EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) L4 Full HTML
Highlight
Free Access
Issue
A&A
Volume 557, September 2013
Article Number L4
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201322151
Published online 14 August 2013

© ESO, 2013

1. Introduction

Planetesimals, the seeds of planets, are believed to form by coagulation of dust grains in protoplanetary disks. How micron-sized dust grains grow to kilometer-sized planetesimals has been an unsolved problem in the complete planet formation theory; the intermediate-sized bodies are believed to be poorly sticky (Zsom et al. 2010), easily disrupted by collisions (Blum & Wurm 2008), or liable to fall quickly onto the central star (Adachi et al. 1976; Weidenschilling 1977).

Several possibilities have been proposed to overcome these barriers (Johansen et al. 2007; Pinilla et al. 2012; Windmark et al. 2012; Lambrechts & Johansen 2012; Ros & Johansen 2013; Garaud et al. 2013). However, there has not yet been any coherent scenario explaining planetesimal formation from dust grains that avoids all of the barriers.

thumbnail Fig. 1

Schematic drawing to illustrate dust growth via fluffy aggregates. a) The dust aggregate hits another aggregate to be stick. This reduces dust density and occurs in a very early stage of dust growth. b) When the collisional speed is high enough to disrupt the dust aggregates, they are compressed. c) Dust aggregates have a velocity difference against gas, and they feel the ram pressure by the gas. The ram pressure statically compresses the dust aggregates. d) When the dust aggregates become so massive that they do not support their structure, they are compressed by their own self-gravity.

The internal structure evolution is a key to understanding how dust coagulation forms planetesimals. Figures 1a and b show the schematic diagram of the structure evolution previously considered. Dust grains become porous aggregates composed of sub-micron monomer particles by coagulation in protoplanetary disks, as illustrated in Fig. 1a (Smirnov 1990; Meakin 1991; Kempf et al. 1999; Blum & Wurm 2000; Krause & Blum 2004; Paszun & Dominik 2006). When the dust aggregates become massive, they are gradually compacted or disrupted in dust-dust collisions because of the increase in the impact energy, as illustrated in Fig. 1b (Dominik & Tielens 1997; Wada et al. 2007, 2008, 2009; Suyama et al. 2008, 2012; Paszun & Dominik 2008, 2009; Okuzumi et al. 2012).

Growth via fluffy aggregates has been proposed to be one possible scenario to overcome the barriers in Okuzumi et al. (2012). They have shown that fluffy aggregates rapidly coagulate to avoid the radial drift problem. On the other hand, although the aggregates are compressed by dust-dust collisions, their internal density remains ρ ~ 10-5 g/cm3 (Suyama et al. 2008; Okuzumi et al. 2012). This is not consistent with the fact that planetesimals are believed to have ρ ~ 0.1 g/cm3 as well as comets, the remnants of planetesimals (A’Hearn 2011). Therefore other mechanisms to compress the fluffy aggregates are required.

In this paper, we introduce the static compression of aggregates due to ram pressure of the disk gas and self-gravity in protoplanetary disks, as illustrated in Figs. 1c and d. We use the compressive strength of porous aggregates numerically derived by Kataoka et al. (2013) to obtain the porosity (equivalent to the internal density) of dust aggregates. We show how much the dust aggregates are compressed by the disk gas and by self-gravitational compression in their growth. Moreover, we investigate whether the growth is rapid enough to avoid the radial drift barrier by comparing the dust growth and radial drift timescale.

2. Method

The compressive strength of a highly porous dust aggregate, P, is given by (Kataoka et al. 2013) 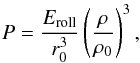(1)where ρ is the mean internal density of the dust aggregate, r0 the monomer radius, ρ0 the material density, and Eroll the rolling energy, which is the energy for rolling a particle over a quarter of the circumference of another particle (Dominik & Tielens 1997; Wada et al. 2007). In this paper, we adopt ρ0 = 1.0 g/cm3, r0 = 0.1 μm, and Eroll = 4.74 × 10-9 erg, which correspond to icy particles. Eroll is proportional to the critical displacement, which has an uncertainty from 2 Å to 30 Å (Dominik & Tielens 1997; Heim et al. 1999). For later discussion, we note that the dust density is proportional to 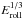and thus the uncertainty little affects the resulting dust density.

When a dust aggregate feels a pressure that is higher than its compressive strength, the aggregate is quasi-statically compressed until its strength equals the pressure. We define the dust internal density where the  compressive  strength  equals  a given

pressure as an equilibrium density ρeq. Using Eq. (1), we obtain ρeq as 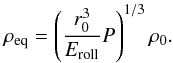(2)We consider a source of the pressure to be ram pressure of the disk gas or self-gravity of the aggregate.

We obtain ram pressure of the disk gas as follows. We consider a dust aggregate of mass m and radius r, which is moving in the disk gas with velocity v against the gas. The pressure Pgas against the aggregate can be defined as the gas drag force divided by the geometrical cross section: Pgas ≡ Fdrag/A, where Fdrag = mv/ts, A = πr2, and ts is the stopping time of the aggregate. While the pressure has both compressive and tensile components, we assume that the pressure is compressive. Thus, we obtain the pressure as 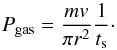(3)The typical gas drag law is adopted to obtain ts and v. The gas drag law is the Epstein regime, when the dust radius is less than 4/9 times the mean free path of gas. On the other hand, it is the Stokes regime if the Reynolds number is less than unity (see Eq. (4) in Okuzumi et al. 2012, for example). When the Reynolds number exceeds unity, the gas drag law changes as a function of Reynolds number (see Eqs. (8a) to (8c) in Weidenschilling 1977). The drag force is determined by the relative velocity of the gas and dust. The relative velocity is induced by Brownian motion, radial drift, azimuthal drift, and turbulence. We use the closed formula of the turbulence model (Ormel & Cuzzi 2007) and assume the turbulent parameter αD = 10-3, except for the strong turbulence case, where αD = 10-2.

We assume the minimum mass solar nebula (MMSN), which was constructed based on our solar system (Hayashi 1981). At a radial distance R from the central star, the gas-surface density profile is 1700 g/cm2 × (R/1 AU)-1.5 and the dust-to-gas mass ratio is 0.01. The temperature profile adopted is 137 K × (R/1 AU)− 3/7, which corresponds to midplane temperature (Chiang et al. 2001). This is cooler than optically thin disk models to focus on the dust coagulation in the midplane.

thumbnail Fig. 2

Equilibrium dust density at 5 AU in an MMSN disk. The blue thick solid line represents the equilibrium density of gas pressure, where the ram pressure of gas is equal to the compressive strength of the dust aggregate. The thin dotted lines represent the component of gas ram pressure, which is induced by the velocity difference between gas and dust, such as Brownian motion, radial drift motion, azimuthal motion, and turbulent motion. The red solid line represents the equilibrium density of self-gravity. The blue and red shaded region represents where the compressive strength of the dust aggregate is lower than the pressure of gas or self-gravity, so these aggregates are compressed until their density becomes the equilibrium density. We also plot the dust growth path without static compression (Okuzumi et al. 2012).

We also calculate the self-gravitational pressure as follows. Although the gravitational pressure has distribution in the aggregates, we simply assume a uniform pressure inside the aggregates. We define the force on the dust aggregates as F = Gm2/r2, and the area A = πr2. Thus, the self-gravitational pressure is 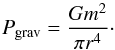(4)We note that the equilibrium density of self-gravitational compression depends only on dust mass and internal density and not on the disk properties.

3. Results

First, we calculate the equilibrium density of dust aggregates in a wide range in mass, where their compressive strength is equal to the gas or self-gravitational pressure. Figure 2 shows the equilibrium dust density against dust mass at 5 AU in the disk. If the gas or self-gravitational pressure is higher than the compressive strength, the dust aggregate is compressed to achieve the equilibrium density because the strength is higher in denser dust aggregates. In other words, the equilibrium density represents a lower limit of the dust density in the disk. We also plot the collisional growth path without static compression (Okuzumi et al. 2012); the dust aggregates initially grow with a fractal dimension of 2, and when the impact energy of dust-dust collisions reaches the rolling energy, the internal density becomes almost constant. The evolutional track should trace the higher density of the growth with collisional compression and the equilibrium density of static compression. Therefore, we conclude that dust growth is initially fractal, and then the gas compression becomes effective before collisional compression occurs at 5 AU in the disk.

thumbnail Fig. 3

Pathways in the planetesimal formation in the minimum mass solar nebula model. The gray line shows the constant density evolutional track, which corresponds to the compact growth. The black, green, blue, and red lines are the evolutional track through dust coagulation via fluffy aggregates. Each line represents different mechanisms of dust coagulation, which are hit-and-stick, collisional compression, gas compression, and self-gravity compression. The red shaded region represents where the radial drift timescale is less than the growth timescale, which is equivalent to radial-drift region. The brown squares indicate the properties of comets, and the triangles represent their upper limit. The radii of dust aggregates for 1 μm, 1 cm, 1 m, 100 m, and 10 km are also written. Top left: for 5 AU in orbital radius. Top right: for 8 AU in orbital radius. The cross point represents where the dust falls onto the central star. Bottom left: for 5 AU in strong turbulence model where αD = 10-2. Bottom right: for 8 AU in two times as massive as MMSN model.

Figure 3 shows the pathways of the dust growth in mass-density space at 5 and 8 AU from the central star. Here, we assume that the dust aggregates have no mass or volume distribution. The first growth mode is hit-and-stick, where the fractal dimension is 2. As dust aggregates become massive, the gas compression becomes effective. Once gas compression occurs, the equilibrium density is higher in more massive aggregates until the Stokes number (i.e., the stopping time normalized by the orbital timescale) becomes unity; consequently, the aggregates always keep the equilibrium density in coagulation. The gas compression remains effective until the dust aggregates grow so massive that self-gravitational compression is more effective than gas compression. The self-gravitational compression is effective when the mass is ~1011 g. Once the gravitational compression is effective, the density increases with the mass of the power of 5/2. However, the gas compression makes the dust density almost constant because of the constant velocity difference of the gas and dust of the head wind in azimuthal direction. Therefore, the final stage is determined by self-gravitational compression. We find that the dust aggregates should be compressed to a density of 0.1 g/cm3 when their mass is ~1018 g.

The density and mass of the final product are close to comets, which are considered to be the remnants of planetesimals. We also plot the properties of several comets that are well known in the density and mass in Fig. 3 (A’Hearn 2011). The comets have a mass of ~1016 g and an internal mass density of ~0.1 g/cm3. There is a two-orders-of-magnitude discrepancy in mass between the final product of our calculation and the comets. The mass of comets would be finally determined by collisional fragmentation or melting of planetesimals.

We estimate the dust growth timescale by coagulation and the radial drift timescale. Assuming that aggregates have no mass or volume distribution, the growth time is defined as m/ρdπr2Δv, where ρd is the spatial mass density of dust aggregates and Δv is the velocity difference between the dust aggregates, which is assumed be the root mean square of Brownian motion and turbulent motion (see Eq. (32) in Okuzumi et al. 2012). For the velocity induced by turbulence, we use the velocity difference of dust and gas as dust-dust velocity for simplicity. We include the dust sedimentation by considering the dust scaleheight (Brauer et al. 2008). The drift timescale is defined as the orbital radius divided by the radial drift velocity. We define the dust aggregates as where the drift timescale is less than 30 times the growth timescale drift to the central star (Okuzumi et al. 2012).

We show that the revealed pathway still overcomes the radial drift problem. Figure 3 also illustrates the region where the dust aggregates radially drift inward before they grow. Even when the dust aggregates become massive and their Stokes number is unity, the dust growth time is still shorter than the drift at 5 AU. In the outer radius of the disk (e.g., at 8 AU), the dust aggregates drift inward before growth (top right of Fig. 3). However, if the disk is two times as massive as MMSN, the dust aggregates successfully break the radial drift problem (bottom right of Fig. 3). Therefore, the fluffy dust can grow to planetesimals more inside in protoplanetary disks.

Fluffy dust also breaks through the bouncing barrier. Solid bodies have been shown to bounce in some situations (Güttler et al. 2010). However, both numerical simulations and experiments have shown that highly porous aggregates do not bounce when φ ≲ 0.15 (Langkowski et al. 2008; Wada et al. 2011; Seizinger & Kley 2013; Kothe et al. 2013). Thus, the bouncing is not a major difficulty for the growth of highly porous aggregates.

The fragmentation barrier is not a serious problem when considering icy particles. The dust aggregates are not significantly fragmented and grow through collisions as long as their collision velocity is <60 m/s (Wada et al. 2009). The collisional velocity becomes maximum when the Stokes number is unity. It is the square root of αD times the sound speed of gas. In the case of αD = 10-3, the maximum velocity is ~17 m/s at 5 AU, so the dust aggregates can avoid significant disruption. In the case of αD = 10-2, on the other hand, the velocity reaches ~54 m/s, comparable to the critical velocity. Thus, we should carefully discuss the fragmentation in strong turbulent disks. We note that the turbulent velocity is lower than the original MMSN model, where the temperature is determined by the balance between the stellar radiation and the reemission for each position. This is because we focus on the midplane, where the temperature is lower; thus the velocity is also lower than the irradiated surface.

However, when considering silicate particles, it is difficult to break through the fragmentation barrier. Inside the snowline, the ice is sublimated and the dominant material is silicate particles. The critical velocity of fragmentation of silicate is ~6 m/s (Wada et al. 2009). Thus, the silicate planetesimal formation is still an open question.

In the final stage of coagulation, the runaway growth begins. We estimate the dust mass where the dust-dust collision velocity induced by turbulence exceeds the escape velocity of the dust. When the dust becomes as massive as ~1015 g, the runaway growth starts. The dust internal density is still as small as ~10-2, which means that the geometrical cross section is larger than the compact case. This will make the runaway growth faster, but the whole scenario does not change, as shown in the N-body simulations (Kokubo & Ida 1996).

In conclusion, we revealed the pathway of the porosity evolution of dust aggregates to form planetesimals by introducing static compression. We also showed that icy dust growth on the pathway avoids the bouncing, fragmentation, and radial drift barriers. This scenario can provide a planetesimal distribution as a concrete initial condition of the later stages of planet formation.

Acknowledgments

A.K. is supported by the Research Fellowship from JSPS for Young Scientists (24·2120).

References

  1. Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theoret. Phys., 56, 1756 [CrossRef] [Google Scholar]
  2. A’Hearn, M. F. 2011, ARA&A, 49, 281 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blum, J., & Wurm, G. 2000, Icarus, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
  4. Blum, J., & Wurm, G. 2008, ARA&A, 46, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Chiang, E. I., Joung, M. K., Creech-Eakman, M. J., et al. 2001, ApJ, 547, 1077 [NASA ADS] [CrossRef] [Google Scholar]
  7. Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
  8. Garaud, P., Meru, F., Galvagni, M., & Olczak, C. 2013, ApJ, 764, 146 [NASA ADS] [CrossRef] [Google Scholar]
  9. Güttler, C., Blum, J., Zsom, A., Ormel, C. W., & Dullemond, C. P. 2010, A&A, 513, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Hayashi, C. 1981, Prog. Theoret. Phys. Suppl., 70, 35 [CrossRef] [Google Scholar]
  11. Heim, L.-O., Blum, J., Preuss, M., & Butt, H.-J. 1999, Phys. Rev. Lett., 83, 3328 [NASA ADS] [CrossRef] [Google Scholar]
  12. Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
  13. Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 554, A4 [Google Scholar]
  14. Kempf, S., Pfalzner, S., & Henning, T. K. 1999, Icarus, 141, 388 [NASA ADS] [CrossRef] [Google Scholar]
  15. Kokubo, E., & Ida, S. 1996, Icarus, 123, 180 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kothe, S., Blum, J., Weidling, R., & Güttler, C. 2013, Icarus, 225, 75 [NASA ADS] [CrossRef] [Google Scholar]
  17. Krause, M., & Blum, J. 2004, Phys. Rev. Lett., 93, 021103 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  18. Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
  19. Langkowski, D., Teiser, J., & Blum, J. 2008, ApJ, 675, 764 [NASA ADS] [CrossRef] [Google Scholar]
  20. Meakin, P. 1991, Rev. Geophys., 29, 317 [NASA ADS] [CrossRef] [Google Scholar]
  21. Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
  22. Ormel, C. W., & Cuzzi, J. N. 2007, A&A, 466, 413 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Paszun, D., & Dominik, C. 2006, Icarus, 182, 274 [NASA ADS] [CrossRef] [Google Scholar]
  24. Paszun, D., & Dominik, C. 2008, A&A, 484, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Paszun, D., & Dominik, C. 2009, A&A, 507, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Pinilla, P., Birnstiel, T., Ricci, L., et al. 2012, A&A, 538, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Seizinger, A., & Kley, W. 2013, A&A, 551, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Smirnov, B. M. 1990, Phys. Rep., 188, 1 [NASA ADS] [CrossRef] [Google Scholar]
  30. Suyama, T., Wada, K., & Tanaka, H. 2008, ApJ, 684, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  31. Suyama, T., Wada, K., Tanaka, H., & Okuzumi, S. 2012, ApJ, 753, 115 [NASA ADS] [CrossRef] [Google Scholar]
  32. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2007, ApJ, 661, 320 [NASA ADS] [CrossRef] [Google Scholar]
  33. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2008, ApJ, 677, 1296 [NASA ADS] [CrossRef] [Google Scholar]
  34. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
  35. Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2011, ApJ, 737, 36 [NASA ADS] [CrossRef] [Google Scholar]
  36. Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
  37. Windmark, F., Birnstiel, T., Güttler, C., et al. 2012, A&A, 540, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1

Schematic drawing to illustrate dust growth via fluffy aggregates. a) The dust aggregate hits another aggregate to be stick. This reduces dust density and occurs in a very early stage of dust growth. b) When the collisional speed is high enough to disrupt the dust aggregates, they are compressed. c) Dust aggregates have a velocity difference against gas, and they feel the ram pressure by the gas. The ram pressure statically compresses the dust aggregates. d) When the dust aggregates become so massive that they do not support their structure, they are compressed by their own self-gravity.
In the text
thumbnail Fig. 2

Equilibrium dust density at 5 AU in an MMSN disk. The blue thick solid line represents the equilibrium density of gas pressure, where the ram pressure of gas is equal to the compressive strength of the dust aggregate. The thin dotted lines represent the component of gas ram pressure, which is induced by the velocity difference between gas and dust, such as Brownian motion, radial drift motion, azimuthal motion, and turbulent motion. The red solid line represents the equilibrium density of self-gravity. The blue and red shaded region represents where the compressive strength of the dust aggregate is lower than the pressure of gas or self-gravity, so these aggregates are compressed until their density becomes the equilibrium density. We also plot the dust growth path without static compression (Okuzumi et al. 2012).
In the text
thumbnail Fig. 3

Pathways in the planetesimal formation in the minimum mass solar nebula model. The gray line shows the constant density evolutional track, which corresponds to the compact growth. The black, green, blue, and red lines are the evolutional track through dust coagulation via fluffy aggregates. Each line represents different mechanisms of dust coagulation, which are hit-and-stick, collisional compression, gas compression, and self-gravity compression. The red shaded region represents where the radial drift timescale is less than the growth timescale, which is equivalent to radial-drift region. The brown squares indicate the properties of comets, and the triangles represent their upper limit. The radii of dust aggregates for 1 μm, 1 cm, 1 m, 100 m, and 10 km are also written. Top left: for 5 AU in orbital radius. Top right: for 8 AU in orbital radius. The cross point represents where the dust falls onto the central star. Bottom left: for 5 AU in strong turbulence model where αD = 10-2. Bottom right: for 8 AU in two times as massive as MMSN model.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.