| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A19 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321868 | |
| Published online | 14 August 2013 | |
New evolutionary sequences for extremely low-mass white dwarfs
Homogeneous mass and age determinations and asteroseismic prospects ⋆,⋆⋆
Grupo de Evolución Estelar y Pulsaciones. Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, CONICET-CCT. Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar; mmiller@fcaglp.unlp.edu.ar; acorsico@fcaglp.unlp.edu.ar
Received: 9 May 2013
Accepted: 27 June 2013
Context. The number of detected extremely low-mass (ELM) white dwarf stars has increased drastically in recent years, thanks to the results of many surveys. In addition, some of these stars have been found to exhibit pulsations, making them potential targets for asteroseismology.
Aims. We provide a fine and homogeneous grid of evolutionary sequences for helium (He) core white dwarfs for the whole range of their expected masses (0.15 ≲ M∗/M⊙ ≲ 0.45), including the mass range for ELM white dwarfs (M∗/M⊙ ≲ 0.20). The grid is appropriate for mass and age determination of these stars, as well as for studying their adiatabic pulsational properties.
Methods. White dwarf sequences have been computed by performing full evolutionary calculations that consider the main energy sources and processes of chemical abundance changes during white dwarf evolution. Realistic initial models for the evolving white dwarfs have been obtained by computing the nonconservative evolution of a binary system consisting of an initially 1 M⊙ ZAMS star and a 1.4 M⊙ neutron star for various initial orbital periods. To derive cooling ages and masses for He-core white dwarfs, we perform a least square fitting of the M(Teff,g) and Age(Teff,g) relations provided by our sequences by using a scheme that takes into account the time spent by models in different regions of the Teff − g plane. This is particularly useful when multiple solutions for cooling age and mass determinations are possible in the case of CNO-flashing sequences. We also explore in a preliminary way the adiabatic pulsational properties of models near the critical mass for the development of CNO flashes (~0.2 M⊙). This is motivated by the discovery of pulsating white dwarfs with stellar masses near this threshold value.
Results. We obtain reliable and homogeneous mass and cooling age determinations for 58 very low-mass white dwarfs, including three pulsating stars. Also, we find substantial differences in the period spacing distributions of g-modes for models with stellar masses near ~ 0.2 M⊙, which could be used as a seismic tool to distinguish stars that have undergone CNO flashes in their early cooling phase from those that have not. Finally, for an easy application of our results, we provide a reduced grid of values useful to obtain the masses and ages of He-core white dwarfs.
Key words: white dwarfs / binaries: general / stars: evolution / stars: oscillations / stars: interiors
Table 2 is available in electronic form at http://www.aanda.org
The tracks and the data presented in the middle and lower panels of Figs. 5, 6 are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A19
© ESO, 2013
1. Introduction
White dwarf stars are routinely used to constrain the age and past history of the Galactic populations, including the solar neighborhood and open and globular clusters (Von Hippel & Gilmore 2000; Hansen et al. 2007; Winget et al. 2009; García-Berro et al. 2010; Bono et al. 2013, and references therein). In addition, they are used to place constraints on properties of elementary particles, such as axions (Isern et al. 1992; 2008; Córsico et al. 2012a,b) and neutrinos (Winget et al. 2004), or on alternative theories of gravitation (García-Berro et al. 1995; 2011). These and other potential applications of white dwarfs require a detailed and precise knowledge of the main physical processes that control their evolution (see Fontaine & Brassard 2008; Winget & Kepler 2008, and Althaus et al. 2010a, for a review).
The white dwarf mass distribution includes a population of low-mass remnants, most of them expected to have a helium (He) core in their interiors (see Kepler et al. 2007). In recent years, the number of detected white dwarfs with very low stellar masses, commonly referred to as extremely low-mass (ELM) white dwarfs, has increased considerably thanks to the result of many surveys, particularly the ELM survey and the SPY and WASP surveys (see Koester et al. 2009; Brown et al. 2010, 2012; Maxted et al. 2011). Because of the very low stellar mass values that characterize these ELM white dwarfs (lower than about 0.20 M⊙1), they are believed to be the result of compact binary evolution, during which the envelope of a red giant star is removed before the core reaches enough mass to ignite helium. The evolution of He-core white dwarfs has been studied by Driebe et al. (1998), Sarna et al. (2000), Althaus et al. (2001), Serenelli et al. (2002), Nelson et al. (2004), Benvenuto & De Vito (2005), Panei et al. (2007), and more recently by Gautschy (2013).
A major step towards the understanding of the formation and evolution of ELM white dwarfs has been the recent discovery of three pulsating He-core white dwarfs with stellar masses below 0.23 M⊙ and effective temperatures less than 10 000 K (Hermes et al. 2012; 2013). This new class of pulsating white dwarfs most probably belongs to a low-mass extension of the ZZ Ceti instability strip to much cooler effective temperatures. It is expected that the application of the tools of asteroseismology to these and other pulsating ELM white dwarfs found in the future will reveal details of their internal structure and evolutionary status; see Steinfadt (2010) and Córsico et al. (2012) for the first exploration of the adiabatic properties of these objects.
The development of a fine and homogeneous grid of evolutionary sequences for He-core white dwarfs and especially ELM white dwarfs, which are derived consistently from binary evolution, is therefore a pressing necessity for precise mass and cooling age determinations, and asteroseismological inferences for these stars. This is the main aim of this paper. As shown by Sarna et al. (2000), a proper treatment of the binary evolution leading to the formation of these stars is of utmost importance for the correct assessment of their evolutionary properties. This is particularly true regarding the mass of the hydrogen envelope that is left after the end of binary evolution. In particular, Sarna et al. (2000) found that for stellar masses lower than ≈0.25 M⊙, binary evolution calculations yield more massive hydrogen envelopes than those found by arbitrarily abstracting mass to a red giant star. These authors also reported that an active hydrogen burning shell remains during the evolution through the stages of approximately constant luminosity that follow the end of binary evolution and also during most of the cooling branch. This delays the evolution of ELM white dwarfs by several Gyr. In this connection, Sarna et al. (2000) found that the evolutionary times during the stages of constant luminosity are strongly dependent on the mass of the white dwarf remnant. Hence, for a proper assessment of evolutionary timescales and mass-radius relations, the binary nature that leads to the formation of ELM white dwarfs must be taken into account. This has been the approach we adopted in this work to generate the initial models for the evolving white dwarfs. Specifically, we considered the nonconservative angular-momentum evolution of a binary system consisting of an initially 1 M⊙ ZAMS component and a 1.4 M⊙ neutron star component. In particular, our white dwarf sequences start shortly after the end of Roche lobe phase.
In addition to the discussion of the evolutionary expectations of our sequences, we extend the scope of the paper by presenting a preliminary exploration of the adiabatic pulsational properties of our evolutionary models near the critical stellar mass for the development of CNO flashes on the cooling branch. We show in particular that seismic tools exploiting these properties can be used to extract information about the occurrence of CNO flashes in prior stages and the consequent age dichotomy expected in low-mass He-core white dwarfs. Our interest in this aspect is motivated by the fact that the three pulsating ELM white dwarfs discovered by Hermes et al. (2013) have stellar mass near the threshold value for the occurrence of CNO flashes.
The paper is outlined as follows. In Sect. 2 we briefly describe the input physics of the evolutionary code employed in our calculations, as well as the procedure and assumptions we consider for the computation of binary evolution that leads to the formation of ELM white dwarfs. In total, nine initial ELM white dwarf models with stellar masses between 0.155 and 0.20 M⊙ were derived for initial orbital periods at the beginning of the Roche lobe phase in the range 0.9 to 2 d. Additional binary calculations have been conducted for binary configurations with initial orbital periods up to 300 d to cover the whole mass range expected for He-core white dwarfs. In Sect. 3 we present the main evolutionary characteristics of our sequences, while in Sect. 4 we describe the method adopted to derive ages and masses for He-core white dwarfs from these sequences. In this section we also present a new and homogeneous determination of masses and, for the first time, cooling ages of a large sample of recently discovered low-mass (most of them ELM) white dwarfs, in addition to a simple algorithm for easy use of our sequences. In Sect. 5 we describe the main basic expectations of our sequences for the adiabatic pulsation properties of models representative of the observed pulsating ELM white dwarfs.
2. Numerical tools
The evolutionary calculations presented in this work have been done using the LPCODE stellar evolutionary code (Althaus et al. 2003; 2005; 2012). This code has recently been used to produce very accurate white dwarf models (see García-Berro et al. 2010; Althaus et al. 2010b; Renedo et al. 2010; Miller Bertolami et al. 2011a,b, and references therein). The code has also been used to study the formation of subdwarf stars from the post-red giant branch (RGB) hot-flasher scenario (Miller Bertolami et al. 2008), as well as the role of thermohaline mixing for the surface composition of low-mass giant stars (Wachlin et al. 2011). A complete description of the input physics and numerical procedures can be found in these works. The nuclear network accounts explicitly for the following elements: 1H, 2H, 3He, 4He, 7Li, 7Be, 12C, 13C, 14N, 15N, 16O, 17O, 18O, 19F, 20Ne, and 22Ne, together with 34 thermonuclear reaction rates for the pp-chains, CNO bi-cycle, helium burning, and C ignition that are identical to those described in Althaus et al. (2005), with the exception of 12C + p → 13N + γ → 13C + e+ + νe and 13C(p, γ)14N, which are taken from Angulo et al. (1999). Radiative opacities are those of OPAL (Iglesias & Rogers 1996). Conductive opacities are from Cassisi et al. (2007). The equation of state during the main sequence evolution is that of OPAL for hydrogen- and helium-rich composition. Finally, updated low-temperature molecular opacities with varying C/O ratios are used. To this end, we adopted the low-temperature opacities computed at Wichita State University (Ferguson et al. 2005) and presented by Weiss & Ferguson (2009). In LPCODE, molecular opacities are computed by adopting the opacity tables with the correct abundances of the unenhanced metals (e.g., Fe) and C/O ratio. Interpolation is carried out by means of separate cuadratic interpolations in R = ρ/T63, T and XH, but linearly in NC/NO.
For the evolutionary stages following the end of mass loss and for the white dwarf regime, we use the equation of state of Magni & Mazzitelli (1979) for the whole star. We also take into account the effects of element diffusion due to gravitational settling and chemical and thermal diffusion of 1H, 3He, 4He, 12C, 13C, 14N, and 16O (see Althaus et al. 2003, for details). In particular, the metal mass fraction Z in the envelope of our models is specified by scaling it to the local abundance of the CNO elements at each layer. For the white dwarf regime and for effective temperatures lower than 10 000 K, outer boundary conditions for the evolving models are derived from nongrey model atmospheres (Rohrmann et al. 2012). Recently, LPCODE has been tested against other white dwarf code. Uncertainties in white dwarf cooling ages arising from different numerical implementations of stellar evolution equations were found to be below 2% (Salaris et al. 2013).
Realistic initial models of ELM white dwarfs have been obtained by mimicking the binary evolution of progenitor stars. Since hydrogen shell burning is the main source of star luminosity during most of the evolution of ELM white dwarfs, the computation of realistic initial white dwarf structures is a fundamental issue, in particular concerning the correct assessment of the hydrogen envelope mass left by progenitor evolution (see Sarna et al. 2000). We assume that the evolution of the binary system is fully nonconservative, i.e., the total mass and angular momentum of the system are not conserved. It is worth mentioning that changes in the orbital separation resulting from changes in the mass assumed to be lost from the system are small (see Sarna et al. 2000, for details). To this end, we follow the formalism of Sarna et al. (2000). We denote with M1 the mass of the secondary (mass-losing) star, M2 the mass of the neutron star (primary), and with Ṁ1 the mass-loss rate of the secondary. The change of the total orbital angular momentum (J) of the binary system can be written 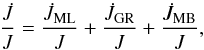 (1)where
(1)where 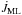 ,
, 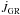 , and
, and 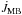 are, respectively, the angular momemtum loss from the system due to mass loss, gravitational wave radiation, and magnetic braking (which is relevant when the secondary has an outer convection zone). To compute these quantities we follow Sarna et al. (2000; see also Muslimov & Sarna 1993):
are, respectively, the angular momemtum loss from the system due to mass loss, gravitational wave radiation, and magnetic braking (which is relevant when the secondary has an outer convection zone). To compute these quantities we follow Sarna et al. (2000; see also Muslimov & Sarna 1993): 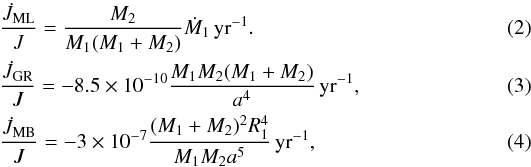 where a is the semiaxis of the orbit and R1 the radius of the secondary. All quantities are given in solar units. The mass-loss rate from the secondary is calculated as in Chen & Han (2002). Mass loss is considered as long as the secondary fills its Roche lobe rL, given by
where a is the semiaxis of the orbit and R1 the radius of the secondary. All quantities are given in solar units. The mass-loss rate from the secondary is calculated as in Chen & Han (2002). Mass loss is considered as long as the secondary fills its Roche lobe rL, given by 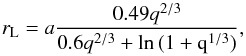 (5)where q = M1/M2 is the mass ratio. The semiaxis of the orbit is found by integrating the equation for the rate of change of a. If mass lost by the secondary is completely lost from the system, i.e. nothing of the mass lost by the secondary is accreted by the primary, a is then given by (see Muslimov & Sarna 1993)
(5)where q = M1/M2 is the mass ratio. The semiaxis of the orbit is found by integrating the equation for the rate of change of a. If mass lost by the secondary is completely lost from the system, i.e. nothing of the mass lost by the secondary is accreted by the primary, a is then given by (see Muslimov & Sarna 1993) 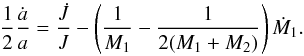 (6)Mass loss is continued until the secondary star shrinks within its Roche lobe. As a result of a hydrogen thermonuclear flash occurring on the white dwarf cooling branch, the secondary may fill its Roche lobe during the flash for the second time. In this case, mass loss becomes operative again on a very short timescale. We want to mention that the present treatment for mass loss is not completely self-consistent in the sense that the mass-loss rate is not considered as an unknown quantity during the iteration procedure to solve the stellar structure equations. Instead, it is fixed beforehand for each model. Nonetheless, this procedure constitutes a better approach for deriving physically sound initial ELM white dwarf models than arbitrarily removing mass to an evolving low-mass star. It is enough for the purpose of this work, which is focused on the cooling and structural properties of ELM white dwarfs.
(6)Mass loss is continued until the secondary star shrinks within its Roche lobe. As a result of a hydrogen thermonuclear flash occurring on the white dwarf cooling branch, the secondary may fill its Roche lobe during the flash for the second time. In this case, mass loss becomes operative again on a very short timescale. We want to mention that the present treatment for mass loss is not completely self-consistent in the sense that the mass-loss rate is not considered as an unknown quantity during the iteration procedure to solve the stellar structure equations. Instead, it is fixed beforehand for each model. Nonetheless, this procedure constitutes a better approach for deriving physically sound initial ELM white dwarf models than arbitrarily removing mass to an evolving low-mass star. It is enough for the purpose of this work, which is focused on the cooling and structural properties of ELM white dwarfs.
All of our He-core white dwarf initial models have been derived from evolutionary calculations for binary systems consisting of an evolving low-mass component of initially 1 M⊙ and a 1.4 M⊙ neutron star as the other component. Metallicity is assumed to be Z = 0.01. A total of 14 initial He-core white dwarf models with stellar masses between 0.155 and 0.435 M⊙ were derived for initial orbital periods at the beginning of the Roche lobe phase in the range 0.9 to 300 d. In particular, nine sequences span the range of masses corresponding to ELM white dwarfs (M ≲ 0.20 M⊙). At this point, it is worth mentioning that the envelope mass of the resulting white dwarf, a key factor in dictating the cooling times, is only weakly dependent on the initial mass of the secondary (mass-losing) star (Nelson et al. 2004). However, different angular-momentum loss prescriptions due to mass loss, which could have an impact on the final envelope mass, have not been explored in this paper.
In Table 1, we provide some main characteristics of the whole set of initial He-core white dwarf models that we calculated. The further evolution of these initial models has been computed down to the range of luminosities of cool white dwarfs, including the stages of multiple thermonuclear CNO flashes during the beginning of cooling branch. The numbers between brackets in the first column denote the stellar mass of the remnant that is left after the occurrence of a second stage of Roche lobe overflow during the CNO flash. Indeed, during the course of the CNO flash, the white dwarf remnant may be forced to fill its Roche lobe again, thus leading to a new mass transfer episode. We note also from Table 1 that, in good agreement with previous studies (Sarna et al. 2000; Althaus et al. 2001) there exists a threshold in the stellar mass value (at ~ 0.18 M⊙), below which CNO flashes are not expected.
3. Evolutionary results
As an example of the evolution of the white dwarf progenitor during the mass transfer stage, we show in Fig. 1 the Hertzsprung-Russell diagram for the evolution of the initially 1.0 M⊙ secondary star. Evolution of the secondary starts from the ZAMS and is followed until the end of core hydrogen burning and the further stages. Two tracks are shown, which correspond to initial orbital periods of 0.90 and 1.40 d. At the points denoted by RL, the secondary fills its Roche lobe for the first time, and mass loss from the system begins. We note that from that moment on the secondary evolves at almost constant radius, until its stellar mass decreases below ~0.4 M⊙. Mass loss continues until the secondary shrinks within its Roche lobe. The evolutionary tracks for our He-core white dwarf models start precisely after the end of Roche lobe overflow.
Characteristics of our initial He-core white dwarf models.
The evolution in the plane surface gravity versus effective temperature for all of our He-core white dwarf sequences is shown in Fig. 2, together with selected post-RGB low-mass objects that are presumably He-core white dwarfs (most of them ELM white dwarfs); see Table 2. In Fig. 3 we display on the same plot the results for the ELM sequences that do not experience CNO flashes on the cooling branch, together with the lowest mass He-core white dwarf sequence that experiences CNO flashes, the 0.18213 M⊙ sequence (see Table 1). The figure illustrates the evolutionary stages corresponding to the first 7 Gyr of evolution after the end of mass loss. The main remarkable characteristic of the no-flashing sequences is their slow evolution over most of their life, which is due to the residual hydrogen shell burning being the main source of surface luminosity, even at very advanced stages of evolution. In particular, for the least massive of our ELM sequences, the evolutionary timescales involved in reaching the white dwarf cooling branch from the end of mass loss amount to about 1 Gyr. This means that these objects should have a large chance of being observed during those stages. Also noticeable is the very slow rate of evolution at intermediate effective temperatures on the cooling branch. In fact, we note that evolution takes about several Gyr to reach Teff ~ 9000 K because stable hydrogen shell burning still provides the main energy source, even at such advanced stages. It is clear that for these ELM white dwarfs, an appropriate treatment of progenitor evolution is required for a correct assessment of the evolutionary timescales.
In contrast, the behavior is entirely different for sequences that experience unstable hydrogen shell burning on their early cooling branch, as can be appreciated by inspecting the track corresponding to the 0.18213 M⊙ sequence in Fig. 3. This sequence experiences nine CNO flashes before reaching the quiescent terminal white dwarf cooling branch. Several points are worthy of comment. We note that during the final cooling branch evolution proceeds on a timescale that is much shorter than the evolutionary timescale characterizing the sequences with M < 0.18 M⊙. This is because CNO flashes markedly reduce the hydrogen content of the star, with the result that residual nuclear burning is much less relevant when the remnant reaches the final cooling branch. Hence, sequences that go through several episodes of CNO flashes are expected to evolve below Teff = 5000 K in a time much less than the Hubble time. This contrasts with the situation for the least massive ELM sequences, where nuclear burning substantially delays their evolution by several Gyr at higher effective temperatures. This age dichotomy, which results from the interplay of element diffusion and nuclear burning during the flash episodes, is a remarkable property of very low-mass He-core white dwarfs with important observational consequences, as we reported in previous investigations (see Althaus et al. 2001; Panei et al. 2007, and references therein).
 |
Fig. 1 Hertzsprung-Russell diagram for the evolution of the initially 1.0 M⊙ secondary star. The tracks corresponding to initial orbital periods of 0.90 and 1.40d are depicted. The final mass at the end of Roche lobe overflow is, respectively, 0.15540 and 0.18685 M⊙. RL marks the locations in the diagram when the secondary star fills its Roche lobe for the first time and mass loss begins. The color scale to the right shows the stellar mass of the secondary star. |
 |
Fig. 2 Surface gravity – effective temperature diagrams for our He-core white dwarf sequences. Sequences with masses in the range 0.18 M⊙ ≲ MWD ≲ 0.4 M⊙ undergo CNO flashes during the early cooling phase, leading to the apparent loops in the g–Teff diagram. Filled circles and triangles correspond, respectively, to the observed post-RGB low-mass stars from Silvotti et al. (2012) and Brown et al. (2013), and asterisks correspond to the pulsating ELM white dwarfs detected by Hermes et al. (2013), see Table 2. |
It is worth noting that, in the case of CNO-flashing sequences, the rate of evolution slows down during the stages just prior to the occurrence of the CNO flashes on the early cooling branches. This is illustrated by Fig. 4, which shows the evolutionary speed of some selected CNO-flashing sequences in the log Teff − log g diagram. The slower evolution just before the occurrence of the CNO flashes is apparent. Hence, the observational counterparts of these remnants also have a chance of being detected during these evolutionary stages. This should be taken into account when attempting to assess the stellar mass and age of He-core white dwarfs from evolutionary sequences that experience several CNO flashes, because multiple solutions are possible from such sequences, at intermediate effective temperatures (see Silvotti et al. 2012). This can be clearly understood by inspecting Fig. 2. We develop this issue in the next section.
 |
Fig. 3 Surface gravity – effective temperature diagram for ELM white dwarf sequences with 0.15540, 0.16115, 0.16499, 0.17064, 0.17624 M⊙ (thick lines, from right to left), together with the lowest mass He-core white dwarf sequence that undergoes CNO flashes (0.18213 M⊙, thin line). Tracks correspond to the first 7 Gyr of evolution after the end of mass loss when the secondary shrinks within its Roche lobe. The color scale to the right displays the cooling age in Gyr. We note the much faster evolution of the 0.18213 M⊙ sequence after the occurrence of the CNO flashes. Black and grey circles represent observed nonpulsating post-RGB low-mass stars, and red asterisks represent pulsating ELM white dwarfs, as detailed in Table 2. |
 |
Fig. 4 Evolutionary speed of the sequences in the log Teff − log g diagram – for 0.36304 M⊙, 0.27242, and 0.18213 M⊙ (top, middle, and bottom panels, respectively). Thin black lines denote evolutionary stages faster than the upper boundary of the color coding. We note the much faster evolution of the more massive sequences before entering the white dwarf cooling sequence. |
4. Mass and age determination
Our grid of He-core white dwarf sequences is appropriate for homogeneous mass and cooling age determinations of observed low-mass white dwarfs for all evolutionary stages where these stars have chances of being observed: the final cooling branch, the stages at constant luminosity following the end of Roche lobe overflow (particularly in the case of ELM white dwarfs), and the evolutionary stages prior to the occurrence of CNO flashes on the early cooling branches. These evolutionary stages are highlighted in Fig. 4 for some selected CNO-flashing sequences. Because of the occurrence of several CNO flashes, special care must be taken when assessing the age and mass from theoretical He-core evolutionary sequences. Usually, white dwarf masses and cooling ages are derived from their log g − log Teff values by means of theoretical white dwarf tracks and isochrones in the log g − log Teff plane. Performing linear interpolation among available tracks and isochrones is usually enough to obtain masses and cooling ages directly from the log g − log Teff values. However, in the case of low-mass He-core white dwarfs, the problem is rather involved. As can be seen in Fig. 2 for high effective temperatures, He-core white dwarf tracks cross each other in the log g − log Teff plane, leading to multiple possible solutions, both for mass and cooling age, for a given measured value for log g and log Teff. This multiplicity of the age and mass solutions would be almost irrelevant if the evolutionary stages at which the tracks cross each other (loops) were fast and consequently the probability of finding a star at those stages were low. Unfortunately, the time spent during these loops is not negligible2, and thus several solutions are possible for a given measured value for log g and log Teff. Consequently, the determination of masses and ages of He-core white dwarfs calls for some kind of statistical approach to weight the time spent by each model in each region of the log g − log Teff diagram.
 |
Fig. 5 Top panel: M(log Teff,log g) relation as obtained directly from stellar evolution simulations. Middle panel: M(log Teff,log g) relation derived from the weighted least square scheme described in Sect. 4. Bottom panel: uncertainty σM of the derived M(log Teff,log g) relation. Symbols correspond to the observed post-RGB low-mass stars listed in Table 2. In particular, green circles correspond to the pulsating ELM white dwarfs detected by Hermes et al. (2013). White regions in the middle and bottom panels indicate either fast evolutionary stages for which not enough points were available to obtain an accurate fit (in the case of CNO-flashing sequences) or simply that no tracks are available at that region. |
In this connection, we adopted the following scheme to determine masses and cooling ages of He-core white dwarfs from our sequences. To weight the time spent by each model at different locations of the log g − log Teff diagram, we created random values of cooling age (t) and mass (M∗) and computed their corresponding theoretical values of log g − log Teff from our sequences. Thus we are left with a set of points whose density in the log g − log Teff diagram is directly related to the probability of finding a model of a given mass at that location of the log g − log Teff diagram. Because interpolation between different tracks is not possible, we adopted for each mass value that of our closest model. In the absence of better knowledge of He-core white dwarf progenitor lifetimes and masses, we assumed uniform distribution in mass and cooling age within the ranges M∗ ∈ (0.14965 M⊙, 0.50742 M⊙) and t ∈ (0 Gyr,7 Gyr). Within these assumptions we computed 2 × 107 points to have a good sampling of the log g − log Teff-Mass-Age relationship. For each observed He-core white dwarf star with known values of log g − log Teff (see Table 2), we performed a least square polynomial fitting of the log g − log Teff-Mass-Age relationship within an ellipse around the (log gstar, 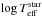 ) values of the star and derived its mass and age. We adopted the dispersion around the fitted polynom as an estimation of the errors in mass and cooling age. The size of the ellipse and the degree of the polynomial expression were chosen to allow for a good representation of different regions of the log g − log Teff plane. For the region where the “knees” of the tracks are located (log g < − 12.1 + 4.5 × log Teff), we adopted
) values of the star and derived its mass and age. We adopted the dispersion around the fitted polynom as an estimation of the errors in mass and cooling age. The size of the ellipse and the degree of the polynomial expression were chosen to allow for a good representation of different regions of the log g − log Teff plane. For the region where the “knees” of the tracks are located (log g < − 12.1 + 4.5 × log Teff), we adopted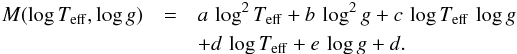 (7)For values of log g > − 12.1 + 4.5 × log Teff, a first-degree polynom was adopted.
(7)For values of log g > − 12.1 + 4.5 × log Teff, a first-degree polynom was adopted. 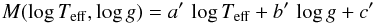 (8)Similar expressions were adopted in the same regions for the t(log Teff,log g) relation.
(8)Similar expressions were adopted in the same regions for the t(log Teff,log g) relation.
To select the points to be used in each fitting we adopted 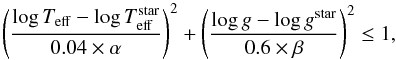 (9)where α and β have to be chosen in such a way as to allow enough points for the least square fit but, at the same time, must be kept small enough so that the t(log Teff,log g) and M(log Teff,log g) can be reproduced by the simple polynomial expressions of Eqs. (7) and (8). In particular α and β were taken as
(9)where α and β have to be chosen in such a way as to allow enough points for the least square fit but, at the same time, must be kept small enough so that the t(log Teff,log g) and M(log Teff,log g) can be reproduced by the simple polynomial expressions of Eqs. (7) and (8). In particular α and β were taken as 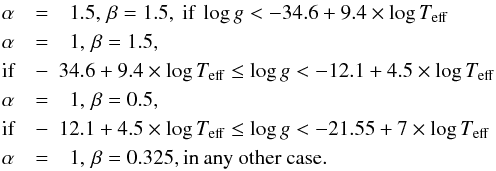 (10)In Figs. 5 and 6 we can see the M(log Teff,log g) and t(log Teff,log g) relations as given directly by our stellar evolution sequences (top panels) together with the weighted least square fitted M(log Teff,log g) and t(log Teff,log g) relations described above (middle panels), and the estimated uncertainties of the least squared fit procedure (bottom panel). The relatively large uncertainties of the interpolated M(log Teff,log g) relation (Fig. 5, bottom panel) at log g ≲ 6.5 and log Teff ≳ 4.3 are a natural consequence of the fact that sequences of different masses spend similar times in that region, so that it is populated by stars of different masses. Hence, multiple solutions (with a dispersion of 0.03 M⊙) for the inferred stellar mass are possible at that region. A similar situation can be appreciated in the t(log Teff,log g) relation at 5.5 ≲ log g ≲ 6.5 and log Teff ≳ 4.1, where the uncertainty of the derived cooling ages is of about a few hundred Myr. In addition, the t(log Teff,log g) relation becomes very uncertain (σt ~ 1 Gyr) around log g ~ 6.5 and 3.9 ≲ log Teff ≲ 3.95. This is because at that region of the log g − log Teff diagram it is expected the age dichotomy between the very low-mass sequences (M∗ ≲ 0.18 M⊙), which do not undergo CNO flashes and evolve very slowly and the higher mass sequences (M∗ ≳ 0.18 M⊙), which undergo CNO flashes and consequently evolve much faster during the final cooling branch.
(10)In Figs. 5 and 6 we can see the M(log Teff,log g) and t(log Teff,log g) relations as given directly by our stellar evolution sequences (top panels) together with the weighted least square fitted M(log Teff,log g) and t(log Teff,log g) relations described above (middle panels), and the estimated uncertainties of the least squared fit procedure (bottom panel). The relatively large uncertainties of the interpolated M(log Teff,log g) relation (Fig. 5, bottom panel) at log g ≲ 6.5 and log Teff ≳ 4.3 are a natural consequence of the fact that sequences of different masses spend similar times in that region, so that it is populated by stars of different masses. Hence, multiple solutions (with a dispersion of 0.03 M⊙) for the inferred stellar mass are possible at that region. A similar situation can be appreciated in the t(log Teff,log g) relation at 5.5 ≲ log g ≲ 6.5 and log Teff ≳ 4.1, where the uncertainty of the derived cooling ages is of about a few hundred Myr. In addition, the t(log Teff,log g) relation becomes very uncertain (σt ~ 1 Gyr) around log g ~ 6.5 and 3.9 ≲ log Teff ≲ 3.95. This is because at that region of the log g − log Teff diagram it is expected the age dichotomy between the very low-mass sequences (M∗ ≲ 0.18 M⊙), which do not undergo CNO flashes and evolve very slowly and the higher mass sequences (M∗ ≳ 0.18 M⊙), which undergo CNO flashes and consequently evolve much faster during the final cooling branch.
As an application of our He-core white dwarf sequences and the interpolation algorithm described above, we have determined the stellar masses and cooling ages for the sample of post-RGB low-mass stars (most of them ELM white dwarfs) listed in Silvotti et al. (2012) and Brown et al. (2013). We assume that these stars have a He core. The derived values of mass and cooling age for each star are shown in Table 2, together with the estimated uncertainties (fourth and fifth columns). For such white dwarfs, the age values listed in Table 2 constitute the first assessment of their cooling ages. As a check, we compared our derived values with those derived by the standard interpolation approach, which can be performed for white dwarfs with masses M∗ < 0.18 M⊙3, and found that the difference in the masses and ages is well within the quoted uncertainties. Some differences appear between the inferred stellar mass from our sequences and stellar mass values quoted by Silvotti et al. (2012) and Brown et al. (2013). This is particularly true in the case of the ELM white dwarf sample of Brown et al. (2013). For most of their sample, they found a stellar mass value of 0.17 M⊙, in contrast with our analysis, which yields stellar mass values in the range 0.17 M⊙–0.21 M⊙. This difference is due to the fact that Brown et al. (2013) adopted the final cooling track (after all the flashes) as the representative one for the sequences which undergo CNO flashes. As shown in Fig. 4, it is the first entrance to the white dwarf cooling phase that is slower and takes a longer time. Thus, for sequences which undergo CNO flashes a star of a given mass is more likely to be found during its first entrance (which occurs at lower effective temperatures) than during its final entrance to the white dwarf cooling zone. Choosing the final cooling track to derive masses at gravities log g ≲ 6 leads to an underestimation of the stellar mass of up to 20%. We note that the differences in the evolutionary speeds of different sequences are naturally taken into account in the scheme presented in the previous section.
We also checked the estimations performed by the scheme presented here by comparing our results with the analysis performed by Silvotti et al. (2012) on KIC 6614501. They assumed that the binary component is a He-core white dwarf and discussed two possibilities: i) its mass is M1 ~ 0.185 M⊙ and the star is on the final cooling track after all the CNO flashes. Because in this case evolution occurs at a faster pace, this possibility is thus less probable (see Fig. 4.) and ii) its mass is M1 ≳ 0.19 M⊙ and the star is still on one of the cooling branches during the CNO-flash stage. In the second case the mass of the star should be constrained between 0.19−0.24 M⊙, from a comparison with Althaus et al. (2001) tracks and the cooling age should be between 30 and 290 Myr. In the first and less probable case, the age derived by Silvotti et al. (2012) is 180 Myr. By looking at Table 2, we see that our mass and cooling age determination scheme gives a value of M1 = 0.210 ± 0.0209 M⊙ and tage = 368 ± 239 Myr for KIC 6614501. Then our mass derivation is in very good agreement with the values derived for option ii of Silvotti et al. (2012) and the same happens for the cooling age of the star. We note, in particular, that the large derived uncertainty in the mass and age within our approach is because many different tracks go through that region of the log g − log Teff plane at similar paces; consequently, a better determination of mass and age just from log g and log Teff is not possible.
4.1. A quick way to assess mass and cooling age of He-core white dwarfs
To provide other authors with an easy way to estimate the masses and cooling ages of He-core white dwarf stars from our tracks, we computed M∗ and t with the previously described algorithm at a small grid of points in the log g − log Teff diagram. Such a grid is presented in Table 3 and can be used via direct bilinear interpolation to obtain the masses and cooling ages at any point in the log g − log Teff diagram. Because the grid is not regularly spaced in log Teff (for the sake of economy), interpolation must be performed first in log Teff and then in log g. As an example, the results from these approximated estimations are listed in columns six and seven of Table 2 and compared with those directly computed from the scheme presented in the previous section. While some differences are present in the derived cooling ages between the full scheme and the bilinear interpolation of Table 3, these differences are moderate and similar to the quoted uncertainties. In particular, for the ELM KIC 6614501 analysed by Silvotti et al. (2012), a simple bilinear interpolation from Table 3 gives straightforwardly M1 ~ 0.217 M⊙ and tage ~ 287 Myr, which is very similar to the values derived by Silvotti et al. (2012). On the other hand, masses derived by the bilinear interpolation of the grid presented in Table 3 are in excellent agreement with those derived from the full scheme. Globally, bilinear interpolation of the values presented in Table 3 allows a very fast and easy way to derive masses and cooling ages for He-core white dwarfs. However, in the case of age derivation, bilinear interpolation within the rather coarse grid of Table 3 does not offer a good representation for the stars close to the age dichotomy that appears at higher gravities and lower temperatures. For those stars a more precise cooling age and mass derivation than those presented in Sect. 4 can be inferred from direct interpolation of the terminal cooling branch of our evolutionary sequences.
5. Prospects for an asteroseismic tool
Masses and cooling ages at a grid in the log (g) − log Teff plane.
We have carried out exploratory computations of the g-mode adiabatic pulsation properties of our ELM white dwarf models, in particular for sequences with stellar masses near the critical mass for the development of CNO flashes (M∗ ≈ 0.2 M⊙). This was motivated by the fact that at least two of the three ELM pulsating white dwarfs reported by Hermes et al. (2013) have stellar masses near this threshold value. A full exploration of the adiabatic and nonadiabatic pulsation properties of our complete set of low-mass and ELM white dwarfs is underway and will be presented in a future paper. Our pulsation computations were performed with the Newton-Raphson nonradial pulsation code described in Córsico & Althaus (2006). Here, we focus on the most massive ELM sequence that does not experience CNO flashes on the cooling branch (M∗ = 0.1762 M⊙), and the lowest mass ELM white dwarf sequence that experiences CNO flashes (M∗ = 0.1805 M⊙). In Figs. 7 and 8 we display the chemical profiles and the propagation diagrams for two models at Teff ~ 9500 K. It is noteworthy that the internal chemical distribution is very different despite the fact that the difference in the stellar mass of these two models is almost negligible (ΔM∗ = 0.0043 M⊙). In particular, the M∗ = 0.1762 M⊙ model has a pure H envelope that is ~ 65 times thicker than the M∗ = 0.1805 M⊙ model. Also, the shape of the He/H transition region is markedly different in both cases. Indeed, for the more massive model this chemical interface is still characterized by a double-layered structure, while for the less massive model it has already attained a single-layered structure due to the action of element diffusion. This significantly different behavior is a signature of the occurrence of CNO flashes in the 0.1805 M⊙ sequence and can be understood by examining Fig. 3. In fact, as a result of the less important role of residual H burning after the occurrence of the CNO flashes4, the 0.18213 M⊙ sequence evolves much faster than the 0.1762 M⊙ sequence. Hence, the chemical profile in the 0.18213 M⊙ sequence is not expected to be completely separated out by diffusion processes, as in the case of the less massive sequence.
 |
Fig. 7 Internal chemical profiles of He and H and the propagation diagram, the run of the logarithm of the squared Brunt-Väisälä and Lamb (with ℓ = 1) frequencies, corresponding to an 0.1762 M⊙ ELM white dwarf model at Teff ~ 9500 K. |
The differences in the shape of the He/H interface for both models are translated into distinct features in the run of the squared critical frequencies, in particular in the Brunt-Väisälä frequency (N2). This can be appreciated in Figs. 7 and 8, which also depict the propagation diagrams (Unno et al. 1989) corresponding to these models. In fact, for the M∗ = 0.1805 M⊙ model, N2 is characterized by two bumps, as expected for a double-layered chemical structure at the He/H. At variance with this, for the M∗ = 0.1762 M⊙ model the Brunt-Väisälä frequency has only one bump. It is located at log (1 − Mr/M∗) ~ − 1.9, which is notoriously more pronounced than its counterpart in the M∗ = 0.1805 M⊙ model.
In pulsating stars in general, the structure of the g-mode period spectrum is sensitive to the spatial run of the Brunt-Väisälä frequency. This is particularly true for pulsating white dwarfs, in which the bumps of N2 induced by chemical gradients are responsible for mode-trapping effects (Bradley 1996; Córsico et al. 2002). A clear signature of mode trapping is that the forward period spacing, defined as ΔΠk( ≡ Πk + 1 − Πk), exhibits strong departures from uniformity when plotted in terms of the pulsation period Πk. The period difference between an observed mode and adjacent modes (Δk ± 1) can be used as an observational diagnostic of mode trapping. For stellar models characterized by a single chemical interface, like the one of M∗ = 0.1762 M⊙ we are considering here, local minima in ΔΠk usually correspond to modes trapped in the H envelope, in contrast local maxima in ΔΠk are associated with modes trapped in the core region. In Fig. 9 we show the forward period spacing in terms of the dipole periods for the same models with M∗ = 0.1762 M⊙ and M∗ = 0.1805 M⊙ described in Figs. 7 and 8. We depict with a red horizontal line the asymptotic period spacing, computed as in Córsico et al. (2012). From this figure, mode-trapping signatures are clearly noticeable for both models, particularly for periods shorter than ~ 2500 s. Longer periods seem to fit the asymptotic predictions, although small departures from constant period spacing are still appreciable.
Focusing on the nonasymptotic regime (Πk ≲ 2500 s), we found appreciable differences in the period spacing distributions of the two models in spite of the fact that both models have virtually the same stellar mass. In particular, for the M∗ = 0.1805 M⊙ model the amplitude of the departure from uniform period spacing due to mode trapping is appreciably larger than for the M∗ = 0.1762 M⊙ one. This could be thought as a useful seismic tool for discriminating stars that have undergone CNO flashes in their early cooling phase from those that have not, provided that enough consecutive low- and intermediate-order (200 ≲ Π ≲ 2000 s) g-modes with the same ℓ value were detected in pulsating ELM white dwarfs. At least two of the pulsating ELM white dwarfs reported by Hermes et al. (2013) with stellar mass near the threshold value for the occurrence of CNO flashes are potential candidates to test these ideas.
 |
Fig. 9 Forward period spacing in terms of the (ℓ = 1) periods for the model with M∗ = 0.1762 M⊙ (upper panel) and M∗ = 0.1805 M⊙ (lower panel), and a Teff ~ 9500 K. The red horizontal line corresponds to the asymptotic period spacing. |
6. Conclusions
In view of the discovery of numerous ELM white dwarfs from different surveys (Brown et al. 2012, 2013, and references therein) and the recent detection of pulsations in some of them (Hermes et al. 2012, 2013), we present in this paper a detailed grid of evolutionary sequences for He-core white dwarfs by considering the binary evolution that leads to their formation. These new evolutionary models are intended for homogeneous mass and cooling age determinations as well as for potential asteroseismological applications of these stars.
Evolutionary calculations were done with the amply used and well-tested LPCODE stellar evolutionary code, appropriately modified to simulate the binary evolution of progenitor stars. Binary evolution was assumed to be fully nonconservative, and the loss of angular momemtum due to mass loss, gravitational wave radiation, and magnetic braking was considered. All of our He-core white dwarf initial models were derived from evolutionary calculations for binary systems consisting of an evolving low-mass component of initially 1 M⊙ and a 1.4 M⊙ neutron star as the other component. Metallicity is assumed to be Z = 0.01. A total of 14 initial He-core white dwarf models with stellar masses between 0.155 and 0.435 M⊙ were computed for initial orbital periods at the beginning of the Roche lobe phase in the range 0.9 to 300 d, see Table 1. In particular, nine sequences span the range of masses corresponding to ELM white dwarfs (M ≲ 0.20 M⊙). It should be mentioned that in this paper we have not considered different values of the initial mass of the secondary (mass-losing) star. Although the envelope mass of the resulting white dwarf, a key factor in dictating the cooling times, is expected to be only weakly dependent on the initial mass of the mass-losing star (Nelson et al. 2004), different orbital angular-momentum loss prescriptions due to mass loss could have an impact on the final envelope mass. This issue has not been considered in this paper. We also did not explore other physical processes, such as pulsar irradiation, which could reduce the resulting envelope mass of the He-core white dwarf (Ergma et al. 2001).
In agreement with previous studies, we found that multiple CNO flashes are expected for stellar masses larger than about 0.18 M⊙. Because of this, special care must be taken at assessing the cooling age and mass from evolutionary sequences, since multiple solutions are, in principle, possible from such sequences, at intermediate effective temperatures. To get reliable mass and cooling age determination from our sequences (given the surface gravity and effective temperature), we devised an interpolation algorithm that accounts for precisely the several possible solutions for stellar mass and cooling age in the case of CNO-flashing sequences. As an application of our He-core white dwarf sequences, we determined the stellar masses and cooling ages for the sample of post RGB low-mass stars considered in Silvotti et al. (2012) and Brown et al. (2013). Finally, we provided a simple scheme that allows our evolutionary sequences to be straightforwardly used for mass and age inferences of He-core white dwarfs.
Finally, we explored the pulsation properties of ELM white dwarf models for sequences with stellar masses near the critical mass for the development of CNO flashes (~ 0.2 M⊙). This was motivated by the fact that at least two of the three ELM pulsating white dwarfs reported by Hermes et al. (2013) have stellar masses near this threshold value. Specifically, we compared the period spacings of a model with M∗ = 0.1762 M⊙, corresponding to the most massive ELM sequence that does not experience CNO flashes on the cooling branch, with the period spacings of a model with M∗ = 0.1805 M⊙, corresponding to the lowest mass He-core white dwarf sequence that experiences CNO flashes. Despite the small difference in their stellar masses, we found that these models have appreciably different internal chemical structures, which impact quite differently on the mode-trapping properties of the models for periods shorter than about 2500 s. Thus, we can envisage an asteroseismic diagnostic tool for distinguishing stars that have undergone CNO flashes in their early cooling phase from those that have not, provided that enough consecutive pulsation periods of g-modes with low- and intermediate-radial orders and the same harmonic degree were detected in pulsating ELM white dwarfs.
Finally, although the cooling age and mass of observed He-core white dwarfs can be directly inferred from the information provided in this paper, the complete set of our evolutionary sequences can be found at our web site http://www.fcaglp.unlp.edu.ar/evolgroup and at the CDS.
Online material
Selected post-RGB low-mass stars.
As we mentioned, most of this time corresponds to the stages just prior to the occurrence of the CNO flashes, see Fig. 4.
Theoretical sequences with masses M∗ < 0.18 M⊙ do not cross each other, and the sequences with masses M∗ > 0.18 M⊙ spend negligible time in the region of the tracks with lower masses. Thus no degeneracy of the possible solutions exists, making it possible to use a standard approach to determine masses and cooling ages of ELM white dwarfs.
Acknowledgments
We warmly acknowledge the comments and suggestions of our referee, which strongly improved the original version of this paper. This research was supported by PIP 112-200801-00940 from CONICET and by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR.
References
- Althaus, L. G., Serenelli, A. M., & Benvenuto, O. G. 2001, MNRAS, 323, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010a, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010b, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 537, 33 [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., & De Vito, M. A. 2005, MNRAS, 362, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Salaris, M., & Gilmozzi, R. 2013, A&A, 549, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradley, P. A. 1996, ApJ, 468, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allende Prieto, C., & Kenyon, S. J. 2010, ApJ, 723, 1072 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allende Prieto, C., & Kenyon, S. J. 2012, ApJ, 744, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Kilic, M., Allende Prieto, C., Gianninas, A., & Kenyon, S. J. 2013, ApJ, 769, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Han, Z. 2002, MNRAS, 335, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Benvenuto, O. G., & Serenelli, A. M. 2002, A&A, 387, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., et al. 2012a, MNRAS, 424, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Romero, A. D., et al. 2012b, JCAP, 12, 10 [Google Scholar]
- Córsico, A. H., Romero, A. D., Althaus, L. G., & Hermes, J. J. 2012c, A&A, 547, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Driebe, T., Schönberner, D., Blöcker, T., & Herwig, F. 1998, A&A, 339, 123 [NASA ADS] [Google Scholar]
- Ergma, E., Sarna, M. J., & Gerskevits-Antipova, J. 2001, MNRAS, 321, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Hernanz, M., Isern, J., & Mochkovitch, R. 1995, MNRAS, 277, 801 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Torres, S., Althaus, L. G., & Isern, J. 2011, J. Cosmology Astropart. Phys., 5, 21 [Google Scholar]
- Gautschy, A. 2013 [arXiv:1303.6652] [Google Scholar]
- Hansen, B. M. S., Anderson, J., Brewer, J., et al. 2007, ApJ, 671, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Winget, D. E., et al. 2012, ApJ, 750, L28 [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Winget, D. E., et al. 2013, ApJ, 765, 102 [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Hernanz, M., & García-Berro, E. 1992, ApJ, 392, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., García-Berro, E., Torres, S., & Catalán, S. 2008, ApJ, 682, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Kleinman, S. J., Nitta, A., et al. 2007, MNRAS, 375, 1315 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., Voss, B., Napiwotzki, R., et al. 2009, A&A, 505, 441 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Maxted, P. F. L., Anderson, D. R., Burleigh, M. R., et al. 2011, MNRAS, 418, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Olano, C., & Jiménez, N. 2011a, MNRAS, 415, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Rohrmann, R. D., Granada, A., & Althaus, L. G. 2011b, ApJ, 743, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Sarna, M. J. 1993, MNRAS, 262, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, L. A., Dubeau, E., & MacCannell, K. A. 2004, ApJ, 616, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Panei, J. A., Althaus, L. G., Chen, X., & Han, Z. 2007, MNRAS, 382, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., García-Berro, E., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 546, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarna, M. J., Ergma, E., & Antipova, J. 2000, MNRAS, 316, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A. M., Althaus, L. G., Rohrmann, R. D., & Benvenuto, O. G. 2002, MNRAS, 337, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R., Ostensen, R. H., Bloemen, S., et al. 2012, MNRAS, 424, 1752 [NASA ADS] [CrossRef] [Google Scholar]
- Steinfadt, J. D. R., Bildsten, L., & Arras, P. 2010, ApJ,718, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars, 2nd. edn. (University of Tokyo Press) [Google Scholar]
- von Hippel, T., & Gilmore, G. 2000, AJ, 120, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, A., & Ferguson, J. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARAA, 46, 157 [Google Scholar]
- Winget, D. E., Sullivan, D. J., Metcalfe, T. S., Kawaler, S. D., & Montgomery, M. H. 2004, ApJ, 602, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Hertzsprung-Russell diagram for the evolution of the initially 1.0 M⊙ secondary star. The tracks corresponding to initial orbital periods of 0.90 and 1.40d are depicted. The final mass at the end of Roche lobe overflow is, respectively, 0.15540 and 0.18685 M⊙. RL marks the locations in the diagram when the secondary star fills its Roche lobe for the first time and mass loss begins. The color scale to the right shows the stellar mass of the secondary star. |
| In the text | |
 |
Fig. 2 Surface gravity – effective temperature diagrams for our He-core white dwarf sequences. Sequences with masses in the range 0.18 M⊙ ≲ MWD ≲ 0.4 M⊙ undergo CNO flashes during the early cooling phase, leading to the apparent loops in the g–Teff diagram. Filled circles and triangles correspond, respectively, to the observed post-RGB low-mass stars from Silvotti et al. (2012) and Brown et al. (2013), and asterisks correspond to the pulsating ELM white dwarfs detected by Hermes et al. (2013), see Table 2. |
| In the text | |
 |
Fig. 3 Surface gravity – effective temperature diagram for ELM white dwarf sequences with 0.15540, 0.16115, 0.16499, 0.17064, 0.17624 M⊙ (thick lines, from right to left), together with the lowest mass He-core white dwarf sequence that undergoes CNO flashes (0.18213 M⊙, thin line). Tracks correspond to the first 7 Gyr of evolution after the end of mass loss when the secondary shrinks within its Roche lobe. The color scale to the right displays the cooling age in Gyr. We note the much faster evolution of the 0.18213 M⊙ sequence after the occurrence of the CNO flashes. Black and grey circles represent observed nonpulsating post-RGB low-mass stars, and red asterisks represent pulsating ELM white dwarfs, as detailed in Table 2. |
| In the text | |
 |
Fig. 4 Evolutionary speed of the sequences in the log Teff − log g diagram – for 0.36304 M⊙, 0.27242, and 0.18213 M⊙ (top, middle, and bottom panels, respectively). Thin black lines denote evolutionary stages faster than the upper boundary of the color coding. We note the much faster evolution of the more massive sequences before entering the white dwarf cooling sequence. |
| In the text | |
 |
Fig. 5 Top panel: M(log Teff,log g) relation as obtained directly from stellar evolution simulations. Middle panel: M(log Teff,log g) relation derived from the weighted least square scheme described in Sect. 4. Bottom panel: uncertainty σM of the derived M(log Teff,log g) relation. Symbols correspond to the observed post-RGB low-mass stars listed in Table 2. In particular, green circles correspond to the pulsating ELM white dwarfs detected by Hermes et al. (2013). White regions in the middle and bottom panels indicate either fast evolutionary stages for which not enough points were available to obtain an accurate fit (in the case of CNO-flashing sequences) or simply that no tracks are available at that region. |
| In the text | |
 |
Fig. 6 Same as Fig. 5 but for the t(log Teff,log g) relation and its corresponding uncertainty σt. |
| In the text | |
 |
Fig. 7 Internal chemical profiles of He and H and the propagation diagram, the run of the logarithm of the squared Brunt-Väisälä and Lamb (with ℓ = 1) frequencies, corresponding to an 0.1762 M⊙ ELM white dwarf model at Teff ~ 9500 K. |
| In the text | |
 |
Fig. 8 Same as in Fig. 7, but for a 0.1805 M⊙ ELM white dwarf model. |
| In the text | |
 |
Fig. 9 Forward period spacing in terms of the (ℓ = 1) periods for the model with M∗ = 0.1762 M⊙ (upper panel) and M∗ = 0.1805 M⊙ (lower panel), and a Teff ~ 9500 K. The red horizontal line corresponds to the asymptotic period spacing. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


