| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321853 | |
| Published online | 14 August 2013 | |
Herschel imaging and spectroscopy of the nebula around the luminous blue variable star WRAY 15-751 ⋆,⋆⋆
1 Institut d’Astrophysique et de Géophysique, Université de Liège, Allée du 6 août, 17 – Bât. B5c, 4000 Liège, Belgium
e-mail: vamvatira@astro.ulg.ac.be
2 Instituut voor Sterrenkunde, Katholieke Universiteit Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
3 Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussels, Belgium
Received: 7 May 2013
Accepted: 28 June 2013
We have obtained far-infrared Herschel-PACS imaging and spectroscopic observations of the nebular environment of the luminous blue variable (LBV) WRAY 15-751. The far-infrared images clearly show that the main, dusty nebula is a shell of radius 0.5 pc and width 0.35 pc extending outside the Hα nebula. Furthermore, these images reveal a second, bigger and fainter dust nebula that is observed for the first time. Both nebulae lie in an empty cavity, very likely the remnant of the O-star wind bubble formed when the star was on the main sequence. The kinematic ages of the nebulae are calculated to be about 2 × 104 and 8 × 104 years, and we estimated that each nebula contains ~0.05 M⊙ of dust. Modeling of the inner nebula indicates a Fe-rich dust. The far-infrared spectrum of the main nebula revealed forbidden emission lines coming from ionized and neutral gas. Our study shows that the main nebula consists of a shell of ionized gas surrounded by a thin photodissociation region illuminated by an “average” early-B star. We derive the abundance ratios N/O = 1.0 ± 0.4 and C/O = 0.4 ± 0.2, which indicate a mild N/O enrichment. From both the ionized and neutral gas components we estimate that the inner shell contains 1.7 ± 0.6 M⊙ of gas. Assuming a similar dust-to-gas ratio for the outer nebula, the total mass ejected by WRAY 15-751 amounts to 4 ± 2 M⊙. The measured abundances, masses and kinematic ages of the nebulae were used to constrain the evolution of the star and the epoch at which the nebulae were ejected. Our results point to an ejection of the nebulae during the red super-giant (RSG) evolutionary phase of an ~40 M⊙ star. The multiple shells around the star suggest that the mass-loss was not a continuous ejection but rather a series of episodes of extreme mass-loss. Our measurements are compatible with the recent evolutionary tracks computed for an ~40 M⊙ star with little rotation. They support the O–BSG–RSG–YSG–LBV filiation and the idea that high-luminosity and low-luminosity LBVs follow different evolutionary paths.
Key words: circumstellar matter / stars: massive / stars: mass-loss / stars: variables: S Doradus / stars: individual: WRAY 15-751
© ESO, 2013
1. Introduction
Luminous blue variables (LBVs), or S Doradus variables, represent a short stage (~104 − 105 yr) in the evolution of massive stars with initial mass ≥30 M⊙ (Maeder & Meynet 2010). They are located in the upper left part of the Hertzsprung-Russell diagram (HRD), although some of them undergo occasional excursions to the right of the HRD. Their main characteristics are a) photometric variability, from giant eruptions, ≥ 2 mag, to small oscillations, ~0.1 mag; b) high luminosity, ~106 L⊙; and c) high mass-loss rates, ~10-5 − 10-4 M⊙ yr-1 (Humphreys & Davidson 1994).
According to current evolutionary scenarios (Maeder & Meynet 2010), an early-type O star evolves into a Wolf-Rayet (WR) star by losing a significant fraction of its initial mass. Progressively, the outer layers of the star are removed, revealing a “bare core” that becomes a WR star. One way to lose mass is through stellar winds. However, in the past few years the mass-loss rates of O stars have been revised downward by up to one order of magnitude (Fullerton et al. 2006) and more often by a factor of a few (Bouret et al. 2005; Puls et al. 2008), highlighting the key role played by episodes of extreme mass-loss in an intermediate evolutionary phase (LBV or red supergiant phase).
Most LBVs are surrounded by ejected nebulae (Hutsemékers 1994; Nota et al. 1995). The H ii nebulae have diameters of 0.5−2 pc, expansion velocities of a few tens of km s-1, and dynamical ages of 3 × 103 to 5 × 104 yr. Their morphologies are usually axisymmetric, from mildly to extremely bipolar or elliptical. Previous infrared and millimeter studies of LBV nebulae have revealed not only dust but also molecular gas (CO) (McGregor et al. 1988; Hutsemékers 1997; Nota et al. 2002).
There are many questions about the detailed evolution of these massive stars. For instance, we still do not know when and how the nebulae are ejected, what causes the strong mass-loss phases and what leads to the giant eruptions observed in some of them. Also, important quantities such as the nebular mass and the gas composition (CNO abundances) are very uncertain.
WRAY 15-751 (=Hen 3-591 = IRAS 11065-6026) was first considered to be a possible WR star by Henize (Roberts 1962) because of a perceptibly widened Hα emission line. Carlson and Henize (1979) included it in their sample of southern peculiar emission-line stars and classified it as a Bep star on the basis of the strong [Fe ii] emission lines characterizing its spectrum. Based on a photometric and spectroscopic study in the optical, Hu et al. (1990) concluded that WRAY 15-751 is a variable star with spectral type O9.5. After estimating its distance (r > 5 kpc) and temperature (Teff = 30 000 K), these authors calculated a lower limit of log L/L⊙ equal to 5.7. By plotting these data in an evolutionary diagram, they revealed that WRAY 15-751 is located in the region of LBV stars, with a lower limit on the initial mass of approximately 50 M⊙. De Winter et al. (1992) made an extensive comparative study of the optical and ultraviolet characteristic of this star with those of the LBVs AG Car and HR Car. They concluded that WRAY 15-751 was a LBV in a phase of quiescence surrounded by a cold dusty circumstellar shell with strong emission in the far-infrared, like HR Car.
Based on the available photometry, Sterken et al. (2008) showed that WRAY 15-751 exhibits strong variability, confirming that the star belongs to the S Dor class. Its variations have an amplitude of about two magnitudes in V and a cycle length of several decades, similar to the observed variations of AG Car. The star moved from V ≃ 12.5 and Teff ≃ 30 000 K in 1989, to V ≃ 10.5 and Teff ≃ 9000 K in 2008.
Hutsemékers and Van Drom (1991, hereafter HVD) studied WRAY 15-751 with optical photometric and spectroscopic data. They found that the star is surrounded by a ring nebula of ionized gas with a diameter of about 22″. The nebula appeared non-uniform in brightness and is apparently not detached from the central star. This fact led them to conclude that the nebula might arise from a continuous mass-loss instead of from a sudden outburst. Based on their spectral analysis, they also suggested that the nebula is expanding almost symmetrically at 26 km s-1.
The first infrared study of the nebula around WRAY 15-751 was made by Voors et al (2000). By modeling ground-based infrared images taken at about 10 μm and ISO spectroscopic observations, they derived some properties of the circumstellar dust around the star: the distribution of emission is roughly spherical, the dust shell is detached and slightly elongated; there is neutral gas outside the dust shell and ionized gas only in the inner part of it; the dust shell contains on the average large grains and a minor population of warm very small grains.
Weis (2000) made a detailed kinematic and morphological study of the nebula and found that, in addition to a nearly spherical shell, it also displays a bipolar-like structure (caps). Duncan & White (2002) studied this nebula at radio wavelengths (3 and 6 cm) and confirmed the almost attached nebula surrounding the central star. Moreover, the subtraction of the central star as a point source revealed a two-component inner structure, which was interpreted by the authors as a disk or torus, suggesting a possible mass transfer from a companion star.
 |
Fig. 1 PACS images of the nebula around WRAY 15-751 at 70 μm, 100 μm and 160 μm, from left to right. Top: original images. Bottom: images deconvolved using the MCS method. The size of each image is 1′× 1′. The scales on the right correspond to the surface brightness (arbitrary units). North is up and east is to the left. |
Van Genderen et al. (1992) calculated a lower limit of 4–5 kpc for the distance to WRAY 15-751, based on the photometry of field stars. This value agrees with the suggestion of Hu et al. (1990). HVD found a larger distance of 7 kpc, determined from the kinematics of the [N ii] lines. Pasquali et al. (2006) adopted a distance of 6 ± 1 kpc in their study of the birth-cluster of WRAY 15-751 based on the radial velocity of the star and its surrounding H ii region. In this paper we adopt a distance of 6 ± 1 kpc, which encompasses all measurements.
We analyze the images and the spectrum of the WRAY 15-751 nebula taken by PACS (Photodetector Array Camera and Spectrometer, Poglitsch et al. 2010), one of the three instruments onboard the Herschel Space Observatory (Pilbratt et al. 2010). The paper is organized as follows. The observations and the data reduction are presented in Sect. 2. In Sect. 3 a description of the nebula far-infrared morphology is given, while in Sect. 4 we give an overview of the spectrum. In Sect. 5 we model the dust continuum emission. The emission line spectrum is presented and analyzed in Sect. 6. A general discussion follows in Sect. 7 and conclusions appear in Sect. 8.
2. Observations and data reduction
2.1. Infrared observations
The infrared imaging and spectroscopic observations were carried out using PACS as part of the Mass-loss of Evolved StarS (MESS) guaranteed time key program (Groenewegen et al. 2011).
The imaging observations of the WRAY 15-751 nebula were carried out on January 2, 2010, which corresponds to the 233 observational day (OD) of Herschel. The scan map mode was used. In this observing mode, the telescope slews at constant speed (20″/s in our case) along parallel lines to cover the required area of the sky. For each filter, two orthogonal scan maps were obtained so that our final data set consists of maps at 70, 100 and 160 μm. The observation identification numbers (obsID) of the four scans are 1342188849, 1342188850, 1342188851, and 1342188852. The duration of each one is 157 s.
The data reduction was performed using the Herschel interactive processing environment (HIPE, Ott 2010). The “highpassFilter” task was used to produce the final images as detailed in Groenewegen et al. (2011). The images were oversampled by a factor of 3.2 with respect to the original pixel size, hence leading to pixel sizes in the final maps of 1″ in the blue (70, 100 μm) channel and 2″ in the red (160 μm) channel. Since the highpassFilter task filters out the largest structures, an independent data reduction was performed in all three wavelengths using the Microwave Anisotropy Dataset mapper (MADmap) algorithm (Cantalupo et al. 2010) to investigate emission at large scales. This algorithm, also provided within HIPE, accounts for the significant detector drift.
Deconvolution was applied to the three PACS images, produced with the highpassFilter task, in an effort to better reveal the morphology of the inner nebula. For this purpose, the point-spread functions (PSFs) of Vesta and the MCS deconvolution method (Magain et al. 1998) were used. The advantage of this method is that it does not violate the sampling theorem. Indeed, the image is not deconvolved by the total PSF, which leads to an infinite resolution, but the deconvolution makes use of a partial PSF chosen to respect the desired resolution of the final deconvolved image. The Herschel-PACS PSF full widths at half maximum (FWHMs) are 5.2″, 7.7″ and 12″ at 70 μm, 100 μm and 160 μm, respectively. After the deconvolution with the corresponding PSF, the final spatial resolution is twice as good as the initial one.
The spectrum of the WRAY 15-751 nebula was taken on November 26, 2009 (OD 196) during the calibration phase of the instrument. The PACS integral-field spectrometer covers the wavelength range from 52 μm to 220 μm in two channels that operate simultaneously in the blue, 52–98 μm band (second order: B2A 52–73 μm and B2B 70–105 μm, third order: B3A 52–73 μm), and the red, 102–220 μm band (first order: R1A 133–220 μm and R1B 102–203 μm). It has a resolving power of λ/δλ ~ 940 − 5500, depending on the wavelength. It provides simultaneous imaging of a 47″ × 47″ field of view, resolved in 5 × 5 square spatial pixels (i.e., spaxels). An image slicer employing reflective optics is used to re-arrange the two-dimensional field-of-view along a 1 × 25 pixels entrance slit for the gratings. We used the spectral energy distribution (SED) observing template, which provides a complete coverage between 52 and 220 μm. The two obsIDs of these observations are 1342187236 and 1342187237. The data reduction was also performed using HIPE, following the standard data reduction steps, in particular the subtraction of the background spectrum obtained through nodding.
2.2. Visible observations
The optical images of WRAY 15-751 and its nebula were obtained on March 14, 1994, with the 3.6-m telescope at the European Southern Observatory (ESO), La Silla, Chile. The EFOSC1 camera was used in its coronographic mode: the 6″ circular coronographic mask was inserted in the aperture wheel and positioned on the central star, while the Lyot stop was inserted in the grism wheel (Melnick et al. 1989). A series of short (1 s) and long (300 s) exposures were secured in a Hα+[N ii] filter (λc = 6560.5 Å; FWHM = 62.2 Å), and in a continuum filter just redward (λc = 6644.7 Å; FWHM = 61.0 Å). The CCD pixel size was 0 605 on the sky. The night was photometric and the seeing around 1
605 on the sky. The night was photometric and the seeing around 1 6. The frames were bias-corrected and flat-fielded. The continuum images were subtracted from the Hα+[N ii] ones after correcting for the position offsets and for the different filter transmissions, using field stars. The resulting averaged images show more detail than those displayed in HVD. They can be compared to those obtained at the ESO New Technology Telescope (NTT) with the STSci coronograph (Nota 1999; Weis 2000).
6. The frames were bias-corrected and flat-fielded. The continuum images were subtracted from the Hα+[N ii] ones after correcting for the position offsets and for the different filter transmissions, using field stars. The resulting averaged images show more detail than those displayed in HVD. They can be compared to those obtained at the ESO New Technology Telescope (NTT) with the STSci coronograph (Nota 1999; Weis 2000).
3. Morphology of the nebula
 |
Fig. 2 Hα+[N ii] image of the nebula around WRAY 15-751. The size of the image is 1′× 1′. The scale on the right corresponds to the surface brightness (arbitrary units). North is up and east is to the left. The central star is occulted by the coronograph spot. |
The images of the WRAY 15-751 nebula at the three PACS wavelengths, 70 μm, 100 μm and 160 μm, are illustrated in Fig. 1. Note that the star is not visible at these wavelengths. While the ionized gas does not appear to be detached from the star (HVD; Duncan & White 2002; Fig. 2), the dust emission seen in these images shows an almost symmetric ring-like morphology, as suggested by Voors et al. (2000) on the basis of mid-infrared imaging. This ring shape is more clearly seen at 70 μm, the wavelength at which the spatial resolution is the highest. The central part of the nebula is clearly fainter than the ring. The very inner nebula, which is unresolved in the optical but was detected at radio wavelengths by Duncan & White (2002), is not seen in the PACS images.
 |
Fig. 3 PACS 100 μm image of the nebula obtained using the MADmap reduction algorithm. The size of the image is 10′ × 10′. The scale on the bottom corresponds to the surface brightness (arbitrary units). North is up and east is to the left. A faint extended elliptical nebulosity is seen around the bright shell, the size of which is marked with the horizontal and vertical bars. Both appear located inside a cavity in the interstellar medium. |
 |
Fig. 4 Two-color (70 μm in blue and 160 μm in red) image from the Hi-GAL survey of the complex environment of WRAY 15-751 (the blue spot at the center of the image marked with a white arrow). The size of the image is 1°× 1°. North is up and east is to the left. A bubble ~25′ in diameter and offset from the star is tentatively seen around WRAY 15-751. |
In the 70 μm deconvolved image, the ring extends up to ~ 18″ in radius with a width of ~ 12″. Adopting a distance of 6 kpc, these values corresponds to a nebular radius of about 0.5 pc and to a ring width of 0.35 pc. The surface brightness seems to be non-uniform, as the northeastern part of the nebula is brighter than the other parts. This asymmetry in the brightness distribution was also detected at optical and mid-infrared wavelengths (HVD; Voors et al. 2000).
Figure 2 illustrates the nebula around WRAY 15-751 in the Hα+[N ii] light. The nebula essentially appears disk-like with a circular rim 22″ in diameter, in agreement with the measurement of HVD. It appears slightly elongated, with small caps (Weis 2000) along the main axis (PA ~ 155°, east of north). The eastern part of the nebula is definitely brighter than the western one. A similar morphology is observed at radio wavelengths (Duncan & White 2002). No diffuse emission can be detected in the images obtained within the adjacent continuum filter. The Hα+[N ii] rim, which corresponds to the ionized gas region, is inside the dust ring, which extends farther out.
In Fig. 3, we illustrate the large-scale infrared emission around WRAY 15-751, obtained after the reduction with the MADmap algorithm. A much larger, very faint ellipsoidal nebula can be seen circumscribing the WRAY 15-751 bright ring nebula. This outer nebula is detected at all three wavelengths but it is more clearly seen at 100 μm. Its size is roughly 2.1′× 2.5′, which corresponds to a mean radius of 2 pc at a distance of 6 kpc. This nebula is elongated along the same PA as the Hα+[N ii] inner shell (Fig. 2), supporting its physical association to WRAY 15-751. It is also interesting to note that it lies in a cavity, probably cleaned up prior to the ejection of the nebula. The radius of this empty cavity is about 4′, which corresponds to 7 pc at a distance of 6 kpc.
The kinematic age of the two nebulae can be estimated, assuming that the expansion velocity is the same in both cases. HVD measured the expansion velocity to be vexp ~ 26 km s-1. Adopting this value, the inner nebula, of radius r = 0.5 pc, has a kinematic age tkin = r/vexp of 1.9 × 104 years, while the outer nebula, of mean radius 2 pc, has a kinematic age of 7.5 × 104 years.
To explore the environment of WRAY 15-751 in more detail, we considered the PACS observations of the field obtained in the framework of the Herschel Infrared Galactic Plane survey (Hi-GAL, Molinari et al. 2010). The observations, made immediately public for legacy, were retrieved from the archive processed up to level 2. The two orthogonal scans were added.
A two-color image is displayed in Fig. 4, illustrating the complex interstellar environment around WRAY 15-751. In particular, we can see a series of filaments that form a roughly circular structure around WRAY 15-751. We tentatively interpret this structure as the bubble formed by the O-star progenitor, although we cannot exclude a foreground/background structure. Velocity mapping would be needed to ascertain the physical association. WRAY 15-751 appears to be offset with respect to the bubble, possibly because of higher density material northwest of the star. The radius of this bubble is about 12′, which corresponds to 20 pc at 6 kpc.
4. Spectrum of the nebula: overview
The footprint of the PACS spectral field-of-view on the image of the nebula at 70 μm is shown in Fig. 5. This figure allows us to identify which spaxel corresponds to which part of the nebula. It must be noted that the whole inner ring nebula is inside the spectral field of view although the center of the nebula is not exactly at the central spaxel (2,2).
 |
Fig. 5 Footprint of the PACS spectral field of view on the image of the nebula at 70 μm. Each number pair is the label of a specific spaxel. The size of the image is 1′ × 1′. North is up and east is to the left. |
The spectrum of the nebula, integrated over the nine central spaxels, is shown in Fig. 6. The shape of the continuum below 55 μm results from a yet-imperfect spectral response correction in this range. Above 190 μm the continuum shape results from a light leak from the second diffraction order of the grating to the first one.
The following forbidden emission spectral lines are detected: [N iii] λ 57 μm, [O i] λλ 63, 146 μm, [O iii] λ 88 μm, [N ii] λλ 122, 205 μm, and [C ii] λ 158 μm. The highest ionization lines indicate an H ii region around WRAY 15-751, while the lowest ionization lines reveal a photo-dissociation region (PDR). Apart from these emission lines and the dust continuum, no other dust features have been detected. It should be noted that Voors et al. (2000) did not detect the [O i] λ 63 μm line on their ISO-LWS spectrum: only the lines [O iii] λ 88 μm and [N ii] λ 122 μm were clearly visible.
 |
Fig. 6 PACS spectrum of WRAY 15-751, integrated over the nine central spaxels. Indicated are the lines [Niii], [Oi], [Oiii], [Nii] and [Cii]. The continuum shape below 55 μm results from a yet-imperfect spectral response function correction, while above 190 μm it results from a light leak, from the second diffraction order of the grating in the first one. The different bands are indicated with different colors. |
5. Dust continuum emission
Aperture photometry was performed on the PACS images and integrated flux densities derived for the bright nebular shell. Table 1 presents the Herschel-PACS flux density measurements, along with data taken from the archives of the Infrared Astronomical Satellite (IRAS) mission (Neugebauer et al. 1984), the Infrared Space Observatory (ISO) mission (Kessler et al. 1996) and the Infrared Astronomical Mission AKARI (Murakami et al. 2007). We did not include the IRAS observation at 100 μm because it is only an upper limit, and the AKARI observation at 160 μm because of its low quality. Note that the beam size of the IRAS and AKARI observations is large enough to fully encompass the ring nebula.
Photometric color correction was applied to all flux densities derived from the data of these four space missions. This correction is needed to convert monochromatic flux densities that refer to a constant energy spectrum, to the true object SED flux densities at the photometric reference wavelengths of each instrument.
On the ISO-CAM image1 the nebular flux density was measured through aperture photometry, subtracting the contribution from the central object. For the color correction of the IRAS data, we used the flux density ratios to derive the color temperature and then chose the corresponding color correction factor (Beichman et al. 1988). The ratio R (25,60) corresponds to a temperature of 190 K, while R (12,25) corresponds to 125 K. We decided to correct the flux density at 60 μm using the factor at 190 K. For the flux densities at 12 and 25 μm we calculated the corrections using both the low and the high temperatures and finally considered the average of the two corrected flux densities, the difference being accounted for in the errors. To estimate the color correction of AKARI FIS and IRC data, we fitted a black body to the two datasets independently, using the 25 μm IRAS observation because we needed a measurement near the maximum of the curve. These fits led us to adopt the color correction factors that correspond to a temperature of 200 K for FIS (Yamamura et al. 2010) and 150 K for IRC data (Rosario et al. 2008). To color-correct the Herschel-PACS data, we fitted a black body, considering again the 25 μm IRAS observation. This fit gave a temperature of 200 K, therefore we adopted the corresponding correction factor (Müller et al. 2011). For the color correction of the ISO data we used the correction factors given in the corresponding handbooks (Blommaert et al. 2003; Laureijs et al. 2003). Finally, the mid-infrared flux density derived from ground-based imaging at ESO with the TIMMI instrument was taken from Voors et al. (2000).
Color-corrected nebular flux densities.
All these measurements, presented in Table 1, were considered to model the dust continuum of the nebula, along with the PACS spectrum, integrated over the full field of view (25 spaxels) and the archived ISO-LWS spectrum discussed in Voors et al. (2000).
In Fig. 7, we show the infrared SED of WRAY 15-751 obtained at different epochs with the various instruments. Within the uncertainties, all these measurements agree excellently. First, the agreement between the PACS and ISO-LWS spectra obtained at different epochs, taking into account that at longer wavelengths the ISO PSF (100′′ FWHM at 180 μm) becomes larger than the aperture (84′′) so that some nebular flux is likely lost, while this is not the case with PACS (PSF of 14′′ FWHM at 200 μm for a 47′′ × 47′′aperture and a diameter of the nebula smaller than 40′′). Second, the agreement between the spectra and the photometric data points, indicating that broad-band photometry is dominated by the dust continuum, and that the dust shell is well within the PACS spectroscopic field of view.
5.1. Modeling the dust nebula
To model and interpret the dust emission spectrum and the far-infrared images, we used the publicly available two-dimensional radiative transfer code 2-Dust (Ueta and Meixner 2003). 2-Dust is a versatile code that can be supplied with various grain size distributions and optical properties as well as complex axisymmetric density distributions.
 |
Fig. 7 Infrared spectrum of WRAY 15-751 from data collected at different epochs: IRAS LRS from 8 to 22 μm (1983, magenta), ISOPHOT from 2.5 to 11 μm and ISO LWS from 45 to 140 μm (1996, green), Herschel-PACS from 55 to 180 μm (2010, blue). The ISOPHOT data at λ < 5 μm are corrected for extinction using E(B − V) = 1.8. At λ > 100 μm, the flux density from ISO LWS is not reliable, the LWS aperture is too small for the ISO PSF. Color-corrected photometric measurements are superimposed (red symbols). The spectrum at λ < 5 μm comes from the central star, the bump at ~10 μm from silicates and very small out-of-equilibrium dust grains, and the spectrum at λ > 20 μm from the bulk of the dust shell. Results of the 2-Dust model fitting are illustrated. Top: best fits of the IRAS/ISO data assuming R⋆/Teff = 80/18 000, amin/amax = 0.05/1.5 (solid line) and amin/amax = 0.2/0.5 (dashed line). Bottom: fits of the AKARI/Herschel data using the same dust shell properties but with R⋆/Teff = 320/9000. Results for a lower-luminosity star R⋆/Teff = 240/9000 and amin/amax = 0.2/0.5 are also displayed (dotted line). |
Modeling the WRAY 15-751 dust nebula has previously been carried out by Voors et al. (2000) using IRAS and ISO near- to far-infrared spectroscopy, mid-infrared (10 μm) ground-based imaging and a one-dimensional radiative transfer code. Using the same data and adopting their input parameters for both the dust and the nebular properties, we derived quasi-identical results using 2-Dust (e.g. dust emission spectrum, temperature and mass). In the following, we use in addition the new PACS imaging and spectroscopic data, together with AKARI archive data to further constrain the dust shell properties.
Voors et al. (2000) showed that the discrepancy between their model and the data at ~10 μm (Fig. 7) is probably caused by a small amount of tiny, warm, out-of-equilibrium carbon grains in addition to silicates. These warm grains do not significantly contribute to the bulk of the dust mass at the origin of the emission at λ > 20 μm. Their mid-infrared image may thus not represent the main dust component. We then re-derived the inner radius of the dust shell using the PACS 70 μm image. We first assumed that the dust shell around WRAY 15-751 is spherically symmetric. This is a good proxy to the overall geometry and limits the number of free parameters. We also assumed that the dust density in the nebula runs as r-2. By comparing the PACS images with the synthetic ones produced by 2-Dust and convolved with the PACS PSF (Fig. 8), we determined the inner radius of the dust shell, rin = 7″. This agrees with the radius derived by Voors et al. (2000). We also adopted rout = 3 × rin. At a distance of 6 kpc, this corresponds to rin = 0.20 pc and rout = 0.60 pc. These results are similar to the measurements discribed in Sect. 3, considering the errors.
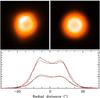 |
Fig. 8 Top left: the 1′ × 1′ image of the nebula around WRAY 15-751 observed with PACS at 70 μm. North is up and east to the left. Top right: the synthetic image computed with 2-Dust using rin = 7″ and rout = 21″ and convolved with the PACS PSF. Bottom: East-west cuts through the central part of the nebula, observed (black) and synthetic (red). The upper plots correspond to the 70 μm image, the lower ones to the 100 μm image. |
Like other LBVs, WRAY 15-751 exhibits long-term strong photometric variations. Since the reaction (heating/cooling) of typical dust grains to luminosity changes is quasi-instantaneous (e.g. Bode and Evans 1979), the stellar parameters corresponding to the different epochs of observation must be considered. In a detailed study, Sterken et al. (2008) showed that the star was in a minimum (i.e., minimum V brightness), hot phase in 1989 and in a maximum, cooler phase in 2008. They suggested that WRAY 15-751 moved in the HR diagram from log L/L⊙ = 5.9 ± 0.15, log Teff = 4.46 ± 0.02 in 1989 to log L/L⊙ = 5.4 ± 0.15, log Teff = 3.92 ± 0.02 in 2008. By interpolating, we estimated Teff = 18 000 K in 1996, at the epoch of the ISO observations. A good fit of the ISOPHOT stellar spectrum at λ < 5 μm is obtained with R⋆ = 80 R⊙, which corresponds to a stellar luminosity log L/L⊙ = 5.8. Unfortunately, the photometric measurements are very scarce before 1989. From the V light curve displayed by Sterken et al. (2008), the brightness of the star seems nevertheless similar in 1983, the epoch of the IRAS observations. We then adopted Teff = 18 000 K and R⋆ = 80 R⊙ as input for the 2-Dust modeling of both the IRAS and ISO data sets. At the epoch of the AKARI and Herschel observations in 2007–2010, the star is much cooler and apparently less luminous. This is quite surprising given the good agreement of the IRAS/ISO and the AKARI/Herschel spectroscopic and photometric data seen in Fig. 7. Although AKARI/Herschel flux densities might be marginally lower than the IRAS/ISO ones, this constitutes a strong constraint for the modeling since the nebula itself cannot have significantly changed between 1996 and 2007–2010. To model the 2007–2010 data, we considered two sets of stellar parameters: a constant-luminosity, low-temperature model with Teff = 9000 K, R⋆ = 320 R⊙, and a low-luminosity, low-temperature one with Teff = 9000 K, R⋆ = 240 R⊙ (i.e., log L/L⊙ = 5.5) which better agrees with the most recent position of WRAY 15-751 in the HR diagram estimated by Sterken et al. (2008). Note that we neglected the delay in the response of the different parts of the dust shell to stellar changes, at most about four years in the observer frame for a shell radius of 0.6 pc. Such a delay will mostly smear out the effects of the stellar variations over some years.
Voors (1999) and Voors et al. (2000) found that the dust in the WRAY 15-751 nebula is dominated by amorphous silicates, with little contribution from crystalline species. They also obtained a best fit of the spectrum using pyroxenes and a 50/50 Fe to Mg abundance. We therefore started with a similar dust composition, using the optical constants given by Dorschner et al. (1995), extrapolated to a constant refraction index in the far-ultraviolet. We assumed the size distribution for the dust grains of Mathis et al. (1977, hereafter MRN): n(a) ∝ a-3.5 with amin < a < amax, a denoting the grain radius. By varying the opacity, which controls the strength of the emission, and amax (or amin), which controls the 20 μm/100 μm flux density ratio, several good fits can be obtained (we did not attempt to fit the 10 μm bump, which is due to out-of-equilibrium dust, only a minor contributor to the dust mass). Acceptable values of amax range between 0.5 and 1.5 μm, confirming the presence of large ~1 μm dust grains in the nebula. In all cases the nebula is optically thin, the opacity is lower than 0.01 at 25 μm.
However, when a good fit of the IRAS/ISO data was obtained with the hot R⋆/Teff = 80/18 000 stellar parameters, we were unable to reproduce the AKARI/Herschel data using the same dust shell properties with the cooler star, even when using the constant luminosity 320/9000 model. A higher luminosity central star would be needed to compensate for the shift of stellar energy output from lower to higher wavelengths. We then tried to increase the near-infrared dust absorptivity by increasing the Fe to Mg ratio. Using the optical data of pyroxenes with a higher Fe to Mg ratio provided by Dorschner et al. (1995), the fit can be improved, but not sufficiently so. We then used the silicate dust with the highest available near-infrared absorptivity, i.e., the optical data given by Ossenkopf et al. (1992) for cold O-rich silicate with Fe inclusions (see also Fig. 7 of Dorschner et al. 1995), with an average bulk density ρ = 3.5 g cm-3. Using a narrow range of dust radii, amin = 0.2 < a < amax = 0.5, we were finally able to fit both the IRAS/ISO data with the R⋆/Teff = 80/18 000 model and the AKARI/Herschel data with the R⋆/Teff = 320/9000 model (Fig. 7). The observed dust emission cannot be reproduced when using the low-luminosity stellar parameters R⋆/Teff = 240/9000 suggested by Sterken et al. (2008) for the 2007–2010 epoch.
In summary, the nebular dust emission can be reproduced for both the hot and cool stellar phases, assuming a constant stellar luminosity and Fe-rich dust grains. The adopted range of grain radii is unrealistically narrow, but numerical tests show that wider ranges can be considered if the near-infrared absorptivity is increased even more. As supported by the modeling, the fact that the dust emission does not significantly change from 1996 to 2010 suggests that stellar variations occur at essentially constant luminosity, as found in several LBVs (Wolf et al. 1981; Humphreys and Davidson 1994). Our results are not entirely incompatible with those of Sterken et al. (2008) since the uncertainties on the stellar luminosity are large and possibly underestimated, as quoted by the authors themselves. Our results demonstrate that the far-infrared dust emission from dust shells can be used to constrain the luminosity variations of the central star.
The mass and temperature of the dust shell we derive from the modeling depend little on the exact stellar parameters and dust sizes, provided that a good fit of the spectrum is obtained. We find that the total dust mass in the nebula is Mdust = 4.5 ± 0.5 × 10-2M⊙ and that Tdust varies from 95 K at rin to 66 K at rout. The quoted uncertainty of Mdust only accounts for the dispersion of the values obtained with different models and is therefore underestimated. Our value of Mdust is higher than the one derived by Voors et al. (2000) mainly because we used a larger distance to WRAY 15-751.
It is interesting to compare these estimates with those determined using empirical methods. Indeed, Mdust can be derived using 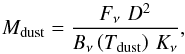 (1)where \begin{lxirformule}$K_{\nu}$\end{lxirformule} is the mass absorption coefficient, Bν the Planck function and D the distance to the nebula (Hildebrand 1983). Kν is roughly independent of the grain radius and behaves as νβ in the far-infrared. For the cold O-rich silicates of Ossenkopf et al. (1992), K60 = 50 cm2 g-1 at 60 μm and β = 2.1. By fitting a modified black-body with β = 2.1 to the λ ≥ 18 μm photometric data points (Fig. 7), we obtain Tdust = 87 K, not far from the mean value of the temperatures found with 2-Dust. The higher Tdust and lower β obtained in Vamvatira-Nakou et al. (2011) are due to the inclusion in the fit of the data at ~10 μm. Using Eq. (1) and the color-corrected IRAS flux density F60 = 129 Jy, we obtain Mdust ≃ 3.5 × 10-2M⊙, which agrees reasonably well with the value derived with 2-Dust, given the large uncertainties. The lower values of Mdust reported in Hutsemékers (1994; 1997) using the same method are essentially due to the use of different values of Kν and β.
(1)where \begin{lxirformule}$K_{\nu}$\end{lxirformule} is the mass absorption coefficient, Bν the Planck function and D the distance to the nebula (Hildebrand 1983). Kν is roughly independent of the grain radius and behaves as νβ in the far-infrared. For the cold O-rich silicates of Ossenkopf et al. (1992), K60 = 50 cm2 g-1 at 60 μm and β = 2.1. By fitting a modified black-body with β = 2.1 to the λ ≥ 18 μm photometric data points (Fig. 7), we obtain Tdust = 87 K, not far from the mean value of the temperatures found with 2-Dust. The higher Tdust and lower β obtained in Vamvatira-Nakou et al. (2011) are due to the inclusion in the fit of the data at ~10 μm. Using Eq. (1) and the color-corrected IRAS flux density F60 = 129 Jy, we obtain Mdust ≃ 3.5 × 10-2M⊙, which agrees reasonably well with the value derived with 2-Dust, given the large uncertainties. The lower values of Mdust reported in Hutsemékers (1994; 1997) using the same method are essentially due to the use of different values of Kν and β.
5.2. Properties of the outer nebula
We now estimate the temperature and the mass of the outer nebula (shown in Fig. 3).
After carefully subtracting the background and the bright inner dust shell, we measured F100 = 5.0 ± 0.5 Jy at 100 μm where the outer nebula is best seen, and F70 = 6.0 ± 0.5 Jy at 70 μm. At 160 μm, we estimated F160 = 5.0 ± 1.5 Jy, but this value strongly depends on the reduction procedure and background subtraction.
Assuming the same dust composition for the outer shell as for the inner one, i.e., β ≃ 2 (silicates), we derived Tdust = 40 ± 5 K by fitting a modified black-body to the flux densities measured at 70 and 100 μm. Within the uncertainties, the flux density at 160 μm is barely compatible with this temperature, most likely due to background contamination. The temperature of the nebula is higher than the temperature of the nearby background emission measured around Tdust ≃ 20 K, thus supporting the association of the outer nebula with WRAY 15-751. It is also interesting to note that for silicates, Tdust is expected to vary as as r− 1/3 (e.g. Tielens 2005), so that the second shell of radius ~70′′ should have Tdust ≃ 45 K extrapolating from the average temperature of the inner shell. This is consistent with the measured value.
Using F100 ≃ 5.0 ± 0.5 Jy, K100 = 18 cm2 g-1 and Tdust = 40 ± 5 K in Eq. (1), we find Mdust = 5 ± 2 × 10-2M⊙. Although uncertain, the mass of dust in the outer shell appears at least as large as the mass in the bright inner shell.
6. Emission line spectrum
6.1. Line flux measurements
Line fluxes from the summed spectrum
We measured the emission line intensities in each one of the 25 spectra (Fig. 5) by fitting a Gaussian to the line profiles using IRAF. The detailed measurements are given in Appendix A. Only at the central spaxel (2, 2) are all the lines detected. At this spaxel the intensities of almost all lines reach their highest values. Most of the flux is detected in the 3 × 3 spaxels central area. In contrast, the outer 16 spaxels contribute significantly less to the line fluxes.
To investigate whether there are differences in the properties of the gas in different parts of the nebula, we also computed for each spaxel the flux ratios of every detected line to the line [N ii] λ 122 μm, which is the strongest one. There is some evidence that the ratio [C ii] 158 μm/[N ii] 122 μm might be higher in the outer spaxels than in the central ones. However, this trend is not significant given the large errors. Consequently, we cannot conclude that there is any clear trend with the distance to the center.
To measure the total emission line fluxes in the nebula with a reasonable accuracy, in particular to compute diagnostic flux ratios, we used the sum of the spectra that correspond to the 9 (3 × 3) central spaxels. The 16 outer spaxels are not included in the sum because they bring more noise than signal especially for the faint lines. We again calculated the line flux by fitting a Gaussian profile to each one of the detected forbidden emission lines. The results are given in Table 2. This table contains the detected ions, the wavelength of each line, the corresponding spectral waveband in which they were detected, and the fluxes with their errors. The quoted uncertainties are the sum of the line fitting uncertainty plus the uncertainty due to the position of the continuum, to which we quadratically added an error of 20% to account for the uncertainty of the PACS absolute flux calibration. Note that within a given waveband, relative flux uncertainties are smaller, on the order of 10%. There is a good agreement between the fluxes measured in two different bands for a given emission line so that weighted mean values are computed. The line [N ii] λ 205 μm had a problematic calibration in PACS. Therefore, to be able to use the corresponding flux values for the following analysis, we calculated a correction factor using objects from the MESS collaboration (Groenewegen et al. 2011) observed with both PACS and SPIRE. Then, from the SPIRE/PACS cross calibration we found that the measured [N ii] λ 205 μm flux should be multiplied by a correction factor of 5.5. The error of the final corrected [N ii] 205 μm fluxes is assumed to be 25%.
When using the central 3 × 3 spaxel region, some nebular flux is lost, the amount of which depends on the wavelength as the beam size, with consequences on the flux ratios. On the other hand, the spectrum summed over all 25 spaxels encompasses the full ring nebula, as shown in Fig. 5 and supported by the agreement with the photometric measurements (Sect. 5). Thus, assuming that the spectral lines originate from the same regions as the dust continuum, we used the ratio of the 9-spaxel continuum spectrum to the 25-spaxel continuum spectrum to estimate the correction factor, which varies roughly linearly from 0.85 at 50 μm to 0.65 at 210 μm. Corrected flux values are given in the rightmost column of Table 2. For the two lines reasonably detected outside the central area, i.e., [N ii] λ 122 μm and [C ii] λ 158 μm (Table A.1), we directly measured the fluxes integrated over the 25 spaxels. We found F = 5.0 ± 1.0 × 10-15 W m-2 for [N ii] and F = 1.31 ± 0.18 × 10-15 W m-2 for [C ii], in good agreement with the corrected values given in Table 2.
6.2. Photoionization region characteristics
The emission lines associated to the H ii region detected in the spectrum of the inner nebula are [N iii] 57 μm, [O iii] 88 μm, and [N ii] 122, 205 μm. The other three emission lines originate from a region of transition between ionized and neutral hydrogen, indicating a photodissociation region (PDR). Extensive analysis and discussion of the latter lines is given in the next section.
6.2.1. Hα flux
The Hα flux from the nebula was estimated by integrating the surface brightness over the whole nebula (Fig. 2). Contamination by field stars was corrected for, and emission from the central part extrapolated using the mean surface brightness. The contribution of the strong [N ii] lines was removed using the [N ii]/Hα ratio measured in HVD and the transmission curve of the Hα+[N ii] filter. The conversion to absolute flux was made with the help of spectrophotometric standard stars observed in the same filter. Adopting a color excess E(B − V) = 1.8 ± 0.3 based on the available optical studies of the nebula (Hu et al. 1990; HVD 1991; Voors et al. 2000; Garcia-Lario et al. 1998), we finally derived F0(Hα) = 3.1 × 10-11 ergs cm-2 s-1 (=3.1 × 10-14 W m-2). The uncertainty of this value amounts to ~20%. It is more accurate than –and agrees with– the value given by Hutsemékers (1994).
6.2.2. Electron density
The [N ii] 122/205 μm ratio, equal to 3.71 ± 1.17, provides a diagnostics for the electron density, ne. To calculate it we used the package nebular of the IRAF/STSDAS environment (Shaw & Dufour 1995). This algorithm makes use of the fact that the nebular cooling-rate is dominated by ions, most of which have either p2, p3 or p4 ground-state electron configurations. These configurations have five low-lying levels. The main physical assumption is that only these five levels are considered to calculate the emission line spectrum. For all the following calculations, an electron temperature constant throughout the nebula and equal to Te = 104 K was assumed with an uncertainty of 20%. This value is reasonable since we observe higher excitation (i.e., the [N iii] 57 μm and [O iii] 88 μm lines) than in the AG Car nebula, for which Smith et al. (1997) calculated an electron temperature between 5900 to 7000 K. The electron density, using the [N ii] 122/205 μm ratio, is found to be 164 ± 90 cm-3.
The [S ii] 6716/6731 Å ratio is also an electron density diagnostics. The value of this ratio measured by HVD is equal to 1.1 ± 0.1, which yields to an electron density of 423 ± 183 cm-3, using the same tool and hypothesis. For the following analysis, we used the average electron density, i.e. ne = 210 ± 80 cm-3, a typical value for LBV nebulae (Nota et al. 1995).
6.2.3. Ionizing flux
It should be noted here that the recombination time in our case is much longer than the timescale of the variability exhibited by the central star of the nebula. More precisely, the recombination time is equal to τrec = 1/neαB = (1.22 × 105/ne) yr (Draine 2011), where αB is the recombination coefficient. Using the measured electron density, we estimated that the recombination time is about 440 yr. Consequently, the stellar variations of ~10 yr cannot change the photoionization/recombination timescale significantly and an average nonvariable star can be considered.
The rate of emission of hydrogen-ionizing photons, Q0, and the Strömgren radius of the ionized hydrogen region, RS, can thus be determined. The nebula was considered to be spherical with an uniform density. Q0 and RS were first determined using the estimated Hα flux and second based on the radio flux density, Sν = 24 mJy at 6 cm (4.9 GHz) which was taken from the study of Duncan & White (2002), adopting a typical error of 0.5 mJy. It should be mentioned here that the nebula is optically thin at 4.9 GHz, as the optical depth, calculated using Eq. (B.15), is lower than one.
The following equation gives the RS in pc (see Appendix B) 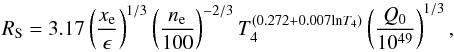 (2)where, using the Hα flux, Q0 (in photons s-1) is given by
(2)where, using the Hα flux, Q0 (in photons s-1) is given by 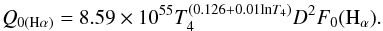 (3)When using the radio flux, Q0 (in photons s-1) is given by
(3)When using the radio flux, Q0 (in photons s-1) is given by 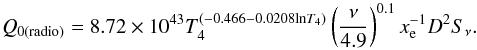 (4)In these equations xe = ne/np, i.e. the fraction of the electron density to the proton density, ϵ is the filling factor, T4 = Te/(104 K), ν is the radio frequency (4.9 GHz in this case) and D is the distance of the nebula in kpc. The Hα flux, F0(Hα), is in ergs cm-2 s-1, while the radio flux, Sν, is in mJy.
(4)In these equations xe = ne/np, i.e. the fraction of the electron density to the proton density, ϵ is the filling factor, T4 = Te/(104 K), ν is the radio frequency (4.9 GHz in this case) and D is the distance of the nebula in kpc. The Hα flux, F0(Hα), is in ergs cm-2 s-1, while the radio flux, Sν, is in mJy.
Using the above equations and assuming xe = 1 (the star is not hot enough to significantly ionize He), ϵ = 1 (the whole volume of the nebula is filled by ionized gas) and T4 = 1, the rate of emission of hydrogen-ionizing photons is found to be Q0(Hα) = (9.6 ± 3.7) × 1046 photons s-1 and Q0(radio) = (7.5 ± 2.5) × 1046 photons s-1. Within the uncertainties, these two results agree well. This also means that the adopted value of E(B − V) is essentially correct. The mean value is Q0 = (8.2 ± 2.1) × 1046 photons s-1 and corresponds to an early-B star, Teff ~ 22 000 K (Panagia 1973), in agreement with the average spectral type of the star (Hu et al. 1990; Sterken et al. 2008).
The Strömgren radius calculated from Eq. (2) is RS = 0.46 ± 0.17 pc. By definition, the Strömgren radius is the radius of an ionization bounded nebula. In Sect. 3 the radius of the nebula in the optical, which is the radius of the ionized gas region which surrounds the central star, was found to be 0.32 pc. As both radii agree within the errors, we can conclude that the nebula can be ionization bounded, in agreement with the presence of PDR lines in the spectrum.
6.2.4. Abundances
The N/O abundance ratio can be estimated using the lines [N iii] 57 μm and [O iii] 88 μm and the equation ![\begin{equation} \frac{\mathrm{N}}{\mathrm{O}}=\frac{\langle \mathrm{N}^{++}\rangle} {\langle \mathrm{O}^{++}\rangle} =\frac{F_{[\ion{N}{iii}]57}/\varepsilon_{[\ion{N}{iii}]57}} {F_{[\ion{O}{iii}]88}/\varepsilon_{[\ion{O}{iii}]88}} , \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq180.png) (5)where F is the observed line flux and ε is the volume emissivity. Considering Te = 104 K and ne = 210 cm-3, we derived the emissivities using the package nebular. From the measured line intensities (Table 2), the N/O abundance ratio is then found to be 1.00 ± 0.38. The N/O ratio is much higher than the solar value of 0.14 (Grevesse et al. 2010). Compared with the N/O ratios of other LBVs nebulae (Smith 1997; Smith et al. 1998; Lamers et al. 2001), the value in the WRAY 15-751 nebula is one of the lowest and almost the same as the value found for the LMC R127 nebula, 0.9 ± 0.4.
(5)where F is the observed line flux and ε is the volume emissivity. Considering Te = 104 K and ne = 210 cm-3, we derived the emissivities using the package nebular. From the measured line intensities (Table 2), the N/O abundance ratio is then found to be 1.00 ± 0.38. The N/O ratio is much higher than the solar value of 0.14 (Grevesse et al. 2010). Compared with the N/O ratios of other LBVs nebulae (Smith 1997; Smith et al. 1998; Lamers et al. 2001), the value in the WRAY 15-751 nebula is one of the lowest and almost the same as the value found for the LMC R127 nebula, 0.9 ± 0.4.
An estimate of the N/H abundance number ratio can also be made, based on the observed Hα 6562.8 Å, [N iii] 57 μm, [N ii] 122 μm and 205 μm lines, considering that 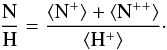 (6)The flux ratios, F/F0(Hβ) were calculated for the three infrared lines of nitrogen. The observed values of F were taken from Table 2. To calculate the Hβ flux, given the dereddened Hα flux, we assumed a case-B recombination with Te = 104 K. The ionic abundances N+/H+ and N+ +/H+ where then derived using again the package nebular. Their sum gives the N/H abundance number ratio, calculated to be (4.3 ± 2.0) × 10-4. This value is equivalent to a logarithmic N/H abundance of 12 + log (N/H) = 8.63 ± 0.20, higher than the solar value of 7.83 (Grevesse et al. 2010). This value is similar to the N/H abundances of other LBV nebulae (Smith 1997; Smith et al. 1998; Lamers et al. 2001).
(6)The flux ratios, F/F0(Hβ) were calculated for the three infrared lines of nitrogen. The observed values of F were taken from Table 2. To calculate the Hβ flux, given the dereddened Hα flux, we assumed a case-B recombination with Te = 104 K. The ionic abundances N+/H+ and N+ +/H+ where then derived using again the package nebular. Their sum gives the N/H abundance number ratio, calculated to be (4.3 ± 2.0) × 10-4. This value is equivalent to a logarithmic N/H abundance of 12 + log (N/H) = 8.63 ± 0.20, higher than the solar value of 7.83 (Grevesse et al. 2010). This value is similar to the N/H abundances of other LBV nebulae (Smith 1997; Smith et al. 1998; Lamers et al. 2001).
6.2.5. Mass of the ionized gas
The mass of the ionized gas can be estimated based on the Hα and the radio emissions. For this calculation the equations derived in Appendix B were used.
Since the temperature of the central star is lower than 30 000 K, we can assume that the ionization of He is negligible (y+ = 0). Assuming also ϵ = 1, the mass of the ionized nebula is Mi(Hα) = 1.04 ± 0.53 M⊙ and Mi(radio) = 0.92 ± 0.46 M⊙. The average value is Mi = 0.97 ± 0.35 M⊙. If the nebula is considered to be a shell and not a sphere, with inner radius 7′′ (assuming that the Hα shell has the same inner radius as the infrared dust shell) and outer radius 11′′, which is the limit of the Hα nebula as described in Sect. 3, its ionized mass is Mi = 0.84 ± 0.31 M⊙. Considering the errors, the ionized mass in the case of a shell nebula is not significantly different from the spherical case.
6.3. Photodissociation region characteristics
The fine structure lines [O i] 63, 146 μm and [C ii] 158 μm indicate a PDR in the nebula because they are among the important coolants in PDRs (Hollenbach & Tielens 1997). In this region, which surrounds the ionized region of the nebula, the gas is neutral and the far-ultraviolet (FUV) photons (with hν < 13.6 eV) play a significant role in the chemistry and the heating. The first detection of a PDR in an LBV nebula, through the presence of fine structure lines, was made by Umana et al. (2009) in their Spitzer study of the nebula that surrounds HR Car. One year later a PDR was found in the nebula around the LBV candidate HD 168625 (Umana et al. 2010), this time through spectral features indicating the presence of polycyclic aromatic hydrocarbons (PAHs).
The three infrared fine structure lines mentioned above can be used to determine the physical conditions in the PDR. But before that, any possible contribution of the H ii region to the observed line intensities must be determined and subtracted. Neutral oxygen can be found only in neutral regions, because its ionization potential (13.62 eV) is very close to the ionization potential of hydrogen. Consequently, the lines [O i] 63, 146 μm arise exclusively from the PDR (Malhorta et al. 2001). However, carbon is the fourth-most abundant element and has an ionization potential (11.26 eV) lower than that of hydrogen, so that C+ can be found both in PDRs and H ii regions. Therefore, the line [C ii] 158 μm may arise from the H ii region of the nebula WRAY 15-751 and/or from the associated PDR (Heiles 1994).
A first estimate of the contribution of the PDR to the flux of the line [C ii] 158 μm can be obtained following the empirical method described by Goicoechea et al. (2004). For each spaxel where the [N ii] 122 μm is detected (see Appendix A), the [C ii] 158 μm emission that comes from the ionized gas should scale with the [N ii] 122 μm, since the latter arises exclusively in ionized regions. Figure 9 shows the correlation between the [C ii] 158 μm and the [N ii] 122 μm flux for each spaxel where these two lines are detected. This correlation is described by ![\begin{equation} F_{[\ion{C}{ii}]158} = (0.16\pm 0.02) \, F_{[\ion{N}{ii}]122}+ (0.03 \pm 0.01), \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq198.png) (7)where F[C ii] 158 is the 158 μm line flux and F[C ii] 122 is the 122 μm line flux in units of 10-15 W m-2. The constant term of this relation represents the average [C ii] 158 μm flux per spaxel that arises in the PDR. Assuming that the PDR extends as the dust nebula, i.e., over 18′′ in radius or ~11 spaxels, we then find
(7)where F[C ii] 158 is the 158 μm line flux and F[C ii] 122 is the 122 μm line flux in units of 10-15 W m-2. The constant term of this relation represents the average [C ii] 158 μm flux per spaxel that arises in the PDR. Assuming that the PDR extends as the dust nebula, i.e., over 18′′ in radius or ~11 spaxels, we then find ![\hbox{$F_{[\ion{C}{ii}]158}^{\mathrm{PDR}} \simeq (0.33 \pm 0.11)\times 10^{-15}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq202.png) W m-2.
W m-2.
 |
Fig. 9 Correlation between the [C ii] 158 μm and [N ii] 122 μm line fluxes for each spaxel where these two lines are detected. |
Another estimate of the contribution of the PDR and the H ii regions to the flux of [C ii] 158 μm line can be also obtained. As the [N ii] 122 μm line arises exclusively in the ionized gas regions, measurements of its flux can give an estimate of the contribution of the H ii region to the flux of [C ii] 158 μm line, ![\hbox{$F_{[\ion{C}{ii}]158}^{\ion{H}{ii}}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq203.png) through a model. We define
through a model. We define ![\hbox{$F_{[\ion{C}{ii}]158}^{\ion{H}{ii}} =\alpha F_{[\ion{C}{ii}]158}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq204.png) , where F[C ii] 158 is the total flux of the [C ii] 158 μm line from Table 2 and α a factor that has to be determined. The ratio of fractional ionization is given, as previously, by
, where F[C ii] 158 is the total flux of the [C ii] 158 μm line from Table 2 and α a factor that has to be determined. The ratio of fractional ionization is given, as previously, by ![\begin{equation} \frac{\langle \mathrm{C}^{+}\rangle}{\langle \mathrm{N}^{+}\rangle}= \frac{F_{[\ion{C}{ii}]158}^{\ion{H}{ii}}/\varepsilon_{[\ion{C}{ii}]158}} {F_{[\ion{N}{ii}]122}/\varepsilon_{[\ion{N}{ii}]122}} \cdot \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq205.png) (8)Malhorta et al. (2001) provided an estimate for this relation only for the high, ne ≫ ncrit, and the low, ne ≪ ncrit, electron density limit, where ncrit = 3.1 × 102 cm-3 for [N ii] 122 μm and ncrit = 50 cm-3 for [C ii] 158 μm. As neither of these two limits apply to our case, the emissivities were calculated using the package nebular for the assumed Te and the measured ne. Assuming ⟨ C+ ⟩ / ⟨ N+ ⟩ = C/N, we find
(8)Malhorta et al. (2001) provided an estimate for this relation only for the high, ne ≫ ncrit, and the low, ne ≪ ncrit, electron density limit, where ncrit = 3.1 × 102 cm-3 for [N ii] 122 μm and ncrit = 50 cm-3 for [C ii] 158 μm. As neither of these two limits apply to our case, the emissivities were calculated using the package nebular for the assumed Te and the measured ne. Assuming ⟨ C+ ⟩ / ⟨ N+ ⟩ = C/N, we find ![\begin{equation} \label{eq:cnratio} \frac{F_{[\ion{C}{ii}]158}^{\ion{H}{ii}}}{F_{[\ion{N}{ii}]122}}= (0.45 \pm 0.06) \ \frac{\mathrm{C}}{\mathrm{N}} \cdot \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq212.png) (9)Since N/O has been estimated to be 1, we find that
(9)Since N/O has been estimated to be 1, we find that 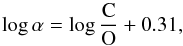 (10)using the observed ratio F[C ii] 158/F[N ii] 122 = 0.222 ± 0.054.
(10)using the observed ratio F[C ii] 158/F[N ii] 122 = 0.222 ± 0.054.
To derive the temperature and density of the PDR as well as the C/O abundance ratio, we plot the theoretical F[O i] 63/F[O i] 146 ratio against the ![\hbox{$F_{[\ion{O} {i}]63}/F_{[\ion{C}{ii}]158}^{\mathrm{PDR}}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq216.png) ratio normalized to the solar (C/O)⊙ = 0.5 abundance ratio (Fig. 10), following a similar study by Liu et al. (2001). To calculate the populations of the fine-structure levels of C+ and O0, we solved the two- and three-level atom equilibrium equations, respectively, considering that collisions with atomic hydrogen dominate in the PDR (Draine 2011). The radiative transition probabilities, Aij, for the [C ii] and [O i] fine-structure lines and the electron collision strengths, Ωij, were taken from Draine (2011). The collisional rate coefficients for the fine-structure excitation by hydrogen were taken from Barinovs et al. (2005) for [C ii] and from Abrahamsson et al. (2007) for [O i]. A simple analytic extrapolation was made for temperatures higher than those given in these two references2. Furthermore, if we assume that there is pressure equilibrium between the H ii region and the PDR, we have (Tielens 2005)
ratio normalized to the solar (C/O)⊙ = 0.5 abundance ratio (Fig. 10), following a similar study by Liu et al. (2001). To calculate the populations of the fine-structure levels of C+ and O0, we solved the two- and three-level atom equilibrium equations, respectively, considering that collisions with atomic hydrogen dominate in the PDR (Draine 2011). The radiative transition probabilities, Aij, for the [C ii] and [O i] fine-structure lines and the electron collision strengths, Ωij, were taken from Draine (2011). The collisional rate coefficients for the fine-structure excitation by hydrogen were taken from Barinovs et al. (2005) for [C ii] and from Abrahamsson et al. (2007) for [O i]. A simple analytic extrapolation was made for temperatures higher than those given in these two references2. Furthermore, if we assume that there is pressure equilibrium between the H ii region and the PDR, we have (Tielens 2005) 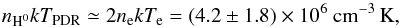 (11)where nH0 is the atomic hydrogen number density and TPDR is the temperature of the PDR. This relation defines a locus of possible values in the diagram of Fig. 10.
(11)where nH0 is the atomic hydrogen number density and TPDR is the temperature of the PDR. This relation defines a locus of possible values in the diagram of Fig. 10.
 |
Fig. 10 Temperature-density PDR diagnostic diagram. The grid of flux ratios F[O i] 63/F[O i] 146 versus |
Given the observed ratio F[O i] 63/F[O i] 146 = 8.4 ± 2.8 and the constraints from Eq. (11), we can derive from Fig. 10 log![\hbox{$(F_{[\ion{O} {i}]63}/F_ {[\ion{C}{ii}]158}^{\mathrm{PDR}})$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq232.png) + [C/O] = 0.63, where [C/O] ≡ log(C/O)−log (C/O)⊙. Recalling that
+ [C/O] = 0.63, where [C/O] ≡ log(C/O)−log (C/O)⊙. Recalling that ![\hbox{$F_{[\ion{C}{ii}]158}^{\mathrm{PDR}}=(1-\alpha)F_{[\ion{C}{ii}]158}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq233.png) and considering the above relation between C/O and α (Eq. (10)), the observed value of the line ratios yields α = 0.82 ± 0.07 and C/O = 0.40 ± 0.19. Considering the errors, the C/O abundance ratio of the nebula has the solar value. C/H is then (1.7 ± 1.3) × 10-4 from the N/H, C/O and N/O abundance ratios. The contribution of the H ii region to [C ii] 158 μm is then
and considering the above relation between C/O and α (Eq. (10)), the observed value of the line ratios yields α = 0.82 ± 0.07 and C/O = 0.40 ± 0.19. Considering the errors, the C/O abundance ratio of the nebula has the solar value. C/H is then (1.7 ± 1.3) × 10-4 from the N/H, C/O and N/O abundance ratios. The contribution of the H ii region to [C ii] 158 μm is then ![\hbox{$F_{[\ion{C}{ii}]158}^ {\ion{H}{ii}} =(0.99\pm0.16)\times 10^{-15}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq236.png) W m-2 while the contribution of the PDR is
W m-2 while the contribution of the PDR is ![\hbox{$F_{[\ion{C}{ii}]158}^{\mathrm{PDR}} = (0.22\pm0.09)\times 10^{-15}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq237.png) W m-2. This value agrees with the one obtained using the empirical method.
W m-2. This value agrees with the one obtained using the empirical method.
The diagram in Fig. 10 also provides us with the values of the density and the temperature of the PDR of the nebula, from the observed F[O i] 63/F[O i] 146 ratio: log nH0 = 2.38 ± 0.18 and TPDR > 4000 K. Given the constraints from Eq. (11), we estimate that TPDR ~ 17 500 K but this value is very uncertain, within a factor of 2.
The incident FUV radiation field, G0, along with the density nH0, describes the structure of the PDR. Expressed in terms of the average interstellar radiation field, which corresponds to a unidirectional radiation field of 1.6 × 10-3 erg cm-2 s-1, it is given by (Tielens 2005) 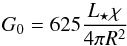 (12)at the distance R from the star, with L⋆ the stellar luminosity and χ the fraction of the luminosity above 6 eV. For an early B star, χ ~ 0.7 (Young Owl et al. 2002). Considering L⋆ = 105.8 L⊙ (Sect. 5.1) and the radius of the ionized gas region, which is surrounded by the PDR, R = 0.32 pc, the incident FUV radiation field is found to be G0 ≃ 8.5 × 104 for the PDR of the WRAY 15-751 nebula. This value is consistent with the estimated PDR density, as our results are reasonably compatible with the diagnostic diagrams of the PDR models of Kaufman et al. (1999, Figs. 4 and 5).
(12)at the distance R from the star, with L⋆ the stellar luminosity and χ the fraction of the luminosity above 6 eV. For an early B star, χ ~ 0.7 (Young Owl et al. 2002). Considering L⋆ = 105.8 L⊙ (Sect. 5.1) and the radius of the ionized gas region, which is surrounded by the PDR, R = 0.32 pc, the incident FUV radiation field is found to be G0 ≃ 8.5 × 104 for the PDR of the WRAY 15-751 nebula. This value is consistent with the estimated PDR density, as our results are reasonably compatible with the diagnostic diagrams of the PDR models of Kaufman et al. (1999, Figs. 4 and 5).
The FUV radiation given by G0 is also absorbed and re-emitted by the dust in the FIR. The radiative equilibrium gives us the dust temperature, Tdust, which in case of silicates (i.e., β = 2) is given by (Tielens 2005) 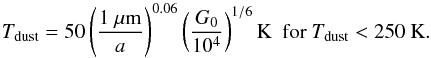 (13)As the small grains dominate the average cross-section, a typical grain size of a = 0.1 μm can be assumed, which leads to a dust temperature of Tdust = 81 K, in excellent agreement with the results of the 2-Dust model.
(13)As the small grains dominate the average cross-section, a typical grain size of a = 0.1 μm can be assumed, which leads to a dust temperature of Tdust = 81 K, in excellent agreement with the results of the 2-Dust model.
The total mass of hydrogen in the PDR, MH, can be estimated from the [C ii] 158 μm line flux derived for the PDR (Tielens 2005), using the equation given in Appendix C. For the above PDR density, temperature, distance and C/H abundance, the neutral hydrogen mass in the PDR is estimated to be MH = 0.43 ± 0.35 M⊙.
6.4. Total gas mass
The total gas mass of the nebula is the sum of the mass in the ionized nebula and the mass in the PDR, corrected for the presence of helium, i.e., 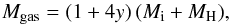 (14)where y = nHe/nH. Assuming a solar abundance for helium of 12+log(He/H) = 10.93 ± 0.01 (Grevesse et al. 2010), the gas mass is Mgas = 1.7 ± 0.6 M⊙. Considering the calculated dust mass (Sect. 5.1), the dust-to-gas mass ratio for the inner nebula is Mdust/Mgas = 0.026 ± 0.010, i.e., ~3%. If the He abundance is higher, as expected for an evolved star, the total gas mass will be higher, typically 20% for a He/H abundance ratio corresponding to the observed N/O abundance ratio.
(14)where y = nHe/nH. Assuming a solar abundance for helium of 12+log(He/H) = 10.93 ± 0.01 (Grevesse et al. 2010), the gas mass is Mgas = 1.7 ± 0.6 M⊙. Considering the calculated dust mass (Sect. 5.1), the dust-to-gas mass ratio for the inner nebula is Mdust/Mgas = 0.026 ± 0.010, i.e., ~3%. If the He abundance is higher, as expected for an evolved star, the total gas mass will be higher, typically 20% for a He/H abundance ratio corresponding to the observed N/O abundance ratio.
7. Discussion
Parameters of WRAY 15-751
A summary of the measurements obtained in the previous sections is given in Table 3. The luminosity, effective temperature and distance of the central star are given first (from Hu et al.1990; Sterken et al. 2008, and this work), followed by the parameters of the inner and the outer dust shells, i.e., the radius, the expansion velocity (from HVD; assumed to be identical for both shells), the kinematic age, the electron density and the assumed temperature of the ionized gas, the abundance ratios, and the dust and gas masses.
The Herschel-PACS far-infrared images of WRAY 15-751 reveal the dust nebula as a shell of radius 0.5 pc and width 0.35 pc. These observations also unveiled a second dust nebula, four times bigger, lying in an empty cavity. As in the case of WR stars (Marston 1996), the empty cavity probably corresponds to the interior of O-star wind bubble formed when the star was on the main sequence.
Our study consistently shows that the main nebula is illuminated by an average early-B star and consists of a shell of ionized gas surrounded by a thin photodissociation region. Both these regions are mixed with dust. The mass of this nebula amounts to ~2 M⊙ ejected ~2 × 104 years ago. The second, larger and older nebula contains a similar amount of mass if we assume a similar dust-to-gas ratio so that, in total, ~4 M⊙ of gas have been ejected within ~6 × 104 years. This also indicates that the star had multiple episodes of intense mass-loss. Moreover, it is possible that the very inner dense nebula spectroscopically detected by HVD and resolved by Duncan & White (2002) constitutes a third ejection some 103 years ago, assuming an angular radius of 1″ (Duncan & White 2002) and an expansion velocity of 26 km s-1, the same as for the main ring nebula.
The N/O abundance ratio appears to be enhanced by a factor 8 with respect to the solar abundances given in Ekström et al. (2012). This confirms the presence of processed material in the nebula. The C/O ratio, measured for the first time in a LBV nebula, is solar within the uncertainties. These ratios correspond to an enhancement in N/H by a factor 6 and a depletion in C/H and O/H by a factor 1.4 with respect to the solar abundances.
 |
Fig. 11 Evolutionary path in the HR diagram of a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The thicker lines emphasize the part of the tracks compatible with the measurements (cf. Figs. 12 and 13). For clarity, the tracks are stopped at the beginning of the blue loop (data point No 210 in Ekström et al. 2012). |
 |
Fig. 12 Evolution of the N/O versus the C/O surface abundance ratios for a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The dashed lines correspond to the values measured for the inner shell around WRAY 15-751, with their errors. The thicker lines emphasize the part of the tracks compatible with the measurements. For clarity, the tracks are stopped at the beginning of the blue loop (data point No 210 in Ekström et al. 2012). |
The N/O ratio of 1.00 ± 0.38 is quite similar to the ratio measured in the nebula around the LMC LBV R127 (Smith et al. 1998). The 12+log(N/H) abundance of 8.63 ± 0.20 is between the values for the LBVs AG Car and η Car (Smith et al. 1998). The conclusion of Smith et al. (1997, 1998) that LBV nebulae contain only mildly enriched material with respect to CNO equilibrium values and thus were ejected during a previous red supergiant (RSG) or yellow supergiant (YSG) phase therefore applies to WRAY 15-751, especially as the star is less luminous, log L/L⊙ = 5.7 ± 0.2, i.e., just at or below the Humphreys-Davidson limit. In addition, the nebula has a relatively low expansion velocity of 26 km s-1, more compatible with RSG outflows than the higher velocities measured in more luminous LBVs such as AG Car. The ejection of the WRAY 15-751 nebula during an RSG phase was also proposed by Voors et al. (2000) on the basis on its dust composition.
 |
Fig. 13 Evolution of the N/O surface abundance ratio as a function of the mass-loss rate for a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The dashed lines correspond to the values measured for the inner shell around WRAY 15-751, with their errors. The thicker lines emphasize the part of the tracks compatible with the measurements. For clarity, the tracks are stopped at the beginning of the blue loop (data point no 210 in Ekström et al. 2012). |
Our observations can be used to constrain the evolutionary path of the star and the epoch of ejection of the nebula. Given its luminosity, WRAY 15-751 is expected to result from the evolution of a star of initial mass in the range 40–60 M⊙. Figures 11−13 show the evolution of some properties of a 40 M⊙ star using the models of Ekström et al. (2012). Four different cases of stellar rotation are considered, from no rotation to a rotation rate of v/vcrit = 0.4. The tracks are first compared with the observed N/O and C/O abundance ratio to identify the part of the tracks where the computed surface abundances match the observed nebular abundances (Fig. 12). Possible tracks were additionally constrained when compared with the observed mass-loss rate (Fig. 13). The mass-loss rate is estimated from the mass of the inner nebula divided by the duration of the enhanced mass-loss episode (estimated from the kinematic age), i.e., the time needed to cover the ring width: log Ṁ = −3.8 ± 0.2, accounting for an increase of the mass of 20% due to the higher He/H abundance at that time. These constraints are finally reported in the HR diagram (Fig. 11) to identify the locus of the ejection of the inner nebula. The model appears to remarkably agree with the observations, supporting the scenario of an ejection of the nebula during the RSG phase3. The N/H enhancement factor as well as the C/H and O/H depletion factors predicted by the model also agree with the observed values. The mild N/O enrichment indicates that the star cannot be a fast rotator, the v/vcrit = 0.4 track being clearly excluded. A similar result is obtained for a 45 M⊙ star except that the only possible tracks have v/vcrit = 0.0 and 0.1. For a 50 M⊙ star, no track satisfies the observational constraints.
The time between the ejections of the outer and the inner nebulae, about 6 × 104 years, is compatible with the duration of the RSG phase of a 40 M⊙ star, as computed by the model. Thus, the outer nebula could also have been ejected during this phase, especially in the models with v/vcrit < 0.2 for which the inner, younger nebula is ejected closer to the end of the RSG phase than to the beginning (Fig. 11). The total mass lost during the RSG phase amounts to 8–9 M⊙ in the model. Although higher, this is compatible with our value of 4 ± 2 M⊙, recalling that the value for the outer nebula is particularly uncertain due to the unknown dust-to-gas ratio and He abundance.
Our results suggest that the ejection of the nebula does not occur because the star is rotating close to the critical velocity, as proposed by Meynet et al. (2011). Moreover, the existence of multiple nebular shells points to an instability mechanism at work during the RSG evolutionary stage and not to a continuous wind. In particular, models by Stothers & Chin (1996) suggest that LBV nebulae can result from strong, closely spaced mass-loss episodes in the RSG phase and not from a continuous wind. For a 45 M⊙ star, they found that about 4 M⊙ can be ejected, in agreement with our measurements.
While our results support the scenario of an ejection of LBV in the RSG phase, the study of Lamers et al. (2001) reached the conclusion that LBV nebulae were ejected during the BSG phase with high rotational velocities, and not during the RSG stage. However, Lamers et al. (2001) only considered very luminous LBVs (log L/L⊙ > 5.8), while WRAY 15-751 is a lower luminosity LBV. Moreover, the nebula around WRAY 15-751 is only weakly bipolar compared with other LBV nebulae such as those around AG Car or HR Car, in qualitative agreement with little effect of rotation. Finally, the discovery of a dusty LBV-like ring nebula around the yellow supergiant Hen3-1379, which is very similar to WRAY 15-751, also supports the ejection of nebulae during the RSG phase (Hutsemékers et al. 2013). Therefore, high-luminosity and low-luminosity LBVs probably follow different evolutionary paths.
Our results are compatible with the evolutionary model of an ~40 M⊙ star and the O–BSG–RSG–YSG–LBV filiation. According to Toalá & Arthur (2011), an ~40 M⊙ star creates a bubble of radius ~25 pc as a main- sequence O star, in agreement with the structure tentatively observed in Fig. 4. Then, when an RSG, the star ejects several solar masses of material in the cavity previously created, forming the observed dusty nebulae. It is interesting to note that in this scenario, the age of WRAY 15-751 since the ejection of the last nebula is only ~2 × 104 years, which corresponds in the computed tracks of Fig. 11 to the loop at log Teff ~ 4.1. Higher temperatures are only reached ~105 years later. It is not clear whether a star at that location in the HR diagram, which corresponds to a hot YSG, can have the LBV-like instability properties currently displayed by WRAY 15-751. This might indicate that the LBV phenomenon could occur at different evolutionary stages. Determining the surface abundances of WRAY 15-751 in its present stage might help to constrain this scenario more closely.
8. Conclusions
We have presented the analysis of Hershel PACS imaging and spectroscopic data of the nebula around the LBV Wray 15-751, together with new optical-imaging data. The far-infrared images clearly show that the main, dusty nebula is a shell extending outside the well-known Hα nebula. Furthermore, these images reveal a second, bigger and fainter dust nebula that is observed for the first time. The two nebulae lie in an empty cavity, very likely the remnant of the O-star wind bubble formed when the star was on the main sequence.
The dust parameters of the main nebula were determined based on dust modeling. This model shows that the far-infrared emission did not significantly change during the different phases of the S Dor cycle. This stability points to a stellar variation under essentially constant luminosity. We also found that Fe-rich dust is needed to reproduce the data. This is not unexpected in LBV nebulae as a consequence of depletion of C and O with respect to heavier elements (Gail et al. 2005).
The far-infrared spectrum of the main nebula contains forbidden emission lines coming from an ionized region and from a photodissociation region, from which we derived the gas parameters, such as the C, N, O abundances and the ejected gas mass, with the C/O ratio measured for the first time in an LBV nebula. As a result of this study, the main shell nebula consists of an ionized gas region which is surrounded by a thin PDR, both regions being mixed with the dust. As expected for such an evolved star, the nebula shows N enrichment and C, O depletion.
The measured abundances, masses and kinematic ages of the nebulae were used to constrain the evolution of the star and the epoch at which the nebulae were ejected. Our results point to an ejection of the nebulae during the RSG evolutionary phase of an ~40 M⊙ star. The multiple shells around the star suggest that the mechanism of mass-loss is not a continuous wind but instead a series of short episodes of extreme mass-loss.
This scenario is compatible with the recent evolutionary tracks computed for an ~40 M⊙ star with little rotation, in particular the O–BSG–RSG–YSG–LBV filiation although it should be stressed that post-main-sequence evolutionary tracks of massive stars are still very uncertain, in particular since they rely on poorly known mass-loss mechanisms and rates. If the evolutionary tracks are correct, our results support the idea that high-luminosity and low-luminosity LBVs follow different evolutionary paths. The forthcoming analysis of similar data for higher luminosity LBVs (e.g., AG Car) and for LBVs known to be fast rotators (e.g., HR Car) should allow us to constrain this scenario more closely.
The 10.5 μm ISO-CAM image of the nebula is very similar to the ground-based mid-infrared images presented in Voors et al. (2000) but its spatial resolution is much lower.
Acknowledgments
We thank Xiaowei Liu, Daniel Pequignot and Evelyne Roueff for help with the PDR diagnostic diagram construction. C.V.N., P.R., D.H., Y.N., K.E. and M.A.T.G. acknowledge support from the Belgian Federal Science Policy Office via the PRODEX Programme of ESA. The Liège team acknowledges also support from the FRS-FNRS (Comm. Franç. de Belgique). PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). Data presented in this paper were analyzed using HIPE, a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology.
References
- Abrahamsson, E., Krems, R. V., & Dalgarno, A. 2007, ApJ, 654, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Barinovs, Ğ., van Hemert, M. C., Krems, R., & Dalgarno, A. 2005, ApJ, 620, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Beichman, C. A., Neugebauer, G., Habing, H. J., Clegg, P. E., & Chester, T. J. 1988, Infrared Astronomical Satellite (IRAS) Catalogs and Atlases, 1, Explanatory Supplement (Pasadena: California Institute Technology) [Google Scholar]
- Blommaert, J., Siebenmorgen, R., Coulais, A., et al. 2003, The ISO Handbook, Volume II: CAM-The ISO Camera (Paris: European Space Agency) [Google Scholar]
- Bode, M. F., & Evans, A. 1979, A&A, 79, 113 [NASA ADS] [Google Scholar]
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantalupo, C. M., Borrill, J. D., Jaffe, A. H., Kisner, T. S., & Stompor, R. 2010, ApJS, 187, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Carlson, E. D., & Henize, K. G. 1979, Vistas Astron., 23, 213 [Google Scholar]
- de Winter, D., Perez, M. R., Hu, J. Y., & The, P. S. 1992, A&A, 257, 632 [NASA ADS] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Duncan, R. A., & White, S. M. 2002, MNRAS, 330, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gail, H.-P., Duschl, W. J., Ferrarotti, A. S., & Weis, K. 2005, ASPC, 332, 317 [NASA ADS] [Google Scholar]
- Garcia-Lario, P., Riera, A., & Manchado, A. 1998, A&A, 334, 1007 [NASA ADS] [Google Scholar]
- Goicoechea, J. R., Rodriguez-Fernandez, N. J., & Cernicharo, J. 2004, 600, 214 [Google Scholar]
- Grevesse, N., Asplund, M., Sauval, A. J., & Scott, P. 2010, Ap&SS, 328, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Waelkens, C., Barlow, M. J., et al. 2011, A&A, 526, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C. 1994, ApJ, 436, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, J. Y., de Winter, D., The, P. S., & Perez, M. R. 1990, A&A, 227, 17 [Google Scholar]
- Humphreys R.M., & Davidson K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Hutsemékers, D. 1994, A&A, 281, L81 [NASA ADS] [Google Scholar]
- Hutsemékers, D. 1997, ASPC, 120, 316 [Google Scholar]
- Hutsemékers, D., & van Drom, E. 1991, A&A, 251, 620 (HVD) [NASA ADS] [Google Scholar]
- Hutsemékers, D., Cox, N. L. J., & Vamvatira-Nakou, C. 2013, A&A, 552, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Nota, A., Panagia, N., Smith, L. J., & Langer, N. 2001, ApJ, 551, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R. J., Klaas, U., Richards, P. J., Schulz, B., & Ábrahám, P. 2003, The ISO Handbook, Volume IV: PHT - The Imaging Photo-Polarimeter (European Space Agency) [Google Scholar]
- Liu, X.-W., Barlow, M. J., Cohen, M., et al. 2001, MNRAS, 323, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2010, New Astron. Rev., 54, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P., Courbin, F., & Sohy, S. 1998, ApJ, 494, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Malhorta, S., Kaufman, M. J., & Hollenbach, D. 2001, ApJ, 561,766 [Google Scholar]
- Marston, A. P. 1996, AJ, 112, 2828 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McGregor, P. J., Hyland, A. R., & Hillier, D. J. 1988, ApJ, 324, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, J., Dekker, H., & D’Odorico, S. 1989, EFOSC, ESO operating manual 4 [Google Scholar]
- Meynet, G., Georgy, C., Hirschi, R., et al. 2011, BSRSL, 80, 266 [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T., Okumura, K., & Klaas, U. 2011, PACS Photometer Passbands and Colour Correction Factors for Various Source SEDs [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nota, A. 1999, IAU Colloq. 169, Lect. Not. Phys., 523, 62 [Google Scholar]
- Nota, A., Livio, M., Clampin, M., & Schulte-Ladbeck, R. 1995, ApJ, 448, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Nota, A., Pasquali, A., Marston, A. P., et al. 2002, AJ, 124, 2920 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., Henning, T., & Mathis, J. S. 1992, A&A, 261, 567 [NASA ADS] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (University sciences books) [Google Scholar]
- Ott, S. 2010, ASP Conf. Ser., 434, 139 [Google Scholar]
- Panagia, N. 1973, AJ, 78, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquali, A., Comerón, F., & Nota, A. 2006, A&A, 448, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, A2 [Google Scholar]
- Puls, J., Markova, N., & Scuderi, S. 2008, ASPC, 388, 101 [NASA ADS] [Google Scholar]
- Roberts, M. S. 1962, AJ, 67, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Rosario, L., Takashi, O., Yoshifusa, I., et al. 2008, AKARI IRC Data User Manual [Google Scholar]
- Shaw, R. A., & Dufour, R. J. 1995, PASP, 107, 896S [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J. 1997, ASPC, 120, 310 [Google Scholar]
- Smith, L. J., Stroud, M. P., Esteban, C., & Vilchez, J. M. 1997, MNRAS, 290, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Nota, A., Pasquali, A., et al. 1998, ApJ, 503, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Sterken, C., van Genderen, A. M., Plummer, A., & Jones, A. F. 2008, A&A, 484, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stothers, R. B., & Chin, C.-W. 1996, ApJ, 468, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge University Press) [Google Scholar]
- Toalá, J. A., & Arthur, S. J. 2011, ApJ, 737, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Ueta, T., & Meixner, M. 2003, ApJ, 586, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Umana, G., Buemi, C. S., Trigilio, C., et al. 2009, ApJ, 694, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Umana, G., Buemi, C. S., Trigilio, C., et al. 2010, ApJ, 718, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Vamvatira-Nakou, C., Royer, P., Hutsemékers, D., et al. 2011, Bull. Soc. Roy. Sci. Liège, 80, 43 [Google Scholar]
- van Genderen, A. M., The, P. S., & de Winter, D. 1992, A&A, 258, 316 [NASA ADS] [Google Scholar]
- Voors, R. H. M. 1999, Infrared studies of hot stars with dust, Ph. D. Thesis, Universiteit Utrecht, The Netherlands [Google Scholar]
- Voors, R. H. M., Waters, L. B. F. M., de Koter, A., et al. 2000, A&A, 356, 501 [NASA ADS] [Google Scholar]
- Weis, K. 2000, A&A, 357, 938 [NASA ADS] [Google Scholar]
- Wolf, B., Appenzeller, I., & Stahl, O. 1981, A&A, 103, 94 [NASA ADS] [Google Scholar]
- Yamamura, I., Makiuti, S., Ikeda, N., et al. 2010, AKARI/FIS All-Sky Survey Bright Source Catalogue, Version 1.0, Release Note [Google Scholar]
- YoungOwl, R. C., Meixner, M. M., Fong, D., et al. 2002, ApJ, 578, 885 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Emission line fluxes for each spaxel
Table A.1 gives the results of the emission line flux measurements for each spaxel. The first column contains the detected ions along with the spectral band in which the corresponding line was measured. The following columns contain the line fluxes, expressed in W/m2, along with their errors. The spaxel numbers (Fig. 5) are mentioned in every cell of the table. No spectral lines were detected in the western column of the spectrometric camera (spaxels [0, 0] to [4, 0]), and these spaxels were hence not included in the table. The quoted uncertainties are the sum of the line-fitting uncertainty plus the uncertainty due to the position of the continuum.
Appendix B: Ionized nebula
The formulae needed to estimate the nebular mass and the ionizing flux from both Hα and radio emissions are re-derived here for consistency of hypotheses and notations.
Appendix B.1: Hα emission
The luminosity in the Hα recombination line, integrated over the volume V of the nebula, is given by (Osterbrock & Ferland 2006) 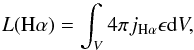 (B.1)where ϵ is the filling factor that gives the fraction of the volume of the nebula that is filled by ionized gas, and jHα is the Hα line emission coefficient. The flux received by the observer is
(B.1)where ϵ is the filling factor that gives the fraction of the volume of the nebula that is filled by ionized gas, and jHα is the Hα line emission coefficient. The flux received by the observer is 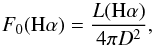 (B.2)where D is the distance to the nebula. By integrating over the volume, assuming a spherical uniform nebula of radius R and considering the effective recombination coefficient αeff = (4πj)/(nenphν), we have
(B.2)where D is the distance to the nebula. By integrating over the volume, assuming a spherical uniform nebula of radius R and considering the effective recombination coefficient αeff = (4πj)/(nenphν), we have 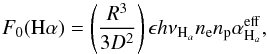 (B.3)where ne is the electron density, np is the proton density, h is the Plank’s constant and νHa is the frequency of the Hα line.
(B.3)where ne is the electron density, np is the proton density, h is the Plank’s constant and νHa is the frequency of the Hα line.
The mass of the ionized nebula, Mi, is equal to 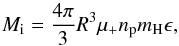 (B.4)with mH being the H atomic mass and μ+ the mean ionic mass per H ion. By replacing ne in the Eq. (B.3) with ne = xenp and combining it with Eq. (B.4), the ionized mass can be written as
(B.4)with mH being the H atomic mass and μ+ the mean ionic mass per H ion. By replacing ne in the Eq. (B.3) with ne = xenp and combining it with Eq. (B.4), the ionized mass can be written as 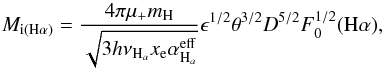 (B.5)where θ is the angular radius of the nebula (R = θD) in Hα. By replacing the effective recombination coefficient with the following formula, taken from Draine (2011),
(B.5)where θ is the angular radius of the nebula (R = θD) in Hα. By replacing the effective recombination coefficient with the following formula, taken from Draine (2011), 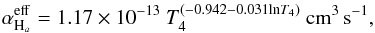 (B.6)where T4 = Te/(104 K) and Te is the electron temperature, we obtain the following expression for the ionized mass of the nebula in solar masses
(B.6)where T4 = Te/(104 K) and Te is the electron temperature, we obtain the following expression for the ionized mass of the nebula in solar masses  (B.7)where θ is in arcsec, D is in kpc and F0(Hα) is in ergs cm-2 s-1. With nH+ = np, nHe+ and nHe+ + the ionized hydrogen, ionized helium and doubly ionized helium number densities, respectively, xe = ne/np ≃ 1 + nHe+/nH+ = 1 + y+ and μ+ ≃ 1 + 4 nHe+/nH+ = 1 + 4y+ assuming nHe+ + = 0 and denoting y+ = nHe+/nH+.
(B.7)where θ is in arcsec, D is in kpc and F0(Hα) is in ergs cm-2 s-1. With nH+ = np, nHe+ and nHe+ + the ionized hydrogen, ionized helium and doubly ionized helium number densities, respectively, xe = ne/np ≃ 1 + nHe+/nH+ = 1 + y+ and μ+ ≃ 1 + 4 nHe+/nH+ = 1 + 4y+ assuming nHe+ + = 0 and denoting y+ = nHe+/nH+.
The number of hydrogen ionizing photons per unit time, Q(H0), emitted by a nebula in equilibrium is given by (Osterbrock & Ferland 2006) 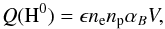 (B.8)where αB is the recombination coefficient given by the following equation, taken from Draine (2011),
(B.8)where αB is the recombination coefficient given by the following equation, taken from Draine (2011), 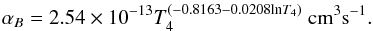 (B.9)The combination of the two previous equations gives us the radius, RS, which is the radius of the Strömgren sphere
(B.9)The combination of the two previous equations gives us the radius, RS, which is the radius of the Strömgren sphere 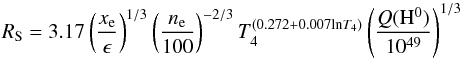 (B.10)in units of pc. By combining this equation with the Eq. (B.3), with R = RS (ionization bounded nebula), the rate of emission of hydrogen-ionizing photons for a given Hα flux, in photons per second is
(B.10)in units of pc. By combining this equation with the Eq. (B.3), with R = RS (ionization bounded nebula), the rate of emission of hydrogen-ionizing photons for a given Hα flux, in photons per second is 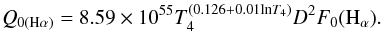 (B.11)
(B.11)
Line fluxes in each spaxel. A dash indicates a poor signal-to-noise ratio or a non-detection.
Appendix B.2: Continuum radio emission
In the radio frequency region, where hν ≪ kT, the Plank law can be written as 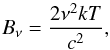 (B.12)where Bν = jν/κν, with jν and κν the emission and absorption coefficients at a given frequency ν, respectively.
(B.12)where Bν = jν/κν, with jν and κν the emission and absorption coefficients at a given frequency ν, respectively.
The radio flux density at a distance D from the nebula is given by 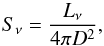 (B.13)with Lν = ∫V4πjνϵdV. Assuming that the nebula is an optically thin sphere of radius R, the radio flux density can then be written
(B.13)with Lν = ∫V4πjνϵdV. Assuming that the nebula is an optically thin sphere of radius R, the radio flux density can then be written 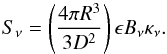 (B.14)The continuum free-free effective absorption coefficient at radio frequencies is given by (Osterbrock & Ferland 2006)
(B.14)The continuum free-free effective absorption coefficient at radio frequencies is given by (Osterbrock & Ferland 2006) 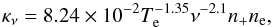 (B.15)where the temperature Te is in K and the frequency ν is in GHz. The ion density is equal to n+ = nH+ + nHe+ = ne.
(B.15)where the temperature Te is in K and the frequency ν is in GHz. The ion density is equal to n+ = nH+ + nHe+ = ne.
The ionized mass of the nebula is defined by Eq. (B.4). By adopting the same formalism as in the first part of this Appendix, the ionized mass in solar masses is finally found to be 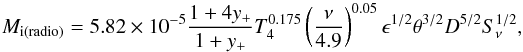 (B.16)where ν is the radio frequency in GHz, θ is the angular radius of the ionized nebula in arcsec, D is the distance to the nebula in kpc and Sν is the radio flux density in mJy.
(B.16)where ν is the radio frequency in GHz, θ is the angular radius of the ionized nebula in arcsec, D is the distance to the nebula in kpc and Sν is the radio flux density in mJy.
The rate of emission of hydrogen-ionizing photons, for a given radio flux density, can be found by combining Eqs. (B.10) and (B.14): 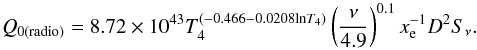 (B.17)
(B.17)
Appendix C: Photodissociation region
According to Tielens (2005), the total mass of hydrogen in the PDR is given by ![\appendix \setcounter{section}{3} \begin{equation} M_{\mathrm{H}}=\frac{4\pi D^2 m_{\mathrm{H}}} {X_{\mathrm{C}}A_{\mathrm{ul}}E_{\mathrm{lu}}} \left(\frac{g_{\rm l}}{g_{\rm u}}\mathrm{exp} [E_{\mathrm{lu}}/kT_{\rm PDR}]+1\right)F_{[\ion{C}{ii}]}, \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq355.png) (C.1)where XC is the C/H abundance in number, TPDR the temperature of the gas, gl, glu, Aul and Elu the statistical weights, transition probability and energy difference of the levels involved to this transition, D the distance to the star and F[C ii] the observed [C ii] 158 μm flux. From the cooling law, we have that (Tielens 2005)
(C.1)where XC is the C/H abundance in number, TPDR the temperature of the gas, gl, glu, Aul and Elu the statistical weights, transition probability and energy difference of the levels involved to this transition, D the distance to the star and F[C ii] the observed [C ii] 158 μm flux. From the cooling law, we have that (Tielens 2005) ![\appendix \setcounter{section}{3} \begin{equation} n_{\mathrm{u}}A_{\mathrm{ul}}h\nu_{\mathrm{ul}}=\frac{(g_{\mathrm{u}} /g_{\mathrm{l}})\mathrm{exp}[-h\nu_{\rm ul}/kT_{\rm PDR}]} {1+n_{\mathrm{crit}}/n_\mathrm{H^0}+(g_{\mathrm{u}} /g_{\mathrm{l}})\mathrm{exp}[-h\nu_{\rm ul}/kT_{\rm PDR}]+1}, \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq363.png) (C.2)where nH0 is the number density of atomic hydrogen and the ncrit the critical density, given by
(C.2)where nH0 is the number density of atomic hydrogen and the ncrit the critical density, given by 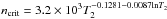 cm-3 where T2 = TPDR/(102 K) (Draine 2011). By replacing the known parameters with their values and by considering that TPDR ≫ Eul/k = 92K, we finally have
cm-3 where T2 = TPDR/(102 K) (Draine 2011). By replacing the known parameters with their values and by considering that TPDR ≫ Eul/k = 92K, we finally have ![\appendix \setcounter{section}{3} \begin{equation} M_{\mathrm{H}}({M}_{\odot}) = 4.93\times10^9 \left(1+\frac{n_\mathrm{crit} / n_\mathrm{H^0}}{3}\right) D^2 \left(\frac{F_{[\ion{C}{ii}]}}{X_{\mathrm{C}}}\right) , \end{equation}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq368.png) (C.3)where D is in kpc and F[C ii] is in W m-2.
(C.3)where D is in kpc and F[C ii] is in W m-2.
All Tables
Line fluxes in each spaxel. A dash indicates a poor signal-to-noise ratio or a non-detection.
All Figures
 |
Fig. 1 PACS images of the nebula around WRAY 15-751 at 70 μm, 100 μm and 160 μm, from left to right. Top: original images. Bottom: images deconvolved using the MCS method. The size of each image is 1′× 1′. The scales on the right correspond to the surface brightness (arbitrary units). North is up and east is to the left. |
| In the text | |
 |
Fig. 2 Hα+[N ii] image of the nebula around WRAY 15-751. The size of the image is 1′× 1′. The scale on the right corresponds to the surface brightness (arbitrary units). North is up and east is to the left. The central star is occulted by the coronograph spot. |
| In the text | |
 |
Fig. 3 PACS 100 μm image of the nebula obtained using the MADmap reduction algorithm. The size of the image is 10′ × 10′. The scale on the bottom corresponds to the surface brightness (arbitrary units). North is up and east is to the left. A faint extended elliptical nebulosity is seen around the bright shell, the size of which is marked with the horizontal and vertical bars. Both appear located inside a cavity in the interstellar medium. |
| In the text | |
 |
Fig. 4 Two-color (70 μm in blue and 160 μm in red) image from the Hi-GAL survey of the complex environment of WRAY 15-751 (the blue spot at the center of the image marked with a white arrow). The size of the image is 1°× 1°. North is up and east is to the left. A bubble ~25′ in diameter and offset from the star is tentatively seen around WRAY 15-751. |
| In the text | |
 |
Fig. 5 Footprint of the PACS spectral field of view on the image of the nebula at 70 μm. Each number pair is the label of a specific spaxel. The size of the image is 1′ × 1′. North is up and east is to the left. |
| In the text | |
 |
Fig. 6 PACS spectrum of WRAY 15-751, integrated over the nine central spaxels. Indicated are the lines [Niii], [Oi], [Oiii], [Nii] and [Cii]. The continuum shape below 55 μm results from a yet-imperfect spectral response function correction, while above 190 μm it results from a light leak, from the second diffraction order of the grating in the first one. The different bands are indicated with different colors. |
| In the text | |
 |
Fig. 7 Infrared spectrum of WRAY 15-751 from data collected at different epochs: IRAS LRS from 8 to 22 μm (1983, magenta), ISOPHOT from 2.5 to 11 μm and ISO LWS from 45 to 140 μm (1996, green), Herschel-PACS from 55 to 180 μm (2010, blue). The ISOPHOT data at λ < 5 μm are corrected for extinction using E(B − V) = 1.8. At λ > 100 μm, the flux density from ISO LWS is not reliable, the LWS aperture is too small for the ISO PSF. Color-corrected photometric measurements are superimposed (red symbols). The spectrum at λ < 5 μm comes from the central star, the bump at ~10 μm from silicates and very small out-of-equilibrium dust grains, and the spectrum at λ > 20 μm from the bulk of the dust shell. Results of the 2-Dust model fitting are illustrated. Top: best fits of the IRAS/ISO data assuming R⋆/Teff = 80/18 000, amin/amax = 0.05/1.5 (solid line) and amin/amax = 0.2/0.5 (dashed line). Bottom: fits of the AKARI/Herschel data using the same dust shell properties but with R⋆/Teff = 320/9000. Results for a lower-luminosity star R⋆/Teff = 240/9000 and amin/amax = 0.2/0.5 are also displayed (dotted line). |
| In the text | |
 |
Fig. 8 Top left: the 1′ × 1′ image of the nebula around WRAY 15-751 observed with PACS at 70 μm. North is up and east to the left. Top right: the synthetic image computed with 2-Dust using rin = 7″ and rout = 21″ and convolved with the PACS PSF. Bottom: East-west cuts through the central part of the nebula, observed (black) and synthetic (red). The upper plots correspond to the 70 μm image, the lower ones to the 100 μm image. |
| In the text | |
 |
Fig. 9 Correlation between the [C ii] 158 μm and [N ii] 122 μm line fluxes for each spaxel where these two lines are detected. |
| In the text | |
 |
Fig. 10 Temperature-density PDR diagnostic diagram. The grid of flux ratios F[O i] 63/F[O i] 146 versus |
| In the text | |
 |
Fig. 11 Evolutionary path in the HR diagram of a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The thicker lines emphasize the part of the tracks compatible with the measurements (cf. Figs. 12 and 13). For clarity, the tracks are stopped at the beginning of the blue loop (data point No 210 in Ekström et al. 2012). |
| In the text | |
 |
Fig. 12 Evolution of the N/O versus the C/O surface abundance ratios for a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The dashed lines correspond to the values measured for the inner shell around WRAY 15-751, with their errors. The thicker lines emphasize the part of the tracks compatible with the measurements. For clarity, the tracks are stopped at the beginning of the blue loop (data point No 210 in Ekström et al. 2012). |
| In the text | |
 |
Fig. 13 Evolution of the N/O surface abundance ratio as a function of the mass-loss rate for a 40 M⊙ star of solar metallicity and for initial rotation rates v/vcrit from 0 to 0.4, using the models of Ekström et al. (2012). The dashed lines correspond to the values measured for the inner shell around WRAY 15-751, with their errors. The thicker lines emphasize the part of the tracks compatible with the measurements. For clarity, the tracks are stopped at the beginning of the blue loop (data point no 210 in Ekström et al. 2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\hbox{$F_{[\ion{O} {i}]63}/F_{[\ion{C}{ii}]158} ^{\mathrm{PDR}}$}](/articles/aa/full_html/2013/09/aa21853-13/aa21853-13-eq225.png)