EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 557 (September 2013) A&A, 557 (2013) A87 Full HTML
Free Access
Issue
A&A
Volume 557, September 2013
Article Number A87
Number of page(s) 12
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201321753
Published online 06 September 2013

© ESO, 2013

1. Introduction

Many close binaries are believed to have encountered an unstable phase of mass transfer leading to a common-envelope (CE) phase (Paczynski 1976). The CE phase is a short-lived phase in which the envelope of the donor star engulfs the companion star. Subsequently, the companion and the core of the donor star spiral inward through the envelope. If sufficient energy and angular momentum is transferred to the envelope, it can be expelled, and the spiral-in phase can be halted before the companion merges with the core of the donor star. The CE phase plays an essential role in binary star evolution and, in particular, in the formation of short-period systems that contain compact objects, such as post-common-envelope binaries (PCEBs), cataclysmic variables (CVs), the progenitors of Type Ia supernovae, and gravitational wave sources, such as double white dwarfs.

Despite of the importance of the CE phase and the enormous efforts of the community, all effort so far have not been successful in understanding the phenomenon in detail. Much of the uncertainty in the CE phase comes from the discussion of which and how efficient certain energy sources can be used to expel the envelope (e.g. orbital energy and recombination energy, Iben & Livio 1993; Han et al. 1995; Webbink 2008), or if angular momentum can be used (Nelemans et al. 2000; van der Sluys et al. 2006). Even though hydrodynamical simulations of parts of the CE phase (Ricker & Taam 2008, 2012; Passy et al. 2012) have become possible, simulations of the full CE phase are not feasible yet due to the wide range in time and length scales that are involved (see Taam & Sandquist 2000; Taam & Ricker 2010; Ivanova et al. 2013, for reviews).

In this study, a binary population synthesis (BPS) approach is used to study CE evolution in a statistical way. BPS is an effective tool to study mechanisms that govern the formation and evolution of binary systems and the effect of a mechanism on a binary population. Particularly interesting for CE research is the population of PCEBs (defined here as close, detached WDMS-binaries with periods of less than 100d that underwent a CE phase) for which the evolution of the binary and its stellar components is relatively simple. Much effort has been devoted to increase the observational sample and to create a homogeneously selected sample of PCEBs (e.g. Schreiber & Gänsicke 2003; Rebassa-Mansergas et al. 2007; Nebot Gómez-Morán et al. 2011).

In recent years, it has become clear that there is a discrepancy between PCEB observations and BPS results. BPS studies (de Kool & Ritter 1993; Willems & Kolb 2004; Politano & Weiler 2007; Davis et al. 2010) predict the existence of a population of long period PCEBs (>10 d) that have not been observed (e.g. Nebot Gómez-Morán et al. 2011). It is unclear if the discrepancy is caused by a lack of understanding of binary formation and evolution or by observational biases. This study aims to clarify this by considering the observational selection effects that are inherent to the PCEB sample into the BPS study. Using the BPS code SeBa, a population of binary stars is simulated with a realistic model of the Galaxy and magnitudes and colors of the stellar components. In Sect. 2, we describe the BPS models, and in Sect. 3, we present the synthetic PCEB populations generated by the models. In Sect. 3.1, we incorporate the selection effects in our models that are specific to the population of PCEBs found by the SDSS. Comparing this to the observed PCEB sample (Nebot Gómez-Morán et al. 2011; Zorotovic et al. 2011a) leads to a constrain on CE evolution, which will be discussed in Sect. 4.

2. Method

2.1. SeBa – a fast stellar and binary evolution code

We employ the binary population synthesis code SeBa (Portegies Zwart & Verbunt 1996; Nelemans et al. 2001; Toonen et al. 2012) to simulate a large amount of binaries. We use SeBa to evolve stars from the zero-age main sequence until remnant formation. At every timestep, processes as stellar winds, mass transfer, angular momentum loss, common envelope, magnetic braking, and gravitational radiation are considered with appropriate recipes. Magnetic braking (Verbunt & Zwaan 1981) is based on Rappaport et al. (1983). A number of updates to the code has been made since Toonen et al. (2012), which are described in Appendix A. The most important update concerns the tidal instability (Darwin 1879; Hut 1980) in which a star is unable to extract sufficient angular momentum from the orbit to remain in synchronized rotation, leading to orbital decay and a CE phase. Instead of checking at RLOF, we assume that a tidal instability leads to a CE phase instantaneously when tidal forces become affective i.e. when the stellar radius is less than one-fifth of the periastron distance.

SeBa is incorporated in the Astrophysics Multipurpose Software Environment, or AMUSE. This is a component library with a homogeneous interface structure and can be downloaded for free at amusecode.org (Portegies Zwart et al. 2009).

2.2. The initial stellar population

The initial stellar population is generated on a Monte Carlo based approach, according to appropriate distribution functions. These are (1)where Mi is the initial mass of the more massive star in a specific binary system, the initial mass ratio is defined as qi ≡ mi/Mi with mi the initial mass of the less massive star, ai is the initial orbital separation and ei the initial eccentricity. Furthermore, KTG93 represents Kroupa et al. (1993), A83 Abt (1983), and H75 Heggie (1975).

2.3. Common-envelope evolution

For CE evolution, two evolutionary models are adopted that differ in their treatment of the CE phase. The two models are based on a combination of different formalisms for the CE phase. The α-formalism (Tutukov & Yungelson 1979) is based on the energy budget, whereas the γ-formalism (Nelemans et al. 2000) is based on the angular momentum balance. In model αα, the α-formalism is used to determine the outcome of the CE phase. For model γα, the γ-prescription is applied unless the CE is triggered by a tidal instability rather than dynamically unstable Roche lobe overflow (see Toonen et al. 2012).

In the α-formalism, the α-parameter describes the efficiency with which orbital energy is consumed to unbind the CE according to 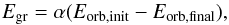(2)where Eorb is the orbital energy and Egr is the binding energy of the envelope. The orbital and binding energy are as shown in Webbink (1984), where Egr is approximated by 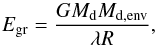(3)where Md is the donor mass, Md,env is the envelope mass of the donor star, R is the radius of the donor star, and in principle, λ depends on the structure of the donor (de Kool et al. 1987; Dewi & Tauris 2000; Xu & Li 2010; Loveridge et al. 2011).

Table 1

Common-envelope prescription and efficiencies for each model.

In the γ-formalism, γ-parameter describes the efficiency with which orbital angular momentum is used to expel the CE according to 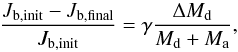(4)where Jb,init and Jb,final are the orbital angular momentum of the pre- and post-mass transfer binary respectively, and Ma is the mass of the companion.

The motivation for the γ-formalism comes from the observed distribution of double WD systems that could not be explained by the α-formalism nor stable mass transfer for a Hertzsprung gap donor star (see Nelemans et al. 2000). The idea is that angular momentum can be used for the expulsion of the envelope, when there is a large amount of angular momentum available such as in binaries with similar-mass objects. However, the physical mechanism remains unclear.

In the standard model in SeBa, we assume γ = 1.75 and αλ = 2, based on the evolution of double WDs (Nelemans et al. 2000, 2001). However lower CE efficiencies have been claimed (Zorotovic et al. 2010), and therefore, we construct a second set of models assuming αλ = 0.25. See Table 1 for an overview of the models that are used in this paper.

2.4. Galactic model

thumbnail Fig. 1

Color−color diagrams for the full population of PCEBs with orbital periods less than 100 d and for a limiting magnitude of g = 15−20 for model αα2. On the left, it shows the u−g vs. g−r diagram, in the middle, the g−r vs. r−i diagram, and on the right, the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars.

thumbnail Fig. 2

Color−color diagrams for the visible population of PCEBs for model αα2. On the left it shows the u−g vs. g−r diagram, in the middle the g−r vs. r−i diagram and on the right the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars.

When studying populations of stars that are several Gyr old on average, the star formation history of the Galaxy becomes important. We follow Nelemans et al. (2004) in taking a realistic model of the Galaxy based on Boissier & Prantzos (1999). In this model, the star formation rate is a function of time and position in the Galaxy. It peaks early in the history of the Galaxy and has decreased substantially since then. We assume the Galactic scale height of our binary systems to be 300 pc (Roelofs et al. 2007b,a). The resulting population of PCEBs at a time of 13.5 Gyr is analysed.

2.5. Magnitudes

For WDs, the absolute magnitudes are taken from the WD cooling curves of pure hydrogen atmosphere models (Holberg & Bergeron 2006; Kowalski & Saumon 2006; Tremblay et al. 2011, and references therein1). These models cover the range of temperatures of Teff = 1500−100   000 K and of surface gravities of log = 7.0−9.0 for WD masses between 0.2 and 1.2 M⊙. For MS stars of spectral type A0-M9, we adopt the absolute magnitudes as given by Kraus & Hillenbrand (2007). Overall, the colours correspond well to colours from other spectra, such as the observational spectra from Pickles (1998, with colors by Covey et al. 2007 and synthetic spectra (Munari et al. 2005) from Kurucz’s code (Kurucz & Avrett 1981; Kurucz 1993). For both the MS stars and WDs, we linearly interpolate between the brightness models. For MSs and WDs that are not included in the grids, the closest gridpoint is taken.

To convert absolute magnitudes to apparent magnitudes, the distance from the sun is used as given by the Galactic model. Furthermore, we adopt the total extinction in the V filter band from Nelemans et al. (2004), which is based on Sandage’s extinction law (Sandage 1972). We assume the Galactic scale height of the dust to be 120 pc (Jonker et al. 2011). To evaluate the magnitude of extinction in the different bands of the ugriz-photometric system, we use the conversion of Schlegel et al. (1998), which are based on the extinction laws of Cardelli et al. (1989) and O’Donnell (1994) with RV = 3.1.

2.6. Selection effects

We assume that WDMS binaries can be observed in the magnitude range 15−20 in the g-band. As WDs are inherently blue and MS are inherently red, we assume that WDMS binaries can be distinguished from single MS stars if 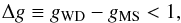(5)where gWD and gMS are the magnitude in the g band of the WD and the MS respectively, and distinguished from single WDs if 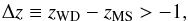(6)where zWD and zMS are the z band magnitudes of the WD and the MS respectively. The g-band is used instead of the u-band, because the u−g colours of late-type MS stars are fairly uncertain (Munari et al. 2005; Bochanski et al. 2007). The effect of (varying) the cuts will be discussed in forthcoming sections.

3. Results

Figures 1 and 2 show the full and visible population of PCEBs in ugriz color−color space for model αα2. The full population of PCEBs lies close to the unreddened MS. Most PCEB systems will be observed as apparent single MS stars. On the other hand, the visible population of PCEBs is by construction clearly distinguished from the MS in the u−g vs. g−r color−color diagram. In the r−i vs. i−z diagram and g−r vs. r−i diagram, most visible systems lie close to the MS indicating that the WD components are generally cold (see Augusteijn et al. 2008, Fig. 2). The u−g vs. g−r diagram also shows that the majority of systems is relatively red confirming that samples of PCEBs that are discovered by their blue colors (e.g. Schreiber & Gänsicke 2003), are severely biased and incomplete. The color−color diagrams for model αα1, model γα1, and model γα2 are very comparable to those of model αα2.

The space density of visible PCEBs follows directly from our models where the position of the PCEBs in the Galaxy is given by the Galactic model (see Sect. 2.4). The space density (see Table 2) is calculated in a cylindrical volume with height above the plane of 200 pc and radii of 200 pc and 500 pc centred on the Sun. At small distances (≲100 pc) from the Sun, our data is noisy due to low number statistics, and at larger distances, the PCEB population is magnitude limited. The observed space density of PCEBs (6−30) × 10-6   pc-3 (Schreiber & Gänsicke 2003) is fairly uncertain and consistent with all BPS models.

Table 2

Space density of visible PCEBs within 200 and 500 pc from the Sun in 10-6   pc-3 for different models of CE evolution.

Figures 3−5 show the distribution of MS mass, WD mass, and orbital period of the visible population of PCEBs. Model γα1, αα1 and γα2 show PCEB systems with periods between 0.05−100 d, whereas model αα2 shows a narrower period range of about 0.05−10 d. Few PCEBs exist at periods of less than a few hours, as these systems come in contact and possibly evolve into CVs. Figure 4 shows a relation between MS and WD mass that is different for each model. The masses of WDs in visible PCEBs are roughly between 0.2 and 0.8 M⊙; most WDs have either helium (He) or carbon-oxygen (CO) cores. Figure 5 shows that the model γα1 and model γα2 periods at a given WD mass can be longer than for model αα1 and model αα2. This is because the CE phase leads to a strong decrease in the orbital separation according to the α-prescription, while this is not necessarily true in the γ-prescription.

Varying the cuts that determine which PCEBs are visible (see Sect. 2.6), does not change our results much. The limiting magnitude of g = 15−20 does not affect the relations between WD mass, MS mass, and period, but it can effect the space density of visible PCEBs. If the sensitivity of the observations increases to g = 21, the space density within 200 pc and 500 pc increases by about 15−30% and 30−50% respectively.

The cut that distinguishes WDMS from apparent single WDs (see Eq. (6)) has a small effect on the population of PCEBs. If we assume a more conservative cut, less massive MS stars are visible at a given WD temperature. Varying the cut between Δz > 0 and Δz > −2 does not affect the space density significantly. The distribution of periods is not affected. Making a cut in the i-band instead of the z-band has a similar effect on the visible PCEB population as varying Δz.

Varying the cut that distinguishes WDMS from apparent single MS stars (see Eq. (5)) is important for the space density and the MS mass distribution of PCEBs, as the WD is less bright than the secondary star for most systems. If a more conservative cut is appropriate, i.e. Δg > 0, the space density decreases by about 30−40%, and the less massive MS stars are visible at a given WD temperature. The space density increases by 40−50% when assuming Δg > 2. Varying the cut between Δg > 0 and Δg > 2 affects the maximum MS mass in PCEBs by ±0.1 M⊙. Most importantly, the correlations of MS mass with WD mass and period are, however, not affected. The effect on the visible PCEB population of making a cut in the u-band is comparable to that in the g-band.

thumbnail Fig. 3

Visible population of PCEBs as a function of orbital period and mass of the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.

thumbnail Fig. 4

Visible population of PCEBs as a function of mass of the WD and the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.

thumbnail Fig. 5

Visible population of PCEBs as a function of orbital period and WD mass for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.

3.1. The SDSS PCEB sample

thumbnail Fig. 6

Color−color diagrams for the visible population of PCEBs in the SDSS for model αα2. On the left, it shows the u−g vs. g−r diagram, in the middle, the g−r vs. r−i diagram, and on the right, the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars. The color−color diagrams are very comparable to those of model αα1, model γα1, and model γα2.

thumbnail Fig. 7

Visible population of PCEBs in the SDSS as a function of orbital period and mass of the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

thumbnail Fig. 8

Visible population of PCEBs in the SDSS as a function of mass of the WD and the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

thumbnail Fig. 9

Visible population of PCEBs in the SDSS as a function of orbital period and WD mass for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

To compare our models with the results of Nebot Gómez-Morán et al. (2011) and Zorotovic et al. (2011b), we place two additional constraints on the visible population of PCEBs in comparison to those described in Sect. 2.6. Following these authors, we only consider WDs that are hotter than 12 000 K and MS stars of the stellar classification M-type. However, there is a discrepancy in the relation between spectral type and stellar mass used in those papers and that of Kraus & Hillenbrand (2007) due to the uncertainty in stellar radii of low-mass stars. Where the former (based on Rebassa-Mansergas et al. 2007) finds that M-type stars have masses of less than 0.472 M⊙, Kraus & Hillenbrand (2007) find that the M-dwarf mass range is extended to 0.59 M⊙. To do a consistent comparison, we will adopt the relation between spectral type and stellar mass of Rebassa-Mansergas et al. (2007) and the relation between magnitudes and spectral types of Kraus & Hillenbrand (2007). The effect of this discrepancy is further discussed in the Sect. B.

Comparing the color−color diagrams of the visible PCEB population (see Fig. 2) with that of the fraction that is visible in the SDSS (see Fig. 6) shows that the observed population is biased toward late-type secondaries and hot WDs (see Augusteijn et al. 2008, Fig. 2). The bias against systems containing early-type secondaries is in accordance with the findings of Rebassa-Mansergas et al. (2010) for the WDMS population from the SDSS.

Nebot Gómez-Morán et al. (2011) studied the observed period distribution of observed PCEBs. They find the distribution follows approximately a log-normal distribution that peaks at about 10.3 h and ranges from 1.9 h to 4.3 d (see points in Fig. 7). They also find that the period distribution of the PCEBs found by the SDSS is very comparable to that of previously known PCEBs. However, Nebot Gómez-Morán et al. (2011) point out that the dearth of long-period systems is in contradiction with the results of binary population synthesis studies (see de Kool & Ritter 1993; Willems & Kolb 2004; Politano & Weiler 2007; Davis et al. 2010) indicating a low α-CE efficiency, if selection effects do not play a role. Figure 7 shows that the selection effects does not cause a dearth of PCEBs with long periods in model αα1, γα1, and γα2. Only the results of model αα2 with a reduced α-CE efficiency are consistent with the observed period distribution.

Another observational constraint for our models can come from the relative population sizes. Although the space density of PCEBs is not known very accurately, it has become possible to determine the fraction of PCEBs amongst WDMS systems of all periods. From SDSS observations, Nebot Gómez-Morán et al. (2011) find that the fraction of PCEBs amongst unresolved WDMS with M-dwarf companions is 27 ± 2%. Wide WDMS that are blended or fully resolved are not included in their sample. To compensate for this effect, we exclude those WDMS systems from our WDMS sample for which the angular size of an object is larger than twice the seeing, where the size of the object is approximated by the orbital separation, and where the distance to the WDMS is given by the Galactic model (see Sect. 2.4). The seeing limit is varied between the median seeing of SDSS of 1.4′′ and an upper limit for over 90% of the SDSS data of 2′′. Furthermore, the SDSS PCEB identification method is based on radial velocity measurements, and, as such dependent on the number of spectra taken, the temporal sampling of the measurements and the accuracy of the radial velocity measurement. Nebot Gómez-Morán et al. (2011) find that their identification method is not sensitive to systems with periods of more than a few tens of days, however, the observed period distribution that cuts off at a few days is not dramatically affected by this bias. To account for the long-period bias, we exclude long-period PCEBs from the PCEB sample (but include them in the WDMS sample). As the sensitivity of the SDSS PCEB identification method depends on the orbital period of the system (see Fig. 10 of Nebot Gómez-Morán et al. 2011), the limiting period is varied between 10 d and 50 d. The fraction of visible PCEBs amongst unresolved WDMS for all models are consistent with the observed value within a factor of two (see Table 3). Based on a sample of WDs with near-infrared emission observed with the Hubble Space Telescope, Farihi et al. (2010) also found a ratio of about 25%.

Zorotovic et al. (2011b) studied the mass dependencies of the orbital period distribution and found that systems containing high-mass secondaries tend to have longer orbital periods. Figure 7 shows a similar trend in our models, however due to the period distribution model αα2 reproduces the observations best. The relation between WD and secondary mass cannot be used to differentiate between CE theories, because the models show very similar distributions (see Fig. 8), which is contrary to the complete visible PCEB sample (see Fig. 4). However, the models match well to the observed systems in Fig. 8 for WD masses less than about 0.7 M⊙. The models show a lack of PCEBs with massive WD components (see Sect. 4 for a discussion). Disregarding WDs with masses more than about 0.8 M⊙, Fig. 9 shows a good match between the observations and the predictions of model αα2 regarding the distribution of orbital period versus WD mass. The discrepancy between the observed period distribution and the synthetic ones from model αα1, model γα1, and model γα2 is mainly found in PCEBs with helium WD components. For He-core WDs (i.e. MWD < 0.5 M⊙), all models show an increase in orbital period with WD mass. Although the observations are not in contradiction with this, statistical evidence of this relation in the current observed sample has not been found (Zorotovic et al. 2011b). In addition, less than half of the observed systems contains a He WD, which is in contradiction with our models for which at least 70% of PCEB WDs are helium rich (see Table 4).

3.2. Variable CE efficiency

Next, we consider the possibility that CE evolution occurs differently for different types of donor stars or types of instabilities. We differentiate between red giant (RG) donors and asymptotic giant branch (AGB) donors and between dynamical (DY) and tidal (TI) instabilities. The majority of PCEBs is formed through a dynamical instability initiated by a RG (see Table 5, RG-DY). This evolutionary path is not much affected by processes other than the CE phase, as the evolution is relatively simple: for example the donor stars do not suffer from superwinds as AGB stars. For this path, only the PCEBs from model αα2 with a reduced CE efficiency of αλ = 0.25 are consistent with the observed period distribution and its mass dependencies. Any other CE model produces a high number of PCEBs at periods larger than 10 d.

Subsequently, we study CE evolution in the other evolutionary channels with two hypotheses. First, we assume that CE interactions with red giant donors suffer from a low CE efficiency and that those with AGB donors suffer from a high CE efficiency (RG-DY and RG-TI according to model αα2, AGB-DY and AGB-TI according to model γα1 or αα1). However, the PCEB population from this hypothesis does not reproduce the observed period and mass distributions significantly better or worse than model αα2. The percentage of systems containing a He WD improves slightly to about 60% and 50% for AGB-DY and AGB-TI according to model γα1 and αα1 respectively. The second hypothesis is that all systems evolving through dynamical instabilities suffer from low CE efficiency and that systems evolving through a tidal instability do not (RG-DY and AGB-DY according to model αα2 and RG-TI and AGB-TI according to model αα12). However, also this hypothesis does not lead to a significant improvement (or worsening) in the period and mass distributions compared to model αα2. The percentage of systems containing a He WD is about 75%. Concluding, at current we cannot constrain the CE evolution or efficiencies of the evolutionary channels RG-TI, AGB-DY and AGB-TI, although the percentage of systems with helium WDs improves when assuming that the CE efficiency is lower when the CE phase is initiated by a RG star than for an AGB star.

Table 3

Fraction of visible PCEBs amongst unresolved WDMS for different models of CE evolution.

4. Discussion and conclusion

We have studied common-envelope evolution by theoretical modelling of the formation and evolution of post-common-envelope binaries with constraints from observations. We have considered four models of CE evolution that differ in the CE prescription and CE efficiency. The SDSS has played an important role in providing the largest and most homogeneous sample of PCEBs, however, the visible population of PCEBs is still affected by strong selection effects. We presented here the first binary population models that consider the selection effects that are inherent to the population of visible PCEBs.

We find that although selection effects are important, e.g. for the secondary mass distribution, they do not lead to a dearth of long-period systems as is observed (e.g., Nebot Gómez-Morán et al. 2011). Furthermore, we find that the main evolutionary path of visible PCEBs in the SDSS consists of a CE phase caused by a red giant that fills its Roche lobe in a dynamically unstable manner. Most importantly, we find that the efficiency for this channel at which orbital energy can be used to expel the envelope in the CE phase is low – to reproduce the observed period distribution with few systems at 10−100 d. Secondary evolutionary paths cannot be constrained at present; low and high CE efficiencies for energy consumption or angular momentum consumption are consistent with observations.

Besides the distribution of orbital periods, the results from the model with the reduced α-CE efficiency are consistent with the observed space density, the fraction of PCEBs amongst WDMS, and the WD mass vs. MS mass distribution, however, the fraction of PCEBs containing He WDs is overestimated. When assuming that the CE efficiency is higher when the CE phase is initiated by an AGB star rather than a RG star, the fraction of He WDs in PCEBs is in better agreement with the observations. At face value, an overestimation of the fraction of He WDs companions in PCEBs exaggerates the importance of the RG-DY channel, however, the conclusion about the low CE efficiency for RG systems is based on the short periods that are observed for PCEBs with He WD components.

Table 4

Percentage of helium WDs and carbon/oxygen (including oxygen/neon) WDs in visible PCEBs in the SDSS for different models of CE evolution.

Table 5

Percentage of visible PCEBs in the SDSS from different evolutionary paths for different models of CE evolution.

The fraction of He WDs amongst PCEBs depends on the CE efficiency as shown by Table 4 (see also de Kool & Ritter 1993; Willems & Kolb 2004) and the initial distribution of mass ratios and orbital separations. Willems & Kolb (2004) showed that the effect of the CE efficiency and the initial mass ratios on the He-WD ratio for the full PCEB population cannot be distinguished, but that the effect of the initial mass ratio distribution for low CE efficiencies (αλ = 0.1) becomes negligible. Furthermore the He WD fraction is affected by the cooling curves of WDs. We have adopted the cooling curves of Holberg & Bergeron (2006); Kowalski & Saumon (2006); Tremblay et al. (2011) that assume a carbon and carbon-oxygen composition of the core. However, He-core WDs for a given stellar mass have a longer cooling time as the specific heat is larger (Althaus, Miller Bertolami, priv. comm.). If we systematically underestimated the brightness of He WDs compared to CO WDs, the synthetic fraction of He WDs in visible PCEBs would be even higher.

thumbnail Fig. B.1

Visible population of PCEBs in the SDSS assuming the spectral type-mass relation of Kraus & Hillenbrand (2007) for model αα2.

So far, we have studied the CE efficiency (α) assuming a constant envelope-structure parameter (λ). In other words we studied the combination αλ. While the CE efficiency is not well known, the structure parameter has been calculated by several studies (Dewi & Tauris 2000; Xu & Li 2010; Loveridge et al. 2011). For low mass stars of M < 3 M⊙, on average at the onset of the CE phase λ ≈ 1.1−1.3 on the RG and λ ≈ 0.5−0.8 on the AGB (van der Sluys et al. 2010, including internal energy in the envelope binding energy). Therefore, our result of a small value for αλ is not due to a small value for λ; the CE efficiency is low.

The SDSS has observed six (possibly eight) PCEBs with high WD masses of more than 0.8 M⊙. The number of massive WDs is small, but they represent about 10% of the observed sample. Although our models do create massive WDs with M-dwarf companions, the relative number to other PCEB systems is not reproduced by our models. If the observed number of these systems increases to a statistical significant amount, it would be interesting to look in more detail in the evolution of these systems, because it is hard to envision how to form a high number of these systems with the current IMF and initial mass ratio distribution. It is particularly interesting in the context of CV-progenitors, as WDs in CVs are on average significantly more massive than single WDs (e.g. Warner 1995; Savoury et al. 2011).

Constraints on CE evolution other than this study have come from reconstruction methods of the evolution of observed binaries. From observed PCEBs, Zorotovic et al. (2010) deduces a value of α = 0.2−0.3 for the CE efficiency when including the internal energy of the envelope into the energy balance equation. They find that the internal energy is important for CE evolution when the CE phase is initiated by AGB donors, but the effect is not significant for RG donors. We therefore conclude that our results are consistent with those of Zorotovic et al. (2010).

From reconstructing the evolution of post-CE binaries (mostly pre-SDSS PCEBs and some SdB+MS binaries), De Marco et al. (2011) found that the CE efficiency decreases with mass ratio (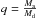). The effect, however, has not been observed in the SDSS PCEB population (Zorotovic et al. 2011b).

Portegies Zwart (2013) reconstructs the formation and evolution of the cataclysmic variable HU Aquarius. The two planets that orbit this CV play an important role in constraining the CE efficiency. Portegies Zwart (2013) find a low CE efficiency of αλ = 0.45 ± 0.17 for this system consistent with our conclusion.

From reconstructing the evolution of double He WDs, Nelemans et al. (2000) deduces two constraints on CE evolution. First, CE evolution occurs very efficiently (i.e. αλ = 2) in a binary system with a giant donor and a WD companion. The physical interpretation of this is that more energy sources than orbital energy are used to expel the envelope. An example of a possible energy source is the internal energy of the envelope including recombination energy (e.g. Han et al. 1995; Webbink 2008). Second, neither the α-CE prescription nor stable mass transfer is able to explain the observations for the first phase of mass transfer in the evolution of progenitor systems of double He WDs, and therefore, Nelemans et al. (2000) proposed the γ-prescription. Furthermore, Nelemans et al. (2001) showed in a BPS study that the population of Galactic double WDs is well modelled when assuming γ = 1.75 and αλ = 2, whereas the standard α-prescription does not. Recently, Woods et al. (2012, see also Woods et al. 2010 suggested a new evolutionary model to create double WDs that involves stable, non-conservative mass transfer between a RG and a MS star. The effect on the orbit is a modest widening with a result alike to the γ-description.

Summarizing, the CE phase is a crucially important phase in the formation and evolution of binaries, however, it is not well understood. BPS and evolutionary reconstruction studies have lead to valuable constraints on CE evolution that contribute to the formation of a coherent picture of CE evolution over mass ratios and stellar types involved in the CE phase. In our option, the emerging picture of CE evolution with non-degenerate companions thus far is that:

  • in approximately equal mass binaries that lead to the formation ofdouble WDs, mass transfer leads to a modest widening of theorbit;

  • in binaries with low mass ratios (q ≈ 0.2−0.5) that lead to the formation of PCEBs, CE evolution leads to a strong contraction of the orbital separation;

  • in binaries with extreme low mass ratios (q ≲ 0.2) the CE phase is caused by a tidal instability rather than a dynamical instability and the CE phase might evolve differently for that reason.

2

Note that model γα1 is identical to model αα1 for systems evolving through a tidal instability.

Acknowledgments

We thank Kars Verbeek, Simo Scaringi, and Kevin Covey for very helpful discussions on colours and magnitudes of main-sequence stars. This work was supported by the Netherlands Research Council NWO (grant VIDI [# 639.042.813]) and by the Netherlands Research School for Astronomy (NOVA).

References

  1. Abt, H. A. 1983, ARA&A, 21, 343 [Google Scholar]
  2. Augusteijn, T., Greimel, R., van den Besselaar, E. J. M., Groot, P. J., & Morales-Rueda, L. 2008, A&A, 486, 843 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Berger, D. H., Gies, D. R., McAlister, H. A., et al. 2006, ApJ, 644, 475 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bochanski, J. J., West, A. A., Hawley, S. L., & Covey, K. R. 2007, AJ, 133, 531 [NASA ADS] [CrossRef] [Google Scholar]
  5. Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
  8. Covey, K. R., Ivezić, Ž., Schlegel, D., et al. 2007, AJ, 134, 2398 [NASA ADS] [CrossRef] [Google Scholar]
  9. Darwin, G. 1879, Phil. Trans. Roy. Soc., 170, 447 [Google Scholar]
  10. Davis, P. J., Kolb, U., & Willems, B. 2010, MNRAS, 403, 179 [NASA ADS] [CrossRef] [Google Scholar]
  11. de Kool, M., & Ritter, H. 1993, A&A, 267, 397 [NASA ADS] [Google Scholar]
  12. de Kool, M., van den Heuvel, E. P. J., & Pylyser, E. 1987, A&A, 183, 47 [NASA ADS] [Google Scholar]
  13. De Marco, O., Passy, J.-C., Moe, M., et al. 2011, MNRAS, 411, 2277 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dewi, J. D. M., & Tauris, T. M. 2000, A&A, 360, 1043 [NASA ADS] [Google Scholar]
  15. Farihi, J., Hoard, D. W., & Wachter, S. 2010, ApJS, 190, 275 [NASA ADS] [CrossRef] [Google Scholar]
  16. Han, Z., Podsiadlowski, P., & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
  17. Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hillenbrand, L. A., & White, R. J. 2004, ApJ, 604, 741 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
  20. Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hut, P. 1980, A&A, 92, 167 [NASA ADS] [Google Scholar]
  23. Iben, Jr., I., & Livio, M. 1993, PASP, 105, 1373 [Google Scholar]
  24. Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
  25. Jonker, P. G., Bassa, C. G., Nelemans, G., et al. 2011, ApJS, 194, 18 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kowalski, P. M., & Saumon, D. 2006, ApJ, 651, L137 [Google Scholar]
  27. Kraus, A. L., & Hillenbrand, L. A. 2007, AJ, 134, 2340 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kurucz, R. L. 1993, SYNTHE spectrum synthesis programs and line data [Google Scholar]
  30. Kurucz, R. L., & Avrett, E. H. 1981, SAO Special Report, 391 [Google Scholar]
  31. López-Morales, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] [Google Scholar]
  32. Loveridge, A. J., van der Sluys, M. V., & Kalogera, V. 2011, ApJ, 743, 49 [Google Scholar]
  33. Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Nebot Gómez-Morán, A., Gänsicke, B. T., Schreiber, M. R., et al. 2011, A&A, 536, A43 [CrossRef] [Google Scholar]
  35. Nelemans, G., Verbunt, F., Yungelson, L. R., & Portegies Zwart, S. F. 2000, A&A, 360, 1011 [NASA ADS] [Google Scholar]
  36. Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Nelemans, G., Yungelson, L. R., & Portegies Zwart, S. F. 2004, MNRAS, 349, 181 [NASA ADS] [CrossRef] [Google Scholar]
  38. O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
  39. Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [Google Scholar]
  40. Passy, J.-C., De Marco, O., Fryer, C. L., et al. 2012, ApJ, 744, 52 [NASA ADS] [CrossRef] [Google Scholar]
  41. Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
  42. Politano, M., & Weiler, K. P. 2007, ApJ, 665, 663 [NASA ADS] [CrossRef] [Google Scholar]
  43. Portegies Zwart, S. 2013, MNRAS, 429, L45 [NASA ADS] [Google Scholar]
  44. Portegies Zwart, S. F., & Verbunt, F. 1996, A&A, 309, 179 [NASA ADS] [Google Scholar]
  45. Portegies Zwart, S., McMillan, S., Harfst, S., et al. 2009, New A, 14, 369 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
  47. Rebassa-Mansergas, A., Gänsicke, B. T., Rodríguez-Gil, P., Schreiber, M. R., & Koester, D. 2007, MNRAS, 382, 1377 [NASA ADS] [CrossRef] [Google Scholar]
  48. Rebassa-Mansergas, A., Gänsicke, B. T., Schreiber, M. R., Koester, D., & Rodríguez-Gil, P. 2010, MNRAS, 402, 620 [NASA ADS] [CrossRef] [Google Scholar]
  49. Reimers, D. 1975, Mem. Soc. Roy. Sci. Liège, 8, 369 [Google Scholar]
  50. Ricker, P. M., & Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
  51. Ricker, P. M., & Taam, R. E. 2012, ApJ, 746, 74 [NASA ADS] [CrossRef] [Google Scholar]
  52. Roelofs, G. H. A., Groot, P. J., Benedict, G. F., et al. 2007a, ApJ, 666, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  53. Roelofs, G. H. A., Nelemans, G., & Groot, P. J. 2007b, MNRAS, 382, 685 [NASA ADS] [CrossRef] [Google Scholar]
  54. Sandage, A. 1972, ApJ, 178, 1 [NASA ADS] [CrossRef] [Google Scholar]
  55. Savoury, C. D. J., Littlefair, S. P., Dhillon, V. S., et al. 2011, MNRAS, 415, 2025 [NASA ADS] [CrossRef] [Google Scholar]
  56. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  57. Schreiber, M. R., & Gänsicke, B. T. 2003, A&A, 406, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Taam, R. E., & Ricker, P. M. 2010, New A Rev., 54, 65 [Google Scholar]
  59. Taam, R. E., & Sandquist, E. L. 2000, ARA&A, 38, 113 [NASA ADS] [CrossRef] [Google Scholar]
  60. Toonen, S., Nelemans, G., & Portegies Zwart, S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Tremblay, P.-E., Bergeron, P., & Gianninas, A. 2011, ApJ, 730, 128 [NASA ADS] [CrossRef] [Google Scholar]
  62. Tutukov, A., & Yungelson, L. 1979, in Mass Loss and Evolution of O-Type Stars, eds. P. S. Conti, & C. W. H. De Loore, IAU Symp., 83, 401 [Google Scholar]
  63. van der Sluys, M. V., Verbunt, F., & Pols, O. R. 2006, A&A, 460, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. van der Sluys, M., Politano, M., & Taam, R. E. 2010, in AIP Conf. Ser. 1314, eds. V. Kologera, & M. van der Sluys, 13 [Google Scholar]
  65. Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
  66. Warner, B. 1995, Cambridge Astrophys. Ser., 28 [Google Scholar]
  67. Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
  68. Webbink, R. F. 2008, in Astrophys. Space Sci. Lib. 352, eds. E. F. Milone, D. A. Leahy, & D. W. Hobill, 233 [Google Scholar]
  69. Willems, B., & Kolb, U. 2004, A&A, 419, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Woods, T. E., Ivanova, N., van der Sluys, M., & Chaichenets, S. 2010, in AIP Conf. Ser. 1314, eds. V. Kologera, & M. van der Sluys, 24 [Google Scholar]
  71. Woods, T. E., Ivanova, N., van der Sluys, M. V., & Chaichenets, S. 2012, ApJ, 744, 12 [NASA ADS] [CrossRef] [Google Scholar]
  72. Xu, X.-J., & Li, X.-D. 2010, ApJ, 716, 114 [NASA ADS] [CrossRef] [Google Scholar]
  73. Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
  74. Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Zorotovic, M., Schreiber, M. R., & Gänsicke, B. T. 2011a, A&A, 536, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., et al. 2011b, A&A, 536, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Population synthesis code SeBa

We present here the most important changes that we made to the population synthesis code SeBa, since Toonen et al. (2012). First, the method of modelling a tidal instability (Darwin 1879) is updated. This instability takes place in systems of extreme mass ratios in which there is insufficient orbital angular momentum to keep the stars in synchronous rotation (Hut 1980). The tidal forces that are responsible for the orbital decay are strongly dependent on the ratio of the stellar radius and the distance between the stars (Zahn 1977). Instead of checking at RLOF, we assume tidal forces are effective if the stellar radius is less than one-fifth of the periastron distance between the stars and that the orbital decay proceeds instantaneously.

In addition, the winds of hydrogen-poor helium-burning stars are updated. We adopt the formalism of Hurley et al. (2000) which consists of the maximum of the wind mass-loss of Reimers (1975) and a Wolf-Rayet-like wind-mass loss.

Finally, the responses of the radius of helium stars to mass loss are updated. The adiabatic response ζad and the thermal response ζeq (see Eqs. (A.14) and (A.18) in Toonen et al. 2012) are used to determine the stability of Roche lobe overflow. For helium MS-stars and helium hertzsprung-gap stars, we assume ζad = 4. For helium giants, ζad is based on the prescription of Hjellming & Webbink (1987). For helium hertzsprung-gap stars and helium giants, we assume ζth = −2.

Appendix B: The spectral type – mass relation

In the last decade, it has become clear that there is a discrepancy between theoretical models of and observationally determined radii and masses of low-mass stars, challenging our understanding of stellar evolution, structure, and atmospheres (see e.g. Hillenbrand & White 2004; Berger et al. 2006; López-Morales 2007; Boyajian et al. 2012). To exclude these uncertainties from the comparison with the SDSS observations (see Sect. 3.1), we have used the relation between spectral type and mass, as determined by Rebassa-Mansergas et al. (2007) and the relation between spectral type and magnitudes, as given by Kraus & Hillenbrand (2007). There is a good agreement between the effective temperatures as a function of spectral type of Rebassa-Mansergas et al. (2007) and Kraus & Hillenbrand (2007). For comparison, we show the synthetic populations of visible PCEBs in SDSS in Fig. B.1 where we assume the relation between spectral type and mass from Kraus & Hillenbrand (2007). The population is significantly extended to higher secondary masses when compared to those shown in Figs. 7 and 8.

All Tables

Table 1

Common-envelope prescription and efficiencies for each model.

In the text
Table 2

Space density of visible PCEBs within 200 and 500 pc from the Sun in 10-6   pc-3 for different models of CE evolution.

In the text
Table 3

Fraction of visible PCEBs amongst unresolved WDMS for different models of CE evolution.

In the text
Table 4

Percentage of helium WDs and carbon/oxygen (including oxygen/neon) WDs in visible PCEBs in the SDSS for different models of CE evolution.

In the text
Table 5

Percentage of visible PCEBs in the SDSS from different evolutionary paths for different models of CE evolution.

In the text

All Figures

thumbnail Fig. 1

Color−color diagrams for the full population of PCEBs with orbital periods less than 100 d and for a limiting magnitude of g = 15−20 for model αα2. On the left, it shows the u−g vs. g−r diagram, in the middle, the g−r vs. r−i diagram, and on the right, the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars.
In the text
thumbnail Fig. 2

Color−color diagrams for the visible population of PCEBs for model αα2. On the left it shows the u−g vs. g−r diagram, in the middle the g−r vs. r−i diagram and on the right the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars.
In the text
thumbnail Fig. 3

Visible population of PCEBs as a function of orbital period and mass of the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.
In the text
thumbnail Fig. 4

Visible population of PCEBs as a function of mass of the WD and the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.
In the text
thumbnail Fig. 5

Visible population of PCEBs as a function of orbital period and WD mass for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale.
In the text
thumbnail Fig. 6

Color−color diagrams for the visible population of PCEBs in the SDSS for model αα2. On the left, it shows the u−g vs. g−r diagram, in the middle, the g−r vs. r−i diagram, and on the right, the r−i vs. i−z diagram. The intensity of the grey scale corresponds to the density of objects on a linear scale. The solid line corresponds to the unreddened MS from A-type to M-type MS stars. The color−color diagrams are very comparable to those of model αα1, model γα1, and model γα2.

In the text
thumbnail Fig. 7

Visible population of PCEBs in the SDSS as a function of orbital period and mass of the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

In the text
thumbnail Fig. 8

Visible population of PCEBs in the SDSS as a function of mass of the WD and the MS star for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

In the text
thumbnail Fig. 9

Visible population of PCEBs in the SDSS as a function of orbital period and WD mass for all models: (a) model γα1, (b) model αα1, (c) model γα2, and (d) model αα2. The intensity of the grey scale corresponds to the density of objects on a linear scale. Overplotted are the observed PCEBs taken from Zorotovic et al. (2011a). Thick points represent systems that are found by the SDSS, and thin points represent previously known PCEBs with accurately measured parameters. The previously known sample of PCEBs is affected by other selection effects than the SDSS sample or the synthetic sample. Note that Ik Peg has been removed from the sample as its MS component is not an M-dwarf.

In the text
thumbnail Fig. B.1

Visible population of PCEBs in the SDSS assuming the spectral type-mass relation of Kraus & Hillenbrand (2007) for model αα2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.