| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321364 | |
| Published online | 02 September 2013 | |
The CN/C15N isotopic ratio towards dark clouds ⋆,⋆⋆
1
Université Joseph Fourier and CNRS, Institut de Planétologie et
d’Astrophysique, 38041
Grenoble, France
e-mail: Pierre.Hily-Blant@obs.ujf-grenoble.fr
2
Université Paris-Orsay and CNRS, Institut d’Astrophysique
Spatiale, 91405
Orsay,
France
3
LRA/CNRS, Observatoire de Paris & École normale
supérieure, 75005
Paris,
France
Received:
26
February
2013
Accepted:
26
June
2013
Understanding the origin of the composition of solar system cosmomaterials is a central question, not only in the cosmochemistry and astrochemistry fields, and requires various approaches to be combined. Measurements of isotopic ratios in cometary materials provide strong constraints on the content of the protosolar nebula. Their relation with the composition of the parental dark clouds is, however, still very elusive. In this paper, we bring new constraints based on the isotopic composition of nitrogen in dark clouds, with the aim of understanding the chemical processes that are responsible for the observed isotopic ratios. We have observed and detected the fundamental rotational transition of C15N towards two starless dark clouds, L1544 and L1498. We were able to derive the column density ratio of C15N over 13CN towards the same clouds and obtain the CN/C15N isotopic ratios, which were found to be 500 ± 75 for both L1544 and L1498. These values are therefore marginally consistent with the protosolar value of 441. Moreover, this ratio is larger than the isotopic ratio of nitrogen measured in HCN. In addition, we present model calculations of the chemical fractionation of nitrogen in dark clouds, which make it possible to understand how CN can be deprived of 15N and HCN can simultaneously be enriched in heavy nitrogen. The non-fractionation of N2H+, however, remains an open issue, and we propose some chemical way of alleviating the discrepancy between model predictions and the observed ratios.
Key words: ISM: abundances / ISM: clouds / ISM: general / ISM: molecules / astrochemistry
Appendices are available in electronic form at http://www.aanda.org
The reduced spectra (in FITS format) are available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/557/A65
© ESO, 2013
1. Introduction
Spectroscopic properties of the observed species and transitions.
Understanding the origin of the elements in the solar system is a crucial issue at the crossroads of astrophysics, cosmochemistry, and astrobiology. In this respect, comets play a particular role because they are considered the most ancient relics of the formation of the solar system from the protosolar nebula, 4.567 Gyr ago. If it is certain that all cometary material has an interstellar origin, what is unclear is whether there is any chemical species present in e.g. cometary ices that have remained unaltered since their incorporation into those ices. The central issue is to determine the origin of the elements that are detected in comets and interplanetary dust particles and to unveil their chemical link with the pristine interstellar matter. The detection of glycine in 81P/Wild 2 cometary samples by Elsila et al. (2009) makes the question of the presence of glycine in the interstellar medium (ISM) still a crucial one. Direct analysis of interplanetary dust particles and meteorites provides clues to the composition of the solar system (e.g. Bonal et al. 2010), but due to their thermal and physical evolution since their formation, it is not always easy to trace the origins of the cosmomaterials back to the nascent protosolar system or even to the parental dark cloud. Isotopic composition may be a better tool in this respect. Isotopic ratios have proven extremely powerful in providing quantitative constraints on the composition of the protosolar disk from which the solar system formed (Chaussidon & Gounelle 2007; Jehin et al. 2009). For carbon, the isotopic ratio 12C/13C measured in comets shows a remarkable homogeneity, with a mean value of 91 that agrees with the solar value of 90 and is also very close to the value of 70 determined in the local ISM (Milam et al. 2005; Asplund et al. 2009; Manfroid et al. 2009). For oxygen, measurements in comets lead to 16O/18O ratios between 500 and 600, which again are in good agreement with the solar and local ISM value of 500 (Wilson & Rood 1994).
However, for nitrogen, which is the next most abundant element, measurements in various environments, such as the Sun, the solar system, and the ISM, draw a much more contrasted picture. The Genesis mission has recently allowed Marty et al. (2011) to measure the nitrogen isotopic ratio in the solar wind, yielding 14N/15N = 441 ± 5 for the protosolar nebula. This value is significantly larger than the terrestrial value of 272. A review of the 14N/15N measurements in primitive matter of the solar system (Mumma & Charnley 2011) confirms the idea of a strongly variable 14N/15N ratio in the solar system. Observations of the 14N/15N ratio in protoplanetary disks may also be directly compared to the value from the Genesis mission. Unfortunately, measurements of isotopic ratios in the most evolved gas-poor disks like TW Hya (Kastner et al. 2010) are extremely difficult, except for carbon and oxygen-bearing molecular species (e.g. CO Dutrey et al. 1997, 2007), whose large abundances make their major isotopologues detectable. This is in contrast with cold and dense starless cores, where N-bearing molecules (HCN, HNC, CN, NH3, N2H+, NO) are routinely observed (Gerin et al. 1992; Crapsi et al. 2005, 2007; Hily-Blant et al. 2010b; Padovani et al. 2011), together with their 15N isotopologues (Ikeda et al. 2002; Gerin et al. 2009; Lis et al. 2010). The recent observation of N15NH+ towards the starless core L 1544 by Bizzocchi et al. (2010) leads to an isotopic ratio N2H+/N15NH+ = 446 ± 71, a value equal to that of the protosolar nebula. Similar values were obtained by Gerin et al. (2009) in other cold dense cores using NH2D, though with much larger uncertainties. These values contrast with the HCN measurements by Ikeda et al. (2002) and Lucas & Liszt (1998), who find ratios of 150 and 240 in dark and diffuse molecular gas respectively. More recently, Adande & Ziurys (2012) found similar values based on HCN and CN observations towards warm (T > 25 K) molecular clouds, with ratios from 150 to 350. Even more recently, Hily-Blant et al. (2013, hereafter HB13) report HCN isotopic ratios between 140 and 360, where the range of values is shown to reflect genuine spatial variations of the ratio. HB13 also suggest that the large variations of the 14N/15N ratio in cosmomaterials, in dark clouds, and in the more diffuse ISM may indeed be rooted in the interstellar nitrogen chemistry. The underlying idea is that there are two reservoirs of interstellar nitrogen characterized by different isotopic ratios: nitrile carriers (such as HCN) are systematically enriched in 15N with respect to the Sun’s value, whereas hydrides (such as ammonia) show values encompassing that measured in the Sun. The differential fractionation of these two reservoirs may originate in the interstellar chemistry of nitrogen. This is because nitriles essentially derive from atomic nitrogen, whereas hydrides derive from molecular nitrogen.
Because atomic and molecular nitrogen, which are presumably the main reservoirs of nitrogen, are not directly observable in the dense ISM, the determination of the bulk 14N/15N is indirect and relies on the observation of minor N-bearing molecules. To which extent the abundance ratio of two isotopologues of a given molecule is representative of the elemental isotopic ratio depends on so-called fractionation processes: the stronger these processes, the larger the departure of the molecular abundance ratio from the elemental ratio. Fractionation processes are of two types: chemical and selective photodissociation effects. The latter effect can safely be ignored in dark clouds, which are dense and shielded regions. Chemical effects are potentially important in cold gas (Watson et al. 1976; Langer et al. 1984). Regarding nitrogen, Terzieva & Herbst (2000, hereafter TH00) investigated chemical fractionation in dense and cold clouds (nH = 2×4 cm-3, T = 10 K), and found essentially no fractionation of any nitrogen-bearing molecule. This was further investigated by Charnley & Rodgers (2002), who showed, in contrast, that in situations where OH is strongly depleted from the gas-phase, there is more atomic nitrogen available for fractionation. Indeed, large fractionation levels are predicted, e.g. for NH3, at early times in their calculations. However, these models also predict strong fractionation of N2H+, which is not observed. Therefore, none of the two available models of nitrogen fractionation in dark clouds are able to reproduce the observational constraints.
The CN radical plays a peculiar role in the nitrogen chemistry because it is a mediator of the atomic-to-molecular conversion (HB13). CN is also coupled with the dominant nitriles such as HCN and HNC, which derive from atomic nitrogen. Thus, the nitrogen fractionation level of CN potentially provides interesting constraints on the fractionation pathways. In this paper, we report the detection of C15N towards two starless cores, L1544 and L1498. Put in conjunction with the N2H+ and HCN fractionation measurements available towards L1544, it is expected that these new observations will strongly constrain models.
The paper is structured as follows. In Sect. 2, we present the observations and column density derivation. In Sect. 3, we present our fractionation model, to which we compare the 14N/15N measured in CN and other molecules. The discussion is the subject of Sect. 4.
Line properties towards L1544 and L1498 and associated column density ratios from LVG calculations.
2. Observations
The N = 1–0 rotational spectrum of C15N is split into fine and
hyperfine structures, which arise from the electron spin and the I = 1/2
nuclear spin of the 15N atom. There are two groups of lines due to the fine
structure, which are distant by 300 MHz (see Table 1). The strongest hyperfine component is the 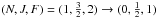 transition at 110024.590 MHz, with a
relative intensity of 0.417 (Saleck et al. 1994). The
next strongest transitions have relative intensities of 17%, with frequencies of 109689.610
and 110023.540 MHz. All six hyperfine components were observed simultanously towards L1498
and L1544 at the IRAM 30m telescope in May 2012 (≈16 h per source) under good weather
conditions. The VESPA autocorrelator was used as a spectrometer to provide us with
high-resolution spectra, namely, 20 kHz or 0.054 km s-1 at 110 GHz. The
typical receiver temperature achieved with the EMIR detectors (Carter et al. 2012) was ≈40 K, resulting in system temperatures ≈120 K.
Amplitude calibration was performed using the three-phase IRAM method typically every 10
min. Pointing and focus sessions using strong continuum sources were repeated every one and
two hours respectively. The wobbler-switching mode (140′′ throw) was used to provide us with
high-quality baselines, such that residual bandpass calibration effects could be handled
with first-order polynomial fitting. The HC15N(1–0) data reported in this paper
are taken from Hily-Blant et al. (2010b). The
13CN(1–0) rotational spectrum also presents fine and hyperfine structures,
which are described in Bogey et al. (1984). For the
present analysis, we use only the brightest hyperfine component, at 108780.201 (Hily-Blant et al. 2008). The spectroscopic properties of
both species and observed transitions are summarized in Table 1. Towards L1544, the 13CN spectrum is taken from Hily-Blant et al. (2010b), and towards L1498, it is taken
from unpublished spectra of Padovani et al. (2011).
Data reduction was done using the CLASS software (Hily-Blant
et al. 2005). All plots were done in the GILDAS environment provided by IRAM (Pety 2005). The J2000 coordinates for L1498 and L1544 are
α,δ = 04:10:51.50, 25:09:58.0 and 05:04:16.90, 25:10:47.0 respectively.
transition at 110024.590 MHz, with a
relative intensity of 0.417 (Saleck et al. 1994). The
next strongest transitions have relative intensities of 17%, with frequencies of 109689.610
and 110023.540 MHz. All six hyperfine components were observed simultanously towards L1498
and L1544 at the IRAM 30m telescope in May 2012 (≈16 h per source) under good weather
conditions. The VESPA autocorrelator was used as a spectrometer to provide us with
high-resolution spectra, namely, 20 kHz or 0.054 km s-1 at 110 GHz. The
typical receiver temperature achieved with the EMIR detectors (Carter et al. 2012) was ≈40 K, resulting in system temperatures ≈120 K.
Amplitude calibration was performed using the three-phase IRAM method typically every 10
min. Pointing and focus sessions using strong continuum sources were repeated every one and
two hours respectively. The wobbler-switching mode (140′′ throw) was used to provide us with
high-quality baselines, such that residual bandpass calibration effects could be handled
with first-order polynomial fitting. The HC15N(1–0) data reported in this paper
are taken from Hily-Blant et al. (2010b). The
13CN(1–0) rotational spectrum also presents fine and hyperfine structures,
which are described in Bogey et al. (1984). For the
present analysis, we use only the brightest hyperfine component, at 108780.201 (Hily-Blant et al. 2008). The spectroscopic properties of
both species and observed transitions are summarized in Table 1. Towards L1544, the 13CN spectrum is taken from Hily-Blant et al. (2010b), and towards L1498, it is taken
from unpublished spectra of Padovani et al. (2011).
Data reduction was done using the CLASS software (Hily-Blant
et al. 2005). All plots were done in the GILDAS environment provided by IRAM (Pety 2005). The J2000 coordinates for L1498 and L1544 are
α,δ = 04:10:51.50, 25:09:58.0 and 05:04:16.90, 25:10:47.0 respectively.
3. Results
Among the three brightest C15N lines, only the strongest, with a relative intensity of 42%, is clearly detected towards both sources. The line properties, which are derived from Gaussian fits, are summarized in Table 2. We also give the properties of the 13CN(1–0) line obtained in a similar fashion. We note a 0.1 km s-1 discrepancy between the velocities of the 13CN and C15N lines towards L1498, which could not be ascribed to any obvious technical issue. We note, however, that the uncertainty on the rest frequency reported in the Cologne Database for Molecular Spectroscopy (Müller et al. 2005) is 0.1 MHz, or 0.25 km s-1, which could account for the observed shift. New observation of the 13CN(1–0) towards L1498 should be performed to check this discrepancy. We are, however, most confident that the detected lines are 13CN and C15N, since we searched for other lines at those frequencies in public databases and could not find any likely candidate. There is a marginal detection of the 110023.540 MHz line towards L1544, which has a peak intensity of 20 mK. This intensity well matches what would be expected from the relative intensities (17% that of the strongest line), which suggests that the lines are optically thin. This secondary component is not detected towards L1498, though there is some emission at the expected velocity (within the 0.1 MHz uncertainty), with an upper limit that is consistent with the relative intensities of these two components. The analysis below is based solely on the strongest C15N line at 110024.590 MHz.
Line intensities towards L1544 are stronger than towards L1498 and are also broader by a factor ≈2. This is likely due to the L1544 lines presenting two closeby velocity components (Hily-Blant et al. 2010b), which are not resolved in the C15N spectrum. These two velocity components may be related to the collapse signature recently evidenced by the inverse P-Cygni profile of a water line (Caselli et al. 2012).
To derive column densities from the emission lines, we performed radiative transfer calculations with the RADEX code (van der Tak et al. 2007), using the large velocity gradient (LVG) approximation for an expanding sphere. The hyperfine rate coefficients for C15N and 13CN were derived from the rate coefficients computed by Kalugina et al. (2012) for CN+H2 using the infinite-order-sudden approximation (see Appendix C). We assumed that the source has a constant density and temperature and that it uniformly fills the telescope beam. The line width was held fixed at 0.2 km s-1 for L1498 and at 0.4 km s-1 for L1544. The intensity of the observed 13CN(1–0) transition was computed for varying 13CN column density (N(13CN)), H2 density (nH2), and kinetic temperatures (T). The kinetic temperatures considered span the range 7 to 12 K by steps of 1 K. Figure B.1 shows the resulting line intensity for a kinetic temperature of 10 K. A continuum range of solutions matches the observation constraints summarized in Table 2, with densities to a few 105 cm-3 and associated 13CN column densities from 6×13 to 2.5×12 cm-2. Refined calculations were then performed across this range for both 13CN and C15N. For C15N, a similar ensemble of solutions was found. Even though the density and column density are degenerate, the 13CN and C15N solutions are characterized by a constant 13CN/C15N column density ratio across the full range of solutions. Finally, refined calculations were done in which the C15N column density was such that 6 ≤ N(13CN)/N(C15N) ≤ 9. The 13CN/C15N column density ratios are 7.5 and 7 for L1544 and L1498 respectively. Although the density and column density are degenerate, equal excitation temperatures (within 0.1 K) of 3−5 K are found for the 13CN and C15N, across the full range of solutions. The 13CN line is found to be only marginally thin, with an opacity close to unity, whilst the C15N line can safely be assumed to be thin. It is of interest to note that LTE calculations using excitation temperatures in the range 3–4 K provide abundance ratios which agree reasonably well with the above LVG calculations.
On chemical grounds, both species follow similar formation and destruction routes and are thus expected to coexist spatially hence the above column density ratios are representative of their abundance ratios. If we now assume that 12CN/13CN = 12C/13C and adopt for the latter the value of 68 from Milam et al. (2005), we derive an isotopic ratio CN/C15N = 476 ± 70 in L1498 and CN/C15N = 510 ± 70 in L1544, where conservative uncertainties are applied (see Table 2). Altogehter, these values give CN/C15N = 500 ± 75.
The 13CN column density may also be compared with the H13CN column density, which is 1.8×12 cm-2 towards L1498 (Padovani et al. 2011) and 4.6×12 cm-2 towards L1544 (HB13). The 13CN:H13CN ratios are thus 0.6 and 1.7 for L1498 and L1544 respectively, which are in harmony with ratios found by Hily-Blant et al. (2010b) towards several starless cores.
4. Comparison to model predictions
4.1. Fractionation of nitriles and hydrides
The CN/C15N abundance ratios inferred in the two starless cores are thus only slightly larger than the protosolar value of 14N/15N = 441, but significantly larger the HCN/HC15N ratio derived by HB13 towards L183 and L1544, which are smaller than the protosolar ratio. In contrast, the CN/C15N ratio is similar to that measured in hydrides (NH3, N2H+) towards dark clouds by Bizzocchi et al. (2010), Gerin et al. (2009), and Lis et al. (2010). At first glance, this is at odds with the suggestion that hydrides and nitriles present different fractionation degrees (HB13), because one would have expected CN to behave more like HCN than like NH3. Yet, it must be recognized that CN plays a particular role in the chemistry of nitrogen: though it is a nitrile, it reacts directly with N to form N2 from which hydrides derive. Hence, the non-fractionation of CN may not be in contradiction with the chemical picture proposed in by HB13.
4.2. Model calculations
We thus wish to understand how the CN radical gets deprived in 15N and at the
same time HCN is enriched in 15N. To this aim, we implemented the fractionation
reactions of TH00 into a dark cloud chemical network based on Flower & Pineau des Forêts (2003), in which the nitrogen chemistry
has been fully revised. The most important changes regard the dissociative recombinations
of ions such as 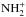 ,
, 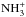 , and
, and
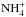 , which are critical for the production of
hydrides. Following Dislaire et al. (2012), the
dissociative recombination of N2H+ possesses a channel producing NH
with a branching ratio of ≈5% (Vigren et al.
2012). The gas phase ortho-to-para conversion of H2 through proton
exchange reactions has also been fully updated (Rist et
al. 2013, and references therein) since the rate of the key reaction
N+ + H2 depends critically on the ortho-to-para ratio of
H2 (Dislaire et al. 2012). Other
important reactions have been updated, based on the recent laboratory work of Daranlot et al. (2012). In a first approach, the
updated chemical network of Le Gal was simplified by ignoring the ortho- and para- forms
of H2,
, which are critical for the production of
hydrides. Following Dislaire et al. (2012), the
dissociative recombination of N2H+ possesses a channel producing NH
with a branching ratio of ≈5% (Vigren et al.
2012). The gas phase ortho-to-para conversion of H2 through proton
exchange reactions has also been fully updated (Rist et
al. 2013, and references therein) since the rate of the key reaction
N+ + H2 depends critically on the ortho-to-para ratio of
H2 (Dislaire et al. 2012). Other
important reactions have been updated, based on the recent laboratory work of Daranlot et al. (2012). In a first approach, the
updated chemical network of Le Gal was simplified by ignoring the ortho- and para- forms
of H2, 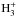 , and other nitrogen-bearing molecules.
This means that the rate of the reaction N+ + H2 was held fixed at a
value corresponding to an ortho:para ratio of H2, of 10-3, in a
similar fashion as in Dislaire et al. (2012).
, and other nitrogen-bearing molecules.
This means that the rate of the reaction N+ + H2 was held fixed at a
value corresponding to an ortho:para ratio of H2, of 10-3, in a
similar fashion as in Dislaire et al. (2012).
The chemical fractionation reactions considered by TH00 are ion-neutral reactions,
because they are the fastest and are hence expected to be the most efficient. These
reactions consist in forward and backward reactions, 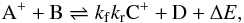 where ΔE is the zero-point
energy difference between the products and reactants, such that ΔE > 0
if the reaction is exothermic. The rates of the forward and backward reactions are related
through
where ΔE is the zero-point
energy difference between the products and reactants, such that ΔE > 0
if the reaction is exothermic. The rates of the forward and backward reactions are related
through ![\begin{eqnarray*} k_{\rm f} / k_{\rm r} = f(B,m) \exp[\Delta E / kT], \end{eqnarray*}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq63.png) where
f(B,m) is a factor that depends on the masses and
partition functions of the reactants and products. The values of ΔE and
f(B,m) are taken from the work of TH00 and are listed
in Table A.2. At temperatures smaller than
ΔE, the forward reaction proceeds much faster than the backward
reaction, thus shifting the steady-state abundances towards the reactants. In implementing
the fractionation reactions of TH00 in our network, we adopted a single Langevin rate of
10-9 cm3 s-1 for all forward reactions. The
remaining reactions involving nitrogen atoms in our network have been duplicated to
include their 15N homologue. The total number of species and reactions are 144
and 870 respectively. We do not consider freeze-out of any species in these models. We
follow the time evolution of the chemical state of a parcel of gas of density
(nH = 104 cm-3) and kinetic
temperature of 10 K, which was exposed to a cosmic-ray ionisation rate
ζ = 1.3 × -17 s-1 and shielded from the ambient UV field by
20 mag of visual extinction, such that external UV photons do not play any significant
role. However, secondary photons, which result from the fluorescence of H2
molecules excited by collisions with the electrons produced by cosmic-rays are explicitly
taken into account and are responsible for a significant fraction of the ionisation. The
initial abundances are given in Table A.1, where an
elemental isotopic ratio of nitrogen ℛ0 = 440 was adopted (Marty et al. 2011).
where
f(B,m) is a factor that depends on the masses and
partition functions of the reactants and products. The values of ΔE and
f(B,m) are taken from the work of TH00 and are listed
in Table A.2. At temperatures smaller than
ΔE, the forward reaction proceeds much faster than the backward
reaction, thus shifting the steady-state abundances towards the reactants. In implementing
the fractionation reactions of TH00 in our network, we adopted a single Langevin rate of
10-9 cm3 s-1 for all forward reactions. The
remaining reactions involving nitrogen atoms in our network have been duplicated to
include their 15N homologue. The total number of species and reactions are 144
and 870 respectively. We do not consider freeze-out of any species in these models. We
follow the time evolution of the chemical state of a parcel of gas of density
(nH = 104 cm-3) and kinetic
temperature of 10 K, which was exposed to a cosmic-ray ionisation rate
ζ = 1.3 × -17 s-1 and shielded from the ambient UV field by
20 mag of visual extinction, such that external UV photons do not play any significant
role. However, secondary photons, which result from the fluorescence of H2
molecules excited by collisions with the electrons produced by cosmic-rays are explicitly
taken into account and are responsible for a significant fraction of the ionisation. The
initial abundances are given in Table A.1, where an
elemental isotopic ratio of nitrogen ℛ0 = 440 was adopted (Marty et al. 2011).
 |
Fig. 1 Fractional abundances (left) and abundance ratios (right) of selected species. The observed isotopic ratios towards L1544 for HCN and CN, as well as towards L1498 for CN, are shown as hatched areas (right panel). The 15N atom is noted N., such that CN. matches C15N, etc. The dotted line shows the adopted reference elemental isotopic ratio, 14N/15N = 440 (Marty et al. 2011). |
4.3. Chemical considerations
The resulting abundances and abundance ratios of selected species are shown in Fig. 1. As is evident, all species reach a steady state after typically 5 Myrs, similar to what was found by Flower et al. (2006). This timescale is comparable to the lifetime of molecular clouds (Tassis & Mouschovias 2004) but is larger than the free-fall timescale and slightly larger than the ambipolar diffusion one (e.g. Walmsley et al. 2004). Those dynamical timescales are mostly relevant for the inner and dense parts of dark clouds and are not directly applicable to the rather low density material modelled here. It is possible, but not certain, that the nitrogen-bearing species have reached steady-state. In any case, it must be recognized that the chemical timescale depends strongly on the initial abundances adopted.
In our calculations, the steady state is characterized by an N:N2 abundance ratio close to unity, suggesting near equipartition between these two reservoir species. This is in sharp contrast to the calculations of Hily-Blant et al. (2010a), who found N2 to be 30–40 times more abundant than N. Unfortunately, the use of two different chemical networks, namely OSU 2009 in the latter case, impedes any direct comparison but undoubtedly calls for further investigation. Still, our predicted ratio is similar to that determined by Flower et al. (2006) with an older version of our chemical network. Another characteristic is the HNC:HCN ≈ 1 ratio. We also see that NH3 is the most abundant of the three hydrides, with an abundance of 1.2×-8, when NH and NH2 have abundances of 5.1×-9 and 4.3×-9 respectively. The predicted abundance of ammonia is close to its value of 1.5–5.0×-8 in the cold envelope of IRAS 16293-2422. The latter estimate is a revision of the value published in Hily-Blant et al. (2010a). It is based on non-LTE radiative transfer calculations using the publicly available RATRAN and LIME codes, and taking into account all the observed ammonia lines, including the 572 GHz fundamental line (Hogerheijde & van der Tak 2000; Brinch & Hogerheijde 2010). These calculations will be detailed elsewhere. There is also a good agreement for the abundances of NH and NH2. The predicted CN:HCN abundance ratio of 0.2 is smaller than the observed value, a discrepancy already noted by Hily-Blant et al. (2010b).
We now examine the predicted fractionation degree, that is, the enrichment or depletion in 15N with respect to the elemental ratio, of several nitrogen-bearing species, which is our main concern. The right panel of Fig. 1 shows the abundance ratios of nitrogen-bearing isotopologues as a function of time. Probably the main result is that our model does predict large variations of the isotopic ratio in several species, contrary to the calculations of TH00, who found very small fractionation for all species. Our model predicts that the isotopic ratio of N, which we note ℛ(N), is ≈630, and that ℛ(N2) ≈ 400 (see Table 3). Since these species are also the reservoirs of nitrogen, this implies that most of the nitrogen is fractionated, either enriched or deprived in 15N and any enrichment/depletion of N in 15N implies depletion/enrichment of N2. Another striking feature is that until a few 106 Myrs, isotopic ratios remain close to the initial value of 440. Beyond this time, three types of behaviour may be emphasized: species that are enriched in 15N, those that are deprived in 15N, and those that are not fractionated. The latter group includes NH2 and NH3. The positively fractionated molecules are HCN, HNC, and NH, for which the steady-state isotopic ratio is ≈330, and the depleted ones are N, NO, and CN. (see Table 3). The latter exhibits an isotopic ratio of ≈550.
The depletion of atomic nitrogen in 15N is due to the fractionation reactions
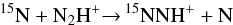 (1)and
(1)and 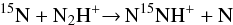 (2)that are strongly favoured at low temperature
with respect to the reverse process, due to a large ΔE = 36 K (see Table
A.2). The ratios predicted for N and NO are very
close, and that of CN, although smaller, follows the same trend. The former result is
easily explained by recognizing that NO and 15N O are produced and destroyed by
the same two reactions:
(2)that are strongly favoured at low temperature
with respect to the reverse process, due to a large ΔE = 36 K (see Table
A.2). The ratios predicted for N and NO are very
close, and that of CN, although smaller, follows the same trend. The former result is
easily explained by recognizing that NO and 15N O are produced and destroyed by
the same two reactions:  For 15NO, the main formation
channel is through reaction with 15N, whilst the destruction channel is through
reaction with N. Hence the steady-state abundances of NO and 15N O are given
respectively by
For 15NO, the main formation
channel is through reaction with 15N, whilst the destruction channel is through
reaction with N. Hence the steady-state abundances of NO and 15N O are given
respectively by ![\begin{eqnarray*} {[\ensuremath{\rm NO}]} = f_1/d_1 \times [\ensuremath{\rm OH}] \end{eqnarray*}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq75.png) and
and ![\begin{eqnarray*} {[\ensuremath{\rm ^{15}NO}]} = f_1/d_1 \times [\ensuremath{\rm ^{15}N}][\ensuremath{\rm OH}] / [\ensuremath{\rm N}], \end{eqnarray*}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq76.png) leading to an isotopic ratio
NO/15N O = N/15N. The situation is similar for CN, but as already
noted, the isotopic ratio of CN is lower than that of N (and NO). This is because
C2N+ and H2CN+ are efficiently fractionated
by the ion-neutral reactions of TH00 (see Table A.2), such that their isotopic ratios become smaller than ℛ0. The
dissociative recombination of these ions, which are normally negligible in producing CN,
contributes to about 10% to the formation of C15N. As a result, C15N
does not strictly follow the same behaviour as N and NO. Because HCN and HNC are primarily
formed through the dissociative recombination of H2CN+, their
isotopic ratios are similar to that of H2CN+.
leading to an isotopic ratio
NO/15N O = N/15N. The situation is similar for CN, but as already
noted, the isotopic ratio of CN is lower than that of N (and NO). This is because
C2N+ and H2CN+ are efficiently fractionated
by the ion-neutral reactions of TH00 (see Table A.2), such that their isotopic ratios become smaller than ℛ0. The
dissociative recombination of these ions, which are normally negligible in producing CN,
contributes to about 10% to the formation of C15N. As a result, C15N
does not strictly follow the same behaviour as N and NO. Because HCN and HNC are primarily
formed through the dissociative recombination of H2CN+, their
isotopic ratios are similar to that of H2CN+.
We now turn our attention to nitrogen hydrides. To understand the different behaviour of
NH on the one hand and NH2 and NH3 on the other hand, we first need
to understand what determines the relative abundances of
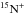 and N+. The N+ ion
is mostly produced by the reaction of N2 with He+. This is also true
for
and N+. The N+ ion
is mostly produced by the reaction of N2 with He+. This is also true
for 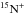 , but the fractionation reaction
, but the fractionation reaction
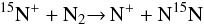 presents an exothermicity of 28 K. The
forward process leading to N15N is therefore enhanced at low temperature with
respect to the reverse process, and this is why ℛ(N2) < ℛ(N+). As
N2H+ is a daughter molecule of N2, this also explains
how ℛ(N2H+) < ℛ0, in addition to reactions (1)–(2). In turn, the enrichment of N2H+ in 15N
propagates into NH because, as Dislaire et al.
(2012) have shown, the dissociative recombination of N2H+
dominates the formation of NH over the
presents an exothermicity of 28 K. The
forward process leading to N15N is therefore enhanced at low temperature with
respect to the reverse process, and this is why ℛ(N2) < ℛ(N+). As
N2H+ is a daughter molecule of N2, this also explains
how ℛ(N2H+) < ℛ0, in addition to reactions (1)–(2). In turn, the enrichment of N2H+ in 15N
propagates into NH because, as Dislaire et al.
(2012) have shown, the dissociative recombination of N2H+
dominates the formation of NH over the 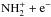 channel. Therefore, we find that
ℛ(NH) < ℛ0. To explain how NH2 and NH3 behave
differently, we recall that these two molecules result from the dissociative recombination
of
channel. Therefore, we find that
ℛ(NH) < ℛ0. To explain how NH2 and NH3 behave
differently, we recall that these two molecules result from the dissociative recombination
of 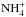 , which itself results from successive
hydrogen abstraction reactions initiated by N+ + H2. The
fractionation of NH2 and NH3 therefore reflects that of
N+. Hence, ℛ(NH) reflects that of N2, which is smaller than
ℛ0, whereas ℛ(NH2) and ℛ(NH3) reflect that of
N+, which is larger than ℛ0.
, which itself results from successive
hydrogen abstraction reactions initiated by N+ + H2. The
fractionation of NH2 and NH3 therefore reflects that of
N+. Hence, ℛ(NH) reflects that of N2, which is smaller than
ℛ0, whereas ℛ(NH2) and ℛ(NH3) reflect that of
N+, which is larger than ℛ0.
However, as is evident from Fig. 1 and Table 3, ℛ(NH2) and ℛ(NH3) are not
strictly equal to ℛ(N+), as we would expect from the above reasoning. Indeed,
the fractionation levels of N+, NH+,
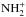 ,
, 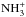 , and
, and
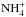 , are 480, 470, 450, 434, and 429
respectively. This shows that there is some enrichment in 15N at each step
along the reaction chain which begins with N+ + H2 and terminates
with
, are 480, 470, 450, 434, and 429
respectively. This shows that there is some enrichment in 15N at each step
along the reaction chain which begins with N+ + H2 and terminates
with  . The reason is that, because
ℛ(NH) > ℛ0, the reaction H+ + 15NH is faster than
the similar reaction H+ + NH and thus becomes non-negligible in the formation
of 15NH+. As a consequence, ℛ(NH+) < ℛ(N+).
In a similar fashion, the two reactions
. The reason is that, because
ℛ(NH) > ℛ0, the reaction H+ + 15NH is faster than
the similar reaction H+ + NH and thus becomes non-negligible in the formation
of 15NH+. As a consequence, ℛ(NH+) < ℛ(N+).
In a similar fashion, the two reactions 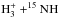 and HCO+ + 15NH
contribute to the formation of
and HCO+ + 15NH
contribute to the formation of  , whereas their 14N-homologues
do not. This explains how the positive fractionation of NH propagates in the other two
hydrides, though at a small level. Now, the next ions in the sequence, namely
, whereas their 14N-homologues
do not. This explains how the positive fractionation of NH propagates in the other two
hydrides, though at a small level. Now, the next ions in the sequence, namely
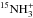 and
and
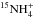 , are further enriched in 15N
with respect to
, are further enriched in 15N
with respect to 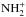 because 15NH3 starts
to contribute to their synthesis by reacting with H+,
because 15NH3 starts
to contribute to their synthesis by reacting with H+,
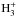 , and C+. In contrast, the
14N-homologues of these reactions are negligible in forming NH3.
As we see, minute variations of the isotopic ratio of a given species propagate into the
chemical network because the increase in the relative abundance of the
15N-isotopologue enhances reactions that are usually negligible, thus opening
new formation paths.
, and C+. In contrast, the
14N-homologues of these reactions are negligible in forming NH3.
As we see, minute variations of the isotopic ratio of a given species propagate into the
chemical network because the increase in the relative abundance of the
15N-isotopologue enhances reactions that are usually negligible, thus opening
new formation paths.
Finally, the above chemical considerations may be summarized as follows. Atomic nitrogen is depleted in 15N with respect to N2 because of the fractionation reactions (1)–(2). Other reactions decrease ℛ(H2CN+) below ℛ0, with the consequence that both ℛ(HCN) and ℛ(HNC) are lower than ℛ0. Species that derive primarily from atomic nitrogen, like NO and CN (see e.g. HB13), have isotopic ratios close to that of N. Yet, for CN, ℛ(C2N+) < ℛ0 drives ℛ(CN) to values lower than ℛ(N) and ℛ(NO). Among hydrides, the positive fractionation of NH derives from that of N2H+, which is inherited from that of N2. In contrast, NH2 and NH3 are neither enriched nor depleted in 15N because they derive principally from N+, which is only very slightly fractionated.
Since the rate of the key reaction N+ + H2 depends on the ortho:para ratio of H2, we performed a series of calculations with ortho:para ratios of H2 ranging from 10-6 to 10-3. The predicted isotopic ratios do not change by more than 10%, except those of NH2 and NH3 which follow the same trend, decreasing from 427 to 305 when o:p is 10-3 and 10-6 respectively. In the process, the ratio of NH decreases only from 326 to 317. The reason is that as o:p of H2 decreases, the rate of the reaction N+ + H2 drops and the reaction NH + H+ starts to dominate the formation NH+ and 15NH+. This explains how the ratios of NH2 and NH3 become closer to that of NH. Apart from this moderate change affecting NH2 and NH3, we conclude that the above results do not depend on the assumed value of o:p of 10-3.
4.4. Comparisons to the observations
The present model predictions are now compared to the CN and HCN isotopic ratios observed in L1544 and L1498 (right panel of Fig. 1). The isotopic ratio of HCN are ℛ(HCN) = 230−350 and 190–280 towards the central positions of L1544 towards L183 respectively (HB13). This value is not available in the case of L1498. For CN, we take the values determined in Sect. 3. As is evident, the model predictions agree well with all the observational constraints. In particular, the isotopic ratios of CN and HCN estimated in L1544 are well reproduced by our model calculations.
More problematic is the case of N2H+. The constraints on
N2H+/N15NH+ from Bizzocchi et al. (2010), who found 446 ± 71, are plotted in Fig. 1. Our model predicts a significant enrichment for
N15NH+, with ℛ(N2H+) = 280. The
fractionation of N15NH+ is associated with the reaction of
N2H+ with 15N. From Table 3, we note that the fractionation of N15NH+ is
larger than that of 15NNH+, a result of the different zero-point
energy differences of the two reactions  and
and 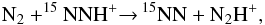 whose exothermicities are respectively
ΔE = 10.7 and 2.25 K. These reactions may proceed either by breaking an
N-H bond or an N-N bond. In the latter case, the reaction likely requires a strong
activation energy. If we artificially switch off these two reactions, we note that the
fractionations of 15NNH+ and N15NH+ become
equal, as expected, with a isotopic ratio of 340. Yet, this value is only slightly larger
than the value in Table 3 and is still outside the
permitted value from Bizzocchi et al. (2010) by a
small factor. The same argument may apply even more likely to the fractionation reactions
N + N2H+, which proceeds through N-N bond breaking. Suppressing
the latter reactions has a much stronger effect on the fractionation picture because these
reactions are responsible for the fractionation of atomic nitrogen (see the discussion
above). In particular, NH becomes less fractionated and CN and N2H+
have similar isotopic ratios ≈400, whereas HCN fractionation remains unaffected. This
further illustrates the dichotomy suggested by HB13. Observations of
15NNH+ would enable the first suggestion to be tested.
whose exothermicities are respectively
ΔE = 10.7 and 2.25 K. These reactions may proceed either by breaking an
N-H bond or an N-N bond. In the latter case, the reaction likely requires a strong
activation energy. If we artificially switch off these two reactions, we note that the
fractionations of 15NNH+ and N15NH+ become
equal, as expected, with a isotopic ratio of 340. Yet, this value is only slightly larger
than the value in Table 3 and is still outside the
permitted value from Bizzocchi et al. (2010) by a
small factor. The same argument may apply even more likely to the fractionation reactions
N + N2H+, which proceeds through N-N bond breaking. Suppressing
the latter reactions has a much stronger effect on the fractionation picture because these
reactions are responsible for the fractionation of atomic nitrogen (see the discussion
above). In particular, NH becomes less fractionated and CN and N2H+
have similar isotopic ratios ≈400, whereas HCN fractionation remains unaffected. This
further illustrates the dichotomy suggested by HB13. Observations of
15NNH+ would enable the first suggestion to be tested.
The models presented here have a C/O abundance ratio of 0.50, which falls in between the low–metal-abundance value of 0.41 from Wakelam & Herbst (2008) and the value of 0.67 from Flower & Pineau des Forêts (2003). We also performed model calculations with C/O = 0.40, for which all the above reasoning applies equally, though predicting a smaller ℛ(CN) whilst maintaining a fractionation of HCN close to the case C/O = 0.50. We thus found a better agreement with the calculations having C/O = 0.50. Exploring the effects of the initial abundances is an important area of investigation. However, it is beyond the scope of the present work and is deferred to a subsequent paper.
5. Conclusions and perspectives
Combining observations of C15N and 13CN and assuming a CN:13CN isotopic ratio, we have estimated the CN:C15N ratio towards two dark clouds. In both cases, the CN molecule appears slightly depleted in 15N with respect to the solar wind elemental ratio, with a CN:C15N ratio ≈500 ± 75 or depletion values δ15 = [272/ℛ(CN) − 1] = −527 to −360‰ . Towards L1544, additional constraints are provided by the HCN:HC15N ratio. We performed chemical model calculations, which include ion-neutral fractionation reactions for nitrogen-bearing species. Our gas-phase model predicts significant fractionation of many species. This is in sharp contrast to the former predictions of Terzieva & Herbst (2000). Even though the model of Charnley & Rodgers (2002) also produces fractionation of nitrogen-bearing species, the comparison with our calculations is not direct because the freeze-out of CO onto dust particles is a prerequisite to fractionation in their calculations. In contrast, we note that our model calculations predict fractionation without the need for depletion. Quite interestingly, our model is able to reproduce simultaneously 15N-poor CN and 15N-rich HCN, as is observed towards L1544. This indeed also demonstrates that these two observational facts do not contradict the chemical argument of HB13, according to which there are two families of nitrogenated species, namely nitriles, and hydrides, which present different sensitivity to fractionation. However, the present work allowed us to explore the mechanisms responsible for the differential fractionation among nitrogenated species and, in particular, to understand how CN can be slightly depleted in 15N and at the same time HCN be enriched in 15N. The differential fractionation of CN and HCN is at odds with observations in comets (Bockelée-Morvan et al. 2008; Manfroid et al. 2009), where similar isotopic ratios are obtained for both species. These two observational facts could be reconciled by assuming that CN is a daughter molecule of HCN (e.g. by photolysis) (for a discussion, see e.g. Mumma & Charnley 2011). Another limitation in our model is brought to light by the isotopic ratios of N2H+/N15NH+ and N2H+/15NNH+ which are predicted below 380, whilst observationally the former is 461 ± 71. We suggest that observations of 15NNH+ would bring strong constraints on the fractionation processes at work. In particular, whether these two ratios are equal or different would suggest that some of the underlying fractionation reactions present large activation energy. Another possibility, not considered in this work, is that depletion of gas-phase elements, (in particular CO, which is a predator of N2H+) plays a significant role for the fractionation of N2H+. On more general grounds, the present calculations suggest that a thorough comparison of the Ohio State University (OSU) chemical network with the one used here will potentially provide insights to the chemical processes at work.
From an astrochemical point of view, observations of as many species as possible is most welcome. However, C15N detection is time demanding, and further progress may rather benefit from observations of HC15N and H15N C towards a larger sample of sources. In addition, observations of 15NH3 would bring extremely interesting constraints, but the discrepancy between the results of Lis et al. (2010) and Gerin et al. (2009) suggests that the interpretation of such observations may not be straightforward. Observations of 15NO would also be most valuable. However, this molecule presents both fine and hyperfine splittings such that the intensity may be diluted within too many components, making this species particularly difficult to detect. The hypothesis of Hily-Blant et al. (2013) could also be pushed forward by observing isotopologues of more complex nitriles, such as HC3N and beyond.
Online material
Appendix A: Chemical model
We implemented the fractionation reactions of TH00, assuming a symmetry factor f(B,m) of unity for all reactions, unless N2 appears as a reactant or as a product. In these cases, f(B,m) = 0.5 or 1 respectively. A constant Langevin rate of 10-9 cm3 s-1 was adopted for these ion-neutral reactions. The zero-point energy differences are taken from TH00. The reactions and their rate coefficients are listed in Table A.2.
Elemental abundances (taken from Flower & Pineau des Forêts 2003), except for O. Numbers in parentheses are powers of 10.
Fractionation reactions and rate coefficients (k(T) = α(T/300)βexp(−ΔE/T) cm3 s-1) implemented in our chemical network (from TH00).
Appendix B: Collisional rate coefficients
The hyperfine rate coefficients for 13CN+H2 and C15N+H2 were derived from the fine-structure rate coefficients computed by Kalugina et al. (2012) for CN+H2. The latter coefficients were determined from fully quantum close-coupling (CC) calculations based on a highly correlated potential energy surface. Rate coefficients were deduced for temperatures ranging from 5 to 100 K. Full details can be found in Kalugina et al. (2012).
The 13C (with nuclear spin I = 1/2) and 15N
(I = 1/2) substitutions in CN (in which 14N has a nuclear
spin I = 1) significantly modify the hyperfine structure of the
molecule. Yet, the fine-structure rate coefficients can be considered nearly identical
for the three isotopologues. To derive the 13CN and C15N hyperfine
rate coefficients, we used the infinite-order-sudden (IOS) approximation applied to the
CN fine-structure rate coefficients of Kalugina et al.
(2012). Within this approximation, where the fine-structure energy spacings are
ignored compared to the collision energy, the rate coefficients between fine-structure
levels
(kNj → N′j′(T)
for a 2Σ state molecule) can be obtained directly from the “fundamental”
fine-structure rate coefficients (those out of the lowest N = 0 level)
as follows: ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{iosrot} k^{IOS}_{Nj \to N'j'}(T) &= (2j'+1)\sum_L \frac{2L+1}{L+1} \left(\begin{array}{ccc} j' & L & j \\ -1/2 & 0 & 1/2 \end{array}\right)^{2} \nonumber \\ & \quad \times \frac{1}{2}\left[1-\epsilon (-1)^{j+j'+L}\right] k^{IOS}_{0,1/2 \to L,L+1/2}(T), \end{eqnarray}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq126.png) (B.1)where ϵ is equal to +1 if
the parity of initial and final rotational Nj level is the same or –1
if the parity of initial and final rotational Nj level differ1.
(B.1)where ϵ is equal to +1 if
the parity of initial and final rotational Nj level is the same or –1
if the parity of initial and final rotational Nj level differ1.
 |
Fig. B.1 LVG predictions at T = 10 K towards L1544 (left) and L1498 (right). In each panel, the grey scale shows the predicted intensity of the 110024.590 MHz component of the C15N(1–0) hyperfine multiplet. The boxes (full line) delineate the solutions for the C15N (cyan) and the 13CN lines (white). The dashed box shows the C15N solutions when the C15N column density is multiplied by factors of 7.5 and 7 for L1544 and L1498 respectively. |
For C15N, which possesses a single non-zero nuclear spin, the IOS rate
coefficients among hyperfine-structure levels can be obtained from the
 rate coefficients as
rate coefficients as ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{REEQ2} & & k^{IOS}_{NjF \to N'j'F'} (T) = (2j+1)(2j'+1) (2F'+1)\sum_{L} \frac{2L+1}{L+1} \nonumber \\ & & \times \left( \begin{array}{ccc} j' & L & j \\ -1/2 & 0 & 1/2 \end{array} \right)^2 \left\{ \begin{array}{ccc} j & j' & L \\ F' & F & I \end{array} \right\}^2 \nonumber \\ & & \times \frac{1}{2}\left[1+\epsilon (-1)^{j+j'+L}\right] k^{IOS}_{0,1/2 \to L,L+1/2}(T), \end{eqnarray}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq130.png) (B.2)where I = 1/2 is the
nuclear-spin of 15N. In practice, the CN fine-structure energy spacings are
not negligibly small and the IOS approximation is expected to fail at low temperature
(T < 100 K). However, since it correctly predicts the relative
rates among hyperfine levels (because the propensity rules are properly included through
the Wigner coefficients), a simple method to correct the low temperature results is to
scale the IOS results, as originally suggested by Neufeld & Green (1994):
(B.2)where I = 1/2 is the
nuclear-spin of 15N. In practice, the CN fine-structure energy spacings are
not negligibly small and the IOS approximation is expected to fail at low temperature
(T < 100 K). However, since it correctly predicts the relative
rates among hyperfine levels (because the propensity rules are properly included through
the Wigner coefficients), a simple method to correct the low temperature results is to
scale the IOS results, as originally suggested by Neufeld & Green (1994): 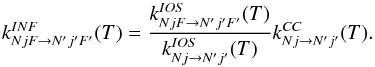 (B.3)In this approach the CC rate coefficients
kCC(0,1/2 → L,L + 1/2)
must be employed as the IOS fundamental rates in both Eqs. (B.1) and (B.2). The scaling procedure thus ensures that
(B.3)In this approach the CC rate coefficients
kCC(0,1/2 → L,L + 1/2)
must be employed as the IOS fundamental rates in both Eqs. (B.1) and (B.2). The scaling procedure thus ensures that 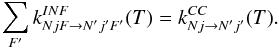 (B.4)It should be noted that the propensity rule
Δj = ΔF predicted by the recoupling approach is also
properly reproduced by IOS approximation, as discussed in Faure & Lique (2012). We note that for CN there is also a strong
propensity for transitions with even ΔNKalugina et al. (2012). In practice, the first 22 hyperfine levels of
C15N were considered, corresponding to rate coefficients for all 210
transitions among levels with N ≤ 5.
(B.4)It should be noted that the propensity rule
Δj = ΔF predicted by the recoupling approach is also
properly reproduced by IOS approximation, as discussed in Faure & Lique (2012). We note that for CN there is also a strong
propensity for transitions with even ΔNKalugina et al. (2012). In practice, the first 22 hyperfine levels of
C15N were considered, corresponding to rate coefficients for all 210
transitions among levels with N ≤ 5.
For 13CN, which possesses two non-zero nuclear spins, the IOS rate
coefficients among hyperfine structure levels can be obtained similarly, including an
additional coupling: ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{REEQ3} && k^{IOS}_{NjF_1F \to N'j'F_1'F'} (T) = (2j\!+\!1)(2j'\!+\!1)(2F_1\!+\!1)(2F_1'\!+\!1)(2F'\!+\!1) \nonumber \\[0.5mm] && \times \sum_{L} \frac{2L+1}{L+1} \left( \begin{array}{ccc} j' & L & j \\ -1/2 & 0 & 1/2 \end{array} \right)^2 \left\{ \begin{array}{ccc} j & j' & L \\ F_1' & F_1 & I_1 \end{array} \right\}^2 \ \left\{ \begin{array}{ccc} j & j' & L \\ F' & F & I_2 \end{array} \right\}^2 \nonumber \\[0.5mm] && \times \frac{1}{2}\left[1-\epsilon (-1)^{j+j'+L}\right] k^{IOS}_{0,1/2 \to L,L+1/2}(T), \end{eqnarray}](/articles/aa/full_html/2013/09/aa21364-13/aa21364-13-eq138.png) (B.5)where I1 = 1/2
and I2 = 1 are the nuclear spins of 13C and
14N respectively. The propensity rule is in this case
Δj = ΔF1 = ΔF and the
scaling formula writes
(B.5)where I1 = 1/2
and I2 = 1 are the nuclear spins of 13C and
14N respectively. The propensity rule is in this case
Δj = ΔF1 = ΔF and the
scaling formula writes 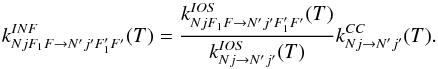 (B.6)In practice, the first 62 hyperfine levels
of 13CN were considered, corresponding to rate coefficients for all 1676
transitions among levels with N ≤ 5.
(B.6)In practice, the first 62 hyperfine levels
of 13CN were considered, corresponding to rate coefficients for all 1676
transitions among levels with N ≤ 5.
Note that there is a typo regarding the sign of ϵ in Eq. (7) of Faure & Lique (2012).
Acknowledgments
We acknowledge the comments of the anonymous referee, which helped to improve the scientific quality of the manuscript. Funding for this project was provided by grants from la Région Rhône-Alpes and from the Physico-Chimie du Milieu Interstellaire program. R.L.G. helds a doctoral fellowship from la Région Rhône-Alpes.
References
- Adande, G. R., & Ziurys, L. M. 2012, ApJ, 744-758, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Caselli, P., & Dore, L. 2010, A&A, 510, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Biver, N., Jehin, E., et al. 2008, ApJ, 679, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Bogey, M., Demuynck, C., & Destombes, J. L. 1984, Can. J. Phys., 62, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Bonal, L., Huss, G. R., Krot, A. N., et al. 2010, Geochim. Cosmochim Acta, 74, 6590 [Google Scholar]
- Brinch, C., & Hogerheijde, M. R. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carter, M., Lazareff, B., Maier, D., et al. 2012, A&A, 538, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Keto, E., Bergin, E. A., et al. 2012, ApJ, 759, L37 [Google Scholar]
- Charnley, S. B., & Rodgers, S. D. 2002, ApJ, 569, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Chaussidon, M., & Gounelle, M. 2007, Comptes Rendus Geoscience, 339, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, C. M., et al. 2005, ApJ, 619, 379 [Google Scholar]
- Crapsi, A., Caselli, P., Walmsley, M. C., & Tafalla, M. 2007, A&A, 470, 221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daranlot, J., Hincelin, U., Bergeat, A., et al. 2012, PNAS, 109, 10233 [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dutrey, A., Guilloteau, S., & Guélin, M. 1997, A&A, 317, L55 [NASA ADS] [Google Scholar]
- Dutrey, A., Henning, T., Guilloteau, S., et al. 2007, A&A, 464, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elsila, J. E., Glavin, D. P., & Dworkin, J. P. 2009, Meteorit. Planet. Sci., 44, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Faure, A., & Lique, F. 2012, MNRAS, 425, 740 [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forêts, G., & Walmsley, C. M. 2006, A&A, 456, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Viala, Y., Pauzat, F., & Ellinger, Y. 1992, A&A, 266, 463 [NASA ADS] [Google Scholar]
- Gerin, M., Marcelino, N., Biver, N., et al. 2009, A&A, 498, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Pety, J., & Guilloteau, S. 2005, CLASS evolution: I. Improved OTF support, Tech. rep., IRAM [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 2008, A&A, 480, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Maret, S., Bacmann, A., et al. 2010a, A&A, 521, L52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 2010b, A&A, 513, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hily-Blant, P., Bonal, L., Faure, A., & Quirico, E. 2013, Icarus, 223, 582 [Google Scholar]
- Hogerheijde, M. R., & van der Tak, F. F. S. 2000, A&A, 362, 697 [NASA ADS] [Google Scholar]
- Ikeda, M., Hirota, T., & Yamamoto, S. 2002, ApJ, 575, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Jehin, E., Manfroid, J., Hutsemékers, D., Arpigny, C., & Zucconi, J.-M. 2009, Earth Moon and Planets, 105, 167 [CrossRef] [Google Scholar]
- Kalugina, Y., Lique, F., & Kłos, J. 2012, MNRAS, 422, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Kastner, J. H., Hily-Blant, P., Sacco, G. G., Forveille, T., & Zuckerman, B. 2010, ApJ, 723, L248 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Wootten, A., Gerin, M., & Roueff, E. 2010, ApJ, 710, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. 1998, A&A, 337, 246 [NASA ADS] [Google Scholar]
- Manfroid, J., Jehin, E., Hutsemékers, D., et al. 2009, A&A, 503, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marty, B., Chaussidon, M., Wiens, R. C., Jurewicz, A. J. G., & Burnett, D. S. 2011, Science, 332, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, Annu. Rev. Astron. Astrophys., 49, 471 [Google Scholar]
- Neufeld, D. A., & Green, S. 1994, ApJ, 432, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Walmsley, C. M., Tafalla, M., Hily-Blant, P., & Pineau des Forêts, G. 2011, A&A, 534, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 (EDP Science) [Google Scholar]
- Rist, C., Faure, A., Hily-Blant, P., & Le Gal, R. 2013, J. Phys. Chem. A, in press [Google Scholar]
- Saleck, A. H., Simon, R., & Winnewisser, G. 1994, ApJ, 436, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Tassis, K., & Mouschovias, T. C. 2004, ApJ, 616, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vigren, E., Zhaunerchyk, V., Hamberg, M., et al. 2012, ApJ, 757, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, W. D., Anicich, V. G., & Huntress, W. T. 1976, ApJ, 205, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, Annu. Rev. Astron. Astrophys., 32, 191 [Google Scholar]
All Tables
Line properties towards L1544 and L1498 and associated column density ratios from LVG calculations.
Elemental abundances (taken from Flower & Pineau des Forêts 2003), except for O. Numbers in parentheses are powers of 10.
Fractionation reactions and rate coefficients (k(T) = α(T/300)βexp(−ΔE/T) cm3 s-1) implemented in our chemical network (from TH00).
All Figures
 |
Fig. 1 Fractional abundances (left) and abundance ratios (right) of selected species. The observed isotopic ratios towards L1544 for HCN and CN, as well as towards L1498 for CN, are shown as hatched areas (right panel). The 15N atom is noted N., such that CN. matches C15N, etc. The dotted line shows the adopted reference elemental isotopic ratio, 14N/15N = 440 (Marty et al. 2011). |
| In the text | |
 |
Fig. B.1 LVG predictions at T = 10 K towards L1544 (left) and L1498 (right). In each panel, the grey scale shows the predicted intensity of the 110024.590 MHz component of the C15N(1–0) hyperfine multiplet. The boxes (full line) delineate the solutions for the C15N (cyan) and the 13CN lines (white). The dashed box shows the C15N solutions when the C15N column density is multiplied by factors of 7.5 and 7 for L1544 and L1498 respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


