| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321364 | |
| Published online | 02 September 2013 | |
Online material
Appendix A: Chemical model
We implemented the fractionation reactions of TH00, assuming a symmetry factor f(B,m) of unity for all reactions, unless N2 appears as a reactant or as a product. In these cases, f(B,m) = 0.5 or 1 respectively. A constant Langevin rate of 10-9 cm3 s-1 was adopted for these ion-neutral reactions. The zero-point energy differences are taken from TH00. The reactions and their rate coefficients are listed in Table A.2.
Elemental abundances (taken from Flower & Pineau des Forêts 2003), except for O. Numbers in parentheses are powers of 10.
Fractionation reactions and rate coefficients (k(T) = α(T/300)βexp(−ΔE/T) cm3 s-1) implemented in our chemical network (from TH00).
Appendix B: Collisional rate coefficients
The hyperfine rate coefficients for 13CN+H2 and C15N+H2 were derived from the fine-structure rate coefficients computed by Kalugina et al. (2012) for CN+H2. The latter coefficients were determined from fully quantum close-coupling (CC) calculations based on a highly correlated potential energy surface. Rate coefficients were deduced for temperatures ranging from 5 to 100 K. Full details can be found in Kalugina et al. (2012).
The 13C (with nuclear spin I = 1/2) and 15N
(I = 1/2) substitutions in CN (in which 14N has a nuclear
spin I = 1) significantly modify the hyperfine structure of the
molecule. Yet, the fine-structure rate coefficients can be considered nearly identical
for the three isotopologues. To derive the 13CN and C15N hyperfine
rate coefficients, we used the infinite-order-sudden (IOS) approximation applied to the
CN fine-structure rate coefficients of Kalugina et al.
(2012). Within this approximation, where the fine-structure energy spacings are
ignored compared to the collision energy, the rate coefficients between fine-structure
levels
(kNj → N′j′(T)
for a 2Σ state molecule) can be obtained directly from the “fundamental”
fine-structure rate coefficients (those out of the lowest N = 0 level)
as follows: 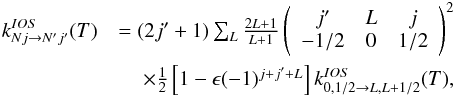 (B.1)where ϵ is equal to +1 if
the parity of initial and final rotational Nj level is the same or –1
if the parity of initial and final rotational Nj level differ1.
(B.1)where ϵ is equal to +1 if
the parity of initial and final rotational Nj level is the same or –1
if the parity of initial and final rotational Nj level differ1.
 |
Fig. B.1
LVG predictions at T = 10 K towards L1544 (left) and L1498 (right). In each panel, the grey scale shows the predicted intensity of the 110024.590 MHz component of the C15N(1–0) hyperfine multiplet. The boxes (full line) delineate the solutions for the C15N (cyan) and the 13CN lines (white). The dashed box shows the C15N solutions when the C15N column density is multiplied by factors of 7.5 and 7 for L1544 and L1498 respectively. |
| Open with DEXTER | |
For C15N, which possesses a single non-zero nuclear spin, the IOS rate
coefficients among hyperfine-structure levels can be obtained from the
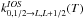 rate coefficients as
rate coefficients as 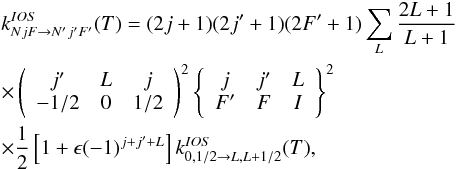 (B.2)where I = 1/2 is the
nuclear-spin of 15N. In practice, the CN fine-structure energy spacings are
not negligibly small and the IOS approximation is expected to fail at low temperature
(T < 100 K). However, since it correctly predicts the relative
rates among hyperfine levels (because the propensity rules are properly included through
the Wigner coefficients), a simple method to correct the low temperature results is to
scale the IOS results, as originally suggested by Neufeld & Green (1994):
(B.2)where I = 1/2 is the
nuclear-spin of 15N. In practice, the CN fine-structure energy spacings are
not negligibly small and the IOS approximation is expected to fail at low temperature
(T < 100 K). However, since it correctly predicts the relative
rates among hyperfine levels (because the propensity rules are properly included through
the Wigner coefficients), a simple method to correct the low temperature results is to
scale the IOS results, as originally suggested by Neufeld & Green (1994): 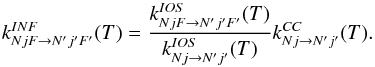 (B.3)In this approach the CC rate coefficients
kCC(0,1/2 → L,L + 1/2)
must be employed as the IOS fundamental rates in both Eqs. (B.1) and (B.2). The scaling procedure thus ensures that
(B.3)In this approach the CC rate coefficients
kCC(0,1/2 → L,L + 1/2)
must be employed as the IOS fundamental rates in both Eqs. (B.1) and (B.2). The scaling procedure thus ensures that 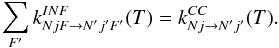 (B.4)It should be noted that the propensity rule
Δj = ΔF predicted by the recoupling approach is also
properly reproduced by IOS approximation, as discussed in Faure & Lique (2012). We note that for CN there is also a strong
propensity for transitions with even ΔNKalugina et al. (2012). In practice, the first 22 hyperfine levels of
C15N were considered, corresponding to rate coefficients for all 210
transitions among levels with N ≤ 5.
(B.4)It should be noted that the propensity rule
Δj = ΔF predicted by the recoupling approach is also
properly reproduced by IOS approximation, as discussed in Faure & Lique (2012). We note that for CN there is also a strong
propensity for transitions with even ΔNKalugina et al. (2012). In practice, the first 22 hyperfine levels of
C15N were considered, corresponding to rate coefficients for all 210
transitions among levels with N ≤ 5.
For 13CN, which possesses two non-zero nuclear spins, the IOS rate
coefficients among hyperfine structure levels can be obtained similarly, including an
additional coupling: 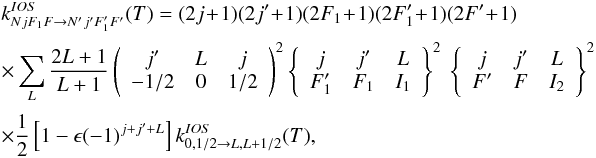 (B.5)where I1 = 1/2
and I2 = 1 are the nuclear spins of 13C and
14N respectively. The propensity rule is in this case
Δj = ΔF1 = ΔF and the
scaling formula writes
(B.5)where I1 = 1/2
and I2 = 1 are the nuclear spins of 13C and
14N respectively. The propensity rule is in this case
Δj = ΔF1 = ΔF and the
scaling formula writes 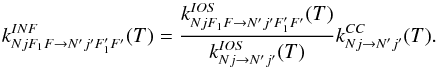 (B.6)In practice, the first 62 hyperfine levels
of 13CN were considered, corresponding to rate coefficients for all 1676
transitions among levels with N ≤ 5.
(B.6)In practice, the first 62 hyperfine levels
of 13CN were considered, corresponding to rate coefficients for all 1676
transitions among levels with N ≤ 5.
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


