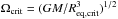| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321359 | |
| Published online | 12 September 2013 | |
Star formation with disc accretion and rotation
I. Stars between 2 and 22 M⊙ at solar metallicity
Geneva Observatory, University of Geneva, Maillettes 51, 1290 Sauverny, Switzerland
e-mail: lionel.haemmerle@unige.ch
Received: 25 February 2013
Accepted: 24 June 2013
Context. The way angular momentum is built up in stars during their formation process may have an impact on their further evolution.
Aims. In the framework of the cold disc accretion scenario, we study how angular momentum builds up inside the star during its formation for the first time and what the consequences are for its evolution on the main sequence (MS).
Methods. Computation begins from a hydrostatic core on the Hayashi line of 0.7 M⊙ at solar metallicity (Z = 0.014) rotating as a solid body. Accretion rates depending on the luminosity of the accreting object are considered, which vary between 1.5 × 10-5 and 1.7 × 10-3 M⊙ yr-1. The accreted matter is assumed to have an angular velocity equal to that of the outer layer of the accreting star. Models are computed for a mass-range on the zero-age main sequence (ZAMS) between 2 and 22 M⊙.
Results. We study how the internal and surface velocities vary as a function of time during the accretion phase and the evolution towards the ZAMS. Stellar models, whose evolution has been followed along the pre-MS phase, are found to exhibit a shallow gradient of angular velocity on the ZAMS. Typically, the 6 M⊙ model has a core that rotates 50% faster than the surface on the ZAMS. The degree of differential rotation on the ZAMS decreases when the mass increases (for a fixed value of vZAMS/vcrit). The MS evolution of our models with a pre-MS accreting phase show no significant differences with respect to those of corresponding models computed from the ZAMS with an initial solid-body rotation. Interestingly, there exists a maximum surface velocity that can be reached through the present scenario of formation for masses on the ZAMS larger than 8 M⊙. Typically, only stars with surface velocities on the ZAMS lower than about 45% of the critical velocity can be formed for 14 M⊙ models. Reaching higher velocities would require starting from cores that rotate above the critical limit. We find that this upper velocity limit is smaller for higher masses. In contrast, there is no restriction below 8 M⊙, and the whole domain of velocities to the critical point can be reached.
Key words: stars: formation / stars: rotation / stars: evolution / accretion, accretion disks
© ESO, 2013
1. Introduction
Stars are formed from the fragmentation and the collapse of large molecular clouds. Since the collapse proceeds in a non-homologous way (McNally 1964; Bodenheimer & Sweigart 1968; Larson 1969), hydrostatic equilibrium is first reached by a central core, while the rest of the cloud is still collapsing. A part of the remaining mass is then accreted by the central core, while it is already evolving through a slow Kelvin-Helmholtz (KH) contraction. The rest is ejected to infinity. This is the star formation scenario through accretion (Shu 1977; Stahler et al. 1980a,b, 1986b,a).
It is currently believed that this scenario holds for low-mass, intermediate-mass and massive stars (e.g. Nakano 1989; Bernasconi & Maeder 1996; Yorke & Bodenheimer 2008; Kuiper et al. 2010). While the general picture seems to be well defined, our knowledge of accretion history is far from being complete, and many questions regarding as to how the accretion history depends on the physics of the cloud (metallicity, turbulence) or of the already formed stars are still open. The complex hydrodynamics of the accretion process itself is also a very active area of research (e.g. Peters et al. 2010, 2011; Kuiper et al. 2010, 2011; Girichidis et al. 2011).
For the first time in the frame of the accretion scenario, the aim of the present work is to study the role of rotation during the pre-MS phase of intermediate-mass stars. We would like to know how the angular momentum builds up inside the forming star and which kind of rotation profile is obtained when the star enters the core hydrogen-burning phase on the zero-age main sequence (ZAMS), which is defined as the point when central hydrogen abundance has decreased by 3?. One can indeed expect that different distributions of the angular velocity inside the star can be obtained with some impact on the evolution during the MS phase, depending on the accretion history.
This work is the first in a series of papers exploring these effects. Here, we consider the case of stars with masses on the ZAMS between 2 and 22 M⊙ at solar metallicity. In Sect. 2, we describe the physical ingredients used for the computation of our models, while the results are presented in Sect. 3. Implications of these results for explaining the observed surface velocities of Herbig Ae/Be objects are discussed in Sect. 4. Possible impact of the pre-MS evolution on the evolution of stars on the MS phase are presented in Sect. 5, and conclusions are given in Sect. 6.
2. Physical ingredients of the models
The models are computed with the Geneva stellar evolution code (Eggenberger et al. 2008) with the same treatment as Ekström et al. (2012) for the rotational instabilities and with the following modifications to account for the pre-MS phase:
-
The burning of D, 6Li and 7Li is included, through the following reactions:
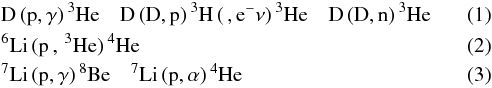 The corresponding reaction rates are those of Caughlan & Fowler (1988). Let us recall that 6Li- and 7Li-burning have a negligible impact in terms of energy generation. The main contribution to the nuclear energy generation rate comes from D-burning. This contribution becomes significant for temperatures in stellar interiors around 1 − 2 × 106 K.
The corresponding reaction rates are those of Caughlan & Fowler (1988). Let us recall that 6Li- and 7Li-burning have a negligible impact in terms of energy generation. The main contribution to the nuclear energy generation rate comes from D-burning. This contribution becomes significant for temperatures in stellar interiors around 1 − 2 × 106 K. -
Mixing in convective zones is assumed to be instantaneous for all chemical species, except for D. For this fragile element (see above), mixing is treated as a diffusive process with a diffusion coefficient deduced from the mixing-length theory (Bernasconi 1997). It is given by
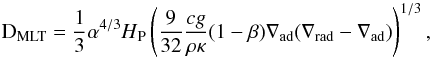 (4)where α is the mixing-length coefficient, HP is the pressure-scale height, c the speed of light, g is the gravitational acceleration, ρ is the mass density, κ is the opacity, β is the ratio of gas pressure to total pressure, ∇ad is the adiabatic gradient, and ∇rad is the radiative gradient.
(4)where α is the mixing-length coefficient, HP is the pressure-scale height, c the speed of light, g is the gravitational acceleration, ρ is the mass density, κ is the opacity, β is the ratio of gas pressure to total pressure, ∇ad is the adiabatic gradient, and ∇rad is the radiative gradient. -
We suppose that accretion occurs through the scenario of cold disc accretion (Hosokawa et al. 2010). It means that matter is gently deposited at the surface of the star with an internal energy content equal to that contained in the outer layers of the accreting stars. This procedure is the same as in Yorke & Bodenheimer (2008) and Hosokawa et al. (2010). It could result, for instance, from interactions between the stellar radiation field and the infalling matter, leading to a thermal coupling between this material and the stellar photosphere. The angular velocity Ω of the new material is also taken to equal that of the surface of the accreting star before the new layer is accreted. This accretion law corresponds to the smoothest way to accrete angular momentum. A weak magnetic field could be sufficient to drag the infalling matter along the field lines and to obtain such an accretion law for the angular momentum1. It turns out that the resulting time derivative of the total angular momentum,
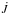 , is nearly proportional to the mass accretion rate, Ṁ. This implies that the mean specific angular momentum accreted at each evolution step is almost constant all along the birthline.
, is nearly proportional to the mass accretion rate, Ṁ. This implies that the mean specific angular momentum accreted at each evolution step is almost constant all along the birthline.
2.1. Mass accretion rate
We use the same accretion law as in Behrend & Maeder (2001). Let us recall a few points about this accretion law. Firstly, it is based on an empirical relation, which was established by Churchwell (1998) and confirmed by Henning et al. (2000), between the mass outflow rate, Ṁout, and the bolometric luminosity, L, of the accreting object in ultra-compact HII regions: 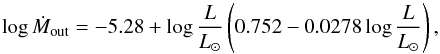 (5)where Ṁout is in solar masses per year. To deduce an accretion rate from Ṁout, Behrend & Maeder (2001) made the hypothesis that a constant fraction f of the mass collapsing from the accretion reservoir is accreted by the star. The other fraction, (1 − f), produces the outflow of Eq. (5). Thus, we have a very simple relation between the rate of mass outflow and the rate of mass accretion
(5)where Ṁout is in solar masses per year. To deduce an accretion rate from Ṁout, Behrend & Maeder (2001) made the hypothesis that a constant fraction f of the mass collapsing from the accretion reservoir is accreted by the star. The other fraction, (1 − f), produces the outflow of Eq. (5). Thus, we have a very simple relation between the rate of mass outflow and the rate of mass accretion 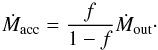 (6)In the following we adopt a value of 1/3 for f, as in Behrend & Maeder (2001). This implies that the accretion rate is equal to half of the mass outflow. This accretion law gives accretion rates between 1.5 × 10-5 M⊙ yr-1 for objects with luminosities around 10 L⊙ and 10-3 M⊙ yr-1 for luminosities equal to 104 L⊙.
(6)In the following we adopt a value of 1/3 for f, as in Behrend & Maeder (2001). This implies that the accretion rate is equal to half of the mass outflow. This accretion law gives accretion rates between 1.5 × 10-5 M⊙ yr-1 for objects with luminosities around 10 L⊙ and 10-3 M⊙ yr-1 for luminosities equal to 104 L⊙.
It has to be noted that the empirical relation obtained by Churchwell (1998), which is used here, does not necessarily describe an evolutionary sequence. It may, for instance, result from a relation between the mass outflow rate and the luminosity when the outflow rate reaches some maximum value and is thus detectable. Implicitly, we assume here that most of the star is built up during events following the above relation and that other accretion phases (if any) would have a negligible impact. Let us note that there are observational and theoretical arguments for justifying the use of the present accretion law. 1) There are still many uncertainties on the accretion rates, and we think that the present choice remains an interesting possibility, since the birthline resulting from this law fits well with the observed upper envelope in the HR diagram of the positions of Herbig Ae/Be objects (see Fig. 1 in Behrend & Maeder 2001). 2) The present accretion rates are in the range of values expected by theoretical considerations. The typical accretion rate 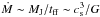 for a cloud’s temperature of 10−20 K is ~10-5 M⊙ yr-1. This rate is expected for solar-type stars. For stars around 50 M⊙, the Kelvin-Helmholtz time is ~5 × 104 yr, so that a simple argument about timescales (M/Ṁ < tKH) imposes an accretion rate higher than ~10-3 M⊙/yr. 3) Accretion rates in the same ranges have been used by recent similar works modelling massive star formation through accretion. For instance, Hosokawa & Omukai (2009) calculate their pre-MS evolution with constant mass accretion rates spanning values between 10-6 and 6 × 10-3 M⊙ yr-1.
for a cloud’s temperature of 10−20 K is ~10-5 M⊙ yr-1. This rate is expected for solar-type stars. For stars around 50 M⊙, the Kelvin-Helmholtz time is ~5 × 104 yr, so that a simple argument about timescales (M/Ṁ < tKH) imposes an accretion rate higher than ~10-3 M⊙/yr. 3) Accretion rates in the same ranges have been used by recent similar works modelling massive star formation through accretion. For instance, Hosokawa & Omukai (2009) calculate their pre-MS evolution with constant mass accretion rates spanning values between 10-6 and 6 × 10-3 M⊙ yr-1.
2.2. Initial model
We begin the computations with a hydrostatic core of 0.7 M⊙, as in Behrend & Maeder (2001), with L = 7.69 L⊙, Teff = 3852 [K], and Z = 0.014. We take the chemical abundances of Asplund et al. (2005), and the Ne value from Cunha et al. (2006). For the light elements, we take mass fractions of X2 = 5 × 10-5, X6 = 9 × 10-10, and X7 = 1 × 10-8 (Xi being the mass fraction of the isotope of mass number i). This value for X2 is the same as in Behrend & Maeder (2001). The chemical composition of the accreted material is taken equal to the initial stellar composition.
This choice of L and Teff corresponds to the case of spherical accretion. When the pre-stellar cloud collapses, the disc is expected to form only after an initial phase of spherical accretion, so that the relevant scenario for the formation of the initial model is the scenario of spherical accretion, even if we consider cold disc accretion during the rest of the pre-MS evolution. We assume that a spherical accretion was responsible for the growth of the star until a mass of about 0.7 M⊙ is reached. From this stage onwards, we pursue the evolution assuming that accretion proceeds through a cold disc. In Sect. 3.4, we briefly mention how the choice of an initial model built by disc accretion would modify our results, but a more detailed study of the impact of the initial model is postponed to a forthcoming work.
The initial model is fully convective, and solid-body rotation is assumed in convective zones. The rotation of the initial model is thus determined by a single angular velocity Ωini for all layers, so that we can choose it as a free parametre. Since the accretion of angular momentum during the subsequent evolution is linked to the rotation of the accreting object, the value we choose for Ωini has an impact on the angular momentum accretion rate for all the subsequent phases.
2.3. Models
We compute models for different final masses on the ZAMS MZAMS from 2 M⊙ to 22 M⊙. In each case, we begin with the initial model described in Sect. 2.2, that is accreting mass at a rate given by Eqs. (5) and (6). When the mass of the star reaches the value MZAMS, we turn off accretion, and the star continues its evolution at constant mass, while the star keeps contracting towards the ZAMS. For each MZAMS, we compute models with different Ωini, between 0 and 2.25 × 10-5 s-1. This last value corresponds to the critical angular velocity of the initial hydrostatic core2.
 |
Fig. 1 Birthline with rotation (Ωini = 2.1 × 10-5 s-1, solid blue line) and birthline without rotation with three contractions (long-dashed blue lines). Some points of the birthline of Behrend & Maeder (2001) are displayed for comparison (filled squares). The short-dashed lines indicate the ZAMS of Ekström et al. (2012) without rotation (black) and the pre-MS tracks at constant mass corresponding to the contractions displayed (red). The numbers along the birthline are rotational velocities (in km s-1) along the birthline with rotation at M = 2, 6 and 14 M⊙. Letters along the birthline indicate the evolutionary stages described in the text (Sect. 3.1). Straight dotted lines are iso-radii of 0.1, 1, 10, 100 and 1000 R⊙ from bottom left to top right. |
 |
Fig. 2 Evolution of the radius and the internal structure of the star on the birthline without rotation (upper panel) and with rotation (Ωini = 2.1 × 10-5 s-1, lower panel). In each panel, the upper solid line is the radius and shaded areas correspond to convective regions. The dotted lines indicate the iso-masses. That is, the radius corresponding to fixed values of the lagrangian coordinate Mr (Mr = 1, 2, 3, ... [M⊙]). Letters along the radius on the upper panel indicate the evolutionary stages described in the text (Sect. 3.1). Numbers along the radius on the lower panel correspond to rotational velocities (in km s-1) at M = 1, 2, 3, ... [M⊙]. |
 |
Fig. 3 Upper panel: vertical component of the meridional circulation for the 6 M⊙ model with Ωini = 9 × 10-6 s-1 (i.e., model of the grid described in Sect. 3.3) at an age of 200 000 years just at the end of the accretion phase (see Fig. 6). Lower panel: diffusion coefficient for the transport by shear instability for the same model. |
3. Results
3.1. The accretion phase
The birthline without rotation and the birthline with Ωini = 2.1 × 10-5 s-1 are visible in Fig. 1. Note that the shape of the birthline and the sequence of events described below would be very similar for other choices of the core initial angular velocity. For comparison, we added some points of the birthline of Behrend & Maeder (2001). The evolution of the radius of the star and of its internal structure is given in Fig. 2.
 |
Fig. 4 Angular velocity on the birthline with Ωini = 2.1 × 10-5 s-1 (value needed to obtain vZAMS/vcrit = 0.40 for the 14 M⊙). Upper panel: angular velocity at the surface and in the centre of the star, along the birthline as a function of the total mass. Letters indicate the evolutionary stages described in the text (Sect. 3.1), and triangles indicate the appearance of the convective core. Lower panel: rotation profiles on the birthline at different masses from 2 M⊙ to 14 M⊙, by steps of 1 M⊙. |
The evolution on the birthline follows roughly five stages, delimited by capital letters in Figs. 1 and 2, with each one corresponding to a contraction or an expansion phase:
-
1.
A → B: at the beginning of the evolution, the central temperature of the star is too low for nuclear reactions to occur at a significant rate. Weak D-burning takes place in deep regions, but the corresponding energy generation rate ϵD is negligible (~10-16 [erg g-1 s-1]). The energy comes from gravitational contraction, and luminosity decreases, as in the case of a classical Hayashi line.
-
2.
B → C: when the central temperature reaches ~106 [K], D-burning becomes significant and its abundance decreases in the centre. The star expands and its luminosity increases.
-
3.
C → D: when the central mass fraction of D becomes too low (≲5 × 10-6), the energy liberated by D-burning is no longer sufficient to sustain the star and gravitational contraction starts again. The stellar luminosity stops growing for a while, but the central temperature continues to increase. When the central temperature reaches ~2.8 × 106 [K], the opacity is low enough for radiative equilibrium to establish in the centre.
-
4.
D → E: while the radiative core grows, the changes in the structure of the star produce a steep increase in its radius. This expansion is enhanced in that the accreted D can no longer reach the centre and burns now in an off-centre shell.
-
5.
E → F: once the star is completely radiative, the radius decreases again, while its luminosity continues to grow. A convective core develops before the ZAMS, when the energy liberated by the CN-cycle becomes significant.
As we can see in Fig. 1, the differences between our birthline and that of Behrend & Maeder (2001) are very modest and are mainly due to differences in the initial chemical composition. In Behrend & Maeder (2001), an initial metallicity of Z = 0.020 was considered, while we take Z = 0.014 here.
Figures 1 and 2 show that the effects of rotation along the birthline are small. This is indeed expected for the following two reasons:
-
The rotation velocities considered here are always far fromcritical values and do not imply strong deformations of theaccreting star (see Fig. 10).
-
Transport processes (meridional currents and shear instabilities) are inefficient during the pre-MS phase for stars with masses on the ZAMS in the mass range considered here. Figure 3 illustrates this: it shows the vertical component of the meridional circulation velocity, U, and the diffusion coefficient for the transport by shear instability, Dshear, for the 6 M⊙ model with Ωini = 9 × 10-6 s-1 at an age of 200 000 years (just after the end of accretion). We see that the typical value for U is 10-4−10-3 cm s-1. For a radius R ≳ 5 R⊙ (this inequality holds for the whole accretion phase), this leads to a typical timescale of meridional currents equal to R/U ≳ 107 yr, which is much longer than the pre-MS timescale of a few 105 yr for the 6 M⊙ star. The timescale for the transport by shear instability is given by R2/Dshear. Figure 3 shows that the typical value of Dshear is 107 − 108 cm2 s-1, leading to a similar timescale than for meridional circulation. Therefore, there is no chance for these processes to have a strong impact on the distribution of Ω and of the chemical elements. For stars with lower MZAMS, things may be different. The transport processes have an impact on the surface abundances in light elements (Eggenberger et al. 2012).
Figure 4 shows how the angular velocity profile builds up inside the accreting object. We see that the accreting star rotates as a solid body up to a mass of about 3 M⊙. This comes from the star that is completely convective up to this point (see Fig. 2), and we assume that convective zones rotate as solid bodies. As soon as the radiative core appears and expands, above about 5 M⊙, an internal gradient of Ω develops with a typical ratio of 2 to 3 between the rotation rate of the core and that of the surface. Note that starting accretion from a core with a lower rotation velocity produces less steep gradients of Ω at the end of the accretion phase. This can be seen comparing the distribution of Ω in the 6 M⊙ model at the end of the accretion phase, when Ωini = 9.00 × 10-6 s-1 (see Fig. 7) and the curve corresponding to 6 M⊙ in Fig. 4 obtained with Ωini = 2.10 × 10-5 s-1.
In more general terms, the effect of varying Ωini on the value of Ω during the evolution is the following: the angular velocity of a given layer at a given evolutionary stage depends almost linearly on Ωini. This is due to the angular velocity at each time step of the accreted layer is defined from the previous surface velocity. Since the transport of angular momentum is negligible on pre-MS timescales, as mentioned above, the specific angular momentum (r2Ω) remains constant and thus the angular velocity of each layer keeps at each stage a linear dependence on the initial value.
At the end of the accretion phase and for the masses considered here, the star still needs to contract towards the ZAMS. In the next sub-section, we describe in more details the complete pre-MS and MS evolution of our models with MZAMS = 6 and 14 M⊙.
3.2. Pre-MS of a 6 and 14 M⊙ model with accretion and rotation
Complete evolutionary tracks for models with MZAMS = 6 M⊙ computed with and without rotation are shown in Fig. 5. The initial velocity of the rotating model (Ωini = 9 × 10-6 s-1) is chosen to obtain a star rotating at 40% of the critical velocity on the ZAMS. This value of v/vcrit = 0.4 on the ZAMS is adopted in the continuity of the computation of a large grid of rotating models at solar metallicity by Ekström et al. (2012) and is representative of the rotation velocity of young B-type stars, according to Huang et al. (2010).
 |
Fig. 5 Evolutionary tracks for the models with MZAMS = 6 M⊙ with rotation (solid blue line) and without rotation (dashed red line). The numbers along the track of the rotating model indicate the rotation velocity (in km s-1) at M = 1, 2, ..., 6 [M⊙], on the ZAMS, and on the terminal-age main sequence (TAMS). The right dotted line represents the birthline, and the left dotted line represents the ZAMS of Ekström et al. (2012) without rotation. The end of accretion is indicated by filled squares. The ZAMS and the TAMS of the models are indicated by empty squares. |
The evolution of the radius and of the internal structure of the star during the pre-MS is shown in Fig. 6 for the non-rotating model (upper panel) and the rotating one (lower panel).
 |
Fig. 6 Similar figure as Fig. 2, following the evolution with time of the 6 M⊙ model. Time 0 is taken at the beginning of the computation starting from the 0.7 M⊙ core. Filled squares indicate the end of accretion. |
The model with MZAMS = 6 M⊙ follows the birthline almost until the end of the expansion due to the development of the radiative core (point E in Fig. 2).
We see that the rotating model reaches a given evolutionary stage at a slightly larger age than the non-rotating one. The age of the star on the ZAMS (counted here from the beginning of the accretion on the 0.7 M⊙ core) is 7.4% larger with rotation than without rotation. This effect comes from the centrifugal force that decreases the effective gravity inside the star and thus slows down the contraction.
Figure 7 shows the variation in Ω inside the 6 M⊙ at different stages during the contraction phase.
 |
Fig. 7 Angular velocity of the model with MZAMS = 6 M⊙. Upper panel: angular velocity at the surface and in the centre of the star as a function of the age. Circles indicate the stages for which the rotation profiles are shown in the lower panel. The filled square corresponds to the end of accretion, and the triangle indicates the appearance of the convective core. Lower panel: rotation profiles during the contraction phase at different stages indicated by circles on the upper panel. The thickest line corresponds to the ZAMS. |
An interesting question is to know which kind of distribution of Ω is obtained on the ZAMS. Is the star rotating as a solid body or not? When accretion stops, we have a nearly solid-body rotating star. We see that the contraction phase increases the contrast between the rotation rate of the core and the rotation rate of the envelope. However, this contrast remains modest and the rotation law of the star on the ZAMS is not far from a solid-body rotation law. The core is rotating 36% faster than the surface.
The evolution of the structure of the 14 M⊙ model is shown in Fig. 8.
Again, the value of Ωini is chosen, so that v/vcrit = 0.4 on the ZAMS: Ωini = 2.1 × 10-5 s-1. As in the case of the 6 M⊙ model, we note that a given evolutionary stage is reached at slightly larger ages, when rotation is included. The effect is however small; the time spent on the pre-MS increases by only 3.1% when rotational effects are considered.
Figure 9 shows the variation in Ω inside the 14 M⊙ model at different stages during the contraction phase. In contrast with the results obtained for the 6 M⊙ model, the contraction phase, which is much shorter than for the 6 M⊙ stellar model, decreases the contrast between the rotation rate of the core and the surface. Indeed, we see that the ratio of the angular velocity at the centre and at the surface is approximately equal to 2 at the end of the accretion, while it is about 1.2 on the ZAMS. Thus the core is rotating about 20% faster than the surface on the ZAMS in the case of the 14 M⊙ model, while it is rotating 36% faster in the case of the 6 M⊙ model. For the 2 M⊙ model again with v/vcrit = 0.4 on the ZAMS (not shown here), the same ratio is about 80%. We conclude that in this scenario the degree of differential rotation on the ZAMS decreases when MZAMS increases for a given v/vcrit = 0.4 on the ZAMS.
This can be understood by looking at Fig. 1. We see that the degree of global contraction, starting from the birthline to the ZAMS, increases when the mass decreases. This favours stronger gradient of Ω inside lower mass stars.
3.3. Grid of rotating pre-MS models
We compute the accretion and contraction phases for models with masses MZAMS between 2 and 14 M⊙ by steps of 1 M⊙. As explained above, we chose a value of Ω for the initial core for each final mass such that an equatorial velocity of about 40% of the critical velocity is reached on the ZAMS. These initial values are given in Table 1.
The models with MZAMS of 6 and 14 M⊙ are the same as those described in Sect. 3.2. For the accretion law considered here, the value of Ωini increases linearly with the final mass. The ratio of the surface velocity to the critical velocity at a given time is always below 80% during the whole pre-MS and MS phase. Figure 10 shows the ratio v/vcrit as a function of MZAMS at different stages of the evolution.
 |
Fig. 10 Ratio v/vcrit as a function of MZAMS at different stages of the evolution, for the models described in Sect. 3.3. The dotted line indicates the maximum value of v/vcrit reached during the pre-MS. |
There are many interesting points that can be noted from this figure.
-
We see that v/vcrit decreases during the accretion process. This comes from the radius of the accreting star that remains around 10 R⊙ during most of the accretion phase, while the mass is growing. Consequently, the surface gravity and, hence, vcrit increase.
-
For low- and intermediate-mass stars (<8 M⊙), the surface velocity at the end of the accretion phase is still far from the one reached on the ZAMS, while the difference between these velocities decreases when more massive stars are considered. This is expected because the formation timescale (M/Ṁ) for the higher mass range becomes of the same order of magnitude as the Kelvin-Helmholtz timescale (typical timescale of the contraction), and thus, the birthline is very close or even follows the ZAMS (Beech & Mitalas 1994; Bernasconi & Maeder 1996).
-
An important point is that these models have difficulties to form stars more massive than about 20 M⊙ and have a surface velocity on the ZAMS equal or superior to about 40% of the critical velocity. We see indeed that one should start from initial cores rotating near the critical limit to obtain these models, which does not seem reasonable.
-
A similar problem exists for producing very fast rotators on the ZAMS in the whole mass range considered here. We develop this point further in Sect. 3.4.
The pre-MS tracks of this grid are shown in Fig. 11. Tables for the pre-MS evolution of these models can be obtained from the website3. An example of a table (the one for MZAMS = 6 M⊙) is displayed in Table 2.
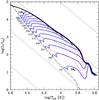 |
Fig. 11 Grid of pre-MS models with MZAMS from 2 to 14 M⊙, by steps of 1 M⊙, with Ωini ∝ MZAMS (i.e. models described in Sect. 3.3, solid blue lines). Two birthlines (without rotation and with the higher Ωini) are plotted (solid black lines). The dashed line indicates the ZAMS of Ekström et al. (2012) and dotted lines correspond to iso-radius of 0.1, 1, 10 and 100 R⊙ from left to right. Equatorial surface velocities on the ZAMS are indicated (in km s-1) at the end of each track. Dot-dashed red lines indicate isochrones of 2 × 105, 5 × 105 and 2 × 106 yr from top to bottom. |
 |
Fig. 12 Evolution of the surface velocity of the models described in Sect. 3.3. Filled squares correspond to the end of the accretion, while empty squares indicate the ZAMS and the TAMS. |
The evolution of vsurf up to the end of the MS is plotted in Figs. 12 and 13 for all these models. Surface equatorial velocities during the MS phase are typically between 150 and 250 km s-1. These values encompass the observed average equatorial velocities measured for these types of stars on the MS band (Huang et al. 2010). This means that the pre-MS evolutions obtained here, provided our accretion history is reasonable, may be considered as representative for a significant fraction of the stars in this mass range.
We see that these models keep a surface velocity between 10 and 100 km s-1 during most of the accretion phase. A decrease of the surface velocity occurs when the star inflates during central D-burning, because Ṁ is still low. When Ṁ becomes high enough, the surface velocity increases, even during the expansion resulting from the growing of the radiative core. For the low- and intermediate-mass stars, the contraction phase produces a very substantial increase in the surface velocity. Figure 13 shows that the surface velocity for the 2 M⊙ stellar model increases by a factor 8.
 |
Fig. 13 Same as Fig. 12 but focused on the contraction phase. This time the x-axis is the fraction of the total contraction time, so that the end of accretion corresponds to 0 and the ZAMS to 1. |
For the 14 M⊙, the increase is more modest by only a factor 1.3 due to the proximity of the birthline with the ZAMS. Interestingly, we see that the surface velocity does not go through a local maximum just before reaching the ZAMS for models with MZAMS inferior or equal to 7 M⊙, as it is in the case of more massive stars. This is related to the degree of differential rotation on the ZAMS that increases, when the mass on the ZAMS decreases. This reduces the velocity of the meridional currents, which slow down the outer layers and accelerate the inner regions at the very beginning of the MS phase (see the discussion in Denissenkov et al. 1999).
3.4. Maximum surface velocities on the ZAMS
As mentioned in Sect. 3.3, we cannot form stars with masses ≳20 M⊙ and v/vcrit ≳ 0.4 on the ZAMS in the context of the accretion scenario and with the assumptions considered here. Even for masses around 10−15 M⊙, there are difficulties to produce fast rotators on the ZAMS. This is because the ratio v/vcrit in this scenario has two peaks during the pre-MS: one at the beginning of the birthline and the other one around the ZAMS. The first peak is responsible for the limitation of the surface velocities on the ZAMS.
For each final mass, we estimate the maximum value for the surface velocity that can be reached on the ZAMS, vsurf(max). The results are shown in Fig. 14.
 |
Fig. 14 Maximum surface velocities on the ZAMS as a function of MZAMS for models between 2 and 22 M⊙. The dotted line in the upper panel indicates the critical velocity. |
We see that the present scenario does not limit the range of v/vcrit that can be obtained on the ZAMS below 8 M⊙. For 9 M⊙, the maximum surface velocity on the ZAMS is 82% of the critical velocity, while this ratio is 68% for 10 M⊙. For these masses, the present scenario cannot produce very fast rotators on the ZAMS. Above 15 M⊙, the maximum possible value of vZAMS/vcrit is below 0.4. For 22 M⊙, the limit is 0.29, which corresponds to vsurf(max) = 207 km s-1. If evolved on the MS, such a star would have a time averaged velocity around 150 km s-1, a value below the typical surface velocity of a star of such a mass (Huang et al. 2010).
To be more explicit about the cause of this limitation, we show how the surface velocity evolves with time for models ending with different masses on the ZAMS in Fig. 15, starting with a core that rotates at its maximal velocity Ωini = 2.25 × 10-5 s-1.
 |
Fig. 15 Evolution of the surface velocity during the pre-MS for models with Ωini = 2.25 × 10-5 s-1 and MZAMS between 9 and 22 M⊙. The thickest line is the corresponding birthline, and the empty squares indicate the ZAMS. Letters correspond to the stages described in Sect. 3.1. |
These models correspond to the fastest rotators that can be produced with the present accretion scenario. For MZAMS ≤ 8 M⊙, the critical velocity is reached during the KH contraction phase. Thus, it suffices to chose a smaller value of Ωini to reach the critical velocity on the ZAMS for these models, as already mentioned above. Above 8 M⊙, the star reaches the ZAMS with vsurf(max) < vcrit, so that velocities between vsurf(max) and vcrit are not allowed.
We also see that the ZAMS velocity is a decreasing function of MZAMS for a given Ωini. This is related to the mean specific angular momentum accreted at each time that is almost constant along the birthline. This results in a specific angular momentum at the surface of the star on the ZAMS nearly independent of the mass. As the radius of a ZAMS star increases with its mass, the relation jsurf ∝ R × vsurf leads to a vsurf decreasing with the mass on the ZAMS. Since vcrit on the ZAMS increases with the mass, v/vcrit on the ZAMS also decreases with the mass. This is the cause of the problem for fast rotators. To produce stars with masses superior to 15 M⊙ with v/vcrit ≥ 0.4 on the ZAMS, we need to change the pre-MS scenario. At that point we leave the problem open. It is however interesting to note two points: 1) any disc locking mechanism during the contraction phase will make the problem still more severe; 2) the limitation concerns only masses above 8 M⊙. Does this indicate that more massive stars follow a different accretion history than low- and intermediate-mass stars? We shall investigate that question in a forthcoming study. In particular, the effect of varying the accretion law for mass and angular momentum will be studied in a forthcoming paper (Haemmerlé et al., in prep.). We shall see whether a different accretion history will allow to produce fast rotators among massive stars.
Another issue is the impact of the properties of the initial model on the velocity limitation on the ZAMS. In the present models, all the computations started with a model corresponding to spherical accretion. One wonders if the choice of an initial model built also by disc accretion allows us to reach higher surface velocities on the ZAMS for massive stars. Disc accretion allows the accreted material to radiate its internal energy in the disc before being accreted, so that a model built by disc accretion has less internal energy and consequently, a smaller radius than a model of the same mass built by spherical accretion. As a consequence, the critical velocity of an initial model built by disc accretion is higher than for the present initial model. We then can start the computations with a higher Ωini but not with a higher angular momentum: for solid-body rotation at the critical velocity, one has 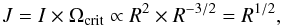 (7)so that a smaller radius leads to a smaller angular momentum. This remark concerns the total angular momentum of the star itself but also the specific angular momentum of the accreted material, which remains constant during all the accretion phase. At the end of the accretion phase, the total amount of angular momentum gathered by a star built from an initial core rotating at its critical velocity is even smaller, if the initial model is built by disc accretion than with the present initial model. As the radius and the density profile on the ZAMS are fixed, the surface velocity of a ZAMS star decreases when its angular momentum decreases. The conclusion is that the velocity limitation on the ZAMS is even stronger with an initial model coming from disc accretion than with the present one. It has to be noted that a longer initial phase of spherical accretion would lead to larger radii for a given mass. Is it possible to significantly relax the velocity limitation on the ZAMS by delaying the transition between spherical and disc accretion phases? We shall discuss this point in a forthcoming paper.
(7)so that a smaller radius leads to a smaller angular momentum. This remark concerns the total angular momentum of the star itself but also the specific angular momentum of the accreted material, which remains constant during all the accretion phase. At the end of the accretion phase, the total amount of angular momentum gathered by a star built from an initial core rotating at its critical velocity is even smaller, if the initial model is built by disc accretion than with the present initial model. As the radius and the density profile on the ZAMS are fixed, the surface velocity of a ZAMS star decreases when its angular momentum decreases. The conclusion is that the velocity limitation on the ZAMS is even stronger with an initial model coming from disc accretion than with the present one. It has to be noted that a longer initial phase of spherical accretion would lead to larger radii for a given mass. Is it possible to significantly relax the velocity limitation on the ZAMS by delaying the transition between spherical and disc accretion phases? We shall discuss this point in a forthcoming paper.
4. Comparisons with observed velocities of Herbig Ae/Be stars
Figure 16 shows the pre-MS evolutionary tracks in the log g versus log Teff diagram.
 |
Fig. 16 Diagram log Teff – log g. Solid lines are evolutionary tracks of the grid described in Sect. 3.3 (with the non-rotating birthline). Dashed lines are iso-velocities of 50, 100, 150 and 200 km s-1 of these models (from right to left). Dots indicate observations of Herbig Ae/Be stars with measured vsini from Alecian et al. (2013). The symbol and its colour depends on the value of w = vsini4/π: red triangles are used for w < 50 km s-1, orange diamonds for 50 km s-1<w< 100 km s-1, yellow squares for 100 km s-1<w< 150 km s-1, green pentagons for 150 km s-1<w< 200 km s-1 and blue stars for 200 km s-1<w< 250 km s-1. A mean error bar is displayed, which corresponds to the averaged error over the stars for which an error is given. |
In this figure, the bottom line is the birthline and the upper ends of the tracks correspond to the ZAMS. Theoretically, one expects that pre-MS stars with masses between 2 and 14 M⊙ should be observed in the colored region of the diagram. The colored regions correspond to different ranges of surface velocities:
-
red: v < 50 km s-1;
-
orange: 50 km s-1 ≤ v< 100 km s-1;
-
yellow: 100 km s-1 ≤ v< 150 km s-1;
-
green: 150 km s-1 ≤ v< 200 km s-1; and
-
blue: v ≥ 200 km s-1.
As expected, the surface velocity predicted by the models increases, when the surface gravity increases and when the effective temperature increases.
Overplotted on this diagram are the observed positions of Herbig Ae/Be stars studied by Alecian et al. (2013) and Folsom et al. (2012). Many stars show a log g equal to 4.0, which reflects the difficulty of measuring this quantity. This is also reflected by the large error bars on the determined gravity. This has, of course, to be kept in mind when comparisons are made with models. We see also that the density of points is the greatest in regions corresponding to the lower mass range, where the pre-MS evolution lasts the longer and where the initial mass function predicts a large number of objects.
To compare the measured rotational velocities to the results of our models, we use different symbols and colours for the observations. If the predictions of the models agreed with these observations, the points of a given colour should appear in the region of the corresponding colour. Unsurprisingly, we see that very few observational points lie in their expected region. Indeed, the track for each mass corresponds to only one peculiar initial condition, while one expects a distribution of initial conditions in reality, in particular with Ωini. Moreover, what is measured is vsini and not v. Even if we try to correct for this effect by multiplying the observed vsini values by the inverse of the average of sini (4/π), we cannot pretend that the plotted values correspond to the true velocities. In the present state, it is thus not possible to draw any strong conclusion from these comparisons. We can however note that there appears to be a general trend for having the fastest rotators (blue and green points) on average at a higher gravity and effective temperature than slow rotators (orange and yellow points), in accordance with the trend expected from the models. This trend needs however to be confirmed with respect to the difficulties mentioned above. We hope however that this attempt of comparing the models with the observations will stimulate further observations and theoretical modelling.
5. Impact of pre-MS evolution on the MS evolution
We have seen above that, with the accretion law considered here, the stars do not rotate as solid-body when arriving on the ZAMS, as assumed, for example, in Ekström et al. (2012). Let us now study the consequence of this small differential rotation in the present models on the evolution during the whole MS phase. For this purpose, we compute additional models for 6 and 14 M⊙, which started on the ZAMS with an initially flat rotation profile (labelled ZAMS), as in Ekström et al. (2012). The models labelled ZAMS(vsurf) were computed with a chosen Ωini, such that vsurf on the ZAMS is the same as in the corresponding model with accretion labelled PMS(accr). In a similar manner, the models denoted ZAMS(J) were computed with an Ωini, such that the total angular momentum content, J, on the ZAMS, is the same as in the corresponding model with accretion.
 |
Fig. 17 HR diagram showing the main-sequence evolution of the five models of 6 M⊙, as described in Sect. 5. |
The MS tracks of these different models are displayed in Fig. 17 for the 6 M⊙ case (with the models labelled HAYA, as described below). A comparison of the evolution of the surface velocity of the same models are shown in Fig. 18. Finally, Fig. 19 shows the comparison of their internal rotation profiles.
Figure 17 shows that there is no significant difference in the MS tracks of the various models considered. Comparing the evolution of the surface velocities (see Fig. 18), we see that the ZAMS(vsurf) model presents a strong decrease of the surface velocity at the beginning of the MS phase. This is due to the meridional currents that have a high velocity and that advect angular momentum from the surface to the central region when Ω is constant inside the star. This occurs until an equilibrium situation is achieved between this advection process, which builds and maintains the gradient of Ω, and the shear turbulence, which tends to erode it (Zahn 1992; Denissenkov et al. 1999; Meynet & Maeder 2000).
In the present models with accretion and internal transport of angular momentum during the pre-MS phase, we obtain a shallow internal gradient of Ω on the ZAMS. This implies that meridional currents will have an easier job for building the equilibrium profile. A decrease that is less strong of the surface velocity at the beginning of the MS phase is then obtained for these models than for models starting from the ZAMS. This is very apparent in Fig. 18. We see that models accounting for the pre-MS phase do not show the decrease of the surface velocity shown by models starting from the ZAMS.
We saw that the gradient of Ω on the ZAMS in pre-MS models with accretion decreases with the mass. This is why a small decrease in the surface velocity can be seen for higher masses (see the small peak of velocity just before the ZAMS in Fig. 12).
 |
Fig. 18 Evolution of the surface velocity during the main sequence for the five models of 6 M⊙, as described in Sect. 5. |
 |
Fig. 19 Rotation profiles on the main sequence for the five models of 6 M⊙, as described in Sect. 5. The upper panel shows the profiles on the ZAMS, while the lower panel shows the profiles 107 yr after the ZAMS (i.e. at around 15% of the time spent on the MS). Filled squares indicate the surface of the star. |
The same behaviour is found for the ZAMS(J) model. The main difference is the level of the surface velocity that is reached when the equilibrium situation is reached. While in the ZAMS(vsurf) model, the surface velocity that reached after equilibrium is below that which is reached in the PMS(accr) model by about 15−20%. The surface velocity of the ZAMS(J) model reaches the same level as in the PMS(accr) model.
Importantly, the comparison of the evolution of the surface velocities between the ZAMS(vsurf) and PMS(accr) models shows that two stars with the same initial mass, position in the HR diagram, and initial surface velocity may show very different evolutions for the surface velocities during the MS phase, depending on their total content of angular momentum. When the total angular momentum is the same in both models, the evolution of the surface velocities are the same except at the very beginning of the MS phase.
It is interesting now to look at the evolution of the internal distribution of Ω and of the surface chemical enrichments. These two features are strongly related, since the main drivers of the surface enrichments are the gradients of Ω. Comparing the distributions of Ω, we note the following differences:
-
After 15% of the total MS time, the rotation profiles of all themodels are similar in terms of ∇Ω.
-
At this stage, the only remaining differences are simple shifts in the absolute value of Ω, due to the differences of total angular momentum content of the star.
-
While this shift is negligible in ZAMS(J) models, it is more pronounced in ZAMS(vsurf) models (~15−20%).
This shift in the rotation profile is at the origin of the shift in vsurf previously mentioned. Except for this global shift, we see that the various rotation profiles converge in a short amount of time compared to the total MS time. As a consequence, there is no significant differences in the surface enrichments during the MS phase of all these models. These remarks are true for both the 6 and 14 M⊙ models.
From the above considerations, we can conclude that the assumption of solid-body rotation on the ZAMS is justified and provides evolution during the MS phase that quite agree with the evolution obtained from models accounting for the pre-MS phase with accretion. However, this is true only if models to be compared start their MS evolution with the same total angular momentum content.
It is also interesting to compare the PMS(accr) models to models starting on the Hayashi line and evolving at constant mass on the ZAMS. These initial conditions mimic stars following a very strong initial episode of accretion, which bring the model at the top of the Hayashi line. In a similar manner to what was done above, we computed models labelled HAYA(vsurf) and HAYA(J), starting on the Hayashi line with initial rotation rates where vsurf and J on the ZAMS respectively, are the same as in PMS(accr) models. Results of these models are shown in Figs. 17−19. We see that the results obtained from the HAYA models are all similar to the results of the PMS(accr) model. In contrast with the ZAMS models, they do not show a very marked decrease in the surface velocity at the beginning of the MS phase, as already noted above. This comes from stars that are not rotating as solid bodies at that stage (see Fig. 19). A noticeable difference with respect to the PMS(accr) models is that the HAYA models allow us to reach much higher velocities on the ZAMS. This will be studied in a forthcoming work with accretion rates that are very strong in a first phase and that then decrease with time.
6. Conclusions and perspectives
We have studied the pre-MS evolution of stars with masses on the ZAMS between 2 and 22 M⊙, considering rotation and accretion in the framework of the cold disc accretion scenario with an accretion rate increasing with the mass. Our main results are the following:
-
Stars reach the ZAMS with a rotation profile that is not far fromsolid-body rotation with small (but non-zero) gradient of angularvelocity. The core rotates between 20%(14 M⊙) and 80% (2 M⊙) faster than the surface for a fixed ratio v/vcrit = 0.4 on the ZAMS.
-
For all the cases considered in the present work, models of a given mass and total angular momentum content present very similar MS evolutions in terms of evolutionary tracks, surface velocities, and abundances, independent of their formation history. This is fortunate: if it would not be the case, then the evolution of stars would not only depend on the mass, metallicity, rotation, magnetic field, multiplicity but also depend on the formation history. This does not appear to be the case.
-
Above 8 M⊙, the present scenario cannot produce the whole range of surface velocities on the ZAMS. Only velocities below an upper limit can be achieved. For instance, it is not possible to produce 15 M⊙ with rotational velocities on the ZAMS equal or higher than v/vcrit = 0.4.
This last conclusion leads to the question of the origin of the massive fast rotators. We can identify different lines of research for future studies: 1) as was briefly indicated above, it may be that a different history for the mass accretion rate may be a solution. 2) Here, we also suppose that the accreted layer is deposited onto the star with the same angular momentum as the surface. In the disc, matter rotates with a Keplerian velocity, which is equivalent to the critical velocity. It may be that the matter accreted have a specific angular momentum is higher than the surface. This would, of course, change the results obtained here, even
when keeping the same mass accretion law. 3) Finally, it may be also that some stars acquire their high velocity through tidal interactions or mass transfer in close binaries (de Mink et al. 2013).
This assumption corresponds to the lower limit for the accretion of angular momentum. The upper limit is given when the material is accreted with a quasi-keplerian velocity (i.e. quasi-critical velocity), which is expected to be the velocity of the material in the disc. We shall investigate the impact of this other limiting case in a forthcoming work.
Acknowledgments
Part of this work was supported by the Swiss National Science Foundation.
References
- Alecian, E., Wade, G. A., Catala, C., et al. 2013, MNRAS, 429, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, & F. N. Bash, ASP Conf. Ser., 336, 25 [Google Scholar]
- Beech, M., & Mitalas, R. 1994, ApJS, 95, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Behrend, R., & Maeder, A. 2001, A&A, 373, 190 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernasconi, P. A. 1997, Ph.D. Thesis, Université de Genève [Google Scholar]
- Bernasconi, P. A., & Maeder, A. 1996, A&A, 307, 829 [NASA ADS] [Google Scholar]
- Bodenheimer, P., & Sweigart, A. 1968, ApJ, 152, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Caughlan, G. R., & Fowler, W. A. 1988, Atomic Data and Nuclear Data Tables, 40, 283 [Google Scholar]
- Churchwell, E. 1998, The Origin of Stars and Planetary Systems, eds. C. Lada, & N. Kylafis (Alphen-sur-le-Rhin: Kluwer) [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, L143 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., Ivanova, N. S., & Weiss, A. 1999, A&A, 341, 181 [NASA ADS] [Google Scholar]
- Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Folsom, C. P., Bagnulo, S., Wade, G. A., et al. 2012, MNRAS, 422, 2072 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Girichidis, P., Federrath, C., Banerjee, R., & Klessen, R. S. 2011, MNRAS, 413, 2741 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Lapinov, A., Schreyer, K., Stecklum, B., & Zinchenko, I. 2000, A&A, 364, 613 [NASA ADS] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, T., Yorke, H. W., & Omukai, K. 2010, ApJ, 721, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., Gies, D. R., & McSwain, M. V. 2010, ApJ, 722, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2010, ApJ, 722, 1556 [CrossRef] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, T. 2011, ApJ, 732, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
- McNally, D. 1964, ApJ, 140, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Nakano, T. 1989, ApJ, 345, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Klessen, R. S., Mac Low, M.-M., & Banerjee, R. 2010, ApJ, 725, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., & Mac Low, M.-M. 2011, ApJ, 729, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980a, ApJ, 241, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980b, ApJ, 242, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Palla, F., & Salpeter, E. E. 1986a, ApJ, 308, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W., Palla, F., & Salpeter, E. E. 1986b, ApJ, 302, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Yorke, H. W., & Bodenheimer, P. 2008, in Massive Star Formation: Observations Confront Theory, eds. H. Beuther, H. Linz, & T. Henning, ASP Conf. Ser., 387, 189 [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Birthline with rotation (Ωini = 2.1 × 10-5 s-1, solid blue line) and birthline without rotation with three contractions (long-dashed blue lines). Some points of the birthline of Behrend & Maeder (2001) are displayed for comparison (filled squares). The short-dashed lines indicate the ZAMS of Ekström et al. (2012) without rotation (black) and the pre-MS tracks at constant mass corresponding to the contractions displayed (red). The numbers along the birthline are rotational velocities (in km s-1) along the birthline with rotation at M = 2, 6 and 14 M⊙. Letters along the birthline indicate the evolutionary stages described in the text (Sect. 3.1). Straight dotted lines are iso-radii of 0.1, 1, 10, 100 and 1000 R⊙ from bottom left to top right. |
| In the text | |
 |
Fig. 2 Evolution of the radius and the internal structure of the star on the birthline without rotation (upper panel) and with rotation (Ωini = 2.1 × 10-5 s-1, lower panel). In each panel, the upper solid line is the radius and shaded areas correspond to convective regions. The dotted lines indicate the iso-masses. That is, the radius corresponding to fixed values of the lagrangian coordinate Mr (Mr = 1, 2, 3, ... [M⊙]). Letters along the radius on the upper panel indicate the evolutionary stages described in the text (Sect. 3.1). Numbers along the radius on the lower panel correspond to rotational velocities (in km s-1) at M = 1, 2, 3, ... [M⊙]. |
| In the text | |
 |
Fig. 3 Upper panel: vertical component of the meridional circulation for the 6 M⊙ model with Ωini = 9 × 10-6 s-1 (i.e., model of the grid described in Sect. 3.3) at an age of 200 000 years just at the end of the accretion phase (see Fig. 6). Lower panel: diffusion coefficient for the transport by shear instability for the same model. |
| In the text | |
 |
Fig. 4 Angular velocity on the birthline with Ωini = 2.1 × 10-5 s-1 (value needed to obtain vZAMS/vcrit = 0.40 for the 14 M⊙). Upper panel: angular velocity at the surface and in the centre of the star, along the birthline as a function of the total mass. Letters indicate the evolutionary stages described in the text (Sect. 3.1), and triangles indicate the appearance of the convective core. Lower panel: rotation profiles on the birthline at different masses from 2 M⊙ to 14 M⊙, by steps of 1 M⊙. |
| In the text | |
 |
Fig. 5 Evolutionary tracks for the models with MZAMS = 6 M⊙ with rotation (solid blue line) and without rotation (dashed red line). The numbers along the track of the rotating model indicate the rotation velocity (in km s-1) at M = 1, 2, ..., 6 [M⊙], on the ZAMS, and on the terminal-age main sequence (TAMS). The right dotted line represents the birthline, and the left dotted line represents the ZAMS of Ekström et al. (2012) without rotation. The end of accretion is indicated by filled squares. The ZAMS and the TAMS of the models are indicated by empty squares. |
| In the text | |
 |
Fig. 6 Similar figure as Fig. 2, following the evolution with time of the 6 M⊙ model. Time 0 is taken at the beginning of the computation starting from the 0.7 M⊙ core. Filled squares indicate the end of accretion. |
| In the text | |
 |
Fig. 7 Angular velocity of the model with MZAMS = 6 M⊙. Upper panel: angular velocity at the surface and in the centre of the star as a function of the age. Circles indicate the stages for which the rotation profiles are shown in the lower panel. The filled square corresponds to the end of accretion, and the triangle indicates the appearance of the convective core. Lower panel: rotation profiles during the contraction phase at different stages indicated by circles on the upper panel. The thickest line corresponds to the ZAMS. |
| In the text | |
 |
Fig. 8 Same as Fig. 6 but for MZAMS = 14 M⊙. |
| In the text | |
 |
Fig. 9 Same as Fig. 7 but for MZAMS = 14 M⊙. |
| In the text | |
 |
Fig. 10 Ratio v/vcrit as a function of MZAMS at different stages of the evolution, for the models described in Sect. 3.3. The dotted line indicates the maximum value of v/vcrit reached during the pre-MS. |
| In the text | |
 |
Fig. 11 Grid of pre-MS models with MZAMS from 2 to 14 M⊙, by steps of 1 M⊙, with Ωini ∝ MZAMS (i.e. models described in Sect. 3.3, solid blue lines). Two birthlines (without rotation and with the higher Ωini) are plotted (solid black lines). The dashed line indicates the ZAMS of Ekström et al. (2012) and dotted lines correspond to iso-radius of 0.1, 1, 10 and 100 R⊙ from left to right. Equatorial surface velocities on the ZAMS are indicated (in km s-1) at the end of each track. Dot-dashed red lines indicate isochrones of 2 × 105, 5 × 105 and 2 × 106 yr from top to bottom. |
| In the text | |
 |
Fig. 12 Evolution of the surface velocity of the models described in Sect. 3.3. Filled squares correspond to the end of the accretion, while empty squares indicate the ZAMS and the TAMS. |
| In the text | |
 |
Fig. 13 Same as Fig. 12 but focused on the contraction phase. This time the x-axis is the fraction of the total contraction time, so that the end of accretion corresponds to 0 and the ZAMS to 1. |
| In the text | |
 |
Fig. 14 Maximum surface velocities on the ZAMS as a function of MZAMS for models between 2 and 22 M⊙. The dotted line in the upper panel indicates the critical velocity. |
| In the text | |
 |
Fig. 15 Evolution of the surface velocity during the pre-MS for models with Ωini = 2.25 × 10-5 s-1 and MZAMS between 9 and 22 M⊙. The thickest line is the corresponding birthline, and the empty squares indicate the ZAMS. Letters correspond to the stages described in Sect. 3.1. |
| In the text | |
 |
Fig. 16 Diagram log Teff – log g. Solid lines are evolutionary tracks of the grid described in Sect. 3.3 (with the non-rotating birthline). Dashed lines are iso-velocities of 50, 100, 150 and 200 km s-1 of these models (from right to left). Dots indicate observations of Herbig Ae/Be stars with measured vsini from Alecian et al. (2013). The symbol and its colour depends on the value of w = vsini4/π: red triangles are used for w < 50 km s-1, orange diamonds for 50 km s-1<w< 100 km s-1, yellow squares for 100 km s-1<w< 150 km s-1, green pentagons for 150 km s-1<w< 200 km s-1 and blue stars for 200 km s-1<w< 250 km s-1. A mean error bar is displayed, which corresponds to the averaged error over the stars for which an error is given. |
| In the text | |
 |
Fig. 17 HR diagram showing the main-sequence evolution of the five models of 6 M⊙, as described in Sect. 5. |
| In the text | |
 |
Fig. 18 Evolution of the surface velocity during the main sequence for the five models of 6 M⊙, as described in Sect. 5. |
| In the text | |
 |
Fig. 19 Rotation profiles on the main sequence for the five models of 6 M⊙, as described in Sect. 5. The upper panel shows the profiles on the ZAMS, while the lower panel shows the profiles 107 yr after the ZAMS (i.e. at around 15% of the time spent on the MS). Filled squares indicate the surface of the star. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.