| Issue |
A&A
Volume 557, September 2013
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 23 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219165 | |
| Published online | 06 September 2013 | |
Binary black holes in nuclei of extragalactic radio sources
1
Institut d’Astrophysique, UPMC Univ. Paris 06, CNRS, UMR 7095,
98bis Bd Arago,
75014
Paris,
France
e-mail:
roland@iap.fr
2
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69,
53121
Bonn,
Germany
3
Núcleo de Astrofísica Teórica, Universidade Cruzeiro do Sul,
R. Galvão Bueno 868, Liberdade,
01506-000
São Paulo, SP, Brazil
4
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
Received:
5
March
2012
Accepted:
5
June
2013
If we assume that nuclei of extragalactic radio sources contain binary black hole systems, the two black holes can eject VLBI components, in which case two families of different VLBI trajectories will be observed. Another important consequence of a binary black hole system is that the VLBI core is associated with one black hole, and if a VLBI component is ejected by the second black hole, one expects to be able to detect the offset of the origin of the VLBI component ejected by the black hole that is not associated with the VLBI core. The ejection of VLBI components is perturbed by the precession of the accretion disk and the motion of the black holes around the center of gravity of the binary black hole system. We modeled the ejection of the component taking into account the two pertubations and present a method to fit the coordinates of a VLBI component and to deduce the characteristics of the binary black hole system. Specifically, this is the ratio Tp/Tb where Tp is the precession period of the accretion disk and Tb is the orbital period of the binary black hole system, the mass ratio M1/M2, and the radius of the binary black hole system Rbin. From the variations of the coordinates as a function of time of the ejected VLBI component, we estimated the inclination angle io and the bulk Lorentz factor γ of the modeled component. We applied the method to component S1 of 1823+568 and to component C5 of 3C 279, which presents a large offset of the space origin from the VLBI core. We found that 1823+568 contains a binary black hole system whose size is Rbin ≈ 60 μas (μas is a microarcsecond) and 3C 279 contains a binary black hole system whose size is Rbin ≈ 420 μas. We calculated the separation of the two black holes and the coordinates of the second black hole from the VLBI core. This information will be important to link the radio reference-frame system obtained from VLBI observations and the optical reference-frame system obtained from Gaia.
Key words: astrometry / galaxies: jets / galaxies: individual: 1823+568 / galaxies: individual: 3C 279
© ESO, 2013
1. Introduction
VLBI observations of compact radio sources show that the ejection of VLBI components does not follow a straight line, but undulates. These observations suggest a precession of the accretion disk. To explain the precession of the accretion disk, we assumed that the nuclei of radio sources contain binary black hole systems (BBH system, see Fig. 1).
A BBH system produces three pertubations of the VLBI ejection due to
-
1.
the precession of the accretion disk;
-
2.
the motion of the two black holes around the center of gravity of the BBH system; and
-
3.
the motion of the BBH system in the galaxy.
In this article, we do not take into account the possible third pertubation due to the motion of the BBH system in the galaxy.
 |
Fig. 1 BBH system model. The two black holes can have an accretion disk and can eject VLBI components. If it is the case, we observe two different families of trajectories and an offset between the VLBI core and the origin of the VLBI component if it is ejected by the black hole that is not associated with the VLBI core. The angles Ω1 and Ω2 between the accretion disks and the rotation plane of the BBH system can be different. |
A BBH system induces several consequences, which are that
-
1.
even if the angle between the accretion disk and the plane of rotation of the BBH system is zero, the ejection does not follow a straight line (due to the rotation of the black holes around the center of gravity of the BBH system);
-
2.
the two black holes can have accretion disks with different angles with the plane of rotation of the BBH system and can eject VLBI components; in that case we observe two different families of trajectories; a good example of a source with two families of trajectories is 3C 273, whose components C5 and C9 follow two different types of trajectories (see Fig. 2); and
-
3.
if the VLBI core is associated with one black hole, and if the VLBI component is ejected by the second black hole, there will be an offset between the VLBI core and the origin of the ejection of the VLBI component; this offset will correspond to the radius of the BBH system.
The precession of the accretion disk can be explained using a single rotating black hole (Lense-Thirring effect) or by the magnetically driven precession (Caproni et al. 2006). However, a single black hole and a BBH system have completely different consequences. In the case of a BBH system, one has an extra perturbation of the ejected component due to the motions of the black holes around the center of gravity of the BBH system. One can expect to observe two different families of trajectories (if the two black holes eject VLBI components) and an offset of the origin of the ejected component if it is ejected by the black hole that is not associated with the VLBI core.
 |
Fig. 2 Trajectories of the VLBI components C5 and C9 of 3C 273 using MOJAVE data (Lister et al. 2009b). We observe two different types of trajectories, suggesting that they are ejected from two different black holes. |
We modeled the ejection of the VLBI component using a geometrical model that takes into account the two main perturbations due to the BBH system, i.e.
-
1.
the precession of the accretion disk; and
-
2.
the motion of the two black holes around the center of gravity of the BBH system.
Modeling the ejection of VLBI components using a BBH system has been developed in previous articles, for instance Britzen et al. (2001) modeled 0420-014, Lobanov & Roland (2005) modeled 3C 345, and Roland et al. (2008) modeled 1803+784. Observationnal VLBI studies have been performed to directly detect BBH systems in active galactic nuclei (Burke-Spolaor 2011; Tingay & Wayth 2011).
In Sect. 2 we recall the main lines of the model. The details of the model can be found in Roland et al. (2008).
We determined the free parameters of the model by comparing the observed coordinates of the VLBI component with the calculated coordinates of the model.
This method requires knowing of the variations of the two coordinates of the VLBI component as a function of time. Because these observations contain the kinematical information, we will be able to estimate the inclination angle of the source and the bulk Lorentz factor of the ejected component.
In this article we present a method to solve this problem, either for a precession model or for a BBH system model, based on understanding the space of the solutions.
Practically, two different cases can occur when we try to solve this problem.
-
1.
Either the VLBI component is ejected from the VLBI core, orthe offset is smaller than or on the order of the smallest error bars ofthe VLBI positions of the ejected component (case I);
-
2.
or the VLBI component is ejected with an offset larger than the smallest error bars of the VLBI positions of the ejected component (case II).
Case II is much more complicated to solve than case I, because the observed coordinates contain an unknown offset that is larger than the error bars. Therefore, we first have to find the offset, then correct the VLBI data from the offset, and finally find the solution corresponding to the corrected data.
We present the method for solving the problem in Sect. 3. To illustrate case I, we solve the fit of component S1 of 1823+568 using MOJAVE data in Sect. 4. To illustrate case II, we solve the fit of component C5 of 3C 279 using MOJAVE data in Sect. 5.
2. Model
2.1. Introduction: two-fluid model
We describe the ejection of a VLBI component in the framework of the two-fluid model (Sol et al. 1989; Pelletier & Roland 1989, 1990; Pelletier & Sol 1992). The two-fluid description of the outflow is adopted with the following assumptions:
-
1.
The outflow consists of an e−−e+ plasma (hereafter the beam) moving at a highly relativistic speed (with corresponding Lorentz factor1γb ≤ 30) surrounded by an e− − p plasma (hereafter the jet) moving at a mildly relativistic speed of vj ≤ 0.4 × c.
-
2.
The magnetic field lines are parallel to the flow in the beam and the mixing layer, and are toroidal in the jet (see Fig. 3).
Muxlow et al. (1988) and Roland et al. (1988) found that the Cygnus A hot spots could be explained by a an e− − p plasma moving at a mildly relativistic speed, i.e. vj ≤ 0.4 × c. Consequently, the two-fluid model was introduced to explain superluminal radio sources observed in the nuclei of radio sources.
 |
Fig. 3 Two-fluid model. The outflow consists of an e− − e+ plasma, the beam, moving at a highly relativistic speed, surrounded by an e− − p plasma, and of the jet, moving at a mildly relativistic speed. The magnetic field lines are parallel to the flow in the beam and the mixing layer, and are toroidal in the jet. |
The e− − p jet carries most of the mass and the kinetic energy ejected by the nucleus. It is responsible for the formation of kpc-jets, hot spots, and extended lobes (Roland & Hetem 1996). The relativistic e± beam moves in a channel through the mildly relativistic jet and is responsible for the formation of superluminal sources and their γ-ray emission (Roland et al. 1994). The relativistic beam can propagate when the magnetic field B is parallel to the flow in the beam and in the mixing layer between the beam and the jet, and when it is greater than a critical value (Pelletier et al. 1988; Achatz & Schlickeiser 1993). The magnetic field in the jet becomes rapidly toroidal as a function of distance from the core (Pelletier & Roland 1990).
The observational evidence for the two-fluid model has been discussed by e.g. Roland & Hetem (1996). Observational evidence for relativistic ejection of an e± beam comes from the γ-ray observations of MeV sources (Roland & Hermsen 1995; Skibo et al. 1997) and from VLBI polarization observations (Attridge et al. 1999).
The formation of X-ray and γ-ray spectra, assuming relativistic ejection of e± beams, has been investigated by Marcowith et al. (1995, 1998) for Centaurus A.
The possible existence of VLBI components with two different apparent speeds has been pointed out for the radio galaxies Centaurus A (Tingay et al. 1998), Virgo A (Biretta et al. 1999) and 3C 120 (Gómez et al. 2001). If the relativistic beam transfers some energy and/or relativistic particles to the jet, the relativistic particles in the jet will radiate and a new VLBI component with a mildly relativistic speed will be observed (3C 120 is a good example of a source showing this effect).
2.2. Geometry of the model
We call Ω the angle between the accretion disk and the orbital plane
(XOY) of the BBH system. The component is ejected on a cone (the
precession cone) with its axis in the Z′OZ
plane and of opening angle Ω. We assumed that the line of sight is in the plane
(YOZ) and forms an angle io with the axis
Z′OZ (see Fig. 4). The axis η corresponds to the mean ejection
direction of the VLBI component projected in a plane perpendicular to the line of sight,
so the plane perpendicular to the line of sight is the plane (ηOX). We
call ΔΞ the rotation angle in the plane perpendicular to the line of sight to transform
the coordinates η and X into coordinates
N (north) and W (west), which are directly comparable
with the VLBI observations. We have 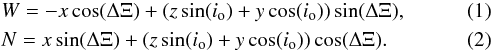 The
sign of the coordinate W was changed from Roland et al. (2008) to use the same definition as VLBI observations.
The
sign of the coordinate W was changed from Roland et al. (2008) to use the same definition as VLBI observations.
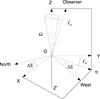 |
Fig. 4 Geometry of the problem. The planes X–η and west–north are perpendicular to the line of sight. In the west–north plane, the axis η corresponds to the mean ejection direction of the VLBI component. Ω is the opening angle of the precession cone. |
2.3. General perturbation of the VLBI ejection
For VLBI observations, the origin of the coordinates is black hole 1, i.e. the black hole
ejecting the VLBI components. For the sake of simplicity, we assumed that the two black
holes have circular orbits, i.e. e = 0. Therefore, the coordinates of the moving
components in the frame of reference where black hole 1 is considered the origin are
(Roland et al. 2008) ![\begin{eqnarray} \label{eq:xc} x_{\rm c} &=& [R_{\rm o}(z) \cos(\omega_{\rm p}t-k_{\rm p}z(t)+\phi_{\rm o}) \nonumber\quad\quad\quad \\ &&\quad + x_{1} \cos(\omega_{\rm b}t-k_{\rm b}z(t)+\psi_{\rm o}) - x_{1} \cos(\psi_{\rm o})] \exp(-t/T_{\rm d}), \quad\quad\quad\\ \label{eq:yc} y_{\rm c} & = & [R_{\rm o}(z) \sin(\omega_{\rm p}t-k_{\rm p}z(t)+\phi_{\rm o}) \nonumber \quad\quad\quad\\ &&\quad + y_{1} \sin(\omega_{\rm b}t-k_{\rm b}z(t)+\psi_{\rm o}) - y_{1} \sin(\psi_{\rm o})] \exp(-t/T_{\rm d}), \quad\quad\quad\\ \label{eq:zc} z_{\rm c} &=& z_{\rm c}(t), \end{eqnarray}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq32.png) where
where
-
Ro(z) is the amplitude of the precession perturbation, given by Ro(z) = Rozc(t)/(a + zc(t)), with a = Ro/(2tanΩ);
-
ωp is ωp = 2π/Tp, where Tp is the precession period, and kp is defined by kp = 2π/TpVa, where Va is the speed of the propagation of the perturbations;
-
ωb is ωb = 2π/Tb, where Tb is the BBH system period and kb is defined by kb = 2π/TbVa;
-
Td is the characteristic time of the damping of the perturbation;
![\begin{eqnarray} R_{\rm bin} = \left[\frac{T_{\rm b}^{2}}{4\pi^{2}}G(M_{1}+M_{2}) \right]^{1/3}. \label{eq:Rbin} \end{eqnarray}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq49.png) (7)In
mas units (milli arc second units), it is
(7)In
mas units (milli arc second units), it is ![\begin{eqnarray} R_{\rm bin} \approx 2.06 \times 10^{8} \; \left[\frac{T_{\rm b}^{2}}{4\pi^{2}}G(M_{1}+M_{2}) \right]^{1/3} / D_{\rm a} , \label{eq:Rbin_mas} \end{eqnarray}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq50.png) (8)where
Da = Dl/(1 + z)2
is the angular distance, Dl is the luminosity distance, and
z is the redshift of the source.
(8)where
Da = Dl/(1 + z)2
is the angular distance, Dl is the luminosity distance, and
z is the redshift of the source.
The differential equation governing the evolution of
zc(t) can be obtained by defining the speed
of the component, namely 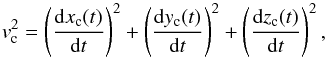 (9)where
vc is related to the bulk Lorentz factor by
(9)where
vc is related to the bulk Lorentz factor by
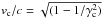 .
.
Using (3)–(5), we find from (9)
that dzc/dt is the
solution of the equation 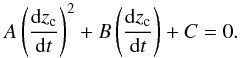 (10)The calculation of
the coefficients A, B and C can be
found in Appendix A of Roland et al. (2008).
(10)The calculation of
the coefficients A, B and C can be
found in Appendix A of Roland et al. (2008).
Equation (10) admits two solutions corresponding to the jet and the counter-jet.
Following Camenzind & Krockenberger (1992),
if we call θ the angle between the velocity of the component and the line
of sight, we have 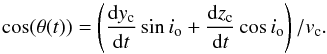 (11)The Doppler beaming
factor δ, characterizing the anisotropic emission of the moving
component, is
(11)The Doppler beaming
factor δ, characterizing the anisotropic emission of the moving
component, is ![\begin{equation} \delta_{\rm c}(t) = \frac{1}{\gamma_{\rm c} \left[1 - \beta_{\rm c} \cos(\theta(t))\right]}, \label{eq:delta} \end{equation}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq65.png) (12)where
βc = vc/c.
The observed flux density is
(12)where
βc = vc/c.
The observed flux density is 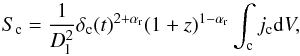 (13)where
Dl is the luminosity distance of the source,
z its redshift, jc is the emissivity of the
component, and αr is the synchrotron spectral index (it is
related to the flux density by
S ∝ ν− αr).
As the component is moving relativistically toward the observer, the observed time is
shortened and is given by
(13)where
Dl is the luminosity distance of the source,
z its redshift, jc is the emissivity of the
component, and αr is the synchrotron spectral index (it is
related to the flux density by
S ∝ ν− αr).
As the component is moving relativistically toward the observer, the observed time is
shortened and is given by ![\begin{equation} t_{\rm obs} = \int_{0}^{t}\left[1- \beta_{\rm c} \cos(\theta(t'))\right]\left(1+z\right){\rm d}t'. \label{eq:tobs} \end{equation}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq71.png) (14)
(14)
2.4. Coordinates of the VLBI component
Solving (10), we determine the coordinate zc(t) of a point-source component ejected relativistically in the perturbed beam. Then, using (3) and (4), we can find the coordinates xc(t) and yc(t) of the component. In addition, for each point of the trajectory, we can calculate the derivatives dxc/dt, dyc/dt, dzc/dt and then deduce cosθ from (11), δc from (12), Sν from (13) and tobs from (14).
After calculating the coordinates xc(t), yc(t) and zc(t), they can be transformed to wc(t) (west) and nc(t) (north) coordinates using (1) and (2).
As explained in Britzen et al. (2001), Lobanov & Roland (2005), and Roland et al. (2008), the radio VLBI component has to
be described as an extended component along the beam. We call
nrad the number of points (or integration steps along the
beam) for which we integrate to model the component. The coordinates
Wc(t),
Nc(t) of the VLBI component are then
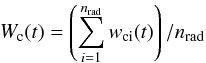 (15)and
(15)and
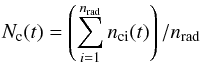 (16)and
can be compared with the observed coordinates of the VLBI component, which correpond to
the radio peak intensity coordinates provided by model-fitting during the VLBI data
reduction process.
(16)and
can be compared with the observed coordinates of the VLBI component, which correpond to
the radio peak intensity coordinates provided by model-fitting during the VLBI data
reduction process.
When, in addition to the radio, optical observations are available that peak in the light curve, this optical emission can be modeled as the synchrotron emission of a point source ejected in the perturbed beam, see Britzen et al. (2001) and Lobanov & Roland (2005). This short burst of very energetic relativistic e± is followed immediately by a very long burst of less energetic relativistic e±. This long burst is modeled as an extended structure along the beam and is responsible for the VLBI radio emission. In that case the origin to of the VLBI component is the beginning of the first peak of the optical light curve and is not a free parameter of the model.
2.5. Parameters of the model
In this section, we list the possible free parameters of the model. They are
-
io the inclination angle;
-
φo the phase of the precession at t = 0;
-
ΔΞ the rotation angle in the plane perpendicular to the line of sight (see Eqs. (1) and (2));
-
Ω the opening angle of the precession cone;
-
Ro the maximum amplitude of the perturbation;
-
Tp the precession period of the accretion disk;
-
Td the characteristic time for the damping of the beam perturbation;
-
M1 the mass of the black hole ejecting the radio jet;
-
M2 the mass of the secondary black hole;
-
γc the bulk Lorentz factor of the VLBI component;
-
ψo the phase of the BBH system at t = 0;
-
Tb the period of the BBH system;
-
to the time of the origin of the ejection of the VLBI component;
-
Va the propagation speed of the perturbations;
-
nrad is the number of steps to describe the extension of the VLBI component along the beam;
-
ΔW and ΔN the possible offsets of the origin of the VLBI component.
We will see that the parameter Va can be used to study the degeneracy of the solutions, so we can keep it constant to find the solution. The range of values that we study for parameter Va is 0.01 × c ≤ Va ≤ 0.45 × c2.
The parameter nrad is known when the size of the VLBI component is known.
This means that, pratically, the problem we have to solve is a 15 free parameter problem.
We have to investigate the different possible scenarios with regard to the sense of the rotation of the accretion disk and the sense of the orbital rotation of the BBH system. These possibilities correspond to ±ωp(t − z/Va) and ±ωb(t − z/Va). Because the sense of the precession is always opposite to the sense of the orbital motion (Katz 1997), we study the two cases denoted by +− and −+, where we have ωp(t − z/Va), −ωb(t − z/Va) and −ωp(t − z/Va), ωb(t − z/Va), respectively.
3. Method for solving the problem
3.1. Introduction
In this section, we explain the method for fitting VLBI observations using either a precession model or a BBH system model. The software is freely available on request to J. Roland3.
This method is a practical one that provides solutions, but the method is not unique and does not guarantee that all possible solutions are found.
We calculate the projected trajectory on the plane of the sky of an ejected component and
determine the parameters of the model to simultaneously produce the best fit with the
observed west and north coordinates. The parameters found minimize 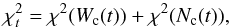 (17)where
χ2(Wc(t)) and
χ2(Nc(t)) are
the χ2 calculated by comparing the VLBI observations with the
calculated coordinates Wc(t) and
Nc(t) of the component. For instance, to
find the inclination angle that provides the best fit, we minimize
(17)where
χ2(Wc(t)) and
χ2(Nc(t)) are
the χ2 calculated by comparing the VLBI observations with the
calculated coordinates Wc(t) and
Nc(t) of the component. For instance, to
find the inclination angle that provides the best fit, we minimize
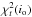 .
.
A good determination of the 1σ (standard deviation) error bar can be
obtained using the definition 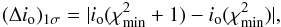 (18)which
provides two values (Δio)1σ + and
(Δio)1σ − (see Lampton et al. 1976 and Hébrard et al. 2002).
(18)which
provides two values (Δio)1σ + and
(Δio)1σ − (see Lampton et al. 1976 and Hébrard et al. 2002).
The concave parts of the surface χ2(io) contain a minimum. We can find solutions without a minimum; they correspond to the convex parts of the surface χ2(io) and are called mirage solutions.
 |
Fig. 5 Example of a possible profile of the solution χ2(io). There are two possible solutions for which χ2(Sol1)≈ χ2(Sol2). They correspond to the concave parts of the surface χ2(io). However, solution 2 is more robust than solution 1, i.e. it is the deepest one, and it will be the solution we adopt. |
To illustrate the properties of the surface χ2(io) we plot in Fig. 5 a possible example of a profile of the solution χ2(io). In Fig. 5, there are two possible solutions for which χ2(Sol1)≈ χ2(Sol2), solution 2 is more robust than solution 1, i.e. it is the deepest one, and it will be the solution we will keep.
We define the robustness of the solution as the square root of the difference between the smallest maximum close to the minimum and the minimum of the function χ2. A solution of robustness 3 is a 3σ solution, i.e. 3σ ⇔ Δχ2 = 9.
The main difficulties we have to solve are the following:
-
1.
find all possible solutions;
-
2.
eliminate the mirage solutions;
-
3.
find the most robust solutions.
For a given inclination angle of the BBH system problem, there exists a parameter that allows us to find the possible solutions. This fundamental parameter is the ratio Tp/Tb, where Tp and Tb are the precession period of the accretion disk and the binary period of the BBH system respectively (see details in paragraph 2 of Sects. 3.3, A.4, and B.5).
Any minimum of the χ2 function can be a local minimum and not a global minimum. However, because we investigate a wide range of the parameter Tp/Tb, namely 1 ≤ Tp/Tb ≤ 1000, we expect to be able to find all possible solutions (the limit Tp/Tb ≤ 1000 is given as an indication, in practice a limit of Tp/Tb ≤ 300 is enough).
Note that when the solution is found, it is not unique, but there exists a family of solutions. The solution shows a degeneracy and we will see that the parameter to fix the degeneragy or to find the range of parameters that provide the family of solutions is Va, the propagation speed of the perturbation along the beam.
Generally, for any value of the parameters, the surface χ2(λ) is convex and does not present a minimum. Moreover, when we are on the convex part of the surface χ2(λ), one of the important parameters of the problem can diverge. The two important parameters of the problem that can diverge are
-
1.
the bulk Lorentz factor of thee± beam, which has to be γb ≤ 30. This limit is imposed by the stability criterion for the propagation of the relativistic beam in the subrelativistic e− − p jet;
-
2.
the total mass of the BBH system.
The most frequent case of divergence we can find corresponds to γb → ∞. These mirage solutions are catastrophic and must be rejected. As we will see, generally, we have to study the robustness of the solution in relation to the parameters Tp/Tb, M1/M2, γ and io.
3.2. Solution of the precession model
In a first step, we fit a simple precession model without a BBH system. This corresponds to the precession induced by a spinning BH (Lense-Thirring effect) or by the magnetically driven precession (Caproni et al. 2006). This has the advantage of determining whether the solution corresponds to case I or to case II and of preliminarily determining the inclination angle and the bulk Lorentz factor of the ejected component.
We have to investigate the different possible scenarios with regard to the sense of the rotation of the accretion disk. These possibilities correspond to ±ωp(t − z/Va). Accordingly, we study the two cases.
Assuming a simple precession model, these are the steps to fit the coordinates X(t) and Y(t) of a VLBI component:
-
Determining the solution χ2(io) and the time origin of thecomponent ejection. In this section we assume thatVa = 0.1c (as χ2(Va) remains constant when Va varies, any value of Va can be used, see details in the next paragraph). We calculate χ2(io), i.e., we minimize
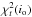 when the inclination angle varies gradually between two values. At each step of
io, we determine each free parameter
λ such that
when the inclination angle varies gradually between two values. At each step of
io, we determine each free parameter
λ such that 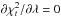 . Firstly, the important
parameter to determine is the time origin of the ejection of the VLBI component. We
compare the times of the observed peak flux with the modeled peak flux. The time
origin is obtained when the two peak fluxes occur at the same time. The solutions
corresponding to case II show a significant difference between the time origin of
the ejection of the VLBI component deduced from the fit of the peak flux and the
time origin obtained from the interpolation of the core separation. Second, we can
make a first determination of the inclination angle and of the bulk Lorentz factor.
. Firstly, the important
parameter to determine is the time origin of the ejection of the VLBI component. We
compare the times of the observed peak flux with the modeled peak flux. The time
origin is obtained when the two peak fluxes occur at the same time. The solutions
corresponding to case II show a significant difference between the time origin of
the ejection of the VLBI component deduced from the fit of the peak flux and the
time origin obtained from the interpolation of the core separation. Second, we can
make a first determination of the inclination angle and of the bulk Lorentz factor.
-
2.
Determining the family of solutions. The solution previously found is not unique and shows a degeneracy. The parameter Va can be used to study the degeneracy of the solution. Indeed, if we calculate χ2(Va) when Va varies, we find that χ2(Va) remains constant. For the inclination angle found in the previous section and the parameters of the corresponding solution, we calculate χ2(Va) when Va varies between 0.01c ≤ Va ≤ 0.45c and deduce the range of the precession period.
-
3.
Determining the possible offset of the origin of the VLBI component. In this section, we keep Va = 0.1c and using the inclination angle previously found and the corresponding solution, we calculate χ2(Δx,Δy) when Δx and Δy vary (Δx and Δy are the possible offsets of the VLBI origin). Solutions corresponding to case II show a significant offset of the space origin. Note that determining the offsets of the VLBI coordinates does not depend on the value of the inclination angle.
3.3. Solution of the BBH model
We have to investigate the different possible scenarios with regard to the sense of the rotation of the accretion disk and the sense of the orbital rotation of the BBH system. Because the sense of the precession is always opposite to the sense of the orbital motion, we study the two cases where we have ωp(t − z/Va), −ωb(t − z/Va) and −ωp(t − z/Va), ωb(t − z/Va), respectively.
Assuming a BBH model, this is the method for fitting the coordinates X(t) and Y(t) of a VLBI component:
-
1.
Determining the BBH system parameters for various values of Tp/Tb.In this section, we keep the inclination angle previously found andVa = 0.1c. We determine the BBH system parameters for different values of Tp/Tb, namely Tp/Tb = 1.01, 2.2, 4.6, 10, 22, 46, 100, and 220 for a BBH system with M1 = M2 (these values of Tp/Tb are chosen because they are equally spaced on a logarithmic scale). Generally, the BBH systems obtained with a low value of Tp/Tb, namely Tp/Tb = 1.01, 2.2, or 4.6 are systems with a large radius and the BBH systems obtained with a high value of Tp/Tb, namely Tp/Tb = 10, 22, 46, 100, or 220 are systems with a small radius.
-
2.
Determining the possible solutions: the χ2(Tp/Tb) – diagram. In this section, we keep the inclination angle previously found, Va = 0.1c and M1 = M2. The crucial parameter for finding the possible solutions is Tp/Tb, i.e., the ratio of the precession period and the binary period. Starting from the solutions found in the previous section, we calculate χ2(Tp/Tb) when Tp/Tb varies between 1 and 300. We find that the possible solutions characterized by a specific value of the ratio Tp/Tb. We note that some of the solutions can be mirage solutions, which have to be detected and excluded.
-
3.
Determining the possible offset of the space origin. In this section, we keep the inclination angle previously found, Va = 0.1c and M1 = M2. Starting with the solution found in the previous section, we calculate χ2(Δx,Δy) when Δx and Δy vary (Δx and Δy are the possible offsets of the VLBI origin). If we find that an offset of the origin is needed, we correct the VLBI coordinates by the offset to continue. Note that determining the offsets of the VLBI coordinates does not depend on the value of the inclination angle.
-
4.
Determining the range of possible values of Tp/Tb. In this section, we keep Va = 0.1c, M1 = M2. Previously, we found a solution characterized by a value of Tp/Tb for a given inclination. Therefore we calculate χ2(io) when io varies with a variable ratio Tp/Tb. We obtain the range of possible values of Tp/Tb and the range of possible values of io.
-
5.
Preliminary determination of io, Tp/Tb and M1/M2. In this section, we keep Va = 0.1c. This section is the most complicated one and differs for solutions corresponding to case I and case II. We indicate the main method and the main results (the details are provided in Sect. A.7 for the fit of component S1 of 1823+568 solutions and in Sect. B.7 for the fit of component C5 of 3C 279). We calculate χ2(io) for various values of Tp/Tb and M1/M2. Generally, we find that there exist critical values of the parameters Tp/Tb and M1/M2, which separate the domains for which the solutions exist or become mirage solutions. The curves χ2(io) show a minimum for given values (io)min and if necessary, we study the robustness of the solution in relation to the parameter γ, therefore we calculate χ2(γ) at io = (io)min for the corresponding values of Tp/Tb and M1/M2. When these critical values are obtained, we find the domains of Tp/Tb and M1/M2, which produce the solutions whose robustness is greater than 1.7σ and the corresponding inclination angle io.
-
6.
Determining a possible new offset correction. Using the solution found in the previous section, we calculate again χ2(Δx,Δy) when Δx and Δy vary. When a new offset of the origin is needed, we correct the VLBI coordinates by the new offset to continue. Note that this new offset correction is smaller than the first one found previously.
-
7.
Characteristics of the final solution to the fit of the VLBI component. We are now able to find the BBH system parameters that produce the best solution for the fit with the same method as described in point 5, Preliminary determination of io, Tp/Tb and M1/M2.
-
8.
Determining the family of solutions. The solution previously found is not unique and shows a degeneracy. The parameter Va can be used to study the degeneracy of the solution. Indeed, when we calculate χ2(Va) for varying Va, we find that χ2(Va) remains constant. Using the solution found in the previous section and the parameters of the corresponding solution, we calculate χ2(Va) when Va varies between 0.01c ≤ Va ≤ 0.45c and deduce the range of the precession period, the binary period, and the total mass of the BBH system.
-
9.
Determining the size of the accretion disk. Because we know the parameters of the BBH system, we can deduce the rotation period of the accretion disk and its size.
4. Method – Case I
4.1. Introduction: fitting the component S1 of 1823+568
Case I corresponds to a VLBI component ejected either from the VLBI core or to one where the offset of the origin of the ejection is smaller than or on the order of the smallest error bars of the VLBI component coordinates. It is the simplest case to solve. To illustrate the method of solving the problem corresponding to case I, we fit the component S1 of the source 1823+568 (Figs. 6 and 7).
4.2. VLBI data of 1823+568
1823+568 is an quasar at a redshift of 0.664 ± 0.001 (Lawrence et al. 1986). The host galaxy is elliptical according to HST observations (Falomo et al. 1997). The jet morphology on kpc-scales is complex – a mirrored S in observations with the MTRLI at 1666 MHz and with the VLA at 2 and 6 cm (O’Dea et al. 1988). The largest extension of 1823+568 is 15′′, corresponding to 93 kpc. On pc-scales the jet is elongated and points in a southern direction from the core (Pearson & Readhead 1988) – in accordance with the kpc-structure. Several components could be identified in the jet, e.g., Gabuzda et al. (1989) and Gabuzda et al. (1994), Gabuzda & Cawthorne (1996), Jorstad et al. (2005). A VSOP Space VLBI image of 1823+568 has been obtained by Lister et al. (2009a). All identified components show strong polarization. The linear polarization is parallel to the jet ridge direction. Most of the components show slow apparent superluminal motion. The fast component S1 moved with an apparent velocity of about 20c ± 2c until 2005 and subsequently decreases (Glück 2010). Twenty-two VLBA observations obtained at 15 GHz within the 2-cm MOJAVE survey between 1994.67 and 2010.12 have been re-analyzed and model-fitted to determine the kinematics of the individual components. For details of the data reduction and analysis see Glück (2010).
The radio map of 1823+568, observed 9 May 2003, is shown in Fig. 6. The data are taken from Glück (2010).
 |
Fig. 6 15 GHz natural weighted VLBI image of 1823+568 with fitted circular Gaussian components observed 9 May 2003 (Glück 2010). The map peak flux density was 1.27 Jy/beam, where the convolving beam was 0.58 × 0.5 mas at position angle (PA) − 2.09°. The contour levels were drawn at 0.15, 0.3, 0.6, 1.2, 2.4, 4.8, 9.6, 19.2, 38.4, and 76.8% of the peak flux density. |
4.3. Preliminary remarks
The redshift of the source is zs ≈ 0.664, and using for the Hubble constant Ho ≈ 72 km/s/Mpc, the luminosity distance of the source is Dl ≈ 3882 Mpc and the angular distance is Da = Dl/(1 + z)2.
For details of the values of the data and of their error bars see Glück (2010). At 15 GHz, calling the beam size Beam,
we adopted for the minimum values Δmin of the error bars of the observed VLBI
coordinates, the values in the range: 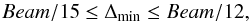 (19)see Sect. C for details concerning this choice.
(19)see Sect. C for details concerning this choice.
For 1823+568, observations were performed at 15 GHz and the beam size is mostly circular
and equal to Beam ≈ 0.5 mas. We adopted as minimum values of the error
bars the values
(ΔW)min ≈ Beam/12 ≈ 40
μas and
(ΔN)min ≈ Beam/12 ≈ 40
μas for the west and north coordinates of component S1, i.e., when the
error bars obtained from the VLBI data reduction were smaller than
(ΔW)min or (ΔN)min, they were
enlarged to the minimum values. The minimum values were chosen empirically, but the
adopted values were justified a posteriori by comparing the χ2
value of the final solution and the number of constraints to make the fit and to obtain a
reduced χ2 close to 1. For the component S1, we have
(χ2)final ≈ 51 for 56 constraints, the reduced
χ2 is 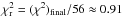 .
Lister & Homan (2005) suggested that the
positional error bars should be about 1/5 of the beam size. However, if
we had chosen
(ΔW)min = (ΔN)min ≈ Beam/5 ≈ 100
μas, we would have
(χ2)final ≪ 56, indicating that the minimum error
bars would be overestimated (see details in Sect. C).
.
Lister & Homan (2005) suggested that the
positional error bars should be about 1/5 of the beam size. However, if
we had chosen
(ΔW)min = (ΔN)min ≈ Beam/5 ≈ 100
μas, we would have
(χ2)final ≪ 56, indicating that the minimum error
bars would be overestimated (see details in Sect. C).
To obtain a constant projected trajectory of the VLBI component in the plane perpendicular to the line of sight, the integration step to solve Eq. (10) changes when the inclination angle varies. The integration step was Δt = 0.8 yr when io = 5°. When io varied, it was Δt = 0.8(sin(5°)/sin(io)) yr.
The trajectory of component S1 is not long enough to constrain the parameter Td, i.e., the characteristic time for the damping of the beam perturbation. We fit assuming that Td ≤ 2500 yr; this value produced a good trajectory shape.
The time origin of the ejection of the component S1, deduced from the interpolation of VLBI data, is to ≈ 1995.6 (Fig. 7).
 |
Fig. 7 Separation from the core for the different VLBI components for the source 1823+568 from MOJAVE data (Lister et al. 2009b). For details concerning the plot and the line fits see Lister et al. (2009b). We fit component S1 corresponding to component 4 from the MOJAVE survey. Component S1 moves fast, which may indicate that two families of VLBI components exist in the case of 1823+568. If this is the case, the nucleus of 1823+568 could contain a BBH system. |
Close to the core, the size of S1 is ≈ 0.24 mas, therefore we assumed that nrad = 75, where nrad is the number of steps to describe the extension of the VLBI component along the beam. At io = 5° with an integration step Δt = 0.8 yr, we calculated the length of the trajectory corresponding to each integration step. The size of the component is the sum of the first nrad = 75 lengths.
4.4. Final fit of component S1 of 1823+568
Here we present the solution to the fit of S1, the details for the fit can be found in Sect. A.
We studied the two cases ±ωp(t − z/Va). The final solution of the fit of component S1 using a BBH system corresponds to +ωp(t − z/Va) and −ωb(t − z/Va).
The main characteristics of the solution of the BBH system associated with 1823+568 are that
-
the radius of the BBH system isRbin ≈ 60 μas ≈ 0.42 pc;
-
the VLBI component S1 is not ejected by the VLBI core, and the offsets of the observed coordinates are ΔW ≈ +5 μas and ΔN ≈ 60 μas;
-
the ratio Tp/Tb is 8.88 ≤ Tp/Tb ≤ 9.88; and
-
the ratio M1/M2 is 0.095 ≤ M1/M2 ≤ 0.25.
The results of the fits obtained for Tp/Tb = 8.88 and Tp/Tb = 9.88 are given in Sect. A.9. The solutions found with Tp/Tb ≈ 8.88 are slightly more robust, but both solutions can be used.
To continue, we arbitrarily adopted the solution with Tp/Tb ≈ 8.88 and M1/M2 ≈ 0.17. We deduced the main parameters of the model, which are that
-
the inclination angle is io ≈ 3.98°;
-
the angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 0.28° (this is also the opening angle of the precession cone);
-
the bulk Lorentz factor of the VLBI component is γc ≈ 17.7; and
-
the origin of the ejection of the VLBI component is to ≈ 1995.7.
The variations of the apparent speed of component S1 are shown in Fig. 8.
 |
Fig. 8 Apparent speed of component S1 increases at the begining, then it is ≈ 17.5c until 2005, and finally, it decreases slowly assuming a constant bulk Lorentz factor γc ≈ 17.7. |
We can determine the Doppler factor (Eq. (12)), and consequently, we can estimate the observed flux density (Eq. (13)). This was used to fit the temporal position of the peak flux and to determine the temporal origin of the ejection of the VLBI component (see Sect. A.1 for the details).
The fit of the two coordinates W(t) and N(t) of the component S1 of 1823+568 is shown in Fig. 9. The points are the observed coordinates of component S1 that were corrected by the offsets ΔW ≈ +5 μas and ΔN ≈ 60 μas, and the red lines are the coordinates of the component trajectory calculated using the BBH model assuming the solution parameters, i.e., Tp/Tb ≈ 8.88, M1/M2 ≈ 0.17, io ≈ 3.98°, etc.
Finally, we compared this solution with the solution obtained using the precession model.
The 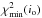 is about 51 for the fit
using the BBH system and about 67 for the precession model (see Sect. A.1), i.e., the BBH system solution is a 4σ better
solution. To fit the ejection of component S1 we used 56 observations (the west and north
coordinates corresponding to the 28 epochs of observation), so the reduced
χ2 is
is about 51 for the fit
using the BBH system and about 67 for the precession model (see Sect. A.1), i.e., the BBH system solution is a 4σ better
solution. To fit the ejection of component S1 we used 56 observations (the west and north
coordinates corresponding to the 28 epochs of observation), so the reduced
χ2 is 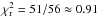 ,
indicating that the minimum values used for the error bars are correct.
,
indicating that the minimum values used for the error bars are correct.
 |
Fig. 9 Fit of the two coordinates W(t) and N(t) of component S1 of 1823+568. They correspond to the solution with Tp/Tb ≈ 8.88, M1/M2 ≈ 0.17, and io ≈ 3.98°. The points are the observed coordinates of component S1 that were corrected by the offsets ΔW ≈ +5 μas and ΔN ≈ 60 μas (the VLBI coordinates and their error bars are taken from Glück 2010). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
4.5. Determining the family of solutions
For the inclination angle previously found, i.e., io ≈ 3.98°, Tp/Tb ≈ 8.88, M1/M2 ≈ 0.17, and Rbin ≈ 60 μas, we gradually varied Va between 0.01c and 0.45c. The function χ2(Va) remained constant, indicating a degeneracy of the solution. We deduced the range of variation of the BBH system parameters. They are given in Table 1.
The period of the BBH system is not obviously related to a possible periodicity of the radio or the optical light curve.
4.6. Determining the size of the accretion disk
From the knowledge of the mass ratio M1/M2 ≈ 0.17 and the ratio Tp/Tb ≈ 8.88, we calculated in the previous section the mass of the ejecting black hole M1, the orbital period Tb, and the precession period Tp for each value of Va.
The rotation period of the accretion disk, Tdisk, is given by
(Britzen et al. 2001) 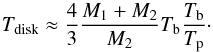 (20)Thus we
calculated the rotation period of the accretion disk, and assuming that the mass of the
accretion disk is Mdisk ≪ M1, the
size of the accretion disk Rdisk is
(20)Thus we
calculated the rotation period of the accretion disk, and assuming that the mass of the
accretion disk is Mdisk ≪ M1, the
size of the accretion disk Rdisk is 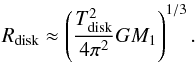 (21)We found that the
size of the accretion disk does not depend on
Va and is
Rdisk ≈ 0.090pc ≈ 0.013mas.
(21)We found that the
size of the accretion disk does not depend on
Va and is
Rdisk ≈ 0.090pc ≈ 0.013mas.
5. The method – Case II
5.1. Introduction: application to component C5 of 3C 279
Case II corresponds to an ejection of the VLBI component with an offset of the origin of the component larger than the smallest error bars of the VLBI component coordinates. This is the most difficult case to solve because data have to be corrected by an unknown offset That is larger than the smallest error bars.
When we apply the precession model, there are two signatures of case II, which are
-
1.
the problem of the time origin of the VLBI component, and
-
2.
the shape of the curve
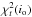 .
.
Using the precession model, we modeled the flux and compared the time position of the first peak flux with the time position of the observed peak flux. If the origin time deduced from interpolating the VLBI data was very different than the origin time deduced from the precesion model, we concluded that there is a time origin problem (see Sect. B.1). We show that this origin-time problem is related to the offset of the space origin of the VLBI component, i.e., the VLBI component is not ejected by the VLBI core and this offset is larger than the smallest error bars (see Sect. B.3).
Ranges for the BBH system parameters.
When the offset of the space origin is larger than the smallest error bars of the
component positions and the VLBI coordinates are not corrected by this offset, the curve
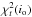 can have a very
characteristic shape:
can have a very
characteristic shape:
-
1.
the inclination angle is limited to a specific interval, i.e.,imin ≤ io ≤ imax;
-
2.
when io → imax and when io → imin, the bulk Lorentz factor of the VLBI component diverges, i.e., γc → ∞; and
-
3.
the function
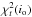 does not have a minimum in the interval
imin ≤ io ≤ imax.
does not have a minimum in the interval
imin ≤ io ≤ imax.
See Fig. B.1 corresponding to the precession model applied to component C5 of 3C 279.
5.2. MOJAVE data of 3C 279
The radio quasar 3C 279 (z = 0.536 Marziani et al. 1996) is one of the brightest extragalactic radio sources and has been observed and studied in detail for decades. Superluminal motion in the outflow of the quasar was found by Whitney et al. (1971) and Cohen et al. (1971). Thanks to the increasing resolution and sensitivity of modern observation techniques, a more complex picture of 3C 279 appeared, including multiple superluminal features moving along different trajectories downstream the jet (Unwin et al. 1989). The apparent speed of these components span an interval between 4c and 16c (Cotton et al. 1979; Wehrle et al. 2001).
We used the MOJAVE observations of 3C 279 (Lister et al. 2001). Seventy-six VLBA observations obtained at 15 GHz within the 2-cm MOJAVE survey between 1999.25 and 2007.64 were re-analyzed and model-fitted to determine the coordinates of the VLBI components. We used the NRAO Astronomical Image Processing System (AIPS) to calibrate the data. We performed an amplitude calibration and applied a correction for the atmospheric opacity for the high-frequency data (ν > 15 GHz). The parallactic angle correction was taken into account before we calibrated the phases using the pulse-scale signal and a final fringe fit. The time- and frequency-averaged data were imported to DIFMAP (Shepherd 1997), were we used the CLEAN and MODELFIT algorithm for imaging and model fitting, respectively.
The fully calibrated visibilities were fitted in DIFMAP using the algorithm MODELFIT and 2D circular Gaussian components. These components were characterized by their flux density, Smod, position rmod, position angle (PA), θmod (measured from north through east), and their full-width at half-maximum (FWHM). Since the number of fitted Gaussians was initially not limited, we only then added a new component when the χ2 value decreased significantly. This approach led to a minimum number of Gaussians that can be regarded as a reliable representation of the source. We modeled each epoch separately to avoid biasing effects. The kinematics of the source could thus be analyzed by tracking the fitted components. The average beam for the 15 GHz observations is 0.51 mas × 1.34 mas.
The radio map of 3C 349, observed 15 june 2003, is shown in Fig. 10. The data are taken from Lister et al. (2009a).
 |
Fig. 10 15 GHz natural-weighted VLBI image of 3C 279 with fitted circular Gaussian components observed 15 June 2003 (Lister et al. 2009a). The map peak flux density was 8.3 Jy/beam, where the convolving beam was 1.3 × 0.5 mas at position angle (PA) −6.0°. The contour levels were drawn at 0.2, 0.5, 1.0, 2.0, 4.0, 8.0, 16, 32, 64, and 80% of the peak flux density. Component C4 is a stationary component (see Fig. 11). |
 |
Fig. 11 Separation from the core for the different VLBI components for the source 3C 279 from MOJAVE data (Lister et al. 2009b). For the obtaining of the plotted line fits see Lister et al. (2009b). We fit component C5. Component C5 is ejected from an origin with a large offset from the VLBI core. |
5.3. Preliminary remarks
The redshift of 3C 279 is z ≈ 0.536, and using for the Hubble constant Ho ≈ 72 km/s/Mpc, the luminosity distance of the source is Dl ≈ 3070 Mpc and the angular distance is Da = Dl/(1 + z)2.
For details of the values of the data see Lister et al. (2009a). Because the observations were performed at 15 GHz and the beam size was 0.51 mas × 1.34 mas, we adopted for the minimum values of the error bars the values (ΔW)min ≈ Beam/15 ≈ 34 μas and (ΔN)min ≈ Beam/15 ≈ 89 μas for the west and north coordinates of component C5. The adopted values were justified a posteriori by comparing the χ2 value of the final solution and the number of constraints to make the fit and to obtain a reduced χ2 close to 1. For the component C5, we have (χ2)final ≈ 150 for 152 constraints, thus the reduced χ2 is: (χ2)r ≈ 0.99. It has been suggested by Lister & Homan (2005) that the positional error should be within 20% of the convolving beam size, i.e., ≈ Beam/5. See Sect. C for details concerning the choice adopted in this article and the determination of the χ2, the characteristics of the solution using minimum erros bars are as large as ≈ Beam/5.
The integration step used to solve Eq. (10) is Δt = 0.8 yr when io = 5°. When io varies, it is Δt = 0.8(sin(5°)/sin(io)) yr.
The trajectory of component C5 is not long enough to constrain the parameter Td, i.e., the characteristic time for the damping of the beam perturbation. We fit assuming that Td ≤ 2000 yr.
The time origin of the ejection of the component C5 cannot be deduced easily from the interpolation of VLBI data (Lister et al. 2009b). However, we show in Sect. B.1 how, using the precession model, it is possible to obtain the minimum time origin of the VLBI component by comparing the time position of the calculated first peak flux with the observed time position of the first peak flux.
Close to the core, the size of C5 is ≈ 0.25 mas, therefore we assumed that nrad = 75, where nrad is the number of steps to describe the extension of the VLBI component along the beam.
5.4. Final fit of component C5 of 3C 279
Here we present the solution to the fit of C5, the details for the fit can be found in Sect. B. The fit of component C5 using a BBH system corresponds to −ωp(t − z/Va) and +ωb(t − z/Va).
The main characteristics of the solution of the BBH system associated with 3C 279 are that
-
the radius of the BBH system isRbin ≈ 420 μas ≈ 2.7 pc;
-
the VLBI component C5 is not ejected by the VLBI core and the offsets of the observed coordinates are ΔW ≈ +405 μas and ΔN ≈ +110 μas;
-
the ratio Tp/Tb is Tp/Tb ≈ 140; and
-
the ratio M1/M2 is M1/M2 ≈ 2.75.
The results of the fits obtained for Tp/Tb ≈ 140 and M1/M2 ≈ 2.75 are given in Appendix B.9.
Adopting the solution with Tp/Tb ≈ 140 and M1/M2 ≈ 2.75, we deduced the main parameters of the model.
-
The inclination angle is io ≈ 10.4°.
-
The angle between the accretion disk and the rotation plane of the BBH system is Ω ≈ 2.4° (this is also the opening angle of the precession cone).
-
The bulk Lorentz factor of the VLBI component is γc ≈ 16.7.
-
The origin of the ejection of the VLBI component is to ≈ 1999.0.
The variations of the apparent speed of component C5 are shown in Fig. 12.
 |
Fig. 12 Apparent speed of component C5 varies between 17c and 9c assuming a constant bulk Lorentz factor γc ≈ 16.7. |
We can determine the Doppler factor (Eq. (12)), and consequently we can estimate the observed flux density (Eq. (13)). Using the precession model, we fitted the temporal position of the peak flux and determined the temporal origin of the ejection of the VLBI component (see Sect. B.1 for the details). Using the BBH model, we calculated and plotted in Fig. 13 the flux variations of C5 using Eq. (A.1). We found that the time origin of the ejection of component C5 is to ≈ 1999.03. Although Eq. (A.1) is a rough estimate of the flux density variations, it allows us
-
to check the time origin of the ejection of the VLBI componentfound using the BBH model;
-
to compare the time positon of the modeled first peak flux with the observed first peak flux;
-
to obtain a good shape of the variation of the flux density during the first few years and explain the difference between the radio and the optical light curves. In some cases, in addition to the radio, optical observations show a light curve with peaks separated by about one year, see for instance the cases of 0420-016 (Britzen et al. 2001) and 3C 345 (Lobanov & Roland 2005). Using Eq. (A.1), the optical emission can be modeled as the synchrotron emission of a point source ejected in the perturbed beam (Britzen et al. 2001; Lobanov & Roland 2005). This short burst of very energetic relativistic e± is followed immediately by a very long burst of less energetic relativistic e±. This long burst is modeled as an extended structure along the beam and is responsible for the VLBI radio emission.
The fit of both coordinates W(t) and N(t) of component C5 of 3C 279 are shown in Fig. 14. The points are the observed coordinates of component C5 that were corrected for the offsets ΔW ≈ +405 μas and ΔN ≈ +110 μas, the red lines are the coordinates of the component trajectory calculated using the BBH model assuming the solution parameters, i.e., Tp/Tb ≈ 140, M1/M2 ≈ 2.75, io ≈ 10.4°, etc.
 |
Fig. 13 Flux variations of component C5 using the BBH model. The time origin of the ejection of C5 is 1999.03. |
 |
Fig. 14 Fit of the two coordinates W(t) and N(t) of component C5 of 3C 279. They correspond to the solution with Tp/Tb ≈ 140, M1/M2 ≈ 2.75, and io ≈ 10.4°. The points are the observed coordinates of component C5 that were corrected for the offsets ΔW ≈ +405 μas and ΔN ≈ +110 μas. VLBI coordinates are taken from Lister et al. (2009a). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
Finally, we compared this solution with the solution obtained using the precession model.
The 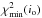 is about 151.4 for the fit
using the BBH system and >1000 for the precession model (see Sect. B.1). To fit the ejection of component C5 we used 152
observations (76 epochs), so the reduced χ2 is
is about 151.4 for the fit
using the BBH system and >1000 for the precession model (see Sect. B.1). To fit the ejection of component C5 we used 152
observations (76 epochs), so the reduced χ2 is
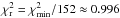 .
.
5.4.1. Determining the family of solutions
The solution is not unique, but there exists a family of solutions. For the inclination angle previously found, i.e., io ≈ 10.4° and using the parameters of the corresponding solution, i.e., Tp/Tb ≈ 140, M1/M2 ≈ 2.75 and Rbin ≈ 420 μas, we gradually varied Va between 0.01c and 0.45c. The function χ2(Va) remains constant, indicating a degeneracy of the solution, and we deduced the range of variation of the BBH system parameters. They are given in Table 2.
Ranges for the BBH system parameters.
5.4.2. Determining the size of the accretion disk
From the knowledge of the mass ratio M1/M2 ≈ 2.75 and the ratio Tp/Tb ≈ 140, we calculated in the previous section the mass of the ejecting black hole M1, the orbital period Tb, and the precession period Tp for each value of Va.
We calculated the rotation period of the accretion disk, Tdisk, using (20). Assuming that the mass of the accretion disk is Mdisk ≪ M1, the size of the accretion disk Rdisk is calculated using (21).
We found that the size of the accretion disk does not depend on Va and is Rdisk ≈ 0.26 pc ≈ 0.041 mas.
5.4.3. Comparing of the trajectories of C5 and C10
We see from Fig. 11 that
-
components C5 and C6 probably follow probably the same trajectories;
-
component C10 follows a different trajectory than C5 and C6.
Thus, using the MOJAVE data (Lister et al. 2009b), we plot in Fig. 15 the trajectories of C5 and C10. We found that
-
component C10 is probably ejected by the VLBI core;
-
component C5 is ejected with a large offset from the VLBI core; and
-
components C5 and C10 follow two different trajectories and are not ejected from the same origins, indicating that the nucleus of 3C 279 contains a BBH system.
 |
Fig. 15 Using the MOJAVE data (Lister et al. 2009b), we plot the trajectories of C5 and C10. Component C10 is probably ejected by the VLBI core and component C5 is ejected with a large offset from the VLBI core. Components C5 and C10 follow two different trajectories and are ejected from different origins, indicating that the nucleus of 3C 279 contains a BBH system. Note that the origin of this caption corresponds to the origin of the ejection of component C5, thus all MOJAVE coordinates have been corrected for the offsets ΔW ≈ +405 μas and ΔN ≈ +110 μas. |
6. Discussion and conclusion
We showed how from the knowledge of the coordinates West(t) and North(t) of the ejected VLBI component one can find the characteristics of the BBH system in both cases. To illustrate case I, we fitted component S1 of 1823+568, and to illustrate case II, we fitted component C5 of 3C 279.
From the fit of the coordinates of component S1 of 1823+568, the main characteristics of the final solution of the BBH system associated with 1823+568 are that
-
the radius of the BBH system is Rbin ≈ 60 μas ≈ 0.42 pc;
-
the VLBI component S1 is not ejected by the VLBI core, and the offsets of the observed coordinates are ΔW ≈ +5 μas and ΔN ≈ 60 μas;
-
the ratio Tp/Tb is 8.88 ≤ Tp/Tb ≤ 9.88;
-
the ratio M1/M2 is 0.095 ≤ M1/M2 ≤ 0.25;
-
the inclination angle is io ≈ 4.0°;
-
the bulk Lorentz factor of the VLBI component is γc ≈ 17.7; and
-
the origin of the ejection of the VLBI component is to ≈ 1995.7.
From the fit of the coordinates of component C5 of 3C 279, the main characteristics of the final solution of the BBH system associated with 3C 279 are that
-
the radius of the BBH system is Rbin ≈ 420 μas ≈ 2.7 pc;
-
the VLBI component C5 is not ejected by the VLBI core and the offsets of the observed coordinates are ΔW ≈ +405 μas and ΔN ≈ +110 μas;
-
the ratio Tp/Tb is Tp/Tb ≈ 140;
-
the ratio M1/M2 is M1/M2 ≈ 2.75;
-
the inclination angle is io ≈ 10.4°;
-
the bulk Lorentz factor of the VLBI component is γc ≈ 16.7; and
-
the origin of the ejection of the VLBI component is to ≈ 1999.0.
If, in addition to the radio observations, one can obtain optical, X-ray, or γ-ray observations that show a light curve with peaks, the simultaneous fit of the VLBI coordinates and this light curve put stronger constraints on the characteristics of the BBH system. The high-frequency emission can be modeled as the synchrotron emission or the inverse Compton emission of a point source ejected in the perturbed beam, see Britzen et al. (2001) for PKS 0420-014 and Lobanov & Roland (2005) for 3C 345. This short burst of very energetic relativistic e± is followed immediately by a very long burst of less energetic relativistic e±. This long burst is modeled as an extended structure along the beam and is responsible for the VLBI radio emission. The simultaneous fit of the VLBI coordinates and the optical light curve using the same method as the one developed in this article has to be achieved.
Observations of compact radio sources in the first mas show that the VLBI ejections do not follow a straight line, and modeling the ejection shows in each case studied that the nucleus contains a BBH system. Accordingly, Britzen et al. (2001) assumed that all radio sources contain a BBH system. If extragalactic radio sources are associated with galaxies formed after the merging of galaxies and if the formation of extragalactic radio sources is related to the presence of binary black hole systems in their nuclei, we can explain
-
why extragalactic radio sources are associated with elliptical galaxies;
-
why more than 90% of the quasars are radio-quiet quasars, e.g., Kellermann et al. (1989) and Miller et al. (1990).
Radio-quiet quasars are active nuclei that contain a single black hole and can be associated with spiral galaxies (Peacock et al. 1986). Although it has not been proven yet that radio-quiet quasars only contain a single black hole, the hypothesis for distinguishing between radio-loud and radio-quiet quasars on the basis of the binarity of the central engine is supported by comparing the optical properties of the two classes (Goldschmidt et al. 1999). Recent observations of the central parts of radio galaxies and radio-quiet galaxies show a systematic difference between the two classes (Kharb et al. 2012).
Because Gaia will provide positions of extragalactic radio sources within ≈ 25 μas, the link between the Gaia reference frame from optical observations of extragalactic radio sources and the reference frame obtained from VLBI observations will have to take into account the complex structure of the nuclei of extragalactic radio sources, because with a resolution of ≈ 25 μas, probably all these sources will appear as double sources, and the radio core, obtained from VLBI observations and the optical core obtained by Gaia will not necessarily be the same.
We conclude, remarking that if the inner parts of the accretion disk contain a warp or precess faster than the precession of the outer part, this will produce a very small perturbation that will produce a day-to-month variability of the core flux (Roland et al. 2009).
Acknowledgments
J.R. thanks Alain Lecavelier des Etangs and Simon Prunet for useful discussions and comments. This research has made use of data from the MOJAVE database that is maintained by the MOJAVE team (Lister et al. 2009a) and part of this work was supported by the COST Action MP0905 Black Holes in a Violent Universe.
References
- Achatz, U., & Schlickeiser, R. 1993, A&A, 274, 165 [NASA ADS] [Google Scholar]
- Attridge, J. M., Roberts, D. H., & Wardle, J. F. C. 1999, ApJ, 518, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Biretta, J. A., Sparks, W. B., & Macchetto, F. 1999, ApJ, 520, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Britzen, S., Roland, J., Laskar, J., et al. 2001, A&A, 374, 784 [Google Scholar]
- Burke-Spolaor, S. 2011, MNRAS, 410, 2113 [NASA ADS] [CrossRef] [Google Scholar]
- Camenzind, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Caproni, A., Livio, M., Abraham, Z., & Mosquera Cuesta, H. J. 2006, ApJ, 653, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., Cannon, W., Purcell, G. H., et al. 1971, ApJ, 170, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Cotton, W. D., Counselman, III, C. C., Geller, R. B., et al. 1979, ApJ, 229, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Falomo, R., Urry, C. M., Pesce, J. E., et al. 1997, ApJ, 476, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Fey, A. L., Gordon, D. G., Jacobs, C. S. 2009, IERS Technical Note No. 35 (Frankfurt: Bundesamts für Kartographie und Geodäsie) [Google Scholar]
- Gabuzda, D. C., & Cawthorne, T. V. 1996, MNRAS, 283, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gabuzda, D. C., Cawthorne, T. V., Roberts, D. H., & Wardle, J. F. C. 1989, ApJ, 347, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Gabuzda, D. C., Mullan, C. M., Cawthorne, T. V., Wardle, J. F. C., & Roberts, D. H. 1994, ApJ, 435, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Glück, C. B. 2010, in Diplomarbeit, Universität zu Köln [Google Scholar]
- Goldschmidt, P., Kukula, M. J., Miller, L., & Dunlop, J. S. 1999, ApJ, 511, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, J.-L., Marscher, A. P., Alberdi, A., Jorstad, S. G., & Agudo, I. 2001, ApJ, 561, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Lemoine, M., Vidal-Madjar, A., et al. 2002, ApJS, 140, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, J. I. 1997, ApJ, 478, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., Shaffer, D. B., & Green, R. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kharb, P., Capetti, A., Axon, D. J., et al. 2012, AJ, 143, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Lawrence, C. R., Pearson, T. J., Readhead, A. C. S., & Unwin, S. C. 1986, AJ, 91, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., & Homan, D. C. 2005, AJ, 130, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Tingay, S. J., Murphy, D. W., et al. 2001, ApJ, 554, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, H. D., Aller, M. F., et al. 2009a, AJ, 137, 3718 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009b, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lobanov, A. P., & Roland, J. 2005, A&A, 431, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Marcowith, A., Henri, G., & Pelletier, G. 1995, MNRAS, 277, 681 [NASA ADS] [Google Scholar]
- Marcowith, A., Henri, G., & Renaud, N. 1998, A&A, 331, L57 [NASA ADS] [Google Scholar]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [Google Scholar]
- Miller, L., Peacock, J. A., & Mead, A. R. G. 1990, MNRAS, 244, 207 [NASA ADS] [Google Scholar]
- Muxlow, T. W. B., Pelletier, G., & Roland, J. 1988, A&A, 206, 237 [NASA ADS] [Google Scholar]
- O’Dea, C. P., Barvainis, R., & Challis, P. M. 1988, AJ, 96, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., Miller, L., & Longair, M. S. 1986, MNRAS, 218, 265 [NASA ADS] [Google Scholar]
- Pearson, T. J., & Readhead, A. C. S. 1988, ApJ, 328, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, G., & Roland, J. 1989, A&A, 224, 24 [NASA ADS] [Google Scholar]
- Pelletier, G., & Roland, J. 1990, in Parsec-scale radio jets, eds. J. A. Zensus, & T. J. Pearson (Cambridge University Press), 323 [Google Scholar]
- Pelletier, G., & Sol, H. 1992, MNRAS, 254, 635 [NASA ADS] [Google Scholar]
- Pelletier, G., Sol, H., & Asseo, E. 1988, Phys. Rev. A, 38, 2552 [NASA ADS] [CrossRef] [Google Scholar]
- Roland, J., Britzen, S., Kudryavtseva, N. A., Witzel, A., & Karouzos, M. 2008, A&A, 483, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roland, J., Britzen, S., Witzel, A., & Zensus, J. A. 2009, A&A, 496, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roland, J., & Hermsen, W. 1995, A&A, 297, L9 [NASA ADS] [Google Scholar]
- Roland, J., & Hetem, A. 1996, in Cygnus A – Study of a Radio Galaxy, eds. C. L. Carilli, & D. E. Harris (Cambridge University Press), 126 [Google Scholar]
- Roland, J., Pelletier, G., & Muxlow, T. W. B. 1988, A&A, 207, 16 [NASA ADS] [Google Scholar]
- Roland, J., Teyssier, R., & Roos, N. 1994, A&A, 290, 357 [NASA ADS] [Google Scholar]
- Schlüter, W., & Behrend, D. 2007, J. Geodesy, 81, 379 [Google Scholar]
- Shepherd, M. C. 1997, in Astronomical Data Analysis Software and Systems VI, eds. G. Hunt, & H. Payne, ASP Conf. Ser., 125, 77 [Google Scholar]
- Skibo, J. G., Dermer, C. D., & Schlickeiser, R. 1997, ApJ, 483, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Sol, H., Pelletier, G., & Asseo, E. 1989, MNRAS, 237, 411 [NASA ADS] [Google Scholar]
- Tingay, S. J., & Wayth, R. B. 2011, AJ, 141, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Tingay, S. J., Jauncey, D. L., Reynolds, J. E., et al. 1998, AJ, 115, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Unwin, S. C., Cohen, M. H., Hodges, M. W., Zensus, J. A., & Biretta, J. A. 1989, ApJ, 340, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Wehrle, A. E., Piner, B. G., Unwin, S. C., et al. 2001, ApJS, 133, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Whitney, A. R., Shapiro, I. I., Rogers, A. E. E., et al. 1971, Science, 173, 225 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Fit of component S1 of 1823+568
Appendix A.1: Fit of S1 using the precession model
To fit the ejection of component S1, we used 56 observations (28 epochs).
We studied the two cases ±ωp(t − z/Va). The final solution of the fit of component S1 of 1823+568 using a BBH system corresponds to +ωp(t − z/Va), therefore we discuss only this case in this appendix. In this section, we assume that Va = 0.1c.
The range of inclination we explore is 0.5° ≤ io ≤ 10°.
An important parameter for the fit is the time origin of the ejection of the VLBI
component. We model the flux using equation 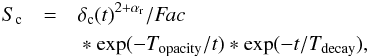 (A.1)where
Fac is a scaling factor, Topacity is the
characteristic time to describe the synchrotron opacity, and
Tdecay is the characteristic time to describe the losses.
This is the simplest way to model the flux and does not take into account in situ
re-acceleration of the relativistic particles along the beam and synchrotron, inverse
Compton, or expansion losses. We do not aim to fit the flux light curve, but we wish to
compare the time position of the modeled first peak flux with the observed first peak
flux (Fig. A.1). This provides the minimum for the
time origin of the ejection of the VLBI component. For S1 we find
to ≥ 1995.65. This value agrees well with the time origin
obtained from VLBI data interpolation, which is to ≈ 1995.60
(Glück 2010). This case corresponds to case I,
i.e., if there is an offset of the VLBI ejection, it is smaller than or on the order of
the smallest error bars of the VLBI component coordinates. In the following we keep
to as a free parameter in the range
1995.65 ≤ to ≤ 1995.90.
(A.1)where
Fac is a scaling factor, Topacity is the
characteristic time to describe the synchrotron opacity, and
Tdecay is the characteristic time to describe the losses.
This is the simplest way to model the flux and does not take into account in situ
re-acceleration of the relativistic particles along the beam and synchrotron, inverse
Compton, or expansion losses. We do not aim to fit the flux light curve, but we wish to
compare the time position of the modeled first peak flux with the observed first peak
flux (Fig. A.1). This provides the minimum for the
time origin of the ejection of the VLBI component. For S1 we find
to ≥ 1995.65. This value agrees well with the time origin
obtained from VLBI data interpolation, which is to ≈ 1995.60
(Glück 2010). This case corresponds to case I,
i.e., if there is an offset of the VLBI ejection, it is smaller than or on the order of
the smallest error bars of the VLBI component coordinates. In the following we keep
to as a free parameter in the range
1995.65 ≤ to ≤ 1995.90.
 |
Fig. A.1 Fit of the first peak flux of component S1 of 1823+568 using the precession model. The time origin deduced from the fit of the peak flux is to ≥ 1995.65 and is comparable with the time origin deduced from VLBI observations interpolation, i.e., to ≈ 1995.60. |
Because the function 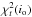 is mostly flat between 4
and 10 degrees, to continue we abitrarily adopted the inclination angle
io ≈ 6°. The main results of the fit for the
precession model are that
is mostly flat between 4
and 10 degrees, to continue we abitrarily adopted the inclination angle
io ≈ 6°. The main results of the fit for the
precession model are that
-
the opening angle fo the precession cone is Ω ≈ 0.46°;
-
the bulk Lorentz factor of S1 is γc ≈ 20;
-
the origin of S1 is to ≈ 1995.7; and
-
χ2(io ≈ 6°) ≈ 67.4.
Appendix A.2: Determining the family of solutions
The solution is not unique. For the inclination angle previously found, i.e.,
io ≈ 6° and using the parameters of the
corresponding solution, we gradually varied
Va between 0.01c and
0.45c. At each step of
Va, we minimized the function
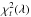 , where λ
are the free parameters. The function
χ2(Va)
remained constant, indicating a degeneracy of the solution, and we obtained the range of
possible values for the precession period given in Table A.1.
, where λ
are the free parameters. The function
χ2(Va)
remained constant, indicating a degeneracy of the solution, and we obtained the range of
possible values for the precession period given in Table A.1.
Range for the precession period.
Appendix A.3: Determining the BBH system parameters
Because the precession is defined by +ωp(t − z/Va), the BBH system rotation is defined by −ωb(t − z/Va). In this section, we kept the inclination angle previously found, i.e., io ≈ 6° and Va = 0.1c.
To determine the BBH system parameters corresponding to a value of
Tp/Tb, we
minimized 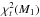 when the mass of the
ejecting black hole M1 varied gradually between 1
M⊙ to a value corresponding to
M1/M2 = 2
with a starting value of M2, such that
106 ≤ M2 ≤ 109. During the
minimization M2 is a free parameter, and at each step of
M1, we minimized the function
when the mass of the
ejecting black hole M1 varied gradually between 1
M⊙ to a value corresponding to
M1/M2 = 2
with a starting value of M2, such that
106 ≤ M2 ≤ 109. During the
minimization M2 is a free parameter, and at each step of
M1, we minimized the function
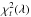 , where λ
are the free parameters. Thus we constrained the parameters of the BBH system when the
two black holes have the same masses, i.e.,
M1 = M2.
, where λ
are the free parameters. Thus we constrained the parameters of the BBH system when the
two black holes have the same masses, i.e.,
M1 = M2.
We determined the parameters of the BBH system model for different values of the parameter Tp/Tb, namely Tp/Tb = 4.6, 10, 22, 46, 100, and 220.
For a given value of Tp/Tb, we found the radius of the BBH system defined by Eq. (8). Note that the radius of the BBH system does not depend on the starting value of M2.
Appendix A.4: χ2(Tp/Tb) – diagram
In this section, we kept the inclination angle previously found, i.e., io ≈ 6°, Va = 0.1c and assumed M1 = M2.
The diagram χ2(Tp/Tb) provides the possible solutions at a given inclination angle. Some of the solutions can be mirage solutions when io varies.
We calculated χ2(Tp/Tb) for 1 ≤ Tp/Tb ≤ 300. We started for each value of the BBH system parameters found in the previous section, i.e., corresponding to the values of Tp/Tb = 4.6, 10, 22, 46, 100, and 220, and covered the complete interval 1 ≤ Tp/Tb ≤ 300. For instance, if we started at Tp/Tb = 22, we covered the ranges varying Tp/Tb from 22 to 1 and from 22 to 300. We found the possible solutions of the BBH system, i.e,. the solutions that correspond to the minima of χ2(Tp/Tb). They are given in Table A.2.
Main solutions found for io ≈ 5.98°.
Solutions 1 and 5 are excluded because they have γc > 30. There are three possible solutions, the best one is Solution 2, which corresponds to a BBH system whose radius is Rbin ≈ 60 μas. In the following, we continue with Solution 2.
Appendix A.5: Possible offset of the origin of the ejection
In this section, we kept the inclination angle previously adopted, i.e., io ≈ 6°. We assumed that Va = 0.1c, M1 = M2, Tp/Tb = 11.45 and used the parameters of Solution 2 previously found.
To test whether the VLBI component is ejected from the VLBI core or from the second
black hole, we calculated
χ2(ΔW,ΔN), where
ΔW and ΔN are offsets in the west and north
directions. The step used in the west and north directions is 5μas. At
each step of ΔW and ΔN, we minimized the function
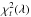 , where λ
are the free parameters (Fig. A.2). The radius of
the BBH system was left free to vary during the minimization.
, where λ
are the free parameters (Fig. A.2). The radius of
the BBH system was left free to vary during the minimization.
 |
Fig. A.2 Calculation of χ2(ΔW,ΔN) using the BBH model. Non-zero offsets are possible, but the size of the offset must be the same as the radius of the BBH system calculated at this point. This is the case if the offsets are ΔW1 ≈ 0.010 mas and ΔN1 ≈ 0.070 mas. We determined the offset at io ≈ 6°; it does not depend on the value of the adopted inclination angle. |
The minimum of χ2(ΔW,ΔN) is ≈ 49.5, and we see from Fig. A.2 that the corresponding non-zero offsets are with ΔN ≥ 0.060 mas. However, all points with the smallest χ2(ΔW,ΔN) are not possible. Indeed, for a point with the smallest χ2, the size of the offset offset must be equal to the radius of the BBH system calculated at this point. This is the case if the offsets are ΔW1 ≈ +0.010 mas and ΔN1 ≈ +0.070 mas. The radius of the BBH system at this point is Rbin ≈ 70 μas and the offset size is ≈ 71 μas, i.e., the offset and the radius of the BBH system are the same at this point.
Therefore we conclude that
-
the VLBI component S1 is not ejected from the VLBI core, but from the second black hole of the BBH system;
-
the radius of the BBH system is Rbin ≈ 71 μas. It is about twice the smallest error bars of the observed VLBI component coordinates (the component positions), but it is significantly detected (2σ from Fig. A.2).
We must correct the VLBI coordinates from the offset before we continue.
Note that determining the offset of the origin does not depend on the value adopted for the inclination angle. This was shown by calculating the offset at different inclination angles, i.e., io ≈ 4°, 5°, 7°.
Appendix A.6: Determining Tp/Tb
From this point onward, the original coordinates of the VLBI component S1 are corrected for the offsets ΔW1 and ΔN1 found in the previous section. In this section, we assumed that Rbin = 71 μas, M1 = M2 and Va = 0.1c.
Previously, we found that Solution 2 is characterized by Tp/Tb ≈ 11.45 for io ≈ 6°. In this section we obtain the range of possible values of Tp/Tb when io varies.
We calculated the funtion χ2(io) in the inteval 2° ≤ io ≤ 7°, assuming that the ratio Tp/Tb is free. The relation between Tp/Tb and io is plotted in Fig. A.3.
 |
Fig. A.3 Tp/Tb as function of io obtained by minimizing χ2(io). |
Knowing of the possible values of the ratio Tp/Tb allows us to calculate in the next section the function χ2(io) for various values of the ratios Tp/Tb and M1/M2 and then estimate the mass ratio M1/M2 of the BBH system.
Appendix A.7: Preliminary determination of io, Tp/Tb and M1/M2.
In this section, we assumed that Va = 0.1c and the radius of the BBH system is Rbin = 71 μas.
We varied io between 2 and 7 degrees and calculated χ2(io) for various values of Tp/Tb and M1/M2. The values of Tp/Tb investigated are Tp/Tb = 11.45, 8.88, 8.11, 7.76, and 7.62. The values of M1/M2 investigated are M1/M2 = 1.0, 0.5, 0.37, 0.25, and 0.1. For each value of M1/M2 we calculated χ2(io) for all values of Tp/Tb. The plots χ2(io) for M1/M2 = 1.0 and 0.37 are shown in Fig. A.4.
 |
Fig. A.4 Function χ2(io). It stops at large inclination angles because the bulk Lorentz factor becomes greater than 30. Top figure: the ratio M1/M2 is M1/M2 = 1. When Tp/Tb increases, the minimum decreases and disappears. This means that the function χ2(io) does not show a minimum and is a mirage solution. Bottom figure: the ratio M1/M2 = 0.37. The function χ2(io) has a minimum for Tp/Tb ≈ 8.88 and io ≈ 4. The robustness of this solution, defined as the square root of the difference χ2(γ = 30) − χ2(min), is ≈ 1.8 × σ. |
The main results are that
-
when io is larger than about 6 degrees, the bulk Lorentz factor increases and becomes greater than 30, which is excluded;
-
the critical value of M1/M2 ≈ 0.5;
-
if M1/M2 > 0.5, the solution χ2(io) is a mirage solution;
-
if M1/M2 < 0.5, the solution χ2(io) has a minimum;
-
the solutions with a robustness larger than 1.7σ are those with M1/M2 < 0.37 (see Table B.1);
-
when M1/M2 decreases, the solutions are more robust, but they are of lower quality, i.e., their χ2(min) increases (see Table B.1); and
-
when M1/M2 < 0.5, the value of Tp/Tb that produces the best fit is Tp/Tb ≈ 8.88, independently of the value of M1/M2.
We present in Table A.3 the results of solutions corresponding to Tp/Tb ≈ 8.88 and M1/M2 = 0.1, 0.25 and 0.37.
Solutions found for Tp/Tb ≈ 8.88.
Appendix A.8: Determining a possible new offset correction
In this section, we assumed Va = 0.1c. Using the solution found in the previous section (Table B.1), we can verify whether if there is an additional correction to the offset of the origin of the VLBI component. For this, we calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions. We assumed the radius of the BBH system to be free to vary. We found that a small additional correction is needed ΔW2 ≈ −0.005 mas and ΔN2 ≈ −0.010 mas.
Finally, we found that the total offset is ≈ 60 μas and the radius of the BBH system is also Rbin ≈ 60 μas.
Appendix A.9: Final fit of component S1 of 1823+568
From this point onward, the coordinates of the VLBI component S1 are corrected for the new offsets ΔW2 and ΔN2 found in the previous section. In this section, we assumed Va = 0.1c and Rbin = 60 μas.
We can now find the final solution for S1. We calculated χ2(io) for various values of Tp/Tb assuming M1/M2 ≈ 0.25. We found that the best range for Tp/Tb is: 8.88 ≤ Tp/Tb ≤ 9.88. With this we can estimate the range of the mass ratio assuming Tp/Tb ≈ 8.88 and Tp/Tb ≈ 9.88. We defined the range of the mass ratio in the following way:
-
1.
we found the mass ratio that produces a solution of at least1.7σ robustness, and
-
2.
we found the mass ratio that produces a solution that is poorer by 1σ than the previous one, but that is more robust.
The results of the fit are presented in Tables A.4 and A.5. The improvement of the solutions of Tables A.4 and A.5 compared to the solutions of Table A.3 is due to the new offset and the new value of the BBH system radius.
The range of M1/M2 when Tp/Tb ≈ 8.88.
The range of M1/M2 when Tp/Tb ≈ 9.88.
We see that the solutions found with Tp/Tb ≈ 8.88 are slightly more robust, but both solutions can be used.
The characteristics of the final solution of the BBH system associated with 1823+568 are given in Sect. 4.4.
Appendix B: Fit of component C5 of 3C 279
Appendix B.1: Fit of C5 using the precession model
To fit the ejection of component C5 we used 152 observations (76 epochs).
We studied the two cases ±ωp(t − z/Va). The final solution of the fit of component C5 of 3C 279 using a BBH system corresponds to −ωp(t − z/Va), therefore we discuss only this case in this appendix.
To fit the component C5, we assumed Td ≤ 2000 yr.
In this section, we assume that Va = 0.1c.
The range of inclination explored is 0.5° ≤ io ≤ 10°.
To begin, we allowed the time origin of the VLBI component to be a free parameter. We
assumed 1997.0 ≤ to ≤ 1998.5. We found that the function
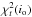 is characteristic of a
function corresponding to case II (see Sect. 5.1),
and the possible range for the inclination angle is [0.5,5.5]. The time
origin is to ≈ 1997.52 when
io → 0.55, and the time origin is
to ≈ 1998.15 when io → 5.5. We
plotted the first peak flux corresponding to the solution
to ≈ 1998.15 and io → 5.5
(solution with the smallest χ2) and found that it is too
early by at least eight months (dash line in Fig. B.2). As indicated in Sect. A.1, we do
not aim to fit the flux light curve, but we wish to compare the time position of the
modeled first peak flux with the observed first peak flux (Fig. B.2).
is characteristic of a
function corresponding to case II (see Sect. 5.1),
and the possible range for the inclination angle is [0.5,5.5]. The time
origin is to ≈ 1997.52 when
io → 0.55, and the time origin is
to ≈ 1998.15 when io → 5.5. We
plotted the first peak flux corresponding to the solution
to ≈ 1998.15 and io → 5.5
(solution with the smallest χ2) and found that it is too
early by at least eight months (dash line in Fig. B.2). As indicated in Sect. A.1, we do
not aim to fit the flux light curve, but we wish to compare the time position of the
modeled first peak flux with the observed first peak flux (Fig. B.2).
Next, we allowed to to be a free parameter in the range
1998.80 ≤ to ≤ 1999.10 and calculated the new function
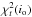 . The possible range for
the inclination angle is reduced to
0.8° ≤ io ≤ 4.3°. The plots of
. The possible range for
the inclination angle is reduced to
0.8° ≤ io ≤ 4.3°. The plots of
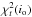 and
γ(io) are presented in Fig. B.1. We plotted the first peak flux corresponding to
the solution to ≈ 1998.80 and
io → 4.3 (solid line in Fig. B.2). From Fig. B.2, we conclude that
the minimun time for the ejection of C5 is to ≥ 1998.80.
and
γ(io) are presented in Fig. B.1. We plotted the first peak flux corresponding to
the solution to ≈ 1998.80 and
io → 4.3 (solid line in Fig. B.2). From Fig. B.2, we conclude that
the minimun time for the ejection of C5 is to ≥ 1998.80.
 |
Fig. B.1 Precession model applied to the component C5 of 3C 279. We assumed that the time origin is 1998.80 ≤ to ≤ 1999.10. Top figure: the function χ2(io) is limited to 0.8° ≤ io ≤ 4.3° and has no minimum in this interval. It stops at io ≈ 4.3° and io ≈ 0.8° because at these points the bulk Lorentz factor becomes larger than 30. Bottom figure: the bulk Lorentz factor diverges when io → 4.3° and io → 0.8°. |
The behavior of the functions χ2(io) and γc(io) are the second signature of case II, i.e., the offset is larger than the smallest error bars of the VLBI component coordinates.
 |
Fig. B.2 Determination of the minimum time for the ejection of component C5. We fit the first peak flux of component C5 of 3C 279 using the precession model. The peak flux corresponding to an ejection at to ≈ 1998.15 is shown (dash line), it is too early by at least 8 months. The precession model can fit the position of the first peak flux for to ≥ 1998.80 (solid line). |
We see from Fig. B.1 that the bulk Lorentz factor is γc ≥ 22. Because the function χ2(io) does not show a minimum, we arbitrarily chose an inclination angle such that 22 ≤ γ ≤ 26 and the corresponding χ2(io) is the smallest. To continue, we chose io ≈ 2.98° and the corresponding parameters of the precession solution (the χ2 of this solution is χ2 ≈ 1211 and its bulk Lorentz factor is γ ≈ 22.6). We used this solution to apply the method explained in Sect. 3 and we will see in the following how the BBH system model allows us to find the concave part of the funtion χ2(io).
Appendix B.2: Determining the family of solutions (precession model)
The solution is not unique. For the inclination angle previously found, i.e., io ≈ 2.98° and using the parameters of the corresponding solution, we gradually varied Va between 0.01c and 0.45c. The function χ2(Va) remains constant, indicating a degeneracy of the solution, and we obtained the range of possible values for the precession period given in Table B.1.
Range for the precession period.
Appendix B.3: Possible offset of the origin of the ejection (precession model)
In this section, we kept the inclination angle previously found, i.e., io ≈ 2.98°. We assumed that Va = 0.1 and used the parameters of the solution previously found.
To test whether the VLBI component is ejected from the VLBI core or if it is ejected with an offset of the origin, we calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions, using the precession model. The step used in West and North directions is 10μas.
 |
Fig. B.3 Using the precession model, we calcuated χ2(ΔW,ΔN) corresponding to the solution with io ≈ 2.98°. Non-zero offsets are possible and the smallest offsets are ΔW ≈ 0.300 mas and ΔN ≈ 0.280 mas, which corresponds to a BBH system of radius Rbin ≥ 410 μas. |
We see from Fig. B.3, that non-zero offsets are possible and the smallest offsets of the coordinates are ΔW ≈ +0.300 mas and ΔN ≈ +0.280 mas, which, a priori, corresponds to an offset of the space origin of ≥410 μas or to a BBH system of radius Rbin ≥ 410 μas. This minimum offset corresponds to an improvement of about 28σ. If the offset of the space origin can be estimated using the precession model, it cannot be explained if we assume that the nucleus contains a single black hole, but it can be explained if we assume that the nucleus contains a BBH system.
It is important to note that the offset does not depend on the inclination angle chosen in Sect. B.1. Indeed, we took the solution corresponding to io ≈ 1.5°, whose χ2 is χ2 ≈ 1610 and whose bulk Lorentz factor is γ ≈ 24, and we calculated χ2(ΔW,ΔN), which yielded the same result.
It is easy to prove that the value of the offset of the space origin is related to the time origin problem. Indeed, Fig. B.3 shows that there is a significant offset of the space origin when we assume that the time origin of component C5 of 3C 279 is to ≥ 1998.80. Now, using again the precession model, we calculated the possible offset of the space origin assuming that the time origin is a free parameter (Fig. B.4). We see from Fig. B.4 that non-zero offsets are possible and the smallest offsets of the coordinates are ΔW ≈ 100 μas and ΔN ≈ +150 μas, at this point, the time origin is to ≈ 1998.45. This time origin corresponds to an ejection that is about seven months too early.
 |
Fig. B.4 Calculation of χ2(ΔW,ΔN) using the precession model and assuming that the time origin is a free parameter. We find that non-offset are possible and the smallest offset corresponds to the point ΔW ≈ 100 μas and ΔN ≈ +150 μas. At this point, the time origin is to ≈ 1998.45 which is ≈ 7 months too early. |
To continue, two possibilities arise:
-
1.
either we keep the original VLBI coordinates anddetermine the parameters of the BBH system and theχ2(Tp/Tb) – diagram. Then, we determine a first offset correction using the BBH model, and after a preliminary determination of Tp/Tb and M1/M2, we determine a second offset correction using the BBH model;
-
2.
or we apply the precession offset correction to the VLBI coordinates and then we determine the parameters of the BBH system and the χ2(Tp/Tb) – diagram. Then we determine a first offset correction using the BBH model, and after a preliminary determination of Tp/Tb and M1/M2, we determine a second offset correction using the BBH model.
For component C5 of 3C 279, the two possibilities were followed. We found that they provide the same result in the end. In this article, we present the first one.
The determination of the offsets of the origin of the ejection does not depend on the inclination angle.
Appendix B.4: Determining the BBH system parameters
Because the precession is defined by −ωp(t − z/Va), the BBH system rotation is defined by +ωb(t − z/Va). In this section we kept the inclination angle previously found, i.e., io ≈ 2.98° and Va = 0.1c.
In the previous section, we saw that the BBH system has a large radius, i.e., Rbin ≥ 410 μas. Therefore, we determined the parameters of a BBH system with small Tp/Tb and a radius for the BBH system that is a free parameter (solutions with small Tp/Tb have large radii), i.e., we determined the parameters of a BBH system with Tp/Tb = 1.01 and calculated the corresponding χ2(Tp/Tb) – diagram.
Appendix B.5: χ2(Tp/Tb) – diagram
In this section, we kept the inclination angle previously found, i.e., io ≈ 2.98°, Va = 0.1c and assumed M1 = M2. Furthermore we assumed that the radius of the BBH system is a free parameter.
We calculated χ2(Tp/Tb) for 1 ≤ Tp/Tb ≤ 300. We started for BBH system parameters corresponding to the values of Tp/Tb = 1.01 and cover the complete interval of Tp/Tb. The result is shown in Fig. B.5.
 |
Fig. B.5 Calculation of χ2(Tp/Tb). The curve corresponds to the minimization when Tp/Tb varies from 1 to 300. There is one solution S1. |
We found the one solution given in Table B.2.
Solution found for io ≈ 2.98°.
Appendix B.6: Determining the offset of the origin of the ejection (BBH model)
In this section, we kept the inclination angle previously found, i.e., io ≈ 2.98°. We assumed that Va = 0.1c, M1 = M2.
We calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions. The step used in the west and north directions is 5 μas. The radius of the BBH system and Tp/Tb are free parameters during the minimization.
We calculated χ2(ΔW,ΔN) starting with the parameters of solution S1 found in the previous section. The result is shown in Fig. B.6.
 |
Fig. B.6 Calculation of χ2(ΔW,ΔN) using the BBH model. Contour levels are 246, 247, 250, 255, etc., corresponding to the minimum, 1σ, 2σ, 3σ, etc. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is true when the offsets are ΔW1 ≈ +0.490 mas and ΔN1 ≈ 0.005 mas. |
We see from Fig. B.6 that non-zero offsets are possible. However, all points with the smallest χ2(ΔW,ΔN) are not possible. Indeed, for a point with the smallest χ2, the offset size must be equal to the radius of the BBH system calculated at this point. This is the case if the offsets are ΔW1 ≈ +0.490 mas and ΔN1 ≈ +0.005 mas.
The radius of the BBH system at this point is Rbin ≈ 487 μas and the offset size is ≈ 490 μas, i.e., the offset and the radius of the BBH system are the same at this point.
Therefore we conclude that
-
the VLBI component C5 is not ejected from the VLBI core, but from the second black hole of the BBH system, and
-
the radius of the BBH system is Rbin ≈ 490 μas. It is more than ten times the smallest error bars of the VLBI component coordinates.
Note that if the size of the offset found with the BBH model is the same as the size of the offset found with the precession model, the first offsets are not the same for the coordinates. However, after the preliminary determination of the ratios Tp/Tb and M1/M2, the second and third offset corrections provide the same final offset corrections (the two methods indicated in Sect. B.3 provide the same corrections in the end).
Appendix B.7: Preliminary determination of io, Tp/Tb and M1/M2
From this point onward, the original coordinates of the VLBI component C5 are corrected for the offsets ΔW1 and ΔN1 found in the previous section. In this section, we assumed that Va = 0.1c and the radius of the BBH system is Rbin = 490 μas.
For given values of the ratio M1/M2 = 1.0, 1.25, 1.50, 1.75, and 2.0, we varied io between 3.0 and 10 degrees and calculated χ2(io) assuming that the ratio Tp/Tb is variable.
We found that χ2(io) is minimum for the parameters
-
io ≈ 5.9°;
-
M1/M2 ≈ 1.75; and
-
Tp/Tb ≈ 14.6.
Appendix B.8: Detemining a possible new offset correction
In this section, we assumed Va = 0.1c.
With io ≈ 5.9°, with a variable ratio Tp/Tb, M1/M2 ≈ 1.75 and the parameters of the solution found in the previous section, we can verify whether there is an additional correction to the offset of the origin of the VLBI component. We calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions. We assumed that the radius of the BBH system is left free to vary. The result is shown in Fig. B.7. We found that an additional correction is needed, namely ΔW2 ≈ −0.085 mas and ΔN2 ≈ +0.105 mas.
At this point the total offset is ≈ 418 μas and the radius of the BBH system is Rbin ≈ 420 μas.
 |
Fig. B.7 Calculation of χ2(ΔW,ΔN) using the BBH model. Contour levels are 162, 163, 166, 171, etc corresponding to the minimum, 1σ, 2σ, 3σ, etc. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case when the offsets are ΔW2 ≈ −0.085 mas and ΔN2 ≈ +0.105 mas. |
Appendix B.9: Final fit of component C5 of 3C 279
The coordinates of the VLBI component C5 are corrected for the new offsets ΔW2 and ΔN2. In this section, we assumed Va = 0.1c and Rbin = 420 μas.
We can now find the final solution for the fit of C5. We calculated χ2(io) for various values of Tp/Tb and M1/M2, namely Tp/Tb ≤ 1000 and M1/M2 ≤ 3.5 with a typical step Δ(M1/M2) = 0.25.
The first important result is that when the ratio Tp/Tb is high enough, we can find non-mirage solutions in relation to the variable γ. To illustrate this result, we plot in Fig. B.8 the function γ(Tp/Tb) corresponding to M1/M2 = 1.75.
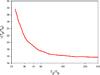 |
Fig. B.8 Calculation of γ(Tp/Tb). For a given value of M1/M2, the bulk Lorentz factor decreases when Tp/Tb increases, showing that if the ratio Tp/Tb is high enough, we can find solutions that are not mirage solutions in relation to the variable γ. |
The determination of the solution used an iterative method. Starting with a given value of Tp/Tb, we calculated χ2(io) for various values of M1/M2. Then we calculated for the parameters corresponding to the solution found the function χ2(Tp/Tb) to determine the new value of Tp/Tb that minimizes the function χ2(Tp/Tb). Starting with the new value of Tp/Tb, we repeated the procedure.
At each step of the procedure, we calculated χ2(γ) to check that the solution corresponds to the concave part and is not a mirage solution.
The best fit is obtained for Tp/Tb ≈ 140 and M1/M2 ≈ 2.75. The results of the fits are presented in Table B.3.
Solutions found for Tp/Tb = 140.
We plot in Fig. B.9 the calculation of χ2(γ) corresponding to the solution characterized by Tp/Tb = 140 and M1/M2 = 2.75. It shows that the solution is not a mirage solution in relation to γ.
 |
Fig. B.9 Calculation of χ2(γ) for the solution with Tp/Tb = 140 and M1/M2 = 2.75. It shows that the solution is not a mirage solution in relation to γ. The minimum corresponds to γ ≈ 16.7. |
The best fit is obtained for Tp/Tb ≈ 140 (see Fig. B.10). When the ratio Tp/Tb increases, the χ2 remains mostly constant but the robustness of the solution in relation to γ increases.
 |
Fig. B.10 Calculation of χ2(Tp/Tb) for the solution with M1/M2 = 2.75. |
Finally, we plot in Fig. B.11 the function χ2(io).
 |
Fig. B.11 Calculation of χ2(io) for the solution with Tp/Tb = 140 and M1/M2 = 2.75. |
The characteristics of final solution of the BBH system associated with 3C 279 are given in Sect. 5.4.
Appendix C: Error bars
Appendix C.1: Minimum error bar values
Observations used to fit the components S1 of 1823+568 and C5 of 3C 279 were performed at 15 GHz. We adopted for the minimum values of the error bars, Δmin, values in the range Beam/15 ≤ Δmin ≤ Beam/12.
There are three important points concerning the minimum values used for the error bars:
-
1.
The minimum values are chosen empirically, but the adoptedvalues are justified a posteriori by comparing of the value ofχ2 of the final solution and the number of constraints used to make the fit. Indeed, the reduced χ2 has to be close to 1.
-
2.
The minimum value of the error bars used at 15 GHz produces a value of (χ2)final concistent with the value of the realistic error obtained from the VLBI Service for Geodesy and Astrometry (Schlüter & Behrend 2007), which is a permanent geodetic and astrometric VLBI program. It has been monitoring the position of thousands of extragalactic radio sources for more than 30 years. In 2009, the second realization of the International Celestial Reference Frame (ICRF2) was released (Fey et al. 2009), obtained after the treatment of about 6.5 millions of ionosphere-corrected VLBI group delay measurements at 2 and 8 GHz. This catalog is currently the most accurate astrometric catalog, giving absolute positions of 3414 extragalactic bodies at 8 GHz. The observations at 2 GHz are used for the ionospheric correction only. Therefore, the positions at 2 GHz are not provided. The ICFR2 is found to have a noise floor of only 40 microseconds of arc (μas), which is five to six times better than the previous ICRF realization (Ma et al. 1998). The positions of more than 200 radio sources are known with a precision (inflated error, or “realistic” error) better than 0.1 mas. Since the ICRF2 release, the positional accuracy of the sources has increased, and it is likely that the next VLBI realization of the ICRF will have a noise floor lower than 40 μas.
-
3.
The adopted minimum value of the error bars also includes typical errors due to opacity effects, which shift the measured position at different frequencies (Lobanov 1998).
It has been suggested by Lister & Homan (2005) that the positional error bars should be about 1/5 of the beam size. To study the influence of the minimum values of the error bars on the characteristics of the solution, we calculate in the next sections the solution of the fit of the component C5 assuming for the minimum values of the error bars the value suggested by Lister & Homan (2005), i.e. the value Δmin = Beam/5 , or (ΔW)min ≈ 102 μas and (ΔN)min ≈ 267 μas.
Appendix C.2: Fit of C5 using the precession model
We look for a solution with −ωp(t − z/Va) and to ≥ 1980.80 (see Sect. B.1).
In this section, we assumed that Va = 0.1c.
The range of inclination explored is 0.5° ≤ io ≤ 10°.
We allowed to to be a free parameter in the range
1998.80 ≤ to ≤ 1999.10 and calculated the function
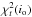 . The possible range for
the inclination angle is
0.74° ≤ io ≤ 4.3°. The plots of
. The possible range for
the inclination angle is
0.74° ≤ io ≤ 4.3°. The plots of
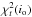 and
γ(io) are presented in Fig. C.1.
and
γ(io) are presented in Fig. C.1.
 |
Fig. C.1 Precession model applied to the component C5 of 3C 279 assuming high values for the minimum error bars. We assumed that the time origin is 1998.80 ≤ to ≤ 1999.10. Top figure: the function χ2(io) is limited to 0.8° ≤ io ≤ 4.3° and has no minimum in this interval. It stops at io ≈ 4.3° and io ≈ 0.8° because at these points the bulk Lorentz factor becomes larger than 30. Bottom figure: the bulk Lorentz factor diverges when io → 4.3° and io → 0.8°. |
The behavior of the functions χ2(io) and γc(io) are the second signature of case II.
Comparison of Figs. C.1 and B.1 shows that the range of the inclination angle, and the values of the bulk Lorentz factor in this range, are the same for the different values of the minimum error bars used.
Appendix C.3: Possible offset of the origin of the ejection (precession model)
In this section, we kept the inclination angle used in Sect. B.3, i.e., io ≈ 3.3°. We assumed that Va = 0.1 and used the parameters of the solution found in Sect. C.2.
We calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions, using the precession model. The step used in the west and north directions is 10μas. The result of the calculation is plotted in Fig. C.2.
 |
Fig. C.2 Using the precession model, we calcuated χ2(ΔW,ΔN). The contour levels 68, 71, 76, etc correspond to 1σ, 2σ, 3σ, etc. Non-zero offsets are possible and the smallest offsets are ΔW ≈ 0.320 mas and ΔN ≈ 0.280 mas, which corresponds to a BBH system of radius Rbin ≥ 425 μas. |
Comparison of Fig. C.2 with Fig. B.3 shows that
-
the smallest offsets of the coordinates are ΔW ≈ +0.320 mas and ΔN ≈ +0.280 mas. They are similar to the offsets found assuming that the minimum error bars are Δmin = Beam/15 (see Sect. B.3),
-
the value of χ2 at the minimum is
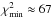 instead of
instead of
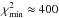 when the minimum error
bars are Δmin = Beam/15. The
reduced
when the minimum error
bars are Δmin = Beam/15. The
reduced 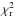 is
is
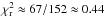 , indicating that the
minimum error bars are too large.
, indicating that the
minimum error bars are too large.
Accordingly, with high values for the minimum values of the error bars, we find using the precession model that the component C5 is ejected with an offset of the space origin of at least 0.425 mas with a robustness higher than 11σ. The offset of the space origin can be estimated using a single black hole and the precession of the accretion disk. It cannot be explained when we assume that the nucleus contains a single black hole, but it can be explained when we assume that the nucleus contains a BBH system.
Appendix C.4: χ2(Tp/Tb) – diagram
Because the precession is defined by −ωp(t − z/Va), the BBH system rotation is defined by +ωb(t − z/Va). As in Sect. B.4, we calculated the BBH parameters for the inclination angle io ≈ 2.98° and the ratio Tp/Tb = 1.01 and calculated the corresponding χ2(Tp/Tb) – diagram assuming M1 = M2 and Va = 0.1c.
We calculated χ2(Tp/Tb) for 1 ≤ Tp/Tb ≤ 300. The result is shown in Fig. C.3.
 |
Fig. C.3 Calculation of χ2(Tp/Tb). There is one solution Sol 1. |
We found a possible solution of the BBH system given in Table C.1.
Solution found for io ≈ 2.98°.
Comparison of Tables B.2 and C.1 and of Figs. B.5 and C.3 shows that the solutions S1 and Sol1 are mostly identical.
Appendix C.5: Determining the offset of the origin of the ejection (BBH model)
In this section, we kept the inclination angle previously found, i.e., io ≈ 2.98°. We assumed that Va = 0.1c, M1 = M2.
We calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions. The step used in the west and north directions is 5 μas. The radius of the BBH system and Tp/Tb are free parameters during the minimization.
We calculated χ2(ΔW,ΔN) starting with the parameters of solution Sol 1 found in the previous section. The result is shown in Fig. C.4.
 |
Fig. C.4 Calculation of χ2(ΔW,ΔN) using the BBH model. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case if the offsets are ΔW1 ≈ +0.495 mas and ΔN1 ≈ 0.005 mas. The corresponding radius of the BBH system is Rbin ≈ 495 μas. |
We see from Fig. C.4 that non-zero offsets are possible. However, all points with the smallest χ2(ΔW,ΔN) are not possible. Indeed, for a point with the smallest χ2, the size offset must be equal to the radius of the BBH system calculated at this point. This is the case if the offsets are ΔW1 ≈ +0.495 mas and ΔN1 ≈ +0.005 mas.
The radius of the BBH system at this point is Rbin ≈ 495 μas and the offset size is ≈ 495 μas, i.e. the offset and the radius of the BBH system are the same at this point.
Comparison of the result found in Sect. B.6 and of Figs. C.4 and B.6 show that the offset determined using large error bars is the same as the offset calculated with the small error bars.
Therefore we conclude that the VLBI component C5 is not ejected from the VLBI core but from the second black hole of the BBH system.
Appendix C.6: Determining a possible new offset correction
From this point onward, the original coordinates of the VLBI component C5 are corrected for the offsets ΔW1 and ΔN1 found in the previous section.
In this section, we assumed Va = 0.1c.
As in Sect. B.7, we preliminarily determined the parameters Tp/Tb, M1/M2 and io.
With io ≈ 5.9°, using the ratios Tp/Tb free and M1/M2 ≈ 1.75, we can verify whether there is an additional correction to the offset of the origin of the VLBI component. We calculated χ2(ΔW,ΔN), where ΔW and ΔN are offsets in the west and north directions. We assumed that the radius of the BBH system is let free to vary. The result is shown in Fig. C.5. We found that an additional correction is needed, namely ΔW2 ≈ −0.085 mas and ΔN2 ≈ +0.085 mas.
At this point the total offset is ≈ 419 μas and the radius of the BBH system is Rbin ≈ 419 μas.
 |
Fig. C.5 Calculation of χ2(ΔW,ΔN) using the BBH model. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case if the offsets are ΔW2 ≈ −0.085 mas and ΔN2 ≈ 0.085 mas. The corresponding radius of the BBH system is Rbin ≈ 419 μas. |
Thus, using for the highest values of the error bars the values Δmin = Beam/5, we found that the final offset is ΔWt ≈ +0.410 mas, and ΔNt ≈ +0.090 mas, and the radius of the BBH system is Rbin ≈ 0.419 mas.
These values have to be compared with the values obtained assuming for the lowest error bars the value used Δmin = Beam/15, which are ΔWt ≈ +0.405 mas, and ΔNt ≈ +0.110 mas, and the radius of the BBH system is Rbin ≈ 0.420 mas.
Appendix C.7: Final solution
The characteristics of the final solution determined assuming for the minimum value of the error bars the value Δmin = Beam/5 are
-
Tp/Tb ≈ 140;
-
M1/M2 ≈ 2.75;
-
io ≈ 11.0°; and
-
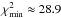 .
.
Thus the reduced χ2 at the minimum is
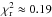 ,
indicating that the minimum error bars are too large.
,
indicating that the minimum error bars are too large.
Appendix C.8: Conclusion
We determined the characteristics of the solution, assuming for the minimum value of the error bars the value Δmin = Beam/5 suggested by Lister & Homan (2005). We found that
-
1.
the characteristics of the solution are the sameas those of the solution determined assumingfor the minimum value of the error bars the valueΔmin = Beam/15, and
-
2.
the corresponding reduced χ2 is
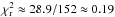 , indicating that the
minimum error bars are too large.
, indicating that the
minimum error bars are too large.
The correct value for the minimum error bars at 15 GHz is Beam/15 ≤ Δmin ≤ Beam/12.
This value
-
1.
produces a reduced χ2,
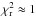 ;
; -
2.
the minimum value agrees with the value of the realistic error obtained from the VLBI Service for Geodesy and Astrometry (Schlüter & Behrend 2007), and
-
3.
the fit of VLBI coordinates of components of 3C 345 (work in progress) indicates that the adopted values for the minimun values of the error bars, i.e., Beam/15 ≤ Δmin ≤ Beam/12, are correct for frequencies between 8 GHz and 22 GHz.
All Tables
All Figures
 |
Fig. 1 BBH system model. The two black holes can have an accretion disk and can eject VLBI components. If it is the case, we observe two different families of trajectories and an offset between the VLBI core and the origin of the VLBI component if it is ejected by the black hole that is not associated with the VLBI core. The angles Ω1 and Ω2 between the accretion disks and the rotation plane of the BBH system can be different. |
| In the text | |
 |
Fig. 2 Trajectories of the VLBI components C5 and C9 of 3C 273 using MOJAVE data (Lister et al. 2009b). We observe two different types of trajectories, suggesting that they are ejected from two different black holes. |
| In the text | |
 |
Fig. 3 Two-fluid model. The outflow consists of an e− − e+ plasma, the beam, moving at a highly relativistic speed, surrounded by an e− − p plasma, and of the jet, moving at a mildly relativistic speed. The magnetic field lines are parallel to the flow in the beam and the mixing layer, and are toroidal in the jet. |
| In the text | |
 |
Fig. 4 Geometry of the problem. The planes X–η and west–north are perpendicular to the line of sight. In the west–north plane, the axis η corresponds to the mean ejection direction of the VLBI component. Ω is the opening angle of the precession cone. |
| In the text | |
 |
Fig. 5 Example of a possible profile of the solution χ2(io). There are two possible solutions for which χ2(Sol1)≈ χ2(Sol2). They correspond to the concave parts of the surface χ2(io). However, solution 2 is more robust than solution 1, i.e. it is the deepest one, and it will be the solution we adopt. |
| In the text | |
 |
Fig. 6 15 GHz natural weighted VLBI image of 1823+568 with fitted circular Gaussian components observed 9 May 2003 (Glück 2010). The map peak flux density was 1.27 Jy/beam, where the convolving beam was 0.58 × 0.5 mas at position angle (PA) − 2.09°. The contour levels were drawn at 0.15, 0.3, 0.6, 1.2, 2.4, 4.8, 9.6, 19.2, 38.4, and 76.8% of the peak flux density. |
| In the text | |
 |
Fig. 7 Separation from the core for the different VLBI components for the source 1823+568 from MOJAVE data (Lister et al. 2009b). For details concerning the plot and the line fits see Lister et al. (2009b). We fit component S1 corresponding to component 4 from the MOJAVE survey. Component S1 moves fast, which may indicate that two families of VLBI components exist in the case of 1823+568. If this is the case, the nucleus of 1823+568 could contain a BBH system. |
| In the text | |
 |
Fig. 8 Apparent speed of component S1 increases at the begining, then it is ≈ 17.5c until 2005, and finally, it decreases slowly assuming a constant bulk Lorentz factor γc ≈ 17.7. |
| In the text | |
 |
Fig. 9 Fit of the two coordinates W(t) and N(t) of component S1 of 1823+568. They correspond to the solution with Tp/Tb ≈ 8.88, M1/M2 ≈ 0.17, and io ≈ 3.98°. The points are the observed coordinates of component S1 that were corrected by the offsets ΔW ≈ +5 μas and ΔN ≈ 60 μas (the VLBI coordinates and their error bars are taken from Glück 2010). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| In the text | |
 |
Fig. 10 15 GHz natural-weighted VLBI image of 3C 279 with fitted circular Gaussian components observed 15 June 2003 (Lister et al. 2009a). The map peak flux density was 8.3 Jy/beam, where the convolving beam was 1.3 × 0.5 mas at position angle (PA) −6.0°. The contour levels were drawn at 0.2, 0.5, 1.0, 2.0, 4.0, 8.0, 16, 32, 64, and 80% of the peak flux density. Component C4 is a stationary component (see Fig. 11). |
| In the text | |
 |
Fig. 11 Separation from the core for the different VLBI components for the source 3C 279 from MOJAVE data (Lister et al. 2009b). For the obtaining of the plotted line fits see Lister et al. (2009b). We fit component C5. Component C5 is ejected from an origin with a large offset from the VLBI core. |
| In the text | |
 |
Fig. 12 Apparent speed of component C5 varies between 17c and 9c assuming a constant bulk Lorentz factor γc ≈ 16.7. |
| In the text | |
 |
Fig. 13 Flux variations of component C5 using the BBH model. The time origin of the ejection of C5 is 1999.03. |
| In the text | |
 |
Fig. 14 Fit of the two coordinates W(t) and N(t) of component C5 of 3C 279. They correspond to the solution with Tp/Tb ≈ 140, M1/M2 ≈ 2.75, and io ≈ 10.4°. The points are the observed coordinates of component C5 that were corrected for the offsets ΔW ≈ +405 μas and ΔN ≈ +110 μas. VLBI coordinates are taken from Lister et al. (2009a). The red lines are the coordinates of the component trajectory calculated using the BBH model. |
| In the text | |
 |
Fig. 15 Using the MOJAVE data (Lister et al. 2009b), we plot the trajectories of C5 and C10. Component C10 is probably ejected by the VLBI core and component C5 is ejected with a large offset from the VLBI core. Components C5 and C10 follow two different trajectories and are ejected from different origins, indicating that the nucleus of 3C 279 contains a BBH system. Note that the origin of this caption corresponds to the origin of the ejection of component C5, thus all MOJAVE coordinates have been corrected for the offsets ΔW ≈ +405 μas and ΔN ≈ +110 μas. |
| In the text | |
 |
Fig. A.1 Fit of the first peak flux of component S1 of 1823+568 using the precession model. The time origin deduced from the fit of the peak flux is to ≥ 1995.65 and is comparable with the time origin deduced from VLBI observations interpolation, i.e., to ≈ 1995.60. |
| In the text | |
 |
Fig. A.2 Calculation of χ2(ΔW,ΔN) using the BBH model. Non-zero offsets are possible, but the size of the offset must be the same as the radius of the BBH system calculated at this point. This is the case if the offsets are ΔW1 ≈ 0.010 mas and ΔN1 ≈ 0.070 mas. We determined the offset at io ≈ 6°; it does not depend on the value of the adopted inclination angle. |
| In the text | |
 |
Fig. A.3 Tp/Tb as function of io obtained by minimizing χ2(io). |
| In the text | |
 |
Fig. A.4 Function χ2(io). It stops at large inclination angles because the bulk Lorentz factor becomes greater than 30. Top figure: the ratio M1/M2 is M1/M2 = 1. When Tp/Tb increases, the minimum decreases and disappears. This means that the function χ2(io) does not show a minimum and is a mirage solution. Bottom figure: the ratio M1/M2 = 0.37. The function χ2(io) has a minimum for Tp/Tb ≈ 8.88 and io ≈ 4. The robustness of this solution, defined as the square root of the difference χ2(γ = 30) − χ2(min), is ≈ 1.8 × σ. |
| In the text | |
 |
Fig. B.1 Precession model applied to the component C5 of 3C 279. We assumed that the time origin is 1998.80 ≤ to ≤ 1999.10. Top figure: the function χ2(io) is limited to 0.8° ≤ io ≤ 4.3° and has no minimum in this interval. It stops at io ≈ 4.3° and io ≈ 0.8° because at these points the bulk Lorentz factor becomes larger than 30. Bottom figure: the bulk Lorentz factor diverges when io → 4.3° and io → 0.8°. |
| In the text | |
 |
Fig. B.2 Determination of the minimum time for the ejection of component C5. We fit the first peak flux of component C5 of 3C 279 using the precession model. The peak flux corresponding to an ejection at to ≈ 1998.15 is shown (dash line), it is too early by at least 8 months. The precession model can fit the position of the first peak flux for to ≥ 1998.80 (solid line). |
| In the text | |
 |
Fig. B.3 Using the precession model, we calcuated χ2(ΔW,ΔN) corresponding to the solution with io ≈ 2.98°. Non-zero offsets are possible and the smallest offsets are ΔW ≈ 0.300 mas and ΔN ≈ 0.280 mas, which corresponds to a BBH system of radius Rbin ≥ 410 μas. |
| In the text | |
 |
Fig. B.4 Calculation of χ2(ΔW,ΔN) using the precession model and assuming that the time origin is a free parameter. We find that non-offset are possible and the smallest offset corresponds to the point ΔW ≈ 100 μas and ΔN ≈ +150 μas. At this point, the time origin is to ≈ 1998.45 which is ≈ 7 months too early. |
| In the text | |
 |
Fig. B.5 Calculation of χ2(Tp/Tb). The curve corresponds to the minimization when Tp/Tb varies from 1 to 300. There is one solution S1. |
| In the text | |
 |
Fig. B.6 Calculation of χ2(ΔW,ΔN) using the BBH model. Contour levels are 246, 247, 250, 255, etc., corresponding to the minimum, 1σ, 2σ, 3σ, etc. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is true when the offsets are ΔW1 ≈ +0.490 mas and ΔN1 ≈ 0.005 mas. |
| In the text | |
 |
Fig. B.7 Calculation of χ2(ΔW,ΔN) using the BBH model. Contour levels are 162, 163, 166, 171, etc corresponding to the minimum, 1σ, 2σ, 3σ, etc. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case when the offsets are ΔW2 ≈ −0.085 mas and ΔN2 ≈ +0.105 mas. |
| In the text | |
 |
Fig. B.8 Calculation of γ(Tp/Tb). For a given value of M1/M2, the bulk Lorentz factor decreases when Tp/Tb increases, showing that if the ratio Tp/Tb is high enough, we can find solutions that are not mirage solutions in relation to the variable γ. |
| In the text | |
 |
Fig. B.9 Calculation of χ2(γ) for the solution with Tp/Tb = 140 and M1/M2 = 2.75. It shows that the solution is not a mirage solution in relation to γ. The minimum corresponds to γ ≈ 16.7. |
| In the text | |
 |
Fig. B.10 Calculation of χ2(Tp/Tb) for the solution with M1/M2 = 2.75. |
| In the text | |
 |
Fig. B.11 Calculation of χ2(io) for the solution with Tp/Tb = 140 and M1/M2 = 2.75. |
| In the text | |
 |
Fig. C.1 Precession model applied to the component C5 of 3C 279 assuming high values for the minimum error bars. We assumed that the time origin is 1998.80 ≤ to ≤ 1999.10. Top figure: the function χ2(io) is limited to 0.8° ≤ io ≤ 4.3° and has no minimum in this interval. It stops at io ≈ 4.3° and io ≈ 0.8° because at these points the bulk Lorentz factor becomes larger than 30. Bottom figure: the bulk Lorentz factor diverges when io → 4.3° and io → 0.8°. |
| In the text | |
 |
Fig. C.2 Using the precession model, we calcuated χ2(ΔW,ΔN). The contour levels 68, 71, 76, etc correspond to 1σ, 2σ, 3σ, etc. Non-zero offsets are possible and the smallest offsets are ΔW ≈ 0.320 mas and ΔN ≈ 0.280 mas, which corresponds to a BBH system of radius Rbin ≥ 425 μas. |
| In the text | |
 |
Fig. C.3 Calculation of χ2(Tp/Tb). There is one solution Sol 1. |
| In the text | |
 |
Fig. C.4 Calculation of χ2(ΔW,ΔN) using the BBH model. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case if the offsets are ΔW1 ≈ +0.495 mas and ΔN1 ≈ 0.005 mas. The corresponding radius of the BBH system is Rbin ≈ 495 μas. |
| In the text | |
 |
Fig. C.5 Calculation of χ2(ΔW,ΔN) using the BBH model. There is a valley of possible offsets, but the size of the offset must be the same as the radius of the BBH system. This is the case if the offsets are ΔW2 ≈ −0.085 mas and ΔN2 ≈ 0.085 mas. The corresponding radius of the BBH system is Rbin ≈ 419 μas. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation} x_{1} = y_{1} = -\frac{ M_{2}}{M_{1}+M_{2}} \times \left[\frac{T_{\rm b}^{2}}{4\pi^{2}}G(M_{1}+M_{2}) \right]^{1/3}. \end{equation}](/articles/aa/full_html/2013/09/aa19165-12/aa19165-12-eq48.png)