| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201321919 | |
| Published online | 05 August 2013 | |
Hyperfine structure investigations of atomic niobium with optogalvanic and laser-induced fluorescence spectroscopy in the near-infrared wavelength range
1
Istanbul University, Faculty of SciencePhysics Department,
34134 Vezneciler, Istanbul, Turkey
e-mail: gbasar@istanbul.edu.tr
2
Istanbul Technical University, Faculty of Science and Letters,
Physics Engineering Department, 34469 Maslak, Istanbul, Turkey
3
Hochschule für Technik und Wirtschaft Berlin,
Fachbereich 1, Wilhelminenhofstr.
75A, 12459
Berlin,
Germany
e-mail: sophie.kroeger@htw-berlin.de
Received:
19
May
2013
Accepted:
29
June
2013
Aims. The aim of this work is to increase the amount of hyperfine structure data of atomic niobium (Nb I), which is needed for astrophysicists for the detailed analysis of new stellar spectra. Particular emphasis was placed on the investigation of energy levels with unknown hyperfine structure constants.
Methods. The hyperfine structure in the spectrum of Nb I was studied using laser-induced fluorescence spectroscopy and laser optogalvanic spectroscopy with a tuneable single-mode cw Ti:Sa laser in the wavelength range from 750 nm to 865 nm. The Nb atoms were produced and excited in a liquid-nitrogen-cooled hollow-cathode plasma.
Results. We measured and analysed 81 spectral lines, 19 of which are not previously known from the literature. In total, the magnetic dipole hyperfine structure constants A were determined for 28 energy levels of even and 53 energy levels of odd parity. The electric quadrupole hyperfine structure constants B were only determined in a few cases, when the spectra were clearly resolved and/or when a level was found from several transitions. The magnetic dipole hyperfine structure constants A of 13 even and 11 odd levels as well as the electric quadrupole hyperfine structure constants B of 13 even and 17 odd levels are presented for the first time. For the other levels, improved values of hyperfine structure constants are given.
Conclusions. The hyperfine structure can have a significant effect on stellar absorption line profiles, and the corresponding abundances can be substantially overestimated if these effects are not taken into account. Therefore, a detailed consideration of the hyperfine structure is important for stellar abundance determinations. The present work substantially increases the knowledge of hyperfine structure of Nb, which plays an important role in investigating the nucleosynthesis of heavy elements.
Key words: atomic data / line: profiles / techniques: spectroscopic / methods: laboratory
© ESO, 2013
1. Introduction
We here continue our earlier systematic investigations of the spectrum of Nb I (Kröger & Bouzed 2003; Kröger et al. 2004, 2007, 2010; Başar et al. 2008; Er et al. 2011). Our purpose is to supplement hyperfine structure (hfs) data for this element, in particular, to fill gaps for all energy levels of even parity with unknown hyperfine structure (hfs) constants.
Niobium1 (Nb) is the third element of 4d shell transition elements and belongs to the very few elements with only one stable isotope. The astrophysical interest of Nb hfs data was already extensively discussed in Kröger et al. (2010). A lot of work has already been done over the past 35 years to investigate the hfs of Nb using various spectroscopic methods. For the low-lying energy levels hfs constants have been determined with very high accuracy using atomic-beam magnetic-resonance method by Büttgenbach et al. (1975). Other high-resolution measurements have been made by Fraenkel et al. (1988) using laser and radio-frequency spectroscopy, and by some of us (Başar et al. 2008), using Doppler-reduced saturation absorption spectroscopy. Doppler-limited measurements of hfs constants have been made using Fourier transform spectroscopy (Kröger et al. 2010; Er et al. 2011) and Doppler-limited laser spectroscopic methods (Singh & Rao 1989; Singh et al. 1992; Bouzed et al. 2003; Kröger 2007). In addition to the experimental investigations, a theoretical analysis of hfs of atomic Nb has been performed by Büttgenbach & Dicke (1975), Kröger & Bouzed (2003), and Kröger et al. (2007).
Despite all this effort, for many energy levels the hfs constants are still unknown, some of them lying relatively low, i.e. lower than 25 000 cm-1. Until now, the magnetic dipole hfs constants A of 57 levels of even and 136 levels of odd parity as well as the electric quadrupole hfs constants B of 32 levels of even and 30 levels of odd parity are known. In the present work, we increase the data by 24 A (13 for even and 11 for odd parity levels), filling all gaps for levels of even parity, which have had not yet known A constants. Additionally, 31 new B constants (13 for even and 18 for odd parity levels, respectively) were determined.
2. Experimental details
The Nb atoms were produced and excited in a cooled hollow-cathode plasma. The hollow-cathode lamp consists of mainly two anodes and a 20 mm long hollow cathode with a 3 mm inner diameter in which a 0.125-mm-thick niobium foil was inserted. The hollow cathode was cooled by liquid nitrogen to reduce the Doppler width. A detailed explanation of the construction of the hollow-cathode lamp is given in Messnarz & Guthöhrlein (2000). The discharge was operated at a Ne pressure of about 2 mbar and a current of 10 to 50 mA. The current was chosen depending on the signal-to-noise ratio of the spectral line. The low current is favourable to reduce the Doppler width, whereas the high current increases the signal.
A continuous wave tuneable titan-sapphire (Ti:Sa) laser (Coherent MBR-110 pumped by Coherent Verdi 18 W) was used in the wavelength range from 750 nm to 865 nm with a power of about 1.5 W. Two small parts of the laser beam were split off by a beam sampler to measure spectral properties. The first beam part was directed to a home-made temperature stabilized confocal Fabry-Perot interferometer (FPI) with a free spectral range of about 300 MHz, which was used to measure the variation of the relative frequency during the scan of the laser wavelength. The spectrum from the FPI was used to calibrate the simultaneously measured atomic spectrum. The second part of the laser beam was coupled to a wavemeter (High Finesse WS6-200), which has an accuracy for the absolute frequency of 200 MHz or 0.007 cm-1. By using a couple of dielectric mirrors, the main laser beam went through the hollow-cathode lamp after passing from the backside through the hole of the large diameter mirror that has a hole in the middle (outer diameter: ?= 100 mm, hole diameter: ?= 3 mm).
The experimental setup was constructed so that both the laser optogalvanic spectroscopy (LOGS) and laser-induced fluorescence spectroscopy (LIFS) could be applied simultaneously (see Fig. 1). The laser beam was amplitude-modulated by a mechanical chopper to apply a lock-in technique that recovered the signal deduced from LOGS and LIFS.
The optogalvanic signal was produced when the wavelength of the laser was resonant with the differences of energy levels of Nb or noble gas atoms. The change of voltage was measured across a ballast resistor. A detailed explanation of the optogalvanic effect can be found in Sasso (1990).
For LIFS measurements, the large-diameter hole mirror collected the divergent fluorescence light from the hollow cathode. The fluorescence light was collimated by a lens, directed to the monochromator by two large diameter mirrors (?= 100 mm) and focused on the entrance slit by another lens. The monochromator (McPherson 607, 0.67 m focal length and a (120 mm × 140 mm) large grating with 1200 lines/mm; photomultiplier PM R928 from Hamamatsu) was used as a fixed wavelength filter to measure only the fluorescence light arising from transition including one of the energy levels, which are involved in the transition excited by the laser. A detailed explanation of the LIFS method can be found in Shamim et al. (2011).
 |
Fig. 1 Schematic overview of the experimental setup used for laser optogalvanic spectroscopy and laser-induced fluorescence spectroscopy; M: mirror, L: lens, BS: beam sampler, FPI: Fabry-Perot interferometer, R: resistor, C: capacitor, HC: hollow-cathode lamp, DMM: digital multimeter, PD: photodiode, HM: hole mirror, PM: photomultiplier, HV: high-voltage power supply. |
The two signals from LOGS and LIFS could be observed simultaneously. By scanning the laser wavelength, the hfs of the investigated spectral lines could be detected. For some lines, the signal-to noise ratio was better using LOGS than LIFS. For other lines, it was the opposite. For each line, the best method was chosen. For LIFS measurements, different fluorescence transitions were tried and the best was picked up.
In LOGS measurements, some lines were overlapping within their hfs pattern with other Nb or Ne lines. For these lines, LIFS was very convenient and offered the possibility to separate the lines by using different fluorescence channels. An example for overlapping hfs patterns is given in Fig. 2. The spectrum recorded with LOGS is compared with two spectra measured with LIFS using two different fluorescence wavelength. Only by using LIFS with two different fluorescence wavelengths was it possible to separate the lines.
 |
Fig. 2 Example for blended lines: a) Spectrum recorded by LOGS at around 12 715 cm-1 showing the overlap of two Nb lines as well as another spurious line. b) Spectrum recorded by LIFS with fluorescence λf = 532.15 nm: transition from 14 899.26 cm-1, J = 5/2 − → 27 614.10 cm-1, J = 5/2 at λair = 786.266 nm or σvac = 12 714.84 cm-1. c) Spectrum recorded by LIFS with fluorescence λf = 581.94 nm: transition from 17 476.22 cm-1, J = 11/2 − → 30 191.25 cm-1, J = 13/2 at λair = 786.255 nm or σvac = 12 715.03 cm-1. |
3. Selection of lines
As mentioned above, the aim of the present work was to fill up gaps in the knowledge of hfs constants A, especially for levels of even parity. The classification program Class_lw from Windholz & Guthöhrlein (2003) was used to search for transitions involving levels with unknown A constants. A comprehensive list of experimental wavelengths and classifications for Nb I and II, as well as a list of corresponding energy levels is given by Humphreys & Meggers (1945) (nearly 70 years, old but still very useful). This list provides the basis for the classification program, supplemented by new energy levels from more recent references (Kröger et al. 2004, 2007), (resulting in the same list as the current state of the level list, given in the NIST atomic spectra database (NIST 2013)). The program additionally contains information about magnetic dipole and electric quadrupole hfs constants A and B, if available. Using the Ritz combination principle and taking into account the selection rule for electric dipole transitions (ΔJ = 0, ± 1; J = 0 ↮ 0), the program calculates all possible transitions to and from a chosen energy level. The program does not consider transition probabilities and of course provides much more lines than listed in the wavelength table of Humphreys & Meggers (1945). Therefore, not all transitions calculated by the Ritz combination principle could be found with our experimental conditions.
We measured and classified 81 spectral transitions (see Table 1). Sixty-two of these lines have already been listed in the wavelength tables from Humphreys & Meggers (1945), 14 without classification. The classification for these lines was deduced from the classification program Class_lw using the hfs patterns as fingerprint. Nineteen lines were not previously known from the literature.
4. Hyperfine structure analysis
Nb i lines investigated by means of laser optogalvanic spectroscopy (LOGS) or laser-induced fluorescence spectroscopy (LIFS).
The hyperfine structure (hfs) describes higher-order interactions of the nuclear moments
with the magnetic and electric fields produced by the electrons at the site of the nucleus.
It results in a splitting of a fine structure energy level E,
(characterized by the total electronic angular momentum quantum number J),
into hfs sublevels when an isotope has a nuclear spin I greater than zero.
The hfs sublevels are characterized by the total angular momentum quantum number
F, which can take values from | J − I |
to (J + I). Hence, the number of hfs sublevels is equal to
the minimum of (2J + 1) or (2I + 1). The hfs interaction
energy Ehfs of a hfs sublevel is given by 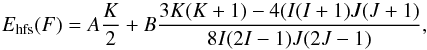 (1)where A and B
are the hfs constants for the magnetic dipole and electric quadrupole interaction,
respectively, and
(1)where A and B
are the hfs constants for the magnetic dipole and electric quadrupole interaction,
respectively, and 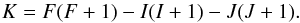 The first term in Eq. (1) is caused by the magnetic dipole interaction
and the second term by the electric quadrupole interaction. A and
B are specific for each fine structure level. If only the magnetic dipole
hfs is taken into account, the energy difference between hfs sublevels can be simply
calculated by the Landé interval rule:
The first term in Eq. (1) is caused by the magnetic dipole interaction
and the second term by the electric quadrupole interaction. A and
B are specific for each fine structure level. If only the magnetic dipole
hfs is taken into account, the energy difference between hfs sublevels can be simply
calculated by the Landé interval rule: 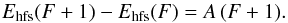 (2)The selection rule for optical transitions
between hfs sublevels is given by
(2)The selection rule for optical transitions
between hfs sublevels is given by 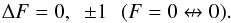 The relative intensity of hfs transitions is
given by
The relative intensity of hfs transitions is
given by 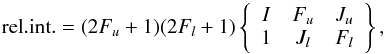 (3)where the indices u and
l indicate the upper and lower level, respectively. Transitions with
ΔJ = ΔF have the highest intensity.
(3)where the indices u and
l indicate the upper and lower level, respectively. Transitions with
ΔJ = ΔF have the highest intensity.
The only stable niobium isotope 93Nb has a nuclear spin of I = 9/2 and a large magnetic dipole moment of μI = + 6.1705 (3) μN (Lederer & Shirley 1978). Therefore it is reasonable to apply Doppler-limited experimental techniques to determine the magnetic dipole hfs constants A. The comparatively small electric quadrupole moment of Q = −0.36 (7) barn (Lederer & Shirley 1978) leads to a weak deviation of the hyperfine splitting from the interval rule (see Eq. (2)), which is not always detectable in Doppler-limited spectra.
For analysing the recorded spectra, the wave number axis were linearised using the free spectral range of the FPI. The free spectral range is calibrated to 299.0010 (8) MHz, which corresponds to a relative accuracy of 3 × 10-4%.
To obtain the hfs constants A and B, the linearised spectra were fitted using the program Fitter (Guthöhrlein 2004), which takes into consideration Eq. (1). The fit parameters were
-
the centre of gravity of the total hfs;
-
the A and B constants of the upper and the lower level;
-
the intensities and the Gaussian and Lorentzian parts of the Voigt profile of the individual hfs components;
-
two parameters to take into account height and slope of the background.
For all measured lines the observed intensity ratios of the hfs components differ from the theoretical intensity ratios given in Eq. (3). This is caused by hyperfine pumping and by the saturation effect due to the high power of the laser. This effect results in an intensity reduction and broadening of the strong hfs components and leads to an apparent intensity increase of the weak components. As a consequence, the ratio of the intensities of the components is not in accordance with the theoretical ratios. The Lorentzian contribution differs for the individual hfs components, whereas the Gaussian contribution is the same for all hfs components of a line. For this reason, the parameter for the Gaussian half width was set to the same value for all hfs components of a line, whereas the parameters for Lorentz half width and intensity may vary. To illustrate the magnitude of intensity increase of the weak components, a spectrum of a fully resolved line is shown in Fig. 3 together with the theoretical relative intensities, given as arrows. The arrows are normalised to the strongest hfs component. Intensity increases up to factors higher than 6 are measured.
Depending on the discharge current and on the wavelength, the Gaussian line width varied from 540 MHz to 820 MHz for the different lines.
As discussed above, the influence of the electric quadrupole interaction on the hfs is small. Therefore, it was possible to determine reliable values for the B constants only when a line had at least four clearly resolved individual hfs components. In these cases, the B constants were fitted as free parameters. In all other cases, the B constants were fixed to be equal to zero (except for a few unresolved lines, where A and B constants for one level were fixed equal to previously known values, see below).
 |
Fig. 3 Fully resolved line to illustrate the magnitude of intensity increase of the weak components. Theoretical relative intensities calculated following Eq. (3) are given as arrows; the arrows are normalised to the strongest hfs component: transition from 9 043.14 cm-1, J = 5/2 − → 20 837.98 cm-1, J = 5/2 at λair = 847.596 nm or σvac = 11 794.84 cm-1. |
All spectra with clearly resolved hfs components (as for example the line shown in Fig. 3) are fitted with individual Lorentz half widths and individual intensity parameters for each hfs component. In some cases, for the weakest hfs components of these lines, the fit leads to unreliable values of the Lorentz half width. Then, these parameters were coupled to the same parameter of an other hfs component with the same ΔF.
To analyse the spectra that showed only partly resolved hfs, the number of parameters had to be reduced. This was made in different gradings, as described in the following. Due to the dependence of the saturation effect from the intensity of the hfs components, it made sense to couple profile parameters of hfs components with the same ΔF value, because their intensities are similar in size.
As a first measure, for lines with a partly resolved hfs (as for example shown in Fig. 4a) the parameter for the Lorentzian width were coupled to the same value for each group of hfs components with same ΔF.
If this was not sufficient, depending on the degree of resolution, in some cases the parameter for the Lorentzian width were coupled to the same value for all hfs components and the intensity parameters were additionally coupled for one or more groups of hfs components with the same ΔF according to the theoretical ratios. An example for such a line is given in Fig. 4b.
Some lines look as if they are completely resolved, although this is not the case and most peaks include two or three hfs components. This occurred when one of the involved levels had a very low A constant (i.e. lower than 50 MHz with FWHM of about 600 MHz). For example, the lowest curve in Fig. 2 exhibits this behaviour. To highlight the hfs components, this line is shown again in Fig. 4c together with the fit results.
To analyse spectra with almost unresolved hfs, the number of parameters had to be reduced even more. For this purpose, in addition to all couplings discussed above, the hfs constants A and B of one level were fixed when they were previously known from the literature. An example for such a line is given in Fig. 4d. A list of the hfs constants from the literature and from this work that were fixed during a fit is given in Table 2.
 |
Fig. 4 Hyperfine spectra of the Nb i lines measured with LIFS or LOGS together with the best fitted curve. The hyperfine components are marked by the difference ΔF of the total angular momenta of the lower and upper hyperfine levels. In the lower part of the each figure the residuals between experimental and best fitted curves are given, multiplied by the factor indicated at left side of the graphs. a) Example for a line with a rather well resolved hfs, fitted with coupled parameters for the Lorentzian width for each group of hfs components with same ΔF: transition from 13 145.71 cm-1, J = 9/2 − → 25 199.81 cm-1, J = 9/2 at λair = 829.365 nm or σvac = 12 054.10 cm-1. b) Example for a partly resolved line, fitted with same parameter for the Lorentzian width for all hfs components and coupled intensity parameters for all hfs components with ΔF = 0: transition from 12 357.70 cm-1, J = 9/2 − → 24 203.05 cm-1, J = 11/2 at λair = 843.981 nm or σvac = 11 845.35 cm-1. c) Example for a line that looks like completely resolved, but most peaks include two or three hfs components: transition from 17 476.22 cm-1, J = 11/2 − → 30 191.25 cm-1, J = 13/2 at λair = 786.255 nm or σvac = 12 715.03 cm-1. d) Example for an unresolved line fitted with coupled profile parameters, B constants fixed to zero and fixed A constant of the lower level: transition from 19 568.72 cm-1, J = 5/2 − → 32 654.48 cm-1, J = 5/2 at λair = 763.979 nm or σvac = 13 085.76 cm-1. |
Hyperfine structure constants A and B from the literature and from this work, which were fixed during a fit.
Experimental hyperfine structure constants Aexp and Bexp (in MHz) of the levels of even parity of Nb i together with comparative values Aref and Bref, if available.
Experimental hyperfine structure constants Aexp and Bexp (in MHz) of the levels of odd parity of Nb i together with comparative values Aref and Bref, if available.
5. Results and discussion
Altogether, 81 spectral lines were investigated by laser excitation i.e LOGS and LIFS. They are listed in Table 1 along with their wavelengths in air λair, wave numbers in vacuum σvac, intensities and classifications. In the last column of Table 1, the experimental method used, LOGS or LIFS, is specified. When LIFS was used, the corresponding fluorescence wavelength is given in the last column. The wave numbers in vacuum were calculated as energy differences from the upper and lower level: σvac = Eu − El. The experimental centre of the gravity wave number in vacuum of the lines can be determined by using the start wave number of laser scan and fitting the centre of gravity of the hfs. These experimental values agree within an interval of ± 0.02 cm-1 with the calculated wave number σvac given in Table 1. The wavelengths in air were calculated from the wave numbers in vacuum using the dispersion relation (Peck & Reader 1972). The intensities and classifications are given according to Humphreys & Meggers (1945) when a line was listed in this wavelength table. Nineteen lines are new lines, which mean they have not previously been published. They are denoted as “nl”. Additionally, 16 lines measured in the present work were given in the wavelength tables of Humphreys & Meggers (1945) without classification. They have newly been classified here and are denoted as “nc”. When a line is overlapping within its hfs pattern with another Nb or with a Ne line, this is commented as “B” (blend) in Table 1.
The resulting hfs constants Aexp and Bexp are listed in Tables 3 and 4 for the levels of even and odd parity, respectively. Level energies are given according to Humphreys & Meggers (1945) and Kröger et al. (2004, 2007), configurations and terms according to Kröger & Bouzed (2003) for levels of even parity and according to Kröger et al. (2007) for levels of odd parity. The wavelength λair given in the fifth column specifies the line that was used to determine the hfs constants Aexp and Bexp. All spectra were recorded and fitted five times or more, depending on the signal-to-noise ratio. The given Aexp and Bexp are the statistic mean value of the fit results of all measurements, the measurement uncertainty being twice the corresponding standard. These errors refer only to the statistical variation of the fit and do not include systematic errors, which may occur because of the coupling of profile or intensity parameters during the fit. Hence the measurement uncertainty may be higher than the given statistical error bar. This fact can be exemplified by some hfs constants Aexp or Bexp, determined from different lines, which do not agree with each other within the limits of given errors. Nevertheless, the statistical errors convey an idea of the accuracy of the fit value.
When a hfs constant of a level was measured by two or more lines, the weighted mean value Amean and Bmean was taken, using the error limits of Aexp and Bexp as weight. The measurement uncertainties given for the mean values Amean are twice the standard deviations corresponding to this average.
6. Conclusion and outlook
In total, we have determined the magnetic dipole hyperfine structure constants A for 81 energy levels of atomic Nb and additionally the electric quadrupole hyperfine structure constants B for 41 of these levels. For 13 levels of even parity and for 11 levels of odd parity the A constants were measured for the first time. Additionally, the electric quadrupole hfs constants B for 30 levels were measured for the first time. Beyond that, already known A and B constants were verified and in some cases the accuracy was improved.
The present work constitutes another contribution to complete the hfs data of atomic Nb and provides this data for users, especially in astrophysics. Including the new results of the present work, the magnetic dipole hfs constants A are now known for all known energy levels of even parity.
Based on these data, it is highly recommended that an improved theoretical analysis for levels of even and odd parity is undertaken. Additionally, the search for new fine structure energy levels should proceed. From an atomic physical point of view, it would be of great interest to measure the hfs constants, especially the electric quadrupole constants B, with higher accuracy using Doppler-free experimental methods.
Acknowledgments
Gö. Başar thanks for the research fund of the Istanbul University Scientific Research Projects with project number No. 6222. I. K. Öztürk thanks for the research fund of the Istanbul University Scientific Research Projects with project number No. 6221. We thank Ali Sami Gözükırmızı for the data acquisition program.
References
- Başar, G., Başar, G., Bayram, B., & Kröger, S. 2008, Phys. Scr., 78, 015303 [NASA ADS] [CrossRef] [Google Scholar]
- Bouzed, A., Kröger, S., Zimmermann, D., Kronfeldt, H.-D., & Guthöhrlein, G. 2003, Eur. Phys. J. D, 23, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Büttgenbach, S., & Dicke, R. 1975, Z. Phys. D, 275, 197 [NASA ADS] [Google Scholar]
- Büttgenbach, S., Dicke, R., Gebauer, H., Herschel, M., & Meisel, G. 1975, Z. Phys. D, 275, 193 [NASA ADS] [Google Scholar]
- Er, A., Öztürk, I., Başar, G., et al. 2011, J. Phys. B: At. Mol. Opt. Phys., 44 [Google Scholar]
- Fraenkel, L., Bengtsson, C., Hanstorp, D., Nyberg, A., & Persson, J. 1988, Z. Phys. D, 8, 171 [Google Scholar]
- Guthöhrlein, G. H. 2004, University of Bundeswehr Hamburg, unpublished [Google Scholar]
- Humphreys, C. J., & Meggers, W. F. 1945, J. Res. Nat. Bur. Stand, 34, 478 [CrossRef] [Google Scholar]
- Kröger, S. 2007, Eur. Phys. J. D, 41, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kröger, S., & Bouzed, A. 2003, Eur. Phys. J. D, 23, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kröger, S., Scharf, O., & Guthöhrlein, G. 2004, Europhys. Lett., 66, 344 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kröger, S., Öztürk, I. K., Acar, F. G., et al. 2007, Eur. Phys. J. D, 41, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kröger, S., Er, A., Öztürk, I. K., et al. 2010, A&A, 516, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lederer, C. M., & Shirley, V. S. 1978, Table of isotopes, 7th edn (New York: Wiley) [Google Scholar]
- Messnarz, D., & Guthöhrlein, G. H. 2000, Eur. Phys. J. D, 12, 269 [Google Scholar]
- NIST 2013, NIST Atomic Spectra Database Version 5, Website [Google Scholar]
- Peck, R., & Reader, K. 1972, JOSA, 62 [Google Scholar]
- Sasso, A. 1990, Rev. Mod. Phys., 82, 603 [Google Scholar]
- Shamim, K., Siddiqui, I., & Windholz, L. 2011, Eur. Phys. J. D, 64 [Google Scholar]
- Singh, R., & Rao, G. N. 1989, Phys. Scr., 40, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, R., Thareja, R. K., & Rao, G. N. 1992, J. Opt. Soc. Am. B, 9, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Windholz, L., & Guthöhrlein, G. H. 2003, Phys. Scr. T, 105, 55 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Nb i lines investigated by means of laser optogalvanic spectroscopy (LOGS) or laser-induced fluorescence spectroscopy (LIFS).
Hyperfine structure constants A and B from the literature and from this work, which were fixed during a fit.
Experimental hyperfine structure constants Aexp and Bexp (in MHz) of the levels of even parity of Nb i together with comparative values Aref and Bref, if available.
Experimental hyperfine structure constants Aexp and Bexp (in MHz) of the levels of odd parity of Nb i together with comparative values Aref and Bref, if available.
All Figures
 |
Fig. 1 Schematic overview of the experimental setup used for laser optogalvanic spectroscopy and laser-induced fluorescence spectroscopy; M: mirror, L: lens, BS: beam sampler, FPI: Fabry-Perot interferometer, R: resistor, C: capacitor, HC: hollow-cathode lamp, DMM: digital multimeter, PD: photodiode, HM: hole mirror, PM: photomultiplier, HV: high-voltage power supply. |
| In the text | |
 |
Fig. 2 Example for blended lines: a) Spectrum recorded by LOGS at around 12 715 cm-1 showing the overlap of two Nb lines as well as another spurious line. b) Spectrum recorded by LIFS with fluorescence λf = 532.15 nm: transition from 14 899.26 cm-1, J = 5/2 − → 27 614.10 cm-1, J = 5/2 at λair = 786.266 nm or σvac = 12 714.84 cm-1. c) Spectrum recorded by LIFS with fluorescence λf = 581.94 nm: transition from 17 476.22 cm-1, J = 11/2 − → 30 191.25 cm-1, J = 13/2 at λair = 786.255 nm or σvac = 12 715.03 cm-1. |
| In the text | |
 |
Fig. 3 Fully resolved line to illustrate the magnitude of intensity increase of the weak components. Theoretical relative intensities calculated following Eq. (3) are given as arrows; the arrows are normalised to the strongest hfs component: transition from 9 043.14 cm-1, J = 5/2 − → 20 837.98 cm-1, J = 5/2 at λair = 847.596 nm or σvac = 11 794.84 cm-1. |
| In the text | |
 |
Fig. 4 Hyperfine spectra of the Nb i lines measured with LIFS or LOGS together with the best fitted curve. The hyperfine components are marked by the difference ΔF of the total angular momenta of the lower and upper hyperfine levels. In the lower part of the each figure the residuals between experimental and best fitted curves are given, multiplied by the factor indicated at left side of the graphs. a) Example for a line with a rather well resolved hfs, fitted with coupled parameters for the Lorentzian width for each group of hfs components with same ΔF: transition from 13 145.71 cm-1, J = 9/2 − → 25 199.81 cm-1, J = 9/2 at λair = 829.365 nm or σvac = 12 054.10 cm-1. b) Example for a partly resolved line, fitted with same parameter for the Lorentzian width for all hfs components and coupled intensity parameters for all hfs components with ΔF = 0: transition from 12 357.70 cm-1, J = 9/2 − → 24 203.05 cm-1, J = 11/2 at λair = 843.981 nm or σvac = 11 845.35 cm-1. c) Example for a line that looks like completely resolved, but most peaks include two or three hfs components: transition from 17 476.22 cm-1, J = 11/2 − → 30 191.25 cm-1, J = 13/2 at λair = 786.255 nm or σvac = 12 715.03 cm-1. d) Example for an unresolved line fitted with coupled profile parameters, B constants fixed to zero and fixed A constant of the lower level: transition from 19 568.72 cm-1, J = 5/2 − → 32 654.48 cm-1, J = 5/2 at λair = 763.979 nm or σvac = 13 085.76 cm-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


