| Issue |
A&A
Volume 556, August 2013
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321410 | |
| Published online | 17 July 2013 | |
Evidence of quiet-Sun chromospheric activity related to an emerging small-scale magnetic loop
1
Astronomical Institute of the Slovak Academy of Sciences,
05960
Tatranská Lomnica,
Slovakia
e-mail:
gomory@astro.sk
2
Leibniz-Institut für Astrophysik Potsdam,
An der Sternwarte 16,
14482
Potsdam,
Germany
e-mail: hbalthasar@aip.de; kgp@aip.de
Received: 5 March 2013
Accepted: 14 June 2013
Aims. We investigate the temporal evolution of magnetic flux emergence in the quiet-Sun atmosphere close to disk center.
Methods. We combined high-resolution SoHO/MDI magnetograms with TRACE observations taken in the 1216 Å channel to analyze the temporal evolution of an emerging small-scale magnetic loop and its traces in the chromosphere.
Results. We find signatures of flux emergence very close to the edge of a supergranular network boundary located at disk center. The new emerging flux appeared first in the MDI magnetograms in form of an asymmetric bipolar element, i.e., the patch with negative polarity is roughly twice as weak as the corresponding patch with opposite polarity. The average values of magnetic flux and magnetic flux densities reached 1.6 × 1018 Mx, − 8.5 × 1017 Mx, and 55 Mx cm-2, –30 Mx cm-2, respectively. The spatial distance between the opposite polarity patches of the emerged feature increased from about 2.″5 to 5.″0 during the lifetime of the loop, which was 36 min. A more precise lifetime-estimate of the feature was not possible because of a gap in the temporal sequence of the MDI magnetograms. The chromospheric response to the emerged magnetic dipole occurred ~9 min later than in the photospheric magnetograms. It consisted of a quasi-periodic sequence of time-localized brightenings visible in the 1216 Å TRACE channel for ~14 min that were co-spatial with the axis connecting the two patches of opposite magnetic polarity.
Conclusions. We identify the observed event as a small-scale magnetic loop emerging at photospheric layers that subsequently rose to the chromosphere. We discuss the possibility that the fluctuations detected in the chromospheric emission probably reflect magnetic-field oscillations which propagate to the chromosphere in the form of waves.
Key words: Sun: magnetic topology / Sun: surface magnetism / Sun: photosphere / Sun: chromosphere
© ESO, 2013
1. Introduction
Magnetic structures emerging in form of small-scale loops in the quiet-Sun atmosphere and associated dynamics have recently come to the center of attention. Systematic studies of these features became possible mainly through space-born observations acquired with a new generation of instruments such as the spectro-polarimeter (SP; Lites et al. 2001) of the Solar Optical Telescope (SOT; Tsuneta et al. 2008) onboard the Japanese space mission Hinode (Kosugi et al. 2007) or the Imaging Magnetograph eXperiment (IMaX; Martínez Pillet et al. 2011) of the balloon-borne observatory SUNRISE (Solanki et al. 2010) because they provide extended time-series of data with very high spatial resolution, which is needed for the loop detection (see e.g. works of Centeno et al. 2007; Martínez González & Bellot Rubio 2009; Ishikawa et al. 2010; Wiegelmann et al. 2010; Martínez González et al. 2010, 2011, 2012; Guglielmino et al. 2012; Orozco Suárez & Katsukawa 2012; Palacios et al. 2012; Viticchié 2012). However, Martínez González et al. (2007) and Gömöry et al. (2010) showed that also observations obtained with ground-based instruments that are equipped with an adaptive-optics system (e.g., the German Vacuum Tower Telescope, VTT; Schröter et al. 1985, with the Kiepenheuer Adaptive Optics System, KAOS; von der Lühe et al. 2003) are suitable to study processes related to small-scale loop emergence.
Small-scale loops represent a significant fraction of the magnetic flux in the quiet photosphere (Martínez González et al. 2007) and are thus important for a more complex description of the latter. Martínez González & Bellot Rubio (2009) performed an extensive statistical analysis of 69 emerging loops and found that 16 of these features even reach the transition between the upper photosphere and the lower chromosphere and that ten of them can be seen yet in emission in Ca ii H filtergrams. However limitations in the used datasets did not allow them to identify any loop in the layers sampled by Hα emission. This evidence was given by Yurchyshyn et al. (2010), who observed the trailing part of an active region and found that even a very small dipole (spatial extent of ~0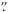 5) can rise high enough and heat up sufficiently to be detected in the upper chromosphere, where it exhibits significant activity.
5) can rise high enough and heat up sufficiently to be detected in the upper chromosphere, where it exhibits significant activity.
 |
Fig. 1 Context images showing the common FoV for all observations. Left panel: SoHO/MDI magnetogram at the best visibility of the emerging feature. The color scale is in Mx cm-2 with red (blue) indicating positive (negative) polarity. An artificial saturation at ±150 Mx cm-2 has been chosen to highlight regions of weak magnetic polarity on the solar surface. Middle panel: image taken in the TRACE white-light channel during the emergence of the analyzed feature demonstrating the absence of strong magnetic fields in the FoV (quiet Sun). Right panel: temporal average of TRACE images taken in the 1216 Å channel during the feature emergence showing long-living chromospheric network elements. Squares enclose the region enlarged in Fig. 2. (This figure is available in color in electronic form.) |
These observational results support findings of Trujillo Bueno et al. (2004), who argued that the magnetic energy stored in the quiet photosphere can balance the radiative losses of the chromosphere. Similar results were found by Ishikawa et al. (2008) for plage regions. Moreover, MHD simulations of Isobe et al. (2008) suggested that small-scale loops that emerge in the photosphere can indeed reach chromospheric heights and become reconnected with the local expanding vertical magnetic fields, thus heating the surrounding chromospheric plasma. All these facts assign an important role to small-scale magnetic loops in the transport and dissipation of magnetic energy for heating the chromosphere. However, different mechanisms capable for the transfer of energy into upper photospheric layers have still to be confirmed, especially with respect to results showing a lack of total energy flux transported to the chromosphere by acoustic waves (Carlsson et al. 2007), although more recent results obtained by Bello González et al. (2009, 2010) pointed out that the acoustic energy flux might have been underestimated in the past due to insufficient spatial resolution. In contrast, Beck et al. (2013a) suggested that magnetic heating processes are more important for the chromospheric energy balance than commonly assumed, when they compared photospheric magnetic fields obtained from spectro-polarimteric observations in the Fe i 630.25 nm line of the Polarimetric Littrow Spectrograph (POLIS; Beck et al. 2005) with results retrieved after applying a recently developed LTE-inversion strategy (Beck et al. 2013b) on POLIS Ca ii H spectra.
However, while some simulations show that emerging loops can reach the chromosphere, simulations of magneto-convection by Stein & Nordlund (2006) predicted that these loops probably disintegrate as they rise through the lower solar atmosphere, which makes an energy transport connected to these features implausible. Moreover, a broad variety of chromospheric dynamics can be modeled with a wave-driven reconnection (e.g. De Pontieu et al. 2009). This could indicate that the small-scale emerging fields are at least not the only contributor to the chromospheric energy balance.
The discrepancies mentioned above do not allow general conclusions in this research field so far, thus emphasizing the need of more observational studies. A complete understanding of magnetic flux emergence in the quiet Sun could considerably improve not only our knowledge about the photosphere, but also shed light on the problem of chromospheric heating.
We present a case study of an emerging small-scale loop that appeared close to a supergranular network boundary at the disk center and exhibited significant chromospheric activity.
2. Data and data reduction
The analyzed data-set was obtained within the Joint Observing Program JOP 171 that was performed during several days in the second half of October 2005. This observing program was dedicated to studying properties of the quiet solar atmosphere from photospheric layers to the corona1. To do so, several instruments onboard the Solar and Heliospheric Observatory (SoHO) and the Transition Region And Coronal Explorer (TRACE) were involved in the data acquisition process.
We analyzed a particular dataset of a quiet-Sun region close to disk center obtained on 25 October 2005 between 13:17 and 13:56 UT. We focused on the time-series of high-resolution magnetograms from the Michelson Doppler Imager (MDI) onboard SoHO (Scherrer et al. 1995) and TRACE (Handy et al. 1999a) filtergrams taken in the 1216 Å channel. Context images showing the common field of view (FoV) in all observations are displayed in Fig. 1.
The MDI longitudinal magnetograms have a FoV of 614′′ × 384′′ (1024 × 640 pixels). Their spatial resolution in the high-resolution observing mode was 1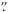 25 with a corresponding pixel size of 0
25 with a corresponding pixel size of 0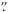 6 × 0
6 × 0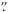 6. The instrumental detection threshold for the magnetic flux density is approximately 17 Mx cm-2 (Schrijver et al. 1997). Therefore, all pixels with a signal below this limit were excluded from the subsequent analysis. The magnetograms were taken with a regular 1-min cadence, but their sequence was interrupted between 13:45–13:53 UT. All MDI data were downloaded in the pre-processed form.
6. The instrumental detection threshold for the magnetic flux density is approximately 17 Mx cm-2 (Schrijver et al. 1997). Therefore, all pixels with a signal below this limit were excluded from the subsequent analysis. The magnetograms were taken with a regular 1-min cadence, but their sequence was interrupted between 13:45–13:53 UT. All MDI data were downloaded in the pre-processed form.
The TRACE data cover a FoV of 384′′ × 384′′ (768 × 768 pixels) with a spatial resolution of 1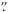 0 and a corresponding pixel size of 0
0 and a corresponding pixel size of 0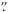 5. The sequence of 1216 Å filtergrams was taken with a cadence of ~45 s which was interrupted several times by a cycle of exposures acquired in white-light, 1550 Å, 1600 Å, 171 Å, and 196 Å channels. These additional data were taken for context and coalignment purposes. All raw images acquired by TRACE were corrected for instrumental effects (i.e., subtracting dark-current and pedestal, correcting for exposure time, for radiation spikes, and for saturated pixels) using the standard procedures included in the Solar Software (SSW) IDL package provided by the TRACE team (Freeland & Handy 1998). The data were corrected also for solar rotation.
5. The sequence of 1216 Å filtergrams was taken with a cadence of ~45 s which was interrupted several times by a cycle of exposures acquired in white-light, 1550 Å, 1600 Å, 171 Å, and 196 Å channels. These additional data were taken for context and coalignment purposes. All raw images acquired by TRACE were corrected for instrumental effects (i.e., subtracting dark-current and pedestal, correcting for exposure time, for radiation spikes, and for saturated pixels) using the standard procedures included in the Solar Software (SSW) IDL package provided by the TRACE team (Freeland & Handy 1998). The data were corrected also for solar rotation.
Note that the data acquired in the 1216 Å TRACE channel do not only include the desired Ly α emission, but also signals from UV emissions near 1550 Å and longer wavelengths. The reason is a double peak in spectral response of the detector with one peak located at ~1216 Å and a second peak situated at ~1550 Å. The bandwidth of both transmission windows is similar and amounts to 84 Å for the one centered at 1216 Å. Handy et al. (1999b) described a method of extracting only Ly α emission from observations taken in the 1216 Å channel using filtergrams acquired in the 1600 Å channel. Because of the absence of a co-temporal sequence of 1600 Å images in our dataset, we were unable to apply this method for the present data. The same authors claimed that only ~60% of the signal recorded in the 1216 Å channel originates from Ly α emission. Moreover, the emission recorded in this channel covers the temperature range 1.0–3.0 × 104 K (Handy et al. 1999a), i.e., not only the formation temperature of the Ly α line, which is ~2.0 × 104 K (e.g. Vourlidas et al. 2001). Therefore, we considered the TRACE 1216 Å data only as an approximation of chromospheric emission and drew no conclusions about absolute intensity changes.
A precise coalignment of the MDI and TRACE data had to be performed before the analysis. We used white-light images recorded simultaneously with both instruments for this purpose. As an independent check, we used the co-spatiality between the brightest chromospheric structures visible in the 1216 Å channel (chromospheric network) and magnetic features.
3. Results
We visually inspected the SoHO/MDI high-resolution magnetograms for emerging magnetic dipoles that also exhibit some activity in chromospheric emission. The evolution of such a feature emerging in the vicinity of a network boundary is presented in Fig. 2. Note that we used a nonlinear timescale to present the sequence of TRACE 1216 Å images with superimposed contours of SoHO/MDI magnetograms to provide a better description of the various phases taking place during the evolutionary process.
In the first two snapshots (taken at 13:14:15 UT and 13:16:36 UT) several magnetic elements are visible. These features represent the pre-existing magnetic field forming the network boundary, which also remains detectable during and after the time span under investigation. Between 13:17:10–13:18:20 UT, a new patch of positive polarity and subsequently (at 13:20:05 UT) also a tiny area of new negative polarity become apparent. Finally, at 13:21:15 UT, the new magnetic feature is clearly visible. Since longitudinal magnetograms are blind to horizontal fields, we were unable to correctly describe the complex topology of the emerged feature. However, such bipolar events can be best explained either by an emerging ∩-like loop or a submerging feature with a ∪-like shape. In both cases, the patches of opposite polarity correspond to the footpoints of the emerging feature.
Later on, at 13:25:59 UT, chromospheric brightenings co-spatial with the new patch of negative polarity appear and persist. After several minutes (at 13:28:32 UT) enhanced chromospheric emission becomes visible also in regions covered by the positive-polarity patch. From 13:30:51 UT to 13:33:11 UT enhanced chromospheric activity is apparent along the whole axis of the feature, where we define the axis as the straight line connecting the two patches of opposite polarity. From 13:34:21 UT until 13:40:42 UT, the 1216 Å channel emission becomes again spatially separated and brightenings related to the negative patch start to weaken at the end of this period. Between 13:41:51 UT and 13:45:21 UT, the northern negative-polarity footpoint is still visible in the magnetograms, but does no longer leave its detectable fingerprints in chromospheric emission. Finally, at 13:53:10 UT and later, there is no clear evidence of the negative footpoint or its recurrent appearance (we recall that there is a gap in the magnetograms between 13:45–13:53 UT).
 |
Fig. 2 Temporal evolution of the emerging magnetic dipole. Background images have been taken in the TRACE 1216 Å channel. The superimposed contours represent the magnetic signal detected in the SoHO/MDI data. The magnetic-field contours are plotted at ±25, ±40, ±55 and ±70 Mx cm-2 with red (blue) contours referring to positive (negative) magnetic polarity. The yellow contours mark the pixels that were used for calculating the magnetic flux density and the total magnetic flux at the footpoints of the emerging loop. The recording time of the particular 1216 Å images is presented in the upper right corner of each subpanel. The corresponding magnetograms are almost co-temporal (with a maximal time difference <30 s). (This figure is available in color in electronic form.) |
Concerning the southern positive-polarity patch, we note that its interaction and consecutive merging with the nearby network boundary complicates its lifetime-estimate, although significant emission in the co-spatial area in the chromosphere persists even after its disappearance. Interaction and the consecutive merging with the network boundary can be best seen from the contours related to the positive polarity patch in Fig. 2 at 13:30:51 UT and later on.
Figure 3 shows the temporal evolution of the longitudinal magnetic flux densities at the footpoints (upper panel) and the chromospheric emission along the axis of the emerging magnetic feature (lower panel). We calculated the longitudinal magnetic flux densities at particular positions across the footpoints by averaging over all pixels that are located perpendicular to the loop axis and that do not exceed the lateral extension of the two patches of opposite polarity. The changes in flux density show a time delay between the two opposite polarity patches and point to an asymmetric nature of the detected dipole. While the longitudinal magnetic flux densities related to the positive polarity patch reach roughly 55 Mx cm-2 and remain more or less constant during the whole lifetime of the small-scale magnetic feature, the negative polarity patch reaches only − 30 Mx cm-2 on average. Nevertheless, the magnetic flux densities of both polarities have very similar values at the very beginning of the event, when the negative patch also reaches ~53 Mx cm-2. Corresponding values of the total magnetic flux related to the positive and negative polarity patches (not shown here) are roughly 1.6 × 1018 Mx and − 8.5 × 1017 Mx, respectively. As for the flux density, the total flux related to the small-scale feature is also at least balanced at the beginning of the feature emergence, with an absolute value of the total magnetic flux of ~1.5 × 1018 Mx for both polarities. Magnetic flux density and total magnetic flux were calculated within the areas highlighted by yellow contours in Fig. 2.
Physical parameters of the detected bipolar magnetic feature compared with typical values determined for emerging small-scale magnetic loops by Martínez González & Bellot Rubio (2009).
The spatial distance between the footpoints of the emerging feature at photospheric level is steadily increasing during first phases of the event from ~2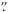 5 up to ~5
5 up to ~5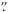 0. However, just toward the end of its lifetime the emerging small-scale magnetic loop seems to again slightly decrease its axial extension. The lifetime of the detected feature can be estimated only very roughly to no longer than 36 min because of the gap in the MDI data (Fig. 3, upper panel).
0. However, just toward the end of its lifetime the emerging small-scale magnetic loop seems to again slightly decrease its axial extension. The lifetime of the detected feature can be estimated only very roughly to no longer than 36 min because of the gap in the MDI data (Fig. 3, upper panel).
The lower panel of Fig. 3 outlines the delay of ~9 min between magnetic feature emergence and chromospheric response, the latter being first visible in the region co-spatial to the negative polarity patch. Later on, the chromospheric brightenings appear in form of isolated, quasi-periodical bursts, which are visible along the whole axis connecting the two patches of opposite polarity. The duration of the observed chromospheric activity is ~14 min.
The quasi-periodic nature of the chromospheric emission related to the flux emergence is also visible in Fig. 4. This plot shows the 1216 Å channel emission at locations of the emerging feature associated with strongest magnetic field. The increase of the chromospheric signals visible during the main phase of activity shows time delays in the range of 2.3 to 3.7 min. However, we were unable to assign any characteristic period to this oscillatory behavior. Nevertheless, although the intensity enhancements show a time delay between the patches of positive and negative polarity, the temporal differences between the particular peaks are the same for both footpoints (at least within the temporal resolution of the data), thus increasing the statistical significance of these events.
 |
Fig. 3 Space-time maps showing the evolution of longitudinal magnetic flux densities and chromospheric emission along the axis connecting the two patches of opposite magnetic polarity of the emerging feature. (This figure is available in color in electronic form.) |
4. Discussion
In Table 1, we compare the physical parameters of the detected bipolar magnetic feature with typical values determined for small-scale magnetic loops emerging from the photosphere to higher atmospheric layers (Martínez González & Bellot Rubio 2009). Note that a proper determination of the magnetic field strength from the derived longitudinal magnetic flux densities was impossible because of the missing information about azimuth, inclination, and filling factor of the magnetic-field lines forming the emerging feature. Since the magnetic field should be more or less vertical at the footpoints (because of the geometry of the loop), the lacking information concerning the inclination is not that crucial. If we assume a filling factor close to unity for these areas, then the real magnetic field strength is roughly equal to the measured magnetic flux density. However, when assuming a much smaller filling factor, the real magnetic field strength would increase easily up to kG values. The comparison of the individual parameters shows that the values estimated for the magnetic feature are consistent with typical characteristics of small-scale magnetic loops reaching chromospheric heights. Exceptions are the determined longitudinal magnetic flux values in the two footpoints, which are at least one magnitude higher than those of typical loops, which makes them comparable instead with extreme cases of the latter features. This might be due to the limited spatial resolution of the MDI magnetograms, resulting in an overestimation of the total area covered by the footpoints of the emerging dipole and the calculated total magnetic flux values. This together with the fact that the emerging dipole was first detected in the magnetograms and only later also at chromospheric heights supports the hypothesis that the observed structure can be identified as a rising small-scale magnetic loop, exhibiting significant activity in the upper atmosphere.
On the other hand, one might object that the almost ideal co-spatiality of the patches harboring opposite magnetic polarity with the 1216 Å emissions points to a non-loop-like shape of the detected feature. The expected quasi-circular topology of the detected feature would require that the spatial extent between areas of chromospheric emissions should be smaller than the distance between the patches of opposite polarity. However, Martínez González et al. (2010) demonstrated that at the first stages, during the loop emergence into photospheric layers, the loop has a flattened geometry and keeps its shape throughout the photosphere. However, when passing the transition between photosphere and chromosphere, the magnetic field at the footpoints becomes almost vertical and the loop has a ∩-like (or arch-like) shape. Given this result, the co-spatiality detected in our data even strengthens our interpretation.
 |
Fig. 4 Temporal evolution of the 1216 Å emission at locations of the emerging feature that are associated with strongest photospheric magnetic field (upper curve: negative polarity; lower curve: positive polarity). The standard deviation for each intensity value is marked by errorbars. Different values of Δt depict individual time intervals between consecutive intensity peaks. |
The axial distance between the footpoints of the loop shows a steady increase in the early phase of the event (Fig. 3, upper panel). After reaching a maximum distance, the footpoints retain their position nearly constant to each other until the disappearance of the loop. This is a typical behavior for a small-scale magnetic loop within a granule. These loops are first advected by granular flows, and their size increases. The almost linear increase of the axial loop dimension indicates that the footpoints do not undergo a free random walk. Later, when they reach the intergranular lanes, the footpoints remain stable and the loop does not change its axial extension significantly anymore. However, a small decrease of the axial loop extension visible after ~13:36 UT might indicate a subsequent submergence of the loop, which is also supported by the co-temporal weakening of chromospheric emission that vanishes at the end. However, the decrease in the axial extension of the loop toward the end of its lifetime could just reflect the noisy behavior of the SoHO/MDI magnetograms.
This noisy behavior also did not allow us to directly study possible oscillations of the magnetic flux density at the footpoints. However, we clearly detected a quasi-periodic behavior of the emissions recorded in the 1216 Å channel (Fig. 4). We estimated the damping time of these fluctuations to ~14 min and their related periods to 2.3–3.7 min. These results agree well with findings of Martínez González et al. (2011) for stronger magnetic patches. The latter authors analyzed high-resolution spectro-polarimetric data obtained with SUNRISE/IMaX and found that areas of circular polarization patches, containing constant magnetic flux, can oscillate, implying that the magnetic flux density fluctuates in antiphase. Typical periods of these oscillations range between 4 and 11 min for weaker flux patches and between 3 and 5 min for stronger ones. The detected oscillations can be strongly damped or amplified within a time interval of 5–30 min. The authors proposed that these oscillations could propagate even up to chromospheric layers in form of waves and dissipate their energy through the formation of shocks. Thus the pattern detected in the 1216 Å intensity evolution of our data might also be the result of such events.
Additional evidence of magnetic-flux oscillations were found in relation to plages and pores (Fujimura & Tsuneta 2009), confirming that this phenomenon is also present in other solar features. Beck et al. (2013a) also suggested that magnetic heating processes are more important for the chromospheric energy budget than commonly assumed. However, whether acoustic waves or magneto-acoustic waves related with, e.g., small-scale magnetic loops suffice in heating the solar chromosphere might be answered only by future high spatial resolution observations that combine photospheric spectro-polarimetry and chromospheric spectroscopy, e.g. by parallel observations with the GREGOR Fabry-Pérot Interferometer (GFPI; Puschmann et al. 2012a,b,c) and the planned Blue Imaging Solar Spectrometer (BLISS; Puschmann et al. 2012b, 2013) at the 1.5-m GREGOR solar telescope (Schmidt et al. 2012a,b).
The small-scale loop emerged as a dipole whose polarities exhibit different field strengths most of its lifetime. Thus the total magnetic flux of the emerging feature seems to be unbalanced. However, this unexpected result could just reflect the difficulties in separating the positive footpoint of the loop from the stronger network fields nearby because of its permanent interaction with the latter and its final merge. Another possible explanation could be based on the different spatial extension of both footpoints. The magnetic flux in the positive polarity patch could be concentrated within a much smaller area, implicating flux densities well above the detection threshold, while for the negative polarity the opposite could be the case. Similar conditions can even lead to measurements of unipolar fields in the quiet Sun (Lamb et al. 2008).
5. Conclusions
We observed a magnetic feature present in SoHO/MDI magnetograms and TRACE 1216 Å channel filtergrams with a time lack of ~9 min in the latter. We identified this structure as a small-scale magnetic loop that emerged into the photosphere and subsequently reached chromospheric heights. We interpreted quasi-periodic variations found in the chromospheric emission related to the loop as a consequence of magnetic-field oscillations at the footpoints, resulting in a wave propagation toward higher layers. The asymmetric appearance of the loop could indicate that the footpoints cover areas of different sizes.
JOP 171 details: http://sohowww.nascom.nasa.gov/soc/JOPs/jop171
Acknowledgments
This work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number BA 1875/7-1, the Science Grant Agency – project VEGA 2/0108/12, and the Slovak Research and Development Agency under the contract No. APVV-0816-11. MDI is part of SOHO, the Solar and Heliospheric Observatory, which is a project of international cooperation between ESA and NASA. The Transition Region and Coronal Explorer, TRACE, is a mission of the Stanford-Lockheed Institute for Space Research, and part of the NASA Small Explorer program. We thank J. Rybák for his help with the data coalignment. The authors thank an anonymous referee for constructive comments and valuable suggestions. This research has made use of NASA’s Astrophysics Data System.
References
- Beck, C., Schmidt, W., Kentischer, T., & Elmore, D. 2005, A&A, 437, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013a, A&A, 553, A73 [NASA ADS] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Puschmann, K. G. 2013b, A&A, 549, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Flores Soriano, M., Kneer, F., & Okunev, O. 2009, A&A, 508, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Franz, M., Martínez Pillet, V., et al. 2010, ApJ, 723, L134 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., de Pontieu, B., et al. 2007, PASJ, 59, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Centeno, R., Socas-Navarro, H., Lites, B., et al. 2007, ApJ, 666, L137 [NASA ADS] [CrossRef] [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Hansteen, V. H., & Schrijver, C. J. 2009, ApJ, 701, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimura, D., & Tsuneta, S. 2009, ApJ, 702, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Gömöry, P., Beck, C., Balthasar, H., et al. 2010, A&A, 511, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guglielmino, S. L., Martínez Pillet, V., Bonet, J. A., et al. 2012, ApJ, 745, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999a, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Handy, B. N., Tarbell, T. D., Wolfson, C. J., Korendyke, C. M., & Vourlidas, A. 1999b, Sol. Phys., 190, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Ishikawa, R., Tsuneta, S., Ichimoto, K., et al. 2008, A&A, 481, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishikawa, R., Tsuneta, S., & Jurčák, J. 2010, ApJ, 713, 1310 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, H., Proctor, M. R. E., & Weiss, N. O. 2008, ApJ, 679, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Kosugi, T., Matsuzaki, K., Sakao, T., et al. 2007, Sol. Phys., 243, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Lamb, D. A., DeForest, C. E., Hagenaar, H. J., Parnell, C. E., & Welsch, B. T. 2008, ApJ, 674, 520 [Google Scholar]
- Lites, B. W., Elmore, D. F., & Streander, K. V. 2001, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation, ed. M. Sigwarth, ASP Conf. Ser., 236, 33 [Google Scholar]
- Martínez González, M. J., & Bellot Rubio, L. R. 2009, ApJ, 700, 1391 [CrossRef] [Google Scholar]
- Martínez González, M. J., Collados, M., Ruiz Cobo, B., & Solanki, S. K. 2007, A&A, 469, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez González, M. J., Manso Sainz, R., Asensio Ramos, A., & Bellot Rubio, L. R. 2010, ApJ, 714, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Asensio Ramos, A., Manso Sainz, R., et al. 2011, ApJ, 730, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, M. J., Manso Sainz, R., Asensio Ramos, A., & Hijano, E. 2012, ApJ, 755, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D., & Katsukawa, Y. 2012, ApJ, 746, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Palacios, J., Blanco Rodríguez, J., Vargas Domínguez, S., et al. 2012, A&A, 537, A21 [Google Scholar]
- Puschmann, K. G., Balthasar, H., Bauer, S.-M., et al. 2012a, in Second ATST-EAST Meeting: Magnetic fields from the photosphere to the corona, eds. T. R. Rimmele, A. Tritschler, F. Wöger, et al., ASP Conf. Ser., 463, 423 [Google Scholar]
- Puschmann, K. G., Balthasar, H., Beck, C., et al. 2012b, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. MacLean, S. K. Ramsay, & H. Takami, SPIE Conf. Ser., 8446, 79 [Google Scholar]
- Puschmann, K. G., Denker, C., Kneer, F., et al. 2012c, Astron. Nachr., 333, 880 [NASA ADS] [Google Scholar]
- Puschmann, K. G., Denker, C., Balthasar, H., et al. 2013, Opt. Eng. 52, in press, DOI: 10.1117/1.OE.52.8.081606 [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012a, Astron. Nachr., 333, 796 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., von der Lühe, O., Volkmer, R., et al. 2012b, in Second ATST-EAST Meeting: Magnetic fields from the photosphere to the corona, eds. T. R. Rimmele, A. Tritschler, F. Wöger, et al., ASP Conf. Ser., 463, 365 [Google Scholar]
- Schrijver, C. J., Title, A. M., Hagenaar, H. J., & Shine, R. A. 1997, Sol. Phys., 175, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vistas Astron., 28, 519 [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2006, ApJ, 642, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, Sol. Phys., 249, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Viticchié, B. 2012, ApJ, 747, L36 [NASA ADS] [CrossRef] [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics, eds. S. L. Keil, & S. V. Avakyan, SPIE Conf. Ser., 4853, 187 [Google Scholar]
- Vourlidas, A., Klimchuk, J. A., Korendyke, C. M., Tarbell, T. D., & Handy, B. N. 2001, ApJ, 563, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Solanki, S. K., Borrero, J. M., et al. 2010, ApJ, 723, L185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yurchyshyn, V. B., Goode, P. R., Abramenko, V. I., et al. 2010, ApJ, 722, 1970 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical parameters of the detected bipolar magnetic feature compared with typical values determined for emerging small-scale magnetic loops by Martínez González & Bellot Rubio (2009).
All Figures
 |
Fig. 1 Context images showing the common FoV for all observations. Left panel: SoHO/MDI magnetogram at the best visibility of the emerging feature. The color scale is in Mx cm-2 with red (blue) indicating positive (negative) polarity. An artificial saturation at ±150 Mx cm-2 has been chosen to highlight regions of weak magnetic polarity on the solar surface. Middle panel: image taken in the TRACE white-light channel during the emergence of the analyzed feature demonstrating the absence of strong magnetic fields in the FoV (quiet Sun). Right panel: temporal average of TRACE images taken in the 1216 Å channel during the feature emergence showing long-living chromospheric network elements. Squares enclose the region enlarged in Fig. 2. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 2 Temporal evolution of the emerging magnetic dipole. Background images have been taken in the TRACE 1216 Å channel. The superimposed contours represent the magnetic signal detected in the SoHO/MDI data. The magnetic-field contours are plotted at ±25, ±40, ±55 and ±70 Mx cm-2 with red (blue) contours referring to positive (negative) magnetic polarity. The yellow contours mark the pixels that were used for calculating the magnetic flux density and the total magnetic flux at the footpoints of the emerging loop. The recording time of the particular 1216 Å images is presented in the upper right corner of each subpanel. The corresponding magnetograms are almost co-temporal (with a maximal time difference <30 s). (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 3 Space-time maps showing the evolution of longitudinal magnetic flux densities and chromospheric emission along the axis connecting the two patches of opposite magnetic polarity of the emerging feature. (This figure is available in color in electronic form.) |
| In the text | |
 |
Fig. 4 Temporal evolution of the 1216 Å emission at locations of the emerging feature that are associated with strongest photospheric magnetic field (upper curve: negative polarity; lower curve: positive polarity). The standard deviation for each intensity value is marked by errorbars. Different values of Δt depict individual time intervals between consecutive intensity peaks. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


