| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | L6 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201321999 | |
| Published online | 10 July 2013 | |
First observational application of a connectivity-based helicity flux density
1 LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris-Diderot, 92195 Meudon, France
e-mail: kevin.dalmasse@obspm.fr
2 Mullard Space Science Laboratory, Univ. College London, UK
Received: 31 May 2013
Accepted: 23 June 2013
Context. Measuring the magnetic helicity distribution in the solar corona can help in understanding the trigger of solar eruptive events because magnetic helicity is believed to play a key role in solar activity due to its conservation property.
Aims. A new method for computing the photospheric distribution of the helicity flux was recently developed. This method takes into account the magnetic field connectivity whereas previous methods were based on photospheric signatures only. This novel method maps the true injection of magnetic helicity in active regions. We applied this method for the first time to an observed active region, NOAA 11158, which was the source of intense flaring activity.
Methods. We used high-resolution vector magnetograms from the SDO/HMI instrument to compute the photospheric flux transport velocities and to perform a nonlinear force-free magnetic field extrapolation. We determined and compared the magnetic helicity flux distribution using a purely photospheric as well as a connectivity-based method.
Results. While the new connectivity-based method confirms the mixed pattern of the helicity flux in NOAA 11158, it also reveals a different, and more correct, distribution of the helicity injection. This distribution can be important for explaining the likelihood of an eruption from the active region.
Conclusions. The connectivity-based approach is a robust method for computing the magnetic helicity flux, which can be used to study the link between magnetic helicity and eruptivity of observed active regions.
Key words: magnetic fields / methods: numerical / Sun: photosphere / Sun: corona
© ESO, 2013
1. Introduction
Magnetic helicity globally characterizes the geometrical properties of the magnetic field in a volume, generalizing more local properties such as twist and shear (e.g., Moffatt 1969). Because of its conservation property (see Berger 1984), magnetic helicity is believed to play a key role in solar eruptivity. In particular, it has been argued that magnetic helicity accumulation and/or annihilation can be involved in the generation and dynamics of solar flares and coronal mass ejections (CMEs; e.g., Low 1997; Kusano et al. 2002).
Observationally, evidence of magnetic helicity accumulation and annihilation can be obtained from studying the photospheric distribution of the magnetic helicity flux in active regions (ARs) prior to flaring activity (e.g. Moon et al. 2002; Chae et al. 2004; LaBonte et al. 2007). Magnetic helicity accumulation is straightforward when the helicity flux is uniformly distributed in sign. In a given magnetic system, a sequential injection of helicity of different signs would reduce the accumulated helicity. Magnetic helicity annihilation, by contrast, necessitates a distribution with opposite helicity fluxes since the annihilation of helicity requires the reconnection of magnetic domains of opposite helicity. Linton et al. (2001) showed that magnetic reconnection can release more energy when it occurs between systems of opposite helicity, and Kusano et al. (2002, 2004) developed a model of solar flares based on the interaction of magnetic structures of opposite helicity.
Observational studies were therefore carried out to detect ARs with opposite helicity fluxes (e.g., Chandra et al. 2010; Romano et al. 2011; Jing et al. 2012; Vemareddy et al. 2012). The helicity flux distribution in ARs is measured by computing a helicity flux density proxy, since helicity is not a local quantity (see Pariat et al. 2005). The proxies usually employed only require the photospheric evolution of AR vector magnetograms. These proxies do not allow a direct interpretation of the helicity flux density distribution when opposite signals of helicity flux are present, and can even introduce spurious, i.e., fake, signals (see Pariat et al. 2005, 2007).
Pariat et al. (2005) proposed a new proxy of the helicity flux density that takes into account the magnetic field connectivity, and Dalmasse et al. (2013) developed a method to compute such a proxy in practice. Based on analytical case studies and numerical simulations, they showed that this method can reliably and accurately determine the injection of helicity, and can reveal the real mixed signals of the helicity flux. Therefore, this method should be used to map the helicity flux in observational studies.
As an example, recent observational studies of the photospheric distribution of the magnetic helicity flux in NOAA 11158 found mixed signals of the helicity flux in the AR as reported by Jing et al. (2012) and Vemareddy et al. (2012). These authors argued that the pattern can be associated to the injection of opposite helicity and that magnetic helicity annihilation can be responsible for triggering some major flares observed in the AR. However, they employed the purely photospheric proxy only instead of a connectivity-based helicity flux density method to compute the photospheric distribution of the helicity flux in the AR. We can therefore wonder if these mixed signals are real or spurious. In particular, how much are the helicity flux distribution and the signal intensity modified when using a connectivity-based helicity flux density proxy? Hence, can the obtained helicity flux distribution give hints of the action of magnetic helicity annihilation in the activity of NOAA 11158?
In the present letter, we address these questions by comparing the helicity flux distribution in NOAA 11158 computed with the purely photospheric as well as the connectivity-based proxy. We present the first observational application of the connectivity-based helicity flux density method introduced in Dalmasse et al. (2013) and test the robustness of this method.
2. Observations and analysis
2.1. Method
Pariat et al. (2005) demonstrated that the helicity flux can be expressed as the summation of the relative rotation rate of all pairs of elementary magnetic flux tubes weighted by their magnetic flux. From this definition, they introduced a purely photospheric proxy of helicity flux density, Gθ, such that 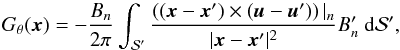 (1)where S′ is the photospheric-surface where the helicity flux is computed, x and x′ are the photospheric magnetic footpoints of elementary magnetic flux tubes, B and B′ are their associated magnetic fields (index n or t denotes the normal or transverse component of a vector), and u and u′ are their respective flux transport velocities defined by (e.g., Démoulin & Berger 2003):
(1)where S′ is the photospheric-surface where the helicity flux is computed, x and x′ are the photospheric magnetic footpoints of elementary magnetic flux tubes, B and B′ are their associated magnetic fields (index n or t denotes the normal or transverse component of a vector), and u and u′ are their respective flux transport velocities defined by (e.g., Démoulin & Berger 2003): 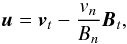 (2)where v is the photospheric plasma velocity.
(2)where v is the photospheric plasma velocity.
Equations (1) and (2) show that at a given time, t, the photospheric distribution of helicity flux, Gθ, can be computed from a timeseries of vector magnetograms. However, as pointed out by Pariat et al. (2005), a helicity flux density is only meaningful when considering a whole elementary magnetic flux tube/field line. Such an extension implies taking into account the magnetic field connectivity, which is not included in Gθ. To solve this problem, Pariat et al. (2005) defined a connectivity-based helicity flux density proxy, GΦ, such that 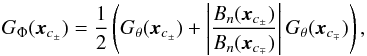 (3)where c is a closed elementary magnetic flux tube, i.e., a field line, anchored in the photosphere at the magnetic footpoints xc±.
(3)where c is a closed elementary magnetic flux tube, i.e., a field line, anchored in the photosphere at the magnetic footpoints xc±.
Dalmasse et al. (2013) introduced a method for computing Eq. (3) based on magnetic field line integration, which requires the knowledge of the magnetic field in the volume above the region of interest. Because magnetic field measurements are mostly realized at the photospheric level, we performed magnetic field extrapolations to obtain the coronal magnetic field and to compute the photospheric distribution of the magnetic helicity from Eq. (3).
Additionally, we computed the true density of the helicity flux for each elementary magnetic flux tube c, i.e., the helicity flux per unit magnetic flux, dhΦ/dt, defined by (see Pariat et al. 2005) 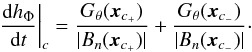 (4)By definition from Eqs. (3) and (4), GΦ and dhΦ/dt are defined only for closed magnetic field lines. For open magnetic field lines, we set GΦ = Gθ and did not compute dhΦ/dt. Finally, closed magnetic field lines with Bn(xc±) lower than 10 Gauss at one footpoint were treated as open field lines to avoid problems related to the presence of bald patches that would result in very high/infinite values of the helicity flux density, and that would prevent the conservation of the total helicity flux.
(4)By definition from Eqs. (3) and (4), GΦ and dhΦ/dt are defined only for closed magnetic field lines. For open magnetic field lines, we set GΦ = Gθ and did not compute dhΦ/dt. Finally, closed magnetic field lines with Bn(xc±) lower than 10 Gauss at one footpoint were treated as open field lines to avoid problems related to the presence of bald patches that would result in very high/infinite values of the helicity flux density, and that would prevent the conservation of the total helicity flux.
2.2. Data
NOAA 11158 appeared on 2011 February 10 at the heliographic coordinates S19 E42. This AR was the result of strong and fast magnetic flux emergence that resulted in the formation of two large-scale bipoles, a northern and a southern one (e.g., Schrijver et al. 2011). Its emergence was associated to several C-, M-, and X-class flares and CMEs during 2011 February 10−20 (e.g., Sun et al. 2012).
We used the 12 min cadence and high-resolution vector magnetograms from the SDO/HMI instrument at 06:22 and 06:34 UT on 2011 February 14 prior to a C-class flare observed at 06:51 UT. For both vector magnetograms, the 180° ambiguity was removed using the method of Metcalf et al. (2006). These vector magnetograms were used to compute the photospheric flux transport velocity field using the differential affine velocity estimator for vector magnetograms (DAVE4VM; Schuck 2008) with a window size of 19 pixels (as in Liu & Schuck 2013).
We assumed that the computed flux transport velocity field is equivalent to an instantaneous flux transport velocity at ~06:28 UT. We then constructed the associated vector magnetogram by averaging the magnetic data measurements taken at 06:22 and 06:34 UT (Fig. 1a).
We performed a nonlinear force-free magnetic field (NLFFF) extrapolation to obtain the coronal magnetic field from the vector magnetogram at ~06:28 UT using the magnetofrictional relaxation method developed in Valori et al. (2005, 2010). The data were first rebinned to 1′′ per pixel and preprocessed toward the force-free condition using the method of Fuhrmann et al. (2007). The extrapolation domain covers ~208 × 202 × 145 Mm3. A set of selected magnetic field lines is represented in Fig. 1b.
3. Results
In the following, the positive and negative polarities of the northern or southern bipole are referred to as NP and NN, or SP and SN, respectively (see Fig. 1a).
The full photospheric xy-domain of the NLFFF extrapolation was considered to derive the helicity flux density maps displayed in Fig. 2. In this domain, the closed magnetic field – for which GΦ has been computed – encloses 73% of the total unsigned magnetic flux. The remaining magnetic flux corresponds to open-like magnetic fields (see Sect. 2.1). These regions, where GΦ = Gθ, are mainly located at the eastern and western extremities of the AR.
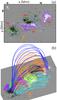 |
Fig. 1 Solar active region NOAA 11158 at ~06:28 UT on 2011 February 14. a) Photospheric vertical magnetic field (Bz) in grayscale overplotted with the flux transport velocity field (blue/green arrows) and the polarity labels (red). b) 3D views of the NLFFF magnetic field extrapolation with selected magnetic field lines. Each field line color corresponds to a different quasi-connectivity domain (separated by QSLs; see Sect. 4). The orange arrow shows the viewing angle relatively to panel a). The magnetic field values are saturated at ±1500 Gauss. Solid pink and dashed cyan lines are ±500 Gauss magnetic field isocontours, respectively. |
We compared the total fluxes computed from both Gθ and GΦ maps displayed in Fig. 2. The helicity flux of the closed magnetic field and the total helicity flux computed with the proxy Gθ are 3.7 × 1021 Wb2 s-1 and 2.3 × 1021 Wb2 s-1, respectively. The total helicity flux is lower because of the strong contribution of negative helicity in the open magnetic field. The same fluxes computed with the proxy GΦ are 3.9 × 1021 Wb2 s-1 and 2.5 × 1021 Wb2 s-1. The ratio of these fluxes computed with GΦ compared with Gθ are 1.05 and 1.08, respectively. Therefore, the global helicity flux between the two proxies agrees very well.
 |
Fig. 2 Solar active region NOAA 11158 at ~06:28 UT on 2011 February 14. a), b) Helicity flux density distributions in units of 107 Wb2 m-2 s-1 with the same color scale: a) Gθ and b) GΦ maps. All photospheric maps are overplotted with ±500 Gauss isocontours of Bz. |
In Fig. 2b, the GΦ map also displays mixed signals. This implies that there are real mixed signs of the helicity flux in the AR, as found in previous studies (e.g., Jing et al. 2012; Vemareddy et al. 2012). However, the distribution is different from the results of the Gθ map (Fig. 2a) except in the regions of open magnetic fields. In SN, the weak positive signal has almost entirely been replaced by negative helicity flux. In NP, GΦ presents enhanced positive values on the left side and an intrusion of negative values in the central part. Finally, the weak negative signal present between NN and SP in Gθ (≈− 2.5 × 106 Wb2 m-2 s-1) is now positive in GΦ (≈2.5 × 106 Wb2 m-2 s-1). Otherwise, the distribution of GΦ and Gθ is similar in NN and SP because field lines are linking similar values of Gθ.
Considering only the closed magnetic field, we summed the positive and then the negative helicity flux signals for both Gθ and GΦ. We found that the ratio of these fluxes computed with GΦ compared with Gθ are 0.84 and 0.57, respectively. We summed the absolute value of these positive and negative fluxes to obtain the total unsigned helicity flux for both GΦ and Gθ, and found a ratio equal to 0.76. Overall, it shows that the intensity of the signal in Gθ tends to be overestimated.
In Fig. 3, we represent the 3D distribution of the helicity flux density per elementary magnetic flux tubes/field lines. In this figure, each magnetic field line is colored according to the associated true helicity flux density computed from Eq. (4). The 3D representation of the true helicity flux density shows us that the helicity flux density map (Fig. 2b) is the result of two magnetic structures of strong opposite helicity flux: an inner system with positive helicity flux overlaid by an outer system of negative helicity flux.
We also computed the helicity flux distribution using a potential magnetic field extrapolation. The results also show mixed helicity flux signals. Compared with the NLFFF case, the differences are mostly located in the highly sheared region between SP and NN where the electric currents are the strongest. In particular, the intensity of the signal is different, but not its sign. This mutual consistency between the application to potential and NLFFF extrapolations, together with the tests performed in Dalmasse et al. (2013), provides us with additional confidence that our method for computing GΦ is robust when applied to observational data.
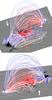 |
Fig. 3 Two 3D views of the NLFFF magnetic field extrapolations with the same selected magnetic field lines as in Fig. 1b. Field lines are colored according to their associated helicity flux density value computed from Eq. (4), red or blue for positive or negative values. The values are saturated at ±1.5 × 108 Wb s-1. Arrows show the viewing angles relative to Fig. 1 (orange) and to the bottom panel (white). |
4. Conclusions and discussion
We presented the first observational application of a connectivity-based helicity flux density proxy to NOAA 11158 using the method developed in Dalmasse et al. (2013). We showed that the method can be reliably applied to observational data, and should be used to monitor the injection of magnetic helicity in ARs.
By computing the photospheric mapping of the helicity flux using this method with an NLFFF extrapolation, we provided direct and reliable evidence that real opposite helicity fluxes were observed in NOAA 11158 on 2011 February 14. However, the intensity and the distribution of the helicity flux are different from what has been found in previous studies (Jing et al. 2012; Vemareddy et al. 2012). The connectivity-based helicity flux density proxy shows that (1) the intensity of the fluxes tends to be overestimated with Gθ; and (2) that two magnetic structures with opposite helicity flux are present, one on top of the other.
Although it is not included here, we computed the photospheric mapping of quasi-separatrix layers (QSLs; see review by Démoulin 2006, and references therein). These are regions of sharp gradients of the magnetic field connectivity and are preferential sites for current layers formation, and thus, for magnetic reconnection (e.g. Janvier et al. 2013). Comparing the QSLs mapping with the distribution of helicity flux, we found several locations where the interface between the regions of opposite helicity flux coincides with QSLs. One such particularly interesting region is located in the northern part of the southern bipole. There, we found a flux rope (green field lines in Fig. 1b) linking SN to SP, with a net positive helicity flux (Fig. 3). The negative footpoints of this flux rope are below surrounding twisted and arcade field lines (purple field lines on the north of SP in Fig. 1b) which are associated to a strong negative helicity flux (Fig. 3). Hence, the helicity flux pattern could possibly play a role in the initiation and dynamics of the C-class flare observed in this region at 06:51 UT, i.e., 20 min after our extrapolation and helicity injection map. Assuming that these opposite helicity fluxes correspond to a transfer of opposite helicity from the convection zone toward the corona, NOAA 11158 would be a good candidate for studying solar eruptivity related to magnetic helicity annihilation (e.g., Kusano et al. 2002, 2004).
Overall, the temporal evolution study of the connectivity-based helicity flux density and of the helicity flux density per elementary magnetic flux tube is needed to obtain information on the role of helicity injection in the flaring activity observed in ARs, and on the nature of the emerging magnetic flux tube(s) creating these ARs.
Acknowledgments
This work used the DAVE4VM code written and developed by P. Schuck at the Naval Research Laboratory. The research leading to these results has received funding from the European Commission’s Seventh Framework Programme (FP7/2007-2013) under the grant agreement eHeroes (project N° 284461, http://www.eheroes.eu). Lucie Green is grateful to the Royal Society for funding through their University Research Fellowships. The data used here are courtesy of the NASA/SDO and the HMI science team.
References
- Berger, M. A. 1984, Geophys. Astrophys. Fluid Dyn., 30, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Moon, Y.-J., & Park, Y.-D. 2004, Sol. Phys., 223, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, R., Pariat, E., Schmieder, B., Mandrini, C. H., & Uddin, W. 2010, Sol. Phys., 261, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Dalmasse, K., Pariat, E., Démoulin, P., & Aulanier, G. 2013, Sol. Phys., in press [Google Scholar]
- Démoulin, P. 2006, Adv. Space Res., 37, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Berger, M. A. 2003, Sol. Phys., 215, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, M., Seehafer, N., & Valori, G. 2007, A&A, 476, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Aulanier, G., Pariat, E., & Démoulin, P. 2013, A&A, in press [Google Scholar]
- Jing, J., Park, S.-H., Liu, C., et al. 2012, ApJ, 752, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2002, ApJ, 577, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2004, ApJ, 610, 537 [NASA ADS] [CrossRef] [Google Scholar]
- LaBonte, B. J., Georgoulis, M. K., & Rust, D. M. 2007, ApJ, 671, 955 [CrossRef] [Google Scholar]
- Linton, M. G., Dahlburg, R. B., & Antiochos, S. K. 2001, ApJ, 553, 905 [Google Scholar]
- Liu, Y., & Schuck, P. W. 2013, Sol. Phys., 283, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. 1997, in Coronal Mass Ejections, eds. N. Crooker, J. Joselyn, & J. Feynman, AGU Geophys. Monogr, 99, 39 [Google Scholar]
- Metcalf, T. R., Leka, K. D., Barnes, G., et al. 2006, Sol. Phys., 237, 267 [Google Scholar]
- Moffatt, H. K. 1969, J. Fluid Mech., 35, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Moon, Y.-J., Chae, J., Choe, G. S., et al. 2002, ApJ, 574, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Démoulin, P., & Berger, M. A. 2005, A&A, 439, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Démoulin, P., & Nindos, A. 2007, Adv. Space Res., 39, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Pariat, E., Sicari, M., & Zuccarello, F. 2011, A&A, 525, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J., Aulanier, G., Title, A. M., Pariat, E., & Delannée, C. 2011, ApJ, 738, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, X., Hoeksema, J. T., Liu, Y., et al. 2012, ApJ, 748, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Valori, G., Kliem, B., & Keppens, R. 2005, A&A, 433, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valori, G., Kliem, B., Török, T., & Titov, V. S. 2010, A&A, 519, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vemareddy, P., Ambastha, A., Maurya, R. A., & Chae, J. 2012, ApJ, 761, 86 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Solar active region NOAA 11158 at ~06:28 UT on 2011 February 14. a) Photospheric vertical magnetic field (Bz) in grayscale overplotted with the flux transport velocity field (blue/green arrows) and the polarity labels (red). b) 3D views of the NLFFF magnetic field extrapolation with selected magnetic field lines. Each field line color corresponds to a different quasi-connectivity domain (separated by QSLs; see Sect. 4). The orange arrow shows the viewing angle relatively to panel a). The magnetic field values are saturated at ±1500 Gauss. Solid pink and dashed cyan lines are ±500 Gauss magnetic field isocontours, respectively. |
| In the text | |
 |
Fig. 2 Solar active region NOAA 11158 at ~06:28 UT on 2011 February 14. a), b) Helicity flux density distributions in units of 107 Wb2 m-2 s-1 with the same color scale: a) Gθ and b) GΦ maps. All photospheric maps are overplotted with ±500 Gauss isocontours of Bz. |
| In the text | |
 |
Fig. 3 Two 3D views of the NLFFF magnetic field extrapolations with the same selected magnetic field lines as in Fig. 1b. Field lines are colored according to their associated helicity flux density value computed from Eq. (4), red or blue for positive or negative values. The values are saturated at ±1.5 × 108 Wb s-1. Arrows show the viewing angles relative to Fig. 1 (orange) and to the bottom panel (white). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


