| Issue |
A&A
Volume 555, July 2013
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 6 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201321482 | |
| Published online | 05 July 2013 | |
Stray-light correction in 2D spectroscopy
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6,
79104
Freiburg,
Germany
e-mail:
schliche@kis.uni-freiburg.de
Received:
15
March
2013
Accepted:
22
May
2013
Context. In solar physics, spectropolarimeters based on Fabry-Pérot interferometers are commonly used for high spatial resolution observations. In the data pipeline, corrections for scattered light may be performed on each narrow band image.
Aims. We elaborate on the effects of stray-light corrections on Doppler maps.
Methods. First, we demonstrate the basic correction effect in a simplified situation of two profiles that suffer from stray light. Then, we study the correction effects on velocity maps by transforming a Hinode SP map into a two-dimensional spectroscopic data set with i(x,y) at each wavelength point, which mimicks narrow band images. Velocity maps are inferred from line profiles of original and stray-light corrected data.
Results. The correction of scattered light in narrow band images affects the inferred Doppler velocity maps: relative red shifts always become more red, and relative blue shifts become more blue. This trend is independent of whether downflows have dark or bright intensities. As a result, the effects of overcorrection produce both downflows and upflows.
Conclusions. In 2D spectropolarimetry, corrections for scattered light can improve the image intensity and velocity contrast but inherently produce downflow signatures in the penumbra. Hence, such corrections are justified only if the properties of the stray light (seeing, telescope, and instrument) are well known.
Key words: techniques: imaging spectroscopy / methods: data analysis / techniques: image processing / methods: observational
© ESO, 2013
1. Introduction
The magnetohydrodynamic processes on the Sun are a subject of numerous research projects, since the Sun serves as a laboratory to explore the manifold and complex interactions between magnetic fields, highly ionized plasma, and radiation. One prominent example is how magnetoconvection in a sunspot penumbra produces the observed brightness. While it is commonly accepted that magnetoconvective processes are present, various models with distinct flow fields have been presented (see e.g., Rempel & Schlichenmaier 2011). The observational challenge is now to indisputably measure the morphology of the flow field. For comparing theoretical expectations with observations, the method of spectropolarimetry is crucial: velocity fields and magnetic fields in the atmosphere of the Sun alter the transport of radiation via the Doppler and Zeeman effects, and the respective imprints of those fields can be measured in spectral profiles of the polarimetric components of light.
To acquire spectropolarimetric data, two approaches are most commonly used: (1) grating spectrographs amended by a modulator measure polarimetric and spectral properties of a one-dimensional image. The solar image is scanned across a slit to construct maps of spectropolarimetric profiles (e.g., VTT/TIP, Hinode SOT/SP, DST/DLSP, THEMIS/MTR). Here, the recorded spectra have a spatial and a spectral direction (see Beck et al. 2011, for a recent study on stray-light issues). (2) Spectropolarimeters based on Fabry-Pérot interferometers are used as tunable filters to scan in wavelength, while acquiring narrow-band images of the different polarization states (e.g., DST/IBIS, SST/CRISP, VTT/TESOS, VTT/GFPI, Sunrise/IMaX). Here, narrow-band images are recorded at each wavelength.
Two-dimensional spectrometers produce spatial images at given wavelength points. These images can be corrected for scattered light to increase the contrast. Stray-light correction has recently been applied to data of a penumbra, which led to the finding of penumbral downflows in dark filaments (Scharmer et al. 2011; Joshi et al. 2011). As actually already pointed out by Joshi et al. (2011, cf. their Fig. 4), stray-light corrections however, may substantially enhance the red shifts. Here, we go a step further and make the case that downflows – under certain circumstances – are an artifact of stray-light correction.
In this contribution, we elaborate on unwanted artifacts in inferred velocity maps that may result from stray-light overcorrections. We find that downflows inevitably result from stray-light corrections. In Sect. 2, we demonstrate the overcorrection effect using a simplified situation. Methods of stray-light correction for two-dimensional image data are introduced and compared in Sect. 3. To demonstrate that elongated penumbral downflows are inherently generated by a stray-light correction, we utilize Hinode SP data. We construct narrow-band images from an SP scan across a sunspot (cf. Sect. 4). We compare velocity maps of uncorrected and corrected velocity maps. In Sect. 5, we conclude that downflows can be produced by overcorrections.
2. Effect of stray-light correction on line profiles
In this section, we use a simplified two-profile model to show that a stray-light correction always enhances the fluctuations (“contrast”) in velocity maps; that is, relative red shifts are shifted to the red, and relative blue shifts are shifted to the blue.
We consider two profiles that are Doppler shifted with respect to each other:
ib,t(λ) &
ir,t(λ). The index “t”
denotes true profiles, and “b” and “r” denote blue- and red-shifted profiles, respectively.
The observed profiles, ib,o(λ)
& ir,o(λ), suffer from
stray-light, and assuming a stray-light fraction, β, we measure:
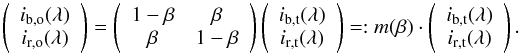 (1)β varies
between 0 and 0.5: β = 0 means no mixing, and β = 0.5
corresponds to entire mixing, such that both observed profiles are identical. Inverting the
matrix, m(β), the stray-light corrected profiles,
ib,c(λ) &
ir,c(λ) are obtained by
(1)β varies
between 0 and 0.5: β = 0 means no mixing, and β = 0.5
corresponds to entire mixing, such that both observed profiles are identical. Inverting the
matrix, m(β), the stray-light corrected profiles,
ib,c(λ) &
ir,c(λ) are obtained by
 with
an estimate for the stray-light fraction,
with
an estimate for the stray-light fraction,  .
The true profile is only retrieved if
.
The true profile is only retrieved if  . Plotting the profiles for
. Plotting the profiles for
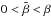 , the corrected profiles lies
between the observed and true profile. In any case,
, the corrected profiles lies
between the observed and true profile. In any case, 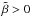 yields corrected profiles with
enhanced red and blue shift with respect to the observed profiles.
yields corrected profiles with
enhanced red and blue shift with respect to the observed profiles.
 |
Fig. 1 Effect of stray-light overcorrection: two true profiles (solid lines), which are red- and blue-shifted with respect to each other, are subject to stray light (dashed lines). The vertical lines mark the line wing positions of the lines. The three panels differ with respect to the continuum intensities in blue- and red-shifted true profiles. |
In Fig. 1, we focus on the effects of overcorrection
of 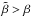 . To this end, we assume that
the observation suffers from a stray light with β = 20%, but the correction
is performed with
. To this end, we assume that
the observation suffers from a stray light with β = 20%, but the correction
is performed with  . For the
two true profiles (solid lines), we choose Gaussian line shapes that have a similar line
depth (0.7) and width (15 pm) to Fe I 630.15 nm. The two true profiles are shifted relative
to each other by 2.0 km s-1 (~4.3 pm). The observed profiles are shown by the
dashed lines. The corresponding corrected profiles are shown as dotted lines. The vertical
solid, dashed, and dotted lines mark the respective Doppler shifts as measured in the line
wing1 The four different panels in Fig. 1 differ only in the continuum intensity level for the two
true profiles. Figure 1a shows the typical situation of
a brighter blue-shifted profile with a continuum intensity
icont = 1.03 and a darker red-shifted profiles with
icont = 0.97. The two observed profiles (dashed line) turn out
to be shifted relative to each other by 1.1 km s-1. For the overcorrected profile
(dotted line), the difference increases to 3.1 km s-1. Thus, the velocity
difference of the overcorrected profiles is too large by 1.1 km s-1 relative to
the true velocity difference. Note that the difference in continuum intensity of the two
profiles is 6% (true), 4% (obs), and 10% (corrected).
. For the
two true profiles (solid lines), we choose Gaussian line shapes that have a similar line
depth (0.7) and width (15 pm) to Fe I 630.15 nm. The two true profiles are shifted relative
to each other by 2.0 km s-1 (~4.3 pm). The observed profiles are shown by the
dashed lines. The corresponding corrected profiles are shown as dotted lines. The vertical
solid, dashed, and dotted lines mark the respective Doppler shifts as measured in the line
wing1 The four different panels in Fig. 1 differ only in the continuum intensity level for the two
true profiles. Figure 1a shows the typical situation of
a brighter blue-shifted profile with a continuum intensity
icont = 1.03 and a darker red-shifted profiles with
icont = 0.97. The two observed profiles (dashed line) turn out
to be shifted relative to each other by 1.1 km s-1. For the overcorrected profile
(dotted line), the difference increases to 3.1 km s-1. Thus, the velocity
difference of the overcorrected profiles is too large by 1.1 km s-1 relative to
the true velocity difference. Note that the difference in continuum intensity of the two
profiles is 6% (true), 4% (obs), and 10% (corrected).
To demonstrate that the red and blue shifts are enhanced in any case, we present the case of equally bright blue and red shift in Fig. 1b, the case of a darker blue shift where icont = 0.97, and a brighter red shift where icont = 1.03 in Fig. 1c. In both cases, the velocity differences between overcorrected red and blue shifts increase. In case 1b, all profiles have unity continuum intensity, thus, the line shifts are enhanced even without intensity contrast. In case 1c, the contrast is the same as in 1a, but now the red-shifted profile is brighter than the blue-shifted one. Hence, the red shift is enhanced in all cases, but the intensity level may increase or decrease. That is, a stray-light correction can have different effects on intensity and line position.
In Fig. 1d, the intensity difference of the true profiles is larger than in 1a. The blue-shifted profile has icont = 1.2, and the red-shifted profile has icont = 0.8. The other parameters are as before. Here, the velocity difference of the corrected profiles is larger than in 1a. The corrected red-shifted profile has a line wing shift of 1.9 km s-1 with the red shift of the true profile being 1 km s-1. In case 1a, the corrected profile has only 1.6 km s-1. Hence, the larger intensity contrast further enhances the effect of overcorrection and leads to profiles that are shifted even stronger to the red.
This two-profile model demonstrates that stray-light corrections have an immediate impact on the values of the velocities. An overcorrection results in an enhancement of existing velocity fluctuations. Hence, significant red shifts (i.e., downflows) can be produced by stray-light overcorrection. This effect is further enhanced with increasing intensity contrast (cf. case 1d).
Another effect of stray-light correction is the modification of the asymmetry of the line. In our model all true profiles are symmetric, that is, they have a vertical bisector. Yet, this is not true for the corrected profiles. For example, the mean bisector velocity of the line core (intensities between 70% and 100% of the line depression) in Fig. 1d amounts to 1.55 km s-1, while the line wing bisector velocity is 1.92 km s-1.
3. Stray-light correction method
If a stray-light correction is not only applied to two profiles as in the previous section but also applied to narrow-band images, a deconvolution, instead of a simple superposition (as in Eq. (1)), needs to be performed.
The effect of stray-light contained in the observed image, io,
can be described2 by a stray-light function,
s(x,y), with a normalized integral over area,
∫s(x,y) dxdy = 1,
convolved with the true image, it, by 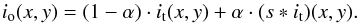 (2)The parameter
α, whose values range from 0 ≤ α ≤ 1, denotes the
fractional amount of stray light. The “∗” sign abbreviates the convolution. Employing the
δ-function and the identity,
(2)The parameter
α, whose values range from 0 ≤ α ≤ 1, denotes the
fractional amount of stray light. The “∗” sign abbreviates the convolution. Employing the
δ-function and the identity,  and
taking advantage that the convolution is distributive, one can write
and
taking advantage that the convolution is distributive, one can write ![\begin{equation} \label{eq:stray2} i_{\rm o}(x,y) = [ (1-\alpha) \cdot \delta + \alpha \cdot s] \ast i_{\rm t} (x,y) . \end{equation}](/articles/aa/full_html/2013/07/aa21482-13/aa21482-13-eq38.png) (3)The stray-light function
may consist of a superposition of Gaussians with different widths and amplitudes. In the
case of two Gaussians, it would be written as:
(3)The stray-light function
may consist of a superposition of Gaussians with different widths and amplitudes. In the
case of two Gaussians, it would be written as:  with
α = α1 + α2. The
area integral of each Gaussian is unity. Obviously, more than two functions and other types
of functions may also be used. In the following, we shall restrict our consideration to
with
α = α1 + α2. The
area integral of each Gaussian is unity. Obviously, more than two functions and other types
of functions may also be used. In the following, we shall restrict our consideration to
![\begin{eqnarray*} s= g(\sigma) = \frac{2\sigma}{\pi}\exp \left[ -\left(x^2+y^2\right)/\left(2 \sigma^2\right) \right] \end{eqnarray*}](/articles/aa/full_html/2013/07/aa21482-13/aa21482-13-eq41.png) with
the first factor normalizing the integral and the full width at half maximum corresponding
to 2.35σ. We can rewrite Eq. (3) with
p(α,σ): = (1 − α)δ + αg(σ),
with
the first factor normalizing the integral and the full width at half maximum corresponding
to 2.35σ. We can rewrite Eq. (3) with
p(α,σ): = (1 − α)δ + αg(σ),
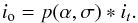 (4)A convolution in
real space becomes a multiplication in spatial frequency space. If we denote the Fourier
transforms in frequency space with capital letters, the latter equation can therefore be
solved for It as
(4)A convolution in
real space becomes a multiplication in spatial frequency space. If we denote the Fourier
transforms in frequency space with capital letters, the latter equation can therefore be
solved for It as 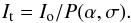 (5)Note that
P(α,σ) does not drop to zero for large frequencies,
since the δ component produces a constant offset in frequency space. The
stray-light corrected image, it, is then retrieved by
transforming It back into real space.
(5)Note that
P(α,σ) does not drop to zero for large frequencies,
since the δ component produces a constant offset in frequency space. The
stray-light corrected image, it, is then retrieved by
transforming It back into real space.
Comparison with Scharmer et al. (2011):
Scharmer et al. use the same approach as described above. In an experiment, we use a
speckle reconstructed image taken with the broad band imager at GREGOR (von der Luhe et
al. 2012) that has a granulation contrast of 5.6% (root mean square deviations of
intensity). If we use α = 0.58 and
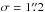 , which are the values used by
Scharmer et al., the contrast of the GREGOR image increases from 5.6% to 12.4%.
, which are the values used by
Scharmer et al., the contrast of the GREGOR image increases from 5.6% to 12.4%.
 |
Fig. 2 A comparison of the inverse Wiener filter F-1 used by
(Joshi et al. 2011) (dashed line) and our
deconvolution with |
Comparison with Joshi et al. (2011):
Joshi et al. modify a Wiener filter used by Sobotka et
al. (1993) such that the filter equals unity for large spatial frequencies. Their
formula is based on a Gaussian with  and contains the free parameter
c. For the comparison, we use the same GREGOR image as in the previous
paragraph. To obtain the same contrast amplification with their and our (Eq. (5)) method, we find α = 0.34.
A comparison is displayed in Fig. 2. The left panel
compares their F-1 with
and contains the free parameter
c. For the comparison, we use the same GREGOR image as in the previous
paragraph. To obtain the same contrast amplification with their and our (Eq. (5)) method, we find α = 0.34.
A comparison is displayed in Fig. 2. The left panel
compares their F-1 with
 . In the right panel, we plot
the power spectra for uncorrected and the two corrected images. The difference between the
two methods (dashed and dotted lines) are small. Both methods increase the contrast of our
GREGOR image from 5.6% to 8.12%. The map of the differences of the corrected images
reveals a standard deviation of 1.4%, and extreme values of up to 12%.
. In the right panel, we plot
the power spectra for uncorrected and the two corrected images. The difference between the
two methods (dashed and dotted lines) are small. Both methods increase the contrast of our
GREGOR image from 5.6% to 8.12%. The map of the differences of the corrected images
reveals a standard deviation of 1.4%, and extreme values of up to 12%.
4. Effects of scattered light corrections
In this section, we elaborate on how stray-light corrections in 2D spectroscopy affect the line shifts in realistic data. For the latter, we utilized a scan with Hinode SP to mimic a 2D spectrometer. Then we compare the line shifts of uncorrected data to those where a stray-light correction was applied to the images.
4.1. Mimicking a 2D spectrometer
Maps of I(y,λ) [x] with y along the slit and x in the scanning (perpendicular) direction are transformed into images at each wavelength I(x,y) [λ]. These images are used to mimic a 2D spectroscopic data set that was acquired by a Fabry-Pérot system.
The stray-light properties of Hinode are well studied (Danilovic et al. 2008; Wedemeyer-Böhm & Rouppe van der Voort 2009; van Noort 2012). However, we do not attempt to correct the flow maps for the true stray-light. Here, we want to study the effects of stray-light correction on the observed velocity maps.
 |
Fig. 3 Upper left: original velocity map derived from the shifts of the line wing of Fe I 630.15 nm for AR 10923 at θ ≈ 8°. The coordinates are in arcsec relative to disc center. The large inlay is a magnification of the black box. The values along the back slice in the box are plotted in Fig. 4. The other three maps show the velocity map with varying stray-light fractions: α = 0.20 (upper right), α = 0.40 (lower left), and α = 0.60 (lower right). The width of the Gaussian is σ = 2″ in all cases. |
4.2. Uncorrected velocity maps
We performed our analysis for two sunspot maps acquired with Hinode SP: (1) AR 10923, 14 Nov. 2006, scan start at 07:15 UT, where the center of the spot is at a heliocentric angle of θ ≈ 8° and (2) AR 10933, 5 Jan. 2007, scan start at 12:34 UT, θ ≈ 3°.
The upper left panel of Fig. 3 displays the uncorrected Hinode Doppler flow map of AR 10923. The Doppler velocity is determined from the shift in the line wing (cf. FS09 and footnote 1 in Sect. 2). The zero velocity is defined as the average of those umbral areas that display antisymmetric V-profiles as in FS09. Although the center of the spot is only some 150′′ away from the disk center, the projection of the horizontal Evershed outflow is clearly seen: the top penumbra part is on average blue-shifted, and the lower part is red-shifted. Yet, the blue-shifted center-side penumbra also show patches of red shifts (as reported by FS09). We discard horizontal inflows as the source of these redshifts and interpret them as down flows.
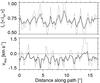 |
Fig. 4 Slice through penumbra is denoted by the black curved line in Fig. 3. Upper panel: normalized intensity along the slice. The solid line corresponds to uncorrected data and the dotted line to stray-light corrected data with (α = 0.6 and σ = 2″). Lower panel: same as upper panel but for velocity. It is seen that the dotted line shows significant patches of downflows (υ > 0). |
4.3. Flow maps with stray-light correction
Applying Eq. (5) to the pseudonarrow band images and computing the velocity as in the uncorrected map, we infer velocity maps for the following stray-light parameters: We use σ = 2″ and vary α = 0.2 to α = 0.4 and then to α = 0.6. The corresponding three velocity maps are displayed in Fig. 3 next to the uncorrected map. The inlets in the lower left part of the image display a magnification of the black square in the center-side penumbra. The curved line in the black square corresponds to the plots in Fig. 4.
Inspecting these images with increasing α, three findings can be inferred: (1) the contrast, that is, the pixel-to-pixel differences of the velocity maps are increasing in the quiet Sun and in the penumbra, which means that the local red shifts become more red and the local blue shifts become more blue. (2) In particular in the inlet, it is seen that the area of penumbral downflows (yellow-redish color) increases with the increasing values of α. (3) Elongated downflow patches on the center-side penumbra become more and more prominent with increasing α.
In the corresponding intensity image, the downflows tend to be located in dark penumbral filaments, which is a typical effect of overcorrection (cf. Sect. 2). Strong elongated downflows, as seen in the lower right panel of Fig. 3, are produced by effects of overcorrection, since we have used α = 0.6. However, Danilovic et al. (2008) find α-values for Hinode, which are clearly less than 0.1.
Figure 4 plots uncorrected (solid lines) and corrected (α = 0.6, dashed lines) intensities (upper panel) and velocities (lower panel) along the black curve (within the black square of Fig. 3). Both the intensity and velocity variations along the cut for the corrected values are larger than those for the uncorrected data. Before corrections, there are only two locations with very small downflow velocities (υ < 100 m/s). After the stray-light correction, there are several patches of significant downflows along the slice with a peak velocity higher than 1.5 km s-1!
Tables 1 and 2 for AR 10923 and AR 10933 provide the root mean square deviations (abbreviated by “rms”) of intensity and velocity and the mean velocities for quiet Sun and penumbra. The rms(v) and the rms(i) increase for increasing α values. Comparing α = 0 and α = 0.6 in the quiet sun for the two tables, both values for i and υ increase by the same scaling factor of about 2.5. In the penumbra, rms(i) and rms(υ) are larger in the uncorrected image and increase less strongly. However, the scaling factors here for υ and i are different: rms(i) increases by a factor of about 1.5, and rms(υ) increases by a factor of 2 for AR10923 and 2.5 for AR 10933. This demonstrates that the penumbral velocity maps are very sensitive to stray-light correction, and overcorrections easily produce strong red and blue shifts.
While a stray-light correction preserves the mean intensity of each filtergram, it should also be noted that it produces a mean red shift in the velocity maps: in the case of AR 10933, the quiet Sun velocity mean increases from − 0.29 km s-1 (α = 0) to + 0.11 km s-1 (α = 0.6). This is because the blue shifts are associated predominantly with bright structures while red shifts tend to occur in dark structures (upflows in granules and downflows in intergranules). This property is also present in our simplified example in Fig. 1d, where the red-shifted profile is darker than the blue-shifted one: the mean of the two observed and the two corrected velocities increase from − 0.13 to + 0.29 km s-1 by 0.42 km s-1.
5. Discussion and conclusions
We study the effects of stray-light correction on velocity maps in 2D spectroscopy, in which narrowband images scanned in wavelength constitute the 3D data set, i(x,y,λ). As corrections for scattered light change the distribution of intensity in individual narrow band images, the line profiles and their positions are affected. Working out the essential effect in a simplified model (cf. Sect. 2), we demonstrate that the amplitudes of up and downflows are enhanced when performing a stray-light correction. Applying a stray-light correction to penumbral pseudo-images (Sect. 4), elongated penumbral downflows in dark filaments result in a natural way.
The important questions then are: (1) what is the amount of stray light present in the recorded data? (2) How does the stray-light vary spatially? Is it legitimate to assume a Gaussian distribution? If correct answers are lacking, stray-light corrections can falsify the retrieved velocity maps. If one corrects for more stray light than actually present in the data, there is a risk of retrieving erroneous downflows or too strong upflows. One should also be aware that the velocity mean is typically red-shifted by a few 100 m/s (cf. Tables 1 and 2) while stray-light corrections conserve the mean intensity.
Joshi et al. (2011) compare the granular contrast of their observation with IMAX measurements (Martínez Pillet et al. 2011) to estimate the amount of stray light (α ≈ 0.34, cf. Fig. 2) in their data. Similarly, Scharmer et al. (2011) determine large α-values (α ≈ 0.58) from a comparison of quiet Sun intensity contrast in their observation and in numerical simulations (de la Cruz Rodríguez et al. 2011). In both cases, they apply stray-light corrections with large α-values and idealized spatial distributions to claim the detection of elongated patches of red shifts. We believe that their justification is not without doubt. Here, we demonstrate that a stray-light correction alway produces significant (relative) red shifts. Therefore, we think that their red shifts could be produced by effects of overcorrection. To avoid overcorrection, a reliable assessment of the stray-light properties (amount and spatial distribution) would be necessary.
The line-wing position are bisector shifts at a line intensity of 0.9 as in Franz & Schlichenmaier (2009, hereafter FS09).
We follow Bello González et al. (2013).
Acknowledgments
We are grateful to Nazaret Bello González for fruitful discussions and to Franz Kneer for providing various IDL routines. M.F. acknowledges financial supported by the Leibniz-Gemeinschaft within the “Pakt für Forschung und Innovation”. Hinode is a Japanese mission developed and launched by ISAS/JAXA with NAOJ as domestic partner and NASA and STFC (UK) as international partners. It is operated by these agencies in cooperation with ESA and NSC (Norway).
References
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bello González, N., Danilovic, S., & Kneer, F. 2013, A&A, On the structure and dynamics of Ellerman bombs, submitted [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Cruz Rodríguez, J., Kiselman, D., & Carlsson, M. 2011, A&A, 528, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franz, M., & Schlichenmaier, R. 2009, A&A, 508, 1453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joshi, J., Pietarila, A., Hirzberger, J., et al. 2011, ApJ, 734, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Schlichenmaier, R. 2011, Liv. Rev. Sol. Phys., 8, 3 [Google Scholar]
- Scharmer, G. B., Henriques, V. M. J., Kiselman, D., & de la Cruz Rodríguez, J. 2011, Science, 333, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Sobotka, M., Bonet, J. A., & Vazquez, M. 1993, ApJ, 415, 832 [NASA ADS] [CrossRef] [Google Scholar]
- van Noort, M. 2012, A&A, 548, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von der Lühe, O., Volkmer, R., Kentischer, T. J., & Geißler, R. 2012, Astron. Nachr., 333, 894 [NASA ADS] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Effect of stray-light overcorrection: two true profiles (solid lines), which are red- and blue-shifted with respect to each other, are subject to stray light (dashed lines). The vertical lines mark the line wing positions of the lines. The three panels differ with respect to the continuum intensities in blue- and red-shifted true profiles. |
| In the text | |
 |
Fig. 2 A comparison of the inverse Wiener filter F-1 used by
(Joshi et al. 2011) (dashed line) and our
deconvolution with |
| In the text | |
 |
Fig. 3 Upper left: original velocity map derived from the shifts of the line wing of Fe I 630.15 nm for AR 10923 at θ ≈ 8°. The coordinates are in arcsec relative to disc center. The large inlay is a magnification of the black box. The values along the back slice in the box are plotted in Fig. 4. The other three maps show the velocity map with varying stray-light fractions: α = 0.20 (upper right), α = 0.40 (lower left), and α = 0.60 (lower right). The width of the Gaussian is σ = 2″ in all cases. |
| In the text | |
 |
Fig. 4 Slice through penumbra is denoted by the black curved line in Fig. 3. Upper panel: normalized intensity along the slice. The solid line corresponds to uncorrected data and the dotted line to stray-light corrected data with (α = 0.6 and σ = 2″). Lower panel: same as upper panel but for velocity. It is seen that the dotted line shows significant patches of downflows (υ > 0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


