EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) L9 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number L9
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201321590
Published online 22 May 2013

© ESO, 2013

1. Introduction

Several very bright quasars have been detected already at z > 6. This suggests that some supermassive black holes (SMBHs) with masses of ≃109  M⊙ already existed when the Universe was less than 1 Gyr old (Fan 2006). Explaining how such massive SMBHs could have assembled so soon after the Big Bang presents quite a challenge. The main questions concern how and when the seeds of these SMBHs formed and how their subsequent growth proceeded.

Several pathways leading to the formation of seed black holes (SBHs) have already been proposed. One group of scenarios suggests that SBHs formed via the direct collapse of metal-free/very metal-poor gas in halos with Tvir ≳ 104  K, at redshifts ~5–10, resulting in SBHs with M ~ 104 − 105  M⊙ (see, e.g., Bromm & Loeb 2003; Koushiappas et al. 2004; Begelman et al. 2006; Lodato & Natarajan 2006; Spaans & Silk 2006; Schleicher et al. 2010b; Latif et al. 2013). For efficient gas collapse to occur, fragmentation must be suppressed, which is possible if the gas in the halo is kept hot (large Jeans mass). Hence, the formation of H2 must be inhibited so cooling can occur only through atomic H, as otherwise H2 cooling will lower temperatures to ~200 K.

Several mechanisms have been suggested that suppress H2 cooling. The most accepted of these mechanisms requires a critical level of Lyman-Werner radiation to photo-dissociate H2 and keep its abundance very low. The critical intensity needed to suppress H2 in the massive halos where direct gas collapse can occur is large compared to the expected cosmic UV background at the relevant redshifts. However, the distribution has a long bright-end tail, and halos irradiated by supercritical intensities would be a small subset of all halos (Dijkstra et al. 2008). Another mechanism proposes that the dissipation of a sufficiently strong magnetic field can heat the gas in the halo to ~104 K, which causes H2 to be destroyed by collisional dissociation (Sethi et al. 2010).

A variety of mechanisms exist for generating magnetic fields early in the Universe, both before and after recombination (for a review, see, e.g., Widrow et al. 2012), and also for amplifying an existing field. In the case of a collapsing halo, the most important ones are gravitational compression, the small-scale turbulent dynamo, the large-scale dynamo in protostellar and galactic disks, and magneto-rotational instability (MRI).

Gravitational compression increases the magnetic field as 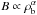when the field is coupled to the gas. For spherically symmetric collapse, α = 2/3, but if the collapse proceeds preferentially along one axis, the scaling is closer to α = 1/2. In realistic cases, intermediate values are often found (e.g., Schleicher et al. 2009; Hocuk et al. 2012).

Non-helical turbulent flows can act as small-scale dynamos, which produce disordered, random magnetic fields (Kazantsev 1968). The magnetic field amplification results from the random stretching and folding of the field lines by the turbulent random flow. During gravitational collapse, turbulence is generated by the release of gravitational energy and the infall of accreted gas on the inner, self-gravitating core. This means that, in the context of star and galaxy formation, a strong tangled magnetic field may already be generated during the collapse phase by the small-scale dynamo (Schleicher et al. 2010a). For the formation of SBHs, it implies that the existence of an accretion disk may cause the magnetic field to be further amplified (by a large-scale dynamo and/or the MRI) which provides additional stability and hence reduces fragmentation.

2. The model

The evolution of a cloud of primordial gas is followed from initial expansion to a high-density core, using a one-zone model, in which the physical variables involved are regarded as those at the cloud center. The model uses standard cosmology, with cosmological parameters given by WMAP7 (Larson et al. 2011).

2.1. Density evolution

The spherical collapse model for a top-hat overdensity is used to compute the matter density. At the moment of turnaround, the gas decouples from the dark matter and becomes self-gravitating. Any effects due to rotation are neglected for simplicity. The baryonic matter collapse is expected to proceed like the Larson-Penston similarity solution (for the isothermal case; Larson 1969; Penston 1969), as generalized to polytropic cases by Yahil (1983). According to this solution, the cloud consists of two parts, a central core region and an envelope. The central core region has a flat density distribution, whereas the density in the envelope decreases outwards. The size of the central flat region is roughly given by the local Jeans length, 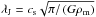, with 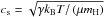the sound speed in the central region and ρm the total matter density in the central region. The collapse in the core proceeds approximately at the free-fall rate, although additional heat input due to magnetic energy dissipation, for example, may delay gravitational collapse. The mean baryonic density evolution in the central part is described by 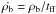, where tff is the free-fall time .

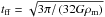2.2. Chemical network

The species that are included in the chemical network of this model are H, H+, H−, H2, H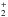, and e−; HD or other molecules involving deuterium are not included. Reactions with He are not taken into account, but He is considered in the calculation of the mean molecular mass. The He mass fraction is taken to be ~0.248 (corresponding to an abundance xHe ≈ 0.0825) and stays constant throughout the time integration. The fractional abundances of H, H2, and e− are explicitly followed during the integration.

The evolution of the fractional abundance of electrons xe is given by the equation (see, e.g., Peebles 1993, for further details) (1)The first term represents the recombination and photo-ionization of the primordial plasma, the second term is the collisional recombination term, and the third term represents collisional ionization (H + e− → H+ + 2e−).

The evolution of the fractional abundance of molecular hydrogen xH2 is given by the equation (Shang et al. 2010; Sethi et al. 2010) 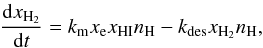(2)where 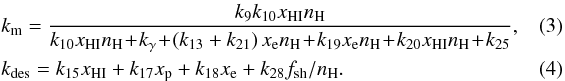Here, km is the net rate of formation of H2 through the H− channel, kdes is the net destruction rate of H2, and kγ is the destruction rate of H− by CMB photons. The reaction rates can be found in Appendix A of Shang et al. (2010), numbered as above. For sufficiently large column densities, H2 can shield itself from radiation in the Lyman-Werner bands. The self-shielding factor fsh is given by Draine & Bertoldi (1996). The updated fsh from Wolcott-Green et al. (2011) results in decreased shielding and may thus enhance our results.

2.2.1. Radiation background

A sufficiently intense UV radiation background can either directly photo-dissociate H2, or photo-dissociate the intermediary H−. The relevant criterion for suppressing H2 formation is that the photo-dissociation timescale must be shorter than the formation timescale, which results in Jcrit ∝ ρ. The intensity is written as J21, which denotes the specific intensity just below 13.6 eV in the units of 10-21  erg cm-2 sr-1 s-1 Hz-1. Here, two different UV spectra are considered. They are both Planck spectra with a blackbody temperature of either T∗ = 104 or 105 K (T4 and T5, respectively). The T4 spectrum is meant to approximate the mean spectrum of a normal stellar population (Pop. II), whereas the T5 spectrum is closer to the harder spectrum expected to be emitted by the first generation of stars (Pop. III; Tumlinson & Shull 2000; Bromm et al. 2001; Schaerer 2002).

2.3. Magnetic field evolution

Gravitational compression and the small-scale dynamo can amplify the magnetic field strength B, while ambipolar diffusion will decrease B. If the flux-freezing condition applies, the magnetic field depends on the density as 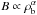, where α lies in the range 2/3–1/2. Hence, B will increase during gravitational collapse. It is assumed that gas is continually falling in, so the turbulence generated by accretion will not decay, but is instead constantly replenished. However, this depends on the ambient gas reservoir and may in reality be more complicated. It has been shown that the injection scale of such accretion-driven turbulence is close to the size of the system under consideration (thus, λJ) (Klessen & Hennebelle 2010; Federrath et al. 2011). The turbulent velocity on the injection scale is expected to be comparable to the velocity of the infalling gas, and for a roughly isothermal density profile, the free-fall velocity is independent of radius. So, while the injection scale changes during the collapse, the injected velocity vin stays the same and is approximately equal to the virial velocity (Greif et al. 2008; Wise & Abel 2007; Wise et al. 2008). On scales smaller than the injection scale, the turbulent velocity is expected to scale as v ∝ lβ, with β = 1/3 for Kolmogorov turbulence (incompressible gas) and β = 1/2 for Burgers turbulence (strongly compressed gas).

The magnetic field on a scale l typically grows exponentially on the eddy turnover time ted = l/v, where v is the turbulent velocity on the scale l. However, the magnetic field will saturate when the magnetic energy corresponds to a fraction 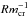of the kinetic energy; Rmcr is the critical magnetic Reynolds number. If Rm > Rmcr, the magnetic field grows through dynamo action. The maximum magnetic field strength is thus given by 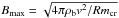(Subramanian & Barrow 1998). However, the exact value of the saturation field strength is still somewhat uncertain. Once B > Bmax on a certain scale, it is no longer amplified by the small-scale dynamo; however, it is still amplified by gravitational compression (∝ρα). It can then in principle increase above the saturation level (which only increases ∝ρ1/2), but in this case it is subject to turbulent decay. On a given scale, this decay will probably also occur on ted. As a result, the magnetic field strength tends to stay close to Bmax on that scale.

The most important contribution to the total magnetic energy comes from the integral scale, the scale on which the magnetic field is largest. Schleicher et al. (2010a) have shown that in an atomic cooling halo, the integral scale increases very rapidly to the maximum scale on which the magnetic field is coherent after the start of the simulation. For this reason, only the evolution of the magnetic field at this scale of maximal coherence is followed here. Since the magnetic field is distorted by the gravitational collapse, the largest possible coherence length is always smaller than the Jeans length by some factor fd; its precise value is uncertain. We adopted a fiducial value of 0.1; changing this by a factor of a few does not significantly affect the results.

Ambipolar diffusion (AD) is important in a mostly neutral medium where a tangled magnetic field is present. The AD heating rate can be estimated as 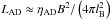(Shang et al. 2002; Schleicher et al. 2008), where ηAD is the AD resistivity (Pinto et al. 2008; Pinto & Galli 2008) and lB is the coherence length of the magnetic field, which is approximated by the minimum of the Alvén damping scale and the integral scale.

The evolution of the magnetic field energy EB = B2/8π is then calculated as 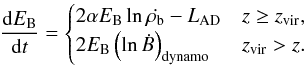(5)

2.4. Thermal evolution

The evolution of the temperature T is given by the equation (see, e.g., Peebles 1993; Sethi et al. 2008) (6)The first term is the adiabatic heating/cooling rate due to collapse/expansion, the second term incorporates various other heating (magnetic energy dissipation by AD and turbulent dissipation, discussed below) and cooling (through H2 and H) volume rates, and the third term represents Compton heating/cooling.

Part of the turbulent energy will go to driving the small-scale dynamo, and part of it will be transferred from large scales to smaller ones in a cascade process, until it is dissipated by viscosity at small enough scales. The rate (per unit mass) at which energy is injected into the system is 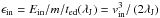(Shu 1992). The volume heating rate from the accretion-driven turbulence (ADT) can then be estimated as LADT = ftρbϵin, where ft is the fraction of the injected energy that is dissipated. Its fiducial value is taken to be 0.1; changing this by a factor of a few does not significantly affect the results.

The model is initialized at a redshift of 800. The dissipation of magnetic fields into the IGM after recombination can significantly influence its temperature and ionization, so this early start provides the proper initial conditions. We follow the evolution of a 109M⊙ halo that virializes at z = 10. The radiation background is switched on at turnaround (z ≈ 15); an earlier or slightly later turn-on is also possible, but does not change the results significantly. The integration is stopped when nb ≈ 107  cm-3. The model is not suitable for higher densities; this would require the inclusion of additional physical processes, e.g., three-body interactions which increase the H2 formation rate.

3. Results

After the radiation background is turned on, H2 is destroyed rapidly. It cannot self-shield as the density is too low; this happens even for a low intensity of J21 = 1. The cooling is dominated by H, so the temperature is high and the ionized fraction becomes elevated, which in turn aids the formation of H2. For intensities that are low enough, H2 succeeds in reforming, and becomes the dominant coolant. The density at which this occurs depends on the radiation intensity, and is higher for higher intensities. However, at a certain intensity H2 cannot reform fast enough to become an important coolant. If turbulence is unimportant and the initial magnetic field is ≤ 0.01  nG (virtually identical to the zero-field case), this critical intensity is found to be 10 < J21 ≤ 102 for a T4 background and 104 < J21 ≤ 105 for a T5 background. Similar results are found for B0 = 1  nG, always assuming α = 2/3. However, if the magnetic field is increased to 2 nG, H2 never becomes an important coolant for a T4 background with J21 = 10, while for J21 = 1 an instability occurs at high densities. Here, the AD heating becomes too strong to be compensated by the H2 cooling and the temperature suddenly increases, because much of the H2 is destroyed by collisional dissociation and H cooling is still very strongly suppressed below ~8 × 103 K. The gas stays hot afterwards, with cooling dominated by H. For a T5 background with the same B0, a similar instability occurs for J21 = 104, while with B0 = 3 nG the H2 fraction is never large enough for significant cooling at this intensity. Thus, when turbulence is not important, a larger initial magnetic field decreases the critical intensity required to keep the gas in the halo hot, as illustrated in Fig. 1.

thumbnail Fig. 1

Gas temperature as a function of density for a T4 background with J21 = 10 (left) and a T5 background with J21 = 104 (right), for several different initial magnetic field strengths (no turbulence). The dotted vertical line indicates virialization.

During collapse, turbulence quickly brings the magnetic field strength to Bmax through the small-scale dynamo, either by amplifying smaller fields or by draining energy from larger fields. Since Bmax only increases as ∝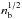, heating from turbulent dissipation always dominates over AD heating, and because H2 cooling grows more steeply with density than turbulent heating does, the gas always cools through H2 when there is no radiation background present. Since heating is dominated by turbulence, halos with different B0 converge to approximately the same evolutionary track; the turbulence has a moderating effect.

The effects of different radiation intensities of a T4 and T5 background on the temperature, electron fraction, and H2 fraction are shown in Fig. 2 for a turbulent halo with B0 = 1  nG. However, the critical intensity does not depend on B0 when turbulent effects are important. The critical intensity is found to be 1 < J21 ≤ 10 for a T4 background and 103 < J21 ≤ 104 for a T5 background.

thumbnail Fig. 2

Gas temperature, electron fraction, and H2 fraction as a function of density for a turbulent halo with B0 = 1  nG, a T4 (left) and a T5 (right) background, and different J21 as indicated in the top panels. The dotted vertical line indicates virialization.

4. Discussion

The effects of magnetic fields and turbulence on the critical intensity of a UV radiation background were examined. Note that these results only hold in a zero or very low metallicity environment, because metals and dust are much more efficient coolants than H2. For a halo not significantly influenced by turbulence or magnetic fields, the critical intensity was found to be 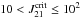for a T4 background, and 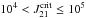for a T5 background. These limits are consistent with those found by Shang et al. (2010) and lower by a factor ~10 than previous estimates by e.g., Omukai (2001) and Bromm & Loeb (2003), most likely as a result of the different H2 dissociation rates used. For B0 = 1  nG, these limits do not change; however, when the field is increased to ~2 nG, the critical intensity is lowered by a factor ~10, and the stronger the field, the lower 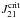. Such magnetic fields alone do not give rise to sufficient AD heating to overcome H2 cooling, but in combination with a radiation background they do influence the ability of the gas to stay hot. Note that the amount of AD heating depends on the scaling of B with ρ; it is therefore important to obtain a correct model for this relationship. The current upper limit on the primordial magnetic field is ~1 nG comoving (Schleicher & Miniati 2011; Trivedi et al. 2012), so a 2 nG field would be reached by the ~2σ upward fluctuations.

In a 109M⊙ turbulent halo, the critical intensity was found to be 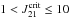for a T4 background, and 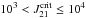for a T5 background; these are a factor ~10 lower than for a halo not affected by turbulence or magnetic fields. Since this is due to the turbulent heating in such halos, larger halos and/or halos with stronger turbulent heating will have an even lower 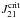. Note that the results for the non-turbulent halos are independent of halo mass. Interestingly, in turbulent halos with M ≳ 1011  M⊙ (depending on the strength of the turbulence), the turbulent heating alone is able to keep the gas hot without any UV background.

The fact that the values of 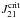that have been found here are smaller than previous estimates is quite important. The mean cosmic UV background is expected to be around 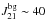, which is smaller than the critical intensities, especially in the case of a T5 background. However, the background will fluctuate spatially, and thus a fraction of all halos will be irradiated by a supercritical intensity. Then, the lower the critical intensity, the larger the fraction of halos which are suitable candidates for direct SMBH formation; e.g., according to the distribution proposed by Dijkstra et al. (2008), a decrease in 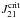from 104 to 103 means an increase in the fraction of irradiated Tvir ≈ 104  K halos from negligibly small (≲10-8) to ~10-6. For 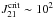, the halo fraction even increases to ~10-3. With a sufficiently low 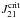, one could argue that this mechanism provided many, if not all, seeds for the SMBHs observed in galaxies today.

Acknowledgments

C. Van Borm acknowledges research funding by the German Science Foundation (DFG) under grant SFB 963/1 (project A12).

References

  1. Begelman, M. C., Volonteri, M., & Rees, M. J. 2006, MNRAS, 370, 289 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bromm, V., & Loeb, A. 2003, ApJ, 596, 34 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bromm, V., Kudritzki, R. P., & Loeb, A. 2001, ApJ, 552, 464 [NASA ADS] [CrossRef] [Google Scholar]
  4. Dijkstra, M., Haiman, Z., Mesinger, A., & Wyithe, J. S. B. 2008, MNRAS, 391, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  5. Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Fan, X. 2006, New A Rev., 50, 665 [Google Scholar]
  7. Federrath, C., Sur, S., Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2011, ApJ, 731, 62 [NASA ADS] [CrossRef] [Google Scholar]
  8. Greif, T. H., Johnson, J. L., Klessen, R. S., & Bromm, V. 2008, MNRAS, 387, 1021 [NASA ADS] [CrossRef] [Google Scholar]
  9. Hocuk, S., Schleicher, D. R. G., Spaans, M., & Cazaux, S. 2012, A&A, 545, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Kazantsev, A. P. 1968, Sov. J. Exp. Theor. Phys., 26, 1031 [Google Scholar]
  11. Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Koushiappas, S. M., Bullock, J. S., & Dekel, A. 2004, MNRAS, 354, 292 [NASA ADS] [CrossRef] [Google Scholar]
  13. Larson, R. B. 1969, MNRAS, 145, 271 [NASA ADS] [CrossRef] [Google Scholar]
  14. Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
  15. Latif, M. A., Schleicher, D. R. G., Schmidt, W., & Niemeyer, J. 2013, MNRAS, submitted [arXiv:1304.0962] [Google Scholar]
  16. Lodato, G., & Natarajan, P. 2006, MNRAS, 371, 1813 [NASA ADS] [CrossRef] [Google Scholar]
  17. Omukai, K. 2001, ApJ, 546, 635 [NASA ADS] [CrossRef] [Google Scholar]
  18. Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton University Press) [Google Scholar]
  19. Penston, M. V. 1969, MNRAS, 144, 425 [NASA ADS] [CrossRef] [Google Scholar]
  20. Pinto, C., & Galli, D. 2008, A&A, 484, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Pinto, C., Galli, D., & Bacciotti, F. 2008, A&A, 484, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Schaerer, D. 2002, A&A, 382, 28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Schleicher, D. R. G., & Miniati, F. 2011, MNRAS, 418, L143 [NASA ADS] [Google Scholar]
  24. Schleicher, D. R. G., Banerjee, R., & Klessen, R. S. 2008, Phys. Rev. D, 78, 083005 [NASA ADS] [CrossRef] [Google Scholar]
  25. Schleicher, D. R. G., Galli, D., Glover, S. C. O., et al. 2009, ApJ, 703, 1096 [NASA ADS] [CrossRef] [Google Scholar]
  26. Schleicher, D. R. G., Banerjee, R., Sur, S., et al. 2010a, A&A, 522, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Schleicher, D. R. G., Spaans, M., & Glover, S. C. O. 2010b, ApJ, 712, L69 [NASA ADS] [CrossRef] [Google Scholar]
  28. Sethi, S. K., Nath, B. B., & Subramanian, K. 2008, MNRAS, 387, 1589 [NASA ADS] [CrossRef] [Google Scholar]
  29. Sethi, S., Haiman, Z., & Pandey, K. 2010, ApJ, 721, 615 [NASA ADS] [CrossRef] [Google Scholar]
  30. Shang, H., Glassgold, A. E., Shu, F. H., & Lizano, S. 2002, ApJ, 564, 853 [NASA ADS] [CrossRef] [Google Scholar]
  31. Shang, C., Bryan, G. L., & Haiman, Z. 2010, MNRAS, 402, 1249 [NASA ADS] [CrossRef] [Google Scholar]
  32. Shu, F. H. 1992, Physics of Astrophysics, Vol. II (University Science Books) [Google Scholar]
  33. Spaans, M., & Silk, J. 2006, ApJ, 652, 902 [NASA ADS] [CrossRef] [Google Scholar]
  34. Subramanian, K., & Barrow, J. D. 1998, Phys. Rev. D, 58, 083502 [NASA ADS] [CrossRef] [Google Scholar]
  35. Trivedi, P., Seshadri, T. R., & Subramanian, K. 2012, Phys. Rev. Lett., 108, 231301 [NASA ADS] [CrossRef] [Google Scholar]
  36. Tumlinson, J., & Shull, J. M. 2000, ApJ, 528, L65 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  37. Widrow, L. M., Ryu, D., Schleicher, D. R. G., et al. 2012, Space Sci. Rev., 166, 37 [NASA ADS] [CrossRef] [Google Scholar]
  38. Wise, J. H., & Abel, T. 2007, ApJ, 665, 899 [NASA ADS] [CrossRef] [Google Scholar]
  39. Wise, J. H., Turk, M. J., & Abel, T. 2008, ApJ, 682, 745 [NASA ADS] [CrossRef] [Google Scholar]
  40. Wolcott-Green, J., Haiman, Z., & Bryan, G. L. 2011, MNRAS, 418, 838 [NASA ADS] [CrossRef] [Google Scholar]
  41. Yahil, A. 1983, ApJ, 265, 1047 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Gas temperature as a function of density for a T4 background with J21 = 10 (left) and a T5 background with J21 = 104 (right), for several different initial magnetic field strengths (no turbulence). The dotted vertical line indicates virialization.
In the text
thumbnail Fig. 2

Gas temperature, electron fraction, and H2 fraction as a function of density for a turbulent halo with B0 = 1  nG, a T4 (left) and a T5 (right) background, and different J21 as indicated in the top panels. The dotted vertical line indicates virialization.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.