| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 6 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201321431 | |
| Published online | 17 May 2013 | |
Connection between dense gas mass fraction, turbulence driving, and star formation efficiency of molecular clouds⋆
1
Max-Planck-Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg
Germany
e-mail:
jtkainul@mpia.de
2 Monash Centre for Astrophysics, School of Mathematical
Sciences, Monash University, Vic 3800, Australia
Received: 7 March 2013
Accepted: 18 April 2013
We examine the physical parameters that affect the accumulation of gas in molecular clouds to high column densities where the formation of stars takes place. In particular, we analyze the dense gas mass fraction (DGMF) in a set of self-gravitating, isothermal, magnetohydrodynamic turbulence simulations that include sink particles to model star formation. We find that the simulations predict close to exponential DGMFs over the column density range N(H2) = 3−25 × 1021 cm-2 that can be easily probed via, e.g., dust extinction measurements. The exponential slopes correlate with the type of turbulence driving and also with the star formation efficiency. They are almost uncorrelated with the sonic Mach number and magnetic-field strength. The slopes at early stages of cloud evolution are steeper than at the later stages. A comparison of these predictions with observations shows that only simulations with relatively noncompressive driving (b ≲ 0.4) agree with the DGMFs of nearby molecular clouds. Massive infrared dark clouds can show DGMFs that agree with more compressive driving. The DGMFs of molecular clouds can be significantly affected by how compressive the turbulence is on average. Variations in the level of compression can cause scatter to the DGMF slopes, and some variation is indeed necessary to explain the spread of the observed DGMF slopes. The observed DGMF slopes can also be affected by the clouds’ star formation activities and statistical cloud-to-cloud variations.
Key words: ISM: clouds / ISM: structure / stars: formation / turbulence
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Star formation is ultimately controlled by the processes that regulate the formation of density enhancements in molecular clouds. In our current picture, the density statistics of the interstellar medium are heavily affected by supersonic turbulence (for a review, see Hennebelle & Falgarone 2012). The density statistics depend on characteristics, such as the total turbulent and magnetic energy (e.g., Padoan et al. 1997a; Nordlund & Padoan 1999; Vázquez-Semadeni & García 2001; Kowal et al. 2007; Molina et al. 2012; Federrath & Klessen 2013, FK13 hereafter), the driving mechanism of the turbulence (e.g., Federrath et al. 2010b; Federrath & Klessen 2012, FK12, hereafter), the equation of state (e.g., Passot & Vázquez-Semadeni 1998; Gazol & Kim 2013), and the driving scale (e.g., Fischera & Dopita 2004; Brunt et al. 2009). Constraining these characteristics is fundamental for virtually all analytic star formation theories.
We have previously employed near-infrared dust extinction mapping in analyzing column density statistics of molecular clouds (Kainulainen et al. 2009, 2011a,b; Kainulainen & Tan 2013, KT13 hereafter). This technique is sensitive and well-calibrated at low column densities, making it suitable to study the molecular cloud mass reservoirs. Exploiting this advantage, we studied how the clouds gather gas to the regime where star formation occurs. We used an easily accessible characteristic to quantify this, namely the dense gas mass fraction1 (DGMF, hereafter), defined as a function that gives the fraction of the cloud’s mass above a column density value 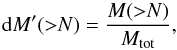 (1)where M(>N) is the mass above the column density N, and Mtot is the total mass. The DGMF is linked to the probability density function (PDF), p(N), of column densities, which gives the column density probability between [N,N + dN], via
(1)where M(>N) is the mass above the column density N, and Mtot is the total mass. The DGMF is linked to the probability density function (PDF), p(N), of column densities, which gives the column density probability between [N,N + dN], via 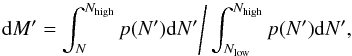 (2)where [Nlow,Nhigh] is the probed column density range. The reason for analyzing DGMFs instead of PDFs is simply the intuitive connection to the total mass reservoir of the cloud. Previously, DGMFs have been analyzed by, e.g., Kainulainen et al. (2009), who show that starless clouds contain much less dense gas than star-forming clouds, and by Lada et al. (2010) who used them to derive a star-formation threshold.
(2)where [Nlow,Nhigh] is the probed column density range. The reason for analyzing DGMFs instead of PDFs is simply the intuitive connection to the total mass reservoir of the cloud. Previously, DGMFs have been analyzed by, e.g., Kainulainen et al. (2009), who show that starless clouds contain much less dense gas than star-forming clouds, and by Lada et al. (2010) who used them to derive a star-formation threshold.
 |
Fig. 1 DGMFs of four simulations (black lines) with ℳs = 10, processed to mimic those observed with a near-infrared dust extinction mapping technique. The solid lines show the DGMFs at t = 0 and the dotted lines at time steps SFE = { 1,3,10 } %. The panels also show with dashed lines the mean DGMF of nearby starless clouds (blue) and of Taurus (Kainulainen et al. 2009, red), and of a sample of IRDCs (KT13, green). |
From the theoretical point-of-view, the form of the DGMF can be controlled by any of the forces affecting the cloud’s density structure. The key parameters describing these forces are2 i) the sonic Mach number, ℳs; ii) the turbulence driving (Federrath et al. 2008, 2010b), which is commonly denoted by b, with b = 1/3 corresponding to purely solenoidal driving and b = 1 to fully compressive driving; and iii) the magnetic field strength, B, reflected by the Alfvén Mach number, ℳA. These parameters relate to density fluctuations via (Nordlund & Padoan 1999; Price et al. 2011; Molina et al. 2012) 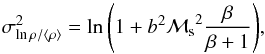 (3)where σlnρ/ ⟨ ρ ⟩ is the standard deviation of logarithmic, mean-normalized densities, and
(3)where σlnρ/ ⟨ ρ ⟩ is the standard deviation of logarithmic, mean-normalized densities, and 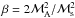 . This form of Eq. (3) (Molina et al. 2012) is valid up to moderate magnetic field strengths, ℳA ≳ 6. The strength of the ℳs – density coupling is very important for analytic star formation theories, because it directly affects the star formation rates and efficiencies (SFE) they predict (e.g., Krumholz & McKee 2005; Hennebelle & Chabrier 2011; Padoan & Nordlund 2011, see FK12).
. This form of Eq. (3) (Molina et al. 2012) is valid up to moderate magnetic field strengths, ℳA ≳ 6. The strength of the ℳs – density coupling is very important for analytic star formation theories, because it directly affects the star formation rates and efficiencies (SFE) they predict (e.g., Krumholz & McKee 2005; Hennebelle & Chabrier 2011; Padoan & Nordlund 2011, see FK12).
In this work, we estimate how the different physical parameters affect the observed DGMFs of molecular clouds. To this goal, we analyze numerical turbulence simulations and derive predictions for observable DGMFs. We then compare the predictions to the results of Kainulainen et al. (2009, 2011b) and KT13 (see also Lada et al. 2010).
2. Simulation data
We analyze a set of magneto-hydrodynamic simulations of isothermal, driven turbulence in a periodic box, including self-gravity and sink particles to follow gas accretion onto protostars (see FK12). Each simulation is a time series that starts (t = 0) when the turbulence is fully developed and the gravity is switched on. Then, the evolution is followed as a function of SFE, defined as the fraction of mass accreted into sink particles. The formation of the first sink particle occurs at SFE = 0%. The sink particles affect their surroundings because of gas accretion, and we eliminated them from the simulations. The issue is described in Appendix A.1. Here we quote the main result: the DGMFs of ℳs = 10 simulations (which we directly compare with observations) with 5123 cells are unaffected by sink particles below N(H2) < 11 × 1021 cm-2. They are 70% accurate up to N(H2) ≈ 25 × 1021 cm-2. We also show in Appendix A.2 that the resolution does not affect the DGMFs in this range.
 |
Fig. 2 Exponential slopes of the DGMFs as a function of b (left), B (center), and ℳs (right). The solid black lines show the time step t = 0, and the dotted lines SFE = { 0,1,...,10 } %. The blue, red, and green shaded regions indicate the slopes observed in starless and star-forming nearby clouds (Kainulainen et al. 2009) and in IRDCs (KT13, however, see the discussion on these data in Sect. 3.2). The median masses of each set of the clouds, M1/2, are shown in the panels. |
The simulations were scaled so that their virial parameters, 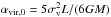 where σv is the 3D velocity dispersion and L the size of the simulation, were close to unity. Observations have shown that molecular clouds, on average, show αvir,0 ≈ 1 (e.g., Heyer et al. 2009). However, this definition is an idealized approximation. The actual virial parameters, αvir = 2|Ekin |/| Epot |, vary by more than an order of magnitude in the simulations. However, the actual virial parameters do not affect density PDFs greatly (FK12). If the virial parameter is “low-enough” to allow some collapse, the density structure is determined by other parameters (FK12; Molina et al. 2012).
where σv is the 3D velocity dispersion and L the size of the simulation, were close to unity. Observations have shown that molecular clouds, on average, show αvir,0 ≈ 1 (e.g., Heyer et al. 2009). However, this definition is an idealized approximation. The actual virial parameters, αvir = 2|Ekin |/| Epot |, vary by more than an order of magnitude in the simulations. However, the actual virial parameters do not affect density PDFs greatly (FK12). If the virial parameter is “low-enough” to allow some collapse, the density structure is determined by other parameters (FK12; Molina et al. 2012).
To make a realistic comparison with observations, we processed the simulations with ℳs = 5−10 to mimic data derived using near-infrared dust extinction mapping (Lombardi & Alves 2001). First, column density data from simulations was regridded to 60″/pixel and smoothed to the FWHM = 120″ resolution (0.09 pc at 150 pc distance). The native resolution of the simulations with ℳs > 10 is coarser than this, and we could not smooth them. We do not compare them with the lower ℳs simulations. Then, the column densities outside N(H2) = [3,25] × 1021 cm-2 were discarded, approximating the dynamic range of extinction mapping. The lower limit of the range was chosen to be high enough that it is possible to define separate structures in simulations using (approximately) closed contours of constant column density. This is because, observationally, clouds are commonly defined in this manner (e.g., Lada et al. 2010). Finally, Gaussian noise with σ(N) = 0.018N(H2) + 0.2 × 1021 cm-2 was added, following typical uncertainties in the data of Kainulainen et al. (2009). This procedure was repeated for three different projections of the simulation data, and the DGMFs from them were averaged to form the final DGMF.
We examined the effects of the resolution and noise to the DGMFs. We experimented with the resolution of 0.03 pc that studies employing Herschel data of nearby clouds will reach (e.g., Schneider et al. 2013). Similar resolution is reached by combined near- and mid-infrared extinction mapping when applied to infrared dark clouds (IRDCs, KT13). The effect of the resolution and noise to the DGMFs was practically negligible.
3. Results and discussion
3.1. Dependence of the DGMF on physical parameters
We derived the DGMFs for the simulations up to SFE = 10%. Figure 1 shows the DGMFs of four simulations with ℳs = 10 and b = { 1/3,0.4,1 }. For the case b = 0.4, both a nonmagnetized and a magnetized simulation are shown. The DGMFs at early stages (t = 0 and SFE = 0%) are well-described by exponential functions, dM′ ∝ eαN. When star formation begins, the DGMFs flatten. Their shapes remain close to an exponential function or curve upwards approaching a powerlaw shape. This behavior is similar in all models. Since the DGMFs are close to exponential functions in the range N(H2) = 3−11 × 1021 cm-2, we quantified their shapes through fits of exponentials. This yielded the range α = [−0.41, −0.023] in all models.
We examined the dependence of the DGMF slopes on the driving of turbulence and magnetic field strength (B) in the simulations with ℳs = 10. The results are shown in Fig. 2 (left and center). Most importantly, the DGMF slope responds most sensitively to the turbulence driving, changing by a factor of 4.8−8.5 when b changes from 1/3 to 1. The slopes clearly depend less on B. The nonmagnetic simulations show significantly shallower slopes than magnetized ones, but if B ≳ 3 μG, the slopes are uncorrelated with it.
The DGMF slopes depend on the SFE. The dependency is stronger in magnetized than in nonmagnetized simulations: the spreads of the slopes in the range SFE = [1,10] % for these cases are 0.09 and 0.03, respectively. The mean difference in the slopes of nonmagnetized and magnetized runs is 0.05. The early stages (t = 0, SFE = 0%) show clearly steeper slopes than the higher SFEs. We also examined the relationship between the DGMF slopes and ℳs. For this, we derived the DGMFs in the native resolution of the simulations (smoothing would greatly reduce the size of the low-ℳs runs). Therefore, the results should be compared to observations with caution. Figure 2 shows the DGMF slopes and ℳs in simulations with b = 1/3. The slopes do not respond to ℳs, except when ℳs = 5.
The DGMFs can vary also due to i) the random nature of turbulence (“cloud-to-cloud” variations) and ii) projection effects. The former can be examined by comparing simulations that have the same input parameters, but different random number seeds (e.g., #12, 14, and 17, see Table A.1). Unfortunately, we only had three simulation pairs with varying random number seeds. The mean difference in the DGMF slopes among these was 0.08 at the early stages (t = 0, SFE = 0%). However, for time steps SFE ≥ 1 the mean difference was only 0.02. The projection effects were studied by examining the standard deviation of the slopes derived for three different projections of all models. The mean standard deviation of the slopes in all models was 0.03.
We note that the effective Reynolds numbers of our simulations (≲104) are lower than that of the interstellar medium (~107). It is not clear how this affects the predicted statistical properties. Aluie (2013) has rigorously shown that the direct influence of driving on the kinetic energy is restricted to scales larger than the smallest scale at which the turbulence is stirred. However, numerical (Federrath et al. 2010b) and analytic (Galtier & Banerjee 2011) works have found differences in flow statistics in the range that can be considered to be the “inertial range” of compressible turbulence simulations. Resolution studies of the simulations suggest that the driving-induced differences remain when the Reynolds number increases. As this issue cannot be addressed with the current computational methods, our results are also subject to it.
3.2. Comparing the predictions with observations
Figures 1 and 2 show observed DGMFs to be compared with the simulated ones. Figure 1 shows the mean DGMF of quiescent clouds (LDN1719, Lupus V, Cha III, and Musca), a DGMF of Taurus that is a typical star-forming cloud (Kainulainen et al. 2009), and a mean DGMF of ten IRDCs from KT13. Figure 2 shows the ranges of the observed slopes from Kainulainen et al. (2009), which span α = [−0.17, −0.45] for 13 nearby star-forming clouds and α = [−0.35, −1.2] for four quiescent clouds. The range of IRDC slopes from KT13 is also shown. We note that the DGMFs of IRDCs in KT13 were derived from a slightly different column density range than those of nearby clouds. They begin from N(H2) ≈ 7 × 1021 cm-2, and therefore, comparing them with the other data should be considered only suggestive.
The dependence of the DGMF slopes on the turbulence driving allows us to constrain b (see Fig. 2). None of the simulations shows the steep slopes observed in starless clouds. From the nonmagnetized simulations, only those with b = 1/3 agree with the nearby star-forming clouds. Magnetic fields can steepen the slopes by about 0.05 (Fig. 2, center). Therefore, from the magnetized runs, those with b = 1/3, or b = 0.4 and B ≥ 3 μG agree with star-forming clouds. The fully compressive simulations produce a much higher fraction of dense gas than observed in nearby clouds. The comparison suggests a low b for nearby molecular clouds on average, possibly lower than previously estimated by Padoan et al. (1997b) and Brunt (2010) in Taurus, b ≈ 0.5.
The DGMF slopes correlate with the SFE, depending on whether the cloud is magnetized or not. Since in the current view, clouds have magnetic fields (Crutcher 2012), the spread of slopes is likely the most realistic in magnetized simulations (i.e., 0.1, see Fig. 2). Thus, it seems that part of the spread in the observed slopes originates in the SFEs of the clouds. We used a Monte Carlo simulation to estimate whether all the variation in the observed slopes can originate from changes in the SFE and statistical variations. We assumed that the changes due to SFE are uniformly distributed between [0,0.1] and the statistical variations are normally distributed with σ = 0.04. The test showed that the probability that 13 clouds span a range >0.28 is 0.2%. However, the range of the observed slopes can be wider. KT13 showed that IRDCs possibly have flatter DGMFs than nearby clouds (Fig. 2). In conclusion, it seems likely that the spread of the observed DGMF slopes cannot be explained by statistical variations and changes in the SFE alone. Changes in the clouds’ average compression provide one possible source to account for this variation.
One interesting question for the future is to examine if the DGMFs correlate with cloud mass. There are no very massive clouds in the nearby cloud sample (median mass 0.5 × 104 M⊙). In contrast, the median mass of the IRDCs is 5 × 104 M⊙, which is ten times higher. This could contribute to the differences seen in the slopes of the two cloud sets, however, as discussed earlier, comparing DGMFs of IRDCs with nearby clouds is not without caveats. The question could be properly addressed by a study of a statistical sample of IRDCs or a study of the nearest high-mass clouds (e.g., Orion, Cygnus, Rosette) employing Herschel data.
The weak dependence of the DGMF slopes on ℳs appears to be an effect of the narrow column density range we examine, even though the results derived from simulations that have differing physical resolutions are only suggestive. The density PDF is expected to respond to ℳs following Eq. (3), which should reflect on the DGMFs. However, it appears that in the range of N(H2) = 3−11 × 1021 cm-2 the effect is insignificant. This result agrees with Goodman et al. (2009), who did not detect any dependence between column density PDF widths and CO linewidths in Perseus. However, we recently measured the column density PDF widths using a high-dynamic-range technique (KT13) and concluded that if a wider range is examined, the PDF widths correlate with ℳs.
When comparing observed DGMFs with simulations, it should be kept in mind that in simulations “driving” is well-defined and ideal: energy is injected on large scales, with certain characteristics such as the divergence and curl. In real clouds, energy is likely injected on multiple scales, and the characteristics of the driving can depend on the scale. However, if some of these driving modes excite more compression than others, particular regions in a cloud, hence also clouds on average, can show characteristics of the flows produced with ideal driving with different mixtures of solenoidal and compressive modes.
Finally, we comment on the relation between the DGMFs and column density PDFs. The column density PDFs of nearby clouds are lognormal below N(H2) ≲ 3 × 1021 cm-2. In the range N(H2) = 3−25 × 1021 cm-2, they agree with either powerlaws or (wide) lognormals (KT13). The PDF shapes above N(H2) ≳ 3 × 1021 cm-2 are not well-constrained. They may be either lognormals (KT13) or powerlaws (Schneider et al. 2013, see Fig. B.1). It follows from Eq. (2) that a lognormal PDF yields an exponential DGMF and a powerlaw PDF yields a powerlaw DGMF. The simulated DGMFs appear exponential in the range N(H2) ≳ 3−25 × 1021 cm-2 at the early stages. Therefore, the column density PDFs are close to lognormals. When the simulations evolve, the DGMFs become closer to powerlaws. This means that the underlying column density PDF transits from a lognormal to a powerlaw.
4. Conclusions
We have examined the relationship between the dense gas mass fraction (DGMF), star formation, and turbulence properties in molecular clouds by comparing DGMFs derived from isothermal, magneto-hydrodynamic, self-gravitating turbulence simulations to observed ones. Our conclusions are as follows.
-
1.
Simulations predict close-to exponential DGMFsfor molecular clouds in the column density range ofN(H2) = 3−11 × 1021 cm-2. The DGMF slopes span the range α = [−0.41, −0.023], and they are clearly steeper at the early stages of the simulations compared to the stages when stars are forming (SFE ≥ 1%). These predictions are accurate on a 70% level up to N(H2) ≈ 25 × 1021 cm-2.
-
2.
The DGMF slopes depend strongly on the turbulence driving (b). They depend less, but significantly, on the exact SFE. The dependence on the SFE is stronger in magnetized than nonmagnetized cases. Generally, the effect of the magnetic field to the DGMF is small. Also ℳs has a negligible effect on the slopes in the examined column density range. The statistical variations are comparable to those arising from varying SFE. However, how compressive the turbulence is (i.e., parameter b) is the largest single factor in determining the slope of the DGMF in the simulations.
-
3.
The observed DGMFs can be used to constrain the turbulence-driving parameter b. The DGMFs of nearby clouds are only reproduced by simulations that are driven by relatively noncompressive forcing, i.e., b = 1/3 or 0.4. The fully compressive simulations (b = 1) overestimate the DGMFs greatly. Massive IRDCs can show flatter DGMFs that are in agreement with more compressive driving. The spread of the observed DGMFs cannot be explained by different SFEs and statistical variations alone. Variations in the clouds’ average compression level offer one explanation to account for the observed spread.
Online material
Appendix A: Numerical effects on the DGMFs
Appendix A.1: Effect of sink particles
Simulation properties (adapted from FK13).
Sink particles (Federrath et al. 2010a) in the simulations accrete material into them after their creation and affect the density structure of their immediate surroundings in the simulation (and the DGMFs). In the following, we consider the effects of sink particles to the DGMFs.
As described in FK12, the sink particles are created on a certain, resolution-dependent volume density and always have a radius of 2.5 pixels in the native resolution of the simulation. It follows that the sink particles have a resolution-dependent minimum density, which can be converted further into a minimum mean column density. Sink particles are created when a series of collapse criteria are fulfilled (see FK12), and when the local volume density exceeds 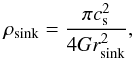 (A.1)where cs is the isothermal speed of sound and rsink the radius of the sink particle. It follows that the mean column density of a sink particle at the moment of its creation is
(A.1)where cs is the isothermal speed of sound and rsink the radius of the sink particle. It follows that the mean column density of a sink particle at the moment of its creation is 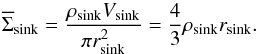 (A.2)The sink particle properties are listed in Table A.1 for different physical resolutions.
(A.2)The sink particle properties are listed in Table A.1 for different physical resolutions.
The sink particle column densities listed in Table A.1 represent levels below which the DGMFs are not affected by sink particles, regardless of whether the sinks are removed or not. In the most conservative interpretation, the DGMFs are reliable only below these column density limits. Therefore, we use the upper limit of N(H2) = 11 × 1021 cm-2, which is the sink particle column density for the ℳs = 10 simulations 5123 cells in size, in the analysis performed in this paper.
However, it is not at all certain that the DGMF shape immediately above N(H2)sink is greatly affected by the sink particles. Above N(H2)sink, there are lines-of-sight whose column density is higher than the sink particle column density, but the local volume densities do not reach high enough values for sink particles to form. In fact, these lines-of-sight are more numerous in the simulations compared to those that contain sinks, especially at early times when the overall SFE is low.
We dealt with sink particles in this work by disregarding the lines-of-sight affected by them directly from the simulation data. While this procedure, in principle, eliminates the effects of sink particles, it removes mass from high column densities and can bias the DGMF downwards (steepen it). Consequently, it is important to note that the flattening of the DGMFs seen in the simulations (see Sect. 3.1) at around N(H2) ≈ 10−15 × 1021 cm-2 cannot be due to sink particle treatment, any associated incompleteness would bias the determination downwards, not upwards.
We can quantify the incompleteness due to sink particle removal by comparing DGMFs derived with and without the elimination of sink particles. This experiment is shown in Fig. A.1, which shows the ratio of the DGMFs with and without the sink particle elimination as a function of column density. The plot is shown for the model in which the effect of sinks in the examined column density range is expected to be strongest, i.e., the solenoidal simulation with 2563 cell resolution. Higher resolution increases the sink particle column density (cf. Table A.1), and more compressive forcing increases the relative amount of high column densities, thereby reducing the error in the examined column density regime. The figure shows that the error due to incompleteness (i.e., removal of high-column densities) is less than 30% below N(H2) ≲ 25 × 1021 cm-2 for SFEs up to 10%.
In summary, it can be concluded that the DGMFs derived for ℳs = 10 simulations are unaffected by the sink particles (or by their removal) below the N(H2)sink values. In addition, the error in the predicted DGMFs is less than 30% when the range up to N(H2) ≈ 25 × 1021 cm-2 is considered.
Appendix A.2: Effect of the simulation resolution
The simulations of FK12 are either 1283, 2563, 5123, or 10243 computational cells in size. In this work, we used all but those simulations that are 1283 cells in size. It is possible that the different computational resolutions used in the simulations affect the DGMFs, because especially high column densities are potentially better resolved by high-resolution simulations. We examined the possible effect of the simulation resolution to the DGMFs by comparing the DGMFs of simulations that were run with the same physical parameters, but have different computational resolution.
Figure A.2 shows as an example a comparison of DGMFs derived for models #10 and #11 that are 2563 and 5123 cells in size, respectively. All other parameters are same in these two models. The DGMF of model #10 is in good agreement with that of model #11 below the sink particle column density, N(H2) = 11 × 1021 cm-2. At higher column densities, the lower resolution simulation (#10) begins to underestimate the column densities slightly. However, it is still within 30% of the higher resolution one up to the column density of N(H2) ≈ 25 × 1021 cm-2. We conclude that the effect of resolution is less than the uncertainty due to the projection effects in the column density range N(H2) = 11 × 1021 cm-2 and accurate to 70% level up to N(H2) = 25 × 1021 cm-2.
 |
Fig. A.1 Error (incompleteness) in the derived DGMFs due to removal of sink particles. The figure shows the ratio of DGMFs derived with and without sink particle removal as a function of column density for time steps up to SFE = 10%. The curves for t = 0 and SFE = 0% are indistinguishable from unity. The plot is shown for simulation #10 (ℳs = 10, 2563 cells in size, b = 1/3). The error in other ℳs = 10 models is expected to be smaller, because of the higher sink particle column density and more compressive turbulence driving. |
 |
Fig. A.2 Effect of simulation resolution to the DGMFs. The red line shows the DGMF of simulation #10 (2563 cells in size) divided by the DGMF of simulation #11 (5123 cells in size). The physical parameters of the two simulations are the same. The dashed lines show the DGMFs calculated for different projections of model #11 divided by the mean DGMF of model #11. |
Appendix B: Illustration of column density PDFs
 |
Fig. B.1 Column density PDFs of models #11 (b = 1/3) and #24 (b = 1), and the PDF of the Taurus molecular cloud. Both models have ℳs = 10 and B = 0 μG, and they are 5123 computational cells in size. The black histograms show the PDFs of model #11 at t = 0 (solid line) and SFE = 5% (dotted line). The blue line shows the PDF of model #24. The red line shows the PDF of Taurus from Kainulainen et al. (2009). The dynamic range of the Taurus PDF ends at about lnN(H2) = 3.2. The black dashed line shows, for reference, a lognormal function. The PDFs in the range N(H2) = 3−11 × 1021 cm-2 can be described by a lognormal function, but also reasonably well by a powerlaw function (which would be a linear curve in the given presentation). |
Figure B.1 show a comparison of the column density PDFs derived for models #11 and #24, and the PDF of the Taurus molecular cloud from Kainulainen et al. (2009). The higher relative amount of high-column density material predicted by fully compressive simulations (#24) causes a flatter PDF. In the column density range N(H2) = 3−25 × 1021 cm-2, the PDF of simulation #11 is close to what is observed in Taurus. In this narrow range, the PDF is in reasonable agreement with either a lognormal function (shown for a reference in the figure) or a powerlaw function.
However, see the discussion on the caveat related to the simulation Reynolds numbers in Sect. 3.1.
Acknowledgments
The work of J.K. was supported by the Deutsche Forschungsgemeinschaft priority program 1573 (“Physics of the Interstellar Medium”). C.F. acknowledges a Discovery Projects Fellowship from the Australian Research Council (grant DP110102191).
References
- Aluie, H. 2013, Physica. D Nonlinear Phenomena, 247, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M. 2010, A&A, 513, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brunt, C. M., Heyer, M. H., & Mac Low, M.-M. 2009, A&A, 504, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 156 (FK12) [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 (FK13) [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Banerjee, R., Clark, P. C., & Klessen, R. S. 2010a, ApJ, 713, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., et al. 2010b, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischera, J., & Dopita, M. A. 2004, ApJ, 611, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Galtier, S., & Banerjee, S. 2011, Phys. Rev. Lett., 107, 134501 [NASA ADS] [CrossRef] [Google Scholar]
- Gazol, A., & Kim, J. 2013, ApJ, 765, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Pineda, J. E., & Schnee, S. L. 2009, ApJ, 692, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2011, ApJ, 743, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53, KT13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Alves, J., Beuther, H., et al. 2011a, A&A, 536, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., et al. 2011b, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kowal, G., Lazarian, A., & Beresnyak, A. 2007, ApJ, 658, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molina, F. Z., Glover, S. C. O., Federrath, C., & Klessen, R. S. 2012, MNRAS, 423, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å. K., & Padoan, P. 1999, in Interstellar Turbulence, Proc. Conf. (CUP), 218 [Google Scholar]
- Padoan, P., & Nordlund, Å. 2011, ApJ, 730, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Nordlund, A., & Jones, B. J. T. 1997a, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Jones, B. J. T., & Nordlund, A. P. 1997b, ApJ, 474, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Federrath, C., & Brunt, C. M. 2011, ApJ, 727, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., & García, N. 2001, ApJ, 557, 727 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 DGMFs of four simulations (black lines) with ℳs = 10, processed to mimic those observed with a near-infrared dust extinction mapping technique. The solid lines show the DGMFs at t = 0 and the dotted lines at time steps SFE = { 1,3,10 } %. The panels also show with dashed lines the mean DGMF of nearby starless clouds (blue) and of Taurus (Kainulainen et al. 2009, red), and of a sample of IRDCs (KT13, green). |
| In the text | |
 |
Fig. 2 Exponential slopes of the DGMFs as a function of b (left), B (center), and ℳs (right). The solid black lines show the time step t = 0, and the dotted lines SFE = { 0,1,...,10 } %. The blue, red, and green shaded regions indicate the slopes observed in starless and star-forming nearby clouds (Kainulainen et al. 2009) and in IRDCs (KT13, however, see the discussion on these data in Sect. 3.2). The median masses of each set of the clouds, M1/2, are shown in the panels. |
| In the text | |
 |
Fig. A.1 Error (incompleteness) in the derived DGMFs due to removal of sink particles. The figure shows the ratio of DGMFs derived with and without sink particle removal as a function of column density for time steps up to SFE = 10%. The curves for t = 0 and SFE = 0% are indistinguishable from unity. The plot is shown for simulation #10 (ℳs = 10, 2563 cells in size, b = 1/3). The error in other ℳs = 10 models is expected to be smaller, because of the higher sink particle column density and more compressive turbulence driving. |
| In the text | |
 |
Fig. A.2 Effect of simulation resolution to the DGMFs. The red line shows the DGMF of simulation #10 (2563 cells in size) divided by the DGMF of simulation #11 (5123 cells in size). The physical parameters of the two simulations are the same. The dashed lines show the DGMFs calculated for different projections of model #11 divided by the mean DGMF of model #11. |
| In the text | |
 |
Fig. B.1 Column density PDFs of models #11 (b = 1/3) and #24 (b = 1), and the PDF of the Taurus molecular cloud. Both models have ℳs = 10 and B = 0 μG, and they are 5123 computational cells in size. The black histograms show the PDFs of model #11 at t = 0 (solid line) and SFE = 5% (dotted line). The blue line shows the PDF of model #24. The red line shows the PDF of Taurus from Kainulainen et al. (2009). The dynamic range of the Taurus PDF ends at about lnN(H2) = 3.2. The black dashed line shows, for reference, a lognormal function. The PDFs in the range N(H2) = 3−11 × 1021 cm-2 can be described by a lognormal function, but also reasonably well by a powerlaw function (which would be a linear curve in the given presentation). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


