| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321053 | |
| Published online | 17 May 2013 | |
RX J0440.9 + 4431: a persistent Be/X-ray binary in outburst
1 ISDC Data Center for Astrophysics, Université de Genève, chemin d’Écogia 16, 1290 Versoix, Switzerland
e-mail: Carlo.Ferrigno@unige.ch
2 Dipartimento di Fisica, Università di Ferrara, via Saragat 1, 44100 Ferrara, Italy
3 CRESST & University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA
4 NASA Goddard Space Flight Center, Astrophysics Science Division, Code 661, Greenbelt, MD 20771, USA
5 IAAT, Abt. Astronomie, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
6 ESAC, ISOC, Villañueva de la Cañada, Madrid, Spain
Received: 7 January 2013
Accepted: 15 March 2013
The persistent Be/X-ray binary RX J0440.9 + 4431 flared in 2010 and 2011 and has been followed by various X-ray facilities (Swift, RXTE, XMM-Newton, and INTEGRAL). We studied the source timing and spectral properties as a function of its X-ray luminosity to investigate the transition from normal to flaring activity and the dynamical properties of the system. We have determined the orbital period from the long-term Swift/BAT light curve, but our determinations of the spin-period are not precise enough to constrain any orbital solution. The source spectrum can always be described by a bulk-motion Comptonization model of black body seed photons attenuated by a moderate photoelectric absorption. At the highest luminosity, we measured a curvature of the spectrum, which we attribute to a significant contribution of the radiation pressure in the accretion process. This allows us to estimate that the transition from a bulk-motion-dominated flow to a radiatively dominated one happens at a luminosity of ~2 × 1036 erg s-1. The luminosity dependency of the size of the black body emission region is found to be rBB ∝ LX0.39±0.02 . This suggests that either matter accreting onto the neutron star hosted in RX J0440.9 + 4431 penetrates through closed magnetic field lines at the border of the compact object magnetosphere or that the structure of the neutron star magnetic field is more complicated than a simple dipole close to the surface.
Key words: X-rays: binaries / X-rays: individuals: RX J0440.9+4431 / stars: neutron
© ESO, 2013
1. Introduction
LS V +44 17/RX J0440.9+4431 was classified as one of the rare persistent neutron star Be/X-ray binaries based on the outcomes of the first dedicated RXTE monitoring campaign performed by Reig & Roche (1999). The source distance was later estimated at (~3.3 ± 0.5) kpc by Reig et al. (2005). RX J0440.9+4431 is also reported in the seven-year and nine-year INTEGRAL all-sky survey (Krivonos et al. 2010b, 2012). From the former to the latter catalog, the average flux of the source increased from (0.95 ± 0.15) mCrab to (4.0 ± 0.1) mCrab1 (17–60 keV) as it underwent several episodes of enhanced X-ray activity in 2010 and 2011 (see later in this section). The flux estimate given in the seven-year catalog is consistent with what has been measured previously by Reig & Roche (1999) and can thus be considered as the persistent level of the source. A similar flux (0.9 ± 0.5) mCrab2 was also reported in the 54-month Palermo BAT Survey in the 15–150 keV band (Cusumano et al. 2010).
The first observed outburst from RX J0440.9 + 4431, which we are aware of, was detected on 2010 March 26, and lasted until April 15 (Morii et al. 2010; Finger & Camero-Arranz 2010). The Swift/BAT light curve (Fig. 1) showed that the source reached a peak luminosity of about 200 mCrab (15–150 keV) six days after the onset of the event. It remained in this state for eight days, and then turned off to its persistent luminosity level in about ten days. The outburst was also observed by the RXTE All Sky Monitor (2–10 keV, ASM). In the ASM light curve, the source reached about 10 cts/s (i.e., ~130 mCrab). A detailed study of the first outburst from RX J0440.9 + 4431 was presented by Usui et al. (2012). The authors show that the broad-band spectrum of the source could be described well by a combination of a black body component, a cut-off power law, and an iron line with a centroid energy of ~6.4 keV. They also find a pronounced dip in the pulse profile interpreted as being due to obscuration of the X-ray emission from the neutron star by the accretion stream.
A second outburst from RX J0440.9 + 4431 was detected by INTEGRAL on 2010 September 1 (Fig. 1). The measured average and peak fluxes during the event were ~30 mCrab and (77 ± 17) mCrab (17–60 keV), respectively (Krivonos et al. 2010a). The Swift/BAT and RXTE/ASM light curves showed that the outburst had a rise and decay time of about five days, with a compatible peak luminosity of ~80 mCrab. The analysis of the combined Swift, INTEGRAL, and RXTE data led to identifying a possible cyclotron absorption feature at ~30 keV, suggesting a surface magnetic field of B ≃ 3 × 1012 G for the accreting neutron star hosted in this system. This magnetic field intensity would be compatible with the measured properties of the source broad-band noise in the X-ray domain (Tsygankov et al. 2012).
The two intense X-ray emission episodes recorded from RX J0440.9 + 4431 showed the typical properties of the so-called “Type I” outbursts, usually displayed when the neutron star in a Be/X-ray binary approaches the system periastron and interacts with the companion equatorial disk. The presence of a neutron star in RX J0440.9 + 4431 is secured by the detection of pulsations in its persistent and outburst emission. The measured pulse period increased from ≈ 202 s in 1999 (Reig & Roche 1999) to ≈ 206 s during the latest observations, thus evidencing an average spin down trend. The first estimate of the source orbital period was reported by Reig (2011) at ~150 d using the orbit-to-spin period relation for Be/X-ray binaries. This period would be compatible with the recurrence time of the source outbursts (150–160 d Morii et al. 2010; Krivonos et al. 2010a; Tsygankov et al. 2012).
A deep (20 ks) XMM-Newton observation of RXJ0440.9+ 4431 was carried out on 2011 March 18 to study the properties of its persistent emission (La Palombara et al. 2012). During this observation, the source displayed an average flux of 6 × 10-11 erg cm-2 s-1 (0.3–12 keV) and the corresponding spectrum could be well described using a power law plus a black body model. The estimated radius for the thermal emission component was compatible with the size of a hot-spot on the surface of a strongly magnetized neutron star (~1012 G). Pulsations at ≈ 205 s were detected throughout the observation. No significant spectral variability with the spin phase could be measured, although an indication of hardening was found at the pulse minimum.
In this paper, we report on the last detected outburst from the source which occurred on February 2011 (Fig. 1). On this occasion, we triggered our pre-approved RXTE target of opportunity observations and performed a simultaneous monitoring campaign at the softer X-ray energies with Swift/XRT to study the evolution of the source spectrum with luminosity and improve the measurement of the source orbital period. We have also re-analyzed all available RXTE, Swift/XRT, XMM-Newton, and INTEGRAL (Bradt et al. 1993; Gehrels et al. 2004; Jansen et al. 2001; Winkler et al. 2003) observations performed in the direction of RX J0440.9 + 4431 in 2010 and 2011 to compare the source emission properties across two orders of magnitude in luminosity. The data analysis technique is described in Sect. 2, and all the results are reported in Sect. 3. Our discussions and conclusions are given in Sects. 4 and 5, respectively.
 |
Fig. 1 Light curve of RX J0440.9 + 4431 and times of the observations reported in this paper. Black points with errors: Swift/BAT daily averaged light curve. Red vertical bars: times of the RXTE observations. Blue horizontal bar: time span of the INTEGRAL data used in this paper. Green diamonds: times of the Swift observations used in our analysis. The first vertical yellow bar indicates the occurrence of the first maximum in the light curve; the others correspond to the times of the following maxima predicted by our orbital period determination. MJD 55 280, 55 430, and 55 580 correspond to 2010, March 25, 2010, August 22, and 2011, January 19, respectively. |
2. Data analysis
We have analyzed RXTE and Swift data using the heasoft software package (v. 6.12) while all spectral fits have been performed using XSPEC version 12.6.0u (Arnaud 1996).
For RXTE, we have followed the suggested analysis threads3 and we considered only PCA (2–60 keV, Jahoda et al. 1996) data from the PCU2 unit, which was always active. Good time intervals (GTI) were created by imposing that at least 30 min passed after the satellite exited the SAA, and the elevation on the Earth limb was ≥ 10°. We additionally imposed an electron ratio ≤ 0.15 and modeled the background using the provided estimator v3.8. Events were extracted in the mode GoodXenon (time resolution 0.95 μs and 255 energy channels). The instrument specific response matrices were generated taking into account the corrected energy bounds and the gain corrections performed by the EDS. The average PCA spectrum was obtained from the standard2 mode without further rebinning and fitted above standard channel 4 (~3 keV) up to the higher energy at which the source signal was detectable (i.e., about 20 keV, for short observations or faint source states, higher otherwise). Spectra were assumed to have a systematic uncertainty of 0.5%, as recommended by the instrument team4.
For Swift/XRT (0.5–11 keV), we followed standard analysis procedures (Burrows et al. 2005) and considered both window timing (WT) and photon counting (PC) data, but limited our spectral range to 0.8–10 keV to avoid calibration uncertainties. XRT spectra were grouped to have at least 50 counts in each energy channel using grppha. We extracted separated spectra for data accumulated in each satellite orbit and used the proper exposure map to account for bad columns, hot pixels, vignetting, and PSF losses.
We extracted the source spectrum from the INTEGRALIBIS/ISGRI (20–100 keV, Ubertini et al. 2003) and JEM-X (5–30 keV, Lund et al. 2003) data of the 2010 outburst taken from 2010, September 1 to September 10 using the Off-line Science Software (OSA, v.10) distributed by the ISDC (Courvoisier et al. 2003). The JEM-X spectrum is extracted in the standard 16 bins defined in OSA, while the IBIS/ISGRI one in user defined 62 bins.
XMM-Newton data have been processed using XMM Science Analysis System (SAS) version 12.0.1. We have extracted only the EPIC-PN (0.5–10 keV, Strüder et al. 2001) spectrum from a region of 0.6 arcmin centered on the source. Background and pile-up corrections were neglected (La Palombara et al. 2012). The spectrum was adaptively re-binned using the SAS tool specgroup in order to have at least 25 counts per energy bin and, at the same time, to prevent oversampling of the energy resolution by more than a factor of three.
3. Results
3.1. Orbital period
To search for the source orbital period, we exploited the daily averaged light curve obtained from the hard X-ray transient monitor page of Swift/BAT5. These data cover almost continuously the time interval MJD 53 414–56 282 (2005 February 13 – 2012 December 31), owing to the large field of view of the instrument and the spacecraft pointing strategy. We first used the Lomb-Scargle periodogram method in the range 32–200 days. The highest significance period is found at ~150 days. We have also exploited the epoch folding technique on the same data by assuming 32 phase bins and assigning weights of 1/σ2 to the individual bins (here σ is the reported uncertainty on the source count rate). The most prominent peak (χ2 = 942) is found also in this case at ~150 days with evident harmonics at multiple frequencies (see inset in Fig. 2). We have refined our determination of the orbital period by limiting our search with the above methods around the most significant peak and using 130 phase bins. The best value is found at (150.0 ± 0.2) days. The uncertainty at 68% c.l. on this measurement is obtained by bootstrapping 1000 light curves with count rates randomly distributed within the uncertainty of the measurements, and then computing the standard deviation of the period determinations. We have folded the light curve at this period and obtained the profile shown in Fig. 2. This is reminiscent of what is usually observed from Be/X-ray binaries, with most of the emission concentrated during the periastron passage (phase 0.6 in the figure). We have fit the folded light curve with a constant plus a Gaussian to estimate the time of the light curve maximum. The Gaussian is centered at orbital phase 0.641 ± 0.001, which can be converted into the time of occurrence of the first flare by taking into account the best orbital period: it corresponds to MJD 55 293.2 ± 0.3, i.e., the time of the brightest flare observed so far from RX J0440.9 + 4431. We have plot this time interval in Fig. 1, left section, as a vertical shaded region. We have then propagated the uncertainty on the orbital period to the following two flares observed in our campaign and plot them as shaded regions in the other two sections of the light curve.
Interestingly, when limiting ourselves to the time range before MJD 55 280 (2010 March 25), the orbital modulation was not detectable and no prominent peaks are clearly visible over the red noise. This indicates that the X-ray active phase of the source began only in April 2010 when it was detected in outburst for the first time, since the availability of modern X-ray monitors.
 |
Fig. 2 Folded Swift/BAT light curve (15–150 keV) of RXJ0440.9+4431 at the best determined orbital period, (150.0 ± 0.2) days. The inset shows the periodogram obtained from the epoch folding technique applied to the Swift/BAT light curve. |
3.2. Timing analysis and spin period measurements
To search for the ~200 s source spin period and its possible variations, we performed a timing analysis of all RXTE data (event mode GoodXenon). Swift pointings were on average too short to perform a similar analysis. We first extracted the background corrected PCA light curves in the 3–35 keV energy range (time bin 2 s), and barycenter-corrected them using the known optical position (Reig et al. 2005). For each observation we removed the variability on time scales longer than the expected pulsed signal6 and determined the pulse period with the epoch folding technique.
We obtained the best determined period for all the available RXTE observations using an optimal number of phase bins (from 16 to 64 depending on the S/N), and estimated the uncertainties by running 100 simulations of the input light curves with rates estimated from Poisson distributions centered on the real measured values. The results are reported in Table 1. Some variability in the measured values is evident from the table, but the limited number and accuracy of our determinations are not sufficient to disentangle unambiguously the effects of the orbital motion and/or possible accretion torques.
Measurements of the spin period of RX J0440.9 + 4431 obtained from all the RXTE observations analyzed in the present work.
Log of observations of the 2010-2011 outbursts used in this paper.
3.3. Broad-band spectral analysis
The availability of quasi-simultaneous INTEGRAL, RXTE, and Swift data permitted to investigate the broad-band spectral properties of RX J0440.9 + 4431 (note that part of the data were already presented: Tsygankov et al. 2012; Usui et al. 2012). The broad-band quasi-simultaneous data set is shown in Table 2 with a conventional ID of the corresponding multi-instrument observations: A, S, 1, 2, 3, 4. For the INTEGRAL data reduction we took advantage of the most updated IBIS/ISGRI calibrations included in the OSA v.107.
To compare our findings with those reported previously by Tsygankov et al. (2012), and test the effect of the improved INTEGRAL calibrations, we used the same data set as in the above paper (INTEGRAL data from MJD 55 440–55 449, RXTE/PCA data from OBSID 95418-01-03-00 and Swift/XRT pointing OBSID 00031690003, i.e., observation S in Table 2). We restricted the selection of pointings to a maximum off-axis angle of 7° to minimize the systematic uncertainties on the IBIS instrumental response. The total effective exposure time of the final IBIS/ISGRI spectrum was 56 ks. This corresponds to an effective exposure time for JEM-X2 of 64 ks (owing to the lower dead-time of the detector).
A spectral model comprising a cut-off power law and a black body component could fit the data reasonably well (χ2/d.o.f. = 1.09/558). Normalization constants (fixed to 1 for Swift/XRT) were also included in the fit to account for source variability and instrument inter-calibrations. Photoelectric absorption is accounted for using the model phabs with abundances from Anders & Grevesse (1989). Some residuals are present at ≳ 30 keV, as reported by Tsygankov et al. (2012). However, we found that an additional Lorentzian absorption feature with σ = 6 keV at ~ 30 keV, as proposed by these authors, did not significantly improve the fit (χ2/d.o.f. = 1.05/556, 33% chance improvement probability).
Best fit parameters for the absorbed bmc with exponential cut-off model for the broad band spectral fits of the 2010 outburst (uncertainties are at 90% c.l.).
A better description of the spectrum could be obtained by using the general Comptonization model bmc (Titarchuk et al. 1997) with an exponential cutoff at high energy (bmc × exp(−E/EFold), χ2/d.o.f. = 0.92/559). Because of the general shape of the convolutional kernel, this model can be applied to Comptonization spectra of both optically thin and optically thick regimes, and considering the cases in which thermal or thermal plus bulk Comptonization dominate (Farinelli et al. 2013). The emerging spectrum of the bmc model can be expressed as ![\begin{eqnarray} \label{eq:bmc} F(E)=\frac{N_{\rm BMC}}{1+A}\left[ S(E) + A S(E) \ast G(E,E_0)\right], \end{eqnarray}](/articles/aa/full_html/2013/05/aa21053-13/aa21053-13-eq103.png) (1)where G(E,E0) is the Green’s function of the Componization energy operator, and S(E) is the seed photon black body spectrum. The quantity A/(A + 1) empirically provides the fraction of seed photons which are Compton scattered; it is related to the geometrical configuration of the system and to the seed photon spatial distribution in the Comptonization region. Actually, log 10(A) is the model parameter returned by XSPEC. The Green’s function G(E,E0) is a broken powerlaw ∝ Eα + 3 for E < E0 and ∝ E − α for E > E0. The value of the powerlaw energy index α is related to the efficiency of the Comptonization process. From the normalization of the model, it is possible to infer the effective radius of the region in which the seed black body radiation is generated by using the relation
(1)where G(E,E0) is the Green’s function of the Componization energy operator, and S(E) is the seed photon black body spectrum. The quantity A/(A + 1) empirically provides the fraction of seed photons which are Compton scattered; it is related to the geometrical configuration of the system and to the seed photon spatial distribution in the Comptonization region. Actually, log 10(A) is the model parameter returned by XSPEC. The Green’s function G(E,E0) is a broken powerlaw ∝ Eα + 3 for E < E0 and ∝ E − α for E > E0. The value of the powerlaw energy index α is related to the efficiency of the Comptonization process. From the normalization of the model, it is possible to infer the effective radius of the region in which the seed black body radiation is generated by using the relation 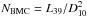 (here L39 is the luminosity in units of 1039 erg/s and D10 the distance in units of 10 kpc):
(here L39 is the luminosity in units of 1039 erg/s and D10 the distance in units of 10 kpc): 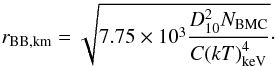 (2)Here C = 1 for a spherical geometry and C = 0.25 for a circular slab. Assuming for RX J0440.9 + 4431 a distance of 3.3 kpc, the relation above can be written as
(2)Here C = 1 for a spherical geometry and C = 0.25 for a circular slab. Assuming for RX J0440.9 + 4431 a distance of 3.3 kpc, the relation above can be written as 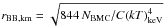 .
.
The best fit parameters obtained using the absorbed bmc with exponential cut-off model are reported in Table 3. We found that this description of the source continuum emission permitted to constrain the optical depth of the previously suggested Lorentzian shaped absorption feature to <0.1 (see the residuals from the best fit in in Fig. 3).
 |
Fig. 3 Broad-band spectrum of the quasi-simultaneous INTEGRAL/ISGRI (green), INTEGRAL/JEM-X2 (blue), RXTE/ PCA (red), and Swift/XRT (black) observations performed in September 2010. The best fit is obtained with the absorbed bmc with exponential cut-off model. The residuals from this fit are also shown in the bottom panel. |
To test further the applicability of the spectral model introduced above to RX J0440.9 + 4431, we carried out a second fit to the quasi-simultaneous Swift/XRT and RXTE/PCA observations performed in April 2010 (observation A in Table 2). At this epoch, the source was brighter (F2−30 keV ≃ 3.8 × 10-9 erg s-1 cm-2) than in observation S, PCA data could be used from 3 to 45 keV and an iron line was needed to fit the data (we modeled this as a thin additional Gaussian component centered at ~6.4 keV; Usui et al. 2012). No evidence was found for the Lorentzian shaped absorption feature (width 6 keV, centroid energy < 42 keV) suggested by Tsygankov et al. (2012). We obtained a 90% c.l. upper limit of 0.03 on its optical depth. We also note that Usui et al. (2012) did not find evidence of any absorption feature in the combined RXTE/PCA and HEXTE spectrum of the source. We conclude that the absorption feature reported by Tsygankov et al. (2012) was probably due to systematic biases in the joint analysis of data from several instruments and/or a inadequate modeling of the continuum emission.
 |
Fig. 4 Results of the spectral fits to the RXTE/PCA observations (filled circles) performed during the outbursts of RX J0440.9 + 4431 occurred in 2010 and 2011 (Table 2). The best fit spectral parameters obtained from the XMM-Newton observation (2011 March 18) are also included and represented with a star (uncertainties are at 68% c.l. and lower limits at 90% c.l.).The bmc model was used for all fits, but during the two observations performed when the source reached the highest flux, an exponential cut-off at high energy was needed to properly fit the data (see Sect. 3.4). The black body radius rBB is obtained from Eq. (2) setting C = 1. The red solid lines in the right panels represents the best fit relations of Eq. (3), (4) obtained from the PCA data only. |
3.4. Spectral variability
To study possible changes in the spectral parameters of the source at different luminosity states, we fit here all the available RXTE/PCA data, which provided an unbiased monitoring of the source across all different states, by assuming the continuum model for the source broad-band emission discussed in Sect 3.3. A log of the observations is given in Table 2, where we report also the source flux and luminosity. The lower energy threshold of the RXTE/PCA is 3 keV and it does not permit a precise measurement of the absorption column density in the direction of RX J0440.9 + 4431. Thus, we have fixed it to the weighted average value measured from all the available Swift/XRT and RXTE quasi-simultaneous observations characterised by high enough signal-to-noise ratio (S/N) to significantly constrain our parameter of interest (the observations with a conventional ID in Table 2). We find NH = (2.8 ± 0.1) × 1021 cm-2. In several fits the value of log 10(A) in the bmc model could only be poorly constrained. Where possible, we estimated a lower limit at 90% c.l. by using the XSPEC command steppar. For the lower statistic spectra we fixed it to log 10(A) = 1.5. During the observations performed when the source reached the highest flux (observation IDs 95418-01-01-00 and 95418-01-02-00, April 2010) an exponential cut-off at high energy (i.e., exp( − E/EFold)) was needed to properly fit the data: we have found EFold = (30 ± 6) keV and (33 ± 8) keV, respectively. For all the other observations, we have verified that the lower limit on the cut-off energy is outside the energy range covered by our data (~50 keV), consistently with the value derived using INTEGRAL/ISGRI data (see Sect. 3.3). The results obtained from all the fits are reported in Fig. 4. We include in the figure also the EPIC-PN data from the XMM-Newton observation that caught RX J0440.9 + 4431 in its persistent low state (La Palombara et al. 2012). Note that the bmc model also provided a fully acceptable fit to these data (χ2/d.o.f. = 1.1/183) and yielded log 10A > 1.2, kT = (1.02 ± 0.03) keV, α = 0.81 ± 0.08, rBB = (0.73 ± 0.04) km, and a column density NH = (5.4 ± 0.2) × 1021 cm-2 (uncertainties at 90% c.l.). The absorption column density measured with XMM-Newton/EPIC-PN was higher than that measured with Swift/XRT. We verified that fitting the PCA data with this higher value of NH would not affect the results discussed below.
 |
Fig. 5 Hardness-intensity diagram of all the available PCA observation of RX J0440.9 + 4431. Different symbols refer to different outbursts: diamonds are for the outburst in April 2010 (MJD 55 292–55 301), stars for the outburst of September 2010 (MJD 55 447–55 450), and black dots for the outburst of February 2011 (MJD 55 594–55 606). |
From the plots in Fig. 4, we note that the parameter log 10(A) could be only poorly constrained and α shows a not very pronounced downwards trend for increasing source flux. Conversely, both the effective radius and temperature of the thermal emission component increase with the source flux. For the effective radius, we find ( /d.o.f. = 0.6/19):
/d.o.f. = 0.6/19): 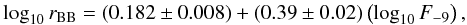 (3)where rBB is the effective radius of the black body seed photons expressed in km and F-9 is the 2–30 keV flux expressed in units of 10-9erg cm-2 s-1. This relation is equivalent to
(3)where rBB is the effective radius of the black body seed photons expressed in km and F-9 is the 2–30 keV flux expressed in units of 10-9erg cm-2 s-1. This relation is equivalent to 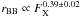 or
or 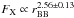 . Similarly for the black body temperature, we find (
. Similarly for the black body temperature, we find (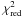 /d.o.f.=0.6/19):
/d.o.f.=0.6/19): 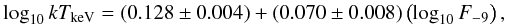 (4)where kTkeV is the black body temperature expressed in keV. In Eqs. (3), (4) uncertainties are given at 1σ c.l. To prove the variations in the source spectral properties in the different observations in a model-independent way, we also report in Fig. 5 the hardness-intensity diagram of the RXTE/PCA data (as shown by, e.g., Reig & Nespoli 2013). From this figure we note that during all outbursts the source X-ray emission becomes harder at higher fluxes and there is an evident change of the overall slope at PCU2 count rates >100 cts/s (the persistent emission level of RX J0440.9 + 4431 corresponds to a PCU2 count rate of about 1–3 cts/s) We verified that different choices of the energy bands would not significantly affect this result.
(4)where kTkeV is the black body temperature expressed in keV. In Eqs. (3), (4) uncertainties are given at 1σ c.l. To prove the variations in the source spectral properties in the different observations in a model-independent way, we also report in Fig. 5 the hardness-intensity diagram of the RXTE/PCA data (as shown by, e.g., Reig & Nespoli 2013). From this figure we note that during all outbursts the source X-ray emission becomes harder at higher fluxes and there is an evident change of the overall slope at PCU2 count rates >100 cts/s (the persistent emission level of RX J0440.9 + 4431 corresponds to a PCU2 count rate of about 1–3 cts/s) We verified that different choices of the energy bands would not significantly affect this result.
An interpretation of the spectral changes in RXJ0440.9+ 4431 is provided in Sect. 4.3.
4. Discussion
4.1. The long-term X-ray variability and the orbital period
The Swift/BAT data allowed us to measure with a fairly good accuracy the orbital period of the source owing to its enhanced X-ray activity in 2010 and 2011. Before this period, the available data revealed that RX J0440.9 + 4431 was a persistent X-ray emitter at a level of about 1 mCrab in hard X-rays (15–150 keV) and no significant orbital modulation could be detected from its light curve. Be/X-ray systems are rarely persistent X-ray sources, but many of them showed in the past only sporadic episodes of enhanced X-ray activity. The latter is thought to be originated by variations in the extension of the Be star equatorial disk (see, e.g., Reig 2011). The existence of persistent Be systems supports the idea that the fainter long-term X-ray activity of these sources is most likely related to the accretion of the NS from the tenuous wind of the companion, while the outbursts occur as a consequence of the interaction at the system periastron between the compact object and the Be equatorial disk (see also, Rothschild et al. 2012, for the quiescent emission of A 0535+26). From the shaded regions of Fig. 1, we note that the maxima of the second and third flares do not correspond exactly to a multiple of our best candidate orbital period: one lies slightly before, the other after. In Be/X-ray binary systems, some variability of the orbital phase occurrence of outburst is expected, but in absence of orbital ephemeris based on pulse period modulation, we cannot speculate further on this subject.
4.2. The broad-band spectral model
Previous works on persistent Be pulsars (Reig & Roche 1999) showed that their spectra can usually be well described by a model comprising a power law component and a black body with an emitting radius of a few hundreds meters (La Palombara & Mereghetti 2006, 2007; La Palombara et al. 2009, 2012). These sources are characterized by a spin period of the order of hundreds seconds, orbital period of hundreds of days and a persistent luminosity of 1034 − 35 erg s-1. The direct black body emission is commonly interpreted as being due to the thermal mound at the base of the neutron star accretion column (with a size proportional to the width of the accretion stream), while the power law is the signature of Comptonization of the thermal photons by the in falling plasma. Following this interpretation and using data from several X-ray observatories, we have verified that also the broad-band spectrum of RX J0440.9 + 4431 could be reasonably well described by this phenomenological model, although our wide energy range requirers the introduction of an exponential roll-over at high energies.
A more insightful description of the parameters regulating the X-ray emission from the source can be obtained by using the bmc model. This permits to describe in a self-consistent way the process in which part of the thermal seed photons are Comptonized and up-scattered to higher energies, giving rise to a power-law shaped emission with part of the photons escaping the Comptonizzation to reach directly the observer. The model is a general solution of the process of Comptonization of a spherically symmetric in-falling plasma but has the major limitation that the high energy roll-over, due to either the thermal motion of electrons or the deviation from a free-fall velocity profile of the moving plasma, is not taken into account. This can be empirically introduced by means of an additional exponential cut-off (exp( − E/EFold), Farinelli et al. 2013), still preserving the advantage of having a self-consistent treatment of the Compton up-scattering process.
Several other models describe the process of Compton up-scattering of seed photons, with different degrees of complication and various limitations. The models comptt and compst (see Titarchuk 1994, and references therein) describe a thermal Comptonization in a static plasma so, despite the possibility of obtaining statistically satisfactory results in terms of X-ray spectral fitting, they are not suitable to be applied to accreting sources at highly sub-Eddington rates as RX J0440.9 + 4431 (in these cases the accreting material is expected to be nearly in free-fall).
The model comptb (Farinelli et al. 2008) has been proposed to describe the emission of low-mass X-ray binaries for both the cases of simply thermal or thermal plus bulk Comptonization. However, the correlation between the electron temperature kTe, the spectral index α and the bulk parameter δ does not yield an independent determination of the whole parameter set. Assuming that bulk Comptonization is an important effect, the model implementation requires that the parameter kTe is fixed or allowed to vary in a very narrow range, inferred from other considerations. It is also important to note that the comptt, compps, and comptb models do not consider the presence of a magnetic field so that the classical Thomson or Klein-Nishina electron scattering cross-sections are assumed. The Be X-ray binary nature of RX J0440.9 + 4431, together with its relatively high pulsed fraction (Usui et al. 2012), suggests that the NS in this system is endowed with a magnetic field significantly higher than in the low-mass systems. This is expected to funnel efficiently the accreting material onto the neutron star’s polar caps, leading to an electron temperature that is hardly predictable a priori.
The model proposed by Becker & Wolff (2007) is also not appropriate to describe the X-ray emission observed from RX J0440.9 + 4431, as it assumes a velocity profile for the inflowing plasma in which an intense radiation field originates a collision-less shock above the NS surface. In this case, the radiation creeps through the lateral walls of the accretion stream giving rise to the so-called “fan beam”. In the case of RX J0440.9 + 4431, the emission pattern from the NS is expected to assume rather the shape of a “pencil beam”, as at low luminosity the radiation is believed to be able to escape directly in the direction of the accretion stream and no dramatic changes in the pulse profile could be revealed over two orders of magnitude in luminosity (La Palombara et al. 2012; Usui et al. 2012). The latter assumption can be roughly demonstrated in the present case by comparing the magnitude of the gravitational force of the neutron star and the radiation pressure from the polar cap where matter is thermalized. We find that 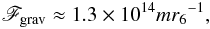 (5)where m and r6 are the neutron mass in solar masses and the distance from the surface in units of 106 cm, respectively. On the other hand, the radiative force per unit mass is given by
(5)where m and r6 are the neutron mass in solar masses and the distance from the surface in units of 106 cm, respectively. On the other hand, the radiative force per unit mass is given by 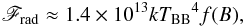 (6)where kTBB is the temperature of the thermal mound and f(B) ≤ 1 is a correction factor to the Thomson cross-section due to the presence of the magnetic field. For photons propagating along the vertical direction, thus almost parallel to the magnetic field, the Thomson cross-section is strongly reduced, with f(B) ≪ 1 (Becker & Wolff 2007). For a typical neutron star mass and using the best fit values of kTBB reported in Tables 3 and 4, it is evident that Frad ≪ Fgrav.
(6)where kTBB is the temperature of the thermal mound and f(B) ≤ 1 is a correction factor to the Thomson cross-section due to the presence of the magnetic field. For photons propagating along the vertical direction, thus almost parallel to the magnetic field, the Thomson cross-section is strongly reduced, with f(B) ≪ 1 (Becker & Wolff 2007). For a typical neutron star mass and using the best fit values of kTBB reported in Tables 3 and 4, it is evident that Frad ≪ Fgrav.
Best fit parameters of the compmag model using a free-fall velocity profile of the accreting matter.
The model of Becker & Wolff (2007) was extended recently (compmag; Farinelli et al. 2012). In this new implementation, it is possible to tune the velocity profile of the in-falling material. A broad-band spectral coverage is however necessary to obtain suitable constraints in the physical parameters of compmag, and thus the single PCA spectra could not be used for this purpose. More satisfactory results were obtained in the multi-instrument broad band spectral analysis of the outbursts in April 2010 and September 2010. We have chosen to use a free-fall like profile with fixed parameter η = 0.5, we have also fixed the albedo at the NS surface to one, while the other parameters are determined by the spectral fit. They are the flow velocity at the NS surface (β0, expressed in unities of c), the accretion column radius (r0, expressed in Schwarzschild radii), the seed black body temperature (kTBB), the electron temperature in the accretion stream (kTe), their opticsl depth (τ), and the model normalization (N). A summary of these results is reported in Table 4. The temperature of the seed thermal photons is in fair agreement with the bmc model. The increase of the electron temperature at decreasing luminosity can be identified as the origin of the increased cut-off energy, while the normalization, N, of compmag is defined such that Rkm = N1/2D10, and thus gives an estimate of the apparent blackbody emitting area. It is worth noting that compmag assumes a uniform blackbody photon field distribution across the accreting column, so the inferred value Rkm does not actually represent the hot spot dimension on the neutron star surface, but rather the total area obtained by emission at different heights above the neutron star surface (so that in general Rkm > r0). This is confirmed here: we obtain Rkm ~ 6.5 and Rkm ~ 3.5 for the first and second observation, respectively (at a source distance of 3.3 kpc), while the column radius remains constant within the uncertainties at about 1 km.
We note that the absorbing column as measured by XMM-Newton/PN is significantly higher than the Swift/XRT determinations, while the spectral parameters of the bmc slightly deviate from the trend derived from the PCA data set (Fig. 4). This can be due to the different energy ranges over which spectra are measured which can lead to a difference in the determination of the spectral slope and thus of the absorbing column. Furthermore, we note that according to Romano et al. (2005), the PN detector yields spectral parameter for the calibration source PSR B0540 − 69 which deviate from EPIC/MOS and Swift/XRT in the same direction as our data, i.e., higher NH, although by a smaller amount. Therefore, we cannot exclude that the apparent discrepancy we have found is influenced by the calibration systematics. We have verified that using a different absorption model (tbabs) with the abundances of Wilms et al. (2000) does not remove the discrepancy and yields an equally acceptable fit with compatible parameter value, except the absorbing column, which is systematically higher than in the model used in this paper. We remark that the absolute value of the absorbing column is of marginal importance for the results discussed here, and that the relatively low-resolution spectra analyzed here do not allow us to distinguish between the models. The values we have derived are similar with the one determined by Tsygankov et al. (2012), while Usui et al. (2012) use just RXTE data (above 3 keV) and get absorbing column roughly one order of magnitude in excess: we have verified that excluding the Swift/XRT data, we would have obtained similar values, which we conclude to be inaccurate as they are hampered by the lack of low-energy coverage.
Among all these different spectral models, the bmc is able to provide a self-consistent and robust physical description of the accretion process in RX J0440.9 + 4431 over the different luminosity levels even exploiting a limited energy band. The compmag model is able to provide complementary information on the accretion process, which are not present in the bmc model, although with more structured assumptions on the geometrical properties of the accretion stream, in particular a significant vertical extent of the emitting plasma above the NS surface. However, it generally requires a large energy coverage and it is of limited use when data are not available to provide constraints on the source emission above ~20 keV.
4.3. Spectral parameters
The observations of RX J0440.9 + 4431 in 2010 and 2011 allowed us to study spectral changes in the X-ray emission from the source over two orders of magnitude in X-ray flux and mass accretion rates (~1014 − 16 g s-1). To compare the results of our spectral analysis at different accretion rates, we plot in Fig. 6 a selection of our bmc best-fit unfolded spectral models obtained at increasing flux levels from the fits to the RXTE data. We note that the spectra of the lower persistent state are rather soft, they become harder at intermediate states, and display a more pronounced curvature at the highest luminosities. This is in agreement with the measurement of a high-energy exponential cut-off at ~30 keV in the RXTE/PCA data during the two observations performed when the source flux was ≥ 10-9 erg cm-2 s-1. The photon index of the Comptonization Green’s function slightly decreases in comparison to the observations performed at the intermediate flux level, also indicating a hardening of the source X-ray emission. At the intermediate state, INTEGRAL/ISGRI data were available to provide coverage at the higher energies, an exponential cut-off was measured at 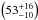 keV. This suggests that the cut-off energy increases at lower luminosities so that the hard X-ray spectrum presents the hard tail expected when bulk Comptonization is the dominant reprocessing channel (Becker & Wolff 2005). Observations performed at the lower fluxes ( ≤ 10-10 erg cm-2 s-1) showed a steeper Comptonization index and a cooler thermal photon temperature, they are thus characterized by a significantly softer emission. These results are confirmed by the model-independent analysis of the source emission provided by the HID in Fig. 5. The observations in which a cut-off energy of 30 keV was measured are represented with the two blue diamonds located in the upper right corner of the plot. The PCA observations performed at intermediate levels, for which quasi-simultaneous INTEGRAL/ISGRI data were also available, are represented with the two green stars located immediately below the blue diamonds. The source emission hardens remarkabley at count rates ~80–100 cts/s, i.e., where the change in the cut-off energy is also revealed by the spectral fitting. The flux corresponding to the lowering of the cut-off energy is 1.3 ÷ 1.8 × 10-9 erg cm-2 s-1, and translates into a luminosity ~2 × 1036 erg s-1.
keV. This suggests that the cut-off energy increases at lower luminosities so that the hard X-ray spectrum presents the hard tail expected when bulk Comptonization is the dominant reprocessing channel (Becker & Wolff 2005). Observations performed at the lower fluxes ( ≤ 10-10 erg cm-2 s-1) showed a steeper Comptonization index and a cooler thermal photon temperature, they are thus characterized by a significantly softer emission. These results are confirmed by the model-independent analysis of the source emission provided by the HID in Fig. 5. The observations in which a cut-off energy of 30 keV was measured are represented with the two blue diamonds located in the upper right corner of the plot. The PCA observations performed at intermediate levels, for which quasi-simultaneous INTEGRAL/ISGRI data were also available, are represented with the two green stars located immediately below the blue diamonds. The source emission hardens remarkabley at count rates ~80–100 cts/s, i.e., where the change in the cut-off energy is also revealed by the spectral fitting. The flux corresponding to the lowering of the cut-off energy is 1.3 ÷ 1.8 × 10-9 erg cm-2 s-1, and translates into a luminosity ~2 × 1036 erg s-1.
According to the discussion of Becker et al. (2012), at low luminosity (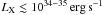 ) matter strikes the NS surface after passing through a gas-mediated shock. At higher luminosity, the radiation pressure begins to affect the accretion process so that a radiative shock forms, and plasma deceleration takes place through Coulomb interactions in an vertically extended atmosphere. At this stage, the efficiency of the thermal cooling of the high-energy electrons responsible for the Comptonized emission increases significantly and can produce the observed change in the cut-off energy. However, the luminosity level at which this transition happens is not well predicted on theoretical basis and is here tentatively identified on observational grounds at ~2 × 1036 erg s-1. It is worth noticing that in all observations, RX J0440.9 + 4431 remains relatively faint in the X-rays compared to the giant outbursts of transient Be/X-ray binaries (LX ~ 1038 erg s-1). As a consequence, the HID does not show the typical upper branch turning towards softer colors typically observed during the brightest outbursts of these sources, which might be interpreted as the onset of the fully radiation dominated accretion column (Reig & Nespoli 2013; Becker et al. 2012).
) matter strikes the NS surface after passing through a gas-mediated shock. At higher luminosity, the radiation pressure begins to affect the accretion process so that a radiative shock forms, and plasma deceleration takes place through Coulomb interactions in an vertically extended atmosphere. At this stage, the efficiency of the thermal cooling of the high-energy electrons responsible for the Comptonized emission increases significantly and can produce the observed change in the cut-off energy. However, the luminosity level at which this transition happens is not well predicted on theoretical basis and is here tentatively identified on observational grounds at ~2 × 1036 erg s-1. It is worth noticing that in all observations, RX J0440.9 + 4431 remains relatively faint in the X-rays compared to the giant outbursts of transient Be/X-ray binaries (LX ~ 1038 erg s-1). As a consequence, the HID does not show the typical upper branch turning towards softer colors typically observed during the brightest outbursts of these sources, which might be interpreted as the onset of the fully radiation dominated accretion column (Reig & Nespoli 2013; Becker et al. 2012).
 |
Fig. 6 Selection of unfolded RXTE/PCA spectra at different luminosity states based on the bmc model. The corresponding observation ID is also indicated. |
To test further our understanding of the accretion processes in RX J0440.9 + 4431 given above, we have estimated from the bmc best-fit parameters the terminal velocity of the accretion flow at the NS surface for all the RXTE spectra and reported our results in Fig. 6. For this purpose, we follow Eqs. (91), (92) of Becker & Wolff (2007) adapted to the notation used in the previous sections of our paper. By equating the energy flux dissipated by the thermally emitting surface to the flux of kinetic energy, we obtain 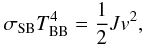 (7)where σSB is the Stefan-Boltzmann constant, TBB the black body temperature, v the stream velocity, and
(7)where σSB is the Stefan-Boltzmann constant, TBB the black body temperature, v the stream velocity, and 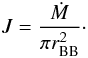 (8)The radius of the hot spot emitting the thermal radiation, rBB, can be derived from the measured spectral parameters using Eq. (2). We use also the standard conversion between mass accretion rate and X-ray luminosity:
(8)The radius of the hot spot emitting the thermal radiation, rBB, can be derived from the measured spectral parameters using Eq. (2). We use also the standard conversion between mass accretion rate and X-ray luminosity: 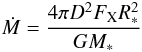 (9)where D is the source distance, FX is approximated by F2 − 30 keV, G is the gravitation constant, R∗ and M∗ are the NS radius and mass. By taking into account that
(9)where D is the source distance, FX is approximated by F2 − 30 keV, G is the gravitation constant, R∗ and M∗ are the NS radius and mass. By taking into account that 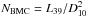 (see Eq. (2)) and expressing the free-fall velocity at the NS surface as
(see Eq. (2)) and expressing the free-fall velocity at the NS surface as 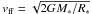 , we obtain that
, we obtain that 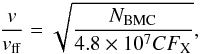 (10)where C is the geometrical factor of Eq. (2) and FX is expressed in erg cm-2 s-1. By assuming that the thermal emitting surface is a circular slab (C = 0.25), we derive a terminal velocity of the accretion stream which is ≈ 0.85vff for all the observations, apart for the two corresponding to the highest luminosities (Fig. 7). In these cases the terminal velocity marginally exceeds the free-fall limit. This might indicate that the thermal mound is building-up on the NS surface so that the geometrical factor C of the thermally emitting region increases and approaches that of the spherical geometry case (C = 1). This indication agrees with the interpretation that the spectral change at the peak of the flaring activity of RX J0440.9 + 4431 is due to the formation of a radiatively dominated accretion column suggested by the decreasing cut-off energy. We note that the above calculations agree fairly well with the base velocity of the compmag best-fit parameters (β0 ≈ 0.5 ≈ 0.8vff/c).
(10)where C is the geometrical factor of Eq. (2) and FX is expressed in erg cm-2 s-1. By assuming that the thermal emitting surface is a circular slab (C = 0.25), we derive a terminal velocity of the accretion stream which is ≈ 0.85vff for all the observations, apart for the two corresponding to the highest luminosities (Fig. 7). In these cases the terminal velocity marginally exceeds the free-fall limit. This might indicate that the thermal mound is building-up on the NS surface so that the geometrical factor C of the thermally emitting region increases and approaches that of the spherical geometry case (C = 1). This indication agrees with the interpretation that the spectral change at the peak of the flaring activity of RX J0440.9 + 4431 is due to the formation of a radiatively dominated accretion column suggested by the decreasing cut-off energy. We note that the above calculations agree fairly well with the base velocity of the compmag best-fit parameters (β0 ≈ 0.5 ≈ 0.8vff/c).
 |
Fig. 7 Luminosity dependency of the velocity of the accreted matter at the NS surface obtained from Eq. (10) assuming C = 0.25. |
Throughout the whole luminosity range, the variation of the parameters of the thermal emision component in RX J0440.9 + 4431 could be satisfactorily described by the relations: 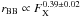 ,
, 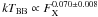 (see Sect. 3.3 and Fig. 4). In the case of accretion onto a neutron star from the stellar wind, it is expected that the radius of the hot spot is inversely correlated to the luminosity, as at higher accretion rate matter should penetrate along magnetic field lines which are more and more concentrated towards the NS magnetic poles (Arons & Lea 1980). Conversely, if the transfer of matter is mediated by an accretion disk, the area of the hot spot is proportional to the ratio R∗/RAlfven
(see Sect. 3.3 and Fig. 4). In the case of accretion onto a neutron star from the stellar wind, it is expected that the radius of the hot spot is inversely correlated to the luminosity, as at higher accretion rate matter should penetrate along magnetic field lines which are more and more concentrated towards the NS magnetic poles (Arons & Lea 1980). Conversely, if the transfer of matter is mediated by an accretion disk, the area of the hot spot is proportional to the ratio R∗/RAlfven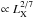 (see, e.g., Lamb et al. 1973; White et al. 1983). The correlation determined from the fits to the data thus support the idea that RX J0440.9 + 4431 is continuously accreting from a surrounding disk (despite the opposite would be expected for the persistent activity of a Be/X-ray binary, see Sect. 4.1). However, the measured relation between rBB and the source luminosity is much steeper than expected in the case of disk accretion8. This might indicate either that matter penetrates through closed magnetic field lines at the border of the magnetosphere or that the neutron star magnetic field structure is a more complicated than a simple dipole close to the surface. The former idea was suggested to justify the magnetospheric instabilities observed in the outbursts of EXO 2030+375 (Klochkov et al. 2011) and A 0535+262 (Postnov et al. 2008). The latter has been invoked, e.g., by Ferrigno et al. (2009) to interpret the soft component in the broad-band spectrum of 4U 0115+63 and can be related also to accretion-induced deformations of the magnetic field and instabilities in the accretion mound which are shown to exist on the base of recent numerical simulations (Mukherjee et al. 2013).
(see, e.g., Lamb et al. 1973; White et al. 1983). The correlation determined from the fits to the data thus support the idea that RX J0440.9 + 4431 is continuously accreting from a surrounding disk (despite the opposite would be expected for the persistent activity of a Be/X-ray binary, see Sect. 4.1). However, the measured relation between rBB and the source luminosity is much steeper than expected in the case of disk accretion8. This might indicate either that matter penetrates through closed magnetic field lines at the border of the magnetosphere or that the neutron star magnetic field structure is a more complicated than a simple dipole close to the surface. The former idea was suggested to justify the magnetospheric instabilities observed in the outbursts of EXO 2030+375 (Klochkov et al. 2011) and A 0535+262 (Postnov et al. 2008). The latter has been invoked, e.g., by Ferrigno et al. (2009) to interpret the soft component in the broad-band spectrum of 4U 0115+63 and can be related also to accretion-induced deformations of the magnetic field and instabilities in the accretion mound which are shown to exist on the base of recent numerical simulations (Mukherjee et al. 2013).
The way in which the accreting matter penetrates the NS magnetosphere and accretes onto the compact star surface is also producing significant changes in its spin period. In Sect. 3.2, we have shown that the spin period values measured from the observations of RX J0440.9 + 4431 are not precise enough to constrain the source orbital properties and/or evaluate accretion torques. However, we note that RX J0440.9 + 4431 showed a remarkable spin-down over the past 12 years from 202 s (Reig & Roche 1999) to ≈ 206 s. If we assume that RX J0440.9 + 4431 is accreting from a disk at a non negligible rate, then the measured spin down can be interpreted in terms of coupling between the neutron star magnetic field lines and the external regions of the accretion disk located beyond the so-called corotational radius (Wang 1995, 1996). This assumption has been sometimes used to constrain the NS magnetic field. As pointed out by Bozzo et al. (2009), the uncertainties on the location and the extension of the boundary layer in the disk accretion models for magnetized neutron stars are relatively large. Therefore, we could just derive that the magnetic field for the NS in RX J0440.9 + 4431 is of the order of few × 1012 G. This is in agreement with the timing signatures of the broad-band noise discussed in Tsygankov et al. (2012). The non-detection of the previously reported cyclotron scattering absorption line discussed in Sect. 3.3 is not a counter argument to this magnetic field estimate, as these features are not ubiquitous in the spectra of accreting magnetized neutron stars.
5. Conclusions
In this work, we reported on the analysis of the last outbursts detected from the persistent Be X-ray binary RX J0440.9 + 4431, and used all archival observations of this source performed in 2010 and 2011 to investigate its spectral properties in a broad X-ray energy domain (0.3–150 keV).
We obtained the most accurate measurement of the source orbital period so far at (150.0 ± 0.2) days and performed a detailed analysis of the source spectrum covering more than two orders of magnitude in luminosity. We used the bulk motion Comptonization model (bmc, Titarchuk et al. 1997), which provided a self-consistent picture of the accretion processes in RX J0440.9 + 4431. In particular, we found a coherent dependency of the size and temperature of the thermal emitting region as a function of the luminosity. These quantities do not follow the relations expected for accretion onto strongly magnetized neutron stars, and we argue that either accreting matter penetrates through closed magnetic field lines at the border of the magnetosphere or that the neutron star magnetic field configuration deviates from a dipole close to the surface.
Analyzing the spectral changes at the hard X-ray band (>10 keV), we have identified the luminosity level at which the accretion flow dynamics begin to be affected by radiation pressure (LX ≈ 2 × 1036 erg s-1). We estimated the in-falling plasma velocity close to the neutron star, which is consistent with the predictions from a physically motivated model. This provided an independent indication of the building-up of a radiative accretion column at the highest luminosity reached by RX J0440.9 + 4431 from the likely bending of the thermal emission surface. RX J0440.9 + 4431 was particularly well suited for this study because the variations of its thermal emission could be unambiguously revealed during the higher and lower X-ray active states. This is not the case for other Be X-ray binaries (see, e.g., the controversy on the spectral modeling of EXO 2020+375, Reig & Roche 1999; Klochkov et al. 2007; Wilson et al. 2008).
We compared our findings on the accretion process in RX J0440.9 + 4431 by exploring the most recent spectral models accounting for thermal emission and its Comptonization in a strong magnetic field. The compmag model could provide a number of further details for the interaction between the neutron star hosted in this source and the in-falling plasma, but the usability of this model is limited by the statistics of the available data. More sensitive missions will hopefully cover the required broad energy range (2–50 keV) (e.g., LOFT, Feroci et al. 2012) and will allow us to study in greater detail the accretion process at the lower end of the luminosity range of Be/X-ray binaries by means of complex physically motivated models, which cannot be significantly constrained at present.
To infer the thermal component radius from the model parameters, we have assumed a constant geometry (parameter C of Eq. (2)).
Acknowledgments
This research has made use of data obtained through the High Energy Astrophysics Science Archive Research Center Online Service, provided by the NASA/Goddard Space Flight Center. We thank the Swift PI and the schedulers for having performed the target of opportunity observations used in this work in correspondence with the planned RXTE TOOs.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, 101, 17 [NASA ADS] [Google Scholar]
- Arons, J., & Lea, S. M. 1980, ApJ, 235, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2005, ApJ, 630, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, P. A., Klochkov, D., Schönherr, G., et al. 2012, A&A, 544, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bozzo, E., Stella, L., Vietri, M., & Ghosh, P. 2009, A&A, 493, 809 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bradt, H. V., Rothschild, R. E., & Swank, J. H. 1993, A&AS, 97, 355 [NASA ADS] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Courvoisier, T., Walter, R., Beckmann, V., et al. 2003, A&A, 411, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cusumano, G., La Parola, V., Segreto, A., et al. 2010, A&A, 524, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Titarchuk, L., Paizis, A., & Frontera, F. 2008, ApJ, 680, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., Ceccobello, C., Romano, P., & Titarchuk, L. 2012, A&A, 538, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farinelli, R., Amati, L., Shaposhnikov, N., et al. 2013, MNRAS, 428, 3295 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., Stella, L., van der Klis, M., et al. 2012, Exp. Astron., 34, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrigno, C., Becker, P. A., Segreto, A., Mineo, T., & Santangelo, A. 2009, A&A, 498, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finger, M. H., & Camero-Arranz, A. 2010, The Astronomer’s Telegram, 2537, 1 [NASA ADS] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, Proc. SPIE, 2808, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Horns, D., Santangelo, A., et al. 2007, A&A, 464, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klochkov, D., Staubert, R., Santangelo, A., Rothschild, R. E., & Ferrigno, C. 2011, A&A, 532, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivonos, R., Tsygankov, S., Lutovinov, A., Turler, M., & Bozzo, E. 2010a, The Astronomer’s Telegram, 2828, 1 [NASA ADS] [Google Scholar]
- Krivonos, R., Tsygankov, S., Revnivtsev, M., et al. 2010b, A&A, 523, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivonos, R., Tsygankov, S., Lutovinov, A., et al. 2012, A&A, 545, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Palombara, N., & Mereghetti, S. 2006, A&A, 455, 283 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Palombara, N., & Mereghetti, S. 2007, A&A, 474, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Palombara, N., Sidoli, L., Esposito, P., Tiengo, A., & Mereghetti, S. 2009, A&A, 505, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Palombara, N., Sidoli, L., Esposito, P., Tiengo, A., & Mereghetti, S. 2012, A&A, 539, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, F. K., Pethick, C. J., & Pines, D. 1973, ApJ, 184, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Lund, N., Budtz-Jørgensen, C., Westergaard, N. J., et al. 2003, A&A, 411, L231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morii, M., Kawai, N., Sugimori, K., et al. 2010, The Astronomer’s Telegram, 2527, 1 [NASA ADS] [Google Scholar]
- Mukherjee, D., Bhattacharya, D., & Mignone, A. 2013, MNRAS, 430, 1976 [NASA ADS] [CrossRef] [Google Scholar]
- Postnov, K., Staubert, R., Santangelo, A., et al. 2008, A&A, 480, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., & Nespoli, E. 2013, A&A, 551, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reig, P., & Roche, P. 1999, MNRAS, 306, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P., Negueruela, I., Fabregat, J., Chato, R., & Coe, M. J. 2005, A&A, 440, 1079 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, P., Cusumano, G., Campana, S., et al. 2005, UV, 5898, 369 [Google Scholar]
- Rothschild, R., Markowitz, A., Caballero, I., et al. 2012, ApJ, submitted [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L., Mastichiadis, A., & Kylafis, N. D. 1997, ApJ, 487, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Tsygankov, S. S., Krivonos, R. A., & Lutovinov, A. A. 2012, MNRAS, 421, 2407 [NASA ADS] [CrossRef] [Google Scholar]
- Ubertini, P., Lebrun, F., Di Cocco, G., et al. 2003, A&A, 411, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usui, R., Morii, M., Kawai, N., et al. 2012, PASJ, 64, 79 [NASA ADS] [Google Scholar]
- Wang, Y.-M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
- Wang, Y.-M. 1996, ApJ, 465, L111 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Swank, J. H., & Holt, S. S. 1983, ApJ, 270, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. A., Finger, M. H., & Camero-Arranz, A. 2008, ApJ, 678, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, C., Courvoisier, T., Di Cocco, G., et al. 2003, A&A, 411, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Measurements of the spin period of RX J0440.9 + 4431 obtained from all the RXTE observations analyzed in the present work.
Best fit parameters for the absorbed bmc with exponential cut-off model for the broad band spectral fits of the 2010 outburst (uncertainties are at 90% c.l.).
Best fit parameters of the compmag model using a free-fall velocity profile of the accreting matter.
All Figures
 |
Fig. 1 Light curve of RX J0440.9 + 4431 and times of the observations reported in this paper. Black points with errors: Swift/BAT daily averaged light curve. Red vertical bars: times of the RXTE observations. Blue horizontal bar: time span of the INTEGRAL data used in this paper. Green diamonds: times of the Swift observations used in our analysis. The first vertical yellow bar indicates the occurrence of the first maximum in the light curve; the others correspond to the times of the following maxima predicted by our orbital period determination. MJD 55 280, 55 430, and 55 580 correspond to 2010, March 25, 2010, August 22, and 2011, January 19, respectively. |
| In the text | |
 |
Fig. 2 Folded Swift/BAT light curve (15–150 keV) of RXJ0440.9+4431 at the best determined orbital period, (150.0 ± 0.2) days. The inset shows the periodogram obtained from the epoch folding technique applied to the Swift/BAT light curve. |
| In the text | |
 |
Fig. 3 Broad-band spectrum of the quasi-simultaneous INTEGRAL/ISGRI (green), INTEGRAL/JEM-X2 (blue), RXTE/ PCA (red), and Swift/XRT (black) observations performed in September 2010. The best fit is obtained with the absorbed bmc with exponential cut-off model. The residuals from this fit are also shown in the bottom panel. |
| In the text | |
 |
Fig. 4 Results of the spectral fits to the RXTE/PCA observations (filled circles) performed during the outbursts of RX J0440.9 + 4431 occurred in 2010 and 2011 (Table 2). The best fit spectral parameters obtained from the XMM-Newton observation (2011 March 18) are also included and represented with a star (uncertainties are at 68% c.l. and lower limits at 90% c.l.).The bmc model was used for all fits, but during the two observations performed when the source reached the highest flux, an exponential cut-off at high energy was needed to properly fit the data (see Sect. 3.4). The black body radius rBB is obtained from Eq. (2) setting C = 1. The red solid lines in the right panels represents the best fit relations of Eq. (3), (4) obtained from the PCA data only. |
| In the text | |
 |
Fig. 5 Hardness-intensity diagram of all the available PCA observation of RX J0440.9 + 4431. Different symbols refer to different outbursts: diamonds are for the outburst in April 2010 (MJD 55 292–55 301), stars for the outburst of September 2010 (MJD 55 447–55 450), and black dots for the outburst of February 2011 (MJD 55 594–55 606). |
| In the text | |
 |
Fig. 6 Selection of unfolded RXTE/PCA spectra at different luminosity states based on the bmc model. The corresponding observation ID is also indicated. |
| In the text | |
 |
Fig. 7 Luminosity dependency of the velocity of the accreted matter at the NS surface obtained from Eq. (10) assuming C = 0.25. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


