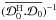| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220882 | |
| Published online | 17 May 2013 | |
Applying full polarization A-Projection to very wide field of view instruments: An imager for LOFAR
1
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot,
5 place Jules Janssen,
92190
Meudon,
France
e-mail: cyril.tasse@obspm.fr
2
Department of Physics & Electronics, Rhodes
University, PO Box
94, 6140
Grahamstown, South
Africa
3
SKA South Africa, 3rd Floor, The Park, Park Road,
7405
Pinelands, South
Africa
4
Sterrewacht Leiden, PO Box 9513, 2300 RA
Leiden, The
Netherlands
5
Netherlands Institute for Radio Astronomy (ASTRON),
Postbus 2,
7990 AA
Dwingeloo, The
Netherlands
6
National Radio Astronomy Observatory, Socorro, NM
87801,
USA
Received:
11
December
2012
Accepted:
9
February
2013
The required high sensitivities and large fields of view of the new generation of radio interferometers impose high dynamic ranges, e.g., ~1:106 to 1:108 for the Square Kilometre Array (SKA). The main problem for achieving these high ranges is the calibration and correction of direction dependent effects (DDE) that can affect the electro-magnetic field (antenna beams, ionosphere, Faraday rotation, etc.). It has already been shown that the A-Projection is a fast and accurate algorithm that can potentially correct for any given DDE in the imaging step. With its very wide field of view, low operating frequency (~30–250 MHz), long baselines, and complex station-dependent beam patterns, the LOw Frequency ARray (LOFAR) is certainly the most complex SKA pathfinder instrument. In this paper we present a few implementations of the A-Projection in LOFAR which can deal nondiagonal Mueller matrices. The algorithm is designed to correct for all DDE, including individual antennas, projection of the dipoles on the sky, beam forming, and ionospheric effects. We describe a few important algorithmic optimizations related to LOFAR’s architecture that allowed us to build a fast imager. Based on simulated datasets we show that A-Projection can dramatically improve the dynamic range for both phased array beams and ionospheric effects. However, certain problems associated with the calibration of DDE remain (especially ionospheric effects), and the effect of the algorithm on real LOFAR survey data still needs to be demonstrated. We will be able to use this algorithm to construct the deepest extragalactic surveys, comprising hundreds of days of integration.
Key words: instrumentation: interferometers / techniques: interferometric / techniques: image processing
© ESO, 2013
1. Introduction: LOFAR and direction-dependent effects
With the building or development of many large radio telescopes (LOFAR, EVLA, ASKAP, MeerKAT, MWA, SKA, e-Merlin), radio astronomy is undergoing a period of rapid development. New issues arise with the development of new types of interferometers, and certain approximations applicable to imaging with the older generation of instruments are not valid anymore. Specifically, they have wide fields of view and will be seriously affected by direction dependent effects (DDE). Dealing with DDE represents serious challenges, in the theoretical, numerical, and technical aspects of calibration and imaging (see Bhatnagar 2009, for a detailed review).
 |
Fig. 1 LOFAR stations are phased arrays characterized by a large field of view. X/Y polarimetric measurements made with it are therefore nontrivial compared to a radio telescope using dishes: we have to take into account the projection of the dipoles that are generally nonorthogonal on the sky and the fact that this angle varies across the field of view. This figure shows the Mueller matrix corresponding to baseline (01) in a given time and frequency slot, normalized by the Mueller matrix at the phase center (see text). Each pixel in the plot (i,j) shows the amplitude of the (i,j) Mueller matrix element in a certain direction s using a logarithmic scale. Even in this normalized version, the off-diagonal Mueller terms are as high as 10% and cannot be neglected. |
This is particularly true for the LOw Frequency ARray (LOFAR), an instrument that observes in a mostly unexplored frequency range (ν ≲ 240 MHz), and will be one of the largest radio telescopes ever built in terms of collecting area. LOFAR’s design is based on a combination of phased array and interferometer concepts (see de Vos et al. 2009, for a description of the LOFAR system). It presently consists of 40 stations in the Netherlands, and 8 international stations (5 in Germany, and 1 each in France, Sweden, and the United Kingdom). Each high band antenna station (110–240 MHz, HBA hereafter) comprises 24 to 96 tiles of 4 × 4 coherently summed antennas, while in a low band antenna station (10–80 MHz, LBA) they are clustered in groups of 96 elements. At the station level, the signals from the individual antennas or tiles (for LBA and HBA, respectively) are phased and summed by the beamformer. This step amounts to forming a virtual antenna pointing towards the targeted field location. The data are transported from the various stations of the LOFAR array to the correlator. The whole process and the pipeline architecture are described in more detail in Heald et al. (2010). LOFAR is affected by many complex baseline-time-frequency4 dependent DDE, consisting mainly of effects in the antenna/station beams and the ionosphere. We currently have models of both the high-band and low-band station beams (HBA and LBA, respectively).
As shown in Bhatnagar et al. (2008), A-Projection allows sky images to be estimated, taking all possible complicated effects associated with DDE into account (see also Bernardi et al. 2011; Mitchell et al. 2012; Sullivan et al. 2012, in the context of the Murchison Widefield Array and forward modeling). However, unlike dish-based interferometers, whose fields of view are typically 0.5 degree and where the beam shape and polarization angle are affected by pointing errors and rotated on the sky by the parallactic angle (depending on the dish mount), LOFAR is based on phased arrays that have very wide fields of view (up to ~12 degrees), and nontrivial and quickly varying beams, thereby driving complicated polarization effects. Technically speaking, very wide field-of-view instruments that aim to reach a high dynamic range have to deal with baseline-dependent nondiagonal Mueller matrices (see Sect. 2 for a detailed discussion). For the VLA, due to its relatively small field of view, it was sufficient for A-Projection to take only the diagonal terms of the Mueller matrices into account to demonstrate corrections for instrumental polarization. This is not possible for LOFAR, however, due to its heavily nondiagonal baseline-associated Mueller matrices, where all 4 × 4 Mueller terms have to be taken into account (see Sect. 3 for a detailed discussion).
We show in this paper that the scheme described in Bhatnagar et al. (2008) can indeed deal with the heavily nondiagonal Mueller matrices associated with the very wide field of view of phased arrays. Our imaging algorithm can take any model or calibration solution or ionosphere phase screen as input. In Sect. 2 we describe the issues related with the usage of phased arrays in interferometers, and focus on LOFAR-related issues, i.e., polarization aspects and baseline dependence of DDE. We describe a few important algorithmic optimizations related to LOFAR’s architecture, which allow us to build a fast imager1. In Sect. 3 we describe the A-Projection algorithm first presented in Bhatnagar et al. (2008), and the various implementations and optimizations we have found that make it reasonably fast in the case of LOFAR. We present the results in Sect. 4 and show that beam and ionosphere corrections can both be performed at high accuracy. We summarize and discuss the next developments in Sect. 5.
 |
Fig. 2 Correction |
2. Polarization effects associated with very wide fields of view interferometers
In this section we describe the polarizations effects associated with the complex structure of DDE that are inherent in the use of phased arrays with very wide fields of view and nondiagonal, baseline-dependent Mueller matrices (or nonunitary Jones matrices in the case of interferometers having similar antennas, see Fig. 1 and the discussion in Sect. 2.1).
For an instrument with long baselines, large fractional bandwidth, very wide field of view, and station-dependent effective Jones matrices (due to beam, ionosphere, Faraday rotation), the Mueller matrices to be considered are not only nondiagonal, but also baseline-dependent. To highlight some of the main complications associated with very wide field-of-view instruments, in Sect. 2.1 we describe in detail the structure of the linear operator introduced by Bhatnagar et al. (2008). In Sect. 2.2 we propose a method to approximately correct for the associated effects corrupting the image plane (see also Rau & Cornwell 2011, for other examples of the use of linear operators in the context of image synthesis and deconvolution).
2.1. Description of baseline-dependence, DDE, and polarization effects
For convenience, in this section and throughout the paper, we do not show the sky term
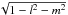 that usually divides the sky to account for the projection of the celestial sphere onto
the plane, as this has no influence on the results. The DDE below are baseline-dependent,
since is the case for LOFAR, and the measurement equation formalism can properly model
those effects (for extensive discussions on the validity and limitations of the
measurement equation see Hamaker et al. 1996; Smirnov 2011, and see Appendix A for a short review of our requirements). If
that usually divides the sky to account for the projection of the celestial sphere onto
the plane, as this has no influence on the results. The DDE below are baseline-dependent,
since is the case for LOFAR, and the measurement equation formalism can properly model
those effects (for extensive discussions on the validity and limitations of the
measurement equation see Hamaker et al. 1996; Smirnov 2011, and see Appendix A for a short review of our requirements). If
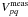 is the set
of four-polarization measurement (XX, XY, YX, YY) and
Gp is the direction independent Jones
matrix of antenna-p, then the corrected visibilities on
baseline pq are
is the set
of four-polarization measurement (XX, XY, YX, YY) and
Gp is the direction independent Jones
matrix of antenna-p, then the corrected visibilities on
baseline pq are ![\hbox{$V^{\rm corr}_{pq}=[G_{t\nu,p}]^{-1}.V^{\rm meas}_{pq}.[G^{\rm H}_{t\nu,q}]^{-1}$}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq16.png) ,
and we can write
,
and we can write 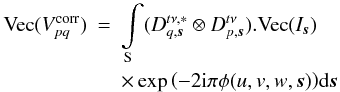 (1)where
I is the four-polarization sky, ⊗ the Kronecker
product, Vec the operator12 that transforms a 2 × 2 matrix
into a four-dimensional vector, and
(1)where
I is the four-polarization sky, ⊗ the Kronecker
product, Vec the operator12 that transforms a 2 × 2 matrix
into a four-dimensional vector, and 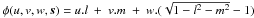 models
the product of the effects of correlator, sky brightness and array geometry. The matrix
models
the product of the effects of correlator, sky brightness and array geometry. The matrix
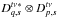 is a
4 × 4 matrix, and throughout the text we refer to it as the Mueller
matrix2. We can also write Eq. (1) in terms of a series of linear
transformations:
is a
4 × 4 matrix, and throughout the text we refer to it as the Mueller
matrix2. We can also write Eq. (1) in terms of a series of linear
transformations: 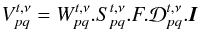 (2)where
(2)where
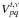 are the
are the
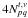 visibility
measurement points in the time-frequency block in which the DDE are assumed to be
constant. If Npix is the number of pixels in the sky model,
the true sky image vector I has a size of
4Npix, and it contains the full polarization information
(XXx,XYx,YXx,XYx)
on the xth pixel at the 4x position. Then,
visibility
measurement points in the time-frequency block in which the DDE are assumed to be
constant. If Npix is the number of pixels in the sky model,
the true sky image vector I has a size of
4Npix, and it contains the full polarization information
(XXx,XYx,YXx,XYx)
on the xth pixel at the 4x position. Then,
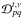 contains
the DDE, and is a
(4Npix) × (4Npix) block diagonal
matrix. On a given baseline (p,q), each of its 4 × 4 block is the
contains
the DDE, and is a
(4Npix) × (4Npix) block diagonal
matrix. On a given baseline (p,q), each of its 4 × 4 block is the
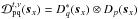 Mueller matrix evaluated at the
location of the xth pixel. F is the Fourier transform
operator of (4Npix) × (4Npix).
Each of its (4 × 4) blocks is a scalar matrix, the scalar being the kernel of the Fourier
basis
exp(−2iπφ(u,v,w,s)). The
matrix
Mueller matrix evaluated at the
location of the xth pixel. F is the Fourier transform
operator of (4Npix) × (4Npix).
Each of its (4 × 4) blocks is a scalar matrix, the scalar being the kernel of the Fourier
basis
exp(−2iπφ(u,v,w,s)). The
matrix 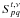 is the
uv-plane sampling function for that visibility, of size
is the
uv-plane sampling function for that visibility, of size
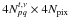 , and
, and
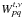 is the
diagonal
is the
diagonal 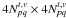 matrix
containing the weights associated with the
matrix
containing the weights associated with the 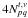 visibilities.
visibilities.
We show in Fig. 1 that the Mueller matrix is
nondiagonal for LOFAR. The various panels show the amplitude of the direction dependent
Mueller matrix using our beam model alone (therefore it does not include Faraday rotation
and ionosphere), for the baseline (p,q) = (0,1) in a
given time and frequency slot. To minimize the off-diagonal elements, we computed
![\hbox{$\mathcal{D}_{0}(\vec{s})=[\mathcal{D}(\vec{s_0})]^{-1}.\mathcal{D}(\vec{s})$}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq43.png) in the direction s,
where s0 is the
phase center direction. Intuitively, the normalization of the Mueller matrix by
in the direction s,
where s0 is the
phase center direction. Intuitively, the normalization of the Mueller matrix by
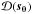 makes the projected dipoles on the sky orthogonal at the phase centre (off-diagonal
elements are zero there), while this becomes less true as we go further from the targeted
location. The off-diagonal elements can be as high as ~10% at a few degrees from the
pointed location and, unlike most interferometers, they cannot be neglected in the case of
LOFAR.
makes the projected dipoles on the sky orthogonal at the phase centre (off-diagonal
elements are zero there), while this becomes less true as we go further from the targeted
location. The off-diagonal elements can be as high as ~10% at a few degrees from the
pointed location and, unlike most interferometers, they cannot be neglected in the case of
LOFAR.
We are generally interested in using the total set of visibilities over baselines, time,
and frequencies, having 4NV points. We can
write 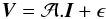 (3)where
ϵ is the noise, and
(3)where
ϵ is the noise, and 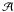 a (4NV) × (4Npix)
matrix made of all
a (4NV) × (4Npix)
matrix made of all 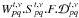 matrices on
top of each other. Then
matrices on
top of each other. Then 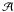 has dimensions
has dimensions 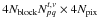 , where
Nblock is the total number of time-frequency-baseline
blocks. We can also write
, where
Nblock is the total number of time-frequency-baseline
blocks. We can also write 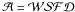 ,
where
,
where 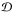 has size
4NblocksNpix × Npix
and has all the
has size
4NblocksNpix × Npix
and has all the 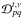 effects on
top of each other. ℱ is the block-diagonal Fourier transform operator of size
4NblocksNpix × 4NblocksNpix,
with all of its blocks
4Npix × 4Npix equal to the
matrix F appearing in Eq. (2).
effects on
top of each other. ℱ is the block-diagonal Fourier transform operator of size
4NblocksNpix × 4NblocksNpix,
with all of its blocks
4Npix × 4Npix equal to the
matrix F appearing in Eq. (2).  and
and  are the sampling and weight matrices of size
(4NV) × (4NblocksNpix)
and
(4NV) × (4NV)
respectively. The transformation of Eq. (3)
is exact. Estimating a sky from a sparsely sampled measured set of
visibilities is less trivial, however.
are the sampling and weight matrices of size
(4NV) × (4NblocksNpix)
and
(4NV) × (4NV)
respectively. The transformation of Eq. (3)
is exact. Estimating a sky from a sparsely sampled measured set of
visibilities is less trivial, however.
2.2. Estimating a sky image: polarization effects
There are different ways to solve for I from the set of
visibilities, and reversing Eq. (3) relies
on the linearity of the sky term in the measurement equation. As mentioned above, our
deconvolution scheme uses A-Projection. This generalization of CS-CLEAN is now better
understood in the framework of compressed sensing, which includes other new techniques
(see McEwen & Wiaux 2011, for a review). In
this section we describe a method of approximately correcting the polarization effects in
the image plane. To highlight the issues associated with polarization and the baseline
dependence of the DDE, we simply write the sky least square solution
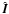 as the pseudo inverse:
as the pseudo inverse: 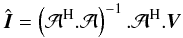 (4)where
the term
(4)where
the term 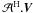 is the 4Npix dirty image, and
is the 4Npix dirty image, and
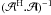 is the (4Npix) × (4Npix) image
plane deconvolution matrix. Its structure is rather complicated, and its size makes its
estimation prohibitive.
is the (4Npix) × (4Npix) image
plane deconvolution matrix. Its structure is rather complicated, and its size makes its
estimation prohibitive.
In the simple case of a matrix 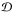 being unity (no DDE), we can see that each 4 × 4 block number (x,y) of
the matrix
being unity (no DDE), we can see that each 4 × 4 block number (x,y) of
the matrix 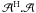 is the instrumental response to a source centered on the location of the
xth pixel, evaluated at the yth pixel. Therefore,
computing
is the instrumental response to a source centered on the location of the
xth pixel, evaluated at the yth pixel. Therefore,
computing 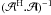 would involve estimating the point spread function (PSF) centered on the location of each
pixel and inverting a
4Npix × 4Npix matrix. In the
presence of nontrivial baseline-dependent DDE involving nondiagonal Mueller matrices, the
problem becomes more complex. However, we show below that under some assumptions, the
operator
would involve estimating the point spread function (PSF) centered on the location of each
pixel and inverting a
4Npix × 4Npix matrix. In the
presence of nontrivial baseline-dependent DDE involving nondiagonal Mueller matrices, the
problem becomes more complex. However, we show below that under some assumptions, the
operator 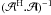 (sometimes called the deconvolution matrix) affected by DDE is
decomposable in a classical deconvolution matrix (containing information on the PSF), and
a simple correction performed separately on each pixel.
(sometimes called the deconvolution matrix) affected by DDE is
decomposable in a classical deconvolution matrix (containing information on the PSF), and
a simple correction performed separately on each pixel.
Following the notation introduced above, we can write
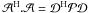 as a 4Npix × 4Npix matrix, with
as a 4Npix × 4Npix matrix, with
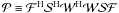 of size
4NblocksNpix × 4NblocksNpix.
The latter matrix is block diagonal, and each of its
4Npix × 4Npix blocks describes
the PSF of the instrument for a given baseline-time-frequency block. Their
4 × 4 xy-blocks are scalar matrices, the scalar
pt,ν,pq(x,y) being the
response of the instrument evaluated at the yth pixel to a source being
centered at the xth pixel in the given baseline-time-frequency block. We
then have
of size
4NblocksNpix × 4NblocksNpix.
The latter matrix is block diagonal, and each of its
4Npix × 4Npix blocks describes
the PSF of the instrument for a given baseline-time-frequency block. Their
4 × 4 xy-blocks are scalar matrices, the scalar
pt,ν,pq(x,y) being the
response of the instrument evaluated at the yth pixel to a source being
centered at the xth pixel in the given baseline-time-frequency block. We
then have  = \displaystyle\sum\limits_{t,\nu,pq}p_{t,\nu,pq}(x,y)\mathcal{D}^{\rm H}_{t,\nu,pq}(y)\mathcal{D}_{t,\nu,pq}(x). \label{eq:aproj5} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq77.png) (5)It
is virtually impossible to compute this matrix, and this illustrates the difficulty of
doing an image plane deconvolution in the presence of time-frequency-baseline dependent
DDE. To apply a first-order correction to the image plane, we assume that the DDE are
constant enough across time, frequency, and baseline. Then we can write
(5)It
is virtually impossible to compute this matrix, and this illustrates the difficulty of
doing an image plane deconvolution in the presence of time-frequency-baseline dependent
DDE. To apply a first-order correction to the image plane, we assume that the DDE are
constant enough across time, frequency, and baseline. Then we can write
 \sim N_{t,\nu,pq} p(x,y)\overline{\mathcal{D}^{\rm H}\mathcal{D}}(x,y) $$](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq78.png) where
Nt,ν,pq is the number of
baseline-time-frequency blocks,
where
Nt,ν,pq is the number of
baseline-time-frequency blocks, 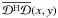 is a 4 × 4 matrix that is
the average of
is a 4 × 4 matrix that is
the average of 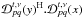 over baselines, time, and
frequency, and p(x,y) is the PSF stacked in baselines,
time, and frequency. If the uv-coverage is good enough, then
over baselines, time, and
frequency, and p(x,y) is the PSF stacked in baselines,
time, and frequency. If the uv-coverage is good enough, then
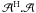 is block diagonal (p(x,y) = 0 for
x ≠ y, p(x,y) = 1
otherwise). All the x ≠ y terms cancel out in the final
product, and in the relevant part of the
is block diagonal (p(x,y) = 0 for
x ≠ y, p(x,y) = 1
otherwise). All the x ≠ y terms cancel out in the final
product, and in the relevant part of the 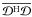 matrix the Npix 4 × 4 blocks are on the diagonal. Applying
matrix the Npix 4 × 4 blocks are on the diagonal. Applying
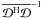 to
to 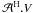 can then be done on each pixel separately, by computing the product
can then be done on each pixel separately, by computing the product
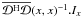 , where
Ix contains the full polarization
information
(XXx,XYx,YXx,XYx)
for the xth pixel. This provides a way to estimate an approximate
least-square clean-component value from a flux density in the dirty image in a given
direction sx. The details of
this image-plane normalization are discussed further in Sect. 3.1. Although a few assumptions underlie this normalization, from the
simulations presented in Sect. 4.3 we argue that the
complex 4 × 4 matrix normalization per pixel presented here brings clear improvement.
However, it does not seem necessary for the sky solutions to convergence (see Sect. 7).
, where
Ix contains the full polarization
information
(XXx,XYx,YXx,XYx)
for the xth pixel. This provides a way to estimate an approximate
least-square clean-component value from a flux density in the dirty image in a given
direction sx. The details of
this image-plane normalization are discussed further in Sect. 3.1. Although a few assumptions underlie this normalization, from the
simulations presented in Sect. 4.3 we argue that the
complex 4 × 4 matrix normalization per pixel presented here brings clear improvement.
However, it does not seem necessary for the sky solutions to convergence (see Sect. 7).
3. Implementation of A-Projection for LOFAR
As explained above, the full polarization A-Projection scheme has been described in Bhatnagar et al. (2008). However, for the VLA implementation only the diagonal Mueller matrix terms had to be taken into account. As explained in Sect. 2, LOFAR has very wide fields of view, and the baseline-dependent Mueller matrices associated to the four-polarization correlation products are nondiagonal. This basically means that each individual polarization cannot be treated independently of the others. In this section we describe in detail a few implementations of A-Projection that allow correcting for the nondiagonal Mueller matrices. We propose optimizations in relation to the telescope architecture. We show in Sect. 4 that this algorithm can indeed deal with the heavily nondiagonal Mueller matrices associated with LOFAR’s wide fields of view.
Following Bhatnagar et al. (2008), we built our
implementation of A-Projection on top of a traditional Cotton & Schwab CLEAN
algorithm (Schwab 1984). It is an iterative
deconvolution algorithm that consists of two intricate steps. The CLEAN and A-Projection
algorithms perform a series of operations that can be described in the following way:
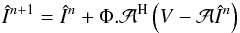 (6)where
the true sky estimate În + 1
at step n + 1 is built from its estimate
În at step n and Φ is a
nonlinear operator. It basically estimates the deconvolved sky from the residual dirty image
(6)where
the true sky estimate În + 1
at step n + 1 is built from its estimate
În at step n and Φ is a
nonlinear operator. It basically estimates the deconvolved sky from the residual dirty image
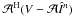 .
The minor cycle performs operations that approximate
.
The minor cycle performs operations that approximate 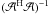 as discussed in Sect. 2, and takes the estimated image
vector to zero but at the strongest components above a certain threshold. For the sky
solutions to converge, the predict step
as discussed in Sect. 2, and takes the estimated image
vector to zero but at the strongest components above a certain threshold. For the sky
solutions to converge, the predict step 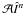 or degridding) has to be accurate and unbiased. A-Projection is a fast way
to apply
or degridding) has to be accurate and unbiased. A-Projection is a fast way
to apply 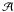 or
or 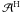 .
If we separate the phase of the Fourier kernel in Eq. (1) as the sum of
φ0(u,v,s) = u.l + v.m
and
.
If we separate the phase of the Fourier kernel in Eq. (1) as the sum of
φ0(u,v,s) = u.l + v.m
and 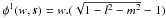 , then
following Bhatnagar et al. (2008) invoking the
convolution theorem Eq. (1) becomes
, then
following Bhatnagar et al. (2008) invoking the
convolution theorem Eq. (1) becomes
![\begin{eqnarray} \label{eq:aproj} V^{t,\nu}_{pq}(u,v,w,i)&=& \mathcal{F}\left(\displaystyle\sum\limits^4_{j=1}\mathcal{D}_{pq}^{t,\nu}(i,j,\vec{s})W(w,\vec{s}) I_j(l,m)\right) \nonumber\\ &=& \displaystyle\sum\limits^4_{j=1}\bigg[ \mathcal{F} \left( \mathcal{D}_{pq}^{t,\nu}(i,j,\vec{s}) W(w,\vec{s}) \right)\nonumber\\ && \ \ \ \ \ *\ \mathcal{F} \left( I_j\left( l,m \right) \right) \bigg] \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq105.png) (7)where
∗ is the convolution product, ℱ is a 2D Fourier transform,
(7)where
∗ is the convolution product, ℱ is a 2D Fourier transform,
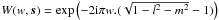 , and
i and j index the polarization number (running over (XX,
XY, YX, YY)). This method is efficient because the DDE are smooth on the
sky, meaning the support of the corresponding convolution function can be small (no high
frequency terms). Indeed, as shown in Fig. 1 the LOFAR
station beam is very smooth, and depending on the field of view, the typical support is of
the order of 5–11 pixels.
, and
i and j index the polarization number (running over (XX,
XY, YX, YY)). This method is efficient because the DDE are smooth on the
sky, meaning the support of the corresponding convolution function can be small (no high
frequency terms). Indeed, as shown in Fig. 1 the LOFAR
station beam is very smooth, and depending on the field of view, the typical support is of
the order of 5–11 pixels.
3.1. Naive implementation
The operation 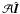 in Eq. (6) converts a sky model into
visibilities. To apply this operator to a massive amount of data in an algorithmically
efficient way, we apply the scheme outlined in Eq. (7). First a two-dimensional, fast Fourier transform (FFT) is applied to
the sky model image Î, independently on the 4 polarizations. Then for
each baseline in a time-frequency block Δ(t,ν), where the DDE are assumed
to be constant, the 16 convolution functions are computed as the Fourier transform of the
image plane Kronecker product of the DDE. For the LOFAR beam on a given baseline this
block is typically 10 min and 0.2 MHz wide. The residual visibilities in each polarization
are interpolated from the sum in Eq. (7).
In practice, to minimize the support of the W-term and associated aliasing effects, we
multiply the DDE in the image plane by a Prolate spheroidal function (see Appendix B for more details).
in Eq. (6) converts a sky model into
visibilities. To apply this operator to a massive amount of data in an algorithmically
efficient way, we apply the scheme outlined in Eq. (7). First a two-dimensional, fast Fourier transform (FFT) is applied to
the sky model image Î, independently on the 4 polarizations. Then for
each baseline in a time-frequency block Δ(t,ν), where the DDE are assumed
to be constant, the 16 convolution functions are computed as the Fourier transform of the
image plane Kronecker product of the DDE. For the LOFAR beam on a given baseline this
block is typically 10 min and 0.2 MHz wide. The residual visibilities in each polarization
are interpolated from the sum in Eq. (7).
In practice, to minimize the support of the W-term and associated aliasing effects, we
multiply the DDE in the image plane by a Prolate spheroidal function (see Appendix B for more details).
The predicted visibilities are removed from the measured visibilities by computing the
residual visibilities 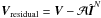 . Then
. Then
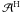 applies a correction to the residual visibilities, projects the result onto a grid (the
gridding step) and Fourier transforms it. In practice this is done as
applies a correction to the residual visibilities, projects the result onto a grid (the
gridding step) and Fourier transforms it. In practice this is done as
![\begin{eqnarray} V^{(t,\nu),(p,q)}_{\textrm{corr},u,v,w,i} &=& \displaystyle\sum\limits^4_{j=1}\bigg( \mathcal{F} \left( \mathcal{D}_{pq}^{*t,\nu}\left(j,i,\vec{s}\right) W^*\left(w,\vec{s}\right) \right)\nonumber\\ && \ \ \ \ \ *\ V^{(t,\nu),(p,q)}_{\textrm{residual},u,v,j}\bigg)\bigg]\bigg) \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq114.png) (8)and
(8)and
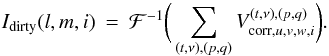 (9)The
resulting dirty image is still corrupted by the phased-array beam-related effects
discussed in Sect. 2.2. Before the minor cycle we can
either multiply each xth four-polarization
Idirty(x) pixel by the 4 × 4 matrix
(9)The
resulting dirty image is still corrupted by the phased-array beam-related effects
discussed in Sect. 2.2. Before the minor cycle we can
either multiply each xth four-polarization
Idirty(x) pixel by the 4 × 4 matrix
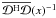 ,
or simply normalize each polarization of Idirty by
,
or simply normalize each polarization of Idirty by
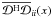 , the diagonal elements of
, the diagonal elements of
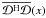 . As shown in Sect. 4.3, fully applying
. As shown in Sect. 4.3, fully applying
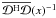 to each pixel in Idirty lead to a minor improvement.
to each pixel in Idirty lead to a minor improvement.
The computational cost of taking DDE into account using A-Projection depends on
(i) whether its baseline dependence; (ii) the angular size at which the effect needs to be
sampled (thereby constraining the size support of the convolution function); and (iii) the
amplitude of the terms of the 4 × 4 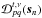 matrix. In the case of the full
polarization A-Projection, the data need to be corrected per baseline, time, and frequency
slot. For each of those data chunks, to recover the corrected four-polarization
visibilities, one needs to take all 16 terms of the
4 × 4
matrix. In the case of the full
polarization A-Projection, the data need to be corrected per baseline, time, and frequency
slot. For each of those data chunks, to recover the corrected four-polarization
visibilities, one needs to take all 16 terms of the
4 × 4 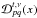 Mueller matrix into account,
along with the four visibilities built from the 2D Fourier transform of the sky model.
Therefore in addition to the 16 convolution function estimates per baseline and
time-frequency slot, in the gridding and degridding steps one needs to compute
Mueller matrix into account,
along with the four visibilities built from the 2D Fourier transform of the sky model.
Therefore in addition to the 16 convolution function estimates per baseline and
time-frequency slot, in the gridding and degridding steps one needs to compute
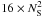 operations
per four-polarization visibility point, where NS is the
support of the convolution function. The algorithmic complexity is discussed further in
Sect. 4.4, but this implementation is too slow to
be practical.
operations
per four-polarization visibility point, where NS is the
support of the convolution function. The algorithmic complexity is discussed further in
Sect. 4.4, but this implementation is too slow to
be practical.
3.2. Separating antenna beam pattern and beam-former effects
Depending on the assumptions and system architecture one can find powerful algorithmic
optimizations. We show here that in the case of LOFAR, we can use the fact that although
stations are rotated with respect to each other, the elementary antennas are parallel. The
effective phased-array beam
Bp,s of
station p is modeled as
Bp,s = ap,s.Ep,s,
where ap,s is
the array factor, and
Ep,s is the
element beam pattern. The term
ap,s
depends on the phased array geometry and on the delays applied to the signal of the
individual antennas before the summation (by the beam-former of each
individual LOFAR stations). The term
Ep,s
models both the individual element antenna sensitivity over the sky and its projection on
the sky. We have 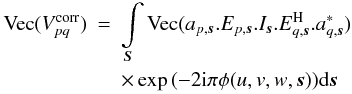 (10)where
ap,s is
scalar valued and
Ep,s
nondiagonal because (intuitively) the element beam projection on the sphere depends on the
direction. Applying the convolution theorem to Eq. (10) we obtain
(10)where
ap,s is
scalar valued and
Ep,s
nondiagonal because (intuitively) the element beam projection on the sphere depends on the
direction. Applying the convolution theorem to Eq. (10) we obtain ![\begin{eqnarray} \label{eq:sepel} \textrm{Vec}(V^{\rm corr}_{pq}) &=& \mathcal{F}[E^*_{q,\vec{s}} \otimes E_{p,\vec{s}}]\nonumber\\[4mm] &&*\ \mathcal{F} \left[a_{p,\vec{s}}.a^*_{q,\vec{s}}.\exp{\left(-2 {\rm i}\pi \phi^{1}(w,\vec{s})\right)}\right] \nonumber\\[4mm] &&*\int\limits_{\vec{S}} I_{\vec{s}} .\exp{\left(-2 {\rm i} \pi \phi^{0}(u,v,\vec{s})\right)} {\rm d}\vec{s}. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq130.png) (11)All
LOFAR stations have different layouts on the ground, so the scalar-valued array factor
ap,s is
station dependent. However, all individual antennas of all stations point in the same
direction, and we can assume that the Mueller matrix is baseline independent, i.e.
(11)All
LOFAR stations have different layouts on the ground, so the scalar-valued array factor
ap,s is
station dependent. However, all individual antennas of all stations point in the same
direction, and we can assume that the Mueller matrix is baseline independent, i.e.
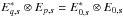 .
Although this requires an additional correction step of the gridded uv-plane visibilities,
as we see below this is an interesting algorithmic shortcut because the element-beam
correction can be applied to the baseline-stacked grids.
.
Although this requires an additional correction step of the gridded uv-plane visibilities,
as we see below this is an interesting algorithmic shortcut because the element-beam
correction can be applied to the baseline-stacked grids.
The element beam is very smooth over the sky, and in most cases it can be assumed to be
constant on time scales of an hour, so that the polarization correction step does not need
to be applied often. The degridding step goes as follows. (i) In each time-frequency slot
Δ(t,ν)E where the Mueller matrix of the element beam is
assumed to be constant, the polarization correction is applied to the (XX, XY, YX, YY)
grids as the sum of convolved grids by the terms of
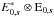 .
We then loop3 over baseline (pq),
and time-frequency range Δ(t,ν)a where the
array factor and w-coordinate are assumed to be constant
within Δ(t,ν)E. For each step in the loop; (ii) the
oversampled convolution function for baseline (pq) is estimated in
Δ(t,ν)a for the term in the second line of
Eq. (11); and (iii) it is used to
interpolate the predicted visibilities at the given uv-coordinate, separately on each
polarization.
.
We then loop3 over baseline (pq),
and time-frequency range Δ(t,ν)a where the
array factor and w-coordinate are assumed to be constant
within Δ(t,ν)E. For each step in the loop; (ii) the
oversampled convolution function for baseline (pq) is estimated in
Δ(t,ν)a for the term in the second line of
Eq. (11); and (iii) it is used to
interpolate the predicted visibilities at the given uv-coordinate, separately on each
polarization.
As explained in Sect. 4.4, the computing time for estimating the convolution functions can be quite significant, and this scheme allows us to compute only one convolution function per baseline instead of 16, and 4 gridding/degridding steps instead of 16. We note, however, that the assumption of baseline independence of the Mueller matrix on which this optimization is based starts to become invalid in case of direction-dependent differential Faraday rotation, or for the longer baselines where the curvature of the earth starts to be important (in that case the element beams are not parallel). As discussed in Sect. 4.4, the computing time of this implementation is dominated by the convolution function estimate.
3.3. Separating the W-term: hybrid w-stacking
The support of the A-term is determined by the minimum angular scale to be sampled in the image plane. The beam or ionospheric effects are in general very smooth on the sky so that only small numbers of pixels are needed to fully describe the effects, thus corresponding to a small convolution function support size (typically 11 × 11 pixels). The highest spatial frequency in the image plane is the W-term and its support can be as large as ~500 × 500 pixels for the long baselines in wide fields of view, when the target field is at low elevation. This forces us to (i) compute a convolution function with a large support; and (ii) grid each individual baseline using the large, W-term-dominated convolution function.
We note, however, that the W-term is in itself baseline independent4: two baselines characterized by different ionosphere and beams, but
with the same w-coordinate, will have the same W-term. We therefore slightly changed the
piping of the algorithm at this point by taking the A-Term and the W-term into account
separately, as follows ![\begin{eqnarray} \label{eq:wstack} \textrm{Vec}(V^{\rm corr}_{pq}) &=& \mathcal{F}[E^*_{\vec{s}} \otimes E_{\vec{s}}]\nonumber\\ && *\ \mathcal{F}\left[\exp{\left(-2 {\rm i} \pi \phi^{1}(w_{\rm plane},\vec{s})\right)}\right]\nonumber \\ && *\ \mathcal{F}\left[a_{p,\vec{s}}.a^*_{q,\vec{s}}.\exp{\left(-2 {\rm i} \pi \phi^{1}(\Delta w,\vec{s})\right)}\right]\nonumber\\ &&*\int\limits_{\vec{S}} I_{\vec{s}} .\exp{\left(-2 {\rm i} \pi \phi^{0}(u,v,\vec{s})\right)} {\rm d}\vec{s}. \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq138.png) (12)We
consecutively grid or degrid the data in w-slices, i.e., which have similar w-coordinates.
This algorithm is also known as W-stacking5. In
addition, we take into account that the points can lie either above or below the
associated w-plane central coordinate, using the term
exp(−2iπφ1(Δw,s)),
where Δw = w − wplane. This
step is similar to the traditional w-projection algorithm. If we have enough w-stacking
planes, Δw is small, and the support of the baseline-time-frequency
dependent convolution function remains small, leading to a dramatic decrease in the total
convolution function estimation time. Conversely, given a convolution function support we
can find the maximum usable Δw and derive the number of w-stacking planes
as a function of the observation’s maximum w coordinate (see Sect. 4.4.3 for more detailed discussion). In the case of
LOFAR, choosing a convolution function support of ~21 pixel gives a number of w-stacking
planes of ~30.
(12)We
consecutively grid or degrid the data in w-slices, i.e., which have similar w-coordinates.
This algorithm is also known as W-stacking5. In
addition, we take into account that the points can lie either above or below the
associated w-plane central coordinate, using the term
exp(−2iπφ1(Δw,s)),
where Δw = w − wplane. This
step is similar to the traditional w-projection algorithm. If we have enough w-stacking
planes, Δw is small, and the support of the baseline-time-frequency
dependent convolution function remains small, leading to a dramatic decrease in the total
convolution function estimation time. Conversely, given a convolution function support we
can find the maximum usable Δw and derive the number of w-stacking planes
as a function of the observation’s maximum w coordinate (see Sect. 4.4.3 for more detailed discussion). In the case of
LOFAR, choosing a convolution function support of ~21 pixel gives a number of w-stacking
planes of ~30.
This requires yet an additional step as compared to the implementation described in
Sect. 3.2, the degridding
step 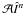 ,
which can be described as follows. First, following the notation introduced above, (i) in
each time-frequency interval Δ(t,ν)E we correct the
four-polarization grids from the element beam (including projection effects) using
,
which can be described as follows. First, following the notation introduced above, (i) in
each time-frequency interval Δ(t,ν)E we correct the
four-polarization grids from the element beam (including projection effects) using
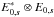 .
Then (ii) we loop over the number of w-planes (ranging from
−wmax to wmax, see Sect. C), and convolve the grid obtained in (i) by the
associated w-term (appearing in the second line of 12). Finally in (iii) for each w-plane obtained in each step of the
loop (ii), we loop over the set of baselines (pq)w and the
time-frequency range Δ(t,ν)a,w associated
with the given w-plane. We interpolate the predicted visibilities at the given
uv-coordinate, separately for each polarization, based on the oversampled
.
Then (ii) we loop over the number of w-planes (ranging from
−wmax to wmax, see Sect. C), and convolve the grid obtained in (i) by the
associated w-term (appearing in the second line of 12). Finally in (iii) for each w-plane obtained in each step of the
loop (ii), we loop over the set of baselines (pq)w and the
time-frequency range Δ(t,ν)a,w associated
with the given w-plane. We interpolate the predicted visibilities at the given
uv-coordinate, separately for each polarization, based on the oversampled
![\hbox{$\mathcal{F}[a_{p,\vec{s}}.a^*_{q,\vec{s}}.\exp{(-2 {\rm i}\pi \phi^{1}(\Delta w,\vec{s}))}]$}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq148.png) convolution function. As
discussed in Sect. 4.4.3, this is the fastest
implementation of A-Projection we have obtained so far.
convolution function. As
discussed in Sect. 4.4.3, this is the fastest
implementation of A-Projection we have obtained so far.
4. Simulations
 |
Fig. 3 Essential part of the A-Projection algorithm relies on the predict step, which transforms a 2D sky image (the projection of the celestial sphere on a plane) into a set of visibilities. We have simulated a dataset having one off-axis source, where the true visibilities (black dashed line) have been estimated using Eq. (1), taking the beam into account. This plot shows the comparison in all measured polarizations between the exact value of the visibility of a given baseline and the A-Projection estimate (gray line). Contrary to a traditional predict step, the visibilities are modulated by the beam amplitude (dotted line), and we have time-dependent polarization leakage. The overplotted graph shows a zoom in the small region shown in the top-right panel. In the degridding step, we use a computationally efficient closest-neighbor interpolation, creating steps in the predicted visibilities. |
 |
Fig. 4 Dramatic differences between the estimated deconvolved sky when using three different modified CLEAN algorithms on a simulated dataset containing 100 sources. The visibilities have been generated by taking (i) the individual antennas; (ii) their projection on the sky and (iii) the beam-forming step (the scalar array factor) into account. The top-left image shows the deconvolved sky as estimated with a traditional imager not taking time, frequency, baseline, direction-dependent effects into account. The top right and lower left images have been generated by considering, respectively, the array factor only and both the array factor and the element beam. The lower right panel shows that the input flux densities are correctly recovered. |
To test the algorithmic framework described above, we performed a series of tests on LOFAR simulated datasets. In this section we summarize those results and discuss the computational costs of A-Projection for LOFAR.
4.1. One off-axis strongly polarized source
As discussed above, by using A-Projection we can compute the exact value
of the four-polarization visibilities on a given baseline at a given time and frequency,
from (i) the sky model and (ii) the baseline-time-frequency-direction dependent effects.
In a first step, we focus on testing the full polarization A-Projection degridding (or
predict) step (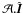 ).
The accuracy of this step is vital for the convergence of the CLEAN/A-Projection
algorithm. Our experience suggests that any small numerical systematic bias in this
operation can lead to strong divergence of CLEAN.
).
The accuracy of this step is vital for the convergence of the CLEAN/A-Projection
algorithm. Our experience suggests that any small numerical systematic bias in this
operation can lead to strong divergence of CLEAN.
To test this transformation, we simulated a dataset having only one strongly polarized off-axis point-like source in a low-band 62 MHz LBA dataset. The four-polarization visibilities were generated using BBS (BlackBoard Selfcal6), which directly calculates the visibilities following Eq. (1). It takes the beams of the individual elementary antennas into account (and their projection on the sky), as well as the phasing of the individual antenna within a LOFAR station (the array factor). We located the simulated source a few degrees from the phase center, and its flux density is strongly polarized, in a nonphysical way (with Stokes parameters of I,Q,U,V = 100, 40, 20, 10 Jy). Figure 3 shows the real part of BBS and A-Projection predicted visibilities on baseline (01). The residuals are centered at zero, and A-Projection performs very well in predicting the four-polarization visibilities, taking the complicated effects of the LOFAR phased array station beams into account. A traditional predict using simple Fourier transform, facets, or W-Projection would suffer from much higher residuals, driving systematics in the deconvolution, and thereby limiting the dynamic range. Here the residual errors are dominated by the type of interpolation we use in the uv domain (closest neighborhood, see Appendix B for details).
4.2. Dataset with many sources
4.2.1. LOFAR station beam
To test our modified implementation of the entire CLEAN algorithm (involving gridding and degridding steps), we simulated a dataset containing 100 sources, with the source count slope following the 1.4 GHz NVSS source count (Condon et al. 1998). Most of these sources have flux densities between 10-2 and 1 Jy, to which we added two much stronger sources of 100 and 10 Jy, respectively.
As in the dataset described above, the visibilities are generated using BBS6. We have considered the Jones matrices of the individual
elementary antennas, as well as the array-factor (the beam-forming step). As explained
in Sect. 3.2 and shown in Fig. 3, because the LOFAR stations are rotated with respect to each other,
all baselines will be affected differently by beam effects. We have applied first-order
corrections for the beam effect to the visibilities by computing
![\hbox{$V^{t,\nu}_{pq,{\rm corr}}=[D^{t,\nu}_p]^{-1}_{\vec{s}_0}V^{t,\nu}_{pq}[D^{t,\nu,H}_q]^{-1}_{\vec{s}_0}$}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq152.png) ,
where
Dp(s0)
is the Jones matrix of station p computed at the center of the field.
This mostly compensates for the element beam effects, in particular the projection of
the dipoles on the sky. However, as shown below, the LOFAR fields are large, and the
projections of the dipoles vary across the field of view.
,
where
Dp(s0)
is the Jones matrix of station p computed at the center of the field.
This mostly compensates for the element beam effects, in particular the projection of
the dipoles on the sky. However, as shown below, the LOFAR fields are large, and the
projections of the dipoles vary across the field of view.
Figure 4 shows the restored images produced using three different modified CLEAN algorithms. Each of the images is ~3000 × 3000 pixels in size, and is ~6 degrees wide. We used 15 w-stackings, 128 Δw-planes (see Sect. 3.3), a maximum baseline of 5 kλ, a Briggs7 weighting scheme, a cycle factor of 2.5 and 10 000 minor cycle iterations. The first map was generated using W-Projection (Cornwell et al. 2008) as implemented in CASA8. Strong artifacts are present around the brightest off-axis source, and the dynamic range is only 1:230. In the second image we used our implementation of A-Projection taking the array factor only into account. This has reduced the effect of the residual visibility levels on each individual baselines and raised the dynamic range to ~1:3.400. In the third image we have taken into account all LOFAR beam effects: individual antenna sensitivity, spatially varying projections, and the array factor. The dynamic range increased to ~1:12.000 9.
The source flux densities in the restored maps were determined using the LOFAR source extraction software pyBDSM10. As shown in Fig. 4, the input flux densities are very well recovered.
4.2.2. LOFAR station beam and the ionosphere
To test the ionospheric correction with A-Projection, we simulated a dataset containing 100 sources, affected by a simulated ionosphere. The ionospheric effects essentially consist of a purely scalar, direction-dependent phase, without including Faraday rotation. In addition to these purely scalar ionospheric phase effects, the visibilities are affected by the direction-dependent LOFAR station beam effects discussed above.
 |
Fig. 5 Dirty images at the location of a bright source in a simulated dataset. The images are 1deg in diameter. Without applying the A-Projection correction for an ionospheric phase screen (left panel) the dirty image shows important distortions as a result of ionospheric effects. Application of this correction (right panel) clearly shows improvements. |
The ionosphere is modeled as an infinitesimally thin layer at a height of 200 km. The total electron content (TEC) values at a set of sample points11 are generated by a vector autoregressive random process. As described in van der Tol (2009) the spatial correlation is given by Kolmogorov turbulence, and the TEC values needed to construct the phase screen are determined using Kriging interpolation.
 |
Fig. 6 This figure shows the deconvolved image synthesized from the simulated dataset described in Sect. 4.2.2. In the left panel, the ionospheric effects are not taken into account, and our deconvolution scheme naturally produces severe artifacts and high residuals in the reconstructed sky. The deconvolved image shown in the right panel has been estimated using our implementation of A-Projection with the time-dependent ionospheric phase screen. |
Figure 5 shows dirty images at the location of a bright source before and after A-Projection correction of beam and ionosphere. This suggests that the dirty undistorted sky is properly recovered from the corrupted visibilities. We compare in Fig. 6 the cleaned image with and without the A-Projection correction. These simulations demonstrate that A-Projection can indeed deal with the complicated effects associated with the ionosphere.
 |
Fig. 7 The evolution of the estimated flux density as a function of the major cycle iteration for one polarized off-axis source. From top to bottom, and left to right, the panels show results generated by using (i) W-Projection only; (ii) AW-Projection with the array factor only; (iii) AW-Projection taking the full beam model into account; and (iv) image plane corrections as described in Sect. 2.2. |
4.3. Convergence
We have also studied the influence of the various corrections described in this paper on the convergence speed of the flux densities estimated through the major cycle loop. For this we used the dataset described in Sect. 4.1 containing one off-axis source having Stokes parameters (IQUV) = (100,40,20,10) Jy.
Figure 7 shows the evolution of the estimated flux density as a function of the major cycle iteration number for different algorithms. Using only the W-Projection merely shows a weak convergence towards the observed flux density (i.e., to the “beam-multiplied” sky). The situation improves somewhat when we apply a full polarization A-Projection without the element beam (therefore assuming the dipole projections on the sky are constant across the field of view). We note that in the absence of polarization, the situation is not as bad. Taking the element beams into account, the algorithm makes the estimated flux densities converge to the true values to within one percent. In this version of the algorithm, the image plane correction is the same in all polarizations and just a scalar, the average primary beam normalization. The situation improves slightly in terms of convergence speed by applying the image-plane renormalization described in Sect. 2.2.
In any case, the accuracy of the recovered flux densities seems to be guaranteed by the accuracy of the degridding step. Our experience in implementing A-Projection suggests that any small systematic error in the degridding step can lead to biases in the recovered flux densities or even to divergence in the more severe cases. Adding the image-plane polarization correction seems to improve the convergence speed, but does not appears to be necessary.
4.4. Computational and memory-related costs
Given the large amount of data that has to be processed for imaging an interferometric dataset, reducing the algorithmic complexity is of primary importance.
4.4.1. Memory-related issues
The A-term is generally very smooth in the image plane, with corresponding small support convolution functions, and under those conditions the A-Projection algorithm is virtually free interms of computing time as explained in Bhatnagar et al. (2008) (and in Cornwell et al. 2008, in the case of W-Projection): the A-term and the low w-coordinate convolution function support is less than, or comparable to, the spheroidal function support that needs to be applied anyway in a traditional gridder/degridder. However, as described in Sect. 3.2, all LOFAR stations are rotated with respect to each other, and the synthesized stations beams are all different in a given direction. This gives rise to a serious algorithmic complication because it makes convolution functions baseline-dependent: the number of possible convolution functions are 16 × Ntimes × NFreqs × NStations × (NStations − 1)/2. With ~800 to ~1500 baselines, even with only one convolution function every ten minutes, a typical observing run of eight hours, one frequency channel, and an average support size of ~30 pixels (taking the w-term into account), this requires ~100 Gbytes of storage. This is optimistic because in the case of other DDE such as the ionosphere, the A-term will have to be evaluated every 30 s. Even if the storage is done at the minimum necessary resolution, those numbers are clearly prohibitive for storing the convolution into memory. The convolution functions therefore have to be computed on the fly, and algorithmically, this represents an additional cost.
4.4.2. Naive and element-beam-separated A-Projection
The LOFAR station beams are smooth on the sky, and the corresponding convolution
function supports are small (typically 11–15 pixel complex images), while the W-term
needs up to ≳ 500 pixels depending on the w-coordinate (with an average of
~30 pixels). The computing time depends on the convolution function
support NS, and for the implementations described in
Sects. 3.1 and 3.2, we have  (13)where
the subscripts S, Ap,
Aq and W stand for the
prolate spheroidal (~7–11 pixels), A-terms of antenna p
and q, and W-term, respectively. For a typical field-of-view, we have
NS(A) = 9−15 and
(13)where
the subscripts S, Ap,
Aq and W stand for the
prolate spheroidal (~7–11 pixels), A-terms of antenna p
and q, and W-term, respectively. For a typical field-of-view, we have
NS(A) = 9−15 and
 ,
where D is the field-of-view diameter and w is the
W-coordinate of the given baseline in the given time-slot (see Appendix B). For that baseline, time and frequency slot we can
write the total computing time as
,
where D is the field-of-view diameter and w is the
W-coordinate of the given baseline in the given time-slot (see Appendix B). For that baseline, time and frequency slot we can
write the total computing time as  , where
, where
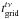 and
and
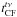 are the
estimated gridding and convolution function times, respectively. For LOFAR data, in most
cases we
have NS ~ NS(W)
and
are the
estimated gridding and convolution function times, respectively. For LOFAR data, in most
cases we
have NS ~ NS(W)
and 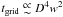 . Our experience has
shown that tCF is dominated by the computing time of the
Fourier transform of the zero-padded convolution function (see Fig. 8), whose size is
. Our experience has
shown that tCF is dominated by the computing time of the
Fourier transform of the zero-padded convolution function (see Fig. 8), whose size is 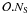 ,
where
,
where 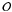 is the oversampling parameter that controls the quality of the nearest neighborhood
interpolation. If
is the oversampling parameter that controls the quality of the nearest neighborhood
interpolation. If 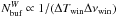 is the number of
visibility buffers associated with the W-plane (ΔTwin and
Δνwin are the time/frequency window intervals in which the
DDE are assumed to be constant), then we have
is the number of
visibility buffers associated with the W-plane (ΔTwin and
Δνwin are the time/frequency window intervals in which the
DDE are assumed to be constant), then we have 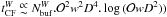 . The gridding time for a
given w-plane is simply
. The gridding time for a
given w-plane is simply 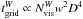 , where
, where
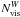 is the
number of visibilities associated with the w-plane. The total computing time can then be
written as
is the
number of visibilities associated with the w-plane. The total computing time can then be
written as ![\begin{eqnarray} t_{\rm tot}\sim N_{\rm el}t_{\rm el}+ \bigg( \displaystyle\sum\limits_{W-{\rm planes}}\bigg[at^W_{\rm grid}+bt^W_{\rm CF}\bigg]\bigg) \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq183.png) (14)where
a and b are constants,
Nel the number of time/frequency blocks in which the
element beam is assumed to be constant, and
(14)where
a and b are constants,
Nel the number of time/frequency blocks in which the
element beam is assumed to be constant, and  is the computing time needed to
apply the element beam to the grids (c = 16 for full polarization
imaging, and c = 8 for only I-stokes). For the
implementation described in Sect. 3.1, we have
tel = 0, but both a
and b are 16 times higher (8 for only I-stokes) than
in the case of the algorithm described in Sect. 3.2. Figure 8 shows the estimated gridding
and convolution function times as a function of the w-coordinate of the given baseline
in the given time slots. From this figure it is clear that the W-term is the most
important limiting factor and that the estimate of the convolution function represents a
major limitation of those implementations, especially in cases of a rapidly varying DDE,
such as the ionosphere, where the convolution function calculation would largely
dominate.
is the computing time needed to
apply the element beam to the grids (c = 16 for full polarization
imaging, and c = 8 for only I-stokes). For the
implementation described in Sect. 3.1, we have
tel = 0, but both a
and b are 16 times higher (8 for only I-stokes) than
in the case of the algorithm described in Sect. 3.2. Figure 8 shows the estimated gridding
and convolution function times as a function of the w-coordinate of the given baseline
in the given time slots. From this figure it is clear that the W-term is the most
important limiting factor and that the estimate of the convolution function represents a
major limitation of those implementations, especially in cases of a rapidly varying DDE,
such as the ionosphere, where the convolution function calculation would largely
dominate.
4.4.3. Hybrid W-stacking and A-Projection
As explained in Sect. 3.3 for the W-staking
implementation, the baseline-time-frequency-dependent oversampled convolution function
is the Fourier transform of the zero-padded image-plane product of the spheroidal and
A-terms, plus a W-term accounting for the Δw-distance between the given
visibilities and the corresponding w-planes. The larger the support of the convolution
function, the fewer w-planes we need to fully correct for the w-term. As explained in
Appendix B, in order to properly sample the
w-term in the image plane, to a given w-coordinate and field of view corresponds a
certain convolution function support. We can then obtain
Δw = a.NS/D2
(with 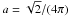 ), and
the necessary number of w-planes between −wmax and
wmax is
NW = wmaxD2/(a.NS).
Because we compute the W-term convolution in the image plane, the cost of this step is
), and
the necessary number of w-planes between −wmax and
wmax is
NW = wmaxD2/(a.NS).
Because we compute the W-term convolution in the image plane, the cost of this step is
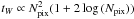 . The total computing time is
then
. The total computing time is
then ![\begin{eqnarray} t_{\rm tot} \sim bN_{\rm vis}N_{\rm S}^2+cN_{\rm buf}\mathcal{O}^2N_{\rm S}^2\log (\mathcal{O}N_{\rm S}) +N_{\rm el} \left[t_{\rm el}+N_Wt_W\right] \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq198.png) (15)where
Nel is the number of time/frequency buffers in which the
element beam is assumed to be constant, Nbuf is the number
of time/frequency buffers in which the A-/Δw-terms are assumed to be
constant, and b and c are constants. In Table 1 we present the typical computing times for a major
cycle with the implementation discussed here and presented in Sect. 3.3.
(15)where
Nel is the number of time/frequency buffers in which the
element beam is assumed to be constant, Nbuf is the number
of time/frequency buffers in which the A-/Δw-terms are assumed to be
constant, and b and c are constants. In Table 1 we present the typical computing times for a major
cycle with the implementation discussed here and presented in Sect. 3.3.
 |
Fig. 8 This figure shows the computing time of both the gridding and convolution function steps for a 10 degree diameter field of view, a maximum w-coordinate of 104 m and a time-window of Twindow = 1200 s. When the DDE vary rapidly (such as in the case of the ionosphere), a baseline-dependent convolution function is often required, and the convolution function computing time can largely exceed the gridding computing time. Our hybrid W-staking algorithm is not affected by this scaling law. |
5. Summary and future work
The new generation of low-frequency interferometers (EVLA, MWA, LWA) and pathfinders and precursors of the SKA (LOFAR, ASKAP, MeerKAT) cannot be used properly and efficiently without the development of new calibration and imaging techniques that take the many DDE that influence the electro-magnetic field into account. These effects mainly include complicated antenna/station beam effects, fast ionosphere phase, and amplitude variations, along with the associated Faraday rotation.
In this paper we have focused on the issues associated with the application of new techniques for the LOFAR elementary antenna and station beams, which involves using few levels of phased arrays (see Sect. 1). Using the measurement equation formalism, the associated high complexity (wide field of view, individual station rotations, projection of the elementary dipoles on the sky), the problem of imaging and deconvolution LOFAR calibrated datasets can be solved by applying the A-Projection algorithm described in Bhatnagar et al. (2008). Because of its very large field of view (~5–10 degrees in diameter), a full-polarization A-Projection implementation dealing with nondiagonal Mueller matrices is needed for LOFAR. We showed that A-Projection can indeed deal with the heavily baseline-dependent, nondiagonal, direction-dependent Mueller matrices associated with LOFAR baselines. We also demonstrated that efficient ionospheric corrections can be performed using A-Projection. We proposed a series of implementations of A-Projection for LOFAR, taking nondiagonal Mueller matrices into account, aiming at accuracy and computing efficiency.
5.1. Optimizations
As explained in Sect. 4.4 the DDE, although varying rapidly, are smooth on the sky, so the convolution functions have a small support. However, in the case of LOFAR, the wide field of view requires considering (i) the W-term; and (ii) the off-diagonal terms of the Mueller matrices (due to the varying projection of the dipoles on the sky or to Faraday rotation). In addition (iii), the baseline dependence renders the storage of the convolution functions prohibitive, so they have to be computed on the fly.
In our first implementation (Sect. 3.1), the constraint (i) often makes the W-term convolution function support dominant; while (ii) requires the implementation of a complicated gridding and degridding step, taking all polarizations into account to correct for polarization leakage. In the case of a quickly varying DDE such as the ionosphere; step (iii) can completely dominate the computing time (usually set by gridding/degridding operations).
Using the fact that LOFAR station elementary antennas (responsible for the complicated projection effects) are parallel, although the station layouts are rotated with respect to each other, we could separate the first implementation into two steps (Sect. 3.2). The first is a purely scalar gridding/degridding, which suffers from (i) and (iii), while the second is only affected by (ii). As the nondiagonality of the Mueller matrix is corrected in the baseline-stacked uv-plane, we win a computational factor of 10 to 16 as compared to the first implementation. It is important to note that this optimization breaks down when the nondiagonal Mueller matrix becomes baseline-dependent, as in the case of very long baselines (due to the earth’s curvature) or due to the ionosphere’s differential Faraday rotation.
In the last implementation (Sect. 3.3), we still applied the direction-dependent nondiagonal Mueller matrix of the baseline-independent element-beam, but go further by separating the W-term from the A-Term. The former is responsible for the large support sizes and is baseline independent (around a given w-plane), while the latter has small support and is baseline dependent. In this implementation, we grid/degrid the data based on a small support baseline-dependent, oversampled convolution function, and convolve the input and output grids (forward and backward steps, respectively) with the non-oversampled W-term convolution function. We saved computing time by calculating the oversampled convolution function of a generally much smaller support, giving a net gain of two to ten over the second implementation (Sect. 3.2, and Table 1).
Such optimizations are vital for the feasibility of the LOFAR extragalactic surveys, given their huge total integration times of hundreds of days. Also for the SKA, it will be important to take such algorithmic optimizations into account, which are linked to the instrument and system architecture, because they can reduce the algorithmic complexity by orders of magnitude.
5.2. Application to LOFAR survey data and future work
We conducted many experiments on real LOFAR data in order to test our imager. Specifically, we repeatedly observed the same set of objects, each time shifting their pointing centers by a few degrees. Our implementation of A-Projection gives coherent corrected flux densities at the level of 5–10% on the edge of the field. However, although we have shown in this paper that the algorithm gives excellent results in simulated datasets, it shows little or no dynamic range improvement in the resulting images, as compared to a traditional imager.
LOFAR is a very complex machine and feeding the imager with an incorrect direction-dependent calibration solution will not lead to any improvement in the deconvolved sky, and can even decrease the dynamical range. To improve LOFAR’s dynamic range we will have to make progress in understanding the calibration aspects of DDE, especially those related to ionosphere and differential Faraday rotation. Much effort is being given to this, and DDE calibration algorithms of low complexity are under development or have already been achieved, such as SAGECal (Yatawatta 2008).
On the imager side, other ongoing developments include (i) implementation on GPU, of the gridding, degridding, or the convolution function calculations; (ii) compressed sensing in the image plane; (iii) uv-plane interpolation techniques different from zero-padding FFT; and (iv) wide-band A-Projection Bhatnagar et al. (in prep.). Ionosphere and true beam calibration, in combination with peeling techniques, will hopefully allow us to use the framework presented in this paper to reach the high ~105−106 dynamic range needed to construct the deepest extragalactic LOFAR surveys.
See for example Maxim Voronkov’s presentation at http://www.astron.nl/calim2010/presentations in the context of ASKAP.
See http://www.lofar.org/wiki/doku.php?id=public:documents:lofar_documents&s[]=bbs for a review of BBS functionalities.
With a robust parameter of 0, see http://www.aoc.nrao.edu/dissertations/dbriggs
It seems the accuracy of the output images of our imager is presently limited to ~10-4 due to some numerical precision problem: throughout the code, single-precision floating-point numbers are used, and the rounding-off of products and sums involved in the algorithm seem to generate limitations at this level. Detailed tests based on comparing of single and multi-threading consistently show an instability at this level. For the LOFAR surveys we might not need higher accuracy however, since we plan to use direction-dependent peeling to subtract the brightest sources.
See http://www.lofar.org/wiki/doku.php for more information.
For each station, the sample points correspond to the piercing points in the ionosphere of five directions located at the four corners and the center of the field of view. This way the ionospheric layer is sampled in the most relevant area and there are at least five sample points within the field of view of each station.
Acknowledgments
This work was done using the R&D branch of the CASA code base. We would like to thank the CASA Group and casacore team for the underlying libraries. We thank Sarod Yatawatta for useful discussions of the element beam modeling that lead to powerful optimizations. We are grateful to our anonymous referee and to Wim van Driel for his extensive and constructive look at the form and content of this paper.
References
- Bernardi, G., Mitchell, D. A., Ord, S. M., et al. 2011, MNRAS, 413, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatnagar, S. 2009, in The Low-Frequency Radio Universe, eds. D. J. Saikia, D. A. Green, Y. Gupta, & T. Venturi, ASP Conf. Ser., 407, 375 [Google Scholar]
- Bhatnagar, S., Cornwell, T. J., Golap, K., & Uson, J. M. 2008, A&A, 487, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Cornwell, T. J., Golap, K., & Bhatnagar, S. 2008, IEEE J. Select. Top. Signal Proc., 2, 647 [NASA ADS] [CrossRef] [Google Scholar]
- de Vos, M., Gunst, A. W., & Nijboer, R. 2009, IEEE Proc., 97, 1431 [Google Scholar]
- Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G., McKean, J., Pizzo, R., et al. 2010, in ISKAF2010 Science Meeting [Google Scholar]
- McEwen, J. D., & Wiaux, Y. 2011 [arXiv:1110.6137] [Google Scholar]
- Mitchell, D. A., Wayth, R. B., Bernardi, G., Greenhill, L. J., & Ord, S. M. 2012, J. Astron. Instrument., 1, 50003 [NASA ADS] [Google Scholar]
- Rau, U., & Cornwell, T. J. 2011, A&A, 532, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwab, F. R. 1984, AJ, 89, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, O. M. 2011, A&A, 527, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sullivan, I. S., Morales, M. F., Hazelton, B. J., et al. 2012, ApJ, 759, 17 [Google Scholar]
- van der Tol, S. 2009, Ph.D. Thesis, TU Delft [Google Scholar]
- Yatawatta, S. 2008 [arXiv:0809.0208] [Google Scholar]
Appendix A: Measurement equation formalism
To model the complex direction-dependent effects (DDE – station beams, ionosphere,
Faraday rotation, etc.), we make extensive use of the measurement equation formalism
developed by Hamaker et al. (1996), which provides a
model of a generic interferometer. Each of the physical phenomena that transform or
convert the electric field before the correlation is computed is modeled by linear
transformations (2 × 2 matrix). If 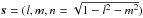 is a
sky direction, and H stands for the Hermitian transpose operator, then the
correlation matrix Vpq between
antennas p and q can be written as
is a
sky direction, and H stands for the Hermitian transpose operator, then the
correlation matrix Vpq between
antennas p and q can be written as
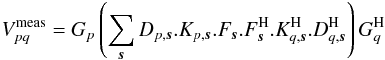 (A.1)where
Dp,s is the
product of direction-dependent Jones matrices corresponding to antenna p
(e.g., beam, ionosphere phase screen and Faraday rotation),
Gp is the product of
direction-independent Jones matrices for antenna p (like electronic gain
and clock errors). The matrix
Kp,s
describes the effect of the array geometry and correlator on the observed phase shift of a
coherent wavefront between antenna p and a reference antenna. This effect
is purely scalar, so it is reducible to the product of a scalar and the unity matrix and
we can write
(A.1)where
Dp,s is the
product of direction-dependent Jones matrices corresponding to antenna p
(e.g., beam, ionosphere phase screen and Faraday rotation),
Gp is the product of
direction-independent Jones matrices for antenna p (like electronic gain
and clock errors). The matrix
Kp,s
describes the effect of the array geometry and correlator on the observed phase shift of a
coherent wavefront between antenna p and a reference antenna. This effect
is purely scalar, so it is reducible to the product of a scalar and the unity matrix and
we can write 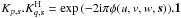 , where
(u,v,w) is the baseline vector between antennas p
and q in wavelength units and 1 is the unity
matrix. We then have
, where
(u,v,w) is the baseline vector between antennas p
and q in wavelength units and 1 is the unity
matrix. We then have 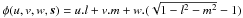 , where
the −1 term models the correlator effect when phasing the signals in the direction of
w. Finally, the product
, where
the −1 term models the correlator effect when phasing the signals in the direction of
w. Finally, the product 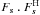 is the sky
contribution in the direction s and is the true underlying
source coherency matrix [[XX,XY], [YX, YY]].
is the sky
contribution in the direction s and is the true underlying
source coherency matrix [[XX,XY], [YX, YY]].
This elegant formalism enables us to model the full polarization of the visibility as a
function of the true underlying electric field correlation. In a simple
and consistent way it takes the direction dependent and direction independent effects into
account. Indeed, most of the Jones matrices in the measurement equations have a fairly
simple formulation, and radio calibration problems amount to finding the various
components of G and E, given a sky model
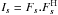 .
.
The measurement equation introduced above can be written in a more extended and
continuous form that is better suited to imaging by applying the Vec operator12 to 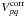 . We obtain
. We obtain
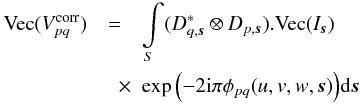 (A.2)where
⊗ is the Kronecker product, Vec is the operator that transforms a 2 × 2 matrix into a
dimension 4 vector.
(A.2)where
⊗ is the Kronecker product, Vec is the operator that transforms a 2 × 2 matrix into a
dimension 4 vector.
Appendix B: Further algorithm details
In this section we describe some important details of the various implementations of A-Projection for LOFAR. In particular, we make extensive use of the Prolate spheroidal function for resolution adaptation and zero-padding for uv-plane interpolation.
As explained in Sect. 3, since LOFAR stations are characterized by different primary beams, the gridding and degridding steps are baseline dependent. Therefore the convolution functions cannot be computed once and then kept stored in memory as is done for W-projection. Instead, they have to be computed on the fly (see Sect. 4.4). However, because the station’s beam model is fairly complex and costly to evaluate (coordinates transformation, estimate of the Element beam Jones matrix), we only store the 4-polarization image plane beams in memory (their Jones matrices) at the minimal resolution. The necessary resolution is simply estimated as λ/(2.Dstation), where Dstation is the given station’s diameter.
The W-term is also estimated only once and stored in memory at the minimal resolution.
This amounts to finding the maximum frequency to be sampled in the image plane, and the
corresponding number of pixels corresponding to the minimum support required for the
W-term convolution function. If the image has an angular diameter
Dim, the resolution needed to properly sample to W-term is
the inverse of the highest spatial frequency, located in one of its corners. The support
of the W-term is then 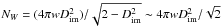 .
.
To interpolate the visibilities on the grid in the gridding step (or conversely in the
degridding step), or to adapt the resolution of the A and W-terms we use a zero-padding
interpolation. Since this scheme can produce artifacts due to the presence of sharp edges
and aliasing problems, we have to make extensive use of a Prolate spheroidal function. It
is computed at the maximum resolution in the image plane. We then Fourier-transform it,
find its support 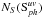 , “cut” it down to that size,
and store it in the uv-plane (hereafter
, “cut” it down to that size,
and store it in the uv-plane (hereafter 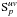 ).
).
For the various algorithms presented in this paper, we have to compute the products of
various DDE in the image plane. For example for the algorithm described in Sect. 3.1, we have to adapt the A and W-term resolutions before
multiplying them in the image plane. We first have to find the support
NS of the convolution function as in
Eq. (13). We first compute the image
plane spheroidal at the resolutions of the A and W-terms
(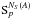 and
and
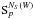 respectively), as follows
respectively), as follows ![\appendix \setcounter{section}{2} \begin{eqnarray} \mathrm{S}_p^{N_S(A)}&=&\mathcal{F}^{-1}\mathcal{Z}^{N_S(A)}\mathrm{S}^{uv}_p\nonumber\\[3mm] \mathrm{S}_p^{N_S(W)}&=&\mathcal{F}^{-1}\mathcal{Z}^{N_S(W)}\mathrm{S}^{uv}_p \end{eqnarray}](/articles/aa/full_html/2013/05/aa20882-12/aa20882-12-eq245.png) (B.1)where
ℱ is the Fourier transform, and
(B.1)where
ℱ is the Fourier transform, and 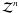 the zero-padding operator that puts the input into a grid of size n. To
estimate the A-term interpolated on an
NS × NS
pixel image:
the zero-padding operator that puts the input into a grid of size n. To
estimate the A-term interpolated on an
NS × NS
pixel image: 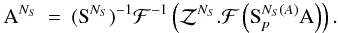 (B.2)We
obtain the image plane effects at the same resolution and multiply them according to the
specific needs of the various implementations described in Sect. 3 and obtain the image plane product Pim. We
then compute the oversampled convolution function as
(B.2)We
obtain the image plane effects at the same resolution and multiply them according to the
specific needs of the various implementations described in Sect. 3 and obtain the image plane product Pim. We
then compute the oversampled convolution function as
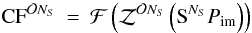 (B.3)where
the resulting interpolated convolution function
(B.3)where
the resulting interpolated convolution function 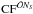 has
has 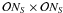 pixels, with
pixels, with  as the oversampling parameter. If the final image is
Npix × Npix pixels, because we
have used the spheroidal function, after applying the inverse Fourier transform, we have
to normalize the dirty image by the spheroidal function
as the oversampling parameter. If the final image is
Npix × Npix pixels, because we
have used the spheroidal function, after applying the inverse Fourier transform, we have
to normalize the dirty image by the spheroidal function
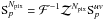 .
.
As outlined above, all LOFAR stations are different, and the convolution functions are baseline dependent. The for loops described in Sect. 3 are therefore parallelized on baseline. For the degridding step from a common read-only grid, the residual visibilities are estimated independently using different threads. The code has been created in the LOFAR package and depends on the casacore and casarest packages.
Appendix C: Limiting the maximum w-coordinate
 |
Fig. C.1 The W-term increases for lower elevations of the target field. Using the W-Projection algorithm, the computing time increases with w2. This figure shows the normalized cumulative distribution of the w-coordinate (left panel) for a typical LOFAR observation, and the corresponding normalized cumulative computing time (right panel). We can see that rejecting the ~5% of the points with w > 104 saves ~70% of the computing time. |
For the traditional interferometers operating at relatively high frequencies compared to
LOFAR, in general the field of view is small enough so that the W-term can always be
neglected (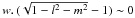 ).
However, for the new wide fields of view, long-baseline interferometers, the W-term is
very important, and not taking it into account produces artifacts and considerably reduces
the dynamic range. For a given field of view
).
However, for the new wide fields of view, long-baseline interferometers, the W-term is
very important, and not taking it into account produces artifacts and considerably reduces
the dynamic range. For a given field of view
or a given angular distance to the phase center, the importance of the W-term increases as the w-coordinate value, i.e., when the targeted field is at low elevation. It is therefore important to stress that wide fields of view or long baselines do not directly mean that the W-term will be important: irrespective of its baseline or field of view, a planar array that would observe at zenith would always have a null w-coordinate.
Algorithmically, for A-Projection, the W-term is one of the main limiting factors. Using the W-Projection algorithm (Cornwell et al. 2008) and assuming the W-term support is higher than the Prolate spheroidal support, the gridding time evolves as tgrid,w ∝ w2.D4, because the highest spatial frequency in the image plane has to be properly sampled. We found that in a typical LOFAR dataset this nonlinear behavior generally makes the ≲5% of the points with the highest w-coordinates responsible for ≳ 70% of the computing time (as in Fig. C.1). This small amount of data does not necessarily add to the overall sensitivity or resolution. Setting a wmax value above which the visibilities are not gridded significantly increases the computational efficiency, without losing sensitivity or resolution. Not that our hybrid W-stacking (Sect. 3.3) algorithm is not affected by these limitations.
All Tables
All Figures
 |
Fig. 1 LOFAR stations are phased arrays characterized by a large field of view. X/Y polarimetric measurements made with it are therefore nontrivial compared to a radio telescope using dishes: we have to take into account the projection of the dipoles that are generally nonorthogonal on the sky and the fact that this angle varies across the field of view. This figure shows the Mueller matrix corresponding to baseline (01) in a given time and frequency slot, normalized by the Mueller matrix at the phase center (see text). Each pixel in the plot (i,j) shows the amplitude of the (i,j) Mueller matrix element in a certain direction s using a logarithmic scale. Even in this normalized version, the off-diagonal Mueller terms are as high as 10% and cannot be neglected. |
| In the text | |
 |
Fig. 2 Correction |
| In the text | |
 |
Fig. 3 Essential part of the A-Projection algorithm relies on the predict step, which transforms a 2D sky image (the projection of the celestial sphere on a plane) into a set of visibilities. We have simulated a dataset having one off-axis source, where the true visibilities (black dashed line) have been estimated using Eq. (1), taking the beam into account. This plot shows the comparison in all measured polarizations between the exact value of the visibility of a given baseline and the A-Projection estimate (gray line). Contrary to a traditional predict step, the visibilities are modulated by the beam amplitude (dotted line), and we have time-dependent polarization leakage. The overplotted graph shows a zoom in the small region shown in the top-right panel. In the degridding step, we use a computationally efficient closest-neighbor interpolation, creating steps in the predicted visibilities. |
| In the text | |
 |
Fig. 4 Dramatic differences between the estimated deconvolved sky when using three different modified CLEAN algorithms on a simulated dataset containing 100 sources. The visibilities have been generated by taking (i) the individual antennas; (ii) their projection on the sky and (iii) the beam-forming step (the scalar array factor) into account. The top-left image shows the deconvolved sky as estimated with a traditional imager not taking time, frequency, baseline, direction-dependent effects into account. The top right and lower left images have been generated by considering, respectively, the array factor only and both the array factor and the element beam. The lower right panel shows that the input flux densities are correctly recovered. |
| In the text | |
 |
Fig. 5 Dirty images at the location of a bright source in a simulated dataset. The images are 1deg in diameter. Without applying the A-Projection correction for an ionospheric phase screen (left panel) the dirty image shows important distortions as a result of ionospheric effects. Application of this correction (right panel) clearly shows improvements. |
| In the text | |
 |
Fig. 6 This figure shows the deconvolved image synthesized from the simulated dataset described in Sect. 4.2.2. In the left panel, the ionospheric effects are not taken into account, and our deconvolution scheme naturally produces severe artifacts and high residuals in the reconstructed sky. The deconvolved image shown in the right panel has been estimated using our implementation of A-Projection with the time-dependent ionospheric phase screen. |
| In the text | |
 |
Fig. 7 The evolution of the estimated flux density as a function of the major cycle iteration for one polarized off-axis source. From top to bottom, and left to right, the panels show results generated by using (i) W-Projection only; (ii) AW-Projection with the array factor only; (iii) AW-Projection taking the full beam model into account; and (iv) image plane corrections as described in Sect. 2.2. |
| In the text | |
 |
Fig. 8 This figure shows the computing time of both the gridding and convolution function steps for a 10 degree diameter field of view, a maximum w-coordinate of 104 m and a time-window of Twindow = 1200 s. When the DDE vary rapidly (such as in the case of the ionosphere), a baseline-dependent convolution function is often required, and the convolution function computing time can largely exceed the gridding computing time. Our hybrid W-staking algorithm is not affected by this scaling law. |
| In the text | |
 |
Fig. C.1 The W-term increases for lower elevations of the target field. Using the W-Projection algorithm, the computing time increases with w2. This figure shows the normalized cumulative distribution of the w-coordinate (left panel) for a typical LOFAR observation, and the corresponding normalized cumulative computing time (right panel). We can see that rejecting the ~5% of the points with w > 104 saves ~70% of the computing time. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.