EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A110 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A110
Number of page(s) 10
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/201219840
Published online 17 May 2013

© ESO, 2013

1. Introduction

Sedna is the observed trans-Neptunian object (TNOs) with the farthest perihelion q = 76 AU. Besides this, Sedna also has a large semi-major axis a = 542 AU and a small inclination i = 11.9°. It was first observed by Brown et al. (2004), in a survey of far objects that began in November 2001 in Palomar observatory. Sedna may be considered as the first observed object belonging to an inner Oort Cloud (IOC), because its orbit cannot be formed by dynamical mechanisms that could produce the orbits of other known populations of TNOs like the Kuiper belt, the scattered disk (SDOs) and the detached objects (Gomes 2003; Gomes et al. 2005a; Duncan & Levison 1997; Elliot et al. 2006). Two other objects are in the neighborhood of the IOC, 2000 CR105 with orbital elements a = 220 AU, q = 44.0 AU, and i = 22.8° (Buie et al. 2003) and 2004 VN112 with a = 346 AU, q = 47.3 AU, and i = 25.5° (Elliot et al. 2005). These objects may be classified as components of the IOC, like Sedna, although 2000 CR105 can be marginally explained by the resonant mechanisms responsible for the orbital formation of other detached objects (Gomes et al. 2005a). Several scenarios have been proposed to explain the peculiar dynamics of Sedna-like objects (Gladman & Chan 2006; Brasser et al. 2006; Gomes et al. 2006; Kaib et al. 2011). Here we compare two of these scenarios: the planetary mass solar companion (PMSC, Gomes et al. 2006) and the stellar dense cluster scenario (Brasser et al. 2006). The latter is possibly the most consistent since it reproduces the orbit of Sedna well and is based on the likely primordial Sun’s birth environment. The choice of the PMSC scenario is motivated by being based on a putative, unknown solar system object, whose existence should be put on trial through possible signatures that a PMSC can produce on known solar system objects.

Gomes et al. (2006) propose that the orbits of Sedna-type objects are formed by means of perturbations from a putative PMSC. In that work, this hypothesis was tested through numerical simulations using several values of masses, semi-major axes, eccentricities, and inclinations of the solar companion. Their aim was to determine orbital elements of the companion that could produce objects belonging to the inner border of the IOC. Many simulations were done using a model with massless particles and the four giant planets in their actual orbits, and the total time of the integration is at most 109 years. They also did a numerical integration considering a more realistic model of planetary evolution including the giant planets in initially compact orbits and a disk of massive planetesimals beyond the farthest planet. They show that the effect of the companion’s perturbations on the objects of the scattered disk could produce objects near the region of Sedna for companions with diverse orbital elements and masses. Considering the low values of the eccentricities, a relation exists between the companion mass and its semi-minor axis compatible with the production of orbits similar to Sedna’s. A companion with Neptune’s mass and semi-major axis a = 2000 AU, or one Jupiter mass and a = 5000 AU, or 8 Jupiter masses at 10   000 AU all produce IOCs which include the orbit of Sedna. It is also shown that a companion with an Earth mass (see also Gladman & Chan 2006), a = 1000 AU, eccentricity e = 0.94, and inclination i = 5° may detach objects to the region of Sedna. We thus conclude that PMSCs of various masses and orbital elements are efficient in producing detached objects with large perihelion distances and semi-major axes.

Brasser et al. (2006, 2007, 2008) have improved the work originally developed by Gaidos (1995), Fernández (1997), and Fernández & Brunini (2000), in which the Sun was probably formed in a much denser stellar environment than the current one. They developed the stellar encounter scenario. The fundamental hypothesis of that work is that the Sun originated in a stellar cluster immersed in gas and that in this initial phase the number of stellar encounters with the primordial Sun was high. The perturbations from the stellar encounters added to the gas potential are able to detach the perihelion of the planetesimals scattered by Jupiter and Saturn (during the phase of formation of those planets) to regions beyond the close encounter gravitational domain of these two planets, creating, in this way, IOCs that are compatible with the orbit of Sedna (see also Morbidelli & Levison 2004; Kenyon & Bromley 2004). The authors conclude that planetesimals scattered by Jupiter and Saturn are detached to the region of Sedna ideally for central cluster densities λ0 = 104   M⊙ pc-3 (solar masses /parsec-3) and that the higher the initial central density, the more internal to the solar system is the inner border of the resultant IOC.

A recent observational survey of distant objects has been carried out by Schwamb et al. (2010), using the Samuel Oschin telescope at Palomar Observatory (the telescope that detected Sedna for the first time). A total of 52 objects pertaining to the Kuiper belt and Centaurs were detected, 25 of which were observed for the first time. Sedna was observed again, but no other object like Sedna with perihelion greater than 45 AU was obtained, even though the observational survey had a precision that detected slow objects at up to 1000 AU with visual magnitude 21.5. Based on their observations and assuming that Sedna-type objects were formed according to Brasser’s scenario, Schwamb et al. (2010) argue that the only plausible value for the central initial density of the stellar cluster in which the Sun emerged would be 104   M⊙ pc-3.

In a recent work, Brasser et al. (2011) extend their previous work to include the formation of the Oort Cloud by means of stellar encounters and gas potential for different clusters. Among the modifications, they used an n-body numerical integrator to simulate the gravitational interaction between the bodies. They also included the gas ejection from the cluster and used a second type of potential − the Hernquist potential. They conclude that Sedna type objects are formed for all assumed clusters in their work and that the inner cloud would be formed beyond 100 AU. They also conclude that the formation efficiency of the IOC was 2% for the Plummer potential and 5% for the Hernquist potential, significantly less than previously obtained, 2%−18%.

thumbnail Fig. 1

Orbital distribution in semi-major axis vs. perihelion distances for the scenario of the star cluster, for three central cluster densities, after 3 × 106 ys. The small circles represent planetesimals and triangles represent CR105, VN112, and Sedna.

thumbnail Fig. 2

Orbital distribution of semi-major axis vs. perihelion distance for the scenario of the star cluster after 3 × 106 ys: the small circles represent planetesimals and triangles represent CR105, VN112, and Sedna. Panels from left to right respectively denote star orbits close to the cluster center, intermediate, and far from the cluster center, corresponding to a density in the cluster center of 104   M⊙ pc-3.

It is timely to argue for the plausible of the existence of a PMSC. Among the possible mechanisms for the peculiar orbital formation of a PMSC, we cite the scattering of a planet by Jupiter in a primordial solar system followed by a subsequent increase in the perihelion by tidal effects generated by a primordial stellar cluster or capture of a PMSC during the phase in which the Sun was inside a primordial cluster. The fact that floating planets (Sumi et al. 2011; Delorme et al. 2012) have likely been observed, associated to the probability that wide stellar binaries were formed by a capture event during the dissipation of the gas in a stellar cluster (Levison et al. 2010a; Kouwenhoven et al. 2012), strongly suggests that at least as many companions of planetary mass may exist in the vicinity of stars as wide binaries of stellar mass (estimated by Kouwenhoven et al. 2012 in about 1−30%), considering just a possible mechanism for the formation of PMSCs.

It is important to mention that both scenarios are not incompatible. In particular, the Sun could have been formed in a dense cluster of stars that induced the formation of the IOC, and during this phase, a planet could have been captured by the Sun. In this work, nevertheless, we consider the scenarios as independent ones. Our idea is that, even though the likely presence of the Sun in the primordial cluster must have induced the increase in the perihelion of some scattered objects, this mechanism could form an Oort Cloud that is incompatible with the existence of Sedna. Thus, the consideration of the companion scenario means that the companion itself induced the formation of Sedna type objects, although the cluster scenario could have yielded more distant IOC objects.

In this work we develop an observational simulator (OS) of objects so as to compare the results obtained for the formation of Sedna-type objects by Gomes et al. (2006) with Brasser et al. 2006. The main purpose of the OS is to artificially introduce bias in the numerically produced populations to prepare them to be compared with real observations.

In Sect. 2, we briefly describe the Sedna formation scenarios. In Sect. 3 we describe the OS. In Sect. 4, we apply the OS to both models, and in Sect. 5 we present the conclusions.

thumbnail Fig. 3

Orbital distribution of semi-major axis vs. pericenter distance for the PMSC model after 4.5 × 109 Gy. The small circles represent planetesimals and triangles represent CR105, VN112, and Sedna. The parameters for the companion are a = 1500 AU, e = 0.4, i = 80°, and M = 10-4   M⊙.

2. Reproducing the scenarios for the formation of Sedna-type objects

We reproduce the mechanisms mentioned in the previous section that describe the orbital formation of Sedna type objects. Such objects are considered in this work as all objects with semi-major axes 300 ≤ a ≤ 1000 AU and perihelion q ≥ 50 AU. This choice is justified since objects with semi-major axes below 300 AU can have he perihelion detached from the gravitational effect of the planets by means of the mechanism described in Gomes et al. (2005a), and objects with semi-major axes above 1000 AU can have their perihelions increased by galactic tidal effects. In all integrations, we used a modified version of the symplectic integrator Mercury (Chambers 1999).

The stellar cluster scenario described by Brasser et al. (2006) considers that the genesis of the Sun and its primordial evolution took place while it was a member of this stellar cluster. Torques triggered by passing stars and by the cluster gas could have increased the perihelion of objects initially scattered by Jupiter and Saturn in such a way that these objects became fossilized in positions free of planetary encounters, after the Sun left the cluster about three million years after its formation. We reproduced the results obtained by Brasser et al. (2006) for densities 104, 3 × 104, and 105   M⊙ pc-3 for a total evolution of three million years in a system of 2000 initially cold massless particles, uniformly distributed between 4 and 12 AU with Jupiter and Saturn in initially closer orbits according to the Nice model (aJ = 5.45 AU, aS = 8.65 AU; Tsiganis et al. 2005). We recommend the work by Brasser et al. (2006) for further details about the method used in the construction of our results. In Fig. 1, we show the results obtained for the three different cluster central densities described above. Objects that in the end of the numerical integration had perihelia inside 50 AU are discarded since from a combination of the galactic tides with planetary perturbations they may be displaced from that region in the solar system lifetime. In Fig. 2 we show the results for the clusters initial central density 104   M⊙ pc-3, for a Sun-like star that (1) orbits near the center of the cluster; (2) has an intermediate orbit; and (3) orbits most of the time far from the cluster center. A Sun-like star that initially had an orbit in the densest parts of the cluster forms a population of Sedna-like objects closer to the Sun-like star than a population produced by another Sun-like star that initially had an orbit farther from the center of the cluster.

We now analyze the PMSC scenario. Gomes et al. (2006) propose that the orbits of Sedna-type objects could be formed by means of perturbations from a hypothetical PMSC placed in the Oort Cloud. The secular gravitational perturbation of this companion on the planetesimals that were initially scattered by the giant planets may increase their perihelia, as in the cluster scenario. In this work we present the results from a numerical integration including a PMSC with the orbital parameters a = 1500 AU, e = 0.4, i = 80°, and mass M = 10-4   M⊙. This choice was based on parameters from one of the companions in Gomes et al. (2006) that yielded a good Sedna-like population. In this numerical integration, the planetesimals have masses that induce the migration of the four giant planets, for a total simulation time of 4.5 Gy. The initial semi-major axes of the planets were 5.45, 8.18,11.50, and 14.20 AU, and the disk of planetesimals extended between 15.5 AU and 34 AU with a surface density proportional to r-1. This disk was initially composed of one thousand particles, and each particle cloned 50 times just after the instability among planets associated with the Nice model so that in the end the remaining particles can be considered as coming from a set of 50   000 equal, massive particles, with a total mass of 35 M⊕. The planets and planetesimals that compose the disk have initial inclinations and eccentricities near zero. The planetary migration is induced by the interaction between the disk of planetesimals and planets, according to the Nice model (Gomes et al. 2005b; Tsiganis et al. 2005; Morbidelli et al. 2005). We also included galactic tides in the numerical integration through the same model as in Gomes et al. (2006 and references therein). In this model, the accelerations in the directions defined by the galactic fram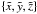e are 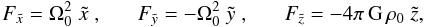(1)with Ω0 = 26 km s-1 kpc-1, ρ0 = 0.1   M⊙/pc3, and G is the gravitational constant.

Briefly, the planetesimals interact with the planets by exchanging energy and angular momentum, which brings the planets to a migration phase from their initially compact orbits to orbits near their present configuration. The massive planetesimals are scattered to orbits with large semi-major axes and eccentricities. The planetesimals with semi-major axes beyond 1000 AU experience a strong influence from the galactic tides, which tend to increase their perihelia, removing them from the zone of planetary close encounters, thus forming the Oort Cloud. The gravitational perturbation from the PMSC allows the increase in the perihelion distances of intermediately distant planetesimals. In Fig. 3, we present the semi-major axis vs. perihelion distribution of planetesimals orbits that were scattered by the giant planets during their migration and were deposited in the IOC by the perturbations from the PMSC. These same perturbations induce these planetesimals to sporadically return to the zone of close encounters with the giant planets. Thus, the objects of the IOC cloud formed by the above mechanism stay dynamically active. Companions with different masses may produce similar results, since the companion semi-minor axis is conveniently changed (Gomes et al. 2006).

thumbnail Fig. 4

Distribution of semi-major axis a), eccentricity b), inclination c), and perihelion distance d) for objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained by the scenario of the star cluster.

3. The observational simulator

We constructed an OS based on the probability of a certain object being observed, given its size, albedo, and distance from the Earth and Sun. We initially chose a set of orbits generated by a theoretical model. The orbits are characterized by their orbital elements: semi-major axis, eccentricity, inclination, longitude of the ascending node, and longitude of the perihelion for a heliocentric system. We randomly chose an object from the above set of orbits. We then associated a mean longitude for such object, randomly chosen between 0° and 360°. Finally we assigned a radius for this object, by means of a cumulative power law size distribution, given by 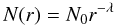(2)where N(r) represents the number of objects with radius larger than r, N0 is a constant, r is the radius of the object, and λ is the power law slope. Fraser et al. (2010) obtained values of λ for the hot and cold populations of the Kuiper belt as λcold = 4.1 and λhot = 1.8 (hot population objects  →  38  ≤  a  ≤  55 AU and i ≥ 5°, cold population objects  →  38  ≤  a  ≤  55 AU and i ≤ 5°). Assuming a value for the radius of the largest body rL we have N(rL) = 1, which determines N0 and, for the smallest body, we choose a radius (rs) such that it yields a visual magnitude V = 23 at a distance of 30 AU. We randomly generate an integer between 1 and N(rs) and thus obtain the radius r for the object through the distribution equation above.

Once the position of the object in its orbit has been obtained, we compute its distance from the Sun (ds). The distance of the object from the Earth (de) is obtained from the equation 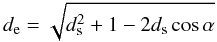(3)where α is randomly chosen between 0 and 90 deg, and is considered the distance from the Sun to the Earth as 1 AU. Assuming an average albedo (al) of 0.20 for all objects we compute the visual magnitude (V) for the object through 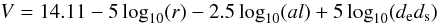(4)where the distances are in AU and the radius in km.

If the visual magnitude of the object is less than a given value, the object is considered observed. The OS also allows constraining the values of latitude in which the observations are realized. Sedna was discovered in an all-sky survey by Brown et al. (2004). Here we consider, besides the all-sky survey, latitudes restricted to the ranges  ±5°,  ±10° and  ±15°. In the next section, we make comparisons between the described scenarios using the OS. The simulator is executed 300 times for each population, each run being interrupted when an object is inside the IOC (defined as the set of objects with 300 ≤ a ≤ 1000 AU and q ≥ 50 AU). Then we identify the number of SDOs observed when this first member of the IOC is observed and compare it to the number of real SDOs for one Sedna.

4. Applying the observational simulator to models of formation of the inner Oort Cloud

We apply the simulator to the stellar cluster scenario, for an initial central density of the stellar cluster 104   M⊙ pc-3, following arguments by Schwamb et al. (2010) that, by means of observational restrictions, constrain this value as the more plausible for a cluster in which the Sun would have appeared. For this model, the integration total time was 3 My, which represents the average time of gas dispersion from the cluster. In such a case, only Jupiter and Saturn are considered, and consequently, the planetesimals are initially scattered by these two planets and may have their perihelion increased by the tidal forces from Plummer’s potential and close encounters between the Sun and passing stars. Estimates of the initial mass in the region between Jupiter and Saturn are about 200 M⊕, where 50 M⊕ is needed to form 10 M⊕ rocky nuclei that are able to accrete gaseous material and, therefore, to form the giant planets (Levison et al. 2010b). This leaves about 150 M⊕ to be scattered by these planets.

Small objects (diameters smaller than  ≈30 km) cannot reach large distances to be affected by the tidal forces and by stellar encounters, as a consequence of the drag effect exerted by the circumstellar gas, in such a way that only 50−75 M⊕ of the solid material reach large enough distances to be affected by tides (Brasser et al. 2007). The analysis is made only for one of the results, in which Sedna appears as a member of the inner edge of the Oort Cloud, obtained for the star with the innermost orbit with respect to the stellar cluster center for the initial central density of 104   M⊙ pc-3 (see Fig. 2). In Fig. 4 we plot the histograms for the semi-major axis distribution, eccentricity, inclination, and perihelion of objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained by means of this scenario. Around 50% of the objects have semi-major axes in the range 300 ≤ a ≤ 700 AU and 90% present eccentricity larger than 0.50. Thirty percent of the objects have inclinations less than 30°, and 40% of the objects have perihelion distances smaller than 100 AU.

thumbnail Fig. 5

Variation in the power law slope with the average number of observations needed to obtain a Sedna-like object for the scenario of the star cluster, considering three values for the radius of the largest body in the the distribution. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation for the largest object with two Pluto radii in the larger panel.

thumbnail Fig. 6

Variation in the power law slope vs. average number of observations to obtain a Sedna-like object for the scenario of the star cluster, considering four values for the allowed latitude range. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation without restriction in latitude.

Since the total time span of the numerical integration considered for this model is 3 My, we consider, in our statistical analysis for the stellar cluster scenario, just those objects that are in a region limited by q ≥ 50 AU and a ≤ 1000 AU. For the complete evolution of 4.5 Gy, objects with perihelion smaller than 50 AU could leave the IOC through the combined perturbations of the Galactic tide and Neptune. Since we wish to compare the observations of objects in the IOC with the observations of scattered objects, we do a numerical integration of the orbits of the four giant planets and a disk of 50 000 equally massive planetesimals (with a total mass of 35 M⊕ for the disk) for a total time of 4.5 Gy, according to the Nice model, so that at the end of the integration we obtain a disk of scattered planetesimals to be added to the objects obtained in the stellar cluster scenario. Nevertheless, since each simulated planetesimal in the stellar cluster model is around 36 times as massive as each planetesimal obtained by the Nice model simulation (considering a scattered mass by Jupiter and Saturn initially of 50 M⊕ equally distributed among the 2000 planetesimals), objects obtained were cloned in the former scenario, aiming at assigning the same mass for each object in either model, so as to apply the OS in a consistent manner. In this cloning we keep the same orbital elements of the original particles, except for the mean longitude, which is randomly chosen between 0° and 360°.

thumbnail Fig. 7

Distribution of semi-major axis a); eccentricity b); inclination c); and perihelion distances bf d) of objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained by the PMSC scenario.

thumbnail Fig. 8

Variation in the power law slope vs. the average number of observations to obtain a Sedna-like object for the scenario of the PMSC, considering three values for the radius of the largest body in the distribution The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation for the largest object with two Pluto radius.

thumbnail Fig. 9

Variation in the power law slope vs. the average number of observations to obtain a Sedna-like object for the scenario of the PMSC, considering four values for the allowed latitude range of observation. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation without restriction in latitude.

The efficiency in the formation of the IOC obtained in Brasser et al. (2006) is approximately 10%, and for the more complete model presented in Brasser et al. (2011) the efficiency is approximately 2%. Thus, once we reproducing the previous model (Brasser et al. 2006) reduced accordingly the number of objects cloned by 20%, aiming a more realistic analysis. For a distribution of planetesimals obtained by the stellar cluster scenario added to the scattered population, we ran 300 realizations of the observational simulator, and in each realization, ended the code when an object of the IOC is observed, so that in the end could compute an average number of SDOs observations needed to obtain an object with an orbit similar to Sedna.

thumbnail Fig. 10

The first 30 largest radius of SDOs. The continuous line stands for the real objects. The dotted line refers to sizes determined by the OS on a population affected by the PMSC. The dashed line stands for the no-companion model.

The scattered disk comes from a scattering by the giant planets during the late heavy bombardment (Tsiganis et al. 2005), and the IOC originated in the primordial scattering of objects during the planetary formation phase (Brasser et al. 2006), we considered a slope fixed at λ = 2.0 for the scattered disk (in agreement with the estimates by Fraser et al. 2010), and varied the values of λ for the IOC. In Fig. 5 we present a plot of the distribution slope vs. average number of observations (before an IOC object is detected), for ρ0 = 104   M⊙ pc-3, in which we varied the power law size distribution slope between 1.7 ≤ λ ≤ 4.2 (roughly between the slopes for the hot and cold populations of the Kuiper belt), for the three largest size parameters in the power law distribution, which are r = 2 Pluto radii (circle), 1 Mars radius (triangle), and 2 Mars radii (square). The higher the value of λ, the more observations are necessary to obtain an object belonging to the IOC. Now we have to compare this average number of observations before a Sedna-like object is observed with real observations. Sedna was the 82nd object observed with scattered disk characteristics. On the other hand, no other Sedna-like objects has been observed to date in a total of 158 SDOs, so we compare the average order of observing Sedna through the simulator with the range 82−158. Still in Fig. 5, we present a zoom of the region 2.7 ≤ λ ≤ 3.4, where it is possible to notice that a Sedna-type object is detected on an average of 82−158 SDO observations for a value of λ between 2.8 and 3.3, with an insignificant difference when we consider the three largest size parameters in the distribution. A similar analysis is presented in Fig. 6, where the radius of the largest body in the distribution is fixed at r = 2 Pluto radii. In this figure we restricted the observations to latitudes  ±5° (triangle),  ±10° (square),  ±15° (diamond), and no restriction in latitude (circle). The figure presents the variation in the slope λ (in the range 1.7 to 4.2) vs. the average number of observations necessary to obtain a Sedna. As expected, the larger λ, the larger the average number of necessary observations. Sedna is obtained from an average of 82−158 observations for λ values between 2.8 and 3.3, as in Fig. 5.

thumbnail Fig. 11

Probability of obtaining an object of type Sedna for the star cluster and the PMSC scenarios for a number of 14 or fewer objects observed, following observational research by Schwamb et al. (2010).

For the PMSC, the total integration time was 4.5 Gy, in a coherent model of orbital evolution, so that the final results of numerical integration must consistently represent all trans-Neptunian populations (hot Kuiper belt, scattered disk, and Oort Cloud). Here we also run the OS for the population of objects obtained by this mechanism, and stop the simulator when a Sedna-type object appears. In Fig. 7 we present the histograms of the distributions in semi-major axis, eccentricity, inclination, and perihelion distance of the objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained for this scenario. Around 50% of the objects have semi-major axes ranging in 300 ≤ a ≤ 700 AU, and 70% present eccentricity above 0.50. Around 20% of the objects have inclinations less than 30° and present a uniform distribution between the prograde and retrograde orbits. Ten percent of the objects have perihelia below 100 AU. Figure 8 is like Fig. 5 now for the PMSC scenario. The main difference between Figs. 5 and 8 lies in the value of λ. For the PMSC scenario, a Sedna is obtained on an average of 82−158 observations, for the distribution slope in the range 2.2 ≤ λ ≤ 2.7. Varying the latitude range of allowed observation (Fig. 9), we obtain a Sedna from an average of 82−158 observations, for a smaller λ when we consider no latitude restriction. As expected, for a fixed λ, a smaller average number of observations necessary to obtain a Sedna is needed for wider latitude windows. Considering unrestricted latitudes, a Sedna is detected as one in the 82−158 range for smaller λ as compared with the cluster scenario.

The OS also determines the sizes of the observed objects. It is instructive to compare the sizes of the objects obtained by the simulator to real ones. For this comparison we chose the size distribution power law with the largest size as two Pluto radii and slope 2.2. Then we compared the 30 largest sizes observed by the OS obtained as an average of the 30 largest sizes of each of the 300 realizations of the simulator, both for the companion and cluster models (Fig. 10). For the real objects, the largest radius (Eris’s) is plotted according to its determined size by Sicardy et al. (2011) and the other sizes are determined by comparing the absolute magnitude of the SDOs1, with the first three terms on the right side of Eq. (4), which corresponds to the absolute magnitude. We selected an albedo of 0.2 for compatibility with the OS. We also restricted our analysis to the realizations of the simulator that yielded 80 to 160 SDOs observations before a Sedna-like object was obtained. Figure 10 shows some compatibitiy of the sizes obtained by the simulator and real ones, although somewhat larger radii are obtained by the simulator with respect to real sizes. If we consider realizations in which there are fewer SDOs at the discovery of the first Sedna, we get better matches among the curves. Now the size of the first Sedna-like object found is usually smaller than Sedna’s real size. Considering the same realizations of the simulator as just above we find that, for the companion case in 68% of the realizations, we detect the first IOC object smaller than Sedna. For the no-companion case, this fraction is 90%.

In 2010, the results of an observational survey performed at Palomar Observatory by Schwamb and collaborators was presented. The purpose of that survey was to observe slow trans-Neptunian bodies, with sensitivity in the semimajor axis of 1000 AU, magnitude up to 21.3, and latitude window of  ±30°. Fifty-two objects were observed among Centaurs, Kuiper belt objects, and scattered disk objects, including Sedna, but no other object like Sedna was detected. Among all objects, 14 were scattered disk objects. Thus, we decided to apply the OS to this specific survey. To do this, we used the same observational constraints as the survey’s (V < 21.3 and latitudes restricted to  ±30°.) and considered that Sedna was one observed IOC object among 14 SDOs. For each value of distribution slope between 1.7 and 4.2, we carried out a total of 1000 OS realizations and calculated the probability of obtaining a Sedna-type object in 14 observations or fewer (Fig. 11). As a result, the greater probability of obtaining a Sedna-type object is roughly 24% (star cluster) and 11% (PMSC) for a distribution slope between 1.8 and 2.0, and a probability of 3% for both scenarios for a slope around 3.0. It can be argued that, since the objects of the inner Oort Cloud comes from the scattered disk in the PMSC scenario, it is expected that the distribution slope of Sedna-like objects is similar to that of the scattered disk, estimated at 2.0 (Fraser et al. 2010), which leads to a probability of obtaining an object like Sedna around 8%. For the star cluster scenario, we cannot as easily determine what the distribution slope would be for that population. Considering a distribution slope similar to that of the scattered disk, the probability of observing an object like Sedna considering the scenario of star cluster is evaluated at around 18%.

In a sense it is more consistent to apply the OS to a specific survey that observed Sedna since we can consistently apply the survey parameters suck as the faintest visual magnitude and latitude range. The general conclusion is that Sedna was unexpectedly observed too early for both scenarios, as suggested by Fig. 11 and also implicitly in Schwamb et al. (2010). Also, Sedna’s size compared to the size of the first IOC object obtained by the OS is indicative of Sedna’s premature observation. On the other hand, we understand that it is important to include observations from multiple surveys even though we cannot consistently use a specific faintest magnitude and latitude range. This can be justified on the grounds that several other surveys that did not find Sedna or any other Sedna-like object could potentially have found one. The multiple surveys comparisons possibly bring more accurate information about the probability of finding a Sedna-like object. As to the comparison between scenarios, if we consider just Schwamb’s survey, there is a small preference for the cluster model, and for the multiple survey analysis, there is a slight preference for the companion model. These are, however, statistically insignificant, suggesting that new objects must be observed for a possible future decision about the best scenario.

5. Conclusions

When we reconstructed the scenarios that yield the orbits of objects in the IOC (defined here as the set of all objects within 300 ≤ a ≤ 1000 AU and q ≥ 50 AU), we found out that the companion model presents a more uniform distribution of objects in semi-major axes, while the stellar cluster presents a greater accumulation of objects with smaller semi-major axes. The distribution in eccentricities is almost identical, with a small difference only in the percentage of objects with eccentricity below 0.5. The PMSC scenario also presents a more uniform distribution of prograde and retrograde orbits than the cluster scenario. Neverthless the cluster model yields more orbits with inclinations less than 30° for the parameters used in our paper. Possibly as suggested by the inclination distributions in Figs. 4 and 7, the distinction between models should be assessed through the distribution of orbital inclinations of a reasonable number of new observed Sedna-like objects.

Using the OS, we analyzed the likelihood of obtaining objects similar to Sedna. As a comparison parameter we used the fact that Sedna is one in 82−158 SDO’s with a ≥ 50 AU and q ≥ 30 AU. Two complementary analyses were done. First, we analyzed the dependence on the size distribution slope λ of the average number of observations needed to obtain a Sedna-type object, for three values of the largest object in the power law distribution. In the second analysis we fixed the largest radius in the size distribution, and considered the observations in four latitude ranges, including an all-sky survey.

We achieved the following results using the OS

  • 1.

    For the stellar cluster scenario, which is fixλ = 2 for the scattered disk size distribution, a Sedna type object is obtained in an average of 82−158 observations, for a value of λ for the IOC between 2.80 and 3.30. Furthermore, the correlation between the size of the largest body distribution of objects and the average number of observations demonstrates be weak.

  • 2.

    For this same model, a Sedna-type object was obtained on an average of 82−158 SDO observations for the IOCs λ still between 2.80 and 3.30, when we considered restrictions in latitudes of observation, and we noticed that, according to intuition, we obtained a Sedna-type object fewer observations when the survey is undertaken using a wider window of observation latitudes.

  • 3.

    With respect to the PMSC scenario, an object similar to Sedna was obtained on an average of 82−158 SDO’s observations for λ between 2.20 and 2.70;

  • 4.

    Considering latitudes restriction, a Sedna is obtained in an average of 82−158 SDO observations, for λ roughly between 2.3 and 2.9.

It is noteworthy that, for the PMSC model, a Sedna-type object is obtained as one in 82−158 observed SDO when we consider a slope for the size distribution that is not much more than what is presently estimated for the scattered disk. For the star cluster model consistency was obtained when we considered a slope for the cumulative size distribution in the IOC around 3.0, which is greater than the collisional equilibrium slope around 2.5, which may also be the case for the objects that were scattered by the gas giants in their final phase of formation.

We also compared the PMSC and star cluster scenarios by restricting our analysis to the objects observed in the survey by Schwamb et. al. (2010), and obtained the probability of observing an object like Sedna with 14 or fewer observed scattered objects. For size-distribution slopes close to 2.0, the probability is twice as high for the star cluster model than for the PMSC model, peaking near 30% for a slope at 1.8 and gradually decreasing to 2% for slopes near 3.0. On the other hand, for both scenarios, it is not very likely that we would observe Sedna and just 14 SDOs in the same survey. In this sense we might say that Sedna was observed earlier than expected if we consider a population formed by either scenario considered in this paper. This is somehow confirmed by Schwamb et al. (2010) did not find any other Sedna-like object in their survey. Also that it has not been found in any other survey to date seems to strengthen this idea. On the other hand, the results with observations not restricted to one particular survey suggest that we are not far from detecting a new object of the inner Oort Cloud.

According to Gomes et al. (2006), the PMSC scenario is robust with respect to different masses and orbital elements of the companion, provided that a strength parameter proportional to the planet’s mass and inversely proportional to the semi-minor axis to the third power is kept constant. This strength parameter is compatible with most PMSCs that would otherwise be detected due to its stronger visual magnitude. This fact be important to provide a more sensitive differentiation between the

scenarios when new observations are available in the future. A fundamental difference between the population of objects produced by the PMSC model and by the stellar cluster model is that the objects produced in the former case are dynamically active, while the objects obtained in the stellar cluster are fossilized at their positions. This can produce important signatures in the distribution of other TNOs objects, which will be analyzed in a future work.

Our final conclusion is that both the stellar cluster and the PMSC scenario are able to describe the dynamical formation of Sedna-type objects. More observations of other members of Sedna population are necessary to determine which is the more plausible scenario for representing the physical reality in the formation of these objects.

References

  1. Binney, J., & Tremaine, S. 1987, Galactic Dynamics (UK: Princeton University Press) [Google Scholar]
  2. Buie, M. W., Wasserman, L. H., Elliot, J. L., et al. 2003, Earth, Moons Planets, 92, 113 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brandner, W. 2006, Planet Formation: theory, observations and experiments, eds. H. Klahr, & W. Brandner (New York: Cambridge University Press) [Google Scholar]
  4. Brasser, R., Duncan, M. J., & Levison, H. F. 2006, Icarus, 184, 59 [NASA ADS] [CrossRef] [Google Scholar]
  5. Brasser, R., Duncan, M. J., & Levison, H. F. 2007, Icarus, 191, 413 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brasser, R., Duncan, M. J., & Levison, H. F. 2008, Icarus, 196, 274 [NASA ADS] [CrossRef] [Google Scholar]
  7. Brasser, R., Duncan, M. J., Levison, H. F., Schwamb, M. E., & Brown, M. E. 2011, Icarus, 217, 1 [Google Scholar]
  8. Brown, M. E., Trujillo, C., & Rabinowitz, D. 2004, ApJ, 617, 645 [NASA ADS] [CrossRef] [Google Scholar]
  9. Brouwer, D., & Clemence, G. M. 1961, Meth. Cel. Mech. (New York: Academic Press Inc) [Google Scholar]
  10. Buie, M. W., Wasserman, L. H., Millis, R. L., et al. 2006, Dynamical Structure of the Kuiper Belt. NOAO Proposal ID #2006B-0413 [Google Scholar]
  11. Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  12. Delorme, P., Gagné, J., Malo, L., et al. 2012, A&A, 548, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Duncan, M. J., & Levison, H. F. 1997, Science, 276, 1670 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Elliot, J. L., Kern, S. D., Clancy, K. B., et al. 2005, ApJ, 129, 1117 [Google Scholar]
  15. Fernández, J. A. 1997, Icarus, 129, 106 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fernández, J. A., & Bruníni, A. 2000, Icarus, 145, 580 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fraser, W. C., Brown, M. E., & Schwamb, M. E. 2010, Icarus, 210, 944 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gaidos, E. J. 1995, Icarus 114, 258 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gladman, B., & Chan, C. 2006, ApJ, 643, 135 [Google Scholar]
  20. Gomes, R. S. 2003, Icarus, 161, 404 [Google Scholar]
  21. Gomes, R. S., & Soares, J. S. 2009, IAU Symp., 263, 67 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gomes, R. S., Gallardo, T., Fernández, J. A., & Brunini, A. 2005a, Celest. Mech. Dyn. Astron., 91, 109 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gomes, R. S., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005b, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Gomes, R. S., Matese, J., & Lissauer, J. 2006, Icarus, 184, 589 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kaib, N. A., Roskar, R., & Quinn, T. 2011, Icarus, 215, 491 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kenyon, S. J., & Bromley, B. C. 2004, Nature 432, 598 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  27. Kouwenhoven, M. B. N., Goodwin, S. P., Parker, R. J., et al. 2012, MNRAS, 404, 1835 [Google Scholar]
  28. Levison, H. F., Thommes, E., & Duncan, M. J. 2010a, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
  29. Levison, H. F., Duncan, M. J., Brasser, R., & Kaufmann, D. E. 2010b, Science, 329, 187 [NASA ADS] [CrossRef] [Google Scholar]
  30. Morbidelli, A., & Levison, H. F. 2004, AJ, 128, 2564 [NASA ADS] [CrossRef] [Google Scholar]
  31. Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Oort, J. H. 1950, Bull. Astron. Inst. Neth., 11, 91 [Google Scholar]
  33. Schwamb, M. E., Brown, M. E., Rabinowitz, D. L., & Ragozzine, D. 2010, ApJ, 720, 1691 [NASA ADS] [CrossRef] [Google Scholar]
  34. Sicardy, B., Ortiz, J. L., Assafin, M., et al. 2011, Nature, 478, 493 [NASA ADS] [CrossRef] [Google Scholar]
  35. Sumi, T., Kamiya, K., Bennett, D. P., et al. 2011, Nature, 473, 349 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  36. Tsiganis, K., Gomes, R. S., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

All Figures

thumbnail Fig. 1

Orbital distribution in semi-major axis vs. perihelion distances for the scenario of the star cluster, for three central cluster densities, after 3 × 106 ys. The small circles represent planetesimals and triangles represent CR105, VN112, and Sedna.
In the text
thumbnail Fig. 2

Orbital distribution of semi-major axis vs. perihelion distance for the scenario of the star cluster after 3 × 106 ys: the small circles represent planetesimals and triangles represent CR105, VN112, and Sedna. Panels from left to right respectively denote star orbits close to the cluster center, intermediate, and far from the cluster center, corresponding to a density in the cluster center of 104   M⊙ pc-3.
In the text
thumbnail Fig. 3

Orbital distribution of semi-major axis vs. pericenter distance for the PMSC model after 4.5 × 109 Gy. The small circles represent planetesimals and triangles represent CR105, VN112, and Sedna. The parameters for the companion are a = 1500 AU, e = 0.4, i = 80°, and M = 10-4   M⊙.
In the text
thumbnail Fig. 4

Distribution of semi-major axis a), eccentricity b), inclination c), and perihelion distance d) for objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained by the scenario of the star cluster.
In the text
thumbnail Fig. 5

Variation in the power law slope with the average number of observations needed to obtain a Sedna-like object for the scenario of the star cluster, considering three values for the radius of the largest body in the the distribution. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation for the largest object with two Pluto radii in the larger panel.
In the text
thumbnail Fig. 6

Variation in the power law slope vs. average number of observations to obtain a Sedna-like object for the scenario of the star cluster, considering four values for the allowed latitude range. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation without restriction in latitude.
In the text
thumbnail Fig. 7

Distribution of semi-major axis a); eccentricity b); inclination c); and perihelion distances bf d) of objects belonging to the IOC (q ≥ 50 AU and 300 ≤ a ≤ 1000 AU) obtained by the PMSC scenario.
In the text
thumbnail Fig. 8

Variation in the power law slope vs. the average number of observations to obtain a Sedna-like object for the scenario of the PMSC, considering three values for the radius of the largest body in the distribution The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation for the largest object with two Pluto radius.
In the text
thumbnail Fig. 9

Variation in the power law slope vs. the average number of observations to obtain a Sedna-like object for the scenario of the PMSC, considering four values for the allowed latitude range of observation. The small panel represents a zoom for the range 70−170 observations. The thick curve represents the simulation without restriction in latitude.
In the text
thumbnail Fig. 10

The first 30 largest radius of SDOs. The continuous line stands for the real objects. The dotted line refers to sizes determined by the OS on a population affected by the PMSC. The dashed line stands for the no-companion model.
In the text
thumbnail Fig. 11

Probability of obtaining an object of type Sedna for the star cluster and the PMSC scenarios for a number of 14 or fewer objects observed, following observational research by Schwamb et al. (2010).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.