| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201321356 | |
| Published online | 03 April 2013 | |
Radio continua modulated by waves: Zebra patterns in solar and pulsar radio spectra?
Astronomical Institute of the Academy of Sciences of the Czech
Republic,
25165
Ondřejov,
Czech Republic
e-mail:
karlicky@asu.cas.cz
Received: 24 February 2013
Accepted: 8 March 2013
Aims. We aim to answer the question how waves with plasma density variations affect the radio continua generated by the plasma emission mechanism.
Methods. We built a simple semi-empirical model of the radio continuum modulation. Assuming that the waves with density variations are in the source of this radio continuum, we modeled the artificial radio spectrum, which we compared with observed spectra.
Results. We show that the waves with density variations modulate the radio continua generated by the plasma emission mechanism. Considering a single slow magnetoacoustic wave, we model the radio spectra, which resemble solar zebra patterns. We show that this modulation generates zebra effects even when the radio continuum is composed of many spiky bursts. Generalizing from one single wave to a wave turbulence we find that the computed radio spectrum is similar to so-called lace bursts. Finally, using the same procedure, but for fast magnetoacoustic waves, we modeled the radio spectrum similar to that observed during the interpulse phase of the radio emission of the Crab Nebula pulsar.
Key words: Sun: radio radiation / pulsars: individual: Crab Nebula pulsar / waves
© ESO, 2013
1. Introduction
The plasma emission mechanism is considered to be a two-level process: At locations where the electron distribution function has a positive derivative in the velocity space (e.g., bump-on-tail, loss-cone distributions) the plasma (Langmuir) or upper-hybrid waves are generated by various instabilities. Then these waves are converted into the electromagnetic waves on fundamental or harmonic plasma (upper-hybrid) frequencies (Melrose 1980). Because these frequencies depend on the plasma density, it is expected that the observed radio spectra generated by this mechanism can be modulated by the waves connected with density variations.
The fine structures of the solar radio emission are an important source of information on plasma parameters and processes in solar flares.
There are many types of solar radio bursts, one of which are type IV radio bursts, which can be characterized as broadband smooth radio continua. They frequently exhibit several types of fine-structures such as zebra patterns, and fiber bursts, see the catalog of Slottje (1981).
Zebra patterns (or zebras) have been presented in many papers, see e.g. Slottje (1972), Aurass & Chernov (1983), Jiřička et al. (2001), Aurass et al. (2003), Chernov et al. (2003), Chen et al. (2011), and others.
Many mechanisms have been proposed to explain them (Kuijpers 1975; Zheleznyakov & Zlotnik 1975; Chernov 1976; Mollwo 1983; Winglee & Dulk 1986; Ledenev et al. 2001; Yasnov & Karlický 2004; Bárta & Karlický 2006; LaBelle et al. 2003; Kuznetsov & Tsap 2007; Zlotnik 2013); for review of these models, see Chernov (2010).
The most frequently used model is based on the emission at the double plasma resonance: 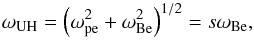 (1)where ωUH,ωpe, and ωBe are the upper-hybrid, electron-plasma, and electron-cyclotron frequencies, and s is an integer harmonic number (e.g. Zlotnik 2013). In addition, there are models based on interferometric effects (Bárta & Karlický 2006; Ledenev et al. 2006), trapping of the upper-hybrid waves in density resonators (LaBelle et al. 2003), and the ion-cyclotron maser (Treumann et al. 2011).
(1)where ωUH,ωpe, and ωBe are the upper-hybrid, electron-plasma, and electron-cyclotron frequencies, and s is an integer harmonic number (e.g. Zlotnik 2013). In addition, there are models based on interferometric effects (Bárta & Karlický 2006; Ledenev et al. 2006), trapping of the upper-hybrid waves in density resonators (LaBelle et al. 2003), and the ion-cyclotron maser (Treumann et al. 2011).
However, zebras were also observed in the radio emission of the Crab Nebula pulsar (Hankins & Eilek 2007). Several models explaining these zebras have been proposed, e.g., by Hankins & Eilek (2007), or recently by Zheleznyakov et al. (2012).
Treumann et al. (1990) suggested that the fiber bursts, which are another fine structure of type IV bursts, are generated by a modulation of the background type IV by a traveling MHD wave. Based on this idea, Kuznetsov (2006) and Karlický et al. (2013) built models in which fiber bursts are produced by a modulation of the radio continuum by the fast sausage magnetoacoustic waves (or wave trains).
These fiber models gave rise to the question of what happens when we assume that the radio continuum is affected by other magnetohydrodynamic waves, e.g., by slow magnetoacoustic waves (Roberts et al. 1984).
In the present paper, we study this modulation. We found that this process can explain some aspects of the observed solar zebras. We used a similar model and simulated pulsar zebras.
The paper is organized as follows: Sect. 2 is devoted to solar zebras. Here we show an example of the solar zebra, describe our semi-empirical model, and present the simulation results. Section 3 shows a typical pulsar zebra compared with a simulated spectrum. Finally, in Sect. 4 we discuss our results.
 |
Fig. 1 Zebra pattern observed during the 18 March 2003 event by the Ondřejov radiospectrograph. |
2. Solar zebras
2.1. Example of the radio spectrum with zebra pattern
Figure 1 shows the radio spectrum with zebra pattern observed during the 18 March 2003 flare by the Ondřejov radiospectrograph (Jiřička et al. 1993). The zebra consists of about four zebra lines that slowly drift to lower frequencies. The frequency drift is about − 10 MHz s-1. It is interesting that in this case the zebra looks to be composed of many spiky structures. An example of the frequency profile of this zebra at 12:23:55.5 UT is shown in Fig. 7 with a full line. The frequency interval between the zebra lines is about 100 MHz. Similarly, as known from the literature (e.g. Zlotnik 2013), the frequency interval between neighboring zebra lines slowly increases with increasing frequency.
2.2. Modeled solar zebras
In agreement with Kuznetsov (2006) and Karlický et al. (2013), we assumed that the radio continuum emission is produced at the double (harmonic) upper-hybrid frequency ωUH as a result of a coalescence of two upper-hybrid waves generated, e.g., by the loss-cone instability. In solar flare conditions the electron-cyclotron frequency ωce is much lower than the electron-plasma frequency ωpe, therefore in the following we assumed ωUH ≈ ωpe and neglected the role of the magnetic field.
 |
Fig. 2 Density model of the solar atmosphere with (full line) and without (dashed line) the slow sausage magnetoacoustic wave (the wave density amplitude is nR = 0.01). The horizontal full lines depict the plasma densities corresponding to the highest and lowest frequencies considered in the radio spectrum. The vertical dashed lines limit this density interval. The dotted line shows the lowest height of the zebra radio source corresponding to 2.5 GHz. |
Furthermore, we assumed that radio continuum is generated in some height interval of the solar atmosphere, which is in the hydrostatic equilibrium. The electron plasma density ne in this atmosphere is described as 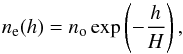 (2)where no is the density at h = 0, h is the height in the solar atmosphere, and H is the height scale. We here assumed no = 4 × 1010 cm-3, and H = 25 Mm. The electron density profile is shown by the dashed line in Fig. 2.
(2)where no is the density at h = 0, h is the height in the solar atmosphere, and H is the height scale. We here assumed no = 4 × 1010 cm-3, and H = 25 Mm. The electron density profile is shown by the dashed line in Fig. 2.
First, we assumed that an each height unit of the radio source in the solar atmosphere (in the studied 2000–3000 MHz frequency interval) emits the same radio flux. Then, the resulting radio flux at the specific frequency f can be expressed as a sum of the emissions from the height units with a frequency of fpe = ωpe/2π close to f/2. Accordingly, the intensity of the radio emission at some specific frequency only depends on the spatial gradient of plasma density. A maximum radio flux will be reached at the frequency that corresponds to the location where the absolute value of the density gradient is lowest, and vice versa. Owing to a slight change of the density gradient in the studied height interval (see vertical dashed lines in Fig. 2), the radio flux in the frequency space slowly increases towards lower frequencies. To obtain a flat radio continuum spectrum (as observed in this frequency range) we multiplied the unit height emission by the weighting function we(h). Its value is close to 1 and slightly increases at lower heights.
Then we assumed that in the radio continuum source there is the wave propagating along the magnetic field lines in the vertical direction in the solar atmosphere. The most appropriate one in this case looks to be slow sausage magnetoacoustic wave traveling along dense loops (waveguides) (for a description of this wave, see e.g. Roberts et al. 1984). In our model, we added this wave as a density perturbation to the unperturbed atmosphere as follows: ![\begin{equation} n_{\rm e} (h) = n_{\mathrm{o}} \exp \left(-\frac{h}{H}\right) \left(1 + n_{\rm R} \cos [2 \pi (h - h_0 - c_{\rm s} t)/ L_{\rm w}]\right), \end{equation}](/articles/aa/full_html/2013/04/aa21356-13/aa21356-13-eq25.png) (3)where nR is the ratio between the amplitude of the wave nw and unperturbed atmospheric density ne, cs is the velocity of the slow sausage magnetoacoustic wave (approximately equal to the sound velocity), t is the time, and Lw is the wavelength. An example of the atmosphere with the wave (nR = 0.01 and Lw = 2400 km) is shown by the full line in Fig. 2.
(3)where nR is the ratio between the amplitude of the wave nw and unperturbed atmospheric density ne, cs is the velocity of the slow sausage magnetoacoustic wave (approximately equal to the sound velocity), t is the time, and Lw is the wavelength. An example of the atmosphere with the wave (nR = 0.01 and Lw = 2400 km) is shown by the full line in Fig. 2.
To simulate the radio spectrum with a zebra similar to that in Fig. 1 we considered the following wave parameters: cs = 117 km s-1, Lw = 2400 km, and nR = 0.005. The positive value of the velocity means that the wave propagates towards higher heights in the solar atmosphere. Because the zebra was observed only at frequencies below 2.5 GHz (Fig. 1) we take the wave only at heights above the height corresponding to the frequency 2.5 GHz (see the dotted vertical line in Fig. 2). Then we recalculated the emission from height units to frequencies; the resulting spectrum we show in Fig. 3. The density wave changes densities in the radio source and thus changes emitting frequencies. These changes in emitting frequencies change the frequency spectrum from the flat spectrum without the wave to the radio spectrum with the zebra lines in the case with the wave.
Because the observed zebra (Fig. 1) shows spiky structures, we tried to simulate these with the following procedure. Using the random number generator, we generated the emission weighting function we(h,t) in the height-time space as shown in Fig. 4. The physical meaning of this weighting function is that the radio emission is localized in bright regions, which appear only for some limited time intervals. To generate this function we used the Gaussian functions in space and in time. We added this weighting function and computed the radio spectrum, which is shown in Fig. 5. To simulate these spiky structures only at the zebra, we used the weighting function only in the space above the horizontal and slowly drifting line, see Fig. 4. As a result of this weighting function, which represents bright emission regions in the radio source, the spiky structures appear in the radio spectrum; compare Figs. 3 and 5.
 |
Fig. 3 Computed solar radio spectrum with the zebra pattern generated by a modulation of the radio continuum by a single wave; the wave density amplitude is nR = 0.005. Compare the spectrum with that in Fig. 1. |
 |
Fig. 4 Radio emission structure (weighting function) generated randomly in time and heights in the solar atmosphere. Only the emission structure at heights above the horizontal slowly drifting line was used to compute the radio spectrum shown in Fig. 5. |
During computations we changed the wave amplitude and found that the depth of zebra flux modulation increases with increasing amplitude, see Fig. 6. However, it is valid up to the wave amplitude that has a zero density gradient in the radio source – the critical amplitude. One wave bump on the unperturbed density profile with an amplitude lower than the critical one generates one maximum on the radio spectrum, the bump with an amplitude greater than the critical one generates two maxima.
Finally, we tried to fit the zebra frequency profile (Fig. 7) and found that the best fit was obtained for the wave amplitude corresponding to nR = 0.005. The peaks (zebra lines in the spectrum) of the computed frequency profile in Fig. 7 (dashed line) are at 2065, 2165, 2273, and 2385 MHz. This means the frequency interval between neighboring zebra lines increases with increasing frequency, which agrees with observations. A detailed analysis shows that this is caused by a change of the global density gradient that depends on the height in the unperturbed atmosphere.
 |
Fig. 5 Computed solar radio spectrum with the zebra pattern generated by a modulation of the radio continuum by a single wave together with the radio emission structure shown in Fig. 4. The wave density amplitude is nR = 0.005. Compare the spectrum with that in Fig. 1. |
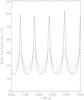 |
Fig. 6 Computed radio flux variations as a function of frequency for three wave density amplitudes: nR = 0.01 (full line), nR = 0.005 (dashed line), and nR = 0.003 (dotted line). |
 |
Fig. 7 Comparison of the radio flux as a function of frequency observed at 12:23:55.5 UT during the 18 March 2003 zebra event (full line) with that computed for the wave density amplitude nR = 0.005 (dashed line). |
 |
Fig. 8 Example of the radio spectrum generated by a modulation of the radio continuum by the wave turbulence. |
2.3. Radio spectrum with wave turbulence
Now, instead of one single wave, we considered a 1D wave turbulence (along the vertical magnetic field lines in the solar atmosphere). We considered ten waves with wavelengths in the interval Lw = 125−4000 km, with an amplitude according to the Kolmogorov spectral index i = −5/3 with random phases and with cs = ± 117 km s-1. The positive and negative value of the velocity means that one half of the waves propagate toward higher heights and the second half of the waves toward lower heights in the solar atmosphere. The ratio of the density amplitude of the longest wave to the coronal density is 0.05.
Using the same procedure as in the previous paragraph, we computed the radio spectrum, which is shown in Fig. 8. It shows a very complex structure. This structure resembles the so-called lace bursts, which are only rarely observed (Karlický et al. 2001).
 |
Fig. 9 Zebra pattern spectrum in microwave emission from the Crab Nebula pulsar (Hankins & Eilek 2007). |
3. Pulsar zebras
Zebra patterns similar to those analyzed in solar observations were observed in the radio emission of the Crab Nebula pulsar (Hankins & Eilek 2007), see Fig. 9. They were observed in the interpulse phase. Hankins & Eilek (2007) discussed several possible explanations of these zebras, and concluded that the interpulse zebras do not match the predictions of any current model. Recently, these zebras were interpreted by Zheleznyakov et al. (2012) using the double-plasma resonance model. This explains many observed features of these zebras. However, the main problem of the model is that it requires relatively low magnetic field in the pulsar radio source.
In our simulations we assumed that in the pulsar atmosphere the radio continuum is generated at the double-plasma frequency 2ωpe from two coalescing plasma (Langmuir) waves. Furthermore, in the radio continuum source we assumed a fast magnetoacoustic wave. This wave propagates at Alfvén speed, which for our case with a very high magnetic field B, is close to the speed of light c (Gedalin 1993): 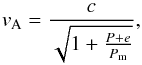 (4)where e is the total energy density of plasma particles, P is the total plasma pressure and Pm = B2/8 π is the magnetic field pressure.
(4)where e is the total energy density of plasma particles, P is the total plasma pressure and Pm = B2/8 π is the magnetic field pressure.
The density model for our simulations depends on the pulsar model. We consider the model of Zheleznyakov et al. (2012). They proposed that the observed frequency of the zebra f′ corresponds to the frequency in the radio source f as 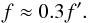 (5)This yields the density range in the radio source: the radio frequency f′ = 8 GHz and f′ = 10.5 GHz corresponds to the density 1.77 × 1010 cm-3 and 3.06 × 1010 cm-3, respectively, see horizontal lines in Fig. 10. In our density model the global density profile is given by the exponential function with a height scale of 12.5 km. This steep density profile can be caused by a strong gravity in the radio source or it is only transient one.
(5)This yields the density range in the radio source: the radio frequency f′ = 8 GHz and f′ = 10.5 GHz corresponds to the density 1.77 × 1010 cm-3 and 3.06 × 1010 cm-3, respectively, see horizontal lines in Fig. 10. In our density model the global density profile is given by the exponential function with a height scale of 12.5 km. This steep density profile can be caused by a strong gravity in the radio source or it is only transient one.
We propose that the frequency drift of the observed zebra is caused by the propagating fast magnetoacoustic wave. It gives us the spatial scale in the density model (Fig. 10). The wave velocity is vA ≈ c, the amplitude of density wave used and the wave wavelength is nR = 0.01 and 1.5 km. Due to the positive frequency drift of the observed zebra lines, the assumed wave propagates toward lower heights in the present density model.
 |
Fig. 10 Density model used for the pulsar zebra simulation. This density model is based on the pulsar model of Zheleznyakov et al. (2012). For high Lorentz factors this model has to be re-scaled depending on the Lorentz factor. |
 |
Fig. 11 Computed pulsar radio spectrum with the zebra pattern generated by a modulation of the radio continuum caused by the fast magnetoacoustic wave. The radio continuum is also modulated in time according to the smoothed time burst profile shown in the upper part of Fig. 9. |
We used the same procedure as in the solar case. To also mimic the observed time variation of this zebra, we smoothed the time profile of the pulsar emission shown in the upper part of Fig. 9 and used it as the weighting function we(t). The computed radio spectrum is shown in Fig. 11.
In other models, e.g., in the model of Hankins & Eilek (2007), the radio source is in the highly relativistic jet with the plasma density 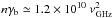 cm-3, where γb is the Lorentz factor estimated as γb ~ 102−103. For these high Lorentz factors our density model has to be rescaled according to the Lorentz factor. We expect that in these cases the radio spectra will be similar to the spectrum presented in Fig. 11.
cm-3, where γb is the Lorentz factor estimated as γb ~ 102−103. For these high Lorentz factors our density model has to be rescaled according to the Lorentz factor. We expect that in these cases the radio spectra will be similar to the spectrum presented in Fig. 11.
4. Discussion and conclusions
Based on the results presented here, we can answer the question from the title of this paper. Yes, some solar zebra patterns can be explained by waves in radio continuum sources. The slow sausage magnetoacousic wave looks to be an appropriate wave type in the solar zebra case. Similarly, some waves (maybe the fast magnetoacoustic ones) can modulate the radio emission of pulsars and produce zebras. However, in both the cases we need a more detailed analysis and comparisons with other zebra models.
One way to verify this model could be based on the fact that the density wave only re-distributes the emission energy in the frequency space; the emission energy with and without the wave is the same. Assuming that the emission is the same in all parts of the source volume, this means that an increase of the radio flux at some frequencies equals the radio flux decrease at other frequencies.
But real radio sources are not homogenous. Emissions from different source locations differ. In our model this aspect is included by the weighting function, which depends not only on locations, but also on time. We used this function to show the spiky structure of the zebra observed in March 18, 2003.
Note that in our case, the highest radio flux increase corresponds to the lowest absolute value of the density gradient and vice versa. In principle, this enables to invert the problem, i.e. to estimate the wave density profile in the radio source from the zebra frequency profile.
We found that the depth of the radio flux modulation increases with an increase of the wave amplitude. However, this is valid only up to the wave amplitude that yields a zero density gradient at some locations. Except for the case with the turbulence, the assumed wave amplitudes give the negative density gradients everywhere in both models. We found that the radio flux modulation vs. frequency in the March 18, 2003 zebra can be fitted by a wave with an amplitude nR = 0.005.
Furthermore, it was shown that the global change of the density gradient in the atmosphere can explain the observed increase of the frequency interval between neighboring zebra lines with the frequency increase.
It is commonly accepted that the slow magnetoacoustic waves are strongly damped, which could modify our model. Some works based on observations show such a damping, see, e.g., Kim et al. (2012). On the other hand, recently, Liu et al. (2012) presented a slow magnetoacoustic wave propagating along a tube in the solar atmosphere without significant damping across a propagation distance of about 33 Mm. This distance is ten times greater than in our solar zebra case (117 km s-1 × 25 s = 2.9 Mm). Furthermore, Liu and collaborators found that the wavelength of this wave is about 5000 km, the wave speed 101 km s-1, and the wave density amplitude 0.084. The wavelength and velocity are similar to those considered in our model. The observed value of the density amplitude is higher than all amplitudes used in our computations. Although slowly damped slow magnetoacoustic waves were observed, the question about their damping remains open, and more studies in this field are necessary. For example, a continuous driving of these waves during reconnection in the region close to an X-point is the interesting possibility to reduce their damping. If this is the case, zebras would occur in the vicinity of such an X-point in reconnection, and their bandwidth combined with the coronal density gradient would yield information about the zone around the reconnection site.
In our solar model we assumed hydrostatic equilibrium of the solar atmosphere. To explain the observed frequency drift of the March 18, 2003 zebra, we assumed a height scale as 25 Mm, i.e. the atmospheric temperature of 5 × 105 K. However, this result also depends on the assumption about the vertical propagation of wave and about the emission on the harmonic frequency. For the emission on the fundamental frequency the modulation effect will be more complex due to wave cutoffs.
We presented computations with a single wave and obtained artificial radio spectra similar to some observed zebras. Then we generalized this single-wave case to the radio source with wave turbulence. The obtained spectrum was found to be similar to the rarely observed lace bursts.
We simulated pulsar zebras using the pulsar model of Zheleznyakov et al. (2012). For models with high Lorentz factors, the density model needs to be re-scaled to obtain the similar radio spectra. Thus, the parameters used in our model for the pulsar zebra are not unique. To better specify them a more specific model of the pulsar radio continuum is needed. We aim to do this in our future work.
In the present work the waves were modeled using the cosinus function. In future work it is necessary to include the non-linear character of these waves, which influences the form of these waves, especially for higher amplitudes and during their propagation through non-homogeneous atmospheres.
The present model describes a simple effect of the modulation of the radio continuum emission. It does not consider any special frequencies for the zebra emission lines, as mentioned in the introduction. On the other hand, density waves are highly probable in any radio sources, therefore this modulation effect should be considered also in more sophisticated models of the zebra patterns.
Acknowledgments
The author thanks the anonymous referee for comments that improved the paper. This research was supported by grants P209/12/0103 (GA CR), and the Marie Curie PIRSES-GA-2011-295272 RadioSun project.
References
- Aurass, H., & Chernov, G. P. 1983, Sol. Phys., 84, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Aurass, H., Klein, K.-L., Zlotnik, E. Y., & Zaitsev, V. V. 2003, A&A, 410, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bárta, M., & Karlický, M. 2006, A&A, 450, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, B., Bastian, T. S., Gary, D. E., & Jing, J. 2011, ApJ, 736, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P. 1976, Soviet Astron. 20, 449 [Google Scholar]
- Chernov, G. P. 2010, Res. Astron. Astrophys., 10, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, G. P., Yan, Y. H., & Fu, Q. J. 2003, A&A, 406, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gedalin, M. 1993, Phys. Rev. E 47, 4354 [Google Scholar]
- Hankins, T. H., & Eilek, J. A. 2007, ApJ, 670, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Jiřička, K., Karlický, M., Kepka, O., & Tlamicha, A. 1993, Sol. Phys., 147, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Jiřička, K., Karlický, M., Mészárosová, H., & Snížek, V. 2001, A&A, 375, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlický, M., Bárta, M., Jiřička, K., et al. 2001, A&A, 375, 638 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karlický, M., Mészárosová, H., & Jelínek, P. 2013, A&A, 550, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, S., Nakariakov, V. M., & Shibasaki, K. 2012, ApJ, 756, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijpers, J. 1975, Sol. Phys., 44, 143 [Google Scholar]
- Kuznetsov, A. A. 2006, Sol. Phys., 237, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsov, A. A., & Tsap, Yu. T. 2007, Sol. Phys., 241, 127 [NASA ADS] [CrossRef] [Google Scholar]
- LaBelle, J., Treumann, R. A., Yoon, P. H., & Karlický, M. 2003, ApJ, 593, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Ledenev, V. G., Karlický, M., Yan, Y., & Fu, Q. 2001, Sol. Phys., 202, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Ledenev, V. G., Yan, Y., & Fu, Q. 2006, Sol. Phys., 233, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Zhou, Z., Wang, Y., et al. 2012, ApJ, 758, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Mollwo, L. 1983, Sol. Phys., 83, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1980, Plasma Astrophysics (New York, USA: Gordon and Breach Science Publ.) [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 865 [NASA ADS] [Google Scholar]
- Slottje, C. 1972, Sol. Phys., 25, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Slottje, C. 1981, Atlas of fine structures of dynamic spectra of solar type IV-dm and some type II radio bursts, Dwingeloo [Google Scholar]
- Treumann, R. A., Güdel, M., & Benz, A. O. 1990, A&A, 236, 242 [NASA ADS] [Google Scholar]
- Treumann, R. A., Nakamura, R., Baumjohann, W. 2011, Ann. Geophys., 29, 1673 [NASA ADS] [CrossRef] [Google Scholar]
- Winglee, R. M., & Dulk, G. A. 1986, ApJ, 307, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Yasnov, L. V., & Karlický, M. 2004, Sol. Phys., 219, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., & Zlotnik, E. Y. 1975, Sol. Phys., 44, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Zheleznyakov, V. V., Zaitsev, V. V., & Zlotnik, E. Y. 2012, Astron. Lett., 38, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Zlotnik, E. Y. 2012, Sol. Phys., online first [Google Scholar]
All Figures
 |
Fig. 1 Zebra pattern observed during the 18 March 2003 event by the Ondřejov radiospectrograph. |
| In the text | |
 |
Fig. 2 Density model of the solar atmosphere with (full line) and without (dashed line) the slow sausage magnetoacoustic wave (the wave density amplitude is nR = 0.01). The horizontal full lines depict the plasma densities corresponding to the highest and lowest frequencies considered in the radio spectrum. The vertical dashed lines limit this density interval. The dotted line shows the lowest height of the zebra radio source corresponding to 2.5 GHz. |
| In the text | |
 |
Fig. 3 Computed solar radio spectrum with the zebra pattern generated by a modulation of the radio continuum by a single wave; the wave density amplitude is nR = 0.005. Compare the spectrum with that in Fig. 1. |
| In the text | |
 |
Fig. 4 Radio emission structure (weighting function) generated randomly in time and heights in the solar atmosphere. Only the emission structure at heights above the horizontal slowly drifting line was used to compute the radio spectrum shown in Fig. 5. |
| In the text | |
 |
Fig. 5 Computed solar radio spectrum with the zebra pattern generated by a modulation of the radio continuum by a single wave together with the radio emission structure shown in Fig. 4. The wave density amplitude is nR = 0.005. Compare the spectrum with that in Fig. 1. |
| In the text | |
 |
Fig. 6 Computed radio flux variations as a function of frequency for three wave density amplitudes: nR = 0.01 (full line), nR = 0.005 (dashed line), and nR = 0.003 (dotted line). |
| In the text | |
 |
Fig. 7 Comparison of the radio flux as a function of frequency observed at 12:23:55.5 UT during the 18 March 2003 zebra event (full line) with that computed for the wave density amplitude nR = 0.005 (dashed line). |
| In the text | |
 |
Fig. 8 Example of the radio spectrum generated by a modulation of the radio continuum by the wave turbulence. |
| In the text | |
 |
Fig. 9 Zebra pattern spectrum in microwave emission from the Crab Nebula pulsar (Hankins & Eilek 2007). |
| In the text | |
 |
Fig. 10 Density model used for the pulsar zebra simulation. This density model is based on the pulsar model of Zheleznyakov et al. (2012). For high Lorentz factors this model has to be re-scaled depending on the Lorentz factor. |
| In the text | |
 |
Fig. 11 Computed pulsar radio spectrum with the zebra pattern generated by a modulation of the radio continuum caused by the fast magnetoacoustic wave. The radio continuum is also modulated in time according to the smoothed time burst profile shown in the upper part of Fig. 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


