| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201321148 | |
| Published online | 03 April 2013 | |
Mid-infrared observations of the circumstellar disks around PDS 66 and CRBR 2422.8-3423
University of Kiel, Institute for Theoretical Physics and
Astrophysics,
Leibnizstrasse 15,
24118
Kiel,
Germany
e-mail:
cgraefe@astrophysik.uni-kiel.de
Received:
22
January
2013
Accepted:
6
March
2013
Aims. We present mid-infrared observations and photometry of the circumstellar disks around PDS 66 and CRBR 2422.8-3423, obtained with VISIR/VLT in the N band and for the latter also in the Q band. Our aim is to resolve the inner regions of these protoplanetary disks, which carry potential signatures of intermediate or later stages of disk evolution and ongoing planet formation.
Methods. We determined the radial brightness profiles of our target objects and the corresponding PSF reference that were observed before and after our target objects. Background standard deviations, the standard errors, and the seeing variations during the observations were considered. Adopting a simple radiative transfer model based on parameters taken from previous studies, we derived constraints on the inner-disk hole radius of the dust disk.
Results. Neither of the circumstellar disks around our science targets are spatially resolved in our observations. However, we are able to constrain the inner-disk hole radius to <15.0-0.5+0.5 AU and <10.5-1.0+0.5 AU for PDS 66 and CRBR 2422.8-3423, respectively. The photometry we performed yields N-band flux densities of 599 ± 8 mJy for PDS 66 and 130 ± 14 mJy for CRBR 2422.8-3423, as well as a Q-band flux density of 858 ± 109 mJy for CRBR 2422.8-3423.
Key words: protoplanetary disks / stars: pre-main sequence / stars: individual: PDS 66 / stars: individual: CRBR 2422.8-3423 / planets and satellites: formation / radiative transfer
© ESO, 2013
1. Introduction
As a consequence of the conservation of angular momentum during star formation, young stars are generally surrounded by dust and gas-rich circumstellar disks. These disks are known to dissipate over time (~106−107 yr; Haisch et al. 2001) by means of stellar winds or photoevaporation by either the radiation of the central star or some external radiation (e.g., Hollenbach et al. 2000; Clarke et al. 2001; Alexander & Armitage 2007), accretion onto the central star (Hartmann et al. 1998), grain growth and fragmentation (e.g., Dullemond & Dominik 2005; Dominik et al. 2007; Natta et al. 2007; Birnstiel et al. 2011; Sauter & Wolf 2011; Garaud et al. 2013; Ubach et al. 2012), and the formation of planets (e.g., Pollack et al. 1996; Boss 2002; Armitage 2007, 2010; Fortier et al. 2013). Knowledge of the structure of inner regions of disks and how they dissipate is crucial for our understanding of planet formation. Some protoplanetary disks show inner-disk clearings, such as gaps or holes, as an implication of the ongoing evolution of these disks. Their presence may indicate that planets have already formed in the disk and cleared their orbits. However, photoevaporation is also capable of producing inner-disk clearings. The study of such disks can therefore constrain models of planet formation and allows the roles of the different disk-clearing mechanisms to be evaluated.
To date, spectrophotometric methods are most widely used to identify inner-disk clearings (Forrest et al. 2004; Robitaille et al. 2007; D’Alessio 2009; Espaillat et al. 2008, 2010, 2012), but they usually do not provide an unequivocal solution. Conclusions obtained using spectral energy distribution (SED) modeling are much more model-dependent and degenerate than using resolved images. Therefore, imaging of protoplanetary disks provides an independent check of SED modeling and a far less ambiguous method for studying the disk structure (e.g., Eisner et al. 2009; Hughes et al. 2009; Sauter et al. 2009; Madlener et al. 2012; Gräfe et al. 2013). Various efforts to resolve the inner emission holes through direct imaging observations have been undertaken (e.g. in the (sub)millimeter wavelength range by Hughes et al. 2007, 2009; Brown et al. 2008, 2009; Andrews et al. 2011). However, owing to their limited sensitivity, submillimeter and millimeter observations have so far only provided information about the large reservoirs of cold dust in the outer regions, and they hardly probe the inner hot regions since their thermal emission is very faint at (sub)mm wavelengths. Thus, high-resolution mid-infrared imaging of protoplanetary disks is essential for obtaining information about the warm dust in the innermost regions of the disk, for detecting inner-disk clearings as signatures of the disk dissipation mechanisms, and investigating the structure close to the star, hence the regions where planets potentially form (e.g., Wolf et al. 2007). Efforts to spatially resolve circumstellar disks in the mid-infrared have been accomplished by, e.g., Pantin et al. (2005), Chen et al. (2008), Churcher et al. (2011), Gräfe et al. (2011), and Honda et al. (2012).
In this work we present high-resolution mid-infrared observations obtained with VISIR/VLT of the two well-studied circumstellar disks around PDS 66 and CRBR 2422.8-3423, reaching the limit of the angular resolution of today’s single-dish, ground-based telescopes. An even higher resolution in this wavelength range can only be achieved by means of interferometric observations, e.g., with MIDI/VLTI (e.g., Schegerer et al. 2009), which are still limited to the mid-infrared brightest sources. Our target objects are characterized in Sect. 2, while the observations and data reduction are found in Sect. 3. In Sect. 4 we describe the analysis of the data and the applied model in detail and finally present and discuss our results in Sect. 5.
2. Target objects
2.1. PDS 66
PDS 66, also known as MP Mus and Hen 3-892, is a K1 IVe classical T Tauri star (cTTS) and a member of Lower Centaurus Crux (Gregorio-Hetem et al. 1992; Mamajek et al. 2002). It exhibits excess infrared emission at λ > 3 μm that has been interpreted as arising from a primordial circumstellar disk (e.g., Silverstone et al. 2006; Hillenbrand et al. 2008). A distance d of only 86 pc makes it to one of the nearest known protoplanetary disks (Mamajek et al. 2002). Despite its old age of ~13 Myr, which is substantially beyond the median age for cTTS (e.g., Pascucci et al. 2007; Cortes et al. 2009), the disk of PDS 66 is in a stage between a primordial and a transitional disk, evolving toward the transition disk population, not showing indications of any large cleared inner regions in its spectral energy distribution (SED) yet (e.g., Preibisch & Mamajek 2008; Cortes et al. 2009). It is still actively accreting with a mass accretion rate of 5 × 10-9 M⊙ yr-1 resulting from modeling the Hα line profile (Pascucci et al. 2007). Figure 1 shows the SED of PDS 66. In Table 1 all available flux measurements are compiled.
 |
Fig. 1 Spectral energy distribution of PDS 66. A star with T⋆ = 5035 K is shown as the dashed line. |
2.2. CRBR 2422.8-3423
CRBR 2422.8-3423 is a Class I source located in the ρ Ophiuchus dark cloud at a distance of 120 pc (Comeron et al. 1993; Motte et al. 1998; Brandner et al. 2000). Its near-infrared appearance is dominated by a bipolar reflection nebula intersected by a central dust lane, similar to the well-studied edge-on disk of the Butterfly Star in Taurus (Brandner et al. 2000; Pontoppidan et al. 2005; Gräfe et al. 2013). The southeastern lobe of the reflection nebula is 11 times fainter than the northwestern lobe in the K band (Brandner et al. 2000), showing that the disk has an inclination deviating ~20° from edge-on orientation (Thi et al. 2002). No signatures of accretion or outflow are detected. Pontoppidan et al. (2005) detected ices in the disk using spectroscopy obtained with the Spitzer Space Telescope. Due to the lower than edge-on disk inclination of CRBR 2422.8-3423, the upper parts of the disk become optically thinner in the mid-infrared along the line of sight and allow one the detection of continuum emission from the warm, inner disk. Figure 2 shows the SED of CRBR 2422.8-3423 with its strong infrared excess resulting from the circumstellar disk. In Table 2 the available flux measurements are compiled.
 |
Fig. 2 Spectral energy distribution of CRBR 2422.8-3423 including a SST/IRS spectrum in the range 7.4−14.5 μm (Pontoppidan et al. 2005). |
3. Observations and data reduction
The mid-infrared observations of our two targets, PDS 66 and CRBR 2422.8-3423, were carried out on February 24 and May 21, 2011, respectively, using the Very Large Telescope (VLT) spectrometer and imager for the mid-infrared (VISIR) (Lagage et al. 2004) in the SIV filter and for CRBR 2422.8-3423 also in the Q2 filter. The properties of the observations are listed in Table 3. To achieve the highest possible angular resolution, the small field objective was used (0.075′′/pixel). A standard chop/nod-procedure to remove sky and telescope emission with a chop of 8″ in the north-south direction and a perpendicular 8″ nod as well as a jitter width of 1′′ were applied for the observations. Calibration observations of standard stars within a few degrees of the science object were taken immediately before and after the science observations. The standard stars were chosen from the mid-infrared spectrophotometric standard star catalog of the VLT based on Cohen et al. (1999). All observations were executed in service mode.
Observation properties.
Raw data were reduced using the VISIR data reduction pipeline provided by ESO. A full-resolution background map was created for every observed image using the Source Extractor software (Bertin & Arnouts 1996) and subtracted from the image to remove the background. This approach provides a more reliable estimate of the background than the assumption of a constant one. Owing to the small chopping and nodding throw in the observations, the observed source is always present in the field of view of the instrument such that the source is detected four times in the reduced image. To increase the signal-to-noise ratio (S/N) by a factor of two, these four detections of the source were averaged. The resulting reduced and averaged images of our two targets as well as the corresponding standard star images were used for the data analysis (Sect. 4).
4. Data analysis
The data analysis presented here is similar to previous work (Gräfe et al. 2011). For both target objects the mid-infrared emission is dominated by the circumstellar disk.
4.1. Radial brightness profiles
If the circumstellar disk surrounding the central star is spatially resolved, we expect the observed brightness distribution of this object to be significantly broadened compared to the corresponding point spread function (PSF). The observed standard stars are considered to be point sources and therefore used as PSF references in the data analysis. An appropriate comparison between science object and corresponding standard star observation clarifies if the circumstellar disk is spatially resolved.
We characterize the brightness distribution of an observed object by its peak-normalized
azimuthally averaged radial brightness profile. The averaging is performed with respect to
the center of each object which is determined by fitting a two-dimensional Gaussian
profile. Assuming azimuthal symmetry, this averaging method yields a much better
brightness profile than a simple cut through the object and also considerably improves the
S/N by a factor of 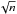 ,
where n is the number of pixels in every annulus. Azimuthally symmetric
disk images can be expected if the disks are seen in face-on orientation or if they are
unresolved but the PSF is approximately circular. The effect of the disk inclination on
our results is discussed in Sect. 5.
,
where n is the number of pixels in every annulus. Azimuthally symmetric
disk images can be expected if the disks are seen in face-on orientation or if they are
unresolved but the PSF is approximately circular. The effect of the disk inclination on
our results is discussed in Sect. 5.
We compile a radial brightness profile for each science object and standard star. For this purpose, the two standard star observations of each science object observation are averaged. Subtracting the standard star profile from the corresponding science object profile results in a residual flux profile produced by the extended star-disk system. Significant residual flux implies that the circumstellar disk is spatially resolved.
4.2. Detection threshold
To investigate whether the derived residual flux is significant, we define a detection threshold such that any residual flux above this threshold is caused by an extension of the star-disk system, i.e., a spatially resolved disk surrounding the star.
Our detection threshold takes into account the standard deviation of the background flux
(background noise, σbg) of the science and standard star
image, respectively, each standard error (σSE) resulting from
the averaging of the brightness profiles of both images as well as the seeing variations
during the observation. Owing to the azimuthal averaging, the background noise of the
brightness profiles depends on the radius (r) and declines with
increasing radius. We impose the constraint that the residual flux must be higher than
3σbg. The standard error is also a function of
r and is determined by 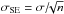 where σ is the standard deviation of the averaged flux of the brightness
profile. The seeing which varies during observations increases the
full-width-at-half-maximum (FWHM) of the observed object. In the data analysis, such
variations can cause a residual flux profile similar to the case of an extended star-disk
system, thus mimic a spatially resolved disk. Therefore, it is crucial to determine these
variations during the observation. To estimate the seeing variations we observed the
standard stars before and after the science object. Assuming that the seeing has a normal
distribution during the observations, the variations can be calculated as the half of the
absolute difference of the residual flux profiles of both standard star observations. This
method yields a radial profile reflecting a conservative estimate of the seeing variations
during the observations. In addition to the already mentioned constrains, the derived
residual flux profiles are considered significant only if they are three times larger than
the derived seeing variations.
where σ is the standard deviation of the averaged flux of the brightness
profile. The seeing which varies during observations increases the
full-width-at-half-maximum (FWHM) of the observed object. In the data analysis, such
variations can cause a residual flux profile similar to the case of an extended star-disk
system, thus mimic a spatially resolved disk. Therefore, it is crucial to determine these
variations during the observation. To estimate the seeing variations we observed the
standard stars before and after the science object. Assuming that the seeing has a normal
distribution during the observations, the variations can be calculated as the half of the
absolute difference of the residual flux profiles of both standard star observations. This
method yields a radial profile reflecting a conservative estimate of the seeing variations
during the observations. In addition to the already mentioned constrains, the derived
residual flux profiles are considered significant only if they are three times larger than
the derived seeing variations.
Our detection threshold is now defined as the sum of 3σbg and σSE of the science and standard star profile, respectively, and three times the seeing variations. The contribution of each of the components to this threshold is exemplarily represented for PDS 66 in Fig. 3, emphasizing the necessity for a reliable determination of the seeing variations.
 |
Fig. 3 Contribution of each of the components to the detection threshold for PDS 66. |
4.3. Model
During the evolution of circumstellar disks, inner-disk clearings like holes are expected to form (see also Sect. 1). Such objects are often referred to as transitional disks and are considered to represent an evolved stage of the accretion disks. In the mid-infrared, the surface brightness distribution of the circumstellar disk is dominated by the inner disk rim, which is directly illuminated by the central star. It is our aim to give constraints on the inner-disk hole radius of the observed objects adopting a simple model based on parameters taken from previous studies.
Our model consists of a parameterized disk that is described with a radially and
vertically dependent density distribution based on the work of Shakura & Sunyaev (1973): ![\begin{equation} \rho_{\rm disk} = \rho_0 \left(\frac{r_0}{r_{\rm cyl}}\right)^{\alpha} {\rm exp}\left(-\frac{1}{2}\left[\frac{z}{h(r_{\rm cyl})}\right]^2\right)\cdot \label{Eq:density} \end{equation}](/articles/aa/full_html/2013/04/aa21148-13/aa21148-13-eq81.png) (1)Here, z
is the cylindrical coordinate with z = 0 corresponding to the disk
midplane and rcyl is the radial distance from this
z-axis. The parameter ρ0 is determined by
the total dust mass mdust of the disk. The quantity
r0 is a reference radius and has a typical value of 100 AU
whereas h is the vertical scale height and a function of
rcyl
(1)Here, z
is the cylindrical coordinate with z = 0 corresponding to the disk
midplane and rcyl is the radial distance from this
z-axis. The parameter ρ0 is determined by
the total dust mass mdust of the disk. The quantity
r0 is a reference radius and has a typical value of 100 AU
whereas h is the vertical scale height and a function of
rcyl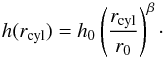 (2)The parameters
α and β describe the radial density profile and the
disk flaring, respectively. The disk extends from an inner cylindrical radius
rin to an outer one rout. This
ansatz has already been successfully applied to other circumstellar disks, such as, e.g.,
the Butterfly Star (Gräfe et al. 2013), HH 30
(Madlener et al. 2012), and CB 26 (Sauter et al. 2009). Integrating Eq. (1) along the z-axis yields the
surface density
(2)The parameters
α and β describe the radial density profile and the
disk flaring, respectively. The disk extends from an inner cylindrical radius
rin to an outer one rout. This
ansatz has already been successfully applied to other circumstellar disks, such as, e.g.,
the Butterfly Star (Gräfe et al. 2013), HH 30
(Madlener et al. 2012), and CB 26 (Sauter et al. 2009). Integrating Eq. (1) along the z-axis yields the
surface density 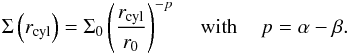 (3)The density structure
described in Eq. (1) is given by the gas in
the disk. As the dust in the disk is assumed to be coupled to the gas, its density
distribution is also described by this equation. The sizes of the dust grains in our model
are distributed according to a power law of the form
(3)The density structure
described in Eq. (1) is given by the gas in
the disk. As the dust in the disk is assumed to be coupled to the gas, its density
distribution is also described by this equation. The sizes of the dust grains in our model
are distributed according to a power law of the form 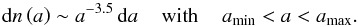 (4)Here,
a is the dust grain radius and n(a)
the number of dust grains with a specific radius. The parameters used in our model are
listed in Table 4. Most of them are taken from
previous studies of both objects. For the grain size distribution we use the commonly
known MRN distribution by Mathis et al. (1977) and
we fix the disk scale height at 100 AU at a typical value of 10 AU (e.g., Gräfe et al. 2013; Sauter et al. 2009; Pinte et al. 2008).
Using the relation α = 3(β − 0.5), which results from
viscous accretion theory (Shakura & Sunyaev
1973), and the given surface density exponent
p = α − β, the parameters
α and β amount to 2.25 and 1.25, respectively. The
inner disk radius is used as variable parameter.
(4)Here,
a is the dust grain radius and n(a)
the number of dust grains with a specific radius. The parameters used in our model are
listed in Table 4. Most of them are taken from
previous studies of both objects. For the grain size distribution we use the commonly
known MRN distribution by Mathis et al. (1977) and
we fix the disk scale height at 100 AU at a typical value of 10 AU (e.g., Gräfe et al. 2013; Sauter et al. 2009; Pinte et al. 2008).
Using the relation α = 3(β − 0.5), which results from
viscous accretion theory (Shakura & Sunyaev
1973), and the given surface density exponent
p = α − β, the parameters
α and β amount to 2.25 and 1.25, respectively. The
inner disk radius is used as variable parameter.
To allow us a comparison with the observations, the simulated images, that are constructed using the radiative transfer code MC3D (Wolf et al. 1999; Wolf 2003), are convolved with the corresponding standard star observations. Following the method described in Sect. 4.1 a residual flux profile is determined for every synthetic image. If the disk is spatially resolved in the observation we can reproduce the residual flux profile with the described model by varying the inner disk radius and thus determine the inner-disk hole radius of the object. For disks that could not be spatially resolved our model allows us to estimate an upper limit to the inner-disk hole radius.
Adopted model parameters.
4.4. Photometry
The flux densities of the two observed objects are determined using the VISIR photometry package by Hönig et al. (2010). For photometry, the science targets can be considered as point sources such that each science and calibrator beam is fitted by a two-dimensional Gaussian. The flux densities are then obtained by calculating conversion factors from the integrated intensity of the Gaussian fits of the calibrators and using these factors to evaluate the respective integrated Gaussian intensity of the science targets.
5. Results and discussion
The resulting constraints on the inner-disk hole radii and the photometry of the observed circumstellar disks are compiled in Table 5. In the following, we discuss the analysis of PDS 66 and CRBR 2422.8-3423 in detail.
Constraints on the inner-disk hole radii and photometry of the observed objects.
 |
Fig. 4 Left: observed residual flux of PDS 66 including the determined detection threshold. Right: modeled residual flux for several inner-disk hole radii including the detection threshold. |
 |
Fig. 5 Left: observed residual flux of CRBR 2422.8-3423 N band including the determined detection threshold. Right: modeled residual flux for several inner-disk hole radii including the detection threshold. |
For both objects, the difference in the object and standard star flux profiles is below the
detection threshold, i.e., no significant extension of the star-disk system is detected (see
Fig. 4, left and Fig. 5, left). Using our model, we can investigate at which inner-disk hole radius we
would have detected a significant extension of the star-disk system, thus determine an upper
limit to the inner-disk hole radius. We infer the inner radii to be smaller than
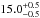 AU
and
AU
and 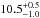 AU
for PDS 66 and CRBR 2422.8-3423, respectively (see Fig. 4, right and Fig. 5, right). The
uncertainties result from the uncertainty of the disk inclination which is 32° ± 5° for
PDS 66 (Cortes et al. 2009) and 70° ± 5° for
CRBR 2422.8-3423 (Thi et al. 2002). The constraints
on the inner-disk hole radii we give here are the first for these two objects and consistent
with what is known about both objects from the literature. The quality of the
Q-band observation of CRBR 2422.8-3423 and also the corresponding
standard star is too low to be used for our analysis. This is also reflected in the
uncertainty of the flux measurement (Table 5).
Therefore, we do not give any constraints on the inner-disk hole radius of CRBR 2422.8-3423
resulting from the Q-band observations.
AU
for PDS 66 and CRBR 2422.8-3423, respectively (see Fig. 4, right and Fig. 5, right). The
uncertainties result from the uncertainty of the disk inclination which is 32° ± 5° for
PDS 66 (Cortes et al. 2009) and 70° ± 5° for
CRBR 2422.8-3423 (Thi et al. 2002). The constraints
on the inner-disk hole radii we give here are the first for these two objects and consistent
with what is known about both objects from the literature. The quality of the
Q-band observation of CRBR 2422.8-3423 and also the corresponding
standard star is too low to be used for our analysis. This is also reflected in the
uncertainty of the flux measurement (Table 5).
Therefore, we do not give any constraints on the inner-disk hole radius of CRBR 2422.8-3423
resulting from the Q-band observations.
Owing to its old age, the disk around PDS 66 is very likely to already have formed an inner-disk hole or at least inner regions that are depleted. Unfortunately, this could not be confirmed by our observations. Nevertheless, our analysis gives an upper limit on the inner-disk hole and future observations will hopefully resolve or further constrain it. In contrast to PDS 66, CRBR 2422.8-3423 is a Class I object, thus its disk is not expected to already have created large inner-disk clearings. This is also supported by our analysis providing a low upper limit for an inner-disk hole.
As shown in Fig. 3 the seeing variations are the major component of the detection threshold. A proper estimate of them is crucial to prevent the detection of a supposed extended star-disk system that is not caused by a circumstellar disk but by variations in the observing conditions during observation leading to a broadening of the brightness profile.
The diffraction limit for VLT/VISIR in the N band is ~0.3″. For PDS 66
with a distance of 86 pc this means that it is in principle possible to spatially resolve
structures with a radius as small as 13 AU. Our upper limit on the inner-disk hole radius
of 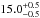 AU
is just above the diffraction limit. For CRBR 2422.8-3423 with a distance of 120 pc,
structures of 18 AU in radius can be spatially resolved at the diffraction limit. However,
we determine an upper limit for the inner-disk hole radius of
AU
is just above the diffraction limit. For CRBR 2422.8-3423 with a distance of 120 pc,
structures of 18 AU in radius can be spatially resolved at the diffraction limit. However,
we determine an upper limit for the inner-disk hole radius of
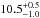 AU
which is below the diffraction limit and thus seems odd at first. This result can be easily
explained by the fact that the location of the inner-disk radius influences the temperature
distribution on larger scales. Therefore, based on the underlying disk model (density
distribution, dust properties), the location of the inner rim can be constrained from the
mid-infrared brightness distribution on larger scales. However, this statement only applies
if the observed brightness distribution is not solely given by the inner rim (face-on
orientation) but dominated by the re-emission of these outer regions. The latter is the case
for the disk around CRBR 2422.8-3423 which is seen at an inclination of 70°, where the inner
rim cannot be seen directly.
AU
which is below the diffraction limit and thus seems odd at first. This result can be easily
explained by the fact that the location of the inner-disk radius influences the temperature
distribution on larger scales. Therefore, based on the underlying disk model (density
distribution, dust properties), the location of the inner rim can be constrained from the
mid-infrared brightness distribution on larger scales. However, this statement only applies
if the observed brightness distribution is not solely given by the inner rim (face-on
orientation) but dominated by the re-emission of these outer regions. The latter is the case
for the disk around CRBR 2422.8-3423 which is seen at an inclination of 70°, where the inner
rim cannot be seen directly.
As described in Sect. 4.1 we characterize the brightness distribution of an observed object by its peak-normalized azimuthally averaged radial brightness profile. This method can be used without hesitation for stars surrounded by face-on orientated disks. However, this method can also be applied to inclined disks yielding a more conservative result for the broadening of the object with respect to the corresponding PSF. Since the model uses the same inclination and PSF as the observation, a comparison between both is feasible with this method.
The photometry for our two observed objects yields, in the N band, a flux density of 599 ± 8 mJy for PDS 66 and 130 ± 14 mJy for CRBR 2422.8-3423 and in the Q2 band 858 ± 109 mJy for CRBR 2422.8-3423. As a complement to already known flux densities at other wavelengths, they will be useful for constraining the SEDs of these two objects and modeling their circumstellar disks.
Acknowledgments
This work is supported by the DFG through the research group 759 “The Formation of Planets: The Critical First Growth Phase” (WO 857/4-2) and project WO 857/12-1. We are grateful to the anonymous referee for providing useful suggestions that improved this paper.
References
- Alexander, R. D., & Armitage, P. J. 2007, MNRAS, 375, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2007, Lecture notes on the formation and early evolution of planetary systems [arXiv:astro-ph/0701485] [Google Scholar]
- Armitage, P. J. 2010, Astrophysics of Planet Formation [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2011, A&A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 2002, Earth Planet. Sci. Lett., 202, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Brandner, W., Sheppard, S., Zinnecker, H., et al. 2000, A&A, 364, L13 [NASA ADS] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., Dullemond, C. P., & Wilner, D. J. 2008, ApJ, 675, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Wolf, S., Schreyer, K., Launhardt, R., & Henning, T. 2005, AJ, 129, 1049 [Google Scholar]
- Chen, C. H., Fitzgerald, M. P., & Smith, P. S. 2008, ApJ, 689, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Churcher, L., Wyatt, M., & Smith, R. 2011, MNRAS, 410, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., Gendrin, A., & Sotomayor, M. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Walker, R. G., Carter, B., et al. 1999, AJ, 117, 1864 [NASA ADS] [CrossRef] [Google Scholar]
- Comeron, F., Rieke, G. H., Burrows, A., & Rieke, M. J. 1993, ApJ, 416, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Cortes, S. R., Meyer, M. R., Carpenter, J. M., et al. 2009, in AIP Conf. Ser. 1158, eds. T. Usuda, M. Tamura, & M. Ishii, 119 [Google Scholar]
- D’Alessio, P. 2009, in Rev. Mex. Astron. Astrofis., 35, 33 [Google Scholar]
- Dominik, C., Blum, J., Cuzzi, J. N., & Wurm, G. 2007, Protostars and Planets V, 783 [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisner, J. A., Monnier, J. D., Tuthill, P., & Lacour, S. 2009, ApJ, 698, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Calvet, N., Luhman, K. L., Muzerolle, J., & D’Alessio, P. 2008, ApJ, 682, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Ingleby, L., Hernández, J., et al. 2012, ApJ, 747, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Forrest, W. J., Sargent, B., Furlan, E., et al. 2004, ApJS, 154, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K.-M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garaud, P., Meru, F., Galvagni, M., & Olczak, C. 2013, ApJ, 764, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfe, C., Wolf, S., Roccatagliata, V., Sauter, J., & Ertel, S. 2011, A&A, 533, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gräfe, C., Wolf, S., Guilloteau, S., et al. 2013, A&A, in press, DOI: 10.1051/0004-6361/201220720 [Google Scholar]
- Gregorio-Hetem, J., Lepine, J. R. D., Quast, G. R., Torres, C. A. O., & de La Reza, R. 1992, AJ, 103, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., Carpenter, J. M., Kim, J. S., et al. 2008, ApJ, 677, 630 [Google Scholar]
- Hollenbach, D. J., Yorke, H. W., & Johnstone, D. 2000, Protostars and Planets IV, 401 [Google Scholar]
- Honda, M., Maaskant, K., Okamoto, Y. K., et al. 2012, ApJ, 752, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Gandhi, P., et al. 2010, A&A, 515, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hughes, A. M., Wilner, D. J., Calvet, N., et al. 2007, ApJ, 664, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A. M., Andrews, S. M., Espaillat, C., et al. 2009, ApJ, 698, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Lagage, P. O., Pel, J. W., Authier, M., et al. 2004, The Messenger, 117, 12 [NASA ADS] [Google Scholar]
- Madlener, D., Wolf, S., Dutrey, A., & Guilloteau, S. 2012, A&A, 543, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., Meyer, M. R., & Liebert, J. 2002, AJ, 124, 1670 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Andre, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] [Google Scholar]
- Natta, A., Testi, L., Calvet, N., et al. 2007, Protostars and Planets V, 767 [Google Scholar]
- Pantin, E., Bouwman, J., & Lagage, P. O. 2005, A&A, 437, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascucci, I., Hollenbach, D., Najita, J., et al. 2007, ApJ, 663, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Padgett, D. L., Ménard, F., et al. 2008, A&A, 489, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Dullemond, C. P., van Dishoeck, E. F., et al. 2005, ApJ, 622, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., & Mamajek, E. 2008, The Nearest OB Association: Scorpius-Centaurus (Sco OB2), ed. B. Reipurth, 235 [Google Scholar]
- Ricci, L., Testi, L., Natta, A., & Brooks, K. J. 2010, A&A, 521, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Sauter, J., & Wolf, S. 2011, A&A, 527, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sauter, J., Wolf, S., Launhardt, R., et al. 2009, A&A, 505, 1167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schegerer, A. A., Wolf, S., Hummel, C. A., Quanz, S. P., & Richichi, A. 2009, A&A, 502, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schütz, O., Meeus, G., & Sterzik, M. F. 2005, A&A, 431, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Silverstone, M. D., Meyer, M. R., Mamajek, E. E., et al. 2006, ApJ, 639, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W. F., Pontoppidan, K. M., van Dishoeck, E. F., Dartois, E., & d’Hendecourt, L. 2002, A&A, 394, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ubach, C., Maddison, S. T., Wright, C. M., et al. 2012, MNRAS, 425, 3137 [NASA ADS] [CrossRef] [Google Scholar]
- van Kempen, T. A., van Dishoeck, E. F., Salter, D. M., et al. 2009, A&A, 498, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, S. 2003, Comput. Phys. Comm., 150, 99 [Google Scholar]
- Wolf, S., Henning, T., & Stecklum, B. 1999, A&A, 349, 839 [NASA ADS] [Google Scholar]
- Wolf, S., Moro-Martín, A., & D’Angelo, G. 2007, Planet. Space Sci., 55, 569 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectral energy distribution of PDS 66. A star with T⋆ = 5035 K is shown as the dashed line. |
| In the text | |
 |
Fig. 2 Spectral energy distribution of CRBR 2422.8-3423 including a SST/IRS spectrum in the range 7.4−14.5 μm (Pontoppidan et al. 2005). |
| In the text | |
 |
Fig. 3 Contribution of each of the components to the detection threshold for PDS 66. |
| In the text | |
 |
Fig. 4 Left: observed residual flux of PDS 66 including the determined detection threshold. Right: modeled residual flux for several inner-disk hole radii including the detection threshold. |
| In the text | |
 |
Fig. 5 Left: observed residual flux of CRBR 2422.8-3423 N band including the determined detection threshold. Right: modeled residual flux for several inner-disk hole radii including the detection threshold. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


