| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220844 | |
| Published online | 20 March 2013 | |
Self-consistent 2D models of fast-rotating early-type stars
1 Université de Toulouse, UPS-OMP, IRAP, 31062 Toulouse, France
e-mail: francisco.espinosa@irap.omp.eu
2 CNRS, IRAP, 14 avenue Édouard Belin, 31400 Toulouse, France
Received: 4 December 2012
Accepted: 24 January 2013
Aims. This work aims at presenting the first two-dimensional models of an isolated rapidly rotating star that include the derivation of the differential rotation and meridional circulation in a self-consistent way.
Methods. We use spectral methods in multidomains, together with a Newton algorithm to determine the steady state solutions including differential rotation and meridional circulation for an isolated non-magnetic, rapidly rotating early-type star. In particular we devise an asymptotic method for small Ekman numbers (small viscosities) that removes the Ekman boundary layer and lifts the degeneracy of the inviscid baroclinic solutions.
Results. For the first time, realistic two-dimensional models of fast-rotating stars are computed with the actual baroclinic flows that predict the differential rotation and the meridional circulation for intermediate-mass and massive stars. These models nicely compare with available data of some nearby fast-rotating early-type stars like Ras Alhague (α Oph), Regulus (α Leo), and Vega (α Lyr). It is shown that baroclinicity drives a differential rotation with a slow pole, a fast equator, a fast core, and a slow envelope. The differential rotation is found to increase with mass, with evolution (here measured by the hydrogen mass fraction in the core), and with metallicity. The core-envelope interface is found to be a place of strong shear where mixing will be efficient.
Conclusions. Two-dimensional models offer a new view of fast-rotating stars, especially of their differential rotation, which turns out to be strong at the core-envelope interface. They also offer more accurate models for interpreting the interferometric and spectroscopic data of early-type stars.
Key words: stars: rotation / stars: interiors / stars: early-type
© ESO, 2013
1. Introduction
One of the main challenges of current stellar physics is to understand the overall dynamics of stars. Indeed, the new detailed observations of stars that report either on magnetic fields (Petit et al. 2009, 2010) or on abundance patterns in clusters (Hunter et al. 2008; Brott et al. 2011) both crucially depend on the fluid flows that pervade the interior of stars. Thermal convection has long been related to the generation of magnetic fields, but the dynamics of convectively stable radiative regions has been considered for at least twenty years as the cornerstone in understanding surface abundances in stars. Moreover, the heart of these large-scale dynamics is the ubiquitous rotation of stars. It is now well-known that rotation is a key parameter for stellar dynamos (Petit et al. 2008), but it is also crucial to the macroscopic transport through stably stratified radiative regions. There, the baroclinic (or other) flows along with some small-scale turbulence determine the so-called rotational mixing that is now a key process in interpreting stellar abundances (Maeder & Meynet 2000). As a result, progress toward understanding stars and interpreting the new data sets that come from spectropolarimetry (magnetic fields), spectroscopic surveys, interferometry, and seismology requires a precise account of the distribution and evolution of angular momentum in stars.
The most common implementation of rotation and rotational mixing in stellar evolution codes is the prescription of Zahn (1992) and its subsequent improvements (Talon & Zahn 1997; Maeder & Zahn 1998). This modelling is designed for one-dimensional codes. It relies on an averaging of the differential rotation, which becomes purely radial (shellular), and of the meridional transport, which, thanks to some natural hypothesis on the turbulence in a radiative zone, reduces to an effective diffusion for chemicals or a simple advection and diffusion for angular momentum (see Chaboyer & Zahn 1992; Zahn 1992). As underlined by Zahn (1992), this model rests on the conjecture that all deviations from equilibrium can be represented by a single spherical harmonic, namely Y2(cosθ) also standing for the first effect of centrifugal distortion. The formal expansion, including the whole spherical harmonics series, has been derived in Mathis & Zahn (2004, 2005) and is currently included in the one-dimensional code STAREVOL (Decressin et al. 2009), but deviations from sphericity must remain small. Such models are therefore expected to be valid for slow rotation since fast rotation generates more complicated flows and a significant distortion of the star. However, exploration of the various stellar situations requires investigating cases where slow rotation is not possible (e.g. Ekström et al. 2012). Clearly, we lack a more detailed view of the large-scale and long-time-scale dynamics of stars, in the first place to put bounds on the validity of 1D-models.
A closer view at the stellar (fluid) dynamics clearly requires laying aside the spherically symmetric models. Modelling dynamics needs more than one dimension, thus a general use of two-dimensional models is the obvious next step in stellar modelling.
However, jumping into the multidimensional modelling of stars is not a sinecure. Attempts have followed one another since the first polytropes of James (1964, see also Rieutord 2006b, for a review of the historical landmarks of 2D-models), but presently no code can represent stellar evolution in two (or more) space dimensions, including self-consistently the large-scale dynamics. Most of the present models impose an ad hoc law of internal rotation. The reason is that computing the baroclinic flows (or others), together with the stellar structure, is difficult numerically because equations are stiff.
These foreseeable difficulties motivated the dedicated studies of Rieutord (2006a) and Espinosa Lara & Rieutord (2007). In Rieutord (2006a) the specific features of baroclinic flows were investigated through a simplified model using the Boussinesq approximation. The next step (Espinosa Lara & Rieutord 2007) has been to compute a completely radiative star enclosed in a spherical container. With this configuration we could self-consistently compute the flows and the hydrostatic structure of the interior of a fast-rotating star. Although this computation has already given a good idea of the differential rotation and the meridional circulation that may be expected in radiative zones of rotating stars, the spherical shape of the container enclosing the star is not appropriate to give the surface characteristics of such stars, which are important from the point of view of observations. In addition the computation remained limited to the interior of the star since polar pressure was always more than 10-5 times the central one (realistic values are of the order of 10-12 or less). The natural next step that we present here therefore demanded serious effort to overcome the simplification of the previous models. We required that the geometry of the coordinates follows the surface of the star so that boundary conditions could be correctly implemented and that solutions extend up to the true surface of the star as given by an optical depth condition.
While heading to that goal, it turned out that computating velocity fields was more difficult than ever, essentially because of the huge variations in density along the radius of the star (typically more than eight orders of magnitude).
The present paper aims at reporting these latest advances in the building of the two-dimensional models of rapidly rotating stars. In the following section we summarize our strategy for constructing these models and report on the tests that were made to validate them. In Sect. 3, we discuss the problem of the velocity fields and present the boundary layer analysis necessary for using asymptotic solutions. The next section presents some preliminary results including a comparison with observational data and a first survey of the dependence of differential rotation on the general parameters of intermediate-mass stars. Some conclusions end the paper.
2. Construction of 2D-models
2.1. Hypothesis
As in Espinosa Lara & Rieutord (2007), we restrict our models to those describing isolated rotating stars that are in a steady state. This idealization, which neglects both chemical evolution and any mass loss, is of course a first approach to the much more complex reality. In addition, we consider the star strictly axisymmetric. Breaking of this symmetry comes from turbulence and magnetic fields. Turbulence is not a problem in principle, since we are interested in long-term averages. Effects of turbulence should be quasi-steady and axisymmetric (although their correct modelling is still a major issue). Magnetic fields, on the contrary, cannot be ignored a priori. Non-axisymmetric, steady magnetic fields are known to exist in some rotating stars (i.e. roAp stars for instance). However, as progress from simple to complicate commands it, we first ignore magnetic fields. This may not be so bad for some A stars like Vega, whose surface magnetic fields are rather weak (Petit et al. 2010).
2.2. Equations
The partial differential equations that determine the steady state of a lonely rotating star are the following: 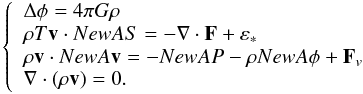 (1)There, one recognizes Poisson’s equation (φ is the gravitational potential, ρ the density, and G the gravitation constant), the equation of entropy S (T is the temperature, v the velocity, F the heat flux, and ε∗ the nuclear heat sources), the momentum equation written here in an inertial frame (P is the pressure and Fv the viscous force), and lastly the equation of mass conservation.
(1)There, one recognizes Poisson’s equation (φ is the gravitational potential, ρ the density, and G the gravitation constant), the equation of entropy S (T is the temperature, v the velocity, F the heat flux, and ε∗ the nuclear heat sources), the momentum equation written here in an inertial frame (P is the pressure and Fv the viscous force), and lastly the equation of mass conservation.
These differential equations need to be completed by constitutive laws. We write the expression of the heat flux as 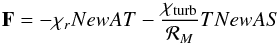 (2)where χr is the radiative conductivity and χturb a turbulent heat conductivity. Here, ℛM = ℛ/ℳ where ℛ is the ideal gas constant and ℳ the mean molecular mass of the fluid. We hypothesize that turbulent convection is equivalent to the diffusion of entropy. As for the viscous force, the similar level of modelling turbulence leads us to use a turbulent viscosity. We therefore assume that
(2)where χr is the radiative conductivity and χturb a turbulent heat conductivity. Here, ℛM = ℛ/ℳ where ℛ is the ideal gas constant and ℳ the mean molecular mass of the fluid. We hypothesize that turbulent convection is equivalent to the diffusion of entropy. As for the viscous force, the similar level of modelling turbulence leads us to use a turbulent viscosity. We therefore assume that 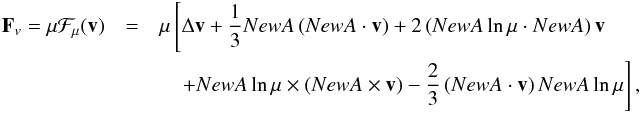 (3)where μ is the dynamical viscosity of the gas.
(3)where μ is the dynamical viscosity of the gas.
The equations are also completed by the relations 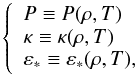 (4)which respectively give the equation of state, the opacity, and the nuclear heat generation. We recall that in radiative diffusive equilibrium, heat conductivity is related to opacity by
(4)which respectively give the equation of state, the opacity, and the nuclear heat generation. We recall that in radiative diffusive equilibrium, heat conductivity is related to opacity by 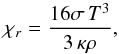 (5)where σ is the Stefan-Boltzmann constant. For the energy generation we use an analytical formula that represents hydrogen burning either in CNO or pp-chains, namely:
(5)where σ is the Stefan-Boltzmann constant. For the energy generation we use an analytical formula that represents hydrogen burning either in CNO or pp-chains, namely: 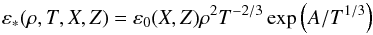 (6)as in Espinosa Lara & Rieutord (2007). It is completed by the use of OPAL tables for computing the opacity and deriving the density from the equation of state (X = 0.7 and Z = 0.02 with solar composition of Grevesse & Noels 1993).
(6)as in Espinosa Lara & Rieutord (2007). It is completed by the use of OPAL tables for computing the opacity and deriving the density from the equation of state (X = 0.7 and Z = 0.02 with solar composition of Grevesse & Noels 1993).
2.3. Boundary conditions
The foregoing partial differential equations require boundary conditions for the solutions to be fully determined. These apply at the star centre and surface. The conditions at the centre are that the solutions should simply be regular. Surface boundary conditions are more involved.
The first outer boundary condition is on the gravitational potential, which should match that of a field in the vacuum, vanishing at infinity. A way of solving this difficulty is to use the analytical solution of Poisson’s equation using the Green function. This is the so-called self-consistent field method developed by Ostriker & Mark (1968) and used in 2D models of Jackson et al. (2005). We prefer another technique that consists in computing this field in a surrounding empty domain bounded by a sphere where simple boundary conditions can be applied (see Rieutord & Espinosa Lara 2012).
The next boundary conditions are those to be imposed on the velocity field. For an isolated star it is natural to use stress-free conditions: ![\begin{eqnarray*} \vv\cdot \vn =0 \quad {\rm and}\quad ([\sigma]\vn)\wedge\vn =\vzero \end{eqnarray*}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq30.png) where [σ] is the stress tensor. The fluid is assumed to not flow outside the star and to feel no horizontal stress (n is the outer normal of the star).
where [σ] is the stress tensor. The fluid is assumed to not flow outside the star and to feel no horizontal stress (n is the outer normal of the star).
Finally, the temperature field requires its boundary conditions. We assume that the star radiates locally as a black body so impose 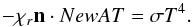 (7)Both of the velocity and temperature boundary conditions need to be applied on the surface of the star, which is ill-defined. It depends on an arbitrary criterion like the value of an optical depth (most commonly).
(7)Both of the velocity and temperature boundary conditions need to be applied on the surface of the star, which is ill-defined. It depends on an arbitrary criterion like the value of an optical depth (most commonly).
In non-rotating models, surface pressure is commonly estimated by 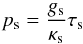 (8)where subscript “s” indicates surface quantities, and τs is the optical depth at the photosphere usually set to 2/3, but τs = 1 is also used (Morel 1997).
(8)where subscript “s” indicates surface quantities, and τs is the optical depth at the photosphere usually set to 2/3, but τs = 1 is also used (Morel 1997).
Similarly, we define the bounding surface of the star, i.e. the surface where boundary conditions are taken, as the isobar where the pressure is 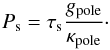 (9)On this isobar, T = Teff only at the pole. On this surface (7) is therefore not met except at the pole. In fact, to determine the temperature field, we just need to give the temperature on this surface as a function of latitude. For that, we assume that the part of the star that rests above this bounding surface can be described by a polytrope of index n. Thus the pressure verifies
(9)On this isobar, T = Teff only at the pole. On this surface (7) is therefore not met except at the pole. In fact, to determine the temperature field, we just need to give the temperature on this surface as a function of latitude. For that, we assume that the part of the star that rests above this bounding surface can be described by a polytrope of index n. Thus the pressure verifies 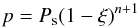 (10)where ξ is a non-dimensional variable measuring the height above the bounding surface. Because this “atmosphere” is polytropic, we have
(10)where ξ is a non-dimensional variable measuring the height above the bounding surface. Because this “atmosphere” is polytropic, we have 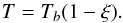 (11)The top of the atmosphere is the true surface of the star as defined by a given optical depth τs. There the pressure is
(11)The top of the atmosphere is the true surface of the star as defined by a given optical depth τs. There the pressure is 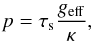 which depends on the co-latitude θ. On the pole, obviously p = Ps. The height of the atmosphere is given by
which depends on the co-latitude θ. On the pole, obviously p = Ps. The height of the atmosphere is given by 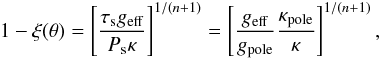 however, on the true surface T = Teff, therefore
however, on the true surface T = Teff, therefore 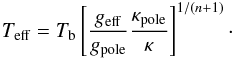 We therefore find the temperature profile along the bounding surface
We therefore find the temperature profile along the bounding surface 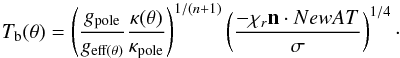 (12)Finally, on the bounding surface we only need to set
(12)Finally, on the bounding surface we only need to set 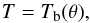 (13)which is quite simple to implement. The polytropic index may be chosen from a power-law fit of the opacity in the temperature/density range spanned by the atmosphere. We indeed know that if κ ∝ ρℓT− m, then n = (m + 3)/(ℓ + 1). This is not a rigorous description of these layers, which are also baroclinic, but it should be a reasonable approximation to determine the fundamental parameters of the star. Nevertheless, if required, a more realistic atmospheric model can be used to determine Tb(θ). In the following calculations we use τs = 1 and n = 3. Finally, we also note that the true equatorial radius is slightly larger than the equatorial radius of the bounding surface, but the actual difference is always less than 10-3 and is therefore neglected.
(13)which is quite simple to implement. The polytropic index may be chosen from a power-law fit of the opacity in the temperature/density range spanned by the atmosphere. We indeed know that if κ ∝ ρℓT− m, then n = (m + 3)/(ℓ + 1). This is not a rigorous description of these layers, which are also baroclinic, but it should be a reasonable approximation to determine the fundamental parameters of the star. Nevertheless, if required, a more realistic atmospheric model can be used to determine Tb(θ). In the following calculations we use τs = 1 and n = 3. Finally, we also note that the true equatorial radius is slightly larger than the equatorial radius of the bounding surface, but the actual difference is always less than 10-3 and is therefore neglected.
2.4. Angular momentum condition
Even with the foregoing boundary conditions, the problem is not fully constrained because the total angular momentum is not specified. To complete the formulation of the problem we may either enforce the total angular momentum L or specify the surface equatorial velocity of the star Veq. In the first case we may write 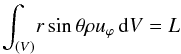 or
or 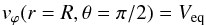 in the second case.
in the second case.
2.5. Numerical method
We now briefly summarize on the numerical method we use. We refer the reader to Rieutord & Espinosa Lara (2012) for a more detailed account. To apply (more) easily boundary conditions we use coordinates that follow the spheroidal shape of the star. The stellar domain is divided into subdomains. Inside such a subdomain the relation between spherical coordinates (r,θ,ϕ) and our new spheroidal coordinates (ζ,θ′,ϕ′) is simply ![\begin{equation} \left\{ \begin{array}{l} r=a_i\zeta+A_i(\zeta)[R_{i+1}(\theta)-a_i\eta_{i+1}]+B_i(\zeta)[R_i(\theta)-a_i\eta_i]\\ \theta=\theta'\\ \varphi=\varphi' \end{array}\right. \end{equation}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq61.png) (14)in the ith domain such that ηi ≤ ζ ≤ ηi + 1. In this expression, Ri(θ) is the radius of the ith bounding surface, and Ai(ζ),Bi(ζ) are third-order polynomials chosen so that, with the choice of the constants ai the mapping is continuous and derivable (see Rieutord & Espinosa Lara 2012; Bonazzola et al. 1998, for more details). These coordinates are the natural coordinates associated with the shape of the star, but unfortunately they are not orthogonal (see Rieutord & Espinosa Lara 2012).
(14)in the ith domain such that ηi ≤ ζ ≤ ηi + 1. In this expression, Ri(θ) is the radius of the ith bounding surface, and Ai(ζ),Bi(ζ) are third-order polynomials chosen so that, with the choice of the constants ai the mapping is continuous and derivable (see Rieutord & Espinosa Lara 2012; Bonazzola et al. 1998, for more details). These coordinates are the natural coordinates associated with the shape of the star, but unfortunately they are not orthogonal (see Rieutord & Espinosa Lara 2012).
The spatial discretization of the equations is done by using spectral methods so as to minimize the size of matrices that arise. The fields are expanded into a series of spherical harmonics for their horizontal dependence on the θ′ coordinate, and the radial functions are sampled on the Gauss-Lobatto collocation nodes, which are associated with Chebyshev polynomials.
The nonlinear equations of the stellar structure are solved iteratively. Two methods have been tested: the first is a relaxation method also known as the fixed-point scheme inspired by Bonazzola et al. (1998) and Espinosa Lara & Rieutord (2007), while the second is the well-known Newton method. The fixed-point scheme can be easily coded, while Newton’s scheme coding is rather involved. However, it turns out that the first scheme is really efficient in simple configurations (polytropes or slowly rotating stars), while Newton’s scheme converges in most cases rather rapidly (typically in ten iterations when a non-rotating model is given as a starting point). We therefore kept Newton’s method.
2.6. Calibrations
The solutions can be tested in various ways. First, the internal accuracy is easily accessible with spectral methods since the spectral expansion readily shows whether the spatial resolution is appropriate or not. A slight change in the initial guess of the solutions allows us to test the influence of the round-off errors.
When the iterations have converged, we test the solution in two ways: first with the virial theorem, which relates integral quantities derived from the momentum equation and, second, with an energy test that also checks integral quantities but from the energy equation. Details of these tests may be found in Espinosa Lara & Rieutord (2007) or Rieutord & Espinosa Lara (2012). The virial test is usually passed with an accuracy better than a few 10-12, while the energy test may show errors up to 10-5. This much looser behaviour of the energy side comes from the use of the opacity tables, which generate some noise (either of numerical or physical origin).
Comparison of the results between the ESTER code without rotation and the one-dimensional code TGEC.
Comparison of the results between the 2D models of Deupree et al. (2012) and ours for α Ophiuchi.
Finally, we compared the solutions given by our code at zero rotation with solutions given by other codes using completely different numerical methods. We show in Table 1 one such comparison with the one-dimensional code TGEC (Toulouse-Geneva Evolution Code, see Hui-Bon-Hoa 2008; Théado et al. 2012). Similar results are obtained with the CESAM code (Morel 1997). The small discrepancies between our code and the foregoing codes comes from the absence of evolution in our code, which allows us to use an analytic formula for the heating by nuclear reactions, i.e. (6). We also find similar agreement with the values published by Deupree et al. (2012), although with a slight (4%) discrepancy on the equatorial radius (see Table 2).
3. The velocity field
3.1. General preliminaries
The velocity field deserves special attention because it is the solution of stiff partial differential equations. In an isolated steady, rotating star, flows come from Reynolds stresses and baroclinic torques. The baroclinic torques are created by the misalignment of pressure and density gradients and have to be balanced by the gradient of angular velocity, so that the star rotates differentially (e.g. Rieutord 2006c).
In an inertial frame the velocity field is governed by 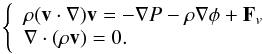 (15)If we scale the velocity setting v = 2Ω0Rw and use the equatorial radius R as the length scale (Ω0 is an angular velocity to be specified later), we can rewrite these two equations in their non-dimensional form:
(15)If we scale the velocity setting v = 2Ω0Rw and use the equatorial radius R as the length scale (Ω0 is an angular velocity to be specified later), we can rewrite these two equations in their non-dimensional form: 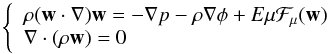 (16)where the pressure and the potential have been scaled appropriately. We thus introduced the Ekman number
(16)where the pressure and the potential have been scaled appropriately. We thus introduced the Ekman number 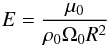 (17)where μ0 is a typical value of the dynamical viscosity and ρ0 is the scale of density.
(17)where μ0 is a typical value of the dynamical viscosity and ρ0 is the scale of density.
The axisymmetry of the solution suggests the decomposition of the velocity field into two contributions: the differential rotation Ω(r,θ) and the meridional circulation u(r,θ). We thus write 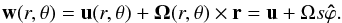 (18)Here, (r,θ,ϕ) are the usual spherical coordinates and s = rsinθ is the distance to the rotation axis.
(18)Here, (r,θ,ϕ) are the usual spherical coordinates and s = rsinθ is the distance to the rotation axis.
Following (18), the momentum equation can be split into an azimuthal part 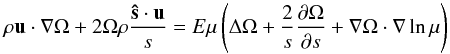 (19)and a meridional part
(19)and a meridional part 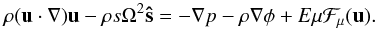 (20)Taking the curl of this expression (divided by ρ) we obtain the vorticity equation associated with the meridional component of the velocity field
(20)Taking the curl of this expression (divided by ρ) we obtain the vorticity equation associated with the meridional component of the velocity field 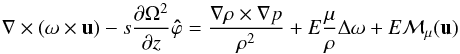 (21)with
(21)with 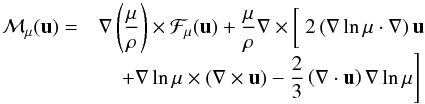 (22)where ω = ∇ × u is the vorticity of the meridional circulation. Only the ϕ-component of this equation is non-zero.
(22)where ω = ∇ × u is the vorticity of the meridional circulation. Only the ϕ-component of this equation is non-zero.
Equation (19) can be easily transformed into an equation for the transport of angular momentum 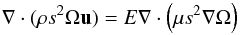 (23)establishing that, for the fluid to be in a stationary state, the transport of angular momentum by the viscous force must be balanced by the transport induced by the meridional circulation.
(23)establishing that, for the fluid to be in a stationary state, the transport of angular momentum by the viscous force must be balanced by the transport induced by the meridional circulation.
3.2. Viscosity in stars
For the stars we are considering that have no convective envelope, the physical conditions are such that radiative viscosity largely dominates that of collisional origin. In Fig. 1, we plot the values of this viscosity along with the associated Ekman number based on the radius of the star and an angular velocity corresponding to a rotation period of 12 h. This figure shows that the radiative viscosity leads to Ekman numbers always less than 10-10.
 |
Fig. 1 Top: profiles of the radiative (black) and turbulent (red) viscosity as a function of the normalized radius, for three stellar models of ZAMS stars of 3 M⊙, 7 M⊙, and 10 M⊙. Bottom: the associated profiles of the Ekman number ν/2ΩR2 based on the radius of the star and a rotation period of 12 h. |
Because of these low values, some turbulence may develop as a result of the shear of the differential rotation. Zahn (1992) proposes that the induced turbulent vertical viscosity reads as 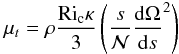 where Ric is the critical Richardson number. Assuming that Ric ~ 1/4, we show in Fig. 1 the values of the turbulent Ekman number, with the same scalings as above, computed from the differential rotation of a 2D-model. Although it is a few orders of magnitude larger, the turbulent Ekman number of fast-rotating stars is still very small compared to unity (always less than 10-7).
where Ric is the critical Richardson number. Assuming that Ric ~ 1/4, we show in Fig. 1 the values of the turbulent Ekman number, with the same scalings as above, computed from the differential rotation of a 2D-model. Although it is a few orders of magnitude larger, the turbulent Ekman number of fast-rotating stars is still very small compared to unity (always less than 10-7).
3.3. Inviscid solution and the occurrence of a boundary layer
The extremely low values of the stellar Ekman numbers lead us to look for solutions to the velocity equations that are valid in the asymptotic regime E → 0. In this regime, the viscous force is not able to maintain a solid body rotation. It therefore carries angular momentum. In a steady state, this flux is balanced by the meridional flow according to (23). This expression gives the order of magnitude of this meridional flow. Thus, we have 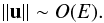 (24)Using this result, the meridional flow can be decoupled from the rest of the equations. Indeed, all the terms depending on u in the other components of the momentum equation are O(E2) and can be neglected. In particular, the meridional projection will become
(24)Using this result, the meridional flow can be decoupled from the rest of the equations. Indeed, all the terms depending on u in the other components of the momentum equation are O(E2) and can be neglected. In particular, the meridional projection will become 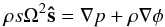 (25)and the vorticity equation
(25)and the vorticity equation 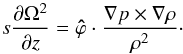 (26)In principle, Eq. (26) can be used to calculate the rotation profile for a given configuration. Unfortunately, without adequate boundary conditions, the rotation profile is undetermined by a function of s; that is if Ω(r) is a solution, Ω′2(r) = Ω2(r) + F(s) is also a solution.
(26)In principle, Eq. (26) can be used to calculate the rotation profile for a given configuration. Unfortunately, without adequate boundary conditions, the rotation profile is undetermined by a function of s; that is if Ω(r) is a solution, Ω′2(r) = Ω2(r) + F(s) is also a solution.
This degeneracy is removed by viscosity. Indeed, the free surface of the star is assumed to support no stress, so the angular velocity should verify 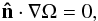 (27)where
(27)where 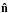 is the unit vector normal to the surface. However, this condition is incompatible with (26). This is a standard problem that is solved using a boundary layer analysis. The main idea is to take advantage of the existence of a thin layer in the vicinity of the boundary where viscosity is not negligible and where the flow adapts its properties to fulfil the boundary conditions. Doing this, we can separate the problem into two domains, an interior one where viscosity can be neglected and a thin boundary layer, dominated by viscosity. In our case, the thickness of the boundary layer depends on the Ekman number. It is infinitesimally thin when E → 0, which is used to simplify the equations, since the vertical gradient of a boundary layer quantity is much larger than the horizontal one. This procedure has been successfully used to derive baroclinic flows in a Boussinesq model of a star (see Rieutord 2006a). We now adapt it to realistic stellar models.
is the unit vector normal to the surface. However, this condition is incompatible with (26). This is a standard problem that is solved using a boundary layer analysis. The main idea is to take advantage of the existence of a thin layer in the vicinity of the boundary where viscosity is not negligible and where the flow adapts its properties to fulfil the boundary conditions. Doing this, we can separate the problem into two domains, an interior one where viscosity can be neglected and a thin boundary layer, dominated by viscosity. In our case, the thickness of the boundary layer depends on the Ekman number. It is infinitesimally thin when E → 0, which is used to simplify the equations, since the vertical gradient of a boundary layer quantity is much larger than the horizontal one. This procedure has been successfully used to derive baroclinic flows in a Boussinesq model of a star (see Rieutord 2006a). We now adapt it to realistic stellar models.
3.4. Stretched coordinates
It is useful to define a new set of stretched coordinates (ξ,τ,ϕ) to represent the fluid inside the boundary layer. The vertical coordinate ξ measures the distance to the surface scaled by a parameter ε that represents the thickness of the boundary layer. The angular coordinate τ is equal to the colatitude of the nearest point on the surface, so that τ = θ when ξ = 0. When choosing that ξ increases outwards, ξ is negative inside the star. The azimuthal coordinate ϕ coincides with the corresponding spherical coordinate.
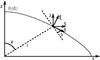 |
Fig. 2 A schematic view of the local basis adapted to the analysis of the Ekman layer. |
The unit vectors 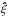 and
and 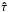 are perpendicular and parallel to the surface, respectively. They can be expressed as
are perpendicular and parallel to the surface, respectively. They can be expressed as 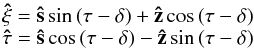 (28)where ŝ and ẑ are the unit vectors associated with the cylindrical coordinates, and δ is defined as
(28)where ŝ and ẑ are the unit vectors associated with the cylindrical coordinates, and δ is defined as 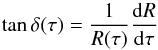 (29)and accounts for the deformation of the surface due to the centrifugal force. Figure 2 sketches out this new local frame. The relation between (ξ,τ) and the cylindrical coordinates (s,z) is given by
(29)and accounts for the deformation of the surface due to the centrifugal force. Figure 2 sketches out this new local frame. The relation between (ξ,τ) and the cylindrical coordinates (s,z) is given by 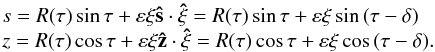 (30)The coordinates (ξ,τ,ϕ) form a set of orthogonal coordinates with scale factors
(30)The coordinates (ξ,τ,ϕ) form a set of orthogonal coordinates with scale factors 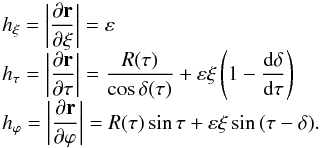 (31)We are interested in a very thin layer below the surface, thus ε ≪ 1 and to leading order
(31)We are interested in a very thin layer below the surface, thus ε ≪ 1 and to leading order 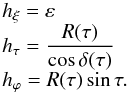 (32)
(32)
3.5. Scale analysis
We start the analysis of the boundary layer by deriving the order of magnitude of the dependent variables. As we have noted before (Eq. (24)), the meridional velocity in the interior inviscid domain is u ~ O(E), while the rest of the variables are supposed to be ~O(1). Since the flow is steady, mass conservation imposes 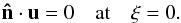 (33)Using the boundary layer coordinates, it reads
(33)Using the boundary layer coordinates, it reads 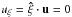 , so the normal velocity uξ should go from a value O(E) at the base of the boundary layer to zero. Thus
, so the normal velocity uξ should go from a value O(E) at the base of the boundary layer to zero. Thus 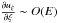 , since ξ is a stretched variable. Using the new coordinates (ξ,τ,ϕ), the continuity equation now reads as (see Appendix A)
, since ξ is a stretched variable. Using the new coordinates (ξ,τ,ϕ), the continuity equation now reads as (see Appendix A) 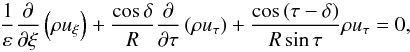 (34)from where we see that uτ ~ O(E/ε).
(34)from where we see that uτ ~ O(E/ε).
On the surface, the tangential stress should vanish, according to the stress-free boundary condition. Using the boundary layer coordinates, this condition reduces to 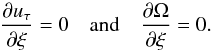 (35)We now go back to the vorticity Eq. (21). If the vertical gradient of angular velocity vanishes on the surface, the inviscid vorticity Eq. (26) cannot, in general, be verified. Thus, within the boundary layer, the balance of forces requires the viscous force whose dominant term
(35)We now go back to the vorticity Eq. (21). If the vertical gradient of angular velocity vanishes on the surface, the inviscid vorticity Eq. (26) cannot, in general, be verified. Thus, within the boundary layer, the balance of forces requires the viscous force whose dominant term 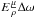 should be of order unity. The vorticity of the meridional velocity field is
should be of order unity. The vorticity of the meridional velocity field is 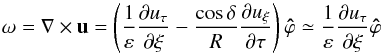 (36)and
(36)and 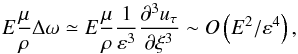 (37)then the scale of the boundary layer must be
(37)then the scale of the boundary layer must be 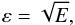 (38)as expected. Normal and meridional velocities are O(ε2) and O(ε), respectively. It is useful to define the scaled boundary layer corrections
(38)as expected. Normal and meridional velocities are O(ε2) and O(ε), respectively. It is useful to define the scaled boundary layer corrections 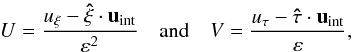 (39)where uint ~ O(ε2) is the interior meridional circulation.
(39)where uint ~ O(ε2) is the interior meridional circulation.
Back to the meridional component of the momentum Eq. (20), the viscous force is O(ε2) in the direction of 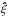 and O(ε) in the direction of
and O(ε) in the direction of 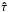 and, in the limit ε → 0, the inviscid equation is still valid within the boundary layer. Then we suppose that the rest of the dependent variables p, ρ, φ are not perturbed in the boundary layer and can be treated as functions of τ alone, because their vertical derivatives
and, in the limit ε → 0, the inviscid equation is still valid within the boundary layer. Then we suppose that the rest of the dependent variables p, ρ, φ are not perturbed in the boundary layer and can be treated as functions of τ alone, because their vertical derivatives 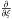 are O(ε).
are O(ε).
The angular velocity Ω is slightly perturbed within the boundary layer: its vertical derivative should change from some finite value to zero, thus we set 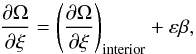 (40)where the vertical variation of β is not negligible inside the boundary layer.
(40)where the vertical variation of β is not negligible inside the boundary layer.
3.6. Boundary layer equations
In short, we have to solve for three variables in the boundary layer: the boundary layer corrections of the normal and tangential components of the meridional velocity field U and V, and of the vertical gradient of rotation that we have called β. The equations describing the flow in the boundary layer are obtained from the vorticity Eq. (21), the conservation of angular momentum (19) and the continuity equation ∇·(ρu) = 0. At leading order in ε and after subtracting the interior inviscid equations, these equations read as (see Appendix A) 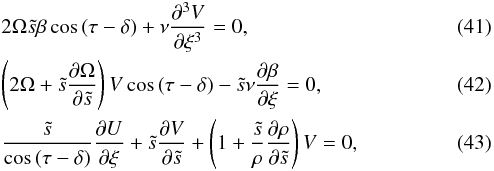 where we have defined
where we have defined 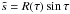 and ν = μ/ρ,
and ν = μ/ρ, 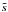 is the radial cylindrical coordinate at the surface, and ν is the non-dimensional kinematic viscosity. These equations are completed with boundary conditions. On the surface (ξ = 0), the conservation of mass and the stress-free boundary conditions become
is the radial cylindrical coordinate at the surface, and ν is the non-dimensional kinematic viscosity. These equations are completed with boundary conditions. On the surface (ξ = 0), the conservation of mass and the stress-free boundary conditions become 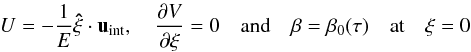 (44)where
(44)where 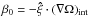 . The corrections should also vanish in the interior, then
. The corrections should also vanish in the interior, then 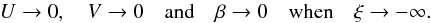 (45)Combining (41) and (42), we obtain
(45)Combining (41) and (42), we obtain 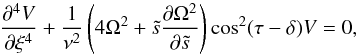 (46)whose solution is
(46)whose solution is ![\begin{equation} V=V_0(\ts)\mathrm{e}^{B\xi}\left[\cos\,(B\xi)+V_1(\ts)\sin\,(B\xi)\right], \end{equation}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq183.png) (47)with
(47)with 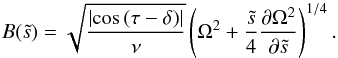 (48)Here, we have used the fact that V should vanish when ξ → − ∞. Using the boundary condition at the surface (44), we see that V1 = −1 and therefore
(48)Here, we have used the fact that V should vanish when ξ → − ∞. Using the boundary condition at the surface (44), we see that V1 = −1 and therefore ![\begin{equation} \label{eq:bl_V} V=V_0(\ts)\mathrm{e}^{B\xi}\left[\cos\, (B\xi)-\sin\, (B\xi)\right]. \end{equation}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq187.png) (49)In the previous expressions we have considered that B is real. For that, Ω must satisfy the condition
(49)In the previous expressions we have considered that B is real. For that, Ω must satisfy the condition 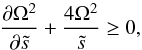 (50)which is equivalent to
(50)which is equivalent to 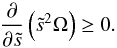 (51)In other words, the specific angular momentum must increase with the distance to the axis of rotation. This is in fact Rayleigh’s criterion for the centrifugal stability of the differential rotation profile.
(51)In other words, the specific angular momentum must increase with the distance to the axis of rotation. This is in fact Rayleigh’s criterion for the centrifugal stability of the differential rotation profile.
Using (41) we get β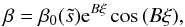 (52)and the condition
(52)and the condition 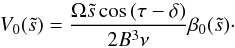 (53)Finally, using the continuity Eq. (43) we obtain the expression for U
(53)Finally, using the continuity Eq. (43) we obtain the expression for U![\begin{equation} \label{eq:bl_U} U=-U_0(\ts)\mathrm{e}^{B\xi}\cos\,(B\xi) -U_1(\ts)\xi\mathrm{e}^{B\xi}\left[\cos\,(B\xi)-\sin\,(B\xi)\right], \end{equation}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq193.png) (54)where
(54)where 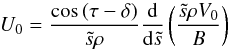 (55)and
(55)and 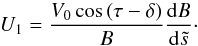 (56)The foregoing expression of the boundary layer correction are those of the classical Ekman layer adapted for a spheroidal stress-free surface. Like the Ekman layer, these corrections suffer from the equatorial singularity. This singularity is associated with the vanishing of
(56)The foregoing expression of the boundary layer correction are those of the classical Ekman layer adapted for a spheroidal stress-free surface. Like the Ekman layer, these corrections suffer from the equatorial singularity. This singularity is associated with the vanishing of 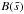 at equator, which is the inverse of the layer’s thickness. This is a quantity of order unity except at the equator where it vanishes (τ → π/2 and δ → 0). As was shown by Roberts & Stewartson (1963), the boundary layer changes scale in this region which extends in latitude as
at equator, which is the inverse of the layer’s thickness. This is a quantity of order unity except at the equator where it vanishes (τ → π/2 and δ → 0). As was shown by Roberts & Stewartson (1963), the boundary layer changes scale in this region which extends in latitude as 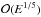 . There, the boundary layer thickness is
. There, the boundary layer thickness is 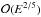 , which is slightly larger than E1/2. The influence of this singularity tends to zero when the Ekman number vanishes.
, which is slightly larger than E1/2. The influence of this singularity tends to zero when the Ekman number vanishes.
3.7. Surface differential rotation
The normal velocity in the boundary layer (54) should verify the boundary condition at the surface, as expressed in Eq. (44), namely, 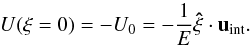 (57)We see now that this leads to the appropriate boundary condition on the Ω profile at the surface. As the fluid flow is axisymmetric and ∇·(ρuint) = 0, the meridional velocity may be described by a stream function ψ, defined as
(57)We see now that this leads to the appropriate boundary condition on the Ω profile at the surface. As the fluid flow is axisymmetric and ∇·(ρuint) = 0, the meridional velocity may be described by a stream function ψ, defined as  (58)then
(58)then 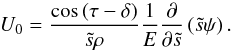 (59)Using Eq. (55) we see that, on the surface
(59)Using Eq. (55) we see that, on the surface 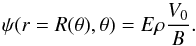 (60)Using Eqs. (48) and (53), we calculate
(60)Using Eqs. (48) and (53), we calculate 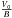
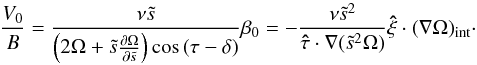 (61)Equations (60) and (61) lead to the condition for the interior rotation profile, now expressed using only interior variables
(61)Equations (60) and (61) lead to the condition for the interior rotation profile, now expressed using only interior variables 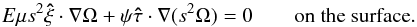 (62)This boundary condition is to be imposed to the differential rotation and lifts the indetermination of the inviscid solution of the baroclinic flow (26). Indeed these solutions are determined up to an arbitrary function of the radial cylindrical coordinate s. This new condition leads to the differential equation that determines this arbitrary function. It couples the horizontal derivative of the angular velocity
(62)This boundary condition is to be imposed to the differential rotation and lifts the indetermination of the inviscid solution of the baroclinic flow (26). Indeed these solutions are determined up to an arbitrary function of the radial cylindrical coordinate s. This new condition leads to the differential equation that determines this arbitrary function. It couples the horizontal derivative of the angular velocity 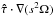 with its vertical derivative
with its vertical derivative 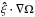 . Thus, solving for this nonlinear boundary condition with the equations of dynamics, leads directly to a self-consistent differential rotation without having to solve the Ekman boundary layer. This part of the solution may be recovered using Eqs. (49), (52), and (54).
. Thus, solving for this nonlinear boundary condition with the equations of dynamics, leads directly to a self-consistent differential rotation without having to solve the Ekman boundary layer. This part of the solution may be recovered using Eqs. (49), (52), and (54).
Remarkably enough, this boundary condition is smooth at the equator: the above-mentioned equatorial singularity is removed with the rest of the Ekman layer.
3.8. Numerical validation
To validate the new boundary condition (62) to be imposed to the inviscid baroclinic flows, we solved numerically the full viscous equation in the simplified set-up of a star enclosed in a spherical box as in Espinosa Lara & Rieutord (2007). As in this previous work we considered a one solar mass of an ideal gas, whose opacities are given by Kramer’s power laws and which rotates at half the break-up angular velocity. The dynamical viscosity of the gas is set to a constant μc. The interior is fully radiative, and the polar pressure is set to 2 × 10-4 the central pressure. The latter condition reduces the density variations and makes the full viscous solution more easily computable.
Because of the imposed constant dynamical viscosity, density variations induce variations of the kinematic viscosity and thus of the Ekman number (17). In Fig. 3, we show the convergence of the surface differential rotation towards the one prescribed by Eq. (62), when the (central) Ekman number Ec = μ/ρc2ΩR2 decreases from 10-4 to 10-6. In Fig. 4 we show the meridional stream function in the asymptotic case and for a viscous solution with E = 10-7. We note that the two solutions agree nicely.
Finally, we computed the boundary layer corrections for the three components of the velocity both from the full numerical solution and from the asymptotic formulae (49), (52), and (54). As shown by Fig. 5, we see that, provided that the Ekman number is sufficiently low, the two solutions also agree.
 |
Fig. 3 Surface rotation (in cycles per day) as a function of colatitude for different values of the Ekman number. The profile approaches the inviscid solution (dashed line) as the Ekman number decreases. |
 |
Fig. 4 Streamlines of the meridional circulation for the inviscid solution with E → 0 (left) and for the full problem (E = 10-7) including the viscous force (right). Solid lines and dashed lines represent counter-clockwise and clockwise circulation, respectively. In the viscous solution, the streamlines are closed inside the boundary layer. For these calculations, one solar mass of ideal gas with Kramers’ opacities was enclosed in a bounding sphere at the pole of which the pressure is 10-4 times the central value (see Espinosa Lara & Rieutord 2007, for a description of this model). |
 |
Fig. 5 Boundary layer corrections for the normal velocity (left), latitudinal velocity (centre), and normal gradient of angular velocity (right) for different values of the Ekman number E. The corrections are computed at a colatitude θ = π/4 and are in normalized units. Solid lines show the corrections calculated from the difference between the full solution and the inviscid model. Dashed lines show the corrections as predicted by the asymptotic solutions (49), (52), and (54). |
4. Results
4.1. The core-envelope interface
The core-envelope interface (thereafter CEI) is the locus of a complex dynamics that is important to understand for its consequences on the lifetime of the stars and the chemical enrichments of their surface layers. As a consequence of the baroclinic torque balance (26), strong density gradient at the CEI (driven for instance by the chemical evolution of the core) forces a strong angular velocity gradient at this same place. In our models, which neglect viscous effect in the interior and any diffusion of elements, this velocity gradient is represented by a jump in the angular velocity. This jump is controlled by the latitudinal variations in the pressure along the CEI. Indeed, the CEI is a surface where the Brunt-Väisälä frequency squared changes sign. If there is a density jump there,  behaves there as a Dirac, and the baroclinic torque is not defined. However, since pressure must be continuous, its latitudinal variations on the CEI just inside and just outside the core must be the same. From the projection of (25) on a tangent vector eT of the CEI, we can therefore derive the following jump condition
behaves there as a Dirac, and the baroclinic torque is not defined. However, since pressure must be continuous, its latitudinal variations on the CEI just inside and just outside the core must be the same. From the projection of (25) on a tangent vector eT of the CEI, we can therefore derive the following jump condition 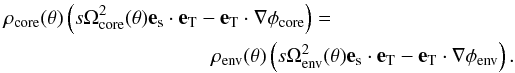 (63)This interface conditions shows that if the density is discontinuous, so is the angular velocity, since ∇φ is continuous.
(63)This interface conditions shows that if the density is discontinuous, so is the angular velocity, since ∇φ is continuous.
Numerics show that if the core is denser than the envelope, it rotates faster, as illustrated in Fig. 6. We note that this faster rotation of the core and the ensuing velocity gradient builds up on the thermal time scale of the star. This is indeed the time scale that controls the baroclinic modes and therefore the action of the baroclinic torque. This time scale is usually smaller than that of nuclear evolution, and therefore this velocity jump has time to build up when the core gets denser as nuclear evolution proceeds.
The foregoing shear is obviously smoothed by diffusion processes, in particular by viscosity. However, this smoothing is not simple. The balance of forces requires the occurrence of a Stewartson layer that develops on the tangent cylinder of the core-envelope interface as illustrated in Fig. 7. Such a layer is triggered by any discontinuity that appears on this interface. As shown in the original analysis of Stewartson (1966), this internal layer is composed of nested layers whose thicknesses scale with some fractional power of the viscosity (E1/4, E2/7 and E1/3 are the main non-dimensional scales). Such scalings are not included in our solution, which only retains the balance between viscous force and meridional advection on a macroscopic scale.
In Fig. 7, we clearly see the meridional flows induced by the core-envelope interface. Their spectral expansion on spherical harmonics is not converged well as a consequence of the hidden discontinuities. The foregoing remarks aim at underlining that such flows should be considered as not fully computed. This is why we do not comment on the transport they may achieve, although this is one of the key parts of rotational mixing. The core-envelope shear layer is clearly reminiscent of the tachocline of low-mass stars, although the mechanisms at work are different. As for this layer, we should expect some dynamo effect driven by the shear. Further work is clearly needed.
Fortunately, the differential rotation is computed much better and does not suffer from the approximate treatment of the Stewartson layer. This is most probably because the influence of this layer vanishes as the viscosity vanishes.
4.2. Comparison with observational data
The most important test of the foregoing models naturally comes from a comparison with observational data. The recent progress in optical and infrared interferometry have led to the derivation of new precise measurements of the fundamental parameters of some early-type stars of intermediate mass.
We have selected three such stars, namely α Lyr (M ~ 2.2 M⊙), α Oph (M ~ 2.2 M⊙), and α Leo (M ~ 4.1 M⊙). The star α Oph (Ras Alhague) has also been successfully modelled by Deupree et al. (2012).
Data from these three stars comes from the interferometric observations with CHARA (Aufdenberg et al. 2006; Zhao et al. 2009; Che et al. 2011; Monnier et al. 2012). In addition, α Oph is the primary of binary system whose orbit constrains its mass to the interval 2.03 ≤ M/M⊙ ≤ 2.63 (Hinkley et al. 2011). It has also been recently identified as a δ-Scuti star displaying 57 frequencies (Monnier et al. 2010). All these data make Ras Alhague an interesting test bed for models of rapidly rotating stars. Because Vega is a photometric standard, it has been studied in detail for many years (e.g. Aufdenberg et al. 2006; Takeda et al. 2008; Monnier et al. 2012, and references therein). Regulus is also an interesting case because it may owe its fast rotation to the swallowing of the envelope of its now white dwarf companion (Rappaport et al. 2009).
In Tables 3–5, we compare our models to these data. Three parameters have been adjusted: the mass, the angular velocity, and the mass fraction of hydrogen in the core. The last parameter allows us to take the hydrogen depletion into account in the core due to time evolution. This is our proxy for time evolution on the main sequence. A solar metallicity is used for the envelope (X = 0.7 and Z = 0.02), except for Vega where we use Z = 0.0093 and X = 0.7546 following Yoon et al. (2008).
 |
Fig. 6 Angular velocity (in rd/s) as a function of the radial distance (in R⊙) along the rotation axis (θ = 0) for the Vega model of Table 4. The angular velocity discontinuity at the core-envelope interface is clearly visible. |
The comparison shown by these tables is quite encouraging. We shall not discuss the matching between data and models in more detail. Indeed, the observed quantities are model dependent; actually, they have been derived using a Roche model with solid body rotation and ad hoc gravity darkening laws. A full discussion, which should include the spectral energy distribution and the oscillation spectrum when relevant, would require a dedicated work and is therefore beyond the scope of the present paper.
4.3. Surface convection
 |
Fig. 7 Meridional streamlines from the model of α Leo. The vertical solid line illustrates the tangent cylinder associated with the core-envelope interface. |
While the most important convective region for stars with a mass above two solar masses is the core, some residual convection may affect the surface layers. In Fig. 8, we display the regions where the squared Brunt-Väisälä frequency is negative for a Vega-like model. It shows that a thin convective layer affects the surface due to the hydrogen ionization peak. Two other layers associated with the first and second ionizations of helium are also shown. As an effect of rotation, these layers thicken and deepen in the equatorial region. In the more massive star α Leo, the unstably stratified layers are below the surface in the polar regions, but the equatorial temperature drop lets the outermost layer almost touch the surface (see Fig. 9). These regions, if they actually develop some thermal convection, may participate in the line broadening with micro- or macroturbulence.
Comparison between observationally derived (Monnier et al. 2010) parameters of the star α Oph and our model.
4.4. Differential rotation of intermediate-mass stars
The essential progress that has been accomplished in these 2D-models with respect to previous attempts is that differential rotation is no longer arbitrary. It is the solution of fluid dynamics equations and is the response to the actual baroclinic torque that exists in all rotating stars. When stars rotate rapidly and do not lose angular momentum, this torque is the main driver of the differential rotation. Reynolds stresses from the convective core are also possibly influential, but presently their functional form is unknown.
To have an idea of the resulting differential rotation in intermediate-mass stars, we explore, in a rather systematic manner, the dependence of differential rotation with general quantities that may influence it. We therefore examine the dependence with mass, metallicity, and angular velocity.
We first note that in all cases investigated, this differential rotation is stable with respect to the centrifugal instability: the z-component of the specific angular momentum always increases with the distance to the rotation axis, except for a small jump at the CEI when the core is evolved. This is a consequence of the weak differential rotation generated by the baroclinic torques as shown below.
A first general view of the differential rotation is given in Fig. 10 for the model of Regulus. As emphasized by the surface latitudinal and radial variations on a ZAMS (homogeneous) three solar mass star model, the differential rotation never exceeds 7% horizontally and 25% radially (see Figs. 11 and 14). As shown in Fig. 11 the differential rotation is not necessarily a monotonous function of the latitude and, at fast rotation rates, latitudes at ±40° rotate slightly more rapidly (2%) than the equator. This is at odds with our previous result (Espinosa Lara & Rieutord 2007). The difference likely comes from the unrealistic boundary conditions used in Espinosa Lara & Rieutord (2007) where the star was confined in a spherical container. The non-monotonous behaviour is only present in the outer part of the envelope. It is related to the change in the temperature variation with latitude on an isobar, since these variations control the baroclinic torque (Espinosa Lara & Rieutord 2007). Indeed as shown in Fig. 12 in the interior the temperature decreases from pole to equator, while it increases near the surface. Such a change affects the baroclinic torque and the ensuing velocity field. The reason to this change is not clear. The effective temperature representing the radiative flux, as shown in Fig. 13, always decreases from pole to equator, as expected.
 |
Fig. 8 Convectively unstable layers in the outer layers of Vega’s model as shown by the squared Brunt-Väisälä frequencyN2. Left: a general view showing the regions where N2 < 0. These are limited by the solid lines. In the top panel, there are two convective layers, and the shallowest one reaches the surface of the star. The dashed line marks the minimum of N2. The layers associated with helium ionization region clearly appear. Left: closer view of the surface layer. The grey scale represents the values of N2 in squared radians per second. |
The radial profiles displayed in Fig. 14 show the almost rigid rotation of the core (as there is no baroclinic torque there). As noted above, the radial variations are stronger than the latitudinal ones, but they are essentially concentrated near the core (namely between rc and 2rc). Since the latitudinal differential rotation is much less, we note that in this neighbourhood of the core, the differential rotation is essentially shellular (see also Fig. 10). This remark prompted us to compare the radial differential with that obtained from the previous 1D-models, including rotation according to the approach of Zahn (1992). Works like those of Denissenkov et al. (1999) and Meynet & Maeder (2000) have shown that an initial solid body rotation rapidly relaxes towards a quasi-steady shellular differential rotation like the one displayed in Fig. 14. Our model shows that this shellular flow is just the differential rotation driven by the baroclinic torque of the configuration so does not depend on a prescription for the viscosity. As a consequence the 1D and 2D models are in good agreement for the amplitude of this differential rotation. For the 20 M⊙-model of Meynet & Maeder (2000), we find a δΩ/Ω ~ 0.18, while their 1D-model gives δΩ/Ω ~ 0.21.
 |
Fig. 9 Layers with unstable stratification in the upper envelope of the model for α Leo. |
 |
Fig. 10 Differential rotation of Regulus. Dashed isocontours and dark background represent slower regions, while clear or white background and solid isocontours show faster regions. |
The dependence of differential rotation with respect to the mass of the stars is illustrated in Fig. 15. There we see that the trend is for radial differential rotation to decrease with mass, while latitudinal variations increase. This is a consequence of the variations in the Brunt-Väisälä frequency  with mass. As mass increases, the peak of
with mass. As mass increases, the peak of  near the core decreases, and therefore the baroclinic torque is weaker, leading to a milder radial differential rotation.
near the core decreases, and therefore the baroclinic torque is weaker, leading to a milder radial differential rotation.
Decreasing metallicity obviously increases differential rotation as shown by Fig. 16. The stronger latitudinal differential rotation is conspicuous. We understand this effect as a consequence of the reduction of the opacity when metals are removed. The gas is then more efficient at heat transport, so temperature gradients are steeper, making the baroclinic torque and the differential rotation stronger.
Finally, we tried to evaluate the effects of time evolution along the main sequence. For early-type stars, the variations in the hydrogen mass fraction in the convective core can serve as a proxy of this evolution. Figure 17 (top and middle) clearly shows that at a given fraction of the break-up angular velocity, hydrogen burning leads to an increasing radial differential rotation and a decreasing latitudinal variation. This is related to the building up of a density jump at the core-envelope interface as discussed above. As a consequence, the angular velocity shows a rapid variation on this interface as shown in Fig. 17 (bottom).
 |
Fig. 11 Latitudinal differential rotation on the surface of a 3 M⊙ ZAMS star for several values of the equatorial rotation velocity (Ωeq). The group of lower curves shows the latitudinal variations of angular velocity at the core-envelope boundary. |
 |
Fig. 12 Latitudinal variations of temperature on an isobar at various depth. The change from a decreasing function to an increasing one occurs near the isobar that crosses the rotation axis at a fractional radius of r ~ 0.6. |
 |
Fig. 13 Latitudinal variations of effective temperature on an isobar at various depth. Here, the effective temperature is defined as |
 |
Fig. 14 Radial profile of differential rotation at the equator (top) and the pole (bottom) of a 3 M⊙ star for several values of the equatorial rotation velocity (Ωeq). |
 |
Fig. 15 Top: radial differential rotation, taken at equator, for ZAMS (homogeneous) models as a function of mass. Bottom: surface differential rotation for the same stars. The chemical composition is solar. |
 |
Fig. 17 Top: variation in the radial differential rotation with mass fraction of hydrogen in the core. The value in the envelope is held fixed at 0.7, while that of the core is decreased as would be the case when the stars evolve. The angular velocity is half of the break-up: Ωeq = 0.5 Ωk. Middle: same as top but for the surface differential rotation. Bottom: the ratio of the angular velocity at the pole of the core and at the bottom of the envelope on the rotation axis. |
5. Conclusions
We have presented the first realistic two-dimensional models of a rotating star where the differential rotation and the meridional circulation are calculated self-consistently with the stellar structure. In particular, we have devised a method of computing the velocity field without having to compute the Ekman boundary layers. These layers are indeed extremely thin and would require too much spatial resolution to be included in the solution. The account of the boundary layer is, however, needed to lift the indetermination of the inviscid solution with respect to geostrophic flows. The present solution therefore includes the minimum viscosity for making the differential rotation well-defined and insuring the balance of angular momentum flux between meridional advection and diffusion. This simplification does not allow the inclusion of a Stewartson layer, which requires the full viscosity terms around the core.
The accuracy of the models have been certified through various tests:
-
the spectral convergence;
-
the monitoring of round-off errors;
-
the virial test;
-
the energy balance test.
The first three tests usually show relative errors less than 10-10, while the energy balance yields much higher errors of the order of 10-5 because of the rapid variations in opacity. Of course, the computation of models close to break-up is less precise because of the development of the equatorial cusp (making θ-derivatives singular).
The resulting models have been compared to one-dimensional models computed with well-tested codes like CESAM or TGEC in the non-rotating case. Slight differences of the order of or less than a percent are perceptible. They most probably come from our use of an analytic formula for the nuclear heating instead of a nuclear network as is standard in 1D codes.
Finally, we compared our models to the observational data of some rapidly rotating stars: namely α Lyr, α Oph, and α Leo. These stars have recently been studied in detail with interferometers operating in the visible or infrared. Our models nicely match the observationally derived parameters of these stars, suggesting that they are not far from reality and confirming the previous good matching of the gravity darkening found by Espinosa Lara & Rieutord (2011).
From these reassuring results we have studied the properties of the differential rotation of baroclinic origin that pervade the radiative envelope of intermediate-mass stars. The results show that it remains small for a homogeneous star: a few percent in latitude on the surface and less than 25% radially. Differential rotation seems to decrease with increasing mass and metallicity. Besides, core evolution increases the radial differential rotation because of the torque coming from the density jump at the core-envelope interface. As shown in Fig. 17, by the end of the main sequence, the core rotation may reach three times that of the envelope. This result is important in view of the interpretation of the core rotation of red giants stars descending from intermediate-mass stars. This rotation is now available from asteroseismology (Mosser et al. 2012). Before the advent of a full account of dynamical evolution in two-dimensional models, our results suggest that baroclinic torques may lead to red giants with fast-rotating cores.
The foregoing two-dimensional models give a new view of the structure and the dynamics of rapidly rotating stars, but they raise many new questions as well. We have mentioned that of the temperature profile on isobars that behaves non-monotonically and for which no simple explanation was found, but the most challenging questions are certainly those around the core-envelope interface, including the Stewartson layer that inevitably develops along the tangent cylinder of the convective core. Solutions require the account of viscosity and the diffusion of elements. However, Ekman layers still need to be avoided because they are much too thin to be solved numerically. The complete solution likely necessitates a combination of the asymptotic solution that we derived in this work and a numerical solution of the full viscous operator in the interior of the star. The density variations of the core-envelope boundary induced by core evolution should also be smoothed by some diffusion effects; nevertheless, they lead to a strong gradient of angular velocity that emphasizes the mixing of the core and the base of the envelope. One may naturally wonder if this dynamical feature would lead to some faked core overshooting that is confused with a true overshoot.
Finally, the next challenging issue in this modelling of rapidly rotating stars will be including time evolution so as to monitor the evolution of the distribution of angular momentum and determine the consequences of the famous rotational mixing that is at the heart of the specific chemical evolution of rotating stars (Maeder & Meynet 2000).
Acknowledgments
We are grateful to Sylvie Theado for providing us with 1D-models computed with the Toulouse-Geneva Evolution Code, to Yveline Lebreton for letting us use the one-dimensional CESAM code, and to the referee Georges Meynet for his detailed comments on the first version of our manuscript. The authors acknowledge the support of the French Agence Nationale de la Recherche (ANR), under grant ESTER (ANR-09-BLAN-0140). This work was also supported by the Centre National de la Recherche Scientifique (CNRS, UMR 5277), through the Programme National de Physique Stellaire (PNPS). The numerical calculations have been carried out on the CalMip machine of the “Centre Interuniversitaire de Calcul de Toulouse” (CICT), which is gratefully acknowledged.
References
- Aufdenberg, J. P., Mérand, A., Coudé du Foresto, V., et al. 2006, ApJ, 645, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., & Marck, J.-A. 1998, Phys. Rev. D, 58, 104020 [NASA ADS] [CrossRef] [Google Scholar]
- Brott, I., Evans, C. J., Hunter, I., et al. 2011, A&A, 530, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
- Che, X., Monnier, J. D., Zhao, M., et al. 2011, ApJ, 732, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Mathis, S., Palacios, A., et al. 2009, A&A, 495, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., Ivanova, N. S., & Weiss, A. 1999, A&A, 341, 181 [NASA ADS] [Google Scholar]
- Deupree, R. G., Castañeda, D., Peña, F., & Short, C. I. 2012, ApJ, 753, 20 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2007, A&A, 470, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and evolution of the elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Cassé (Cambridge Univ. Press), 15 [Google Scholar]
- Hinkley, S., Monnier, J. D., Oppenheimer, B. R., et al. 2011, ApJ, 726, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Hui-Bon-Hoa, A. 2008, Ast. Space Sc., 316, 55 [Google Scholar]
- Hunter, I., Brott, I., Lennon, D. J., et al. 2008, ApJ, 676, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, S., MacGregor, K. B., & Skumanich, A. 2005, ApJS, 156, 245 [NASA ADS] [CrossRef] [Google Scholar]
- James, R. A. 1964, ApJ, 140, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Zahn, J. P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J.-P. 2005, A&A, 440, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Monnier, J. D., Townsend, R. H. D., Che, X., et al. 2010, ApJ, 725, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Monnier, J., Che, X., Zhao, M., et al. 2012, ApJ, 761, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostriker, J. P., & Mark, J. W.-K. 1968, ApJ, 151, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Petit, P., Dintrans, B., Morgenthaler, A., et al. 2009, A&A, 508, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Lignières, F., Wade, G. A., et al. 2010, A&A, 523, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rappaport, S., Podsiadlowski, P., & Horev, I. 2009, ApJ, 698, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Rieutord, M. 2006a, A&A, 451, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M. 2006b, in SF2A Proc. 2006, eds. F. Casoli, et al. [arXiv:astro-ph/0702384] [Google Scholar]
- Rieutord, M. 2006c, in Stellar Fluid dynamics and numerical simulations: From the Sun to Neutron Stars, eds. M. Rieutord, & B. Dubrulle, EAS Publ. Ser., 21, 275 [Google Scholar]
- Rieutord, M., & Espinosa Lara, F. 2012, in SeIsmology for studies of stellar Rotation and Convection, eds. M.-J. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. Green in Lect. Notes Phys. (Springer), in press [arXiv:astro–ph/1208.4926] [Google Scholar]
- Roberts, P., & Stewartson, K. 1963, ApJ, 137, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Stewartson, K. 1966, J. Fluid Mech., 26, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, Y., Kawanomoto, S., & Ohishi, N. 2008, ApJ, 678, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Talon, S., & Zahn, J.-P. 1997, A&A, 317, 749 [Google Scholar]
- Théado, S., Alecian, G., LeBlanc, F., & Vauclair, S. 2012, A&A, 546, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, J., Peterson, D. M., Zagarello, R. J., Armstrong, J. T., & Pauls, T. 2008, ApJ, 681, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zhao, M., Monnier, J. D., Pedretti, E., et al. 2009, ApJ, 701, 209 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Boundary layer equations
Appendix A.1: Differential operators using boundary layer coordinates
The boundary layer coordinates (ξ, τ, ϕ) defined in Sect. 3.4 form a set of orthogonal coordinates with scale factors 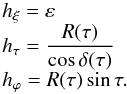 (A.1)It is useful to define a new coordinate
(A.1)It is useful to define a new coordinate  that depends on τ alone:
that depends on τ alone: 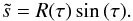 (A.2)The relation between
(A.2)The relation between 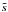 - and θ-derivatives is given by
- and θ-derivatives is given by 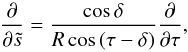 (A.3)and the associated scale factor is
(A.3)and the associated scale factor is 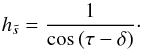 (A.4)Based on the scale factors, the common differential operators can be expressed as Gradient:
(A.4)Based on the scale factors, the common differential operators can be expressed as Gradient: 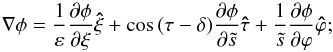 (A.5)
(A.5)
Appendix A.2: Vorticity equation
Let us recall the general form of the vorticity equation
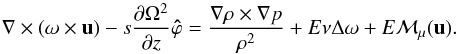 (A.10)On the other hand, the interior inviscid solution satisfies the equation
(A.10)On the other hand, the interior inviscid solution satisfies the equation 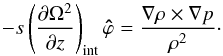 (A.11)Subtracting the two equations, we have
(A.11)Subtracting the two equations, we have 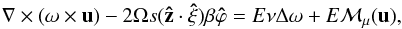 (A.12)where we have used
(A.12)where we have used 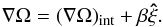 (A.13)Within the boundary layer, the two components (uξ, uτ), of the velocity field can be written as
(A.13)Within the boundary layer, the two components (uξ, uτ), of the velocity field can be written as  where the interior solution uint is ~O(ε2). The associated vorticity is
where the interior solution uint is ~O(ε2). The associated vorticity is 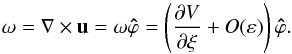 (A.16)It can be shown that the first term in (A.12) is
(A.16)It can be shown that the first term in (A.12) is 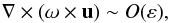 (A.17)while the last term depends on second derivatives of the velocity field, so
(A.17)while the last term depends on second derivatives of the velocity field, so 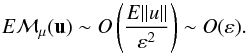 (A.18)However, the remaining term EνΔω is ~ O(1). Indeed,
(A.18)However, the remaining term EνΔω is ~ O(1). Indeed,
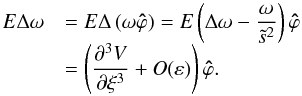 (A.19)Introducing this in (A.12) and rearranging terms, we obtain at leading order in ε
(A.19)Introducing this in (A.12) and rearranging terms, we obtain at leading order in ε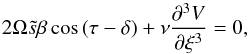 (A.20)where we have used the fact that, in the boundary layer,
(A.20)where we have used the fact that, in the boundary layer,  and
and  .
.
Appendix A.3: Transport of angular momentum
We start with the general equation in its compact form 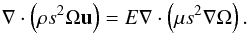 (A.21)Both terms in the equation are ~O(ε2) for the interior variables, but they are ~O(ε) within the boundary layer. Let us start with the right-hand side
(A.21)Both terms in the equation are ~O(ε2) for the interior variables, but they are ~O(ε) within the boundary layer. Let us start with the right-hand side 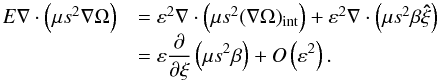 (A.22)The term ∇·(μs2(∇Ω)int) only depends on interior variables, so it is ~O(1). The vertical derivative of an interior variable with respect to ξ is ~O(ε), so we can write
(A.22)The term ∇·(μs2(∇Ω)int) only depends on interior variables, so it is ~O(1). The vertical derivative of an interior variable with respect to ξ is ~O(ε), so we can write 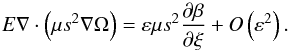 (A.23)Now, we calculate the remaining term
(A.23)Now, we calculate the remaining term 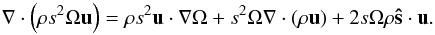 (A.24)From the continuity equation, we know that ∇·(ρu) = 0, then
(A.24)From the continuity equation, we know that ∇·(ρu) = 0, then 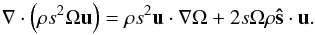 (A.25)Substituting
(A.25)Substituting 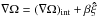 and
and 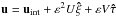 , we have
, we have 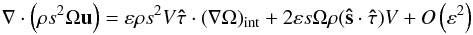 (A.26)since uint ~ O(ε2). Substituting (A.26) and (A.23) into (A.21), up to leading order in ε, we get
(A.26)since uint ~ O(ε2). Substituting (A.26) and (A.23) into (A.21), up to leading order in ε, we get 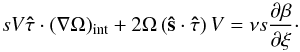 (A.27)We know that, in the boundary layer,
(A.27)We know that, in the boundary layer, 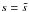 and
and 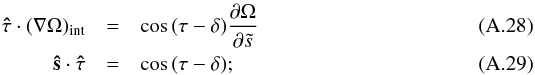 then, rearranging terms we obtain the final form
then, rearranging terms we obtain the final form 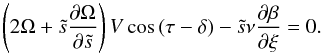 (A.30)
(A.30)
All Tables
Comparison of the results between the ESTER code without rotation and the one-dimensional code TGEC.
Comparison of the results between the 2D models of Deupree et al. (2012) and ours for α Ophiuchi.
Comparison between observationally derived (Monnier et al. 2010) parameters of the star α Oph and our model.
All Figures
 |
Fig. 1 Top: profiles of the radiative (black) and turbulent (red) viscosity as a function of the normalized radius, for three stellar models of ZAMS stars of 3 M⊙, 7 M⊙, and 10 M⊙. Bottom: the associated profiles of the Ekman number ν/2ΩR2 based on the radius of the star and a rotation period of 12 h. |
| In the text | |
 |
Fig. 2 A schematic view of the local basis adapted to the analysis of the Ekman layer. |
| In the text | |
 |
Fig. 3 Surface rotation (in cycles per day) as a function of colatitude for different values of the Ekman number. The profile approaches the inviscid solution (dashed line) as the Ekman number decreases. |
| In the text | |
 |
Fig. 4 Streamlines of the meridional circulation for the inviscid solution with E → 0 (left) and for the full problem (E = 10-7) including the viscous force (right). Solid lines and dashed lines represent counter-clockwise and clockwise circulation, respectively. In the viscous solution, the streamlines are closed inside the boundary layer. For these calculations, one solar mass of ideal gas with Kramers’ opacities was enclosed in a bounding sphere at the pole of which the pressure is 10-4 times the central value (see Espinosa Lara & Rieutord 2007, for a description of this model). |
| In the text | |
 |
Fig. 5 Boundary layer corrections for the normal velocity (left), latitudinal velocity (centre), and normal gradient of angular velocity (right) for different values of the Ekman number E. The corrections are computed at a colatitude θ = π/4 and are in normalized units. Solid lines show the corrections calculated from the difference between the full solution and the inviscid model. Dashed lines show the corrections as predicted by the asymptotic solutions (49), (52), and (54). |
| In the text | |
 |
Fig. 6 Angular velocity (in rd/s) as a function of the radial distance (in R⊙) along the rotation axis (θ = 0) for the Vega model of Table 4. The angular velocity discontinuity at the core-envelope interface is clearly visible. |
| In the text | |
 |
Fig. 7 Meridional streamlines from the model of α Leo. The vertical solid line illustrates the tangent cylinder associated with the core-envelope interface. |
| In the text | |
 |
Fig. 8 Convectively unstable layers in the outer layers of Vega’s model as shown by the squared Brunt-Väisälä frequencyN2. Left: a general view showing the regions where N2 < 0. These are limited by the solid lines. In the top panel, there are two convective layers, and the shallowest one reaches the surface of the star. The dashed line marks the minimum of N2. The layers associated with helium ionization region clearly appear. Left: closer view of the surface layer. The grey scale represents the values of N2 in squared radians per second. |
| In the text | |
 |
Fig. 9 Layers with unstable stratification in the upper envelope of the model for α Leo. |
| In the text | |
 |
Fig. 10 Differential rotation of Regulus. Dashed isocontours and dark background represent slower regions, while clear or white background and solid isocontours show faster regions. |
| In the text | |
 |
Fig. 11 Latitudinal differential rotation on the surface of a 3 M⊙ ZAMS star for several values of the equatorial rotation velocity (Ωeq). The group of lower curves shows the latitudinal variations of angular velocity at the core-envelope boundary. |
| In the text | |
 |
Fig. 12 Latitudinal variations of temperature on an isobar at various depth. The change from a decreasing function to an increasing one occurs near the isobar that crosses the rotation axis at a fractional radius of r ~ 0.6. |
| In the text | |
 |
Fig. 13 Latitudinal variations of effective temperature on an isobar at various depth. Here, the effective temperature is defined as |
| In the text | |
 |
Fig. 14 Radial profile of differential rotation at the equator (top) and the pole (bottom) of a 3 M⊙ star for several values of the equatorial rotation velocity (Ωeq). |
| In the text | |
 |
Fig. 15 Top: radial differential rotation, taken at equator, for ZAMS (homogeneous) models as a function of mass. Bottom: surface differential rotation for the same stars. The chemical composition is solar. |
| In the text | |
 |
Fig. 16 Same as Fig. 15 but stars with Z = 0 metallicity. |
| In the text | |
 |
Fig. 17 Top: variation in the radial differential rotation with mass fraction of hydrogen in the core. The value in the envelope is held fixed at 0.7, while that of the core is decreased as would be the case when the stars evolve. The angular velocity is half of the break-up: Ωeq = 0.5 Ωk. Middle: same as top but for the surface differential rotation. Bottom: the ratio of the angular velocity at the pole of the core and at the bottom of the envelope on the rotation axis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



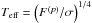
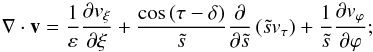
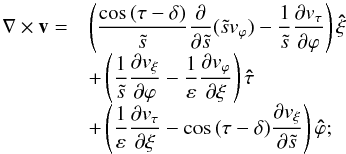
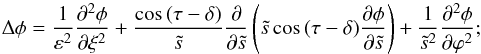
![\appendix \setcounter{section}{1} \begin{equation} \begin{array}{l} (\vec u\cdot\nabla)\vec v= \displaystyle \left[\frac{u_\xi}{\varepsilon}\frac{\partial v_\xi}{\partial\xi} +\cos\,(\tau-\delta)u_\tau\frac{\partial v_\xi}{\partial\ts} +\frac{u_\varphi}{\ts}\frac{\partial v_\xi}{\partial\varphi} \right]\vec{\hat\xi}\\[1mm] \qquad+\displaystyle \left[\frac{u_\xi}{\varepsilon}\frac{\partial v_\tau}{\partial\xi} +\cos\,(\tau-\delta)\left( u_\tau\frac{\partial v_\tau}{\partial\ts} -\frac{u_\varphi v_\varphi}{\ts}\right) +\frac{u_\varphi}{\ts}\frac{\partial v_\tau}{\partial\varphi} \right]\vec{\hat\tau}\\[4mm] \qquad+\displaystyle \left[\frac{u_\xi}{\varepsilon}\frac{\partial v_\varphi}{\partial\xi} +\cos\,(\tau-\delta)\left( u_\tau\frac{\partial v_\varphi}{\partial\ts} +\frac{u_\varphi v_\tau}{\ts}\right) +\frac{u_\varphi}{\ts}\frac{\partial v_\varphi}{\partial\varphi} \right]\vec{\hat\varphi}. \end{array} \end{equation}](/articles/aa/full_html/2013/04/aa20844-12/aa20844-12-eq293.png)