| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220836 | |
| Published online | 21 March 2013 | |
Chandra observation of the Galactic supernova remnant CTB 109 (G109.1–1.0)
1
Institut für Astronomie und Astrophysik, Universität Tübingen,
Sand 1,
72076
Tübingen,
Germany
e-mail:
sasaki@astro.uni-tuebingen.de
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden
Street, Cambridge,
MA
02138,
USA
3
INAF − Osservatorio Astronomico di Palermo, Piazza del Parlamento
1, 90134
Palermo,
Italy
Received: 3 December 2012
Accepted: 4 February 2013
Context. We study the X-ray emission of the Galactic supernova remnant (SNR) CTB 109 (G109.1−1.0), which is well-known for its enigmatic half-shell morphology both in radio and in X-rays and is associated with the anomalous X-ray pulsar (AXP) 1E 2259+586.
Aims. We want to understand the origin of the X-ray bright feature inside the SNR called the Lobe and the details of the interaction of the SNR shock wave with the ambient interstellar medium (ISM).
Methods. The Lobe and the northeastern part of the SNR were observed with Chandra ACIS-I. We analysed the spectrum of the X-ray emission by dividing the entire observed emission into small regions. The X-ray emission is best reproduced with one-component or two-component non-equilibrium ionisation models depending on the position. In the two-component model, one emission component represents the shocked ISM and the other the shocked ejecta.
Results. We detect enhanced element abundances, in particular for Si and Fe, in and around the Lobe. There is one particular region next to the Lobe with a high Si abundance of 3.3 (2.6−4.0) times the solar value. This is the first, unequivocal detection of ejecta in CTB 109.
Conclusions. The new Chandra data confirm that the Lobe was created by the interaction of the SNR shock and the supernova ejecta with a dense and inhomogeneous medium in the environment of SNR CTB 109. The newly calculated age of the SNR is t ≈ 1.4 × 104 yr.
Key words: shock waves − ISM: supernova remnants − X-rays: ISM − X-rays: individuals: SNR CTB 109
© ESO, 2013
1. Introduction
The Galactic supernova remnant CTB 109 (G109.1−1.0) is the host of the anomalous X-ray pulsar (AXP) 1E 2259+586 (Fahlman & Gregory 1981) and represents one of the most exotic and interesting objects in the X-ray sky. The study of an SNR associated with an AXP provides valuable information on the environment in which it formed and an independent estimate of the age of the objects. Given that there are only three firm associations of SNRs with AXPs (Mereghetti 2008), detailed studies of each association will produce progress in our understanding not only of SNRs but also of the AXPs.
The SNR CTB 109 has a spectacular semi-circular morphology in both the X-ray and the radio. At a distance of 3.2 ± 0.2 kpc (Kothes & Foster 2012), it is located next to a giant molecular cloud (GMC) complex and is one of the most striking examples of an interaction of an SNR with a molecular cloud. Since there is neither X-ray (see Fig. 1 in Sasaki et al. 2004) nor radio emission (Hughes et al. 1981) where the western part of the shell would be expected, the semi-circular morphology of CTB 109 implies that the shock has been greatly impeded or even stopped entirely by the GMC complex in the west. A linear feature in CO (“CO arm”) extends from the GMC complex to the local X-ray minimum in the northern half of the SNR (Tatematsu et al. 1987). Therefore, at least a part of the GMC complex extends in front of the remnant. CTB 109 has an X-ray bright interior region known as the “Lobe”. The Lobe is brighter than any part of the shell. Although it has been suggested that this feature is a jet associated with the AXP 1E 2259+586 (Gregory & Fahlman 1983), high-resolution images from ROSAT HRI (Hurford & Fesen 1995), Chandra (Patel et al. 2001), as well as XMM-Newton (Sasaki et al. 2004), show no morphological connection with the pulsar. Furthermore, the X-ray spectrum from the Lobe obtained with XMM-Newton is completely thermal (Sasaki et al. 2004).
We believed that the bright X-ray emission is the result of the interaction between the SNR shock and a molecular cloud complex and therefore performed an observation with the Chandra X-ray Observatory (Weisskopf et al. 2002) using the Advanced CCD Imaging Spectrometer (ACIS, Garmire et al. 2003) in order to study this interaction region in more detail. The first analysis of the high resolution data obtained with ACIS-I in combination with new high resolution CO data from the Five College Radio Observatory has revealed regions with signs of interaction between the SNR shock and CO clouds (Sasaki et al. 2006). In this paper we present the results of the spectral analysis of the entire northeastern part of the SNR, which was observed with ACIS-I.
2. Chandra data
We observed the northeast part of the SNR in an 80 ksec pointing of Chandra with ACIS-I as the prime instrument (ObsID 4626). The Lobe and the northeastern part of the remant shell were completely covered by the ACIS-I array (Fig. 1). The data were analysed with CIAO 4.4. and CALDB 4.4.8.
 |
Fig. 1 Exposure-corrected Chandra ACIS-I intensity map (0.35−8.0 keV). The big red circle indicates the position of the Lobe, the yellow ellipse that of the CO arm. |
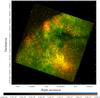 |
Fig. 2 Two-colour image with red (0.35−0.8 keV) and green (1.0−8.0 keV). |
2.1. Images
Figure 1 shows the exposure-corrected intensity map of the ACIS-I data (0.35−8.0 keV). The events were binned with a bin size of 4 pixels and the image has been smoothed with a Gaussian kernel of 3 and 4 pixels in Figs. 1 and 2 (see below), respectively.
Compared to the XMM-Newton image (Sasaki et al. 2004), the Chandra image reveals more point sources. Also, structures in the dark region absorbed by the CO arm, as well as filamentary structures in the Lobe, are resolved. The two-colour image (Fig. 2), in which the soft band (0.35−0.8 keV) is presented in red and the hard band (1.0−8.0 keV) in green, shows colour variations in the Lobe. There is a bright yellow structure in the central part of the Lobe, while the outer diffuser parts are green (harder) in the east and red (softer) in the west. The two-colour image shows spectral variations that are either intrinsic or due to absorption or perhaps a combination of the two. The diffuse emission in the CO arm appears to have harder spectra consistent with higher absorption. A detailed spectral analysis would possibly distinguish between intrinsic spectral variations and variable absorption.
 |
Fig. 3 Extracted regions overlaid on the intensity map. Point sources are removed. |
For further analysis, we divided the diffuse emission of the SNR into small regions with similar surface brightness and X-ray colour, and extract spectra for each region. To study the spectra of only the diffuse emission, we first performed source detection on the whole data (wavdetect) and excluded all detected point and point-like sources in each region. The regions used are shown in Fig. 3. The number of counts in the regions varies from ~4000−20 000 cts. The spectra are binned with a minimum of 20 counts per bin so that Gaussian statistics may be assumed in the fitting.
2.2. Spectral analysis
We analysed the spectra using the X-ray spectral fitting package XSPEC Ver. 12.7.1. The analysis of XMM-Newton data showed that the emission from CTB 109 is thermal with no indication of nonthermal emission (Sasaki et al. 2004). Furthermore, the thermal emission suggests that the plasma is not in collisional ionisation equilibrium (CIE). Therefore, we fitted the extracted ACIS-I spectra with non-equilibrium ionisation (NEI) models. The foreground absorbing column density NH was modeled using TBABS (Wilms et al. 2000). We used abundances relative to solar values reported by Wilms et al. (2000).
 |
Fig. 4 Contour diagram of the parameters kT and τ for the fit with one VNEI model of region 49. The contours correspond to confidence levels of 60%, 90%, and 99%. |
2.2.1. One-component NEI model
First, we fitted all spectra assuming one VNEI component, similar to what was used to analyse the XMM-Newton data (Sasaki et al. 2004). Initially, the abundances were all fixed to solar values. In regions 49 and 57, which correspond to the outer shock, we get relatively good fits with NH = 9.6(8.8−10.5)1Allerrorsinthispaperare90%confidenceerrors. × 1021 cm-2, 1.2(1.1−1.3) × 1022 cm-2, kT = 0.25 (0.22−0.27) keV, 0.25 (0.23−0.26) keV, and net > 7.2 × 1011 s cm-3, > 2.3 × 1010 s cm-3, with reduced χ2 = 1.4 for 107 and 99 degrees of freedom for regions 49 and 57, respectively (see Fig. 4). The best fit values for the ionisation timescale are net = 4.9 × 1013 s cm-3 and 2.1 × 1013 s cm-3 indicating CIE in these regions.
We also freed the abundances, but the one-component description of the data is not satisfactory in about 25% of the regions with reduced χ2 > 1.5, ranging up to reduced χ2 = 2.0 (see Fig. 5, upper left diagram).
2.2.2. Two-component NEI model
 |
Fig. 5 Left: Chandra ACIS-I spectrum of an interior region 39 with the best fit single-component VNEI model (upper diagram, reduced χ2 = 2.0 for 103 degrees of freedom) and two-component model (lower diagram, reduced χ2 = 1.1 for 100 degrees of freedom). Middle: spectrum of the outermost region 57 in the east (upper) and an interior region 54 (lower) with the best fit 2 VNEI model. The relative flux of the ejecta component (dotted) with respect to the ISM component (dashed) in region 57 is lower than in most other regions. Right: spectrum of region 17 with enhanced Si xiii emission (upper diagram). The Mg xi, Si xiii, and S xv triplets are marked. For comparison, the spectrum of region 08, which is the brightest region in the Lobe next to region 17, is shown (lower diagram). The best fit 2 VNEI model is additionally plotted in the diagrams. |
Therefore, in the next step we assumed two thermal VNEI components: 1) to model the emission of the shocked ISM and 2) to verify the existence of emission from shocked ejecta. This two-component model improves the fits in a number of regions (see below), especially in region 39, which had a reduced χ2 = 2.0 (103 degrees of freedom) for the one-component VNEI model and can be fitted with a reduced χ2 = 1.1 (100 degrees of freedom) with a two-component VNEI model (Fig. 5, left panels).
For the ISM component, we use kT1 = 0.25 keV and net1 = 1 × 1012 s cm-3 as starting values, representing the best fit parameters of the single-component VNEI model for regions 49 and 57. All abundances of this component were fixed to solar values. The second component, which was introduced to model the ejecta emission, was fitted with variable abundances for elements showing strong emission lines. The fits required a higher temperature of kT2 ≈ 0.6 keV. The ejecta component with the higher temperature dominates the spectrum for energies higher than ~1 keV in most of the spectra (see Fig. 5, middle panels). The abundances of Mg, Si, S, for which emission lines are visible in the spectra, as well as Fe, were freed for the second (ejecta) model component and fitted. In some regions, higher abundances are found for Si and Fe in particular (see Fig. 5, right panels).
2.2.3. F-test
To verify how much the fits improve by including a second VNEI component, we performed an F-test for the one-component VNEI and two-component VNEI models for all regions. In 27 out of 58 regions, the two models differ with probabilities higher than 99.9%. In order to visualise the variations of the spectral properties, we created a map of the spectral parameters by filling each region with the corresponding parameter value. In the top row of Fig. 6 we show the distribution of the temperature parameter kT of the one-component VNEI model for regions in which the F-test indicated no necessity of an additional component (left) and the distributions of kT1 (ISM) and kT2 (ejecta) of the two-component VNEI model (middle and right, respectively). Regions in which the F-test confirmed an improvement of the fits after including the second VNEI component are marked with white crosses. The middle and bottom rows in Fig. 6 show the same for the ionisation timescales τ (left) and τ2 (right) and the foreground column densities NH for the one-component (left) and two-component (right) fits.
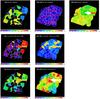 |
Fig. 6 Top: best fit temperature parameters for the one-component VNEI model (kT) in regions in which the F-test indicated that the one-component model fits the spectrum sufficiently well (left) and temperature parameters kT1 and kT2 for the two-component fits for all regions (middle and right, respectively). Middle: best fit values for the ionisation timescale τ for the one-component VNEI model (left) and the ionisation timescale τ2 for the dominating ejecta component for the two-component fits (right). Bottom: best fit values for the foreground NH for the one-component VNEI model (left) and for the two-component fits (right). The crosses mark the regions in which the F-test indicated that the two-VNEI component model yields a better fit (see Sect. 2.2.3). |
3. Discussion
The analysis of the Chandra ACIS spectra of the northeastern part of the SNR CTB 109, divided into small regions, has shown that the spectra can be well fitted by a one-component VNEI model in many regions. However, in 50% of the regions a two-component model consisting of two thermal VNEI models with two different temperatures improves the fit significantly. In this model, the first component is used to describe the emission from the shocked ISM, while the second component reproduces the emission from the ejecta. Therefore, we believe that there are at least two emission components in all regions. In cases in which the one-component model yields a sufficiently good fit, the temperature and the ionisation timescale most likely tend towards values of the component of the multi-temperature spectrum that dominates the emission. We base our discussion on the results obtained with the two-component spectral fits for all regions. The diagrams in Fig. 7 show the relations between some parameters derived from the fits (see following subsections for further discussion).
The temperature of the ISM component (Fig. 6, upper middle) is comparable in all regions and is low (~0.1−0.3 keV), while the temperature of the ejecta component is higher (~0.4−0.9 keV, Fig. 6, upper right). The ionisation timescale of the ejecta component is τ2 = 1011−12 s cm-3 (Fig. 6, middle right panel) except for regions at and around the CO arm, in which τ2 tends to be higher. The higher values for τ2 in the CO arm regions indicate a higher density as we can assume that these regions have been shocked at a similar time to the rest of the remnant.
The NH images (Fig. 6, lower panels) show that the foreground absorption is high near the CO arm (NH> 1.1 × 1022 cm-2). Around and, in particular, west of the Lobe, the foreground absorption is lower (NH< 1.0 × 1022 cm-2), while it seems to be higher southeast of the Lobe.
 |
Fig. 7 Distribution of the parameter values for the fit with two VNEI components. The labels of the data points are region numbers. The lines in the diagrams for surface brightness norm1,2/A against temperature kT1,2 (upper and middle panels) show the isobars for p/k = 106 cm-3 K (blue) and 107 cm-3 K (green) for different values of the filling factors in the remnant and the size of the emitting volume along the line of sight. The line for each filling factor with the lowest norm1,2/A are marked with a thicker line and labelled with the f1,2 value. The lines in the diagram showing the surface brightness as norm2/A against the ionisation timescale τ2 (bottom panel) are isochrones for t = 10 000, 20 000, 50 000, and 100 000 yr. A range for all isochrones is shown for each t covering the range of variation in the depth of the emitting volume. |
3.1. Filling factors and ejecta mass
CTB 109 is an evolved SNR in the Sedov phase. In such a remnant, which also shows interactions with denser molecular clouds, we can assume that the reverse shock has already propagated to the centre and thus heated most or all of the ejecta. The spectral model provides us with the normalisation parameter 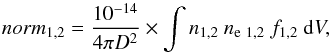 (1)with f1 and f2 being the filling factors of the ISM and ejecta components, respectively (f1 + f2 = 1). For the distance to the SNR, we use D = 3.0 ± 0.5 kpc as estimated by Kothes et al. (2002) and confirmed by Kothes & Foster (2012, 3.2 ± 0.2 kpc). To calculate the filling factor for the ejecta component f2 we assume pressure equilibrium between the two thermal components. Applying momentum conservation for the shock propagating through these components, we get
(1)with f1 and f2 being the filling factors of the ISM and ejecta components, respectively (f1 + f2 = 1). For the distance to the SNR, we use D = 3.0 ± 0.5 kpc as estimated by Kothes et al. (2002) and confirmed by Kothes & Foster (2012, 3.2 ± 0.2 kpc). To calculate the filling factor for the ejecta component f2 we assume pressure equilibrium between the two thermal components. Applying momentum conservation for the shock propagating through these components, we get 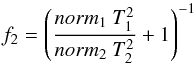 (2)(see Bocchino et al. 1999).
(2)(see Bocchino et al. 1999).
The resulting parameter map for the filling factor of the ejecta component of the two-component VNEI fits is shown in Fig. 8 for all regions. We indeed see a trend in the parameter value distribution map in Fig. 8, in which the inner (western) regions tend to have higher f2 values than the outer regions.
 |
Fig. 8 Distribution of the filling factor for the ejecta component f2 derived from the fits with the two-component VNEI model. |
We can estimate the total ejected mass using the filling factor f2 and the density n2 derived for the ejecta component from Eq. (1). We assume that the SNR is a half sphere with a radius of as determined from the XMM-Newton EPIC images by Sasaki et al. (2004). For D = 3.0 ± 0.5 kpc, R = 16 ± 3 pc = 5.0 ± 0.8 × 1019 cm. Since we have performed spectral analysis using a model with two thermal components only in regions that have been observed with Chandra ACIS-I, we use the median values of f2 and n2 from the two-component fits to estimate the total mass of the ejecta. With f2,median = 0.44 and n2,median = 0.62 cm-2, the total ejecta mass under the assumption of a half sphere as seen, e.g., in the XMM-Newton mosaic image, is Mejecta = 60 M⊙. The density n2 in the regions observed with Chandra varies from 0.23 to 0.81 cm-2, while the filling factor f2 has values between 0.29 and 0.91. Therefore, these estimates have uncertainties of ~50%, whereas the volume may also have an uncertainty of the same order since the X-ray emitting hot gas might not fill the entire volume applied for the estimate. In addition the ejecta might be clumped and thus not uniformly distributed in the assumed volume. If we suppose that the ejecta only fills 30% of the volume, the ejecta mass will be as low as Mejecta = 20 M⊙. Therefore, one should keep in mind that Mejecta is a very crude estimate. However, even the lower limit of Mejecta = 20 M⊙ would rule out a Type Ia supernova as the origin of CTB 109.
3.2. Pressure
In the norm1,2/A-kT1,2 diagrams in Fig. 7 (upper two diagrams) we have plotted lines of constant pressure with p/k = 106 cm-3 K (blue) and 107 cm-3 K (green) for different values of filling factors and depths of the emitting volume in the SNR. These lines were calculated from the best fit parameters assuming pressure equilibrium between the ISM and ejecta components. All the data points are consistent with a thermal pressure of p/k ≈ 107 cm-3 K, corresponding to 1.4 × 10-13 dyne cm-2. The scatter is mainly due to the different filling factors and the uncertainties in the size of the emitting volume along the line of sight.
3.3. Age estimate
In the τ2-norm2/A plot in Fig. 7 (lower diagram), we plot the ionisation timescale τ2 of the ejecta component versus the normalisation norm2 per area A of each region.
To study the dependence of the X-ray surface brightness, measured as the normalisation parameter per area norm2/A, and the ionisation timescale τ2, we can replace ne by τ/t in Eq. (1). We then get norm2/A as a function of τ for a given t. The value of norm2 depends on the emitting volume, thus on the depth of the volume along the line of sight for each region. Assuming that the AXP is located at the centre of the circle corresponding to the SNR shell, we calculated the minimum and maximum distances from the AXP for each region. The calculated isochrones for different t values are also shown in the τ2-norm2/A plot. The two lines for each time t show the possible ranges for the depth of the remnant. This diagram indicates that the age of the shocked plasma, derived from the ejecta component (2) is ~2 × 104 yr.
The fits have shown that the temperature of the ISM component (1) is between 0.1 keV and 0.3 keV. For the outer regions 49 and 57, the single component VNEI fit yields kT = 0.25 keV (Sect. 2.2.1). The high and not well-constrained values of the ionisation timescale τ in the single-component fits, as well as the τ1 in the two-component fits, suggest that the plasma of the shocked ISM is close to CIE. If we assume that this temperature is more or less representative of the shocked plasma, the blast wave velocity is 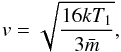 (3)with a mean mass per free particle for a fully ionised plasma of
(3)with a mean mass per free particle for a fully ionised plasma of 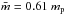 . For a temperature of kT1 = 0.25 ± 0.03 keV, we get v = 460 ± 30 km s-1. The radius is R = 5.0 ± 0.8 × 1019 cm (Sasaki et al. 2004). Using the Sedov similarity solution (Sedov 1959; Taylor 1950; von Neumann 1947), the age of the remnant can be estimated as
. For a temperature of kT1 = 0.25 ± 0.03 keV, we get v = 460 ± 30 km s-1. The radius is R = 5.0 ± 0.8 × 1019 cm (Sasaki et al. 2004). Using the Sedov similarity solution (Sedov 1959; Taylor 1950; von Neumann 1947), the age of the remnant can be estimated as 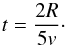 (4)We thus obtain t = (14 ± 2) × 103 yr from the ISM component, which is a little higher than the value obtained from the XMM-Newton data (Sasaki et al. 2004) for which we only assumed one spectral component. Interestingly, this new value for the age of the SNR is in agreement with the age estimate obtained from the fits of the ejecta component.
(4)We thus obtain t = (14 ± 2) × 103 yr from the ISM component, which is a little higher than the value obtained from the XMM-Newton data (Sasaki et al. 2004) for which we only assumed one spectral component. Interestingly, this new value for the age of the SNR is in agreement with the age estimate obtained from the fits of the ejecta component.
3.4. Ejecta
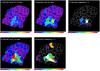 |
Fig. 9 Best fit abundances assuming a thermal model consisting of two VNEI components. The shown parameters are: abundances for elements other than Si, S, and Fe fitted for the ejecta emission a), Si abundance fitted for the ejecta emission b) and its significance calculated as (abundance of the Si – abundance of the other elements)/error of the abundance of Si c), Fe abundance and its significance (d) and e), respectively). |
As can be seen in the Si-abundance and Fe-abundance distribution images in Fig. 9, the abundances measured for the ejecta emission are all comparable to or lower than solar values, except for the Lobe. While the Ne, Mg, and S abundances seem to agree with those of the other elements, Si and Fe abundances are higher, especially in and around the Lobe. The enhanced abundances in the Lobe suggest that its emission has a contribution from an ejecta clump or a conglomeration of ejecta clumps and shocked clouds. There is one particular region (region 17) with significantly enhanced Si abundance within the Lobe (3.3 [2.6−4.0], see Figs. 9b, c). The spectrum of region 17 is shown together with that of an adjacent region with lower Si abundance in Fig. 5 (right panels).
Another possible process that can cause enhanced emission for particular elements in thermal plasma is charge exchange. However, to produce charge exchange emission there must be a phase of cold neutral gas next to or inside the hot X-ray emitting plasma. CO data show no emission at the position of the Lobe or west of it, where the Si abundance enhancement is observed in X-rays (Sasaki et al. 2006). For a mature SNR like CTB 109 we can assume that the reverse shock has propagated all the way through the SNR and, therefore, there should be no unionised gas in the interior of CTB 109. Furtheremore, if the enhanced emission of Si is due to charge exchange, one would expect even higher indication of charge exchange for O or Ne for solar or cosmic abundances. Since no emission enhancement is observed for these lower Z elements, we can rule out that the enhanced emission of particular elements is caused by charge exchange.
The detection of ejecta emission is also very important for the study of the AXP 1E 2259+586, as it will give information on its progenitor. Together with soft gamma-ray repeaters (SGRs) and the sub-class of rotation-powered high-magnetic field pulsars, the AXPs are believed to form a class of neutron stars with extremely high magnetic fields. So far, there are only a few confirmed associations between SNRs and high-magnetic field neutron stars1: SNR G292.2−0.5 and the pulsar J1119−6127, SNR Kes 75 and the pulsar J1846−0258, SNR Kes 73 and AXP 1E 1841−045, SNR CTB 109 and AXP 1E 2259+586, SNR G327.2−0.1 and AXP 1E 1547.0−5408, SNR G337.0−0.1 and SGR 1627−41, SNR G042.8+00.6 and SGR 1900+14, and SNR N 49 and SGR 0526−66 in the LMC. Recently, Park et al. (2012) detected ejecta emission in a deep observation of the SNR N 49 with Chandra (120 ks exposure). However, the element abundance ratio derived from the emission seems to be more consistent with a Type Ia supernova, which would rule out the association between the SNR and the SGR, and requires further investigation. Lopez et al. (2011) measured enhanced abundances of Mg, Si, and S in SNR Kes 73 associated with the AXP 1E 1841−045, whereas Safi-Harb & Kumar (2012) reported on possible abundance enhancement in the X-ray spectra of SNR G292.2−0.5 and SNR Kes 73.
Ejecta emission is also detected in other middle-aged remnants, e.g., in the Galactic SNR G349.7+0.2 (Lazendic et al. 2005), which is interacting with a molecular cloud, or SNRs in the Large Magellanic Cloud (LMC) 0548−70.4, 0534−69.9 (Hendrick et al. 2003), and N49B (Park et al. 2003). Clumping of ejecta seems to be common in core-collapse SNRs. Ejecta clumps have also been found in evolved SNRs like the Vela, both in the interior (Miceli et al. 2008) and outside the main shell (Aschenbach et al. 1995). Kifonidis et al. (2003) have shown in two-dimensional simulations that macroscopic mixing occurs in core-collapse supernova explosions forming clumps of metals. Rayleigh-Taylor instabilities grow in the layers of metals during the expansion, and these layers fragmentate into ejecta clumps.
We created narrow band images for the elements Mg and Si, as prominent emission lines of these elements are visible in the spectra of some regions (Sect. 2.2). The continuum emission has been subtracted from the line emission. Figure 10 shows a three-colour image with red for the soft band XMM-Newton image (0.3−0.9 keV) presented by Sasaki et al. (2004), green for Mg emission ([1.25−1.45 keV band] – surrounding continuum), and blue for Si emission ([1.7−2.1 keV band] – continuum). There is one small region bright in Si emission, covered by the extraction region 17 with enhanced Si line emission (see Sect. 2.2). The Mg emission is distributed broadly; soft emission is bright in the Lobe and the small region in the northeast shell (region 41), which has a relatively low foreground absorption of NH = 0.80 (0.70−0.94) × 1022 cm-2.
Kaplan et al. (2009) measured the proper motions of the AXP 1E 2259+586 using Chandra ACIS-S observations in 2000 and 2006 pointed at the AXP. The suggested initial position at which the supernova occured and the AXP was born is north of the AXP and might even have been in the area coinciding with the CO arm, depending on the real age of the SNR. On the other hand, new near-infrared observations of the counterpart of the AXP with the Keck II telescope using laser guide star adaptive optics have been performed to measure the proper motion of the AXP. These data indicate that the initial position of the AXP was closer to the position of X-ray Lobe, approximately half way between today’s position of the AXP and the Si clump seen in blue in Fig. 10 (Tendulkar et al., in prep.). Both results show that the position of the initial supernova explosion was located west to northwest of the Lobe and suggest that the interaction of the blast wave with a dense molecular cloud produced the X-ray Lobe and, at the same time, caused the formation of the reverse shock, which then ran into ejecta enhanced in Si or Fe. However, one has to keep in mind that the alignment of the Si enhanced region and the Lobe might well be a projection effect.
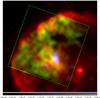 |
Fig. 10 Three-colour image consisting of a red image for the soft band XMM-Newton image (0.3−0.9 keV, Sasaki et al. 2004), a green image for Mg (1.25−1.45 keV) – continuum, and a blue image for Si (1.7−2.1 keV) – continuum. The Mg and Si images were created from the Chandra data. The green dashed box indicates the field of view of the Chandra ACIS-I. The yellow cross indicates the present position of the AXP 1E 2259+586. |
4. Conclusions
Through the analysis of the deep high-resolution data of the Lobe and the northeastern part of the SNR CTB 109 taken with Chandra ACIS-I, we confirm ejecta emission inside the remnant. There is an enhancement in element abundances especially in the X-ray bright Lobe. We have thus unambiguously detected ejecta emission from an SNR associated with an AXP. The ISM and ejecta emission indicate an age of ~10−20 kyr for the shocked X-ray emitting plasma.
As one can see in the XMM-Newton intensity image (Fig. 1, Sasaki et al. 2004) the SNR shell is brighter in the north and the south, while it is darker with diffuse structures in the outer parts of the same sector in which the Lobe is located (east-northeast). The analysis of Chandra data has shown that the foreground absorption NH is lower in and around the Lobe (Fig. 6, lower panels), while the Fe L-shell emission is enhanced in the Lobe, with one smaller region with significantly enhanced Si abundance. The bright feature seen as the Lobe can be explained by the following scenario: the blast wave hit a dense cloud, evaporating and maybe encompassing it. Due to the interacton with the cloud, a reverse shock was formed and propagated towards the centre heating the ejecta. The evaporated cloud is now visible as the Lobe with stronger X-ray emission.
Castro et al. (2012) report the detection of a GeV source with Fermi at the position of CTB 109. The Fermi source is located southwest of the Lobe where the SNR appears dark, and thus most likely highly absorbed in X-rays. Assuming that the γ-rays are produced in π0-decays caused by the interaction of the SNR shock with a dense interstellar cloud now visible as the Lobe, Castro et al. (2012) derive a density of ~120 cm-3 for the cloud. They point out the discrepancy between this value and the density of 0.9 cm-3, which we calculated from the X-ray data (Sasaki et al. 2006). However, as the density of the Lobe of 0.9 cm-3 refers to the hot shocked X-ray emitting gas, which is likely to have a lower density than the original cold cloud, the new result from Castro et al. (2012) is consistent, rather than incompatible, with our results. As we have pointed out (Sasaki et al. 2006) and confirmed in the new spectral analysis, the foreground absorption south of the Lobe (regions 38 and 51 in this work) is high with NH = 1.3(1.1−1.5) × 1022 cm-2 and comparable to that in the CO arm. Therefore, our new Chandra study as well as the new Fermi results by Castro et al. (2012) confirm that there was and still is interaction between the shock wave of CTB 109 with the ambient dense material. The remainder of this interaction is still visible as CO clouds presented in Sasaki et al. (2006).
Acknowledgments
M.S. acknowledges support by the Deutsche Forschungsgemeinschaft through the Emmy Noether Research Grant SA 2131/1. P.P.P. and T.J.G. acknowledge support from NASA contract NAS8-03060.
References
- Aschenbach, B., Egger, R., & Trumper, J. 1995, Nature, 373, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchino, F., Maggio, A., & Sciortino, S. 1999, A&A, 342, 839 [NASA ADS] [Google Scholar]
- Castro, D., Slane, P., Ellison, D. C., & Patnaude, D. J. 2012, ApJ, 756, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Fahlman, G. G., & Gregory, P. C. 1981, Nature, 293, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Garmire, G. P., Bautz, M. W., Ford, P. G., Nousek, J. A., & Ricker, Jr., G. R. 2003, in X-Ray and Gamma-Ray Telescopes and Instruments for Astronomy, eds. J. E. Truemper, & H. D. Tananbaum, Proc. SPIE, 4851, 28 [Google Scholar]
- Gregory, P. C., & Fahlman, G. G. 1983, in Supernova Remnants and their X-ray Emission, IAU Symp., 101, 429 [NASA ADS] [Google Scholar]
- Hendrick, S. P., Borkowski, K. J., & Reynolds, S. P. 2003, ApJ, 593, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, V. A., Harten, R. H., & van den Bergh, S. 1981, ApJ, 246, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hurford, A. P., & Fesen, R. A. 1995, MNRAS, 277, 549 [NASA ADS] [Google Scholar]
- Kaplan, D. L., Chatterjee, S., Hales, C. A., Gaensler, B. M., & Slane, P. O. 2009, AJ, 137, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Kifonidis, K., Plewa, T., Janka, H.-T., & Müller, E. 2003, A&A, 408, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kothes, R., & Foster, T. 2012, ApJ, 746, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Kothes, R., Uyaniker, B., & Yar, A. 2002, ApJ, 576, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Lazendic, J. S., Slane, P. O., Hughes, J. P., Chen, Y., & Dame, T. M. 2005, ApJ, 618, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, L. A., Ramirez-Ruiz, E., Huppenkothen, D., Badenes, C., & Pooley, D. A. 2011, ApJ, 732, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Miceli, M., Bocchino, F., & Reale, F. 2008, ApJ, 676, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Hughes, J. P., Slane, P. O., et al. 2003, ApJ, 592, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Hughes, J. P., Slane, P. O., et al. 2012, ApJ, 748, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, S. K., Kouveliotou, C., Woods, P. M., et al. 2001, ApJ, 563, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Safi-Harb, S., & Kumar, H. S. 2012, ArXiv e-prints [Google Scholar]
- Sasaki, M., Plucinsky, P. P., Gaetz, T. J., et al. 2004, ApJ, 617, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, M., Kothes, R., Plucinsky, P. P., Gaetz, T. J., & Brunt, C. M. 2006, ApJ, 642, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Tatematsu, K., Fukui, Y., Nakano, M., et al. 1987, A&A, 184, 279 [NASA ADS] [Google Scholar]
- Taylor, G. I. 1950, Proc. Roy. Soc. London A, 201, 159 [NASA ADS] [CrossRef] [Google Scholar]
- von Neumann, J. 1947, Los Alamos Sci. Lab. Tech. Ser., 7 [Google Scholar]
- Weisskopf, M. C., Brinkman, B., Canizares, C., et al. 2002, PASP, 114, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Exposure-corrected Chandra ACIS-I intensity map (0.35−8.0 keV). The big red circle indicates the position of the Lobe, the yellow ellipse that of the CO arm. |
| In the text | |
 |
Fig. 2 Two-colour image with red (0.35−0.8 keV) and green (1.0−8.0 keV). |
| In the text | |
 |
Fig. 3 Extracted regions overlaid on the intensity map. Point sources are removed. |
| In the text | |
 |
Fig. 4 Contour diagram of the parameters kT and τ for the fit with one VNEI model of region 49. The contours correspond to confidence levels of 60%, 90%, and 99%. |
| In the text | |
 |
Fig. 5 Left: Chandra ACIS-I spectrum of an interior region 39 with the best fit single-component VNEI model (upper diagram, reduced χ2 = 2.0 for 103 degrees of freedom) and two-component model (lower diagram, reduced χ2 = 1.1 for 100 degrees of freedom). Middle: spectrum of the outermost region 57 in the east (upper) and an interior region 54 (lower) with the best fit 2 VNEI model. The relative flux of the ejecta component (dotted) with respect to the ISM component (dashed) in region 57 is lower than in most other regions. Right: spectrum of region 17 with enhanced Si xiii emission (upper diagram). The Mg xi, Si xiii, and S xv triplets are marked. For comparison, the spectrum of region 08, which is the brightest region in the Lobe next to region 17, is shown (lower diagram). The best fit 2 VNEI model is additionally plotted in the diagrams. |
| In the text | |
 |
Fig. 6 Top: best fit temperature parameters for the one-component VNEI model (kT) in regions in which the F-test indicated that the one-component model fits the spectrum sufficiently well (left) and temperature parameters kT1 and kT2 for the two-component fits for all regions (middle and right, respectively). Middle: best fit values for the ionisation timescale τ for the one-component VNEI model (left) and the ionisation timescale τ2 for the dominating ejecta component for the two-component fits (right). Bottom: best fit values for the foreground NH for the one-component VNEI model (left) and for the two-component fits (right). The crosses mark the regions in which the F-test indicated that the two-VNEI component model yields a better fit (see Sect. 2.2.3). |
| In the text | |
 |
Fig. 7 Distribution of the parameter values for the fit with two VNEI components. The labels of the data points are region numbers. The lines in the diagrams for surface brightness norm1,2/A against temperature kT1,2 (upper and middle panels) show the isobars for p/k = 106 cm-3 K (blue) and 107 cm-3 K (green) for different values of the filling factors in the remnant and the size of the emitting volume along the line of sight. The line for each filling factor with the lowest norm1,2/A are marked with a thicker line and labelled with the f1,2 value. The lines in the diagram showing the surface brightness as norm2/A against the ionisation timescale τ2 (bottom panel) are isochrones for t = 10 000, 20 000, 50 000, and 100 000 yr. A range for all isochrones is shown for each t covering the range of variation in the depth of the emitting volume. |
| In the text | |
 |
Fig. 8 Distribution of the filling factor for the ejecta component f2 derived from the fits with the two-component VNEI model. |
| In the text | |
 |
Fig. 9 Best fit abundances assuming a thermal model consisting of two VNEI components. The shown parameters are: abundances for elements other than Si, S, and Fe fitted for the ejecta emission a), Si abundance fitted for the ejecta emission b) and its significance calculated as (abundance of the Si – abundance of the other elements)/error of the abundance of Si c), Fe abundance and its significance (d) and e), respectively). |
| In the text | |
 |
Fig. 10 Three-colour image consisting of a red image for the soft band XMM-Newton image (0.3−0.9 keV, Sasaki et al. 2004), a green image for Mg (1.25−1.45 keV) – continuum, and a blue image for Si (1.7−2.1 keV) – continuum. The Mg and Si images were created from the Chandra data. The green dashed box indicates the field of view of the Chandra ACIS-I. The yellow cross indicates the present position of the AXP 1E 2259+586. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


