| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118629 | |
| Published online | 26 March 2013 | |
Nebular gas drag and planetary accretion with eccentric high-mass planets⋆
1 Univ. Estadual Paulista – UNESP, Grupo de Dinâmica Orbital & Planetologia, Guaratinguetá, , CEP 12516-410, SP, Brazil
e-mail: thierry@feg.unesp.br, ocwinter@gmail.com
2 Univ. Estadual Paulista – UNESP, DCCE – IBILCE, São Jose do Rio Preto, 01405900 SP, Brazil
e-mail: tsuchida@ibilce.unesp.br
Received: 12 December 2011
Accepted: 23 January 2013
Aims. We investigate the dynamics of pebbles immersed in a gas disk interacting with a planet on an eccentric orbit. The model has a prescribed gap in the disk around the location of the planetary orbit, as is expected for a giant planet with a mass in the range of 0.1–1 Jupiter masses. The pebbles with sizes in the range of 1 cm to 3 m are placed in a ring outside of the giant planet orbit at distances between 10 and 30 planetary Hill radii. The process of the accumulation of pebbles closer to the gap edge, its possible implication for the planetary accretion, and the importance of the mass and the eccentricity of the planet in this process are the motivations behind the present contribution.
Methods. We used the Bulirsch-Stoer numerical algorithm, which is computationally consistent for close approaches, to integrate the Newtonian equations of the planar (2D), elliptical restricted three-body problem. The angular velocity of the gas disk was determined by the appropriate balance between the gravity, centrifugal, and pressure forces, such that it is sub-Keplerian in regions with a negative radial pressure gradient and super-Keplerian where the radial pressure gradient is positive.
Results. The results show that there are no trappings in the 1:1 resonance around the L4 and L5 Lagrangian points for very low planetary eccentricities (e2 < 0.07). The trappings in exterior resonances, in the majority of cases, are because the angular velocity of the disk is super-Keplerian in the gap disk outside of the planetary orbit and because the inward drift is stopped. Furthermore, the semi-major axis location of such trappings depends on the gas pressure profile of the gap (depth) and is a = 1.2 for a planet of 1 MJ. A planet on an eccentric orbit interacts with the pebble layer formed by these resonances. Collisions occur and become important for planetary eccentricity near the present value of Jupiter (e2 = 0.05). The maximum rate of the collisions onto a planet of 0.1 MJ occurs when the pebble size is 37.5 cm ≤ s < 75 cm; for a planet with the mass of Jupiter, it is15 cm ≤ s < 30 cm. The accretion stops when the pebble size is less than 2 cm and the gas drag dominates the motion.
Key words: planets and satellites: formation / minor planets, asteroids: general / accretion, accretion disks
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
The Sun, like other stars, was formed as a result of the gravitational collapse of a large volume of interstellar dust and gas (Shu et al. 1987). Because this interstellar material has a certain amount of angular momentum, the largest part of it could not fall directly into the sun and has formed part of a disk of gas and dust (the solar nebula) in orbit around the protosun. In fact, the interstellar material was incorporated into the nebula through a process of accretion, and part of it lost its angular momentum and precipitated into the primitive Sun. Therefore, most of this material formed part of the protosun, and only a small fraction of it remained in a disk to give rise to the solar planetary system. Given a purely Keplerian gas flow (axially symmetric) in the solar nebula, it is known that a pebble pushing towards the central star follows a spiral trajectory. If we consider a pressure gradient, the flow ceases to be purely Keplerian because of the systematic difference between the velocity of the gas, which is supported by the pressure, and the velocity that characterises the purely Keplerian motions (Weidenschilling 1977). If these pebbles are disturbed by a planet, the formation of co-orbital systems can occur.
The formation of these systems that occur when the pebbles cross the planet have been studied extensively by Kary & Lissauer (1995) and Chanut et al. (2008). It was shown that the efficiency of trapping at the Lagrangian points not only depends on the pebble size but also on the planet mass ratio and eccentricity. Recently, Ormel & Klahr (2010) have performed simulations of the two-dimensionally restricted, three-body problem for the accretion of small bodies onto protoplanets of a few hundred kilometres in two regimes of velocity (Stokes and Epstein). They have shown that the impact probability agrees with the findings of Kary et al. (1993) for pebbles in the Stokes regime. Moreover, Muto & Inutsuka (2009) find that the trapping of pebbles in resonance with low-mass planets is apparently independent of the pebble size or Stokes number, and the minimum mass planet for a dust gap opening has over 10 M⊕.
In an accretion disk, the material loses angular momentum and spirals towards the central object, while a viscous mechanism, due to the gas, redistributes the angular momentum in the disk. Lin & Papaloizou (1980) showed that the redistribution of viscous angular momentum is overloaded when the planet mass ratio μ2 exceeds 10-4. In the presence of a nebula there are formations of spiral density waves, and if they are non-linear and form shocks at the point where they are launched at Lindblad resonances, then it leads to a gap formation. When the gap is formed, it is expected that the surface density changes and, consequently, that the angular velocity changes (Peale 1993). In terms of observational data, Wolf et al. (2002) show that ALMA will be able to detect a gap at 5.2 AU caused by the presence of a Jupiter-mass planet in a disk 140 pc away from the Taurus star-forming region.
Planet formation is, generally speaking, still an unsolved puzzle. The particle-disk-planet interaction has not been fully explored. For example, two-dimensional flat disks with planets were modelled by Bryden et al. (1999), Kley (1999), and Lubow et al. (1999) by applying a locally isothermal assumption for the radial distribution. Klahr & Kley (2006) have performed a full 3D radiation hydrodynamical simulation of embedded protoplanets in disks and compared the results to the standard isothermal approach. They show that the mean torques and the migration rates are not strongly affected by thermodynamics. D’Angelo et al. (2003a) have shown that the two-dimensional approximation works reasonably well, as long as the planetary mass is higher than a tenth of the mass of Jupiter.
On the other hand, it is well known that Jupiter is more enriched in solids than to the Sun. If Jupiter was formed by means of gravitational instability, it would have had to accrete these solids in a later stage. Thus, Paardekooper & Mellema (2004, 2006) have performed simulations of a 2D gas and dust cloud with the presence of planets of 0.1 MJ and 0.5 MJ. According to the results, pebbles smaller than 10 cm do not enrich a newly formed giant planet. Moreover, only pebbles larger than 1 cm may accrete a planet with a mass of Jupiter, and the accretion stops after hundreds to thousands of orbits in the 2D simulation of the gap opening (Paardekooper 2007). The low accretion rate lies in the mechanism of resonance trapping (Weidenchilling & Davis 1985), where inward-moving pebbles are captured in mean motion resonances (MMRs). However, Fouchet et al. (2007) stated that accumulation of pebbles closer to the gap edge, which is formed by high-mass planets, is unlikely to be associated with planetary resonances. The process of the accumulation of pebbles closer to the gap edge, its possible implication for the planetary accretion, and the importancy of the mass and the eccentricity of the planet in this process are the motivations of the present contribution.
In the literature, only Patterson (1987), Kary & Lissauer (1995) and Chanut et al. (2008) have considered a planet in eccentric orbit, and none of them considered a gap in the nebular disk. Kary & Lissauer (1995) have worked with small planets, which clearly justifies the assumption that the disk is unperturbed. However, it is necessary to model a gap in the disk when we consider a system with high-mass planets (≥10-4 M⊙). Lubow et al. (1999) suggested that the mass-flow rate through the gap surrounding an eccentric high-mass planet may be higher than that for a corresponding circular orbit planet, but they did not show this in their work.
In the present work we propose to investigate the behaviour of pebbles that encounter a planet in an eccentric orbit when the planet is large enough (μ2 ≥ 10-4) to open a gap in the nebula. The main goal is to determine the fractions of pebbles that collide with the giant planet, become trapped at exterior resonances, become trapped in a 1:1 mean motion resonance (co-orbital) or cross the orbital semi-major axis of the planet. We analyse the evolution of these pebbles with different masses and orbit eccentricities of the giant planet. The dependence on the value of the gas drag parameter k, which represents the size of the pebbles, is also investigated. The scenario described in this work might not be directly applied to our solar system (e.g. Gomes et al. 2005; Walsh et al. 2011), but the numerous examples of eccentric exoplanets shows that it may be important in a number of systems. In Sect. 2, we describe the nebular model and present the gap effects in detail. In Sect. 3, we present the equations of motion and the nebular drag that we use in this work. Then, we show the initial conditions of the simulations in Sect. 4. We describe the simulation results in Sect. 5 and discuss them in Sect. 6. Conclusions are given in Sect. 7.
2. Nebular model
Peale (1993) chose the nebular model described by Weidenschiling (1977) to investigate the effects of nebular gas drag on pebbles near the Lagrangians points L4 and L5. In a steady state of the nebula, where all of the gas is in a circular orbit, the density ρ is constant at each radial distance r, and the motion is governed by 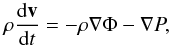 (1)where v is the velocity vector, Φ is the gravitational potential per unit of mass, and P is the pressure, where the effects of viscosity are neglected. With
(1)where v is the velocity vector, Φ is the gravitational potential per unit of mass, and P is the pressure, where the effects of viscosity are neglected. With 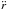 ,
, 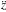 ,
, 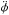 , ṙ, and ż all equal to zero in the steady state, the equation above in cylindrical coordinates r, φ, z becomes
, ṙ, and ż all equal to zero in the steady state, the equation above in cylindrical coordinates r, φ, z becomes 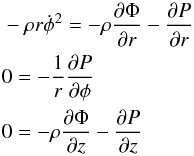 (2)with P(r,z) = ρ(r,z)kBTmp(r)/m for T = Tmp (midplane temperature) being constant in the z direction, where m is the mean molecular mass (~3.8 × 10-24 g), and kB the Boltzmann’s constant, or with P = Pmp(r) [ρ(r,z)/ρmp(r)] γ for an adiabatic temperature gradient in the z direction, and Φ = − GM⊙/(r2 + z2)1/2 for a negligible disk mass, where G is the gravitational constant and M⊙ is the solar mass. Thus, the last of Eqs. (2) can be solved to give
(2)with P(r,z) = ρ(r,z)kBTmp(r)/m for T = Tmp (midplane temperature) being constant in the z direction, where m is the mean molecular mass (~3.8 × 10-24 g), and kB the Boltzmann’s constant, or with P = Pmp(r) [ρ(r,z)/ρmp(r)] γ for an adiabatic temperature gradient in the z direction, and Φ = − GM⊙/(r2 + z2)1/2 for a negligible disk mass, where G is the gravitational constant and M⊙ is the solar mass. Thus, the last of Eqs. (2) can be solved to give 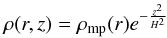 (3)or
(3)or 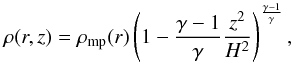 (4)for the two temperature gradients in the z direction. Here γ is the ratio of the specific heats, and H is the scale height, which is given by
(4)for the two temperature gradients in the z direction. Here γ is the ratio of the specific heats, and H is the scale height, which is given by 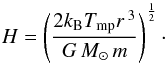 (5)Finally, the shape of Eqs. (3) and (4) simplify if z ≪ r. The surface mass densities Σ(r) for the two cases are found by the integration of Eqs. (3) and (4) over z; thus,
(5)Finally, the shape of Eqs. (3) and (4) simplify if z ≪ r. The surface mass densities Σ(r) for the two cases are found by the integration of Eqs. (3) and (4) over z; thus,  where γ = 7/5 is assumed and H is the scale height evaluated for the midplane temperature. Peale (1993) assumes that Σ = Σ0(a/r)p and T = T0(a/r)q, where Σ0 and T0 are the values of surface mass density and the temperature at the midplane at a Jupiter distance a from the Sun. Weidenschilling (1977) showed some models with 0.5 ≤ q ≤ 1.0. The observations of disks around T Tauri stars imply a surface temperature distribution with q ≈ 1/2 to 3/4 (Beckwith et al. 1990). The surface mass density cannot be described through observation, but theoretical values of p are limited between 1/2 and 2 (Kusaka et al. 1970; Cassen & Moosman 1981; Lissauer 1987). Following Peale (1993), we can fix Σ0 and assume p and q apply only to the local region of interest.
where γ = 7/5 is assumed and H is the scale height evaluated for the midplane temperature. Peale (1993) assumes that Σ = Σ0(a/r)p and T = T0(a/r)q, where Σ0 and T0 are the values of surface mass density and the temperature at the midplane at a Jupiter distance a from the Sun. Weidenschilling (1977) showed some models with 0.5 ≤ q ≤ 1.0. The observations of disks around T Tauri stars imply a surface temperature distribution with q ≈ 1/2 to 3/4 (Beckwith et al. 1990). The surface mass density cannot be described through observation, but theoretical values of p are limited between 1/2 and 2 (Kusaka et al. 1970; Cassen & Moosman 1981; Lissauer 1987). Following Peale (1993), we can fix Σ0 and assume p and q apply only to the local region of interest.
 |
Fig. 1 Distribution of surface mass density of the nebula with a reduction in the surface density at the centre of the gap for p = 0. Here, we show two models of nebular parameters (Peale 1993 and Lubow et al. 1999). |
Because Jupiter creates a large, axially symmetric reduction in the nebular density when it nears its current mass (Lin & Papaloizou 1986, 1993), and assuming that up to 30 M⊕ (M⊕ = Earth’s mass) it does not disturb the distribution of the mass of the nebula, we have ![\begin{eqnarray} &&\rho_{\rm mp}(r)= \frac{\Sigma (r)}{\sqrt{\pi }H(r)} = \frac{\Sigma_{0}}{\sqrt{\pi }H_{0}}\left(\frac{a}{r}\right)^{\frac{3}{2} +p -\frac{q}{2}} \left(1-be^{-\left(\frac{r-a}{H_{0}}\right)^{2}}\right),\\[2mm] && P_{\rm mp}(r)= \frac{k_{\rm B}T_{0}}{m} \left(\frac{a}{r}\right)^{q}\rho_{\rm mp}(r), \end{eqnarray}](/articles/aa/full_html/2013/04/aa18629-11/aa18629-11-eq65.png) where 0 < b < 1. The surface density distribution is shown in Fig. 1 for the chosen value p = 0 and two values of b. We see that the density at the centre of the gap decreases from 10 up to 100 times, depending on the chosen value of b, when the planet reaches 300 M⊕. The reduction of the density depends on the values of the nebular model chosen. However, the local behaviour is in reasonable agreement with the gap shape and size obtained by D’Angelo et al. (2003a) and Klahr & Kley (2006). For example, we obtain a width similar to what is observed in the hydrodynamic simulations for a scale height that is larger by a factor of two. The depth is equal to the one in the isothermal model of Lubow et al. (1999) and the cold model of D’Angelo et al. (2003a) when b = 0.99. For b = 0.9 the depth represents the warm model of D’Angelo et al. (2003a).
where 0 < b < 1. The surface density distribution is shown in Fig. 1 for the chosen value p = 0 and two values of b. We see that the density at the centre of the gap decreases from 10 up to 100 times, depending on the chosen value of b, when the planet reaches 300 M⊕. The reduction of the density depends on the values of the nebular model chosen. However, the local behaviour is in reasonable agreement with the gap shape and size obtained by D’Angelo et al. (2003a) and Klahr & Kley (2006). For example, we obtain a width similar to what is observed in the hydrodynamic simulations for a scale height that is larger by a factor of two. The depth is equal to the one in the isothermal model of Lubow et al. (1999) and the cold model of D’Angelo et al. (2003a) when b = 0.99. For b = 0.9 the depth represents the warm model of D’Angelo et al. (2003a).
 |
Fig. 2 Angular velocity of the nebular gas compared to the Keplerian velocity with and without the gap (b = 0) ) versus the radial distribution of the surface mass density. Here we choose to show the effect of the gap on the angular velocity for three values of b from 0.3 to 0.9. |
Because p = 0 is not realistic for the entire nebula, a flat density distribution should persist around the co-orbital region. The presence of a gap means that the negative pressure radial gradient is enhanced in the inside region of the gap, further reducing the nebular gas angular velocity, but the pressure gradient is reversed outside of the gap, leading to an angular velocity that exceeds the Keplerian value, as shown in the following equation (Peale 1993): 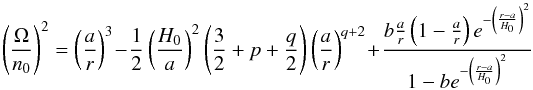 (10)for the nebular angular velocity, where n0 is the mean angular velocity of the pebble, r the radial distance, and a the semi-major axis of the planet. In the absence of a gap (b = 0), Eq. (10) shows that the radial pressure gradient leads to a reduction in the angular velocity below the Keplerian value at all radii. When b ≠ 0, a reversal in the gas angular velocity relative to the Keplerian velocity occurs. We show this behaviour in Fig. 2 for p = 0, q = 1 and four values of b.
(10)for the nebular angular velocity, where n0 is the mean angular velocity of the pebble, r the radial distance, and a the semi-major axis of the planet. In the absence of a gap (b = 0), Eq. (10) shows that the radial pressure gradient leads to a reduction in the angular velocity below the Keplerian value at all radii. When b ≠ 0, a reversal in the gas angular velocity relative to the Keplerian velocity occurs. We show this behaviour in Fig. 2 for p = 0, q = 1 and four values of b.
3. Dynamical system
3.1. Nebular drag
Because the nebular gas rotates around the primary body with a lower angular velocity than the Keplerian value, a pebble orbiting with a Keplerian velocity will suffer a headwind that continuously reduces its orbital energy and angular momentum (Weidenchilling 1977). The drag dynamics are the same as those used by Peale (1993) and Kary & Lissauer (1995). Thus, we can write, for a spherical pebble (e.g., Prantl 1952), 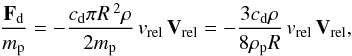 (11)where mp is the pebble mass, R the pebble radius, ρP the pebble density, ρ the gas density, and cd is the drag coefficient which is a function of the Reynolds number. Malhotra (1993) used a simplified form of Peale’s drag force where cd = 0.5 for the Stokes regime. For the densities, we adopt ρ = 10-10 g/cm3 and ρp = 2 g/cm3 (Kary et al. 1993; Kary & Lissauer 1995; Marzari & Scholl 1997). A transition regime between the Stokes drag and the Epstein drag is expected for bodies smaller than 30 cm when the gas density is ten times less than the density used here (i.e., ρ = 10-11 g/cm3; Paardekooper 2007). Moreover, Ormel & Klahr (2010) show that their impact probability agrees with the findings of Kary et al. (1993) for the pebbles in the Stokes regime. In these units, a pebble of a few centimetres still suffers a Stokes drag, and the value of the gas drag parameter k = (3/8)cd(ρ/ρP)/RP is 0.014 per AU of orbital radius for RP = 100 m. Finally,
(11)where mp is the pebble mass, R the pebble radius, ρP the pebble density, ρ the gas density, and cd is the drag coefficient which is a function of the Reynolds number. Malhotra (1993) used a simplified form of Peale’s drag force where cd = 0.5 for the Stokes regime. For the densities, we adopt ρ = 10-10 g/cm3 and ρp = 2 g/cm3 (Kary et al. 1993; Kary & Lissauer 1995; Marzari & Scholl 1997). A transition regime between the Stokes drag and the Epstein drag is expected for bodies smaller than 30 cm when the gas density is ten times less than the density used here (i.e., ρ = 10-11 g/cm3; Paardekooper 2007). Moreover, Ormel & Klahr (2010) show that their impact probability agrees with the findings of Kary et al. (1993) for the pebbles in the Stokes regime. In these units, a pebble of a few centimetres still suffers a Stokes drag, and the value of the gas drag parameter k = (3/8)cd(ρ/ρP)/RP is 0.014 per AU of orbital radius for RP = 100 m. Finally, 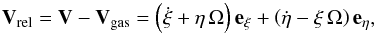 (12)where V is the pebble velocity with components
(12)where V is the pebble velocity with components 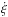 and
and 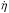 along the orthogonal directions denoted by the unit vectors eξ and eη on the midplane of the nebula, and Ω is the gas angular velocity. All of the motions are confined to the midplane of the nebula.
along the orthogonal directions denoted by the unit vectors eξ and eη on the midplane of the nebula, and Ω is the gas angular velocity. All of the motions are confined to the midplane of the nebula.
3.2. Equations of motion
Here, we consider the dynamic effect of the nebular drag forces on a pebble in the elliptic restricted three-body problem (Murray & Dermott 1999). Thus, the equations of motion of the pebble in the inertial system (ξ,η) are 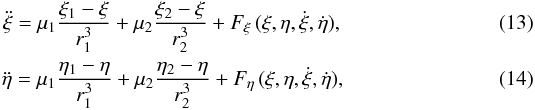 where
where 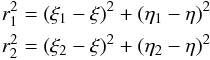 and Fξ and Fη are the ξ and η components of the gas drag, which can be expressed as a function of the position and velocity in the inertial frame.
and Fξ and Fη are the ξ and η components of the gas drag, which can be expressed as a function of the position and velocity in the inertial frame.
4. Numerical simulations
Here we adopt the same model of nebular drag as used by Kary & Lissauer (1995) where q = 1 and H0/a = 0.1 is the scale height that serves to estimate the difference between the gas velocity and the local Keplerian velocity. In this case, the gas velocity is v = 0.995vK. The Bulirsch-Stoer numerical algorithm integrates the Newtonian equations in the planar, elliptical restricted three-body problem with the planet and the pebble orbiting the primary, as in Chanut et al. (2008). The initial position of planet is always taken at its pericentre, and the pebbles are in a ring with a width of 10 to 30 Hill radii (RHill = (μ2/3)1/3 − → RHill ≈ 0.07 for μ2 = 10-3).
At a later stage of planet formation, we know that tidal forces due to the planet open a gap in the disk, typically when the planet reaches a mass close to the mass of Neptune. We choose four values of the planet mass to better cover the ultimate stage of its accretion. We adopt μ2 = 10-4 for the initial mass up to μ2 = 10-3, the actual mass of Jupiter. The initial positions of pebbles are arrayed at each 30° in the ring, and the initial velocities are given by the Keplerian velocity. As a pebble migrates towards the planet, it may follow one of several possible paths. It can be trapped in an exterior resonance with or without a close encounter with the planet. It can also cross the orbit of the planet and continue its migration toward the primary body. Alternatively, the encounter could capture the pebble in a stable libration within a 1:1 mean motion resonance or allow it to collide with the planet and increase the planetary mass. The simulation time is approximately 105 units of time, or approximately 16 000 planetary orbital periods, which is sufficient for the pebbles to reach their final state.
For the gap parameter, we chose values that represent two different decrease functions of the density in the centre of the gap, one presented by Peale (1993) with b = 0.1, 0.25, 0.5, and 0.9 when Jupiter reaches its current mass and the other presented by Lubow (1999) with b = 0.1, 0.3, 0.6, and 0.99. If the pebble continues to orbit the primary body with a semi-major axis within 1 RHill around the orbit of the secondary body, then it is assumed to be trapped in a 1:1 resonance. As in Chanut et al. (2008), we chose two cutoff collision radii, (<0.005 RHill) and (<0.05 RHill). If the pebble comes too close to the secondary body’s centre (collision radius), then the integration is stopped, and a collision is assumed. Similarly, if the pebble’s semi-major axis aP becomes smaller than 0.8, the inferior limit, the integration is stopped.
Theoretically, by considering the dynamical drag effects on a three-body problem, Murray (1994) showed that L4 and L3 move and disappear when 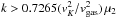 . For example, if vgas/vK = 0.005 and μ2 = 10-4, all of the values of the gas drag parameter higher than k ≈ 2.9 satisfy this condition. We take the lower values of k from 2.5 for μ2 = 10-4 up to 25 for μ2 = 10-3 with the same intervals as our previous work (Chanut et al. 2008). These values of k characterise the size of the pebble: Rp ≈ 3 m for k = 2, 5 and Rp ≈ 30 cm for k = 25 at a Jupiter distance from the Sun. The planets in eccentric orbits are believed to begin their formation in nearly circular orbits because of strong eccentricity damping in the protoplanetary disk and their orbits thus later remain nearly circular (i.e., with eccentricity e2 ≤ 0.1; Lissauer 1993, 1995). For this reason, we increase the eccentricity of the planet up to about 0.1 in comparison with the ultimate value (0.07) taken by Kary & Lissauer (1995) and Chanut et al. (2008) to show what occurs in this interval.
. For example, if vgas/vK = 0.005 and μ2 = 10-4, all of the values of the gas drag parameter higher than k ≈ 2.9 satisfy this condition. We take the lower values of k from 2.5 for μ2 = 10-4 up to 25 for μ2 = 10-3 with the same intervals as our previous work (Chanut et al. 2008). These values of k characterise the size of the pebble: Rp ≈ 3 m for k = 2, 5 and Rp ≈ 30 cm for k = 25 at a Jupiter distance from the Sun. The planets in eccentric orbits are believed to begin their formation in nearly circular orbits because of strong eccentricity damping in the protoplanetary disk and their orbits thus later remain nearly circular (i.e., with eccentricity e2 ≤ 0.1; Lissauer 1993, 1995). For this reason, we increase the eccentricity of the planet up to about 0.1 in comparison with the ultimate value (0.07) taken by Kary & Lissauer (1995) and Chanut et al. (2008) to show what occurs in this interval.
5. Results
5.1. General distribution of the pebbles
In a previous paper (Chanut et al. 2008), we presented numerical results on trapping in a 1:1 mean motion resonance, collisions, crossings, and other events (such as external resonances) related to the dynamics of pebbles under the influence of a planet in a unperturbed nebular disk (without gap). “Crossings” refers to the pebbles that cross the planetary orbit. We listed the percentage of events for two different cutoff collision radii, 0.005 RHill and 0.05 RHIll. These two collision radii correspond to the distances of 3.5 and 35 Jupiter radii. Kary & Lissauer (1997) chose the same values, which are lower than the limit presented by Ormel & Klahr (2010), bgf = 0.06 RHIll, where bgf is the limit radius bellow which there is no trapping in a 1:1 resonance (co-orbital). Moreover, if a circumplanetary disk is considered with a high-density core surrounding the central planet (D’Angelo et al. 2002), the critical radius is where the material inflow to the planet is almost the same, 0.06 RHIll (≈40 Jupiter radii). To understand the results of the present work (a nebular disk with a gap), it is instructive to see the results from Chanut et al. (2008) (a unperturbed nebular disk). A summary of the results of Chanut et al. (2008) is shown in Table 1. The distribution considers several mass ratios of the planet and two cutoff collision radii. In this case, the existence of a nebular gap was not considered. In a unperturbed disk, the crossings dominate the results, with a detectable difference depending on the cutoff radius, and the collision radii determine the accretion percentage.
Distribution of trapping in a 1:1 resonance, collisions, crossings, and trappings that are MMRs or gap trappings due to the equality between the gas disk and pebble angular velocities.
As discussed in the previous section, a planet with a mass ratio μ2 of the order of 10-4 (≈ 0.1 MJ) opens a gap in the density distribution of the nebula disk. The dynamic effects of the gap on the pebble that were generated in our numerical simulations are presented in Table 2. The distribution considers different mass ratios of the planet and two cutoff collision radii. There are no more trappings in a 1:1 resonance (co-orbital) for a nebular gap with very low eccentricity of the planet (less than 0.07). If we consider the gap in the nebula, the collisions represent approximately 40% when the gap is weak (b < 0.3), and when the gap is strong (b ≥ 0.5) there is much more material trapping in the gap: it reaches more than 90%. Table 2 also shows that the accretion rate no longer depends on the cutoff collision radius chosen. Paardekooper (2007) shows that the mass accretion decreases and stops after a few hundred orbital periods for a planet of 1 MJ in a circular orbit. However, we found that it still occurs for an eccentric planet, even for a planet in a very low eccentric orbit (0 < e2 ≤ 0.07). The higher nebular gap density increases the material trapped by gap significantly, and consequently, there is a decrease in the quantity of material that crosses the planet, as shown in the case of μ2 = 6 × 10-4, whose collisions and crossings represent a total of 7% for b = 0.5 and 1% for b = 0.6.
Distribution of trapping in a 1:1 resonance, collisions, crossings, and trappings that are MMRs or gap trappings due to the equality between the gas disk and pebble angular velocities.
 |
Fig. 3 Temporal evolution of the semi-major axis a); eccentricity b); and pebble-gas relative velocity c) of a pebble in a gap trapping. This case considers μ2 = 3 × 10-4, e2 = 0.105, k = 165, and b = 0.3. A gap trapping occurs when the pattern speed matches the angular velocity of the gas (Fig. 2b). |
The eccentricity growth of embedded planets associated with deep annular gaps is discussed by Artymowicz (1992), Lin & Papaloizou (1993), and Goldreich & Sari (2003). Therefore,we extend our simulations to consider a planet with an eccentricity from 0.07 up to 0.1, and the results are presented in Table 3. The distribution considers different mass ratios of the planet and two cutoff collision radii. A low eccentricity (greater than 0.07) favours the accretion rate where 17% of the pebbles collide with a planet with Jupiter’s actual mass, while no eccentricity of the planet orbit favours the accretion rate in an unperturbed disk (Kary & Lissauer 1995). Table 3 shows that the collisions represent yet 37% for b = 0.6 and the higher numbers of collisions occur when the coefficient of the reduction of the gas density in the gap is b = 0.3. The changes in the behaviour of the pebbles are confirmed in Appendix A when the planet eccentricity grow from zero to the maximum value of 0.105 (Table A.1). Another interesting fact is that crossings to the inner disk continue at a very low rate, and trappings in 1:1 resonances (co-orbital) when the gap is still weak (b = 0.1) reappear for planetary eccentricities above 0.07. Examples of trappings in the 1:1 resonance with two planetary eccentricities are presented in Appendix B.
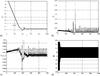 |
Fig. 4 Temporal evolution of the semi-major axis a); eccentricity b); pebble-gas relative velocity c), and resonant angle d) of a pebble trapped in a 6:5 mean motion resonance with the planet. This case considers μ2 = 3 × 10-4, e2 = 0.1, k = 50, and b = 0.3. |
5.2. Resonances
The low accretion rate lies in the mechanism of resonance trapping (Weidenchilling & Davis 1985), where inward moving pebbles are captured in mean motion resonances (MMRs). More recently, Paardekooper (2007) has shown that pebbles in a Stokes gas drag regime could become trapped in MMRs in unperturbed disks (without gap). However, Fouchet et al. (2007) state that accumulation of pebbles closer to the gap edge, which is formed by high-mass planets, is unlikely to be associated with planetary mean motion resonances. The analysis of our results shows that two different phenomena of resonance occur. We refer to the first one as gap trapping. This resonance is a response of the pebbles to the gas density structure (maximum pressure) near the outer edge of the gap. It occurs where the gas velocity is close to the Keplerian velocity value (see Fig. 2b). In this way, a suppression of the headwind and the associated inward drift occur. Figure 3 illustrates the behaviour of a pebble, where the mean pebble-gas relative velocity (Fig. 3c) is nearly cancelled due to the gas pressure structure of the gap and its associated angular velocity. The second resonance phenomenon is due to the commensurability between the mean motions of the pebble and the planet (Murray & Dermott 1999). Such resonances still act against the gas pressure structure of the gap to slow and cancel the inward drift. A pebble trapped in a 6:5 mean motion resonance is presented in Fig. 4, with a planetary mass of 0.3 MJ on an eccentric orbit, e2 = 0.1. The amplitude of the resonant angle, ϕ, is approximately 120° (Fig. 4d). Thus, resonant perturbations that are directed away from the planet balance the drag force that moves the pebble inward. As evidence, Fig. 4c shows that the mean relative velocity between the pebble and the gas remains positive. In the case of gap trapping, it is negative; see Fig. 3c. Now, focusing on the gap trappings, we find that the resonant semi-major axis depends on the planet size. Figure 2 was derived from Eq. (10), and it indicates that, for larger planets and greater b, the angular velocity of the gas equals the Keplerian velocity farther from the planet. To verify this conclusion, we performed some simulations, and the results are presented in Figs. 5 and 6. For the sake of simplicity, we adopted e2 = 0. Figure 5 shows that the inward drift of the pebble stops closer to the gap edge for a planet of 1 MJ, while a planet with 0.3 MJ captures the pebble closer to the planet. Figure 6 shows that pebbles with a small size are highly coupled to the gas, and the motion is dominated by gas drag. Therefore, these small pebbles adhere to the gas velocity, which slows the inward drift, as shown in the temporal evolution of the semi-major axis. On the other hand, the motion of the pebbles that are more decoupled from the gas is more perturbed by gravitational interactions with the planet. The size of the pebble on the right hand side of Fig. 6 is ten times larger than the one to the left, and the amplitude of libration of its eccentricity is larger by a factor of 5.
In unperturbed disks (without a gap), a planet on a circular orbit is statistically more likely to capture pebbles in mean motion resonances. However, a planet with an eccentric orbit exerts a torque on the disk (Goldreich & Tremaine 1980) that increases the pebble eccentricity and enlarges the feeding zone. The chance that the pebble has a close encounter with the planet is higher. The close encounters can trap them in a 1:1 resonance (co-orbital) or remove them toward the inner disk (Kary & Lissauer 1995; Chanut et al. 2008). However, when the planet clears an annular gap in the disk, as is done in the present work, the gap trappings dependence on the planetary eccentricity is weak when the planet reaches a mass higher than 0.3 MJ (see Fig. 7). Nevertheless, the behaviour of the distribution of the resonances for a 0.1 MJ planet is the same as that for a unperturbed disk. For example, for μ2 = 10-4, the resonances are approximately 24% when e2 = 0 and 5% when e2 = 0.1. For μ2 = 10-3, the gap trappings are approximately 6% when e2 = 0 and 5% when e2 = 0.1. In fact, as we diskussed before, the gap trappings must dominate the motion of the pebbles when the planet reaches half of Jupiter’s present mass. We can generally state that the amount of pebbles trapped in these resonances is weakly dependent on the planetary eccentricity, while the MMRs are strongly dependent on the distance from the planet and eccentricity (Kary & Lissauer 1995).
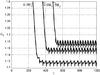 |
Fig. 5 Temporal evolution of the semi-major axis of pebbles trapped by gap for different masses of the planet. In this case, k = 250 for the pebble and the planet is in a circular orbit (e2 = 0). |
 |
Fig. 6 Temporal evolution of the semi-major axis (top) and eccentricity (bottom) of two pebbles trapped by gap. In this case μ2 = 10-3 for the planet in a circular orbit (e2 = 0) and b = 0.99. The value of the gas drag parameter is k = 500 (s = 1.5 cm) on the left side and k = 50 (s = 15 cm) on the right side. |
5.3. Planetary accretion
The role of the eccentricity in the planetary accretion has been emphasised by Kary & Lissauer (1995) in a unperturbed disk for planets with a mass <1 M⊕. Statistically, they showed that, for a nebula without gap, the impact probability decreases exponentially for a planetary eccentricity e2 ≤ 0.028 and is constant for values of 0.028 ≤ e2 < 0.07. In Chanut et al. (2008), we extended the study to other mass ratios, and the tendency is for the impact probability to be constant and not depend on the eccentricity when the planet reaches 0.1 MJ. However, Paardekooper & Mellema (2006) show in 2D simulations of gas and dust with the presence of a planet of ≥ 0.1 MJ that the tendency of the dust accretion, in the circular case, is to stop, and more gas is accreted in comparison to solids. This phenomenon also occurs for a planet of 1 MJ (Paardekooper 2007), where the accretion rate of the amount of pebbles is one order of magnitude below the gas accretion after 500 orbits, which makes further dust accretion negligible. In Appendix C, we show a collision test of a pebble with a large planet on an eccentric orbit. Because the planetary eccentricity promotes close encounters that cause the amplitude of librations to increase, the pebble collide with the planet. In the case of a planet on a circular orbit, the close encounters do not occur, and the pebble remains in the resonance (Fig. 6). To compare, our results of the collisions rates per eccentricity for each planetary mass are shown in Fig. 8. For a weak gap (μ2 = 10-4 or 0.1 MJ), the distribution of the collision rates is similar to our previous results in a unperturbed disk (Chanut et al. 2008). If the gap becomes stronger, the distribution of the collision rates varies with planetary eccentricity. For example, there is no more accretion in the circular case when b ≥ 0.25 (0.3 MJ), and the accretion rate is maximum when e2 = 0.04. When b ≥ 0.3 (Fig. 8b) the maximum rate occurs for e2 = 0.04. Furthermore, when μ2 > 0.5 MJ, the collision rate begins for an eccentricity value e2 near the actual value of Jupiter (0.05) and increases exponentially for a value higher than 0.07. Thus, we show that the non-accretion found by Paardekooper (2007), when e2 = 0, continues for orbits with very low eccentricity.
On the other hand, Paardekooper (2007) has studied the size of the pebbles that accrete onto the planet. In contrast to Kary et al. (1993), who considered low-mass planets that do not disturb the disk, he concluded that only pebbles with 1 cm ≤ s ≤ 1 m for 1 MJ and 10 cm ≤ s ≤ 10 m for 0.1 MJ accrete onto the planet at a higher rate than the gas. Pebbles with s ≥ 10 m are sufficiently decoupled from the gas and the accretion rate is therefore very low. As discussed in Sect. 4, we can calculate the pebble size as a function of the drag parameter k. Because we use the same gas parameters as Malhotra (1993) and Kary & Lissauer (1995), the transition regime occurs for a pebble size of a few centimetres. The behaviour of the collision distribution relative to the gas drag parameter k is shown in Fig. 9. The distribution of size for each planetary mass ratio is in the range defined in Sect. 4. The collision rate generally decreases for high values of k. For 0.1 MJ, the maximum number of collisions occurs for pebbles in the range of sizes of 37.5 cm ≤ s < 75 cm or for k from 10 to 20. For greater planetary masses (0.3 MJ − 1 MJ), the maximum rate of collision occurs for higher k. However, the optimal size increases when the planetary mass increases from k = 250 or s = 3 cm for 0.3 MJ up to k = 50 or s = 15 cm for 1 MJ. Moreover, the collisions stop for k > 400 because the pebbles with this size (s ≈ 2 cm) adhere very well to the gas and are not very perturbed by the gravity of the planet. This value of k makes close approaches difficult even for a planet of 1 MJ with a high eccentricity (0.1). In Fig. 10, we use two models of nebular decrease of the density for all pebble simulations: the weaker model is from Peale (1993) (Fig. 10a), and the other, stronger model is from Lubow et al. (1999) (Fig. 10b). We note that the dominance of the collisions occur for a lower value of the planetary eccentricity (e2 ≤ 0.04) in Fig. 10a than in Fig. 10b (e2 ≥ 0.05). However, the collision rate decreases and equals the resonance rate to eventually dominate and increase exponentially for an eccentricity of e2 ≥ 0.07. In the other case (Fig. 10b), the collision rate does not decrease but increases exponentially for the same eccentricity, e2 ≥ 0.07. These new interesting results show that a moderate planetary eccentricity reverses the cessation of the accretion of pebbles onto high-mass planets. In this way, the stronger the gap density of the gas (e.g. Lubow et al. 1999; D’Angelo, Henning & Kley 2003a; Paardekooper 2007), the higher the planetary eccentricity must be to increase planetary accretion when its mass is near Jupiter’s current value.
 |
Fig. 7 Distribution of pebbles captured by gap or resonances as a function of the eccentricity of the planet for each mass ratio. |
6. Discussion
Currently, we know that over half of the extrasolar planets observed beyond 0.1 AU have eccentricities greater than 0.3. Theorists have suggested numerous mechanisms to excite the orbital eccentricity of giant planets (Artymowicz & Lubow 1996; Goldreich & Sari 2003; Ford & Basio 2008; Moorhead & Adams 2005, 2008). However, only Patterson (1987) and Kary & Lissaeur (1995) have studied the effect of a nonzero eccentricity of the planetary orbit on resonance trapping and accretion. In Chanut et al. (2008), we extended the study for larger planets. However, these studies were only valid for a disk that is unperturbed by the planet. In this paper, we have focused on planets of relatively high mass that open a gap density in the disk.
 |
Fig. 8 Distribution of the collision rates as a function of the planetary eccentricity for each mass ratio. In a), the distribution of the gap coefficient is b = 0.1, 0.25, 0.5, 0.9 (Peale 1993) and, in b), b = 0.1, 0.3, 0.6, 0.99 (Lubow et al. 1999). |
Following Kary et al. (1993), we have shown in a previous work (Table 1) that pebbles have a significant chance to be transferred to interior orbits rather than being accreted to the planet in a disk without a gap. When the planet is massive enough to induce a significant pressure gradient in the disk and the planet is in circular orbit (e2 = 0), the pebbles will be trapped in resonances, and accretion will become insignificant (Paardekoper 2007). In Table 2, we have shown that this result may occur even with a planet on a very low eccentricity orbit (e2 ≤ 0.07) where 99% of the pebbles are trapped by a gap. Figure 4 shows that the mean motion resonances exist for a planet of 0.3 MJ, but, as Fouchet et al. (2007) suggest, the majority of these trappings are due to the pressure maxima gradient in the outer edge of the gap. In fact, Fig. 3c shows that the super-Keplerian velocity of the disk stops the inward drift of the pebbles. We find that the position of such resonances depends on the gas pressure profile in the gap due to the planetary mass (see Fig. 5), and the eccentricity pumping on the pebble size when the planetary gravity dominates the gas drag (see also Fig. 6).
 |
Fig. 9 Distribution of the collisions as a function of the gas drag parameter k for each mass ratio. The highlight of the figure on the top to the right shows the distribution of the collisions with 1 MJ for k ≤ 100. |
On the other hand, it has been shown (Klahr & Kley 2006) that accretion stops after hundreds orbits in non-viscous 2D simulations of gap openings for the circular case (e2 = 0). Paardekooper & Mellema (2006) used 2D simulations of gas and dust with the presence of a planet (≥ 0.1 MJ), to show that the tendency of the dust accretion in the circular case is to stop, and much more gas can be accreted compared to solids. This result also occurs for a planet of 1 MJ (Paardekooper 2007), where the accretion rate of the pebbles is one order of magnitude below that of gas accretion after 500 orbits, which makes further dust accretion negligible. However, it has long been assumed that planets form in nearly circular orbits because of the strong eccentricity damping in the protoplanetary disk, and that their orbits later remain nearly circular (i.e., with an eccentricity of e2 ≤ 0.1; Lissauer 1993, 1995). For this reason, in this work, we have focus on simulating planets with e2 ≤ 0.1. In this way, Kary & Lissauer (1995) showed the impact probability in a unperturbed disk (without gap) for planets smaller than 1 M⊕, in eccentric orbits. Their results were that the impact probability decreases exponentially for a planetary eccentricity ≤0.028 and is constant for values of 0.028 ≤ e2 < 0.07. However, according to our results (with a gap), when μ2 > 0.5 MJ, the collisions rate begins for an eccentricity value e2 higher than 0.04 and increases exponentially for a value over 0.07. Because the gap density of the gas is stronger, the planetary eccentricity must be higher to increase the material accreted onto the planet when its mass is over 0.5 MJ (see also Figs. 8 and 10). Our results have also shown that a planet with a moderate orbital eccentricity (e2 > 0.05) crosses the layer of the pebbles trapped in resonance. Thus, the formation of planetesimals due to the gravitational collapse of the dense pebble layer (Lyra et al. 2009) may not occur with planets on an eccentric orbit. However, by increasing their eccentricities, the pebbles may grow due to collisions between themselves.
We have neglected the self-gravity of the disk. Theoretically, Goldreich & Sari (2003) defined pressure-dominated disks as disks with Kcr ≪ 1 and self-gravity-dominated disk as those with Kcr ≫ 1 where Kcr = (MD/M⊙)(r/H)2. In the model adopted here, Kcr = 1 and, if we diminish the scale height, we are only very slightly in the self-gravity regime.
 |
Fig. 10 Distribution of the collisions and gap resonances rates of the whole set of pebble simulations as a function of the planetary eccentricity. In a), the distribution of the gap coefficient is b = 0.1,0.25,0.5,0.9, and in b), b = 0.1,0.3,0.6,0.99. |
In protostellar disks smaller than the Hill radius of a Jupiter-mass planet, the gas might be at least temporarily trapped in quasi-two-dimensional horseshoe orbits (Goldreich & Sari 2003). D’Angelo, Henning & Kley (2003a) notes that this is the effect of the material lingering around Lagrangian points L4 and L5. With a scale height H/r of approximately 0.04, we can expect that more material will be trapped in the co-orbital region and may collide with the planet or be captured by the planet as a satellite, which does not occur with a higher scale height (0.1). We will investigate these much flattened disks in a future work.
7. Summmary and conclusion
We investigated the dynamics of pebbles interacting with a planet in an orbit that may be eccentric. The standard model of the protostellar disk and the simulation techniques considered the particle phase under gas drag. The model has a prescribed gap around the location of the planet orbit, which is expected for a giant planet with a mass in the range of 0.1–1 Jupiter masses. The angular velocity of the disk was determined by an appropriate balance between the gravity and the centrifugal and pressure forces, such that it is sub-Keplerian in regions with a negative radial pressure gradient and super-Keplerian when the radial pressure gradient is positive. The initial conditions have placed the pebbles with sizes in the range of 1 cm to 3 m in a ring outside the giant planet at distances between 10 and 30 planetary Hill radii. The main goal of this work was to determine the fractions of pebbles that collide with the planet, become trapped in exterior locations, become trapped in a 1:1 resonance (co-orbital), or migrate to the inner disk after 16 000 orbital periods of the planet.
We found that there is no trapping in 1:1 resonance (co-orbital) for very low planetary eccentricities (e2 < 0.07). We showed that the trappings in exterior resonances in their majority are because the angular velocity of the disk is super-Keplerian in the part of the disk gap outside the planetary orbit, so the inward drift is stopped. The value of the resonant semi-major axis depends on the gas pressure profile of the gap (depth) and is located farther from the planet (a = 1.2) when the depth of the gap is maximal (1 MJ).
We found that a planet on an eccentric orbit interact with the pebble layer formed by these resonances. Collisions occur and become important for a planetary eccentricity near Jupiter’s actual value (e2 = 0.05). We showed that the sizes of the pebbles that collide with the different planetary masses agree with those found by Paardekooper (2007) but, due to the eccentricity pumping of the larger pebbles, less coupled to the gas in the region where the planetary gravity dominates the gas drag.
Online material
Appendix A: Behaviour of the pebbles related to the planet mass and eccentricity
The behaviour of the pebbles shown in Tables 2 and 3 is presented here with regards to eccentricity changes. We have chosen six specific values of the planet eccentricity from zero up to the maximum value 0.105 for each mass ratio of the planet. The distribution of the gap coefficient is b = 0.1;0.3;0.6;0.99 (Lubow et al. 1999). The accretion stop for very low values of the planet eccentricity when the planet reaches a mass larger than 0.3 MJ. For the maximum value (e = 0.105) the accretion represents approximately 30% and only a little part crosses the planet orbit.
Distribution of trapping in a 1:1 resonance, collisions, crossings and trappings related to the planet eccentricity.
Appendix B: Trappings in the 1:1 resonance
In Fig. B.1, two examples are shown to compare the time variations of the semi-major axis, eccentricity and longitude of a pebble in the case of the existence of an annular gap in the nebula. The behaviour of the longitude shows that the equilibrium point L5 has not moved forwards. Peale (1993) showed that the reduction of the surface mass density can drive the stationary points back to ± 60° in the circular case. On the other hand, Namouni & Murray (2000), in the case without gas, have suggested that the planetary eccentricity has a reversal effect relative to the drift of the equilibrium points due to the gas (Murray 1994). In a previous work (Chanut et al. 2008), without considering a gap density, we have verified the shift in the position of the equilibrium point. However, for a planetary eccentricity near 0.1 and a gap density in the disk nebula, we show that a position shift does not occur (Fig. B.1). Furthermore, other trappings have been investigated with the same values of k and e2 and show the same tendency as the oscillations of the eccentricity and the longitude of the pebbles trapped in 1:1 resonances (co-orbital), which decrease when the eccentricity of the planet increases. The planetary eccentricity must have had an important role in the origin and the stability of the Trojans and other co-orbital bodies.
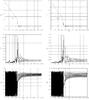 |
Fig. B.1 Temporal evolution of the semi-major axis (top), eccentricity (middle) and longitude (bottom) of a pebble captured in co-orbital motion. In this case μ2 = 10-4 is the mass ratio, k = 2.5 and b = 0.1. The initial conditions are r0 = 1.74 for the pebble and e2 = 0.105 for the planet in the left column and r0 = 1.77 and e2 = 0.091 in the right column. |
Appendix C: Collision test of a pebble with a planet on an eccentric orbit
The early behaviour of the pebble is similar to that shown in Fig. 3. However, Fig. C.1 show that the motion of pebbles that are more decoupled from the gas is more perturbed by gravitational interactions with the planet. Because the planetary eccentricity promotes close encounters that cause the amplitude of librations to increase, the pebble collide with the planet. In the case of a planet on a circular orbit, the close encounters not occur and Paardekooper & Mallema (2006) showed in 2D simulations of gas and dust with the presence of a planet of ≥0.1 MJ that the tendency of the dust accretion is to stop. This phenomenon also occurs for a planet of 1 MJ (Pardekoopeer 2007).
 |
Fig. C.1 Temporal evolution of the semi-major axis a), eccentricity b), relative velocity with the gas c) and radial distance from the planet d) of a pebble that collides with the planet. This case considered μ2 = 3 × 10-4, e2 = 0.07, k = 50 and b = 0.3. |
Acknowledgments
This work was supported by CAPES, CNPq, and Fapesp. We also would like to thank the referee for comments and suggestions that significantly improved this paper.
References
- Bate, M. R., Lubow, S. H., Ogilvie, G. I., & Miller, K. A. 2003, MNRAS, 341, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S., Sargent, A., Chini, R. S., & Güsten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Bryden, G., Chen, X., Lin, D. N. C., Nelson, R. P., & Papaloisou, J. C. B. 1999, ApJ, 514, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Cassen, P., & Moosman, A. 1981, Icarus, 48, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Chanut, T., Winter, O. C., & Tsuchida, M. 2008, A&A, 481, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Henning, Th., & Kley, W. 2002, A&A, 385, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2003a, ApJ, 599, 548 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., Kley, W., & Henning, T. 2003b, ApJ, 586, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., & Rasio, F. A. 2008, ApJ, 686, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Fouchet, L., Maddison, S. T., Gonsalez, J., & Murray, J. R. 2007, A&A, 474, 1037 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldreich, P., & Sari, R. 2003, ApJ, 585, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Kary, D. M., & Lissauer, J. J. 1995, Icarus, 117, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kary, D. M., Lissauer, J. J., & Greenzweig, Y. 1993, Icarus, 106, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., D’Angelo, G., & Henning, T. 2001, ApJ, 547, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Kusaka, T., Nakano, T., & Hayashi, C. 1970, Prog. Theor. Phys., 44, 1580 [NASA ADS] [CrossRef] [Google Scholar]
- Lagrange, J. L. 1889, Mécanique Analytique (Paris: Gauthier-Villars & fils), 4th edn., 2 vols [Google Scholar]
- Lin, D. N. C., & Papaloisou, J. C. B. 1980, MNRAS, 191, 37 [NASA ADS] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. C. B. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. C. B. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine (Tucson: Univ. Arizona Press), 749 [Google Scholar]
- Lissauer, J. J. 1987, Icarus, 69, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J. 1993, ARA&A, 31, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J. 1995, Icarus, 114, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., Seibert, M., & Artymowicz, P. 1999, AJ, 526, 1001 [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2009, A&A, 493, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malhotra, R. 1993, Icarus, 106, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., & Sholl, H. 1997, Icarus, 131, 41 [Google Scholar]
- Moorhead, A. V., & Adams, F. C. 2005, Icarus, 178, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Moorhead, A. V., & Adams, F. C. 2008, Icarus, 193, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D. 1994, Icarus, 112, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge Univ. Press) [Google Scholar]
- Muto, T., & Inutsuka, S. 2009, ApJ, 695, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Namouni, F., & Murray, C. D. 2000, Celest. Mech, 76, 131 [Google Scholar]
- Nelson, A., & Benz, W. 2003a, ApJ, 589, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, A., & Benz, W. 2003b, ApJ, 589, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J. C. B., & Lin, D. N. C. 1984, ApJ, 285, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., Nelson, R. P., Kley, W., Masset, F. S., & Artymowicz, P. 2006 [arXiv:astro-ph/0603196v1] [Google Scholar]
- Paardekooper, S. J. 2007, A&A, 462, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., & Mellema, J. 2004, A&A, 425, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S. J., & Mellema, J. 2006, A&A, 453, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patterson, C. W. 1987, Icarus, 70, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Peale, S. J. 1993, Icarus, 106, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Prantl, L. 1952, Essentials of Fluid Dynamics (New York: Hafner Publishing Company), 174 [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Gueth, F., Henning, T., & Kley, W. 2002, ApJ, 566, L97 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Distribution of trapping in a 1:1 resonance, collisions, crossings, and trappings that are MMRs or gap trappings due to the equality between the gas disk and pebble angular velocities.
Distribution of trapping in a 1:1 resonance, collisions, crossings, and trappings that are MMRs or gap trappings due to the equality between the gas disk and pebble angular velocities.
Distribution of trapping in a 1:1 resonance, collisions, crossings and trappings related to the planet eccentricity.
All Figures
 |
Fig. 1 Distribution of surface mass density of the nebula with a reduction in the surface density at the centre of the gap for p = 0. Here, we show two models of nebular parameters (Peale 1993 and Lubow et al. 1999). |
| In the text | |
 |
Fig. 2 Angular velocity of the nebular gas compared to the Keplerian velocity with and without the gap (b = 0) ) versus the radial distribution of the surface mass density. Here we choose to show the effect of the gap on the angular velocity for three values of b from 0.3 to 0.9. |
| In the text | |
 |
Fig. 3 Temporal evolution of the semi-major axis a); eccentricity b); and pebble-gas relative velocity c) of a pebble in a gap trapping. This case considers μ2 = 3 × 10-4, e2 = 0.105, k = 165, and b = 0.3. A gap trapping occurs when the pattern speed matches the angular velocity of the gas (Fig. 2b). |
| In the text | |
 |
Fig. 4 Temporal evolution of the semi-major axis a); eccentricity b); pebble-gas relative velocity c), and resonant angle d) of a pebble trapped in a 6:5 mean motion resonance with the planet. This case considers μ2 = 3 × 10-4, e2 = 0.1, k = 50, and b = 0.3. |
| In the text | |
 |
Fig. 5 Temporal evolution of the semi-major axis of pebbles trapped by gap for different masses of the planet. In this case, k = 250 for the pebble and the planet is in a circular orbit (e2 = 0). |
| In the text | |
 |
Fig. 6 Temporal evolution of the semi-major axis (top) and eccentricity (bottom) of two pebbles trapped by gap. In this case μ2 = 10-3 for the planet in a circular orbit (e2 = 0) and b = 0.99. The value of the gas drag parameter is k = 500 (s = 1.5 cm) on the left side and k = 50 (s = 15 cm) on the right side. |
| In the text | |
 |
Fig. 7 Distribution of pebbles captured by gap or resonances as a function of the eccentricity of the planet for each mass ratio. |
| In the text | |
 |
Fig. 8 Distribution of the collision rates as a function of the planetary eccentricity for each mass ratio. In a), the distribution of the gap coefficient is b = 0.1, 0.25, 0.5, 0.9 (Peale 1993) and, in b), b = 0.1, 0.3, 0.6, 0.99 (Lubow et al. 1999). |
| In the text | |
 |
Fig. 9 Distribution of the collisions as a function of the gas drag parameter k for each mass ratio. The highlight of the figure on the top to the right shows the distribution of the collisions with 1 MJ for k ≤ 100. |
| In the text | |
 |
Fig. 10 Distribution of the collisions and gap resonances rates of the whole set of pebble simulations as a function of the planetary eccentricity. In a), the distribution of the gap coefficient is b = 0.1,0.25,0.5,0.9, and in b), b = 0.1,0.3,0.6,0.99. |
| In the text | |
 |
Fig. B.1 Temporal evolution of the semi-major axis (top), eccentricity (middle) and longitude (bottom) of a pebble captured in co-orbital motion. In this case μ2 = 10-4 is the mass ratio, k = 2.5 and b = 0.1. The initial conditions are r0 = 1.74 for the pebble and e2 = 0.105 for the planet in the left column and r0 = 1.77 and e2 = 0.091 in the right column. |
| In the text | |
 |
Fig. C.1 Temporal evolution of the semi-major axis a), eccentricity b), relative velocity with the gas c) and radial distance from the planet d) of a pebble that collides with the planet. This case considered μ2 = 3 × 10-4, e2 = 0.07, k = 50 and b = 0.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


