| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118629 | |
| Published online | 26 March 2013 | |
Online material
Appendix A: Behaviour of the pebbles related to the planet mass and eccentricity
The behaviour of the pebbles shown in Tables 2 and 3 is presented here with regards to eccentricity changes. We have chosen six specific values of the planet eccentricity from zero up to the maximum value 0.105 for each mass ratio of the planet. The distribution of the gap coefficient is b = 0.1;0.3;0.6;0.99 (Lubow et al. 1999). The accretion stop for very low values of the planet eccentricity when the planet reaches a mass larger than 0.3 MJ. For the maximum value (e = 0.105) the accretion represents approximately 30% and only a little part crosses the planet orbit.
Distribution of trapping in a 1:1 resonance, collisions, crossings and trappings related to the planet eccentricity.
Appendix B: Trappings in the 1:1 resonance
In Fig. B.1, two examples are shown to compare the time variations of the semi-major axis, eccentricity and longitude of a pebble in the case of the existence of an annular gap in the nebula. The behaviour of the longitude shows that the equilibrium point L5 has not moved forwards. Peale (1993) showed that the reduction of the surface mass density can drive the stationary points back to ± 60° in the circular case. On the other hand, Namouni & Murray (2000), in the case without gas, have suggested that the planetary eccentricity has a reversal effect relative to the drift of the equilibrium points due to the gas (Murray 1994). In a previous work (Chanut et al. 2008), without considering a gap density, we have verified the shift in the position of the equilibrium point. However, for a planetary eccentricity near 0.1 and a gap density in the disk nebula, we show that a position shift does not occur (Fig. B.1). Furthermore, other trappings have been investigated with the same values of k and e2 and show the same tendency as the oscillations of the eccentricity and the longitude of the pebbles trapped in 1:1 resonances (co-orbital), which decrease when the eccentricity of the planet increases. The planetary eccentricity must have had an important role in the origin and the stability of the Trojans and other co-orbital bodies.
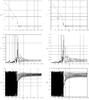 |
Fig. B.1
Temporal evolution of the semi-major axis (top), eccentricity (middle) and longitude (bottom) of a pebble captured in co-orbital motion. In this case μ2 = 10-4 is the mass ratio, k = 2.5 and b = 0.1. The initial conditions are r0 = 1.74 for the pebble and e2 = 0.105 for the planet in the left column and r0 = 1.77 and e2 = 0.091 in the right column. |
| Open with DEXTER | |
Appendix C: Collision test of a pebble with a planet on an eccentric orbit
The early behaviour of the pebble is similar to that shown in Fig. 3. However, Fig. C.1 show that the motion of pebbles that are more decoupled from the gas is more perturbed by gravitational interactions with the planet. Because the planetary eccentricity promotes close encounters that cause the amplitude of librations to increase, the pebble collide with the planet. In the case of a planet on a circular orbit, the close encounters not occur and Paardekooper & Mallema (2006) showed in 2D simulations of gas and dust with the presence of a planet of ≥0.1 MJ that the tendency of the dust accretion is to stop. This phenomenon also occurs for a planet of 1 MJ (Pardekoopeer 2007).
 |
Fig. C.1
Temporal evolution of the semi-major axis a), eccentricity b), relative velocity with the gas c) and radial distance from the planet d) of a pebble that collides with the planet. This case considered μ2 = 3 × 10-4, e2 = 0.07, k = 50 and b = 0.3. |
| Open with DEXTER | |
© ESO, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


