| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 62 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201116551 | |
| Published online | 01 April 2013 | |
The planet search programme at the ESO CES and HARPS⋆,⋆⋆,⋆⋆⋆
IV. The search for Jupiter analogues around solar-like stars
1
Institut für Astrophysik, Georg-August-Universität,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
e-mail: zechmeister@astro.physik.uni-goettingen.de
2
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
3
McDonald Observatory, University of Texas,
Austin, TX
78712,
USA
4
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748
Garching,
Germany
5
Group for Materials Science and Applied Mathematics, School of
Technology, Malmö University, 20506
Malmö,
Sweden
6
Lund Observatory, Lund University, PO Box 43, 22100
Lund,
Sweden
7
Thüringer Landessternwarte Tautenburg (TLS),
Sternwarte 5, 07778
Tautenburg,
Germany
Received:
20
January
2011
Accepted:
13
November
2012
Context. In 1992 we began a precision radial velocity survey for planets around solar-like stars with the Coudé Echelle Spectrograph and the Long Camera (CES LC) at the 1.4 m telescope in La Silla (Chile) resulting in the discovery of the planet ι Hor b. We have continued the survey with the upgraded CES Very Long Camera (VLC) and the HARPS spectrographs, both at the 3.6 m telescope, until 2007.
Aims. In this paper we present additional radial velocities for 31 stars of the original sample with higher precision. The observations cover a time span of up to 15 years and permit a search for Jupiter analogues.
Methods. The survey was carried out with three different instruments/instrument configurations using the iodine absorption cell and the ThAr methods for wavelength calibration. We combine the data sets and perform a joint analysis for variability, trends, and periodicities. We compute Keplerian orbits for companions and detection limits in case of non-detections. Moreover, the HARPS radial velocities are analysed for correlations with activity indicators (CaII H&K and cross-correlation function shape).
Results. We achieve a long-term RV precision of 15 m/s (CES+LC, 1992–1998), 9 m/s (CES+VLC, 1999–2006), and 2.8 m/s (HARPS, 2003–2009, including archive data), respectively. This enables us to confirm the known planetary signals in ι Hor and HR 506 as well as the three known planets around HR 3259. A steady RV trend for ϵ Ind A can be explained by a planetary companion and calls for direct imaging campaigns. On the other hand, we find previously reported trends to be smaller for β Hyi and not present for α Men. The candidate planet ϵ Eri b was not detected despite our better precision. Also the planet announced for HR 4523 cannot be confirmed. Long-term trends in several of our stars are compatible with known stellar companions. We provide a spectroscopic orbital solution for the binary HR 2400 and refined solutions for the planets around HR 506 and ι Hor. For some other stars the variations could be attributed to stellar activity, as e.g. the magnetic cycle in the case of HR 8323.
Conclusions. The occurrence of two Jupiter-mass planets in our sample is in line with the estimate of 10% for the frequency of giant planets with periods smaller than 10 yr around solar-like stars. We have not detected a Jupiter analogue, while the detections limits for circular orbits indicate at 5 AU a sensitivity for minimum mass of at least 1MJup (2MJup) for 13% (61%) of the stars.
Key words: stars: general / planetary systems / techniques: radial velocities / methods: data analysis
Based on observations collected at the European Southern Observatory, La Silla Chile, ESO programmes 50.7-0095, 51.7-0054, 52.7-0002, 53.7-0064, 54.E-0424, 55.E-0361, 56.E-0490, 57.E-0142, 58.E-0134, 59.E-0597, 60.E-0386, 61.E-0589, 62.L-0490, 64.L-0568, 66.C-0482, 67.C-0296, 69.C-0723, 70.C-0047, 71.C-0599, 072.C-0513, 073.C-0784, 074.C-0012, 076.C-0878, 077.C-0530, 078.C-0833, 079.C-0681. Also based on data obtained from the ESO Science Archive Facility.
Appendices are available in electronic form at http://www.aanda.org
Tables of the radial velocities, bisector spans, and
 are available at the CDS via anonymous
ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A78
are available at the CDS via anonymous
ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/552/A78
© ESO, 2013
1. Introduction
The search for extra-solar planets has so far revealed approximately 850 exoplanets1, most of them discovered by the radial velocity (RV) technique. Interestingly, many hot Jupiters have been found, a consequence related to the fact that the RV method as well as the transit method is more sensitive to short period planets. Out of 850 planets discovered so far, 65% have a period shorter than 1 year. Before the discovery of the first extrasolar planet around a solar-like star, the hot Jupiter 51 Peg b (Mayor & Queloz 1995), it was widely expected that planetary systems are in general similar to the solar-system and this was also predicted by most theoretical models as noted by Marcy et al. (2008). In the solar system, Jupiter is the dominant planet amongst all other planets and causes the largest RV amplitude. Therefore surveys were set up to search for planets with masses of 1 MJup and at distances of 5 AU from solar-like stars (e.g. Walker et al. 1995). The regime of Jupiter analogues is still sparsely explored because observations with long time baselines and precise RV measurements are required; e.g. Jupiter orbits the Sun in 12 years and induces an RV semi-amplitude of 12 m/s.
There are many exoplanet search projects e.g. at Lick, AAT (O’Toole et al. 2009; Wittenmyer et al. 2011), Keck (Cumming et al. 2008), ELODIE/SOPHIE (Naef et al. 2005; Bouchy et al. 2009a), CORALIE (Ségransan et al. 2010), and HARPS (Naef et al. 2010; Mayor et al. 2011). These high precision RV projects have discovered a large fraction of the currently known planets and are continuously extending their time baselines. Examples for discovered Jupiter analogues are GJ 777Ab (Naef et al. 2003), a 1.33 MJup planet at 4.8 AU2 around a G6IV star, or HD 154345b (Wright et al. 2008), a 0.95 MJup planet at 4.5 AU around a G8V dwarf (all masses are Msini minimum masses). Two more Jupiter-analogues were also recently reported by Boisse et al. (2012): HD 150706b (2.7 MJup, 7 AU) and HD 222155b (1.9 MJup, 5.1 AU).
The survey described in this paper was begun in 1992 (Endl et al. 2002) with the Coudé Echelle Spectrograph (CES) Long Camera (LC). With the advent of the CES Very Long Camera (VLC) in 1999, it was transferred to this instrument combination, and was continued in 2003 with the HARPS spectrograph. The last observations for this programme were taken in September of 2007, although we have also made use of archival data acquired up to 2009. The survey covers a time span of up to 15 years with RV precisions ranging from 15 m/s down to 2 m/s. A comparable survey was analysed by Wittenmyer et al. (2006) and carried out in the northern hemisphere with the 2.7 m telescope at the McDonald Observatory. It started in 1988 with 24 solar-like stars3 and 7 subgiants. When combined with CFHT data (Walker et al. 1995), it gave an even longer temporal coverage of up to 25 years, albeit with a somewhat lower precision (10–20 m/s).
2. The sample
The original sample of 37 solar-like stars was introduced in detail in Endl et al. (2002). Of these, the monitoring of six stars was stopped: HR 448, HR 753, HR 7373, Barnard’s star, Proxima Centauri, and GJ 433. The first three had been observed temporarily in 1996/97 as once promising metal rich targets, but were soon left out due to limited observing time. The latter three are M dwarfs which were included in a dedicated M dwarf survey with VLT+UVES. For these stars recent and more precise results are published in Zechmeister et al. (2009). So we are left with the 31 stars listed in Table 1 along with some of their properties (spectral type, visual magnitude, distance, and stellar mass).
Targets with their spectral type SpT (Hoffleit &
Jaschek 1991), visual magnitude V (Perryman et al. 1997), distance d (van Leeuwen 2007), secular acceleration
 ,
and stellar mass M.
,
and stellar mass M.
All stars have a brightness of V < 6 mag and spectral types ranging from late F to K. There are two subgiant stars (β Hyi and δ Eri) and two giant stars (HR 3677 and HR 8883) in the sample4.
The sample includes six stars for which planet detections have been claimed. These are HR 506 (Mayor et al.)5, ι Hor (Kürster et al. 2000), ϵ Eri (Hatzes et al. 2000), HR 3259 (Lovis et al. 2006), HR 4523 (Tinney et al. 2011), and recently α Cen B (Dumusque et al. 2012). In Sect. 5 we provide more detailed information on individual objects and we will stress those planet hypotheses.
3. Instruments and data reduction
We used three high resolution spectrographs that are briefly described below with more detail provided for the less known VLC+CES. Table 2 gives an overview of some basic properties of the three instruments.
The three used instruments/configurations with their wavelength reference, chosen spectral coverage and resolving power, and telescope diameter.
3.1. CES + Long Camera
In 1992 the survey started (1992-11-03 to 1998-04-04) with the Coudé Echelle Spectrograph (CES; Enard 1982) and its Long Camera (LC) fed by the 1.4 m Coudé Auxiliary Telescope (CAT) at La Silla (Chile). The CES+LC had a chosen wavelength coverage of 45 Å and a resolution of 100 000 (Table 2). A 2 k × 2 k CCD gathered part of one spectral Echelle order. An iodine gas absorption cell provided the wavelength calibration. More details about the instrument, data analysis, as well as the obtained results can be found in Endl et al. (2002). Table 3 lists the radial velocity results. The median rms is 15.2 m/s when excluding the giants and targets with companions and trends as commented in Table 3 and reflects the typical precision.
Radial velocity results for all targets.
3.2. CES + Very Long Camera
The Very Long Camera (VLC; Piskunov et al. 1997) of the Coudé Echelle Spectrograph (CES) was commissioned at the ESO 3.6 m telescope in La Silla (Chile) in April 1998 and decommissioned in 2007. The VLC was an upgrade of the CES that doubled the resolving power to R = 220 000−235 000 as well as the CCD length so that 80% of the spectral coverage compared to the LC was retained (cf. Table 2). This upgrade together with improved internal stability, and also the larger telescope aperture promised an improvement of the RV precision. For our sample we collected VLC spectra from 1999-11-21 to 2006-05-24.
The VLC was fed by a fibre link from the Cassegrain focus of the 3.6 m telescope. A modified Bowen-Walraven image slicer provided an efficient light throughput at the high resolving power. It redistributed the light from the fibre with a 2′′ aperture via 14 slices to an effective slit width of 0.16′′ and resulted in a complex illumination profile in the spatial direction, i.e. perpendicular to the dispersion axis (Figs. 1 and 2). The right half of a 4 k × 2 k EEV CCD recorded part of one spectral order with the wavelength range of 5376 – 5412 Å. In 2000-06-15 CCD#59 was replaced by CCD#61 and in 2001-11-23 the CES fibre was exchanged.
The CES+VLC employed the same iodine cell as the CES+LC for wavelength calibration. This cell was controlled at a temperature of 50 °C. The RV modelling (Sect. 3.4) requires a high resolution and high signal-to-noise iodine spectrum to reconstruct confidently the instrumental line profile (IP) of the spectrograph. In November 2008 we obtained a laboratory spectrum for our iodine cell with R = 925 000 and S/N ~ 1000 using a Bruker IFS125HR high-resolution Fourier Transform Spectrometer (FTS) at Lund Observatory. A filament lamp was used as a background source. To limit the light from adjacent wavelength regions a set of filters were applied: a coloured glass filter type VG11, a notch-filter to reduce the internal laser light, and a hot mirror to suppress the red spectrum. While the iodine cell laboratory spectrum previously used by Endl et al. (2002) in their analysis of the CES+LC data had only R = 400 000, the new scan ensures an iodine spectrum with a resolution almost 5 times higher than the resolution of the CES+VLC.
 |
Fig. 1 A small section of a VLC raw spectrum (star seen through the iodine cell; broad absorption features are stellar lines whereas narrow lines were introduced by the molecular iodine gas). The 14 slices span 400 pixels. The bright feature to the left near pixel row 2300 is a grating ghost. The area on the left side has a lower bias. The readout register is in the lower right corner of the chip (parallel clocking down, serial clocking to the right). Deeper stellar lines near row 2300 and 2700 have tails to the left and right. The intensity scale is non-linear to bring out the discussed effects. |
 |
Fig. 2 Spatial profile of a VLC spectrum (cross-section for the rows 2400–2410 of the raw spectrum in Fig. 1; linear intensity scale). |
The following properties of the CES+VLC spectra must be considered in the data analysis: the VLC spectra are contaminated by a grating ghost located in the middle of the CCD (Fig. 1) and suffered also from stray light produced by the image slicer. Ripples are visible in the continuum of high S/N (~1000) spectra caused by interference in the fibre. This can be seen, for instance, in flatfield exposures. Also visible in flats are less efficient rows on the chip every 512 pixels, due to a smaller pixel size resulting from the manufacturing process, which affect the wavelength solution. Moreover, as a peculiarity of the CES CCD electronics, a lower bias level is observed to the left of the spectra, caused by an electronic offset that occurs after processing a strong signal. This effect is attributed to the video amplifier electronics and requires the readout of several CCD rows to properly discharge (Sinclair, ESO, 2011, priv. comm.). Hence subsequent CCD rows are affected which may cause systematic spectral line asymmetries and RV shifts depending on the spectral line depth. Moreover, since the iodine lines are weaker, they may not receive the same shift as the stronger stellar lines and cannot correct completely for this effect6.
The spatial profile has a width spanning more than 400 pixels offering a large cross-section for cosmic ray hits (so-called cosmics). For this reason the observing strategy aimed at three consecutive spectra in one night to be able to identify cosmics as outliers. However, we did not use this cosmics detection method because cosmics could also be efficiently identified as deviations from the spatial profile in the optimum extraction.
The VLC spectra were reduced with standard IRAF-tasks including subtraction of the overscan and a nightly master-bias, 2D flat-fielding, scattered light subtraction, and optimum extraction (Horne 1986) which also removes cosmics. The scattered light was defined left and right of the aperture with a low-degree polynomial used to interpolate across the aperture. This was done row-by-row and afterwards “smoothed” in the dispersion direction with a high-order spline to account for the above mentioned features and then as scattered light subtracted from the spectra. Finally, the science spectra were roughly calibrated with a nightly ThAr spectrum to provide an initial guess for the wavelength solution which is later refined with the iodine spectrum in the subsequent modelling process. The whole data reduction process largely removed the artefacts described above, however residual deviations are likely to still exist in the RVs of the VLC data. The typical precision is 9.4 m/s calculated as the median rms in Table 3 for the stars without comments.
3.3. HARPS
With HARPS we monitored our targets from 2003-11-06 to 2007-09-21 (2009-12-19 including archive data). The HARPS spectrograph is described in the literature (e.g. Mayor et al. 2003; Pepe et al. 2004). It is fibre fed from the Cassegrain focus of the 3.6 m telescope and located in a pressure and temperature stabilised environment. An optical fibre sends light from a ThAr lamp to the Cassegrain adapter for wavelength calibration. For the RV computation via cross-correlation with a binay mask 72 Echelle orders ranging from 3800 Å to 6900 Å are available, a region much larger than for the CES.
We made use of the ESO advanced data products (ADP) to complement our time series which sometimes also extended the time base. This archive provides fully reduced HARPS spectra including the final radial velocities processed by the pipeline DRS 7 3.5 (data reduction software). The radial velocities are corrected for the wavelength drift of the spectrograph (if measured by the simultaneous calibration fibre) and the RV uncertainty estimated assuming photon noise 8. The mean RV uncertainties range from 0.2 to 0.8 m/s and do not include calibration errors, guiding errors, and residual instrumental errors. For data analysis a stellar jitter term (≥1.6 m/s) will be added in quadrature (see Sect. 4).
We recomputed with the HARPS DRS some of these archival RVs that suffered in the cross-correlation process from a misadjusted initial RV guess (off by more than 2 km s-1) or from an inappropriate binary correlation mask. A different mask, e.g. K5 instead of G2, can produce RV shifts up to 20 m/s. The publicly available archive data originate from other programs such as short-term asteroseismology campaigns or the HARPS GTO (guaranteed time observations). The latter complemented our data with additional measurements, and in some cases provided a data set that outnumbers our own in terms of number of measurements and time base. We use only data taken in HARPS high accuracy mode (HAM), while we leave out data taken with iodine absorption cell or in high efficiency mode (EGGS, “Extra Good General Spectroscopy”) which uses a different fibre, a different injection method, and no scrambler and has a lower stability and a different zero point. Furthermore, spectra with a signal to noise of S/N < 50 are also left out.
The HARPS data provide an absolute RV scale which is shown in Figs. 19–23 and serves as our references frame into which the other instruments are transferred. Note that relative RV measurements are more precise than the absolute RVs (i.e. more precise than accurate) 9. The median rms in Table 3 is 2.8 m/s for stars without comments. Note that several of our stars are active, so that this value is higher than the precision of 1 m/s usually quoted for HARPS.
To improve the combination of the HARPS and VLC data, spectra were taken in a few nights with both spectrographs immediately after each other making use of an easy switch possible with the common fibre adapter installed in May 2004.
3.4. Details of the RV computation for the CES+VLC data
To compute the RVs of the VLC spectra we used the AUSTRAL code described in Endl et al. (2000) which is based on the modelling technique outlined in Butler et al. (1996). The spectral order was divided into 19 spectral segments (chunks) with a size of 200 pixels (1.8 Å) which we empirically found to yield the optimal RV precision. The reasons could be that for smaller chunks the stellar RV information content becomes too small. For a larger chunk size, on the other hand, probably the assumption that the instrumental profile (IP) is constant over the chunk breaks down, or the discontinuities of the wavelength solution by the mentioned smaller and less efficient pixel rows are more problematic.
The stellar spectrum can be shifted across the CCD by several pixels due to the barycentric velocity of the Earth (calculated with the JPL ephemerides DE200, e.g. Standish 1990) and offsets in the instrument setup. To ensure that the same stellar lines fell in the same chunk, we shifted the chunks to the proper spectral location according to the barycentric correction (1 pixel is ~500 m/s). So instead of having fixed chunk positions with respect to the CCD as originally implemented in the AUSTRAL code, this modification ensures always the same weighting factor for each chunk. The final wavelength solution in each chunk is provided by the iodine lines which record the instrumental drifts and offsets.
Figure 3 illustrates the alignment of the chunks
with respect to the stellar spectrum. This placement of the chunks tries to avoid
splitting up stellar lines between adjacent chunks. As one can see, the chunks contain
only a few deep stellar lines or sometimes none. To quantify this, we calculated the
quality factor Q (Connes 1985;
Butler et al. 1996; Bouchy et al. 2001) for each chunk in a stellar template 10. This factor sums in a flux-weighted way the squared
gradients in a spectrum11, hence measuring its RV
information content. For photon noise, the estimated RV uncertainty is inversely
proportional to Q, i.e.  . Hence, we weight each chunk RV with
Q2 when computing the RV mean. Chunks with
Q < 7 000 were discarded (cf. Fig. 3, right axis). For comparison, the quality factor is
Q = 12 857 for the whole spectral range in Fig. 3 and Q = 67 000 for an iodine spectrum (e.g. the
spectrum of a featureless B-star taken through the iodine cell).
. Hence, we weight each chunk RV with
Q2 when computing the RV mean. Chunks with
Q < 7 000 were discarded (cf. Fig. 3, right axis). For comparison, the quality factor is
Q = 12 857 for the whole spectral range in Fig. 3 and Q = 67 000 for an iodine spectrum (e.g. the
spectrum of a featureless B-star taken through the iodine cell).
For τ Cet (GJ 71; HIP 8102; HR 509; HD 10700) which is known as an RV
constant star (the HARPS data have an rms scatter of ~1.1 m/s HARPS data, Pepe et al. 2011, this work), we achieve with the
CES + VLC a long-term precision of 8.1 m/s (Fig. 19,
Table 3). The internal RV errors of the individual
spectra (~8.8 m/s), calculated as the errors of the mean RV of the chunks
( ), are of the same order as the rms of the
time series implying a fair error estimation.
), are of the same order as the rms of the
time series implying a fair error estimation.
 |
Fig. 3 A VLC spectrum of τ Cet (without iodine cell) and the arrangement of the 200 pixel chunks with their individual Q-factors (blue squares). The intensity maximum of the spectrum is set to unity. The intensity declines to the edges due to instrumental effects (Blaze function). |
3.5. Combining the LC and VLC data
The problem of instrumental offsets, i.e. different radial velocity zero points, occurs when data sets originate from different instruments (e.g. Wittenmyer et al. 2006) or after instrumental changes/upgrades. For instance, an offset of –1.8 m/s was reported by Rivera et al. (2010) after upgrading the Keck/HIRES spectrograph with a new CCD. An offset of only 0.9 m/s was mentioned by Vogt et al. (2010) when combining Keck and AAT data.
As described above we have used three different instruments/instrument configurations and we are also faced with the problem of the instrumental offset. There are basically two different methods for combining the data sets: (1) Simply fitting the offset, i.e. the data sets are considered to be completely independent and the zero points are free parameters in the model fitting. (2) If possible, measuring the offset physically by making use of some known relation between the data sets/instruments to keep the offset fixed.
In fact, we can measure the offset for the LC and VLC data albeit with a limited precision. The LC and VLC spectra were taken through the same iodine cell, i.e. the same wavelength calibrator. Because Endl et al. (2002) calculated the LC RVs with different stellar templates and an iodine spectrum of lower resolution than used in this work, we re-calculated the RVs for all LC spectra with the same VLC stellar template (which is shorter than the LC spectra) and the new iodine cell scan to have the same reference for the LC and VLC. The re-calculated RVs are verified to have a precision similar to the published LC data.
Then we computed the mean of the re-calculated LC and VLC time series. If a star has a
constant RV, one would expect that the means of both time series are the same, i.e. the
offset  within the uncertainties of the means
(σLC and σVLC).
This can be tested with the t-statistics, in particular Welch’s
t-test (for two independent samples with unequal sizes and variances).
We suggest that keeping the offset fixed is valid, if the quantity
within the uncertainties of the means
(σLC and σVLC).
This can be tested with the t-statistics, in particular Welch’s
t-test (for two independent samples with unequal sizes and variances).
We suggest that keeping the offset fixed is valid, if the quantity  (1)is not rejected by the Null-hypothesis. The
parameter s is an estimate for the standard error of the difference in
the means and is calculated from sample variances
(1)is not rejected by the Null-hypothesis. The
parameter s is an estimate for the standard error of the difference in
the means and is calculated from sample variances  and sample sizes
Ni. The variable t
follows a t-distribution with ν degrees of freedom 12. For instance, for | t| > 1.7 and
ν > 30 the difference in the means is significant with a false alarm
probability of FAP < 10%. For some of our stars the FAP for the offset difference is
not significant: δ Eri (64%), ϵ Eri (23%), HR 209 (92%),
and HR 3259 (15%). However, from Fig. 4 it can be
seen that there are also stars having significant offsets leaving doubts whether the
offset can be kept fixed in general.
and sample sizes
Ni. The variable t
follows a t-distribution with ν degrees of freedom 12. For instance, for | t| > 1.7 and
ν > 30 the difference in the means is significant with a false alarm
probability of FAP < 10%. For some of our stars the FAP for the offset difference is
not significant: δ Eri (64%), ϵ Eri (23%), HR 209 (92%),
and HR 3259 (15%). However, from Fig. 4 it can be
seen that there are also stars having significant offsets leaving doubts whether the
offset can be kept fixed in general.
Figure 4 shows that for our sample an average offset of 10.4 m/s (±7.7 m/s) remains for the RV constant stars when comparing the RV means of the VLC and LC data. This offset might be due to systematics in the deconvolution process of the stellar template or in the modelling. For example, due to the different resolution, the LC data have to be modelled with a different chunk size (154 pixels to cover two VLC chunks). We corrected all re-calculated LC RVs for this systematic offset. Finally, we adjusted the RV mean of the published LC time series (Endl et al. 2002) to fit the RV mean of the re-calculated time series. In Figs. 19–23 the LC (Endl et al. 2002) and VLC data are always shown relative to each other with the measured and corrected offset (and not with a fitted RV offsets that could have been taken from our fit results presented below in Sect. 4) to conserve the true measurements.
The uncertainty of the offset found in the sample is rather large for it to be considered
a fixed value. On the other hand the approximately known offset can hold important
information, in particular in the case of HR 2400 or ϵ Ind A. Therefore
we choose a compromise between a fixed offset and a free offset when fitting a function.
Because one expects the difference of the zero point parameters to be zero
(cVLC − cLC ≈ 0), we introduce
in the χ2-fitting a counteracting potential term
η2 (also called penalty function, e.g. Shporer et al. 2010), that increases when the zero point difference
becomes larger  (2)The resulting χ2
(when minimising
(2)The resulting χ2
(when minimising  )
will be higher compared to that obtained when fitting with free offsets but lower than for
fixed offsets. The parameter s determines the coupling between the
offsets. After performing the fit it can be checked, if the fit has spread the zero points
too much (if η ≫ 1 or if there are large jumps in the model curves in
Figs. 19–23).
For s we attributed the uncertainty of the offset correction of 7.7 m/s
leading to a weak coupling.
)
will be higher compared to that obtained when fitting with free offsets but lower than for
fixed offsets. The parameter s determines the coupling between the
offsets. After performing the fit it can be checked, if the fit has spread the zero points
too much (if η ≫ 1 or if there are large jumps in the model curves in
Figs. 19–23).
For s we attributed the uncertainty of the offset correction of 7.7 m/s
leading to a weak coupling.
It is worth mentioning, that in Bayesian analysis  can be identified with the likelihood when assuming a Gaussian distribution for the prior
information that the expected zero point difference is zero.
can be identified with the likelihood when assuming a Gaussian distribution for the prior
information that the expected zero point difference is zero.
 |
Fig. 4 Difference between the means of the VLC and re-computed LC time series for all our stars ordered by spectral type. For RV constant stars (black filled circles) there occurs a systematic offset of 10.4 ± 7.7 m/s (red solid line and red dashed lines). Stars shown with open circles were not included in the offset analysis (for reasons see comments in Table 3). The shown error bars correspond to the uncertainty in the means, i.e. parameter s from Eq. (1). |
3.6. Combining the CES and HARPS data
In principle, VLC and HARPS data could be combined in a similar way. They have different wavelength calibrators, but, since there are some nights with almost simultaneous observations (within minutes), they are closely related in time. The difference between these consecutive measurements should be zero so that it is tempting to bind directly the time series by means of those nights. However, this does not account for fluctuations due to the individual uncertainties. Again a coupling term13 would be a more secure approach.
However, for reasons of simplicity we choose a fully free offset between the HARPS and the CES data. Because the VLC and the HARPS time series overlap well this is less critical, in contrast to the LC and VLC time series which are separated by a 2-year gap. The relative offsets between the CES and HARPS data as illustrated in Figs. 19–23 correspond to the common best fitting model (constant, slope, sinusoid, or Keplerian; cf. Sect. 4).
4. Analysis of the radial velocities
In this section we describe our data analysis and the general results of the survey, while some individual objects are discussed in detail in Sect. 5. The tests which we perform hereafter were repeated on the residuals of the binaries and planet hosting stars to search for additional companions and are indicated as objects with index r in Table 4.
4.1. Preparation of RV data and jitter consideration
Before the data analysis we binned the data into 2-h intervals by calculating weighted means for the temporal midpoint, RV, and RV error. The 2-h interval will especially down-weight nights from asteroseismology campaigns (see Sect. 3.3) and reduce the impact of red noise (Baluev 2013), while resulting in nightly averages for most other nights and still permitting to search for planets with periods as short as one day. Such intervals are also employed for solar-like stars (e.g. Rivera et al. 2010) to average out the stellar jitter, i.e. intrinsic stellar RV variation caused by, e.g., oscillation or granulation in the atmospheres of the stars. While the Sun has an oscillation time scale of ~5 min, its granulation 14 has lifetime ≲25 min (see Dumusque et al. 2011b, for adequate observing strategies). However note, that in our own survey we have usually taken three consecutive spectra in one night covering in total only 5–10 min, which is not sufficient to average out all those intrinsic stellar RV variations. To investigate the short-period jitter, we calculated the weighted scatter 15 in each 2-hr bin with at least 2 measurements and then the weighted mean of these scatters16. Table A.2 lists the jitter estimate σjit,τ from the HARPS data for each star and the mean time scale τ accessible for this estimate within the 2 h bins. Note that these time scales may not sufficiently cover the real jitter time scale in all cases. Therefore these estimated jitter values were not used in a further analysis.
Summary of the tests for excess variability, slope, and periodicities (sinusoidal and Keplerian) for the combined data set.
There can be also a long-term jitter with time scales of few days to weeks related to the rotation period (due to the appearance and disappearance of spots) or up to few years due to the magnetic cycle of a star. Isaacson & Fischer (2010) provide jitter estimates as a function of B − V colour and chromospheric activity index SHK based on Keck observations for more than 2600 main sequence stars and subgiants. Using these relations and the median SHK values in the HARPS data (which in most cases agree well with other literature values; see Table A.2), we estimate the jitter σjit,long for our stars (Table A.2). The jitter terms are usally ≳2 m/s. For GJ 570 A and ϵ Ind A the expected jitter is only 1.6 m/s. Both are K dwarfs with 1.0 < B − V < 1.3 and, according to Isaacson & Fischer (2010), those stars have the lowest level of velocity jitter decoupled from their chromospheric activity. The jitter terms σjit,long were added in quadrature to the internal errors for all stars and lead to a more balanced fit with the CES data. Morevover, to cross-check whether detected RV signals might be caused by those kinds of stellar activity we will also analyse in the HARPS data correlations between the RV data and activity indicators such as Ca II H&K emission and variations of the bisector (BIS) and the FWHM of the cross-correlation profile (Sect. 4.5). All RVs and HARPS activity indicators are online available.
Information about wide companions.
In fitting the data we accounted for the secular acceleration of the RVs (as given in Table 1). This perspective effect can become a measurable positive trend in some high proper motion stars (Schlesinger 1917; Kürster et al. 2003; Zechmeister et al. 2009). In our sample, ϵ Ind A has the highest secular acceleration with 1.8 m/s/yr. Its contribution is depicted in Fig. 23 by a dashed line.
4.2. Excess variability
To investigate objects for excess variability it is common to compare the observed
scatter with a noise estimate. A significantly larger scatter indicates variability.
Because internal errors ΔRVi and jitter estimations
σjit are available, the quality of each measurement is
assessed and allows us to weight the measurements in the
χ2-statistics,  . As the scatter we calculate the weighted
rms which is here defined as
. As the scatter we calculate the weighted
rms which is here defined as  (3)where
W = ∑ wi is the sum of
the weights and ν the number of model parameters. Outliers with a large
uncertainty will contribute less to the rms. The factor
(3)where
W = ∑ wi is the sum of
the weights and ν the number of model parameters. Outliers with a large
uncertainty will contribute less to the rms. The factor
 is a correction that converts the
uncorrected and biased variance into an unbiased variance, i.e. to have an unbiased
estimator for the population variance17. In the
unweighted case (wi = 1,
W = N) we obtain the well known formula for the
unbiased rms:
is a correction that converts the
uncorrected and biased variance into an unbiased variance, i.e. to have an unbiased
estimator for the population variance17. In the
unweighted case (wi = 1,
W = N) we obtain the well known formula for the
unbiased rms:  .
.
Furthermore, we define the weighted mean noise term σ via the mean of
the weights18 (4)Again lower-quality measurements will
contribute less to the mean noise level.
(4)Again lower-quality measurements will
contribute less to the mean noise level.
With these definitions the reduced χ2 can be easily expressed
as the ratio of weighted rms to weighted mean noise level  (5)To test for excess variability we have to fit
a constant and to calculate the scatter around the fit. For the joint analysis we account
for the zero point parameter of each data set when fitting a constant as outlined in Sect.
3.5. Note that the probability for the excess
variability
(5)To test for excess variability we have to fit
a constant and to calculate the scatter around the fit. For the joint analysis we account
for the zero point parameter of each data set when fitting a constant as outlined in Sect.
3.5. Note that the probability for the excess
variability  is directly reliant on a proper estimate
for the noise level σ. Also note that the tests in the next sections
employ model comparisons and the jitter estimate enters only indirectly through fitting
with modified weights. Table 4 summarises for the
combined data set the weighted noise term σ, the weighted rms, and the
χ2-probability for this test. Table A.1 lists additionally the individual rms (Cols. 5–7 labelled
rmsconstant) for each instrument. These values can differ from Table 3, because in Table 4 secular acceleration is accounted for, jitter has been added, the data are
binned, and the LC and VLC offsets are coupled. Because the HARPS data have a much higher
precision, they dominate the statistics.
is directly reliant on a proper estimate
for the noise level σ. Also note that the tests in the next sections
employ model comparisons and the jitter estimate enters only indirectly through fitting
with modified weights. Table 4 summarises for the
combined data set the weighted noise term σ, the weighted rms, and the
χ2-probability for this test. Table A.1 lists additionally the individual rms (Cols. 5–7 labelled
rmsconstant) for each instrument. These values can differ from Table 3, because in Table 4 secular acceleration is accounted for, jitter has been added, the data are
binned, and the LC and VLC offsets are coupled. Because the HARPS data have a much higher
precision, they dominate the statistics.
The small χ2-probabilities for most of the stars indicate
that they are variable with respect to our noise estimate σ. However, 10
stars (and the RV orbit residuals of 8 stars) have
Prob(χ2) > 1%, i.e. they show only low or no excess
variability. In five cases the scatter is smaller than the noise level, i.e.
 , implying an overestimation of the noise
level. Indeed, for four stars (ζ Tuc, τ Cet, HR 2667,
and HR 6998) the jitter estimate σjit,long in Table A.2 is higher than the scatter of the HARPS
measurements (Table A.1). The reason for jitter
overestimation might be a somewhat lower precision of the Keck sample from which the
jitter relation was derived (Isaacson & Fischer
2010).
, implying an overestimation of the noise
level. Indeed, for four stars (ζ Tuc, τ Cet, HR 2667,
and HR 6998) the jitter estimate σjit,long in Table A.2 is higher than the scatter of the HARPS
measurements (Table A.1). The reason for jitter
overestimation might be a somewhat lower precision of the Keck sample from which the
jitter relation was derived (Isaacson & Fischer
2010).
4.3. Long-term trends
Because potential planets or companions can have orbital periods much longer than our
observations, these objects may betray themselves by a trend in the RVs. We searched for
trends by fitting a slope to the data and derived its significance via the fit improvement
with respect to the constant model (previous section) via
 (6)or when expressed with unbiased weighted
variances
(6)or when expressed with unbiased weighted
variances  (7)The associated probability for this
F-value follows a
F1,N−4-distribution (4 parameters: 1 slope, 3
zero points). Again Table 4 summarises the test for
long-term trends. When adopting a false alarm probability threshold of <10-3
fitting a slope improves significantly the rms of all binaries as well as that of
β Hyi, τ Cet, GJ 570 A, ϵ Ind A and
the residuals of HR 506. We note that for β Hyi, α For,
GJ 570 A, HR 6416, HR 7703, ϵ Ind A, and HR 8501 the trend is a
sufficient model (regarding sinusoid and Keplerian fit, see next section), because of the
smaller FAP or weighted rms (i.e. smaller
(7)The associated probability for this
F-value follows a
F1,N−4-distribution (4 parameters: 1 slope, 3
zero points). Again Table 4 summarises the test for
long-term trends. When adopting a false alarm probability threshold of <10-3
fitting a slope improves significantly the rms of all binaries as well as that of
β Hyi, τ Cet, GJ 570 A, ϵ Ind A and
the residuals of HR 506. We note that for β Hyi, α For,
GJ 570 A, HR 6416, HR 7703, ϵ Ind A, and HR 8501 the trend is a
sufficient model (regarding sinusoid and Keplerian fit, see next section), because of the
smaller FAP or weighted rms (i.e. smaller  . For these stars the trend is depicted in
Figs. 19–23.
. For these stars the trend is depicted in
Figs. 19–23.
Some of our stars have known wide visual companions with a known separation
ρ listed in Table 5. Whether
these objects are able to cause the observed trend, can be verified by the estimate
( )
)  (8)with the radial acceleration
(8)with the radial acceleration
 of the observed component A and the
projected separation ρ ≤ r between both components. For
comparison, Jupiter at 5.2 AU can accelerate the Sun by 6.6 m/s/yr. Table 5 summaries the information about known wide companions
and shows that the minimum companion masses derived from the measured slopes are below
0.5 M⊙ for α For, GJ 570 A, HR 6416, HR
7703, and HR 8501. These masses are in agreement with the masses as expected from the
spectral type of their companions. However, ϵ Ind B cannot explain the
trend seen for ϵ Ind A (see Sect. 5
for details).
of the observed component A and the
projected separation ρ ≤ r between both components. For
comparison, Jupiter at 5.2 AU can accelerate the Sun by 6.6 m/s/yr. Table 5 summaries the information about known wide companions
and shows that the minimum companion masses derived from the measured slopes are below
0.5 M⊙ for α For, GJ 570 A, HR 6416, HR
7703, and HR 8501. These masses are in agreement with the masses as expected from the
spectral type of their companions. However, ϵ Ind B cannot explain the
trend seen for ϵ Ind A (see Sect. 5
for details).
 |
Fig. 5 GLS (top) and Keplerian (bottom) periodogram for HR 2667 which is constant to 3.1 m/s. The horizontal lines mark the 10-2, 10-3, and 10-4 false alarm probabilities (FAP). |
The other possibility for a trend is an unknown and unseen companion. Whether the
strength and the long duration of a trend is still compatible with a planetary companion,
can be estimated more conveniently, when Eq. (8) is expressed in terms of the orbital period P which is also
unknown but has to be (for circular orbits) at least twice as large as the time span of
observations T. With Kepler’s 3rd law
 , Eq. (8) can be written as
, Eq. (8) can be written as  (9)For ϵ Ind A we find its
companion to have
msini ≳ 0.97 MJup for
P > 30 yr.
(9)For ϵ Ind A we find its
companion to have
msini ≳ 0.97 MJup for
P > 30 yr.
4.4. Search for periodicities and Keplerian orbits
To search for the best-fitting sinusoidal and Keplerian orbits, we employed the generalised Lomb-Scargle (GLS) algorithm described in Zechmeister & Kürster (2009). It was adapted to treat all three data sets with different offsets and also incorporates the weak offset coupling described before (Sect. 3.5). Searching for sine waves is a robust method to find periodicities and orbits with low eccentricities, while for highly eccentric orbits the Keplerian model should be applied.
Figures 5, 12–15 show the periodograms for some of the stars discussed here. The periodograms
are normalised as 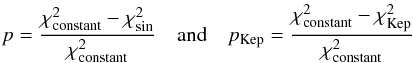 (10)involving the χ2
of the constant, sinusoidal, and Keplerian model, respectively. Analogous to Cumming et al. 2008 and Zechmeister & Kürster (2009), we calculated the probabilities of
the power values for the best-fitting sinusoid and Keplerian orbit
(pbest and pKep,best) via
(10)involving the χ2
of the constant, sinusoidal, and Keplerian model, respectively. Analogous to Cumming et al. 2008 and Zechmeister & Kürster (2009), we calculated the probabilities of
the power values for the best-fitting sinusoid and Keplerian orbit
(pbest and pKep,best) via
 respectively. Compared to the probability
functions given by these authors which account for one offset, here are slight
modifications in the equations (numerator in the fractional terms decreased by 2) arising
from the three zero points, i.e. two more free parameters19.
respectively. Compared to the probability
functions given by these authors which account for one offset, here are slight
modifications in the equations (numerator in the fractional terms decreased by 2) arising
from the three zero points, i.e. two more free parameters19.
The final false alarm probability (FAP) for the period search accounts for the number of
independent frequencies M with the simple estimate
M ≈ fT (Cumming
2004), i.e. the frequency range f and the time baseline
T, and is given by
![\begin{equation} {{\rm FAP}}=1-[1-{\rm Prob}(p>p_{{\rm best}})]^{M} \end{equation}](/articles/aa/full_html/2013/04/aa16551-11/aa16551-11-eq189.png) (13)and can be approximated by
FAP ≈ M·Prob(p > pbest)
for FAP ≪ 1. Since our frequency search interval ranges from 0 to 1 d-1, we
have typically M ~ 5500 for a 15 year time baseline.
(13)and can be approximated by
FAP ≈ M·Prob(p > pbest)
for FAP ≪ 1. Since our frequency search interval ranges from 0 to 1 d-1, we
have typically M ~ 5500 for a 15 year time baseline.
Table 4 summarises the formal best-fitting sinusoidal and Keplerian periods (Psin and PKep) found by the periodograms along with their residual weighted rms and FAP20. Our approach recovers all stars that exhibit long-term trends emulated by long periods and generally decreases the rms down to a few m/s.
We identify for HR 506, ι Hor, and HR 3259 the same periods that were previously announced as planetary signals (Kürster et al. 2000; Mayor et al.; Lovis et al. 2006). In Sect. 5 we derive for HR 506 and ι Hor refined orbital solutions (see also Table 6 and 7) and investigate the correlation between RV and activity indicators.
Orbital parameters for the planetary companion to HR 506.
Orbital parameters for the planetary companion to ι Hor.
For the refinement of the orbital parameters and the error estimation we used the program GaussFit (Jefferys et al. 1988) which can solve general nonlinear fit-problems by weighted least squares and robust estimation. As initial guess we provided the parameters found with the Keplerian periodogram in the previous section. All offsets were free parameters.
We provide also a first orbital solution for the spectroscopic binary HR 2400 (Table 8). However, for κ For, α Cen A+B and the giant HR 3677 it is not possible to give a reliable orbital solution since our measurements cover only a small piece of their orbits. Companion masses are estimated in Sect. 5.
4.5. Correlations with Ca II H&K, BIS, and FWHM
Radial velocity variations can be caused by stellar variability such as oscillations,
granulations, spots, and magnetic activity cycles. They can affect the stellar line
profile and, in case of spots and magnetic cycles, also the amount of Ca II H&K
emission. To test this, one can analyse the  -index and the shape of the
cross-correlation function (CCF) function in particular its full width at half maximum
(FWHM) and bisector span (BIS, Queloz et al. 2001)
which are measures for the averaged stellar line width and asymmetry, respectively. The
activity indicators are products of the HARPS pipeline and the computation of
(SHK and)
-index and the shape of the
cross-correlation function (CCF) function in particular its full width at half maximum
(FWHM) and bisector span (BIS, Queloz et al. 2001)
which are measures for the averaged stellar line width and asymmetry, respectively. The
activity indicators are products of the HARPS pipeline and the computation of
(SHK and)  is described in Lovis et al. (2011). Note that these indicators do not cover the whole
survey, because they cannot be derived from the CES spectra (which do not include the Ca
II region and are contaminated by the iodine lines). The SHK
errors are derived from photon noise (Lovis et al.
2011), the BIS span errors are taken as twice21 the internal RV errors, and the FWHM errors are 2.35 times 22 the internal RV errors.
is described in Lovis et al. (2011). Note that these indicators do not cover the whole
survey, because they cannot be derived from the CES spectra (which do not include the Ca
II region and are contaminated by the iodine lines). The SHK
errors are derived from photon noise (Lovis et al.
2011), the BIS span errors are taken as twice21 the internal RV errors, and the FWHM errors are 2.35 times 22 the internal RV errors.
The time series of the activity indicators and their correlations with RVs are shown for each star in Figs. B.1–B.33. Tables A.4 and A.5 summarise for each star and activity indicator their mean values, scatter, and the correlation coefficients. Statistically significant linear correlations with FAP < 0.01 are highlighted in bold font in the Tables and depicted by a solid line in the figures.
Note that a high statistical correlation does not necessarily mean a physical correlation, in particular when both quantities exhibit just trends which could coincide just by chance and temporarily. However, if the correlation is present during more complex temporal variations, e.g., both quantities have the same period, a planetary hypothesis should be excluded. But note also, that the Sun hosts a Jupiter in a 12 yr orbit and shows a comparably long magnetic cycle (11 yr).
In the sample, τ Cet has the smallest variations in
 (0.005 dex), while
ζ1 Ret has the largest variations (0.048 dex). We find
significant correlations between RV and
(0.005 dex), while
ζ1 Ret has the largest variations (0.048 dex). We find
significant correlations between RV and  for the stars β Hyi, HR
209, ζ1 Ret, α Men, HR 4979, HR 8323, and for
the two stars with planet candidates ι Hor and ϵ Ind A.
However, the correlation seen for α Cen B (probably also HR 7703 and
ϵ Ind A) is artificial since the RV trend is largely caused by a wide
companion, respectively, instead of a magnetic cycle (Sect. 5).
for the stars β Hyi, HR
209, ζ1 Ret, α Men, HR 4979, HR 8323, and for
the two stars with planet candidates ι Hor and ϵ Ind A.
However, the correlation seen for α Cen B (probably also HR 7703 and
ϵ Ind A) is artificial since the RV trend is largely caused by a wide
companion, respectively, instead of a magnetic cycle (Sect. 5).
Orbital parameters for the companion to HR 2400.
Lovis et al. (2011) provide also a relation to
estimate the slope of the RV and  correlations based on the stellar
temperature Teff and metallicity [Fe/H]. After conversion
23 to a slope w.r.t.
correlations based on the stellar
temperature Teff and metallicity [Fe/H]. After conversion
23 to a slope w.r.t.
 by multiplication with a factor of
by multiplication with a factor of
 , these estimates can be compared to the
derived slopes given in Table A.4. As an
additional cross-check, we will do this comparison occasionally in Sect. 5 when we conclude for a magnetic cycle hypothesis. We
note that eight stars24 were included also in a
sample analysed by Lovis et al. (2011) for magnetic
cycles via
, these estimates can be compared to the
derived slopes given in Table A.4. As an
additional cross-check, we will do this comparison occasionally in Sect. 5 when we conclude for a magnetic cycle hypothesis. We
note that eight stars24 were included also in a
sample analysed by Lovis et al. (2011) for magnetic
cycles via  . With the exception of the RV standard
star τ Cet and the subgiant δ Eri, these authors
reported
. With the exception of the RV standard
star τ Cet and the subgiant δ Eri, these authors
reported  cycles/trends for these stars.
cycles/trends for these stars.
Significant correlations between RV and BIS are found for 7 stars (τ Cet, ι Hor, ϵ Eri, α Men, HR 4979, HR 8323, and HR 8883). The correlation for three more stars (α Cen B, GJ 570 A, and HR 8501) should be artificial, since the RV trends can be attributed to a wide stellar companion.
Finally, RV-FWHM correlations are found for 7 stars (β Hyi, HR 209, τ Cet, ζ1 Ret, ζ2 Ret, α Men, and HR 8323). For 6 other stars (HR 2400, HR 3677, α Cen A, α Cen B, GJ 570 A, and probably also ϵ Ind A) the correlations are artificial due the RV trends caused by their wide companions.
RV variations caused by the magnetic cycle should result in positive correlations with all three indicators (Lovis et al. 2011). The stars α Men and HR 8323 are nice showcase examples for this effect. On the other hand, an RV-BIS anti-correlation (cf. the active stars ι Hor, ϵ Eri, and also the giant HR 8883) is expected for rotating spots (Boisse et al. 2011) and should be therefore related to the stellar rotation period.
4.6. Detection limits
To demonstrate the sensitivity of our survey, we have calculated for each star conservative 99.9% detection limits for circular orbits following the method outlined in Zechmeister et al. (2009). As an example, Fig. 6 illustrates the upper mass limit for HR 2667 (one of our most constant stars) showing that we are sensitive approximately to Jupiter analogues. Because the more precise HARPS data typically cover only 1500 d, there is a loss of sensitivity for longer periods indicated by a steep increase of the upper mass limit. The longer time baseline gained with the CES data pushes a bit down the limit at longer periods.
The detection limits of the other stars have a qualitatively similar shape to that shown in Fig. 6. For four stars (ζ Tuc, τ Cet, and the residuals of HR 7703 as well as ϵ Ind A) the upper mass limit is lower than 1 MJup at 5 AU. For 19 stars the limit is still lower than 2 MJup and for 28 stars lower than 4 MJup at 5 AU (see Fig. 7).
 |
Fig. 6 Detection limit for HR 2667 considering circular orbits. The cross marks the distance and msini of a Jupiter analogue for i = 90°. The vertical lines indicate the time baseline of the HARPS and all combined measurements, respectively. |
5. Discussion on individual targets
In this section we discuss individually those stars that exhibit variability.
-
β Hyi:
for β Hyi Endl et al. (2002) announced a trend of 7 m/s/yr with a remaining scatter of 19 m/s. Here the best common trend is only 1.79 m/s/yr depicted with a black solid line in Fig. 19 (plus the secular acceleration of 0.86 m/s). The scatter around the HARPS data decreases to only 2.3 m/s (see Table A.1). However, the trend increases the VLC scatter from 7.4 m/s to 9.0 m/s and the fitted LC-VLC offset departs by 2.2σ (–17 m/s, Table A.3) from the measured offset. Thus, it is unclear whether the trend is steady.
Additionally, we plot the 4300 d period tabulated for β Hyi (Table 4) with a black dashed line in Fig. 19. This period matches that of a Jupiter analogue, while the amplitude of 6.5 m/s would result in a formal minimum mass of 0.56 MJup. Compared to the trend in the previous section the fitted LC-VLC offset is less discrepant (–8.0 m/s), but the sine fit is less significant than trend and still not supported by the VLC data, because their scatter increases from 7.4 m/s to 8.9 m/s. Moreover,
 and FWHM correlate with the RVs. Hence
the long-term variations might be related to the magnetic cycle.
and FWHM correlate with the RVs. Hence
the long-term variations might be related to the magnetic cycle. -
HR 209:
 and FWHM correlate with the RVs. Hence
the RV variations are related to stellar activity probably induced by spots.
and FWHM correlate with the RVs. Hence
the RV variations are related to stellar activity probably induced by spots. -
HR 506 (HD 10647):
a planet candidate was presented by Mayor et al.5 based on CORALIE measurements. Jones et al. (2004) found also weak evidence for a similar signal with the AAT, but did not exclude stellar activity as the cause. Butler et al. (2006) listed AAT RV data and derived orbital parameters.
For HR 506 we clearly recovered the long RV period in the period analysis. Hence, we combine our observations with AAT data and CORALIE data to fit the orbit. Because more cycles have been covered, our combined solution gives a more precise period compared to the solutions given by the other authors (P = (1003 ± 56) d, e = 0.16 ± 0.22 and P = (1040 ± 37) d, e = 0.18 ± 0.08, respectively). For our three combined data sets an eccentric orbit does not fit much better (Table 4) and also in the solution for the five combined data sets the eccentricity vanished. Therefore a circular obit was fitted (e and ω fixed to zero, Table 6, Fig. 8). The semi-major axis and the companion minimum-mass were derived by assuming a stellar mass of 1.17 ± 0.1 M⊕ (Table 1).

Fig. 7 Sensitivity of the survey. For each orbital distance the minimum mass is indicated that could have been detected for 4, 19, and 28 stars of the 31 stars (corresponding to a fraction of 13%, 61%, and 90%) with 99.9% significance. The cross marks again a Jupiter analogue.

Fig. 8 Left: RV time series for HR 506 combined with AAT and CORALIE data. Right: RVs phase folded to the period of P = 995 d and the residuals (bottom).
There is no clear RV-
 correlation
(r = 0.45, FAP = 1.7%). However, when subtracting the 994 d RV
period, there is a significant correlation (r = 0.63, FAP = 0.033%),
implying that the residuals of this active star are affected by stellar activity. The
RV-BIS and RV-FWHM correlations are not significant, also not for the residual RVs.
The RV residuals of HR 506 also have some excess variability and a marginally
significant trend of –2.41 m/s/yr which however increases the rms of the LC data (from
18.8 m/s to 20.0 m/s, Table A.1).
correlation
(r = 0.45, FAP = 1.7%). However, when subtracting the 994 d RV
period, there is a significant correlation (r = 0.63, FAP = 0.033%),
implying that the residuals of this active star are affected by stellar activity. The
RV-BIS and RV-FWHM correlations are not significant, also not for the residual RVs.
The RV residuals of HR 506 also have some excess variability and a marginally
significant trend of –2.41 m/s/yr which however increases the rms of the LC data (from
18.8 m/s to 20.0 m/s, Table A.1). -
τ Cet:
the small trend reduces the scatter from 1.37 m/s to just 1.33 m/s and is just significant due to the large number of observations. However, at this level an instrumental cause is likely for the small trend and the RV-BIS and RV-FWHM correlation. In this respect we also like to point out that the FWHM of τ Cet (but also some others stars, e.g. ζ Tuc) exhibits a noticeable positive long-term trend (Fig. B.7) which might be due to a drifting focus of HARPS. In this case, assuming a constant line equivalent width, a negative trend is expected and indeed seen in the contrast (depth) of the CCF (recently also noted by Gomes da Silva et al. 2012). τ Cet has the smallest variations in
 in the sample.
in the sample. -
κ For:
the RVs of κ For decline over the whole time baseline of 14 yr which indicates an orbital period longer than the estimate of 21 yr given in Endl et al. (2002). The Keplerian period of 10 700 d listed in Table 4 (29.3 yr) is not well constrained. However, again with the slope and Eq. (9) this period might be used to assess a minimum mass of 0.36 M⊙ for the companion. The RV residuals do not exhibit significant variability.
-
ι Hor:
for this active star Kürster et al. (2000) discovered a planet. The signal was also seen by Naef et al. (2001) using the CORALIE spectrograph and by Butler et al. (2001) with the AAT. Using the HARPS data of Vauclair et al. (2008) taken for an asteroseismology campaign, Boisse et al. (2011) searched for short period companions (P < 7 d), but detected no further planet.
In our analysis we recovered the planetary signal seen for ι Hor by Kürster et al. (2000). We refined the orbital parameters with our data sets and included also the AAT (Butler et al. 2006) and CORALIE data (Naef et al. 2001) as shown in Fig. 9. For these two data sets the jitter estimate (from Table A.2) was added to the measurements error. Due to the activity of the star the residuals have a high scatter. The orbital parameters are listed in Table 7. The semi-major axis and the companion minimum-mass were derived by assuming a stellar mass of 1.25 ± 0.02 M⊕ (Table 1). An astrometric upper mass limit of 18.4 MJup was placed by Reffert & Quirrenbach (2011) in combination with the orbital solution of Butler et al. (2006). The orbital period of 307 d is different from the rotation period of ~8 d (see below), while a relation with the magnetic cycle has to be discussed.
Metcalfe et al. (2010) reported that a magnetic activity cycle of ~1.6 yr bears no obvious relation to the orbital period, but we find that there is a moderately significant RV-
 correlation (Fig. B.9) and that the refined orbital period (307 d) is half of the
formal best-fitting period (630 d) for the combined HARPS and SMARTS
SHK-index measurements (Fig. 10; we use the SHK-index instead of
correlation (Fig. B.9) and that the refined orbital period (307 d) is half of the
formal best-fitting period (630 d) for the combined HARPS and SMARTS
SHK-index measurements (Fig. 10; we use the SHK-index instead of
 for the comparison, since Metcalfe et al. (2010) published
SHK-index measurements). However, if the 307 d RV period
were caused by a magnetic cycle, we would expect the same period for the
SHK-index and a positive correlation with the BIS (Lovis et al. 2011), while there is a formal RV-BIS
anti-correlation probably artificially induced by the short-term variations (Fig.
11). Therefore we tend to prefer the planet
hypothesis as a more simple and likely explanation. Moreover, after subtracting the
307 d period, the correlation with
for the comparison, since Metcalfe et al. (2010) published
SHK-index measurements). However, if the 307 d RV period
were caused by a magnetic cycle, we would expect the same period for the
SHK-index and a positive correlation with the BIS (Lovis et al. 2011), while there is a formal RV-BIS
anti-correlation probably artificially induced by the short-term variations (Fig.
11). Therefore we tend to prefer the planet
hypothesis as a more simple and likely explanation. Moreover, after subtracting the
307 d period, the correlation with  remains and the anti-correlation with
BIS increases and becomes more significant.
remains and the anti-correlation with
BIS increases and becomes more significant.The periodogram of the residuals for ι Hor (Fig. 12) shows power at periods of 5.7 d as well as 7.94 d and 8.45 d (also found by Boisse et al. 2011, based on HARPS RVs). The latter peak coincides with periodic variations (8.5 d) found in the SHK index by Metcalfe et al. (2010), which therefore probably indicates the rotation of this star. The residual RVs anti-correlate with BIS which is indeed expected for rotating spots (Boisse et al. 2011).

Fig. 9 (Left) RV time series for ι Hor combined with AAT and CORALIE data. (Right) RVs phase folded to the period of P = 307 d and the residuals (bottom).

Fig. 10 S-index measurements for ι Hor. Metcalfe et al. (2010) published the SMARTS data (blue open circles) and the 566 d period (dotted line). The formal best fit for the combined data set is 630 d (dashed line).
-
α For:
GJ 127 B can explain the trend of –11.5 m/s (Sect. 4.3, Table 5, Fig. 24). So far a trend is a sufficient model. The RV residuals do not exhibit significant variability.
-
ζ1 Ret:
the relatively large scatter of 12.5 m/s is indicative of excess variability and the periodogram of the RVs shows peaks close to our FAP threshold at 21.5 d and 426 d (Fig. 13) with the first giving the lowest for the combined rms value (but increasing the rms of the VLC data). The strong RV-
 (also RV-FWHM) correlation shows that
most of the scatter is due to stellar activity, likely not only the magnetic cycle,
since the observed correlation slope 219 ± 24 m/s/dex exceeds the predicted
value140 ± 7 m/s/dex for a magnetic cycle (Sect. 4.5, assuming 5746 ± 27 K and [Fe/H] = −0.22 ± 0.05 from del Peloso et al. 2000). r = 0.88
indicates that the subtraction of this correlation will reduce the scatter by
(also RV-FWHM) correlation shows that
most of the scatter is due to stellar activity, likely not only the magnetic cycle,
since the observed correlation slope 219 ± 24 m/s/dex exceeds the predicted
value140 ± 7 m/s/dex for a magnetic cycle (Sect. 4.5, assuming 5746 ± 27 K and [Fe/H] = −0.22 ± 0.05 from del Peloso et al. 2000). r = 0.88
indicates that the subtraction of this correlation will reduce the scatter by
 to 5.9 m/s.
ζ1 Ret has the largest
to 5.9 m/s.
ζ1 Ret has the largest
 -variations and a quite high jitter
estimate of 3.8 m/s within our sample.
-variations and a quite high jitter
estimate of 3.8 m/s within our sample. 
Fig. 11 RV vs. BIS for ι Hor. (Top) The linear correlation coefficient is r = −0.53, but the correlation appears more complex and loop-like. (Bottom) After subtracting the 307 d period from the RVs, r is − 0.56.
-
ζ2 Ret:
given the very similar stellar parameters of the binary pair ζ1 Ret and ζ2 Ret, del Peloso et al. (2000) already pointed out the baffling fact of their very different activity level. We do not find any significant RV excess variability for ζ2 Ret. However, there is a significant RV-FHWM correlation and all three activity indicators seem to exhibit a small trend, which might be either due to a magnetic cycle or instrumental (cf. τ Cet).
-
ε Eri:
Hatzes et al. (2000) announced a planet in an eccentric orbit (e = 0.6) around this active star. Benedict et al. (2006) refined the orbital solution and combined the RVs with astrometric observations with the HST Fine Guidance Sensor indicating an orbital inclination of i = 30°. Likewise, Reffert & Quirrenbach (2011) derived a similar value for the inclination and an upper mass limit of 6.1 MJup using Hipparcos astrometry and the RV orbit solution.
However, in the periodogram for ϵ Eri (Fig. 14) we cannot find any evidence for the long-period planet (P = 2500 d) suggested by Hatzes et al. (2000) whose orbital solution is plotted in Fig. 20 for comparison. Due to the higher precision of our data, the combined rms is 8.2 m/s for fitting a constant, while Hatzes et al. (2000) list an rms ranging from 11 to 22 m/s for different instruments in the residuals of their Keplerian model. ϵ Eri is an active star and all three activity indicators are variable, and the BIS shows an anti-correlation with RV. The stellar rotation period is 11.2 d (Donahue et al. 1996; Fröhlich 2007). On a short time scale of 85 min its variability is 0.86 m/s (Table A.2), while the long term jitter estimate is 3.6 m/s (Table A.2). Our best-fitting sine function has a period of 3.11 d, reduces the scatter from 8.2 m/s to only 6.9 m/s, but is not significant. We note that, combining the RVs of HARPS and all the RVs given in Benedict et al. (2006), Anglada-Escudé & Butler (2012) could also not confirm the planet solution, though, without evaluating the significance, they suggested another best fitting, similar long-period.

Fig. 13 GLS periodogram for ζ1 Ret.

Fig. 14 GLS (top) and Keplerian (bottom) periodogram for ϵ Eri. There is no significant power at the period of the putative planet ϵ Eri b (P = 2500 d).
-
α Men:
Eggenberger et al. (2007) reported a companion for α Men which is likely an M3.5 – M6.5 dwarf that was seen at a separation of 3.05′′ with the VLT+NACO. They also mentioned (but did not quantify) a radial velocity drift for α Men seen with the CORALIE spectrograph and suggested that the companion causes this trend. In our data however, the star has no significant excess variability (rms = 3.1 m/s) or trend. Therefore we cannot confirm an RV trend for α Men, whose value should be unchanged over years if induced by an M dwarf with a separation of 3′′. However, since no value for the trend was given by Eggenberger et al. (2007), a quantitative comparison cannot be made.
Moreover, the RVs correlate with all three activity indicators. The observed RV-
 slope of 57 ± 10 m/s/dex (Table A.4) agrees with the predicted sensitivity of
CRV = 69 ± 4 m/s/dex (assuming
Teff = 5594 ± 36 K and [Fe/H] = 0.10 ± 0.05 from Santos et al. 2004) indicating a magnetic cycle as
cause of the RV variations.
slope of 57 ± 10 m/s/dex (Table A.4) agrees with the predicted sensitivity of
CRV = 69 ± 4 m/s/dex (assuming
Teff = 5594 ± 36 K and [Fe/H] = 0.10 ± 0.05 from Santos et al. 2004) indicating a magnetic cycle as
cause of the RV variations. -
HR 2400:
the orbital solution for HR 2400 is given in Table 8. Assuming a stellar mass of 1.2 ± 0.1 M⊕ (Table 1) the companion has a minimum mass of 0.17 M⊙ indicating an M dwarf at a separation of 9.6 AU (0
 26). Hence, HR 2400 is a single-lined
spectroscopic binary (SB1). Figure 24 displays
the RV residuals for HR 2400 which do not have a significant variability. In the FWHM
there seems to be a trend which might be due to stellar activity or spectral
contamination by the companion. In the residuals the RV-FWHM correlation vanished.
26). Hence, HR 2400 is a single-lined
spectroscopic binary (SB1). Figure 24 displays
the RV residuals for HR 2400 which do not have a significant variability. In the FWHM
there seems to be a trend which might be due to stellar activity or spectral
contamination by the companion. In the residuals the RV-FWHM correlation vanished.
-
HR 3259:
for HR 3259 Lovis et al. (2006) reported a planetary system with three Neptune-mass planets with periods (amplitudes) of 8.667 d (3.51 m/s), 31.56 d (2.66 m/s), and 197 d (2.20 m/s). All three periods are seen in the periodogram (Fig. 15) and the corresponding peak heights are in the same order as suggested by the given amplitudes. We refer to Anglada-Escudé & Butler (2012) for a recent and detailed analysis of the HARPS data and updated orbital parameters of the short period planets. We only note that with our own and archive (but without GTO) HARPS data alone we also have seen excess power at these periods, although these peaks did not reach our FAP threshold due to too few observations (only 18 binned HARPS data points) and considerable spectral leakage (aliasing).

Fig. 15 GLS periodogram for HR 3259. The vertical arrows indicate the periods for the three planets announced by Lovis et al. (2006).
-
HR 3677:
the orbit of the companion to the giant HR 3677 is eccentric indicated by the much lower residuals when fitting a Keplerian orbit (8.7 m/s) compared to a circular orbit (35 m/s). Using the slope and Eq. (9) a raw estimate for the minimum companion mass is 0.69 M⊙. The significant excess variability of the RV residuals (Fig. 24) is likely explained by an underestimated jitter of this giant. The RV-FWHM correlation disappears in the residuals.
-
HR 4523:
Tinney et al. (2011) reported a Neptune-like planet with 16 M⊕ minimum mass in a 122 d orbit.
However, the periodogram of our data shows no power at periods of 122 d. Therefore we cannot confirm the planet reported by Tinney et al. (2011). Their 145 measurements over 7 yr with UCLES have a scatter of rms = 3.0 m/s. For comparison, the 62 HARPS RVs over 4.4 yr have also rms = 2.9 m/s. Figure 16 shows the RV data phase folded to the period of the proposed planet. When subtracting the proposed orbital solution, the scatter decreases to 2.56 m/s for UCLES, but increases to 3.29 m/s for HARPS.

Fig. 16 RV data for HR 4523 phase folded to 122.1 d. The dashed curve is an orbital solution proposed by Tinney et al. (2011) based on the UCLES data. HARPS RVs are shown for comparison.
-
HR 4979:
most of the RV variations is likely caused by a magnetic cycle, because the RV correlates with
 and BIS. Moreover, the observed
correlation slope is 81 ± 12 m/s/dex which is of the order of the value expected for
magnetic cycles (65 ± 2 m/s/dex; Sect. 4.5,
assuming Teff = 5729 ± 17 K and [Fe/H] = 0.19 ± 0.01 from
Sousa et al. 2008).
and BIS. Moreover, the observed
correlation slope is 81 ± 12 m/s/dex which is of the order of the value expected for
magnetic cycles (65 ± 2 m/s/dex; Sect. 4.5,
assuming Teff = 5729 ± 17 K and [Fe/H] = 0.19 ± 0.01 from
Sousa et al. 2008). -
α Cen A+B:
we refer to Pourbaix et al. (2002) for the orbital solution for α Cen A+B with a period of 80 yr. We would just like to point out that the fitted trends in Sect. 4.3, although obviously not a sufficient model, can be interpreted as a mean acceleration and that the ratio of these slopes is a measure of the mass ratio
 which agrees with the value of
which agrees with the value of
 derived from Pourbaix et al. (2002).
derived from Pourbaix et al. (2002).Neither the residuals of α Cen A nor α Cen B exhibit a significant variability. However, using HARPS measurements and a very complex analysis, Dumusque et al. (2012) have recently announced a planet candidate for α Cen B with a very small amplitude (0.51 m/s, 3.236 d). Due to the lower number of the (complementary) HARPS measurements in this work (21 vs. 459) we are not sensitive to this planet.
The RV-
 and RV-BIS correlations listed for
α Cen B are only formally significant, since obviously the RV trend
is caused by α Cen A and not by a stellar activity, and vanishes
after subtracting the orbit. The trend seen in
and RV-BIS correlations listed for
α Cen B are only formally significant, since obviously the RV trend
is caused by α Cen A and not by a stellar activity, and vanishes
after subtracting the orbit. The trend seen in  is part of a longer magnetic cycle
which can be seen more clearly when adding recently published HARPS data by Dumusque et al. (2012). We estimate a period of
P ~ 2420 d (Fig. 17) for
the magnetic cycle, but a true periodicity is not secured, since only one cycle is
covered and e.g. Buccino & Mauas (2008)
reported a period of 3061 d with a FAP of 24%.
is part of a longer magnetic cycle
which can be seen more clearly when adding recently published HARPS data by Dumusque et al. (2012). We estimate a period of
P ~ 2420 d (Fig. 17) for
the magnetic cycle, but a true periodicity is not secured, since only one cycle is
covered and e.g. Buccino & Mauas (2008)
reported a period of 3061 d with a FAP of 24%. 
Fig. 17 The time behaviour of
 that shows the magnetic cycle of
α Cen B.
that shows the magnetic cycle of
α Cen B.
Fig. 18 Correlation between bisector span (BIS) and RV for the giant HR 8883.

Fig. 19 Radial velocity time series (unbinned data). The error bars depict the internal measurement errors ΔRVi, i.e. not including jitter. LC (green open circles) and VLC (blue open diamonds) data are displayed with their measured offsets. Jumps in the curves indicates the difference between the measured (Sect. 3.5) and fitted (Sect. 4) LC-VLC offset. HARPS data are in red filled circles. The solid lines indicate significant models, while dashed lines illustrate less or non-significant alternative models. All models include secular acceleration. Model curves are shown for β Hyi (trend and long-period sinusoid, see text for discussion), and HR 506 (sinusoid).

Fig. 20 Radial velocities. Continuation of Fig. 19. Model curves are shown for κ For (Keplerian), ι Hor (Keplerian), and α For (trend). The Keplerian orbit for ϵ Eri taken from Hatzes et al. (2000) is not significant in this work.

Fig. 21 Radial velocities. Continuation of Figs. 19 and 20. Model curves are shown for HR 2400 (Keplerian) and HR 3677 (Keplerian).

Fig. 22 Radial velocities. Continuation of Figs. 19–21. Model curves are shown for α Cen A and α Cen B (Keplerian orbit from Pourbaix et al. 2002), GJ 570 A (trend), and HR 6416 (trend).
-
GJ 570 A:
the trend has a smaller FAP compared to sinusoidal and Keplerian model and is therefore a sufficient model for the RV. GJ 570 BC can explain the trend of –2.7 m/s (Sect. 4.3, Table 5). Also, there is a marginally significant linear correlation of the RVs with BIS and FWHM and therefore stellar activity could contribute to the trend as well.
-
HR 6416:
GJ 666 B can explain the trend of 9.4 m/s (Sect. 4.3, Table 5). A trend is a sufficient model. The residuals do not exhibit significant excess variability.
-
HR 7703:
a trend is a sufficient model and the value of 3.6 m/s (Sect. 4.3, Table 5) can be explained by GJ 783 B. Therefore the formally significant RV-
 correlation should be artificial,
however an additional (positive or negative) contribution to the trend by activity
cannot be excluded. After removing the trend, there is no significant correlation or
excess variability.
correlation should be artificial,
however an additional (positive or negative) contribution to the trend by activity
cannot be excluded. After removing the trend, there is no significant correlation or
excess variability. -
HR 8323:
the listed significant period of 1372 d is caused by a stellar magnetic cycle. All three activity indicators show similar variations and strong correlations with RVs (Fig. B.30, Tables A.4 and A.5). The observed slope of 98 ± 10 m/s/dex (Table A.4) agrees well with the predicted RV-
 sensitivity of
CRV = 108 ± 2 m/s/dex for a magnetic cycle (assuming
Teff = 5937 ± 13 K and [Fe/H] = 0.00 ± 0.01 from Sousa et al. 2008).
sensitivity of
CRV = 108 ± 2 m/s/dex for a magnetic cycle (assuming
Teff = 5937 ± 13 K and [Fe/H] = 0.00 ± 0.01 from Sousa et al. 2008). -
ϵ Ind A:
the trend for ϵ Ind A originally announced by Endl et al. (2002) is probably of highest interest, since it might be caused by a planet. The wide binary brown dwarf companion ϵ Ind B (MBa + MBb = 112 MJup, King et al. 2010) is too far from ϵ Ind A (Table 5, Sect. 4.3). It can induce only an acceleration of 0.009 m/s/yr and hence cannot explain the measured trend. The common slope of 2.4 m/s/yr is predominantly based on the more precise HARPS data. This trend improves the individual rms of the LC and VLC only slightly (see Table A.1), however the rms for both data sets is close to or below the stated precision. The scatter of the VLC data around the trend is even only 4.4 m/s, making it the most precise star in the VLC data set25. In the overall picture the trend seems to be present for the whole observation. The fit places the offset between LC and VLC at –4.0 m/s (Table A.3, visible as the small jump in the fit in Fig. 23, η = 0.52), i.e. is consistent with our physically estimated offset.
With in our sample, ϵ Ind A exhibits comparably large variations in
 (rmsRHK = 0.032 dex, Table
A.4). Since both the RVs and
(rmsRHK = 0.032 dex, Table
A.4). Since both the RVs and
 (as well as FWHM) values have a
long-term trend during the HARPS observations (Fig. B.31), this results in a significant correlation
(r = 0.60). However, both trends could coincide just by chance
temporarily, so that it is still not clear whether they are associated with the same
long-term period (if any). Note also that the last
(as well as FWHM) values have a
long-term trend during the HARPS observations (Fig. B.31), this results in a significant correlation
(r = 0.60). However, both trends could coincide just by chance
temporarily, so that it is still not clear whether they are associated with the same
long-term period (if any). Note also that the last
 observations seem to depart from a
steady trend in contrast to the RVs.
observations seem to depart from a
steady trend in contrast to the RVs. -
HR 8501:
a trend is a sufficient model and GJ 853 B can explain its value of 17.3 m/s (Sect. 4.3, Table 5). The RV-BIS correlation should be artificial and vanishes in the residuals which also do not exhibit significant variability.
-
HR 8883:
the period of 7.6 d found for the giant HR 8883 improves only the HARPS rms, but not the LC and VLC rms (Table A.1). Endl et al. (2002) found strong Ca II H&K emission in a FEROS spectrum (cf. SHK = 0.533 in Table A.2) and mentioned the high X-ray luminosity. Furthermore, the star is indicated in the Hipparcos catalogue (Perryman et al. 1997) as a photometrically variable star (variability flag “U”, i.e. unresolved variable, e.g. irregular or semi-irregular variables). Finally, the large variation of the bisector span and the striking anti-correlation (r = −0.96) with the RVs as seen in the HARPS data (Fig. 18) reveal that the variations and periods of this star are intrinsic to the giant (e.g. rotation, activity, or solar-like oscillations26). The RVs do not correlate with
 or FWHM (Tables A.4 and A.5, Fig. B.33).
or FWHM (Tables A.4 and A.5, Fig. B.33).
6. Summary and conclusion
Our sample consists of three planet hosting stars. These planets are already known and we are able to trace their periodic RV signals allowing confirmation of their reality. The planet hosting stars are ι Hor, discovered by this survey (Kürster et al. 2000), as well as HR 506 (Mayor et al.5) and HR 3259 (Lovis et al. 2006) which even has a system of three planets. However, we have no clear additional planet detection in our sample, while some promising or controversial cases like β Hyi, ϵ Ind A, or ϵ Eri call for follow-up observations.
Compared to our previous results in Endl et al. (2002), we confirm that:
-
κ For, HR 2400, and HR 3677 are SB1 spectroscopic binaries with long periods.
-
α For, HR 6416, and HR 8501 exhibits trends consistent with their wide stellar companions.
-
ϵ Ind A has a steady long-term trend still explained by a planetary companion.
Moreover, we see trends in HR 7703 and GJ 570 A which can also be explained by the known wide stellar companions listed in Table 5. However, the RV trend of 7 m/s/yr reported for β Hyi (Endl et al. 2002) is only 1.8 m/s/yr in the combined data set and is not seen in the VLC data. We cannot confirm a linear drift reported by Eggenberger et al. (2007) for α Men, neither can we confirm the planet HR 4523 b announced by Tinney et al. (2011), nor the planet ϵ Eri b reported by Hatzes et al. (2000). For ϵ Eri b, the astrometric results (Benedict et al. 2006; Reffert & Quirrenbach 2011) seem to confirm the planet, but they do not constitute independent detections, since they rely on the combination with less precise RV measurements. Also the astrometric phase coverage is not complete. However, the same is true for our HARPS measurements. Hence, this planet is not yet fully disproved with our RV non-detection or by imaging non-detections (e.g. Janson et al. 2007, 2008). Furthermore, there are also discussions whether an observed inner disk of warm dust can coexist with this inner planet (Reidemeister et al. 2011).
It has to be pointed out that stellar magnetic cycles (the solar cycle length is 2 × 11 yr)
may cause long-term RV variations which might be mistaken as companions. The CaII H&K
lines are an appropriate indicator to check this (Santos et
al. 2010; Dumusque et al. 2011a; Lovis et al. 2011). Indeed, some stars, like e.g. HR 209,
ζ1 Ret, and HR 8323 exhibit clear
RV- correlations which originates from stellar
activity and prevented us from claiming planets from the RV variations/periods. Hence, also
in the search for Jupiter analouges, it is important to monitor activity indicators.
Unfortunately, only the 4–5 yr of HARPS data contain the CaII H&K lines, so that the
whole time baseline is not covered, which would have been especially desirable for HR 506
and ι Hor.
correlations which originates from stellar
activity and prevented us from claiming planets from the RV variations/periods. Hence, also
in the search for Jupiter analouges, it is important to monitor activity indicators.
Unfortunately, only the 4–5 yr of HARPS data contain the CaII H&K lines, so that the
whole time baseline is not covered, which would have been especially desirable for HR 506
and ι Hor.
We have not detected a Jupiter analogue, while our upper mass limits demonstrate that we are sensitive to Jupiter-mass planets up to 5 AU, i.e. Jupiter analogues (Fig. 7). In our sample the planet candidate with the longest period is HR 506 b (2.7 yr). While it has a minimum mass of one Jupiter mass, its period is still 4 times shorter than that of Jupiter. Although our sample size is too small to provide a meaningful number for the occurrence rate of Jupiters and Jupiter analogues, the two Jupiter-mass planets in our sample imply that our results are in agreement with the planet frequency of other much larger surveys. For example, from the ELODIE survey Naef et al. (2005) estimated a fraction of 7.5 ± 1.5% for stars hosting giant planets with periods less than 10 yr, while Cumming et al. (2008) derived a frequency of 12 ± 1.6% from the Keck survey and Mayor et al. (2011) 9.7 ± 1.3% (for >100 M⊕) from the HARPS/CORALIE survey. For Jupiter analogues, i.e. only in the range of 3–6 AU, Lineweaver & Grether (2003) estimated a frequency of 5 ± 2% which is e.g. consistent with the discovery rate in the AAPS survey (3.3 ± 1.4%, Wittenmyer et al. 2011). Such low observed frequencies are compatible with the non-detection of a Jupiter analogue in our sample and a decreasing frequency of giant planets at larger distances (≳5 AU) is also predicted with core accretion theory (Mordasini et al. 2012).
The main reason for the limited VLC precision of ~9 m/s is the short wavelength coverage of only 39 Å. Useful iodine lines cover a total wavelength range of 1000 Å. If this 25 time larger range could have been used, the extrapolated VLC precision would be 5 times higher, i.e. 1.8 m/s. The actively stabilised HARPS spectrograph has a larger wavelength coverage and an outperforming precision. The higher resolution of the CES+VLC is not necessarily an advantage because the stellar lines are nearly resolved already at the lower resolution of HARPS, i.e. they become not sharper and therefore do not provide much more RV information27. Nevertheless the CES data are valuable for extending the time baseline to 15 years.
The problem of combining long-term precision RV data from different instruments complicates the analysis. We could derive the zero point offset between LC and VLC only with a limited precision which leads to a loss of sensitivity for trends and long periods. However, this problem can occur in long-term surveys quite frequently as spectrographs receive upgrades or survey projects are transferred to new instruments. Long-term access to the same instrument/instrument configuration is therefore important.
While the RV method probes the inner region of the stellar environment, the outer regions can be explored for planets with direct imaging. Since both methods complement each other, their combination leads to a more complete picture about the existence and nature of planets around stars. An example is ϵ Ind A, where despite the high imaging sensitivity with HST/NICMOS and VLT/NACO (Geißler et al. 2007; Janson et al. 2009) the non-detection puts constraints to the companion which induces the observed RV trend of 2.4 m/s/yr. Hence the results and detection limits from our survey can be valuable for other campaigns which target these bright stars.
Some of our nearby and bright stars are also the subject of projects searching and studying surrounding debris disks. Structures in these disks permit conclusions about the presence of outer planets. For example, the Herschel satellite has resolved exo-Kuiper belts around ζ2 Ret (Eiroa et al. 2010) and around HR 506 (q1 Eri, Liseau et al. 2010). In the case of the RV planet-hosting star HR 506, the structure of a ring at 35–40 AU provides a hint for another planet. Similarly, the structure of the known debris disk of ϵ Eri suggests an outer planet (Quillen & Thorndike 2002). But then for HR 8501 that has an RV trend likely due to its wide stellar companion, Eiroa et al. (2010) exclude a cold debris disk.
Online material
Appendix A: Accompanying tables
Residual rms detailed for each instrument resulting from the joint analysis for fitting a constant, slope, sinusoid, and Keplerian orbit.
Jitter estimation.
Offset differences cVLC − cLC [m/s] in the fits.
Correlations of RV with  and BIS for the HARPS data.
and BIS for the HARPS data.
Correlations of RV with FWHM for the HARPS data.
Appendix B: HARPS time series and correlation plots for RVs,
log  , and BIS
, and BIS
 |
Fig. B.1 Activity indictors and correlations with HARPS RVs for ζ Tuc (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.2 Activity indictors and correlations with HARPS RVs for β Hyi (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.3 Activity indictors and correlations with HARPS RVs for HR 209 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.4 Activity indictors and correlations with HARPS RVs for ν Phe (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.5 Activity indictors and correlations with HARPS RVs for HR 506 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.6 Activity indictors and correlations with HARPS RVs for the HR 506 residuals (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.7 Activity indictors and correlations with HARPS RVs for τ Cet (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.8 Activity indictors and correlations with HARPS RVs for κ For (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.9 Activity indictors and correlations with HARPS RVs for ι Hor (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.10 Activity indictors and correlations with HARPS RVs for the ι Hor residuals (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.11 Activity indictors and correlations with HARPS RVs for α For (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.12 Activity indictors and correlations with HARPS RVs for ζ1 Ret (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.13 Activity indictors and correlations with HARPS RVs for ζ2 Ret (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.14 Activity indictors and correlations with HARPS RVs for ϵ Eri (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.15 Activity indictors and correlations with HARPS RVs for δ Eri (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.16 Activity indictors and correlations with HARPS RVs for α Men (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.17 Activity indictors and correlations with HARPS RVs for HR 2400 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.18 Activity indictors and correlations with HARPS RVs for HR 2667 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.19 Activity indictors and correlations with HARPS RVs for HR 3259 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.20 Activity indictors and correlations with HARPS RVs for HR 3677 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.21 Activity indictors and correlations with HARPS RVs for HR 4523 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.22 Activity indictors and correlations with HARPS RVs for HR 4979 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.23 Activity indictors and correlations with HARPS RVs for α Cen A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.24 Activity indictors and correlations with HARPS RVs for α Cen B (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.25 Activity indictors and correlations with HARPS RVs for GJ 570A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.26 Activity indictors and correlations with HARPS RVs for HR 6416 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.27 Activity indictors and correlations with HARPS RVs for HR 6998 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.28 Activity indictors and correlations with HARPS RVs for HR 7703 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.29 Activity indictors and correlations with HARPS RVs for φ2 Pav (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.30 Activity indictors and correlations with HARPS RVs for HR 8323 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.31 Activity indictors and correlations with HARPS RVs for ϵ Ind A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.32 Activity indictors and correlations with HARPS RVs for HR 8501 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
 |
Fig. B.33 Activity indictors and correlations with HARPS RVs for HR 8883 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
The planet was confirmed by Vogt et al. (2005) who revised the semi-major axis to 3.9 AU and discovered a second inner planet (17.1 d, 0.057 MJup).
HR 3677 and HR 8883 were indicated in the Bright Star Catalogue as dwarf stars (Hoffleit & Jaschek 1991). Therefore they entered our sample, however they are giants as indicated by their distances.
HR 506b was announced by Mayor et al. at the XIX th IAP Colloquium in Paris (2003). We found no refereed publication. Information is available on http://obswww.unige.ch/~udry/planet/hd10647.html.
This effect looks similar to charge transfer inefficiency (CTI), which can also cause RV shifts of several m/s (Bouchy et al. 2009b). However, CTI is caused by local defects on the CCD itself.
Systematics in absolute (spectroscopic) RVs arise e.g. from the stellar mask, gravitational red shift and convective blue shift of the star (e.g. Pourbaix et al. 2002).
This template was used in the modelling and obtained via deconvolution from a stellar spectrum taken without iodine cell as described in Endl et al. (2002).
For one simultaneous measurement taken at the time
ts, this term could be written as
 where c is the zero point
parameter, ΔRV(ts) are the individual errors
of the simultaneous measurements, and the indices H (HARPS) and VLC indicate the
instruments. The VLC time series must be a priori adjusted by a zero point such that
RVVLC(ts): = RVH(ts).
where c is the zero point
parameter, ΔRV(ts) are the individual errors
of the simultaneous measurements, and the indices H (HARPS) and VLC indicate the
instruments. The VLC time series must be a priori adjusted by a zero point such that
RVVLC(ts): = RVH(ts).
There is also meso- and supergranulation (life times up to ~30 h) which take place on different size scales Dumusque et al. (2011b).
Note however, that the square root of this variance,
 is not a unbiased estimate of the
population standard deviation (Deakin & Kildea
1999).
is not a unbiased estimate of the
population standard deviation (Deakin & Kildea
1999).
We list the formal, analytic FAP for the Keplerian orbits, but we do not highlight them in the table. As remarked in Zechmeister & Kürster (2009), this FAP is likely to be underestimated due to an underestimated number of independent frequencies. Also Keplerian solutions tend to fit outliers (likely orginating from non-Gaussian noise) making them less robust for period search.
For a Gaussian fit the mean parameter errors for centre (RV) and width
(s) are the same
σRV = σs
(e.g. Eq. (5.8) in Kaper et al. 1966). Moreover,
since for a Gaussian function  , we have
σFWHM = 2.35σRV.
, we have
σFWHM = 2.35σRV.
 where the sensitivity
CRV = CRV(Teff, [Fe/H])
is given by Eq. (9) in Lovis et al. (2011).
where the sensitivity
CRV = CRV(Teff, [Fe/H])
is given by Eq. (9) in Lovis et al. (2011).
ϵ Ind A has the spectral type K which has numerous stellar lines (high quality factor Q, Bouchy et al. 2001) allowing more precise RV measurements.
With a mass estimate of 2.1 M⊙ (Table 1) and a luminosity estimate of
L = 60 L⊙ from visual magnitude V,
distance (Table 1), and bolometric correction
–0.34 mag (Cox 2000), we obtain with scaling
relations for solar-like oscillations (Kjeldsen &
Bedding 1995) an amplitude of  m/s.
m/s.
The thermal line broadening of a line with frequency f is given by
(e.g. Unsöld & Baschek 2002)  and depends on the temperature T and the atomic/molecular
mass m. Therefore resolving hydrogen lines
(mH = 1 amu) in a solar-like star (T = 6000
K) requires a resolution of
and depends on the temperature T and the atomic/molecular
mass m. Therefore resolving hydrogen lines
(mH = 1 amu) in a solar-like star (T = 6000
K) requires a resolution of  and for iron lines
(mFe = 56 amu) R = 135 000. A higher
resolution as provided by the CES leads to an oversampling or stretching of the lines but
does not resolve new lines or sharper features which would improve the RV measurements.
Contrariwise, for iodine gas (T = 323 K,
mI2 = 154 amu) the thermal line broadening
effect corresponds to R = 2 400 000.
and for iron lines
(mFe = 56 amu) R = 135 000. A higher
resolution as provided by the CES leads to an oversampling or stretching of the lines but
does not resolve new lines or sharper features which would improve the RV measurements.
Contrariwise, for iodine gas (T = 323 K,
mI2 = 154 amu) the thermal line broadening
effect corresponds to R = 2 400 000.
Acknowledgments
We are grateful to K. Dennerl and S. Döbereiner for their help with obtaining CES-LC data in the early phase of the survey as well as F. Rodler for obtaining CES-VLC and HARPS data. S. Els helped with the CES-VLC observation and the data reduction. We thank G. Anglada-Escudé for his useful hints and discussions and for providing the HARPS-TERRA software. Discussions with P. Bristow, D. Baade, and P. Sinclair on VLC-CCD effects are gratefully acknowledged. We are thankful to the ESO OPC for generous allocation of observing time to the CES/HARPS planet search programme. M.Z. acknowledges financial support from the Deutsche Forschungsgemeinschaft (DFG) under RE 1664/4-1. The Lund Observatory obtained the IRFTS with support from Knut and Alice Wallenberg Foundation. H.H. and H.N. acknowledge support from the Swedish Research Council (VR) through contract 621-2006-3085 and Linnaeus Grant through Lund Laser Centre.
References
- Anglada-Escudé, G., & Butler, R. P. 2012, ApJS, 200, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Baize, P., & Petit, M. 1989, A&AS, 77, 497 [NASA ADS] [Google Scholar]
- Baluev, R. V. 2013, MNRAS, 429, 2052 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Gatewood, G., et al. 2006, AJ, 132, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Pepe, F., Perrier, C., et al. 2012, A&A, 545, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Pepe, F., & Queloz, D. 2001, A&A, 374, 733 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Hébrard, G., Udry, S., et al. 2009a, A&A, 505, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Isambert, J., Lovis, C., et al. 2009b, in EAS Pub. Ser., 37, ed. P. Kern, 247 [Google Scholar]
- Buccino, A. P., & Mauas, P. J. D. 2008, A&A, 483, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burgasser, A. J., Kirkpatrick, J. D., Cutri, R. M., et al. 2000, ApJ, 531, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Tinney, C. G., Marcy, G. W., et al. 2001, ApJ, 555, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Connes, P. 1985, Ap&SS, 110, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, S&T, 100, 72 [Google Scholar]
- Cumming, A. 2004, MNRAS, 354, 1165 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Deakin, R. E., & Kildea, D. G. 1999, The Australian Surveyor, 44, 74 [Google Scholar]
- del Peloso, E. F., da Silva, L., & Porto de Mello, G. F. 2000, A&A, 358, 233 [NASA ADS] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., & Smith, G. 1993, ApJ, 412, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Dravins, D., Lindegren, L., & Vandenberg, D. A. 1998, A&A, 330, 1077 [NASA ADS] [Google Scholar]
- Dumusque, X., Lovis, C., Udry, S., & Santos, N. C. 2011a, in IAU Symp., 276, eds. A. Sozzetti, M. G. Lattanzi, & A. P. Boss, 530 [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011b, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Eggenberger, A., Udry, S., Chauvin, G., et al. 2007, A&A, 474, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eiroa, C., Fedele, D., Maldonado, J., et al. 2010, A&A, 518, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Enard, D. 1982, in Presented at the SPIE Conf., 331, 232 [Google Scholar]
- Endl, M., Kürster, M., & Els, S. 2000, A&A, 362, 585 [Google Scholar]
- Endl, M., Kürster, M., Els, S., et al. 2002, A&A, 392, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Favata, F., Micela, G., & Sciortino, S. 1997, A&A, 323, 809 [NASA ADS] [Google Scholar]
- Fröhlich, H. 2007, Astron. Nachr., 328, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Geißler, K., Kellner, S., Brandner, W., et al. 2007, A&A, 461, 665 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 1988, Lectures on spectral-line analysis: F, G, and K stars [Google Scholar]
- Hatzes, A. P., Cochran, W. D., McArthur, B., et al. 2000, ApJ, 544, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Heintz, W. D. 1978, ApJS, 37, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffleit, D., & Jaschek, C. 1991, The Bright star catalogue, Yale University Observatory [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Brandner, W., Henning, T., et al. 2007, AJ, 133, 2442 [NASA ADS] [CrossRef] [Google Scholar]
- Janson, M., Reffert, S., Brandner, W., et al. 2008, A&A, 488, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janson, M., Apai, D., Zechmeister, M., et al. 2009, MNRAS, 399, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Jefferys, W. H., Fitzpatrick, M. J., & McArthur, B. E. 1988, Celestial Mechanics, 41, 39 [Google Scholar]
- Jones, H. R. A., Butler, R. P., Tinney, C. G., et al. 2004, in Extrasolar Planets: Today and Tomorrow, eds. J. Beaulieu, A. Lecavelier Des Etangs, & C. Terquem, ASP Conf. Ser., 321, 298 [Google Scholar]
- Kaper, H. G., Smits, D. W., Schwarz, U., Takakubo, K., & van Woerden, H. 1966, Bull. Astron. Inst. Netherlands, 18, 465 [NASA ADS] [Google Scholar]
- King, R. R., McCaughrean, M. J., Homeier, D., et al. 2010, A&A, 510, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kürster, M., Endl, M., Els, S., et al. 2000, A&A, 353, L33 [NASA ADS] [Google Scholar]
- Kürster, M., Endl, M., Rouesnel, F., et al. 2003, A&A, 403, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lineweaver, C. H., & Grether, D. 2003, ApJ, 598, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R., Eiroa, C., Fedele, D., et al. 2010, A&A, 518, L132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Mayor, M., Pepe, F., et al. 2006, Nature, 441, 305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, A&A, submitted [arXiv:1107.5325] [Google Scholar]
- Luyten, W. J., & Hughes, H. S. 1980, in Proper motion survey with the forty-eight inch Schmidt telescope. LV. First supplement to the NLTT catalogue, University of Minnesota, Minneapolis [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2008, Phys. Scr. T, 130, 014001 [CrossRef] [Google Scholar]
- Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Metcalfe, T. S., Basu, S., Henry, T. J., et al. 2010, ApJ, 723, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Mayor, M., Pepe, F., et al. 2001, A&A, 375, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Mayor, M., Korzennik, S. G., et al. 2003, A&A, 410, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Mayor, M., Beuzit, J., et al. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 833 [Google Scholar]
- Naef, D., Mayor, M., Lo Curto, G., et al. 2010, A&A, 523, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Toole, S. J., Jones, H. R. A., Tinney, C. G., et al. 2009, ApJ, 701, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Mayor, M., Queloz, D., et al. 2004, A&A, 423, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Piskunov, N., Edvardsson, B., Magain, P., & Swings, J. P. 1997, http://www.astro.uu.se/obs_ast/ces/ [Google Scholar]
- Pourbaix, D., Nidever, D., McCarthy, C., et al. 2002, A&A, 386, 280 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poveda, A., Herrera, M. A., Allen, C., Cordero, G., & Lavalley, C. 1994, Rev. Mex. Astron. Astrofis., 28, 43 [NASA ADS] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., & Thorndike, S. 2002, ApJ, 578, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Reffert, S., & Quirrenbach, A. 2011, A&A, 527, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reidemeister, M., Krivov, A. V., Stark, C. C., et al. 2011, A&A, 527, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivera, E. J., Butler, R. P., Vogt, S. S., et al. 2010, ApJ, 708, 1492 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlesinger, F. 1917, AJ, 30, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, R., McCaughrean, M. J., Lodieu, N., & Kuhlbrodt, B. 2003, A&A, 398, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ségransan, D., Udry, S., Mayor, M., et al. 2010, A&A, 511, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shporer, A., Winn, J. N., Dreizler, S., et al. 2010, ApJ, 722, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Standish, Jr., E. M. 1990, A&A, 233, 252 [NASA ADS] [Google Scholar]
- Teixeira, T. C., Kjeldsen, H., Bedding, T. R., et al. 2009, A&A, 494, 237 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinney, C. G., Butler, R. P., Jones, H. R. A., et al. 2011, ApJ, 727, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Unsöld, A., & Baschek, B. (eds.) 2002, in Der neue Kosmos (Berlin: Springer-Verlag) [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vauclair, S., Laymand, M., Bouchy, F., et al. 2008, A&A, 482, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2005, ApJ, 632, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Wittenmyer, R. A., Butler, R. P., et al. 2010, ApJ, 708, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G. A. H., Walker, A. R., Irwin, A. W., et al. 1995, Icarus, 116, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Endl, M., Cochran, W. D., et al. 2006, AJ, 132, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Wittenmyer, R. A., Tinney, C. G., O’Toole, S. J., et al. 2011, ApJ, 727, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Worley, C. E., & Douglass, G. G. 1997, A&AS, 125, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApjS, 152, 261 [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 683, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Targets with their spectral type SpT (Hoffleit &
Jaschek 1991), visual magnitude V (Perryman et al. 1997), distance d (van Leeuwen 2007), secular acceleration
 ,
and stellar mass M.
,
and stellar mass M.
The three used instruments/configurations with their wavelength reference, chosen spectral coverage and resolving power, and telescope diameter.
Summary of the tests for excess variability, slope, and periodicities (sinusoidal and Keplerian) for the combined data set.
Residual rms detailed for each instrument resulting from the joint analysis for fitting a constant, slope, sinusoid, and Keplerian orbit.
All Figures
 |
Fig. 1 A small section of a VLC raw spectrum (star seen through the iodine cell; broad absorption features are stellar lines whereas narrow lines were introduced by the molecular iodine gas). The 14 slices span 400 pixels. The bright feature to the left near pixel row 2300 is a grating ghost. The area on the left side has a lower bias. The readout register is in the lower right corner of the chip (parallel clocking down, serial clocking to the right). Deeper stellar lines near row 2300 and 2700 have tails to the left and right. The intensity scale is non-linear to bring out the discussed effects. |
| In the text | |
 |
Fig. 2 Spatial profile of a VLC spectrum (cross-section for the rows 2400–2410 of the raw spectrum in Fig. 1; linear intensity scale). |
| In the text | |
 |
Fig. 3 A VLC spectrum of τ Cet (without iodine cell) and the arrangement of the 200 pixel chunks with their individual Q-factors (blue squares). The intensity maximum of the spectrum is set to unity. The intensity declines to the edges due to instrumental effects (Blaze function). |
| In the text | |
 |
Fig. 4 Difference between the means of the VLC and re-computed LC time series for all our stars ordered by spectral type. For RV constant stars (black filled circles) there occurs a systematic offset of 10.4 ± 7.7 m/s (red solid line and red dashed lines). Stars shown with open circles were not included in the offset analysis (for reasons see comments in Table 3). The shown error bars correspond to the uncertainty in the means, i.e. parameter s from Eq. (1). |
| In the text | |
 |
Fig. 5 GLS (top) and Keplerian (bottom) periodogram for HR 2667 which is constant to 3.1 m/s. The horizontal lines mark the 10-2, 10-3, and 10-4 false alarm probabilities (FAP). |
| In the text | |
 |
Fig. 6 Detection limit for HR 2667 considering circular orbits. The cross marks the distance and msini of a Jupiter analogue for i = 90°. The vertical lines indicate the time baseline of the HARPS and all combined measurements, respectively. |
| In the text | |
 |
Fig. 7 Sensitivity of the survey. For each orbital distance the minimum mass is indicated that could have been detected for 4, 19, and 28 stars of the 31 stars (corresponding to a fraction of 13%, 61%, and 90%) with 99.9% significance. The cross marks again a Jupiter analogue. |
| In the text | |
 |
Fig. 8 Left: RV time series for HR 506 combined with AAT and CORALIE data. Right: RVs phase folded to the period of P = 995 d and the residuals (bottom). |
| In the text | |
 |
Fig. 9 (Left) RV time series for ι Hor combined with AAT and CORALIE data. (Right) RVs phase folded to the period of P = 307 d and the residuals (bottom). |
| In the text | |
 |
Fig. 10 S-index measurements for ι Hor. Metcalfe et al. (2010) published the SMARTS data (blue open circles) and the 566 d period (dotted line). The formal best fit for the combined data set is 630 d (dashed line). |
| In the text | |
 |
Fig. 11 RV vs. BIS for ι Hor. (Top) The linear correlation coefficient is r = −0.53, but the correlation appears more complex and loop-like. (Bottom) After subtracting the 307 d period from the RVs, r is − 0.56. |
| In the text | |
 |
Fig. 12 GLS periodogram on the residuals for ι Hor. In this and the subsequent figures (Figs. 13–15) the horizontal dashed lines depict FAP levels as in Fig. 5. |
| In the text | |
 |
Fig. 13 GLS periodogram for ζ1 Ret. |
| In the text | |
 |
Fig. 14 GLS (top) and Keplerian (bottom) periodogram for ϵ Eri. There is no significant power at the period of the putative planet ϵ Eri b (P = 2500 d). |
| In the text | |
 |
Fig. 15 GLS periodogram for HR 3259. The vertical arrows indicate the periods for the three planets announced by Lovis et al. (2006). |
| In the text | |
 |
Fig. 16 RV data for HR 4523 phase folded to 122.1 d. The dashed curve is an orbital solution proposed by Tinney et al. (2011) based on the UCLES data. HARPS RVs are shown for comparison. |
| In the text | |
 |
Fig. 17 The time behaviour of |
| In the text | |
 |
Fig. 18 Correlation between bisector span (BIS) and RV for the giant HR 8883. |
| In the text | |
 |
Fig. 19 Radial velocity time series (unbinned data). The error bars depict the internal measurement errors ΔRVi, i.e. not including jitter. LC (green open circles) and VLC (blue open diamonds) data are displayed with their measured offsets. Jumps in the curves indicates the difference between the measured (Sect. 3.5) and fitted (Sect. 4) LC-VLC offset. HARPS data are in red filled circles. The solid lines indicate significant models, while dashed lines illustrate less or non-significant alternative models. All models include secular acceleration. Model curves are shown for β Hyi (trend and long-period sinusoid, see text for discussion), and HR 506 (sinusoid). |
| In the text | |
 |
Fig. 20 Radial velocities. Continuation of Fig. 19. Model curves are shown for κ For (Keplerian), ι Hor (Keplerian), and α For (trend). The Keplerian orbit for ϵ Eri taken from Hatzes et al. (2000) is not significant in this work. |
| In the text | |
 |
Fig. 21 Radial velocities. Continuation of Figs. 19 and 20. Model curves are shown for HR 2400 (Keplerian) and HR 3677 (Keplerian). |
| In the text | |
 |
Fig. 22 Radial velocities. Continuation of Figs. 19–21. Model curves are shown for α Cen A and α Cen B (Keplerian orbit from Pourbaix et al. 2002), GJ 570 A (trend), and HR 6416 (trend). |
| In the text | |
 |
Fig. 23 Radial velocities. Continuation of Figs. 19–22. Model curves are shown for HR 7703 (trend), HR 8323 (sinusoid), ϵ Ind A (constant, i.e. only secular acceleration of 1.86 m/s/yr, and trend), and HR 8501 (trend). |
| In the text | |
 |
Fig. 24 Residual RVs (binned as described in Sect. 4) for the spectroscopic binaries. |
| In the text | |
 |
Fig. B.1 Activity indictors and correlations with HARPS RVs for ζ Tuc (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.2 Activity indictors and correlations with HARPS RVs for β Hyi (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.3 Activity indictors and correlations with HARPS RVs for HR 209 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.4 Activity indictors and correlations with HARPS RVs for ν Phe (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.5 Activity indictors and correlations with HARPS RVs for HR 506 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.6 Activity indictors and correlations with HARPS RVs for the HR 506 residuals (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.7 Activity indictors and correlations with HARPS RVs for τ Cet (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.8 Activity indictors and correlations with HARPS RVs for κ For (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.9 Activity indictors and correlations with HARPS RVs for ι Hor (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.10 Activity indictors and correlations with HARPS RVs for the ι Hor residuals (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.11 Activity indictors and correlations with HARPS RVs for α For (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.12 Activity indictors and correlations with HARPS RVs for ζ1 Ret (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.13 Activity indictors and correlations with HARPS RVs for ζ2 Ret (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.14 Activity indictors and correlations with HARPS RVs for ϵ Eri (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.15 Activity indictors and correlations with HARPS RVs for δ Eri (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.16 Activity indictors and correlations with HARPS RVs for α Men (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.17 Activity indictors and correlations with HARPS RVs for HR 2400 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.18 Activity indictors and correlations with HARPS RVs for HR 2667 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.19 Activity indictors and correlations with HARPS RVs for HR 3259 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.20 Activity indictors and correlations with HARPS RVs for HR 3677 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.21 Activity indictors and correlations with HARPS RVs for HR 4523 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.22 Activity indictors and correlations with HARPS RVs for HR 4979 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.23 Activity indictors and correlations with HARPS RVs for α Cen A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.24 Activity indictors and correlations with HARPS RVs for α Cen B (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.25 Activity indictors and correlations with HARPS RVs for GJ 570A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.26 Activity indictors and correlations with HARPS RVs for HR 6416 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.27 Activity indictors and correlations with HARPS RVs for HR 6998 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.28 Activity indictors and correlations with HARPS RVs for HR 7703 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.29 Activity indictors and correlations with HARPS RVs for φ2 Pav (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.30 Activity indictors and correlations with HARPS RVs for HR 8323 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.31 Activity indictors and correlations with HARPS RVs for ϵ Ind A (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.32 Activity indictors and correlations with HARPS RVs for HR 8501 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
 |
Fig. B.33 Activity indictors and correlations with HARPS RVs for HR 8883 (2 h binned data, secular acceleration substracted, see Sect. 4.1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.












