| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 4 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201116542 | |
| Published online | 15 March 2013 | |
Research Note
Properties of multistranded, impulsively heated hydrodynamic loop models
1 INAF – Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese (TO), Italy
e-mail: sur@oact.inaf.it
2 INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
3 Dipartimento di Fisica e Astronomia – Sezione Astrofisica, Università di Catania, via S. Sofia 78, 95123 Catania, Italy
Received: 19 January 2011
Accepted: 8 February 2013
Aims. We investigate the capability of multistranded loop models subject to nanoflare heating to reproduce the properties recently observed in coronal loops at extreme ultraviolet (EUV) wavelengths.
Methods. One-dimensional hydrodynamic simulations of magnetic loop strands were performed with an impulsive, footpoint-localised heating, with a moderate asymmetry between the two loop halves that was produced either by a sequence of identical nanoflares with a given cadence time tC or by a single energy pulse. The temporal evolution of the emission of a multistranded loop was modelled by simply combining the results of independent single-strand simulations, neglecting any spatial interaction among the strands, and was compared with TRACE and SDO/AIA light curves. The density excess with respect to hydrostatic equilibrium (the ψ factor) was evaluated with the filter-ratio technique.
Results. Both loop models exhibit a density excess compared with hydrostatic equilibrium models, which agrees well with the observed values (1 ≲ ψ ≲ 12). However, in the single-pulse model the light curve and density excess maxima do not match. On the other hand, the models with a sequence of nanoflares predict strong emission at lower temperatures that cannot be reconciled with the available observations.
Key words: hydrodynamics / Sun: corona / Sun: UV radiation / methods: numerical
© ESO, 2013
1. Introduction
Observations of coronal loops made at extreme ultraviolet (EUV) wavelengths with the Transition Region And Coronal Explorer (TRACE; Lenz et al. 1999) showed two results that could not be explained by the classical uniform steady-heating model proposed by Rosner et al. (1978). Observed loops are (1) overdense compared with steady-state loop models; and (2) nearly isothermal along their length. These results have been used as strong evidence in support of footpoint-localised, impulsive-heating models, such as the nanoflare model (e.g., Klimchuk 2006). This model is based on the nanoflare heating paradigm as proposed by Parker (1988).
In addition, the observational evidence that loops are generally long-lived (see, e.g. Winebarger et al. 2003) suggests that coronal loops are bundles of individual unresolved threads, heated separately at different times and possibly by different processes – i.e., they are multistranded (e.g., Patsourakos & Klimchuk 2006).
However, Weber et al. (2005) suggested that the higher densities and smaller temperature gradients observed in TRACE loops were the result of applying an isothermal analysis – using the 171-to-195 filter-ratio technique – to a truly multithermal plasma. Schmelz et al. (2010) recently confirmed this suggestion with the 171-to-193 filter-ratio analysis of a loop segment observed with the Atmospheric Imaging Assembly (AIA; e.g., Boerner et al. 2011; Lemen et al. 2011) onboard the Solar Dynamics Observatory (SDO).
In this work, we study two different multistrand models of coronal loops subject to footpoint-localised, impulsive heating with a moderate asymmetry between the two loop halves, neglecting any spatial interaction among the single strands, and apply the filter-ratio technique to derive the “observed” temperature and density of the loop. We describe the density evolution and that of the intensities predicted from the models in the UV and EUV passbands of TRACE and SDO/AIA, and compare them with observations to investigate whether they are capable of reproducing the UV/EUV properties of coronal loops. We show that both models satisfy the observational evidence of overdensity, compared to the hydrostatic equilibrium, although they present several aspects that disagree with current observations.
2. Numerical model
2.1. Hydrodynamic simulations
Parameters of the simulations.
The dynamics of the plasma confined in a magnetic flux tube with a coronal half-length L = 40 Mm and a constant cross-section S = 1015 cm2 was computed with the Adaptively Refined Godunov Solver (ARGOS; see Antiochos et al. 1999) hydro code. The temporal evolution of the temperature T, the electron density n, and the velocity v of the plasma particles, as functions of the space coordinate s along the flux tube, was derived after applying an additional heating term to an initially static loop with an apex temperature Tmax ≃ 0.75 MK and a typical coronal structure (see, e.g., Rosner et al. 1978), obtained with a spatially uniform and constant background heating Ebase = 2 × 10-5 erg cm-3 s-1. The additional heating was chosen to be localised near the loop chromospheric footpoints1. A moderate heating asymmetry between the two footpoints of the flux tube is introduced by specifying an asymmetry parameter f, which expresses the constant ratio of the localised heating at, e.g., the right footpoint to that at the left one. We refer to Susino et al. (2010, hereafter Paper I) for details on the numerical model used for this work.
We discuss two distinct models: model A, in which the additional heating is produced by a single energy pulse, and model B, in which it is produced by a sequence of identical nanoflares. In the last case, the cadence, tC, and the duration, tP, of the energy pulses are kept constant throughout the simulation. In both cases, the heating in the right half of the loop is 75% of that in the left half. The key parameters of the two simulations are listed in Table 1. Models A and B were selected from a series of numerical simulations in which the heating parameters were thoroughly explored. We considered different values for tC (from 250 to 2000 s), EP (from 0.125 to 8 × 1024 erg), and tP (from 125 to 500 s). We also explored the cases f = 1 (symmetric heating) and f = 0.25 (strongly asymmetric heating). The two models were therefore chosen on the basis of their better agreement with the typical properties of observed loops.
2.2. EUV emission
Spatial distributions of the emission and light curves in the AIA and TRACE EUV channels are obtained directly from the single-strand simulations using the relationship ![\begin{equation} I=D\cdot n^2G(T)\ \left[{\rm DN}\ \mathrm{s}^{-1}\ \mathrm{px}^{-1}\right], \end{equation}](/articles/aa/full_html/2013/04/aa16542-11/aa16542-11-eq23.png) (1)where D is the diameter of the loop cross-section and G(T) is the instrument response function for the considered channel. The response functions for the TRACE and AIA passbands (see, e.g., Handy et al. 1999; Boerner et al. 2011) were calculated as functions of the plasma temperature using the Solarsoft routines trace_t_resp.pro and aia_get_response.pro.
(1)where D is the diameter of the loop cross-section and G(T) is the instrument response function for the considered channel. The response functions for the TRACE and AIA passbands (see, e.g., Handy et al. 1999; Boerner et al. 2011) were calculated as functions of the plasma temperature using the Solarsoft routines trace_t_resp.pro and aia_get_response.pro.
A different approach was used to estimate the emission from the UV channels at 1600 Å. The local instantaneous intensity I was calculated by convolving the Solarsoft response functions of the TRACE and AIA 1600 filters with a synthetic spectrum derived from the models. The synthetic spectrum was obtained by summing the free-free and free-bound continua in the spectral range corresponding to the bands – calculated with the CHIANTI (Dere et al 1997, 2009) routines freefree.pro and freebound.pro – to the spectral profiles of the C iv resonance doublet lines at 1548 and 1550 Å, which are the two most intense lines that contribute to the emission in this spectral range. Carbon lines were synthesised from the model according to the collisional-radiative theory approach (see, e.g., Lanza et al. 2001) and taking into account possible deviations from the ionisation equilibrium caused by flows across temperature gradients in the loop and temporal variations of temperature and density in the loop plasma2.
The light curves were obtained by averaging the synthesised intensity along the upper 75% of the coronal portion of the loop, to exclude the contribution from the transition regions at the footpoints.
2.3. Multistranded models
We reconstructed the evolution of a multistranded loop as follows. We assumed that, for the sake of simplicity, all strands belonging to a synthesised loop are identical, except for the switch-on time of the heating. We considered a loop consisting of N = 300 strands, all in the same initial, quasi-static state as in the single strand-simulations.
We turned on the additional heating in each of the elemental strands at a time taken from a uniformly distributed random sequence between 0 and Δt and computed the emission in the SDO/AIA and TRACE passbands by summing the intensities of all strands at a given location and time. We summed both the original models, which are heated more in the right footpoint, and their symmetric with respect to the loop midpoint, which are heated more in the left footpoint. No spatial interaction among the strands was considered.
A critical parameter of the multistranded model is the time delay Δt between the onset of the additional heating in the first strand and that in the last one. If Δt is too short, the strands would be heated roughly in phase, leading to highly concentrated emission along the loop axis, whereas a high value of Δt would produce much more uniform intensity distributions and a longer lifetime of the entire bundle. In this investigation, we considered Δt = 1000 s, which eventually agrees best with the typical lifetimes of warm loops observed in the 171 Å and 195 Å bands of TRACE.
2.4. Density excess factor
To quantify the over/under-dense conditions of the loop with respect to the hydrostatic equilibrium, we defined a density excess factor, ψ, as (see Klimchuk et al. 2010) 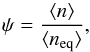 (2)where the angle brackets denote the average of the quantities along the upper 75% of the coronal part of the flux tube and ⟨ neq ⟩ is given by
(2)where the angle brackets denote the average of the quantities along the upper 75% of the coronal part of the flux tube and ⟨ neq ⟩ is given by 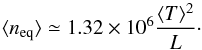 (3)Here L is the loop half-length (in cm). Equation (3) is derived from the Rosner et al. (1978) scaling-law, upon substituting for the pressure using the ideal gas law.
(3)Here L is the loop half-length (in cm). Equation (3) is derived from the Rosner et al. (1978) scaling-law, upon substituting for the pressure using the ideal gas law.
We calculated ⟨ n ⟩, ⟨ T ⟩, and in turn the density excess factor ψ, with the filter-ratio technique. For each time, we inferred the temperature and emission measure, EM, at each position along the strand using the ratio of the TRACE 171 and 195 intensities, and that of the AIA 171 and 193 intensities (following, e.g., Lenz et al. 1999; Schmelz et al. 2010). The density was then derived from the emission measure according to 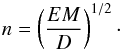 (4)As already pointed out by Klimchuk et al. (2010), determining ψ very likely yields an underestimate of the loop overdensity, since Eq. (3) is an idealised scaling law based on the approximate form of the radiative-loss function, the assumption of no gravitational stratification, and spatially uniform heating. Moreover, Eq. (4) assumes a filling-factor of unity, meaning that the resulting density is a lower limit.
(4)As already pointed out by Klimchuk et al. (2010), determining ψ very likely yields an underestimate of the loop overdensity, since Eq. (3) is an idealised scaling law based on the approximate form of the radiative-loss function, the assumption of no gravitational stratification, and spatially uniform heating. Moreover, Eq. (4) assumes a filling-factor of unity, meaning that the resulting density is a lower limit.
 |
Fig. 1 Synthesised TRACE and AIA intensities (top panel) and density excess factors (bottom panel) as functions of time from the start of the additional heating for model A. TRACE 171 and 195 curves are plotted with dashed lines, SDO/AIA curves with solid lines. The temperatures corresponding to the peaks of the response functions of TRACE and AIA filters are reported in the inset in the top panel. |
3. Results and discussion
Figure 1 shows the light curves in the TRACE and AIA bandpasses together with the density excess factors, as obtained for loop model A (see Table 1).
The loop brightens sequentially from the hotter to the cooler bands as time progresses, as expected for a cooling loop (see, e.g., the light curves of loops 3 and 5 in Winebarger et al. 2003). The time delay between the appearance in the channels 195 and 171 of TRACE, or in the corresponding channels 193 and 171 of AIA, is of about 10 min, in agreement with recent SDO/AIA observations of active region loops (e.g., Viall & Klimchuk 2012). The lifetime of the emission in the two 171 filters, assumed to be equal to the FWHM of a Gaussian fitting the light curve (e.g., Winebarger et al. 2003) is of about 30 min. This values is close to the lower limit of the range of the measured lifetimes, which span from ~1000 s to ~5000 s or longer. The sequence of AIA intensity peaks (211-193-171) is even similar to that obtained both from loop models with nanoflare storm heating (Viall & Klimchuk 2011) and from recent loop observations (e.g., Viall & Klimchuk 2011, 2012; Kamio et al. 2011).
The lack of emission in the 94 and 335 filters of AIA is ascribed to the fact that the response functions for these channels have a dominant component at relatively high temperatures (log T > 6.3), well above the highest temperature reached by the model (log T ≃ 6.1). The emission in the 131, 304, and 1600 filters of AIA is negligible as well, since these channels are principally sensitive to plasma with temperatures below log T ≃ 5.8, i.e., lower than the initial apex temperature of our model. Note, however, that recent results have shown that the Solarsoft response functions of the AIA 94 and 131 filters are missing a significant number of low-temperature lines near 94 Å and 131 Å (e.g., Schmelz et al. 2010). For this reason, simulated light curves for these filters are not fully reliable.
The density excess curves derived from TRACE and AIA filter ratios are quite similar, with marginal differences always within a factor of 2. The common characteristics are (1) an initial phase when ψ is below unity; and (2) a subsequent phase in which the density excess rises, reaches the highest value (~2), and then gradually decreases towards unity.
A close comparison between the evolution of the simulated intensities and the estimated density excess factors shows that, even though the maximum density excess agrees with the values obtained from TRACE observations, ranging between ~1 and ~12 (e.g., Klimchuk et al. 2010), model A achieves the highest overdensities during the radiative cooling phase following the impulsive event (see, e.g., Spadaro et al. 2003), i.e., about 35 min after the loop has brightened in the EUV filters. Therefore the loop would not appear denser than predicted by the canonical hydrostatic scaling laws when its brightness at 195 and 171 Å is highest.
The evolution of the light curves and of the factor ψ obtained for loop model B (see Table 1) is shown in Fig. 2. The peculiarity of model B is that a thermal instability – known as thermal non-equilibrium (e.g., Antiochos et al. 1999; Müller et al. 2004; Karpen et al. 2006; Klimchuk et al. 2010) – develops in the elemental strands during their evolution, as a result of (1) the concentration of the heating at the footpoints; and (2) the very short cadence time of the energy pulses compared to the cooling time of the loop (see Paper I for more details). This instability causes a cyclic “catastrophic” cooling of the plasma located in the coronal part of the loop and the subsequent formation of a plasma condensation moving from the top of the loop to one of the footpoints.
 |
Fig. 2 Same as Fig. 1 for model B. Light curves generated in the UV bands at 1600 Å are also plotted with grey lines. |
The high densities and low temperatures associated with the condensation phase trigger the brightening of the loop in the EUV. The emission lifetime in the 171 passbands is ~1 h, in agreement with the typical values of a few thousand seconds as measured from the observations (Winebarger et al. 2003). The loop also produces a weak emission in the 211 channel of AIA, due to the relatively high temperatures (T ≃ 2.5 MK) in the first phase of its evolution. The time lag between the appearance of the loop in the 211 and 193 filters, as well as that between 193 (TRACE 195) and 171, is of about 1 h. This is somewhat longer than the time lags measured from AIA observations recently reported by Viall & Klimchuk (2012), of the order of 1500 s or less. However, the 211-193-171 sequence is maintained even in this case (as also found by Viall & Klimchuk 2011). Intensities in the other high-temperature AIA filters are negligible for the reasons discussed above.
The ψ factors obtained from TRACE and AIA filter ratios have again small differences, within a factor of 2. ψ is initially below unity, then it abruptly increases when condensations start forming inside the elemental strands, and reaches a highest value (~10 for TRACE, slightly lower for AIA) that agrees well with the observed values and coincides with the highest brightness in the EUV filters, 171 in particular. Finally, the density excess drops to unity when all plasma blobs inside the strands have drained onto the chromosphere, and a new cycle begins.
However, the most striking result for model B is that a considerable emission at 304 Å and 1600 Å is generated during the condensation phase by the cool material (≲0.1 MK) located in the thin transition regions that form at the edges of the condensation itself. To our knowledge, typical active region loops (or “structured emission” along them) are not observed at 304 and 1600 Å. Only recently, Kamio et al. (2011) found evidence of a loop in the core of an active region brightening in the AIA 193, 171, and then 304 filter: the authors explained the 304 Å emission as the signature of a blob of cool plasma falling towards the footpoint region.
4. Conclusions
Our work suggests that multistranded loop models where the individual strands subject to nanoflare heating are treated independently cannot explain all main characteristics of current EUV observations of overdense warm coronal loops. Even though they can predict the observed values of the density excess derived from TRACE and SDO/AIA filter ratios, they place constraints on other observables, i.e. strong emission at lower transition region/chromospheric temperatures along the loop, that cannot be reconciled with the available observations.
On the other hand, 1D numerical models of coronal loops are based on the strong assumption that spatial interactions among the individual strands, and thus the 3D nature of the structures under investigation, can be neglected. Although this simplification is useful because it enables high spatial resolution computations to resolve strong gradients and shocks along the loops or include ionisation processes (see, e.g., Klimchuk 2006), it might be responsible for a missing match between our models and observations. Therefore, the nanoflare heating model may be correct in principle, but the interaction of neighbouring structures on the real Sun may change the appearance of coronal loops. It is worth noting that recent 3D MHD models of the corona have reproduced a temporal and spatial distribution of the heat input that is consistent with a nanoflare heating scenario (see Bingert & Peter 2011, 2013). Moreover, recent observations of a solar active region made at high spatial resolution with the Highresolution Coronal Imager (Hi-C) have shown that magnetic fields at a spatial scale of approximately 150 km are braided, and can release energy into the corona by reconnection events (Cirtain et al. 2013).
Finally, we note that TRACE 195/171 or SDO/AIA 193/171 filter ratios, by themselves, do not appear to provide sufficient constraints to validate a particular model. Multithermal observations are needed to determine the effective temperature and density structure of coronal loops and place significant observational constraints on models of loop heating. SDO/AIA is ideal for this approach, because it has an ensemble of coronal filters that provide high-resolution images of the Sun with a good temperature discrimination and cover the entire active region temperature range. They can be used to perform consistent differential emission-measure (DEM) analyses of the data to derive the temperature distribution of the plasma inside the loops during their evolution (e.g., Schmelz et al. 2010). This is an important observational constraint that a successful model will have to match.
Acknowledgments
We acknowledge financial contribution from the agreement ASI I/013/12/0.
References
- Antiochos, S. K., MacNeice, P. J., Spicer, D. S., & Klimchuk, J. A. 1999, ApJ, 512, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Bingert, S., & Peter, H. 2011, A&A, 530, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bingert, S., & Peter, H. 2013, A&A, 550, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2011, Sol. Phys., 275, 41 [Google Scholar]
- Cirtain, J. W., Golub, L., Winebarger, A. R., et al. 2013, Nature, 493, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., et al. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Handy, B. N., Acton, L. W., Kankelborg, C. C., et al. 1999, Sol. Phys., 187, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & Klimchuk, J. A. 2006, ApJ, 637, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kamio, S., Peter, H., Curdt, W., & Solanki, S. K. 2011, A&A, 532, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A., Karpen, J. T., & Antiochos, S. K. 2010, ApJ, 714, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Spadaro, D., Lanzafame, A. C., et al. 2001, ApJ, 547, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2011, Sol. Phys., 275, 17 [Google Scholar]
- Lenz, D. D., Deluca, E. E., Golub, L., et al. 1999, ApJ, 517, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, D. A. N., Peter, H., & Hansteen, V. H. 2004, A&A, 424, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Patsourakos, S., & Klimchuk, J. A. 2006, ApJ, 647, 1452 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Schmelz, J. T., Kimble, J. A., Jenkins, B. S., et al. 2010, ApJ, 725, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Spadaro, D., Lanza, A. F., Lanzafame, A. C., et al. 2003, ApJ, 582, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Susino, R., Lanzafame, A. C., Lanza, A. F., & Spadaro, D. 2010, ApJ, 709, 499 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2011, ApJ, 738, 24 [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2012, ApJ, 753, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, M. A., Schmelz, J. T., DeLuca, E. E., & Roames, J. K. 2005, ApJ, 635, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Winebarger, A. R., Warren, H. P., & Seaton, D. B. 2003, ApJ, 593, 1164 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Synthesised TRACE and AIA intensities (top panel) and density excess factors (bottom panel) as functions of time from the start of the additional heating for model A. TRACE 171 and 195 curves are plotted with dashed lines, SDO/AIA curves with solid lines. The temperatures corresponding to the peaks of the response functions of TRACE and AIA filters are reported in the inset in the top panel. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for model B. Light curves generated in the UV bands at 1600 Å are also plotted with grey lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


