| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 10 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201220914 | |
| Published online | 04 March 2013 | |
On high-contrast characterization of nearby, short-period exoplanets with giant segmented-mirror telescopes
Max-Planck Institüt für Astronomie, Königstuhl 17,
69117
Heidelberg,
Germany
e-mail:
ianc@mpia.de
Received: 14 December 2012
Accepted: 21 January 2013
Measurements of the frequency with which short-period planets occur around main sequence stars allows a direct prediction of the number and types of such planets that will be amenable to characterization by high-contrast instruments on future giant segmented-mirror telescopes (GSMTs). Adopting conservative assumptions, I predict of order 10 planets with radii RP = 1−8 R⊕ and equilibrium temperatures ≲400 K should be accessible around stars within 8 pc of the Sun. These numbers are roughly the same for both near-infrared observations of scattered starlight and mid-infrared observations of planetary thermal emission, with the latter observations demonstrating greater relative sensitivity to smaller and cooler planets. Adopting the conservative assumption that planets with RP = 1−2 R⊕ and 2−4 R⊕ occur with equal frequency, I predict a 40% chance that a planet with RP = 1−2 R⊕ and equilibrium temperature 200–250 K will accessible to high-contrast thermal infrared characterization; this would be a compelling object for further study. To validate these predictions, more detailed analyses are needed of the occurrence frequencies of low-mass planets around M dwarfs, both in the Kepler field and in the solar neighborhood. Several planets already discovered by radial velocity surveys will be accessible to near-infrared high-contrast GSMT observations, including the low-mass planets α Cen Bb and (depending on their albedos) GJ 139c and d, GJ 876b and c, and τ Cet b, c, and d; τ Cet f would be amenable to thermal infrared characterization. Further efforts to model the near-infrared reflectance and mid-infrared emission of these and other short-period planets are clearly warranted, and will pave the way for the interpretation of future high-contrast characterization of a variety of planets around the nearest stars.
Key words: planets and satellites: general / planets and satellites: detection / instrumentation: adaptive optics / methods: numerical / techniques: high angular resolution
© ESO, 2013
1. Introduction
A 1.1 Earth-mass (M⊕) planet candidate has been announced around α Centauri B (Dumusque et al. 2012), and a family of five candidates with minimum masses 2–10 M⊕ has been announced around τ Ceti (Tuomi et al. 2013). If confirmed, the discovery of so many low-mass planets around stars very near the Sun would be a strong sign that such planets are common. Such a conclusion would be consistent with early results from the Kepler mission, which indicate that the frequency of planet candidates increases sharply toward smaller planetary radii (RP ≲ 4 R⊕) for orbital periods P < 250 d (Howard et al. 2012; Dong & Zhu 2012; Fressin et al. 2013). These Kepler results also suggest a dramatic increase in the frequency of small planets (radii RP = 2−4 R⊕) orbiting cooler stars (Howard et al. 2012). Because such stars are more numerous than sun-like stars, there should be many such planets in the Solar neighborhood. Because most of these planets orbit M dwarfs, their equilibrium temperatures Teq are quite cool: typically 200–400 K.
The prospect of numerous temperate, small, low-mass planets orbiting nearby stars is an exciting one. Such planets may lie in their host stars’ “habitable zones” and be capable of supporting liquid water on any solid surface (Huang 1959; Kasting et al. 1993; Pierrehumbert & Gaidos 2011). These planets around nearby stars are also the only ones for which in situ exploration could be even remotely feasible in the foreseeable future (e.g., Crawford 2011, and references therein). For now, the proximity of nearby systems and their attendant high photon fluxes make these planets the most amenable to remote characterization of their atmospheric and/or surface compositions.
In recent years much effort has been devoted to preparing for observations of potential Earth analogues transiting cool M dwarf using, e.g., JWST (Deming et al. 2009; Kaltenegger & Traub 2009). However, because even short period planets are unlikely to transit, the nearest accessible transiting planets will be around rather fainter, more distant stars. The durations of these transits will be short and their signal to noise low, so tens or hundreds of observations will be necessary for significant atmospheric measurements. Phase curve observations provide higher duty cycles and may be able to characterize small, non-transiting planets around stars closer to the Sun (Selsis et al. 2011; Maurin et al. 2012). Spacecraft capable of making such measurements have been proposed (e.g., Vasisht et al. 2008; Swain 2010; Tinetti et al. 2012), but these observations will require extremely stringent spectrophotometric stability (better than 10-4 over periods of days). Considering these various limitations, it is reasonable to explore alternative modes of exoplanetary characterization.
In this Paper I present the first quantitative estimates of the local exoplanet population accessible to ground-based high-contrast observations, and a discussion of how such observations can directly constrain the demographics of the local planet population. Though it has been appreciated for at least a decade that the next generation of ground-based giant segmented-mirror telescopes (GSMTs) can characterize small, cool planets via such observations (Angel 2003; Hawarden et al. 2003), Kepler’s ability to measure planet frequency as a function of P, RP, and stellar effective temperature Teff with unprecedented precision permits the first informed estimate of the number of short-period planets that will be accessible to future large-aperture facilities.
Section 2 discusses simulations of statistically representative planetary systems around nearby stars and an assessment of high-contrast GSMT instruments’ ability to characterize these planets. Section 3 then presents the number of planets accessible to such characterization under various assumptions of planetary occurrence frequency and instrumental capabilities, and discusses the consequences of these assumptions. The main results are summarized in Table 1. In brief, of order 10 planets are predicted to be amenable to such characterization at either near-infrared (NIR, <2.5 μm) or mid-infrared (MIR, ~10 μm) wavelengths, and this number varies by no more than a factor of 2 under rather more optimistic or pessimistic assumptions. In addition, there is significant likelihood (at least 40%) that such observations will be able to characterize an Earth or Venus analogue (RP = 1−2 R⊕, Teq = 200−250 K). Finally, I summarize the results of this work and suggest useful future work in Sect. 4.
Number of short-period planets accessible to high-contrast characterization.
2. Methods
2.1. Defining the local, observable stellar population
To construct an observable sample of nearby stars, I take the 8 pc sample of Kirkpatrick et al. (2012) and remove all white dwarfs and spectral types later than M7 (to avoid brown dwarfs). White and brown dwarfs may have low mass planets, and these planets could even be temperate (Andreeshchev & Scalo 2004; Monteiro 2010), but at present the frequency of planets in such systems remains very poorly constrained. Because high-contrast observations have difficulty attaining the contrast necessary for planet characterization in the presence of nearby bright point sources (mitigation strategies exist but require customized instruments; see e.g., Crepp et al. 2010; Cady et al. 2011), I remove all known binaries with apparent separations ≲5′′. Stars with fainter companions (e.g., Procyon A and Sirius A) are retained. For objects listed by Kirkpatrick et al. (2012) with a range of spectral types, I take the mean of the specified range. Some M dwarfs are listed without any spectral type, and for these I take the spectral types specified by Rojas-Ayala et al. (2012). The final list contains 92, 20, 6, 2, and 4 stars of types M, K, G, F, and A, respectively.
Accurate stellar parameters are not known for all these objects, so I adopt a homogeneous approach and assign Teff and stellar radii using empirical, interferometrically-determined values (Boyajian et al. 2012a,b) for each spectral type. Apparent V-band magnitudes are taken from the UCAC4 Catalogue (Zacharias et al. 2012), converted to absolute V magnitudes using the parallax values in Kirkpatrick et al. (2012), and converted to stellar masses using the mass-luminosity relationship of Henry & McCarthy (1993); using the K band relationship of Delfosse et al. (2000) affects the masses thus derived by roughly 15%, but this does not significantly affect my results. Finally, a BT-Settl stellar model (Allard et al. 2011) is generated by interpolating in log g and Teff to the stellar parameters, and accounting for the star’s size and distance from the Sun.
Note that this 8 pc sample is sufficiently small that high-quality spectra could be obtained for all these targets with relative ease. Spectra at low resolution would provide a useful absolute flux calibration, and spectra at high resolution would permit stellar parameters and abundances to be derived at high precision. Such a homogeneous stellar characterization effort would be highly desirable, and would reduce the need for the assumptions about stellar parameters described above.
2.2. Modeling the local exoplanet population
I estimate the distribution of the local exoplanet population using an analysis of planet frequency as a function of Teff, P, and RP from the Kepler planet candidate sample derived from the first three quarters of Kepler observations (Borucki et al. 2011; Howard et al. 2012). Although these frequencies are computed for planet candidates and not fully validated planets, the occurrence of false positives in the sample is below 15% (Morton & Johnson 2011; Fressin et al. 2013). Furthermore, planet candidates with radii RP = 2−4 R⊕ (the targets most accessible to high-contrast characterization) have a contamination fraction of <7% (Fressin et al. 2013). Thus the Kepler false positive rate has at most a minor effect on the results presented here.
Hot Jupiters are only half as frequent in the Kepler sample as observed by radial velocity surveys (Howard et al. 2012). The authors attribute this discrepancy to the lower metallicity of the Kepler sample, under which conditions fewer massive planets should be expected (Santos et al. 2004; Fischer & Valenti 2005). If this discrepancy is confirmed, then the simulations presented here underestimate the frequency of large planets by as much as a factor of 2; these planets are intrinsically rare, so this is a small effect. The frequency of Neptune-mass and smaller planets depends less strongly on stellar metallicity than does the frequency of Jupiter-mass objects (Sousa et al. 2008; Buchhave et al. 2012); since I show below that smaller planets comprise the bulk of the planet population accessible to high-contrast characterization, differences between the Kepler and local stellar populations should not strongly affect these results (this assumption will be tested in the future by high-precision radial velocity surveys).
I begin by determining the frequency of planets of given RP for each star, based on its Teff. I assume that binary stars have planet frequencies consistent with those of single stars, and that 4−8 R⊕ and 8−32 R⊕ planets occur with frequencies of 1.7% and 0.79%, respectively (see Fig. 8 of Howard et al. 2012). For 2−4 R⊕ planets, I compute a frequency using Eq. (9) of Howard et al. (2012), which was defined using Teff in the range 3600−7100 K. I extend this relation to lower and higher Teff by assuming that beyond the specified range the frequency distribution of planets is uniform and everywhere continuous. In Sect. 3.2 I quantify the effect of this assumption. Howard et al. (2012)’s planet statistics are incomplete for RP < 2 R⊕, but their results suggest 1−2 R⊕ planets are at least as common as 2−4 R⊕ planets. I conservatively assume that planets in these two size ranges occur with equal frequency, consistent with more recent analyses (Dong & Zhu 2012; Fressin et al. 2013). Throughout this work, I assume a uniform distribution of planet sizes within each of the RP ranges noted above.
The preceding steps determine the number of planets of varying RP expected around a given star for P < 50 d. In each of 104 trials I assign to each star either no planet or a planet in one of the four RP bins listed above, with the appropriate frequencies. I then assume that P in each radius range follows that given by Eq. (8) and Table 5 of Howard et al. (2012). Though their planet population statistics are limited to P < 50 d, even over this small range the frequency of planets increases in lnP space for P > 10 d. I conservatively assume that planet frequency is flat for P > 50 d (see also Dong & Zhu 2012). Letting planet frequency increase toward longer periods only slightly increases the number of accessible planets, because the planets most accessible to high-contrast characterization lie on short-period orbits (see Sect. 3.2). Future studies should characterize planet frequency at longer orbital periods (this is a primary goal of the Kepler mission) and should explore the dependence of planet frequency on Teff in greater detail.
The result of this process is a planet population that provides a direct estimate of the frequency of planets with RP and P around each star in the 8 pc sample. Planetary systems may be more diverse than predicted by this simple model: for example, the M dwarf GJ 876 has multiple massive planets (e.g., Baluev 2011) while short-period planets of even very low mass have been excluded around the low-mass Barnard’s Star and Proxima Centauri (Endl & Kürster 2008; Zechmeister et al. 2009; Choi et al. 2013). Nonetheless the modeling approach described above has the advantages of being relatively simple and of providing estimates across a broad range of planetary and stellar parameter space that decently approximate the planet demographics presented by Howard et al. (2012). Future efforts should strive to quantify planet frequency over as broad a range as possible of Teff, P, and RP to obviate the need for some of the assumptions made above.
2.3. Estimating high-contrast instrument performance
Adaptive optics (AO) systems designed to provide very high image quality are often termed “high contrast” systems, a name which emphasizes their sensitivity to faint objects located near much brighter ones; see Oppenheimer & Hinkley (2009) and Mawet et al. (2012) for recent reviews on this topic. At least one high-contrast system is already operating on-sky at the 5 m Hale telescope and reaching contrast levels of ~10-7 (Oppenheimer et al. 2012), and even more capable instruments are under construction for existing 8 m telescopes (Macintosh et al. 2006a; Beuzit et al. 2006). End-to-end simulations and testing of these latter instruments suggest they may reach final contrasts of roughly 10-8 (Mesa et al. 2011; Thomas et al. 2011; Wildi et al. 2011). At this level of performance, short-period exoplanets will likely remain beyond the reach of such instruments (see Sect. 3.3.1).
The next generation of GSMTs will have diameters ranging from 25 m (GMT; Johns 2008) to 30 m (TMT; Nelson & Sanders 2008) to 39 m (E-ELT; Gilmozzi & Spyromilio 2007), and all are projected to rely heavily on AO-assisted, diffraction-limited observations to maximize the science gains of these new facilities. High-contrast NIR instruments have been proposed and studied for all these telescopes (Macintosh et al. 2006b; Matsuo & Tamura 2010; Brandl et al. 2010; Kasper et al. 2010). These initial studies suggest that with moderate and reasonable technological advances, such instruments will be sensitive to objects at separations and contrast levels unprecedented for optical/infrared telescopes.
High contrast instruments generally require highly specialized designs to achieve their goals, and their performance varies across different targets, telescopes, and wavelengths. I estimate the performance of a generic GSMT high-contrast instrument using the analytic relations of Guyon (2005) and adopting the parameters in Table 4 of that work unless noted otherwise (variations of instrument parameters are discussed in Sect. 3.3)1. The instrument is assumed to correct both phase and amplitude errors, sensed via a Mach-Zehnder pupil plane wavefront sensor. The wavefront sensing and science wavelengths are assumed to be identical to minimize chromatic contrast errors (Guyon 2005). The relations used compute raw contrast and not the effective contrast limits for detection; I therefore assume that observational and post-processing techniques can suppress the instantaneous PSF contrast by a factor of 30 at all angular separations; current techniques achieve suppression factors of 20 to several hundred at separations as small as 4.5λ/D (Marois et al. 2008; Crepp et al. 2011; Vogt et al. 2011), so the value assumed here may be somewhat conservative. Finally, following Lunine et al. (2008) I impose an absolute contrast floor of 5 × 10-9 in all cases. The result is a simulation of high-contrast performance with the phenomenologically correct dependencies on wavelength, telescope size, stellar flux, and other parameters2.
In these performance estimates I also crudely account for the effect of finite stellar sizes, which are significant for several of the nearest and largest stars. For example, both α Cen A and Sirius A have angular diameters θ = 8 mas, comparable to the diffraction-limited angular resolution (λ/D) of a 30 m telescope observing at 1.2 μm. Resolved sources cause the effective throughput of high-contrast observations to decrease markedly at the smallest separations (Guyon et al. 2006), though the attainable contrast is not adversely affected for proper choice of coronagraph or other starlight suppression system (Crepp et al. 2009). I approximate the deleterious effects of finite stellar size by imposing a minimum inner working angle (IWA) of (2.2 + 0.4log 10 [θ(λ/D)-1] )λ/D, a relation which approximates the 50% throughput limit of an ideal coronagraph operating at 10-10 contrast (Guyon et al. 2006). This minimum separation increases for larger θ, more extreme contrast levels, and less optimal coronagraph designs. In this work finite stellar size only affects a few star systems (those with the largest θ), and only in the 2λ/D IWA case described in Sect. 3.3.1. Future high-contrast observations probing near or within 1λ/D (Serabyn et al. 2010) should consider these effects in greater detail.
2.4. Estimating the observability of short-period planets
I assess the accessibility of each simulated planet to high-contrast observations by considering both scattered starlight and thermal emission from the planet. I assume that all planets will be observed at quadrature, since radial velocity measurements will allow optimal phasing of most interesting targets. I further assume that all planets are on circular orbits and exhibit Lambertian scattering profiles, and that the observatory can observe all stars in the target sample (under currently published plans GSMTs will be located in both hemispheres).
I assign a Bond and wavelength-independent geometric albedo (AB and Ag, respectively) to each planet by drawing a value from a uniform random distribution spanning 0.0–0.4, a range which is a roughly representative for solar system planets (see also Hu et al. 2012). Although AB and Ag describe different physical quantities (Ag determines the strength of scattering at a given wavelength, while AB determines a planet’s equilibrium temperature Teq, and thus its thermal blackbody emission; see e.g., Seager 2010), for simplicity I use the same value for each planet’s AB and Ag. This equality holds to within a factor of two for planets in the Solar System. At NIR wavelengths most observable planets in the simulations below are only accessible in reflected light, so higher or lower albedos will respectively increase or decrease the size of the accessible planet population; the effect is reversed for observations at thermal infrared wavelengths. To each planet I also assign a heat redistribution factor (f; Seager 2010) drawn from a uniform random distribution spanning the range (0.25, 0.66), where the extrema of this range respectively indicate zero and full redistribution of the incident stellar flux. The redistribution factor does not significantly affect the detectability of planets in reflected light, but would affect the thermal infrared observations described in Sect. 3.3.2.
Using AB, f, and the physical system parameters I then compute Teq for each planet, and I assume that the planet radiates as a blackbody with this temperature. Finally, the planet to star flux contrast in a given bandpass is the ratio of the sum of the planet’s reflected and thermal photon flux to the photon flux from the host star. The planet is assumed to be observable if its contrast lies above the sensitivity limits computed in Sect. 2.3.
3. Simulation results
In this Sect. 1 discuss the local population of planets accessible to characterization by high-contrast observations under a number of different assumptions about planet population parameters and instrumental configurations. I begin by presenting a set of baseline astrophysical and observational parameters in Sect. 3.1. Section 3.2 discusses the effects of varying the parameters of the local planetary population, and Sect. 3.3 discusses the impact of various telescope and instrument design choices. For all cases discussed, the number of planets of various RP and Teq accessible to high-contrast characterization is listed in Table 1.
3.1. Baseline scenario
The baseline observational parameters are a 30 m telescope capable of observing down to an IWA of 3λ/D: this instrument is analogous to TMT’s PFI or SEIT instruments (Macintosh et al. 2006b; Matsuo & Tamura 2010), but with better wavefront sensor performance. This baseline case provides an angular resolution midway between the 25 m GMT and 39 m E-ELT. I adopt a baseline observing wavelength of 1.2 μm (J band), where future AO systems should achieve good correction and which provides good angular resolution. Observations at J band are also interesting because of their potential to descry the 1.27 μm O2 band expected in oxygen-rich planetary atmospheres (e.g., Turnbull et al. 2006; Kawahara et al. 2012). In terms of astrophysical parameters, the baseline scenario assumes that 1−2 R⊕ and 2−4 R⊕ planets occur with equal frequencies (as described in Sect. 2.2, this may be a conservative underestimate), and that planet frequency is flat in lnP space for P > 50 d (the longest periods considered by Howard et al. 2012).
Figure 1 shows a representative planet sample and the computed sensitivity limits as applied to α Cen B. It is notable that the recently discovered low-mass planet candidate α Cen Bb (Dumusque et al. 2012) presents a contrast of 10-7 and is eminently observable in this baseline scenario (assuming a radius of 1.1 R⊕, obtained by converting msini to RP via Eq. (1) of Lissauer et al. 2011). A simulation of the GJ 876 system is shown in Fig. 2; despite the worse contrast achieved on this fainter star, the massive planets GJ 876b and c (Delfosse et al. 1998; Marcy et al. 1998, 2001; Baluev 2011) can be directly characterized if Ag(RP/R⊕)2 ≳ 19 and 6, respectively (Ag ≳ 0.02, with radii estimated as described previously). Though not shown, the currently known planets GJ 139c and d (Pepe et al. 2011) can also be characterized if Ag(RP/R⊕)2 ≳ 0.9 and 1.8, respectively (i.e. Ag ≳ 0.4), and the planet candidates τ Cet b, c, and d could be characterized for Ag(RP/R⊕)2 ≳ 0.08, 0.4, and 1.2, respectively (Ag > 0.04, 0.14, and 0.35). Theoretical efforts to model all these planets’ NIR reflectance are clearly warranted.
 |
Fig. 1 Simulated planet populations for α Cen B in the baseline scenario outlined in Sect. 3.1, observing at 1.2 μm with an instrument similar to TMT/PFI or TMT/SEIT. Planets above and to the right of the dashed line would be accessible to high-contrast spectroscopic characterization. The star symbol indicates α Cen Bb (assuming a radius of 1.1 R⊕). Each circle’s size and color refers to a simulated planet’s RP and Teq, as indicated in the legend. Most of the simulated planets shown are detected in scattered starlight, though thermal emission contributes to the shortest-period planets (including α Cen Bb). |
 |
Fig. 2 Same as Fig. 1, but for the M dwarf GJ 876. From left to right, the star symbols and error bars show the contrast expected for planets c, b, and e over the range of albedos and recirculation parameters described in Sect. 2.4. Planets b and c will be accessible to characterization in scattered light if Ag(RP/R⊕)2 ≳ 19 and 6, respectively. |
The number of accessible planets in this baseline scenario are shown in Fig. 3 as a function of Teq and RP, and these results are summarized in the first row of Table 1. In all results I sort the planets by size (in the ranges described previously) and according to whether Teq is below, within, or above the range 200−300 K (a range which corresponds crudely to the Teq of Mars and a low-albedo Venus). Figure 3 shows that the planets detected in the baseline scenario typically have Teq < 400 K and RP < 4 R⊕: these planets are visible mainly via scattered starlight and not intrinsic thermal emission. Although Howard et al. (2012) show that planets with RP < 4 R⊕ are most frequently found around cooler stars, I find that few planets orbiting M dwarfs are accessible at distances ≳3.5 pc as a result of these stars’ intrinsic faintness, and the consequent degradation of achievable contrast. Finally, I estimate a 6% chance that in this baseline scenario an Earth/Venus analogue (1−2 R⊕, Teq = 200−250 K) can be observed. This probability is likely an underestimate for the reasons described in Sect. 2.2; such a planet would most likely be found around Proxima Centauri or Barnard’s Star. The probability increases to >50% when considering planets with RP = 1−4 R⊕; these temperate planets also most likely to be found around nearby M dwarfs.
 |
Fig. 3 Predicted number of planets (as a function of RP and Teq) expected to be characterized in the baseline high-contrast GSMT observing scenario outlined in Sect. 3.1. The colors and the small numbers in each cell both indicate the expectation value for that combination of RP and Teq, and the histograms show the marginalized distributions. Note that the baseline scenario simulated here conservatively assumes that planets in the two smallest RP ranges occur with equal frequency (see Sects. 2.2 and 3.2). |
3.2. Ability to quantify the local exoplanetary demographics
Several assumptions were made in Sect. 2.2 to extrapolate the Kepler population statistics of Howard et al. (2012) to longer orbital periods and cooler stars, and in this section I test the effects of these assumptions. The results of these tests are all listed in the second section of Table 1.
Howard et al. (2012) find roughly equal occurrence frequencies for 1−2 R⊕ and 2−4 R⊕ planets. The baseline scenario described in Sect. 3.1 conservatively assumes that 2−4 R⊕ planets and 1−2 R⊕ planets occur with equal frequency, an assumption also consistent with more recent results (Dong & Zhu 2012; Fressin et al. 2013). For larger radii, Howard et al. (2012) find a planet frequency ∝ 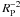 (around sun-like stars). It now appears that this relation does not apply to RP < 2 R⊕; nonetheless, Table 1 shows that approximately equal numbers of planets in the two smallest size ranges would be accessible to characterization if the trend held to smaller radii (i.e., if Kepler’s completeness is significantly overestimated for RP < 2 R⊕; Howard et al. 2012; Dong & Zhu 2012; Fressin et al. 2013). However, because the smaller planets must be closer to their host stars to present the same contrast ratio as the larger planets, the additional 1−2 R⊕ planets have rather warmer temperatures (Teq ~ 400 K) than the baseline population.
(around sun-like stars). It now appears that this relation does not apply to RP < 2 R⊕; nonetheless, Table 1 shows that approximately equal numbers of planets in the two smallest size ranges would be accessible to characterization if the trend held to smaller radii (i.e., if Kepler’s completeness is significantly overestimated for RP < 2 R⊕; Howard et al. 2012; Dong & Zhu 2012; Fressin et al. 2013). However, because the smaller planets must be closer to their host stars to present the same contrast ratio as the larger planets, the additional 1−2 R⊕ planets have rather warmer temperatures (Teq ~ 400 K) than the baseline population.
My baseline scenario conservatively assumes that planet frequency flattens out for P > 50 d, consistent with recent results using additional Kepler data (Dong & Zhu 2012). A recent analysis of the first six quarters of Kepler data extends planet frequency estimates (Dong & Zhu 2012). That work indicates that the frequency of planets in lnP space for P < 250 d appears flat for RP < 4 R⊕, but continues to increase for larger planets; this is consistent with radial velocity surveys, which show that the frequency of massive planets continues to increase out to 2000 d (Cumming et al. 2008). I investigate the impact more frequent planet occurrence on longer periods by letting Howard et al. (2012)’s planet frequency relations increase at longer periods (instead of arbitrarily flattening the distributions). Table 1 shows that compared to the baseline scenario, two additional planets (one each with sizes 4−8 R⊕ and 8−32 R⊕) would be accessible to high-contrast characterization in this scenario. Because these additional planets occur on longer periods, they are rather cooler (Teq < 200 K) than the baseline population.
Perhaps the least conservative assumption in my baseline scenario is the decision to assign planets to stars with Teff < 3600 K, below the range explored by Howard et al. (2012). Large-scale radial velocity campaigns have been conducted for a few such stars and have found no planets down to ~10 M⊕ in short periods (e.g. Proxima Centauri and Barnard’s Star; Endl & Kürster 2008; Zechmeister et al. 2009; Choi et al. 2013). Table 1 shows that even if all cool stars have zero planets, roughly five planets would still remain for future studies.
The immediately preceding assumption is of course overly pessimistic, since planets with msini > 10 M⊕ have been discovered around a number of M dwarfs (e.g., Butler et al. 2004; Bonfils et al. 2005, 2007, 2012). Furthermore, a systematic radial velocity survey of a large number of cool (Teff < 3600 K) has recently indicated a planet occurrence frequency of roughly 90% for msini = 1−100 M⊕, P < 100 d (Bonfils et al. 2013). Using the planet population statistics reported in Table 11 of that survey (instead of extending the Howard et al. 2012, frequencies) for stars with Teff < 3600 K, I predict numbers and types of planets amenable to high-contrast characterization nearly identical to that predicted by the baseline scenario (see Table 1). In this simulation I assume log-uniform frequencies of 2.7% and 3% for planets with 102−103 and 10−102 M⊕, respectively, while the least massive planets (1−10 M⊕) have frequencies of 36% for P = 1–10 d and 52% for longer periods. I convert msini to RP as in Sect. 3.1 (Lissauer et al. 2011), and impose a maximum radius of 1.3 RJ. The close agreement between this simulation and the baseline scenario of Sect. 3.1 hints that the results of Howard et al. (2012) and Bonfils et al. (2013) are consistent for small planets orbiting low-mass stars under fairly simple assumptions. A conclusive test of such a claim is, however, beyond the scope of this work.
3.3. Effects of instrumental capabilities
In this Sect. 1 examine how the accessible exoplanet population depends on various observational parameters: telescope diameter D, inner working angle (IWA), and observing wavelength λ. The results of all these tests are listed in the bottom section of Table 1.
3.3.1. Angular resolution: diameter and inner working angle
As discussed in Sect. 2.3, several GSMT designs have been proposed, each with different diameters D. The baseline instrument used in this work has an IWA defined as 3λ/D, so the angular magnitude of this IWA decreases as D increases. Planets at the smallest separations have the highest observable contrast (in both scattered light and thermal emission), so naturally Table 1 shows that the number of accessible planets increases (by nearly a factor of two) when D increases from 30 m (TMT) to 39 m (E-ELT). The number decreases by a similar factor when D is reduced to 25 m (GSMT).
Table 1 also shows that at most a single short-period planet is predicted to be accessible to high-contrast instruments on current 8 m telescopes, if instruments on these telescopes can reach contrast levels of 5 × 10-9. In this case, the work presented here predicts a >1% chance of accessible planets for only four stars: α Cen AB (15–20% each), Procyon A (5%), and Sirius A (3%). These expectation values drop by only a factor of 2 if such facilities can only achieve contrasts of 10-8. These star systems should therefore be high-priority targets for deep observations in imminent 8 m high-contrast surveys.
Similarly, using a narrower or wider IWA than the baseline scenario of Sect. 3.1 respectively increases or decreases the number of accessible planets, as expected (see Table 1). However, varying IWA has a weaker impact than varying D, even when the angular scale of the IWA is held constant. This result may at first seem surprising: 2λ/D on a 30 m telescope gives a smaller angular separation than does 3λ/D on a 39 m telescope, yet more planets are accessible for characterization under the latter conditions than under the former. The increased sensitivity at larger D for constant angular IWA results from the D-1 dependence of PSF speckle amplitude on phase and amplitude errors (Guyon 2005). Thus for two high-contrast instruments with equal IWA (in angular units), the instrument with the larger primary mirror can reach better contrast levels.
3.3.2. Observing wavelength: scattered starlight and thermal emission
The choice of observing wavelength λ has a number of important consequences: with D it sets the angular scale of the IWA (typically specified in λ/D), it determines the stellar flux available for sensing and correction of phase and amplitude errors, and it modifies the planet/star flux contrast (in this work, by determining the planet’s thermal blackbody emission). Naturally, observations at multiple infrared wavelengths are also desirable to observe spectral features of different molecular species and/or surface compositions (e.g., Kuiper et al. 1947; Hu et al. 2012).
Table 1 shows that the number of planets accessible to high-contrast characterization drops steadily as the observing wavelength increases from 1.0 μm to 3.5 μm. The detected planets are cool and seen in reflective light, so their planet/star contrast remains approximately constant even as angular resolution and the photon flux available for AO wavefront sensing and correction both decrease. Nonetheless, Table 1 suggests that several planets should exist which are accessible to characterization across from at least 1−2.2 μm. The number of Earth/Venus analogues expected to accessible to characterization is a maximum at 1.6 μm, a value which presumably represents a tradeoff between angular resolution and the stellar flux available for wavefront sensing and correction.
Intriguingly, thermal-infrared observations appear to be more attractive than observations at intermediate wavelengths such as 3.5 μm. All three GSMT projects have proposed AO-assisted MIR instruments (Brandl et al. 2010; Tokunaga et al. 2010; Okamoto et al. 2010; Hinz et al. 2012). The longer wavelengths at which these instruments would operate roughly correspond to the Wien peak of cool planets’ blackbody emission, thereby providing a method to measure radiometric radii (Morrison 1973), the surface compositions of airless planets (Hu et al. 2012), and the potential to detect exoplanetary ozone (e.g., Rugheimer et al. 2012, and references therein).
The MIR instrument simulated here is not conservative in one respect: as in this work’s other simulations, I assume that the instrument’s wavefront sensor and science instrument operate at the same wavelength. Current designs for such instruments typically rely on facility AO systems, whose wavefront sensors operate at shorter wavelengths. Under such a strategy, chromatic effects may degrade the achievable contrast to the point that short-period planets become inaccessible (Guyon 2005). Instrument designers should therefore consider the feasibility of MIR wavefront sensing for these instruments, either with a separate MIR wavefront sensor or (to minimize non-common wavefront errors) via phase retrieval and correction using the main science camera (e.g., Malbet et al. 1994; Bordé & Traub 2006).
Figure 4 shows the planet population expected around τ Cet and the expected sensitivity limits for an E-ELT/METIS-like instrument (λ = 10 μm, D = 39 m, and a conservative minimum contrast of 10-7; Brandl et al. 2012). Note that the planet candidate τ Cet f (Tuomi et al. 2013) would be amenable to high-contrast characterization at 10 μm, assuming a reasonable albedo (≲0.7).
 |
Fig. 4 Same as Fig. 1 but for τ Cet in the thermal imaging scenario described in Sect. 3.3.2, observing at 10 μm with an instrument similar to E-ELT/METIS. The planets here are detected mainly via their thermal emission. From left to right, the star symbols and error bars show the contrast expected for planets candidates b, c, d, e, and f (Tuomi et al. 2013) over the range of albedos and recirculation parameters described in Sect. 2.4. If confirmed, planet f would be amenable to direct characterization of its thermal emission. |
A high-contrast MIR instrument has a much-reduced angular resolution compared to NIR observations, but planetary thermal emission boosts the planet/star contrast ratios significantly above the values seen at shorter wavelengths; consequently, comparable numbers of planets are expected to be accessible to NIR and MIR characterization. Figure 5 shows the accessible local planet population as a function of RP and Teq for the thermal imaging simulation, and the last row of Table 1 summarizes these results.
 |
Fig. 5 Predicted number of planets (as a function of RP and Teq) expected to be characterized for the 10 μm imaging scenario described in Sect. 3.3.2. The colors and the small numbers in each cell both indicate the expectation value for that combination of RP and Teq, and the histograms show the marginalized distributions. Compared to the planet population accessible in the baseline NIR case shown in Fig. 3, thermal infrared observations mainly detect thermal emission from cooler planets around warmer stars. Note that the scenario simulated here conservatively assumes that planets in the two smallest RP ranges occur with equal frequency (see Sects. 2.2 and 3.2). |
High-contrast thermal-IR instruments thus offer the potential to directly measure thermal emission from short-period planets down to very small planetary radii. Thermal imaging shifts the distribution of sampled planets to substantially cooler Teq (<200 K) as compared to the NIR baseline scenario of Sect. 3.1 (which is sensitive to rather hotter planets at smaller separations). The number of 1−2 R⊕ planets accessible to thermal infrared characterization is comparable to the number expected in the NIR baseline scenario. However, even these conservative planetary population statistics imply a 40% chance of finding an Earth/Venus analogue (RP = 1−2 R⊕, Teq = 200−250 K); this probability derives mainly from K-type stars with Teff in the range 3900–5500 K, and so may be less sensitive to the assumptions made in Sect. 2.2 for planet frequencies around cooler stars. As discussed in Sects. 2.2 and 3.2, if 1−2 R⊕ planets are 4 × more frequent than 2−4 R⊕ planets then the expectation value increases to 1.6. Thus it may be considered likely that such an object will be found; such an event would excite considerable interest.
4. Conclusions and future work
These simulations of a mostly generic high-contrast instrument indicate that, with reasonable extrapolations of planet frequency rates from the Kepler mission and/or radial velocity surveys (Howard et al. 2012; Bonfils et al. 2013), of order 10 short-period planets will be accessible to characterization via high-contrast imaging and spectroscopy from the next generation of GSMTs. In Table 1, the accessible planet population is summarized and shown to be insensitive to moderate changes in the assumptions made about planet frequencies (see Sect. 3.2) and future instrumental capabilities (see Sect. 3.3).
Targets for future high-contrast characterization are already known today. At wavelengths near 1.2 μm, the planets GJ 876b and c (see Fig. 2) and planet candidates α Cen Bb (see Fig. 1) and τ Cet b should be detectable to the NIR baseline instrument considered in Sect. 3.1. GJ 139c and d and τ Cet c and d should also be detectable if their geometric albedos are >0.15–0.4. Thus perhaps a half-dozen suitable planets with a range of masses (and presumably radii) are already known; this number is large enough that one suspects the modest predictions presented in this work may underestimate the true size of the accessible exoplanet population. This could be the case if the local exoplanet population differs substantially from that observed by Kepler, or if the assumptions made in Sect. 2.2 are shown to be invalid. Future high-precision radial velocity observations, especially of M dwarfs, will enable further tests of these predictions.
Thermal infrared observations will be desirable, because they offer the possibility to directly characterize the thermal emission spectra and energy budgets of these short-period planets, and thus (via radiometric radii) break the radius-albedo degeneracy inherent in reflected light observations. In particular, thermal infrared observations significantly improve the chances of finding Earth or Venus analogues (planets with RP = 1−2 R⊕ and Teq = 200−250 K; see Table 1, and cf. Figs. 3 and 5). The planet candidate τ Cet f (see Fig. 4) is the only currently known planet which could be characterized by these mid-infrared observations, and radial velocity surveys seem likely to provide additional targets in the coming decade.
The opportunity to observe and characterize the atmospheres of relatively small (RP < 4 R⊕) and cool (Teq < 300 K) planets is an exciting one, not least because such planets could be similar to Earth and are particularly compelling objects in the study of exoplanetary habitability. A useful avenue for future study will be to examine in more detail what discernible differences might be used to distinguish Earth-like and Venus-like planets (which exhibit similar infrared emission spectra) on the basis of mid-infrared observations. One initial avenue might be to extend planet classification efforts using optical colors (Crow et al. 2011; Hegde & Kaltenegger 2013) to longer wavelengths.
Future, more detailed simulations are required to estimate the signal to noise with which the accessible planets discussed here can be characterized. Kawahara et al. (2012) have presented an excellent first step toward this goal with their recent determination that GSMTs will allow low-resolution spectroscopy of small planets at 1.27 μm in just a few hours. Further such work at both shorter and longer wavelengths will help determine whether spectroscopy will be possible, or whether characterization will be limited to broadband photometry. Such estimates would also permit predictions of the precision with which high-contrast observations could measure short-period planets’ orbital properties (via astrometry), radiometric radii (via MIR observations), and perhaps eventually measure rotation periods (Ford et al. 2001), variations in climate (Cowan et al. 2012), and perhaps exoplanetary satellites (Robinson 2011; Gómez-Leal et al. 2012). Future efforts would also be useful to extend the work presented here to observations in polarized light (Zugger et al. 2010). Finally, another interesting project would be an assessment of the detectability of extrasolar comets (Jura 2005).
By the end of the current decade, JWST may obtain transmission spectra of a few temperate, 1–3 R⊕ planets around M dwarfs (Deming et al. 2009; Kaltenegger & Traub 2009), but because transmission spectroscopy probes the highest pressures such observations cannot probe deeply into the atmosphere – especially if opaque, high-altitude hazes are as ubiquitous as they seem to be in the atmospheres of hotter planets (Bean et al. 2011; Berta et al. 2012; Pont et al. 2012; Benneke & Seager 2012). Nonetheless, occultation measurements will be essential to inform models of short-period planetary atmospheres and to place future high-contrast GSMT observations in a broader context.
Future observational efforts are necessary to extend the planet demographics measured by Kepler’s initial planet candidate sample (Howard et al. 2012) to smaller planetary radii, cooler stars, and (less importantly for this paper) longer orbital periods, and indeed such efforts are already being published (Dong & Zhu 2012; Fressin et al. 2013). Focused high-precision radial velocity campaigns of the type used to discover planet candidates around α Cen B and τ Cet (Dumusque et al. 2012; Tuomi et al. 2013) should be undertaken for the cool stars nearest the sun, both to compare the frequency of planets in the solar neighborhood to that observed by Kepler, and to discover additional planets for high-contrast GSMT characterization. High-precision spectra of all stars within 8 pc of the Sun should also be obtained to characterize their stellar properties, and thus better estimate the likelihood that they host planets.
Planned GSMTs will have the potential to measure NIR albedos, MIR emission, and consequently the molecular chemistry, energy budgets, and radii, of significant numbers of small, temperate, and potentially Earthlike planets around both M dwarfs and solar-type stars. Given these positive prospects, continued efforts toward a more comprehensive theoretical understanding of temperate exoplanet atmospheres is certainly warranted.
Note that Eqs. (16) and (17) of Guyon (2005) contain an error: the coefficient 0.484 should be 0.0484 (O. Guyon, priv. comm., Jan. 2013).
A Python software module used to calculate these quantities is available from the author’s website, located (as of publication) at http://www.mpia.de/homes/ianc/
Acknowledgments
I thank B. Macintosh and O. Guyon for useful information, advice, and discussions while conducting this study, and the anonymous referee for useful comments. This research has made use of the Exoplanet Orbit Database at http://www.exoplanets.org, the Extrasolar Planet Encyclopedia Explorer at http://www.exoplanet.eu, and free and open-source software provided by the Python, SciPy, and Matplotlib communities.
References
- Allard, F., Homeier, D., & Freytag, B. 2011, 448, 91 [Google Scholar]
- Andreeshchev, A., & Scalo, J. 2004, in IAU Symp., 213, Bioastronomy 2002, Life Among the Stars, eds. R. Norris, & F. Stootman, 115 [Google Scholar]
- Angel, R. 2003, in Earths: DARWIN/TPF and the Search for Extrasolar Terrestrial Planets, eds. M. Fridlund, T. Henning, & H. Lacoste, ESA Spec. Publ., 539, 221 [Google Scholar]
- Baluev, R. V. 2011, Celest. Mech. Dyn. Astron., 111, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Désert, J.-M., Kabath, P., et al. 2011, ApJ, 743, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Feldt, M., Dohlen, K., et al. 2006, The Messenger, 125, 29 [NASA ADS] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 443, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bordé, P. J., & Traub, W. A. 2006, ApJ, 638, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012b, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Brandl, B. R., Uttenhaler, S., Pontoppidan, K. M., et al. 2010, in SPIE Conf. Ser. 7735 [Google Scholar]
- Brandl, B. R., Lenzen, R., Pantin, E., et al. 2012, in SPIE Conf. Ser. 8446 [Google Scholar]
- Buchhave, L. A., Uttenhaler, S., Pontoppidan, K. M., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Cady, E., McElwain, M., Kasdin, N. J., & Thalmann, C. 2011, PASP, 123, 333 [Google Scholar]
- Choi, J., McCarthy, C., Marcy, G. W., et al. 2013, ApJ, 764, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, N. B., Voigt, A., & Abbot, D. S. 2012, ApJ, 757, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, I. A. 2011, Acta Astron., 68, 691 [CrossRef] [Google Scholar]
- Crepp, J. R., Mahadevan, S., & Ge, J. 2009, ApJ, 702, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Crepp, J., Serabyn, E., Carson, J., Ge, J., & Kravchenko, I. 2010, ApJ, 715, 1533 [NASA ADS] [CrossRef] [Google Scholar]
- Crepp, J. R., Pueyo, L., Brenner, D., et al. 2011, ApJ, 729, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Crow, C. A., McFadden, L. A., Robinson, T., et al. 2011, ApJ, 729, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Deming, D., Seager, S., Winn, J., et al. 2009, PASP, 121, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, S., & Zhu, Z. 2012 [arXiv:1212.4853] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Endl, M., & Kürster, M. 2008, A&A, 488, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Ford, E. B., Seager, S., & Turner, E. L. 2001, Nature, 412, 885 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, accepted [arXiv:1301.0842] [Google Scholar]
- Gilmozzi, R., & Spyromilio, J. 2007, The Messenger, 127, 11 [Google Scholar]
- Gómez-Leal, I., Pallé, E., & Selsis, F. 2012, ApJ, 752, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O. 2005, ApJ, 629, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Kuchner, M. J., Collins, B., & Ridgway, S. T. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hawarden, T. G., Dravins, D., Gilmore, G. F., et al. 2003, in SPIE Conf. Ser. 4840, eds. J. R. P. Angel, & R. Gilmozzi, 299 [Google Scholar]
- Hegde, S., & Kaltenegger, L. 2013, Astrobiology, 13, 47 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Henry, T. J., & McCarthy, Jr., D. W. 1993, AJ, 106, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Hinz, P., et al. 2012, in SPIE Conf. Ser. 8446 [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, R., Ehlmann, B. L., & Seager, S. 2012, ApJ, 752, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S.-s. 1959, Am. Sci., 47, 397 [NASA ADS] [Google Scholar]
- Johns, M. 2008, in SPIE Conf. Ser. 6986 [Google Scholar]
- Jura, M. 2005, AJ, 130, 1261 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, M., Beuzit, J., Verinaud, C., et al. 2010, in SPIE Conf. Ser. 7735 [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kawahara, H., Matsuo, T., Takami, M., et al. 2012, ApJ, 758, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Davy, G., Christopher, R., et al. 2012, ApJ, 753, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kuiper, G. P., Wilson, W., & Cashman, R. J. 1947, ApJ, 106, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Ragozzine, D., Fabrycky, D. C., et al. 2011, ApJS, 197, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Lunine, J. I., Fischer, D., Hammel, H., et al. 2008 [arXiv:0808.2754] [Google Scholar]
- Macintosh, B., Troyac, M., Doyond, R., et al. 2006a, in SPIE Conf. Ser. 6272 [Google Scholar]
- Macintosh, B., Thomas, S., Poyneer, L., et al. 2006b, in SPIE Conf. Ser. 6272 [Google Scholar]
- Malbet, F., Shao, M., & Yu, J. W. 1994, in SPIE Conf. Ser. 2201, eds. M. A. Ealey, & F. Merkle, 1135 [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Macintosh, B., Barman, T., et al. 2008, Science, 322, 1348 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Matsuo, T., & Tamura, M. 2010, in SPIE Conf. Ser. 7735 [Google Scholar]
- Maurin, A. S., Selsis, F., Hersant, F., & Belu, A. 2012, A&A, 538, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Krist, J. E., Moody, D. C., et al. 2012, in SPIE Conf. Ser. 8442 [Google Scholar]
- Mesa, D., Gratton, R., Berton, A., et al. 2011, A&A, 529, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monteiro, H. 2010, BASBr, 29, 22 [NASA ADS] [Google Scholar]
- Morrison, D. 1973, Icarus, 19, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, T. D., & Johnson, J. A. 2011, ApJ, 738, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, J., & Sanders, G. H. 2008, in SPIE Conf. Ser. 7012 [Google Scholar]
- Okamoto, Y. K., Packham, C., Tokunaga, A., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Oppenheimer, B. R., & Hinkley, S. 2009, ARA&A, 47, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, B. R., & Hinkley, S. 2012, in SPIE Conf. Ser. 8447 [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierrehumbert, R., & Gaidos, E. 2011, ApJ, 734, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Pont, F., Sing, D. K., Gibson, N. P., et al. 2012 [arXiv:1210.4163] [Google Scholar]
- Robinson, T. D. 2011, ApJ, 741, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Rugheimer, S., Kaltenegger, L., Zsom, A., Segura, A., & Sasselov, D. 2012, Astrobiol., accepted [arXiv:1212.2638] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S. 2010, Exoplanet Atmospheres: Physical Processes [Google Scholar]
- Selsis, F., Wordsworth, R. D., & Forget, F. 2011, A&A, 532, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serabyn, E., Mawet, D., & Burruss, R. 2010, Nature, 464, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Swain, M. R. 2010, in BAAS, 42, AAS/Division for Planetary Sciences Meeting Abstracts #42, 1064 [Google Scholar]
- Thomas, S. J., GiveOn, A. A., Dillon, D., et al. 2011, in SPIE Conf. Ser. 8149 [Google Scholar]
- Tinetti, G., Beaulieu, J. P., Henning, T., et al. 2012, Exp. Astron., 34, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Tokunaga, A. T., Honda, M., Sakon, I., et al. 2010, in SPIE Conf. Ser. 7735 [Google Scholar]
- Tuomi, M., Hugh, R. A., Jones, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turnbull, M. C., Traub, W. A., Jucks, K. W., et al. 2006, ApJ, 644, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Vasisht, G., Swain, M. R., Akeson, R. L., et al. 2008, in SPIE Conf. Ser. 7010 [Google Scholar]
- Vogt, F. P. A., Martinache, F., Guyon, O., et al. 2011, PASP, 123, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Wildi, F., Schmid, H. M., Rigal, F., et al. 2011, in SPIE Conf. Ser. 8151 [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2012, VizieR Online Data Catalog, I/322 [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zugger, M. E., Kasting, J. F., Williams, D. M., Kane, T. J., & Philbrick, C. R. 2010, ApJ, 723, 1168 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Simulated planet populations for α Cen B in the baseline scenario outlined in Sect. 3.1, observing at 1.2 μm with an instrument similar to TMT/PFI or TMT/SEIT. Planets above and to the right of the dashed line would be accessible to high-contrast spectroscopic characterization. The star symbol indicates α Cen Bb (assuming a radius of 1.1 R⊕). Each circle’s size and color refers to a simulated planet’s RP and Teq, as indicated in the legend. Most of the simulated planets shown are detected in scattered starlight, though thermal emission contributes to the shortest-period planets (including α Cen Bb). |
| In the text | |
 |
Fig. 2 Same as Fig. 1, but for the M dwarf GJ 876. From left to right, the star symbols and error bars show the contrast expected for planets c, b, and e over the range of albedos and recirculation parameters described in Sect. 2.4. Planets b and c will be accessible to characterization in scattered light if Ag(RP/R⊕)2 ≳ 19 and 6, respectively. |
| In the text | |
 |
Fig. 3 Predicted number of planets (as a function of RP and Teq) expected to be characterized in the baseline high-contrast GSMT observing scenario outlined in Sect. 3.1. The colors and the small numbers in each cell both indicate the expectation value for that combination of RP and Teq, and the histograms show the marginalized distributions. Note that the baseline scenario simulated here conservatively assumes that planets in the two smallest RP ranges occur with equal frequency (see Sects. 2.2 and 3.2). |
| In the text | |
 |
Fig. 4 Same as Fig. 1 but for τ Cet in the thermal imaging scenario described in Sect. 3.3.2, observing at 10 μm with an instrument similar to E-ELT/METIS. The planets here are detected mainly via their thermal emission. From left to right, the star symbols and error bars show the contrast expected for planets candidates b, c, d, e, and f (Tuomi et al. 2013) over the range of albedos and recirculation parameters described in Sect. 2.4. If confirmed, planet f would be amenable to direct characterization of its thermal emission. |
| In the text | |
 |
Fig. 5 Predicted number of planets (as a function of RP and Teq) expected to be characterized for the 10 μm imaging scenario described in Sect. 3.3.2. The colors and the small numbers in each cell both indicate the expectation value for that combination of RP and Teq, and the histograms show the marginalized distributions. Compared to the planet population accessible in the baseline NIR case shown in Fig. 3, thermal infrared observations mainly detect thermal emission from cooler planets around warmer stars. Note that the scenario simulated here conservatively assumes that planets in the two smallest RP ranges occur with equal frequency (see Sects. 2.2 and 3.2). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


