| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220739 | |
| Published online | 04 March 2013 | |
Multi-site campaign for transit timing variations of WASP-12 b: possible detection of a long-period signal of planetary origin⋆,⋆⋆,⋆⋆⋆
1
Toruń Centre for Astronomy, Nicolaus Copernicus University,
Gagarina 11, 87100
Toruń, Poland
e-mail:
gm@astri.umk.pl
2
Institute of Astronomy, Bulgarian Academy of
Sciences, 72 Tsarigradsko Chausse
Blvd., 1784
Sofia,
Bulgaria
3
Astrophysikalisches Institut und
Universitäts-Sternwarte, Schillergässchen 2–3, 07745
Jena,
Germany
4
Michael Adrian Observatorium, Astronomie Stiftung Trebur, Trebur, Germany
5
University of Applied Sciences, Technische Hochschule Mittelhessen,
Friedberg,
Germany
6
Advanced Astronomy and Space Science Division, Korea Astronomy and
Space Science Institute, Daejeon
305-348, Republic of
Korea
7
Chungbuk National University Observatory,
Cheongju
365-863, Republic of
Korea
8
Max Planck Institute for Astronomy, Königstuhl 17, 69117
Heidelberg,
Germany
9
Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK
10
INAF – Astronomical Observatory of Capodimonte Salita Moiariello
16, 80131
Napoli,
Italy
11
Societá Astronomica Lunae, Castelnuovo Magra,
19030
La Spezia,
Italy
12
Unione Astrofili Italiani, Sezione Stelle Variabili – GRAV,
Italy
13
Institute of Astronomy, The University of Tokyo,
2-21-1 Osawa, Mitaka,
Tokyo
181-0015,
Japan
14
Joint ALMA Observatory, Alonso de C’rdova 3107, Vitacura, Santiago, Chile
15
National Astronomical Observatory of Japan,
2-21-1, Osawa, Miaka,
Tokyo, 181-8588, Japan
16
MTA CSFK, Konkoly Observatory, Konkoly-Thege Mikloś út 15−17, 1121
Budapest,
Hungary
17
ELTE Gothard–Lendület Research Group, 9700
Szombathely,
Hungary
18
Dept. of Exp. Physics & Astronomical Observatory,
University of Szeged, 6720
Szeged,
Hungary
19
Department of Physics, Eötvös University,
Pázmány Péter Sétány 1/A,
1117
Budapest,
Hungary
20
Astronomical Institute, Slovak Academy of Sciences,
05960
Tatranská Lomnica,
Slovakia
21
Aryabhatta Research Institute of Observational
Sciences(ARIES), Manora
Peak, Nainital
263129,
India
22
Institute of Astronomy, National Central University,
300 Jhongda Rd., Jhongli
32001,
Taiwan
Received:
15
November
2012
Accepted:
18
January
2013
Aims. The transiting planet WASP-12 b was identified as a potential target for transit-timing studies because a departure from a linear ephemeris has been reported in the literature. Such deviations could be caused by an additional planet in the system. We attempt to confirm the claimed variations in transit timing and interpret their origin.
Methods. We organised a multi-site campaign to observe transits by WASP-12 b in three observing seasons, using 0.5–2.6-metre telescopes.
Results. We obtained 61 transit light curves, many of them with sub-millimagnitude precision. The simultaneous analysis of the best-quality datasets allowed us to obtain refined system parameters, which agree with values reported in previous studies. The residuals versus a linear ephemeris reveal a possible periodic signal that may be approximated by a sinusoid with an amplitude of 0.00068 ± 0.00013 d and period of 500 ± 20 orbital periods of WASP-12 b. The joint analysis of timing data and published radial velocity measurements results in a two-planet model that explains observations better than do single-planet scenarios. We hypothesise that WASP-12 b might not be the only planet in the system, and there might be the additional 0.1 MJup body on a 3.6-d eccentric orbit. A dynamical analysis indicates that the proposed two-planet system is stable on long timescales.
Key words: planets and satellites: general / stars: individual: WASP-12 / planets and satellites: individual: WASP-12 b
Partly based on (1) data collected with the Nordic Optical Telescope, operated on the island of La Palma jointly by Denmark, Finland, Iceland, Norway, and Sweden, in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, (2) observations made at the Centro Astronómico Hispano Alemán (CAHA), operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC), (3) data collected with telescopes at the Rozhen National Astronomical Observatory, and (4) observations obtained with telescopes of the University Observatory Jena, which is operated by the Astrophysical Institute of the Friedrich-Schiller-University.
Tables 2 and 3 are available in electronic form at http://www.aanda.org
Light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/551/A108
© ESO, 2013
1. Introduction
The transiting extrasolar planet WASP-12 b was found to be one of the most intensely
irradiated planets (Hebb et al. 2009). It orbits a
G-type star on a tight orbit with a semimajor axis of
ab = 0.0229 ± 0.0008 AU and an orbital period of only ~1.09 d.
The planet’s proximity to the star results in a high equilibrium temperature of 2500 K, thus
inducing numerous studies of the properties of the planetary atmosphere (Li et al. 2010; Lai et al. 2010; Fossati et al. 2010b; Croll et al.
2011; Crossfield et al. 2012). In the discovery paper, the planet was found to have a mass of
mb = 1.41 ± 0.10 MJup and an
unexpectedly large radius of Rb = 1.79 ± 0.09
RJup. The host star was found to have an effective temperature
of 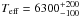 K and a mass of M∗ = 1.35 ± 0.14 M⊙.
Follow-up observations, primarily high-precision photometry, confirmed the large planetary
radius (Maciejewski et al. 2011; Chan et al. 2011). The system parameters were also refined by
Southworth (2012), who used high-precision literature
data in a joint analysis.
K and a mass of M∗ = 1.35 ± 0.14 M⊙.
Follow-up observations, primarily high-precision photometry, confirmed the large planetary
radius (Maciejewski et al. 2011; Chan et al. 2011). The system parameters were also refined by
Southworth (2012), who used high-precision literature
data in a joint analysis.
The orbital eccentricity of WASP-12 b, eb = 0.049 ± 0.015, was
initially determined from the radial velocity (RV) measurements (Hebb et al. 2009). López-Morales et al. (2010) observed occultations whose timing supports a non-circular orbit.
On the other hand, further observations of occultations by Campo et al. (2011) yielded mid-occultation times at orbital phases
0.5010 ± 0.0006 and 0.5006 ± 0.0007, consistent with a circular orbit. The same conclusion
was reached by Husnoo et al. (2011), who analysed
spectroscopic data enhanced by new RV measurements. Croll et al. (2011) observed occultations at a phase equal to
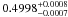 .
These authors re-analysed the available photometric and spectroscopic data and finally
concluded that eb is likely very close to zero.
.
These authors re-analysed the available photometric and spectroscopic data and finally
concluded that eb is likely very close to zero.
A possible non-circular orbit might drive the dissipation of tidal energy. This mechanism, in turn, might be responsible for heating up the planet’s interior and bloating its radius in consequence (Miller et al. 2009). The orbit of WASP-12 b is expected to be circularised on short timescales if the tidal dissipation constant is not significantly larger than a value typical of giant planets (Hebb et al. 2009; Ibgui et al. 2010). Its eccentricity, if real, could be sustained by gravitational perturbations from an additional planet in the system (Hebb et al. 2009; Li et al. 2010). Such a perturbing body could affect the orbital motion of WASP-12 b, causing its transits to exhibit a departure from a linear ephemeris (Miralda–Escudé 2002; Schneider 2004; Holman & Murray 2005; Agol et al. 2005; Steffen et al. 2007).
The transit timing variation (TTV) method has already been used to confirm the planetary nature of systems with multiple transiting planets (e.g. Holman et al. 2010) and to discover an additional planetary companion that cannot be detected with other techniques (Ballard et al. 2011). All these discoveries are based on data acquired with the Kepler space telescope (Borucki et al. 2010) and, to our knowledge, no independently confirmed TTV signal has been detected from the ground so far1. Maciejewski et al. (2011) report a sign of a TTV signal for WASP-12 b and put upper constraints on a mass of a possible perturber. Being encouraged by this result, we organised a multi-site campaign for follow-up timing observations of transits of WASP-12 b.
2. Observations and data reduction
During three consecutive observing seasons, spanning from 2009 Nov. to 2012 Mar., we
acquired 61 complete or partial transit light curves. We used fourteen 0.5–2.6-m telescopes
located in thirteen observatories distributed around the world. A portion of the data was
obtained in collaboration with the Young Exoplanet Transit Initiative (YETI, Neuhäuser et
al. 2011). A list of participating observatories and
instruments (sorted by telescope mirror diameter) is presented in Table 1. To quantify the quality of each light curve, we used
the photometric noise rate (pnr) defined by Fulton et al. (2011) as
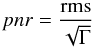 (1)where
the root mean square of the residuals, rms, is calculated from the light curve and a fitted
model, and Γ is the median number of exposures per minute. Observations were recorded in
coordinated universal time (UTC). To exclude systematic errors in the recorded times, local
computer clocks were verified with the network time protocol software, usually accurate to
better than 0.1 s. Observations were performed using the filters in which individual
instruments were the most efficient (usually R). Most of the telescopes
were significantly defocused to reduce flat-fielding noise and decrease the amount of time
lost due to CCD readout. Exposure times were kept fixed during each observing sequence.
Table 2 lists individual observations acquired with
2-m class telescopes, while data obtained with smaller instruments are given in Table 3. Short descriptions of individual instruments,
observation details, and data reduction are given in Sects. 2.1–2.13. In further analysis, three amateur
light curves (Sect. 2.14) were also included.
(1)where
the root mean square of the residuals, rms, is calculated from the light curve and a fitted
model, and Γ is the median number of exposures per minute. Observations were recorded in
coordinated universal time (UTC). To exclude systematic errors in the recorded times, local
computer clocks were verified with the network time protocol software, usually accurate to
better than 0.1 s. Observations were performed using the filters in which individual
instruments were the most efficient (usually R). Most of the telescopes
were significantly defocused to reduce flat-fielding noise and decrease the amount of time
lost due to CCD readout. Exposure times were kept fixed during each observing sequence.
Table 2 lists individual observations acquired with
2-m class telescopes, while data obtained with smaller instruments are given in Table 3. Short descriptions of individual instruments,
observation details, and data reduction are given in Sects. 2.1–2.13. In further analysis, three amateur
light curves (Sect. 2.14) were also included.
Observatories and instruments (with abbreviations identifying datasets) taking part in the campaign.
 |
Fig. 1 Light curves for transits of WASP-12 b observed with 2-m class telescopes. The residuals are shown in the bottom plots. |
2.1. Nordic optical telescope
Five light curves were acquired in the 2011/12 observing season with the Nordic Optical
Telescope (NOT) at the Observatorio del Roque de los Muchachos, La Palma (Spain), through
the P44-102 observing programme (OPTICON 2011B/003). The Andalucia Faint Object
Spectrograph and Camera (ALFOSC) was used in imaging mode, giving a field of view (FoV) of
 . The CCD was binned 2 × 2 to
obtain faster readout. During the first run (2011 Nov. 22–24), we acquired two complete
light curves and one partial light curve, for which some of the data were lost due to bad
weather. The second run (2012 Feb. 1–2) allowed us to observe two almost complete
transits. The beginning of the event on Feb. 2 was lost due to bad weather. Twenty-minute
gaps in light curves on 2011 Nov. 22 and 2012 Feb. 1 are due to the target passing through
zenith, causing rapid motion of the field derotator. Autoguiding guaranteed that stellar
centroids did not change their locations on the detector matrix during each night.
. The CCD was binned 2 × 2 to
obtain faster readout. During the first run (2011 Nov. 22–24), we acquired two complete
light curves and one partial light curve, for which some of the data were lost due to bad
weather. The second run (2012 Feb. 1–2) allowed us to observe two almost complete
transits. The beginning of the event on Feb. 2 was lost due to bad weather. Twenty-minute
gaps in light curves on 2011 Nov. 22 and 2012 Feb. 1 are due to the target passing through
zenith, causing rapid motion of the field derotator. Autoguiding guaranteed that stellar
centroids did not change their locations on the detector matrix during each night.
The photometric measurements were performed with a custom-made pipeline employing differential aperture photometry and standard CCD reduction procedures (debiasing and flat-fielding with sky flats). Only the nearest comparison star was used to minimise the possible flat-field systematics induced by the field rotator (e.g. Moehler et al. 2010). A number of apertures were used, and the light curves with the smallest photometric scatter were taken as the final ones.
2.2. Calar Alto 2.2-m telescope
We observed 15 transits with the 2.2-m telescope at the Calar Alto Observatory (Spain). Most of these observations cover complete events, and only four are partial due to bad weather. In the 2010/11 observing season, ten nights were awarded within the programme F11-2.2-008. We gathered usable data in six nights, and the other four nights were completely lost due to bad weather. In the 2011/12 season, we got seven nights (programme F12-2.2-009) and acquired complete transit light curves in all of them. Two additional light curves were obtained on 2011 Oct. 7 and Nov. 10 as backup observations for the programme H11-2.2-011.
The Calar Alto Faint Object Spectrograph (CAFOS) was used in imaging mode. The original
FoV was windowed to  and 2 × 2 binning was applied
to shorten the read-out time. The telescope was autoguided during all nights except 2012
Feb. 24, when the observers were unable to use the autoguider due to significant telescope
defocusing. The data reduction procedure was similar to that in Sect. 2.1.
and 2 × 2 binning was applied
to shorten the read-out time. The telescope was autoguided during all nights except 2012
Feb. 24, when the observers were unable to use the autoguider due to significant telescope
defocusing. The data reduction procedure was similar to that in Sect. 2.1.
2.3. 2.0-m and 0.6-m telescopes at the National Observatory Rozhen
The 2.0-m Ritchey-Chrétien-Coudé (RCC) telescope at the Bulgarian National Astronomical
Observatory Rozhen was used to observe six complete and four partial transits. During the
2009/10 and 2010/11 seasons, a VersArray 1300B CCD camera (1340 × 1300 pixels, 20
μm pixel size, resolution  per pixel) with an FoV of
per pixel) with an FoV of
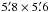 was used as a detector. The
missing part in the beginning of the event on 2009 Nov. 12, as well as gaps on 2010 Nov.
29, were caused by bad weather.
was used as a detector. The
missing part in the beginning of the event on 2009 Nov. 12, as well as gaps on 2010 Nov.
29, were caused by bad weather.
During the 2011/12 season, the same CCD camera was attached to the telescope through the
two-channel focal reducer FoReRo-2, giving a resolution of
0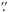 74 per pixel and
an FoV of about 15′ in diameter. Gaps in data on 2011 Nov. 22 and 2012 Jan. 19 were caused
by bad weather conditions. The beginnings of the events on 2011 Dec. 27, 2012 Jan. 18, and
2012 Feb. 23 were lost due to technical problems with the telescope. Red noise is
noticeable in some of the light curves. This effect is principally caused by observing
without autoguiding, as the telescope’s autoguider is unusable in the focal reducer mode.
74 per pixel and
an FoV of about 15′ in diameter. Gaps in data on 2011 Nov. 22 and 2012 Jan. 19 were caused
by bad weather conditions. The beginnings of the events on 2011 Dec. 27, 2012 Jan. 18, and
2012 Feb. 23 were lost due to technical problems with the telescope. Red noise is
noticeable in some of the light curves. This effect is principally caused by observing
without autoguiding, as the telescope’s autoguider is unusable in the focal reducer mode.
In addition, we acquired five transit light curves with the 0.6-m Cassegrain photometric
telescope equipped with an FLI PL09000 CCD camera (3056 × 3056 pixels, 12
μm pixel-size, resolution 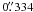 per pixel, FoV: 17′ × 17′).
per pixel, FoV: 17′ × 17′).
Standard idl procedures (adapted from daophot) were used for data reduction (debiasing and flat-fielding with sky flats) and performing differential aperture photometry. Using the method of Everett & Howell (2001), several stars (4 to 6) with photometric precision better than 4 mmag (6 mmag for the 0.6-m telescope) were selected to create an artificial comparison star used for the differential photometry.
2.4. Bohyunsan Optical Telescope
The transit light curve on 2012 Dec. 24 was obtained with the Bohyunsan Optical Telescope
(BOT) at the Bohyunsan Optical Astronomy Observatory (BOAO). The telescope is an alt-az
1.8-m (f/80) reflector operated by the Korea Astronomy and Space Science Institute (KASI),
equipped with the BOAO 4k CCD (15 × 15 μm) imaging instrument. An
available FoV is  on a scale of
on a scale of
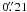 per pixel. We used the 2 × 2
binning mode and windowed the FoV to increase the sampling rate. The autoguider system was
used, and pointing errors were found to be a few tenths of a pixel per exposure.
Observations were reduced in the same way as described in Sect. 2.1.
per pixel. We used the 2 × 2
binning mode and windowed the FoV to increase the sampling rate. The autoguider system was
used, and pointing errors were found to be a few tenths of a pixel per exposure.
Observations were reduced in the same way as described in Sect. 2.1.
2.5. Cassini Telescope
A complete transit of WASP-12 b was observed on 2009 Nov. 11 and a partial one on 2011
Oct. 7 with the 1.52-m Cassini Telescope at the Astronomical Observatory
of Bologna in Loiano (Italy). This telescope was already successfully utilised to follow
up several transiting planets (Southworth et al. 2010, 2012a,b; Mancini et al. 2013). It is equipped with the Bologna Faint Object
Spectrograph & Camera (BFOSC), an instrument built to allow the acquisition of
both images and spectra with a simple configuration change. The detector is a
back-illuminated EEV LN/1300-EB/1 CCD with 1300 × 1340 pixels, giving an FoV of
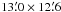 on a scale of
on a scale of
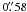 per pixel.
per pixel.
The observations were analysed following standard methods. We created master bias and flat-field images by median-combining sets of bias images and sky flats, and used them to correct the science images. Aperture photometry was performed using the idl/astrolib implementation of daophot (Southworth et al. 2009). The apertures on the target star were placed by eye, and their sizes were set to a wide range of values to find those that gave photometry with the lowest scatter compared to a fitted model. Differential photometry was finally performed using an optimal ensemble of comparison stars.
2.6. 1.5-m Gunma Astronomical Observatory telescope
Transits on 2009 Dec. 26 and 2010 Jan. 18 were observed with the 1.5-m Ritchey-Chrétien
telescope at the Gunma Astronomical Observatory (Japan). An Andor DW432 CCD camera
(1250 × 1152 pixels) was used as a detector providing a
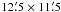 FoV.
FoV.
The photometric data were reduced following standard procedures including subtraction of a median dark frame and dividing by a sky flat field. The relative magnitudes were derived with the aperture photometry method implemented in the customised software pipeline developed for the Semi-Automatic Variability Search sky survey (Niedzielski et al. 2003). An artificial comparison star was generated iteratively using 20–30% of the unsaturated stars with the lowest scatter. A number of aperture radii were tested and the aperture that produced light curves with the smallest scatter was finally chosen.
2.7. Devasthal Fast Optical Telescope
The transit on 2011 Feb. 5 was observed with the 1.3-m Devasthal Fast Optical Telescope (DFOT, Sagar et al. 2012) located at the Devasthal Observatory (India). A set of 2770 exposures was recorded with an exposure time of 5 s. The data reduction was done as described in detail in Joshi et al. (2009). To improve the signal-to-noise ratio, subsets of 20 single frames were co-added to produce the final light curve.
2.8. 1.2-m Michael Adrian Observatory telescope
The 1.2-m T1T telescope at the Michael Adrian Observatory in Trebur
(Germany) was used to observe four and two complete transits in the 2010/11 and 2011/12
seasons, respectively. The telescope has a Cassegrain optical system and is equipped with
a 3072 × 2048-pixel SBIG STL-6303 CCD camera (FoV: 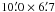 ). The light curve acquired on
2011 Jan. 28 was affected by high airmass at the end of the run. Observations on 2011 Feb.
7 were interrupted by occasional passing clouds. Observations were reduced in the same way
as described in Sect. 2.6.
). The light curve acquired on
2011 Jan. 28 was affected by high airmass at the end of the run. Observations on 2011 Feb.
7 were interrupted by occasional passing clouds. Observations were reduced in the same way
as described in Sect. 2.6.
2.9. Mount Lemmon Optical Telescope
Two complete (2011 Dec. 8 and 2012 Jan. 1) and one partial (2012 Jan. 13) transit light
curves were obtained using the 1.0-m reflector operated by KASI at the Mount Lemmon
Optical Astronomy Observatory (LOAO) in Arizona, USA. For all observations we used the ARC
4k CCD instrument in the 2 × 2 binning mode. The CCD has a pixel size of 15 × 15
μm, a scale of 0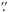 41 per pixel,
and an FoV of 28′ × 28′. During the transits the weather was clear but not photometric
with partial clouds early in the evenings and later clearing up during the runs.
Observations were reduced in the same way as described in Sect. 2.6.
41 per pixel,
and an FoV of 28′ × 28′. During the transits the weather was clear but not photometric
with partial clouds early in the evenings and later clearing up during the runs.
Observations were reduced in the same way as described in Sect. 2.6.
2.10. Konkoly Observatory
Transits on 2011 Jan. 27 and 2011 Dec. 5 were observed with the 1.0-m RCC Telescope at
the Piszkéstető Station of the Konkoly Observatory (Hungary), equipped with a
1340 × 1300-pixel PI VersArray 1300b NTE CCD (FoV: 7′ × 7′, image scale
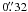 per pixel). Flat-fielding
using sky flats, dark correction, and aperture photometry was performed with standard
iraf routines and a dedicated gnu-r script as described in Szabó et
al. (2010).
per pixel). Flat-fielding
using sky flats, dark correction, and aperture photometry was performed with standard
iraf routines and a dedicated gnu-r script as described in Szabó et
al. (2010).
2.11. Lulin One-meter Telescope
A transit on 2010 Feb. 10 was observed with the Lulin One-meter Telescope (LOT) at the Lulin Observatory, operated by the National Central University of Taiwan. A VersArray:1300B CCD camera with an FoV of 11′ × 11′ was used as a detector. Observations were reduced in the same way as described in Sect. 2.6.
 |
Fig. 3 Additional amateur light curves obtained with 20-cm reflecting telescopes. The mid-transit times were found to be BJDTDB 2 455 865.6130 ± 0.0012 (2011 Oct. 30), 2 455 923.4609 ± 0.0026 (2011 Dec. 27), and 2 455 934.3725 ± 0.0009 (2012 Jan. 07). |
2.12. University Observatory Jena
Five light curves were acquired with the 0.9/0.6-m Schmidt telescope at the University
Observatory Jena in Großschwabhausen near Jena (Germany). The CCD-imager Schmidt Teleskop
Kamera (STK, Mugrauer & Berthold 2010) has
a 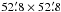 FoV that allows numerous
comparison stars to be observed simultaneously.
FoV that allows numerous
comparison stars to be observed simultaneously.
Data acquired on 2011 Feb. 8, 2011 Mar. 2, and 2011 Mar. 3 were reduced as described in Sect. 2.6. The remaining two nights (2011 Nov. 21 and 22) were reduced with the iraf routines after subtracting dark frames and applying flat-field correction with sky flats. After applying aperture photometry, differential magnitudes were calculated using the algorithm described in Broeg et al. (2005). This algorithm calculates an artificial standard star out of all stars in the field, weighted by their magnitude errors, and compares the brightness of each star, including our target star WASP-12, against this standard star.
2.13. Stará Lesná Observatory
Three light curves were obtained at the Stará Lesná observatory in Slovakia. Observations
were performed with the 0.5-m Newtonian telescope, on which an SBIG ST10 MXE CCD camera
with 2184 × 1472 6.8-μm pixels was mounted. The scale was
0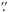 56 per pixel,
corresponding to an FoV of 24′ × 16′.
56 per pixel,
corresponding to an FoV of 24′ × 16′.
The light curve obtained on 2010 Mar. 9 exhibits correlated noise because observations were acquired without autoguiding. Standard correction procedures (bias, dark, and flat-fielding) and then aperture photometry was performed with the C-munipack package2. To generate an artificial comparison star, at least 20−30% of stars with the lowest photometric scatter were selected iteratively from the field stars brighter than 2.5−3 mag below saturation level. To measure instrumental magnitudes, various aperture radii were used. The aperture that gave the smallest magnitude scatter was applied to generate a final light curve.
2.14. Amateur light curves
Light curves for transits on 2011 Oct. 30 and 2012 Jan. 7 were acquired at Castelnuovo Magra (Italy) with a Meade LX200 GPS 10 inch telescope equipped with an f/6.3 focal reducer and an SBIG ST8 XME CCD camera. Science frames were taken through the Baader Yellow 495 Longpass filter with an exposure time of 300 s. The CCD frames were acquired with the MaxIm DL 4 software and then reduced with MaxIm DL 5. The data reduction procedure included removal of dark frames, flat-fielding, and aperture photometry against nearby bright stars.
Observations of the transit on 2011 Dec. 27 were acquired with a CCD camera based on a Sony ICX429ALL sensor, mounted on an 0.2-m Newtonian telescope located near Lucca (Italy). The data were also collected through the Baader Yellow 495 passband filter, and an exposure time of 260 s was used. The equatorial fork mount of the telescope was guided by a modified Webcam coupled with a 60 mm telephoto lens. Images were acquired by the AstroArt v4 software, and a standard data reduction procedure including aperture photometry was performed with the MaxIm DL 5 programme. To generate an artificial comparison star, eight reference stars of magnitudes close to that of WASP-12 were used.
2.15. Light curve pre-processing
Even the best-quality light curves may be affected by photometric trends caused, for instance, by a colour difference between the target and comparison stars and changes in airmass during a run. If they are not removed properly, they may seriously affect transit timing. To remove trends, a model that consists of a transit signal adopted from Maciejewski et al. (2011) and a second-order polynomial were fitted to each light curve analysed in this work. We used the jktebop code (Southworth et al. 2004a,b), which is based on the ebop program (Etzel 1981; Popper & Etzel 1981) and allows photometric trends to be approximated with a polynomial up to order five. A best-fitting trend was subtracted from each light curve and then magnitudes were transformed into fluxes normalised to unit out-of-transit flux level.
3. Results
3.1. System parameters
The Transit Analysis Package3 (tap, version 2.104, Gazak et al. 2012) was used to analyse transit light curves and refine system parameters. TAP uses the Markov chain Monte Carlo (MCMC) approach, with the Metropolis-Hastings algorithm and a Gibbs sampler, to determine model parameters. Wavelet-based techniques are employed to account for correlated noise while estimating error values. It has been shown that this approach provides the most reliable parameter results and error estimates (e.g. Hoyer et al. 2012). The code employs the quadratic limb-darkening (LD) law to model the distribution of the flux on a stellar disc.
To refine the system parameters, the best-quality light curves acquired with 2-m class
telescopes were selected for a simultaneous fit. The selection criteria included
sub-millimagnitude precision of a dataset
(pnr < 1.0 mmag) and transit phase completeness
higher than 75%, including at least an ingress or/and egress preceded or followed by
out-of-transit observations and a flat-bottom phase. Nineteen light curves were found to
fulfil these criteria, including observations on 2010 Feb. 02 by Maciejewski et al. (2011). We ran ten MCMC chains, each containing
106 steps. The individual chains were combined to get final posteriori
probability distributions. The following parameters were linked together for all light
curves: orbital period Pb, orbital inclination
ib, semimajor-axis scaled by stellar radius
ab/R∗,
planetary to stellar radii ratio
Rb/R∗, and
linear (u) and quadratic (v) LD coefficients. The
mid-transit times, airmass slopes, and flux offsets were allowed to vary separately for
individual light curves. A circular orbit was assumed. An analysis of relations between
the parameters reveals significant correlation or anti-correlations (with the Pearson
correlation coefficients ranging from 0.71 to 0.96) between ib
and ab/R∗,
ib and
Rb/R∗,
ab/R∗ and
Rb/R∗,
Rb/R∗ and
v, and u and v. The best-fitting
parameters were determined by taking the median value of marginalised posteriori
probability distributions, which were found to be unimodal. The 15.9 and 85.1 percentile
values of these distributions were taken as upper and lower 1σ errors.
The results are presented in Table 4 where the
impact parameter (defined as  ) is also given. The
final model of WASP-12 b’s transit signature is plotted in Fig. 4.
) is also given. The
final model of WASP-12 b’s transit signature is plotted in Fig. 4.
Parameters of the WASP-12 system from the joint analysis of 19 sub-millimagnitude-precision light curves and the refined linear ephemeris.
The LD coefficients of the best-fitting model were compared to the theoretical values
calculated from the tables from Claret & Bloemen (2011), and derived with the exofast applet4 (Eastman et al. 2013). The
coefficients were bilinearly interpolated from the tables assuming the host star effective
temperature and surface gravity as given by Hebb et al. (2009). The theoretical coefficients, ut = 0.288 and
vt = 0.317, agree with the derived values
(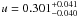 and
and 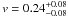 )
within 1σ.
)
within 1σ.
To check for any evolution of the system parameters, for instance as a result of a periastron rotation, the fitting procedure was repeated with ib, ab/R∗, and Rb/R∗ allowed to vary between individual light curves. The linear and quadratic LD coefficients were allowed to vary around values derived in the previous run, under the Gaussian penalty defined by the derived errors. We found that none of these parameters exhibited a statistically significant variation. In addition, we compared individual mid-transit times derived in both approaches, and no discrepancy greater than 1σ was found.
 |
Fig. 4 Best-fitting model of WASP-12 b’s transit (red line) laid over the 19 best-quality, phase-folded light curves. |
The planet WASP-12 b is known to depart significantly from a spherical shape. The ratio
of its polar and sub-stellar-point radii was found to be ~1.14 (Budaj 2011). The observed planetary radius
Rb is the cross section of the planet at inferior
conjunction. It can be calculated from
ab/R∗ and
Rb/R∗
assuming a value of the semi-major axis of ab from Hebb et al.
(2009). The effective planetary radius,
 , which is
more representative of the physical parameters of the planet, is greater. Following the
numerical results of Budaj (2011), we get
, which is
more representative of the physical parameters of the planet, is greater. Following the
numerical results of Budaj (2011), we get
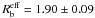 RJup.
This value is identical to 1.90 ± 0.09 RJup determined by
Maciejewski et al. (2011) and within
1σ of the results of Chan et al. (2011) and Southworth (2012). The mean
planetary density was found to be ρb = 0.206 ± 0.043
ρJup. This value is lower than found by previous studies,
because we have accounted for the effective planetary radius in our calculations, but is
consistent with them within 1σ. The surface gravitational acceleration we
find, gb = 9.8 ± 0.4 m s-2, is also noticeably less
than previous studies for the same reason.
RJup.
This value is identical to 1.90 ± 0.09 RJup determined by
Maciejewski et al. (2011) and within
1σ of the results of Chan et al. (2011) and Southworth (2012). The mean
planetary density was found to be ρb = 0.206 ± 0.043
ρJup. This value is lower than found by previous studies,
because we have accounted for the effective planetary radius in our calculations, but is
consistent with them within 1σ. The surface gravitational acceleration we
find, gb = 9.8 ± 0.4 m s-2, is also noticeably less
than previous studies for the same reason.
A faint stellar companion to WASP-12 has been recently discovered at a separation of ~1″ (Bergfors et al. 2012). It is ~4 mag fainter in the i′ band, and its spectral type is in the region of K0 to M0. Since it is not resolved in any of our observations, its light contributes to the total flux of the system. This makes the transit depth shallower by 0.2–0.3 mmag, the precise amount depending on its spectral type. Due to this, we estimate the final planetary radius to be greater by 0.6–1.0%, so ρb and gb will be slightly smaller than the values given above.
The stellar parameters agree with previous studies. We find the stellar radius to be R∗ = 1.63 ± 0.07 R⊙ (assuming the value of ab from Hebb et al. 2009), its mean density to be ρ∗ = 0.315 ± 0.007 ρ⊙, and its surface gravity to be equal log g∗ = 4.14 ± 0.03 (cgs units).
3.2. Transit timing
The individual transit times were determined by fitting a template transit light curve with tap. The fitting procedure started with initial parameters whose values are taken from the best-fitting model (Sect. 3.1, Table 4). They were allowed to vary in the MCMC analysis under Gaussian penalties whose scales were determined by the parameters’ errors. This approach allowed best-model uncertainties to be included in a mid-transit time budget of each light curve. Ten chains of a length of 105 steps were used for each light curve. The first 10% of iterations of each chain were discarded before calculating the parameter values and errors. The mid-transit times, converted to barycentric Julian dates in barycentric dynamical time (BJDTDB, see Eastman et al. 2010), and their errors are given in Tables 2 and 3.
In addition, we re-analysed two datasets from Maciejewski et al. (2011) and obtained mid-transit times 2 455 230.40669 ± 0.00019 and 2 455 254.41871 ± 0.00045 BJDTDB. These values are well within the error bars compared to the original mid-transit times of 2 455 230.40673 ± 0.00011 and 2 455 254.41887 ± 0.00014 BJDTDB, respectively. We also re-analysed a high-accuracy light curve acquired with the 2-m Liverpool Telescope and published in Hebb et al. (2009). The mid-transit time for this early epoch (no. 6) was found to be 2 454 515.52496 ± 0.00043 BJDTDB assuming that the times in original data are in HJDUTC5. The original mid-transit time was not published in Hebb et al. (2009), but it is listed in Campo et al. (2011) as 2 454 515.52542 ± 0.00016 BJDTDB. Both determinations differ by less than 1σ.
Mid-transit times of a single transit observed with different telescopes provide an empirical test of the timing accuracy and error estimates. We collected two or more light curves for twelve transits. Eight of them were observed with two telescopes and four with three telescopes. The median difference between individual times was found to be 0.4σ and never exceeded 1σ. This finding supports the reliability and consistency of our timing survey. Furthermore, we compared mid-transit times derived with tap and jktebop. The latter code offers Monte Carlo (MC) simulations, a bootstrapping algorithm, and the residual-shift (prayer-bead) method to estimate the uncertainties of parameters. The largest of the errors from the methods were conservatively taken. Both codes give consistent results with the median difference between the determined times to a midpoint equal to 13 s or 0.13σ. The median of the ratios of the tap to the jktebop timing errors was found to be 1.33. This value includes partial light curves for which the tap code usually gives errors greater by a factor of up to four.
 |
Fig. 5 O–C diagram for WASP-12 b’s transit timing. The filled circles denote our observations and squares the literature ones with errors smaller than 40 s. The open symbols – circles and squares for our and literature data, respectively – mark points with timing errors greater than 40 s. The open triangles denote the amateur times included in this work. The postulated sinusoidal variation is sketched with a red line. Individual observing seasons, covered by our high-precision observations, are zoomed-in at the bottom. The literature data are taken from Hebb et al. (2009), Chan et al. (2011), Maciejewski et al. (2011), Sada et al. (2012), and Cowan et al. (2012). |
A linear function was fitted to the transit times to determine the orbital period Pb and the time of transit at cycle zero, T0. Cycle zero was taken to be the epoch given by Hebb et al. (2009). We fitted the transit times from new and literature data by the method of least squares. The data point for epoch zero was skipped because it comes from a global fit based on a number of individual light curves (Hebb et al. 2009). We found T0 = 2 454 508.97718 ± 0.00022 BJDTDB and Pb = 1.0914209 ± 0.0000002 d. The individual mid-transit errors were used as weights during the fitting. The reduced χ2 is 1.29, which corresponds to a p-value of 0.06. A null hypothesis assuming constant Pb could therefore not be rejected. The O–C (observed minus calculated) diagram for transit timing is plotted in Fig. 5.
More interestingly, the same conclusion cannot be drawn if the mid-transit time sample is limited to the best-quality data. We now consider only those mid-transit times that have uncertainties below 40 s (i.e. a half of the TTV amplitude suggested in Maciejewski et al. 2011). The linear fit was repeated, resulting in χ2 = 1.99 and a p-value of 1.6 × 10-3. This result allows the null hypothesis to be questioned. Moreover, a coherent pattern in the O–C diagram is noticeable (Fig. 5). In the next step, a model consisting of a linear trend and a sinusoidal variation was fitted. After removing the linear component, a Lomb-Scargle periodogram (Lomb 1976; Scargle 1982) reveals a peak at a period of ~510 epochs (Fig. 6). The false alarm probability (FAP) of this signal is 0.7% and was determined empirically by a bootstrap resampling method. The procedure randomly permutes the O–C values, retaining the original observing epochs, and then calculates the Lomb-Scargle periodogram to determine the power of the strongest signal. After 105 such trials, the FAP of the signal in the original dataset is taken to be the fraction of resampled periodograms that produced higher power than the original dataset. From the least-squares fit, we find that the possible TTV signal has a period of 500 ± 20 epochs and a semi-amplitude of 0.00068 ± 0.00013 d (Fig. 5). The errors are taken from the covariance matrix of the fit. The reduced χ2 of this model is 0.91.
3.3. Two-planet model
A TTV signal shown by the transiting planet may reflect gravitational perturbations driven by an undetected additional planet in the system (e.g. Ballard et al. 2011). To check what planetary configurations may produce timing variations with the postulated periodicity, three-body simulations were performed with the mercury package (Chambers 1999) employing the Bulirsch–Stoer integrator. A hypothetical additional planet of a probe mass of 40 M⊕ was put on orbits with semimajor axes ranging from 0.007 to 0.068 AU (orbital periods between 0.22 and 5.5 d, respectively) with a step equal to 10-6 AU. The semimajor axis of WASP-12 b and the mass of the central star were set to the values found by Hebb et al. (2009). The eccentricity of the perturber, ec, was varied from 0.0 to 0.3 in steps of 0.05. Scenarios with circular and eccentric orbits (eb equal to 0.02, 0.03 and 0.05) of the transiting planet were considered. The simulations assumed coplanar and edge-on orbits. The calculations covered 1500 orbital periods of the transiting planet, i.e. slightly greater than the time span of the timing observations. Lomb-Scargle periodograms were calculated for the synthetic O–C diagrams to determine the dominant periodicity. Numerous solutions that reproduce the postulated TTV signal were identified.
To alleviate the solution degeneracy, the publicly available RV measurements were re-analysed with the Systemic Console software (Meschiari et al. 2009). We used data from Hebb et al. (2009), Husnoo et al. (2011), and Albrecht et al. (2012). The datapoints in transit phase (± 1.6 h from predicted mid-transit times) were removed to avoid interference from the Rossiter–McLaughlin (RM) effect (Rossiter 1924; McLaughlin 1924), which manifests itself as a distortion of the spectral lines of the host star during transit. Data published by Hebb et al. (2009) were collected in the 2007/8 observing season with the SOPHIE spectrograph coupled with the 1.9-m telescope at the Observatoire de Haute Provence. We selected 17 RV measurements with errors between 9 and 13 m s-1 for further analysis. Husnoo et al. (2011) presented further data acquired with SOPHIE in the 2008/9 and 2009/10 seasons. The spectra acquired on 2009 Mar. 21 and 2009 Apr. 13 have half the signal-to-noise ratio and noticeably greater errors than the other observations. This could indicate that these two exposures were affected by clouds which, in turn, could introduce a systematic shift in the RV measurement (N. Husnoo, priv. comm.). We noticed that one of these lower quality points is an outlier at the 3σ level regardless of the RV model under consideration. These two points were therefore not included in any further analysis. It is worth noting that keeping these outlying points does not quantitatively change the ensuing results but noticeably degrades the quality of the fits to the RVs. We also rejected measurements from 2009 Jan. 17 when the signatures of the RM effect were observed. We finally used four and six datapoints from the 2008/9 and 2009/10 seasons, respectively. RVs reported by Albrecht et al. (2012) were acquired in the 2011/12 season with the HIRES spectrograph on the Keck telescope. We used 13 measurements in our study.
 |
Fig. 6 Periodogram of the O–C residuals (continuous black line) and spectral window (dashed red line, multiplied by 10 for clarity). The dashed vertical line shows the empirical FAP level of 1%. The arrow marks the most significant peak, which as can be clearly seen, is not caused by the structure of gaps in the time domain. The shortest period investigated is given by the Nyquist frequency. |
The RV dataset from Husnoo et al. (2011) was split into two separate subsets according to observing season. We noticed that allowing a variation in the RV offsets between individual observing seasons results in significantly better fits. This effect may be caused by the low number of datapoints, the influence of additional bodies on long-term orbits in the system, or instrumental effects. The last is a justifiable possibility because SOPHIE, when operated in high efficiency mode, has been found to produce deviations up to several dozens of m s-1 from a velocity zero point on a timescale of a few months (Husnoo et al. 2011).
In our analysis, the RV signature of tides raised in the host star by the transiting planet is not considered because its expected amplitude of 4.8 m s-1 (Arras et al. 2012) is smaller than the typical errors of the RV measurements.
The periodogram of the RV residuals versus the best-fitting model for WASP-12 b on a circular Keplerian orbit (Fig. 7) shows a signal at approximately 3.6 d. Its empirical FAP was found to be 0.08%, from 105 trials with the bootstrap resampling method. A preliminary Newtonian RV modelling indicate that the residuals may be caused by an additional ~0.1 MJup planet on a non-circular orbit with an eccentricity ec of between 0.2 and 0.3. Intriguingly, our three-body simulations performed with the Mercury code show that a system configuration for a 0.1 MJup perturber may reproduce the postulated timing variations of WASP-12 b if ec is close to 0.3 and eb is between 0.03 and 0.05.
 |
Fig. 7 Periodogram of RV residuals for WASP-12 b on a Keplerian orbit (continuous black line) and the spectral window (dashed red line, multiplied by 10 for clarity). The arrow indicates the strongest peak at 3.58 d that is not associated with significant power in the spectral window. The shortest period is set by the radius of the star. The dashed and dotted horizontal lines show empirical FAP levels of 1% and 0.1%, respectively. |
To model the RV and transit timing datasets simultaneously, we used the Systemic
Console with the Bulirsch–Stoer integrator and a precision parameter of
10-14. The times of RV observations were transformed to BJDTDB. To
put additional constraints on the orbital parameters of WASP-12 b, the transit dataset was
enhanced with five mid-occultation times from Campo et al. (2011) and Croll et al. (2011).
The light-travel time correction of 22.8 s was taken into account. The López-Morales
(2010) mid-occultation point was not considered
in the final iterations because of its much greater uncertainty and possible systematic
timing offset (see Campo et al. 2011 and Croll et
al. 2011 for discussion). The orbital periods,
masses, eccentricities, longitudes of periastron, and mean anomalies were allowed to vary
for both planets. The offsets for individual RV subsets were also free parameters. The
best-fitting model was found iteratively with the simulated annealing and Nelder-Mead
minimisation algorithms. The joint χ2 statistic accounts for
the contributions from the RV and transit time datasets,
 and
and
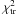 respectively:
respectively: ![\begin{equation} \chi^2= \frac{1}{N_{\rm{RV}}+N_{\rm{tr}}-N_{\rm{fit}}}\left[(N_{\rm{RV}}-N_{\rm{fit}})\chi^{2}_{\rm{RV}}+\lambda \chi^{2}_{\rm{tr}}\right] \end{equation}](/articles/aa/full_html/2013/03/aa20739-12/aa20739-12-eq132.png) (2)where
NRV, Ntr, and
Nfit are the numbers of RV measurements, mid-transit times,
and fitted parameters, respectively, and λ is an arbitrary weight
(Meschiari et al. 2009). The
(2)where
NRV, Ntr, and
Nfit are the numbers of RV measurements, mid-transit times,
and fitted parameters, respectively, and λ is an arbitrary weight
(Meschiari et al. 2009). The
 of the
best-fitting model is approximately five times greater than
of the
best-fitting model is approximately five times greater than
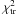 , which
suggests that the RV errors are underestimated. To balance the significance of both data
sets, λ = 5 was specified in the final iterations. The MCMC method was
used to determine parameter uncertainties. The MCMC chain was 106 steps long,
and the first 105 configurations were discarded. The scale parameters were set
empirically in a series of attempts to get the acceptance rate of the MCMC procedure close
to the optimal value of 0.25. For each parameter the standard deviation was taken as the
final error estimate. The best-fitting parameters of the two-planet model are given in
Table 5. Figure 8 shows the RV components from WASP-12 b and the postulated planet, as well as
the modelled TTV signal.
, which
suggests that the RV errors are underestimated. To balance the significance of both data
sets, λ = 5 was specified in the final iterations. The MCMC method was
used to determine parameter uncertainties. The MCMC chain was 106 steps long,
and the first 105 configurations were discarded. The scale parameters were set
empirically in a series of attempts to get the acceptance rate of the MCMC procedure close
to the optimal value of 0.25. For each parameter the standard deviation was taken as the
final error estimate. The best-fitting parameters of the two-planet model are given in
Table 5. Figure 8 shows the RV components from WASP-12 b and the postulated planet, as well as
the modelled TTV signal.
 |
Fig. 8 Joint RV and transit timing model for the WASP-12 system including two planets. Upper: the RV variation produced by WASP-12 b. Middle: the RV signal generated by the postulated planet WASP-12 c. Bottom: the O–C diagram for the transit timing of WASP-12 b with a modelled TTV signal and the residuals shifted by −0.0026 d for clarity. |
Parameters of the two-planet WASP-12 system from the joint analysis of RVs and transit timing.
The RV datasets from the 2008/9 and 2009/10 seasons were found to be shifted against the
2007/8 dataset by −16.4 ± 3.3 and + 1.1 ± 2.9 m s-1, respectively. The value
of the joint χ2 was found to be 3.0 with individual components
 and
and
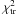 equal to
2.5 and 0.4, respectively. For comparison, a single-planet model with a circular and
eccentric orbit have joint χ2 values of 7.9 and 6.3,
respectively. In the two-planet model, the final rms of the RV dataset was reduced to 7.4
m s-1 from 12.5 m s-1 for a single-planet model with WASP-12 b on a
circular orbit, and from 9.6 m s-1 for a single-planet model with WASP-12 b on
an eccentric orbit.
equal to
2.5 and 0.4, respectively. For comparison, a single-planet model with a circular and
eccentric orbit have joint χ2 values of 7.9 and 6.3,
respectively. In the two-planet model, the final rms of the RV dataset was reduced to 7.4
m s-1 from 12.5 m s-1 for a single-planet model with WASP-12 b on a
circular orbit, and from 9.6 m s-1 for a single-planet model with WASP-12 b on
an eccentric orbit.
3.4. Dynamical stability
The relatively high eccentricity of the postulated planet WASP-12 c raises the question of whether the system is dynamically stable. In this paper, we consider only Newtonian, point-mass mutual interactions as a first-order model of the dynamics of the system. The planet WASP-12 b has an extremely short orbital period, so it is not sufficient to study the long-term evolution of the system with close-in companion WASP-12 c based only on the conservative dynamics. Owing to the close proximity of WASP-12 b to its host star, a full dynamical model would need to account for general relativistic effects, rotational and tidal deformations, and the tidal dissipation of energy (e.g. Mardling & Lin 2002; Migaszewski & Goździewski 2009). If these effects are considered, the orbital geometry and long-term evolution of the whole, mutually interacting system may have been strongly affected ever since its formation, possible migration, and tidal evolution. We postpone this complex problem to another work.
A cursory inspection of the putative system parameters (Table 5) reveals that it is close to the 10b:3c mean-motion resonance (MMR)6. This justifies our interest in the short-term dynamics of the system. We reconstruct the structure of the phase-space in terms of the maximum Lyapunov exponent (Benettin et al. 1976) which is expressed through the so called fast indicator Mean Exponential Growth factor of Nearby Orbits (MEGNO, see e.g. Cincotta & Simó 2000; Cincotta et al. 2003; Goździewski et al. 2001 for details). This dynamical characteristic helps us to classify given sets of initial conditions as regular (leading to quasi-periodic evolution of the system, stable over infinite period of time) or chaotic (leading to irregular phase-space trajectories). The later might lead to geometric changes of the orbits rendering the system unstable in the short-term timescale of 104–105 outer periods (Pc). By the design, the MEGNO indicator when converged to two over any given integration time, guarantees orders of magnitude longer timescale of the dynamical (Lagrange) stability. However, one must be aware that we consider a relatively narrow time window of the system evolution, restricted to the conservative, Newtonian point-mass dynamics.
To visualise the orbital stability and dynamical neighbourhood of the WASP-12 system, we computed a high-resolution dynamical map in the (ac,ec)–plane, see Fig. 9, with the help of our new CPU cluster software mechanic (Słonina et al. 2012). Each point (initial condition) was integrated for 105Pc. Such a timescale is long enough to detect even weak, high-order MMRs. Two MMRs (56c:17b and 33c:10b), which are the closest match to the nominal position of the system (marked with the asterisk symbol), are labelled on the scan. Thanks to the high resolution of the dynamical map, other, even weaker MMRs are also identifiable. The 79c:24b MMR and the 89b:27c MMR (both not labelled), which are between the 23b:7c MMR and 56c:17b MMR, are the closest to the nominal position of the system. Bearing in mind the very small error range of the semimajor axis of the outer planet in the dynamical map, ~10-6 AU (see an explanation below), we found that it might encompass these resonances. Nevertheless, they are very narrow and weak due to their high order. There is only a low probability that the system might be trapped in such resonances. The error range of eccentricity safely separates the WASP-12 system from the zone of global chaos, visible roughly above ec ~ 0.32. This zone appears due to proximity to the orbits’ crossing zone and overlapping of the MMRs.
The dynamical map in Fig. 9 is computed for a
particular, nominal mass of the parent star and all orbital elements, besides those
constituting the map coordinates, are fixed at their best fit values. In general, for a
fixed nominal mass of the star, the semi-major axis derived as osculating element at some
initial epoch is essentially influenced by uncertainties of the planetary masses and
orbital periods in accord with the IIId Kepler law,
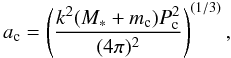 (3)as the most
uncertain parameters (here k is the Gaussian gravitational constant),
though the planetary and stellar mass relation is indirect due to the
N-body observational model. Therefore, the formal error of
ac in the dynamical map should be considered as weakly
dependent on the error of the (fixed) stellar mass.
(3)as the most
uncertain parameters (here k is the Gaussian gravitational constant),
though the planetary and stellar mass relation is indirect due to the
N-body observational model. Therefore, the formal error of
ac in the dynamical map should be considered as weakly
dependent on the error of the (fixed) stellar mass.
If the stellar mass is varied, the relative positions of the mean motion resonances do
not change, because they depend essentially on the mass ratios
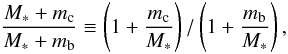 (4)and the ratios of the
orbital periods. As a result, the dynamical map might be considered to be representative
for different masses of the parent star. We also emphasise, following Michtchenko
& Malhotra (2004), that in the limit of low
planetary masses and eccentricities, the Newtonian, conservative three-body dynamics
depend on the mass ratios and semi-major axes, and not on the individual masses and
semi-major axes since the system seems to be well separated from low-order MMRs (see also
Migaszewski & Goździewski 2009).
(4)and the ratios of the
orbital periods. As a result, the dynamical map might be considered to be representative
for different masses of the parent star. We also emphasise, following Michtchenko
& Malhotra (2004), that in the limit of low
planetary masses and eccentricities, the Newtonian, conservative three-body dynamics
depend on the mass ratios and semi-major axes, and not on the individual masses and
semi-major axes since the system seems to be well separated from low-order MMRs (see also
Migaszewski & Goździewski 2009).
 |
Fig. 9 Dynamical map of the WASP-12 system in the (ac,ec)–plane, computed in terms of the MEGNO fast indicator. These two orbital parameters are varied across the map, while other orbital elements and masses are kept at their nominal values from Table 5. The star symbol, located at ac = 0.050681 AU, indicates the nominal system. Colours encode the dynamical stability of the system: yellow is for strongly unstable configurations, and blue is for stable, quasi-periodic systems. A few relevant MMRs are labelled. The raw resolution of this map is 1440 × 900 datapoints. Each initial condition at the map has been integrated for 105 outer orbits. |
4. Discussion
The two-planet model predicts that the eccentricity of WASP-12 b might be non-zero. This,
in turn, might affect the system parameters. The fitting procedure was repeated with
non-zero eb and ωb treated as fixed
parameters, values of which were taken from Table 5.
The noticeable difference was found for ib and
ab/R∗ which
were found to be 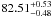 degrees and 2.93 ± 0.02, respectively. Compared to the circular-orbit scenario, the
ib and
ab/R∗
determinations are smaller by 0.5σ and 2.5σ, respectively.
Adopting these values in the calculations results in
degrees and 2.93 ± 0.02, respectively. Compared to the circular-orbit scenario, the
ib and
ab/R∗
determinations are smaller by 0.5σ and 2.5σ, respectively.
Adopting these values in the calculations results in  and
R∗ greater by 4% and 2%, respectively, hence lower values for
ρb, gb,
ρ∗, and log g∗. Since the non-zero
eccentricity of WASP-12 b is speculative, we settle for the scenario with the circular orbit
in Sect. 3.1.
and
R∗ greater by 4% and 2%, respectively, hence lower values for
ρb, gb,
ρ∗, and log g∗. Since the non-zero
eccentricity of WASP-12 b is speculative, we settle for the scenario with the circular orbit
in Sect. 3.1.
Statistical studies of hot Jupiter candidates in the Kepler sample show that these planets are rare in multi-transiting systems (Latham et al. 2011). The occurrence rate is below 5%. The solitariness of hot Jupiters is postulated to be a result of the dynamical evolution of their planetary systems. On the other hand, there are systems with hot Jupiters accompanied by non-transiting planets on wide orbits, e.g. HAT-P-13 (Bakos et al. 2009), HAT-P-17 (Howard et al. 2012), and Qatar-2 (Bryan et al. 2012). These additional planets have been discovered with the RV technique. Their gravitational influence on the transiting planets is too small to be detected through TTVs. Interestingly, single hot or warm Jupiter candidates that exhibit TTV signals have been found in the Kepler sample (Szabó et al. 2012). The frequency of hot Jupiter candidates with periodic TTVs is estimated to be 18%. Some fraction of these positive detections may be perturbative, which allows scenarios with an additional close planet or exomoon to be considered.
The ground-based timing of transiting hot Jupiters has brought no positive results so far, though preliminary detections have been announced. The characteristics of a spurious TTV signal for HAT-P-13 b are the most similar to the case of WASP-12 b. Pál et al. (2011) observed a 0.01 d departure from a linear ephemeris. This finding was confirmed by Nascimbeni et al. (2011) who proposed a sinusoidal variation with a period of ~1150 d and semi-amplitude of 0.005 d. Such a signal could not be caused by the known HAT-P-13 c planet, suggesting there is a third planetary component. Then, Fulton et al. (2011) show that all mid-transit times, except the one from an earlier work by Szabó et al. (2010), are consistent with a linear ephemeris. A similar conclusion was reached by Southworth et al. (2012a), who found no evidence of periodic timing variations.
Bearing in mind the case of HAT-P-13 b, we observed various phases of the TTV signal postulated for WASP-12 b: a maximum (the 2009/10 season), two minima (the 2010/11 and 2011/12 seasons), and portions of ascent and descent trends. Furthermore, we selected mid-transit times of the highest quality for the final analysis. They come from different instruments and data reduction pipelines, thus systematic errors are expected to be minimised. The timing scatter between consecutive transits (up to four in the 2011/12 season) and runs (separated from each other by at least 10–12 epochs) was found to be much smaller than the amplitude of the postulated long-term variation.
Near-ultraviolet (near-UV) transmission spectroscopy during transits of WASP-12 b shows that the planet has an exosphere extending beyond the planet’s Roche lobe (Fossati et al. 2010b). Moreover, these data show that transits begin earlier and are longer than at optical wavelengths. This phenomenon may be interpreted as a fingerprint of an accretion stream escaping from the planet through the inner Lagrangian point (Lai et al. 2010). It is also explicable as the effect of a bow shock induced by the orbital motion of the planet with a magnetic field in the stellar coronal material (Vidotto et al. 2010; Llama et al. 2011). A characteristic of such dynamical interactions is temporal variation implied by the variable magnetic field of the central star (Vidotto et al. 2011). The changes in phases of the early ingress would affect the transit duration, hence the time of a mid-transit. This, in turn, would produce a TTV. The effect of the early ingress, however, is not expected to be detected in the optical bands. In Sect. 3.1 we analysed only complete transits, and found no variation in the transit duration. We also compared the values of the rms in ingress, flat bottom, and egress phases of these light curves after phase folding. Changes in the transit duration would smear the ingress and egress data points in phase, causing a greater rms. We found the rms values of 0.80, 0.76, and 0.77 mmag for ingress, flat bottom, and egress, respectively. These values are compatible with each other, so again we find no sign of transit duration variations (TDV).
Other mechanisms that generate TTVs may also be rejected. An effect induced by an exomoon is expected to produce a number of harmonic frequencies in the periodogram of the timing residuals (Kipping 2009). The interactions with a distant stellar or planetary component on a wide orbit would generate a long-period TTV through the light-travel-time effect (Montalto 2010). The amplitude of the TTV caused by the Applegate mechanism (Applegate 1992), which invokes quasi-periodic variations in the quadrupole moment of magnetically active stars, is expected to be a few seconds over the course of about ten years (Watson & Marsh 2010). The effects of transit parallax (Scharf 2007) and stellar proper motion (Rafikov 2009) are too weak to be detected for the WASP-12 system at present.
Croll et al. (2011) note that
eb is poorly constrained if ωb is
close to 90° or 270°, and this is the case for WASP-12 b. The
literature determinations of this angle range from 270° (Croll et al. 2011) to 286° (Hebb et al. 2009). Our two-planet model gives
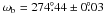 . We obtained values of
ebcosωb = 0.0035 ± 0.0002 and
ebsinωb = −0.0446 ± 0.0034, and
both of them are clearly far from zero. For the latter parameter, the consistency with the
literature determinations is between 1.1 and 1.3σ for Campo et al. (2011) and Croll et al. (2011), respectively. In the case of
ebcosωb, the values are seemingly
discrepant if they are compared to our value obtained for the initial epoch 2 454 509 BJD.
. We obtained values of
ebcosωb = 0.0035 ± 0.0002 and
ebsinωb = −0.0446 ± 0.0034, and
both of them are clearly far from zero. For the latter parameter, the consistency with the
literature determinations is between 1.1 and 1.3σ for Campo et al. (2011) and Croll et al. (2011), respectively. In the case of
ebcosωb, the values are seemingly
discrepant if they are compared to our value obtained for the initial epoch 2 454 509 BJD.
Our model neglects non-Keplerian sources of the apsidal precession including general relativistic effects, the quadrupole field caused by rotational flattening of the star and planet, and tidal potentials of the star and planet. This approach is justified because these effects are usually small, and hence generate precession rates much lower than the precession due to the second planet. However, it has been shown that the precession rate due to the tidal potential of WASP-12 b may be non-negligible (Ragozzine & Wolf 2009). In this case, the precession period is predicted to be several years or decades, depending on the response of the planetary body to a tidal potential.
WASP-12 is a quiet star with no signatures of a structured magnetic field (Fossati et al.
2010a) and a chromospheric activity index
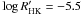 (Knutson et al. 2010; Krejčová & Budaj 2012). To estimate the expected amount of stellar RV jitter generated by
the non-uniform convection (Saar et al. 1998), we
analysed the results of Isaacson & Fischer (2010), who studied RV stability for more than 2600 main sequence and subgiant
stars with spectral types between F5 and M4. We selected a sample of 310 stars whose colour
index B − V and activity index
(Knutson et al. 2010; Krejčová & Budaj 2012). To estimate the expected amount of stellar RV jitter generated by
the non-uniform convection (Saar et al. 1998), we
analysed the results of Isaacson & Fischer (2010), who studied RV stability for more than 2600 main sequence and subgiant
stars with spectral types between F5 and M4. We selected a sample of 310 stars whose colour
index B − V and activity index
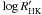 are close to
those of WASP-12. As WASP-12 has B − V = 0.6 mag, we
considered stars with 0.5 ≤ B − V ≤ 0.7 mag and with
are close to
those of WASP-12. As WASP-12 has B − V = 0.6 mag, we
considered stars with 0.5 ≤ B − V ≤ 0.7 mag and with
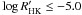 . The median jitter was found to
be 2.6 m s-1. The stellar jitter of WASP-12 is too high in a single-planet model,
being 12.5 and 6.7 m s-1 in the cases of circular and eccentric orbits for
WASP-12 b, respectively. In the two-planet model, the jitter was found to be 2.7
m s-1, which is consistent with the expected value from the Isaacson &
Fischer (2010) survey. To verify the jitter of
WASP-12, we used the Albrecht et al. (2012) RV
dataset, which contains precise measurements from a single night. In such a short time
interval of a few hours, the RV variation is generated by stellar jitter, planets, and
possible instrumental trends. The last two components can be temporarily approximated with a
single Keplerian orbit. This approach yields a jitter of 2.7 m s-1 for WASP-12,
in agreement with the expected value.
. The median jitter was found to
be 2.6 m s-1. The stellar jitter of WASP-12 is too high in a single-planet model,
being 12.5 and 6.7 m s-1 in the cases of circular and eccentric orbits for
WASP-12 b, respectively. In the two-planet model, the jitter was found to be 2.7
m s-1, which is consistent with the expected value from the Isaacson &
Fischer (2010) survey. To verify the jitter of
WASP-12, we used the Albrecht et al. (2012) RV
dataset, which contains precise measurements from a single night. In such a short time
interval of a few hours, the RV variation is generated by stellar jitter, planets, and
possible instrumental trends. The last two components can be temporarily approximated with a
single Keplerian orbit. This approach yields a jitter of 2.7 m s-1 for WASP-12,
in agreement with the expected value.
The radii of known transiting planets with masses close to 0.1 MJup range from 0.21 RJup (Kepler-22 b, Borucki et al. 2012) to 0.73 RJup (Kepler-35(AB) b, Welsh et al. 2012). If the postulated planet transits the host star, the corresponding flux drop is between 0.02% and 0.2%. If the planet is bloated to 1 RJup, the expected transit depth is 0.4%, so such a signal could be detected with a 1-m class telescope. The geometric transit probability for an eccentric orbit (Kane & von Braun 2008) of the postulated planet7 was found to be 13 ± 4%, i.e. almost three times lower than for WASP-12 b. If the system is coplanar, the additional planet could produce grazing transits.
The co-planarity of the system was found to be supported by numerical experiment in which
the mutual inclination of both planets, Δi, was varied from 0 to 30° with a
step size of 2° for Δi < 10° and 5° for
10° ≤ Δi ≤ 30°. The goodness of the fit for the two-planet model was
found to decrease with increasing Δi. Scenarios with
Δi ≤ 10° result in 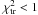 , so the
two-planet WASP-12 system is likely to be coplanar. This finding testifies in favour of
quiescent mechanisms by which planets are transported inwards with the planets’ orbital
orientation preserved (i.e. interactions between planets and protoplanetary discs). On the
other hand, the obliquity of the host star (the sky-projected angle between the stellar spin
and a planetary orbital axis) was found to be
, so the
two-planet WASP-12 system is likely to be coplanar. This finding testifies in favour of
quiescent mechanisms by which planets are transported inwards with the planets’ orbital
orientation preserved (i.e. interactions between planets and protoplanetary discs). On the
other hand, the obliquity of the host star (the sky-projected angle between the stellar spin
and a planetary orbital axis) was found to be 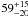 degrees (Albrecht et al. 2012). Such a high value
suggests that WASP-12 b migrated inwards by a process that changes the relative orientation
of the stellar and planetary axes (i.e. planet–planet interactions). It cannot be completely
ruled out that the axial misalignment has a primordial origin unrelated to the evolution of
the planetary system. It has been shown that an interaction between a magnetosphere of a
young magnetic star and circumstellar disc may produce a significant spin–orbit misalignment
(Lai et al. 2011).
degrees (Albrecht et al. 2012). Such a high value
suggests that WASP-12 b migrated inwards by a process that changes the relative orientation
of the stellar and planetary axes (i.e. planet–planet interactions). It cannot be completely
ruled out that the axial misalignment has a primordial origin unrelated to the evolution of
the planetary system. It has been shown that an interaction between a magnetosphere of a
young magnetic star and circumstellar disc may produce a significant spin–orbit misalignment
(Lai et al. 2011).
5. Conclusions
Transit timings of WASP-12 b and precise velocities of its host star give marginally significant support for the presence of the second planet, when both datasets are considered separately. However, a joint analysis results in a two-planet model that explains observations better than single-planet scenarios. This approach removes the degeneracy of solutions, which is typical of the TTV method. Our finding allows us to advance the hypothesis that WASP-12 b is not the only planet in the WASP-12 system and that there is an additional 0.1 MJup body on a 3.6-d period eccentric orbit. The dynamical analysis of the two-planet system shows that it is located in a relatively wide stable zone. This reinforces our hypothesis. However, we note that the putative planetary companion remains under the threshold of reliable detection. Thus, further photometric and spectroscopic follow-up observations of high precision are needed to shed new light on the architecture of the WASP-12 system.
Online material
Transit light curves observed with the ≥1.8-m telescopes.
Transit light curves observed with the <1.8-m telescopes.
It is stated that the light curve is in JDUTC (L. Hebb, priv. comm.). However, the mid-transit time derived by us and the value published in Campo et al. (2011) clearly indicate that the original light curve was converted into HJDUTC.
Acknowledgments
We are grateful to Dr. Simon Albrecht for making radial velocity data available to us at the stage of manuscript publication and to Dr. Leslie Hebb for sharing the Liverpool Telescope light curve. We thank C. Adam and N. Pawellek for trying to obtain more data. We also thank the anonymous referee for suggestions that improved the manuscript. G.M., Ł.B., G.N., and A.N. acknowledge the financial support from the Polish Ministry of Science and Higher Education through the Iuventus Plus grants IP2010 023070 and IP2011 031971. G.M. and A.N. acknowledge funding from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement number RG226604 (OPTICON). D.D. acknowledges the financial support of the projects DO 02-362, and DDVU 02/40-2010 of the Bulgarian National Science Fund. DD and VP gratefully acknowledge observing grant support from the Institute of Astronomy and NAO, Bulgarian Academy of Sciences. S.R., M.K., R.E., A.B., C.G., T.R., and T.O.B.S., together with R.N. would like to acknowledge support from the German national science foundation Deutsche Forschungsgemeinschaft (DFG) in grants NE 515/33-1, 33-2, 34-1, 32-1, 30-1, and 36-1; projects NE 515/33-1, 33-2, and 34-1 are part of the DFG Priority Programme SPP 1385 on The first 10 Myr of the Solar System. Ł.B. acknowledges travel funds from the PAN/BAN exchange and joint research project “Spectral and photometric studies of variable stars”. R.E. also thanks the Abbe-School of Photonics for support. CM thanks the DFG for support through SCHR 665/7-1. K.G. is supported by the Polish Ministry of Science and Higher Education No. N/N203/402739 and “HPC Infrastructure for Grand Challenges of Science and Engineering” (POWIEW) co-financed by the European Regional Development Fund under the Innovative Economy Operational Programme. T.C.H. gratefully acknowledges financial support from the Korea Research Council for Fundamental Science and Technology (KRCF) through the Young Research Scientist Fellowship Program. T.C.H., J.W.L., and C.U.L. acknowledge financial support from KASI grant number 2012-1-410-02. They also expresses their thanks to the BOAO/LOAO support astronomers Hyung-Il, Sang-Min, and Jae-Hyuck Youn. C.G. and M.M. acknowledge support from DFG in MU 2695/13-1. M.M.H., N.T., and R.N. would like to thank the DFG for support in the collaborative research project (Sonderforschungsbereich SFB TR 7) on gravitational wave astronomy, sub-projects C2 and B9. N.T. would like to thank the Carl-Zeiss-Foundation for a scholarship. JS acknowledges financial support from STFC in the form of an Advanced Fellowship. K.T. is financially supported by the Grants-in-Aid for the Scientific Research by the Ministry of Education, Culture, Sports, Science and Technology in Japan (No. 23540277). K.S. and Gy.M.S.z. acknowledge support through the Lendület-2009 Young Researchers’ Programme of the Hungarian Academy of Sciences, the HUMAN MB08C 81013 grant of the MAG Zrt and the Hungarian OTKA Grants K-83790 and K-104607. Gy.M.S.z. is also supported by János Bolyai Research Scholarship of the Hungarian Academy of Sciences. The contribution of M.V. was supported by the Slovak Research and Development Agency under contract No. APVV-0158-11. M.V. also thanks for the support to the project VEGA 2/0094/11. We would like to acknowledge financial support from the Thuringian government (B 515-07010) for the STK CCD camera used in this project. The data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofísica de Andalucía (IAA) under a joint agreement with the University of Copenhagen and NOTSA.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, H. J. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Arras, P., Burkart, J., Quataert, E., & Weinberg, N. N. 2012, MNRAS, 422, 1761 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Howard, A. W., Noyes, R. W., et al. 2009, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Ballard, S., Fabrycky, D., Fressin, F., et al. 2011, ApJ, 743, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Benettin, G., Galgani, L., & Strelcyn, J. 1976, Phys. Rev. A, 14, 2338 [NASA ADS] [CrossRef] [Google Scholar]
- Bergfors, C., Brandner, W., Daemgen, S., et al. 2012, MNRAS, 428, 182 [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Broeg, Ch., Fernández, M., & Neuhäuser, R. 2005, Astron. Nachr., 326, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Bryan, M. L., Alsubai, K. A., Latham, D. W., et al. 2012, ApJ, 750, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Budaj, J. 2011, AJ, 141, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Campo, Ch. J., Harrington, J., Hardy, R. A., et al. 2011, ApJ, 727, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chan, T., Ingemyr, M., Winn, J. N., et al. 2011, AJ, 141, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Cincotta, P. M., & Simó, C. 2000, A&AS, 147, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cincotta, P. M., Giordano, C. M., & Simó, C. 2003, Physica D Nonlinear Phenomena, 182, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowan, N. B., Machalek, P., Croll, B., et al. 2012, ApJ, 747, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Lafreniere, D., Albert, L., et al. 2011, AJ, 141, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Hansen, B. M. S., & Barman, T. 2012, ApJ, 746, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Eastman, J., Gaudi, B. S., & Agol, E. 2013, PASP, 125, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Etzel, P. B. 1981, in Photometric and Spectroscopic Binary Systems (Dordrecht: Kluwert), eds. E. B. Carling, & Z. Kopal, NATO ASI Ser. C., 69, 111 [Google Scholar]
- Everett, M. E., & Howell, S. B. 2001, PASP, 113, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Bagnulo, S., Elmasli, C. A., et al. 2010a, ApJ, 720, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, L., Haswell, C. A., Froning, C. S., et al. 2010b, ApJ, 714, 222 [Google Scholar]
- Fulton, B. J., Shporer, A., Winn, J. N., et al. 2011, AJ, 142, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Gazak, J. Z., Johnson, J. A., Tonry, J., et al. 2012, Adv. Astron., 697, 967 [Google Scholar]
- Goździewski, K., Bois, E., Maciejewski, A. J., & Kiseleva-Eggleton, L. 2001, A&A, 378, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
- Husnoo, N., Pont, F., Hebrard, G., et al. 2011, MNRAS, 413, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Howard, A. W., Bakos, G. Á., Hartman, J., et al. 2012, ApJ, 749, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyer, S., Rojo, P., & López-Morales, M. 2012, ApJ, 748, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Burrows, A., & Spiegel, D. S. 2010, ApJ, 713, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Joshi, Y. C., Pollacco, D., Collier Cameron, A., et al. 2009, MNRAS, 392, 1532 [NASA ADS] [CrossRef] [Google Scholar]
- Kane, S. R., & von Braun, K. 2008, ApJ, 689, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Krejčová, T., & Budaj, J. 2012, A&A, 540, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knutson, H. A., Howard, A. W., & Isaacson, H. 2010, ApJ, 720, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Helling, Ch., & van den Heuvel, E. P. J. 2010, ApJ, 721, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Lai, D., Foucart, F., & Lin, D. N. C. 2011, MNRAS, 412, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Latham, D. W., Rowe, J. F., Quinn, S. N., et al. 2011, ApJ, 732, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L., Miller, N., Lin, D. N. C., & Fortney, J. J. 2010, Nature, 463, 1054 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Llama, J., Wood, K., Jardine, M., et al. 2011, MNRAS, 416, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., Coughlin, J. L., Sing, D. K., et al. 2010, ApJ, 716, 36 [Google Scholar]
- Maciejewski, G., Errmann, R., Raetz, St., et al. 2011, A&A, 528, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancini, L., Southworth, J., Ciceri, S., et al. 2013, A&A, 551, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mardling, R. A., & Lin, D. N. C. 2002, ApJ, 573, 829 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1924, ApJ, 60, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., & Malhotra, R. 2004, Icarus, 168, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Migaszewski, C., & Goździewski, K. 2009, MNRAS, 392, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., Fortney, J. J., & Jackson, B. 2009, ApJ, 702, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda–Escudé, J. 2002, ApJ, 564, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Moehler, S., Freudling, W., Møller, P., et al. 2010, PASP, 122, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M. 2010, A&A, 521, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mugrauer, M., & Berthold, T. 2010, Astron. Nachr., 331, 449 [Google Scholar]
- Nascimbeni, V., Piotto, G., Bedin, L. R., et al. 2011, A&A, 532, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neuhäuser, R., Errmann, R., Berndt, A., et al. 2011, Astron. Nachr., 332, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Niedzielski, A., Maciejewski, G., & Czart, K. 2003, Acta Astron., 53, 281 [NASA ADS] [Google Scholar]
- Pál, A., Sárneczky, K., Szabó, Gy. M., et al. 2011, MNRAS, 413, 43 [Google Scholar]
- Popper, D. M., & Etzel, P. B. 1981, AJ, 86, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2009, ApJ, 700, 965 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ragozzine, D., & Wolf, A. S. 2009, ApJ, 698, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Rossiter, R. A. 1924, ApJ, 60, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., Butler, R. P., & Marcy, G. W. 1998, ApJ, 498, 153 [Google Scholar]
- Sada, P. V., Deming, D., Jennings, D. E., et al. 2012, PASP, 124, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Sagar, R., Kumar, B., Omar, A., & Joshi, Y. C. 2012, in Recent Advances in Star Formation, eds. A. Subramaniam, & S. Anathpindika, ASI Conf. Ser., 4, 113 [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Scharf, C. A. 2007, ApJ, 661, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, J. 2004, in Second Eddington Workshop: Stellar Structure and Habitable Planet Finding, eds. F. Favata, S. Aigrain, & A. Wilson, ESA SP, 538, 407 [Google Scholar]
- Słonina, M., Goździewski, K., & Migaszewski, C. 2012, in Proceedings of the workshop Orbital Couples: Pas de Deux in the Solar System and the Milky Way, eds. F. Arenou, & D. Hestroffer, 125 [Google Scholar]
- Southworth, J. 2012, MNRAS, 426, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004a, MNRAS, 349, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004b, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Hinse, T. C., Jørgensen, U. G., et al. 2009, MNRAS, 396, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Mancini, L., Calchi Novati, S., et al. 2010, MNRAS, 408, 1680 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Bruni, I., Mancini, L., & Gregorio, J. 2012a, MNRAS, 420, 2580 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Mancini, L., Maxted, P. F. L., et al. 2012b, MNRAS, 422, 3099 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Gaudi, B. S., Ford, E. B., Agol, E., & Holman, M. J. 2007, Exoplanet Task Force, submitted [arXiv:0704.0632] [Google Scholar]
- Szabó, Gy. M., Kiss, L. L., Benkő, J. M, et al. 2010, A&A, 523, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szabó, R., Szabó, Gy. M., & Dálya, G. 2012, A&A, submitted [arXiv:1207.7229v2] [Google Scholar]
- Vidotto, A. A., Jardine, M., & Helling, Ch. 2010, ApJ, 722, 168 [Google Scholar]
- Vidotto, A. A., Jardine, M., & Helling, Ch. 2011, MNRAS, 414, 1573 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, C. A., & Marsh, T. R. 2010, MNRAS, 405, 2037 [NASA ADS] [Google Scholar]
- Welsh, W. F., Orosz, J. A., Carter, J. A., et al. 2012, Nature, 481, 475 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Observatories and instruments (with abbreviations identifying datasets) taking part in the campaign.
Parameters of the WASP-12 system from the joint analysis of 19 sub-millimagnitude-precision light curves and the refined linear ephemeris.
Parameters of the two-planet WASP-12 system from the joint analysis of RVs and transit timing.
All Figures
 |
Fig. 1 Light curves for transits of WASP-12 b observed with 2-m class telescopes. The residuals are shown in the bottom plots. |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but for 1.5-m and smaller telescopes. |
| In the text | |
 |
Fig. 3 Additional amateur light curves obtained with 20-cm reflecting telescopes. The mid-transit times were found to be BJDTDB 2 455 865.6130 ± 0.0012 (2011 Oct. 30), 2 455 923.4609 ± 0.0026 (2011 Dec. 27), and 2 455 934.3725 ± 0.0009 (2012 Jan. 07). |
| In the text | |
 |
Fig. 4 Best-fitting model of WASP-12 b’s transit (red line) laid over the 19 best-quality, phase-folded light curves. |
| In the text | |
 |
Fig. 5 O–C diagram for WASP-12 b’s transit timing. The filled circles denote our observations and squares the literature ones with errors smaller than 40 s. The open symbols – circles and squares for our and literature data, respectively – mark points with timing errors greater than 40 s. The open triangles denote the amateur times included in this work. The postulated sinusoidal variation is sketched with a red line. Individual observing seasons, covered by our high-precision observations, are zoomed-in at the bottom. The literature data are taken from Hebb et al. (2009), Chan et al. (2011), Maciejewski et al. (2011), Sada et al. (2012), and Cowan et al. (2012). |
| In the text | |
 |
Fig. 6 Periodogram of the O–C residuals (continuous black line) and spectral window (dashed red line, multiplied by 10 for clarity). The dashed vertical line shows the empirical FAP level of 1%. The arrow marks the most significant peak, which as can be clearly seen, is not caused by the structure of gaps in the time domain. The shortest period investigated is given by the Nyquist frequency. |
| In the text | |
 |
Fig. 7 Periodogram of RV residuals for WASP-12 b on a Keplerian orbit (continuous black line) and the spectral window (dashed red line, multiplied by 10 for clarity). The arrow indicates the strongest peak at 3.58 d that is not associated with significant power in the spectral window. The shortest period is set by the radius of the star. The dashed and dotted horizontal lines show empirical FAP levels of 1% and 0.1%, respectively. |
| In the text | |
 |
Fig. 8 Joint RV and transit timing model for the WASP-12 system including two planets. Upper: the RV variation produced by WASP-12 b. Middle: the RV signal generated by the postulated planet WASP-12 c. Bottom: the O–C diagram for the transit timing of WASP-12 b with a modelled TTV signal and the residuals shifted by −0.0026 d for clarity. |
| In the text | |
 |
Fig. 9 Dynamical map of the WASP-12 system in the (ac,ec)–plane, computed in terms of the MEGNO fast indicator. These two orbital parameters are varied across the map, while other orbital elements and masses are kept at their nominal values from Table 5. The star symbol, located at ac = 0.050681 AU, indicates the nominal system. Colours encode the dynamical stability of the system: yellow is for strongly unstable configurations, and blue is for stable, quasi-periodic systems. A few relevant MMRs are labelled. The raw resolution of this map is 1440 × 900 datapoints. Each initial condition at the map has been integrated for 105 outer orbits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


