| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220679 | |
| Published online | 06 March 2013 | |
GRB 110709B in the induced gravitational collapse paradigm
1 Dip. di Fisica, Sapienza Università di Roma and ICRA, Piazzale Aldo Moro 5, 00185 Roma, Italy
e-mail: ruffini@icra.it; luca.izzo@icra.it; marco.muccino@icra.it; bianco@icra.it; jorge.rueda@icra.it;
2 ICRANet, Piazzale della Repubblica 10, 65122 Pescara, Italy
3 Université de Nice Sophia Antipolis, Nice Cedex 2, Grand Chateau Parc Valrose, France
e-mail: ana.penacchioni@icra.it
Received: 31 October 2012
Accepted: 20 January 2013
Context. Gamma-ray burst (GRB) 110709B is the first source for which Swift-BAT was triggered twice, with a time separation of ~10 min. The first emission (called here episode 1) lasted from 40 s before the first trigger time until 60 s after it. The second emission (hereafter episode 2) lasted from 35 s before the second trigger time until 100 s after it. These features reproduce those of GRB 090618, which has recently been interpreted within the induced gravitational collapse (IGC) paradigm. In line with this paradigm, we assume the progenitor to be a close binary system composed of the core of an evolved star and a neutron star (NS). The evolved star explodes as a supernova (SN) and ejects material that is partially accreted by the NS. We identify this process with episode 1. The accretion process accumulates more than the critical mass of the NS, which gravitationally collapses into a black hole (BH). This process leads to the GRB emission, episode 2. The two trigger episodes have for the first time provided the possibility to cover the X-ray emission observed by XRT both prior to and during the prompt phase of GRB 110709B.
Aims. We analyze the spectra and time variability of episodes 1 and 2 and compute the relevant parameters of the binary progenitor, as well as the astrophysical parameters both in the SN and the GRB phase in the IGC paradigm.
Methods. We performed a time-resolved spectral analysis of episode 1 by fitting the spectrum with a blackbody (BB) plus a power-law (PL) spectral model. From the BB fluxes and temperatures of episode 1 and the luminosity distance dL, we evaluated the evolution with time of the radius of the BB emitter, associated here to the evolution of the SN ejecta. We analyzed episode 2 within the fireshell model, identifying the proper GRB (P-GRB) and simulating the light curve and spectrum. We established the redshift to be z = 0.75, following the phenomenological methods described in the literature, and our analysis of the late X-ray afterglow. It is most remarkable that the determination of the cosmological redshift on the basis of scaling the late X-ray afterglow, which was already verified in GRB 090618 and GRB 101023, is again verified by this analysis.
Results. We find for episode 1 a temperature of the BB component that evolves with time following a broken PL, with the slope of the PL at early times α = 0 (constant function) and the slope of the PL at late times β = −4 ± 2. The break occurs at t = 41.21 s. The total energy of episode 1 is E1iso = 1.42 × 1053 erg. The total energy of episode 2 is E2iso = 2.43 × 1052 erg. We find at transparency a Lorentz factor Γ ~ 1.73 × 102, laboratory radius of 6.04 × 1013 cm, P-GRB observed temperature kTP − GRB = 12.36 keV, baryon load B = 5.7 × 10-3 and P-GRB energy of EP − GRB = 3.44 × 1050 erg. We find a remarkable coincidence of the cosmological redshift by scaling the XRT data and with three other phenomenological methods.
Conclusions. We interpret GRB 110709B as a member of the IGC sources, together with GRB 970828, GRB 090618, and GRB 101023. The existence of the XRT data during the prompt phase of the emission of GRB 110709B (episode 2) offers an unprecedented tool for improving the diagnostic of GRBs emission.
Key words: Gamma-ray burst: individual: GRB 110709B / black hole physics
© ESO, 2013
1. Introduction
Of all the astrophysical processes that are currently being analyzed, few are more fundamental than the one presenting the coincidence of some gamma-ray bursts (GRBs) with the explosion of a supernova (SN). For this, the induced gravitational collapse (IGC) paradigm was first introduced by Ruffini et al. (2001b) and was subsequently analyzed in Ruffini et al. (2007, 2008); Rueda & Ruffini (2012), and Izzo et al. (2012b). Recently, it has been shown that this process can indeed explain the coincidence between the SN and GRB emission, both from an observational and a theoretical point of view (Izzo et al. 2012a; Penacchioni et al. 2012).
In the IGC paradigm (Ruffini et al. 2001b, 2007), a binary system formed by an evolved star and a neutron star (NS) companion is considered as the progenitor.
The IGC paradigm implies a well-determined time sequence. In a close binary system of a massive star in the latest phases of its thermonuclear evolution and an NS companion, the massive star undergoes an SN explosion. The accretion of the early SN material onto the NS companion leads the NS to its critical mass and consequently to its gravitational collapse to form a black hole (BH). The emission of a canonical GRB in the collapse to the BH takes place. A young NS is born out of the SN explosion. Finally, an SN emission is either observed or expected in association with the GRB, ~10 days after the burst in the rest frame. We aim to find sources in which the data are of a sufficiently good quality to allow us to see this complete sequence.
The prototype for the IGC paradigm has recently been given in the analysis of GRB 090618 (Izzo et al. 2012a), following the works of Rueda & Ruffini (2012) and Izzo et al. (2012b). In this work we follow the same line and identify four different episodes in GRB 110709B. Episode 1 starts 40 s before the first trigger time and lasts up to 60 s after it. It is well-fit by a blackbody (BB) plus power-law (PL) spectral model. It corresponds to the trigger of the SN explosion of the compact core and its accretion onto the NS companion. The BB temperature decays with time following a broken PL (Ryde 2004). Episode 2 starts 35 s before the second trigger time and lasts up to 100 s after it. It corresponds to the emission of the canonical GRB emitted in the formation of a BH. Episode 3 starts at 800 s all the way to 106 s. It consists of a standard X-ray emission identified in all systems following the IGC paradigm (Pisani et al., in prep.). Episode 4 corresponds to the observation of the optical SN emission, observable after Tobs = (1 + z)TSN. In the present case, there is no evidence of an associated SN in the optical band. An explanation for this is given by Zauderer et al. (2012), who classified GRB 110709B as dark and stated that its optical emission may have been absorbed by the host galaxy and/or the interstellar medium (ISM). The ensemble of these four episodes characterize the IGC scenario.
As an outcome, at the endpoint of the IGC scenario, a binary system represented by an NS (formed by the SN explosion) and a BH (formed after the GRB explosion) should be expected.
As in the case of GRB 101023, we do not know the cosmological redshift of GRB 110709B due to the lack of optical data. Therefore, we infer it from phenomenological methods: 1) the Amati relation (Amati 2006), 2) the Yonetoku relation (Yonetoku 2004, 2010), 3) the work of Grupe et al. (2007), and 4) the work by Penacchioni et al. (2012), Ruffini (2012), and Pisani et al. (in prep.), which describe a scaling of the late X-ray emission of GRB 090618. In the case of GRB 111228, which we are currently analyzing, we find a striking coincidence between the values of the cosmological redshift determined by these methods for GRB 110709B.
In Sect. 2 we report the observations of the two components of GRB 110709B by the different instruments, in space and on the ground. In Sect. 3 we reduce the Swift data and perform a detailed spectral analysis of both episodes 1 and 2. In Sect. 4 we infer the redshift of the source using the four phenomenological methods mentioned above. In Sect. 5 we determine the radius of the emitting region from the knowledge of the redshift and the BB flux of the first episode. In Sect. 6 we give a brief description of the fireshell model and perform a deeper analysis of episode 2 within this model, reproducing the light curve and the spectrum by a numerical simulation. In Sect. 7 we calculate the parameters of the binary progenitor leading to the IGC of the NS to a BH by the SN explosion. Details on the accretion rate onto the NS, total accreted mass, SN ejecta density, NS mass, and binary orbital period are obtained for selected values of the SN progenitor mass. In Sect. 8 we comment on the radio emission detected by EVLA (Zauderer & Berger 2012). In Sect. 9 we present the conclusions.
2. Observations of GRB 110709B
GRB 110709B has been detected by the Suzaku (Ohmori et al. 2011) and Swift (Cummings et al. 2011) satellites and by the ground-based telescopes GROND (Updike et al. 2011) and Gemini (Berger 2011).
The Burst Alert Telescope (BAT) onboard Swift was triggered a first time at 21:32:39 UT (trigger N° = 456 967). The location of this event is RA = 164.6552, Dec = –23.4550. The light curve is composed of multiple peaks, with the whole emission extending up to 60 s after the trigger (see Fig. 1). What is most interesting is that there was another trigger point at 21:43:25 UT (trigger N° = 456 969), ~11 min after the first trigger time. The onboard calculated location is RA = 164.647, Dec = –23.464. This time Swift did not need to slew, because it was already pointing to that position. This second emission shows a bump that begins 100 s before the second trigger time and lasts around 50 s, followed by several overlapping peaks with a total duration of about 40 s, and another isolated peak of 10 s of duration, 200 s after the second trigger time. Figure 1 shows the complete BAT light curve and Fig. 2 shows the light curve taken by the X-Ray Telescope (XRT) in the 0.3–10 keV band.
There have been no detections in the optical band by Swift-UVOT, which started to observe 70 s after the first BAT trigger time (Holland 2011). The observations with GROND at the La Silla Observatory (Updike et al. 2011) simultaneously in the g′r′i′z′ JHK, reveal two point sources within the 5”.3 XRT error circle reported by Cummings et al. (2011). They suggest that one of them could be an afterglow candidate for GRB 110709B, although it is very faint.
It has been suggested by Zauderer et al. (2012) that this source is an “optically dark” GRB. The possible reasons for this are 1) dust obscuration; 2) an intrinsically dim event; and/or 3) high redshift (optical emission suppressed by Lyα absorption at λobs ≤ 1216 Å (1 + z)). However, they rule out the possibility of a high-redshift event due to the association with an optically detected host galaxy. Furthermore, they have inferred the optical brightness of the afterglow according to the standard afterglow synchrotron model (Granot & Sari 2002; Sari et al. 1999), and from the non-detection in the optical-near-infrared (NIR) wavelengths they find a very high rest-frame extinction for GRB 110709B. This can explain the lack of detections in the optical band.
Fit results of episode 1 with five spectral models: BB, Band, BB+PL, PL and cutoffPL.
There have been detections in the radio band on several occasions by EVLA (Zauderer & Berger 2012), revealing a single unresolved radio source within the XRT error circle, which rebrightened by a factor of 1.6 between 2.1 and 7 days after the burst. The location of the source is RA = 10:58:37.114, Dec = –23:27:16.760.
 |
Fig. 1 BAT light curve of GRB 110709B, including the two trigger times. Here we can appreciate the time separation (about 10 min) between the first and the second trigger. The light curve is in the (15–150 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). The second trigger time was at 331 940 612 s in MET seconds. |
 |
Fig. 2 Count light curve of GRB 110709B obtained from the Swift-XRT detector in the (0.3–10 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). Picture taken from http://www.swift.ac.uk/xrt_curves/00456967/ |
3. Data analysis
In the following we refer to the emission that lasted from 40 s before the first BAT trigger time to 60 s after it as episode 1 (see Fig. 3). We call the emission lasting from 35 s before the second BAT trigger time to 100 s after it as episode 2. We used Swift-BAT data to perform the spectral analysis with XSPEC.
 |
Fig. 3 Count light curve of episode 1 of GRB 110709B obtained from the Swift-BAT detector in the (15–150 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). |
3.1. Episode 1
We performed a time-integrated analysis of the whole episode 1 using five different spectral models, BB, Band (Band et al. 1993), BB+PL, PL, and cutoffPL. The results of the fits are shown in Table 1 and in Fig. 4. The Band function is not well constrained, therefore we excluded it from the following analysis. A statistical test shows that the best models are BB+PL (χ2 = 56.65) and cutoffPL (χ2 = 54.45). Since the difference in the χ2 between these two models is 2.2, the two models are statistically equivalent, therefore we distinguished between these two models based on the physical grounds expected from the IGC scenario. In this scenario, we expect a thermal emission from the expansion of the outer layers of the compact-core SN progenitor. Accordingly, we chose the BB+PL model. We obtain a BB temperature kT = (22 ± 5) keV, a PL index γ = 1.4 ± 0.1 and a χ2 = 56.65 (54 D.O.F.). The flux of the BB component is ~ 12% of the total flux. The total energy of episode 1 is 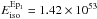 erg. The results of the fit are shown in Table 1. Then we performed a time-resolved spectral analysis with a binning of 5 s fitting the same model and found that the temperature of the BB component follows a broken power-law, as mentioned in Ryde (2004), from 5 s before the trigger time to 55 s after it (see Fig. 5). The broken PL is indeed a constant function plus a simple power-law function. This is the same behavior as observed in the previously analyzed GRB 090618 (Izzo et al. 2012a) and GRB 101023 (Penacchioni et al. 2012). However, the temperatures for this GRB are lower. Nevertheless, the simultaneous presence of a BB and PL component is necessary to obtain an acceptable fit of the data (see Fig. 4).
erg. The results of the fit are shown in Table 1. Then we performed a time-resolved spectral analysis with a binning of 5 s fitting the same model and found that the temperature of the BB component follows a broken power-law, as mentioned in Ryde (2004), from 5 s before the trigger time to 55 s after it (see Fig. 5). The broken PL is indeed a constant function plus a simple power-law function. This is the same behavior as observed in the previously analyzed GRB 090618 (Izzo et al. 2012a) and GRB 101023 (Penacchioni et al. 2012). However, the temperatures for this GRB are lower. Nevertheless, the simultaneous presence of a BB and PL component is necessary to obtain an acceptable fit of the data (see Fig. 4).
 |
Fig. 4 Fit of episode 1 with a BB+PL model. The parameters of the fit are kT = (22 ± 5) keV, BB Amp = 0.2 ± 0.1, γ = 1.4 ± 0.1, PL Amp = 2.2 ± 0.8, Red-χ2 = 1.049 (54 D.O.F.). |
 |
Fig. 5 Evolution of the kT component of the BB+PL model during episode 1. The first data point corresponds to 5 s before the first BAT trigger time. The vertical line corresponds to the trigger time. The time is given in the observer frame. The temperature evolves in time following a broken power-law fit. There is a break at t = 41.21 s. The indices of the PL are α = 0 (consistent with a constant function) and β = −4 ± 2. The presence of the BB, although weaker than in previous cases, is essential to obtain an acceptable fit. |
 |
Fig. 6 Fit of episode 2 with a cutoffPL model. The photon index is γ = 1.0 ± 0.1, the normalization constant is 0.5 ± 0.1, the cutoff energy is E0 = 132 ± 31 and the reduced chi squared of the fit is Red-χ2 = 0.77 (55 D.O.F.). |
Spectral fit of the whole episode 2 with different models: BB, PL, BB+PL, cutoffPL, and Band.
3.2. Episode 2
We also performed a time-integrated spectral analysis of episode 2, whose light curve is shown in Fig. 7. This episode starts 35 s before the second trigger time and last 135 s, until 100 s after the second trigger time. We tried to fit the spectrum with the following spectral models: BB, PL, BB+PL, cutoffPL and Band (see Table 2). We could easily discard the BB and Band models because in one case the Red χ2 is too high and in the other case there is an unconstrained parameter. Because the PL and the BB+PL are nested models, we performed a statistical test to see which one is the best. We obtained a probability Prob = 0.001 that the simpler model is better, therefore the BB+PL dominates over the PL. Then we compared the BB+PL and the cutoffPL models. Because they are not nested, we could not apply the same test. Therefore we chose the model that gives the lowest χ2. We concluded that the model that best fits episode 2 is the cutoffPL model.
It is clear from the analogies with GRB 090618 and GRB 101023 that episode 2 has all the characteristics of a canonical GRB. A difference between GRB 110790B and the already analyzed ones is that the separation between episodes 1 and 2, ~10 min, is much bigger than previously, ~50 s. This remarkable time separation between the two episodes is an additional new fact to propose a different astrophysical origin of these two components.
We now turn to the crucial analysis of the cosmological redshift determination of episode 2.
 |
Fig. 7 Count light curve of episode 2 of GRB 110709B obtained from the Swift-BAT detector in the (15–150 keV) energy band. The time is given with respect to the second trigger time, of 331 940 612 s (in MET seconds). |
4. Cosmological redshift determination
We used four phenomenological methods to constrain the redshift of the source, based on different relations that are detailed below.
4.1. NH column density
We first tried to derive an upper limit for z following the work of Grupe et al. (2007). These authors considered a relation between the absorption column density in excess of the galactic column density, given by ΔNH = NH,fit − NH,gal and the redshift z, through the equation ![\begin{equation} \label{formulaGrupe} \log \,(1+z) < 1.3-0.5[ \log \,(1+\Delta N_{\rm H})]. \end{equation}](/articles/aa/full_html/2013/03/aa20679-12/aa20679-12-eq96.png) (1)We calculated NH,gal from the radio map of the galaxy in the Lab Survey website1 by entering the coordinates of the GRB (RA = 164.64, Dec = –23.46). We obtained NH,gal = 10.5 × 1020 cm-2.
(1)We calculated NH,gal from the radio map of the galaxy in the Lab Survey website1 by entering the coordinates of the GRB (RA = 164.64, Dec = –23.46). We obtained NH,gal = 10.5 × 1020 cm-2.
To obtain the value of NH,fit we took the XRT data from 2000 s to 106 s after the first BAT trigger time and fitted the model phabs*po using the program XSPEC. The XRT data were reduced by the xrtpipeline software, version 0.10.4, which is part of the HEASOFT package, version 6.12. We used the standard response matrix swxpc0to12s6 20010101v013.rmf for the PC mode data. The model phabs represents the photoelectric absorption
20010101v013.rmf for the PC mode data. The model phabs represents the photoelectric absorption 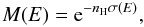 (2)where nH is the equivalent hydrogen column density (in units of 1022 cm-2) and σ(E) is the photoelectric cross section, not including Thompson scattering. We obtained a value of NH,fit = 71.76 × 1020 cm-2. Using these values in (1) we obtained an upper limit for the redshift of z < 1.35.
(2)where nH is the equivalent hydrogen column density (in units of 1022 cm-2) and σ(E) is the photoelectric cross section, not including Thompson scattering. We obtained a value of NH,fit = 71.76 × 1020 cm-2. Using these values in (1) we obtained an upper limit for the redshift of z < 1.35.
4.2. Amati relation
We also tried to determine the redshift of episode 2 through the Amati relation (Amati 2006), which relates the isotropic energy Eiso of the GRB to the peak energy in the rest frame Ep,i of the νFν spectrum (Amati et al. 2009). The analytical expression of Eiso is 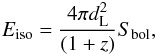 (3)where
(3)where 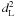 is the luminosity distance, z is the redshift, and Sbol is the bolometric fluence, related to the observed fluence in a given detection band (Emin, Emax) by
is the luminosity distance, z is the redshift, and Sbol is the bolometric fluence, related to the observed fluence in a given detection band (Emin, Emax) by 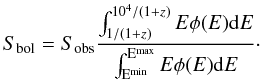 (4)Here, φ is the spectral model considered for the spectral data fit; in this case a Band model (Band et al. 1993), composed of two smoothly connected power-laws. Ep,i is related to the peak energy Ep in the observer frame by
(4)Here, φ is the spectral model considered for the spectral data fit; in this case a Band model (Band et al. 1993), composed of two smoothly connected power-laws. Ep,i is related to the peak energy Ep in the observer frame by 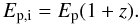 (5)The peak energy is the energy at the peak of the νFν spectrum. It can be written as
(5)The peak energy is the energy at the peak of the νFν spectrum. It can be written as 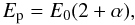 where E0 is the energy at which the two power-laws intersect and α is the slope of the low-energy power-law, according to the Band model.
where E0 is the energy at which the two power-laws intersect and α is the slope of the low-energy power-law, according to the Band model.
We calculated the luminosity distance dL as given by the standard cosmological model 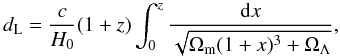 (6)where the Hubble constant is H0 = 70 km s-1 Mpc-1, Ωm = 0.27, ΩΛ = 0.73 and c is the speed of light.
(6)where the Hubble constant is H0 = 70 km s-1 Mpc-1, Ωm = 0.27, ΩΛ = 0.73 and c is the speed of light.
Following the same procedure as described in Penacchioni et al. (2012), we calculated Eiso and Ep,i for different values of z, from 0.1 to 3, at steps of 0.1. Figure 8 shows that the relation is satisfied for values of z > 0.4. This puts a lower limit to the estimation of the redshift.
 |
Fig. 8 Amati relation (solid line) with its 1 − σ uncertainties (doted lines) and peak energy Ep.i vs. Eiso for GRB 110709B, for different values of the redshift, from 0.1 to 3, at steps of 0.1. We can see that the data match the theoretical function within 1 − σ for z > 0.4. |
4.3. Yonetoku relation
We finally obtained a range of possible redshifts by using the Yonetoku relation (Yonetoku 2004). This relation, also known as the Ep–luminosity relation (Ep − L), connects the observed isotropic luminosity L in units of 1052 erg s-1 with the peak energy Ep(1 + z) in the rest frame of the GRB. It is valid for values of Ep between 50 and 2000 keV, and a luminosity range of 1050 − 1054 erg s-1.
The best-fit function for the Ep − L relation is ![\begin{equation} \frac{L}{10^{52}\ \rm{erg\, s}^{-1}}=(2.34^{+2.29}_{-1.76}) \times 10^{-5} \left[\frac{E_{\rm p}(1+z)}{1~ \rm{keV}}\right]^{2.0 \pm 0.2}\cdot \end{equation}](/articles/aa/full_html/2013/03/aa20679-12/aa20679-12-eq137.png) (7)The peak luminosity and the peak energy are calculated by integrating within a 1 s interval around the most intense peak of the light curve, because this is a better distance indicator than the burst average luminosity. However, we took a 10 s interval around the most intense peak to better constrain the value of the parameters (i.e., to increase the number of photons in the spectrum and obtain an error that is smaller than the value of the parameters). The peak luminosity in the rest frame (with the proper K-correction) can be calculated as
(7)The peak luminosity and the peak energy are calculated by integrating within a 1 s interval around the most intense peak of the light curve, because this is a better distance indicator than the burst average luminosity. However, we took a 10 s interval around the most intense peak to better constrain the value of the parameters (i.e., to increase the number of photons in the spectrum and obtain an error that is smaller than the value of the parameters). The peak luminosity in the rest frame (with the proper K-correction) can be calculated as 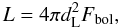 (8)where
(8)where 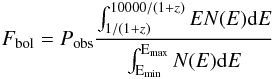 (9)is the energy flux and Pobs is the photon flux.
(9)is the energy flux and Pobs is the photon flux.
Figure 9 shows the Yonetoku relation (solid line) with its uncertainties (dotted lines), and the values of L and Ep,i for each value of z, from 0.1 to 3, at steps of 0.1. We see that the Yonetoku relation is satisfied within 1σ for values of the redshift >0.7, consistent with the results obtained with the Amati relation.
In conclusion, if we put together the three methods, we have a range of possible redshifts of 0.7 < z < 1.35.
 |
Fig. 9 Yonetoku relation (solid line) with its 1 − σ uncertainties (doted lines) and peak luminosity vs. Ep.i for GRB 110709B, for different values of the redshift, from 0.1 to 3, at steps of 0.1. We can see that the data matches the theoretical function within 1 − σ for z > 0.6. |
4.4. Estimate of the redshift using the X-ray afterglow
We previously presented (Penacchioni et al. 2012) a method for estimating the redshift of GRB 101023 by comparing its X-ray light curve to that of GRB 090618, of known redshift (z = 0.54). Here we rescale the X-ray light curve of GRB 090618 as if it were seen at different redshifts and plot it together with GRB 110709B light curve, looking for the values of z for which these light curves overlap at late times. We find a remarkable consistency between this method and the phenomenological methods mentioned above.
To compare the two emissions from the GRBs in a common rest frame, we applied the following operations only to GRB 090618:
-
1)
determination of the starting timeTstart of the late decay emission,
-
2)
spectral analysis of this emission with an absorbed power-law model,
-
3)
extrapolation of this spectral model in a common cosmological rest-frame energy range and, consequently, rescaling of the GRB 090618 light curve for the different energy ranges,
-
4)
cosmological correction for the arrival time by taking into account the different scaling due to cosmological redshift, and
-
5)
correction of the observed flux by changing the redshift of GRB 090618.
A detailed description of the method will be given in a forthcoming publication (Pisani et al., in prep.).
 |
Fig. 10 Plot of GRB 090618 seen as if it were at different redshifts: 0.2 (blue), 0.4 (green), 0.7 (gray), 1.0 (orange), and 2.0 (purple). The red light curve corresponds to GRB 110709B. We can see that it lies between the green and the orange light curves, indicating that the redshift must be between 0.4 and 1.0. |
 |
Fig. 11 GRB 090618 light curve (blue) as if it were seen at z = 0.75 together with the GRB 110709B light curve (red). There is an excellent superposition in the late decay assuming a temporal shift of GRB 090618 of T ∗ = 800 s to the right to align the steep decays of the light curves. |
In this way we directly compared the two light curves for different redshifts of GRB 090618. Figure 10 shows the GRB 090618 light curve seen as if the source were located at different redshifts: 0.2 (blue), 0.4 (green), 0.7 (gray), 1.0 (orange) and 2.0 (purple). The red light curve corresponds to GRB 110709B. We can see that it lies between the green and the orange curves. A more accurate scaling of the late X-ray afterglow suggests a redshift of z = 0.75 for this source.
Figure 11 shows the superposition of the GRB 110709B and GRB 090618 light curves in the observer frame, as if they were located at a redshift z = 0.75.
There is a second aspect, however, which is due to the peculiarity of the turn-on T0 of the XRT detector. At the time BAT was triggered for the second time, XRT was already pointing at the source and was able to detect the emission at very early times, making this GRB probably the first for which XRT has the earliest detection up to date. We shifted the GRB 110709B light curve to align the early steep decays (originating in the prompt in our interpretation). This was done by adding a time T∗ = + 800 s to the GRB 090618 light curve. The superposition is very good. In this way we also aligned the early decays. This factor is arbitrary, but we needed to include it because the GRB 110709B XRT light curve presents many spikes at the beginning, which according to our interpretation correspond not to the steep decay of the X-ray light curve, but to the prompt emission.
For GRB 110709B, because XRT was already active and collecting data at the time of the second BAT trigger time, we were able to follow the behavior of the whole GRB emission of episode 2. This is a key point of our understanding of GRB 110709B, since only in very few cases XRT had a response during the early emission.
In the big flare at ~1000 s after the first BAT trigger time we notice a strong correlation between the emission in X-rays and in γ-rays. We identify this emission as the prompt emission of episode 2. After this prompt phase the traditional plateau phase is observed. After the plateau phase, there is the late decay phase in the X-ray light curve, following a power-law behavior that was also observed in other sources (i.e., GRB 101023, GRB 090618, and GRB 111228). We studied this decay in the IGC paradigm, and considered the possibility that it might be produced by the early emission of the newly born NS. It is interesting to notice that in GRB 110709B the typical flare in X-rays just preceding the plateau phase and following the prompt emission is not observed. This X-ray emission usually occurs without any associated γ-ray emission, since the data are usually below the BAT threshold. In the present case, it is conceivable that the flaring indeed occurred during some of the gaps of ~4000 s in which there are no data due to Earth occultation.
We can then distinguish two types of flares in the X-ray light curve. The first type occurs at early times, previous to the steep decay, and belongs to the prompt emission. These flares can be seen in X-rays only when XRT starts its detection at early enough times, e.g., when the satellite was already pointing at a region near the burst position and did not need much time to slew. The light curve in X-rays generally follows the trend of the light curve in γ-rays. The second type of flares occurs at later times, just preceding the plateau phase. These flares are seen only in X-rays since their photon flux is much lower than the BAT threshold. In the ICG paradigm, we interpret these flares as possible indicators of the breakout of the SN.
We are currently analyzing more sources in the catalog by Margutti et al. (2013) to look for these three very distinct phases, i.e., the flares in the prompt emission, the flares in the afterglow, and the late decay after the plateau, each of which has a different physical origin within the IGC paradigm.
5. Episode 1: radius of the emitting region
Knowing the redshift and parameters of the fit with a BB + PL model, we computed the isotropic energy of the whole episode 1, 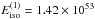 erg.
erg.
With the energy flux of the BB component φBB as a function of time from the time-resolved spectral analysis and the luminosity distance dL, we can compute the value of the radius of the emitter in cm (we then express it in km in Fig. 12) through 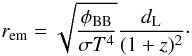 (10)Here φBB is the BB flux in units of erg cm-2 s-1, σ = 5.6704 erg cm2s-1K-4 is the Stefan-Boltzmann constant and dL is the luminosity distance in cm.
(10)Here φBB is the BB flux in units of erg cm-2 s-1, σ = 5.6704 erg cm2s-1K-4 is the Stefan-Boltzmann constant and dL is the luminosity distance in cm.
The best fit of the expanding radius is 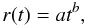 (11)where a = (1.5 ± 1.2) × 104 km s−b and b = 0.32 ± 0.27 (see Fig. 12).
(11)where a = (1.5 ± 1.2) × 104 km s−b and b = 0.32 ± 0.27 (see Fig. 12).
We associate the BB component to the expansion of the ejected material, while the power-law is associated (because we interpret from the IGC paradigm) with the accretion of part of this material onto the NS companion.
 |
Fig. 12 Radius of the emitting region as a function of time (in the cosmological rest frame), corresponding to episode 1. The radius increases with time following a power-law atb, with a = (1.5 ± 1.2) × 104 km s-1 and b = 0.32 ± 0.27. |
6. Analysis of episode 2 in the fireshell model
We recall that the fireshell model (Damour & Ruffini 1975; Ruffini et al. 2000, 2010; Ruffini 2001) is an alternative to the Fireball model, first proposed by Cavallo & Rees (1978), Goodman (1986) and Paczynsky (1986). We assume, within the fireshell model, that all GRBs originate from the gravitational collapse of a star approaching asymptotically the formation of a Kerr-Newmann BH (Wiltshire et al. 2009). An electric field E is created just outside the collapsing core and in between the expanding outer shells that act as a capacitor (Preparata et al. 1998). This electrical field grows until it reaches a critical value, Ec = m2c3/ħe. At this time, vacuum polarization occurs, leading to pair creation at the expenses of the gravitational energy. An optically thick e± plasma forms with total energy 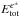 in the range 1049–1054 erg. The e± plasma reaches thermal equilibrium on a timescale of 10-12 s (Aksenov et al. 2007). Because it is optically thick, the plasma self-accelerates due to its internal radiation pressure (Ruffini et al. 1999a,b). After an early expansion in vacuum, the e±-photon plasma engulfs the baryonic matter MB of the outer shells and reaches thermal equilibrium with it. The baryonic matter is described by the dimensionless parameter
in the range 1049–1054 erg. The e± plasma reaches thermal equilibrium on a timescale of 10-12 s (Aksenov et al. 2007). Because it is optically thick, the plasma self-accelerates due to its internal radiation pressure (Ruffini et al. 1999a,b). After an early expansion in vacuum, the e±-photon plasma engulfs the baryonic matter MB of the outer shells and reaches thermal equilibrium with it. The baryonic matter is described by the dimensionless parameter 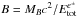 . B must be less than 10-2, otherwise there will not be any relativistic expansion (Ruffini et al. 2000). The optically thick fireshell composed of e±-photon-baryon plasma self-accelerates to ultrarelativistic velocities, finally reaching the transparency condition. A flash of radiation is then emitted. This is the P-GRB (Ruffini et al. 2001a). The amount of energy radiated in the P-GRB is only a fraction of the initial energy
. B must be less than 10-2, otherwise there will not be any relativistic expansion (Ruffini et al. 2000). The optically thick fireshell composed of e±-photon-baryon plasma self-accelerates to ultrarelativistic velocities, finally reaching the transparency condition. A flash of radiation is then emitted. This is the P-GRB (Ruffini et al. 2001a). The amount of energy radiated in the P-GRB is only a fraction of the initial energy 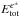 . The remaining energy is stored in the kinetic energy of the optically thin baryonic and leptonic matter fireshell that expands ballistically and starts to slow down through the inelastic collisions with the circumburst medium (CBM). This interaction gives rise to a multi-wavelength emission, the extended afterglow (Ruffini et al. 2001a). We can estimate the characteristic inhomogeneities of the CBM by fitting the luminosity of the X-ray source and imposing the fully radiative condition in the collision between the ultra relativistic baryonic shell and the clouds of the ISM. The complete analytic solution has been developed in Bianco & Ruffini (2004, 2005a,b), together with the analytic expression of the surfaces of equal arrival time of the photons at the detector (EQTS). The afterglow presents three different regimes: a rising part, a peak, and a decaying tail. We therefore define a “canonical GRB” light curve with two sharply different components: 1) the P-GRB and 2) the extended afterglow. What is usually called prompt emission in the current GRB literature mixes the P-GRB with the raising part and the peak of the extended afterglow (Ruffini et al. 2003). The spectrum of the extended afterglow is initially assumed to be thermal in the comoving frame of the expanding shell. Recently, after the analysis of some highly energetic sources observed by Swift and Fermi satellites, this assumption of a pure comoving thermal spectrum has been relaxed and a phenomenological modification by a power-law of the low-energy spectral slope has been introduced (Patriceli et al. 2012). The observed nonthermal spectrum shape is due to a double convolution of thousands of instantaneous comoving spectra, with different temperatures and different Doppler factors, over both the EQTS and the observation time (Ruffini et al. 2004).
. The remaining energy is stored in the kinetic energy of the optically thin baryonic and leptonic matter fireshell that expands ballistically and starts to slow down through the inelastic collisions with the circumburst medium (CBM). This interaction gives rise to a multi-wavelength emission, the extended afterglow (Ruffini et al. 2001a). We can estimate the characteristic inhomogeneities of the CBM by fitting the luminosity of the X-ray source and imposing the fully radiative condition in the collision between the ultra relativistic baryonic shell and the clouds of the ISM. The complete analytic solution has been developed in Bianco & Ruffini (2004, 2005a,b), together with the analytic expression of the surfaces of equal arrival time of the photons at the detector (EQTS). The afterglow presents three different regimes: a rising part, a peak, and a decaying tail. We therefore define a “canonical GRB” light curve with two sharply different components: 1) the P-GRB and 2) the extended afterglow. What is usually called prompt emission in the current GRB literature mixes the P-GRB with the raising part and the peak of the extended afterglow (Ruffini et al. 2003). The spectrum of the extended afterglow is initially assumed to be thermal in the comoving frame of the expanding shell. Recently, after the analysis of some highly energetic sources observed by Swift and Fermi satellites, this assumption of a pure comoving thermal spectrum has been relaxed and a phenomenological modification by a power-law of the low-energy spectral slope has been introduced (Patriceli et al. 2012). The observed nonthermal spectrum shape is due to a double convolution of thousands of instantaneous comoving spectra, with different temperatures and different Doppler factors, over both the EQTS and the observation time (Ruffini et al. 2004).
After fixing the value of the redshift to z = 0.75, we started the analysis of episode 2 within the fireshell model. We first looked for the P-GRB during the first bump of episode 2 (from 100 to 40 s before the second trigger time) by fitting the data with a BB + PL model. We selected several time intervals as the P-GRB during the first bump of episode 2, but in some cases the fits were poor. In some other cases, to reproduce the ratio between the P-GRB energy and the total energy we needed to consider a baryon load B > 10-2 (which is unphysical within the fireshell model) and, in other cases, there was a discrepancy between the observed temperature and the one given by the simulation. Thus we concluded that this bump should belong to episode 1. The reason why we found no strong thermal signature in this bump is that episode 1 starts ~ 10 min before the beginning of the bump and the temperature of the BB component decreases very rapidly following a power-law in the first seconds of emission. Consequently, after such a long time we do not expect to find any signature of a BB from episode 1.
We finally selected the P-GRB as the 9 s from 35 to 26 s before the second trigger, and the following emission from –26 to 100 s as the afterglow. Table 3 shows the parameters of the fit. We calculated a P-GRB energy of EP − GRB = 3.44 × 1050 erg and an isotropic energy of Eiso = 2.43 × 1052 erg.
Fit of the P-GRB and the afterglow of GRB 110709B, episode 2.
We inserted these energy values into our numerical code and calculated the value of the baryon load, B = 5.7 × 10-3. We simulated the light curve and the spectrum, obtaining, at the transparency point, a laboratory radius rtr = 6.04 × 1013 cm, a gamma Lorentz factor Γ = 1.73 × 102 and a P-GRB observed temperature (after cosmological correction) kT = 12.36 keV.
Figures 13a, b show the simulation of the light curve and the spectrum of episode 2. The photon index of the XRT and BAT spectra agree with that predicted by the simulation. Details of this calculation will be given in a forthcoming letter (Penacchioni et al., in prep.). Figure 14 shows the density mask of the ISM, i.e., the density of particles of the interstellar clouds as a function of the distance to the center of the BH. This density has to be interpreted as an effective density because fragmentation may occur in the expanding shell (Ruffini et al. 2007; Dainotti et al. 2007).
 |
Fig. 13 Simulation of the BAT a) light curve and b) spectrum of episode 2. We included XRT data in the fit of the spectrum to show that the slope predicted in the fireshell model agrees with the slope of the X-ray spectrum. |
 |
Fig. 14 Particle density of the ISM clouds as a function of the distance. The mean density is 76 part/cm3. |
7. Nature of the progenitor
Following the works of Rueda & Ruffini (2012) and Izzo et al. (2012b), we suggest for the origin of GRB 110709B a binary system formed by a massive evolved star on the verge of an SN explosion and an NS. The early SN material expanding at non-relativistic velocities is then accreted by the NS companion at times longer than t0,accr, when the material reaches the NS gravitational capture region. The emission observed in episode 1 is associated to this early SN evolution, which is identified with the thermal component, and the accretion process onto the NS, which is possibly related to the nonthermal component. The NS reaches the critical mass in a time t0,accr + Δtaccr and gravitationally collapses to a black hole, emitting the GRB seen in episode 2. We assume the critical mass of a nonrotating NS Mcrit = 2.67 M⊙ as given by Belvedere et al. (2012).
The amount of material that reaches the NS gravitational capture region 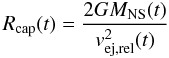 (12)per unit time is given by (see Rueda & Ruffini 2012; Izzo et al. 2012b)
(12)per unit time is given by (see Rueda & Ruffini 2012; Izzo et al. 2012b) 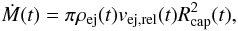 (13)where Rcap is measured from the NS center.
(13)where Rcap is measured from the NS center.
In these expressions, 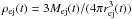 is the density of the ejecta,
is the density of the ejecta, 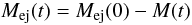 (14)is the total available mass to be accreted by the NS, MNS(t) is the NS mass, and vej,rel(t) is the velocity of the ejecta relative to the NS
(14)is the total available mass to be accreted by the NS, MNS(t) is the NS mass, and vej,rel(t) is the velocity of the ejecta relative to the NS 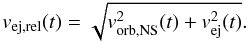 (15)In Eq. (14), Mej(0) is the given initial mass of the ejecta (just at the beginning of the accretion process); we chose different values for it in Table 4. M(t) is the mass of the ejecta that is lost because it passes through the capture region of the NS.
(15)In Eq. (14), Mej(0) is the given initial mass of the ejecta (just at the beginning of the accretion process); we chose different values for it in Table 4. M(t) is the mass of the ejecta that is lost because it passes through the capture region of the NS.
The actual mass accretion rate onto the NS, Ṁaccr(t), is a fraction ηaccr ≤ 1 of Eq. (13), i.e., 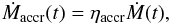 (16)where η is the accretion efficiency onto the NS. Accordingly, there is an amount of material per unit time Ṁout(t) = (1 − ηaccr)Ṁ(t) not accreted by the NS.
(16)where η is the accretion efficiency onto the NS. Accordingly, there is an amount of material per unit time Ṁout(t) = (1 − ηaccr)Ṁ(t) not accreted by the NS.
In Eq. (15), 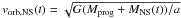 is the orbital velocity relative to the SN core progenitor, a is the separation distance between the NS and the SN core progenitor, and
is the orbital velocity relative to the SN core progenitor, a is the separation distance between the NS and the SN core progenitor, and 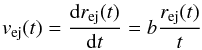 (17)is the expansion velocity of the early SN material, where we have used rej(t) = rem(t), given by Eq. (11).
(17)is the expansion velocity of the early SN material, where we have used rej(t) = rem(t), given by Eq. (11).
We already mentioned that the power-law component in the spectrum of episode 1 might be due to the accretion onto the NS companion. Because this power-law component is present since the beginning of episode 1, we fixed the value of t0,accr to be equal to the starting time of episode 1. This constrains the separation distance a of the binary, which under these conditions is given by 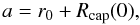 (18)where r0 = rej(0) and Rcap(0) are the radius of the early SN ejecta and the capture radius of the NS companion at the beginning of episode 1. In this case, r0 ≈ 1.75 × 109 cm, see Fig. 12. The separation a is a function of the initial mass of the NS and of the SN core progenitor mass, as well as of the orbital velocity, through Rcap. Clearly, the constraint given by Eq. (18) is a lower limit, since the accretion process onto the NS could have been triggered before by layers at lower densities (e.g. He). In that case, the binary separation a could be higher.
(18)where r0 = rej(0) and Rcap(0) are the radius of the early SN ejecta and the capture radius of the NS companion at the beginning of episode 1. In this case, r0 ≈ 1.75 × 109 cm, see Fig. 12. The separation a is a function of the initial mass of the NS and of the SN core progenitor mass, as well as of the orbital velocity, through Rcap. Clearly, the constraint given by Eq. (18) is a lower limit, since the accretion process onto the NS could have been triggered before by layers at lower densities (e.g. He). In that case, the binary separation a could be higher.
In addition to this constraint, we must take into account that the NS must reach its critical mass Mcrit at the beginning of episode 2, since by that time the NS must collapse to a BH and emit the canonical GRB. This implies that 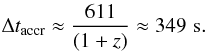 (19)We show in Table 4 the parameters of the binary system leading to IGC of the NS in a time interval equal to the duration of episode 1. We adopted an initial mass for the NS, MNS(0) = 1.4 M⊙ and, correspondingly, an NS radius of RNS(0) = 12.3 km from the mass-radius relation of Belvedere et al. (2012). From the constraint given by Eq. (18), we fixed the binary separation a. We then proceeded with the numerical integration of the accretion rate equations by requiring that MNS(t) = Mcrit at t = Δtaccr, given by Eq. (19), from which we obtained the efficiency ηaccr.
(19)We show in Table 4 the parameters of the binary system leading to IGC of the NS in a time interval equal to the duration of episode 1. We adopted an initial mass for the NS, MNS(0) = 1.4 M⊙ and, correspondingly, an NS radius of RNS(0) = 12.3 km from the mass-radius relation of Belvedere et al. (2012). From the constraint given by Eq. (18), we fixed the binary separation a. We then proceeded with the numerical integration of the accretion rate equations by requiring that MNS(t) = Mcrit at t = Δtaccr, given by Eq. (19), from which we obtained the efficiency ηaccr.
Massive star – neutron star binary progenitor of GRB 110709B.
It is interesting to analyze how the NS can accrete such a large mass, in some cases on the order of 47% of the early SN material (see Col. 5 of Table 4), since one might assume that solid angles of ~ 50% between the early SN material and the accreting NS are hard to obtain. Indeed, during the accretion process the NS is moving with high orbital velocities on the order of 108 cm s-1 relative to the core progenitor (see Col. 7 of Table 4), and consequently travels effective arc-lengths several times longer than the circumference of the orbit (see Col. 8 of Table 4).
Assuming that the gain in gravitational energy of the accreted material onto the NS can be released from the system leads to an upper limit of the luminosity 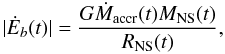 (20)where we take into account the dependence of the NS radius with time, due to the increment of the NS mass by the accretion process. The self-consistent radius is computed at each time from the mass-radius relation of Belvedere et al. (2012).
(20)where we take into account the dependence of the NS radius with time, due to the increment of the NS mass by the accretion process. The self-consistent radius is computed at each time from the mass-radius relation of Belvedere et al. (2012).
The actual luminosity depends on the efficiency ηrad in converting gravitational energy into electromagnetic energy by some still unknown process. Since in our model we assume that the BB component of episode 1 is caused by the early SN expansion, we estimate the efficiency ηrad from the assumption that | Ėb | is responsible for the power-law luminosity LPL, namely 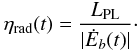 (21)In Fig. 15 we show the evolution of the efficiency ηrad in the first seconds of emission for the binary systems shown in Table 4. We assumed a constant and isotropic power-law luminosity of episode 1, LPL ≈ 1.8 × 1050 erg s-1 ≈ 10-4M⊙ s-1, as found from the spectral analysis. For all cases, we obtain the same evolution of the efficiency with time, i.e., the curves overlap. This is because we constrained all systems to have the same initial NS mass and Δtaccr.
(21)In Fig. 15 we show the evolution of the efficiency ηrad in the first seconds of emission for the binary systems shown in Table 4. We assumed a constant and isotropic power-law luminosity of episode 1, LPL ≈ 1.8 × 1050 erg s-1 ≈ 10-4M⊙ s-1, as found from the spectral analysis. For all cases, we obtain the same evolution of the efficiency with time, i.e., the curves overlap. This is because we constrained all systems to have the same initial NS mass and Δtaccr.
 |
Fig. 15 Theoretical estimation of the efficiency ηrad given by Eq. (21) of the process to convert gravitational energy into radiation as a function of time. For this plot, we assumed a constant and isotropic power-law luminosity of episode 1, LPL ≈ 1.8 × 1050 erg s-1 ≈ 10-4M⊙ s-1. We computed the values of the efficiency for the binary systems shown in Table 4. For all cases, we obtain the same evolution of the efficiency with time, i.e., the curves overlap. The values of ηrad are always <10%. |
8. Radio observations
Zauderer & Berger (2012) reported observations with the EVLA radio telescopes on several occasions between 11 and 16 July 2011, at a frequency of 5.8 GHz. They found a radio source that brightened by about a factor of 1.6 between 2.1 and 7 days after the burst. The coincidence with the XRT position and the rising flux indicate that this is the radio afterglow of GRB 110709B. The position of the source is RA = 10:58:37.114, Dec = –23:27:16.760. We show in Fig. 16 the 5.8 GHz light curve presented in Zauderer et al. (2012), which shows evidence of a radio bump. Following the work of Chevalier & Soderberg (2010), we reproduced the plot of the peak spectral radio luminosity per unit frequency as a function of time (days) at which the peak is produced for different SN associated with GRBs, including GRB 110709B (see Fig. 17). We find that the radio emission of this source is higher than those associated with typical SN.
 |
Fig. 16 X-ray (black), radio (blue) and NIR (red, upper limits) light curves of GRB 110709B. Taken from Zauderer et al. (2012) with kind permission. |
 |
Fig. 17 Plot of the peak spectral radio Luminosity per unit frequency versus the time at which the peak occurs, for different SN associated to GRBs. The circles represent the SN emission associated to SN 2006aj (GRB 060218), SN 1998bw (GRB 980425) and SN 2003lw (GRB 031203). The triangles represent the SN Ib/c for which there are radio observations, namely SN 2002ap, SN 1990B, SN 2008D, SN 1994I, SN 2009bb and SN 2003L. The squares represent the SN IIb: SN 2008ax, SN 2001ig, SN 1993J, SN 2001gd and SN 2003bg. The red cross is the luminosity related to GRB 110709B afterglow. It is higher than the emissions of the other SN, considered “standard”. |
9. Conclusions
GRB 110709B is a very peculiar source, since it is the first for which Swift-BAT was triggered twice. Its Swift-BAT light curve presents two well-defined episodes, episode 1 and episode 2. Episode 1 lasts 100 s and episode 2 lasts 135 s. Particularly interesting is the fact that the X-ray observations started well before the second trigger time. The light curve and spectrum of this source share characteristics with GRB 090618 (Izzo et al. 2012b), GRB 101023 (Penacchioni et al. 2012), and GRB 970828 (Izzo et al. 2012c). It has recently been shown that GRBs that show such distinct emissions, episodes 1 and 2, form a new family of GRBs, which are described by the IGC paradigm (Rueda & Ruffini 2012; Izzo et al. 2012b). Within this scenario, the GRB originates in a binary system formed by a massive star on the verge of an SN and an NS close to its critical mass for the gravitational collapse to a BH. The compact-core SN progenitor ejects material in the very early phases of the SN explosion, which is then accreted by the NS; this process is identified with episode 1. The accretion process onto the NS brings it to the critical mass, which in turn leads to its gravitational collapse to a BH and to emitting the GRB, identified with episode 2. Later on, we see a standard emission in X-rays, which we called episode 3. Several days after the burst, when it is present, we see an optical emission, associated to the SN (episode 4). Following the recent works on GRB 090618 (Izzo et al. 2012b) and GRB 970828 (Izzo et al. 2012c), we here applied the IGC paradigm to GRB 110709B.
The redshift of GRB 110709B is unknown, therefore we used in Sect. 4 four phenomenological methods to constrain it; i.e., Grupe (Grupe et al. 2007), Amati (Amati 2006), Yonetoku (Yonetoku 2004) and the scaling of the X-ray afterglow (Izzo et al. 2012a; Penacchioni et al. 2012). The first method gives an upper limit of z < 1.35. The second and third methods give a lower limit of z > 0.6 and z > 0.7, respectively. The last method gives a precise value of z = 0.75, which lies within the range determined by three of the above mentioned methods. We then decided on this last value as the redshift of GRB 110709B.
The spectral analysis of episode 1 was given in Sects. 3.1 and 5. We found a value of the isotropic energy for episode 1 of 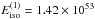 erg (see Table 1). We fit the spectrum with a BB+PL model. The temperature of the BB component evolves with time following a broken power-law (see Fig. 5). The corresponding radius of the BB emitter evolves in time following a power-law given in Eq. (11) and shown in Fig. 12. We associated this radius and the BB component to the evolution of the SN ejecta, while the power-law is associated to the accretion of the ejected material onto the NS companion.
erg (see Table 1). We fit the spectrum with a BB+PL model. The temperature of the BB component evolves with time following a broken power-law (see Fig. 5). The corresponding radius of the BB emitter evolves in time following a power-law given in Eq. (11) and shown in Fig. 12. We associated this radius and the BB component to the evolution of the SN ejecta, while the power-law is associated to the accretion of the ejected material onto the NS companion.
Episode 2 was analyzed in Sects. 3.2 and 6. We found an isotropic energy of 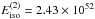 erg (see Table 3). We interpreted this episode as a canonical GRB and simulated its light curve and spectrum within the fireshell model. We found at transparency a Lorentz factor Γ ~ 1.73 × 102, laboratory radius of 6.04 × 1013 cm, P-GRB observed temperature kTP − GRB = 12.36 keV, baryon load B = 5.7 × 10-3, P-GRB energy of EP − GRB = 3.44 × 1050 erg, and a CBM mean density 76 part cm-3. This value is consistent with a “dark GRB”, as cited in Zauderer et al. (2012). The lack of detection of an SN emission for this particular GRB could be due to obscuration by the circumstellar dust in the host galaxy.
erg (see Table 3). We interpreted this episode as a canonical GRB and simulated its light curve and spectrum within the fireshell model. We found at transparency a Lorentz factor Γ ~ 1.73 × 102, laboratory radius of 6.04 × 1013 cm, P-GRB observed temperature kTP − GRB = 12.36 keV, baryon load B = 5.7 × 10-3, P-GRB energy of EP − GRB = 3.44 × 1050 erg, and a CBM mean density 76 part cm-3. This value is consistent with a “dark GRB”, as cited in Zauderer et al. (2012). The lack of detection of an SN emission for this particular GRB could be due to obscuration by the circumstellar dust in the host galaxy.
The nature of the progenitor was discussed in Sect. 7. We indicated that it is a binary system formed by a massive evolved star on the verge of an SN explosion and an NS. We associated the thermal component of episode 1 mainly with the early SN evolution and the power-law component to the accretion process onto the NS. There is the possibility that the accretion process also contributes thermally. The energy from just the thermal component is on the order of 1050 erg, which is reasonable for the expansion of the early SN ejecta. We performed all necessary calculations to obtain the parameters of the binary system. For all our calculations we assumed a fixed NS mass of 1.4 M⊙. We computed the rate at which the early SN material enters the capture region, for given values of the SN core progenitor mass. From this material, only a fraction will be accreted by the NS, therefore we introduced an efficiency factor ηaccr. Because the power-law component is present since the beginning of episode 1, we assumed that this episode starts at the same time t0,accr as the accretion process, namely, when the outermost shell of expanding ejecta reaches the capture radius Rcap of the NS (measured from the center of the NS). This puts a constraint on the separation distance a of the binary. In addition, the NS must reach its critical mass and collapse to a BH at the beginning of episode 2. This puts a constraint on the duration of the accretion process Δtaccr. By integrating the accretion rate equations with these boundary conditions we obtained the efficiency ηaccr. We summarized the results in Table 4 for different values of the core-progenitor mass and the density of the early SN ejecta. Assuming that the power-law radiation comes from the conversion of the binding energy of the accreted material onto the NS, we estimated the efficiency ηrad of this conversion process, which we show in Fig. 15 for an isotropic power-law luminosity LPL ≈ 1.8 × 1050 erg s-1 ≈ 10-4M⊙ s-1 observed in episode 1. For the parameters of the binary system shown in Table 4, we obtained values of ηrad < 10%. The efficiency of the radiation mechanism can be even lower if some beaming or boosting is present. However, we did not address any such possible mechanism in this work.
In Sect. 8 we presented the radio observations of GRB 110709B with the EVLA radio telescopes and the X-ray, radio and NIR light curves taken from Zauderer et al. (2012). We remarked on the presence of a bump in the radio afterglow, at ≈ 10 days after the burst. Because GRB 110709B has been classified as an optically dark burst, we plotted the peak spectral radio luminosity per unit frequency as a function of time and compared it with the luminosities of typical SNe, to see if it was possible to find any coincidences that might indicate the presence of the SN in the radio band. However, the luminosity we found is much higher than those of standard SNe.
We interpreted, within the IGC paradigm, that GRB 110709B is a new member of the IGC family, in addition to GRB 090618, GRB 101023, and GRB 970828.
A remarkable support for the above IGC paradigm comes from the observations of the X-ray afterglow emission of these systems. The X-ray light curve is composed of an early steep decay, a plateau, and a late decay. The analysis of the late decay of the afterglow luminosity has been identified with the cooling of the newly born NS, left by the SN explosion (Negreiros et al. 2012).
Acknowledgments
We are very grateful to the anonymous referee for his/her comments and suggestions that helped to improve the presentation of our results. We thank the Swift team for the support. This work made use of data supplied by the UK Swift Data Centre at the University of Leicester. A.V.P. is supported by the Erasmus Mundus Joint Doctorate Program by Grant Number 2010-1816 from the EACEA of the European Commission. G.B.P. is supported by the Erasmus Mundus Joint Doctorate Program by Grant Number 2011-1640 from the EACEA of the European Commission.
References
- Aksenov, A. G., Ruffini, R., & Vereshchagin, G. V. 2007, Phys. Rev. Lett., 99, 125003 [Google Scholar]
- Amati, L. 2006, MNRAS, 372, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Amati, L., Frontera, F., & Guidorzi, C. 2009, A&A, 508, 173. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Band, D., Matteson, J., Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Belvedere, R., Pugliese, D., Rueda, J. A., et al. 2012, Nucl. Phys. A, 883, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, E. 2011, GCN 12128 [Google Scholar]
- Berger, E., Fox, D. B., Kulkarni, S. R., et al. 2007, ApJ, 660, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, C. L., & Ruffini, R. 2004, ApJ, 605, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, C. L., & Ruffini, R. 2005a, ApJ, 633, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bianco, C. L., & Ruffini, R. 2005b, ApJ, 620, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Frail, D. A., & Sari, R. 2001, ApJ, 121, 2879 [Google Scholar]
- Cavallo, G., & Rees, M. J. 1978, MNRAS, 183, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Soderberg, A. M. 2010, ApJ, 711, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Cummings, J. R., Barthelmy, S. D., Burrows, D. N., et al. 2011, GCN 12122 [Google Scholar]
- D’avanzo, P., Melandri, A., Palazzi, E., et al. 2012, GCN 13069 [Google Scholar]
- Damour, T., & Ruffini, R. 1975, Phys. Rev. Lett., 35, 463 [Google Scholar]
- Dainotti, M. G., Bernardini, M. G., Bianco, C. L., et al. 2007, A&A, 471, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, J. 1986, ApJ, 308, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Granot, J., & Sari, R. 2002, ApJ, 568, 820 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Nousek, J. A., van den Berk, D. E., et al. 2007, AJ, 133, 2216 [NASA ADS] [CrossRef] [Google Scholar]
- Holland, S. 2011, GCN 12157 [Google Scholar]
- Izzo, L., Ruffini, R., Penacchioni, A. V., et al. 2012a, A&A, 543, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzo, L., Rueda, J. A., & Ruffini, R. 2012b, A&A, 548, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izzo, L., Rueda, J. A., Bianco, C. L., et al. 2012c, ApJ, submitted [arXiv:1205.6651] [Google Scholar]
- Krühler, T., Greiner, J., Schady, P., et al. 2011, A&A, 534, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levesque, E. M., Kewley, L. J., Graham, J. F., et al. 2010, ApJ, 712, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Margutti, R., Zainoni, E., Bernardini, M. G., et al. 2013, MNRAS, 428, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Negreiros, R., Ruffini, R., Bianco, C. L., et al. 2012, A&A, 540, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., & Hashimoto, M. 1998, Phys. Rep., 163, 13 [Google Scholar]
- Nomoto, K., Yamakoa, H., Pols, O. R., et al. 1994, Nature, 371, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Ohmori, N., Akiyama, M., Yamauchi, M., et al. 2011, GCN 12172 [Google Scholar]
- Paczynsky, B. 1986, ApJ, 308, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Patricelli, B., Bernardini, M. G., Bianco, C. L., et al. 2012, ApJ, 756, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Penacchioni, A. V., Ruffini, R., Izzo, L., et al. 2012, A&A, 538, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perley, D. A., Cenko, S. B., Bloom, J. S., et al. 2009, AJ, 138, 1690 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Morgan, A. N., Updike, A., et al. 2011, AJ, 141, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Preparata, G., Ruffini, R., & Xue, S.-S. 1998, A&A, 338, L87 [NASA ADS] [Google Scholar]
- Ryde, F. 2004, ApJ, 614, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Rueda, J. A., & Ruffini, R. 2012, ApJ, 758, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R. 2001, in Fluctuating Paths and Fields, eds. W. Janke, A. Pelster, H.-J. Schmidt, & M. Bachmann (Singapore: World Scientific), 771 [Google Scholar]
- Ruffini, R. 2012, Plenary Talk at the Thirteenth MG Meet., Stockholm, Sweden [Google Scholar]
- Ruffini, R., Salmonson, J. D., Wilson, J. R., & Xue, S.-S. 1999a, A&A, 350, 334 [NASA ADS] [Google Scholar]
- Ruffini, R., Salmonson, J. D., Wilson, J. R., & Xue, S.-S. 1999b, A&AS, 138, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruffini, R., Salmonson, J. D., Wilson, J. R., et al. 2000, A&A, 359, 855 [NASA ADS] [Google Scholar]
- Ruffini, R., Bianco, C. L., Fraschetti, F., et al. 2001a, ApJ, 555, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Bianco, C. L., Fraschetti, F., et al. 2001b, ApJ, 555, L117 [Google Scholar]
- Ruffini, R., Bianco, C. L., Chardonnet, P., et al. 2003, in XIth Brazilian School of Cosmology and Gravitation, eds. M. Novello, & S. E. Perez Bergliaffa, AIP Conf. Ser., 782, 16 [Google Scholar]
- Ruffini, R., Bianco, C. L., Chardonnet, P., et al. 2004, IJMPD, 13, 843 [Google Scholar]
- Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2007, ESA-SP, 622, 561 [Google Scholar]
- Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2008, in Proc. 11th Marcel Grosmann Meet. on General Relativity, eds. H. Kleinert, & R. T. Jantzen (World Scientific Publishing), 368 [Google Scholar]
- Ruffini, R., Vereshchagin, G., & Xue, S.-S. 2010, Phys. Rep., 487, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sari, R., Piran, T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Updike, A. C., Olivares, F., Greiner, J., et al. 2011, GCN 12129 [Google Scholar]
- Wiltshire, D. L., Visser, M., & Scott, S. M. 2009, The Kerr Spacetime: Rotating Black Holes in General Relativity (Cambridge University Press) [Google Scholar]
- Xu, D., Fynbo, J. P. O., McCormac, J., et al. 2012, GCN 12764 [Google Scholar]
- Yonetoku, D., Murakami, T., Nakamura, R., et al. 2004, ApJ, 609, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Yonetoku, D., Murakami, T., Tsutsui, R., et al. 2010, PASJ, 62, 1495 [NASA ADS] [Google Scholar]
- Zauderer, B. A., Berger, E., Margutti, R., et al. 2012 [arXiv:1209.4654v1] [Google Scholar]
- Zauderer, B. A., & Berger, E. 2012, GCN 12190 [Google Scholar]
- Zhang, B.-B., Burrows, D., Zhang, B., et al. 2012, ApJ, 748, 132 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Fit results of episode 1 with five spectral models: BB, Band, BB+PL, PL and cutoffPL.
Spectral fit of the whole episode 2 with different models: BB, PL, BB+PL, cutoffPL, and Band.
All Figures
 |
Fig. 1 BAT light curve of GRB 110709B, including the two trigger times. Here we can appreciate the time separation (about 10 min) between the first and the second trigger. The light curve is in the (15–150 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). The second trigger time was at 331 940 612 s in MET seconds. |
| In the text | |
 |
Fig. 2 Count light curve of GRB 110709B obtained from the Swift-XRT detector in the (0.3–10 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). Picture taken from http://www.swift.ac.uk/xrt_curves/00456967/ |
| In the text | |
 |
Fig. 3 Count light curve of episode 1 of GRB 110709B obtained from the Swift-BAT detector in the (15–150 keV) energy band. The time is relative to the first trigger time, of 331 939 966 s (in MET seconds). |
| In the text | |
 |
Fig. 4 Fit of episode 1 with a BB+PL model. The parameters of the fit are kT = (22 ± 5) keV, BB Amp = 0.2 ± 0.1, γ = 1.4 ± 0.1, PL Amp = 2.2 ± 0.8, Red-χ2 = 1.049 (54 D.O.F.). |
| In the text | |
 |
Fig. 5 Evolution of the kT component of the BB+PL model during episode 1. The first data point corresponds to 5 s before the first BAT trigger time. The vertical line corresponds to the trigger time. The time is given in the observer frame. The temperature evolves in time following a broken power-law fit. There is a break at t = 41.21 s. The indices of the PL are α = 0 (consistent with a constant function) and β = −4 ± 2. The presence of the BB, although weaker than in previous cases, is essential to obtain an acceptable fit. |
| In the text | |
 |
Fig. 6 Fit of episode 2 with a cutoffPL model. The photon index is γ = 1.0 ± 0.1, the normalization constant is 0.5 ± 0.1, the cutoff energy is E0 = 132 ± 31 and the reduced chi squared of the fit is Red-χ2 = 0.77 (55 D.O.F.). |
| In the text | |
 |
Fig. 7 Count light curve of episode 2 of GRB 110709B obtained from the Swift-BAT detector in the (15–150 keV) energy band. The time is given with respect to the second trigger time, of 331 940 612 s (in MET seconds). |
| In the text | |
 |
Fig. 8 Amati relation (solid line) with its 1 − σ uncertainties (doted lines) and peak energy Ep.i vs. Eiso for GRB 110709B, for different values of the redshift, from 0.1 to 3, at steps of 0.1. We can see that the data match the theoretical function within 1 − σ for z > 0.4. |
| In the text | |
 |
Fig. 9 Yonetoku relation (solid line) with its 1 − σ uncertainties (doted lines) and peak luminosity vs. Ep.i for GRB 110709B, for different values of the redshift, from 0.1 to 3, at steps of 0.1. We can see that the data matches the theoretical function within 1 − σ for z > 0.6. |
| In the text | |
 |
Fig. 10 Plot of GRB 090618 seen as if it were at different redshifts: 0.2 (blue), 0.4 (green), 0.7 (gray), 1.0 (orange), and 2.0 (purple). The red light curve corresponds to GRB 110709B. We can see that it lies between the green and the orange light curves, indicating that the redshift must be between 0.4 and 1.0. |
| In the text | |
 |
Fig. 11 GRB 090618 light curve (blue) as if it were seen at z = 0.75 together with the GRB 110709B light curve (red). There is an excellent superposition in the late decay assuming a temporal shift of GRB 090618 of T ∗ = 800 s to the right to align the steep decays of the light curves. |
| In the text | |
 |
Fig. 12 Radius of the emitting region as a function of time (in the cosmological rest frame), corresponding to episode 1. The radius increases with time following a power-law atb, with a = (1.5 ± 1.2) × 104 km s-1 and b = 0.32 ± 0.27. |
| In the text | |
 |
Fig. 13 Simulation of the BAT a) light curve and b) spectrum of episode 2. We included XRT data in the fit of the spectrum to show that the slope predicted in the fireshell model agrees with the slope of the X-ray spectrum. |
| In the text | |
 |
Fig. 14 Particle density of the ISM clouds as a function of the distance. The mean density is 76 part/cm3. |
| In the text | |
 |
Fig. 15 Theoretical estimation of the efficiency ηrad given by Eq. (21) of the process to convert gravitational energy into radiation as a function of time. For this plot, we assumed a constant and isotropic power-law luminosity of episode 1, LPL ≈ 1.8 × 1050 erg s-1 ≈ 10-4M⊙ s-1. We computed the values of the efficiency for the binary systems shown in Table 4. For all cases, we obtain the same evolution of the efficiency with time, i.e., the curves overlap. The values of ηrad are always <10%. |
| In the text | |
 |
Fig. 16 X-ray (black), radio (blue) and NIR (red, upper limits) light curves of GRB 110709B. Taken from Zauderer et al. (2012) with kind permission. |
| In the text | |
 |
Fig. 17 Plot of the peak spectral radio Luminosity per unit frequency versus the time at which the peak occurs, for different SN associated to GRBs. The circles represent the SN emission associated to SN 2006aj (GRB 060218), SN 1998bw (GRB 980425) and SN 2003lw (GRB 031203). The triangles represent the SN Ib/c for which there are radio observations, namely SN 2002ap, SN 1990B, SN 2008D, SN 1994I, SN 2009bb and SN 2003L. The squares represent the SN IIb: SN 2008ax, SN 2001ig, SN 1993J, SN 2001gd and SN 2003bg. The red cross is the luminosity related to GRB 110709B afterglow. It is higher than the emissions of the other SN, considered “standard”. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


