| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 10 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220529 | |
| Published online | 01 February 2013 | |
The 2.35 year itch of Cygnus OB2 #9
II. Radio monitoring⋆,⋆⋆
1 Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
e-mail: Ronny.Blomme@oma.be
2 Département AGO, Université de Liège, Allée du 6 Août 17, Bât. B5C, 4000 Liège, Belgium
3 Department of Physics & Astronomy, University College London, Gower Street, London WC1E 6BT, UK
4 School of Physics and Astronomy, The University of Leeds, Woodhouse Lane, Leeds LS2 9JT, UK
5 Research School of Astronomy and Astrophysics, The Australian National University, Australia
Received: 10 October 2012
Accepted: 7 December 2012
Context. Cyg OB2 #9 is one of a small set of non-thermal radio emitting massive O-star binaries. The non-thermal radiation is due to synchrotron emission in the colliding-wind region. Cyg OB2 #9 has only recently been discovered to be a binary system, and a multi-wavelength campaign was organized to study its 2011 periastron passage.
Aims. We want to better determine the parameters of this system and model the wind-wind collision. This will lead to a better understanding of the Fermi mechanism that accelerates electrons up to relativistic speeds in shocks and its occurrence in colliding-wind binaries. We report here on the results of the radio observations obtained in the monitoring campaign and present a simple model to interpret the data.
Methods. We used the Expanded Very Large Array (EVLA) radio interferometer to obtain 6 cm and 20 cm continuum fluxes during the Cyg OB2 #9 periastron passage in 2011. We introduce a simple model to solve the radiative transfer in the stellar winds and the colliding-wind region, and thus determine the expected behaviour of the radio light curve.
Results. The observed radio light curve shows a steep drop in flux sometime before periastron. The fluxes drop to a level that is comparable to the expected free-free emission from the stellar winds, suggesting that the non-thermal emitting region is completely hidden at that time. After periastron passage, the fluxes slowly increase. We use the asymmetry of the light curve to show that the primary has the stronger wind. This is somewhat unexpected if we use the astrophysical parameters based on theoretical calibrations. But it becomes entirely feasible if we take into account that a given spectral type-luminosity class combination covers a range of astrophysical parameters. The colliding-wind region also contributes to the free-free emission, which can help explain the high values of the spectral index seen after periastron passage. Combining our data with older Very Large Array (VLA) data allows us to derive a period P = 860.0 ± 3.7 days for this system. With this period, we update the orbital parameters that were derived in the first paper of this series.
Conclusions. A simple model introduced to explain only the radio data already allows some constraints to be put on the parameters of this binary system. Future, more sophisticated, modelling that will also include optical, X-ray, and interferometric information will provide even better constraints.
Key words: stars: individual: Cyg OB2 #9 / stars: early-type / stars: mass-loss / radiation mechanisms: non-thermal / acceleration of particles / radio continuum: stars
Based on observations with the Expanded Very Large Array (EVLA), which is operated by the National Radio Astronomy Observatory. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
Figure 1 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. Introduction
Among the early-type stars there are a number of non-thermal radio emitters. It is now generally accepted that all such stars are colliding-wind binaries (Dougherty & Williams 2000; De Becker 2007; Blomme 2011). In a massive early-type binary the strong winds from both components collide, leading to the formation of two shocks, one on each side of the contact discontinuity where the two winds collide. Around those shocks a fraction of the electrons is accelerated up to relativistic speeds. This is believed to be due to the Fermi acceleration mechanism (Eichler & Usov 1993). As these electrons spiral around in the magnetic field, they emit synchrotron radiation, which we detect as non-thermal radio emission. In addition, the hot compressed material in the colliding-wind region (CWR) also emits X-rays (Stevens et al. 1992; Pittard & Parkin 2010) and influences the shape of the optical spectral lines (Rauw et al. 2005).
While the general outline of the explanation for non-thermal radio emission is clear, there are still problems when detailed modelling of specific systems is attempted. In modelling the radio flux variations of the short-period variable Cyg OB2 #8A, Blomme et al. (2010) failed to obtain the correct spectral index. For the well-observed WR+O binary WR 140, models fail to explain the behaviour of the radio light curve (Williams et al. 1990; White & Becker 1995; Pittard 2011). Part of the problem is the difficulty in calculating all the effects of the Fermi acceleration ab initio. Another complication is the presence of clumping or porosity in the stellar winds of massive stars, making the estimates of mass-loss rates uncertain. As an added difficulty, the degree of clumping depends on the radius (Puls et al. 2006).
More detailed observations that will help constrain theoretical models are therefore most important. To that purpose a multi-wavelength campaign was started (PI: Y. Nazé) to monitor the 2011 periastron passage of Cyg OB2 #9. That Cyg OB2 #9 is a binary was only discovered relatively recently. The system consists of an O5-5.5If primary and an O3-4III secondary in a highly eccentric (e ≈ 0.7) orbit with a period of ~2.35 yr (Nazé et al. 2008; van Loo et al. 2008). Since its discovery as a binary, Cyg OB2 #9 has passed periastron twice. The 2009 passage was unobservable because it occurred when the system was in conjunction with the Sun. The 2011 periastron passage is therefore the first one that could be observed well.
In Nazé et al. (2012,hereafter Paper I we presented the results from the optical and X-ray monitoring campaign. The CWR was detected in Hα, where it creates enhanced absorption and emission. Owing to the hot material in the CWR, the X-rays show phase-locked behaviour with the flux peaking at periastron. They indicate an adiabatic wind-wind collision for most of the time with the flux following the predicted inverse relation with the separation between the two components. Only close to periastron could the shock be turning radiative. The present paper is the second in the series, analysing the radio observations made by the Expanded Very Large Array (EVLA; Perley et al. 2011). Future papers will discuss the optical interferometry and the modelling of the system.
The non-thermal nature of Cyg OB2 #9 became clear from its high brightness temperature, its non-thermal spectral index, and its variability (White & Becker 1983; Abbott et al. 1984; Bieging et al. 1989; Phillips & Titus 1990). In a series of papers, van Loo et al. (2004, 2005, 2006) tried to explain the non-thermal radio emission by a single star (the binary nature of this star was not yet known at that time). In a single star, it is assumed that the shocks due to the intrinsic instability of the radiation driving mechanism are responsible for the Fermi acceleration (White 1985). However, the increasingly more sophisticated models used by van Loo et al. have failed to explain the observations.
A large set of VLA archive data allowed van Loo et al. (2008) to find a ~2.35 yr period in the fluxes, strongly suggesting binarity. Simultaneously, Nazé et al. (2008) detected the binarity from optical spectroscopy. The orbital information was then refined further using additional optical spectra (Nazé et al. 2010; Paper I). Further evidence for the non-thermal nature of Cyg OB2 #9 comes from Very Large Baseline Array (VLBA) radio observations that clearly show the bow-shaped extended emission typical of a CWR in a binary system (Dougherty & Pittard 2006).
In this paper, we present the EVLA radio observations that were obtained as part of the 2011 Cyg OB2 #9 monitoring campaign. We derive the orbital period from these data. We also introduce a simple numerical model to help us interpret the observations. In Sect. 2 we describe the data reduction of the radio observations. In Sect. 3, we present the radio light curve and derive the binary period. In Sect. 4 we introduce a simple model, which we use in Sect. 5 to analyse and discuss the results, and Sect. 6 summarizes our findings and presents our conclusions.
2. Observations
2.1. EVLA data
Cyg OB2 #9 was monitored with the EVLA during the period January to August 2011. The observations (programme 10C-134) were obtained through the open shared risk observing (OSRO) programme. Eleven observations were made, each time in C-band (4.832–5.086 GHz, 6 cm) and L-band (1.264−1.518 GHz, 20 cm). The observing log is given in Table 1. During the monitoring period, the configuration of the EVLA changed from CnB (giving a lower spatial resolution) to A (the highest spatial resolution).
Each band is covered by 2 × 64 channels, each of 2 MHz width. To calibrate out instrumental and atmospheric effects, the phase calibrator J2007+4029 was used. An observation consisted of a phase calibrator – target – phase calibrator sequence, first in C-band, then in L-band. This sequence was followed by an observation of the flux calibrator (J0542+498=3C 147) in L and C band. The flux calibrator also serves as the bandpass calibrator. Time on target for a single observation is 5 min for C-band and 7 min for L-band.
Observing log, radio fluxes and spectral indexes of the EVLA data on Cyg OB2 #9.
2.2. Data reduction
The data were reduced using the Common Astronomy Software Applications1 (CASA) version 3.3.0 data reduction package. The system already flags a number of problematic data (due to focus problems, incorrect subreflector position, off-source antenna position, or missing antennas), and other flags are applied while reading in the data (shadowing by antennas). Careful attention was given to radio frequency interference (RFI). The small amount of RFI present in the C-band is removed by flagging the visibilities in the relevant channels. For the stronger and more extended RFI in L-band, we applied Hanning smoothing to remove the Gibbs ringing; after that the channels affected by the RFI were flagged.
The calibration sequence starts by assigning the correct flux to the flux calibrator (3C 147), using a model to take into account that this source is slightly resolved. A preliminary gain phase calibration was applied before the delay and bandpass calibration. This was followed by the final gain phase and gain amplitude calibrations. The fluxscale was then transferred from the flux to the phase calibrator (J2007+4029). The phase calibrator fluxes are listed in Table 1: they show the slow flux variations typical of many phase calibrators. The calibrations are then applied to the flux and phase calibrators, as well as to the target. The calibrated data for flux and phase calibrators were inspected visually: if discrepant data were found, they were flagged and the calibration redone.
In L-band (20 cm), the phase calibrator is influenced by the radio galaxy Cyg A, which contributes about 0.05–0.5 Jy (depending on the configuration of the EVLA) to the image, while the phase calibrator itself is about 3 Jy. Since the sidelobes of such a strong source can influence the phase calibrator, we applied self-calibration to improve the gain phases. The visibilities were then inspected and any discrepant data flagged.
In the next step an image was made from the target visibilities. For the C-band, this image covers an area somewhat larger than the primary beam (which is 17′ diameter). To gain computing time, we make the image in the L-band somewhat smaller than the primary beam (which is 60′ diameter). The size of each (square) pixel was chosen such that it oversamples the synthesized beam by a factor of at least 4 in each dimension. The image is cleaned down to a level where the noise in the centre is compatible with the expected noise. Images taken in the low-spatial resolution EVLA configurations contain substantial, extended Galactic background. This was removed by excluding the data on the shortest baselines during the imaging. A strong advantage of the present EVLA data over older VLA continuum data is that the many channels allow a sharp image further away from the field centre. To avoid introducing artefacts in such wide-field imaging (Bhatnagar et al. 2008), we needed to use the specific wide-field options in the CASA cleaning procedure. To handle the smaller-scale extended emission still present in the L-band images, the multi-scale option in the CASA clean procedure was used, with scales chosen to be 5, 10, 20, and 40 times the pixel size. For those images where the Cyg OB2 #9 flux was high enough (≳1 mJy), we also applied a single round of phase-only self-calibration (further rounds of self-calibration no longer improve the image).
Two of our observations in the L-band (20 cm) are strongly affected by flaring from Cyg X-3 (which is within the primary beam). This microquasar consists of a Wolf-Rayet star and a compact object (most likely a black hole), and shows frequent and strong flaring activity. The Cyg X-3 multi-wavelength monitoring campaign reported by Corbel et al. (2012) shows a sharp transition from a quenched state to a major flare, with an onset estimated at MJD 55641.0 ± 0.5 (i.e. March 21). On our March 27 observation, Cyg X-3 has a flux of ~10 Jy; on the April 03 observation this has decreased to ~1 Jy, and on the May 02 observation it has dropped down further to ~0.07 Jy. This behaviour is compatible with the Corbel et al. monitoring results. Because of the decreasing sensitivity away from the field centre, the contribution of Cyg X-3 to our observations is a factor ~3 less than the numbers given above. Nevertheless, for the March 27 and April 03 observations, the sidelobes of Cyg X-3 strongly perturb the cleaning of the image and the measurement of Cyg OB2 #9, which has a flux that is only a few mJy at best. The effect of the Cyg X-3 sidelobes on earlier and later observations is negligible.
For the two most affected observations, we therefore first made an image, limiting the clean components to a small box around Cyg X-3. We used multi-frequency synthesis, resulting in two images, one with the flux (averaged over the frequency band) and another with the spectral index. We then self-calibrated these images using one step of phase-only calibration, followed by one step of amplitude and phase calibration. The clean components of the Cyg X-3 image were then subtracted from the visibility data of the target. These data were then processed in the standard way to make an image and measure the fluxes. The procedure was very successful for the April 03 observation, but in the March 27 observation important residual effects of Cyg X-3 remain. In cleaning the latter image, we therefore do not attain the expected noise level. We did not apply self-calibration to this image either.
For all images resulting from our dataset, we then determined the flux and its corresponding error bar by fitting an elliptical Gaussian to the target. To measure the Cyg OB2 #9 flux, we fixed the size and position angle of the beam to the values of the synthesized beam (which is the shape that a point source should have after cleaning the image). In a number of L-band (20 cm) observations, Cyg OB2 #9 is not detected. In such cases, we assigned an upper limit of three times the root-mean-square (rms) noise measured around the target position.
From the fluxes at 6 cm and 20 cm, we derive the spectral index α, given by Fν ∝ να. The error bar on α is derived from standard error propagation, using the error bars on each of the fluxes. Where the 20 cm flux has an upper limit, only a lower limit for α can be determined.
 |
Fig. 2 Radio fluxes and spectral indexes around the periastron passage of Cyg OB2 #9, as a function of orbital phase. The top figure shows the 6 cm flux, the middle one the 20 cm flux, and the bottom one the spectral index. The older VLA data from van Loo et al. (2008) are plotted with a grey line. The new EVLA data are shown with the thicker solid red line. The length of the line indicates the 1σ error bar on the flux. For the non-detections, upper limits are shown that are 3 × the rms noise in the centre of the image. The fluxes have an additional uncertainty of ~5% due to the absolute flux calibration (not shown on the figure). On the spectral index figure, the dashed line indicates the value for free-free emission (α = + 0.6). Periastron occurs at phase = 0.0. |
3. Results
3.1. Radio light curve
Figure 1 shows contour plots of a small region around Cyg OB2 #9 for each of the 11 observations, at both 6 cm and 20 cm. The 6 cm images show a clear decrease in the flux with time, with a slight increase again towards the end of the series. The 20 cm series mirrors that behaviour, with the star being undetectable from May 20 to August 12. The changing sizes of the synthesized beam reflect the changes of the EVLA antenna configuration. Although we know that Cyg OB2 #9 is a colliding-wind binary, the EVLA data do not allow us to resolve the CWR. Our resolution is at best ~0.5′′ (at 6 cm), but the VLBA data of Dougherty & Pittard (2006) show that the CWR has a size of ~0.015′′ (at 3.6 cm).
The March 27 20 cm observation is of lesser quality, owing to the strong influence of Cyg X-3 on these data (see Sect. 2.2). Our data reduction procedure manages to remove the strongest effects of Cyg X-3, but the quality of the data does not allow us to make an image with a sufficiently high dynamic range.
The measured Cyg OB2 #9 fluxes, their error bars and the spectral indexes are listed in Table 1. Figure 2 plots them as a function of orbital phase, with phase = 0.0 corresponding to periastron. The epoch of periastron passage and the period were taken from this paper (see Sect. 3.2). The comparison with the older 6 cm VLA data from van Loo et al. (2008) shows good agreement, showing that the behaviour of Cyg OB2 #9 repeats very well over a number of orbital cycles. Although each of our data points is based on only 5–7 min on-target time, the quality of these EVLA data is clearly much better than that of the older observations. For the values in the high-flux regime, the main uncertainty is due to the absolute flux calibration (estimated to be at the ~5% level), not to the noise. For the 20 cm data the agreement is also good, though less constraining because of the large error bars and high upper limits of the older VLA data set.
The new data show a steep drop in flux (both at 6 and 20 cm) between the May 02 and May 20 observations, corresponding to phases 0.934–0.955. Before that time, the 6 cm fluxes were in a high-flux regime, but with the flux slowly decreasing. The corresponding 20 cm fluxes are relatively constant during that time. The slight increase in the 20 cm flux between March 27 and April 03 (phase 0.892–0.901) could be due to problems with the data reduction (see Sect. 2.2), but this is less likely for the 6 cm increase.
After the drop in flux, there is still a slight decrease in the 6 cm flux, just up to periastron passage. After periastron the flux starts to slowly increase again. The older VLA data at later phases connect very well with the new data points, also in this low-flux regime. At 20 cm the fluxes are so low that Cyg OB2 #9 is not detected. Only the last data point we have (August 28, phase 0.071) shows a detectable but low flux. Again the new data connect well with the increasing 20 cm flux shown in the older VLA data.
Previously, little information was available about the spectral index (α) and its changes in Cyg OB2 #9 (van Loo et al. 2008). The present data provide interesting information of the important changes of α during periastron passage (Fig. 2, bottom panel). Before periastron, α goes down from 0.43 to 0.23. Since this is well below the + 0.6 value expected for free-free emission, it clearly shows the presence of a non-thermal component. From the May 20 (phase 0.955) observation onwards, the index increases; at times, even the lower limit indicates a value for free-free emission for a spherically symmetric wind, or an even higher value.
One would expect the synchrotron emission from the relativistic electrons in the CWR to reach its maximum close to periastron, where the stellar separation is smallest and the local magnetic field strongest. However, the observed situation here is almost the reverse. Both the drop in flux and the rise in spectral index point to a significant impact of free-free absorption on the synchrotron emission component by the stellar wind material close to periastron passage. This fact emphasizes the importance of orientation effects in the light curve of colliding-wind binaries, notably in the radio domain.
3.2. Period
The new EVLA data, in combination with the older VLA data (van Loo et al. 2008) cover a time span of ~30 years, which is substantially longer than the time span covered by the optical spectroscopy (Paper I). The radio data are thus more suitable to deriving the orbital period of Cyg OB2 #9.
As in van Loo et al. (2008), we used the string-length method (Dworetsky 1983) to determine the period that best fits the data. We limited ourselves to the 6 cm observations, since the coverage at other wavelengths is sparser, and we exclude upper limits. We normalized the fluxes to the maximum flux over the combined VLA and EVLA dataset. This maximum is 8.5 mJy (VLA observation on 1984 November 27). The flux normalization introduces a good balance between phase difference and flux difference in the string-length calculation.
Intrinsically, the string-length method does not provide any error bar on its result. To determine the error bar, we applied the bootstrap technique. We made 5000 Monte-Carlo simulations, where we randomly choose a set of n data points out of the existing n observations (with replacement). We then applied the above string-length method, each time exploring 10 000 periods between 750 and 950 days. We thus end up with a set of 5000 period determinations from which we can derive the best value and the error bar. For the best value, we used the median, and for the error bar we used quantiles to select the middle range that contains 68.3% of the values (this corresponds to ± 1σ for a Gaussian distribution). We find P = 860.0 ± 3.7 days. Within the error bar, this is the same result as listed in Paper I. (That value was based on a preliminary reduction of the radio data.)
With this new value for the period, we redetermined the orbital solution based on the optical spectra from Paper I. The results are presented in Table 2. All phases presented in the present paper are based on this solution.
Orbital solution for Cyg OB2 #9.
We can also check that the epoch of periastron passage detected in the radio corresponds to the one in the optical spectroscopy (Paper I). Naively, one may expect minimum radio flux to occur at periastron passage: at that time the stars are at their closest approach and any non-thermal emission from the CWR will be largely, or totally, absorbed by the stellar wind material. The substantial drop in 6 and 20 cm flux occurs between phase 0.934 and 0.955, i.e. about 1–2 months before periastron passage. The lowest 6 cm flux occurs around phase 0.986–0.999. Fitting a parabola through the six lowest 6 cm fluxes gives the minimum at 0.994. There is therefore a small offset between periastron passage and minimum radio flux.
4. Model
For the further analysis of the radio data it will be interesting to have a simple model. This model should be capable of handling the free-free emission from the stellar winds and the CWR, as well as the non-thermal synchrotron emission from the CWR.
In the model we solve the radiative transfer equation in a three-dimensional grid using an adaptive grid scheme. Our first-level grid has 1283 cells, with the origin at the centre of mass of the binary and the negative z-direction towards the observer. While solving the radiative transfer equation, we refine this grid locally, as needed, to achieve the pre-specified precision on the specific intensity. The grid extends 12 000 R⊙ on either side of the origin. At any phase in the orbit, we position the two stars in our 3D grid. We take the estimated 62° inclination angle into account (Paper I). We next assume a mass-loss rate and terminal velocity for both components. We can then calculate the position of the collision along the line connecting the two stars, as well as the opening angle of the CWR (Eichler & Usov 1993, their Eqs. (1) and (3)). We simplify the shape of the contact discontinuity by assuming it to be a cone that is rotationally symmetric around the axis connecting the two stars (Fig. 3). The size of the CWR is limited to a radius that is proportional to the separation between the two components. We also assign a thickness to the CWR.
At any given point in our grid, the mass density can then be determined from the mass-loss rate and terminal velocity of the relevant star. Within the assumed thickness of the CWR, we increase this density by a factor 4 to account for the (presumed strong) shock the material has gone through. We ignore any possible clumping or porosity in the wind material. We also assign a temperature to each point. For the unperturbed stellar wind material, this value (Twind = 20 000 K) is about half the effective temperature of the star. For the material in the CWR we assign a temperature (TCWR) appropriate for the heated material. This temperature is assumed to be constant over the whole CWR. It is also assumed to be independent of orbital phase. This is mainly motivated by the facts that the CWR temperature is related to the pre-shock velocity and that this velocity is not expected to change significantly along the orbit as the winds will have reached their terminal velocity (except close to periastron). We then solve the radiative transfer equation following the procedure outlined in Wright & Barlow (1975). The radiative transfer takes the free-free absorption and emission into account, both from the CWR and the stellar wind material.
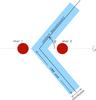 |
Fig. 3 Schematic view of our model for the CWR. The shape of the CWR (shaded in light-blue) is a cone that is rotationally symmetric around the axis connecting the two stars. It has a (half) opening angle θ. |
To include the synchrotron emission in the above model, we manipulate the temperature and opacity we assign to the material. As before, for the unperturbed stellar wind material, we assign a temperature that is about half the effective temperature of the star. For the material in the CWR we assign two temperatures. One represents the hot, non-relativistic material in the CWR. The other temperature is to be interpreted as a brightness temperature, representing the relativistic electrons that are responsible for the synchrotron emission. In this way, we avoid the detailed and complicated calculations needed to determine the exact synchrotron emission. All material emits at either the wind temperature or the combined CWR and synchrotron brightness temperature (if it is in the CWR). For the opacity, the material absorbs at either wind temperature or CWR temperature (the synchrotron brightness temperature does not play a role in absorption). In this way the synchrotron emission can be absorbed by the stellar wind material, as well as by the hot, non-relativistic material in the CWR. We then solve the radiative transfer equation using the adaptive grid scheme, and determine the flux at a number of orbital phases.
5. Analysis and discussion
5.1. Free-free contribution stellar winds
Star and wind parameters of Cyg OB2 #9.
Near minimum the spectral index is close to thermal, suggesting that the non-thermal contribution has dropped to zero. The free-free emission and absorption in the stellar winds of course provide a thermal component and we now check that these low fluxes can be explained by the free-free emission of the winds alone.
In Paper I, we took the stellar parameters from Martins et al. (2005) and assigned the supergiant values of effective temperature (Teff), luminosity (Lbol), and mass (M∗) to both the primary and secondary. From the equations of Vink et al. (2001) we then derive the mass-loss rate (Ṁ) and the terminal velocity (ν∞). We can then use the equations of Wright & Barlow (1975) to calculate the expected radio fluxes of a single-star wind at 6 cm and 20 cm. Combining these results for both components gives a 6 cm free-free flux of ~1 mJy, and a 20 cm flux of ~0.5 mJy. This is much too high compared to the observed 6 cm minimum of 0.27 ± 0.04 mJy and the 20 cm upper limit of 0.15 mJy.
For the purposes of this paper we therefore need more refined values for the stellar and wind parameters. Instead of a single value, we consider the range of values corresponding to the range of spectral types, both for the primary and secondary. In Table 3 we give the star and wind parameters used here, based on the calibration by Martins et al. (2005, theoretical Teff. As in Paper I, we used the Vink et al. (2001) and Wright & Barlow (1975) equations to derive the mass-loss rate, terminal velocity, and expected radio fluxes, as well as the radius where the radial optical depth equals 1. The flux contributions of both stars turn out to be about equal (the radio flux depends on the combination Ṁ/ν∞, which is about the same for these stars). The sum of both fluxes is still higher than the observed 6 cm minimum flux of 0.27 ± 0.04 mJy. The fluxes are lower, however, than the Paper I fluxes because here we used the Martins et al. (2005) giant values instead of supergiant values for the secondary.
A number of effects can lessen the discrepancy between the predicted fluxes and the observed minimum. First of all, the total flux is not given by the straightforward sum of both fluxes. The winds of both stars collide at the contact discontinuity: on each side of this discontinuity there is only material belonging to one star, not to the other. The contact discontinuity falls well within the radii of optical depth = 1 (Table 3). This suggests that a substantial part of the summed flux will be missing. (A more correct description takes into account the material accumulated between the contact discontinuity and the shocks – this is discussed in Sect. 5.2.) There is furthermore some discussion about the distance to the Cyg OB2 association (e.g., Rauw 2011). A larger distance (1.7–2.0 kpc instead of our assumed 1.45 kpc) would explain the discrepancy equally well. Clumping could also be considered as an explanation because it lowers the mass-loss rates by a factor 2–3 (e.g., Puls et al. 2006) compared to the smooth wind models used by Vink et al. (2001). However, the enhanced free-free emission in a clumped wind will compensate for the lower mass-loss rate, rendering the clumping explanation unlikely.
Finally, we note that Muijres et al. (2012) provide improved mass-loss rate estimates compared to the Vink et al. (2001) recipe. The revised mass-loss rates of the primary and secondary are a factor ~2 lower, and the terminal velocities a factor ~1.4 higher than the ones listed in Table 3. This reduces the predicted fluxes by a factor ~4, which leads to values well below the observed minimum flux. Muijres et al., however, note that their terminal velocities are 35–45 % too high compared to observed values.
For the wind momentum ratio 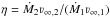 , we find values between 0.97 and 1.76 (using our Table 3 values). Most combinations of wind parameters give a wind momentum ratio that is >1, i.e. the secondary star has the stronger wind. Only the O5I+O4III combination gives a ratio slightly in favour of the primary (η = 0.97). The corresponding (half) opening angles of the CWR can be found using Eq. (3) of Eichler & Usov (1993), giving values between 80° and 90°.
, we find values between 0.97 and 1.76 (using our Table 3 values). Most combinations of wind parameters give a wind momentum ratio that is >1, i.e. the secondary star has the stronger wind. Only the O5I+O4III combination gives a ratio slightly in favour of the primary (η = 0.97). The corresponding (half) opening angles of the CWR can be found using Eq. (3) of Eichler & Usov (1993), giving values between 80° and 90°.
Qualitative constraints on the opening angle can be derived from the VLBA (Very Large Baseline Array) observation presented by Dougherty & Pittard (2006, their Fig. 6). This 3.6 cm observation was taken at phase ~0.6, i.e. close to apastron. The CWR shows a clear bow-shape, curving around an undetected star that is towards the southwest. This star must therefore have the wind with the weaker momentum. At the presumed position of the weak-wind star, the bow-shaped region shows an indentation where flux is missing. At phase 0.6, the stars are separated by ~ 2700 R⊙ (projected on the sky). For the O5I+O3III combination of winds (Table 3), the surfaces of optical depth 1 (at 3.6 cm) nearly touch, and one can therefore expect some, but not all, of the non-thermal radio flux to be absorbed. The VLBA observation therefore seems to favour an unequal-strength wind scenario. In Cyg OB2 #9, a complication arises because the radius where optical depth is 1 (Table 3) is comparable to the separation between the two components. In such a case, absorption by the wind in front can create bow-shaped emission that is purely an absorption effect and which does not relate to the opening angle of the CWR (e.g., Dougherty et al. 2003, their Fig. 11). It is therefore difficult to use the VLBA opening angle to constrain the momentum ratio of the two stars. Furthermore, even in an unequal-wind scenario, it is not possible to conclude from the VLBA data if it is the primary or the secondary that has the weaker wind.
5.2. Free-free contribution colliding-wind region
Since the wind-wind collision is adiabatic through the majority of the orbit (Paper I), the compressed material in the CWR will be at a high temperature. It will therefore also contribute to the free-free emission (Pittard 2010). Observationally, the high value for the spectral index after periastron passage also suggests a thermal (free-free) contribution. The high temperature of the colliding-wind material is furthermore attested by the presence of X-ray emission (Paper I).
To estimate the free-free emission of the CWR we used the model from Sect. 4. For the mass-loss rate and terminal velocity we used the O5I+O3III combination from Table 3 because this has the largest wind contribution to the radio flux. The size of the CWR is limited to a radius that is three times the separation between the two components. We also assigned a thickness of 400 R⊙ to the CWR. This value was chosen since it is a significant fraction of the separation between the two components at periastron (which is ~500 R⊙).
Free-free flux and spectral index of the simple CWR model (no synchrotron emission).
In Table 4, we report the range of flux values found over the phase − 0.2 to + 0.2. We explore a number of values for the temperature of the CWR (TCWR). As a reference, we also list the value for “no CWR”: in that model we have a contact discontinuity, where the material from both winds collides, but the CWR thickness is set to 0. The values listed for the “no CWR” model are only about half of those estimated for the thermal contribution of both stars in Table 3. This is because for each star, all material on the other side of the contact discontinuity is missing, which is roughly half of the material (see Sect. 5.1).
Table 4 shows there is indeed some additional flux due to the CWR, which could influence our interpretation of the Cyg OB2 #9 observations in the low-flux regime. We do need very high temperatures (TCWR = 2 × 107 K) over an extended region to have some detectable influence. This temperature is compatible with what is needed to explain the X-ray observations (Paper I). Because the CWR is adiabatic for most of the orbit, such a high temperature could persist out to large distances from the CWR apex. At periastron the shocks may become radiative (Paper I), so the thermal contribution would be less.
At later orbital phases, material with a similar temperature will be present. Its density will be lower, however. due to the larger separation between the two stars. This will result in a smaller thermal contribution. Observationally, this contribution will furthermore be difficult to disentangle from the much higher non-thermal contribution.
The spectral indexes listed in Table 4 are all higher than the + 0.6 nominal value. This is in part a numerical effect of our simulation: the grid we used covers the 6 cm emitting region well, but is not large enough to cover the full extent of the 20 cm emitting region, and this leads to an artificially high spectral index. The relative differences are significant, however, with a higher temperature leading to a higher spectral index. In a single-star wind, the apparent size increases with wavelength, leading to the + 0.6 spectral index. For our model, we have a fixed size for the CWR, so the spectral index tends towards the + 2.0 value intrinsic to thermal emission (Planck curve). This high spectral index is in qualitative agreement with the post-periastron observations.
In summary, a significant contribution of the thermal free-free emission from the CWR is therefore likely in the low-flux regime around periastron.
5.3. Non-thermal emission
The previous sections have shown that the free-free contribution from both winds, together with free-free emission from the CWR, can explain at least part of the Cyg OB2 #9 flux, while it is in the low-flux regime. The high-flux regime corresponds to a spectral index of 0.2–0.4 (Fig. 2), which is more indicative of non-thermal emission. Indeed, for most of the orbit, Cyg OB2 #9 shows flux values that are nearly independent of wavelength, indicating a flat spectral index (van Loo et al. 2008).
The observed spectral index is still larger than the intrinsic one for non-thermal radiation due to a strong shock, which is expected to be − 0.5. A number of effects can change this value. Weaker shocks would give a more negative index, and therefore cannot explain the present observations. Including the Razin effect can substantially change the spectral index. Blomme et al. (2010) showed that for the shorter-period binary Cyg OB2 #8A the Razin effect can change the index to + 2.0, thereby simulating a thermal value. After including free-free absorption, they found an index of ~+1.0 for Cyg OB2 #8A. The combination of intrinsic synchrotron emission with the Razin effect and free-free absorption can therefore result in a wide range for the spectral index. That the observed values of the spectral index in the high-flux pre-periastron phase are higher than − 0.5 therefore does not contradict non-thermal emission.
There are two phases in the orbit where the projected distance between the two stars shows a local minimum. One is at phase 0.96, which coincides with the strong drop in flux (at phase 0.934–0.955). At this phase, the secondary is closer to us. Because of the high eccentricity of the binary, this situation reverses relatively quickly. At phase 0.03, the projected distance again has a local minimum, but this time the primary is closer to us.
In Sect. 5.1 we found that it was most likely that the primary has the weaker wind, so the synchrotron emission from the CWR should be absorbed less when the primary is in front (i.e. phase 0.03). As this is contradicted by the observations we propose here that the secondary has the weaker wind. This more easily explains the observed radio light curve around periastron: at phase 0.96, the weaker-wind secondary is in front of the CWR and blocks some, but not all, of the synchrotron emission. At phase 0.03, the stronger-wind primary is in front and absorbs more of the synchrotron emission than the secondary did at phase 0.96.
While this seems to contradict the results of Sect. 5.1. we should consider the fact that the relation between spectral type–luminosity class on the one hand and atmospheric parameters on the other hand, is not unique. This is clearly shown by Weidner & Vink (2010), who define spectral-type boxes. These are regions in the Hertzsprung-Russell diagram corresponding to a given spectral subtype and luminosity class. Each spectral-type box has a range in luminosity and effective temperature. From stellar evolution models they also assign a range of masses to such a box. The ranges for the astrophysical parameters are considerably wider than those we list in Table 3 (e.g. for an O5–5.5 I star, log Lbol/L⊙ = 5.85−6.26, while our range is only 5.82−5.87). If we use this wider range to determine the mass-loss rates and terminal velocities, we find wind momentum ratios η = 0.25−1.29. A primary with the stronger wind is therefore likely.
To check in a more quantitative way the hypothesis that a stronger-wind primary can explain the observed radio light curve better, we use a model. A full model would need to include many details, such as the magnetic field, shock strength, and acceleration efficiency, and it would need to track the electrons as they move away from the shock (Pittard et al. 2006; Blomme et al. 2010). We postpone such a detailed model to a subsequent paper (Parkin et al., in prep.). Instead we use the simple model from Sect. 4. We assign two temperatures to the CWR. One is used to represent the hot, non-relativistic material in the CWR, the other one is the brightness temperature that represents the synchrotron emission.
 |
Fig. 4 Comparison between the simple CWR model that includes synchrotron emission (solid line) and the observed Cyg OB2 #9 EVLA fluxes (symbols as in Fig. 2). The model has a strong-wind primary (Ṁ = 1.0 × 10-5 M⊙ yr-1) and a weak-wind secondary (Ṁ = 5.0 × 10-6 M⊙ yr-1). Both stars have ν∞ = 2000 km s-1. |
Since it is not the intention of this paper to present a detailed model we explore only a small part of the parameter range. In Fig. 4 we show a model that presents an acceptable fit to the 6 cm data. It is based on a strong-wind primary (Ṁ = 1.0 × 10-5 M⊙ yr-1) and a weak secondary (Ṁ = 5.0 × 10-6 M⊙ yr-1). These mass-loss rates are roughly the averages from the Weidner & Vink (2010) calibration. Both stars have ν∞ = 2000 km s-1. The size of the CWR is limited to 2 × the separation between the components and its thickness is 200 R⊙. The wind temperature is 20 000 K, the CWR temperature is 106 K, and the brightness temperature of the synchrotron emitting CWR is 4.0 × 108 K. We calculated the resulting flux for the orbital phases covering the range − 0.2 to + 0.2 and plot them on top of the observed Cyg OB2 #9 EVLA fluxes in Fig. 4.
Our simple model is able to reproduce the main features of the observed radio light curve: the asymmetry between pre- and post-periastron behaviour, the strong drop in flux around phase 0.955, the nearly thermal fluxes around periastron, and the slow flux rise after periastron. The asymmetry between pre- and post-periastron behaviour and the slow rise after periastron are direct consequences of our assumption that the primary has the stronger wind. (We cannot reproduce the observed asymmetry in the reverse situation.) The model does have difficulty explaining the more detailed features of the radio light curve. The drop in the flux around phase 0.955 is not as sharp as observed, and the rise in flux after periastron is slower than observed (and later becomes faster than the older VLA observations indicate). We surmise that these are a consequence of the many simplifications in the model. One relevant effect is our neglect of the Coriolis force (Parkin & Pittard 2008). Including this will change the shape of the CWR, which could result in a sharper pre-periastron flux drop and a slower post-periastron flux rise.
We did not attempt to model the 20 cm fluxes or the spectral index. The model has no intrinsic calculation of the synchrotron flux or its spectral index. Since we can easily change many parameters (brightness temperature, CWR size and thickness) to get an acceptable 20 cm light curve, no additional information about the colliding-wind region could be derived from our modelling of the 20 cm fluxes.
6. Conclusions
As part of a multi-wavelength campaign on the 2011 periastron passage of Cyg OB2 #9, we obtained new 6 cm and 20 cm radio observations for this highly eccentric massive O-star binary. They show high non-thermal radio fluxes, attributed to synchrotron radiation emitted by the colliding-wind region in the pre-periastron phase. As the system approaches periastron, the fluxes drop sharply to levels of free-free emission from only the stellar winds. The fluxes then rise again after periastron passage. These new data agree very well with the larger set of VLA data presented by van Loo et al. (2008). The combination of both datasets covers 13 orbits of this system, allowing an accurate determination of the period (P = 860.0 ± 3.7 days).
Based on the spectral types of both components, and using theoretical calibrations (Martins et al. 2005; Vink et al. 2001) one would expect the secondary to have the stronger wind (i.e. the higher wind momentum, Ṁν∞). The calibration of Weidner & Vink (2010), however, allows for a wider range of momentum ratios, including those with a stronger-wind primary. Using a simple model for the synchrotron emission of the CWR, we show that a stronger-wind primary can indeed explain the main features of the observed radio light curve: the asymmetry between the pre- and post-periastron behaviour, the strong drop in flux around phase 0.955, the nearly thermal fluxes around periastron, and the slow flux rise after periastron. Additionally, it is likely that the radio fluxes contain some free-free contribution from the hot and compressed material in the colliding-wind region. This free-free contribution may be important especially in the low-flux regime around periastron passage.
The simple model presented here already allows some constraints to be put on the parameters of this system. Future, more sophisticated, modelling will also include optical, X-ray, and interferometric information. It will thus provide much better constraints and considerably improve our understanding of colliding winds in massive star binaries.
Online material
 |
Fig. 1 Radio images of Cyg OB2 #9. For each of the 11 observations, we show the C-band (6 cm) image at the top, and the L-band image (20 cm) at the bottom. The observation date is shown in each title. Each image shows a small region centred on Cyg OB2 #9. The contour levels are listed at the top of each figure. They are shown as solid/dashed lines for positive/negative values. The levels were chosen so that the lowest positive level is at about 2 × the root-mean-square (rms) level. The highest level is below the peak flux value of Cyg OB2 #9. The synthesized beam is shown by the filled ellipse in the bottom left corner of each figure. The size of the image can be different for different figures (due to the changing configuration of the EVLA). |
Acknowledgments
We are grateful for the help we received from the NRAO staff during the “Data Reduction Workshop Socorro Spring 2012”, where we learned to apply CASA to our EVLA data. We thank J. Vandekerckhove for his help with the reduction of the EVLA data and G. Rauw for comments on an earlier version of the paper. We thank the referee for his/her comments and for pointing out the Weidner & Vink paper. D. Volpi acknowledges funding by the Belgian Federal Science Policy Office (Belspo), under contract MO/33/024. The Liège team acknowledges support from the European Community’s Seventh Framework Programme (FP7/2007-2013) under grant agreement number RG226604 (OPTICON), the Fonds National de la Recherche Scientifique (Belgium), the Communauté Française de Belgique, and the PRODEX XMM and Integral contracts. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France, and NASA’s Astrophysics Data System Abstract Service.
References
- Abbott, D. C., Bieging, J. H., & Churchwell, E. 1984, ApJ, 280, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatnagar, S., Cornwell, T. J., Golap, K., & Uson, J. M. 2008, A&A, 487, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bieging, J. H., Abbott, D. C., & Churchwell, E. B. 1989, ApJ, 340, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Blomme, R. 2011, BSRSL, 80, 67 [Google Scholar]
- Blomme, R., De Becker, M., Volpi, D., & Rauw, G. 2010, A&A, 519, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbel, S., Dubus, G., Tomsick, J. A., et al. 2012, MNRAS, 421, 2947 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M. 2007, A&ARv, 14, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Dougherty, S. M., & Pittard, J. M. 2006, in Proc. 8th European VLBI Network Symp., 49 [Google Scholar]
- Dougherty, S. M., Pittard, J. M., Kasian, L., et al. 2003, A&A, 409, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougherty, S. M., & Williams, P. M. 2000, MNRAS, 319, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Dworetsky, M. M. 1983, MNRAS, 203, 917 [NASA ADS] [Google Scholar]
- Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., De Becker, M., Rauw, G., & Barbieri, C. 2008, A&A, 483, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazé, Y., Damerdji, Y., Rauw, G., et al. 2010, ApJ, 719, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Nazé, Y., Mahy, L., Damerdji, Y., et al. 2012, A&A, 546, A37 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parkin, E. R., & Pittard, J. M. 2008, MNRAS, 388, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., Chandler, C. J., Butler, B. J., & Wrobel, J. M. 2011, ApJ, 739, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, R. B., & Titus, M. A. 1990, ApJ, 359, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M. 2010, MNRAS, 403, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. 2011, BSRSL, 80, 555 [Google Scholar]
- Pittard, J. M., & Parkin, E. R. 2010, MNRAS, 403, 1657 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M., Dougherty, S. M., Coker, R. F., O’Connor, E., & Bolingbroke, N. J. 2006, A&A, 446, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G. 2011, A&A, 536, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G., Crowther, P. A., De Becker, M., et al. 2005, A&A, 432, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- van Loo, S., Runacres, M. C., & Blomme, R. 2004, A&A, 418, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loo, S., Runacres, M. C., & Blomme, R. 2005, A&A, 433, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loo, S., Runacres, M. C., & Blomme, R. 2006, A&A, 452, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Loo, S., Blomme, R., Dougherty, S. M., & Runacres, M. C. 2008, A&A, 483, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weidner, C., & Vink, J. S. 2010, A&A, 524, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. L. 1985, ApJ, 289, 698 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L., & Becker, R. H. 1983, ApJ, 272, L19 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L., & Becker, R. H. 1995, ApJ, 451, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. M., van der Hucht, K. A., Pollock, A. M. T., et al. 1990, MNRAS, 243, 662 [NASA ADS] [Google Scholar]
- Wright, A. E., & Barlow, M. J. 1975, MNRAS, 170, 41 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Free-free flux and spectral index of the simple CWR model (no synchrotron emission).
All Figures
 |
Fig. 2 Radio fluxes and spectral indexes around the periastron passage of Cyg OB2 #9, as a function of orbital phase. The top figure shows the 6 cm flux, the middle one the 20 cm flux, and the bottom one the spectral index. The older VLA data from van Loo et al. (2008) are plotted with a grey line. The new EVLA data are shown with the thicker solid red line. The length of the line indicates the 1σ error bar on the flux. For the non-detections, upper limits are shown that are 3 × the rms noise in the centre of the image. The fluxes have an additional uncertainty of ~5% due to the absolute flux calibration (not shown on the figure). On the spectral index figure, the dashed line indicates the value for free-free emission (α = + 0.6). Periastron occurs at phase = 0.0. |
| In the text | |
 |
Fig. 3 Schematic view of our model for the CWR. The shape of the CWR (shaded in light-blue) is a cone that is rotationally symmetric around the axis connecting the two stars. It has a (half) opening angle θ. |
| In the text | |
 |
Fig. 4 Comparison between the simple CWR model that includes synchrotron emission (solid line) and the observed Cyg OB2 #9 EVLA fluxes (symbols as in Fig. 2). The model has a strong-wind primary (Ṁ = 1.0 × 10-5 M⊙ yr-1) and a weak-wind secondary (Ṁ = 5.0 × 10-6 M⊙ yr-1). Both stars have ν∞ = 2000 km s-1. |
| In the text | |
 |
Fig. 1 Radio images of Cyg OB2 #9. For each of the 11 observations, we show the C-band (6 cm) image at the top, and the L-band image (20 cm) at the bottom. The observation date is shown in each title. Each image shows a small region centred on Cyg OB2 #9. The contour levels are listed at the top of each figure. They are shown as solid/dashed lines for positive/negative values. The levels were chosen so that the lowest positive level is at about 2 × the root-mean-square (rms) level. The highest level is below the peak flux value of Cyg OB2 #9. The synthesized beam is shown by the filled ellipse in the bottom left corner of each figure. The size of the image can be different for different figures (due to the changing configuration of the EVLA). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


