| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220316 | |
| Published online | 04 February 2013 | |
Variable pulse profiles of Hercules X-1 repeating with the same irregular 35 d clock as the turn-ons⋆
1 Institut für Astronomie und Astrophysik, Universität Tübingen, Sand 1, 72076 Tübingen, Germany
e-mail: staubert@astro.uni-tuebingen.de
2 Sternberg Astronomical Institute, 13 Universitetskii pr., 119992 Moscow, Russia
3 Dr. Remeis-Sternwarte, Astronomisches Institut der Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
4 Center for Astrophysics and Space Sciences, University of California at San Diego, La Jolla, CA 92093-0424, USA
Received: 31 August 2012
Accepted: 5 December 2012
The accreting X-ray pulsar Her X-1 shows two types of long-term variations, both with periods of ~35 days: 1) turn-on cycles, a modulation of the flux, with a ten-day long main-on and a five-day long short-on, separated by two off-states, and 2) a systematic variation in the shape of the 1.24 s pulse profile. While there is general consensus that the flux modulation is due to variable shading of the X-ray emitting regions on the surface of the neutron star by the precessing accretion disk, the physical reason for the variation in the pulse profiles has remained controversial. Following the suggestion that free precession of the neutron star may be responsible for the variation in the pulse profiles, we developed a physical model of strong feedback interaction between the neutron star and the accretion disk in order to explain the seemingly identical values for the periods of the two types of variations, which were found to be in basic synchronization. In a deep analysis of pulse profiles observed by several different satellites over the last three decades we now find that the clock behind the pulse profile variations shows exactly the same erratic behavior as the turn-on clock, even on short time scales (a few 35 d cycles), suggesting that there may in fact be only one 35 d clock in the system. If this is true, it raises serious questions with respect to the idea of free precession of the neutron star, namely how the neutron star can change its precessional period every few years by up to 2.5% and how the feedback can be so strong, such that these changes can be transmitted to the accretion disk on rather short time scales.
Key words: binaries: general / stars: individual: Her X-1 / X-rays: binaries / X-rays: stars / pulsars: general
A matrix representing the pulse profile template is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/550/A110
© ESO, 2013
1. Introduction
The binary X-ray pulsar Her X-1 shows a number of periodic modulations of its X-ray flux: the 1.24 s pulse period, the 1.70 d orbital period (through eclipses and the Doppler modulation of the pulse period), a 1.62 d dip period, and a 35 d super-orbital period. The last period is observed first through an on-off cycle with a 10 d main-on and a 5 d short-on (Fig. 1), separated by two 10 d off-states (Tananbaum et al. 1972), and second through a reproduced change in the shape of the 1.24 s pulse profile (Trümper et al. 1986; Deeter et al. 1998; Scott et al. 2000). With respect to these modulations, Staubert et al. (2009) argued that there may be two ~35 d clocks in the system which are generally synchronized by strong feedback.
The 35-day modulation of the X-ray flux is generally explained by the precession of the accretion disk, which quasi-regularly blocks the line of sight to the X-ray emitting regions near the magnetic poles of the neutron star (Gerend & Boynton 1976; Schandl & Meyer 1994). The resulting clock, however, is irregular, showing deviations from regularity of up to ± 10 d. This is generally demonstrated by the (O–C) (observed-minus-calculated) diagram (see Fig. 2), plotting the difference between the observed turn-ons and the calculated turn-ons, under the assumption of a constant period (e.g. 20.5 × P1.7 = 34.850 d; see Staubert et al. 1983; Still & Boyd 2004; Staubert et al. 2007). This diagram has very interesting properties that warrant further attention: 1) a quasi-periodic modulation with a period of ~5 yr, corresponding to a repeated change in the mean precessional period by a few percent, 2) an apparent correlation with the appearance of the anomalous lows, which are thought to be episodes of low tilt (Staubert et al. 2006) or higher twist (Leahy & Dupuis 2010) of the accretion disk leading to a blocking of the line of sight to the X-ray source for some period of time (ranging from a few days to a few years); 3) a possible long-term modulation with ~15.5 yr (Staubert et al. 2011); 4) substructure with a quasi-periodicity of ~2.5 yrs in the UHURU era; 5) a correlation with the X-ray luminosity (Klochkov et al. 2009); and most remarkably; 6) an intriguing correlation with the history of the pulse-period evolution (Staubert et al. 2006). The last two properties require strong physical coupling between the precession of the outer edge of the accretion disk and the accretion torques acting on the neutron star when the material at the inner edge of the accretion disk interacts with the magnetosphere of the neutron star. These facts lend important support for the feedback scenario described in Staubert et al. (2009).
 |
Fig. 1 Average 35 d flux profile of Her X-1, generated by accumulating light curves observed by RXTE/ASM for 35 d turn-ons around binary phase 0.2 (Fig. 3 of Klochkov et al. 2006). The vertical lines indicate the binary eclipses. |
With regard to the systematic variation in shape of the X-ray pulse profiles, the situation is considerably less clear. Trümper et al. (1986; based on observations of Her X-1 by EXOSAT) had proposed that free precession may be the reason for the changing pulse profiles: due to the variation in the angle of the line of sight with respect to the beamed emission from the surface of the spinning neutron star.
Free precession may appear as a fundamental physical property of rigid non-spherical spinning bodies. The simplest case is a spheroid with some small oblateness (a “two-axial” body) in which the axis of angular velocity is not aligned with any principle axis of inertia (e.g., Sommerfeld & Klein 1897). It has been suggested as the underlying reason for the long-period variations, both in timing and spectral properties, observed in several neutron stars (Jones & Andersson 2001; Cutler et al. 2003; Link & Epstein 2001; Haberl et al. 2006). The candidate objects are mostly radio pulsars (including the Crab and Vela pulsars), the isolated X-ray pulsar RXJ0720.4 − 3125 (Haberl et al. 2006) and the accreting binary X-ray pulsar Her X-1. The existence of free precession in neutron stars and its consequences for our understanding of the physics of the interior of neutron stars is extensively discussed in the literature (Anderson & Itoh 1975; Shaham 1977; Alpar & Ögelman 1987; Sedrakian et al. 1999; Wasserman 2003; Levin & D’Angelo 2004; Link 2007). Recently, Link (2007) has emphasized that the question of the reality of free precession in neutron stars has strong implications for our understanding of the properties of matter at supra-nuclear densities.
The idea of free precession in Her X-1 has been taken up by several authors (e.g. Shakura et al. 1998; Ketsaris et al. 2000; Postnov 2004; Staubert et al. 2007; Postnov et al. 2012). Recently, Postnov et al. (2012) have successfully modeled 9–13 keV pulse profiles observed by RXTE under a particular set of assumptions. However, the idea has also been questioned on various grounds (e.g., Bisnovatyi-Kogan et al. 1989; Soong et al. 1987; Scott et al. 2000; Staubert et al. 2010b) and alternative models for the generation of variable pulse profiles, mostly involving the inner edge of the accretion disk and/or the accretion column have been proposed (e.g. Petterson et al. 1991; Scott et al. 2000; Leahy 2004).
Here we present the results of a model independent study of the variation in pulse profiles in comparison to the variation in the 35 d flux modulation. We find, that the two ways to count 35 d cycles – observing the turn-ons and observing the change in pulse profile shape – track each other perfectly, following one and the same irregular clock. First results of this study were presented by Staubert et al. (2010b). It appears, that we cannot talk about two different clocks anymore, but we have to conclude that there is really only one clock in the system. This result shines new light onto the question of how the pulse profiles are generated and what the consequences are for the concept of neutron star free precession in Her X-1.
 |
Fig. 2 Turn-on history of Her X-1: the (O–C) diagram (using 20.5 × Porb as the period to calculate the expected turn-ons). Upper: the anomalous low around MJD 51 500 (AL3) is assumed to last for eighteen 35 d cycles. Lower: the same assuming that there were only seventeen 35 d cycles (see Staubert et al. 2009). The solid line represents the linear best fit to all data, defining a mean period of 34.98 d (which may be used for a rough ephemeris of turn-ons). |
 |
Fig. 3 Representation of the template which describes main-on pulse profiles of Her X-1 in the 9–13 keV range as function of 35 d phase. Left: pulse profiles for every 0.02 in 35 d phase. Right: 3D pulse representation for the 35 d phase range 0.00 to 0.24. The resolution is 128 bins in pulse phase and 48 bins in 35 d phase (resolution 0.005). |
2. 35 d flux modulation and turn-on history
The 35 d modulation shows a sharp increase of flux towards the main-on. It is called turn-on, and defines 35 d phase zero; it generally occurs either around binary phases 0.2 or 0.7 (Giacconi et al. 1973; Levine & Jernigan 1982; see, however, Leahy & Igna 2010). Figure 1 shows the mean flux profile for phase 0.2 turn-ons as observed by RXTE/ASM (Klochkov et al. 2006). The 35 d turn-on clock is fairly irregular, allowing the length of an individual cycle to be either 20.0 × Porb, 20.5 × Porb, or 21.0 × Porb (Staubert et al. 1983) (with a small fraction of cases showing longer or shorter cycles). Adopting P35 = 20.5 × Porb (=34.85 d) as the mean ephemeris period, the turn-on history can be described by the (O–C) diagram. Figure 2 (upper and lower) shows (O–C) since the discovery of Her X-1 until today as a function of time1. The two versions of the diagram (upper and lower) differ in the number of 35 d cycles assumed to have occurred during the 602 day long anomalous low (AL3), which is centered at ~ MJD 51 500. During this gap, the observed X-ray flux was very low because of the blocking by the low inclination accretion disk (optical observations indicate that X-rays are still generated at the neutron star surface, but not seen by a distant observer). For the interpretation of Fig. 2 we refer to Staubert et al. (2009), in the following called the “Two-clocks paper”. In Fig. 2-upper the gap corresponds to 18 cycles with a (short) mean duration of 19.7 × Porb, which is probably the correct physical interpretation for a continued precession of the accretion disk2. In Fig. 2-lower the gap corresponds to 17 cycles with a (long) mean duration of 20.8 × Porb, which can be associated with a semi-regular, long-term clock with a mean period of 20.58 × Porb = 34.98 d. In the “Two-clocks paper” (Staubert et al. 2009) this period is associated with an underlying clock, viewed to be rather regular, namely (free) precession of the neutron star, assumed to be responsible for the observed periodic variation in the shape of the pulse profiles. In this model, it is assumed, that the precession of the neutron star is the master clock and that the precession of the accretion disk is evidently locked to that of the neutron star by existing strong physical feedback in the system, (nearly) synchronizing the periods of the “two clocks”.
3. Pulse profile variations
In observations of Her X-1 by EXOSAT in 1984, Trümper et al. (1986) discovered that the 1.24 s X-ray pulse profiles vary in shape as a function of the phase of the 35 d flux modulation. Observations by Ginga in 1989 (Scott et al. 2000), by HEAO-1 (Soong et al. 1990) and by RXTE starting in 1996 (Staubert et al. 2010a,b), confirmed these findings and added a wealth of detailed information on the combined pulse shape and spectral evolution of the pulsar’s beamed emission. Trümper et al. (1986) had suggested that the systematic variation in pulse shape is due to free precession of the neutron star: the viewing angle towards the X-ray emitting regions of the neutron star varies with the phase of the neutron star precession. Shakura et al. (1998) applied a model of a precessing triaxial shape to pulse profiles of Her X-1 observed by HEAO-1, and Ketsaris et al. (2000) did so for profiles observed by RXTE/PCA. Using all observations by RXTE from 1996 until 2005 we have verified that the shape of the pulse profiles is reproduced every ~35 days. A careful timing analysis was performed of all archived RXTE data on Her X-1 and pulse profiles were generated by folding with the measured pulse periods. Fig. 3 shows two representations of the final template: left: a set of pulse profiles for 35 d phases 0.02 to 0.26 (every 0.02), and right: a 3D-plot for 35 d phases 0.02 to 0.24 with a resolution of 0.005 (the resolution in pulse phase is 128 bins for 0.0 to 1.0). The variation in pulse shape is evident, most pronounced is the gradual disappearance of the left shoulder of the main peak. This systematic analysis had led to the development of the “Two-Clocks-Model” (Staubert et al. 2009) and the successful modeling of the observed pulse profiles by a model of point- and ring-like emission from the polar caps of a neutron star with an offset-dipole field under the assumption of free neutron star precession (Postnov 2004; Postnov et al. 2012).
Staubert et al. (2010b) presented a model-independent investigation of the periodic pulse profile variations based upon constructing a template of those variations for the Her X-1 main-on for photon energies 9–13 keV. A set of observations was selected, providing good coverage of the 35 d phase range –0.05 to 0.15. This template contained flux normalized pulse profiles for every 0.01 in phase. Any 9–13 keV pulse profile observed during a main-on could then be compared to this template and the 35 d phase be determined (by 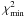 minimization). For the RXTE data, we found that this is generally possible to an accuracy of ± 0.02 in phase. First results of using this template with profiles observed by Ginga, RXTE and INTEGRAL were presented by Staubert et al. (2010a,c), showing that the turn-on history and the history of variations in pulse profiles appeared to be strictly parallel, implying that the neutron star precession (if it is indeed the reason behind the pulse profile variations) is synchronized to the precession of the accretion disk. This raised the important question about how the neutron star would be able to significantly change its precessional period every few years by up to 2.5% and how such changes are relayed to the accretion disk on rather short time scales.
minimization). For the RXTE data, we found that this is generally possible to an accuracy of ± 0.02 in phase. First results of using this template with profiles observed by Ginga, RXTE and INTEGRAL were presented by Staubert et al. (2010a,c), showing that the turn-on history and the history of variations in pulse profiles appeared to be strictly parallel, implying that the neutron star precession (if it is indeed the reason behind the pulse profile variations) is synchronized to the precession of the accretion disk. This raised the important question about how the neutron star would be able to significantly change its precessional period every few years by up to 2.5% and how such changes are relayed to the accretion disk on rather short time scales.
We have since refined this method by constructing an extended template from RXTE/PCA observations of two 35 d cycles, namely cycles no. 313 (Dec. 2001) and no. 323 (Nov. 2002). Together, the data from the observation of these two cycles provide a very well sampled coverage of a complete main-on in the 35 d phase range 0.00 to 0.24 (Fig. A.1). The details of the construction of this template and its exact definition are given in the Appendix. An earlier version of the template (with less resolution) is described in Staubert et al. (2010b). A 3D-representation of the new template (being a matrix of 128 bins in pulse phase by 121 bins in 35 d phase) is given in Fig. 3-right.
Details of RXTE observations of Her X-1 used for the pulse profile analysis.
 |
Fig. 4 Example for finding “pulse profile phase-zero” for the case of cycle 257 main-on, as observed by RXTE/PCA in July 1996. |
4. Results
We compare the characteristics of the two 35 d modulations (of the flux and of the variation in pulse profiles) by plotting both into an (O–C) diagram (Fig. 5). The underlying data are summarized in Table 1, together with the 35 d cycle number and the satellite which performed the corresponding main-on observations of Her X-1.
For the flux modulation, we use the turn-on, also called the “accretion disk phase-zero” and plot the (O–C) as in Fig. 2. Correspondingly, we determine a “pulse profile phase-zero” for all the main-ons for which there is at least one observed pulse profile (for most main-ons there are several profiles). The “pulse profile phase-zero” is defined and calibrated using those cycles which are used to construct the template: for cycles 313 and 323 both types of “phase-zero” are identical (by definition). For any other cycle “pulse profile phase-zero” is found by determining the 35 d phases of all available pulse profiles by comparison with the template and a subsequent linear extrapolation to phase zero. Figure 4 shows an example for the linear extrapolation to find phase zero. For these extrapolations, we use values of the 35 d period which are correct for the time of observation, based on fitting sections of the (O–C) diagram by linear functions, as described in Staubert et al. (2011): to a fairly good approximation, sections (of variable length) can be modeled by a respective constant period. Similar attempts of straight line fittings can be found in Still & Boyd 2004; Jurua et al. 2011. The typical change in the precession period from section to section is on the order of 1.5%. At the re-appearance of Her X-1 after the anomalous low in 1999/2000 (AL3), the precession continued with a rather short period until around MJD 52 000 (see Fig. 5), at which time a rapid increase by 2.5% occurred, on a time scale comparable to two 35 d cycles. We note that within the entire (O–C) data base, the largest change (of ~4%) is found in the early data from UHURU, comparing the initial upward trend in (O–C) to the following downward trend (see Fig. 2).
Using pulse profiles of ten other main-on cycles of Her X-1 observed by RXTE over the last three decades, plus one from Ginga, one from Beppo/SAX, two from Suzaku and one from INTEGRAL, we find that these systematic variations are very stable and reproducible. The constructed template therefore allows one to determine the 35 d phase for any observed main-on pulse profile in the 9–13 keV range.
 |
Fig. 5 (O–C) values in units of days for observed turn-ons (green) and for so far generated “pulse profile phase-zero” values from pulse profile fitting (magenta), using profiles 9–13 keV profiles for several main-ons. The majority of the “pulse profile phase-zero” values are from observations by RXTE. The values based on observations by Ginga, Beppo/SAX, Suzaku and INTEGRAL are marked individually. |
The observational result in the form of an (O–C) diagram is summarized in Fig. 5. The small green points (connected by the solid green line) represent the observed turn-on times (equal to “accretion disk phase-zero”). The magenta points are the times of “pulse profile phase-zero” as determined from the comparison of observed pulse profiles with the pulse profile template and subsequent extrapolation to phase zero. For these cycles the corresponding green points (turn-ons) are enlarged and shown with uncertainties. The observational evidence is clear: within statistical uncertainties, the values for phase-zero as determined by the two different methods are identical (see the last column in Table 1, which gives the differences between the two phase-zero values in units of standard deviations). This means: the “pulse profile clock” is just as irregular as the “turn-on clock”. Both clocks appear to be perfectly synchronized.
We emphasize here, that the above result is completely model independent, it is obtained using only observational data. However, the latest results from the continued effort in modeling the observed pulse profiles by a model assuming free precession of the neutron star (Postnov 2004; Postnov et al. 2012) leads to the same conclusion. This does suggest the need to abandon the concept of “two clocks” and to assume the existence of just one underlying clock which controls the variations of both 35 d zero-phases: that of the turn-ons, and that of pulse profile phase zero.
Figure 5 demonstrates that the Turn-On clock is fairly noisy, with additional quasi-periodic variations on a ~ 5 year time scale. (O–C) correlates with the appearance of the anomalous lows, and it also strongly correlates with the neutron star’s spin period (Staubert et al. 2006).
5. Discussion
What does the above result mean for the concept of (free) precession of the neutron star in Her X-1? We distinguish between two assumptions. First, assuming the precession of the neutron star does indeed exist and is responsible for the variation in pulse profiles and (!) for those of the turn-on times, we would then have to find a physical explanation for two phenomena.
-
1.
How can the neutron star change its precessional period everyfew years by a few percent?
-
2.
How does the mechanism of synchronization between the neutron star precession and the accretion disk precession work? Can the feedback in the system really be strong enough to slave the disk, such that it follows on very short time scales (a few 35 d cycles)?
There seem to be no external forces that are strong enough to change the precessional period, e.g. by applying a torque to the principle axis of inertia. The only possible origin could be inside the neutron star, that is, if glitches occur or if the complex physics of the interior of a highly magnetized neutron star with its crust and liquid core did allow for time variable phenomena (see also Trümper et al. 1986 for discussion of possible mechanisms). For the relevance of free precession to our understanding of matter at supra-nuclear densities, see e.g., Link (2007). The period of free precession Ppr of a two-axial symmetric body with moments of inertia I1 = I2 and I3 (the precession takes place around I3) is related to the spin period P by the Euler equation (Sommerfeld & Klein 1897): Ppr = PI3/(ΔI cosΘ), with Θ being the angle between I3 and the total angular momentum. The period of free precession can change when either ΔI or Θ (or both) change. Postnov et al. (2012) argue that ΔI is probably constant, but that a change in Θ by about one degree, caused e.g. by a sudden relaxation of stresses in the neutron star crust, could lead to a change in precessional period by a few percent (assuming Θ is on the order 50 degree for Her X-1).
Equally challenging is the explanation of how the neutron star, if it is indeed the one master 35 d clock in the system, would be able to transmit its precessional motion to that of the accretion disk (assuming that our long-term concept is correct, that the turn-ons are due to the precession of the accretion disk). We do indeed see strong feedback in the binary system, which has led Staubert et al. (2009) to assume that the precession of the neutron star may be the master clock in the system, under the assumption, however, that the neutron star clock would be rather stable and that the accretion disk would have “a life of its own” providing the freedom to deviate from the strict clocking of the master - as observed in the turn-on history. We now see, that the turn-ons and the pulse profiles vary in strict synchronization, requiring extremely strong feedback. Again, Postnov et al. (2012) show that – under the geometrical conditions believed to be realized in Her X-1 – a sufficiently strong feedback could exist through the dynamical action of the accretion stream on the accretion disk, such that synchronization is enforced. Certainly, precession of a neutron star in an accreting binary would not really be “free” and quantitative model calculations of the interaction between the accretion disk and the magnetized neutron star are clearly needed.
Second, assuming that there is no neutron star precession, we would associate the precession of the accretion disk with the one 35 d clock observed in this system. The generally accepted interpretation of the 35 d flux modulation is that an inclined/ warped/counter-precessing accretion disk blocks our view to the X-ray source for most of the cycle, leaving two stretches of ~10 d and ~5 d, the main-on and short-on, respectively, with a more or less (short-on) clear view to the X-ray source. The disk structure may be viewed as a continuous series of rings of increasing radius and inclination (from inside out), shifted against one another in azimuth (angle of lines of nodes), constituting the twist or warp. For details of such models and corresponding parameters see e.g. Schandl & Meyer (1994); Wijers & Pringle (1999); Scott et al. (2000); Leahy (2002). It is then natural to assume that the disk is also responsible for the changing pulse profile shape, with the inner edge, precessing with the same period as the outer edge (and all other rings), being the prime candidate. Scott et al. (2000), on the basis of Ginga and early RXTE observations, had proposed such a model in which the changes in the shape and in the spectral appearance of the pulses were qualitatively explained by a combination of occultation of the X-ray emitting regions by the precessing inner edge of the accretion disk and by changes in the accretion geometry by a varying relative orientation between the disk and the neutron star magnetosphere. The model by Scott et al. (2000) requires a very small inner radius of the accretion disk of 20 to 40 neutron star radii, which is incompatible with most estimates of the magnetospheric radius (see e.g. the discussion and references in Scott et al. 2000). The magnetospheric radius is usually calculated assuming a spherically symmetric dipolar magnetic field with a surface strengths of a few times 1012 Gauss (as consistently found from both the observed cyclotron line energy of 40 keV and the interpretation of the observed spin-up/spin-down behavior by standard accretion torque theory, e.g. Ghosh & Lamb 1979; Wang 1987; Perna et al. 2006). In addition, we like to point out that the magnetospheric radius in Her X-1 should not be much smaller than the co-rotation radius, since the source is known to live close to its equilibrium with respect to spin-up/spin-down. The co-rotation radius is near 200 neutron star radii.
For completnes, we mention an earlier model which tries to explain the variation in the pulse profile shape between the main-on and the short-on, as proposed by Petterson et al. (1991): here a portion of the inner edge of the warped, counter-precessing accretion disk, rotating synchronously to the neutron star, is raised out of the plane of the disk due to near vertical magnetic pressure. In this model the change in the pulse profiles results entirely from the disk motion. This is consistent with our observations of the variations throughout the main-on and supports the idea of having only one 35 d clock, namely accretion disk precession. But again, the model is only qualitative. A detailed quantitative model for the generation of variable multi-component pulse profiles by accretion disk/magnetospheric effects is not available so far.
Apart from the details of how the pulse profiles are generated, the following basic questions need to be answered:
-
1.
What causes the initial tilt and warp of the disk and what keeps italive over long time scales? In addition to initial conditions (e.g.the relative orientation of neutron star spin and orbital angularmomentum at birth of the X-ray binary), the existence of internalforces on the accretion disk, like coronal winds (Schandl &Meyer 1994), radiation pressure(Pringle 1996; Wijers &Pringle 1999), or the impact of the accretionstream (Shakura et al. 1999) havebeen proposed to produce and maintain the observedconfiguration.
-
2.
What causes the variation of the period of precession (by a few percent) on time scales from a few years to tens of years? – as apparent from the (O–C) diagram (Fig. 2). The accretion disk is subject to a large number of torques. In addition to the three already mentioned above, (1) coronal wind; 2) radiation pressure; 3) impact of the stream, there are three more: 4) torque due to the interaction of the neutron star magnetosphere with the inner edge of the accretion disk; 5) tidal forces by the binary components; and 5) the internal viscosity of the disk. A careful analysis of the overall balance of these torques is needed. But it is evident, considering the various feedback processes working in the binary, that both, the whole system and the accretion disk, live in a “delicate equilibrium”, which allows for deviations from strict regularity (see the discussion in Staubert et al. 2009). It may even be possible that the observed ~ 5 yr modulation (and its overtones of ~ 10 yr and ~ 15 yr) represent a natural ringing frequency of a system of several coupled physical components (Staubert et al. 2009).
-
3.
Finally, we can ask whether a system described above could be secularly stable. Given that the total time span of the existing data base is short (~40 yrs), the observations can not answer the question. For time scales < 40 yrs the (O–C) diagram (in the form of Fig. 2-lower) suggests that there is a mean precession period which could be stable, and there seems to be a “back-driving force” which brings the (O–C) always back to the center line, possibly representing a long-term period. There is, however, evidence that the accretion disk precession may not be stable, or at least – should a long-term stability indeed exist – there can be temporary deviations from stability. The upper part of Fig. 2 shows a dramatic step in (O–C) around MJD 51 500 (AL3). We believe (see footnote 2 and Staubert et al. 2009) that this is the correct description of the physical behavior of the accretion disk, namely that the precessional period of the accretion disk during AL3 and its immediate vicinity was low. So, over the time of this anomalous low the accretion disk has performed “one extra precessional cycle” as compared to the more regular clock (Fig. 2-lower), which in the “Two-clocks model” of Staubert et al. (2009) is associated with the precession of the neutron star. AL3 is a very special event in the long-term evolution of the system and it is not clear whether the notion that the system found back to the usual (albeit non-perfect) regularity after the AL is an adequate description. A comprehensive study is needed about the question of stability, which is beyond the scope of this contribution. If it turns out that the system can not be stable on long time scales and that an external clock is needed, we would see two possibilities: 1) Either: free precession of the neutron star, as discussed earlier. This would also answer the question of how the disk remains in phase with its 35 d clock during long anomalous lows, where the disk lies in or close to the orbital plane. But one would still have to ask, how the free precession can be stable on long time scales, when it does vary on a time scale of a few years. 2) Or: an intrinsic activity cycle of the optical companion HZ Her, leading to variable mass transfer rates with (quasi) periodic properties (Vrtilek et al. 2001; Still & Jurua 2006; Staubert et al. 2006, 2009).
6. Conclusion
Based on our analysis of the variations in pulse profiles of Her X-1 with 35 d phase, as observed for a large number of main-ons by several X-ray satellites (with RXTE being the primary source of data), we conclude that these variations follow the same irregular clock as the flux turn-ons. There seems to be only one ~35 d clock in the system which is responsible for both, the flux modulation and the variation in pulse profile shape. The two phenomena are perfectly synchronized and follow each other on fairly short time scales.
The important physical question is whether the underlying 35 d clock is free precession of the neutron star which could also be responsible for the pulse profile variations. In this case, it needs to be explained how the neutron star can change its precessional period every few years by a few percent, and how the neutron star can slave the accretion disk so tightly, such that the flux modulation follows immediately. If there is no free precession of the neutron star, and the clock is due to the accretion disk alone, then the two most important questions are how the variations in pulse profile are generated and whether the precession of the accretion disk can be secularly stable without the existence of an outside force.
The turn-on times listed by Leahy & Igna (2010) for a restricted period of time are largely consistent with our values.
Acknowledgments
This paper is based on observational data taken by the NASA satellite Rossi X-ray Timing Explorer (RXTE). We like to acknowledge the dedication of all people who have contributed to the great success of this mission. D.V. thanks DLR for financial support through grant 50 OR 0702, and D.K. acknowledges support by the Carl Zeiss Stiftung. We thank the anonymous referee for very valuable comments.
References
- Alpar, A., & Ögelman, H. 1987, A&A, 185, 196 [NASA ADS] [Google Scholar]
- Anderson, P. W., & Itoh, N. 1975, Nature, 256, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., Mersov, G. A., & Sheffer, E. K. 1989, A&A, 221, L7 [NASA ADS] [Google Scholar]
- Cutler, C., Ushomirsky, G., & Linj, B. 2003, ApJ, 588, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Deeter, J. E., Scott, D. M., Boynton, P. E., et al. 1998, ApJ, 502, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Gerend, D., & Boynton, P. E. 1976, ApJ, 209, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Giacconi, R., Gursky, H., Kellogg, E., et al. 1973, ApJ, 184, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., Turolla, R., de Vries, C. P., et al. 2006, A&A, 451, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, D. I., & Andersson, N. 2001, MNRAS, 324, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Jurua, E., Still, M., Meintjes, P. J., Charles, P. A., & Anguma, S. K. 2011, in IAU Symp. 277, eds. C. Carignan, F. Combes, & K. C. Freeman, 325 [Google Scholar]
- Ketsaris, N. A., Kuster, M., Postnov, K., et al. 2000, in Proc. Int. Workshop Hot Points in Astrophysics, JINR, Dubna, ed. V. Belyaev, 192 [arXiv:astro-ph/0010035] [Google Scholar]
- Klochkov, D. K., Shakura, N. I., Postnov, K. A., et al. 2006, Astron. Lett., 32, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Klochkov, D., Staubert, R., Postnov, K., Shakura, N., & Santangelo, A. 2009, A&A, 506, 1261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leahy, D. A. 2002, MNRAS, 334, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A. 2004, ApJ, 613, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., & Dupuis, J. 2010, ApJ, 715, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., & Igna, C. D. 2010, ApJ, 713, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Levin, Y., & D’Angelo, C. 2004, ApJ, 613, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, A. M., & Jernigan, J. G. 1982, ApJ, 262, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B. 2007, Ap&SS, 308, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Link, B., & Epstein, R. I. 2001, ApJ, 556, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Perna, R., Bozzo, E., & Stella, L. 2006, ApJ, 639, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Petterson, J. A., Rothschild, R. E., & Gruber, D. E. 1991, ApJ, 378, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Postnov, K. A. 2004, in Topics in X-ray Astronomy, http://astro.uni-tuebingen.de/staubert65/talks/postnov.pdf [Google Scholar]
- Postnov, K. A., Shakura, N. I., Kochetkova, A., Staubert, R., & Klochkov, D. 2012, MNRAS, submitted [Google Scholar]
- Pringle, J. E. 1996, MNRAS, 281, 357 [NASA ADS] [Google Scholar]
- Schandl, S., & Meyer, F. 1994, A&A, 289, 149 [NASA ADS] [Google Scholar]
- Scott, D. M., Leahy, D. A., & Wilson, R. B. 2000, ApJ, 539, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Sedrakian, A., Wasserman, I., & Cordes, J. M. 1999, ApJ, 524, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Shaham, J. 1977, ApJ, 214, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., Ketsaris, N. A., Prokhorov, M. E., & Postnov, K. A. 1998, MNRAS, 300, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., Prokhorov, M. E., Postnov, K. A., & Ketsaris, N. A. 1999, A&A, 348, 917 [NASA ADS] [Google Scholar]
- Sommerfeld, A., & Klein, F. 1897, Theorie des Kreisels (Dresden: Teubner-Verlag, 1897-1910) [Google Scholar]
- Soong, Y., Gruber, D. E., & Rothschild, R. E. 1987, ApJ, 319, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Soong, Y., Gruber, D. E., Peterson, L. E., & Rothschild, R. E. 1990, ApJ, 348, 634 [NASA ADS] [CrossRef] [Google Scholar]
- Staubert, R., Bezler, M., & Kendziorra, E. 1983, A&A, 117, 215 [NASA ADS] [Google Scholar]
- Staubert, R., Schandl, S., Klochkov, D., et al. 2006, in The Transient Milky Way: A Perspective for MIRAX, eds. J. Braga, F. D’Amico, & R. E. Rothschild, Am. Inst. Phys. Conf. Ser., 840, 65 [Google Scholar]
- Staubert, R., Shakura, N. I., Postnov, K., et al. 2007, A&A, 465, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staubert, R., Klochkov, D., Postnov, K., et al. 2009, A&A, 494, 1025 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staubert, R., Klochkov, D., Postnov, K., et al. 2010a, X-ray Astronomy 2009; Present Status, Multi-Wavelength Approach and Future Perspectives, 1248, 209 [Google Scholar]
- Staubert, R., Klochkov, D., Vasco, D., & Wilms, J. 2010b, in Proc. of the 8th INTEGRAL Workshop, The Restless Gamma-ray Universe, PoS(INTEGRAL 2010)048 [Google Scholar]
- Staubert, R., Klochkov, D., Vasco, D., & Wilms, J. 2010c, in Proc. of the 8th INTEGRAL Workshop, The Restless Gamma-ray Universe, PoS(INTEGRAL 2010)141 [Google Scholar]
- Staubert, R., Klochkov, D., Vasco, D., et al. 2011, in http://astro.ioffe.ru/NS2011 [Google Scholar]
- Still, M., & Boyd, P. 2004, ApJ, 606, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Still, M., & Jurua, E. 2006, in BAAS 38, AAS/High Energy Astrophysics Division #9, 339 [Google Scholar]
- Tananbaum, H., Gursky, H., Kellogg, E. M., et al. 1972, ApJ, 174, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Trümper, J., Kahabka, P., Oegelman, H., Pietsch, W., & Voges, W. 1986, ApJ, 300, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Vrtilek, S. D., Quaintrell, H., Boroson, B., et al. 2001, ApJ, 449, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1987, A&A, 183, 257 [NASA ADS] [Google Scholar]
- Wasserman, I. 2003, MNRAS, 341, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Wijers, R. A. M. J., & Pringle, J. E. 1999, MNRAS, 308, 207 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Generation of the pulse profile template
The X-ray pulse profiles of the 1.24 s pulsation of Her X-1 show systematic variations with phase of the 35 day modulation. Here we describe the process of generation of the pulse profile template for the main-on of Her X-1 in the 9–13 keV range, its characteristics and the way in which the template is used to find the 35 d phase of any 9–13 keV pulse profile. An earlier version of the template (with less resolution) is described in Staubert et al. (2010b). To construct the template we use data of the main-ons of two 35 d cycles, taken by RXTE/PCA: cycles 313 and 323 of Dec. 01 and Nov. 02, respectively (for a definition of pulse profile cycle counting see Staubert et al. 2009). Together the data provide a near continuous coverage of a complete main-on of Her X-1. Figure A.1 shows the two light curves in the energy range 3-20 keV range (adjusted to a common phase zero). Figure A.2 shows examples of pulse profiles for progressive 35 d phases.
For generating the template we proceeded through the following steps of analysis:
-
1.
Generate pulse profiles with 128 phase bins by folding events inthe 9–13 keV range from integration intervalsof typically 0.1–0.2 days (~0.003–0.006 in 35 d phase) with the predetermined best pulse period. From the available data we find 28 pulse profiles at different 35 d phases throughout the main-on.
-
2.
Normalize all profiles such that the minimum is zero and the maximum is 100 cts/s.
-
3.
If necessary, shift profiles such that the “sharp edges” of all profiles coincide at pulse phase 1.0. The sharp edges are defined by the fast decrease in flux after the right shoulder of the main peak into the eclipse-like trough (see Staubert et al. 2009b and Fig. A.3-upper-left).
-
4.
Record the 35 d phase (center of observation interval) for each profile. As 35 d phase zero the observed turn-ons are used: MJD 52 243.05 for cycle no. 313, and MJD 52 594.66 for cycle no. 323.
-
5.
Insert all normalized/shifted profiles (each profile is one line) into a matrix according to the corresponding 35 d phase (which runs along the columns).
-
6.
Perform cubic best fits (see below) with the 35 d phase as variable (along the columns) for each of the 128 pulse profile bins.
-
7.
Calculate template values using the best fit parameters with a resolution of 0.002 in 35 d phase.
Cubic fits of the observed normalized count rate values are performed for each of the 128 columns using the function
 |
Fig. A.1 Main-on light curves of 35 d cycles no. 313 (Dec. 01, red) and cycle no. 323 (Nov. 02, blue) from RXTE/PCA, 9–13 keV. The count rate in cycle 313 is ~ 30 cts/s lower than in cycle 323, here the points are shifted downward by additional 20 cts/s for separation against the data points of cycle 323. |
 |
Fig. A.2 Selected pulse profiles of Her X-1 of 35 day cycles of Dec. 01 (cycle no. 313) and Nov. 02 (cycle no. 323) as a function of 35 day phase (RXTE, 9–13 keV). |
 |
Fig. A.3 Best fit parameters for cubic fits to the evolution of the count rate of normalized pulse profiles for the used 128 pulse phase bins (red points). The reference 35 d phase is C = 0.1. Upper left: A (constant), upper right: B (linear), lower left: D (quadratic), lower right: E (cubic). For comparison, also the pulse profile for 35 d phase 0.122 is shown. For the parameter A, which is basically the profile itself, the “sharp edge” at pulse phase 1.0 is drawn. |
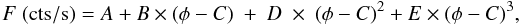 with φ being the 35 d phase (zero phase is turn-on). Figure A.3 shows the evolution of the four fit parameters with pulse phase. The 35 d reference phase was fixed to C = 0.1. For comparison, also the pulse profile of 35 d phase 0.122 is shown.
with φ being the 35 d phase (zero phase is turn-on). Figure A.3 shows the evolution of the four fit parameters with pulse phase. The 35 d reference phase was fixed to C = 0.1. For comparison, also the pulse profile of 35 d phase 0.122 is shown.
The final 9–13 keV template is a smoothed analytical representation of the observed pulse profile matrix. The template covers the main-on in the 35 d phase range 0.00 to 0.24, it is a 128 × 121 matrix of normalized count rate values: each of the 121 lines contains a normalized pulse profile (with 128 bins) corresponding to 35 d phases ranging from 0.00 to 0.24 in steps of 0.002. A graphical 3D-representation of the 9–13 keV template constructed from the data of 35 d cycles 313 and 323 is shown in Fig. 3-right. The template matrix is electronically provided as an ASCII file.
Any 9–13 keV profile observed during a 35 d main-on can then be compared to this template and the 35 d phase can be determined (by 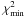 fitting). For the typical RXTE pulse profile, we find that this is generally possible to an accuracy of ± 0.02 in phase. For the comparison, it is, of course, necessary that the profile which is to be tested is adjusted in phase such that the “sharp edge” is at phase 1.0.
fitting). For the typical RXTE pulse profile, we find that this is generally possible to an accuracy of ± 0.02 in phase. For the comparison, it is, of course, necessary that the profile which is to be tested is adjusted in phase such that the “sharp edge” is at phase 1.0.
In Fig. 4 we give an example of how “pulse profile phase-zero” is found using a set of profiles of the main-on of cycle 257 (July 1996) as observed by RXTE/PCA: six different integration intervals were defined for which pulse profiles were generated. The normalized profiles were then compared with the analytical template and for each of them the 35 d phase was determined. These phase values are plotted against the observing time and a linear fit with a constant slope corresponding to the current 35 d period value is performed. For cycle 257 the time of “pulse profile phase-zero” was found to be MJD 50 285.46. This method works with any number of observed pulse profiles per main-on, even with only one profile.
Future work will extend the template to cover also the short-on of the 35 d modulation of Her X-1 and to produce equivalent templates for other energy ranges.
All Tables
All Figures
 |
Fig. 1 Average 35 d flux profile of Her X-1, generated by accumulating light curves observed by RXTE/ASM for 35 d turn-ons around binary phase 0.2 (Fig. 3 of Klochkov et al. 2006). The vertical lines indicate the binary eclipses. |
| In the text | |
 |
Fig. 2 Turn-on history of Her X-1: the (O–C) diagram (using 20.5 × Porb as the period to calculate the expected turn-ons). Upper: the anomalous low around MJD 51 500 (AL3) is assumed to last for eighteen 35 d cycles. Lower: the same assuming that there were only seventeen 35 d cycles (see Staubert et al. 2009). The solid line represents the linear best fit to all data, defining a mean period of 34.98 d (which may be used for a rough ephemeris of turn-ons). |
| In the text | |
 |
Fig. 3 Representation of the template which describes main-on pulse profiles of Her X-1 in the 9–13 keV range as function of 35 d phase. Left: pulse profiles for every 0.02 in 35 d phase. Right: 3D pulse representation for the 35 d phase range 0.00 to 0.24. The resolution is 128 bins in pulse phase and 48 bins in 35 d phase (resolution 0.005). |
| In the text | |
 |
Fig. 4 Example for finding “pulse profile phase-zero” for the case of cycle 257 main-on, as observed by RXTE/PCA in July 1996. |
| In the text | |
 |
Fig. 5 (O–C) values in units of days for observed turn-ons (green) and for so far generated “pulse profile phase-zero” values from pulse profile fitting (magenta), using profiles 9–13 keV profiles for several main-ons. The majority of the “pulse profile phase-zero” values are from observations by RXTE. The values based on observations by Ginga, Beppo/SAX, Suzaku and INTEGRAL are marked individually. |
| In the text | |
 |
Fig. A.1 Main-on light curves of 35 d cycles no. 313 (Dec. 01, red) and cycle no. 323 (Nov. 02, blue) from RXTE/PCA, 9–13 keV. The count rate in cycle 313 is ~ 30 cts/s lower than in cycle 323, here the points are shifted downward by additional 20 cts/s for separation against the data points of cycle 323. |
| In the text | |
 |
Fig. A.2 Selected pulse profiles of Her X-1 of 35 day cycles of Dec. 01 (cycle no. 313) and Nov. 02 (cycle no. 323) as a function of 35 day phase (RXTE, 9–13 keV). |
| In the text | |
 |
Fig. A.3 Best fit parameters for cubic fits to the evolution of the count rate of normalized pulse profiles for the used 128 pulse phase bins (red points). The reference 35 d phase is C = 0.1. Upper left: A (constant), upper right: B (linear), lower left: D (quadratic), lower right: E (cubic). For comparison, also the pulse profile for 35 d phase 0.122 is shown. For the parameter A, which is basically the profile itself, the “sharp edge” at pulse phase 1.0 is drawn. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


