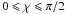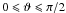| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201220110 | |
| Published online | 01 February 2013 | |
Pulsed high-energy γ-rays from thermal populations in the current sheets of pulsar winds
Institut de Planétologie et d’Astrophysique de Grenoble (IPAG), UMR 5274, 38041 Grenoble, France
e-mail: arkai@obs.ujf-grenoble.fr
Received: 26 July 2012
Accepted: 27 October 2012
Context. More than one hundred pulsars have been detected up to now at GeV energies by the Large Area Telescope (LAT) on the Fermi gamma-ray observatory. Current modelling proposes that the high-energy emission comes from outer magnetospheric gaps, but radiation from the equatorial current sheet that separates the two magnetic hemispheres outside the light cylinder has also been investigated.
Aims. We discuss the region outside the light cylinder, the “near wind” zone. We investigate the possibility that synchrotron radiation emitted by thermal populations in the equatorial current sheet of the pulsar wind in this region can explain the lightcurves and spectra observed by Fermi/LAT.
Methods. We used analytical estimates as well as detailed numerical computation to calculate the γ-ray luminosities, lightcurves, and spectra of γ-ray pulsars.
Results. Many of the characteristics of the γ-ray pulsars observed by Fermi/LAT can be reproduced by our model, most notably the position of these objects in the P − Ṗ diagram, and the range of γ-ray luminosities. A testable result is a sub-exponential cutoff with an index b = 0.35. We also predict the existence of a population of pulsars with cutoff energies in the MeV range. These have systematically lower spindown luminosities than the Fermi/LAT-detected pulsars.
Conclusions. It is possible for relativistic populations of electrons and positrons in the current sheet of a pulsar’s wind immediately outside the light cylinder to emit synchrotron radiation that peaks in the sub-GeV to GeV regime, with γ-ray efficiencies similar to those observed for the Fermi/LAT pulsars.
Key words: pulsars: general / radiation mechanisms: non-thermal / stars: winds, outflows / gamma rays: stars / relativistic processes
© ESO, 2013
1. Introduction
Since the launch of the Fermi space telescope, the sample of gamma-ray pulsars has grown to include more than one hundred objects. All these pulsars, whether young or millisecond, single or in binaries, show spectra consistent with power laws with exponential cutoffs, whose cutoff energy lies in the range 1 − 10 GeV (Abdo et al. 2010). A prominent exception is the Crab pulsar, which has been detected by ground-based Cerenkov arrays in the TeV regime, and whose spectrum can be well fitted by a broken power law (Aliu et al. 2008; McCann 2011). These observations point to the outer gap/slot gap models as the most probable explanation for the pulsed gamma-ray emission, based on population prediction statistics and lightcurve modelling (Gonthier et al. 2010; Decesar et al. 2011; Pierbattista et al. 2011; Venter et al. 2009; Watters & Romani 2011; Venter et al. 2012), although for millisecond pulsars one has to invoke non-dipolar field geometries or displaced polar caps to reach the required energies (Harding & Muslimov 2011). In those models, the emission originates within the light cylinder, defined by the cylindrical radius rLC = c/ω from the pulsar’s rotational axis, where a corotating particle would reach the speed of light. However, it was pointed out by Bai & Spitkovsky (2010) that the emission region must be extended slightly outside the light cylinder to reproduce the double-peaked light curves using the magnetic field configuration from self-consistent, force-free simulations of pulsar magnetospheres.
The idea that high-energy pulsations might come from current sheets near or outside the light cylinder is not new. Lyubarskii (1996) predicted that particles accelerated through reconnection close to the light cylinder might emit gamma-rays through the synchrotron process. Lyubarskii’s emission site is the point where the warped equatorial current sheet that separates regions of opposite magnetic field polarity in the pulsar’s wind meets the current flowing to/from the pulsar’s polar caps, the so-called Y-point (Spitkovsky 2006). Later it was pointed out that pulsed emission naturally arises from the periodicity of the pulsar wind, which is modulated by the star’s rotation in combination with the large bulk Lorentz factors of the outflow (Kirk et al. 2002). This model has been successfully applied to calculate the polarization of optical emission from the Crab pulsar (Pétri & Kirk 2005) and it has also shown promise in explaining the gamma-ray light curves observed by Fermi/LAT (Pétri 2011). In these models the emission is attributed to the inverse Compton process and starts in the wind region far from the light cylinder, r ≫ rLC. In the same context it was proposed that the gamma-ray radiation of the Fermi/LAT band could be synchrotron radiation from power-law electrons in the pulsar wind’s equatorial sheet far from the light cylinder (Kirk et al. 2002; Pétri 2012).
There is, however, no obvious reason why emission should be truncated outside the light cylinder (for magnetospheric gap models) or start at a minimum radius in the far wind zone (for the striped wind model). The emission region should evolve continuously from the outer magnetospheric gaps through the light cylinder and into the equatorial current sheet, possibly affected by the reconnection process that will inevitably occur in the sheet (Bai & Spitkovsky 2010). The region beyond the light cylinder but still in the near wind zone is the area that we are trying to explore. The purpose of this paper is to demonstrate how emission in the 100 MeV − 100 GeV range explored by Fermi/LAT can naturally arise from thermal populations of particles in the striped wind, without going into the details of reconnection physics, but just using a few simple assumptions about the local description of the current sheet. In Sect. 2 we describe our model, including our assumptions, and give some analytical estimates for the emitted radiation. In Sect. 3 we present examples of emission maps and phase-averaged spectra that arise from our model and explore the parameter space to arrive at more general conclusions about the pulsar population observed by Fermi/LAT. Finally we discuss our results and the potential of a more detailed description of the current sheet outside the light cylinder as a source of pulsed energetic radiation.
2. Equatorial current sheet
2.1. Description of the particle population
To describe the wind outside the light cylinder, we will use the “slow-rotator” solution to the magnetohydrodynamics equations that govern the physics of the pulsar wind, which was found by Bogovalov (1999). This solution refers to an electron-positron wind launched by a rotating neutron star, the magnetic axis of which is at an angle χ to its rotational axis. In this description the wind is purely radial and super-fast magnetosonic at launch, and the field can be described by a radial and an azimuthal component of magnitude  where R = r/rLC is the spherical radius normalized to the light cylinder, ϑ is the polar angle, β = (1 − 1/Γ2)1/2 is the bulk speed of the wind, normalized to the speed of light, and BLC is a fiducial magnetic field magnitude at the light cylinder. The adequacy of this solution in describing approximately the structure of the wind for radii as small as the light cylinder has been confirmed by force-free simulations of pulsar magnetospheres (Spitkovsky 2006; Bai & Spitkovsky 2010).
where R = r/rLC is the spherical radius normalized to the light cylinder, ϑ is the polar angle, β = (1 − 1/Γ2)1/2 is the bulk speed of the wind, normalized to the speed of light, and BLC is a fiducial magnetic field magnitude at the light cylinder. The adequacy of this solution in describing approximately the structure of the wind for radii as small as the light cylinder has been confirmed by force-free simulations of pulsar magnetospheres (Spitkovsky 2006; Bai & Spitkovsky 2010).
A prominent feature of Bogovalov’s solution is the warped equatorial current sheet, separating the two magnetic hemispheres, across which the field changes sign. In the mathematical solution the sheet is just a discontinuity, but in reality it should have a finite thickness. Such a current sheet is populated by hot particles, whose pressure balances the magnetic pressure of the cold, strongly magnetized plasma outside the sheet. The sheet oscillates in space and time with a wavelength of λ = 2πβ/ω, and with the pulsar’s frequency ω = 2π/P, where P is the pulsar’s period measured in seconds.
We assumed that in the wind frame (the frame that propagates radially outwards with a Lorentz factor equal to the bulk Lorentz factor of the wind, Γ), the sheet can be locally described by the relativistic Harris equilibrium (Hoh 1966). For this description to be valid, the segment of the sheet under consideration should be approximately flat. For a relativistic outflow, the hydrodynamically causally connected region of the flow has an opening angle of roughly ~ 1/Γ, centred on the direction of motion of the outflow. Since for a pulsar wind Γ ≫ 1, the hydrodynamically connected sheet segment can be considered to be flat and the local Harris sheet description should be a good approximation.
We denote quantities measured in the wind frame with a prime. If we denote the sheet normal direction in the wind frame with a capital X′, and the sheet midplane is at X′ = 0, then locally the field inside and outside the segment can be described by a tangent hyperbolic profile 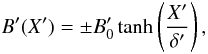 (3)where
(3)where 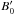 is the magnitude of the field outside the sheet, δ′ is a measure of the sheet thickness and the field is in the direction parallel to the sheet and perpendicular to the direction of current flow, which is locally considered to be Z′. The particle population in the sheet consists of two counter-drifting relativistic Maxwellian distributions whose density falls with X′, and whose drift provides the net current. From the pressure balance across the sheet follows the dependence of the density of each distribution on X′ (Kirk & Skjæraasen 2003):
is the magnitude of the field outside the sheet, δ′ is a measure of the sheet thickness and the field is in the direction parallel to the sheet and perpendicular to the direction of current flow, which is locally considered to be Z′. The particle population in the sheet consists of two counter-drifting relativistic Maxwellian distributions whose density falls with X′, and whose drift provides the net current. From the pressure balance across the sheet follows the dependence of the density of each distribution on X′ (Kirk & Skjæraasen 2003):  where Θ = kBT′/(mc2) is a dimensionless temperature associated with the particle distribution. The condition connecting the particle density, temperature, and current sheet thickness is (Kirk & Skjæraasen 2003; Lyubarsky & Kirk 2001)
where Θ = kBT′/(mc2) is a dimensionless temperature associated with the particle distribution. The condition connecting the particle density, temperature, and current sheet thickness is (Kirk & Skjæraasen 2003; Lyubarsky & Kirk 2001) 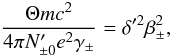 (6)where γ ± and β ± are the Lorentz factor and the corresponding speed, normalized to the speed of light, of the drift of the distributions in the wind frame. Finally, by assuming that the ideal gas law holds for the distribution, we obtain
(6)where γ ± and β ± are the Lorentz factor and the corresponding speed, normalized to the speed of light, of the drift of the distributions in the wind frame. Finally, by assuming that the ideal gas law holds for the distribution, we obtain 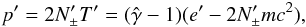 (7)where e′ is the energy density associated with the two counter-streaming distributions. For the relativistic Harris sheet solution, this equation becomes
(7)where e′ is the energy density associated with the two counter-streaming distributions. For the relativistic Harris sheet solution, this equation becomes 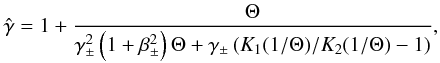 (8)where K1 and K2 are modified Bessel functions of the second kind. In the inner part of the pulsar wind, which is of interest to us, the thermal particles in the distribution are predicted to be highly relativistic, which allows us to set
(8)where K1 and K2 are modified Bessel functions of the second kind. In the inner part of the pulsar wind, which is of interest to us, the thermal particles in the distribution are predicted to be highly relativistic, which allows us to set 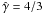 in the above equation and also has as a result that the thermal energy of the particles in the distributions will greatly exceed their rest-mass energy: Θ ≫ 1. Using the approximations
in the above equation and also has as a result that the thermal energy of the particles in the distributions will greatly exceed their rest-mass energy: Θ ≫ 1. Using the approximations  Equation (8) can be simplified to
Equation (8) can be simplified to 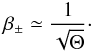 (11)This means that the drift of the distributions in the current sheet is not relativistic, and beaming effects caused by it can be ignored when calculating the emitted radiation. Therefore the distributions can for this purpose be considered to be isotropic in the frame in which the sheet is at rest. With this approximation we can solve Eqs. (5) and (6) for Θ and
(11)This means that the drift of the distributions in the current sheet is not relativistic, and beaming effects caused by it can be ignored when calculating the emitted radiation. Therefore the distributions can for this purpose be considered to be isotropic in the frame in which the sheet is at rest. With this approximation we can solve Eqs. (5) and (6) for Θ and 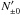 . In doing this, we have to take into account the fact that the angle
. In doing this, we have to take into account the fact that the angle 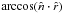 between the sheet normal and the radius unit vector changes when moving from the lab to the wind frame.
between the sheet normal and the radius unit vector changes when moving from the lab to the wind frame.
The magnetic field from the solution of Bogovalov (1999) is always parallel to the sheet, if one ignores reconnection effects. This means that close to the light cylinder and for a radial outflow, one cannot ignore the radial component of the field. The full field in the wind frame will be 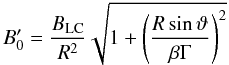 (12)and the toroidal component will prevail in this frame only for R > Γ (we call this region the far wind region). Conversely, in the region R < Γ (which we call the near wind region), it is a good approximation to ignore the second term under the square root and approximate
(12)and the toroidal component will prevail in this frame only for R > Γ (we call this region the far wind region). Conversely, in the region R < Γ (which we call the near wind region), it is a good approximation to ignore the second term under the square root and approximate 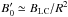 .
.
If one considers a perpendicular rotator (a pulsar with χ = π/2), the temperature and density in a current sheet segment are given by the simple expressions  The dimensionless parameter aLC appearing above is called the strength parameter, and is defined at the pulsar’s light cylinder as
The dimensionless parameter aLC appearing above is called the strength parameter, and is defined at the pulsar’s light cylinder as 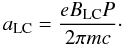 (15)Taking a pulsar’s moment of inertia to be I = 1045 gcm2, the spindown luminosity is calculated by the period and the period derivative as (Abdo et al. 2010)
(15)Taking a pulsar’s moment of inertia to be I = 1045 gcm2, the spindown luminosity is calculated by the period and the period derivative as (Abdo et al. 2010) 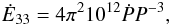 (16)where we have normalized the luminosity to the value 1033 erg/s. The magnetic field (in Gauss units) can then be expressed as
(16)where we have normalized the luminosity to the value 1033 erg/s. The magnetic field (in Gauss units) can then be expressed as 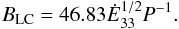 (17)The strength parameter then can be expressed as a function of the spindown luminosity only:
(17)The strength parameter then can be expressed as a function of the spindown luminosity only: 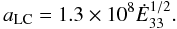 (18)All GeV pulsars detected so far have strength parameters in the range 108−1011.
(18)All GeV pulsars detected so far have strength parameters in the range 108−1011.
Finally, Δ < 1 is the fraction of a half wavelength that a sheet occupies, measured in the radial direction (i.e. not perpendicularly to the local sheet plane), in the lab frame. We assume that Δ is constant with radius for the sake of simplicity, but it is far from clear how this parameter evolves with radius and obliquity χ close to the light cylinder. We also assume that Γ is constant, although generally reconnection in the current sheet has been shown to increase Γ with radius in the far wind zone (Lyubarsky & Kirk 2001; Kirk & Skjæraasen 2003), a result that might also apply to the near wind zone. These assumptions are based on the fact that only a very limited radius interval contributes to the gamma-ray radiation, as we will see below, therefore if the change in Δ and Γ happens with a scale larger than rLC, it is not relevant to the present estimations.
Substituting for aLC in Eq. (13), we obtain 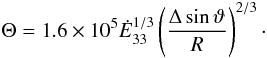 (19)The requirement that Θ ≫ 1 in the near wind region R < Γ translates into
(19)The requirement that Θ ≫ 1 in the near wind region R < Γ translates into 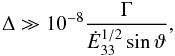 (20)which, as we will see in the following, is easily satisfied for all γ-ray pulsars, provided the emitting region is not very close to the polar axis. In any case, the validity of the Θ ≫ 1 assumption has to be checked a posteriori for all cases of studied pulsars.
(20)which, as we will see in the following, is easily satisfied for all γ-ray pulsars, provided the emitting region is not very close to the polar axis. In any case, the validity of the Θ ≫ 1 assumption has to be checked a posteriori for all cases of studied pulsars.
In the following, all results refer to the near wind region, R < Γ, but still outside the pulsar’s light cylinder, close to which we assume that the current sheet is formed. Therefore we consider a minimum value for the radius of the radiating sheet of Rmin = 1. Our model is valid only for relativistic outflows, therefore we also set a lower limit on Γ of Γmin = 10.
In the next paragraphs, we assume a perpendicular rotator (χ = π/2) to estimate analytically the emitted radiation and the characteristics of the current sheet and its populations. These estimates can be generalized to the oblique rotator (see Appendix B), but the conclusions remain essentially the same as long as the line of sight is not close to the edge of the current sheet, where ζ = π/2 − χ.
2.2. Larmor radius of hot particles
An important condition for the consistency of our model comes from the requirement that the hot particles’ Larmor radius in the full field between the current sheets should be smaller than the sheet width. In the wind frame this requirement translates into 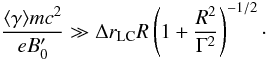 (21)This inequality is equivalent to Θ1/2 ≫ 1, which should hold close to the light cylinder, by the assumptions of the model.
(21)This inequality is equivalent to Θ1/2 ≫ 1, which should hold close to the light cylinder, by the assumptions of the model.
2.3. Energy of emitted photons
The mean Lorentz factor of the electron/positron distribution in the current sheet is ⟨ γ ⟩ ~ 3Θ. Electrons of this ⟨ γ ⟩ gyrating in the field 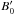 , radiate photons of energy (in the observer’s frame):
, radiate photons of energy (in the observer’s frame): 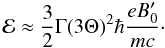 (22)After some manipulation, one finds the highest observable photon energy
(22)After some manipulation, one finds the highest observable photon energy 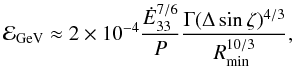 (23)where the photon energy is measured in GeV. In Eq. (23) we have kept only the poloidal component of the magnetic field, since it dominates close to the light cylinder, at R < Γ. All pulsars in the first Fermi/LAT catalogue have
(23)where the photon energy is measured in GeV. In Eq. (23) we have kept only the poloidal component of the magnetic field, since it dominates close to the light cylinder, at R < Γ. All pulsars in the first Fermi/LAT catalogue have 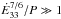 . This is why it is possible for most objects in the catalogue to find an appropriate combination of Γ, Δ and Rmin ≥ 1 that will bring ℰGeV to the regime observed by LAT, while at the same time satisfying all restrictions on Δ, Γ, and R. This is especially easy for the highest luminosity pulsars (Ė33 ≫ 1), or for the very low period ones (P ≪ 1 s, millisecond pulsars), as one can deduce by inspecting Eq. (23). In other words, for pulsars of the same spindown luminosity, millisecond pulsars are more likely to reach GeV energies. Alternatively, if Γ and Δ are the same, millisecond pulsars with lower spindown luminosities than young pulsars can emit in the Fermi/LAT band, a trend that might be observable as our statistics on gamma-ray pulsars increase.
. This is why it is possible for most objects in the catalogue to find an appropriate combination of Γ, Δ and Rmin ≥ 1 that will bring ℰGeV to the regime observed by LAT, while at the same time satisfying all restrictions on Δ, Γ, and R. This is especially easy for the highest luminosity pulsars (Ė33 ≫ 1), or for the very low period ones (P ≪ 1 s, millisecond pulsars), as one can deduce by inspecting Eq. (23). In other words, for pulsars of the same spindown luminosity, millisecond pulsars are more likely to reach GeV energies. Alternatively, if Γ and Δ are the same, millisecond pulsars with lower spindown luminosities than young pulsars can emit in the Fermi/LAT band, a trend that might be observable as our statistics on gamma-ray pulsars increase.
From the constraints on Δ and R, we can calculate an absolute maximum on the peak energy of the emitted spectrum for ζ = π/2: 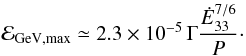 (24)As we will see below, Δ is often more severely constrained by the radiation reaction limit, so the energy ℰGeV,max will not necessarily be reached for all objects.
(24)As we will see below, Δ is often more severely constrained by the radiation reaction limit, so the energy ℰGeV,max will not necessarily be reached for all objects.
The rapid fall of the peak photon energy with radius means that in this simple model the most energetic photons come from close to the light cylinder. In a realistic situation it is to be expected that either Γ or Δ or both will rise with radius, making the fall of ℰGeV with radius less steep, but even if Δ and Γ were to rise linearly with R, the emitted photon energy would still fall as ∝ R-1.
2.4. Energy losses
For the relativistic Harris equilibrium to hold in a quasi-steady state, equilibrium has to be established in the wind frame within a timescale of the order of magnitude 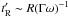 , which is the timescale on which the magnetic field change is comparable to its magnitude δB′ ~ B′. Equilibrium is established in the current sheet within a timescale
, which is the timescale on which the magnetic field change is comparable to its magnitude δB′ ~ B′. Equilibrium is established in the current sheet within a timescale
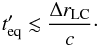 Therefore the requirement
Therefore the requirement 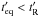 holds close to the light cylinder as long as Δ ≲ Γ-1, while this condition is relaxed with radius to Δ ≲ R/Γ.
holds close to the light cylinder as long as Δ ≲ Γ-1, while this condition is relaxed with radius to Δ ≲ R/Γ.
For the particles not to suffer catastrophic energy losses, their synchrotron cooling timescale 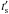 should be longer than
should be longer than 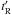 . Comparing the two one finds
. Comparing the two one finds 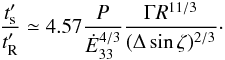 (25)For the lower Ė33 pulsars the inequality
(25)For the lower Ė33 pulsars the inequality 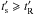 generally holds for R > Rmin, but this may not be the case for some millisecond pulsars, because of the linear dependency of the ratio on the pulsar period P. The steep radius dependence, however, relaxes this condition rapidly, so that when it breaks down, it does so only for a very limited R-range close to the light cylinder.
generally holds for R > Rmin, but this may not be the case for some millisecond pulsars, because of the linear dependency of the ratio on the pulsar period P. The steep radius dependence, however, relaxes this condition rapidly, so that when it breaks down, it does so only for a very limited R-range close to the light cylinder.
If 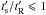 , as is often the case for high spindown pulsars and millisecond pulsars, particles will lose energy rapidly and cool, disturbing the pressure equilibrium between the populations in the current sheet and the magnetic field outside it. The pressure in the sheet will fall, thus causing its compression by the external magnetic field. This can initiate compression-driven magnetic reconnection, a phenomenon previously studied in the context of the interaction of current sheets in a pulsar wind with the wind’s termination shock (Lyubarsky 2003; Pétri & Lyubarsky 2007; Lyubarsky & Liverts 2008; Sironi & Spitkovsky 2011). Reconnection has been shown to be able to accelerate particles to non-thermal distributions above the thermal peak of the particle spectrum (and also, as already mentioned, to accelerate the bulk flow and cause the sheet width to rise). A detailed study of this radiation-loss-induced process is beyond the scope of this work. But if
, as is often the case for high spindown pulsars and millisecond pulsars, particles will lose energy rapidly and cool, disturbing the pressure equilibrium between the populations in the current sheet and the magnetic field outside it. The pressure in the sheet will fall, thus causing its compression by the external magnetic field. This can initiate compression-driven magnetic reconnection, a phenomenon previously studied in the context of the interaction of current sheets in a pulsar wind with the wind’s termination shock (Lyubarsky 2003; Pétri & Lyubarsky 2007; Lyubarsky & Liverts 2008; Sironi & Spitkovsky 2011). Reconnection has been shown to be able to accelerate particles to non-thermal distributions above the thermal peak of the particle spectrum (and also, as already mentioned, to accelerate the bulk flow and cause the sheet width to rise). A detailed study of this radiation-loss-induced process is beyond the scope of this work. But if 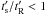 , some acceleration processes ought to be at work to supply the sheet with energetic particles. This will in all likelihood result in power-law distributions in the current sheet, a signature that might be observable in the spectrum above the MeV-GeV peak for the highest luminosity pulsars and for those millisecond pulsars with
, some acceleration processes ought to be at work to supply the sheet with energetic particles. This will in all likelihood result in power-law distributions in the current sheet, a signature that might be observable in the spectrum above the MeV-GeV peak for the highest luminosity pulsars and for those millisecond pulsars with 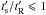 (something that has not been modelled in the present article). Uzdensky & Spitkovsky (2012) recently reported on their investigation of this regime.
(something that has not been modelled in the present article). Uzdensky & Spitkovsky (2012) recently reported on their investigation of this regime.
 |
Fig. 1 Sky maps of the pulsar’s total luminosity shown for two different bulk Lorentz factors Γ = 10 and Γ = 50 and for different χ. In the upper panels χ = π/2, in the middle ones χ = π/3 and in the lower ones χ = π/6. All the plots have been made using the parameters Δ = 0.01 and Rmin = 1. The luminosity is given by integrating ℒν (Eq. (A.4)) over all frequencies and multiplying with d2, where d is the distance of the pulsar from the observer. A beaming factor of ℱΩ = (4π)-1 has been used. |
2.5. Radiation reaction limit and maximum emitted energy
If the particles of mean energy ~3Θmc2 in the current are gaining energy through acceleration in an electric field E ~ ξB with ξ < 1, their acceleration is limited by radiation losses. For radiation-reaction-limited synchrotron emission (in the full-field amplitude 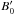 ), energy losses compensate possible energy gain:
), energy losses compensate possible energy gain: ![\begin{equation} \left[\frac{{\rm d}W}{{\rm d}t}\right]_{\rm syn} = e\xi B'_0 c \leqslant e B'_0 c . \end{equation}](/articles/aa/full_html/2013/02/aa20110-12/aa20110-12-eq113.png) (26)From this expression one can calculate an upper limit for Δ:
(26)From this expression one can calculate an upper limit for Δ: 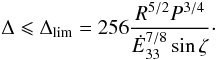 (27)The Ė33 dependence in the denominator implies that for the most powerful pulsars, the sheet is thinner close to the light cylinder. For the Crab we obtain Δlim = 3 × 10-4sin-1ζ at Rmin, whereas for most of the weaker pulsars with Ė33 ≤ 102, Δlim is greater than unity, i.e. it does not present a constraint. All millisecond pulsars detected by Fermi/LAT fall into this category.
(27)The Ė33 dependence in the denominator implies that for the most powerful pulsars, the sheet is thinner close to the light cylinder. For the Crab we obtain Δlim = 3 × 10-4sin-1ζ at Rmin, whereas for most of the weaker pulsars with Ė33 ≤ 102, Δlim is greater than unity, i.e. it does not present a constraint. All millisecond pulsars detected by Fermi/LAT fall into this category.
Inserting Δlim into Eq. (23), one recovers the classical synchrotron limit: 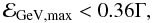 (28)where the factor Γ comes from the boosting of the photon energy to the lab frame. The minimum of Eqs. (24), (28), then, can give an estimate of the maximum value of the GeV cutoff for any individual object.
(28)where the factor Γ comes from the boosting of the photon energy to the lab frame. The minimum of Eqs. (24), (28), then, can give an estimate of the maximum value of the GeV cutoff for any individual object.
Inserting Δlim into Eq. (25), one obtains a lower limit for the ratio 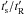 (applicable mainly to higher-spindown pulsars, for which Δlim < 1):
(applicable mainly to higher-spindown pulsars, for which Δlim < 1): ![\begin{equation} \frac{t'_{\rm s}}{t'_{\rm R}} > \left[ \frac{t'_{\rm s}}{t'_{\rm R}}\right]_{\rm min} = 0.23 \Gamma R^2 P^{1/2} \Edot^{-3/4} . \end{equation}](/articles/aa/full_html/2013/02/aa20110-12/aa20110-12-eq122.png) (29)We see that, mainly for young pulsars with a high spindown luminosity, the right-hand side can be less than unity. These pulsars either have smaller Δ to keep
(29)We see that, mainly for young pulsars with a high spindown luminosity, the right-hand side can be less than unity. These pulsars either have smaller Δ to keep 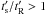 , or rapid reacceleration mechanisms in their current sheets, as argued above (or both). Therefore there should be a trend in the P − Ṗ diagram to observe more objects with acceleration signatures (i.e. power-law tails) in their spectrum as one moves to higher spindown luminosities, or equivalently as one moves to higher Ṗ and lower P (upward left region in a P − Ṗ diagram).
, or rapid reacceleration mechanisms in their current sheets, as argued above (or both). Therefore there should be a trend in the P − Ṗ diagram to observe more objects with acceleration signatures (i.e. power-law tails) in their spectrum as one moves to higher spindown luminosities, or equivalently as one moves to higher Ṗ and lower P (upward left region in a P − Ṗ diagram).
3. Lightcurves, spectra, and γ-ray luminosity
3.1. Lightcurves
The expected lightcurves and spectra produced in the current sheets of a pulsar can be computed numerically by integrating the emission coefficient of the particles in the magnetic field of the current sheet along the line of sight to the observer. The procedure is explained in the appendix.
In the wind model of the pulsar radiation two pulses per period are expected, the separation and the width of which varies with the obliquity χ and the line of sight angle ζ. The width of the pulses depends on the bulk speed of the outflow, with wider pulses for lower Γ (Kirk et al. 2002; Pétri 2011). Examples of the variations of skymaps with χ, ζ and Γ are shown in Fig. 1, where we used a model pulsar of surface magnetic field equal to B = 1010 G and period P = 0.01 s to plot the sky maps of the pulsed total luminosity.
In the left column of Fig. 1 sky maps are shown for Γ = 10, while in the right column the value of the bulk Lorentz factor is Γ = 50. The width of the pulse strongly depends on Γ, as expected. Along with the gamma-ray intensity, we have indicated the position of the radio pulses on the maps with white shading. The discs that represent the radio pulses are only indicative. They are centred on the spot where a sharp radio pulse coming directly from the corresponding pole would appear, and serve to demonstrate the phase lag between the radio and the gamma-ray pulse for different obliquities. As is seen from the sky maps, both pulses are observable only for a limited range of observer angle ζ, and for inclinations higher than χ = π/4. For smaller inclination angles, like in the case χ = π/6, the beam from the pole does not travel through the pulsar wind, the radio pulses are above and below the region of high gamma-ray luminosity in the sky map, and only one of the two kinds can be observed. The exact shape and width of the radio pulse will depend on the geometry of the radiating particle beam above the polar cap. The details of the position calculation of the radio pulse can be found in Pétri (2011).
The upper maps in both columns represent the case of the perpendicular rotator, where χ = π/2, the middle ones are for χ = π/3, and the lower ones for χ = π/6. As the obliquity decreases, the width of the pulse increases while the peak luminosity falls, which causes the overall phase-averaged luminosity to remain essentially constant for different obliquities. The widest pulses are observed for the smallest inclination angles. However, for very small χ the line of sight to the observer has to lie very close to the equatorial plane of the pulsar for the pulse to be observed, since the luminosity is significant only for ζ ≥ π/2 − χ. This is a likely geometry for the objects that are observed to have two wide pulses with a phase separation of δφ ~ 0.5.
From the sky maps for Γ = 10 it can be discerned that there is a slight substructure in the pulses. There is a slight dip in luminosity at the peak of each pulse, resulting in two sub-peaks appearing for all ζ. This is caused by the structure of the current sheet. In the middle of the sheet the magnetic field is exactly zero, rising towards the sides, while the density of the hot particles is highest and falls towards the sides. Therefore the bulk of the radiation of each current sheet segment comes from two regions away from the sheet midplane, where the product of particle density and magnetic field is largest. The double-peaked shape of the pulse reflects the two luminosity peaks within the sheet. Because of the shrinking pulse thickness with rising Γ this phenomenon should be observable only for the lowest bulk Lorentz factors.
It is useful to note here that the highest luminosities in the sky maps are correlated with the highest peak energies ℰGeV, resulting in pulses that become sharper for higher energy photons. This is shown in Fig. 2, where the flux νFν has been plotted in a colour map as a function of emitted energy ℰ (in eV) and phase φ. A horizontal slice of the map shows the lightcurve at a specific energy while a vertical slice shows the spectrum at a given phase. The pulses become narrower with increasing energy, as can be seen from the wider flux variation in a horizontal slice as one moves higher in the map. Also, the peak energy varies by many orders of magnitude within one phase, and is lowest between pulses, something that can be seen when comparing spectra at different phases.
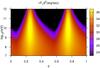 |
Fig. 2 Peak flux νFν (multiplied by the square of the distance to give a luminosity estimate) as a function of phase φ and peak energy ℰ. ℰ ranges from 10 MeV to 1 TeV. The same pulsar parameters were used as in Fig. 1, with χ = π/3 and ζ = π/2. |
In Fig. 3 we show how the lightcurves change when moving the minimum radius Rmin from the light cylinder to a distance in the far wind region, Rmin > Γ. For low Rmin, close to the light cylinder, the pulse shape is almost symmetrical with respect to its peak (also seen in Fig. 1). As one moves towards larger Rmin, the pulses stop being symmetrical and instead present an abrupt rise in luminosity followed by a gradual decrease, which makes them asymmetrical with respect to the peak. Also, the total luminosity in the pulse is reduced by many orders of magnitude as one moves outwards in the wind. In the example of Fig. 3 a change from Rmin = 1 to Rmin = 30 results in a decrease in luminosity by seven orders of magnitude. These results agree with previous investigations of pulses from the far wind region (for example Kirk et al. 2002).
 |
Fig. 3 Variation of the pulsar’s lightcurves for different Rmin. The bulk Lorentz factor in these examples is Γ = 10 and the obliquity is χ = π/3. The rest of the parameters are the same as in Fig. 1. |
From the sky maps we showed we can conclude that the separation of the two pulses depends on χ and ζ, with a separation of Δφ ~ 0.5 when the line of sight lies at the equatorial plane. However, as we have pointed out above, the phase-averaged luminosity changes significantly only if the line of sight lies above the wind, i.e. if ζ < π/2 − χ. In the opposite case the overall luminosity is not sensitive to variations of χ and ζ.
 |
Fig. 4 Phase-averaged spectra for the same model pulsar that was used in Figs. 1 and 3. All the plots have been made using χ = π/2 (perpendicular rotator) and ζ = π/2. Here the variation of the phase-average flux with the parameters Γ, Δ and Rmin is shown. |
 |
Fig. 5 Phase-averaged spectrum and simulated lightrcurve of the millisecond pulsar J1614-2230 as calculated using our model, along with the best-fit power-law plus exponential cutoff fit (Abdo et al. 2009). The parameters that were used are Δ = 0.25, Γ = 20, χ = ζ = π/2 for the millisecond pulsar (left). For the young pulsar in the supernova remnant 3C 58 we used Δ = Δlim, Γ = 80, χ = π/5 and ζ = π/2. |
3.2. Phase-averaged spectra
In Fig. 4 we used the same model pulsar as in the previous section to calculate phase-averaged spectra and their dependence on the model parameters. In the upper plot we show the variation of the spectrum when changing the bulk Lorentz factor Γ. As is expected from Eq. (23), the peak of the spectrum rises linearly with Γ, but the overall luminosity falls with rising Γ. This can be attributed to the diminishing of the area of the sheet from which doppler-boosted radiation is received: the boosted area scales as 1/Γ2, something that is only partly compensated for by the square of the Doppler factor in the calculation of the received flux (given in the appendix). The most strongly boosted radiation comes from the line of sight, but the luminosity of the region that directly intersects the line of sight is not the major contribution to the overall observed luminosity. This is because one observes only the effects of the perpendicular (i.e. azimuthal) field at ϑ = ζ, while the effects of the much stronger poloidal field Br come from a region at angle ~ 1/Γ to the line of sight. Therefore when the line of sight is directly aligned to the edge of the sheet, where ζ = π/2 − χ, still two pulses of the same amplitude are observed, that come from the two parts of the folded current sheet that are at angle ~1/Γ to the line of sight, whereas the edge itself contributes only a little to the overall flux. This is different to what has been predicted in the past (Pétri 2011). However, a single wide pulse will be observed when looking over the edge of the sheet. The disadvantage in this case is that the luminosity decreases quickly with decreasing ζ, which makes such pulses difficult to detect.
In the middle panel the change in the phase-averaged spectrum is shown when varying Δ. The dramatic rise of the cutoff energy and of the luminosity with Δ can be explained by the dependency of the peak of the spectrum on Δ, given in Eq. (23), as well as the rise of the relativistic temperature in the current sheet with Δ as seen in Eq. (19).
In the lower panel we demonstrate the dependence of the cutoff and luminosity on the minimum radius Rmin. The peak frequency of the spectrum and the overall luminosity both rise very strongly with decreasing Rmin, which agrees with Eq. (23) and is also expected because of the dependence of the temperature of the sheet particles on radius, given in Eq. (19). Therefore the bulk of the received high-energy radiation comes from a region of limited range in R close to Rmin.
We would like to note at this point that the spectra that come from thermal distributions have a characteristic slope in the lower frequencies that is the same as the single-particle synchrotron spectrum (with a flux of ℱν ∝ ν1/3). This slope is not clearly seen in the 100 MeV − 10 GeV range for most pulsars, because there is a broad peak in that region. This peak is created mainly by the spread of the magnetic field across the current sheet, which causes different regions in the current sheet to emit photons of different peak energies. Because the emissivity decreases rapidly with radius, the phase-averaged spectrum mainly consists of the radiation emitted by the small part of the current sheet that moves towards the observer, for a very short radius interval, and is dominated by the spectrum at the peak of the pulse. Different spectral slopes could be obtained by assuming the injection of a power-law rather than a thermal distribution, albeit at the price of introducing additional parameters. We return to the question of the particle distribution in Sect. 4.
3.3. Examples
In Fig. 5 we present two examples of spectra and lightcurves of Fermi/LAT-detected pulsars calculated with our model. The first example is the millisecond pulsar PSR J1614-2230, which has a period of P = 3.2 ms and a spindown luminosity of Ė33 = 5. Its spectrum calculated according to our model can be seen in the upper left panel of Fig. 5 along with the best fit power law with exponential cutoff, as given in Abdo et al. (2009). The parameters used were Δ = 0.25, Γ = 20, χ = π/2, and ζ = π/2. The lightcurve corresponding to the same parameters is depicted in the lower left panel. The phase of the two peaks is correctly predicted, but the width of the simulated pulses is narrower than observed. This is because in this example Δ > 1/Γ, and in this case the lightcurve cannot be accurately predicted by our model (as explained in Appendix B).
 |
Fig. 6 P − Ṗ diagram including the pulsars observed by Fermi/LAT and plot of the predicted γ-ray luminosity in the range 0.1 − 10 GeV for a random sample of pulsars. Gamma-ray luminosity Lγ versus the spindown luminosity Lsp for two random samples of millisecond and young pulsars. The lines Lγ = Lsp and |
The second example, shown in the plots on the right side of Fig. 5, is the pulsar PSR J0205+6449, which was discovered by Fermi/LAT in the supernova remnant 3C 58. This pulsar has a high spindown luminosity of Ė33 = 2.7 × 104 and a period of P = 65.7 m s-1. It is a young, energetic pulsar for which Δlim ≃ 1.5 × 10-3. The parameters that we used for these plots are Δ = Δlim, Γ = 80, χ = π/5, and ζ = π/2. The relatively high Lorentz factor needed to reach the cutoff of ℰ ≈ 3 GeV causes the pulses to be rather sharp, which is also observed with Fermi/LAT.
From these two examples and from the phase-averaged spectra shown in Fig. 4 it can be seen that our model predicts a substantially higher energy flux at photon energies above 10 GeV than would be expected using a power-law plus exponential cutoff fit, which implies that for the more energetic pulsars, which have larger bulk Lorentz factors, one could detect radiation in the sub-TeV to TeV regime explored by Cerenkov telescope arrays. Specifically, a good fit to our spectra is given by a power-law with a sub-exponential cutoff: ![\begin{equation} \frac{{\rm d}N}{{\rm d}\mathcal{E}} \propto \mathcal{E}^{-p} \exp\left[ - \left( \frac{\mathcal{E}}{\mathcal{E}_{\rm cutoff}} \right)^b\right] \cdot \end{equation}](/articles/aa/full_html/2013/02/aa20110-12/aa20110-12-eq174.png) (30)Our model predicts a cutoff with b = 0.35. This index is not sensitive to the obliquity χ or the observer angle ζ, as long as the line of sight intersects the equatorial current sheet, i.e. when ζ > π/2 − χ. The index b can reach the value ~ 0.4 for ζ < π/2 − χ, but the very low luminosities that are expected in that case make the majority of those objects unobservable.
(30)Our model predicts a cutoff with b = 0.35. This index is not sensitive to the obliquity χ or the observer angle ζ, as long as the line of sight intersects the equatorial current sheet, i.e. when ζ > π/2 − χ. The index b can reach the value ~ 0.4 for ζ < π/2 − χ, but the very low luminosities that are expected in that case make the majority of those objects unobservable.
3.4. Peak energies and γ-ray luminosities
In Fig. 6 we show a prediction of the region in the P − Ṗ where spectra that peak in the range 0.1 − 10 GeV are espected, according to our model. Two shaded regions are shown that correspond to Δ = 0.1 and Γ = 100 (yellow) and Δ = 0.001 and Γ = 100 (green). We also plotted the lower and upper borders of the region that corresponds to Δ = 0.1 and Γ = 10 (red lines). Obviously almost all pulsars already detected by Fermi/LAT fall in at least one of these regions, from which we conclude that one can accommodate the cutoffs of almost all pulsars with parameters in the range 0.001 ≤ Δ ≤ 0.1 and 10 < Γ < 100.
In principle, the peak energies emitted by the near wind region of a pulsar wind are not constrained to the GeV regime. Peaks at TeV energies are likely excluded by the synchrotron limit given in Eq. (28), but there should be a population of pulsars with spectra peaking in the MeV regime (or lower). These pulsars can be found in a region of the P − Ṗ diagram roughly below the yellow shaded region of the P − Ṗ diagram in Fig. 6. The population of MeV pulsars will include objects with spindown luminosities lower than those detected by Fermi/LAT. This becomes obvious by inspecting Eq. (23): for lower spindown luminosities the same Γ and Δ lead to lower peak energies. For example, a pulsar that is a perpendicular rotator with P = 0.5 s and Ṗ = 10-15 with a bulk Lorentz factor Γ = 10 and Δ = 0.1 will radiate a spectrum that peaks at energies ℰ ≃ 0.3MeV.
The overall luminosity emitted by the near region of a pulsar wind from a perpendicular rotator according to our model can be estimated to within a factor of two by the expression 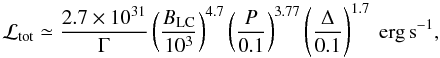 (31)where BLC is given in G and P in s. In terms of spindown luminosity, this can be expressed as
(31)where BLC is given in G and P in s. In terms of spindown luminosity, this can be expressed as 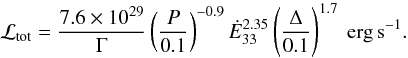 (32)It is obvious from the above expression that, since no trend is observed for γ-ray pulsars to have a γ-ray luminosity that is anti-correlated to their spindown luminosity, the values of Γ and Δ should vary significantly from object to object.
(32)It is obvious from the above expression that, since no trend is observed for γ-ray pulsars to have a γ-ray luminosity that is anti-correlated to their spindown luminosity, the values of Γ and Δ should vary significantly from object to object.
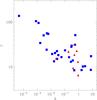 |
Fig. 7 Parameters Δ and Γ estimated for the pulsars in the Fermi/LAT one-year catalogue. Blue squares are the young pulsars and red triangles represent the millisecond pulsars. |
If the peak of the spectrum falls into the γ-ray regime, then Eq. (31) gives a good estimate of the γ-ray luminosity of the pulsar. The dependence of ℒtot on χ and ζ is very weak as long as the line of sight intersects the wind, ζ > π/2 − χ, therefore one can use the above formula to reach approximate conclusions about the γ-ray luminosity of a pulsar. Equations (31) and (23) (which yield an estimate of the peak energy of the phase-averaged spectrum) show that once P and Ṗ are known, the emitted luminosity and peak energy can be fixed essentially by the two parameters Δ and Γ. These two equations can also be inverted to deduce values of Δ and Γ for a sample of pulsars for which P, Ṗ, ℒγ and ℰGeV are known. This was done for the pulsars of the First Fermi/LAT pulsar catalogue and the results are shown in Fig. 7, where Δ and Γ have been plotted for each object of the sample.
The blue squares represent the young pulsars in the catalogue while the red triangles are the millisecond pulsars. For most objects Δ ranges between 10-3 and 1, and a trend is observed for the millisecond pulsars to have higher values of Δ, slightly lower than unity. The bulk Lorentz factor Γ ranges roughly between 10 and 100, and most objects have relatively low Lorentz factors in the range 10 − 30.
For the most part, the deduced Γ and Δ are reasonable, except for five objects for which values Δ > 1 are predicted, which are unphysical since Δ has to be less than unity for the current sheet to be narrower than the wind’s half wavelength. These are: J0633+1746 (the Geminga pulsar), J1057-5226, J1741-2054, J1836+5925, and J2021+4026. These five pulsars are distinct from the rest of the population, in that their estimated γ-ray luminosity is a large part of (and for the last two pulsars even larger than) their spindown luminosity. From Eq. (31) we see that a higher Δ is needed to accommodate a higher ℒγ, which explains the values deduced for these pulsars. The unphysical values of Δ, therefore, may arise because the γ-ray luminosity is estimated from the observational data using too simple an assumption (a beaming factor of value unity). Also, our model is possibly too simple to accommodate all pulsars in the catalogue, and a contribution from another physical mechanism or emission region might result in higher luminosities in the exceptional cases of the objects with Δ > 1.
In the diagram on the right side of Fig. 6 we have plotted the γ-ray luminosity Lγ of two random samples of pulsars (millisecond and young pulsars) with respect to their spindown luminosity Lsp. For this purpose two random samples of pulsars were used, with periods and period derivatives in the ranges − 2 < log P < 0 and − 15 < log Ṗ < − 11 (for the young pulsars) and − 3 < log P < − 2 and − 20 < log Ṗ < − 17 (for the millisecond pulsars). We chose ζ and χ randomly in the interval [0,π/2] , the bulk Lorentz factor in the interval 1 < log Γ < 2, and the sheet thickness either within log Δlim − 2 < log Δ < log Δlim in the case Δlim < 0.1 or within − 3 < log Δ < − 1 if Δlim > 0.1. The γ-ray luminosity was calculated by integrating the phase-averaged flux between 100 MeV and 100 GeV and using a beam correction factor ℱΩ = 1, to obtain a direct comparison with the results of Abdo et al. (2010).
About 12% of all young pulsars in our sample and 30% of the millisecond pulsars have a cutoff within the interval 100 MeV − 10 GeV and are shown in Fig. 6. These percentages reflect our choice of the range in Δ. We constrained Δ to be within two orders of magnitude of the value min(Δmin,0.1). If the range of Δ were narrower, resulting in systematically higher values, the percentages quoted above would rise. Lower choices of Δ lead to lower ℰGeV so there are more pulsars that have peaks below 100 MeV and therefore do not make the cut.
The large beam correction factor used for this plot has as a result the occurrence in some rare cases of objects with Lγ > Lsp, whereas in most cases the γ-ray luminosity is a few percent of Lsp. The young pulsars tend to lie higher in the diagram than millisecond pulsars, which reflects their higher spindown luminosity in combination with the fact that the gamma-ray efficiency is similar in both samples.
In Abdo et al. (2010) a trend was reported that the gamma-ray luminosity is proportional to the square root of the spindown luminosity for the highest luminosities: 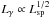 . We have no clear indication of such an effect in our simulated sample, meaning that the gamma-ray efficiency of the highest spindown pulsars is predicted to be similar to that of the lower spindown pulsars. The best-fit line to the points in Fig. 6 gives
. We have no clear indication of such an effect in our simulated sample, meaning that the gamma-ray efficiency of the highest spindown pulsars is predicted to be similar to that of the lower spindown pulsars. The best-fit line to the points in Fig. 6 gives 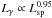 for young and millisecond pulsars, and if the statistical error is taken into account, the relationship is compatible with the proportionality Lγ ∝ Lsp.
for young and millisecond pulsars, and if the statistical error is taken into account, the relationship is compatible with the proportionality Lγ ∝ Lsp.
4. Discussion and conclusions
We have shown how gamma-ray pulses can naturally arise within the framework of the pulsar wind’s equatorial current sheet outside (but close to) the light cylinder. The advantage of this emission model is that it is an intrinsic mechanism that naturally produces peak energies in the MeV-GeV range. It can give meaningful results for almost all pulsars, irrespective of age or environment, employing only a few parameters: the bulk Lorentz factor of the outflow Γ, the sheet thickness Δ, the obliquity χ, and the angle of the rotational axis to the line of sight ζ. To these the minimum radius Rmin can be added (which, in the calculated examples, was set equal to Rmin = 1). However, it is important to note that Rmin has to be sufficiently close to the light cylinder, so that the peak energy of the spectrum reaches the GeV regime. The parameters of the model are constrained by the characteristics of the pulsar and by the physics of the current sheet. The novelty of our model is that it makes an attempt to account for the previously ignored region of the wind between R = 1 and R ≃ Γ, and is therefore able to take advantage of the strong poloidal field close to the light cylinder, something that has not been discussed in previous wind models.
The predictions of our model are the following:
-
1.
Two pulses per pulsar period are expected. The pulses have thesame amplitude.
-
2.
The shape of the pulses is symmetric with respect to their peak, as long as emission starts close to the light cylinder, and becomes increasingly asymmetric with rising Rmin.
-
3.
There is no significant interpulse emission in the GeV range.
-
4.
The width of the pulse decreases with increasing photon energy.
-
5.
The separation of the peaks varies with the obliquity χ and the angle to the line of sight ζ, as in previous models of pulsed radiation from the pulsar wind.
The features of the pulsed emission that cannot be explained by our model, such as the interpulse or the peaks of different intensity, could be accomodated by a model in which radiation comes both from within the light cylinder, possibly in an outer gap, and from the beginning of the wind. The difficulty of outer gap models to produce double-peaked lightcurves, as noted in Bai & Spitkovsky (2010), in combination with the difficulty of our near wind model to produce single pulses, point to the need for a combined model in which the high-energy emission starts within the light cylinder and continues in the equatorial current sheet outside the light cylinder. Therefore the physics of the formation region of the current sheet is very important in the endeavour to understand γ-ray emission from pulsars.
For pulsars in binaries, it is possible that the favoured radiation process is not synchrotron but rather inverse Compton on the low-frequency photons of the massive star, as investigated in Pétri & Dubus (2011). In this case the peak energies and emitted luminosities by the two mechanisms can be comparable, depending on whether the comoving energy density of the low-frequency photons in the wind frame is comparable to the magnetic field energy density close to the light cylinder. For the pulsar B1259-63, which is a member of a binary with a B2e star, the comoving stellar radiation energy density seen by the pairs moving towards the star is 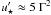 erg s-1, while the comoving magnetic field energy density is
erg s-1, while the comoving magnetic field energy density is 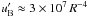 erg s-1 (the radial component dominates when R < Γ). Inverse Compton scattering is dominant if ΓR2/ ≳ 2500, which requires emission to start at 5 − 15 light cylinder radii for values of Γ ≈ 10 − 100. The situation is more favourable to Compton scattering in the other, more compact, gamma-ray binaries where the radiation density is up to 200 times higher (LS 5039).
erg s-1 (the radial component dominates when R < Γ). Inverse Compton scattering is dominant if ΓR2/ ≳ 2500, which requires emission to start at 5 − 15 light cylinder radii for values of Γ ≈ 10 − 100. The situation is more favourable to Compton scattering in the other, more compact, gamma-ray binaries where the radiation density is up to 200 times higher (LS 5039).
A possible problem of our model is that the supersonic solution of Bogovalov (1999) might not apply for the objects of lower bulk Lorentz factors. Particularly, the wind can accelerate, as is predicted in various magnetohydrodynamic models of pulsar winds (Beskin et al. 1998; Kirk et al. 2009). In this case the shape of the current sheet can in reality be different, since there is generally also a polar magnetic field component, which in our model was zero. However, as was mentioned above, the very strong dependence of ℰGeV on R implies that even if the parameters Δ and Γ changed with R, the present model would still be able to explain the main features of the observed spectra. Adding to these considerations the fact that the particle density within the current sheet and the magnetic field decrease as the wind expands to larger R, the conclusion is reached that the emitted luminosity, which depends on  and
and  , will also decrease with radius. This in combination with the decreasing peak of the spectrum means that the main contribution to the spectrum near the cutoff will still come from a very limited region close to Rmin. Therefore, possible changes in the dynamic evolution of the wind should not have a strong effect on the observed spectrum and luminosity, while the exact shape of the current sheet should influence mainly the shape of the pulse, but not the cutoff energy or the emitted luminosity.
, will also decrease with radius. This in combination with the decreasing peak of the spectrum means that the main contribution to the spectrum near the cutoff will still come from a very limited region close to Rmin. Therefore, possible changes in the dynamic evolution of the wind should not have a strong effect on the observed spectrum and luminosity, while the exact shape of the current sheet should influence mainly the shape of the pulse, but not the cutoff energy or the emitted luminosity.
Another possible shortcoming of our model lies in the assumption of a thermal distribution in the current sheet. The Harris distribution has been extensively used in the past in the context of the current sheets in pulsar winds (Kirk & Skjæraasen 2003; Lyubarsky & Kirk 2001; Sironi & Spitkovsky 2011), which makes it the first reasonable assumption when one treats these sheets. It is generally thought, however, that the particle distribution close to the light cylinder should be non-thermal, since the particles are accelerated by electric fields within the light cylinder and possibly by the reconnection process at the Y-point, where the current sheet originates. Nevertheless, using the relativistic Harris equilibrium entails several advantages: it is the simplest self-consistent solution to a relativistic current sheet, and it has only two free parameters: a normalization constant, and the particle temperature. Because of these restrictions there are no degeneracies in our model, as we showed. The observational data uniquely predict the properties of the current sheet for a given pulsar. This makes our model powerful and able to give unambiguous predictions, but also refutable, should it not accomodate the data. In the light of these advantages, we kept the thermal distribution for our current sheets, and dit not resort to a power-law distribution, which would pose fewer restrictions on our model because of the additional free parameters associated with it. In principle, one way to distinguish between power-laws and thermal inputs is the low-energy spectral slope. For thermal distributions the slope asymptotes to 1/3, whereas a wider range is expected for power-laws depending on the distribution index.
It is expected that reconnection will generally alter the physics of the current sheet beyond the pulsar’s light cylinder, and might result in an evolution of the current sheet thickness and the wind Lorentz factor, especially in objects for which the radiative timescales of the thermal particles are very short in comparison to the evolution timescale of the magnetic field (Uzdensky & Spitkovsky 2012). Furthermore, particle acceleration takes place during the reconnection process, which might result in a non-thermal tail to the thermal distribution, the characteristics of which will change as the current sheet evolves with radius. These phenomena will leave their imprint on the pulsed high-energy spectrum, and need to be investigated in a self-consistent way, which is beyond the scope of this article. We can, however, give a simple order-of-magnitude argument about the reconnection-accelerated particles: deep in the current sheet particles can be accelerated by reconnection electric fields to energies higher than the thermal peak. These particles would have Lorentz factors extending to γ ~ ξaLC/Γ (in the wind frame), thus giving rise to photons up to an energy 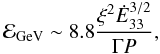 (33)where
(33)where 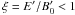 . This could extend beyond the thermal peak for sufficiently large ξ or Ė33, whereas millisecond pulsars are again favoured by the dependence on the inverse of the period. If these high-energy non-thermal particles escape the acceleration site and radiate in the field within the current sheet, their emission could give rise to a power-law tail extending beyond the GeV cutoff (Zenitani & Hoshino 2008). This mechanism should be prominent for objects for which
. This could extend beyond the thermal peak for sufficiently large ξ or Ė33, whereas millisecond pulsars are again favoured by the dependence on the inverse of the period. If these high-energy non-thermal particles escape the acceleration site and radiate in the field within the current sheet, their emission could give rise to a power-law tail extending beyond the GeV cutoff (Zenitani & Hoshino 2008). This mechanism should be prominent for objects for which 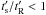 , which tend to cluster at the upper left part of the P − Ṗ diagram, as discussed. It is for these pulsars that acceleration by reconnection could become prominent and be observed in the form of power-law tails in the GeV − TeV regime.
, which tend to cluster at the upper left part of the P − Ṗ diagram, as discussed. It is for these pulsars that acceleration by reconnection could become prominent and be observed in the form of power-law tails in the GeV − TeV regime.
Another possibility is that the particles in the current sheet are already accelerated to a power-law distribution when the sheet starts radiating, in which case a different distribution function would have to be used to calculate the current sheet parameters (Balikhin & Gedalin 2008). This might apply particularly to millisecond pulsars, which have lower surface magnetic fields that lead to lower pair production rates and therefore less dense plasmas in their magnetospheres. In this case a non-thermal particle distribution seems likely to describe the physics of the current sheet in a more consistent way. We defer the investigation of such particle distributions to a future article.
Acknowledgments
We acknowledge support from the EC via contract ERC-StG-200911 and CNES. I.A. would like to thank Jérôme Pétri, Gilles Henri, and Anatoly Spitkovsky for useful discussions.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, Science, 325, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJS, 187, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Aliu, E., Anderhub, H., Antonelli, L. A., et al. 2008, Science, 322, 1221 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bai, X.-N., & Spitkovsky, A. 2010, ApJ, 715, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Balikhin, M., & Gedalin, M. 2008, J. Plasma Phys., 74, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V. S., Kuznetsova, I. V., & Rafikov, R. R. 1998, MNRAS, 299, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V. 1999, A&A, 349, 1017 [NASA ADS] [Google Scholar]
- Decesar, M. E., Harding, A. K., & Miller, M. C. 2011, in AIP Conf. Ser. 1357, eds. M. Burgay, N. D’Amico, P. Esposito, A. Pellizzoni, & A. Possenti, 285 [Google Scholar]
- Gonthier, P. L., Roberts, J. J., Nagelkirk, E., Stam, M., & Harding, A. K. 2010, in AAS/High Energy Astrophysics Division #11, BAAS, 42, 680 [NASA ADS] [Google Scholar]
- Harding, A. K., & Muslimov, A. G. 2011, ApJ, 743, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Hoh, F. C. 1966, Phys. Fluids, 9, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., & Skjæraasen, O. 2003, ApJ, 591, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. G., Skjæraasen, O., & Gallant, Y. A. 2002, A&A, 388, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, J. G., Lyubarsky, Y., & Petri, J. 2009, in Ap&SS Lib., 357, ed. W. Becker, 421 [Google Scholar]
- Lind, K. R., & Blandford, R. D. 1985, ApJ, 295, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarskii, Y. E. 1996, A&A, 311, 172 [NASA ADS] [Google Scholar]
- Lyubarsky, Y. E. 2003, MNRAS, 345, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y., & Kirk, J. G. 2001, ApJ, 547, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubarsky, Y., & Liverts, M. 2008, ApJ, 682, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- McCann, A. for the VERITAS Collaboration 2011, in Proc. of the 32nd International Cosmic Ray Conference (ICRC2011), held 11–18 August, in Beijing, China, OG2.1–2.2: Cosmic Ray Origin and Galactic Phenomena, 7, 207 [Google Scholar]
- Pétri, J. 2011, MNRAS, 412, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J. 2012, MNRAS, 424, 2023 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J., & Dubus, G. 2011, MNRAS, 417, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J., & Kirk, J. G. 2005, ApJ, 627, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Pétri, J., & Lyubarsky, Y. 2007, A&A, 473, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierbattista, M., Grenier, I., Harding, A., & Gonthier, P. L. 2011, in AIP Conf. Ser. 1357, eds. M. Burgay, N. D’Amico, P. Esposito, A. Pellizzoni, & A. Possenti , 249 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2011, ApJ, 741, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Spitkovsky, A. 2006, ApJ, 648, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Uzdensky, D. A., & Spitkovsky, A. 2012 [arXive:1210.3346] [Google Scholar]
- Venter, C., Harding, A. K., & Guillemot, L. 2009 [arXiv:0911.4890] [Google Scholar]
- Venter, C., Johnson, T. J., & Harding, A. K. 2012, ApJ, 744, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Watters, K. P., & Romani, R. W. 2011, ApJ, 727, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Zenitani, S., & Hoshino, M. 2008, ApJ, 677, 530 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Calculation of a received synchrotron spectrum by a relativistically moving sheet
The flux that an observer receives from a relativistically moving source is calculated by the formula (Lind & Blandford 1985): 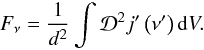 (A.1)
(A.1)
-
Primed quantities are in the wind frame, i.e. the frame where the outflow is at rest. Since the wind is assumed to be flowing radially, at each azimuth and polar angle (ϕ,ϑ) there is a different, local, radially moving wind frame. Quantities pertaining to a point of the wind with coordinates (r,ϑ,ϕ) are calculated in this local wind frame.
-
When calculating the emission coefficient j′ we should take care to calculate it in the direction of the line of sight, taking into account the aberration of photons in the wind frame (we return to this matter below).
-
The volume element is taken in the observer’s frame (or the frame in which the pulsar is at rest) and is dV = r2sinϑdrdϑdϕ.
-
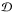 is the doppler factor, which depends on the angle between the line of sight and the direction of motion of the wind. It is calculated by the expression
is the doppler factor, which depends on the angle between the line of sight and the direction of motion of the wind. It is calculated by the expression 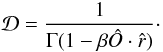 (A.2)The unit vector
(A.2)The unit vector 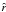 is the radial unit vector in a spherical coordinate system, whose centre is located at the pulsar. Ô is a unit vector in the direction of the observer. The cosine of the angle between these two vectors depends on ϑ and ϕ, and therefore
is the radial unit vector in a spherical coordinate system, whose centre is located at the pulsar. Ô is a unit vector in the direction of the observer. The cosine of the angle between these two vectors depends on ϑ and ϕ, and therefore 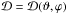 . The observed frequency is
. The observed frequency is 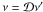 .
. We assume that the direction to the line of sight is at polar angle ζ and at ϕ = 0. In a cartesian system of coordinates, then, we have
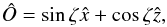 whereas the radial unit vector can be expressed as:
whereas the radial unit vector can be expressed as: 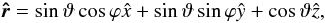 which gives us
which gives us 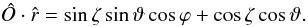 (A.3)
(A.3)-
Finally, d is the distance of the object from the observer. We define a luminosity associated with the pulsar as
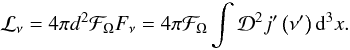 (A.4)The parameter ℱΩ is the beam correction factor, which is taken to be equal to ℱΩ = (4π)-1 in the plots of the pulsar lightcurves and spectra, Figs. 1, 3, and 4. It is, however, taken to be equal to unity ℱΩ = 1 for the Lγ − Lsp plot in Fig. 6.
(A.4)The parameter ℱΩ is the beam correction factor, which is taken to be equal to ℱΩ = (4π)-1 in the plots of the pulsar lightcurves and spectra, Figs. 1, 3, and 4. It is, however, taken to be equal to unity ℱΩ = 1 for the Lγ − Lsp plot in Fig. 6.
Appendix B: Calculation of the emission coefficient
The emission coefficient can be calculated by multiplying the energy distribution of the particles by the single-electron synchrotron spectrum. This implies that the electrons are relativistic, which is, strictly speaking, not true for the whole population, since the distribution starts from γ′ = 1. However, since the temperature of the distribution is relativistic, this approximation will not introduce a significant error. The distribution gives the number of electrons per unit gamma factor, per solid angle, and per unit volume:
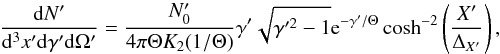 where Θ ≫ 1 is the dimensionless temperature of the distribution in units of mc2 as defined in the text. This distribution is isotropic and its density decreases towards the edge of the sheet. The direction perpendicular to the sheet midplane is denoted by X′ and ΔX′ is the width of the sheet at its local rest frame.
where Θ ≫ 1 is the dimensionless temperature of the distribution in units of mc2 as defined in the text. This distribution is isotropic and its density decreases towards the edge of the sheet. The direction perpendicular to the sheet midplane is denoted by X′ and ΔX′ is the width of the sheet at its local rest frame.
Using the small argument approximation of the modified Bessel function K2, Eq. (10), the distribution function can be expressed as 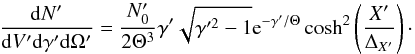 (B.1)This then has to be doubled to take account of both species in the sheet (electrons and positrons). The single-electron synchrotron spectrum is
(B.1)This then has to be doubled to take account of both species in the sheet (electrons and positrons). The single-electron synchrotron spectrum is
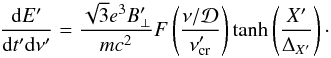 where F(x) is the well-known synchrotron function. In the above expression, we encounter the following:
where F(x) is the well-known synchrotron function. In the above expression, we encounter the following:
-
The field
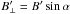 perpendicular to the direction that the photons that reach the observer travel along in the wind frame. α is the angle between the field in the wind frame and the photon trajectory, which can be computed through the scalar product
perpendicular to the direction that the photons that reach the observer travel along in the wind frame. α is the angle between the field in the wind frame and the photon trajectory, which can be computed through the scalar product 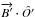 . To calculate this, we need to find the relativistic aberration of photons that follow the line of sight in the lab frame. This is equivalent to calculating the aberration of the vector Ô. The field has only a radial and an azimuthal component, so only the aberration of these two components of the unit vector Ô are needed. These components are
. To calculate this, we need to find the relativistic aberration of photons that follow the line of sight in the lab frame. This is equivalent to calculating the aberration of the vector Ô. The field has only a radial and an azimuthal component, so only the aberration of these two components of the unit vector Ô are needed. These components are 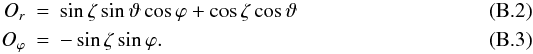 The corresponding primed components in the local wind frame are
The corresponding primed components in the local wind frame are  and the angle α is
and the angle α is 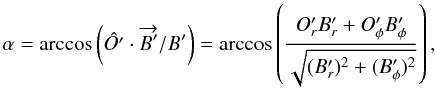 (B.6)while the local magnetic field in the wind frame is
(B.6)while the local magnetic field in the wind frame is  where the superscript LC refers to quantities at the light cylinder.
where the superscript LC refers to quantities at the light cylinder. -
The ratio X′/ΔX′ can be approximately converted to quantities in the lab frame to give:
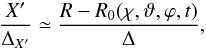 (B.9)where R0(χ,ϑ,ϕ,t) is the location of the current sheet point under consideration at time t.
(B.9)where R0(χ,ϑ,ϕ,t) is the location of the current sheet point under consideration at time t. -
In the general case of the oblique rotator the temperature is given by the expression
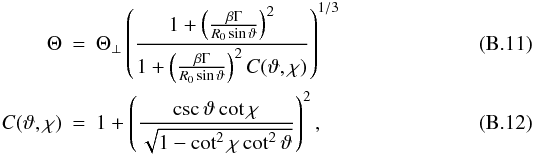 where Θ ⊥ is the value of the temperature for the perpendicular rotator, given in Eq. (19).
where Θ ⊥ is the value of the temperature for the perpendicular rotator, given in Eq. (19).
 |
Fig. B.1 Function C(ϑ,χ) plotted for |
The emission coefficient j′ has to be calculated at the retarded time
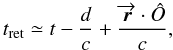 where
where 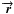 is the position vector of the radiating point in the current sheet, d is the distance of the pulsar from the observer, and t is the time that the observer measures. Normalizing time to 1/ω and distance to rLC the retarded time becomes
is the position vector of the radiating point in the current sheet, d is the distance of the pulsar from the observer, and t is the time that the observer measures. Normalizing time to 1/ω and distance to rLC the retarded time becomes 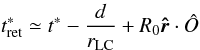 (B.13)(normalized time is denoted with an asterisk).The retarded time enters the computation via the equation for the motion of a current sheet:
(B.13)(normalized time is denoted with an asterisk).The retarded time enters the computation via the equation for the motion of a current sheet:
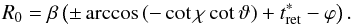 We replace the retarded time in the last equation from (B.13), and move the initial condition for time at t ∗ = d/rLC so that the new observer’s time is
We replace the retarded time in the last equation from (B.13), and move the initial condition for time at t ∗ = d/rLC so that the new observer’s time is 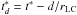 . We obtain an expression for the radius of the current sheet as a function of observer’s time, polar angle and azimuthal angle:
. We obtain an expression for the radius of the current sheet as a function of observer’s time, polar angle and azimuthal angle: 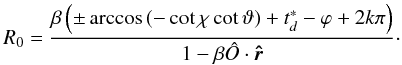 (B.14)Depending on how large or small the dot product
(B.14)Depending on how large or small the dot product 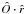 is, the radius R0 where the current sheet part under consideration is located, the radiation from which is received at time
is, the radius R0 where the current sheet part under consideration is located, the radiation from which is received at time 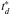 , can vary strongly. This means that at each moment
, can vary strongly. This means that at each moment 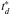 the observer receives radiation that comes from different parts of the current sheet that propagates in the wind, with different coordinates (R0,ϑ,ϕ). We note here that R0 is considered to be the radius at the midplane of the current sheet.
the observer receives radiation that comes from different parts of the current sheet that propagates in the wind, with different coordinates (R0,ϑ,ϕ). We note here that R0 is considered to be the radius at the midplane of the current sheet.
Finally, the flux can be computed, according to the above, as follows: 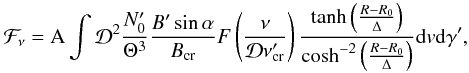 (B.15)with the volume element, the function n(γ′), the constant A, and the magnetic field
(B.15)with the volume element, the function n(γ′), the constant A, and the magnetic field 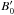 given by
given by ![\appendix \setcounter{section}{2} \begin{eqnarray} {\rm d}v & = &R^2 \sin\vartheta {\rm d}R {\rm d}\vartheta {\rm d}\varphi \\[1mm] n(\gamma') &=&\gamma'\sqrt{\gamma'^2-1}{\rm e}^{-\gamma'/\Theta} \\[1mm] {\rm A} &=& \frac{\sqrt{3}}{4\pi {\rm d}^2} \alpha_f mc^2 \rlc^3 \end{eqnarray}](/articles/aa/full_html/2013/02/aa20110-12/aa20110-12-eq289.png)
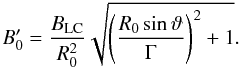 (B.19)The doppler factor has been given in Eq. (A.2) and is calculated with the help of Eq. (A.3). The strength parameter aLC and the density in the middle of the current sheet
(B.19)The doppler factor has been given in Eq. (A.2) and is calculated with the help of Eq. (A.3). The strength parameter aLC and the density in the middle of the current sheet 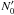 are given in the text. The expression for the flux also includes the sine of angle α, which is calculated by Eq. (B.6). The critical frequency
are given in the text. The expression for the flux also includes the sine of angle α, which is calculated by Eq. (B.6). The critical frequency 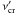 is given in Eq. (B.10), with
is given in Eq. (B.10), with 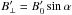 . Finally, the above parameters are calculated at radius R0 with the help of
. Finally, the above parameters are calculated at radius R0 with the help of 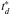 from Eq. (B.14). The purpose of the integration on R is to calculate the integral of the emission coefficient across the sheet, when the sheet midplane is at the point (R0,ϑ,ϕ). The numerical computation of the above integral for each point in time
from Eq. (B.14). The purpose of the integration on R is to calculate the integral of the emission coefficient across the sheet, when the sheet midplane is at the point (R0,ϑ,ϕ). The numerical computation of the above integral for each point in time 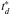 , or equivalently each phase in a pulsar period, and each frequency ν, produces the spectra and lightcurves needed.
, or equivalently each phase in a pulsar period, and each frequency ν, produces the spectra and lightcurves needed.
Finally, the above prescription for the calculation of the pulsar lightcurves is accurate as long as Δ < 1/Γ. In the opposite case, the pulse width is not governed by Γ, but is comparable to Δ, which is not taken into account in the calculation presented here. However, the phase-averaged fluxes calculated by our model are reliable even for Δ > 1/Γ.
All Figures
 |
Fig. 1 Sky maps of the pulsar’s total luminosity shown for two different bulk Lorentz factors Γ = 10 and Γ = 50 and for different χ. In the upper panels χ = π/2, in the middle ones χ = π/3 and in the lower ones χ = π/6. All the plots have been made using the parameters Δ = 0.01 and Rmin = 1. The luminosity is given by integrating ℒν (Eq. (A.4)) over all frequencies and multiplying with d2, where d is the distance of the pulsar from the observer. A beaming factor of ℱΩ = (4π)-1 has been used. |
| In the text | |
 |
Fig. 2 Peak flux νFν (multiplied by the square of the distance to give a luminosity estimate) as a function of phase φ and peak energy ℰ. ℰ ranges from 10 MeV to 1 TeV. The same pulsar parameters were used as in Fig. 1, with χ = π/3 and ζ = π/2. |
| In the text | |
 |
Fig. 3 Variation of the pulsar’s lightcurves for different Rmin. The bulk Lorentz factor in these examples is Γ = 10 and the obliquity is χ = π/3. The rest of the parameters are the same as in Fig. 1. |
| In the text | |
 |
Fig. 4 Phase-averaged spectra for the same model pulsar that was used in Figs. 1 and 3. All the plots have been made using χ = π/2 (perpendicular rotator) and ζ = π/2. Here the variation of the phase-average flux with the parameters Γ, Δ and Rmin is shown. |
| In the text | |
 |
Fig. 5 Phase-averaged spectrum and simulated lightrcurve of the millisecond pulsar J1614-2230 as calculated using our model, along with the best-fit power-law plus exponential cutoff fit (Abdo et al. 2009). The parameters that were used are Δ = 0.25, Γ = 20, χ = ζ = π/2 for the millisecond pulsar (left). For the young pulsar in the supernova remnant 3C 58 we used Δ = Δlim, Γ = 80, χ = π/5 and ζ = π/2. |
| In the text | |
 |
Fig. 6 P − Ṗ diagram including the pulsars observed by Fermi/LAT and plot of the predicted γ-ray luminosity in the range 0.1 − 10 GeV for a random sample of pulsars. Gamma-ray luminosity Lγ versus the spindown luminosity Lsp for two random samples of millisecond and young pulsars. The lines Lγ = Lsp and |
| In the text | |
 |
Fig. 7 Parameters Δ and Γ estimated for the pulsars in the Fermi/LAT one-year catalogue. Blue squares are the young pulsars and red triangles represent the millisecond pulsars. |
| In the text | |
 |
Fig. B.1 Function C(ϑ,χ) plotted for |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.