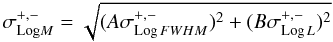| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201220343 | |
| Published online | 09 January 2013 | |
Black-hole masses of type 1 AGN in the XMM-Newton bright serendipitous survey⋆,⋆⋆
1
INAF - Osservatorio Astronomico di Brera, via Brera 28,
20121
Milan,
Italy
e-mail: alessandro.caccianiga@brera.inaf.it
2
Dipartimento di Fisica, Universitá degli Studi di
Milano-Bicocca, Piazza Della
Scienza 3, 20126
Milano,
Italy
3
Instituto de Física de Cantabria (CSIC-UC),
Avenida de los Castros,
39005
Santander,
Spain
4
X-ray & Observational Astronomy Group, Department of
Physics and Astronomy, Leicester University, Leicester
LE1 7RH,
UK
Received: 6 September 2012
Accepted: 15 November 2012
Aims. We derive masses of the central supermassive black hole (SMBH) and accretion rates for 154 type 1 AGN belonging to a well-defined X-ray-selected sample, the XMM-Newton serendipitous sample (XBS).
Methods. We used the most recent “single-epoch” relations, based on Hβ and MgIIλ2798 Å emission lines, to derive the SMBH masses. We then used the bolometric luminosities, computed on the basis of an SED-fitting procedure, to calculate the accretion rates, both absolute and normalized to the Eddington luminosity (Eddington ratio).
Results. The selected AGNs cover a range of masses from 107 to 1010 M⊙ with a peak around 8 × 108 M⊙ and a range of accretion rates from 0.01 to ~50 M⊙/year (assuming an efficiency of 0.1), with a peak at ~1 M⊙/year. The values of Eddington ratio range from 0.001 to ~0.5 and peak at 0.1.
Key words: galaxies: active / galaxies: nuclei / X-rays: galaxies / surveys
Based on observations collected at the Telescopio Nazionale Galileo (TNG) and at the European Southern Observatory (ESO), La Silla, Chile and on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and the USA (NASA).
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2013
1. introduction
The nuclear activity of an active galactic nucleus (AGN) is powered by the accretion of matter into the gravitational well of the central supermassive black hole (SMBH). It has now become clear that the majority of galaxies host an SMBH and that they must have experienced an activity phase during their lifetime (see Merloni & Heinz 2012 for a review). Much observational evidence, like the SMBH mass-bulge relations (e.g. Magorrian et al. 1998; Gültekin et al. 2009), strongly suggest that this activity phase must have played a critical role in galaxy evolution. For these reasons, a better understanding of the accretion mechanism represents a fundamental step not only in improving our knowledge of the AGN physics, but also for general comprehension of the galaxy formation and evolution.
X-rays offer a direct probe of the accretion mechanism since they are produced in the very inner part of the nucleus through a (still poorly understood) mechanism that probably involves the electrons in a “hot” corona and the UV photons produced within the accretion disk (e.g. Haardt & Maraschi 1991, 1993), thus carrying direct information on the physics very close to the SMBH. The highly penetrating capability of X-rays often makes them the only tool for gathering direct information on the nuclear activity when the disk emission, peaked in the UV part of the spectrum, is absorbed and unobservable.
While X-ray observations of single sources can shed light on the complexity of the emission at these energies, a statistical approach based on large samples offers the unique opportunity of studying the link between hot corona and the phenomenon of accretion on the central SMBH (e.g. see Young et al. 2010; Vasudevan & Fabian 2009; Grupe et al. 2010; Lusso et al. 2012, and references therein). To this end, statistically complete and well-defined samples of AGNs equipped with X-ray spectral data and with a reliable estimate of the accretion parameters (SMBH mass, the absolute accretion rate, the accretion rate normalized to the Eddington limit) are required.
The recent availability of statistical relations (see Vestergaard 2009 for a review) that allow the systematic computation of the black-hole mass on large numbers of AGN has made it possible to estimate black-hole masses for very large samples of AGNs (usually optically selected): for instance, the last release of the SDSS QSO catalogue contains a mass estimate for more than 100 000 AGNs (Shen et al. 2011). In spite of these large numbers, the samples that contain information on both black-hole masses and X-ray spectra are significantly smaller. In particular, if we restrict attention to the hard X-ray energies (above 2 keV), where the primary X-ray emission is best observed and studied, the largest samples available for this kind of study contain a few hundred objects at most. The largest samples are often built using X-ray data from the XMM-Newton archive combined with optical data that come from SDSS (Risaliti et al. 2009; Vagnetti et al. 2010), from the literature (Bianchi et al. 2009) or from dedicated observations (Lusso et al. 2012; Grupe et al. 2010). A major problem affecting many samples is that they are often just a collection of sources available in both an X-ray and an optical catalogue so they do not necessarily represent a statistically complete and representative sample of AGNs.
To limit the possible biases deriving from this kind of selection, we present here a new data set containing black-hole masses and accretion rates (both absolute and normalized to the Eddington limit) for a well-defined flux-limited sample of X-ray sources selected from XMM-Newton, the Bright Serendipitous Survey (XBS1, Della Ceca et al. 2004; Caccianiga et al. 2008). The XBS is now almost completely identified (>98%) after ten years of dedicated spectroscopic observations, and it contains, by definition, XMM-Newton data of medium/good quality (from 100 to 104 net counts) that has allowed systematic X-ray spectral analysis for all the selected AGN (Corral et al. 2011). For most of the type 1 AGN contained in this sample, the optical/UV spectral energy distribution has been studied and a reliable estimate (i.e. not based on a bolometric correction) of the bolometric luminosity has already been published (Marchese et al. 2012). In this paper we present the estimate of the black-hole masses, using the single-epoch method. In a companion paper we will use these values, combined with the results of the X-ray analysis, to study the statistical relationship between X-ray properties and the accretion rate on the central SMBH (Fanali et al., in prep.).
The structure of the paper is the following. In Sect. 2 we briefly describe the XBS sample while in Sects. 3 and 4 we present the derivation of black-hole masses and accretion rates, respectively. In Sect. 5 we discuss how the presence of the radiation pressure can change the derived quantities, and in Sect. 6 we summarize results and conclusions.
We assume a flat ΛCDM cosmology with H0 = 65, ΩΛ = 0.7 and ΩM = 0.3.
2. The XBS sample of type 1 AGN
The XBS (Della Ceca et al. 2004; Caccianiga et al. 2008) is a wide-angle (28 sq. deg), high Galactic latitude (|b| > 20 deg) survey based on the XMM-Newton archival data. It is composed of two samples that are both flux-limited (~7 × 10-14 erg s-1 cm-2) in two separate energy bands: the 0.5−4.5 keV band (the BSS sample) and the 4.5−7.5 keV band (the “hard” HBSS sample). A total of 400 sources have been selected, 389 belonging to the BSS sample and 67 to the HBSS sample (56 sources are in common). Selection criteria and the general properties of the 400 objects are discussed in Della Ceca et al. (2004).
To date, the spectroscopic identification has nearly been completed, and 98% of the 400 sources have been spectroscopicaly observed and classified. The details of the classification process are presented in Caccianiga et al. (2007, 2008). In this paper we want to derive the mass of the central SMBH for the type 1 AGNs. In total, the XBS contains 276 type 1 AGN but we have computed the MBH only for the sub-sample of sources that was studied by Marchese et al. (2012) in order to have a reliable estimate of the bolometric luminosity. The sub-sample considered by Marchese et al. contains the type 1 AGN that fall in the area of sky surveyed by GALEX (Martin et al. 2005; Morrissey et al. 2007), therefore it can be considered as representative of the entire XBS sample of type 1 AGN. We have then excluded a few sources whose optical spectrum is either not available or without broad emission lines required to compute the BH mass, leaving us with a total of 154 AGNs. In Fig. 1, we compare the redshift distribution of the 154 type 1 AGN studied here and of the total XBS sample of 276 type 1 AGN. The two distributions are similar, as demonstrated by a KS test (KS probability of 98.6%).
 |
Fig. 1 Redshift distribution for the 154 XBS AGN1 discussed in this paper (continuous black line) compared to the distribution of the total sample of 276 AGN1 (green short-dashed line). Dotted (red) and long-dashed (blue) histograms indicate the objects whose black-hole mass has been derived using the Hβ and MgIIλ2798 Å lines, respectively. |
3. Black-hole mass
To estimate the black-hole masses of the XBS type 1 AGN, we used the “single epoch” (SE) spectral method, which is based on measuring the broad line widths and the continuum emission in a single spectrum (e.g. see Peterson 2010 and Marziani & Sulentic 2012, and references therein). The method assumes both that the BLR traces the gravitational potential due to the presence of the central SMBH and that the virial theorem can be applied. The two input quantities, the velocity dispersion and the size of the system (RBLR), can be inferred directly from the optical/UV spectrum: the line width yields direct information on the velocity dispersion, while the continuum luminosity can be used to estimate the system size through the RBLR/L “scaling relations” (e.g. Kaspi et al. 2000; Bentz et al. 2009). The unknown geometry of the BLR is one fundamental source of uncertainty for this method and, in general, for all methods based on the BLR kinematics (including the reverberation mapping method, Vestergaard 2009). The average value of the “virial factor” that takes the particular geometry of the system into account can be assumed “a priori” (e.g. McLure & Jarvis 2002) or it can be estimated through a comparison with the MBH-σ empirical relation observed in non-active galaxies (Onken et al. 2004; Woo et al. 2010; Graham et al. 2011). That the BLR geometry is probably different from object to object creates an intrinsic dispersion on the “virial factor”, which is one of the most important sources of uncertainty associated to these methods. Besides this “zero point” uncertainty, the SE method has an additional source of uncertainty due to the scatter on the size-luminosity relation. All considered, the total uncertainty on the SE method has been recently estimated to be between 0.35 and 0.46 dex (Park et al. 2012).
The emission lines used for the MBH measurement depend on the redshift of the source. For the XBS sample, the type 1 AGNs cover a redshift range between 0.02 and 2, therefore, the emission lines that can be used for the mass estimate are the Hβ (up to z ~ 0.8) and the MgIIλ2798 Å (from z ~ 0.3). In a number of cases both lines are included in the observed spectral range.
In this paper we adopt the relationships that are anchored to the virial factor estimated by Onken et al. (2004). For the Hβ, we used the relation discussed in Vestergaard & Peterson (2006): 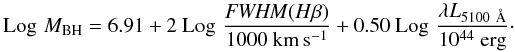 (1)For the MgIIλ2798 Å line we used the relation presented in Shen et al. (2011):
(1)For the MgIIλ2798 Å line we used the relation presented in Shen et al. (2011): 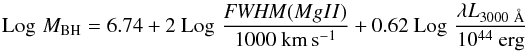 (2)this equation has been obtained by Shen et al. (2011) in such a way that the zero-order point (i.e. the virial factor) is the same as in the Hβ relation presented above (Eq. (1)) so that the masses are consistently derived from these two equations. In both relations, the line widths refer to the broad component, and it is assumed that a narrow component has been subtracted during the fitting procedure.
(2)this equation has been obtained by Shen et al. (2011) in such a way that the zero-order point (i.e. the virial factor) is the same as in the Hβ relation presented above (Eq. (1)) so that the masses are consistently derived from these two equations. In both relations, the line widths refer to the broad component, and it is assumed that a narrow component has been subtracted during the fitting procedure.
In the following sections we describe in detail the methods adopted to compute the two critical input quantities of the equations reported above, i.e. the line widths and the continuum luminosity.
3.1. Line width measurements
The different dependence of MBH on line width and luminosity (see Eqs. (1) and (2)) means that the statistical (i.e. not including the intrinsic dispersion of the relation and the uncertainty on the virial factor) uncertainty of the final MBH estimate will mostly come from the uncertainty on the line width. The line width measurement is then particularly difficult owing to the presence of different spectral components and considering the average quality of our spectra (average S/N ~ 10−11 in the spectral regions close to Hβ and MgIIλ2798 Å emission lines, with ~25% of objects having S/N below 5).
In particular, the correct determination of the width of the broad component of the emission line is hampered by a narrow component (which is particularly important for the Hβ line) and by the iron pseudo-continuum (which is critical for the MgIIλ2798 Å line). A simple component fit, not considering the possible presence of a narrow component, would lead to a systematic under-estimate of the broad line width (Denney et al. 2009). At the same time, not considering the existence of the iron pseudo-continuum may lead to an over-estimate of the line width. A common practice for taking this spectral complexity into account is to subtract a FeII template from the spectrum and, then, fit the subtracted spectrum with a number of narrow and broad components (usually with a Gaussian profile, e.g. see Shen et al. 2011, for details on the method). In the following, we discuss separately the methods used to derive the width of the broad components of the Hβ and MgII.
3.1.1. Hβ
For the fit of the Hβ line we use the method usually adopted in the literature i.e. we subtract an iron template to the spectra and then fit the residuals. To this end, we use the iron template presented in Véron-Cetty et al. (2004) and consider the 3500−6000 Å (rest-frame) spectral region. In this procedure there are three independent parameters that need to be determined: the normalization of the iron template (NFe), the line broadening (σFe), and velocity offset (VFe) of the iron lines. Constraining the lattest two parameters is usually difficult even for good quality spectra. In medium quality spectra (like the one of the SDSS spectra considered by Shen et al. 2011, where S/N ~ 10) these parameters are poorly constrained (e.g. see discussion in Shen et al. 2011). The quality of our spectra is, on average, similar to the ones of the SDSS spectra (and in some cases even lower), so we decided to fix both parameters. After subtracting of the iron template, we fit the resulting spectrum around the Hβ line using a model composed by three components: a PL continuum plus four Gaussians representing, respectively, the narrow and the broad components of the Hβ and the two [OIII] narrow lines. The width of the component describing the narrow Hβ is constrained to be equal to the width of two [OIII] lines. We run the fit in two steps: first we freeze the positions of the Gaussians to the expected wavelengths. In a second step, we leave the positions of the Gaussians describing the emission lines free to vary (with the maximum possible variation in the position of the iron components fixed to ~30 Å to avoid problems with the fitting procedure). The broad and the narrow Hβ components do not necessarily peak at the same wavelength to account for possible velocity offsets between the BLR and the NLR. We show an example of this fitting procedure in Fig. 2.
 |
Fig. 2 Example of a spectral model used to fit the region around the Hβ line. As described in the text, we first subtract an iron template from the spectrum (black line) and then we fit the residual (blue line) with a power-law continuum plus 3 Gaussians describing the narrow Hβ and the two [OIII] lines, plus an additional Gaussian to describe the broad component of the Hβ line. These components are represented by the dashed green lines while the total fit is represented by the red continuous line. |
 |
Fig. 3 Difference between the logarithms of the broad Hβ emission line width derived with two different methods, one based on the subtraction of an iron template where the line widths are fixed and a second method that, instead, leaves the iron line widths free to vary (see text for details). The data are split on the basis of the signal-to-noise around the Hβ line. |
We note that keeping the iron line width and position fixed during the fitting procedure may introduce a certain degeree of uncertainity (even systematic) in the computation of the broad Hβ width. The possibity that the iron lines could be systematically shifted with respect to the Hβ line has been investigated by several authors, and although there have been some claims of systematic large velocity offsets (up to 2000 km s-1) in the spectra of SDSS quasars (Hu et al. 2008), the analysis of good signal-to-noise ratio (S/N) spectra has recently demonstrated that the actual offsets are much smaller (<300 km s-1, Sulentic et al. 2012), if present. The impact of such small offsets on our fitting procedure is not going to be relevant. On the contrary, keeping the iron line width fixed can have a more significant impact on our mass estimates. To quantitatively evaluate this effect, we applied a second fitting method, not based on subtraction of an iron template, using an approach similar to the one used for fitting the MgIIλ2798 Å line (see below). In this method, we adopted a model composed of six Gaussians plus a power-law continuum. Two Gaussians are used to model the Hβ (for the narrow and the broad components), while two Gaussians are used to fit the two [OIII] narrow emission lines. The remaining two Gaussians are used to account for the two strongest FeII components usually observed at 4924 Å and 5023 Å. The widths of these two lines are left free to vary. Then we ran the fitting procedure following the two steps described above and found the best-fit width of the broad Hβ component. The resulting widths were finally compared to those obtained by subtracting the iron template. We carried out this comparison by splitting the sample into two sets: a first data set containing only the low S/N (in the Hβ region) spectra (S/N < 7) and a second data set containing the best spectra we have (S/N > 10). In Fig. 3 we show the distribution of the difference in the widths (in Log) computed using the two procedures, for both data sets. In the case of low S/N spectra there is no systematic difference between the two estimates. This is expected since, in case of very poor quality spectra, it is very difficult to detect any real difference in the iron line width, and all the differences are probably due just to random fluctuations in the fitting procedure. In contrast, for relatively good spectra (S/N > 10), we do observe a significant (~3σ) systematic offset between the line widths, the Hβ being typically larger in the iron template subtraction method (where the iron lines are fixed), when compared to the method where the iron lines are left free to vary. This is probably because, in the first method, part of the iron emission may be included in the broad Hβ component thus producing larger widths. We stress, however, that even in the S/N > 10 data set, the average quality of the spectra (S/N between 10 and 30) is certainly not comparable to the one typically required for a proper spectral deconvolution (>50) and, therefore, there is a high degree of degeneracy in the fitting process. We cannot exclude, for instance, that part of the observed offset is related to an underestimate of the broad Hβ component in the method where the iron widths are left free to vary. For this reason, it is difficult to establish which one of the two methods gives better results. However, the observed offset can be used as an estimate of the possible effect on the broad Hβ width because we have fixed the iron width when subtracting the iron template. The observed offset is 0.057 dex, which translates into an expected offset in the mass computed using the Hβ line of ~0.11. This offset is within the average statistical uncertainty on the masses computed from the Hβ line (~0.18 dex).
We finally note that fitting the Hβ broad line using only one Gaussian is certainly a simplification. The analysis of high S/N spectra of local Seyfert galaxies has revealed a complex phenomenology (e.g. see Sulentic et al. 2000, for a review). Given the typical S/N of our spectra, however, any attempt to provide a more complex fit to the broad Hβ profile would lead to very uncertain results, except for very few cases. Indeed, this is a general problem connected with the systematic application of the SE relation to large samples of spectra whose quality is typically much lower than that of the brightest and best-studied local Seyferts.
3.1.2. MgII
For the MgII we did not follow the same procedure as adopted for the Hβ line due to the difficulty of obtaining a reliable iron template at these wavelengths. We thus decided to include the iron components in the fitting procedure. Specifically, we adopted a model including two Gaussians for the narrow and broad components of MgIIλ2798 Å plus four additional Gaussians to reproduce the iron humps at 2630 Å, 2740 Å, 2886 Å and 2950 Å plus a power-law continuum (see Fig. 4).
 |
Fig. 4 Example of a spectral model to fit the region around the MgIIλ2798 Å line. This method includes the iron lines directly in the fitting procedure rather than subtracting an iron template from the spectrum, as typically done in the literature. The total fit is represented by the solid red line while the different components (the power-law continuum, the narrow and the broad components of the line and the iron humps) are represented by the dashed lines. |
Since, in the case of MgII, we do not have the two [OIII] line as a reference for the narrow line widths, we set the MgII narrow component to be equal to the instrumental resolution, for the spectra with a resolution worse than 500 km s-1. For the very few spectra with better resolution, the width of the narrow component is fixed to 500 km s-1. Again, as a first step we fix the positions of the components to the expected values and, then, we left them free to vary (with a maximum possible variation of 30 Å for the iron components). In fitting the MgII line we have thus assumed that a narrow component is present. It should be noted, however, that for the MgIIλ2798 Å line, the actual presence of a narrow component is less obvious than for the Hβ line. In their work, Vestergaard & Osmer (2009) did not subtract a narrow component during the fitting procedure of the MgII profile (which was modelled with two Gaussians both attributed to the broad component), while other authors (e.g. Mc Lure & Dunlop 2004) have considered a narrow plus a broad component for the MgIIλ298 Å line as in the analysis presented here. The choice of including the narrow component of the MgIIλ2798 Å is somewhat arbitrary. In our analysis, including the narrow MgIIλ2798 Å component gives a slightly better consistency between the masses computed using MgIIλ2798 Å and those computed using Hβ, so we decided to adopt this type of model.
3.1.3. Instrumental resolution
Finally, given the moderate resolution of the spectroscopic observations (~650−1200 km s-1), we applied a correction to the widths of the broad components of both Hβ and MgIIλ2798 Å, resulting from the fitting procedures described above, to account for the instrumental broadening, i.e.,
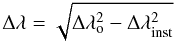 where Δλ, Δλo and Δλinst are the intrinsic, the observed, and the instrumental line width, respectively.
where Δλ, Δλo and Δλinst are the intrinsic, the observed, and the instrumental line width, respectively.
3.2. Monochromatic luminosities
Determination of the monochromatic luminosities at 5100 Å and 3000 Å also requires some caution. In principle we can use the fluxes derived directly from the spectra. This procedure, however, is not accurate for several reasons:
-
the absolute spectro-photometric calibration of our spectra is not always accurate since most of the data have been collected during non-photometric nights;
-
the spectra are often contaminated by the host galaxy light (the slit width used was often relatively large, from 1 to 2 arcsecs, depending to the seeing conditions);
-
the spectra must be corrected for the extinction, both Galactic and at the source. This is a particularly critical point since, given the relatively hard X-ray selection band, the XBS sample contains many type 1 AGNs with moderate levels of absorption (AV up to 1−2 mag, see Caccianiga et al. 2008).
To account for these points, we used the result of a systematic study of the optical/UV spectral energy distribution (SED) of the type 1 AGN of the XBS survey, described in Marchese et al. (2012). In this work we have collected photometric points, both in the optical (most from the SDSS) and in the UV band (from GALEX) and built the SED for each source. In the derivation of the SED we carefully took the presence of the host galaxy into account, on the basis of the strength of the 4000 Å contrast, and excluded it from the final SEDs. We also corrected the photometric points for the extinction, both due to our Galaxy and at the source, using the values of NH derived from the X-ray analysis (Corral et al. 2011) and assuming a Galactic gas-to-dust ratio. This is certainly an approximation since there are well-known examples of AGN where the dust-to-gas ratio is significantly different from what is observed in our Galaxy. However, in the XBS survey we have found generally good agreement between the optical classification (type1/type2 AGN) and the measured levels of NH (lower or greater than 4 × 1021 cm-2), with only a few (<10%) exceptions (Caccianiga et al. 2004; Corral et al. 2011). Therefore, we expect that this problem is not going to have a strong impact on our results, at least from a statistical point of view.
These SEDs have been then fitted with a multi-colour black-body accretion disk model, which includes corrections for temperature distribution near the black hole (for details see DISKPN in the XSPEC 12 software package, Arnaud et al. 1996). From this fit, we computed the rest frame 5100 Å and 3000 Å luminosities to be used in Eqs. (1) and (2) for the mass estimate.
3.3. Computing the BH masses
Using the methods described in the previous sections, we computed the black-hole masses for all the 154 type 1 AGNs of the XBS for which we analysed the SED, as described in Marchese et al. (2012) and for which we acquired an optical spectrum. For 32 objects we only covered the Hβ emission line while for 70 objects we have covered only the MgIIλ2798 Å line. In 52 cases we have detected both lines in the spectrum. In these cases we chose the mass estimate that is considered more accurate, i.e. the one based on the line with the best S/N and/or with the smallest error in the measured width (quite often, one of the two lines is at the edge of the observed spectrum). Overall, the black-hole masses were derived from the Hβ, in 62 cases, and from MgIIλ2798 Å line, in 92 cases.
The masses for the 154 type 1 AGN are reported in Table 1, together with the (statistical) errors. In Table 1 we also report the full width at half maximum (FWHM) of the lines and the values of the monochromatic luminosities used for the mass estimate. The distribution of the masses obtained for the 154 AGN1 of the XBS sample are reported in Fig. 5.
 |
Fig. 5 Distribution of the black-hole masses for the 154 XBS AGN1. Dotted (red) and dashed (blue) histograms show masses derived from Hβ and MgIIλ2798 Å lines respectively. |
3.4. Uncertainties on BH masses
Statistical uncertainities on the BH masses were estimated by combining the statistical errors on both line width and monochromatic luminosity, assuming that the two errors are independent:
where A = 2 and B is equal to 0.5 for the Hβ while it is 0.62 for MgIIλ2798 Å. σ+,− are the asymmetric errors (at the 68% confidence level) to the logarithm of the FWHM and luminosities, respectively.
The errors on the Hβ and MgIIλ2798 Å broad components are derived from the fitting precedure described above, by imposing Δχ2 = ±1. Similarly, the errors on the monochromatic luminosities are computed from the SED fitting procedure by again imposing Δχ2 = ±1 from the best-fit value. As described in Marchese et al. (2012), the SED fitting procedure takes the errors on the photometric points into account. These 1σ uncertainities include both the errors on photometry and additional sources of error due to the correction for the intrinsic extinction and the long term variability (since the used photometric data are not simultaneous). The uncertainty due to the correction for the host galaxy, based on the 4000 Å break, is not folded into these errors. However, in Marchese et al. (2012) we evaluated that by changing the starting value of the 4000 Å break within a reasonable range of values (from 45% to 55%), the variations in the photometric points only produce a negligible (≤14%) change in the best fit luminosity.
The statistical 1-σ errors on the broad line widths, monochromatic luminosities, and on the final black-hole masses are reported in Table 1. We stress that the errors on black-hole masses do not include the uncertainity on the SE method that, as already explained, is expected to be between 0.35 dex and 0.46 dex (Park et al. 2012) i.e. dominant when compared to the average statistical errors (~0.14 dex).
3.5. Comparison of the black-hole mass estimates
With the derived line widths and monochromatic luminosities we computed the MBH for all the AGN1 for which either the Hβ or the MgIIλ2798 Å lines have been observed.
 |
Fig. 6 Comparison between black-hole masses computed on the basis of the MgIIλ2798 Å and the Hβ lines for the XBS AGNs where both lines are included in the spectrum. Red points represent sources with a relatively high S/N (>5) around the line of interest and with lower statistical error bars (<0.2 dex) while grey points are objects with lower S/N spectra and/or larger error bars. As reference we plot the relation 1:1 (solid line), while the two dashed lines represent a scatter of 0.5 dex. |
For the 52 sources where both Hβ and MgIIλ2798 Å are included in the spectrum it is possible to compare the two MBH estimates. To evaluate the presence systematic offsets better, we first considered the objects with a relatively good spectrum (S/N > 5) and excluded the sources with large statistical errors on the final mass estimate (>0.2 dex). The comparison (Fig. 6) shows generally good agreement, without significant offsets and with a spread of ~0.28 dex. Considering all the objects, including those with less accurate determination of the mass the spread increases to ~0.38 dex, and there seems to be a systematic shift probably related to the difficulty of properly accounting for all the components during the spectral fit (in particular the iron lines around the MgIIλ2798 Å line and the narrow component of the Hβ line). In Table 1 we have flagged the masses derived from a problematic fit and those resulting from the analysis of poor S/N (<5) spectra.
As a further test of the reliability of our mass estimate we compared the black-hole masses derived in our work with those computed in Shen et al. (2011) for the few sources in common. Since Shen et al. (2011) presents masses computed using different formulae, we used the ones computed in the same way for the comparison, i.e. the VP06 for Hβ, and the S10 for MgIIλ2798 Å. The result of the comparison is presented in Fig. 7. In some cases, we used the same SDSS spectrum to derive the BH masses while in other cases we acquired an independent spectrum. As before, we first excluded from the test the sources with low S/N (<5) spectra (used in our analysis) and large errors (>0.2 dex) in either our estimate or in the Shen et al. estimate. The comparison shows a spread of ~0.2−0.3 dex and a marginal systematic offset between the two masses, with the ones computed in this work being larger on average by a factor ~0.17 dex. The offset is mainly present in the masses computed from MgIIλ2798 Å. By comparing separately the line widths and the monochromatic luminosities we have established that this offset is mainly attributed to an offset in luminosity rather than in line width. This offset is probably due to the method we used to compute the monochromatic luminosities that corrects for the extinction (both Galactic and at the source), as explained in the previous sections, thus yelding, on average, to higher corrected luminosities, in particular in the blue/UV spectral region. Considering all the sources in common between the two samples the spread increases to ~0.4 dex.
 |
Fig. 7 Comparison between black-hole masses computed in this paper and those computed by Shen et al. (2011), for the XBS AGNs included in the SDSS sample. Red and black points represent the objects with higher signal-to-noise ratio (>5) and smaller uncertainties on the mass derivation (<0.2 dex). Grey points, instead, represent the data with lower S/N and/or larger error bars. Filled (and red, in electronic version) points are sources for which we have used the SDSS spectrum to derive the BH mass, while open points indicate sources for which we used an optical spectrum taken in our own observations. As reference we plot the relation 1:1 (solid line), while the two dashed lines represent a scatter of 0.5 dex. |
4. Eddington ratio and 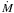
An important parameter that is suspected of regulating a number of observational properties of AGNs is the “normalized” bolometric luminosity, i.e. the so-called Eddington ratio, which is defined as 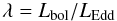 (3)where:
(3)where: 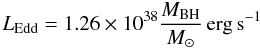 (4)We compute the values of Eddington ratio using the bolometric luminosities taken from Marchese et al. (2012) which was computed, as explained above, by fitting the optical/UV data with a disk model. The photometric points, and therefore the bolometric luminosity, were corrected for reddening as detailed in Marchese et al. (2012). The distribution of Eddington ratios is reported in Fig. 8.
(4)We compute the values of Eddington ratio using the bolometric luminosities taken from Marchese et al. (2012) which was computed, as explained above, by fitting the optical/UV data with a disk model. The photometric points, and therefore the bolometric luminosity, were corrected for reddening as detailed in Marchese et al. (2012). The distribution of Eddington ratios is reported in Fig. 8.
 |
Fig. 8 Distribution of the values of Eddington ratio for the 154 XBS AGN1. Dotted (red) and dashed (blue) histograms show the values based on masses derived from Hβ and MgIIλ2798 Å lines respectively. |
From the bolometric luminosity we can also derive an estimate of the absolute (i.e. not normalized to the Eddington limit) accretion rate: 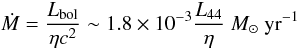 (5)where L44 is the bolometric luminosity in units of 1044 erg s-1 and η is the efficiency of the mass-to-energy conversion. We assume here an efficiency of 0.1 (Marconi et al. 2004). We note that the bolometric luminosities used to compute Ṁ also include the X-ray emission (in addition to the disk component) as described in Marchese et al. (2012). Therefore, by using these bolometric luminosities to compute Ṁ we are implicitly assuming that the energy budget carried by the X-ray emission is directly related to the accretion process. This is, of course, not an obvious assumption, since the origin of the X-ray emission is still an open issue. In any case, we stress that the contribution of the X-ray emission to the bolometric luminosity is, in general, relatively low (~25% on average in our sample) and, therefore, the values of Ṁ are not going to change significantly (on average) if we use only the disk emission in Eq. (5).
(5)where L44 is the bolometric luminosity in units of 1044 erg s-1 and η is the efficiency of the mass-to-energy conversion. We assume here an efficiency of 0.1 (Marconi et al. 2004). We note that the bolometric luminosities used to compute Ṁ also include the X-ray emission (in addition to the disk component) as described in Marchese et al. (2012). Therefore, by using these bolometric luminosities to compute Ṁ we are implicitly assuming that the energy budget carried by the X-ray emission is directly related to the accretion process. This is, of course, not an obvious assumption, since the origin of the X-ray emission is still an open issue. In any case, we stress that the contribution of the X-ray emission to the bolometric luminosity is, in general, relatively low (~25% on average in our sample) and, therefore, the values of Ṁ are not going to change significantly (on average) if we use only the disk emission in Eq. (5).
The distribution of Ṁ is reported in Fig. 9. To facilitate the comparison with previous figures we also show the Ṁ separately for Hβ and MgIIλ2798 Å mass-derived sources, although in this case, the value of Ṁ does not depend on the derived BH mass.
5. The effect of radiation pressure
It has been suggested (Marconi et al. 2008; Marconi et al. 2009) that the black-hole masses derived from the virial theorem can be severely underestimated due to the effect of the radiation pressure. This effect, not considered in the usual SE relations, is expected to be important for accretion rates close to the Eddington limit according to the following equation (Marconi et al. 2008): ![\begin{equation} M_{\rm BH}=M_{\rm BH,0}\left[1+\lambda_0\left(1-a+\frac{a}{\sigma_T N_{\rm H}}\right)\right] \end{equation}](/articles/aa/full_html/2013/01/aa20343-12/aa20343-12-eq57.png) (6)where MBH is the “real” black-hole mass, MBH,0 is the black-hole virial mass computed by neglecting the radiation pressure, λ0 is the Eddington ratio computed using MBH,0, a = Lion/L (i.e. the ratio between the ionizing continuum luminosity and the bolometric luminosity), σT is the Thomson cross-section, and NH the column density of each BLR cloud along the line of sight. As noted by Marconi et al. (2008), for reasonable assumptions on the BLR density (~1023 cm-2) if the accretion is close to the Eddington limit, the correction could be as high as a factor 10. The actual importance of the radiation pressure, however, has been debated in the recent literature. Netzer (2009), for instance, notes that the Eddington ratios of a sample of type 1 AGN from the SDSS (whose black-hole masses were computed using the virial method), when corrected for the radiation pressure, turnes out to be significantly lower when compared to the Eddington ratio distribution of an SDSS sample of type 2 AGN for which the black-hole masses have been computed using a different technique (M-σ relation). In contrast, if no correction is applied, the two distributions are similar.
(6)where MBH is the “real” black-hole mass, MBH,0 is the black-hole virial mass computed by neglecting the radiation pressure, λ0 is the Eddington ratio computed using MBH,0, a = Lion/L (i.e. the ratio between the ionizing continuum luminosity and the bolometric luminosity), σT is the Thomson cross-section, and NH the column density of each BLR cloud along the line of sight. As noted by Marconi et al. (2008), for reasonable assumptions on the BLR density (~1023 cm-2) if the accretion is close to the Eddington limit, the correction could be as high as a factor 10. The actual importance of the radiation pressure, however, has been debated in the recent literature. Netzer (2009), for instance, notes that the Eddington ratios of a sample of type 1 AGN from the SDSS (whose black-hole masses were computed using the virial method), when corrected for the radiation pressure, turnes out to be significantly lower when compared to the Eddington ratio distribution of an SDSS sample of type 2 AGN for which the black-hole masses have been computed using a different technique (M-σ relation). In contrast, if no correction is applied, the two distributions are similar.
Given the difficulty of assessing the actual importance of the radiation pressure, we decided to present both the corrected and the uncorrected masses and Eddington ratios in this paper. The corrected masses, in particular, were computed using the equation above and assuming a = 0.6 and NH = 1023 cm-2 (the values assumed in Marconi et al. 2008).
In Fig. 10 we show the black-hole mass and in Fig. 11 the Eddington ratio distributions corrected for the radiation pressure and compared with the uncorrected quantities. As expected, the corrected masses are shifted towards the higher values, while the Eddington ratio presents a sharp cut off at 0.1 (see discussion in Marconi et al. 2008).
The values of masses and Eddington ratios corrected for the radiation pressure are included in Table 1.
 |
Fig. 10 Distribution of the black-hole masses corrected for the radiation pressure (red continuous line), as described in the text. For comparison we show the distribution of uncorrected masses (black dashed line). |
 |
Fig. 11 Distribution of the Eddington ratios corrected for the radiation pressure (red continuous line), as described in the text. For comparison we show the distribution of uncorrected masses (black dashed line). |
6. Summary and conclusions
We have presented black-hole masses and accretion rates (both absolute and relative to the Eddington limit) for 154 type 1 AGNs belonging to the XBS sample. The masses were derived using the single-epoch method and adopting the most recent scaling relations involving the Hβ and the MgIIλ2798 Å emission lines. The selected sources cover a range of masses from 107 to 1010 M⊙ with a peak around 8 × 108 M⊙ and a range of accretion rates from 0.01 to ~50 M⊙/y (assuming an efficiency of 0.1), with a peak at around 1 M⊙/y. The values of the Eddington ratio range from 0.001 to ~0.5 and peak at 0.1.
We have verified that the computed masses are in broad agreement with the ones presented in Shen et al. (2011) although we found a systematic offset of ~0.17 dex (with our masses being higher) probably because of the different methods adopted in the two works to estimate the continuum luminosity.
We stress that the 154 type 1 AGN presented here constitute a well-defined flux-limited sample of type 1 AGN and not just a collection of data from the literature or from public archives. This characteristic, combined with the systematic availability for all these objects of crucial X-ray information (based on X-ray spectral analysis) and on the optical/UV SED, makes this sample instrumental for statistical studies. In a companion paper (Fanali et al., in prep.), we will use the results presented here to study the link between the hot-corona, responsible for the X-ray emission, and the accretion process onto the central black hole.
Online material
Black-hole masses of the XBS AGN1.
The XBS is one of the research programmes conducted by the XMM-Newton Survey Science Center (SSC, see http://xmmssc-www.star.le.ac.uk), a consortium of 10 international institutions, appointed by the European Space Agency (ESA) to help the XMM-Newton Science Operations Centre (SOC) in developing the software analysis system, to pipeline process all the XMM-Newton data, and to exploit the XMM-Newton serendipitous detections. The Osservatorio Astronomico di Brera is one of the Consortium Institutes.
Acknowledgments
We thank the referee for useful comments that significantly improved the paper and Tommaso Maccacaro for his initial involvement in the XBS project. The authors acknowledge financial support from ASI (grants No. I/088/06/0 and I/009/10/0). S.M. acknowledges financial support by the Spanish Ministry of Economy and Competitiveness, through grant AYA2010-21490-C02-01.
References
- Arnaud, K. A. 1996, Astronomical Data Analysis Software and Systems V, eds. G. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Bianchi, S., Bonilla, N. F., Guainazzi, M., Matt, G., & Ponti, G. 2009, A&A, 501, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Braito, V., et al. 2004, A&A, 416, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Della Ceca, R., et al. 2007, A&A, 470, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Severgnini, P., Della Ceca, R., et al. 2008, A&A, 477, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corral, A., Della Ceca, R., Caccianiga, A., et al. 2011, A&A, 530, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Della Ceca, R., Maccacaro, T., Caccianiga, A., et al. 2004, A&A, 428, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denney, K. D., Peterson, B. M., Dietrich, M., Vestergaard, M., & Bentz, M. C. 2009, ApJ, 692, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, A. W., Onken, C. A., Athanassoula, E., & Combes, F. 2011, MNRAS, 412, 2211 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1993, ApJ, 413, 507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hu, C., Wang, J.-M., Ho, L. C., et al. 2008, ApJ, 687, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2004, MNRAS, 352, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Jarvis, M. J. 2002, MNRAS, 337, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Marchese, E., Della Ceca, R., Caccianiga, A., et al. 2012, A&A, 539, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Axon, D. J., Maiolino, R., et al. 2008, ApJ, 678, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Axon, D. J., Maiolino, R., et al. 2009, ApJ, 698, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Marziani, P., & Sulentic, J. W. 2012, New A Rev., 56, 49 [Google Scholar]
- Merloni, A., & Heinz, S. 2012 [arXiv:1204.4265] [Google Scholar]
- Morrissey, P., Conrow, T., Barlow, T. A., et al. 2007, ApJS, 173, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2009, ApJ, 695, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Park, D., Woo, J.-H., Treu, T., et al. 2012, ApJ, 747, 30 [Google Scholar]
- Peterson, B. M. 2010, IAU Symp., 267, 151 [NASA ADS] [Google Scholar]
- Risaliti, G., Young, M., & Elvis, M. 2009, ApJ, 700, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000, ARA&A, 38, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Marziani, P., Zamfir, S., & Meadows, Z. A. 2012, ApJ, 752, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Vagnetti, F., Turriziani, S., Trevese, D., & Antonucci, M. 2010, A&A, 519, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M. 2009 [arXiv:0904.2615] [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., Joly, M., & Véron, P. 2004, A&A, 417, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestergaard, M., & Osmer, P. S. 2009, ApJ, 699, 800 [Google Scholar]
- Woo, J.-H., Treu, T., Barth, A. J., et al. 2010, ApJ, 716, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2010, ApJ, 708, 1388 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Redshift distribution for the 154 XBS AGN1 discussed in this paper (continuous black line) compared to the distribution of the total sample of 276 AGN1 (green short-dashed line). Dotted (red) and long-dashed (blue) histograms indicate the objects whose black-hole mass has been derived using the Hβ and MgIIλ2798 Å lines, respectively. |
| In the text | |
 |
Fig. 2 Example of a spectral model used to fit the region around the Hβ line. As described in the text, we first subtract an iron template from the spectrum (black line) and then we fit the residual (blue line) with a power-law continuum plus 3 Gaussians describing the narrow Hβ and the two [OIII] lines, plus an additional Gaussian to describe the broad component of the Hβ line. These components are represented by the dashed green lines while the total fit is represented by the red continuous line. |
| In the text | |
 |
Fig. 3 Difference between the logarithms of the broad Hβ emission line width derived with two different methods, one based on the subtraction of an iron template where the line widths are fixed and a second method that, instead, leaves the iron line widths free to vary (see text for details). The data are split on the basis of the signal-to-noise around the Hβ line. |
| In the text | |
 |
Fig. 4 Example of a spectral model to fit the region around the MgIIλ2798 Å line. This method includes the iron lines directly in the fitting procedure rather than subtracting an iron template from the spectrum, as typically done in the literature. The total fit is represented by the solid red line while the different components (the power-law continuum, the narrow and the broad components of the line and the iron humps) are represented by the dashed lines. |
| In the text | |
 |
Fig. 5 Distribution of the black-hole masses for the 154 XBS AGN1. Dotted (red) and dashed (blue) histograms show masses derived from Hβ and MgIIλ2798 Å lines respectively. |
| In the text | |
 |
Fig. 6 Comparison between black-hole masses computed on the basis of the MgIIλ2798 Å and the Hβ lines for the XBS AGNs where both lines are included in the spectrum. Red points represent sources with a relatively high S/N (>5) around the line of interest and with lower statistical error bars (<0.2 dex) while grey points are objects with lower S/N spectra and/or larger error bars. As reference we plot the relation 1:1 (solid line), while the two dashed lines represent a scatter of 0.5 dex. |
| In the text | |
 |
Fig. 7 Comparison between black-hole masses computed in this paper and those computed by Shen et al. (2011), for the XBS AGNs included in the SDSS sample. Red and black points represent the objects with higher signal-to-noise ratio (>5) and smaller uncertainties on the mass derivation (<0.2 dex). Grey points, instead, represent the data with lower S/N and/or larger error bars. Filled (and red, in electronic version) points are sources for which we have used the SDSS spectrum to derive the BH mass, while open points indicate sources for which we used an optical spectrum taken in our own observations. As reference we plot the relation 1:1 (solid line), while the two dashed lines represent a scatter of 0.5 dex. |
| In the text | |
 |
Fig. 8 Distribution of the values of Eddington ratio for the 154 XBS AGN1. Dotted (red) and dashed (blue) histograms show the values based on masses derived from Hβ and MgIIλ2798 Å lines respectively. |
| In the text | |
 |
Fig. 9 Distribution of the values of Ṁ for the 154 XBS AGN1. Line styles as in Fig. 5. |
| In the text | |
 |
Fig. 10 Distribution of the black-hole masses corrected for the radiation pressure (red continuous line), as described in the text. For comparison we show the distribution of uncorrected masses (black dashed line). |
| In the text | |
 |
Fig. 11 Distribution of the Eddington ratios corrected for the radiation pressure (red continuous line), as described in the text. For comparison we show the distribution of uncorrected masses (black dashed line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.