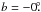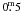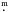| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 13 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201220097 | |
| Published online | 21 December 2012 | |
Strömgren photometric survey in the Galactic anticenter direction⋆,⋆⋆
1 Departament d’Astronomia i Meteorologia and IEEC-ICC-UBUniversitat de Barcelona, Martí i Franquès, 1, 08028 Barcelona, Spain
e-mail: mmonguio@am.ub.es
2 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
Received: 24 July 2012
Accepted: 2 November 2012
Aims. The main purpose is to map the radial variation of the stellar space density for the young stellar population in the Galactic anticenter direction in order to understand the structure and location of the Perseus spiral arm.
Methods. A uvbyHβ Strömgren photometric survey covering 16 deg2 in the anticenter direction was carried out using the Wide Field Camera at the Isaac Newton Telescope. This is the natural photometric system for identifying young stars and obtaining accurate estimates of individual distances and ages. The calibration to the standard system was undertaken using open clusters.
Results. We present a main catalog of 35 974 stars with all Strömgren indexes and a more extended one with 96 980 stars with partial data. The central 8 deg2 have a limiting magnitude of V ~ 17m, while the outer region reaches V ~ 15.m5. These large samples will permit us to analyze the stellar surface density variation associated to the Perseus arm also to study the properties of the stellar component and the interstellar extinction in the anticenter direction.
Key words: Galaxy: structure / methods: observational / surveys / techniques: photometric
Final catalog and catalog with individual measurements are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/549/A78
© ESO, 2012
1. Introduction
While it is well established that spiral arms are important agents driving the evolution of the galactic disks (Sellwood 2011; Fujii et al. 2011), the observational evidence of the spiral arms in the Milky Way are frustratingly inconclusive (Lépine et al. 2011). Key questions are still open: e.g., which is the mechanism of the formation and evolution of the spiral pattern in stellar disks; are they transients or long-lived structures; which are their building blocks, stellar or gaseous? Spitzer/IRAC infrared data (Benjamin 2008) provide new insight into the spiral pattern in the inner region of the Galactic disk, but we have a vague and very confused picture of the outer Milky Way spiral arm structure.
Few projects have studied the anticenter, such as the VLBA project (Reid et al. 2009; Brunthaler et al. 2011) that provides accurate parallaxes for some masers in massive star-forming regions. Vázquez et al. (2008) looked at the third Galactic quadrant using kinematic distances of CO clouds and some open clusters and associations, and propose that the Perseus spiral arm is only defined by gas over a large extent in this direction. Maps of OB-associations and HII-regions (Georgelin & Georgelin 1976; Russeil 2003) and the Galactic distribution of free electrons (Taylor & Cordes 1993) show a four-armed pattern. On the other hand, COBE K-band data (Drimmel 2000) suggest that the non-axisymmetric mass perturbation has a two-rather than a four-armed structure. External galaxies often show a two-armed structure in near-infrared, while they may appear multi-armed in visual bands (Grosbøl et al. 2004). The spiral model of the Milky Way obtained with Spitzer/IRAC infrared data in the Galactic center direction (Benjamin 2008) agrees with this extragalactic scenario. Benjamin (2008) proposes that the Milky Way has two major spiral arms (Scutum-Centaurus and Perseus) with higher stellar densities and two minor arms (Sagittarius and Norma) mainly filled with gas and pockets of young stars.
The Strömgren photometric survey presented here was conducted with the main goal to derive the radial stellar density variation associated to the Perseus arm in the Galactic anticenter. We want to see whether an overdensity of young stars associated to this arm can be identified. The Galactic anticenter direction was chosen because a second step of the project will be to obtain radial velocities for a subset of stars to study the velocity perturbation due to the arm. For this purpose, the anticenter direction is optimal since corrections related to Galactic rotation are negligible in the radial velocity component. Then, accurate distances to individual stars are critical for detecting the radial location of an overdensity. Strömgren uvbyHβ photometry is the natural system for obtaining them. It is also optimal to characterize the outer galaxy with Perseus and Cygnus arms (see Russeil 2003) as candidates for massive spiral arms. Both the strong interstellar extinction in the direction to the Galactic center and the fact that Sagittarius may not be a major arm strongly suggest using the anticenter direction as the better option.
The current paper presents the catalog. In Sect. 2 we describe the requirements for the survey, while in Sect. 3 the data reduction procedures followed to obtain the photometry are explained, as well as the calibrations. Section 4 describes the steps in deriving the mean values in the final catalog from the individual measurements. Internal accuracies, limiting magnitudes, and comparisons with other catalogs can also be found in this section. Finally, Sect. 5 summarizes the characteristics of the survey and briefly discusses the next steps of the project.
2. The Strömgren anticenter survey
The Strömgren anticenter survey must fulfill several requirements in order to have the capability of detecting a possible overdensity of young stars induced by the Perseus arm, expected to be at about 2 kpc (Xu et al. 2006) in the anticenter direction. Important requirements are 1) a limiting magnitude to allow the detection of young stars up to about 3 kpc; 2) a survey area large enough to include a statistically significant number of young stellar objects in the anticenter direction; and 3) precise photometry to derive Strömgren photometric distances beyond the Perseus arm.
Stars with ages between 150 and 500 Myr (such as those with spectral types B5–A3) are the best population to study the possible overdensity due to the Perseus spiral arm, since they are young enough to still have a small intrinsic velocity dispersion (making them respond stronger to a perturbation), but they are also old enough to have approached a dynamic equilibrium with the spiral perturbation. Strömgren uvbyHβ photometry (Strömgren 1966) is the natural system to identify this population, and it allows us to obtain accurate estimates of individual distances and ages.
A statistically significant amount of stars in the photometric survey is needed, and they need to reach at least 3 kpc from the Sun, so the required limiting magnitude is 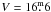 to detect an A0V star and
to detect an A0V star and 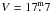 for an A3V star (assuming Av = 1 mag/kpc). To select the survey area needed, Besançon galaxy model simulations were used (Robin et al. 2003). Since it is likely that our galaxy has a relative weak perturbation (i.e. ~ 10% variation in the disk density), approximately 900 B5–A3 stars per radial 1 kpc bin are needed for a 3σ detection. Following the simulations, an 8 deg2 area is needed to achieve this number of stars. This is what we call the central part of the survey. Since the volume covered in the nearby bins is small and also since there are saturation effects, the statistics for these bins are too small, so an extra area with brighter limiting magnitude was added, increasing the survey to 16 deg2. This surrounding area is named the outer part of the survey.
for an A3V star (assuming Av = 1 mag/kpc). To select the survey area needed, Besançon galaxy model simulations were used (Robin et al. 2003). Since it is likely that our galaxy has a relative weak perturbation (i.e. ~ 10% variation in the disk density), approximately 900 B5–A3 stars per radial 1 kpc bin are needed for a 3σ detection. Following the simulations, an 8 deg2 area is needed to achieve this number of stars. This is what we call the central part of the survey. Since the volume covered in the nearby bins is small and also since there are saturation effects, the statistics for these bins are too small, so an extra area with brighter limiting magnitude was added, increasing the survey to 16 deg2. This surrounding area is named the outer part of the survey.
Distances that are more accurate than 25% are needed to identify a 500 pc spiral arm perturbation at 2 kpc distance. This requirement imposes an upper limit on the errors in the absolute magnitude and in the interstellar extinction, both parameters to be derived from the Strömgren photometry. The procedures proposed by Crawford (1978, 1979), Strömgren (1966), allow us to compute the absolute magnitudes for early (B0–A0), intermediate (A0–A3), and late type (A3–F0) stars, respectively. We estimated by simple error propagation that errors in Hβ and c0 smaller than 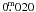 and
and 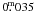 result in distance errors between 25–15% for B5–A0 stars and 25% for A3 type stars. These values were computed assuming an error smaller than
result in distance errors between 25–15% for B5–A0 stars and 25% for A3 type stars. These values were computed assuming an error smaller than 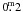 for the visual extinction (AV). Although playing a role in the classification process, the error in other indexes makes no significant contribution to the estimation of distance errors.
for the visual extinction (AV). Although playing a role in the classification process, the error in other indexes makes no significant contribution to the estimation of distance errors.
Due to the Galactic warp, the Galactic plane is expected to be slightly below Galactic latitude b = 0° in the anticenter direction (see Momany et al. 2006). For that reason the center of the survey area was shifted down to 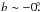 5 in a low-extinction region (Froebrich et al. 2007).
5 in a low-extinction region (Froebrich et al. 2007).
3. Observations and data reduction
3.1. Layout of the observations
The observations were conducted using the Wide Field Camera (WFC) at the Isaac Newton Telescope (INT) located at El Roque de los Muchachos in the Canary Islands. The WFC is a four-chip mosaic of thinned AR-coated EEV 4K × 2K devices with pixels size of 0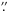 333 and an edge to edge limit of the mosaic of 34
333 and an edge to edge limit of the mosaic of 34 2. The six filters used were Strömgren u, v, b, y, Hβw, Hβn (see the central wavelength and band width in Table 1). Pixel binning of 1 × 1 and slow read-out mode were used for the observations, with a typical seeing of 1″–1
2. The six filters used were Strömgren u, v, b, y, Hβw, Hβn (see the central wavelength and band width in Table 1). Pixel binning of 1 × 1 and slow read-out mode were used for the observations, with a typical seeing of 1″–1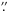 5. The WFC is the only wide-field facility in the northern hemisphere that offers the full set of Strömgren filters.
5. The WFC is the only wide-field facility in the northern hemisphere that offers the full set of Strömgren filters.
Central wavelength and FWHM of the filters used.
 |
Fig. 1 Plot of the 60 WFC fields observed. Red line shows the |
Dates for the observing runs and exposure times for each observation and filter for our program fields.
Data from three different observing runs (2009A, 2010B, and 2011A) were used for the catalog, and data from 2010A were excluded due to cloudy conditions. We were also granted some director’s discretionary time (in 2009 and 2011), but owing to bad weather these nights were not successful. Our 16 deg2 observing area was divided in a grid of 5 × 12 WFC fields (see Fig. 1), with an overlap between them of 3′ in order to check for field-to-field variations.
A different observational strategy was followed for the central and outer regions. For each of the 27 central fields (see Fig. 1), three consecutive observations were obtained, with a shift of 10″ between them, in order to detect cosmic rays and avoid bad pixels. Exposure times for each filter and observation are detailed in Table 2. The observations in the outer region, which includes 33 WFC fields, were planned to increase the statistics for nearby stars in the first kiloparsec distance bins. A single observation with shorter exposure times was conducted for each of these fields (instead of three observations with offsets as in the central region).
The calibration fields used for the transformation to the standard system are given in Table 2. The open cluster NGC 1893 was observed several times during the first two runs. The central part of this cluster has Strömgren photometry available from Tapia et al. (1991) and Marco et al. (2001). To better control the transformation for each of the four WFC chips, several observations of this cluster were done, each time placing the center of the cluster in the center of each of the WFC chips. This strategy ensured that enough bright stars were available in each field, with about 50 stars per chip for the transformation to the standard system. These data were also used to calibrate other stars around the cluster, which were used as secondary standards. During the first observing nights, two anticenter fields were observed repeatedly (namely ac308 and ac406). After their calibration using NGC 1893, they were used as deeper secondary standard fields in the following observing nights. The Coma Berenices (Peña et al. 1993; Crawford & Barnes 1969a) and Praesepe (Crawford & Barnes 1969b; Reglero & Fabregat 1991) open clusters were used as standard fields in some of the runs because they are older than NGC 1893.
3.2. Image pre-reduction and photometry extraction
The images were reduced using several IRAF1 tasks. First, original files were split into four different images, one for each chip, and the bias derived from the overscan areas was subtracted. Bad pixels were replaced by linear interpolation using the nearest good pixels through the fixpix task. The linearity correction proposed on the CASU INT web page2 was applied, as was the transformation factor from ADUs to electrons given in the manual. Flatfielding was applied using the sky flats obtained during the observational runs. A mask was also applied to avoid the vignetted corner of chip 3.
All the stars available in the images were located using the daofind routine. Using the PSF photometry to derive instrumental magnitudes was carefully investigated. But the high dependency on the parameters that define the quality of a particular photometric image (seeing, sky background, etc.) can lead to differences on the order of 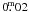 to
to 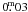 , so the PSF fitting method was rejected and the full survey was reduced using a homogeneous aperture-corrected photometry. Twelve different aperture radii provided twelve different magnitudes for each star. The daogrow algorithm was used to obtain the aperture corrections and the fitted radii. The final instrumental magnitudes were computed from the integration of the derived curve of growth.
, so the PSF fitting method was rejected and the full survey was reduced using a homogeneous aperture-corrected photometry. Twelve different aperture radii provided twelve different magnitudes for each star. The daogrow algorithm was used to obtain the aperture corrections and the fitted radii. The final instrumental magnitudes were computed from the integration of the derived curve of growth.
3.3. Extinction correction
Our calibration fields (see Table 2) were observed at several airmasses each night. Fitting their differences in magnitude vs. the differences in airmass, the extinction coefficients for each night were obtained. An intermediate range of magnitudes for these stars was selected for the fit, avoiding the brightest and the faintest ones. The measurements with airmass differences smaller than 0.1 were also rejected. The fitted function was: 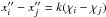 for all the available pairs of measurements i ≠ j from the same star where χ is the airmass for each measurement, and x′′ indicates instrumental magnitudes. The extinction coefficients kx for each of the six filters (u, v, b, y, Hβw, and Hβn) and night are listed in Table A.1, along with the ranges in airmass used. The extinction-corrected magnitudes and indexes (x′) were then computed as
for all the available pairs of measurements i ≠ j from the same star where χ is the airmass for each measurement, and x′′ indicates instrumental magnitudes. The extinction coefficients kx for each of the six filters (u, v, b, y, Hβw, and Hβn) and night are listed in Table A.1, along with the ranges in airmass used. The extinction-corrected magnitudes and indexes (x′) were then computed as 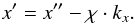 (1)In the case of the Hβ extinction coefficients, we computed and applied the average of the values obtained for Hβw and Hβn. (As known, they are centered on the same wavelength.) This coefficient was applied independently to each filter, which allowed us to take the change in airmass between both exposures into account.
(1)In the case of the Hβ extinction coefficients, we computed and applied the average of the values obtained for Hβw and Hβn. (As known, they are centered on the same wavelength.) This coefficient was applied independently to each filter, which allowed us to take the change in airmass between both exposures into account.
3.4. Transformation to the standard system
The photometry from our calibration fields (see photometric ranges in Table A.2) was used to obtain the transformation coefficients to the standard Strömgren system. Several equations with different color terms were checked in order to select those that minimize the errors and correlations between coefficients, and also to avoid insignificant terms. The selected set of equations were ![% subequation 1536 0 \begin{eqnarray} \label{transf1}&& y'-V_{\mathrm{cat}} = A_1 + B_1\cdot(b-y)_{\mathrm{cat}} , \\[1mm] \label{transf2}&& (b-y)' = A_2 + C_2\cdot(b-y)_{\mathrm{cat}} ,\\[1mm] \label{transf3}&& c_1' = A_3 + B_3 \cdot(b-y)_{\mathrm{cat}} + C_3 \cdot c_{1\mathrm{cat}} ,\\[1mm] \label{transf4}&& (v-b)' = A_4 + B_4\cdot (b-y)_{\mathrm{cat}} + C_4\cdot (v-b) + D_4\cdot c_{1\mathrm{cat}}, \\[1mm] \label{transf5}&& {\rm H}\beta ' = A_5 + B_5 \cdot (b-y)_{\mathrm{cat}} + C_5 \cdot ({\rm H}\beta_{\mathrm{cat}} -2.8), \end{eqnarray}](/articles/aa/full_html/2013/01/aa20097-12/aa20097-12-eq48.png) where the prime indicates instrumental extinction-corrected variables and the subscript cat indicates the standard values. The fitting equation in (v − b) was selected instead of m1, because m1 has a narrower dynamical range for young stars than (v − b). As discussed in Sect. 4, the magnitudes in some individual filters may be missing, especially in the u filter due to the need for very long exposure times. In this case Eqs. (2d) and (2e) had to be modified to avoid the c1 or (b − y) indexes like
where the prime indicates instrumental extinction-corrected variables and the subscript cat indicates the standard values. The fitting equation in (v − b) was selected instead of m1, because m1 has a narrower dynamical range for young stars than (v − b). As discussed in Sect. 4, the magnitudes in some individual filters may be missing, especially in the u filter due to the need for very long exposure times. In this case Eqs. (2d) and (2e) had to be modified to avoid the c1 or (b − y) indexes like 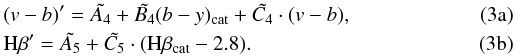 Equations (3a) and (3b) were only used when the initial Eqs. (2d) and (2e) could not be used because some exposure in an individual filter was missing. The obtained coefficients from each night are listed in Tables A.3 and A.4. Chip 3 has a slightly different behavior than the others, as can be seen in coefficients A3 and C5, possibly because it is vignetted. The errors in the photometric indexes are computed from direct error propagation of the coefficients and magnitudes. Correlations among extinction coefficients were taken into account, as well as correlations among coefficients for the transformation to the standard system. Since correlations between both sets have not been taken into account, our errors can be slightly overestimated. However, as our standards have a wide range in both airmasses and colors, the contribution for such correlations should be small.
Equations (3a) and (3b) were only used when the initial Eqs. (2d) and (2e) could not be used because some exposure in an individual filter was missing. The obtained coefficients from each night are listed in Tables A.3 and A.4. Chip 3 has a slightly different behavior than the others, as can be seen in coefficients A3 and C5, possibly because it is vignetted. The errors in the photometric indexes are computed from direct error propagation of the coefficients and magnitudes. Correlations among extinction coefficients were taken into account, as well as correlations among coefficients for the transformation to the standard system. Since correlations between both sets have not been taken into account, our errors can be slightly overestimated. However, as our standards have a wide range in both airmasses and colors, the contribution for such correlations should be small.
The positions in the J2000 coordinate system were determined using wcs and a fifth-order polynomial taking USNO-A2 (Monet 1998) as reference catalog.
 |
Fig. 2 Illumination differences in magnitudes at different field positions. Black lines show the location of the four chips, and coordinates in degrees are centered on the central chip. The illumination differences at each position were computed as the Gaussian-weighted mean (with σ = 0.1°) of the residuals around each point. |
3.5. Illumination correction
Since WFC covers a large field, the importance of the illumination correction must be checked, owing to different illumination of the CCDs. To do that, a field of stars was observed at several positions on the CCDs, and only the y filter was used since the illumination correction is not expected to be color dependent. All the computed instrumental magnitudes for each star, corrected for atmospheric extinction, were averaged to obtain a mean magnitude for each of them. The residuals between each individual magnitude and the computed mean magnitude were computed. Figure 2 shows the smoothed distribution for the residuals across the field of view of the WFC. A weak trend in right ascension was found, reaching values up to +/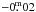 , which is below our general photometric errors. No significant trend was found in declination. The scatter of the data did not justify using anything higher than a second-order fit in right ascension: Δm = aα2 + bα + c. The results of the fit are a = −0.484 ± 0.029 mag/deg2, b = −0.159 ± 0.008 mag/deg, c = 0.005 ± 0.001 mag with residuals of 0.04 mag. This correction was applied to a test area with no significant change in the final mean magnitudes, except for a slight increase in the corresponding errors. Finally, the computed illumination correction was not applied.
, which is below our general photometric errors. No significant trend was found in declination. The scatter of the data did not justify using anything higher than a second-order fit in right ascension: Δm = aα2 + bα + c. The results of the fit are a = −0.484 ± 0.029 mag/deg2, b = −0.159 ± 0.008 mag/deg, c = 0.005 ± 0.001 mag with residuals of 0.04 mag. This correction was applied to a test area with no significant change in the final mean magnitudes, except for a slight increase in the corresponding errors. Finally, the computed illumination correction was not applied.
Number of stars for which mean magnitudes and indexes were computed using N individual measurements.
4. Final catalog
A catalog of 323 794 individual measurements was compiled and is available through the CDS (the detailed content for each column is described in Table A.5). The astrometry for each individual measurement was computed as the mean of the coordinates derived from each of the filter images (six if all the magnitudes are available). Next, a crossmatching process was executed, assuming that two or more measurements belong to the same target if their angular separation was smaller than 3″. This crossmatch radius was selected as the value that minimizes the number of outliers and maximizes the number of assignations, taking into account that it is around two to three times the size of the seeing. STILTS3 tools were used for that purpose, which also allowed us to assign an identifier (ID) to each star. Finally a weighted mean was computed that yielded the final photometric indexes for each target. Details of these computations are 1) those photometric indexes derived from magnitudes having full width at half maximum (FWHM) smaller than two pixels were rejected (assumed to be bad pixels or wrong measurements); 2) a weighted mean was computed, where the weight applied was 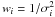 , and σi is the individual error for each index, computed with full propagation errors; 3) outliers were rejected using a 5σ rejection process, obtaining a final number of measurements different for each index (see Table 3); and 4) the weighted standard deviation and the error of the mean were computed for each index. The m1 index was computed from the weighted mean of the individual m1 measurements, so it is not a direct linear combination of the mean (v − b) and (b − y) indexes. The final right ascension and declination coordinates for each target were also computed following a similar procedure.
, and σi is the individual error for each index, computed with full propagation errors; 3) outliers were rejected using a 5σ rejection process, obtaining a final number of measurements different for each index (see Table 3); and 4) the weighted standard deviation and the error of the mean were computed for each index. The m1 index was computed from the weighted mean of the individual m1 measurements, so it is not a direct linear combination of the mean (v − b) and (b − y) indexes. The final right ascension and declination coordinates for each target were also computed following a similar procedure.
Table 3 shows the number of stars with 1, 2, 3, or more measurements. In the outer region, most stars have only one measurement, while in the central region, stars have usually three measurements, but six or nine if they were in an overlap region. Stars in fields ac308 and ac406 were observed up to 20 times. For the stars with a single measurement, the internal standard deviation computed by error propagation in Eqs. (2) and (3) was assigned. For targets with two or more measurements, a flag indicating the coherence between them was computed for each index. This flag gives the number of inconsistent pairs according to a Student’s t-test (t > 90% was adopted). For the V magnitudes, 97% of the stars with more than one measurement have a flag equal to zero; that is, all the measurements are consistent. Similar percentages are obtained for the other indexes.
The catalog with mean magnitudes and color indexes in the anticenter direction contains 96 980 stars (also available through CDS), but not all of them have the full set of indexes. Table 4 shows the statistics of the final photometric data available. A flag with six binary digits indicates the indexes available for each target. As can be seen in Table 4 the catalog contains 35 974 stars with all available indexes. Nonetheless, it is important to emphasize that it contains, in addition, 22 632 stars with all indexes except c1, 22 616 stars with V, (b − y) and Hβ, etc. Reading the last row in Table 4, it can be seen that we have about ~6 × 104 stars with m1 measurements or ~8 × 104 stars with Hβ index.
Statistics of the number of stars as a function of the photometric information available.
Table 5 shows the spectral type distribution obtained by applying the procedure described in Figueras et al. (1991) to the set of 35 974 stars with all photometric indexes. This distribution can be compared with the contents of the Hauck & Mermilliod (1998) catalog, a local volume sample. As expected, our catalog contains a higher percentage of targets belonging to the late type group due to the different limiting magnitude. No stars in common were found between the two catalogs. Our survey area overlaps with the area covered by the North Hemisphere IPHAS survey (González-Solares et al. 2008), with 54 109 stars in common. This overlap between both catalogs will be helpful for detecting stars with emission lines and peculiar features.
Fraction of stars in the catalog for each spectral type.
GSC2 ID is also provided in the catalog and only ~2% of the stars do not have GSC counterparts. In Table A.7, the first ten lines of the catalog are provided, with the description of all the columns in Table A.6.
4.1. Photometric precision
The photometric precision obtained from the error of the mean in each of the indexes is shown in Fig. 3 as a function of V magnitude. For bright stars (V < 16m), internal precisions below 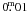 were obtained for V and (b − y) and below
were obtained for V and (b − y) and below 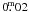 for the other indexes. For fainter stars, the internal precision can reach up to
for the other indexes. For fainter stars, the internal precision can reach up to 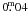 –
–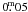 . For stars with a single measurement, the error of the mean could not be obtained, so we plot the internal standard deviation computed by error propagation in Eqs. (2) and (3) (see Fig. 4). For stars brighter than V = 12m the errors increase owing to saturation problems. The bump around V ~ 16–17m is due to some nights with bright sky conditions, leading to larger error in the instrumental magnitudes.
. For stars with a single measurement, the error of the mean could not be obtained, so we plot the internal standard deviation computed by error propagation in Eqs. (2) and (3) (see Fig. 4). For stars brighter than V = 12m the errors increase owing to saturation problems. The bump around V ~ 16–17m is due to some nights with bright sky conditions, leading to larger error in the instrumental magnitudes.
The chip-to-chip variation was also checked using the stars observed several times on different chips, i.e. in the overlap regions. Small variations were seen, but always less than the internal uncertainty. The typical offsets between chips are smaller than 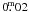 .
.
 |
Fig. 3 Photometric precision, computed as the error of the mean, as a function of V magnitude for the stars with more than one measurement. Lines for the V magnitude and the five standard indexes are plotted. Bins of |
 |
Fig. 4 Internal photometric standard deviation computed by error propagation in Eqs. (2) and (3), as a function of V magnitude for those stars with only one measurement. Lines for the V magnitude and the five standard indexes are plotted. Bins of |
 |
Fig. 5 Astrometric precision, computed as the error of the mean, as a function of V magnitude in right ascension (in red and × ) and declination (in green and ∗) computed for each 0 |
4.2. Astrometric precision
The internal astrometric precision, computed as the error of the mean, is around 0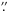 02 (see Fig. 5), less than one tenth of the pixel size (0
02 (see Fig. 5), less than one tenth of the pixel size (0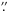 333). Figure 6 shows the comparison between our astrometry with J2000.0 coordinates from UCAC3 (Zacharias et al. 2010), GSC2.3.2 (Lasker et al. 2008), and USNO-A2. Differences up to 0
333). Figure 6 shows the comparison between our astrometry with J2000.0 coordinates from UCAC3 (Zacharias et al. 2010), GSC2.3.2 (Lasker et al. 2008), and USNO-A2. Differences up to 0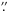 2 with UCAC3 and GSC2.3.2 can be observed, as well as a small trend in V magnitude, more pronounced in USNO-A2. All these effects are explained by the different epochs of the three catalogs (1995–2000, 1988, and 1955 for UCAC3, GSC2, and USNO-A2, respectively). USNO-A2 J2000.0 coordinates were used for the astrometric calibration because it contains stars fainter than UCAC3. However, the mean epoch for USNO-A2 is 1955.0, and since proper motions are not available and cannot be taken into account, our coordinates do not contain the effect induced by the relative Galactic rotation in the anticenter direction with respect to the Sun. This effect does not depend on the distance to the star (assuming a flat rotation curve) and can reach 0
2 with UCAC3 and GSC2.3.2 can be observed, as well as a small trend in V magnitude, more pronounced in USNO-A2. All these effects are explained by the different epochs of the three catalogs (1995–2000, 1988, and 1955 for UCAC3, GSC2, and USNO-A2, respectively). USNO-A2 J2000.0 coordinates were used for the astrometric calibration because it contains stars fainter than UCAC3. However, the mean epoch for USNO-A2 is 1955.0, and since proper motions are not available and cannot be taken into account, our coordinates do not contain the effect induced by the relative Galactic rotation in the anticenter direction with respect to the Sun. This effect does not depend on the distance to the star (assuming a flat rotation curve) and can reach 0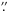 2–0
2–0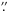 3 for differences in epoch of 50 years. Figure 6 shows that the dispersion increase from top to bottom, again due to the differences between the epochs of our observations and catalog positions. Furthermore, the decrease in the dispersion with increasing magnitude is explained by the effect of the intrinsic motion of the stars, stronger at short distances (so bright magnitudes). We used UCAC3 proper motions to check that the systematic trends disappear when the difference in epochs (2010–1995) is considered. As mentioned, USNO-A2 does not provide proper motions, so the effects were not corrected in our final astrometric data. We verified that these trends have no effect on the crossmatching between our catalog and GSC2.3.2, so the GSC ID is provided as additional information for the user.
3 for differences in epoch of 50 years. Figure 6 shows that the dispersion increase from top to bottom, again due to the differences between the epochs of our observations and catalog positions. Furthermore, the decrease in the dispersion with increasing magnitude is explained by the effect of the intrinsic motion of the stars, stronger at short distances (so bright magnitudes). We used UCAC3 proper motions to check that the systematic trends disappear when the difference in epochs (2010–1995) is considered. As mentioned, USNO-A2 does not provide proper motions, so the effects were not corrected in our final astrometric data. We verified that these trends have no effect on the crossmatching between our catalog and GSC2.3.2, so the GSC ID is provided as additional information for the user.
 |
Fig. 6 Comparison of our astrometry with those from UCAC3 (top), GSC2.3.2 (middle), and USNO-A2 (bottom). Left: differences in αcosδ. Right: differences in δ. In red, mean differences. Green dashed lines show 1σ ranges. All differences are in arcsec. |
 |
Fig. 7 Two-dimensional distribution of the limiting magnitude showing the 90% completeness level. Top: catalog of the 95 255 stars with V magnitudes available. Bottom: subcatalog of the 35 974 stars with all the indexes available (See Table 4). |
4.3. Limiting magnitude
The limiting magnitude was computed as the mean of the magnitudes at the peak star counts in a magnitude histogram and its two adjacent bins, before and after the peak, weighted by the number of stars in each bin. We estimated that the limiting V magnitude computed with this simple algorithm provides the ~90% completeness limit. This was confirmed through the comparison of the V magnitude distribution of our catalog of stars with all available indexes with that of the full catalog containing all the stars with observed V magnitude (see Table 4). This second catalog can be considered complete at the limiting magnitude of the previous one. The limiting magnitude obtained is not the same for all the survey. Data for the outer area were obtained using shorter exposure times. Also for the fields in the central region, the limiting magnitude is slightly variable due to both observation strategy and weather conditions. Figure 7 shows its two-dimensional distribution. As mentioned, the catalog with all the available indexes is limited by the u magnitude. As can be seen in Fig. 7, our catalog of the 35 974 stars with all indexes available reaches ~90% completeness at V ~ 17m and 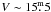 for the central and outer regions, respectively.
for the central and outer regions, respectively.
Figure 8 shows the V-magnitude histogram for the two main areas in our survey (the outer area and the central deeper region). In both cases the comparison between all the stars with available V magnitude and those with all indexes are provided.
 |
Fig. 8 V magnitude histogram. In red, stars with available V magnitudes. In green, stars with all indexes available. Top: stars from the central deeper area. Bottom: stars from the outer area. |
5. Summary and future work
A catalog of Strömgren photometry in the anticenter direction was built, covering a total area of 16 deg2, thereby providing photometric measurements for 96 980 stars. The central 8 deg2 reach ~90% completeness at V ~ 17m, while the outer region of ~8 deg2, mostly observed with only one pointing, reaches this completeness at 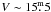 . Photometric internal precisions between
. Photometric internal precisions between 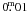 –
–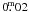 for stars brighter than V = 16m were obtained, increasing to
for stars brighter than V = 16m were obtained, increasing to 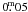 for some indexes and fainter stars (V ~ 18–19m). The catalogs with the individual measurements and the final mean magnitudes and color indexes are available through the CDS.
for some indexes and fainter stars (V ~ 18–19m). The catalogs with the individual measurements and the final mean magnitudes and color indexes are available through the CDS.
In a forthcoming paper the catalog will be used to determine whether there is an stellar overdensity of young stars induced by the Perseus spiral arm in the anticenter direction. That will allow us to fix the locus of the arm and to link this structure with the tracers observed in the second and third Galactic quadrant. The catalog is also being used to select a set of targets for a spectroscopic follow up. Radial velocities are being obtained using WYFFOS multiobject spectrograph installed at the WHT at the Canary Islands. This will allow us to study the possible velocity
perturbation due to the Perseus arm. Undoubtedly this catalog will have other important scientific applications. As an example, it provides photometric metallicities for the FGK stars, from where a statistical analysis of the radial metallicity gradient can be undertaken. Our catalog could also be used to calibrate larger photometric surveys, such as IPHAS, or for future Gaia spectroscopic follow up in the northern hemisphere.
IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation (Tody 1986).
Starlink Tables Infrastructure Library Tool Set, http://www.star.bris.ac.uk/~mbt/stilts/
Acknowledgments
We would like to thank the anonymous referee for his/her comments and suggestions that clearly helped to improve the paper. This work was supported by the MINECO (Spanish Ministry of Economy) – FEDER through grant AYA2009-14648-C02-01 and CONSOLIDER CSD2007-00050. M.M. was supported by a Predoctoral fellowship from the Spanish Ministry (BES-2008-002471 through ESP2006-13855-C02-01 project).
References
- Benjamin, R. A. 2008, ASP Conf. Ser., 387, 375 [NASA ADS] [Google Scholar]
- Brunthaler, A., Reid, M. J., Menten, K. M., et al. 2011, Astron. Nachr., 332, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L. 1978, AJ, 83, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L. 1979, AJ, 84, 1858 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1969a, AJ, 74, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, D. L., & Barnes, J. V. 1969b, AJ, 74, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R. 2000, A&A, 358, 13 [Google Scholar]
- Figueras, F., Torra, J., & Jordi, C. 1991, A&A, 87, 319 [Google Scholar]
- Froebrich, D., Murphy, G. C., Smith, M. D., Walsh, J., & Del Burgo, C. 2007, MNRAS, 378, 1447 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., Baba, J., Saitoh, T. R., et al. 2011, ApJ, 730, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Georgelin, Y. M., & Georgelin, Y. P. 1976, A&A, 49, 57 [NASA ADS] [Google Scholar]
- González-Solares, E. A., Walton, N. A., Greimel, R., et al. 2008, MNRAS, 388, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Grosbøl, P., Patsis, P. A., & Pompei, E. 2004, A&A, 423, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lépine, J. R. D., Cruz, P., Scarano, S. J., et al. 2011, MNRAS, 417, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Marco, A., Bernabeu, G., & Negueruela, I. 2001, AJ, 121, 2075 [NASA ADS] [CrossRef] [Google Scholar]
- Momany, Y., Zaggia, S., Gilmore, G., et al. 2006, A&A, 452, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monet, D. G. 1998, BAAS, 30, 1427 [NASA ADS] [Google Scholar]
- Peña, J. H., Peniche, R., Mujica, R., et al. 1993, Rev. Mex. Astron. Astrofs., 25, 129 [NASA ADS] [Google Scholar]
- Reglero, V., & Fabregat, J. 1991, A&AS, 90, 25 [NASA ADS] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Derrière, S., & Picaud, S. 2003, A&A, 409, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D. 2003, A&A, 397, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sellwood, J. A. 2011, MNRAS, 410, 1637 [NASA ADS] [Google Scholar]
- Strömgren, B. 1966, ARA&A, 4, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Tapia, M., Costero, R., Echevarria, J., & Roth, M. 1991, MNRAS, 253, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. H., & Cordes, J. M. 1993, ApJ, 411, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, Proc. SPIE, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez, R. A., May, J., Carraro, G., et al. 2008, ApJ, 672, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y., Reid, M. J., Zheng, X. W., & Menten, K. M. 2006, Science, 311, 54 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tables
This appendix includes some tables with detailed information about the catalog and the photometric transformation process. Table A.1 shows the extinction coefficients obtained for each night and filter, as well as the airmass ranges covered by the calibration fields. In Table A.2 we detail the range of magnitudes and color indexes covered by our calibration fields. The coefficients for the transformation to the standard system through Eqs. (2) and (3) with their associated errors, for each of the observing nights, are shown in Tables A.3 and A.4, respectively. Tables A.5 and A.6 provide the column description for the two catalogs, which are individual measurements and final mean values, respectively. Table A.7 shows, as an example, the ten first rows of the mean catalog. For the individual measurements catalog, the ten first rows are not provided owing to the large amount of data included, but the full table can be found at the CDS.
Extinction coefficients obtained with the WFC/INT at El Roque de los Muchachos.
Color index photometric ranges for the calibration fields.
Standard transformation coefficients.
Standard transformation coefficients for Eq. (3).
Readme file of the catalog with individual measurements.
Readme file for the catalog with mean measurements.
All Tables
Dates for the observing runs and exposure times for each observation and filter for our program fields.
Number of stars for which mean magnitudes and indexes were computed using N individual measurements.
Statistics of the number of stars as a function of the photometric information available.
Extinction coefficients obtained with the WFC/INT at El Roque de los Muchachos.
All Figures
 |
Fig. 1 Plot of the 60 WFC fields observed. Red line shows the |
| In the text | |
 |
Fig. 2 Illumination differences in magnitudes at different field positions. Black lines show the location of the four chips, and coordinates in degrees are centered on the central chip. The illumination differences at each position were computed as the Gaussian-weighted mean (with σ = 0.1°) of the residuals around each point. |
| In the text | |
 |
Fig. 3 Photometric precision, computed as the error of the mean, as a function of V magnitude for the stars with more than one measurement. Lines for the V magnitude and the five standard indexes are plotted. Bins of |
| In the text | |
 |
Fig. 4 Internal photometric standard deviation computed by error propagation in Eqs. (2) and (3), as a function of V magnitude for those stars with only one measurement. Lines for the V magnitude and the five standard indexes are plotted. Bins of |
| In the text | |
 |
Fig. 5 Astrometric precision, computed as the error of the mean, as a function of V magnitude in right ascension (in red and × ) and declination (in green and ∗) computed for each 0 |
| In the text | |
 |
Fig. 6 Comparison of our astrometry with those from UCAC3 (top), GSC2.3.2 (middle), and USNO-A2 (bottom). Left: differences in αcosδ. Right: differences in δ. In red, mean differences. Green dashed lines show 1σ ranges. All differences are in arcsec. |
| In the text | |
 |
Fig. 7 Two-dimensional distribution of the limiting magnitude showing the 90% completeness level. Top: catalog of the 95 255 stars with V magnitudes available. Bottom: subcatalog of the 35 974 stars with all the indexes available (See Table 4). |
| In the text | |
 |
Fig. 8 V magnitude histogram. In red, stars with available V magnitudes. In green, stars with all indexes available. Top: stars from the central deeper area. Bottom: stars from the outer area. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.