| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A84 | |
| Number of page(s) | 9 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201219952 | |
| Published online | 21 December 2012 | |
Formation and stability of hydrogenated PAHs in the gas phase
Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
e-mail: lha@phys.au.dk
Received: 5 July 2012
Accepted: 30 August 2012
Aims. We report on experimental and computational studies of hydrogenation of polycyclic aromatic hydrocarbon (PAH) cations, HnPAHs, which are relevant to the interstellar medium.
Methods. The yield of the hydrogenated PAH cations produced in a plasma-ion source and by electrospray ionization was measured. DFT calculations at the B3LYP/6-311+G(d, p) and B3LYP/6-31+G(d, p) level of theory were performed to investigate the hydrogenation pattern.
Results. A clear pattern in the yield and binding energies of hydrogen is revealed. Hydrogenated closed shell molecules with an even number of attached hydrogen atoms are significantly more stable than molecules with an odd number of hydrogen atoms and show as a consequence to be more abundant in mass spectra of HnPAHs. The binding energy of a hydrogen atom to Hn−1PAH with an even n is ~2 eV higher than for odd n. The exact distribution in n observed in the experimental mass spectra remains to be solved due to the unknown internal ion source conditions.
Conclusions. The HnPAH cations have been produced under very different conditions, and the measured yield indicates high stability and likely high abundance in the interstellar medium.
Key words: ISM: molecules / methods: laboratory / methods: numerical
© ESO, 2012
1. Introduction
Durent recent years, observational evidence has made it clear that polycyclic aromatic hydrocarbons (PAHs) are ubiquitous in the interstellar medium (ISM; Allamandola et al. 1999). As one of the major molecular species, they are expected to carry 5−10% of the total amount of interstellar carbon (Tielens 2011). Despite this, their role in interstellar chemistry remains largely unexplored. It has been suggested that PAHs may be intimately involved in the molecular origin of life (Ehrenfreund et al. 2006; Herd et al. 2011) and that they may act as interstellar catalysts for the formation of molecular hydrogen (H2; Habart et al. 2004; Rauls & Hornekær 2008), the most abundant molecule in space.
H2 plays a key role in the physical and chemical processes that lead to the formation of new stars and the evolution of interstellar chemical complexity (Williams 1998). The mechanisms behind the formation of H2 in the ISM have been intensely studied, and formation routes on dust grain surfaces, as originally suggested by Hollenbach & Salpeter (1971), have proven efficient in low temperature dense and diffuse interstellar clouds (Katz et al. 1999; Manico et al. 2001; Hornekær et al. 2003; Mennella 2008, 2011) but not under harsher conditions such as those found in photodissociation regions (PDRs; Cazaux & Tielens 2004; Cuppen & Herbst 2005). The presence of PAHs in regions with high rates of H2 formation in PDRs (Habart et al. 2004) has led to the suggestion that PAHs could be the missing H2 catalyst in these regions. The hypothesis is supported by the correlation of H2 and PAH emission in some interstellar regions (Joblin et al. 2000; Habart et al. 2004).
Theoretical studies have supported the hypothesis that PAH cations (Cassam-Chenaï et al. 1994; Bauschlicher 1998; Hirama et al. 2003; Le Page et al. 2009) and superhydrogenated neutrals (Rauls & Hornekær 2008; Rodriques et al. 2010) might act as catalysts for H2 formation. Laboratory experiments have shown that atomic and molecular hydrogen react with benzene and small PAHs (Petrie et al. 1992; Scott et al. 1997; Le Page et al. 1997; Snow et al. 1998). More recently, the formation of superhydrogenated neutral coronene has been observed by scanning tunneling microscopy, thermal desorption measurements, and infrared spectroscopy (Thrower et al. 2011; Mennella et al. 2012; Thrower et al. 2012). Very high superhydrogenation states approaching full superhydrogenation with one excess H atom per carbon atom have been observed (Thrower et al. 2012). Furthermore, both infrared spectroscopy measurements and thermal desorption measurements provided evidence of hydrogen abstraction reactions producing H2, hence shows that PAHs do act as catalysts for molecular hydrogen formation (Mennella et al. 2012; Thrower et al. 2012). The reaction cross-section for these abstraction reactions was found to be 0.06 Å2 pr. excess H atom (Mennella et al. 2012). For PAHs with very high degrees of superhydrogenation, such a cross-section could explain the high H2 formation rates observed in low UV flux PDR regions (Habart et al. 2004). Furthermore, Fu et al. (2012) have recently shown that H2 is formed upon exposure to a doubly hydrogenated PAH with UV-photons and found reaction routes with barriers of 2.3 − 3.4 eV. Multiphton infrared photodissociation studies (Vala et al. 2009, 2011; Szczepanski et al. 2011) also show that H2 is emitted by vibrationally excited hydrogenated PAHs. These findings highlight that, to be able to predict the efficiency of PAHs as an interstellar molecular hydrogen catalyst, we need detailed knowledge of the hydrogenation state of PAHs under interstellar conditions.
Establishment of the presence and hydrogenation state of PAHs is based on correlation between the frequencies of their vibrational modes and the aromatic emission features which appear in the 3−20 μm range throughout the entire galaxy (Tielens 2008). The strong aromatic C-H stretch has a vibrational frequency of 3.3 μm, while the aliphatic (e.g. C bonds to two H atoms) stretch is shifted to 3.4 μm. This emission band is also observed, and hydrogenated PAHs are therefore likely components of the interstellar medium (Schutte et al. 1993; Bernstein et al. 1996; Sloan et al. 1997; Wagner et al. 2000). However, quantitative estimates of the hydrogenation state of interstellar PAH molecules based on observations has so far not been possible.
Besides acting as catalysts for H2 formation, protonated and hydrogenated PAHs have been suggested as possible carriers of the diffuse interstellar bands (DIBs; Tielens 2008). Both computational and experimental results show that protonation and hydrogen addition strongly influence the optical spectra (Pathak & Sarre 2008; Chakraborty et al. 2009; Hammonds et al. 2009; Ricks et al. 2009; Knorke et al. 2009; Garkusha et al. 2011; Alata et al. 2010; Bonaca & Bilalbegovic 2011). This indicates that, although bare and singly protonated PAHs can be ruled out as carriers of the DIBs (Steglich et al. 2011), hydrogenated PAHs cannot.
The hydrogenation state of interstellar PAHs are therefore of great interest to the astrophysical community. We present results on production and stability of a hydrogenated PAH (pentacene) and a hydrogenated nitrogen bearing PAH or PANH (quinoline) in the gas-phase produced by both hard and soft ionization methods. These two linear PAHs (Fig. 1), have been chosen as test-molecules to show the trends of hydrogenation under very different conditions. Contrary to expectations, both methods are shown to produce highly superhydrogenated PAH species, indicating that hydrogenation of PAHs is a robust process and that superhydrogenated PAHs can be formed efficiently and survive even under very hostile conditions, such as those present in a plasma ion source. The experimental data, combined with density functional theory calculations, shed light on the stability of the different PAH hydrogenation states and isomers.
 |
Fig. 1 Quinoline (C9H7N, 129 amu) and pentacene (C22H14, 278 amu). Because of the nitrogen atom, protonated quinoline and its hydrogenated states are easily generated in the electrospray ionization source. Pentacene is solid at room temperature and the radical cation, as well as cationic de- and hydrogenated states, were produced by a Nielsen plasma ion source. |
2. Experimental and computational methods
The experimental techniques involved in the production and mass analysis of hydrogenated PAH cations are described below. Two different ion sources, the Nielsen plasma ion source (Nielsen 1957) and the electrospray-ionization source (Fenn et al. 1989), were mounted on an HV platform where the ions are accelerated to 20 keV. Mass selection was performed by a 90-degree bending magnet. The number of ions as a function of their mass is detected on a micro-channel plate detector located 3 m from the magnet. Ions with 1 amu mass difference are distinguishable in mass spectra obtained by scanning the magnetic field.
In the Nielsen plasma ion source, the analyte molecules are brought into gas phase by heating a solid sample. Ionization of the gas-phase molecules takes place in a plasma generated from electrons evaporated from a tungsten filament and a gas (in this case atmospheric air) let in through a needle valve. The conditions in the plasma are very harsh with 100 − 200 eV electrons, and even multiply charged noble gas cations can be produced in this source. The bombardment of electrons leads to a broad temperature distribution, which has been shown to extend up to 3000 K for fullerene cations produced in the source (Tomita et al. 2001). Most ions are expected to have a temperature of about 800 − 1000 K.
The electrospray-ionization source brings ions diluted in a volatile solvent into gas phase by applying a high voltage (2 − 4 kV) to a droplet of the solution. The droplet will eventually break under Coulomb explosion, and after evaporation of the remaining solvent molecules, the analyte ions remain in gas phase. The molecules are not exposed to sufficient energy exchange to cause fragmentation or change conformation or configuration of the rigid PAHs during ionization by this soft ionization method.
Density functional theory (DFT) calculations were performed for comparison with the experimental results using the Gaussian03 program (Frisch et al. 2004). Structure optimization and energy calculations were carried out at the B3LYP level of theory, using the 6-311+G(d, p) basis set for the smaller molecules, quinoline, and naphthalene, and 6-31+G(d, p) for the bigger, pentacene. Zero point corrections and scaling of the vibrational energies were taken into account. All vibrational frequencies were found to be positive for the optimized structures.
Structure optimization of the hydrogenated PAHs and calculation of their energies is a cumbersome job as hydrogenation can lead to many different isomers. For example, doubly hydrogenated pentacene with two excess H atoms (C22H16, here denoted H2Pen) has 34 different isomers, corresponding to the different positions of the extra hydrogen atoms on the perimeter of the molecule. The experience gained from the calculations for quinoline and naphthalene has therefore been taken into account when performing the calculations for pentacene.
In the following, we define the binding energy of a hydrogen atom to an already hydrogenated PAH according to 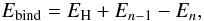 (1)where n is the number of hydrogen atoms attached to the molecule, En the energy of the corresponding molecule, and EH the energy of a hydrogen atom.
(1)where n is the number of hydrogen atoms attached to the molecule, En the energy of the corresponding molecule, and EH the energy of a hydrogen atom.
3. Results and discussion
In the following two sections, the experimentally recorded mass spectra of two linear PAHs are presented and compared with calculations. The hydrogenated state of protonated quinoline and the pentacene cation will be denoted HnQuiH+ and denoted HnPen+.
 |
Fig. 2 Mass spectrum of hydrogenated and dehydrogenated states of protonated quinoline generated in the electrospray ionization source. All hydrogenated states bear a single positive charge. The number of extra hydrogen atoms ascribed to the individual peaks is with reference to the protonated quinoline cation. Note the logarithmic scale. |
3.1. Quinoline
Figure 2 shows the mass spectrum of the hydrogenated and dehydrogenated states of protonated quinoline (C10H7N, 129 amu, shown schematically in Fig. 1), generated by spraying a sample of quinoline dissolved in methanol (a drop of acetic acid was added to the solution to enhance protonation). Only a weak yield of the radical cation (129 amu) and dehydrogenated states is observed as expected considering the preparation method of the ions. Hydrogenated states are produced up to +8H – the same number as the number of edge atoms of the structure. In the mass spectrum, the number of extra hydrogen atoms ascribed to the individual peaks corresponds to the number of extra hydrogen atoms with reference to the protonated molecule.
Mass spectra give an indication of the relative stability of the different species; i.e., the more stable a molecule the higher the expected yield. The binding energies of all the different isomers were calculated for every state of hydrogenation and Table 1 presents the isomers of the lowest energy route of sequential hydrogen addition along with their binding energies, which are plotted in Fig. 3.
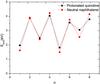 |
Fig. 3 The binding energy of a hydrogen atom of a certain hydrogenated state of protaned quinoline and neutral naphthalene. n corresponds to the total number of hydrogen atoms attached to the PAH and Ebind is calculated according to Eq. (1). The binding energies correspond to the lowest energy route of hydrogenation found. A clear odd-even pattern is clear for both molecules. |
The calculated binding energies are for the isomers of the lowest energy route of sequential hydrogenation. The route of direct hydrogen addition is identical for protonated quinoline and neutral naphthalene. In the supplementary material, a complete list is given of the calculated isomers and the energy differences. The energy difference of the isomers can, in a few cases, be as low as 0.007 eV, less than the accuracy of the calculations.
A clear odd-even pattern in terms of n is visible in Table 1 and Fig. 3: the energy released by attaching a hydrogen atom to give a molecule with an even number of hydrogen atoms is considerably higher (~2 eV) than the energy released when a hydrogen is added to give a molecule with an odd number of hydrogen atoms. For naphthalene, the binding energies reveal that hydrogenation of the second aromatic ring takes place independently of the first ring as Ebind(n) ≃ Ebind(n + 4). This does not apply to quinoline due to the effects of the nitrogen atom.
Quinoline is similar to naphthalene (C10H8), except for the substitution of a carbon and hydrogen atom by a nitrogen atom. The two molecules are isoelectronic, and the substitution is only expected to cause small perturbations to the bond lengths. Protonation of quinoline does not change this. Indeed, the computational results for the binding of hydrogen to protonated quinolines presented in Fig. 3 and Table 1 show that the trends in hydrogenation site of the protonated quinoline cation and neutral naphthalene are the same. Nitrogen substituted PAHs are also very likely components of the interstellar medium, and so hydrogenation of quinoline is thus interesting. One advantage of studying nitrogen substituted PAHs lies in their having a higher proton affinity because of the electronic lonepair of the nitrogen atom, hence making them easier to produce as ions and ideal for electrospray ionization.
The results show, that for +1H, hydrogenation of the carbon atoms nearest to the fusion of the aromatic rings is the more favorable position. For an even number of extra hydrogen atoms, the last hydrogen atom is added adjacent to the previous addition, hence minimizing the number of broken double bonds as expected from the work of Bauschlicher (1998). Up to n = 4, the hydrogenation process is expected to occur on the same ring, thus preserving the aromacity of the other ring. Interestingly, while for most hydrogenated states the hydrogenation of the nitrogen atom is energetically unfavorable, for the +4H case, calculations show that full hydrogenation of the aromatic ring including the protonated nitrogen atom is stable by >0.8 eV compared to partial hydrogenation of both rings. Full hydrogenation of the ring not containing nitrogen (shown in Table 1) is still the stablest isomer by 0.5 eV.
 |
Fig. 4 Mass spectrum of hydrogenated and dehydrogenated states of pentacene generated in the hot Nielsen plasma ion source. All hydrogenated states bear a single positive charge. Note the logarithmic scale. |
After full hydrogenation of the aromatic ring not containing nitrogen, hydrogenation of the other follows the same scheme. Finally, for +8H, hydrogenation of one of the skeleton carbon atoms is energetically more favorable than hydrogenation of the protonated nitrogen atom. The H8QuiH+-state therefore does not correspond to full hydrogenation of the edge atoms, according to the calculations.
A striking feature in the mass spectrum is the relative high abundance of H4QuiH+. Calculations show that this state, together with H2QuiH+, have the highest binding energy. The odd-even pattern is only weakly seen in the mass spectrum (Fig. 2).
 |
Fig. 5 The binding energy of a hydrogen atom of a certain hydrogenated state of pentacene. n corresponds to the total number of hydrogen atoms attached to the PAH and Ebind is calculated according to Eq. (1). The clear odd-even pattern for the neutral is not repeated in the cationic case. |
3.2. Pentacene
Figure 4 shows the mass spectrum of pentacene (C22H14, 278 amu), exhibiting several interesting features. First, the radical cation is produced in significant amounts along with both dehydrogenated and hydrogenated pentacene cations. Some of the hydrogenated pentacene cations are even more prominent than the radical cation, and the higher hydrogenated states yield 100 times more than the lower hydrogenated states. A considerable amount of hydrogen must therefore be present in the ion source. The small peak at 279 amu (corresponding to HPen+) could be ascribed to isotope effects (13C), while no peak is observed at 281 amu (corresponding to H3Pen+) in the spectrum. In this spectrum, the odd-even effect is very prominent. All states with an even number of hydrogen atoms are generated. The dehydrogenated states are probably generated by collisions in the plasma and H/H2 exchange between the PAHs is likely to occur. An additional peak appears at mass 294 amu corresponding to 278 + 16 amu, and this might be ascribed to hydrogenation of the skeleton but this was not investigated further.
An alternative interpretation of the presence of molecules with mass 292 amu would be the substitution of an H atom with a methyl group, the mass of which happens to coincide with full hydrogenation of the edge sites of pentacene. In this scenario, hydrogen atoms would then be stripped off the methyl substituted pentacene cation in the same way as for the radical pentacene cation, resulting in two groups in the mass spectrum corresponding to dehydrogenation of the radical pentacene cation and the methyl substituted pentacene cation. However, since no sign of ions with masses corresponding to substitution of two methyl groups and its dehydrogenated states was seen, we interpret the ions with masses 279 to 292 amu to be hydrogenated states of pentacene.
Figure 5 and Table 2 show the calculated binding energies and the structures of hydrogenated pentacene. The calculations were carried out for both cations and neutrals. The odd-even pattern clearly present in the experimentally obtained mass spectrum is also recognized in the calculations. For the neutral molecules, an even number of extra hydrogen atoms result in higher stability as expected based on electronic shell closing. On the basis of shell closing, one also expects that for the cation the odd hydrogenation numbers will be stabler, which is indeed the case for n > 9 according to calculations. For n < 9, the pattern resembles the neutral pattern, except the differences in energy between the odd and even n’s are not as high in the cationic case. Thus, the odd-even pattern observed in the experiment suggests that in the Nielsen ion source, hydrogenation takes place prior to ionization. Thus, the mass spectrum is related to the stability of the neutral molecules rather than the cations.
The sequential addition of hydrogen atoms follows the same trend as for protonated quinoline and neutral pentacene. Hydrogenation of the end rings happens one at a time, breaking only one double bond at a time. When both outer rings have been fully hydrogenated, hydrogenation of the central rings begins. As mentioned, +10H to +13H all have several stable structures very close in energy, but as for quinoline, the isomers of the lowest energy route of hydrogenation is shown. In the supplementary material, the lowest energy isomers can be found. In the pentacene case, with a PAH skeleton consisting solely of carbon atoms, hydrogenation of the edge atoms is much preferred over the carbon atoms in the ring fusions.
Interestingly, in the mass spectra there is no yield of hydrogenated states below +5H. According to the calculations, this corresponds to full hydrogenation of one of the outer rings and one of the central edge carbon atoms. A large increase in ion yield is observed for the +8H state, after which the height of several of the peaks is even higher than that of the radical ion. The ion abundance from the ion source is related to the stability of the molecules, but also the amount of hydrogen available for hydrogenation in the source and the duration of presence of the molecules in the plasma. The distribution of hydrogenation states may depict an equilibrium of H/H2 exchange of the dehydrogenated and hydrogenated pentacene cations. The gap in abundance below +5H, and the stepwise increase in abundance at +8H are prominent effects, which are probably explained by the internal ion source conditions.
4. Conclusion and outlook
The experimental results show that both protonated quinoline and pentacene can be formed in multiple hydrogenated states under very different conditions and ionization methods. The hydrogenated protonated quinolines have been formed by the soft method of electrospray ionization where the molecules are very unlikely to break apart. Protonation of PAHs by electrospray ionization have previously been reported (Knorke et al. 2009; Vala et al. 2009; Garkusha et al. 2011; Szczepanski et al. 2011; Vala et al. 2011), but here we show that up to full hydrogenation of the edge sites occur. Cationic states of highly hydrogenated pentacene are generated in the harsh environment of the Nielsen plasma ion source, thus demonstrating very high stability.
Our results are supported by calculations (Ricca et al. 2007; Rasmussen et al. 2011). Rasmussen et al. (2011) show that chemical binding of hydrogen to neutral pyrene (a small PAH consisting of four fused aromatic rings) is exothermic by 1.6 eV, and the barrier for further hydrogenation is negligible (0.06 eV). Ricca et al. (2007) find that single hydrogenation of the napthalene cation has no barrier, while double hydrogenation has a slightly higher barrier. In our study, the reaction barriers for hydrogen addition were not calculated, but the measurements show that the barrier can be passed both in solution and in gas-phase, because hydrogenated PAHs are observed from both ion sources, indicating low reaction barriers.
The very clear odd-even pattern in the experimental mass spectrum of the pentacene cations is matched by the binding energies of the neutral hydrogenated pentacene states and not by the hydrogenated pentacene cations. The hydrogenation process is thus likely to take place prior to the ionization in the Nielsen plasma ion source. For protonated quinoline, the binding energy of a hydrogen atom to HnQuiH+ is ~ 2 eV higher for n even than for odd n. The odd-even pattern is only seen weakly in the experimental mass spectrum of protonated quinoline, although H4QuiH+ has the highest abundancy after QuiH+. The trend of hydrogenation site of the investigated molecules agrees with the calculations of Ricca et al. (2007).
This study is motivated by the still unanswered question about H2 formation in intermediate temperature regions of the interstellar medium. Both PAHs and their dehydrogenated and hydrogenated forms have been proposed as catalysts. The shown stability and abundance of highly hydrogenated PAHs encourage further experimental work on the subject, since Mennella et al. (2012) have recently shown that the degree of hydrogenation plays a critical role in the process of H2 formation. It is not possible to compare the results of this study directly to astrophysical objects because the exact conditions in the sources are not known, but the results show that hydrogenated PAHs are indeed stable under very different conditions. The formation of highly hydrogenated PAHs in the gas-phase from bare PAHs underpin the attribution of the 3.4 μm IR feature to the C-H stretch of hydrogenated PAHs. Since PAHs are unarguably components of the interstellar medium and because of the shown stability, we conclude that a wide range of hydrogenated PAHs are very probably components of the interstellar medium.
It has been brought to our attention that mass 294 may be due to oxygen addition to pentacene. If this is the case, the masses immediately below 294 might be due to dehydrogenated states of this species.
Appendix A: Tables of the lowest energy isomers of the hydrogenated PAHs
Acknowledgments
This work was supported by the Lundbeck Foundation, the Carlsberg Foundation, and the Danish Research Agency.
References
- Alata, I., Dedonder, C., Broquier, M., Marceca, E., & Jouvet, C. 2010, J. Am. Chem. Soc., 132, 17483 [CrossRef] [Google Scholar]
- Allamandola, L. J., Hudgins, D. M., & Sandford, S. A. 1999, ApJ, 511, L115 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bauschlicher, C. W. 1998, ApJ, 509, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, M. P., Sandford, S. A., & Allamandola, L. J. 1996, ApJ, 472, L127 [CrossRef] [Google Scholar]
- Bonaca, A., & Bilalbegovic, G. 2011, MNRAS, 416, 1509 [NASA ADS] [CrossRef] [Google Scholar]
- Cassam-Chenaï, P., Pauzat, F., & Ellinger, Y. 1994, in Molecules and Grains in Space, ed. I. Nenner, AIP Conf. Ser., 312, 543 [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, S., Omidyan, R., Alata, I., et al. 2009, J. Am. Chem. Soc., 131, 11091 [CrossRef] [Google Scholar]
- Cuppen, H. M., & Herbst, E. 2005, MNRAS, 361, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenfreund, P., Rasmussen, S., Cleaves, J., & Chen, L. 2006, Astrobiology, 6, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Fenn, J. B., Mann, M., Meng, C. K., Wong, S. F., & Whitehouse, C. M. 1989, Science, 246, 64 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2004, Gaussian 03, Revision C.02 (Wallingford, CT: Gaussian, Inc.) [Google Scholar]
- Fu, Y., Szczepanski, J., & Polfer, N. C. 2012, ApJ, 744, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Garkusha, I., Fulara, J., Nagy, A., & Maier, J. P. 2011, ApJ, 728, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., Walmsley, C. M., & Pineau des Forêts, G. 2004, A&A, 414, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hammonds, M., Pathak, A., & Sarre, P. J. 2009, Phys. Chem. Chem. Phys., 11, 4458 [CrossRef] [Google Scholar]
- Herd, C. D. K., Blinova, A., Simkus, D. N., et al. 2011, Science, 332, 1304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hirama, M., Ishida, T., & Aihara, J.-I. 2003, Comput. Chem., 24, 1378 [CrossRef] [PubMed] [Google Scholar]
- Hollenbach, D., & Salpeter, E. E. 1971, ApJ, 163, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Hornekær, L., Baurichter, A., Petrunin, V. V., Field, D., & Luntz, A. C. 2003, Science, 302, 1943 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joblin, C., Maillard, J. P., Vauglin, I., Pech, C., & Boissel, P. 2000, Molecular Hydrogen in Space (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Knorke, H., Langer, J., Oomens, J., & Dopfer, O. 2009, ApJ, 706, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Keheyan, Y., Bierbaum, V. M., & Snow, T. P. 1997, J. Am. Chem. Soc., 119, 8373 [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2009, ApJ, 704, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Manico, G., Raguní, G., Pirronello, V., Roser, J. E., & Vidali, G. 2001, ApJ, 548, L253 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V. 2008, ApJ, 684, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Mennella, V. 2011, in EAS Pub. Ser. 46, eds. C. Joblin, & A. G. G. M. Tielens (Les Ulis, France: EDP Sciences), 393 [Google Scholar]
- Mennella, V., Hornekær, L., Thrower, J., & Accolla, M. 2012, ApJ, 745, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, K. 1957, Nucl. Instr., 1, 289 [CrossRef] [Google Scholar]
- Pathak, A., & Sarre, P. J. 2008, MNRAS, 391, L10 [NASA ADS] [Google Scholar]
- Petrie, S., Javahery, G., & Bohme, D. K. 1992, J. Am. Chem. Soc., 114, 9203 [CrossRef] [Google Scholar]
- Rasmussen, J. A., Henkelman, G., & Hammer, B. 2011, J. Chem. Phys., 134, 164703 [NASA ADS] [CrossRef] [Google Scholar]
- Rauls, E., & Hornekær, L. 2008, ApJ, 679, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Ricca, A., Bakes, E. L. O., & Bauschlicher, C. W. 2007, ApJ, 659, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Ricks, A. M., Douberly, G. E., & Duncan, M. A. 2009, ApJ, 702, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriques, L. S., Ruette, F., Sanchez, M., & Mendoza, C. 2010, J. Mol. Cat. A, 316, 16 [CrossRef] [Google Scholar]
- Schutte, W. A., Tielens, A. G. G. M., & Allamandola, L. J. 1993, ApJ, 415, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, G. B. I., Fairley, D. A., Freeman, C. G., et al. 1997, J. Phys. Chem., 101, 4973 [CrossRef] [Google Scholar]
- Sloan, G. C., Bregman, J. D., Begalle, T. R., Allamandola, L. J., & Woodward, C. E. 1997, ApJ, 474, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Snow, T., Le Page, V., Keheyan, Y., & Bierbaum, V. 1998, Nature, 391, 59 [CrossRef] [Google Scholar]
- Steglich, M., Bouwman, J., Huisken, F., & Henning, T. 2011, ApJ, 742, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Szczepanski, J., Oomens, J., Steill, J. D., & Vala, M. T. 2011, ApJ, 727, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Thrower, J. D., Nilsson, L., Jørgensen, B., et al. 2011, in EAS Publ. Ser., eds. C. Joblin, & A. G. G. M. Tielens (Les Ulis, France: EDP Sciences), 3 [Google Scholar]
- Thrower, J. D., Jørgensen, B., Friis, E. E., et al. 2012, ApJ, 752, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2011, in EAS Pub. Ser. 46, eds. C. Joblin, & A. G. G. M. Tielens (Les Ulis, France: EDP Sciences), 3 [Google Scholar]
- Tomita, S., Andersen, J. U., Gottrup, C., Hvelplund, P., & Pedersen, U. V. 2001, Phys. Rev. Lett., 87, 073401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vala, M., Szczepanski, J., Oomens, J., & Steill, J. D. 2009, J. Am. Chem. Soc., 131, 5784 [CrossRef] [PubMed] [Google Scholar]
- Vala, M., Szczepanski, J., & Oomens, J. 2011, Int. J. Mass Spectrom., 308, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, D. R., Kim, H., & Saykally, R. J. 2000, ApJ, 545, 854 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Williams, D. A. 1998, Faraday Discuss., 109, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Quinoline (C9H7N, 129 amu) and pentacene (C22H14, 278 amu). Because of the nitrogen atom, protonated quinoline and its hydrogenated states are easily generated in the electrospray ionization source. Pentacene is solid at room temperature and the radical cation, as well as cationic de- and hydrogenated states, were produced by a Nielsen plasma ion source. |
| In the text | |
 |
Fig. 2 Mass spectrum of hydrogenated and dehydrogenated states of protonated quinoline generated in the electrospray ionization source. All hydrogenated states bear a single positive charge. The number of extra hydrogen atoms ascribed to the individual peaks is with reference to the protonated quinoline cation. Note the logarithmic scale. |
| In the text | |
 |
Fig. 3 The binding energy of a hydrogen atom of a certain hydrogenated state of protaned quinoline and neutral naphthalene. n corresponds to the total number of hydrogen atoms attached to the PAH and Ebind is calculated according to Eq. (1). The binding energies correspond to the lowest energy route of hydrogenation found. A clear odd-even pattern is clear for both molecules. |
| In the text | |
 |
Fig. 4 Mass spectrum of hydrogenated and dehydrogenated states of pentacene generated in the hot Nielsen plasma ion source. All hydrogenated states bear a single positive charge. Note the logarithmic scale. |
| In the text | |
 |
Fig. 5 The binding energy of a hydrogen atom of a certain hydrogenated state of pentacene. n corresponds to the total number of hydrogen atoms attached to the PAH and Ebind is calculated according to Eq. (1). The clear odd-even pattern for the neutral is not repeated in the cationic case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


