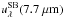EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 549 (January 2013) A&A, 549 (2013) A125 Full HTML
Free Access
Issue
A&A
Volume 549, January 2013
Article Number A125
Number of page(s) 15
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201015257
Published online 10 January 2013

© ESO, 2013

1. Introduction

One of the most important results brought by the Infrared Astronomical Satellite (IRAS) was the detection of a new class of galaxies where the bulk of their bolometric emission lies in the infrared range (Soifer et al. 1984b). This population, named luminous infrared galaxies (LIRG), becomes the dominant extragalactic population at IR luminosities above 1011  L⊙, with a space density higher than all other classes of galaxies of comparable bolometric luminosity (see Sanders & Mirabel 1996, for a complete review of these objects). At the brightest end of this population distribution lie the ultraluminous (ULIRG; LIR > 1012  L⊙) and the hyperluminous infrared galaxies (HLIRG; LIR > 1013  L⊙).

Ever since the discovery of LIRG, two possible origins have been suggested for the observed luminosities: active galactic nuclei (AGN) and/or stellar formation in starburst (SB) episodes (Carico et al. 1990; Condon et al. 1991; Rieke et al. 1980; Soifer et al. 1984a, 1987a; Wright et al. 1984). The AGN/SB relative contributions to the IR output of this kind of sources shows a clear trend with luminosity: while LIRG and low-luminosity ULIRG are SB-dominated sources, the AGN emission is essential for explaining the bolometric luminosity in high-luminosity ULIRG and HLIRG. The fraction of sources harbouring an AGN, and its relative contribution increases with IR luminosity (Farrah et al. 2002a, 2006; Nardini et al. 2010; Rowan-Robinson 2000; Tran et al. 2001; Veilleux et al. 1999, 2002).

Understanding the ultimate physical mechanism that triggers those phenomena and their interplay, particularly in those sources with extreme IR luminosities, is crucial for obtaining a complete view of galaxy evolution. Over the past decade, comprehensive observations from X-rays to radio have produced a consistent paradigm for local ULIRG. Now it is broadly accepted that these objects are dusty galaxies where fierce star formation processes have been triggered by mergers or interactions between gas-rich galaxies (Dasyra et al. 2006; Genzel et al. 2001; Mihos & Hernquist 1994). Only half of them harbour an AGN, which usually is a minor contributor to the total IR emission (cf. Lonsdale et al. 2006, for a complete review).

ULIRG are rare in the Local Universe (Soifer et al. 1987b), but a large number have instead been detected in deep-IR surveys. They are a fundamental constituent of the high-redshift galaxy population (Caputi et al. 2007; Daddi et al. 2005; Elbaz et al. 2002; Farrah et al. 2006; Franceschini et al. 2001; Lonsdale et al. 2004; Magdis et al. 2010, 2011). It has been proposed that ULIRG at high redshift could be at the origin of massive elliptical and S0 galaxies (Franceschini et al. 1994; Genzel & Cesarsky 2000; Genzel et al. 2001; Lilly et al. 1999). A large percentage of stars in present-day galaxies would have been formed during these evolutionary phases. However, the paradigm described above is not as well-grounded for the high-z ULIRG population (Draper & Ballantyne 2012; Niemi et al. 2012; Rodighiero et al. 2011), or for higher luminosity objects like HLIRG.

HLIRG seem to be composite sources, i.e. AGN and SB phenomena are both needed to fully explain their IR emission (Farrah et al. 2002a; Han & Han 2012; Rowan-Robinson 2000; Rowan-Robinson & Wang 2010; Ruiz et al. 2010), and only about a third have been found in interacting systems (Farrah et al. 2002b). This suggests that most HLIRG are not triggered by mergers, as also found for a significant number of high-z ULIRG (Draper & Ballantyne 2012; Niemi et al. 2012; Sturm et al. 2010). If HLIRG and high-z ULIRG share other properties, local HLIRG could be key objects understanding the high-z population of ULIRG, since they are brighter and easier to study with the current astronomical tools. Moreover, as HLIRG could represent the most vigorous stage of galaxy formation with star formation rates (SFR) higher than 1000  M⊙   yr-1, they are unique laboratories for investigating extremely high stellar formation and its connection to super-massive black hole (SMBH) growth.

The relative contributions of AGN and SB to the bolometric luminosity of HLIRG is still being debated. Early studies of small samples of HLIRG found contradictory results, with some authors suggesting that the IR emission arises predominantly from an SB with SFR ~ 1000  M⊙   yr-1 (Frayer et al. 1998, 1999), and other authors suggesting that HLIRG are powered by a dusty AGN (Evans et al. 1998; Granato et al. 1996; Yun & Scoville 1998). The analyses of the IR spectral energy distributions (SED) of larger samples of HLIRG have revealed that about half of these sources are AGN-dominated (Rowan-Robinson 2000; Rowan-Robinson & Wang 2010; Verma et al. 2002). Our analysis of the HLIRG’s broadband (from radio to X-rays) SED (Ruiz et al. 2010) obtained consistent results, showing that both AGN and SB components are needed to reproduce the full emission of these objects. The bolometric luminosity of the AGN is dominant, or at least comparable to, the SB luminosity in ~70% of the studied HLIRG. These studies were, however, based on samples biased toward AGN.

Farrah et al. (2002a, hereafter F02) built a sample of HLIRG with a negligible bias toward AGN, and it was observed with the Submillimetre Common-User Bolometer Array (SCUBA; Holland et al. 1999). Submillimetre data introduced tight constraints on SB luminosities in the IR SED analysis. They found that most HLIRG are AGN-dominated sources, but with a significant contribution (≳20%) due to star formation in all objects.

In Ruiz et al. (2007) we tried to disentangle the AGN and SB emission of HLIRG following a different approach. Since the 2−10 keV X-ray emission above ~1042  erg  s-1 is the “smoking gun” of AGN activity (Mushotzky 2004), we studied the X-ray spectra of a sample of fourteen HLIRG observed by XMM-Newton. We found that all the detected sources (ten out of fourteen) were AGN-dominated in the X-ray band, but most were underluminous in X-rays with respect to the predicted luminosity by the standard AGN SED from Risaliti & Elvis (2004), given their IR luminosities. We also found strong evidence that a significant fraction of these objects are heavily obscured, reaching the Compton-thick (CT) level (hydrogen column, NH > 1024  cm-2), as suggested by previous studies (Iwasawa et al. 2005; Wilman et al. 2003). Such an absorption level only allows, in the best cases, the detection of reflected X-ray emission. To avoid the strong obscuration effects and to obtain a more complete and independent view of these sources, we need to move to another spectral window.

In this paper we present a study of a sample of HLIRG in the mid-infrared (MIR) band, λ = 5−8 μm, a spectral range that is very efficient at detecting AGN emission and less affected by absorption than X-rays. Several diagnostic methods are available to unravel the AGN and SB activity through the MIR spectra, such as the study of high-ionization emission lines and the polycyclic aromatic hydrocarbon (PAH) features (Armus et al. 2007; Farrah et al. 2007; Laurent et al. 2000; Spoon et al. 2007) or the analysis of the continuum around 4 μm (Risaliti et al. 2006). Blind statistical techniques, like principal component analysis, have also been successfully employed with MIR spectra (Hurley et al. 2012; Wang et al. 2011). However, given the limited size of our sample, we cannot apply these statistical methods.

The MIR continuum of pure AGN and pure SB show small dispersion below 10 μm (Brandl et al. 2006; Netzer et al. 2007), allowing the use of universal templates to reproduce the AGN and SB emission in sources where both physical processes are present. As a result, we can unravel the AGN and SB components of composite sources by modelling their MIR spectra with these templates. The key reason for using the continuum emission at λ ≃ 5−8 μm as a diagnostic is the difference in the 6 μm-to-bolometric ratios between AGN and SB (approximately two orders of magnitude higher in the former). This makes the detection of the AGN component possible even when the AGN is heavily obscured and/or bolometrically weak compared to the SB.

SB/AGN continuum spectral decomposition has been successfully applied in ULIRG (Nardini et al. 2008, 2009, 2010; Risaliti et al. 2010) to disentangle the emission of both components. A significant number of HLIRG has been observed with the infrared spectrograph (IRS, Houck et al. 2004) on board Spitzer (Werner et al. 2004), obtaining good quality spectra to apply this diagnostic technique.

The outline of the paper is as follows. Section 2 describes the selected sample of HLIRG. The IRS data reduction is explained in Sect. 3. In Sect. 4 we explain the decomposition process, the adopted model and the results. Section 5 discusses the results of the MIR spectral analysis and Sect. 6 summarizes our conclusions.

The Wilkinson Microwave Anisotropy Probe (WMAP) concordance cosmology has been adopted along the paper: H0 = 70 km s-1 Mpc-1, Ωm = 0.27,ΩΛ = 0.73 (Komatsu et al. 2009).

Table 1

Spitzer observations of HLIRG.

2. The sample

This paper is based on analysis of the F02 sample of HLIRG. Nine out of ten sources in that sample1 have been observed with the Spitzer-IRS in its low-resolution mode, and the data are publicly available in the Spitzer Archive. The F02 sample was originally selected in a manner independent of obscuration, inclination, or AGN content. Moreover, its parent sample is composed of objects found from direct optical follow-up of 60 μm or 850 μm surveys (Rowan-Robinson 2000), so it is statistically homogeneous and complete.

Given these selection criteria, F02 claim that the sample should be entirely free of any AGN bias. However, since the parent sample is composed of sources selected from surveys at different wavelengths, this could produce significant biases for or against “hot” dust, which is more common in AGN than in SB (de Grijp et al. 1985; Soifer et al. 1987a). Thus, objects from 60 μm surveys are more likely to contain hot dust heated by AGN, while those sources from 850 μm surveys will be biased towards cold dust heated by star formation. However, we must note that only a small fraction of the Rowan-Robinson (2000) sample was selected from 850 μm data (less than 10%), and a similar fraction was found in the F02 sample. Moreover, the effect of the AGN hot dust in composite sources with equal AGN and SB bolometric output is severely diminished beyond ~30 μm rest frame (cf. Fig. 1 of Nardini et al. 2009). Only three HLIRG in the F02 sample are at z ~ 1, so the effect of hot dust is minimal. The potential AGN bias is therefore negligible, and we consider the F02 sample suitable for drawing general conclusions about the HLIRG population.

Only five sources of this sample have been observed by XMM-Newton, and just two of these five HLIRG were detected (Ruiz et al. 2007). In order to study the relation between the X-ray and MIR emission for this kind of sources, we included four additional HLIRG in our sample. These objects were selected from the X-ray-selected HLIRG sample we analysed in Ruiz et al. (2007). They all were detected by XMM-Newton and observed with Spitzer-IRS. Three of these additional HLIRG were found via comparisons to known AGN (Tables 2−4 of Rowan-Robinson 2000), and therefore its inclusion leads to a non-negligible bias toward AGN content in our final sample. Nevertheless, on some occasions we could derive conclusions about the overall population of HLIRG restricting our results to the F02 sample (nine out of ten F02 sources are included in our sample).

There are thirteen HLIRG in our final sample. According to their optical spectra, six are type 1 AGN (Seyfert 1 or QSO), four are type 2 AGN (Seyfert 2 or QSO2), and three are SB galaxies (see Table 1). The IR SED of all sources have been observed and studied using radiative transfer models (RTM) over several papers (F02; Rowan-Robinson 2000; Verma et al. 2002). AGN and SB components are both needed to reproduce the IR emission of these HLIRG, the AGN output being dominant in eight out of thirteen sources.

Regarding only the objects in the F02 sample, five are type 1 AGN and four are optically classified as narrow-line (NL) objects. All type 1 sources and one NL object show an AGN-dominated IR SED, and the remaining (three) NL sources show an SB-dominated IR SED, according to the F02 analysis.

The broad band SED (from radio to X-rays) of nine out of thirteen sources have also been studied using observational templates for the AGN and SB components, offering consistent results with those obtained using RTM (Ruiz et al. 2010).

3. Data reduction

All sources from our HLIRG sample have been observed by the IRS on board Spitzer in the low-resolution mode (see Table 1) and the data were publicly available. All observations were operated in the standard staring mode using the two low-resolution modules (SL and LL). The basic calibrated data (BCD) files, bad pixel masks (BMASK), and flux uncertainty files were downloaded from the Spitzer Heritage Archive v1.5. All files are products of the official Spitzer Science Center pipeline (version S18.18).

The BCD pipeline reduces the raw detector images from individual exposures by removing the electronic and optical artefacts (e.g. dark current, droop effect, non-linear effects, detection of cosmic-ray events), jail-bar pattern, and stray light, and performing a flat-field correction. BCD files, along with the corresponding uncertainty images and BMASK files, are reliable inputs for SMART, an IDL-based processing and analysis tool for IRS data (Higdon et al. 2004).

We processed the BCD pipeline files using SMART 8.2.3. We cleaned the BCD files of bad pixels using IRSCLEAN 2.1 and we combined the individual exposures for a given ExpID (uncertainty files were used to perform a weighted-average). To remove the background and low-level rogue pixels we subtracted the two observations in the nodding cycle for each module and order (SL1, SL2, LL1, LL2). We checked that all sources were point-like and well centred in the slits, and finally we ran an automatic, tapered column (window adjusted to the source extent and scaling with wavelength) extraction2 to obtain the flux- and wavelength-calibrated spectra. We checked that individual orders did match in flux after extraction, so no further scaling corrections were needed.

Two spectra were obtained for each source, one for each nod. We calculated an error-weighted average of the two nod spectra3 and they were de-redshifted to rest frame. Figure 1 shows the final spectra.

4. SB/AGN spectral decomposition

4.1. Model for the MIR emission of HLIRG

Thanks to the unprecedent sensitivity of Spitzer-IRS, MIR studies of large samples of luminous AGN and SB have revealed significant spectral homogeneity in the SED of the two separate classes (Brandl et al. 2006; Hernán-Caballero & Hatziminaoglou 2011; Mullaney et al. 2011; Netzer et al. 2007). For high-luminosity sources, this is particularly true within the 5−8 μm range, showing nearly constant shapes of both the PAH complex in SB (Brandl et al. 2006) and the continuum in AGN (Netzer et al. 2007).

This small spectral dispersion allows the use of universal templates to parametrize the observed energy output of objects where both AGN and SB phenomena are present, as in ULIRG or HLIRG, in the wavelength range below 8 μm. This technique has been extensively tested in ULIRG, showing that the observed differences in the PAH equivalent width and strength are caused, in most sources, by the relative contribution of the AGN continuum and its obscuration (Nardini et al. 2008, 2009, 2010).

The bolometric luminosities of HLIRG and ULIRG differ no more than about an order of magnitude (even less for the SB component). Moreover, a significant number of HLIRG seem to share properties with local ULIRG (Ruiz et al. 2010). Thus, we can rely on the model proposed by Nardini et al. (2008, hereafter N08) with reasonable confidence to reproduce the 5−8 μm emission in HLIRG. 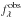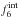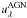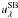The observed flux at wavelength λ, fλobs\hbox{$\Fobs$}, is given by fλobs=f6int[α6uλAGNe−τ(λ)+(1−α6)uλSB],\begin{equation} \label{eq:model} \Fobs = \Fint \left[\alfa~\tempAGN \mathrm{e}^{-\tau(\lambda)} + (1 - \alfa)~\tempSB \right], \end{equation}(1)where α6 is the AGN contribution to f6int\hbox{$\Fint$} (the intrinsic flux density at 6 μm), while uλAGN\hbox{$\tempAGN$} and uλSB\hbox{$\tempSB$} are the AGN and SB emission normalized at 6 μm. 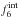This model has only three free parameters: α6, τ6 (the optical depth at 6 μm), and f6int\hbox{$\Fint$} (the flux normalization). Additional high-ionization emission lines and molecular absorption features (due to ices and aliphatic hydrocarbons), whenever present, were fitted using Gaussian profiles.

thumbnail Fig. 1

MIR rest-frame spectra of HLIRG obtained with the Infrared Spectrograph on board Spitzer. The grey shaded area is the 1σ uncertainty region. The vertical dashed lines limit the spectral region where our decomposition technique was applied.

thumbnail Fig. 2

Average SB spectra used as templates in our model: template a) is from N08; templates b)–d) from Hernán-Caballero & Hatziminaoglou (2011, see Sect. 4. The grey shaded area is the estimated 1σ dispersion.

Table 2

Best-fit model parameters (cf. Sect. 4).

thumbnail Fig. 3

5−8 μm spectra and best-fit models (blue solid line). The AGN component is plotted as a red dashed line. For clarity, the SB component (green dotted line) is plotted only on those sources where the AGN and SB contributions are comparable.

thumbnail Fig. 4

Spectral index-optical depth confidence regions for IRAS 07380-2342 (left) and IRAS F16124+3241 (right). The contours represent 1σ, 2σ, and 3σ confidence levels.

Starburst emission

As stated above, starbursts of different luminosities present a small spectral dispersion in their MIR emission below 8 μm. Given all the physical variables (e.g. the initial mass function, the duration and evolution of the burst, dust grain properties) involved in determining the observational properties of an SB, it is in fact surprising to find so much similarity. Brandl et al. (2006) suggest that this homogeneity can derive from the spatial integration of unresolved star-forming spots. We can then assume that an observational template will accurately reproduce the SB emission of our sources in the 5−8 μm range. This emission is characterized by two prominent PAH features at 6.2 and 7.7 μm (Fig. 2).

To increase the robustness of our analysis we employed four different SB templates from N08 (a) and from Hernán-Caballero & Hatziminaoglou (2011) (b–d): a) the average MIR spectrum from the five brightest ULIRG among pure SB sources in the N08 sample; b) the average spectrum of objects optically classified as SB or HII in NED and with νLν(7 μm) < 1044  erg   s-1 (16 sources); c) the average spectrum of SB-dominated objects in the MIR (257 sources); and d) the average spectrum of objects classified as ULIRG (184 sources). As expected, all SB templates show similar features4 and small dispersion below 8 μm (see Fig. 2).

AGN emission

In our range of interest the AGN spectrum is dominated by the cooling of small dust grains that are transiently heated up to temperatures close to the sublimation limit. This process is expected to produce a nearly featureless power law continuum. However, PAH features are found in several quasars (Lutz et al. 2007, 2008; Schweitzer et al. 2006). Netzer et al. (2007) ascribe the FIR emission of a set of luminous PG QSO to cold dust in extended regions, thus probably of stellar origin. After removing this galactic contamination, the average spectrum can be modelled with a single power law from ~3 μm to the 9.7 μm silicate bump. Since the spectral dispersion within this range is small for pure luminous QSO, we can model the AGN emission in our sources with the same power law with a fixed spectral index: fλ ∝ λ0.8. Again, to increase the robustness of our results, we alternatively fitted all sources, allowing the slope of the power law to vary in the range 0.2−1.8. This interval covers the dispersion found in the spectral index for the AGN emission in ULIRG (Nardini et al. 2010).

Our model includes an exponential attenuation in the AGN emission to take the reddening of the NIR radiation due to any compact absorber in the line of sight into account. The optical depth follows the conventional law τ(λ) ∝ λ-1.75 (Draine 1989). The SB emission does not need a similar correction because the possible effects of obscuration are already accounted for in the observational templates.

4.2. Results

The model presented in the previous section was implemented in Sherpa (Freeman et al. 2001), which is the modelling and fitting tool included in the software package CIAO 4.3 (Fruscione et al. 2006). The 5−8 μm spectra were fitted using a Levenberg-Marquardt χ2 minimization algorithm. The errors in the parameters (within 1σ confidence limit) were calculated through Montecarlo simulations.

One object was barely detected by Spitzer, and in two additional sources our model was not suitable (see Sect. 4.3 for a further discussion on these objects), but the spectra of the remaining ten sources were reproduced well by our model (see Fig. 3 and Table 2).

We found no significant difference between the best-fit models using the four SB templates. All templates offer a similar χ2 and consistent values for the model parameters. We have therefore included in Table 2 only the results obtained using the N08 SB template. However, we should note that the use of the ULIRG template provides systematically lower values of α6 in all sources. This result is probably caused by the presence of an AGN component in the template, as expected in an average ULIRG spectrum including high-luminosity objects (Hernán-Caballero & Hatziminaoglou 2011; Nardini et al. 2010).

Allowing the spectral index to vary did not enhance the fit in most sources. A statistically significant improvement (in terms of F-test) was only found in three sources with high optical depth (beside IRAS 18216+6418, which is discussed below). However, we must note that our model is severely degenerated in the optical depth-spectral index plane (see Fig. 4). The shape of the 5−8 μm continuum cannot be fully established in sources showing high absorption. If the spectral index is a free parameter, the minimization algorithm therefore decreases the optical depth while increasing the spectral index. We selected the model with fixed spectral index as our best fit in those sources showing obscuration features outside the 5−8 μm range (e.g. 9.7 μm silicate absorption).

thumbnail Fig. 5

Comparison of the SFR estimated through PAH emission and through IR SED modelling using RTM (Farrah et al. 2002a; Rowan-Robinson 2000; Verma et al. 2002).

The 6 μm emission is largely dominated by the AGN component (α6 ≳ 0.9), which also dominates the whole 5−8 μm spectral range. IRAS F00235+1024 and IRAS F16124+3241 are the only two sources where the SB and AGN components are comparable, but the AGN emission is still above the SB. The PAH emission at ~6.2 and ~7.7 μm in these two sources is adequately reproduced by our SB template, suggesting that our assumption, i.e. the MIR SB emission of HLIRG can be modelled by the MIR emission of SB-dominated ULIRG, is correct.

All sources optically classified as type I AGN show low absorption (except IRAS F10026+4949), while all sources classified as NL or type II AGN show high absorption (except IRAS 12514+1027, which shows a strong 9.7 μm silicate absorption feature).

In two sources (IRAS 09104+4109 and IRAS 12514+1027) we detected a spectral feature at ~7.7 μm that can be modelled as a Gaussian emission line. In both cases the line is statistically significant (in terms of F-test), although it is not needed to obtain a good fit. The line can be interpreted as the unresolved [NeVI] fine-structure line at 7.65 μm. Due to its high ionization energy (126 eV), it seems to be connected to the hardest nuclear activity. This emission feature has been detected in previous studies of local ULIRG (Nardini et al. 2009; Veilleux et al. 2009).

4.3. Notes on particular sources

IRAS 00182-7112

This CT QSO2 shows a heavily absorbed MIR spectrum. At first sight, our model seems to reproduce the spectrum above 6.5 μm well (see Fig. 3a) if two absorption lines at 6.8 and 7.3 μm are included (C-H stretching mode of hydrogenated amorphous carbon, HAC; Furton et al. 1999). However, the lack of the 6.2 μm PAH emission feature and the overall shape of the whole MIR spectrum (see Fig. 1a) strongly suggest that the 7.7 μm feature is actually not associated with PAH emission. Spoon et al. (2004a) suggest that the 5.7−7.7 μm range is dominated by a broad absorption complex owing to water ice and hydrocarbons. Thus, our simple model cannot reproduce the complex spectra of this object (as suggested by the poor fit we obtain, with a reduced χ2 ~ 20).

The spectrum shows no signs of SB activity within the 5−8 μm range, since the PAH features are totally suppressed, and it is very similar to the MIR spectra of deeply obscured AGN (e.g. NGC 4418, NGC 1068). This result, along with additional evidence from other wavelengths, e.g. strong iron Kα emission line with ~1 keV equivalent width in the X-ray spectrum (Ruiz et al. 2007), suggests that the power source hiding behind the optically thick material could be a buried AGN.

Spoon et al. (2004a) present a detailed study of the whole IRS spectrum: the strong absorption and weak emission features in the 4−27 μm spectrum suggest the existence of a dense warm gas cloud close to the nucleus of the source. Based on the strength of the 11.2 μm PAH feature, there is also evidence of star formation activity away from the absorbing region, which could be responsible for up to 30% of the IR luminosity of the system. For further analysis and comparison we have employed this estimate of the SB relative contribution.

IRAS 09104+4109

This is a radio-loud QSO2, and the MIR spectrum is probably dominated by synchrotron radiation, modifying the shape of the AGN emission. Although our model offers an excellent fit in a purely statistical sense (χ2/d.o.f. ≃ 0.6), the selected AGN template only models the reprocessed emission by dust. In this case, the physics predicted by our model could therefore be inaccurate.

IRAS 18216+6418

The continuum of this QSO seems to be flatter than the adopted power law. This is the only non-obscured source where a free spectral index model offers clear improvement in the best fit. The flatter continuum could just be the natural dispersion around the template: a flatter AGN slope has been detected in ~10% of ULIRG (Nardini et al. 2010). However, we must note that this object, although classified as a radio-quiet AGN, shows many properties of radio-loud sources (F02). Thus we cannot reject the possibility that the flatter continuum is caused by synchrotron contamination.

IRAS F23569-0341

This source was barely detected by Spitzer, and the extracted spectrum had a very poor S/N, so it was rejected in the subsequent analysis. It has not been detected with either ISO or SCUBA (F02).

5. Discussion

The 5−8 μm spectra of most ULIRG show signatures of AGN activity, but the relative contribution of the AGN emission at 6 μm spans a broad range, from complete SB-dominated to complete AGN-dominated output (Nardini et al. 2008, 2009, 2010). Our spectral decomposition, on the other hand, clearly states that 5−8 μm spectra of HLIRG are strongly dominated by the nuclear AGN emission reprocessed by the dusty torus. This is consistent with previous studies showing that the fraction of ULIRG harbouring an AGN and the relative contribution of this component increase with IR luminosity (Nardini et al. 2010; Veilleux et al. 1999, 2002).

This result also agrees with previous studies in other wavelengths, which found AGN activity in most HLIRG (F02; Rowan-Robinson 2000; Rowan-Robinson & Wang 2010; Ruiz et al. 2007, 2010; Verma et al. 2002). Moreover, based on the completeness and the negligible AGN bias of the F02’s sample, our analysis is strong direct evidence that all HLIRG harbour an AGN.

5.1. Star formation rate from PAH emission

Many studies have shown the tight correlation between the presence of polycyclic aromatic hydrocarbon (PAH) features in the MIR spectrum and starburst activity (Brandl et al. 2006; Genzel et al. 1998; Rigopoulou et al. 2000). The PAH emission arises in the photo-dissociation region that lies between the HII region of an SB and the surrounding molecular cloud where the stars are formed. The PAH spectral features are, in addition, very uniform, especially below 8 μm (cf. Fig. 1 of N08 or Fig. 2 in Sargsyan & Weedman 2009).

The 5−8 μm spectra of our HLIRG are strongly dominated by the AGN emission, so we cannot obtain a reliable direct measure of the PAH emission. Instead, we estimated the emission of this spectral feature through the SB component obtained with our spectral decomposition. For each source, we calculated a rough estimate of the PAH peak flux at 7.7 μm using the best-fit model5: 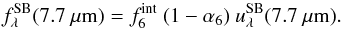fλSB(7.7μm)=f6int(1−α6)uλSB(7.7μm).\begin{equation} \label{eq:sfr} f_{\lambda}^\mathrm{SB}(7.7~\mu\mathrm{m}) = \Fint~(1 - \alfa)~\tempSB(7.7~\mu\mathrm{m}). \end{equation}(2)After converting these fluxes into luminosities, we estimated the SFR using the relation obtained by Sargsyan & Weedman (2009): logSFRPAH=log[λLλSB(7.7μm)]−42.57±0.2,\begin{equation} \label{eq:sfr2} \log {\it SFR}_{\mathrm{PAH}} = \log \left[\lambda L_\lambda^\mathrm{SB}(7.7~\mu\mathrm{m})\right] - 42.57 \pm 0.2, \end{equation}(3)where SFRPAH is the star formation rate in solar masses per year, and λLλSB(7.7μm)\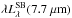hbox{$\lambda L_\lambda^\mathrm{SB}(7.7~\mu\mathrm{m})$} is the PAH luminosity at 7.7 μm in ergs per s.

thumbnail Fig. 6

SFR estimated using the PAH emission at 7.7 μm versus a) total and b) starburst IR luminosities. The open circles mark those sources where our model is inaccurate.

Our estimate of the 7.7 μm flux includes both the PAH emission and the underlying SB continuum due to dust emission, but Eq. (3) is calibrated with respect to the total 7.7 μm flux, including both components. In any case, the continuum contribution is typically just ~10% of the total (Sargsyan & Weedman 2009). Since α6 is close to unity in all our sources, the relative error of the SB contribution at 6 μm is high. Thus our SFR estimates cannot be accurate beyond an order of magnitude.

Figure 5 compares our SFR estimates with those obtained through modelling the IR SED using RTM (Rowan-Robinson 2000; Verma et al. 2002, F02). Both techniques seem to find consistent results. Despite most being AGN-dominated objects (see Sect. 5.2 below), we still found high star-forming activity, with SFR ~ 300−3000  M⊙  yr-1 (see Table 3).

Table 3

SFR and AGN relative contributions to the IR output, along with IR luminosities (in cgs units).

Figure 6 shows the SFR we calculated versus (a) total and (b) SB IR luminosity. We estimated the SB luminosity as 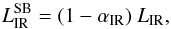LIRSB=(1−αIR)LIR,\begin{equation} L_\mathrm{IR}^\mathrm{SB} = (1 - \alpha_\mathrm{IR})~L_\mathrm{IR}, \end{equation}(4)where αIR is the fractional contribution of the AGN to the total IR luminosity (see Sect. 5.2) and LIR the total IR emission (8−1000 μm) calculated through the IRAS fluxes (Sanders & Mirabel 1996). When only an upper limit is available for the IRAS fluxes at 12 or 25 μm, we have simply assumed one half of this limit. This convention provides a fair approximation of the actual flux densities even for sources at moderate redshifts (Nardini et al. 2009, 2010).

We performed several statistical tests to check any possible correlation between the SFR and the IR luminosities. Since our estimates of LIRSB\hbox{$L_\mathrm{IR}^\mathrm{SB}$} and SFR both depend on the parameter α6 (see Eqs. (2) and (7)), we used a generalized Kendall’s Tau partial correlation test6 (Akritas & Siebert 1996). The result shows that both quantities are correlated with a probability ~99.99% > 3σ. This tight correlation between the star formation and SB IR luminosity is expected from several theoretical results (Draine & Li 2001, 2007; Kennicutt 1998, and references therein).

thumbnail Fig. 7

6 μm-to-IR ratio (R) versus α6. The red dashed line is our best fit for the relation between R and α6 given by Eq. (6). The blue solid line is the best fit obtained by N08 for a sample of ULIRG.

In the case of total IR luminosity versus SFR, we can apply a generalized Kendall’s Tau test7, since the estimate of the IR luminosity is completely independent of our estimate of the SFR. They show a weaker, but slightly significant, correlation (the probability is 98% > 2σ). This slight correlation and the high SFR suggest that SB emission could be a significant contributor to the IR output (see Sect. 5.2).

5.2. AGN contribution to the IR luminosity

We define the 6 μm-to-IR bolometric ratio as R=ν6f6intFIR,\begin{equation} \label{eq:Rdef} R=\dfrac{\nu_6\Fint}{F_\mathrm{IR}}, \end{equation}(5)where FIR is the total IR flux (8−1000 μm) estimated as in Sanders & Mirabel (1996). The hypothesis that the IR and total bolometric fluxes are almost coincident is typically a fair assumption in ULIRG, but in principle we cannot adopt this hypothesis in our sources. The study of the HLIRG’s broad band SED has revealed that, for an important number of sources classified as HLIRG, a non-negligible fraction of the bolometric luminosity is emitted outside the IR range (Ruiz et al. 2010). Therefore we limited our analysis to the IR luminosity.

thumbnail Fig. 8

Comparison of the AGN contribution to the IR luminosity estimated through MIR spectral decomposition and through RTM. The blue squares are type I AGN and the red triangles are type II AGN and SB. The open circles mark those sources where our model is inaccurate. MIR contribution for IRAS 00182-7112 from Spoon et al. (2004a).

We can derive a connection between R and the parameter α6: 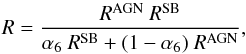R=RAGNRSBα6RSB+(1−α6)RAGN,\begin{equation} \label{eq:Ralpha6} R=\dfrac{\RAGN~\RSB}{\alfa~\RSB + (1-\alfa)~\RAGN}, \end{equation}(6)where RAGN and RSB are the equivalents of R for pure (unobscured) AGN and pure SB, as defined in Eq. (5).

Both R and α6 are known quantities. Assuming α6 as the independent variable and R as the dependent variable, we can fit Eq. (6) to the values observed in our sources, considering RAGN and RSB as free parameters. We found RAGN = 0.36 ± 0.08,RSB = (8 ± 3) × 10-3. In spite of the limited size of our sample and the narrow range for α6, these results are in good agreement with those obtained by N08 for a larger sample of ULIRG: RAGN=0.32-0.08+0.11,RSB=(11.7-0.7+0.9)×10-3\hbox{$\RAGN=0.32^{+0.11}_{-0.08}, \RSB=(11.7^{+0.9}_{-0.7}) \times 10^{-3}$}. Figure 7 shows R versus α6 for our sample of HLIRG, including our best fit and the result from N08.

Using α6, RAGN, and RSB (with the N08 values for the last two quantities), we could estimate the fractional AGN contribution (αIR) to the IR output of each source: 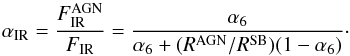αIR=FIRAGNFIR=α6α6+(RAGN/RSB)(1−α6)·\begin{equation} \label{eq:alfaIR} \alpha_\mathrm{IR} = \dfrac{F_\mathrm{IR}^\mathrm{AGN}}{F_\mathrm{IR}} = \dfrac{\alfa}{\alfa + (\RAGN/\RSB)(1-\alfa)}\cdot \end{equation}(7)Figure 8 compares αIR estimated through our MIR spectral analysis and through the analysis of the IR SED using RTM (Rowan-Robinson 2000; Verma et al. 2002, F02). Both estimates seem to be consistent in most sources. Leaving aside those sources where our model is not suitable (IRAS 09104+4109 and IRAS 00182-7112), we found that the IR luminosity of seven out of ten HLIRG is dominated by AGN emission. However, the SB contribution is also significant for all sources, spanning from ~20% to 70% (see Table 3). Using only the sources from the F02 sample, the mean SB contribution is ~30%, close to the 35% obtained by F02. This significant SB contribution is consistent with the correlation we found between SFR and IR luminosity and the high SFR estimated (see Sect. 5.1). Our analysis confirms the idea that star formation and accretion into SMBH are both crucial phenomena in explaining the properties of these extreme objects.

5.3. Covering factor

An important physical parameter for unveiling the distribution of dust in the nuclear environment of an AGN is the dust covering factor (CF), i.e. the fraction of sky covered by dust viewed from the central engine of the AGN. The CF is also critical for understanding the fraction of direct nuclear emission that is absorbed by dust and re-emitted in the IR range and hence has a significant effect on the bolometric luminosity corrections of AGN.

The ratio between the thermal AGN luminosity (i.e., the IR reprocessed emission due to heated dust), 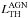LTHAGN\hbox{$L^\mathrm{AGN}_\mathrm{TH}$}, and the primary AGN luminosity (above ~1 μm, i.e., the accretion disk bolometric emission), LBOLAGN\hbox{$L^\mathrm{AGN}_\mathrm{BOL}$}, is commonly interpreted as an estimate of the dust CF (Maiolino et al. 2007; Roseboom et al. 2013; Rowan-Robinson et al. 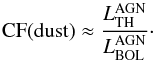2009): CF(dust)≈LTHAGNLBOLAGN·\begin{equation} \mathrm{CF(dust)} \approx \dfrac{L^\mathrm{AGN}_\mathrm{TH}}{L^\mathrm{AGN}_\mathrm{BOL}}\cdot \end{equation}(8)The thermal AGN luminosity can be estimated through the MIR continuum emission. 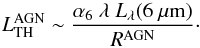Assuming that the IR AGN luminosity is dominated by the dust emission and using the best-fit parameters obtained in our MIR spectral decomposition, the thermal emission is computed as LTHAGN~α6λLλ(6μm)RAGN·\begin{equation} L^\mathrm{AGN}_\mathrm{TH} \sim \dfrac{\alpha_6~\lambda~L_\lambda(6~\mu\mathrm{m})}{\RAGN}\cdot \end{equation}(9)X-ray emission is a primary product of the central engine of AGN, so X-ray luminosity is usually a good proxy for estimating the bolometric AGN luminosity (Maiolino et al. 2007; Rowan-Robinson et al. 2009). We applied the bolometric correction estimated by Marconi et al. 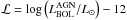(2004): logLBOLAGNLX=1.54+0.24ℒ+0.012ℒ2−0.0015ℒ3,\begin{equation} \label{eq:bolcor} \log \dfrac{L^\mathrm{AGN}_\mathrm{BOL}}{L_\mathrm{X}} = 1.54 + 0.24\mathcal{L} + 0.012\mathcal{L}^2 - 0.0015\mathcal{L}^3, \end{equation}(10)where ℒ=logLBOLAGN(/L⊙)−12\hbox{$\mathcal{L}=\log \left( L^\mathrm{AGN}_\mathrm{BOL}/\Lsun \right) - 12$} and LX the intrinsic (i.e., absorption-corrected) 2−10 keV luminosity.

We can therefore estimate the CF of those sources for which MIR and X-ray data are both available. Eight out of thirteen HLIRG in our sample fulfil this condition. The X-ray luminosities were obtained from Ruiz et al. (2007). IRAS F00235+1024 and IRAS 07380-2342 are probably CT sources (Ruiz et al. 2007, 2010) so the upper limits on their X-ray luminosities have been increased by a factor of 60, the average ratio between intrinsic and observed X-ray luminosities in CT sources (Panessa et al. 2006). IRAS 14026+4341 was not detected in our X-ray analysis, but it has a counterpart in the 2XMMi catalogue (Watson et al. 2009). We estimated its 2−10 keV luminosity using the 2XMMi X-ray fluxes. Since this object seems to be an X-ray absorbed QSO (Ruiz et al. 2010), we applied the correction to the CT objects described above to calculate its intrinsic X-ray luminosity.

thumbnail Fig. 9

CF versus the AGN luminosity at 6 μm. The blue dashed line is the estimated average CF for local QSO (see Sect. 5.3). Symbols as in Fig. 8.

Table 4

AGN luminosities (in cgs units) and CF values.

Table 4 shows all the derived AGN luminosities and final estimates of the dust CF. The covering factors versus the AGN luminosities at 6 μm are plotted in Fig. 9. For comparison, the plot includes the average CF estimated for local QSO8.

Four out of eight objects show a dust CF consistent with ~1 (at 2σ level) and systematically above the average CF of local QSO (~0.5). This result and the heavy X-ray absorption shown by most of these sources (all but one source, IRAS 14026+4341, show signatures of CT absorption in their X-ray emission, see Iwasawa et al. 2005; Ruiz et al. 2007, 2010; Vignali et al. 2011; Wilman et al. 2003) point towards large amounts of gas and dust enshrouding their nuclear environment as found in local ULIRG (Spoon et al. 2004b; Verma et al. 2005; Yan et al. 2010).

We found one source with CF ~ 0.2. This source, IRAS 18216+6418, is a QSO with no sign of X-ray or MIR obscuration. The low CF is consistent with previous studies that find a decrease in the CF of QSO with increasing luminosity (Maiolino et al. 2007; Treister et al. 2008). The decrease could be explained by “receding torus” models (Hasinger 2008; Lawrence 1991; Maiolino et al. 2007): low-luminosity AGN are surrounded by a dust torus of obscuring material covering a large fraction of the central source. High-luminosity AGN would be able to clean out the environment ionizing the surrounding medium or blowing it away through outflowing winds. The opening angle of the torus would thus be larger, and the covered solid angle would be lower (assuming the height of the torus is not luminosity-dependent).

The remaining three sources show CF ≫ 1. A dust CF above unity is usually interpreted as evidence of CT obscuration (Rowan-Robinson et al. 2009). As stated above, two objects (IRAS F00235+1024 and IRAS 07380-2342) were not detected in X-rays (Ruiz et al. 2007) and their broadband SED suggest that their low X-ray emission is due to high obscuration (Ruiz et al. 2010), so the bolometric AGN emission is probably underestimated in these sources. Observational and theoretical studies of CT AGN predict even higher values (i.e., ≫60) for the intrinsic-to-observed X-ray luminosity ratio, depending on the amount of absorption and on the viewing angle with respect to the obscuring torus (Haardt et al. 1994; Iwasawa et al. 1997). The dust CF of these sources would be consistent with unity if the largest correction factor (~1000) were applied.

The third remaining source, IRAS F12509+3122, is a QSO showing an X-ray emission that is significantly lower than the one predicted for a high-luminosity QSO, given its IR luminosity (Ruiz et al. 2010). This suggests that its bolometric AGN emission is also underestimated. However, the low X-ray luminosity of this object cannot be related to X-ray absorption (Ruiz et al. 2007). Alternatively, the X-ray bolometric correction of AGN and the Eddington ratio (λEdd = LBOL/LEdd) seem to be related. The former changes from κX ~ 15−30 for λEdd ≲ 0.1 to κX ~ 70−120 for λEdd ≳ 0.2 (Vasudevan & Fabian 2009). Using the SDSS optical spectrum of IRAS F12509+3122 and the McLure & Jarvis (2002) relation between black hole masses and MgII emission line widths, we estimated λEdd ~ 0.5 for this object. This high Eddington ratio suggests that the X-ray bolometric correction for this source could be higher than obtained in Eq. (10). Further studies are needed to investigate how the Eddington ratio influences the X-ray luminosity of HLIRG.

6. Conclusions

We studied low-resolution MIR spectra of thirteen HLIRG observed with Spitzer, nine of them also observed with XMM-Newton. We modelled their 5−8 μm spectra, using the AGN/SB spectral decomposition technique developed by N08, and we estimated the contribution of each component to the total IR luminosity.

We found that all HLIRG in the sample harbour an AGN that clearly dominates the 5−8 μm spectrum. Given the completeness of the F02 sample (nine out of ten F02 objects are included in our sample), this is strong evidence that all HLIRG harbour an AGN. We also found that the AGN component seems to be the dominant power source of the total IR output in most sources. However, all sources, even the AGN-dominated HLIRG, show significant SB activity, with a mean SB contribution of ~30%. The SFR, estimated through the PAH emission, is also very high in all sources (~300−3000  M⊙   yr-1).

These results agree with previous studies of HLIRG using theoretical models to reproduce their IR SED (F02; Rowan-Robinson 2000; Rowan-Robinson & Wang 2010; Verma et al. 2002), providing further support to the assumptions of these detailed models. The AGN’s relative contribution to the total IR output is also consistent with those estimated through SED modelling. The large mean AGN contribution we found (~70%) is consistent with previous studies of ULIRG, pointing towards an increase in the AGN emission with increasing luminosity (Nardini et al. 2010; Veilleux et al. 2002). Our work confirms the crucial role of both AGN and SB phenomena in explaining the properties of these extreme sources.

Using X-ray and MIR data we were able to estimate the dust CF of these HLIRG, finding that seven out of eight have CF ≳ 1. Most of these sources with large CF also show heavy X-ray absorption and high optical depth or absorption features in their MIR spectrum. This strongly suggests that the nuclear environment of these sources is heavily enshrouded by large amounts of gas and dust, as observed in local ULIRG.

F02 have proposed that HLIRG could be divided into two populations: (1) mergers between gas-rich galaxies, as found in the ULIRG population, and (2) young active galaxies going through their maximum star formation periods whilst harbouring an AGN. In Ruiz et al. (2010) we found strong evidence supporting the two-population hypothesis. Han & Han (2012) studied the same HLIRG sample using AGN and SB 1 theoretical models and Bayesian techniques to fit their IR SED. They find further evidence that the physical properties of AGN and SB harboured by HLIRG could be divided into two populations: SB-dominated HLIRG (corresponding to our “ULIRG-like” objects) show a higher fraction of OB stars and the starburst region is more compact, while AGN-dominated objects show a dustier torus. Additional evidence favouring this two-population idea is presented by Draper & Ballantyne (2012). They suggest, based on recent Herschel observations, that major mergers cannot explain the total population of luminous high-z ULIRG harbouring AGN.

All sources showing CF ~ 1 (except IRAS 14026+4341) were classified as “ULIRG-like” objects in Ruiz et al. (2010), while IRAS 18216+6418, with a significantly lower CF, was classified as a “non-ULIRG” source. Furthermore, IRAS F00235+1024 and IRAS F15307+3252, both sources showing a high CF, were observed by the Hubble Space Telescope (HST) and both present signs of recent mergers. On the other hand, IRAS 18216+6418, also observed by HST, shows no signs of interactions or mergers (Farrah et al. 2002b). The study of the dust CF adds another piece of evidence that HLIRG can be separated into two differentiated populations, although further studies with larger samples of HLIRG are needed to arrive at more definitive conclusions.

1

There were eleven sources in the original sample, but we excluded one object, IRAS 13279+3401, because the redshift in the literature (z = 0.36, Rowan-Robinson 2000) is incorrect, misclassifying the source as an HLIRG. We have shown, using recent optical and MIR spectra (Ruiz et al. 2010), that its redshift is z ~ 0.02. Our estimated IR luminosity for this source is hence 3 × 1010  L⊙.

2

We also tested the advanced optimal (PSF weighted) method (Lebouteiller et al. 2010) to extract the spectra. Since all sources are bright and point-like, the results from both extraction methods were similar. However, we found that the spectra obtained through the advanced optimal method show a strong sinusoidal artefact in most SL2 spectra. We compared our spectra with the Cornell Atlas of Spitzer-IRS Sources (CASIS, Lebouteiller et al. 2011) and found no similar features at those wavelengths. We chose then the tapered column extraction for the subsequent analysis.

3

Averaging the spectra introduces a systematic error related to the flux differences between the two nod spectra. This difference is usually due to the presence of other sources in the slit affecting the background subtraction, or to pointing errors resulting in a slight shift in the dispersion direction (Lebouteiller et al. 2011).

4

Slight differences in the shape of the lines and their intensity ratio are probably caused by variations in the obscuration in the original sources: higher luminosity sources usually show higher obscuration (Rigopoulou et al. 1999).

5

uλSB(7.7μm)\hbox{$\tempSB (7.7~\mu\mathrm{m})$} was estimated by interpolating the N08 SB template at 7.7 μm.

6

Kendall’s Tau test is a non-parametric correlation test based on the Kendall rank coefficient (Kendall & Gibbons 1990). The generalized version is an extension to include censored data (e.g. upper limits). We used the code developed by the Center for Astrostatistics to perform this test (http://astrostatistics.psu.edu/statcodes/cens_tau).

7

We used the ASURV software for this test (Isobe et al. 1986).

8

The average CF was estimated through a direct integration of the Richards et al. (2006) and Hopkins et al. (2007) average AGN SED. The direct AGN emission was calculated by integrating the SED at wavelengths below 1 μm, and the thermal emission integrating the SED at wavelengths above 2 μm.

Acknowledgments

We are grateful to the anonymous referee for the constructive comments and suggestions that improved this paper. A.R. acknowledges support from an IUCAA post-doctoral fellowship and from ASI grant No. ASI I/088/06/0. Financial support for A.R. and F.J.C. was provided by the Spanish Ministry of Education and Science, under project ESP2003-00812 and ESP2006-13608-C02-01. F.J.C. acknowledges financial support under the project AYA2010-21490-C02-01. F.P. acknowledges financial support under the project ASI INAF I/08/07/0. This work is based on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA, and with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. The IRS was a collaborative venture between Cornell University and Ball Aerospace Corporation funded by NASA through the Jet Propulsion Laboratory and Ames Research Center. SMART was developed by the IRS Team at Cornell University.

References

  1. Akritas, M. G., & Siebert, J. 1996, MNRAS, 278, 919 [NASA ADS] [CrossRef] [Google Scholar]
  2. Armus, L., Charmandaris, V., Bernard-Salas, J., et al. 2007, ApJ, 656, 148 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brandl, B. R., Bernard-Salas, J., Spoon, H. W. W., et al. 2006, ApJ, 653, 1129 [NASA ADS] [CrossRef] [Google Scholar]
  4. Caputi, K. I., Lagache, G., Yan, L., et al. 2007, ApJ, 660, 97 [NASA ADS] [CrossRef] [Google Scholar]
  5. Carico, D. P., Sanders, D. B., Soifer, B. T., Matthews, K., & Neugebauer, G. 1990, AJ, 100, 70 [NASA ADS] [CrossRef] [Google Scholar]
  6. Condon, J. J., Huang, Z., Yin, Q. F., & Thuan, T. X. 1991, ApJ, 378, 65 [NASA ADS] [CrossRef] [Google Scholar]
  7. Daddi, E., Dickinson, M., Chary, R., et al. 2005, ApJ, 631, L13 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dasyra, K. M., Tacconi, L. J., Davies, R. I., et al. 2006, ApJ, 638, 745 [NASA ADS] [CrossRef] [Google Scholar]
  9. de Grijp, M. H. K., Miley, G. K., Lub, J., & de Jong, T. 1985, Nature, 314, 240 [NASA ADS] [CrossRef] [Google Scholar]
  10. Draine, B. T. 1989, in Infrared Spectroscopy in Astronomy, ed. E. Böhm-Vitense, ESA SP, 290, 93 [Google Scholar]
  11. Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
  12. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
  13. Draper, A. R., & Ballantyne, D. R. 2012, ApJ, 753, L37 [NASA ADS] [CrossRef] [Google Scholar]
  14. Elbaz, D., Cesarsky, C. J., Chanial, P., et al. 2002, A&A, 384, 848 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Evans, A. S., Sanders, D. B., Cutri, R. M., et al. 1998, ApJ, 506, 205 [NASA ADS] [CrossRef] [Google Scholar]
  16. Farrah, D., Serjeant, S., Efstathiou, A., Rowan-Robinson, M., & Verma, A. 2002a, MNRAS, 335, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  17. Farrah, D., Verma, A., Oliver, S., Rowan-Robinson, M., & McMahon, R. 2002b, MNRAS, 329, 605 [NASA ADS] [CrossRef] [Google Scholar]
  18. Farrah, D., Lonsdale, C. J., Borys, C., et al. 2006, ApJ, 641, L17 [NASA ADS] [CrossRef] [Google Scholar]
  19. Farrah, D., Bernard-Salas, J., Spoon, H. W. W., et al. 2007, ApJ, 667, 149 [NASA ADS] [CrossRef] [Google Scholar]
  20. Franceschini, A., Mazzei, P., de Zotti, G., & Danese, L. 1994, ApJ, 427, 140 [NASA ADS] [CrossRef] [Google Scholar]
  21. Franceschini, A., Aussel, H., Cesarsky, C. J., Elbaz, D., & Fadda, D. 2001, A&A, 378, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Frayer, D. T., Ivison, R. J., Scoville, N. Z., et al. 1998, ApJ, 506, L7 [NASA ADS] [CrossRef] [Google Scholar]
  23. Frayer, D. T., Ivison, R. J., Scoville, N. Z., et al. 1999, ApJ, 514, L13 [NASA ADS] [CrossRef] [Google Scholar]
  24. Freeman, P., Doe, S., & Siemiginowska, A. 2001, in Proc. SPIE, eds. J. L. Starck, & F. D. Murtagh, 4477, 76 [Google Scholar]
  25. Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, in Proc. SPIE, Vol. 6270 [Google Scholar]
  26. Furton, D. G., Laiho, J. W., & Witt, A. N. 1999, ApJ, 526, 752 [CrossRef] [Google Scholar]
  27. Genzel, R., & Cesarsky, C. J. 2000, ARA&A, 38, 761 [NASA ADS] [CrossRef] [Google Scholar]
  28. Genzel, R., Lutz, D., Sturm, E., et al. 1998, ApJ, 498, 579 [NASA ADS] [CrossRef] [Google Scholar]
  29. Genzel, R., Tacconi, L. J., Rigopoulou, D., Lutz, D., & Tecza, M. 2001, ApJ, 563, 527 [NASA ADS] [CrossRef] [Google Scholar]
  30. Granato, G. L., Danese, L., & Franceschini, A. 1996, ApJ, 460, L11 [NASA ADS] [CrossRef] [Google Scholar]
  31. Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
  32. Han, Y., & Han, Z. 2012, ApJ, 749, 123 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hasinger, G. 2008, A&A, 490, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Hernán-Caballero, A., & Hatziminaoglou, E. 2011, MNRAS, 414, 500 [NASA ADS] [CrossRef] [Google Scholar]
  35. Higdon, S. J. U., Devost, D., Higdon, J. L., et al. 2004, PASP, 116, 975 [NASA ADS] [CrossRef] [Google Scholar]
  36. Holland, W. S., Robson, E. I., Gear, W. K., et al. 1999, MNRAS, 303, 659 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  37. Hopkins, P. F., Richards, G. T., & Hernquist, L. 2007, ApJ, 654, 731 [NASA ADS] [CrossRef] [Google Scholar]
  38. Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
  39. Hurley, P. D., Oliver, S., Farrah, D., Wang, L., & Efstathiou, A. 2012, MNRAS, 424, 2069 [NASA ADS] [CrossRef] [Google Scholar]
  40. Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
  41. Iwasawa, K., Fabian, A. C., & Matt, G. 1997, MNRAS, 289, 443 [NASA ADS] [CrossRef] [Google Scholar]
  42. Iwasawa, K., Crawford, C. S., Fabian, A. C., & Wilman, R. J. 2005, MNRAS, 362, L20 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kendall, M., & Gibbons, J. 1990, Rank correlation methods, ed. E. Arnold, A Charles Griffin Book, [Google Scholar]
  44. Kennicutt, R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
  45. Komatsu, E., Dunkley, J., Nolta, M. R., et al. 2009, ApJS, 180, 330 [NASA ADS] [CrossRef] [Google Scholar]
  46. Laurent, O., Mirabel, I. F., Charmandaris, V., et al. 2000, A&A, 359, 887 [NASA ADS] [Google Scholar]
  47. Lawrence, A. 1991, MNRAS, 252, 586 [NASA ADS] [Google Scholar]
  48. Lebouteiller, V., Bernard-Salas, J., Sloan, G. C., & Barry, D. J. 2010, PASP, 122, 231 [NASA ADS] [CrossRef] [Google Scholar]
  49. Lebouteiller, V., Barry, D. J., Spoon, H. W. W., et al. 2011, ApJS, 196, 8 [NASA ADS] [CrossRef] [Google Scholar]
  50. Lilly, S. J., Eales, S. A., Gear, W. K. P., et al. 1999, ApJ, 518, 641 [NASA ADS] [CrossRef] [Google Scholar]
  51. Lonsdale, C., Polletta, M. d. C.,Surace, J., et al. 2004, ApJS, 154, 54 [NASA ADS] [CrossRef] [Google Scholar]
  52. Lonsdale, C. J., Farrah, D., & Smith, H. E. 2006, Ultraluminous Infrared Galaxies, ed. J. W. Mason (Springer Verlag), 285 [Google Scholar]
  53. Lutz, D., Sturm, E., Tacconi, L. J., et al. 2007, ApJ, 661, L25 [NASA ADS] [CrossRef] [Google Scholar]
  54. Lutz, D., Sturm, E., Tacconi, L. J., et al. 2008, ApJ, 684, 853 [Google Scholar]
  55. Magdis, G. E., Elbaz, D., Hwang, H. S., et al. 2010, MNRAS, 409, 22 [NASA ADS] [CrossRef] [Google Scholar]
  56. Magdis, G. E., Elbaz, D., Hwang, H. S., Pep Team, & Hermes Team 2011, in Galaxy Evolution: Infrared to Millimeter Wavelength Perspective, eds. W. Wang, J. Lu, Z. Luo, Z. Yang, H. Hua, & Z. Chen, ASP Conf. Ser., 446, 221 [Google Scholar]
  57. Maiolino, R., Shemmer, O., Imanishi, M., et al. 2007, A&A, 468, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [NASA ADS] [CrossRef] [Google Scholar]
  59. McLure, R. J., & Jarvis, M. J. 2002, MNRAS, 337, 109 [NASA ADS] [CrossRef] [Google Scholar]
  60. Mihos, J. C., & Hernquist, L. 1994, ApJ, 437, 611 [NASA ADS] [CrossRef] [Google Scholar]
  61. Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
  62. Mushotzky, R. 2004, in Supermassive Black Holes in the Distant Universe, ed. A. J. Barger, Astrophys. Space Sci. Lib., 308, 53 [Google Scholar]
  63. Nardini, E., Risaliti, G., Salvati, M., et al. 2008, MNRAS, 385, L130 [NASA ADS] [Google Scholar]
  64. Nardini, E., Risaliti, G., Salvati, M., et al. 2009, MNRAS, 399, 1373 [NASA ADS] [CrossRef] [Google Scholar]
  65. Nardini, E., Risaliti, G., Watabe, Y., Salvati, M., & Sani, E. 2010, MNRAS, 405, 2505 [NASA ADS] [Google Scholar]
  66. Netzer, H., Lutz, D., Schweitzer, M., et al. 2007, ApJ, 666, 806 [NASA ADS] [CrossRef] [Google Scholar]
  67. Niemi, S.-M., Somerville, R. S., Ferguson, H. C., et al. 2012, MNRAS, 421, 1539 [NASA ADS] [CrossRef] [Google Scholar]
  68. Panessa, F., Bassani, L., Cappi, M., et al. 2006, A&A, 455, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
  70. Rieke, G. H., Lebofsky, M. J., Thompson, R. I., Low, F. J., & Tokunaga, A. T. 1980, ApJ, 238, 24 [NASA ADS] [CrossRef] [Google Scholar]
  71. Rigopoulou, D., Spoon, H. W. W., Genzel, R., et al. 1999, AJ, 118, 2625 [NASA ADS] [CrossRef] [Google Scholar]
  72. Rigopoulou, D., Franceschini, A., Aussel, H., et al. 2000, ApJ, 537, L85 [NASA ADS] [CrossRef] [Google Scholar]
  73. Risaliti, G., & Elvis, M. 2004, A Panchromatic View of AGN Supermassive Black Holes in the Distant Universe, ASSL, 308, 187 [Google Scholar]
  74. Risaliti, G., Maiolino, R., Marconi, A., et al. 2006, MNRAS, 365, 303 [NASA ADS] [CrossRef] [Google Scholar]
  75. Risaliti, G., Imanishi, M., & Sani, E. 2010, MNRAS, 401, 197 [NASA ADS] [CrossRef] [Google Scholar]
  76. Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
  77. Roseboom, I. G., Lawrence, A., Elvis, M., et al. 2013, MNRAS, in press [arXiv:1205.4543] [Google Scholar]
  78. Rowan-Robinson, M. 2000, MNRAS, 316, 885 [Google Scholar]
  79. Rowan-Robinson, M., & Wang, L. 2010, MNRAS, 406, 720 [NASA ADS] [Google Scholar]
  80. Rowan-Robinson, M., Valtchanov, I., & Nandra, K. 2009, MNRAS, 397, 1326 [NASA ADS] [CrossRef] [Google Scholar]
  81. Ruiz, A., Carrera, F. J., & Panessa, F. 2007, A&A, 471, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Ruiz, A., Miniutti, G., Panessa, F., & Carrera, F. J. 2010, A&A, 515, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  83. Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
  84. Sargsyan, L. A., & Weedman, D. W. 2009, ApJ, 701, 1398 [NASA ADS] [CrossRef] [Google Scholar]
  85. Schweitzer, M., Lutz, D., Sturm, E., et al. 2006, ApJ, 649, 79 [NASA ADS] [CrossRef] [Google Scholar]
  86. Soifer, B. T., Neugebauer, G., Helou, G., et al. 1984a, ApJ, 283, L1 [NASA ADS] [CrossRef] [Google Scholar]
  87. Soifer, B. T., Rowan-Robinson, M., Houck, J. R., et al. 1984b, ApJ, 278, L71 [NASA ADS] [CrossRef] [Google Scholar]
  88. Soifer, B. T., Neugebauer, G., & Houck, J. R. 1987a, ARA&A, 25, 187 [NASA ADS] [CrossRef] [Google Scholar]
  89. Soifer, B. T., Sanders, D. B., Madore, B. F., et al. 1987b, ApJ, 320, 238 [NASA ADS] [CrossRef] [Google Scholar]
  90. Spoon, H. W. W., Armus, L., Cami, J., et al. 2004a, ApJS, 154, 184 [NASA ADS] [CrossRef] [Google Scholar]
  91. Spoon, H. W. W., Moorwood, A. F. M., Lutz, D., et al. 2004b, A&A, 414, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Spoon, H. W. W., Marshall, J. A., Houck, J. R., et al. 2007, ApJ, 654, L49 [NASA ADS] [CrossRef] [Google Scholar]
  93. Sturm, E., Verma, A., Graciá-Carpio, J., et al. 2010, A&A, 518, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Tran, Q. D., Lutz, D., Genzel, R., et al. 2001, ApJ, 552, 527 [NASA ADS] [CrossRef] [Google Scholar]
  95. Treister, E., Krolik, J. H., & Dullemond, C. 2008, ApJ, 679, 140 [NASA ADS] [CrossRef] [Google Scholar]
  96. Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
  97. Veilleux, S., Kim, D.-C., & Sanders, D. B. 1999, ApJ, 522, 113 [NASA ADS] [CrossRef] [Google Scholar]
  98. Veilleux, S., Kim, D.-C., & Sanders, D. B. 2002, ApJS, 143, 315 [NASA ADS] [CrossRef] [Google Scholar]
  99. Veilleux, S., Rupke, D. S. N., Kim, D.-C., et al. 2009, ApJS, 182, 628 [NASA ADS] [CrossRef] [Google Scholar]
  100. Verma, A., Rowan-Robinson, M., McMahon, R., & Andreas Efstathiou, A. E. 2002, MNRAS, 335, 574 [NASA ADS] [CrossRef] [Google Scholar]
  101. Verma, A., Charmandaris, V., Klaas, U., Lutz, D., & Haas, M. 2005, Space Sci. Rev., 119, 355 [NASA ADS] [CrossRef] [Google Scholar]
  102. Vignali, C., Piconcelli, E., Lanzuisi, G., et al. 2011, MNRAS, 416, 2068 [NASA ADS] [CrossRef] [Google Scholar]
  103. Wang, L., Farrah, D., Connolly, B., et al. 2011, MNRAS, 411, 1809 [NASA ADS] [CrossRef] [Google Scholar]
  104. Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
  106. Wilman, R. J., Fabian, A. C., Crawford, C. S., & Cutri, R. M. 2003, MNRAS, 338, L19 [NASA ADS] [CrossRef] [Google Scholar]
  107. Wright, G. S., Joseph, R. D., & Meikle, W. P. S. 1984, Nature, 309, 430 [NASA ADS] [CrossRef] [Google Scholar]
  108. Yan, L., Tacconi, L. J., Fiolet, N., et al. 2010, ApJ, 714, 100 [NASA ADS] [CrossRef] [Google Scholar]
  109. Yun, M. S., & Scoville, N. Z. 1998, ApJ, 507, 774 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Spitzer observations of HLIRG.

In the text
Table 2

Best-fit model parameters (cf. Sect. 4).

In the text
Table 3

SFR and AGN relative contributions to the IR output, along with IR luminosities (in cgs units).

In the text
Table 4

AGN luminosities (in cgs units) and CF values.

In the text

All Figures

thumbnail Fig. 1

MIR rest-frame spectra of HLIRG obtained with the Infrared Spectrograph on board Spitzer. The grey shaded area is the 1σ uncertainty region. The vertical dashed lines limit the spectral region where our decomposition technique was applied.
In the text
thumbnail Fig. 2

Average SB spectra used as templates in our model: template a) is from N08; templates b)–d) from Hernán-Caballero & Hatziminaoglou (2011, see Sect. 4. The grey shaded area is the estimated 1σ dispersion.
In the text
thumbnail Fig. 3

5−8 μm spectra and best-fit models (blue solid line). The AGN component is plotted as a red dashed line. For clarity, the SB component (green dotted line) is plotted only on those sources where the AGN and SB contributions are comparable.
In the text
thumbnail Fig. 4

Spectral index-optical depth confidence regions for IRAS 07380-2342 (left) and IRAS F16124+3241 (right). The contours represent 1σ, 2σ, and 3σ confidence levels.
In the text
thumbnail Fig. 5

Comparison of the SFR estimated through PAH emission and through IR SED modelling using RTM (Farrah et al. 2002a; Rowan-Robinson 2000; Verma et al. 2002).
In the text
thumbnail Fig. 6

SFR estimated using the PAH emission at 7.7 μm versus a) total and b) starburst IR luminosities. The open circles mark those sources where our model is inaccurate.
In the text
thumbnail Fig. 7

6 μm-to-IR ratio (R) versus α6. The red dashed line is our best fit for the relation between R and α6 given by Eq. (6). The blue solid line is the best fit obtained by N08 for a sample of ULIRG.
In the text
thumbnail Fig. 8

Comparison of the AGN contribution to the IR luminosity estimated through MIR spectral decomposition and through RTM. The blue squares are type I AGN and the red triangles are type II AGN and SB. The open circles mark those sources where our model is inaccurate. MIR contribution for IRAS 00182-7112 from Spoon et al. (2004a).
In the text
thumbnail Fig. 9

CF versus the AGN luminosity at 6 μm. The blue dashed line is the estimated average CF for local QSO (see Sect. 5.3). Symbols as in Fig. 8.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.