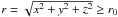| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 9 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219858 | |
| Published online | 14 November 2012 | |
Light echo of V838 Monocerotis: properties of the echoing medium⋆
1 Department for Astrophysics, N. Copernicus Astronomical Center, Rabiańska 8, 87-100 Toruń Poland
e-mail: tylenda@ncac.torun.pl
2 Max-Planck Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 21 June 2012
Accepted: 8 October 2012
Context. The light echo phenomenon that accompanied the 2002 eruption of V838 Mon allows one to study the properties of the diffuse dusty matter in the vicinity of the object.
Aims. We are aiming at obtaining estimates of the optical thickness of the circumstellar matter in front of V838 Mon, as well as optical properties of dust grains in the echoing medium. In particular, we are interested in studying whether the echoing medium can be responsible for the observed faintness of the B-type companion of V838 Mon when compared to three B-type stars that are seen in the vicinty of V838 Mon and are believed to be at the same distance as V838 Mon.
Methods. We used the V838 Mon light echo images obtained by the Hubble Space Telescope (HST) in different filters and epochs. From the images we derived the total brightness of the echo and its surface brightness. The results of the measurements were compared to model light echoes.
Results. The present study allowed us to estimate the optical thickness of the matter in front of the object and the mean cosine value of the scattering angle of dust grains in three HST filters.
Conclusions. The optical thickness of the echoing matter is not sufficient to explain the observed difference in brightness between the B-type companion of V838 Mon and the other three B-type stars observed in the vicinity of V838 Mon. Implications of this result are discussed. Our estimate of the mass of the diffuse matter seen in the light echo shows that the matter cannot have resulted from a past mass loss activity of V838 Mon. We probably observe remnants of an interstellar cloud from which V838 Mon and other members of the observed cluster were formed.
Key words: stars: individual: V838 Monocerotis / stars: peculiar / circumstellar matter
© ESO, 2012
1. Introduction
V838 Monocerotis was discovered as an eruptive star at the beginning of January 2002. The main eruption started at the beginning of February 2002, however, and lasted about two months (see e.g. Munari et al. 2002a; Kimeswenger et al. 2002; Crause et al. 2003). The main characteristic of the eruption, which is different in V838 Mon from other stellar eruptions (e.g. classical novae), was that the object evolved to progressively lower effective temperatures and declined as a very late M-type supergiant (e.g. Tylenda 2005).
Tylenda & Soker (2006) showed that the eruption of V838 Mon cannot be explained by a thermonuclear runaway similar to classical novae, nor by a late He-shell flash. They proposed, following Soker & Tylenda (2003), that the event resulted from a merger of two stars. This idea obtained strong support from an analysis of archive observations of the progenitor of V1309 Sco. The eruption of this object was observed in 2008 and was of the same type as that of V838 Mon (Mason et al. 2010). Tylenda et al. (2011a) showed that the event resulted from a merger of a contact binary.
The eruption of V838 Mon was accompanied by a spectacular light echo. A series of fantastic images of the light echo have been obtained by Hubble Space Telescope (HST, see e.g. Bond et al. 2003; Bond 2007). Analyses of the light echo’s structure and properties allowed astrophysicists to study the dusty medium around V838 Mon (e.g. Tylenda 2004) and to determine the distance to the object (Sparks et al. 2008).
V838 Mon has a spectroscopic companion, a B-type star discovered by Munari et al. (2002b) in September–October 2002, when the eruption remnant became so cool that it almost disappeared from the optical. The spectrum of the companion, classified as B3 V by Munari et al. (2002b), was seen undisturbed until the fall of 2006, when an eclipse-like event was observed (e.g. Munari et al. 2007a). The companion was eclipsed for about two months. In 2004/2005, emission lines of [Fe II] appeared in the spectrum of V838 Mon. The lines strengthened with time and reached a maximum at the time of the eclipse-like event. Tylenda et al. (2009) showed that the profiles and evolution of the [Fe II] emission lines, as well as the eclipse-like event resulted from interactions of the B-type star radiation with the matter ejected by V838 Mon in the 2002 eruption. After reappearance from the eclipse-like event, the companion began to fade again and in 2008 traces of the B-type spectrum, as well as of the [Fe II] emission lines, disappeared. Apparently the companion became completely embedded in the dusty ejecta of V838 Mon (Tylenda et al. 2011b).
Afsar & Bond (2007) found a sparse, young cluster, containing three B-type main-sequence stars, in the field of V838 Mon. The cluster is at a distance of ~6.2 kpc, which is very close to the value of ~6.1 kpc derived by Sparks et al. (2008) for V838 Mon from their analysis of the polarization of the light echo. The reddening of the cluster and that of V838 Mon and its companion are also very similar (EB − V = 0.84 versus 0.9, respectively). It seems very likely that V838 Mon and its B-type companion are also members of the cluster.
However, there is a problem with the observed brightness of the B-type companion of V838 Mon when compared to the magnitudes of the B-type stars of the cluster. Munari et al. (2005) derived V = 16.05 ± 0.05 for the companion of V838 Mon. Using the compilation of photometric data of V. Goranskij1, one derives V = 16.19 ± 0.03 from the data obtained in September–November 2002. The B-type companion is therefore fainter by 1.2–1.4 mag when compared to star 9 (classified as B3 V) in the cluster of Afsar & Bond (2007). Afsar & Bond (2007) interpreted this as evidence that the companion is partly submerged in the dusty ejecta of V838 Mon. However, if a dusty medium results from a stellar eruption, it is very unlikely that it is homogeneous. Therefore, if the ejecta flows in front of a star, one expects to observe a high variability of the stellar light. This was not observed in the case of the B-type companion of V838 Mon until the fall of 2006. As can be seen from the light curve of V838 Mon between fall 2002 and fall 2006 (see e.g. the data of Goranskij1), the U brightness (dominated by the B-type companion in this epoch) remained constant within ± 0.1 mag. The light curve exhibits the same behaviour in the B band after the 2002 eruption (see Munari et al. 2005). As discussed above, interactions of the V838 Mon ejecta with the companion started at the earliest in the fall of 2006 and then indeed resulted in a high variability of the observed light of the companion, eventually leading to the complete disappearance of the star.
Measurements of V838 Mon’s light echo on images obtained with HST/ACS.
The problem of the observed brightness of the B-type companion remains unresolved. A possible explanation is that V838 Mon and its companion suffer from additional, local extinction of ΔAV ≃ 1.3, compared to the three B-type stars of the cluster. A standard extinction of this value would imply additional reddening of ΔEB − V ≃ 0.4. This is significantly higher than the observed difference between the reddening of the V838 Mon and its companion, and that of the cluster (ΔEB − V ≲ 0.1, see above). This implies that the local extinction, if present, would have to be almost grey in the optical, i.e. R = AV/EB − V ≳ 10, which would additionally imply local dust dominated by large grains (a ≳ 0.3 μm).
This idea seems to be conceivable. Young stellar clusters are usually known to contain a significant amount of diffuse matter consisting of remnants of a more massive complex, from which the cluster was formed. For V838 Mon there is observational evidence that diffuse matter is indeed present in the near vicinity of the object. One piece of evidence is the light echo. Radio observations in the CO rotational lines also show the presence of molecular matter, most probably related to the dusty medium seen in the light echo (Kamiński et al. 2007, 2011). The light echo offers possibilities to study parameters and properties of the scattering matter. This is the aim of the present study.
As we show in detail below, an analysis of the brightness of the echo at different wavelengths and its evolution with time allows us to estimate several parameters of the scattering matter. This includes the optical thickness of the matter, as well as dependeces of the scattering coefficient on the wavelength and the scattering angle. In this way we can verify whether the local extinction can be responsible for the relative faintness of the B-type companion of V838 Mon when compared to the other B-type stars of the cluster. The results of the echo study also allow us to derive constraints on the nature of the dust grains and on the mass of the scattering material. The latter is important for discussing the nature of the matter, i.e. whether it is of interstellar origin or rather, as suggested by some authors (e.g. Bond et al. 2003; Bond 2007), that it resulted from past mass loss activity of the progenitor of V838 Mon. This can have consequences for the nature of the progenitor itself and the mechanism of the 2002 eruption.
2. Observational material and its reduction
We have used the archival images of V838 Mon’s light echo obtained with HST in 2002 on April 30, May 20, September 2, October 28, and December 17 (HST proposals 9587, 9588, and 9694). The first image was taken in the F435W filter only. The other ones were obtained in the F435W, F606W, and F814W filters. The observations were performed with the Advanced Camera for Surveys (ACS) combined with the detector of the Wide Field Channel (WCS). Some of the images were taken in the polarimetric mode, the rest in the standard (non-polarimetric) mode. The observations have been described in more detail in Sparks et al. (2008). The pipeline-reduced data, which we extracted from the HST archive, were further processed using the multidrizzle2 package (version 3.3.8). The non-polarimetric observations for a given date and filter were combined in multidrizzle to produce images in units of counts per second. The polarimetric observations were obtained with three retarder angles (0°, 60°, 120°). We first combined frames with the same retarder angle for a given filter and date. Then the polarimetric images were scaled using calibration corrections taken from ACS Data Handbook3. Finally the data were combined into the Stokes I (total intensity) image in each filter.
The following reduction was performed using Starlink4 packages, mainly with KAPPA and GAIA. We measured the background sky level and its variations in each image by performing statistics on a large number of pixels free of stellar and echo emission and instrumental defects. After correcting images for the sky level, those measurements were used to blank all pixels below 1.5σ of sky variations and above the maximum echo brightness for a given date. From the resulting images, we manually removed the remaining parts of stellar diffraction patterns and cosmic-ray hits. Finally, we measured the light echo region.
3. Measurements
The results of the measurements are given in Table 1. The upper, middle, and bottom parts of the table present the results obtained with the F435W, F606W, and F814W filters, respectively. The dates of the observations are given in Col. (1), while Col. (2) notes the observing mode used to obtain the images. Total count rates from the echo are given in Col. (3). Column (4) gives the total number of pixels, which registered a measurable signal from the echo. A total flux from the light echo can be calculated by multiplying the total count rate number by the photflam conversion factor (Sirianni et al. 2005), which is equal to 3.08 × 10-18, 7.725 × 10-19, and 6.94 × 10-19 W m-2 μm-1 per count s-1 for the F435W, F606W, and F814W filters, respectively. The resulted fluxes are presented in Col. (5). The ACS pixel scale is 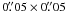 , which allows one to easily calculate a mean surface brightness, SB, from the mean count rate summed over 400 pixels (corresponding to 1 arcsec2) and the photflam. The results are listed in Col. (6).
, which allows one to easily calculate a mean surface brightness, SB, from the mean count rate summed over 400 pixels (corresponding to 1 arcsec2) and the photflam. The results are listed in Col. (6).
The data in Cols. (3)–(6) refer only to the part of the light echo surface that was not contaminated by field stars and V838 Mon itself. The procedure of removing diffraction patterns of field stars introduced uncertainties in the measurements. This is particularly the case for the total flux, which is expected to be systematically underestimated in Col. (5) of Table 1. The effect is difficult to estimate, as each time different parts of the echo were contaminated by stars. The mean surface brightness of the echo is expected to be less vulnerable to the procedure of cutting out the stellar patterns.
We have attempted to correct the measured total flux for this effect. From the radius of the outer rim of the echo measured in Tylenda et al. (2005), we calculated the total number of pixels expected inside the echo. Then we defined a covering factor, fc, as a ratio of the number of pixels that detected the echo (i.e. counted in Col. 4 of Table 1), to the total number expected from the size of the echo. This factor is generally between 0.7–1.0. Assuming that fc is < 1.0 because of the field stars’ patterns and that the mean surface brightness is statistically the same over the echo image, the corrected echo flux can be calculated as the measured flux (listed in Col. 5) devided by fc. The resulting value should, however, be treated as an upper limit to the echo flux. The missing pixels do not result from the field stars only, but also from the fact that there were regions of the echo, not contaminated by stars, where the echo was physically too faint to be measured. Therefore, as a finally corrected flux, we took a mean value from the flux estimated in the above way and the measured flux (Col. 5). For all except the observations from December 17, both fluxes were taken with the same weight when averaging. The echo images obtained on December 17 show empty regions significantly more extended than on earlier dates, so we took the measured flux with a double weight when calculating the finally corrected flux for this date. The echo fluxes corrected with the above procedure and converted to the ST magnitudes (Sirianni et al. 2005) are given in Col. (7) of Table 1. The corrections to the echo total flux were largest for the F435W filter, but even in this case they do not exceed 10% (0.10 mag.).
As noted above, the covering factor, fc, is generally < 1.0, but it varies from image to image. It is usually lowest for the F435W filter and shows a tendency to decrease with the time of observations. As a result the surface brightness listed in Col. (6) of Table 1 is not entirely comparable between different filters and different dates. This may create uncertainties and ambiguities when comparing the results of the echo simulations to the observational measurements. Therefore we also derived another mean surface brightness, which was calculated from the brightest pixels in each image, counted until they fill fc = 0.5. The resulting values, named SB 0.5 below, are listed in Col. (8) of Table 1.
Table 1 lists uncertainties of the obtained values in addition to the results of measurements. The errors of the total flux and the surface brightness (Cols. 5, 6, and 8) are expressed in percent of the values, while those of STmag (Col. 7) are given in magnitudes. When evaluating the errors we took into account count statistics, uncertainities due to subtracting the sky background, uncertainties of the echo dimension, and calibration errors. The first source of errors, which we evaluated from the standard deviation of the mean sky background, was negligible compared to the other ones and resulted in errors ≲ 0.1% in the flux and surface brightness, and ≲ 0.001 mag in STmag. As noted in Sect. 2, before measuring the echo, we clipped the pixels with signal below 1.5σ of the sky variations. This value is of course somewhat arbitrary. To estimate the uncertainties caused by this procedure we repeated measurments by allowing for 1σ variations of the clipping level. The surface brightness, SB, was most vulnerable to this uncertainty, which was 4–7% in the F606W and F814W filters, and 8–16% in the F435W filter. The total flux was uncertain to 0.3–1.3% in the F606W and F814W filters and 2–8% in the F435W filter. SB 0.5 is insensitive to the clipping level. Errors in determining the echo radius derived in Tylenda et al. (2005) propagate through the correction procedure (described above) when deriving STmag, resulting in a ~ 0.05 mag uncertainty. They also affect SB 0.5 through the evaluation of the total number of pixels inside the echo and result in 2.5–3.5% uncertainty. The deriviation of SB does not involve the echo radius. To evaluate uncertainties of the image flux calibration, we selected ten field stars located outside the light echoes and measured their corresponding counts in all images. Calculating mean values and standard deviations, we found that the calibration is uncertain to 7%, 5%, and 4% in the F435W, F606W, and F814W filters, respectively. Propagation of all these errors through the measuring procedure results in the final errors listed in Table 1.
4. The model
Basic assumptions and formulae of the light echo geometry and its modelling can be found in Tylenda (2004) (see also Sparks et al. 2008). Briefly, we assume a single-scattering approximation and that the echo structure is described by the paraboloid equation, i.e. 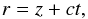 (1)where r is a radial distance of the scattering point from the source of radiation, z is a projection of r on the line of sight of the source, and t is a time delay between the moment of observations of the scattered radiation and that of the radiation directly recorded from the source.
(1)where r is a radial distance of the scattering point from the source of radiation, z is a projection of r on the line of sight of the source, and t is a time delay between the moment of observations of the scattered radiation and that of the radiation directly recorded from the source.
 |
Fig. 1 Cross section, y = 0, of the geometrical model adopted in our light-echo modelling. The source of the light is at x = 0, y = 0, z = 0 (black point in the figure). The observer is at x = 0, y = 0, z = ∞. x and z are in units of ct. Dust is uniformely distributed in the space satisfying z ≤ z0 and |
The geometry assumed in our light-echo simulations is shown in Fig. 1. The echoing medium surrounding the flaring object is uniform and has a semi-infinite geometry. Its boundary is in a form of a plane perpendicular to the line of sight, situated in front of the flaring object at a certain distance, z0, from the object. The medium extends well beyond the object so that the light echo paraboloid never reaches its possible boundary behind the object during the time span covered in our simulations. It was shown in Tylenda (2004) that V838 Mon is situated in a cavity in the surrounding dusty medium. We assume, for simplicity, that this dust-free hole is spherical in respect to the object and has a radius r0.
In the above approximation, the echoing medium is parametrized, apart from z0 and r0, with the optical thickness of the medium along the line of sight of the central object, τ0. The thickness devided by z0 − r0 gives the extinction coefficient, Qext = Qabs + Qsca, where Qabs and Qsca are the absorption and scattering coefficients, respectively. The scattering on dust grains is usually anisotropic, so in order to model it properly, we adopted a standard anisotropy phase function, i.e. 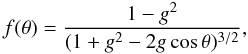 (2)where θ is a scattering angle and g ≡ ⟨ cosθ ⟩ is an anisotropy factor. Generally, the anisotropy factor is determined by properties of dust grains (see e.g. Draine 1985). In our modelling, ⟨ cosθ ⟩ is treated as a free parameter to be determined from fitting the results of simulations to the observational measurements. Extinction of the light travelling through the echoing medium is taken into account in the modelling.
(2)where θ is a scattering angle and g ≡ ⟨ cosθ ⟩ is an anisotropy factor. Generally, the anisotropy factor is determined by properties of dust grains (see e.g. Draine 1985). In our modelling, ⟨ cosθ ⟩ is treated as a free parameter to be determined from fitting the results of simulations to the observational measurements. Extinction of the light travelling through the echoing medium is taken into account in the modelling.
The observed light curve of V838 Mon was obtained in the Johnson-Cousins filters. The HST images of the light echo were obtained with the HST filters, however, which differ from the Johnson-Cousins system. For the purpose of our modelling we converted the photometric measurements of V838 Mon in the B, V, Rc, and Ic, taken from the same references as in Tylenda (2005), into the light curves in F435W, F606W, and F814W using transformation formulae of Sirianni et al. (2005). These light curves were then used to model the evolution of the light echo images.
As discussed in Sect. 2, the observed echo image was contaminated by field stars, in particular by the diffraction pattern of V838 Mon itself. The latter had a typical dimension of ~ 3 arcsec in radius (note that the diffraction cross was much more extended), and was removed in the reduction precedure of all images before measuring the echo. This effect can be easily taken into account in the model simulations and we removed the central circular region of the above radius from calculating the model echo flux and surface brightness.
 |
Fig. 2 Observed expansion of the outer rim of the light echo, as measured in Tylenda et al. (2005) (symbols), compared to our modelling (lines) assuming a distance to V838 Mon of 6.1 kpc. The curves were obtained taking z0 = 2.1 pc (middle curve) ± 10% (outer curves). The outer rim in the simulations was defined as the radius at which the echo surface brightness drops to 10% of its mean value. The light curve of V838 Mon, used in the simulations, is the same as that used to model the light echo in the F435W filter, see upper panel of Fig. 4. |
Following Sparks et al. (2008) and Afsar & Bond (2007), we assume that V838 Mon is at a distance of 6.1 kpc. For a fixed distance, the expansion of the echo outer rim is uniquely determined by z0. The observed expansion of the light echo outer rim, as measured in Tylenda et al. (2005) and compared to the results of our modelling in Fig. 2, results in z0 ≃ 2.1 pc. Following Tylenda (2004) and the adopted distance, we assume r0 = 0.1 pc. Note that the latter value is not crucial for the results of our analysis. The albedo of dust grains, i.e. Qsca/Qext, was taken from the interstellar extinction curve of Weingartner & Draine (2001) with RV = 3.1.
 |
Fig. 3 Evolution of the model echo total flux (in the magnitude scale) as a function of the optical thickness, τ0, along the line of sight of the central source (upper panel) and the anisotropy factor, ⟨ cosθ ⟩ , (bottom panel). Dashed curve in both panels: the light curve of the central source (the same as in the upper panel of Fig. 4). Full curves in the upper panel: the light echo flux evolution with ⟨ cosθ ⟩ fixed at 0.6 but for τ0 varying from 0.05 (bottom curve), through 0.1, 0.2, 0.3, and 0.5 (uppermost curve). Full curves in the bottom panel: the light echo flux evolution with τ0 fixed at 0.2 but for ⟨ cosθ ⟩ varying from 0.0 (bottom curve), through 0.2, 0.4, 0.6, and 0.8 (uppermost curve) |
 |
Fig. 4 Evolution of the light-echo total-flux in the ST magnitude scale as observed in the F435W (upper panel), F606W (middle panel), and F814W (bottom panel) filters. Dashed curve: observed light curve of V838 Mon. Asterisks: observed light-echo magnitudes (Col. 7 in Table 1). Full curve: best fit of the modelled evolution to the observational points. Parameters of the fit can be found in Table 2 upper rows. |
 |
Fig. 5 Evolution of the light-echo surface-brightness in the F435W (upper panel), F606W (middle panel), and F814W (bottom panel) filters. Open symbols and full curve: observed light-echo surface-brightness SB (Col. 6 in Table 1) and its best-fitting model. Filled symbols and dashed curve: the same but for SB 0.5 (Col. 8 in Table 1). Parameters of the fit can be found in Table 2 middle and bottom rows. |
5. Results of model fitting to observations
The results of our modelling with the fixed values of the distance, z0, r0, and albedo, as described in Sect. 4, depend on two parameters, i.e. optical thickness of the echoing matter along the line of sight in front of V838 Mon, τ0, and the scattering anisotropy factor, ⟨ cosθ ⟩ . This is illustrated in Fig. 3. Note that each of the two parameters affects the model results in a different way. As can be seen from the upper panel of Fig. 3, τ0 does not change the shape of the echo flux evolution but it moves the curve vertically in the diagram. On the other hand, ⟨ cosθ ⟩ determines the rate of fading of the light echo with time (see the bottom panel of Fig. 3). Therefore fitting the model results to the observed evolution of the light echo in different filters can constrain the values of these two parameters and their dependence on the wavelength.
Figures 4 and 5 compare the results of our models of the light echo (curves) fitted to the observational measurements (symbols with error bars) collected in Table 1. The fitting was made with the χ2 method. Figure 4 compares the total brightness of the light echo in the ST magnitude scale (data from Col. 7 in Table 1). Here, we also plotted the observed light curves of V838 Mon (dashed curves) that were used to model the echo. Figure 5 presents the observed and model evolution of the mean surface brightness of the echo. Open symbols and full curves refer to the measurments and modelling of SB (data from Col. 6 in Table 1). Filled symbols and dashed curves shows the same but for SB 0.5 (data from Col. 8 in Table 1). The parameters of all models displayed in Figs. 4 and 5 are given in Table 2. The errors of the parameters were obtained from the 90% confidence level of the χ2 fitting.
6. Analysis and discussion
As can be seen from Table 2, the optical thickness of the dusty matter in front of V838 Mon, τ0, as determined from modelling the surface brightness, SB, (middle rows in the table) is systematically higher than the values derived from fitting the total echo flux (upper rows in the table). The difference is within the error bars, however. Modelling of the surface brightness of the bright regions covering 50% of the echo surface, SB 0.5, (bottom rows in the table) gives significantly higher values of τ0 than in the two previous cases. This is not surprising, as brighter regions mean more effective scattering and thus a higher extinction coefficient. The values listed in the upper and middle rows of Table 2 can be considered as typical for the echoing medium of V838 Mon. Those in the bottom rows, when compared to the other ones, illustrate how inhomogeneous the medium is.
The results in Table 2 allow us to study properties of dust grains in the echoing medium. Figures 6 and 7 show values of the scattering coefficient and the anisotropy factor, respectively, as functions of wavelength and compare them to the analogous values obtained by Weingartner & Draine (2001) from modelling the interstellar extinction curve with RV = 3.1 and 5.5.
As can be seen from Fig. 6, our modelling of different observational quantities (total flux, surface brightness) results in a similar wavelength dependence of the scattering coefficient. We can also conclude that this relation is not significantly different from that expected from the standard composition and size distribution of dust grains used to model the interstellar extinction curve of Weingartner & Draine (2001) with RV = 3.1. This suggests that the dusty matter responsible for the observed echo is not significantly different from the typical interstellar dusty medium.
The scattering anisotropy factor, ⟨ cosθ ⟩ , as displayed in Fig. 7, is more sensitive to the observational uncertainties than the scattering coefficient. There are systematic differences in the derived ⟨ cosθ ⟩ values, depending on which quantity was analysed, but the differences are within the error bars. The value of ⟨ cosθ ⟩ is determined from the rate of the echo fading with time. This rate, if derived from the measurements of all pixels detecting emission from the echo, is likely to be distorted because the portion of the echo surface covered by these pixels is different for different dates of the observations. Therefore we expect that the results of fitting the mean surface brightness, SB 0.5, (bottom row in Table 2 and filled circles in Fig. 7) are more reliable than the other two.
Figure 7 shows that our determinations of ⟨ cosθ ⟩ gave values systematically greater than those expected from the interestellar extinction curve with RV = 3.1. They are better reproduced by the extinction curve with RV = 5.5, but even in this case the points mostly lie above the curve. Greater ⟨ cosθ ⟩ is expected for bigger dust grains, but this usually implies that the scattering coefficient is less dependent on the wavelength, which would be in conflict with the points in Fig. 6. However, the model extinction curve and ⟨ cosθ ⟩ depend not only on the grain size, but also on the chemical composition and structure of the grains. It is thus possible that playing with different parameters of the dust grains would allow one to better reproduce the dust properties we obtained from the analysis of the light echo of V838 Mon. This is out of the scope of the present study, however.
Values of τ0 and ⟨ cosθ ⟩ derived from the model fitting to the observations.
 |
Fig. 6 Dependence of the scattering coefficient, Qsca, on the wavelength as derived from modelling of the echo. The values are normalized to Qsca at the effective wavelength of the F814W filter. Asterisks: results of the models fitting the total flux, STmag, (upper rows in Table 2). Open circles: results of the models fitting the mean surface brightness, Sb, (middle rows in Table 2). Filled circles: results of the models fitting the mean surface brightness derived from the brightest pixels filling fc = 0.5, SB 0.5, (bottom rows in Table 2). The horizontal error bars represent the widths of the photometric bands. Open and filled symbols are shifted by ± 0.05 μm in the abscissa axis for clarity. Curves: relations expected from modelling the interstellar extinction curve of Weingartner & Draine (2001) for RV = 3.1 (dotted) and RV = 5.5 (dashed). |
 |
Fig. 7 Dependence of the anisotropy factor, ⟨ cosθ ⟩ , on the wavelength, as derived from our modelling of the echo. The symbols and curves have the same meaning as in Fig. 6. |
We can estimate from Table 2 (upper and middle rows) that the additional extinction of V838 Mon due to local dust responsible for the light echo is AV ≃ 1.2 τ0(F606W) ≃ 0.18 (EB − V ≃ 0.05). Of course, this is the most likely value derived from the mean properties of the local dusty medium seen in the echo. This medium is inhomogeneous, however, as is shown by the uneven distribution of the surface brightness over the echo images. Therefore the real extinction along the line of sight of V838 Mon can be different from the above estimate. Nevertheless, the results obtained from the brighter half part of the echo surface, i.e. from fitting SB 0.5 (bottom rows in Table 2), indicate that it is rather improbable that AV > 0.3. With the observed extinction curve (Fig. 6) this would also imply EB − V ≳ 0.10 from the local dust, which would be too large compared to the observed difference in EB − V between V838 Mon and the three B-type main-sequence stars observed by Afsar & Bond (2007) (see Sect. 1).
Using the standard interstellar-medium relation, AV/NH ≃ 5.3 × 10-22 cm2 (Bohlin et al. 1978), where NH is the column density of hydrogen (atomic plus molecular), and taking AV ≃ 0.18, we obtain a surface density of the echoing matter in front of V838 Mon to be ~8 × 10-4 g cm-2. In 2004 the angular radius of the light echo reached ~1 arcmin (Tylenda et al. 2005). With a distance of 6.1 kpc this allows us to estimate the mass of the diffuse matter of the light echo to be ~35 M⊙. This is a lower limit to the mass of the circumstellar matter of V838 Mon, since, first, in later epochs the echo expanded to even larger radii, second, the estimate is based on the optical thickness in front of V838 Mon only, while the matter almost certainly extends beyond the object. The above estimate can be compared to 90–100 M⊙ obtained by Kamiński et al. (2011) for the molecular complex seen on the CO rotational lines in the vicinity of V838 Mon and a hundred M⊙ estimated by Banerjee et al. (2006) for the mass of the echoing matter in the infrared. All these estimates clearly show that the diffuse matter in the vicinity of V828 Mon, partly seen in the light echo, could not have resulted from a past mass loss activity of V838 Mon, as advocated, e.g. in Bond et al. (2003) and Bond (2007). It is much more probable that we see remnants of an interstellar complex, from which V838 Mon, its companion, and perhaps the other members of the observed cluster were formed.
It is worth noting that Kervella et al. (2012) recently found that the mass of the dusty matter echoing pulsating radiation from the Cepheid RS Pup is ~290 M⊙. It seems therefore that, in general, a stellar light echo to be well resolved in imaging observations requires a flaring star to be associated with a dusty medium of interstellar origin rather than formed from a mass loss activity of the star.
On the basis of our results, we can quite safely conclude that the optical thickness of the dusty matter seen in the light echo is too low to account for the observed dimming of the B-type companion by ~1.3 mag compared to the other B-type stars observed by Afsar & Bond (2007) in the vicinity of V838 Mon (see Sect. 1). Other explanations of this discrepancy have to be considered, e.g. mis-classification of the B-type companion, an evolutionary status of the companion different from that of the three B-type stars of the cluster, or a mistaken distance to V838 Mon and its companion.
The classification of the companion as a B3 main-sequence star comes from Munari et al. (2002b, see also Munari et al. 2007b). This classification was essentially confirmed by Afsar & Bond (2007), but the B-type component in their spectrum, similarly as in the spectrum of Kamiński et al. (2009), was then significantly contaminated by V838 Mon. The observed V brightness of the companion would be in accord with those of the three B-type stars of Afsar & Bond (2007) if it were of a ~B7 V spectral type. The intrinsic colours of such a star would be (B − V)0 = −0.13 and (U − B)0 = −0.43 (Schmidt-Kaler 1982). From Goranskij’s1 compilation of the photometric data we derived V = 16.19 ± 0.03, B − V = 0.55 ± 0.05, and U − B = −0.15 ± 0.07 for the B-type companion. The observed B − V colour can be reconciled with that of the above standard if EB − V ≃ 0.69. But then the reddened U − B colour of the standard star is + 0.08, i.e. it is significantly redder than the observed one. Using the photometric measurements of the B-type companion of Munari et al. (2007b), we obtain EB − V ≃ 0.82 and U − B = + 0.17 for the reddened standard, which is to be compared to the observed one of − 0.06. We thus conclude that B7 V cannot be reconciled with the observed colours of the B-type companion. Note that the best fit of a standard star to the colours derived from the Goranskij data can be obtained taking the spectral type of B2.5 V and EB − V ≃ 0.80, which is not significantly different from the B3 V spectral type obtained by Munari et al. (2002b).
The second possibility is that the B-type companion of V838 Mon is intrinsically fainter because it is in a somewhat different evolutionary stage than the three B-type stars of Afsar & Bond (2007)5. All existing observational data indicate that all four stars are on the main sequence (MS) or not far from it. The only reasonable situation to be discussed in this context is that the B-type companion of V838 Mon has a similar effective temperature but is less luminous (by ~1.3 mag) than star 9 (B3 V) of Afsar & Bond (2007) because it is less massive but is at its hottest stage, namely near the zero age main sequence (ZAMS), while star 9 is more evolved on the MS. Taking the calibrations of the absolute magnitude versus spectral type and luminosity class from Schmidt-Kaler (1982), one easily concludes that to account for a ~1.3 magnitude difference between two B-type stars of a similar spectral type with one of them being on ZAMS, the second star has to be of luminosity class IV, i.e. slightly off MS. This would probably not be in a significant conflict with the spectroscopically determined class V, given the quality of the data of Afsar & Bond (2007). However, the differences in magnitude between star 9, star 8 (B4 V), and star 7 (B6 V) imply that the latter two stars have also to be of luminosity class IV. To have a situation in which three stars of different masses are about to leave or just left MS at the same time, one has to conclude that the three stars have different ages, e.g. star 7 would have to be about twice as old as star 9. This disproves the idea that these three stars form a cluster. Futhermore, a case in which three B-type stars formed at different times happen to lie in a close vicinity in the sky and mimic an isochronic sequence of a cluster in the colour–magnitude diagram is extremely improbable. So is the whole scenario discussed in this paragraph.
If two MS stars of the same spectral type suffer from a similar extinction but are significantly different in the observed brightness then the only reasonable conclusion is that the stars are at different distances. In this way we return to the study of Munari et al. (2007a), where the authors concluded, primarily on the basis of the spectroscopic distance of the B-type companion, that V838 Mon is at a distance of ~10 kpc. In this case V838 Mon and its companion would have nothing to do with the cluster of Afsar & Bond (2007). This possibility creates a problem with the observed linear polarization of the light echo, however, as analysed in Sparks et al. (2008). To reconcile the latter with the distance of 10 kpc, one has to postpone that maximum polarization occurs at a scattering angle of ~60° and not at 90°, as assumed in Sparks et al. (2008). Theoretically this cannot be excluded (e.g. Chap. 4.2 in Kruegel 2008) but requires rather unusual dust grains, e.g. metallic particles.
We performed light echo simulations, similar to those described in Sect. 5, but assuming a distance of 10 kpc. They gave results not significantly different from those obtained in Sect. 5, except that ⟨ cosθ ⟩ was systematically higher by ~20% than the values in Table 2.
We can conclude that if the distance of V838 Mon were ~10 kpc, dust in the echoing medium would have to be quite peculiar, i.e. giving an extinction curve close to the standard one but scattering strongly in forward directions and giving maximum polarization at scattering angles significantly lower than 90°. With the present state of our knowledge of interstellar dust grains, we consider the above result as an argument against a distance as large as ~10 kpc.
In summary, we cannot present any strightforward scenario that could explain the ~1.3 magnitude difference between the B-type companion of V838 Mon and the B3 V star of Afsar & Bond (2007) and which would be in accord with the observed properties of dust in the echoing matter of V838 Mon. Perhaps this could be a dust cloud giving a grey extinction, lying well in front of V838 Mon (not to be seen in the light echo), and not intervening with the lines of sight of the three B-type stars of Afsar & Bond (2007). A detailed spectroscopic study, particularly of the interstellar line profiles (Na I, K I), as well as multi-colour photometric measurements of a large sample of stars in the field of V838 Mon would perhaps enable one to be conclusive in this subject.
Acknowledgments
The research reported on in this paper has partly been supported by a grant no. N N203 403939 financed by the Polish Ministry of Sciences and Higher Education.
References
- Afsar, M., & Bond, H. E. 2007, AJ, 133, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, D. P. K., Su, K. Y. L., Misselt, K. A., & Ashok, N. M. 2006, ApJ, 644, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1979, ApJ, 224, 132 [Google Scholar]
- Bond, H. E. 2007, in The Nature of V838 Mon and its Light Echo, eds. R. L. M. Corradi, & U. Munari, ASP Conf. Ser., 363, 130 [Google Scholar]
- Bond, H. E., Henden, A., Levay, Z. G., et al. 2003, Nature, 422, 405 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Crause, L. A., Lawson, W. A., Kilkenny, D., et al. 2003, MNRAS, 341, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1985, ApJS, 57, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Miller, M., & Tylenda, R. 2007, A&A, 475, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamiński, T., Schmidt, M., Tylenda, R., Konacki, M., & Gromadzki, M. 2009, ApJS, 182, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Tylenda, R., & Deguchi, S. 2011, A&A, 529, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kervella, P., Mérand, A., Szabados, L., et al. 2012, A&A, 541, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kimeswenger, S., Lederle, C., Schmeja, S., & Armsdorfer, B. 2002, MNRAS, 336, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruegel, E. 2008, An Introduction to the Physics of Interstellar Dust (Taylor & Francis Group) [Google Scholar]
- Mason, E., Diaz, M., Williams, R. E., Preston, G., & Bensby, T. 2010, A&A, 516, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Henden, A., Kiyota, S., et al. 2002a, A&A, 389, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Desidera, S., & Henden, A. 2002b, IAU Circ., 8005 [Google Scholar]
- Munari, U., Henden, A., Vallenari, A., et al. 2005, A&A, 434, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Corradi, R. L. M., Henden, A., et al. 2007a, A&A, 474, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Munari, U., Nacasardyan, H., & Villanova, S. 2007b, in The Nature of V838 Mon and its Light Echo, eds. R. L. M. Corradi, & U. Munari, ASP Conf. Ser., 363, 13 [Google Scholar]
- Schmidt-Kaler, Th. 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, eds. K. Schaifers, & H. H. Voigt (Berlin: Springer-Verlag), VI/2b [Google Scholar]
- Sirianni, M., Jee, M. J., Benitez, N., et al. 2005, PASP, 117, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Soker, N., & Tylenda, R. 2003, ApJ, 582, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., Bond, H. E., Cracraft, M., et al. 2008, AJ, 135, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Tylenda, R. 2004, A&A, 414, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R. 2005, A&A, 436, 1009 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., & Soker, N. 2006, A&A, 451, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., Soker, N., & Szczerba, R. 2005, A&A, 441, 1099 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., Kamiński, T., & Schmidt, M. 2009, A&A, 503, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., Hajduk, M., Kamiński, T., et al. 2011a, A&A, 528, A114 [Google Scholar]
- Tylenda, R., Kamiński, T., Schmidt, M., Kurtev, R., & Tomov, T. 2011b, A&A, 532, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Cross section, y = 0, of the geometrical model adopted in our light-echo modelling. The source of the light is at x = 0, y = 0, z = 0 (black point in the figure). The observer is at x = 0, y = 0, z = ∞. x and z are in units of ct. Dust is uniformely distributed in the space satisfying z ≤ z0 and |
| In the text | |
 |
Fig. 2 Observed expansion of the outer rim of the light echo, as measured in Tylenda et al. (2005) (symbols), compared to our modelling (lines) assuming a distance to V838 Mon of 6.1 kpc. The curves were obtained taking z0 = 2.1 pc (middle curve) ± 10% (outer curves). The outer rim in the simulations was defined as the radius at which the echo surface brightness drops to 10% of its mean value. The light curve of V838 Mon, used in the simulations, is the same as that used to model the light echo in the F435W filter, see upper panel of Fig. 4. |
| In the text | |
 |
Fig. 3 Evolution of the model echo total flux (in the magnitude scale) as a function of the optical thickness, τ0, along the line of sight of the central source (upper panel) and the anisotropy factor, ⟨ cosθ ⟩ , (bottom panel). Dashed curve in both panels: the light curve of the central source (the same as in the upper panel of Fig. 4). Full curves in the upper panel: the light echo flux evolution with ⟨ cosθ ⟩ fixed at 0.6 but for τ0 varying from 0.05 (bottom curve), through 0.1, 0.2, 0.3, and 0.5 (uppermost curve). Full curves in the bottom panel: the light echo flux evolution with τ0 fixed at 0.2 but for ⟨ cosθ ⟩ varying from 0.0 (bottom curve), through 0.2, 0.4, 0.6, and 0.8 (uppermost curve) |
| In the text | |
 |
Fig. 4 Evolution of the light-echo total-flux in the ST magnitude scale as observed in the F435W (upper panel), F606W (middle panel), and F814W (bottom panel) filters. Dashed curve: observed light curve of V838 Mon. Asterisks: observed light-echo magnitudes (Col. 7 in Table 1). Full curve: best fit of the modelled evolution to the observational points. Parameters of the fit can be found in Table 2 upper rows. |
| In the text | |
 |
Fig. 5 Evolution of the light-echo surface-brightness in the F435W (upper panel), F606W (middle panel), and F814W (bottom panel) filters. Open symbols and full curve: observed light-echo surface-brightness SB (Col. 6 in Table 1) and its best-fitting model. Filled symbols and dashed curve: the same but for SB 0.5 (Col. 8 in Table 1). Parameters of the fit can be found in Table 2 middle and bottom rows. |
| In the text | |
 |
Fig. 6 Dependence of the scattering coefficient, Qsca, on the wavelength as derived from modelling of the echo. The values are normalized to Qsca at the effective wavelength of the F814W filter. Asterisks: results of the models fitting the total flux, STmag, (upper rows in Table 2). Open circles: results of the models fitting the mean surface brightness, Sb, (middle rows in Table 2). Filled circles: results of the models fitting the mean surface brightness derived from the brightest pixels filling fc = 0.5, SB 0.5, (bottom rows in Table 2). The horizontal error bars represent the widths of the photometric bands. Open and filled symbols are shifted by ± 0.05 μm in the abscissa axis for clarity. Curves: relations expected from modelling the interstellar extinction curve of Weingartner & Draine (2001) for RV = 3.1 (dotted) and RV = 5.5 (dashed). |
| In the text | |
 |
Fig. 7 Dependence of the anisotropy factor, ⟨ cosθ ⟩ , on the wavelength, as derived from our modelling of the echo. The symbols and curves have the same meaning as in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.