| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201219421 | |
| Published online | 20 November 2012 | |
Systematic effect of the Galactic aberration on the ICRS realization and the Earth orientation parameters
1 School of Astronomy and Space Science, Nanjing University, 210093 Nanjing, PR China
e-mail: jcliu@nju.edu.cn
2 SYRTE, Observatoire de Paris, CNRS, UPMC, 61 avenue de l’Observatoire, 75014 Paris, France
e-mail: n.capitaine@obspm.fr
3 Pulkovo Observatory, Pulkovskoe Ch. 65, 196140 St. Peterburg, Russia
4 St. Petersburg State University, Universitetskii pr. 28, 198504 St. Petersburg, Russia
5 Key Laboratory of Modern Astronomy and Astrophysics (Nanjing University), Ministry of Education, 210093 Nanjing, PR China
Received: 16 April 2012
Accepted: 5 October 2012
Context. The curvature of the motion of the solar system barycenter around the Galactic center induces an aberration effect varying linearly with time. It can be called the “Galactic aberration” and is also known as the “secular aberration (drift)” or “aberration in proper motions”. This results in a systematic dipole pattern of the apparent proper motions of an ensemble of distant extragalactic objects, which are used to define the International Celestial Reference System (ICRS).
Aims. The purpose of this paper is to investigate the effect of the Galactic aberration on the ICRS realization and on the Earth orientation parameters (EOP), which refer to the ICRS.
Methods. We first computed the global rotation of the celestial reference system resulting from the Galactic aberration effect on the apparent proper motions of the ensemble of extragalactic objects that realize this system. Then we evaluated the influence of the Galactic aberration on the EOP using CIO based ICRS-to-ITRS coordinate transformation. Numerical evaluations of the effect were performed with the ICRF1 and ICRF2 catalogs over short and long time intervals.
Results. We show that the effect of the Galactic aberration strongly depends on the distribution of the sources that are used to realize the ICRS. According to different distributions of sources (of the ICRF1 and ICRF2 catalogs) the amplitude of the apparent rotation of the ICRS is included between about 0.2 and 1 microarcsecond per year (μas yr-1). We show that this rotation has no component around the axis pointing to the Galactic center and has an zero amplitude in the case of uniform distribution of sources. The effect on the coordinates of the Celestial intermediate pole (CIP) is included between about 1 to 100 μas after one century from J2000.0, while the effects on the Earth rotation angle (ERA) are from 4 to several tens of μas after one century.
Conclusions. We demonstrate that the Galactic aberration is responsible for a variation with time of the orientation of the ICRS axes and consequently for systematic errors on the determination of the EOP, which refer to the ICRS. The effect on the ICRS and EOP increases with time and is not negligible after several tens of years. With high-accuracy astrometry and the increasing length of the available VLBI observation time series, this effect should be considered, particularly in constructing the next realization of the ICRS. Observations of more radio sources, especially in the southern hemisphere should be developed to more homogeneously distribute defining sources in the ICRF to minimize that effect.
Key words: astrometry / catalogs / Galaxy: general / proper motions / reference systems
© ESO, 2012
1. Introduction
The International Celestial Reference Frame (ICRF), regarded as the realization of the International Celestial Reference System (ICRS), is based upon an ensemble of very distant extragalactic sources, whose proper motions are assumed to not be detectable with the current precision of VLBI observations. The first version of the ICRF (hereafter ICRF1) contains 608 compact radio sources in which 212 are selected as defining sources (Ma et al. 1998). The latest version ICRF2 (Fey et al. 2009) contains 3414 radio sources, in which 295 are defining sources. The ICRS is considered as a quasi-inertial reference system under the fundamental assumption that the motion of the solar system barycenter (SSB) is rectilinear, which leads to a dynamically nonrotating barycentric reference system with respect to the rest of the universe. Owing to its motion around the Galactic center (GC), the geodetic precession of the Barycentric Celestial Reference System (BCRS) has been estimated to be about 0.01 μas yr-1 (Brumberg 1991) and thus can be ignored.
The motion of the solar system barycenter in the Galaxy is in fact not rectilinear because of the gravitational attraction from the GC; the velocity vector of the SSB changes with time because of the galactocentic acceleration. This produces non-negligible apparent proper motions of all radio sources (Kovalevsky 2003; Kopeikin & Makarov 2006; Titov 2010). It is responsible for the slow deformation of the celestial reference frames, which cannot be neglected with the advent of microarcsecond astrometry, such as the observations with future VLBI network VLBI2010 (Behrend et al. 2010) and also the increasing length of the available VLBI observation time series, which is sensitive to a cumulative effect.
The acceleration of the SSB in the Galaxy contains two parts: the peculiar acceleration with respect to the local standard of rest (LSR) and the galactocentric acceleration of the LSR. It has already been proved (Kopeikin & Makarov 2006), based on the epicycle theory, that due to the peculiar acceleration of the SSB, the amplitude of apparent proper motions is about 1 μas yr-1, which is about ten times less than the effect of the galactocentric acceleration. Therefore in this paper we only consider the main galactocentric component of the acceleration and we call the corresponding aberration effect “Galactic aberration” after Malkin (2011). This effect has also been called “secular aberration” (Kopeikin & Makarov 2006), “secular aberration drift” (Titov 2010; Titov et al. 2011), or “aberration in proper motions” (Kovalevsky 2003), but no official nomenclature has been adopted so far1.
Titov (2010, 2011) calls attention to the need to take the Galactic aberration effect into account in high-precision astrometric data reductions in the future development of the ICRF and in geodetic/astrometric VLBI software packages. To detect the Galactic aberration effect, Titov et al. (2011) analyzed VLBI data over the period 1990 − 2010 to produce the coordinate time series of 555 radio sources. With the linear proper motions fitted to these series, they obtained the amplitude and apex of the dipole structure, which are consistent, within the error bars, with the theoretical predictions. More recently, Xu et al. (2012) have made a direct estimation of the acceleration of the Sun using 30 years of VLBI data. The apex of the resulting acceleration is about 33° from the Galactic plane to the north because of the very significant value of their estimated z-component acceleration, which is not predicted by the current theory.
To study the influence of the Galactic aberration on the precession parameters, Malkin (2011) analyzed the celestial pole offsets based on 3163 sessions of VLBI observations from 1985 to 2010. Linear trends in the celestial pole offsets, reduced by using radio sources coordinates, were derived, with or without the Galactic aberration effect, and the comparison of these results shows that the influence of the Galactic aberration on the Celestial intermediate pole (CIP) location is up to 0.2 μas yr-1.
 |
Fig. 1 The distribution of radio sources in the ICRF1 (top panel) and ICRF2 (bottom panel) catalogs where the red open circles represent the 212 and 295 defining sources of corresponding catalogs, respectively. The arrows represent the proper motions of the defining sources resulting from the theoretical Galactic aberration. The catalogs are from the ICRS data center operated at Paris Observatory, http://hpiers.obspm.fr/icrs-pc/. |
The aim of this paper is to investigate the systematic effect of the Galactic aberration on the realization of the ICRS and then on the Earth orientation parameters (EOP), which include the CIP coordinates and the Earth rotation angle (ERA). We evaluate the effect using the ICRF1 and ICRF2 source coordinates, which are considered as the first and second benchmark representations of the celestial reference system. Figure 1 shows the distribution of extragalactic sources in the ICRF1 and ICRF2 catalogs in which 212 and 295 sources were selected as defining sources, respectively. The dipole pattern of the apparent proper motions of the defining sources due to the Galactic aberration effect is also shown in the figure. It is important to note that ICRF1 and ICRF2 represent, or realize, the same reference system, namely the ICRS, as the ICRF2 coordinate frame was aligned to that of the ICRF1 (Fey et al. 2009). In this paper, according to recommendations by the IAU working group “Nomenclature for Fundamental Astronomy (NFA)”, we use “ICRS” in a general sense to describe the orientation of the fundamental reference system, while “ICRF” (with or without number) is used to refer to the realization (as a catalog) of the ICRS.
Basic formulas of the Galactic aberration effect are given in Sect. 2. In Sect. 3 we report on the estimated global rotation of the ICRS caused by the Galactic aberration proper motions of radio sources. In Sect. 4, we formulate the corresponding theoretical effect on the CIP coordinates and the ERA and present numerical tests using the ICRF1 and ICRF2 catalogs. Finally, we offer some conclusions about the Galactic aberration effect in Sect. 5.
2. Basic expressions for the Galactic aberration
The observed direction to a radio source measured by a moving observer differs from its true geometric position vector p. The displacement of the position vector owing to the changing velocity of the SSB is such that 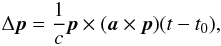 (1)where c is the speed of light, a the centripetal acceleration of the SSB, t0 the initial date, and t the observation date. We can neglect the derivative (and higher order terms) of the acceleration (Kovalevsky 2003), so that a is a constant vector:
(1)where c is the speed of light, a the centripetal acceleration of the SSB, t0 the initial date, and t the observation date. We can neglect the derivative (and higher order terms) of the acceleration (Kovalevsky 2003), so that a is a constant vector: 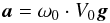 (2)where ω0 and V0 are the angular and linear speed of the SSB in a circular orbit, respectively, and g is the unit vector directed to the GC. The effect of the Galactic aberration due to this galactocentric acceleration of the SSB results in an apparent proper motion of a radio source, which is expressed as
(2)where ω0 and V0 are the angular and linear speed of the SSB in a circular orbit, respectively, and g is the unit vector directed to the GC. The effect of the Galactic aberration due to this galactocentric acceleration of the SSB results in an apparent proper motion of a radio source, which is expressed as 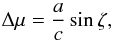 (3)where ζ is the angle between the directions of the GC and the radio source (Kovalevsky 2003). The corresponding aberration effects in Galactic coordinates (longitude, ℓ, and latitude, b) are such that
(3)where ζ is the angle between the directions of the GC and the radio source (Kovalevsky 2003). The corresponding aberration effects in Galactic coordinates (longitude, ℓ, and latitude, b) are such that 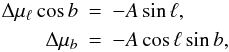 (4)where the quantity
(4)where the quantity 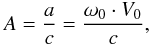 (5)which expresses the magnitude of the Galactic aberration effect (in the unit of proper motion), is called the “Galactic aberration constant” (Malkin 2011). Using Eqs. (1), (2), and (5), one can write the change in the direction of a radio source due to the Galactic aberration as
(5)which expresses the magnitude of the Galactic aberration effect (in the unit of proper motion), is called the “Galactic aberration constant” (Malkin 2011). Using Eqs. (1), (2), and (5), one can write the change in the direction of a radio source due to the Galactic aberration as . \end{eqnarray}](/articles/aa/full_html/2012/12/aa19421-12/aa19421-12-eq24.png) (6)For a radio source with equatorial coordinates (α,δ), the Galactic aberration proper motion in right ascension and declination are such that (Titov 2010):
(6)For a radio source with equatorial coordinates (α,δ), the Galactic aberration proper motion in right ascension and declination are such that (Titov 2010): 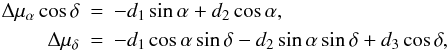 (7)where d1 = Acosα0cosδ0, d2 = Asinα0cosδ0, and d3 = Asinδ0 are the components of the acceleration vector a (cf. Eq. (2)) in the equatorial coordinate system, α0 and δ0 being the right ascension and declination of the GC at J2000.0.
(7)where d1 = Acosα0cosδ0, d2 = Asinα0cosδ0, and d3 = Asinδ0 are the components of the acceleration vector a (cf. Eq. (2)) in the equatorial coordinate system, α0 and δ0 being the right ascension and declination of the GC at J2000.0.
With recent determination of the Galactic constants, the amplitude of A is about 5 μas yr-1 with a relative accuracy of 5% − 10% (Malkin 2011). For all the developments in the following sections, we adopt A = 5 μas yr-1 for the Galactic aberration constant and use (t − t0) for the elapsed time from the initial epoch J2000.0.
3. Effect of the Galactic aberration on the ICRS realized by an ensemble of sources
Malkin (2011) points out that in the ideal case of an uniform distribution of radio sources used in VLBI data reduction, there should be no systematic errors in the CIP location. In reality, the ideal case of an homogeneous distribution of sources is never realized, and there are rotation and deformation of the celestial reference system that is realized by an ensemble of radio sources. In this section we consider the revised celestial reference system, which is denoted as ICRS′ in this paper, defined by the radio sources whose positions include the effect of the Galactic aberration. We first consider (in Sect. 3.1) a very simplified set of radio sources. We then use (in Sect. 3.2) different sets of radio sources that are used to define the ICRS axes in order to evaluate the global rotation of the ICRS and characterize (in Sect. 3.3) the geometry of that rotation in the Galactic coordinate system.
3.1. Simplified set of radio sources
The most straightforward method for obtaining a revised celestial reference system is for each of the three principal axes of the ICRS to tie in with a specific radio source. Obviously, after applying the Galactic aberration effect (Eq. (6)) to the three radio sources, the modified directions of the ICRS coordinate axes are not orthogonal any more, which is clearly unacceptable. For example, after one century, the deviation is 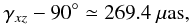 (8)where γxz is the angular separation between the X and Z axes.
(8)where γxz is the angular separation between the X and Z axes.
Alternatively, we assume that only the Z axis to tie in with a radio source and moves according to the Galactic aberration. The three principal directions X, Y, Z of the triad are kept perpendicular to each other. The displacement of the ICRS pole position in this case can be evaluated based on Eq. (6) as 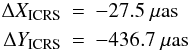 (9)after one century from the basic epoch J2000.0.
(9)after one century from the basic epoch J2000.0.
The next step is to rotate the reference system around the Z axis to apply the correction for the zero point of right ascension, and the amount of this rotation is the statistical average of the right-ascension component of the apparent proper motions 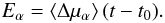 (10)The revised ICRS can be derived by:
(10)The revised ICRS can be derived by: ![\begin{eqnarray} [{\rm ICRS'}] = \mathcal R_3(E_\alpha) \cdot \mathcal R_2(-\Delta X_{\rm ICRS}) \cdot \mathcal R_1(\Delta Y_{\rm ICRS})\cdot[{\rm ICRS}], \end{eqnarray}](/articles/aa/full_html/2012/12/aa19421-12/aa19421-12-eq45.png) (11)where the bracket means the orthogonal triad of the three principal directions in the ICRS and ICRS′.
(11)where the bracket means the orthogonal triad of the three principal directions in the ICRS and ICRS′.
In this method, the Z axis of the ICRS moves along with a single radio source, whose original position vector at J2000.0 is (0,0,1)T, while the other sources are used to provide the zero point correction of right ascension. The precision of the transformed ICRS is restricted by the precision of only one source. We can also use the X, Y axes instead of the Z axis, or any other axis to apply this method, and the results are expected to be different. This approach is not satisfactory either because it is based on too simple an approximation of the ICRF.
3.2. Estimation of the global rotation of the ICRS due to the Galactic aberration effect by a fit to the apparent proper motions
As described in the previous section, the original ICRS is transformed by the apparent Galactic aberration proper motions of the sources that are used to realize the system. Since we impose here that the transformation keeps the orthogonality of the space axes, the ICRS′ can be regarded as being transformed from the original ICRS by three small rigid rotations. Those rotations can be estimated by a least squares fit to the apparent proper motions (cf. Eq. (7)) of an ensemble of radio sources, using the following equations (Mignard & Frœschlé 2000): 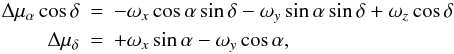 (12)where ωx, ωy, and ωz are the rotation rates around around X, Y, Z axes of the ICRS, respectively. Table 1 provides the estimated values (with their errors) obtained from the fit corresponding to the sources of the ICRF1 and ICRF2 catalogs and the defining-source subsets.
(12)where ωx, ωy, and ωz are the rotation rates around around X, Y, Z axes of the ICRS, respectively. Table 1 provides the estimated values (with their errors) obtained from the fit corresponding to the sources of the ICRF1 and ICRF2 catalogs and the defining-source subsets.
The revised ICRS is such that ![\begin{eqnarray} {\rm [ICRS']}=\mathcal M_{\rm rot}(\psi_x, \psi_y, \psi_z)\cdot{\rm [ICRS]} \label{eq-transformicrs} \end{eqnarray}](/articles/aa/full_html/2012/12/aa19421-12/aa19421-12-eq53.png) (13)where
(13)where 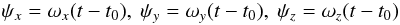 (14)are the rotation angles as linear functions of the elapsed time since J2000.0. Since those angles are small quantities over intervals of several thousands of centuries, the rotation matrix ℳrot(ψx,ψy,ψz) can be written as
(14)are the rotation angles as linear functions of the elapsed time since J2000.0. Since those angles are small quantities over intervals of several thousands of centuries, the rotation matrix ℳrot(ψx,ψy,ψz) can be written as 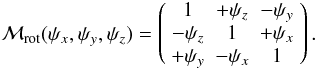 (15)The values for ωx,y,z corresponding to different realizations of the ICRS, reported in Table 1, are such that the amplitude of the total rotation is included between 0.22 μas yr-1 and 1.10 μas yr-1 (i.e. 22 μas cy-1 and 110 μas cy-1, respectively), with formal uncertainties ranging from 0.01 μas yr-1 to 0.1 μas yr-1, according to the realization of the ICRS that is considered (i.e., ICRF1-defining sources, ICRF1, ICRF2-defining sources, or ICRF2). These values should be compared with the stability of the ICRF1 and ICRF2 axes that were reported in Fey et al. (2009) as 20 μas and 10 μas, respectively. This shows that the rotation angles of the ICRS around the X, Y, and Z axes due to the Galactic aberration effect will not be negligible as compared to the stability of the axes after a few decades from the basic epoch t0.
(15)The values for ωx,y,z corresponding to different realizations of the ICRS, reported in Table 1, are such that the amplitude of the total rotation is included between 0.22 μas yr-1 and 1.10 μas yr-1 (i.e. 22 μas cy-1 and 110 μas cy-1, respectively), with formal uncertainties ranging from 0.01 μas yr-1 to 0.1 μas yr-1, according to the realization of the ICRS that is considered (i.e., ICRF1-defining sources, ICRF1, ICRF2-defining sources, or ICRF2). These values should be compared with the stability of the ICRF1 and ICRF2 axes that were reported in Fey et al. (2009) as 20 μas and 10 μas, respectively. This shows that the rotation angles of the ICRS around the X, Y, and Z axes due to the Galactic aberration effect will not be negligible as compared to the stability of the axes after a few decades from the basic epoch t0.
Global rotation of the ICRS around its X, Y, and Z axes due to the Galactic aberration effect.
In the case of the defining sources of the ICRF1 and ICRF2 catalogs, we note that the amplitude of the total rotation is smaller for the ICRF2 catalog than for the ICRF1. This is because the ICRF2 catalog contains more defining sources in the southern hemisphere, and the distribution is therefore more homogeneous (Fey et al. 2009; Lambert & Gontier 2009). The amplitude of the total rotation derived from all the ICRF1 sources is significantly smaller than that derived only from the defining sources, however, the case is not the same for the ICRF2 catalog where the total rotation is larger for all the sources than for only the defining sources. This can be interpreted with reference to Fig. 1: the distribution of all the ICRF2 sources are less uniform than its subset of defining sources, while the ICRF1 is more homogeneous when taking the“candidate” and “other” sources into consideration, besides only the 212 defining sources.
In summary, the minimum effect of the Galactic aberration on the ICRS is for its realization through all the ICRF1 sources, which corresponds to the most uniform distributions of sources (see Fig. 1), while the maximum effect is for its realization through the ICRF1-defining sources, which corresponds to the least uniform distribution of sources. This clearly shows that the rotation resulting from the Galactic aberration strongly depends on the distribution of sources that are used to realize the celestial reference system.
In the least squares fit to apparent proper motions described above, no weights have been used. This may appear unrealistic because, for example, it is well known that, in the case of the ICRF2 defining sources, the source positions in the southern hemisphere are less accurate than those in the northern one. Therefore, an attempt was made to evaluate the impact of this feature on our evaluation. One practical way to use weights is to derive them from the uncertainties in proper motions, the latter being computed by propagating the formal errors of source positions using Eq. (7) along with the law of error propagation. Doing that gives smaller weights to sources in the southern hemisphere, which is similar to having fewer sources in the south. Therefore this changes the distribution of the ICRF2 defining sources to a less uniform one. The result corresponding to this specific weighted fit is provided in the last line of Table 1; it shows that, as expected, the effect is stronger than for the unweighted case (cf. line 3; the total rotation in line 5 is about 5 times as large as in line 3). This weighted case, which corresponds to another practical realization of the ICRS, provides an evaluation of the impact of the uneveness of the formal errors in the positions of the sources on the Galactic aberration effect on the realization of the ICRS. Since real uncertainties of the apparent proper motions are in fact not available, we have limited our study to the unweighted cases.
It is important to note that, besides the rigid rotation developed in this section, the systematic effect of the Galactic aberration on the realization of the ICRS should also include corrections such as distortion and deformation of the reference frame. However, if we want to keep the axes of the revised ICRS perpendicular, only rigid rotation can be applied. Other effects, such as the deformation effect of the reference system, are not considered in this study.
3.3. The geometrical features of the global rotation due to the Galactic aberration effect
The method used in Sect. 3.2 is direct and concise for estimating the rotation of the reference system due to the apparent proper motions of the sources that are used to realize the ICRS; it can be applied to any kind of proper motion patterns. However, this does not reflect the specific geometry of the proper motions due to the Galactic aberration effect.
To best characterize the geometry of that rotation, we use the conventional Galactic coordinate system [XG, YG, ZG] (Blaauw et al. 1960), where the XG axis points to the Galactic center (GC), YG to the direction of the Galactic rotation, and ZG to the north Galactic pole (NGP). Figure 2 shows the feature of the apparent proper motions in the Galactic coordinate system resulting from the Galactic aberration effect: the apparent directions of the radio sources (blue arrows) move along the great circles connecting the anti-Galactic center and the Galactic center. From Fig. 2, we can see that the rotation of the ICRS around the XG axis is zero owing to the pattern of dipole proper motion, no matter how the radio sources are distributed.
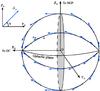 |
Fig. 2 Proper motions resulting from the Galactic aberration. The blue arrows represent the apparent proper motion vectors of sources along great circles connecting the anti-GC and GC. The plane perpendicular to the XG axis is highlighted in gray and the orientation angle, θ, of the total rotation is shown in the top corner. |
The components ωXG, ωYG, and ωZG of the global rotation around the XG, YG, and ZG axes can be obtained from the values for ωx, ωy, and ωz (cf. Table 1), using the following equations: 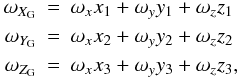 (16)where (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3) are the direction cosines of the XG, YG, and ZG axes, respectively, in the ICRS. The values for those quantities can be derived from the elements of the first, second, and third rows, respectively, of the transformation matrix from the equatorial to Galactic coordinate systems. The commonly used equatorial-to-Galactic transformation matrix,
(16)where (x1,y1,z1), (x2,y2,z2), and (x3,y3,z3) are the direction cosines of the XG, YG, and ZG axes, respectively, in the ICRS. The values for those quantities can be derived from the elements of the first, second, and third rows, respectively, of the transformation matrix from the equatorial to Galactic coordinate systems. The commonly used equatorial-to-Galactic transformation matrix,  , is the one adopted by the Hipparcos team (Perryman et al. 1997), which was first derived by Murray (1989) as
, is the one adopted by the Hipparcos team (Perryman et al. 1997), which was first derived by Murray (1989) as  (17)Another method for estimating the rotations around the XG, YG, and ZG axes consists in a fit to the apparent proper motions (Δμℓcosb, Δμb) in the Galactic coordinate system (cf. Eq. (4)) of an ensemble of radio sources, using the following equations:
(17)Another method for estimating the rotations around the XG, YG, and ZG axes consists in a fit to the apparent proper motions (Δμℓcosb, Δμb) in the Galactic coordinate system (cf. Eq. (4)) of an ensemble of radio sources, using the following equations: 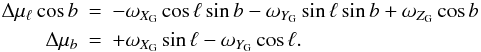 (18)We used the two methods described above for computing the components ωXG, ωYG, and ωZG of the global rotation of the ICRS in the Galactic coordinate system and obtained the same results at the level of 0.01 μas yr-1. The numerical values of ωXG, ωYG, and ωZG in units of μas yr-1 corresponding to the same distributions of sources as in Sect. 3.2 are listed in Table 2. We note that, in all cases, the rotation around the XG axis is very close to zero within the standard error, while the other two rotations depend on the distribution of sources. The values obtained for the total rotations are, in all the cases, the same as in Table 1.
(18)We used the two methods described above for computing the components ωXG, ωYG, and ωZG of the global rotation of the ICRS in the Galactic coordinate system and obtained the same results at the level of 0.01 μas yr-1. The numerical values of ωXG, ωYG, and ωZG in units of μas yr-1 corresponding to the same distributions of sources as in Sect. 3.2 are listed in Table 2. We note that, in all cases, the rotation around the XG axis is very close to zero within the standard error, while the other two rotations depend on the distribution of sources. The values obtained for the total rotations are, in all the cases, the same as in Table 1.
Since the first rotation around the XG axis, pointing to the Galactic center (more precisely, the direction of the acceleration of the SSB), is always zero, we tried to fit only the two rotations ωYG, and ωZG that are in the plane perpendicular to XG (highlighted in gray in Fig. 2). The obtained values that are consistent with that of Table 2 to within the errors of the estimates. In the plane perpendicular to the XG axis, the direction of the total rotation can be described by an angle θ with respect to the YG axis as shown in Fig. 2:  (19)The angle θ also reflects the distribution of sources and its values for different realizations of the ICRS are presented in the last column of Table 2.
(19)The angle θ also reflects the distribution of sources and its values for different realizations of the ICRS are presented in the last column of Table 2.
We also fitted the ωXG, ωYG, and ωZG rotations to the apparent proper motions of an ensemble of randomly distributed sources (i.e. such that any small area on the sphere is expected to contain the same number of points), whose coordinates are simulated as 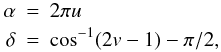 (20)where u and v are random variables on the interval (0,1). The fitted results are in the last line of Table 2. With such random distribution (an approximation of uniform distribution), all three rotations are almost zero. This proves that, for a uniform distribution of the sources, the apparent proper motions resulting from the Galactic aberration would produce no global rotation of the ICRS.
(20)where u and v are random variables on the interval (0,1). The fitted results are in the last line of Table 2. With such random distribution (an approximation of uniform distribution), all three rotations are almost zero. This proves that, for a uniform distribution of the sources, the apparent proper motions resulting from the Galactic aberration would produce no global rotation of the ICRS.
Global rotation around the XG, YG and ZG axes of the Galactic coordinate system due to the Galactic aberration effect.
4. Effect of the Galactic aberration on the Earth orientation parameters
4.1. Theoretical development
Since the ICRS is modified by the Galactic aberration effect, the EOP, which refer to the new ICRS (denoted ICRS′) would have corresponding changes. In this section we calculate these changes based on the results in Sect. 3.
We note that the celestial reference system considered in the celestial-to-terrestrial coordinate transformation is usually the Geocentric Celestial Reference System [GCRS] (e.g. Capitaine & Wallace 2006; Petit & Luzum 2010) to meet the requirements of general relativity. We also note that, according to the IAU 2006 resolution B2, the spatial orientation of the GCRS is assumed to be the same as the ICRS; so it is reasonable to write the transformation formula using [ICRS] for the sake of consistency. Therefore, if we only consider the spatial orientations of these reference systems, the CIO based transformation between the celestial and terrestrial reference system can be written as ![\begin{eqnarray} \label{ITRS1} [{\rm ITRS}] = \mathcal W(x_p, y_p) \cdot \mathcal R_3({\rm ERA}-s) \cdot \mathcal M_\Sigma (X, Y) \cdot[{\rm ICRS}], \end{eqnarray}](/articles/aa/full_html/2012/12/aa19421-12/aa19421-12-eq130.png) (21)xp,yp being components of the polar motion in the terrestrial reference system, s the CIO locator, (X,Y) the GCRS coordinates of the CIP, and
(21)xp,yp being components of the polar motion in the terrestrial reference system, s the CIO locator, (X,Y) the GCRS coordinates of the CIP, and 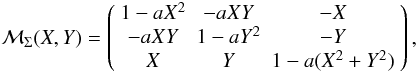 (22)with
(22)with 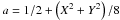 .
.
Since the ITRS triad and the polar motion are not affected by the changes in the ICRS due to Galactic aberration, Eq. (21) becomes ![\begin{eqnarray} \label{ITRS2} [{\rm ITRS}] &=& \mathcal W(x_p, y_p)\cdot \mathcal R_3({\rm ERA}-s+\Delta({\rm ERA}-s)) \nonumber \\ && \times \mathcal M_\Sigma (X+\Delta X, Y+\Delta Y)\cdot[{\rm ICRS'}], \end{eqnarray}](/articles/aa/full_html/2012/12/aa19421-12/aa19421-12-eq136.png) (23)where ΔX, ΔY, and Δ(ERA − s) are the changes in the CIP location and the ERA, respectively, due to the effect of the Galactic aberration on the ICRS. Connecting Eqs. (21) and (23) and inserting Eq. (13), we obtain
(23)where ΔX, ΔY, and Δ(ERA − s) are the changes in the CIP location and the ERA, respectively, due to the effect of the Galactic aberration on the ICRS. Connecting Eqs. (21) and (23) and inserting Eq. (13), we obtain 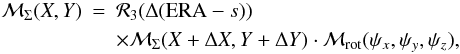 (24)where ψx, ψy, and ψz are the three rotation angles around the ICRS axes that transform the original ICRS to ICRS′ (cf. Eq. (14)).
(24)where ψx, ψy, and ψz are the three rotation angles around the ICRS axes that transform the original ICRS to ICRS′ (cf. Eq. (14)).
Because both of the matrices ℛ3(Δ(ERA − s)) and ℳrot(ψx,ψy,ψz) (cf. Eq. (15)) are orthogonal, we can write Eq. (24) as 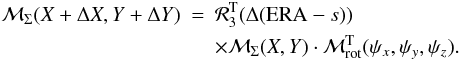 (25)Since on the lefthand side of Eq. (25), the (3, 1) and (3, 2) elements are such that
(25)Since on the lefthand side of Eq. (25), the (3, 1) and (3, 2) elements are such that 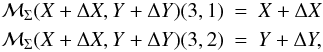 (26)we have
(26)we have 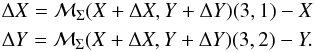 (27)Calculating the (3, 1) and (3, 2) elements of the righthand side of Eq. (25), and noting that the rotation around the Z axis would not affect the (3, 1) and (3, 2) elements, we obtain the solutions for ΔX and ΔY:
(27)Calculating the (3, 1) and (3, 2) elements of the righthand side of Eq. (25), and noting that the rotation around the Z axis would not affect the (3, 1) and (3, 2) elements, we obtain the solutions for ΔX and ΔY: 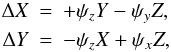 (28)where
(28)where  .
.
To solve for Δ(ERA − s), we note that because the matrix ℳΣ(X,Y) is the product of three individual rotation matrices: 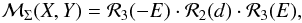 (29)where E and d are the angular coordinates of the CIP in the GCRS, ℳΣ(X,Y) is also orthogonal and we can therefore write Eq. (24) as
(29)where E and d are the angular coordinates of the CIP in the GCRS, ℳΣ(X,Y) is also orthogonal and we can therefore write Eq. (24) as 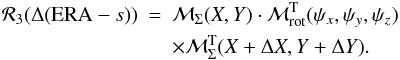 (30)The (1, 2) element on the lefthand side is equal to Δ(ERA − s), which gives
(30)The (1, 2) element on the lefthand side is equal to Δ(ERA − s), which gives 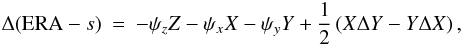 (31)where the terms with an order greater than three in X, Y, and greater than two in the small quantities ψx,y,z, as well as their products with X and Y are neglected. Then inserting Eq. (28) into Eq. (31) gives
(31)where the terms with an order greater than three in X, Y, and greater than two in the small quantities ψx,y,z, as well as their products with X and Y are neglected. Then inserting Eq. (28) into Eq. (31) gives 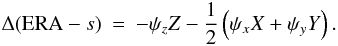 (32)Over short time intervals (several hundred years), the CIP coordinates X and Y are also small quantities, therefore the effect on EOP can be limited to the first order in X, Y, and ψx,y,z:
(32)Over short time intervals (several hundred years), the CIP coordinates X and Y are also small quantities, therefore the effect on EOP can be limited to the first order in X, Y, and ψx,y,z: 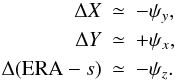 (33)
(33)
4.2. Numerical tests with the ICRF1 and ICRF2 catalogs
4.2.1. Numerical tests over one century
For calculating ΔX, ΔY, and Δ(ERA − s) as functions of time, we use the values for the apparent global rotation of the ICRS obtained in Sect. 3.2 (Table 1). After one century from the basic epoch t0 = J2000.0, the effects of the Galactic aberration on the orientation of the CIP and the ERA are listed in Table 3 (Cols. 2 − 4).
Systematic effects on the Earth orientation parameters after one century from J2000.0.
For defining sources (cf. lines 1 and 3), the magnitudes of ΔX and ΔY (absolute values) due to the Galactic aberration decrease owing to the improvement of the ICRF2, which contains more defining sources and more homogeneous distribution than the ICRF1. Again, for the whole set of sources in the ICRF2 catalog (cf. line 4), the resulting corrections are greater than those derived from only the defining sources. In the case of uniform distribution of sources, the Galactic aberration effect on the EOP would vanish.
 |
Fig. 3 Time series of the effect of Galactic aberration on the CIP location (top plot) and ERA (bottom plot) in ± 500 years around J2000.0, based on the ICRF1 and ICRF2 defining source positions. The CIP location X and Y, necessary for computing ΔX, ΔY, and Δ(ERA − s) are derived from the IAU 2006/2000 precession-nutation model. |
The expressions for ΔX, ΔY, and Δ(ERA − s) as functions of time, for either the ICRF1 and the ICRF2 catalogs, are shown in Fig. 3. For series over intervals covering ± 500 years around J2000.0, we use SOFA ANSI-C functions (IAU SOFA board 2010) to calculate the CIP coordinates based on the IAU 2006/2000 precession-nutation model, which are necessary for calculating the results in Eqs. (28) and (32). The mean rates of ΔX, ΔY, and Δ(ERA − s) are estimated by a linear fit to the ± 500-year time series, and are shown in Cols. 5 − 7 of Table 3.
4.2.2. Comparison with Malkin’s results for precession rates
The rates of change, dΔX/dt, dΔY/dt of the CIP coordinates, from the systematic effect of the Galactic aberration, need special consideration because they have the same form as the Earth’s precession rates and can therefore introduce errors into the estimation of the precession rates from VLBI observations.
We compared the values obtained for dΔX/dt and dΔY/dt in the previous section of this paper with those obtained by Malkin (2011). These two studies are based on (i) the same value for the amplitude of the Galactic aberration effect (i.e. A = 5 μas yr-1); (ii) totally different approaches: Malkin considered the effect of the Galactic aberration on the coordinates of each source used in the least squares solution for the EOP from VLBI observations, while we tried to investigate the global effect of the Galactic aberration on the EOP which refer to different realizations of the ICRS.
The difference in the linear trend of the celestial pole offsets, obtained by Malkin (2011) between the time series of EOP derived with and without applying the Galactic aberration effect to the coordinates of the sources are, in X and Y, 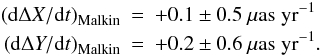 (34)Comparing the above values with dΔX/dt and dΔY/dt of Table 3 (cf. Cols. 5, 6) corresponding to various realizations of the ICRS (ICRF1, ICRF2, etc.), for obtaining the rotation of the ICRS, shows that the effect is, in most cases, of the same order of magnitude, i.e. 0.1 μas yr-1. We note that the discrepancies between Malkin’s results and the various results of Table 3 are of the same order as those between the various values of Table 3. In most cases the values are consistent with Malkin’s results, when taking the corresponding uncertainty in Eq. (34) into account. The difference is not surprising because Malkin’s results are based on a realization of the ICRS that is different from all those reported in Table 3. The best agreement between Malkin’s results and the results of this study corresponds to the realization of the ICRS through the ICRF1 sources (i.e. 2nd line of Table 3).
(34)Comparing the above values with dΔX/dt and dΔY/dt of Table 3 (cf. Cols. 5, 6) corresponding to various realizations of the ICRS (ICRF1, ICRF2, etc.), for obtaining the rotation of the ICRS, shows that the effect is, in most cases, of the same order of magnitude, i.e. 0.1 μas yr-1. We note that the discrepancies between Malkin’s results and the various results of Table 3 are of the same order as those between the various values of Table 3. In most cases the values are consistent with Malkin’s results, when taking the corresponding uncertainty in Eq. (34) into account. The difference is not surprising because Malkin’s results are based on a realization of the ICRS that is different from all those reported in Table 3. The best agreement between Malkin’s results and the results of this study corresponds to the realization of the ICRS through the ICRF1 sources (i.e. 2nd line of Table 3).
The precision of Malkin’s values is on the order of 0.5 μas yr-1, i.e. about five times higher than the effect. With the “theoretical” methods we used in this paper, the differences between the various results indicate that the precision has a similar order of magnitude. The uncertainties given in Table 3 for dΔX/dt and dΔY/dt, which are on the order of 0.1 μas yr-1 in most cases, are optimistic, since they do not consider the practical way the ICRF is realized through the VLBI process.
4.2.3. Numerical tests over a long time interval
For the long-term test of our results (i.e. time interval greater than a few centuries), the use of IAU precession-nutation model is not appropriate, so we adopt the new precession expressions given by Vondrák et al. (2011), which are valid for several thousand centuries. We have calculated ΔX, ΔY and Δ(ERA − s) (cf. Eqs. (28) and (32)) for ± 2000 centuries from the basic epoch J2000.0, when the Galactic aberration effect is taken into account. The time interval covers approximately 16 periods of the CIP precession motion around the north ecliptic pole, which can be clearly seen in Fig. 4. In Eq. (28), the first terms, + ψzY and − ψzX, for ΔX and ΔY are cross terms between the rotation angle ψz and the long periodic components of the precession of the CIP. In long time intervals, they have the same magnitude as the second terms (thus cannot be neglected) and are responsible for the Poisson terms visible in Fig. 4. The long-range secular variations in the ΔX and ΔY are mainly caused by the second terms − ψyZ and + ψxZ in Eq. (28). For the effect of the Galactic aberration on (ERA − s), the terms − ψzZ and 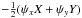 appearing in Eq. (32) are responsible for the secular and periodic variations, respectively.
appearing in Eq. (32) are responsible for the secular and periodic variations, respectively.
 |
Fig. 4 Long-term variations in the CIP location and ERA due to the Galactic aberration effects in ± 2000 centuries, based on the ICRF1 and ICRF2 defining sources. The time series of the CIP location X and Y are derived using the long-term precession expressions provided by Vondrák et al. (2011). |
5. Discussion and conclusion
In this paper, we have investigated the effect of the “Galactic aberration” (resulting from the galactocentric acceleration of the solar system barycenter) on the realization of the ICRS and the estimation of the Earth orientation parameters (EOP). The method used for investigating this effect is as follows: in a first step, we computed the global rotation of the ICRS caused by the Galactic aberration effect on the directions of the ensemble of extragalactic objects that are used to realize the system. In a second step, we evaluated the influence of that global rotation on the observed EOP over short and long time intervals.
In the first step, the apparent proper motions produced by the Galactic aberration (of amplitude A = 5 μas yr-1) were computed for a few ensembles of radio sources based on the ICRF1 and IRCF2 catalogs. The apparent global rotation of the ICRS was then derived from each set of proper motions by a least-squares fit of three rotations around the ICRS axes or the axes of the Galactic coordinate system. The total rotation is included between 0.22 μas yr-1 and 1.10 μas yr-1 according to the distribution of the sources (of the ICRF1 and ICRF2 catalogs). This rotation was shown to have no component around the axis pointing to the Galactic center irrespective of the source distribution and to have a zero amplitude in the case of uniform distribution of sources.
In the second step, we evaluated the influence of the apparent global rotation of the ICRS on the estimation of the EOP over short and long time intervals. As expected, the results show a similar dependence of the effect on the distribution of the sources (of the ICRF1 and ICRF2 catalogs), as mentioned above for the rotation of the ICRS. The amplitude of the systematic effect on the coordinates of the Celestial intermediate pole (CIP) was shown to be included between 1 to 100 μas after one century from J2000.0, while the effects on the ERA are from four to several tens of μas after one century. The order of magnitude of the linear trend of the celestial pole offsets, i.e. 0.1 μas yr-1 ( = 10 μas cy-1), which appears in the same form as a precession effect, agrees, within the formal errors, with Malkin’s results for the same quantities with a totally different method.
The Galactic aberration effect on the radio source positions is an observed one. It is quite different from the precession-nutation of the Earth, which is a physical phenomenon due to the perturbation of the Sun, Moon, and planets on the oblate Earth. However, the spurious global rotation of the ICRS due to the Galactic aberration effect contributes to the linear trend of the celestial pole offsets. This slightly distorts the precession rate estimated from VLBI observations that are processed without taking the Galactic aberration effect into account. The order of magnitude of that distortion is ten times more than the microarcsecond precision of the linear terms of the IAU 2006 precession developments (Capitaine et al. 2003); therefore, the Galactic aberration effect would need to be corrected for, similarly to what was done for other systematic effects before adopting the IAU 2006 precession rate values. This would be possible if that effect could be computed with satisfactory precision; however, as shown in Sect. 4.2.2, the precision can be expected to be on the order of 0.5 μas yr-1 ( = 50 μas cy-1), i.e. 5 times larger than the effect. The computation of the Galactic aberration effect on precession is therefore not sufficiently precise yet to be used for correcting the estimated values for precession, so that effect should be taken directly into account through the apparent proper motions of the sources.
The amplitude of the global rotation of the ICRS as evaluated in this paper is not negligible over the long term (periods of several tens of years) as compared to the ICRF axis stability (Fey et al. 2009). Since the current accuracy for predicting the CIP location is on the order of 2 mas after one century (Capitaine & Wallace 2006), the Galactic aberration effect on the CIP coordinates can be considered as being negligible at present. However, the accuracy for predicting the CIP location is improving with time and can be expected to be better than 100 μas after one century in a near future, thus this effect should be considered. Moreover, because of the permanently changing of VLBI observing programs and networks, hence changing of the source list, the Galactic aberration effect introduces systematic differences between EOP estimations, which are up to tens of microarcseconds over 30 years. This can affect the estimation not only of the precession rate but also of other quantities, such as the amplitudes of the long-period nutation. Such systematic effects should be avoided in VLBI analyzes by taking the apparent proper motions of sources into account.
To conclude, we demonstrated that the Galactic aberration is responsible for a variation with time in the orientation of the ICRS axes and consequently for corresponding errors in determining the EOP referring to the ICRS. We also showed that the effect depends strongly on the homogeneity of distribution of sources that are used to realize the celestial reference system and that its magnitude is close to the accuracy that can be expected in the near future for both the ICRS axis stability and the CIP location. With microarcsecond accuracy in astrometric observations, data reductions, as well as in theories of astronomical reference systems, and also with the increasing length of the available high-accuracy VLBI observation time series, this effect should be considered by the IAU and IERS, particularly in developing the next realization of the ICRS. Since the global effect of Galactic aberration vanishes in the situation of uniform distribution of defining radio sources, effort should be made to homogenize the distribution of the defining sources over the whole sky in order to minimize that effect.
To fully and robustly correct the effect of Galactic aberration, which is attributed to the nonrectilinear motion of the SSB in the Galaxy, one may need a Galactocentric celestial reference system (GalCRS) as a higher level of hierarchy than the Barycentric Celestial Reference System (Klioner & Soffel 1998; Kovalesky 2003; Titov 2010). However, this would require that developments of high-precision theories of the potential and the metric tensor are available for the whole Galaxy (as they are for the solar system in the current IAU models), which may not be the case even when the Gaia (Perryman et al. 2001) mission is completed, owing to imperfect knowledge of the Galaxy.
During the IAU 2012 General Assembly, a new Division A working group (WG) was proposed with the aim of addressing the proper standardization of definitions related to fundamental astronomy. This WG is expected to provide a recommendation on the nomenclature related to the aberration effect considered in this paper.
Acknowledgments
We are grateful to the referee for his/her valuable comments and suggestions for improving the paper. J.C.L. has been supported by China Scholarship Council (CSC) for the joint doctor training program at Department SYRTE (Systèmes de Référence Temps-Espace) of the Paris Observatory (File No. 2011619030). J.C.L. and Z.Z. are also funded by the National Natural Science Foundation of China (NSFC) under grant Nos. 10973009 and 11173014.
References
- Behrend, D., Boehm, J., Charlot, P., et al. 2008, Observing our Changing Earth: Proc. 2007 IAG General Assembly, Perugia, Italy, July 2 − 13, ed. M. G. Sideris, IAG Symp., 133, 833 [Google Scholar]
- Blaauw, A., Gum, C. S., Pawsey, J. L., & Westerhout, G. 1960, MNRAS, 121, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Brumberg, V. A. 1991, Reference Systems, IAU Colloq., 127, 36 [NASA ADS] [Google Scholar]
- Capitaine, N., & Wallace, P. T. 2006, A&A, 450, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2003, A&A, 412, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fey, A., Gordon, D., & Jacobos, C. 2009, The second realization of the International Celestial Reference Frame by Very Long Baseline Interferometry, IERS Technical Note 35 [Google Scholar]
- IAU SOFA Board, IAU SOFA Software Collection, Issue 2010-12-01, available at http://www.iausofa.org [Google Scholar]
- Klioner, S. A., & Soffel, M. 1998, A&A, 334, 1123 [NASA ADS] [Google Scholar]
- Kopeikin, S. M., & Makarov, V. V. 2006, AJ, 131, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, S. B., & Gontier, A.-M. 2009, A&A, 493, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Malkin, Z. M. 2011, Astron. Rep., 55, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F., & Frœschlé, M. 2000, A&A, 354, 732 [NASA ADS] [Google Scholar]
- Murray, C. A. 1989, A&A, 218, 325 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., et al. 1997, The Hipparcos and Tycho Catalogues Vol. 1, ESA SP 1200 (Noordwijk: ESA) [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, G., & Luzum, B. 2010, IERS Conventions (2010), IERS Technical Note No. 36 [Google Scholar]
- Titov, O. 2010, MNRAS, 407, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, O. A. 2011, Astron. Rep., 55, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, O., Lambert, S. B., & Gontier, A.-M. 2011, A&A, 529, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vondrák, J., Capitaine, N., & Wallace, P. 2011, A&A, 534, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, M. H., Wang, G. L., & Zhao, M. 2012, Sci. China Phys. Mech. Astron., 55, 329 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Global rotation of the ICRS around its X, Y, and Z axes due to the Galactic aberration effect.
Global rotation around the XG, YG and ZG axes of the Galactic coordinate system due to the Galactic aberration effect.
Systematic effects on the Earth orientation parameters after one century from J2000.0.
All Figures
 |
Fig. 1 The distribution of radio sources in the ICRF1 (top panel) and ICRF2 (bottom panel) catalogs where the red open circles represent the 212 and 295 defining sources of corresponding catalogs, respectively. The arrows represent the proper motions of the defining sources resulting from the theoretical Galactic aberration. The catalogs are from the ICRS data center operated at Paris Observatory, http://hpiers.obspm.fr/icrs-pc/. |
| In the text | |
 |
Fig. 2 Proper motions resulting from the Galactic aberration. The blue arrows represent the apparent proper motion vectors of sources along great circles connecting the anti-GC and GC. The plane perpendicular to the XG axis is highlighted in gray and the orientation angle, θ, of the total rotation is shown in the top corner. |
| In the text | |
 |
Fig. 3 Time series of the effect of Galactic aberration on the CIP location (top plot) and ERA (bottom plot) in ± 500 years around J2000.0, based on the ICRF1 and ICRF2 defining source positions. The CIP location X and Y, necessary for computing ΔX, ΔY, and Δ(ERA − s) are derived from the IAU 2006/2000 precession-nutation model. |
| In the text | |
 |
Fig. 4 Long-term variations in the CIP location and ERA due to the Galactic aberration effects in ± 2000 centuries, based on the ICRF1 and ICRF2 defining sources. The time series of the CIP location X and Y are derived using the long-term precession expressions provided by Vondrák et al. (2011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


