| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220141 | |
| Published online | 25 October 2012 | |
Superexpansion as a possible probe of accretion in 4U 1820-30
1 SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
e-mail: jeanz@sron.nl
2 Dept. Physics and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
3 National Superconducting Cyclotron Laboratory, Dept. of Physics & Astronomy, and Joint Institute for Nuclear Astrophysics, Michigan State University, East Lansing, MI 48824, USA
4 Los Alamos National Laboratory, B244, Los Alamos, NM 87545, USA
Received: 31 July 2012
Accepted: 2 October 2012
The ultracompact X-ray binary 4U 1820-30 is well known for its ≈170-d superorbital modulation in X-ray flux and spectrum, and the exclusiveness of bursting behavior to the low hard “island” state. In May−June 2009, there was an exceptionally long 51-d low state. This state was well covered by X-ray observations and 12 bursts were detected, 9 with the high-throughput RXTE. We investigate the character of these X-ray bursts and find an interesting change in their photospheric expansion behavior. At the lowest inferred mass accretion rates, this expansion becomes very large in 4 bursts and reaches the so-called superexpansion regime. We speculate that this is due to the geometry of the inner accretion flow being spherical and a decreasing accretion rate: when the flow geometry nearest to the neutron star is spherical and the accretion rate is low, the ram pressure of the accretion disk may become too low to counteract that of the photospheric expansion. In effect, this may provide a novel means to probe the accretion flow. Additionally, we observe a peculiar effect: the well-known cessation of X-ray bursts in the high state is too quick to be consistent with a transition to stable helium burning. We suggest an alternative explanation, that the cessation is due to the introduction of a non-nuclear heat source in the neutron star ocean.
Key words: accretion, accretion disks / X-rays: binaries / X-rays: bursts / stars: neutron / X-rays: individuals: 4U 1820-30
© ESO, 2012
1. Introduction
Low-mass X-ray binaries with neutron stars (NSs) emit X-rays from two distinct locations: the inner region of the accretion disk, including perhaps a boundary layer and corona, and the NS. The former is powered by the liberation of gravitational potential energy and the latter by thermonuclear burning in the surface layers consisting of accreted matter. Per nucleon the thermonuclear energy is just up to a few percent of the gravitational energy and would be hardly distinguishable if it did not have a different time scale. Thermonuclear burning is mostly unstable and “visible” as short bursts of X-ray radiation while gravitational energy is liberated throughout the disk on typical time scales of at least a few weeks. X-ray bursts are characterized by few-second rises and decays at least ten times as slow, and a cooling black body spectrum of temperature kT < 3 keV. For reviews of X-ray bursts, see Lewin et al. (1993) and Strohmayer & Bildsten (2006).
Different kinds of thermonuclear X-ray bursts exist. One distinction that one can make is the presence of photospheric radius expansion (PRE). The luminosity produced in some bursts is so powerful that the Eddington limit is reached and the photosphere is lifted from the NS surface (Grindlay et al. 1980; Ebisuzaki et al. 1983). PRE can be recognized by a temporarily increased emission area of a cooler thermal spectrum and a bolometric flux that remains approximately constant for the same duration. PRE happens in about 20% of the bursts (Galloway et al. 2008). Usually the increase in emission area is approximately tenfold. In 1% of all cases, however, the increase is much larger: 104 or more (or, > 102 in terms of photospheric radius). This is qualified as “superexpansion” (in ’t Zand & Weinberg 2010; see also Hoffman et al. 1978; van Paradijs et al. 1990).
There is an intricate interplay between accretion and burst behavior (e.g., Fujimoto et al. 1981; van Paradijs et al. 1988; Cornelisse et al. 2003). Primarily the accretion rate determines the burst recurrence time: the faster the accretion and ergo fuel supply, the faster the bursts recur. At the highest accretion rates, thermonuclear burning becomes stable and bursts disappear. A second order effect involves the hydrogen abundance: a high abundance may incur a burning regime where stable hydrogen burning co-exists with unstable helium burning.
The aforementioned effects are observationally obvious. It is to be expected, but harder to prove observationally, that there is also a dependence on accretion geometry. Non-isotropic accretion on the NS surface will change the local (or specific) accretion rate and will influence the ignition conditions (e.g., Bildsten 1998) because those may really depend on the specific rather than global rate. A very nice illustration of this is the recently discovered transient IGR J17480–2446 (e.g., Cavecchi et al. 2011; Linares et al. 2012).
In conclusion, accretion parameters (rate, geometry, composition) determine burst parameters such as the recurrence time (e.g., Cornelisse et al. 2003), peak luminosity and duration (and, ergo, fluence; Galloway et al. 2008), PRE and the amplitude of burst oscillations (Muno et al. 2004; Watts 2012). Conversely, thermonuclear bursts may influence the accretion. The luminosity of bursts is sometimes so high that it may affect the accretion flow for a brief period. The influence may be dramatic. Kuulkers et al. (2009) discuss an X-ray burst from Cen X-4 which appears to have turned the accretion disk into a hot state, although it appears at odds with accretion disk theory. Other examples of influence are bursts that cool the accretion disk corona (Chen et al. 2011) and bursts with superexpansion, such as the superburst from 4U 1820-30 (Strohmayer & Brown 2002; Ballantyne & Strohmayer 2004; Keek 2012) and a number of bursts from (candidate) ultracompact X-ray binaries (in ’t Zand & Weinberg 2010). During these bursts, episodes exist when the flux is lower than the pre-burst accretion flux. This implies that accretion was stopped or covered by the optically thick shell. Better yet, strong factor-of-2 fluctuations were recently observed in the decay of several burst light curves that are very probably due to structural disturbances of the accretion disk surface (in ’t Zand et al. 2011b; Palmer 2011; Degenaar et al. 2012).
Because of the influence of superexpansion on the accretion flow, it makes sense to study superexpansion as a function of accretion. Unfortunately, superexpansion is usually a rare phenomenon which makes such a study difficult. However, in 2009 a series of observations was done on 4U 1820-30 when it was gradually changing its accretion rate and presumably geometry. Simultaneously, a series of bursts was observed with different levels of photospheric expansion. We here report our findings of these observations.
4U 1820-30 is the source in which the X-ray burst phenomenon was discovered by Grindlay et al. (1976). It is a persistently bright low-mass X-ray binary (LMXB), viewed at an inclination angle below roughly 50o (Anderson et al. 1997; Ballantyne & Strohmayer 2004). It is located in the globular cluster NGC 6624 at a distance of 8.4 ± 0.6 kpc (Valenti et al. 2004) and is extraordinary since it has the shortest orbital period known for any LMXB: 11.4 min (Stella et al. 1987). The orbital period puts it in the ultracompact X-ray binary regime (Nelson et al. 1986). The donor stars in this group distinguish themselves as being hydrogen-deficient dwarf stars. The donor in 4U 1820-30 is probably a helium white dwarf (Rappaport et al. 1987). From an analysis of burst energetics, Cumming (2003) conclude that the hydrogen abundance X < 0.1. 4U 1820-30 shows a superorbital modulation in the X-ray flux with a period of ≈ 170 d (Priedhorsky & Terrell 1984; Chou & Grindlay 2001; Farrell et al. 2009). The flux resides mostly in a high state, except for few-day periods every ≈ 170 d when the (bolometric) flux decreases by a factor of approximately 2. Zdziarski et al. (2007a) studied the orbital modulation as a function of superorbital phase and found that the orbital amplitude is up to a factor of 2 lower during the superorbital low state (or island state), and that the orbital peak phase shifts. This suggests a different geometry of X-ray emitting and scattering structures on the accretion disk between both states. The nature of the ≈ 170 d periodicity is speculated to be the result of the influence of a third massive body, see Chou & Grindlay (2001) and Zdziarski et al. (2007b), which modulates the orbital eccentricity of the ultracompact system and, thus, the mass accretion rate.
 |
Fig. 1 Evolution of the 3 − 12 keV photon flux relative to that of the Crab source (black curve; RXTE-ASM data) and the 15 − 50 keV photon flux with respect to 0.18 times that of the Crab source (red dash-dotted curve; Swift/BAT data). Vertical lines indicate the bursts detected, solid for those with superexpansion and dashed for those without. Three bursts are indistinguishable because they have too short recurrence times to be visible on this scale (see Table 1). The solid horizontal lines indicate the days that the PCA observed 4U 1820-30 under ObsID 94090. The solid vertical lines in the top left corner indicate the 2σ uncertainties. |
 |
Fig. 2 Measured photon rate time histories for the 9 PCA bursts, from bottom to top chronologically, supplemented with the 2 PCA bursts that are lowest in the color–color diagram (Fig. 4). The subtracted background level is measured from a 150 s time interval prior to the burst and the curves have been normalized to the peak rate. For guidance, the zero level has been indicated by a dotted line. |
It is only during the low states that the source shows X-ray bursts. This is attributed to the difference in accretion rate: in the high state thermonuclear burning is stable and not distinguishable from the accretion radiation while in the low state it is unstable and visible as X-ray bursts (e.g., Chou & Grindlay 2001). 4U 1820-30 is the only confirmed ultracompact hydrogen-deficient X-ray binary to have exhibited carbon-fueled superbursts (Strohmayer & Brown 2002; in ’t Zand et al. 2011a; see also Ballantyne & Strohmayer 2004).
The subject of our study is the bursting behavior during the longest low state ever observed in 4U 1820-30, lasting 51 days in May − June 2009.
2. Observations
Figure 1 shows two light curves of the long low state. The 2 − 12 keV RXTE-ASM data (black; for a description of the ASM, see Levine et al. 1996) show the typical low/high state behavior. At MJD 54 938 the flux sharply decreases from 0.30 Crab units to 0.10 Crab five days later. This endures until MJD 54 994 (51 days later) when there is a sharp increase lasting 4 days and reaching 0.40 Crab. During the low state, the flux shows a slow bowl-shaped change with a minimum halfway through of 0.06 Crab. The bowl is a little skewed, as though there is a slow increase over a time scale longer than the low state.
The 15 − 50 keV BAT data (red curve, as obtained from the Swift/BAT Hard X-ray Transient Monitor web site1; for an instrument description, see Barthelmy et al. 2005) show more or less opposite behavior, with slowly monotonically increasing fluxes during the ASM low state, from 0.05 Crab to 0.16 Crab at the end of the ASM low state.
Twelve bursts were detected during the long low state with three instruments. They are listed in Table 1. Three were detected with BAT, of which one triggered a slew that resulted in a detection of the next burst with XRT and BAT. Nine bursts were detected with the Proportional Counter Array (PCA). Three pairs of bursts had short wait times of 4.2 h (bursts 5 and 6), 3.3 h (bursts 9 and 10) and 1.9 h (bursts 11 and 12). Interestingly, the last burst was detected on the same day as the low state ended with the sharp increase in ASM flux (Fig. 1). The moment of change was not covered by PCA observations.
The nine bursts detected with the high-throughput PCA on RXTE provide much better statistical quality than the others. Therefore, we focus on these. During the low state, 4U 1820-30 was observed 27 times for a total of 134 ks with the RXTE PCA (ObsID 94090). Figure 1 shows the coverage.
The PCA (Jahoda et al. 2006) consists of 5 proportional counter units (PCUs) that are sensitive between 2 and 60 keV and combine to give an effective area of 6000 cm2 at 6 keV. The spectral resolution is about 18% full width at half maximum at 6 keV and the time resolution of the data products for 4U 1820-30 is typically 125 μs. It is rare that all PCUs are active at the same time, particularly at late times in the mission, but the central PCU number 2 (counting from 0) is almost always on. Table 1 indicates which PCUs were on per burst. A wide variety of data products can be requested from the PCA. For our analyses, we used standard-1 (0.125 s resolution and 1 channel for 2 − 60 keV photons) and standard-2 data (16 s resolution and 128 channels) and event mode data E_125us_64M_0_1s (125 μs resolution and 64 energy channels).
Figure 2 shows the light curves of all PCA bursts as drawn from the standard-1 data of all operational PCUs. It is immediately obvious that for bursts 4, 5, 6 and 7 the photon flux drops below the pre-burst level, resulting in the appearance of a precursor implying superexpansion. The photosphere expands while emitting at the Eddington limit. The increase in emission area is compensated by such a strong decrease in radiation temperature that the thermal spectrum shifts out of the PCA bandpass. Additionally, the accretion radiation is cut short by the expanding shell, either sweeping the inner accretion disk or covering the X-ray emitting part of the disk. We note that the XRT burst (number 10) is the first after burst 7, after six days, with sufficient statistical quality to see superexpansion if it were present, but none was detected. The 4 superexpansion bursts are annotated by solid vertical lines in Fig. 1 (three pairs of bursts are indistinguishable in the plot because they occur within a few hours).
We include in our analysis 2 other bursts from the total of 17 detected by the PCA in its 16 year mission (for a discussion of 14 of these, see Keek 2012), because they are the bursts with the least amount of expansion. The top two light curves in Fig. 2 are of these 2 bursts.
 |
Fig. 3 Time-resolved spectroscopy of burst number 7. The top panel shows the measured full-bandpass photon count rates for the PCA Xenon layers (solid line; units of 104 s-1) and propane layers (dashed line; units of 3000 s-1). The propane layer has a somewhat softer response and therefore better tracks the lower energy photons (e.g., Keek 2012). |
 |
Fig. 4 Color–color diagram of all PCU2 measurements of 4U 1820-30 between March 31, 1999, and March 31, 2011. Colors are defined as in Homan et al. (2010): soft color is the count rate in PCU2 channels 10−17 to 6−9 (corresponding to ranges 4.1−7.4 and 2.5−4.1 keV) and hard color is channels 24−40 to 18−23 (17.1−9.9 and 7.4−9.9 keV). Each point is for 128 s of data. Burst data have been excluded. The stars refer to the colors of the 128-s data stretches immediately before the 4 superexpansion bursts, the open circles to those of the other 5 bursts in the low state, squares to all other ordinary bursts and the large cross to the superburst. One ordinary burst is not included here. The burst recurrence time is 2.5 times larger at the group of circles with coordinates (1.95, 1.09) than at the group of stars with coordinates (2.05, 1.25). (This figure is available in color in the electronic form.) |
3. Analysis
3.1. Time-resolved burst spectral analysis
We divided each of the 11 PCA bursts in a number of time bins for which we extracted spectra. The time bins were chosen such as to be able to follow spectral changes promptly. A spectrum of the non-burst emission was extracted from standard-2 data in a time interval between 160 and 16 s prior to each burst. The non-source background (cosmic diffuse emission or particle-induced) was calculated for each extracted spectrum through pcabackest version 3.6 and taken into account in subsequent analyses. The non-burst source emission was modeled by a simple spectral shape (thermal bremsstrahlung) that adhered to the data. Response matrices were calculated for each observation using pcarsp version 11.7.1. Allowance was made for a systematic error of 1% per channel.
The burst spectra were modeled by a Planck function for black body radiation leaving free the temperature and emission area. Allowance was made for the non-burst emission to vary by including the spectral model as obtained for the pre-burst interval, with all parameters fixed, and leaving free its normalization. From the fitted Planck function, bolometric fluxes were calculated. For PRE phases, it is to be expected that the shape of the non-burst emission will change. We do not model this and keep it fixed. Therefore, the black body parameters are expected to be biased for these phases and we do not draw conclusions from them. We did not include low-energy absorption in our models, because the column density (NH ≈ 1 × 1021 cm-2; Kuulkers et al. 2003; Costantini et al. 2012) is too low to be noticeable with the PCA. Figure 3 shows an example of the fit results, for a burst that was measured with 3 PCUs (number 7, see Table 1).
The e-folding decay time τ was measured by fitting to the time history of the bolometric flux, beyond the peak, an exponential decay function. The “precursor time” was determined as the time between the peak of the flux and the start of the precursor. The “gap time” was estimated by investigating the light curve and estimating the time between the end of the precursor decay and the rise of the main burst phase. The burst fluence was determined by combining the integral of the fitted exponential decay function with the assumed fluence before the peak flux which is simply determined by the peak flux times the precursor time. It should be noted that this measures only the nuclear energy that is transformed into radiation. The nuclear energy may also transform into kinetic and gravitational energy of expelled material. A rough estimate of the energy lost to expelled material may be obtained by back-extrapolating the exponential decay to the time of the start of the precursor. We find that this amounts to between 10 and 40% of the (presumed) total nuclear energy. The values are largest for the four superexpansion bursts, mostly because the precursor times are longest there. The results of the measurements are in Table 1 and Fig. 5.
There is little variation in burst fluence and duration. The values vary between 3.2 and 3.6 × 10-7 erg cm-2, a 12% range with a relative 1σ uncertainty of about 5%, and is consistent with being constant (χ2 = 11.4 with 8 d.o.f. for a fit with a constant). The weighted average is (3.39 ± 0.05) × 10-7 erg cm-2. For a 8.4 ± 0.6 kpc distance, the fluence translates to a total energy of Eburst = (2.9 ± 0.4) × 1039 erg. If this is due to a pure layer of helium, with a 3α energy production of Enuc = 5.84 × 1017 erg g-1, the ignition column depth is yign ≈ Eburst/4πR2Enuc = (4.0 ± 0.7) × 108 g cm-2 for a canonical NS radius of 10 km. The upper limit on the variation in fluence (10%) is, unfortunately, not accurate enough to constrain the hydrogen abundance in a manner suggested by Cumming (2003).
3.2. Spectral modeling of accretion-powered radiation
To put the data in perspective, we show in Fig. 4 the commonly used (e.g., Homan et al. 2010) color–color diagram of all PCA data of 4U 1820-30 obtained after March 22, 1999. We exclude earlier data (including one burst) because early gain changes of the detectors preclude straightforward inference of colors. The data show two branches, commonly referred to as the banana state (lower branch) and island state (upper branch) (Hasinger & van der Klis 1989). All low states are equivalent to the island state. Also shown in Fig. 4 are the data points for the 17 PCA bursts detected in this period. These are taken from the 128-s intervals immediately prior to the bursts. Obviously, all bursts occur in the island state. Most notably, the superexpansion bursts occur in the extreme upper part of the island state.
It is difficult to find an unambiguous physical model for the spectra of the accretion radiation, or “persistent spectrum” as we shall call it. Low-resolution LMXB 2−30 keV spectra are most often modeled with a combination of (disk) black body and comptonization components, representative of the thermal radiation from the accretion disk, NS and/or boundary layer, and the comptonization in a corona in the neighborhood of that disk. The geometry of the corona is uncertain. We tested this model against the spectra of the complete observations for each burst, employing PCA standard product spectra. In particular, we employed a simple black body component and a Comptonized component according to the prescription by Titarchuk (1994). In XSPEC they are identified by model names “bbody” and “comptt”. We find that the evidence for the black body component is very uncertain in these data and that including it in the model degrades the accuracy with which comptonization parameters can be measured, due to strong coupling between the two components (both are very broad continua without unambiguous distinctive significantly detected spectral features). Therefore, we choose to ignore the black body component. This implies somewhat worse fits, but the 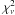 values remain fairly close to acceptable – between 1 and 3.9. The spectra are well represented by the comptonization component within a level of 3% per channel. We here present the fitted parameters, with errors that have been multiplied by a factor of
values remain fairly close to acceptable – between 1 and 3.9. The spectra are well represented by the comptonization component within a level of 3% per channel. We here present the fitted parameters, with errors that have been multiplied by a factor of 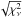 which would be equivalent with a fit with
which would be equivalent with a fit with 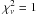 . The resulting 2 − 60 keV fluxes are provided in Table 1 and Fig. 5, plasma temperatures and optical depths (for a disk geometry) are provided in Fig. 5. We note that the energy of the seed photons is always far below the lower bandpass threshold and, thus, not constrained by the data. The spectral results show that the plasma temperature and optical depth vary significantly, the optical depth by a factor of 3, for 2 − 60 keV fluxes that are comparable.
. The resulting 2 − 60 keV fluxes are provided in Table 1 and Fig. 5, plasma temperatures and optical depths (for a disk geometry) are provided in Fig. 5. We note that the energy of the seed photons is always far below the lower bandpass threshold and, thus, not constrained by the data. The spectral results show that the plasma temperature and optical depth vary significantly, the optical depth by a factor of 3, for 2 − 60 keV fluxes that are comparable.
For a 8.4 kpc distance, the 2 − 60 keV fluxes translate to a 2 − 60 keV luminosity range of 3.3 to 5.7 × 1037 erg cm-2 s-1. For a canonical 10 km/1.4 M⊙ NS this is equivalent to a mass accretion rate of 2.8 to 4.8 × 10-9 M⊙ yr-1 or a specific mass accretion rate of 1.4 to 2.4 × 104 g s-1 cm-2.
3.3. Correlation study
We introduce a new empirical parameter to measure the amount and duration of expansion: the equivalent expansion duration (EED). The basis for this is the background-subtracted normalized light curve as shown for all bursts in Fig. 2. The EED is similarly defined as the equivalent width of absorption lines in spectra: it is the loss of photons due to the expansion, expressed in seconds that it would take to emit those photons at the level of the peak flux. The EED is a function of the bandpass and the effective area function, but this is of no consequence here because we use the same instrument in its full bandpass throughout. When superexpansion occurs, the light curve drops to negative values. This will push the EED to even higher values.
We plot various burst parameters against other burst parameters as well as accretion parameters in Fig. 5. The only strong one-to-one correlation exist between EED and the shape of the pre-burst spectrum as measured through the comptonizing plasma parameters.
4. Discussion
The data can be summarized as follows:
-
the fluence and decay rate of all bursts are equal within 6%, except for burst B. The helium content is presumably close to 100%, see below. This implies that the difference in photospheric expansion is unlikely to be the result of a difference in nuclear energy generated or ignition depth;
-
the amount of expansion is strongly correlated with the position of 4U 1820-30 on the color–color diagram in the sense that the 4 bursts with the strongest expansion (superexpansion) are at one extreme end of the island state and those with the smallest expansion at the opposite end. Equivalently, the EED is strongly correlated with the comptonization parameters;
 |
Fig. 5 Diagrams of burst parameters versus persistent emission parameters (left column, except bottom plot) and burst parameters versus burst parameters (right column). The plotted fluence is the measured fluence (see Table 1). The dashed blue data points refer to bursts A and B (top 2 light curves in Fig. 2). The 4 superexpansion bursts are plotted with thick red lines. For additional information a diagram is shown between plasma temperature and optical depth (bottom left plot). (This figure is available in color in the electronic form.) |
All changes in the persistent radiation are thought to be driven by changes in accretion rate. By how much does the accretion rate change? It is well known that fluxes do not directly translate to accretion rates. It appears to be true only on order-of-magnitude scales. One can think of various reasons why there is no 1-to-1 correspondence between flux and accretion rate: the measured persistent flux is not bolometric, the flux may have changing anisotropy factors and the radiation efficiency of transforming gravitational to radiation energy may change. Fortunately, our data provide an independent means of measuring Ṁ changes. The three recurrence times measured for X-ray bursts from 4U 1820-30 (see Sect. 2), in combination with the burst fluences, indicate that the accretion rate at burst 12 (without superexpansion) is 2.5 ± 0.2 times larger than at burst 6 (with super expansion; provided that all nuclear burning is unstable and that the nuclear and gravitational energy liberated per accreted nucleon is constant; i.e., the burst alpha parameter, see Lewin et al. 1993, is constant). For comparison, the 2 − 60 keV persistent flux ratio is only 1.4 ± 0.1 over these bursts. Note that this ratio difference supports the pure helium accretion hypothesis: the pure helium model in Cumming (2003) predicts that Ṁ should be 1.5 to 2 times higher than the value derived from the X-ray flux to have agreement with burst recurrence times and energies in 4U 1820-30.
Changes in spectral shape (as measured via for instance color in Fig. 4 or plasma temperature in Fig. 5) are generally attributed to changes in the geometry of the inner accretion flow, probably as a result of changes in accretion rate. The low/hard and high/soft states are very common in variable LMXBs, disregarding the nature of the accretor (NS or black hole; see reviews by van der Klis 2006; Remillard & McClintock 2006, respectively). These distinct states are usually accompanied by distinct Fourier spectra.
PCA timing and spectral studies of 4U 1820-30 have been the subject of previous papers. Zhang et al. (1998) and Bloser et al. (2000) report on twin kHz quasi-periodic oscillations (QPOs) and find that they, from the lower left banana state to the island state, gradually move in tandem to frequencies twice as small (see also Altamirano et al. 2005). In the banana state, the frequencies saturate (but see Méndez 2002). Bloser et al. (2000) modeled the PCA spectra by a combination of a black body and comptonization component and find that in the island state the plasma temperature increases and the optical depth decreases. We observe the same trend further into the island state (Fig. 5). This behavior is consistent with an interpretation that the QPOs originate in the inner accretion disk (e.g., van der Klis 2006) and that the inner edge of the accretion disk moves outward (recedes) from the lower left banana to the upper island state and that the cleared region is filled by a non-thermal more spherical advection-dominated (i.e., with less radiative efficiency) accretion flow. This is supported by the findings of Zdziarski et al. (2007a) mentioned in Sect. 1.
We note that we have searched for QPOs in the new data, but were able to find only a single, broad QPO around 540 Hz in the combined power spectra of the three observations with a soft color lower than 2.0 (i.e. roughly middle of the island state). A comparison with the power spectra of 4U 1830-30 analyzed in Altamirano et al. (2005) suggests that this QPO is the upper kHz QPO. We note that our data are statistically less constraining than those of Altamirano et al. (2005) due to a smaller number of active PCUs. The other five observations, with soft colors higher than 2.0, extend to more extreme parts of the island state, in which the inner accretion disk edge possibly moves out even further. No high frequency QPO is found in these observations, although indications for a broad (Q = 0.6) feature around 280 Hz are seen.
Expansion into the circumstellar medium will become easier when the ram pressure of the accretion flow becomes smaller. This may happen if the accretion rate decreases or if the geometry changes. The latter may occur, for example, if the accretion is channeled through a disk instead of spherically. A large part of the solid angle as seen from the NS will then open up and allow free expansion. However, all bursts that we observe occur during the island state, when the inner flow is thought to be spherical all the time and the inner edge of the accretion disk is thought to be at some distance from the NS. If the frequency is Keplerian in nature, a factor of 2 decrease in frequency (see above), implies a factor of 22/3 = 1.6 increase in radius from banana to island state.
The change in expansion factor is, therefore, most likely to be directly related to the accretion rate. In the following we attempt to find quantitative support for this. The ram pressure of free falling spherical accretion can be expressed as (Frank et al. 1992) 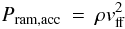 (1)with ρ the density of the infalling matter and vff the free-fall velocity
(1)with ρ the density of the infalling matter and vff the free-fall velocity 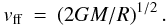 (2)The density can be derived from the continuity equation
(2)The density can be derived from the continuity equation 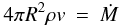 (3)so that Eq. (1) becomes
(3)so that Eq. (1) becomes 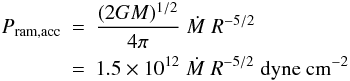 (4)for a 1.4 M⊙ NS, with Ṁ in g s-1 and R in cm.
(4)for a 1.4 M⊙ NS, with Ṁ in g s-1 and R in cm.
The ram pressure of a shell leaving the NS is 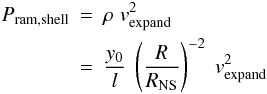 (5)where y0 is the initial column thickness of the shell, l the geometrical thickness and vexpand the expansion velocity of the shell.
(5)where y0 is the initial column thickness of the shell, l the geometrical thickness and vexpand the expansion velocity of the shell.
The shell will be able to leave the NS surface (R = RNS) if Pram,shell > Pram,acc or if 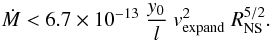 (6)Once the shell has left the NS, it depends on how the shell thickness evolves whether its ram pressure will remain above that of the accretion flow. For a constant shell thickness it does, but for a shell thickness that grows stronger than R0.5 it does not.
(6)Once the shell has left the NS, it depends on how the shell thickness evolves whether its ram pressure will remain above that of the accretion flow. For a constant shell thickness it does, but for a shell thickness that grows stronger than R0.5 it does not.
What values can be applied for the parameters in Eq. (6)? We use the initial rate of increase in the black body radius (see Fig. 3) as a rough estimate of the expansion velocity: vexpand ~ 103 km s-1. The shell column thickness y0 may be derived from the superexpansion duration (see in ’t Zand & Weinberg 2010). It takes about 1 s for the shell to become transparent (at a column thickness of 1 g cm-2) due to dilution that goes as R-2. During that time the shell has expanded to a radius of vexpand × t ~ 103 km. Back extrapolating the dilution implies that y0 ~ 104 g cm-2. This is 10-4 times the ignition of yign ≈ 4 × 108 g cm-2. For the geometrical layer thickness one may use the pressure scale height of a helium atmosphere which is ~33 cm (e.g., Piro & Bildsten 2007). For RNS = 106 cm, Eq. (6) predicts that the shell will be able to lift off if Ṁ ≲ 3 × 10-5 M⊙ yr-1. This is a very loose constraint which is fullfilled under any practical circumstance, 104 times larger than measured for 4U 1820-30. This may be due to the relative arbitrariness of the chosen parameter values. For instance, l may increase substantially during the expansion and vexpand may evolve. If l is ~100 m instead of 33 cm and vexpand 3 times smaller, the constraint in Eq. (6) would be similar to the observed Ṁ. Furthermore, we have used a very simple approach (isotropic spherical free-fall accretion, isotropic shell expansion, constant shell velocity and thickness, ignoring radiation pressure, and ignoring GR corrections). The conclusion is that a quantitative verification of our proposed scenario of the superexpansion behavior in 4U 1820-30 needs detailed modeling which is outside the scope of the present paper.
The constant ignition depth would imply that the expelled shell thickness is similar in all bursts, but that the amount of distance traveled by the shell differs. Usually, it does not travel far, perhaps less than 100 km, before falling back. Only for the superexpansion bursts does it travel far enough to move out of the X-ray band. This is supported by the fact that there is always evidence for a shell, even if there is no superexpansion: all bursts from 4U 1820-30 show a drop in flux within 1 s from the burst onset. This idea is supported by the slower decay of the initial spike for bursts without superexpansion. The shell is moving slower and does not reach high altitudes (i.e., in Fig. 2 the spikes drop the fastest in the superexpansion case).
We note that the superburst in 4U 1820-30 also has superexpansion while it is on the opposite side of the island state in the color–color diagram (Fig. 4). A new analysis of this event (Keek 2012) shows that the energy contained in the precursor is larger than those in ordinary bursts from 4U 1820-30, which may be explained by a shock induced by the carbon detonation and reaching the photosphere. Therefore, the driving of the expansion occurs differently from that in ordinary bursts from 4U 1820-30 and the shell ram pressure is likely to be different.
5. A note on the lack of X-ray bursts in the banana state
As an addendum, we address a peculiar phenomenon in our measurements: X-ray bursting activity seems to react more rapidly to changes in the accretion-induced radiation than expected from crustal heating. The first burst after the flux arrives in the low state is detected within 5 days. The last burst before the persistent flux returns back to the high state is detected only two days before. No bursts were detected in PCA measurements within the next 8 days with a total exposure of 10.4 ks while the recurrence time between the two last bursts was 6.8 ks s, nor with Swift observations. We made a similar but more significant measurement in 2011, when we followed up a PCA burst detection with a 1.2 d long continuous Chandra observation starting 1.3 d after the burst. The jump to the high state occurred in the 1.3 d time frame between both observations. No burst was detected in RXTE data and Chandra data within 2.5 d after the burst with a total exposure time of 1.4 d. In the same time frame there were 0.3 d of exposure time with Swift/BAT, without any X-ray burst detection. We note that a similarly sudden stop of bursting activity was observed in IGR J17473-2721 (Chenevez et al. 2011).
The data suggest that bursting activity stops as suddenly as the low state does. This is peculiar. In the common picture of 4U 1820-30 if X < 0.03 (Cumming 2003), the bursting activity is driven by the temperature of the crust. The crust is heated through pycnonuclear reactions and electron-capture reactions (e.g., Gupta et al. 2007; Haensel & Zdunik 2008) whose rates are a direct function of the accretion rate. However, the thermal time scale of the crust is of order months (e.g., Brown & Cumming 2009), so there should be a delay between a change in the accretion rate and one in the bursting activity. Therefore, the prompt lack of X-ray bursts in the high state of 4U 1820-30, and vice versa, is not explained by stabilization of helium burning by crustal heating.
An alternative explanation might be that in the banana state the inner edge of the accretion disk is probably closer to the NS, see Sect. 4. Depending on the inclination angle and thickness of the inner disk and/or boundary layer, this is perhaps sufficient to block our view of the NS and make X-ray bursts invisible. A test of this hypothesis would be the detection of partly obscured X-ray bursts with a few-hours recurrence times. This has never been observed in 4U 1820-30, despite abundant coverage throughout the history of X-ray astronomy. Furthermore, X-ray bursts have been observed in banana states of other sources (e.g., van der Klis et al. 1990; Muno et al. 2000). Therefore, this explanation is unlikely.
Chenevez et al. (2011) proposed another explanation for the sudden stop of bursting activity in IGR J17473-2721: the occurrence of a superburst during a data gap. However, given the long recurrence time of superbursts (on the order of 1 yr for persistent sources and longer for transients such as IGR J17473-2721), this appears to us an unlikely scenario.
A more promising explanation seems that during the high state the primary heating of the flash layers does not occur by the crust, but by a heat source at a shallower depth. A thermal time scale of ≲ 1 d applies to column depths of ≲1012 g cm-2 (Brown & Cumming 2009) which is in the NS ocean and outside the crust. The heat source is most likely not of nuclear origin. For example, it cannot be CNO burning, because there is no significant abundance of hydrogen in the accreted material. Inogamov & Sunyaev (2010) suggest that for accretion rates in excess of a few percent of the Eddington limit, rotational heating may stabilize helium burning. In this model, the braking of a hypersonic azimuthal flow in the accretion disk by the NS atmosphere results in an additional heat source. Perhaps the accretion flow geometry in the banana state of this source allows for more efficient transfer of angular momentum from the disk to the NS envelope, boosting this heat source and quenching the bursts. Quantitative assessment of this hypothesis requires 2-dimensional multi-zone simulations of nuclear burning, primarily as a function of NS spin, accretion composition and flow geometry. Unfortunately, the NS spin has not been measured yet for 4U 1820-30.
Acknowledgments
We thank Nevin Weinberg (MIT), Ed Brown (MSU) and Tullio Bagnoli (SRON) for useful discussions. J.Z. and L.K. are members of an International Team in Space Science on type-I X-ray bursts sponsored by the International Space Science Institute (ISSI) in Bern and thank ISSI for the hospitality during part of this work. We are grateful to the anonymous referee for constructive comments that helped improve the paper. L.K. is supported by the Joint Institute for Nuclear Astrophysics (JINA; grant PHY08-22648), a National Science Foundation Physics Frontier Center. This paper utilizes data from the Multi-INstrument Burst ARchive (MINBAR). RXTE/ASM and Swift/BAT results were provided by the RXTE/ASM and Swift/BAT team, respectively.
References
- Altamirano, D., van der Klis, M., Méndez, M., et al. 2005, ApJ, 633, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, S. F., Margon, B., Deutsch, E. W., Downes, R. A., & Allen, R. G. 1997, ApJ, 482, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., & Strohmayer, T. E. 2004, ApJ, 602, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Barthelmy, S. D., Barbier, L. M., Cummings, J. R., et al. 2005, Space Sci. Rev., 120, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L. 1998, in The many faces of neutron stars, eds. A. Alpar, L. Buccheri, & J. van Paradijs, NATO ASI (Dordrecht: Kluwer), 419 [Google Scholar]
- Bloser, P. F., Grindlay, J. E., Kaaret, P., et al. 2000, ApJ, 542, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., & Cumming, A. 2009, ApJ, 698, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Cavecchi, Y., Patruno, A., Haskell, B., et al. 2011, ApJ, 740, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-P., Zhang, S., Torres, D. F., et al. 2011, A&A, 534, A101 [Google Scholar]
- Chenevez, J., Altamirano, D., Galloway, D. K., et al. 2011, MNRAS, 410, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, Y., & Grindlay, J. E. 2001, ApJ, 563, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Cornelisse, R., in ’t Zand, J. J. M., Verbunt, F., et al. 2003, A&A, 405, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costantini, E., Pinto, C., Kaastra, J. S., et al. 2012, A&A, 539, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cumming, A. 2003, ApJ, 595, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Altamirano, D., & Wijnands, R. 2012, The Astronomer’s Telegram, 4219, 1 [NASA ADS] [Google Scholar]
- Ebisuzaki, T., Hanawa, T., & Sugimoto, D. 1983, PASJ, 35, 17 [NASA ADS] [Google Scholar]
- Farrell, S. A., Barret, D., & Skinner, G. K. 2009, MNRAS, 393, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. 1992, Accretion power in astrophysics, 2nd edn. (Cambridge University Press) [Google Scholar]
- Fujimoto, M. Y., Hanawa, T., & Miyaji, S. 1981, ApJ, 247, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Grindlay, J., Gursky, H., Schnopper, H., et al. 1976, ApJ, 205, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Grindlay, J. E., Marshall, H. L., Hertz, P., et al. 1980, ApJ, 240, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Brown, E. F., Schatz, H., Möller, P., & Kratz, K.-L. 2007, ApJ, 662, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
- Hoffman, J., Lewin, W., Doty, J., et al. 1978, ApJ, 221, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., van der Klis, M., Fridriksson, J. K., et al. 2010, ApJ, 719, 201 [NASA ADS] [CrossRef] [Google Scholar]
- in ’t Zand, J. J. M., & Weinberg, N. N. 2010, A&A, 520, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J., Serino, M., Kawai, N., & Heinke, C. 2011a, The Astronomer’s Telegram, 3625, 1 [NASA ADS] [Google Scholar]
- in ’t Zand, J. J. M., Galloway, D. K., & Ballantyne, D. R. 2011b, A&A, 525, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 2010, Astron. Lett., 36, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L. 2012, ApJ, 756, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Kuulkers, E., den Hartog, P. R., in ’t Zand, J. J. M., et al. 2003, A&A, 399, 663 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuulkers, E., in ’t Zand, J. J. M., & Lasota, J.-P. 2009, A&A, 503, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levine, A. M., Bradt, H., Cui, W., et al. 1996, ApJ, 469, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Linares, M., Altamirano, D., Chakrabarty, D., Cumming, A., & Keek, L. 2012, ApJ, 748, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez, M. 2002, in Proc. 9th Marcel Grossman Meeting, eds. V. Gurzadyan, R. Jantzen, & R. Ruffini (World Scientific) [arXiv:astro-ph/0207278] [Google Scholar]
- Muno, M. P., Fox, D. W., Morgan, E. H., & Bildsten, L. 2000, ApJ, 542, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Muno, M. P., Galloway, D. K., & Chakrabarty, D. 2004, ApJ, 608, 930 [Google Scholar]
- Nelson, L. A., Rappaport, S. A., & Joss, P. C. 1986, ApJ, 304, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Palmer, D. 2011, The Astronomer’s Telegram, 3663, 1 [NASA ADS] [Google Scholar]
- Piro, A. L., & Bildsten, L. 2007, ApJ, 663, 1252 [NASA ADS] [CrossRef] [Google Scholar]
- Priedhorsky, W., & Terrell, J. 1984, ApJ, 284, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Ma, C. P., Joss, P. C., & Nelson, L. A. 1987, ApJ, 322, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Stella, L., Priedhorsky, W., & White, N. E. 1987, ApJ, 312, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, New views of thermonuclear bursts (Compact stellar X-ray sources), 113 [Google Scholar]
- Strohmayer, T. E., & Brown, E. F. 2002, ApJ, 566, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, E., Ferraro, F. R., & Origlia, L. 2004, MNRAS, 351, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- van der Klis, M. 2006, Rapid X-ray Variability, eds. W. H. G. Lewin, & M. van der Klis (Cambridge University Press), 39 [Google Scholar]
- van der Klis, M., Hasinger, G., Damen, E., et al. 1990, ApJ, 360, L19 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., Penninx, W., & Lewin, W. H. G. 1988, MNRAS, 233, 437 [Google Scholar]
- van Paradijs, J., Dotani, T., Tanaka, Y., & Tsuru, T. 1990, PASJ, 42, 633 [NASA ADS] [Google Scholar]
- Watts, A. L. 2012, ARA&A, 50, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Gierliński, M., Wen, L., & Kostrzewa, Z. 2007a, MNRAS, 377, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Wen, L., & Gierliński, M. 2007b, MNRAS, 377, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, W., Smale, A. P., Strohmayer, T. E., & Swank, J. H. 1998, ApJ, 500, L171 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the 3 − 12 keV photon flux relative to that of the Crab source (black curve; RXTE-ASM data) and the 15 − 50 keV photon flux with respect to 0.18 times that of the Crab source (red dash-dotted curve; Swift/BAT data). Vertical lines indicate the bursts detected, solid for those with superexpansion and dashed for those without. Three bursts are indistinguishable because they have too short recurrence times to be visible on this scale (see Table 1). The solid horizontal lines indicate the days that the PCA observed 4U 1820-30 under ObsID 94090. The solid vertical lines in the top left corner indicate the 2σ uncertainties. |
| In the text | |
 |
Fig. 2 Measured photon rate time histories for the 9 PCA bursts, from bottom to top chronologically, supplemented with the 2 PCA bursts that are lowest in the color–color diagram (Fig. 4). The subtracted background level is measured from a 150 s time interval prior to the burst and the curves have been normalized to the peak rate. For guidance, the zero level has been indicated by a dotted line. |
| In the text | |
 |
Fig. 3 Time-resolved spectroscopy of burst number 7. The top panel shows the measured full-bandpass photon count rates for the PCA Xenon layers (solid line; units of 104 s-1) and propane layers (dashed line; units of 3000 s-1). The propane layer has a somewhat softer response and therefore better tracks the lower energy photons (e.g., Keek 2012). |
| In the text | |
 |
Fig. 4 Color–color diagram of all PCU2 measurements of 4U 1820-30 between March 31, 1999, and March 31, 2011. Colors are defined as in Homan et al. (2010): soft color is the count rate in PCU2 channels 10−17 to 6−9 (corresponding to ranges 4.1−7.4 and 2.5−4.1 keV) and hard color is channels 24−40 to 18−23 (17.1−9.9 and 7.4−9.9 keV). Each point is for 128 s of data. Burst data have been excluded. The stars refer to the colors of the 128-s data stretches immediately before the 4 superexpansion bursts, the open circles to those of the other 5 bursts in the low state, squares to all other ordinary bursts and the large cross to the superburst. One ordinary burst is not included here. The burst recurrence time is 2.5 times larger at the group of circles with coordinates (1.95, 1.09) than at the group of stars with coordinates (2.05, 1.25). (This figure is available in color in the electronic form.) |
| In the text | |
 |
Fig. 5 Diagrams of burst parameters versus persistent emission parameters (left column, except bottom plot) and burst parameters versus burst parameters (right column). The plotted fluence is the measured fluence (see Table 1). The dashed blue data points refer to bursts A and B (top 2 light curves in Fig. 2). The 4 superexpansion bursts are plotted with thick red lines. For additional information a diagram is shown between plasma temperature and optical depth (bottom left plot). (This figure is available in color in the electronic form.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


