| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 16 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201219695 | |
| Published online | 06 November 2012 | |
Characterisation of young stellar clusters⋆
Universidade de São Paulo, IAG, Departamento de Astronomia, Brazil
e-mail: thaisfi@astro.iag.usp.br
Received: 28 May 2012
Accepted: 4 September 2012
Aims. Several embedded clusters are found in the Galaxy. Depending on the formation scenario, most of them can evolve to unbounded groups that are dissolved within 10 Myr to 20 Myr. A systematic study of young stellar clusters that show distinct characteristics provides interesting information on the evolutionary phases during the pre-main sequence. To identify and to understand these phases we performed a comparative study of 21 young stellar clusters.
Methods. Near-infrared data from 2MASS were used to determine the structural and fundamental parameters based on surface stellar density maps, radial density profile, and colour–magnitude diagrams. The cluster members were selected according to their membership probability, which is based on the statistical comparison with the cluster proper motion. Additional members were selected on the basis of a decontamination procedure that was adopted to distinguish field stars found in the direction of the cluster area.
Results. We obtained age and mass distributions by comparing pre-main sequence models with the position of cluster members in the colour–magnitude diagram. The mean age of our sample is ~ 5 Myr, where 57% of the objects is found in the 4–10 Myr range of age, while 43% is <4 Myr old. Their low E(B − V) indicate that the members are not suffering high extinction (AV < 1 mag), which means they are more likely young stellar groups than embedded clusters. Relations between structural and fundamental parameters were used to verify differences and similarities that could be found among the clusters. The parameters of most of the objects show the same trends or correlations. Comparisons with other young clusters show similar relations among mass, radius, and density. Our sample tends to have larger radius and lower volumetric density than embedded clusters. These differences are compatible with the mean age of our sample, which we consider intermediate between the embedded and the exposed phases of the stellar clusters evolution.
Key words: open clusters and associations: general / stars: pre-main sequence / stars: fundamental parameters / infrared: stars
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
It is generally known that most stars are formed in groups or clusters. However, detailed studies of the initial processes of star formation are restricted to isolated dense cores of clouds (Shu et al. 1987; 2004).
The first stages of multiple star formation is usually evaluated through millimetric surveys, which successfully probe the scenario of stellar cluster formation. Based on 1.2 mm data of the Mon OB1 region, for instance, Peretto et al. (2005) discovered 27 proto-stellar cores with diameters of about 0.04 pc and masses ranging from 20 M⊙ to 40 M⊙ associated to the young stellar cluster NGC 2264. These results reveal the physical conditions for multiple massive star formation in a region that shows a wide range of masses (Dahm 2008) and ages (Flaccomio et al. 1997; Rebull et al. 2002) indicating the occurrence of a large variety of young stellar groups.
In addition to millimetric studies, the evolution during the pre-main sequence (pre-MS) is more closely surveyed by using infrared data. Particularly, near-infrared (NIR) provides information about the circumstellar structure of the cluster members, whose physical conditions are directly related to the pre-MS evolutionary stage of the star. Gregorio-Hetem et al. (2009), for instance, have used X-ray results of sources detected in CMa R1, combined with NIR and optical data, to identify the young population associated to this star-forming region. They studied two young clusters with similar mass function, but one of them is older than the other by at least a few Myr. A mixing of populations seems to occur in the inter-cluster region, possibly related to sequential star formation.
Systematic studies of young stellar clusters can directly probe several fundamental astrophysical problems, such as the formation and evolution of open clusters, and more general problems, like the origin and early evolution of stars and planetary systems (Adams et al. 2006; Adams 2010).
Kharchenko et al. (2005) present angular sizes of cluster core and “coronae” for a sample of 520 Galactic open clusters, and Piskunov et al. (2007) revised these data to obtain tidal radius and core size estimated by fitting King profile to the observed density distribution. Carpenter (2000) used 2MASS data to derive surface density maps of stellar clusters associated to molecular clouds, determining cluster radius and number of members based on the distributed population. Adams et al. (2006) explored the relations between cluster radius and stellar distribution in order to study the dynamical evolution of young clusters. Numerical simulations were used to reproduce different initial conditions of cluster formation. The statistical calculations developed by Adams et al. (2006) were based on cluster membership and cluster radius correlations observed in the samples presented by Carpenter (2000) and Lada & Lada (2003), who compiled the first extensive catalogue of embedded clusters providing parameters such as mass, radius, and number of members.
Lada & Lada (2003, hereafter LL03), verified the occurrence of several embedded clusters within molecular clouds in the Galaxy. However, most of these objects probably lose their dynamical equilibrium, which would dissolve the group and turn it into field stars.
Pfalzner (2009) studied the evolution of a sample of 23 massive clusters younger than 20 Myr and suggests two distinct sequences. Depending on size and density, a bimodal distribution is found for the cluster size as a function of age. Based on the mass-radius and density-radius dependence observed in the sample from LL03, Pfalzner (2011) proposes a scenario of sequential formation of “leaky” (exposed) massive clusters. On the other hand, unlike the time sequence proposed by Pfalzner (2011), the relations of cluster properties can be interpreted as formation condition (Adams et al. 2006; Adams 2010).
The structure of embedded clusters traces the physical conditions of their star-forming processes, since the origin and the evolution of stellar clusters are related to the distribution of dense molecular gas in their parental cloud. LL03 propose two basic structural types, according to the cluster surface density. Classical open clusters are characterised by a high concentration in their surface distribution, whose radial profile is smooth and can be reproduced by simple power-law functions or King-like (isothermal) potential. This type of embedded cluster is considered centrally concentrated. On the other hand, hierarchical type clusters exhibit surface density distribution with multiple peaks and show significant structure over a wide range of spatial scale. Although there are clear examples of both types of structures, their relative frequency is unknown.
The main goal of the present work is to characterise a large sample of young stellar clusters and to perform a comparative study aiming to verify their similarities and differences, which are related to their evolutionary stages in the pre-MS. The methods adopted by us have been commonly used in the characterization of open clusters like those developed by Bonatto & Bica (2009a), for instance. Stellar density maps are built from NIR data in order to derive parameters on the basis of radial density profile. These parameters define the structure of the cluster, which is related to its origin and evolution.
The analysis based on radial density profile is unprecedented to 86% of our sample. Considering the lack of systematic studies comparing pre-MS stellar clusters, distributed in different galactic regions, the present work aims to provide sets of structural and fundamental parameters, determined in a uniform data analysis that may contribute to the discussion on the origin of stellar groups.
In Sect. 2 we describe the sample by presenting the selection criteria and the decontamination method for distinguishing cluster members from field stars. Section 3 is dedicated to determining the structural parameters, which are used to accurately estimate distance, age, and mass that are presented in Sect. 4. A comparative analysis is performed in Sect. 5, while Sect. 6 summarises the results and the main conclusions. Finally, Appendix A displays all the plots of the entire sample.
List of clusters and their structural parameters.
2. Description of the sample
Several compilations of open stellar clusters are available in the literature, for example Lynga (1987), Loktin (1994), Mermilliod (1995), LL03, Kharchenko et al. (2005), Piskunov et al. (2007), WEBDA1 and DAML2 (Dias et al. 2002; 2006). In Sect. 2.1 we present the criteria used to select the clusters, while Sect. 2.2 describes the method used to exclude field stars that were found in the same direction as the cluster.
2.1. Cluster selection and observational data
Focussing our study on pre-MS objects, we used the DAML catalogue to select young stellar clusters with ages in the 1–20 Myr range. Distances smaller than 2 kpc were used as selection criterion in order to ensure the good quality of photometric data. Even though our selection is limited to southern objects, they are distributed in different star-forming regions, which enabled us to compare diverse environments. Table 1 gives the list of 21 selected clusters.
A membership probability (P) estimated on the basis of proper motion is given by DAML. To select the stars belonging to the clusters, the values P > 50% were adopted to indicate the possible members, hereafter denoted by P50.
To confirm the cluster centre coordinates available in the literature, we evaluated the distribution of number of stars as a function of right ascension (α) and declination (δ). Gaussian profiles were fitted to these distributions, in order to estimate their centroid. A good agreement with the literature was found, within the errors estimated by the fitting that are Δδ ~ 1 arcmin and 0.75′ < Δα < 2.25′. Table 1 gives the error on α indicated in between parenthesis.
The NIR data, which provide maximum variation among colour–magnitude diagrams (CMDs) of clusters with different ages (Bonatto et al. 2004), were extracted from 2MASS (All Sky Catalogue of Point Sources – Cutri et al. 2003). The JHKs magnitudes were searched for all stars located within a radius of 30 arcmin from the cluster centre. Only good accuracy photometric data were used in our analysis by selecting objects with AAA quality flags that ensure the best photometric and astrometric qualities (Lee et al. 2005).
2.2. Field-star decontamination
Most of our clusters are projected against dense fields of stars in the Galactic disk, making it difficult to distinguish the cluster members. The first step in determining the structural and fundamental parameters is to proceed with field-star decontamination.
This process is based on statistical analysis by comparing the stellar density of the cluster area with a reference region, near to the cluster, according to their characteristics in the CMD. The decontamination algorithm was employed as follows.
-
The whole range of magnitudes and colours is divided intothree-dimensional cells (J, J − H and J − KS).
-
For each cell (i), the stellar density of field stars (σf = nrf/af) is obtained by counting the number of stars (nf) appearing in the reference region (af).
-
Similarly, the total stellar density (σt = nt/ac) is obtained by counting all stars (nt) in the cluster area (ac).
-
The number of field stars (nf), appearing in the cluster area, that have colours and magnitude similar to those estimated in the reference region is calculate by
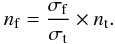 (1)
(1) -
Finally the number of field stars in the cluster area is randomly subtracted in each cell, leaving N = Σi (nti − nfi) members of the cluster.
To minimize errors introduced by the parameters choice and uncertainties on 2MASS data, the decontamination algorithm is applied to several grids by adopting three different positions in the CMD. By defining a cell size ΔJ = 0.5 mag, the algorithm uses a grid starting at Ji and two other grids starting at 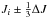 . This dithering is also done for both colours, Δ(J − H) = Δ(J − KS) = 0.1 mag, providing 27 different results for each star. In this way, we obtain the probability that a given object should be considered a field star. All possible members (P50) have 0% probability of being a field star.
. This dithering is also done for both colours, Δ(J − H) = Δ(J − KS) = 0.1 mag, providing 27 different results for each star. In this way, we obtain the probability that a given object should be considered a field star. All possible members (P50) have 0% probability of being a field star.
We considered as candidate members (denoted by P?) those stars that were not removed by the field-star decontamination. Both P50 and P? members were used, but they are weighted differently in the estimation of distance and age, presented in Sect. 4.2.
The adopted decontamination procedure has been used in studies of several types of clusters: objects showing low contrast relative to the field stars (Bica & Bonatto 2005), embedded clusters (Bonatto et al. 2006), and young clusters (Bonatto et al. 2006), among others.
 |
Fig. 1 Left: stellar surface-density map (σ (stars/arcmin2)) obtained for the region of 30 arcmin around Lynga 14. The comparison field-star area is indicated by dashed lines, while the full line indicates the cluster area. Center: a zoom of the σ map uses crosses to indicate the position of objects with membership probability P > 70%. Right: the distribution of the stellar density as a function of radius. The best fitting of observed radial density profile, indicated by the full line, was obtained by using the model from King (1962). A thin (red) line indicates the background density (σbg). |
3. Structural parameters
The structural parameters were determined on the basis of stellar surface density, derived from stellar surface-density maps and radial density profiles that are detailed in Sects. 3.1 and 3.2.
The first step in calculating the stellar surface density is to enhance the contrast between surface distribution of cluster members and field stars by using a colour–magnitude filter.
Pre-MS isochrones were adopted to establish the colour–magnitude filter limiting a CMD region that should only contain cluster members. Once the observed magnitudes were unreddened, using the visual extinction given in the literature, we disregarded all the objects lying out of the range defined by the colour–magnitude filter. This filter is successful at accentuating the structures and reducing the fluctuations caused by the presence of field stars (Bica & Bonatto 2005).
3.1. Stellar surface-density maps
We obtained spatial distribution maps of the stellar surface density (σ) given by the number of stars per arcmin2 for the clusters and their surroundings. Appendix A presents the results for the whole sample, while Fig. 1 shows the map derived for the cluster Lynga 14, as illustration. The left-hand panel shows the entire studied area, whose surface density was calculated in cells of |Δ(αcos(δcenter))| = |Δδ| = 2.5 arcmin2, where Δα and Δδ are the steps on right ascension and declination, respectively.
A zoom view (Fig. 1 central panel) displays a more detailed structure that was obtained by using smaller cells (1.0 arcmin2) for the star-counting process. Following the classification proposed by LL03, the surface density maps were visually inspected to characterise the clusters. The last column of Table 1 indicates if the type is hierarchical (H) or centrally concentrated (CC), according to the definition discussed in Sect. 1. About 38% of the sample (8/21) shows a single major peak of density being classified by CC. Half of the sample (10/21) has multiple peaks and was considered H type, while three objects presenting filamentary density distributions, have undefined type (marked as “??” in Table 1).
3.2. Radial density profile
Aiming to quantify the stellar distribution of the clusters, we evaluated their radial density profile (RDP) by using concentric rings to calculate the surface density. Some of the structural parameters were obtained by fitting a theoretical RDP to the observed data. The adopted function is similar to the empirical model from King (1962), given by 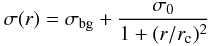 (2)where σ(r) is the stellar surface density (stars/arcmin2), r the radius (arcmin) of each concentric annulus used in the star counting, and σ0 and rc are the density and the radius of the cluster core, respectively. The average density measured in the reference region (σbg) was calculate separately, in order to diminish the number of free parameters in the RDP fitting.
(2)where σ(r) is the stellar surface density (stars/arcmin2), r the radius (arcmin) of each concentric annulus used in the star counting, and σ0 and rc are the density and the radius of the cluster core, respectively. The average density measured in the reference region (σbg) was calculate separately, in order to diminish the number of free parameters in the RDP fitting.
Figure 1 (right panel) shows an example of observed radial distribution of surface density and the best fitting of the King’s profile, which was obtained by adopting the χ2 method based on the parameters σ0 and rc. Aiming to determine the cluster radius (R) more accurately, we verified the point where the cluster stellar density reaches the background density. Figure 1 displays a red line corresponding to σ = σbg, which was used to find R.
A quantitative estimation of how compact the cluster is can be obtained from the density-contrast parameter proposed by Bonatto & Bica (2009a): 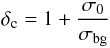 (3)where compact clusters have 7 ≤ δc ≤ 23. According to this criterion, only NGC 6613 can be considered compact (δc ~ 10).
(3)where compact clusters have 7 ≤ δc ≤ 23. According to this criterion, only NGC 6613 can be considered compact (δc ~ 10).
Two other parameters commonly used in comparative analysis are the average density (⟨ n∗ ⟩ ), calculated by dividing the total number of observed members by the cluster area, and the ratio of core size to cluster radius (rc/R). We could expect low values of rc/R for the younger clusters, since their members would not have had enough time to disperse away from the centre. Table 1 gives the structural parameters and the uncertainties derived from the RDP fitting.
Three of our objects are found in the catalogue of Galactic open clusters presented by Piskunov et al. (2007). Based on proper motion, they identified bright stars (V < 14 mag) and used the radial profile of the region containing possible members (P = 14–61%) to define the “coronae” radius of the cluster, while the concentration of the probable members (P > 61%) defines the core radius (Kharchenko et al. 2005). Therefore, their sample is five to ten times less numerous than our sample, which includes low-mass stars detected by 2MASS. Besides, we focussed on the main stellar distribution of the cluster (radius <6′), while they studied larger areas (radius ~ 15′), seeking the tidal radius (Rt).
Fundamental parameters.
These different definitions of cluster radii imply systematically lower values when comparing our results with the structural parameters listed by them. However, these results cannot be directly compared because we are not dealing with the same kind of stellar groups.
In fact, the tidal radius obtained by Piskunov et al. (2007) for NGC 6604 (Rt = 8.8 pc), NGC 2362 (6.2 pc), and Stock 13 (7 pc) is more compatible with the tidal radius that we estimated for these clusters: rt = 7.7 ± 2.3, 8.1 ± 2.4, and 7.0 ± 2.1, respectively, by adopting the expression used by Saurin et al. (2012): 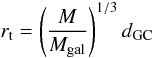 (4)where M is the cluster mass, Mgal the Galactic mass, and dGC the Galactocentric distance, given by
(4)where M is the cluster mass, Mgal the Galactic mass, and dGC the Galactocentric distance, given by 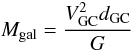 (5)where VGC = 254 ± 16 km s-1 is the circular rotation velocity of the Sun at RGC = 8.4 ± 0.6 kpc (Reid et al. 2009).
(5)where VGC = 254 ± 16 km s-1 is the circular rotation velocity of the Sun at RGC = 8.4 ± 0.6 kpc (Reid et al. 2009).
On the other hand, the R ∝ N0.5 dependence discussed in Sect. 5.1 distinguishes the sample studied by Piskunov et al. (2007) from other young clusters presenting size and membership relations similar to our sample. It seems to be more consistent when comparing the cluster radius that we obtained with the core radius obtained by Piskunov et al. (2007), given as notes in Table 1.
4. Revisiting the fundamental parameters
Adopting the same procedure as described in Sect. 2.2, the field-star decontamination was refined by using the accurate estimative of cluster radius. The size of the reference region was also re-evaluated according to the cluster area, allowing us to define the sample of candidate members more closely. In Sect. 4.1 we adopt the extinction available in the literature to correct the observed colours, which were fitted to the MS intrinsic colours. An iterative fitting process was adopted to accurately determine E(B − V). Even though the distance and age of our clusters are available in the literature, these parameters were checked by us in light of the well-determined structural parameters, as described in Sect. 4.2.
 |
Fig. 2 Left: colour–colour diagram for Lynga 14. The MS and the ZAMS are indicated by full lines, while the locus of giant stars is represented by a dotted line. Reddening vectors from Rieke & Lebofsky (1985) are shown by dot-dashed lines. Right: colour–magnitude diagram showing the isochrones and evolutionary pre-MS tracks from Siess et al. (2000). Cluster members are indicated by open diamonds (P50) and dots (P?). |
4.1. Colour excess
The (J − H) and (H − Ks) colours were used to estimate the extinction, by evaluating the position of the cluster members compared to the MS. In Fig. 2 (left panel), we plot the intrinsic colours of MS and giant stars given by Bessel & Brett (1988), as well as the corresponding reddening vectors given by Rieke & Lebofsky (1985). For comparison, the zero age main-sequence (ZAMS) from Siess et al. (2000) is also plotted, which has much the same distribution of the MS, mainly for massive stars.
After we adopted the normal extinction law AV = 3.09E(B − V) from Savage & Mathis (1979) and the relation 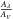 from Cardelli et al. (1989), the observed colours of the cluster members were unreddened and fitted to the MS intrinsic colours. This fitting is based on massive stars, mainly P50 members. Table 2 gives the E(B − V) that provides the best fitting, which is in good agreement with those available in the literature, within the estimated errors. Only a few objects had E(B − V) that was incompatible with the literature. In these cases, the procedure described in Sect. 3 for field-star decontamination by using colour–magnitude filter was reapplied with the extinction derived by us, and the structural parameters were determined for this refined sample of cluster members.
from Cardelli et al. (1989), the observed colours of the cluster members were unreddened and fitted to the MS intrinsic colours. This fitting is based on massive stars, mainly P50 members. Table 2 gives the E(B − V) that provides the best fitting, which is in good agreement with those available in the literature, within the estimated errors. Only a few objects had E(B − V) that was incompatible with the literature. In these cases, the procedure described in Sect. 3 for field-star decontamination by using colour–magnitude filter was reapplied with the extinction derived by us, and the structural parameters were determined for this refined sample of cluster members.
The (J − H)0 and (H − Ks)0 colours were also used to reveal the stars with K-band excess. Young clusters are expected to have several members that show high E(H − Ks) (Lada et al. 1996). These stars appear on the right-hand side of the MS reddening vector in the colour–colour diagram (Fig. 2). The fraction fK was calculated by dividing the number of stars having large (H − Ks)0 by the total number of cluster members.
4.2. Evaluation of distance and age
The unredenned magnitude and colour J0 × (J − H)0 of the cluster members were compared to pre-MS models (Siess et al. 2000), and also to MS Padova models (Girard et al. 2002) that were required to fit the colours of massive stars.
Figure 2 (right panel) shows the CMD obtained for Lynga 14, for illustration. The distances were confirmed by searching for (m − M)Jo, which best fits the position of massive stars. The error bars were estimated from the minimum and the maximum distance module that provide good MS fittings. Within the uncertainties, the distances estimated from the MS fitting are in good agreement with the literature (differences are lower than 30%), except for Trumpler 18. Our results are presented in Table 2 and were used to convert the angular measurements of the structural parameters into parsec.
The number of stars as a function of age was obtained by counting the objects in between different pairs of isochrones in the CMD. We used bins of 5 Myr, except for the two first that correspond to the 0.2–1 Myr and 1–5 Myr ranges. For MS objects (above the 7 M⊙ track) we adopted the age estimated by fitting the data with the Padova model. Figure 3 (left panel) shows the histogram of age distribution as a function of fractional number of members, where possible members (P50) and candidate members (P?) are displayed separately. Figures A3 to A7 show the plots used to evaluate age and mass for the whole sample.
The determination of age on the basis of these histograms may not be obvious. Some of the clusters have members separated into two different ranges, making it difficult to choose between the two options. The first choice of age is based on the most prominent peak formed by the P50 members. If the second peak has a similar number of members, we adopt the lower age value that is listed in Table 2, while the second option is given as notes in the same table.
Because of the large uncertainties on the age estimation, our conclusions are based on mean values. Considering that 12/21 objects of the sample (57%) are in the range of 4–10 Myr, and 9/21 (43%) are younger than 4 Myr, we suggest for our clusters a mean age of ~5 Myr.
 |
Fig. 3 Left: age distribution of Lynga 14 members (thick line) showing the contribution of P50 (dotted line) and P? (dashed line) objects. Right: observed mass distribution indicated by crosses with error bars. The thick line represents the mass function φ(m) fitting. |
4.3. Mass function
Similar to the age estimation, the counting in between the CMD tracks was used to determine the distribution of masses. Nine evolutionary tracks ranging from 0.1 M⊙ to 7 M⊙ were used to estimate the mass of pre-MS stars. For the MS objects we adopted the Padova model that best fits the observed colours, as described in Sect. 4.2. In this way, the sum of MS and pre-MS stars corresponds to the number of observed objects, which is given in Table 2 along with the respective observed mass.
Instead of using a histogram to display the mass distribution, we calculate the mass function given by Kroupa (2001): 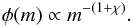 (6)Figure 3 (right panel) displays the observed mass distribution based on the sum of both MS and pre-MS stars. By fitting the observed distribution, we obtained the slope of the mass function, represented by χ (see last column of Table 2).
(6)Figure 3 (right panel) displays the observed mass distribution based on the sum of both MS and pre-MS stars. By fitting the observed distribution, we obtained the slope of the mass function, represented by χ (see last column of Table 2).
About half of the sample has a flatter mass distribution than the initial cluster mass function (ICMF) verified in a wide variety of clusters (e.g. Elmegreen 2006; Oey 2011). The ICMF slope (χ ~ 1.0) is slightly shallower than Salperter’s IMF (χ ~ 1.35).
The IMF suggested by Kroupa (2001) assumes slopes χ = 0.3 ± 0.5 for M < 0.5 M⊙ and Salperter’s IMF for M > 1 M⊙. We used the the observed mass and number of members to estimate the average stellar mass (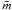 ) and verified that most of them have
) and verified that most of them have 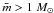 , probably due to a lack of low mass stars in our sample. This is related to the 2MASS detection limit that constrains the presence of faint sources in our sample. A sample incompleteness gives for our clusters large
, probably due to a lack of low mass stars in our sample. This is related to the 2MASS detection limit that constrains the presence of faint sources in our sample. A sample incompleteness gives for our clusters large 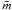 , when compared to embedded clusters. Bonatto & Bica (2010; 2011), for instance, uses
, when compared to embedded clusters. Bonatto & Bica (2010; 2011), for instance, uses 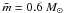 , which is lower than our results by a factor of 2, at least.
, which is lower than our results by a factor of 2, at least.
Based on the IMF fitting of the observed distribution of mass (χ slope), we corrected the incompleteness of our sample by synthetically deriving the number of faint stars that should be considered in the real membership. Table 2 gives the total number of members NT = Nobs + Nimf, where Nobs is related to the observed objects and Nimf is the number of lacking faint stars, estimated by integrating the IMF in the range of low mass (below the limit of detection). The corresponding total mass is also given in Table 2, along with the observed mass. The correction on the sample completeness is needed to improve the estimation of the cluster parameters that are used in the comparison with other samples.
 |
Fig. 4 Comparing our objects (filled circles) with embedded clusters (open squares) studied by LL03 and other samples. Representative error bars are used in a few data points, for illustration. a) Radius of the cluster as a function of number of members. Both our sample and the embedded clusters follow the same dependence R ∝ N0.5 (thick line) found for the stellar clusters (asterisks) studied by Carpenter (2000). Thin lines indicate the limits suggested by Adams et al. (2006). The results obtained by Piskunov et al. (2007) for three objects of our sample (crosses) are used to illustrate differences in the cluster size definition. b) Mass of the cluster as a function of number of members showing the same dependence M ∝ N1 for our sample and embedded clusters (thick line), with limits scaled by a factor ~2 (thin lines). c) Mass-radius dependence showing a mean distribution of M ~ 118 R1.3 (tick line) that spreads by a factor 2 (thin lines). The parameters of massive (“leak”) exposed clusters (triangles) are also plotted, as is the dependence M = 359 R1.7 suggested by Pfalzner (2011) for the embedded clusters (dashed line). d) Volumetric density as a function of radius, showing the dependence ρ = 28 R-1.7 presented by our sample and LL03 data (thick line), limited by thin lines that are scaled by a factor 2. Dashed lines represent the relations proposed by Pfalzner (2011). |
5. Comparative analysis
We investigate possible correlations among the cluster characteristics by comparing the structural and fundamental parameters, respectively from Tables 1 and 2. First, the correlations among mass, radius, and number of members are compared to similar relations obtained by Adams et al. (2006) and Pfalzner (2011) using cluster properties from other works. In Sect. 5.4 the structural parameters (obtained on basis of surface density) are compared, and Sect. 5.5 presents the relations with age.
5.1. Radius
Figure 4a shows the cluster radius distribution as a function of number of members (the same as Fig. 2 in Adams et al. 2006). Our sample is compared with 14 stellar clusters listed by Carpenter (2000) and 34 embedded clusters from LL03, which have available size (radius in pc).
To illustrate the different cluster size definitions discussed in Sect. 3.2, we also plot the cluster radius (Rt) and the respective number of members (N1) that were obtained by Piskunov et al. (2007) for three of our clusters (NGC 2362, NGC 6604, and Stock 13). It can be noted that the relation Rt × N1 is incompatible with the distribution of the other samples (Fig. 4a), possibly because Kharchenko et al. (2005) and Piskunov et al. (2007) study different stellar groups that surpass our clusters (see Sect. 3.2).
We verified that 52% of our sample follows the dependence R = 0.1N0.5, which is the same relation as proposed by Adams et al. (2006) for the clusters listed by Carpenter (2000). Two of our clusters, NGC 6604 and Trumpler 18, as well as three clusters from LL03 (NGC 2282, Gem OB1, and Gem OB4) also follow this trend, but are scaled up by a factor 1.7, which is the superior limit that Adams et al. (2006) suggest for the relation between cluster size and N.
Coinciding with most of the LL03 clusters, 33% of our sample are distributed along the lower curve in Fig. 4a, which is similar to the Carpenter (2000) sample, but scaled down by a factor 1.7. Lynga 14 appears bellow this correlation, suggesting that its membership is larger than the expected number of members, when compared to other clusters having the same size. This characteristic is also noted for some clusters from LL03, in particular SH 2-106 (S 106).
We also evaluate for our sample the commonly used half-mass radius r1/2, which encloses half of the total mass of the cluster. Considering that we do not determine individual mass for each member of the clusters, their observed radial mass distribution cannot be established. To have an approximate estimation of r1/2, we adopted the integrated mass distribution M(r) given by Adams et al. (2006): ![\begin{equation} \frac{M(r/r_{\rm o})}{M_{\rm tot}} = \left[\frac{(r/r_{\rm o})^a}{\left(1 + (r/r_{\rm o})\right)^a}\right]^p \end{equation}](/articles/aa/full_html/2012/11/aa19695-12/aa19695-12-eq207.png) (7)where ro is the scale length that we assume to be the radius of the cluster.
(7)where ro is the scale length that we assume to be the radius of the cluster.
The validity of using Eq. (7) for our sample was checked for Lynga 14, Collinder 205 and Hogg 10, for which we could estimate the observed M(r) and which were used as test cases. The “virial” model, used by Adams et al. (2006) in the simulations for N = 100 members, has coefficients (a = 3 and p ~ 0.41) that seem to reproduce the radial profile of the checked clusters well. We verified that these simulations provide a ratio of r1/2/ro of about 60–63%.
By adopting the relation r1/2 = 0.615 ro, we obtain the range of 0.69–2.5 pc for the half-mass radius estimated in our sample. We compared this result to the study that Adams et al. (2006) developed for NGC 1333, a model that is most like the N = 100 simulations with “cold” starting states (a = 2 and p ~ 0.55) and gives r1/2 = 0.117 to 0.238 for ro = 0.3 to 0.4 pc. The relation r1/2/ro is about 40–60% in this case, which is probably because our clusters are more evolved than the embedded phase.
 |
Fig. 5 Comparing structural parameters: a) background density vs. average density. Cluster radius compared to b) average density; c) core density; and d) distance. e) core radius vs. core density. Age correlations with f) core density; g) the fraction of cluster members showing excess in the K-band; and h) E(B − V). Dotted lines indicate AV ~ 1 mag and the limit of fK = 20%. Triangles are used to indicate objects with two options of age (filled symbols correspond to the first choice, listed in Table 2). |
5.2. Mass
Figure 4b shows the relations between mass and number of members. The LL03 sample has a dependence M = a N1.0, where 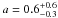 , which means that they are distributed between the lines scaled (up and down) by a factor 2. Our objects also follow this dependence.
, which means that they are distributed between the lines scaled (up and down) by a factor 2. Our objects also follow this dependence.
It is interesting to note that the clusters NGC 2282, Gem OB1, and Gem OB4, from LL03, are found above the superior limit of the distribution. The same occurs for our clusters Trumpler 18 and NGC 6604, which showed a similar trend in the R × N plot (Fig. 4a). The reason for a deviation in the expected relation is that these objects are different from most of the clusters. They have fewer low-mass members, which is confirmed by their flat IMF (χ < 0.4). In the opposite sense, NGC 6178 and Stock 16 are found below the lower limit curve, being compatible with their steep IMF (χ > 1.4).
To discuss whether these differences could be interpreted as a formation condition, as proposed by Adams et al. (2006), or differently if they are related to a time sequence, as suggested by Pfalzner (2011), we compare the relations between mass and radius. Figure 4c shows that our sample has the same dependence as is obtained by fitting the LL03 data: M = 118 R1.3.
Figure 4c also displays the data of the “leaky” massive clusters studied by Pfalzner (2011), who proposes that these objects would be the ending of a time sequence. However, the mass-radius dependence M ~ 359 R1.7, which Pfalzner (2011) used to illustrate the suggested time sequence, is steeper than the distribution of LL03 clusters.
Instead of confirming a sequence that ends in the exposed massive clusters, our results show that clusters from Pfalzner (2011) having radius > 10 pc follow the same M vs. R relation presented by LL03 data and also our sample. On the other hand, the massive clusters with R < 10 pc are found above the upper line in Fig. 4c, similar to Lynga 14 and SH 2-106 (LL03), whose differences we interpret to be as more likely due to different formation conditions.
5.3. Volumetric density
We estimated the volumetric density, by assuming ρ = 3M/(4πR3), which is plotted in Fig. 4d as a function of radius. For both samples, our clusters and those from LL03, we found a similar relation ρ = 28 R-1.7. This is quite similar to the results obtained by Camargo et al. (2010), who find ρ ∝ R-1.92.
Pfalzner (2011) uses a different dependence ρ ~ 100 R-1.3 to represent the LL03 data, which were compared to the relation ρ ∝ R-4 obtained for the massive exposed clusters (Fig. 4c). However, the distribution of our clusters, as well as LL03 data, does not agree with the mass vs. density relation proposed by Pfalzner (2009; 2011). As suggested in Sect. 5.2, the large massive clusters seem to follow the same trend as our clusters, while those with R < 10 pc are scaled up by a factor over 2.
5.4. Surface density
We analysed the structural parameters looking for correlations among the clusters themselves and to verify a possible relation between the cluster and its environment. Hatched areas in Fig. 5 illustrate the trends that were found for most of the clusters. Except for Trumpler 28, the observed average density of the cluster (⟨ n∗ ⟩ ) increases with the background density (σbg), as shown in Fig. 5a. This indicates that dense clusters are found in dense background fields.
Considering that N increases with R (see Fig. 4a), an anti-correlation of ⟨ n∗ ⟩ vs. R is expected, which is indeed noted in Fig. 5b. As a consequence, σbg also appears anti-correlated with R. Core density (σ0) is another structural parameter that also diminishes when cluster radius increases, but a considerable dispersion is seen in Fig. 5c, where almost six clusters are out of the observed trend. Even though R is not expected to be related to the cluster distance (D), Fig. 5d shows a trend toward R increasing with D. This is not surprising, since the similar angular sizes of our objects lead to a large linear size (given in parsec) for more distant clusters.
We plot in Fig. 5e the anti-correlation between core radius (rc) and σ0 that is observed for most of the clusters, excepting Lynga 14 and NGC 3590. The core parameters also show some trends when compared with other structural parameters, such as the correlation between σ0 and δc (density contrast) and rc/R (ratio of core-size to cluster radius) decreasing with the rise in σ0.
The evaluation of structural parameters is unprecedented for most of our objects, but our results are comparable with those available in the literature for other clusters. We verified that the ranges of values obtained by us are compatible with several kinds of young clusters: NGC 6611, an embedded and dynamically evolved cluster (Bonatto et al. 2006); NGC 4755, a post-embedded cluster (Bonatto et al. 2006); the low-mass open clusters NGC 1931, vdB 80, BDSB 96, and Pismis 5 (Bonatto & Bica 2009a); NGC 2239, a possible ordinary open cluster (Bonatto & Bica 2009b); and the dissolving clusters NGC 6823 (Bica et al. 2008), Collinder 197, vdB 92 (Bonatto & Bica 2010) and Trumpler 37 (Saurin et al. 2012).
5.5. Age
It is expected that σ0 should decrease with age once the members of older clusters have had time to disperse, diminishing its surface stellar density. However, no clear trend is observed in Fig. 5f, which displays different symbols to indicate objects that have two options of age, but only one of them was adopted.
The fraction of stars having large E(H − K), fK, is expected to be related to age because of the colour excess in the K-band traces circumstellar matter, which is indicative of youth, as mentioned in Sect. 4.1 (Lada et al. 1996). Figure 5g shows the distribution of fK as a function of age and the fK = 20% limit, above which objects younger than 5 Myr are supposed to be found. Most of our objects have fK > 20%, but three of the youngest clusters are below this limit, showing no correlation of age with fK.
Probably this lack of correlation occurs because some of our clusters have a mixing of populations, which means that part of the members is <4 Myr, while others are 4–10 Myr. On the other hand, the lack of correlation is also found for Stock 16 that has fK = 30% and a mean age of 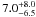 Myr. One explanation is a possible field-stars contamination in the number of objects with K-band excess in the colour–colour diagram, mainly those having 0.1 < (J − H)0 < 0.3 mag. In the colour–magnitude diagram, these stars are counted in the range of ages older than 20 Myr, but should not be considered. The large error bars on both age and fK estimation give us only a qualitative analysis of the relation between these parameters.
Myr. One explanation is a possible field-stars contamination in the number of objects with K-band excess in the colour–colour diagram, mainly those having 0.1 < (J − H)0 < 0.3 mag. In the colour–magnitude diagram, these stars are counted in the range of ages older than 20 Myr, but should not be considered. The large error bars on both age and fK estimation give us only a qualitative analysis of the relation between these parameters.
Age is also expected to be related with other parameters such as colour excess. Since E(B − V) is indicative of visual extinction, it can be used to infer how embedded the cluster is, and by consequence to verify the youth of the cluster. In fact, Fig. 5h shows five of the youngest objects (<4 Myr) appearing above the line representing E(B − V) = 0.3 mag, which means AV > 1 mag. However, six other young clusters are below this limit, which indicates that they are not deeply embedded. For this reason, we concluded that there is no correlation between age and E(B − V) for our sample.
6. Summary of the results and conclusions
We determined the structural parameters as a function of superficial density and radial distribution profile of a sample of 21 clusters, selected on the basis of their youth and intermediate distance. A statistical procedure using colour–magnitude criteria provided a double-checked decontamination of field stars. The remaining stars were considered members, and their observed colours were used to more accurately determine the visual extinction affecting the cluster. The unreddened colours were compared with theoretical isochrones in the CMD aiming to confirm distance and age. The same was done to determine individual masses, based on the cluster members position compared to evolutionary tracks.
In principle, centrally concentrated clusters should be the youngest ones since they would not have had enough time to disperse. In fact, most of our clusters show this characteristic. However, the constrained range of ages in our sample stops us from be more conclusive about differences or similarities in the evolution of the studied clusters.
We conclude that all the 21 studied clusters are very similar, probably due to the selection criteria choosing restricted ranges of size, distance, and age. In consequence, there is no large variation on number of members, radius, and mass of the clusters. On the other hand, the galactic distribution of the objects causes differences among the environments of the clusters.
When compared with other young clusters (LL03, Carpenter 2000), our sample follows the same trends, but has larger radius and lower volumetric density. This means a less concentrated distribution of members that may be related to the expected spatial dispersion, when the cluster gets older.
The distinction between star clusters and associations has been discussed in several works. Following the definitions presented by LL03, our clusters are classified as stellar groups because they have more than 35 physically related stars and their mass density exceeds 1 M⊙/pc-3. Since our objects are optically visible, they cannot be considered embedded clusters. Even considering the large error bars on the age estimation, the mean age of the clusters (~ 5 Myr) is a clear indication that our sample is formed by young stellar associations.
We also checked our sample for the relation between age and crossing time (τcr), following Gieles & Portegies Zwart (2011), for instance. They propose a criterion in which bound systems (open star clusters) would have age/τcr > 1 and unbound systems would have age/τcr < 1. For this test, we adopted the crossing time defined by 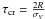 , where R is the cluster radius and the stellar velocity dispersion is given by
, where R is the cluster radius and the stellar velocity dispersion is given by 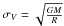 , according to Saurin et al. (2012).
, according to Saurin et al. (2012).
We verified that none of our clusters has stars with age that exceeds the crossing time. Therefore, they probably would evolve like stellar associations. If the error bars on the age/τcr calculations are considered, only Lynga 14 could evolve as an open cluster. This result agrees with the suggestion by LL03 and Pfalzner (2009), for instance, that few star clusters are expected to be bound. However, it must be kept in mind that these are qualitative conclusions, owing the large uncertainties on age estimation.
Our objects are found in the gap between the samples of embedded and exposed clusters studied by Pfalzner (2011); however, our results do not confirm the mass-radius or density-radius dependences suggested by her. In fact, we verified that massive clusters from Pfalzner (2011) are distributed in two groups. Those with large sizes, lower masses, and intermediate ages (4–10 Myr) follow the same trends as shown by embedded clusters (LL03), as well as our sample. The younger massive clusters (<4 Myr) studied by Pfalzner (2011) have smaller sizes and higher masses, appearing out of the correlations shown in Fig. 4, as do Lynga 14 (this work) and SH 2-106 (LL03). As proposed by Adams et al. (2006), the differences among these clusters could be interpreted as a formation condition.
An interesting perspective of the present work is to increase the studied sample by including other clusters having larger radius (4–10 pc), which could complet the gap between our clusters and the sample of massive clusters.
Online material
Appendix A: Plots of the entire sample
All plots used in the analysis of structural and fundamental parameters are displayed in this Appendix. Figure A.1 shows the stellar surface-density maps and the distribution of the stellar density as a function of radius (same as Fig. 1).
Figure A.2 presents colour–colour and colour–magnitude diagrams in the left-hand panel (same as Fig. 2). The centre and right panels show the histogram of age and the mass distribution, respectively (same as Fig. 3).
 |
Fig. A.1 Left: stellar surface-density map (σ (stars/arcmin2)) obtained for the region of 30 arcmin around the clusters. The comparison field-stars area is indicated by dashed lines, while the full line indicates the cluster area. Centre: a zoom of the σ map indicating by crosses the position of objects with membership probability P > 70%. Right: the distribution of the stellar density as a function of radius. The best fitting of observed radial density profile, indicated by the full line, was obtained by using the model from King (1962). A dashed line indicates the background density (σbg). |
 |
Fig. A.1 continued. |
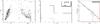 |
Fig. A.2 Left panels: colour–colour and colour–magnitude diagrams. The MS and the ZAMS are indicated by full lines, while the locus of giant stars is represented by a dotted line. Reddening vectors from Rieke & Lebofsky (1985) are shown by dot-dashed lines. The isochrones and evolutionary pre-MS tracks from Siess et al. (2000). Cluster members are indicated by open diamonds (P50) and dots (P?). Centre: age distribution of clusters members (thick line) showing the contribution of P50 (dotted line) and P? (dashed line) objects. Right: observed mass distribution indicated by crosses with error bars. The thick line represents the mass function φ(m) fitting. |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
Acknowledgments
T.S.S. acknowledges financial support from CNPq (Proc. No. 142851/2010-8). J.G.H. acknowledges partial support from CAPES/COFECUB (Proc. No. 712/11). This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, F. C., Porszkow, E. M., Fatuzzo, M., & Myers, P. C. 2006, ApJ, 641, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., & Bonatto, C. 2005, A&A, 443, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bica, E., Bonatto, C., & Dutra, C. M. 2008, A&A, 489, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., & Bica, E. 2009a, MNRAS, 397, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., & Bica, E. 2009b, MNRAS, 394, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., & Bica, E. 2010, A&A, 516, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., & Bica, E. 2011, MNRAS, 415, 2827 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., Bica, E., & Girardi, L. 2004, A&A, 415, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., Santos, J. F. C., & Bica, E. 2006, A&A, 445, 567 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonatto, C., Bica, E., Ortolani, S., & Barbuy, B. 2006, A&A, 453, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camargo, D., Bonatto, C., & Bica, E. 2010, A&A, 521, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2000, AJ, 120, 3139 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri R. M. 2003, The Two Micron All Sky Survey at IPAC (2MASS), California Institute of Technology [Google Scholar]
- Dahm, S. E. 2008, Handbook of Star Forming Regions, Vol. I, 966 [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A, 389, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dias, W. S., Assafin, M., Flório, V., Alessi, B. S., & Libero, V. 2006, A&A, 446, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G. 2006, ApJ, 648, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Flaccomio, E., Sciortino, S., Micela, G., et al. 1997, MmSAI, 68, 1073 [Google Scholar]
- Gieles, M., & Portegies Zwart, S. F. 2011, MNRAS, 410, 6 [Google Scholar]
- Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregorio-Hetem, J., Montmerle, T., Rodrigues, C. V., et al. 2009, A&A, 506, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Rser, S., Schilbach, E., & Scholz, R. D. 2005, A&A, 438, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Alves, J., & Lada, E. A. 1996, AJ, 111, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H. T., Chen, W. P., Zhang, Z.W., & Hu, J. Y. 2005, ApJ, 624, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Loktin, A. V., Matkin, N. V., & Gerasimenko, T. P. 1994, A&AT, 4, 153 [Google Scholar]
- Lynga, G. 1987, A&A, 188, 35 Computer Based Catalogue of Open Cluster [NASA ADS] [Google Scholar]
- Mermilliod, J. C. 1995, ASSL, 203, 127 [Google Scholar]
- Oey, M. S. 2011, ApJ, 739, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., Hennebelle, P., & André, Ph. 2005, SF2A, 729 [Google Scholar]
- Pfalzner, S. 2009, A&A, 498, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S. 2011, A&A, 536, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, A. E., Schilbach, E., Kharchenko, N. V., Roeser, S., & Scholz, R.-D. 2007, A&A, 468, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rebull, L. M., Makidon, R. B., Strom, S. E., et al. 2002, AJ, 123, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al., 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., & Lebofsky, M. J. 1985, ApJ, 288, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Saurin, T. A., Bica, E., & Bonatto, C. 2012, MNRAS, 421, 3206 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., & Mathis, J. S. 1979, ARA&A, 17, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987 ARA&A, 25, 23 [Google Scholar]
- Shu, F. H., Li, Zhi-Yun, & Allen, A. 2004 ApJ, 601, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000 A&A, 358, 593 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left: stellar surface-density map (σ (stars/arcmin2)) obtained for the region of 30 arcmin around Lynga 14. The comparison field-star area is indicated by dashed lines, while the full line indicates the cluster area. Center: a zoom of the σ map uses crosses to indicate the position of objects with membership probability P > 70%. Right: the distribution of the stellar density as a function of radius. The best fitting of observed radial density profile, indicated by the full line, was obtained by using the model from King (1962). A thin (red) line indicates the background density (σbg). |
| In the text | |
 |
Fig. 2 Left: colour–colour diagram for Lynga 14. The MS and the ZAMS are indicated by full lines, while the locus of giant stars is represented by a dotted line. Reddening vectors from Rieke & Lebofsky (1985) are shown by dot-dashed lines. Right: colour–magnitude diagram showing the isochrones and evolutionary pre-MS tracks from Siess et al. (2000). Cluster members are indicated by open diamonds (P50) and dots (P?). |
| In the text | |
 |
Fig. 3 Left: age distribution of Lynga 14 members (thick line) showing the contribution of P50 (dotted line) and P? (dashed line) objects. Right: observed mass distribution indicated by crosses with error bars. The thick line represents the mass function φ(m) fitting. |
| In the text | |
 |
Fig. 4 Comparing our objects (filled circles) with embedded clusters (open squares) studied by LL03 and other samples. Representative error bars are used in a few data points, for illustration. a) Radius of the cluster as a function of number of members. Both our sample and the embedded clusters follow the same dependence R ∝ N0.5 (thick line) found for the stellar clusters (asterisks) studied by Carpenter (2000). Thin lines indicate the limits suggested by Adams et al. (2006). The results obtained by Piskunov et al. (2007) for three objects of our sample (crosses) are used to illustrate differences in the cluster size definition. b) Mass of the cluster as a function of number of members showing the same dependence M ∝ N1 for our sample and embedded clusters (thick line), with limits scaled by a factor ~2 (thin lines). c) Mass-radius dependence showing a mean distribution of M ~ 118 R1.3 (tick line) that spreads by a factor 2 (thin lines). The parameters of massive (“leak”) exposed clusters (triangles) are also plotted, as is the dependence M = 359 R1.7 suggested by Pfalzner (2011) for the embedded clusters (dashed line). d) Volumetric density as a function of radius, showing the dependence ρ = 28 R-1.7 presented by our sample and LL03 data (thick line), limited by thin lines that are scaled by a factor 2. Dashed lines represent the relations proposed by Pfalzner (2011). |
| In the text | |
 |
Fig. 5 Comparing structural parameters: a) background density vs. average density. Cluster radius compared to b) average density; c) core density; and d) distance. e) core radius vs. core density. Age correlations with f) core density; g) the fraction of cluster members showing excess in the K-band; and h) E(B − V). Dotted lines indicate AV ~ 1 mag and the limit of fK = 20%. Triangles are used to indicate objects with two options of age (filled symbols correspond to the first choice, listed in Table 2). |
| In the text | |
 |
Fig. A.1 Left: stellar surface-density map (σ (stars/arcmin2)) obtained for the region of 30 arcmin around the clusters. The comparison field-stars area is indicated by dashed lines, while the full line indicates the cluster area. Centre: a zoom of the σ map indicating by crosses the position of objects with membership probability P > 70%. Right: the distribution of the stellar density as a function of radius. The best fitting of observed radial density profile, indicated by the full line, was obtained by using the model from King (1962). A dashed line indicates the background density (σbg). |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
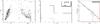 |
Fig. A.2 Left panels: colour–colour and colour–magnitude diagrams. The MS and the ZAMS are indicated by full lines, while the locus of giant stars is represented by a dotted line. Reddening vectors from Rieke & Lebofsky (1985) are shown by dot-dashed lines. The isochrones and evolutionary pre-MS tracks from Siess et al. (2000). Cluster members are indicated by open diamonds (P50) and dots (P?). Centre: age distribution of clusters members (thick line) showing the contribution of P50 (dotted line) and P? (dashed line) objects. Right: observed mass distribution indicated by crosses with error bars. The thick line represents the mass function φ(m) fitting. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


