| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A102 | |
| Number of page(s) | 8 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201219688 | |
| Published online | 06 November 2012 | |
A stacking method to study the gamma-ray emission of source samples based on the co-adding of Fermi-LAT count maps
1
Physik – Institut, Universität Zürich,
Winterthurerstrasse 190,
8057
Zürich,
Switzerland
e-mail: ben.huber@physik.uzh.ch
2
ISDC Data Center for Astrophysics, Center for Astroparticle
Physics, Observatory of Geneva, University of Geneva, Chemin d’Ecogia 16, 1290
Versoix,
Switzerland
3
Oskar Klein Center, Department of Physics, Stockholm University
Center, Albanova University Center, 10691
Stockholm,
Sweden
Received:
25
May
2012
Accepted:
9
September
2012
Aims. We present a stacking method that makes use of co-added maps of gamma-ray counts produced from data taken with the Fermi Large Area Telescope. Sources with low integrated gamma-ray fluxes that are not detected individually may become detectable when their corresponding count maps are added.
Methods. The combined data set is analyzed with a maximum likelihood method taking into account the contribution from point-like and diffuse background sources. For both simulated and real data, detection significance and integrated gamma-ray flux are investigated for different numbers of stacked sources using the public Fermi Science Tools for analysis and data preparation.
Results. The co-adding is done such that potential source signals add constructively, in contrast to the signals from background sources, which allows the stacked data to be described with simply structured models. We show, for different scenarios, that the stacking method can be used to increase the cumulative significance of a sample of sources and to characterize the corresponding gamma-ray emission. The method can, for instance, help to search for gamma-ray emission from galaxy clusters.
Key words: methods: data analysis / methods: statistical / gamma rays: general
© ESO, 2012
1. Introduction
In conjunction with the Energetic Gamma-Ray Experiment Telescope (EGRET) onboard the Compton Gamma-ray Observatory, several studies made use of a stacking method that is based on the adding (co-adding, stacking) of maps of gamma-ray counts and on a subsequent analysis with a maximum likelihood method. These studies were performed to search for gamma-ray emission from, for instance, clusters of galaxies (Reimer et al. 2003), radio and Seyfert galaxies (Cillis et al. 2004), infrared galaxies (Cillis et al. 2005) and potential gamma-ray sources at low galactic latitudes (Cillis et al. 2007).
The basic idea of the co-adding is to add up the data such that the sources of interest are spatially correlated with one other, in contrast to the background sources within the source region. Co-adding can thus increase the signal-to-background ratio, resulting in an increased cumulative significance of the sources in the sample.
Inspired by the EGRET stacking effort, we present a co-adding method for data obtained with the Fermi Large Area Telescope (LAT). The LAT is a pair-conversion telescope onboard the Fermi Gamma-ray Space Telescope (Atwood et al. 2009) that is capable to detect gamma rays with energies from 20 MeV to more than 300 GeV. In comparison to EGRET, the LAT achieves a point source sensitivity that is increased by two orders of magnitude1.
The public Fermi Science Tools provide the stacking tool Composite2 that has recently been applied, for instance, to Milky way satellite galaxies to search for signals from dark matter annihilations (Ackermann et al. 2011). In contrast to the Composite2 method that makes use of summed log -likelihood functions, the co-adding method presented in this paper is based on added maps of counts instead. This may increase the signal-to-background ratio for the sources of interest and a visible excess of counts may be achieved for the stacked signal.
This paper is structured as follows. In Sect. 2, the co-addition of count maps is described together with the resulting likelihood analysis. In Sect. 3, the method is tested with simulated data. As a first step, the stacking of diffuse background is studied, and significance and integrated photon flux upper limits of a hypothetical central point-like source are computed for different numbers of stacked sources. In a second step, the ability to detect point-like emissions with low integral photon fluxes is tested. For this purpose, a simulated faint point-like source is added at the center of each region and the stacking is repeated, investigating the development of source significance and integrated photon flux as well as the dependence on the spectral shape of the source emission. In Sect. 4, the method is applied to real data, first to regions that are free of detected central point-like emission and second to regions that host a known point-like source at their center, that is present in the LAT 2-year point source catalog (The Fermi-LAT Collaboration 2012). In Sect. 5, we discuss the co-adding method and its performance.
For the analysis and data preparation in the following sections, we make use of the Science Tools (v9r23p1)2, together with the P7SOURCE_V6 LAT response functions.
The scripts used for the co-adding analyses in the following sections will become publicly available in the future, or can be directly obtained by the corresponding author.
2. The co-adding method
The co-adding method presented in this paper is based on analyzing stacked data histograms
with a maximum likelihood method. The contents of each individual histogram include
contributions from two classes of background sources and potentially one signal source. The
reason for separating the background contributions into two classes will become clear in
Sect. 2.2. Let
nim denote the content of bin
i in histogram m, and
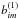 be the estimated contribution from the first class of backgrounds in the same bin. The first
class of background is subtracted from the original histograms individually, before the
stacking. The bin values
be the estimated contribution from the first class of backgrounds in the same bin. The first
class of background is subtracted from the original histograms individually, before the
stacking. The bin values 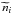 of the co-added histogram are then given by:
of the co-added histogram are then given by:
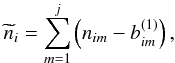 (1)where
j is the number of stacked histograms. These bin values are fit by a
model
(1)where
j is the number of stacked histograms. These bin values are fit by a
model 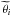 which is the set of bin contents that include a prediction for the potential signal source,
sim, combined with a prediction for the
second class of background events,
which is the set of bin contents that include a prediction for the potential signal source,
sim, combined with a prediction for the
second class of background events, 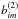 :
:
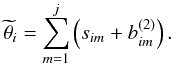 (2)The
normalization of sim and
(2)The
normalization of sim and
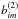 are considered to be free parameters during the fit and varied until a maximum value for the
standard Poisson log-likelihood (Mattox et al. 1996),
are considered to be free parameters during the fit and varied until a maximum value for the
standard Poisson log-likelihood (Mattox et al. 1996),
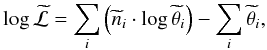 (3)is
found, giving the best-fit value for the amplitude of the potential signal. For each
j ∈ [1,jmax] , where
jmax is the total number of available histograms, the signal
amplitude and the corresponding statistical significance are computed. True detections are
expected to show an increasing trend in significance as more histograms are added to the
stack, while false positives should result in cumulative significances that remain low.
(3)is
found, giving the best-fit value for the amplitude of the potential signal. For each
j ∈ [1,jmax] , where
jmax is the total number of available histograms, the signal
amplitude and the corresponding statistical significance are computed. True detections are
expected to show an increasing trend in significance as more histograms are added to the
stack, while false positives should result in cumulative significances that remain low.
In the following, each histogram represents a region of interest (ROI) and is given by a
three-dimensional histogram called a CountCube. The first class of background sources,
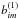 ,
corresponds to known gamma-ray point sources, as they are listed in the LAT 2-year point
source catalog (The Fermi-LAT Collaboration 2012),
while the second class,
,
corresponds to known gamma-ray point sources, as they are listed in the LAT 2-year point
source catalog (The Fermi-LAT Collaboration 2012),
while the second class, 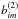 ,
refers to diffuse galactic and extragalactic gamma-ray emissions.
,
refers to diffuse galactic and extragalactic gamma-ray emissions.
2.1. The likelihood function of the standard Fermi-LAT analysis
When the Fermi spacecraft is operated in survey mode, the LAT obtains full sky coverage. Photons that belong to a ROI on the sky, are selected with the tool gtselect which performs the basic regional cuts as well as the selection of defined intervals for observation time and energy (for more details, see Sects. 3 and 4). Here, the selection is done such that the sources of interest are positioned at the center of the corresponding ROIs. The ROI size is chosen large enough to account for the point spread function (PSF) of the instrument (see e.g. Atwood et al. 2009, for details on the PSF). Additional time cuts are performed with the tool gtmktime which takes the pointing and position history of the spacecraft into account and makes sure that only good time intervals are used for the analysis. This removes, for instance, events taken when the spacecraft passes through the South Atlantic Anomaly and photons that come from the earth’s limb (Petry 2005). Afterwards, the tool gtbin is applied to fill the photons into a CountCube. Two dimensions in the CountCube are for the sky position, e.g. right ascension and declination, whereas the third dimension corresponds to the reconstructed energy.
The log -likelihood function that is used for the standard binned analysis of single (not
stacked) ROIs is given by (Mattox et al. 1996):
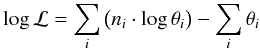 (4)where
ni are the measured number of photon counts
for bin i as they are stored in the CountCube, and
θi are the number of counts predicted by
a model for the same bin. The index i runs over all bins in the
CountCube.
(4)where
ni are the measured number of photon counts
for bin i as they are stored in the CountCube, and
θi are the number of counts predicted by
a model for the same bin. The index i runs over all bins in the
CountCube.
The model that is used to predict the θi
contains the positions and spectral shapes of known point sources in the ROI, and it
includes the expected isotropic contribution from the extragalactic diffuse background
(EGB) and the region-dependent contribution from the galactic diffuse background (GB).
This model is converted into the model-predicted number of counts with the aid of a
SourceMap that takes the integrated exposure time during the observation and the
instrument response functions, mainly PSF, effective area and energy-dependent
corrections, into account and provides the appropriate conversion factors for each bin
i. For every source in the model an individual SourceMap is generated
by the tool gtsrcmaps, using the same spatial and energy binning as in
the underlying CountCube. The model-predicted number of counts
θi in bin i are
calculated through: ![\begin{eqnarray} \label{predictedcounts} \theta_{i} = N_{\rm{GB}}\cdot F_{{\rm{GB}},i}\cdot S_{{\rm{GB}},i} + N_{\rm{EGB}}\cdot F_{{\rm{EGB}},i}\cdot S_{{\rm{EGB}},i} \\ \nonumber + \sum_k \left[N_{0,k}\cdot F_{k,i}(\alpha,...)\cdot S_{k,i}\right]{,} \end{eqnarray}](/articles/aa/full_html/2012/11/aa19688-12/aa19688-12-eq19.png) (5)where
SGB,i,
SEGB,i and
Sk,i represent the SourceMap values for
the GB, EGB and the point sources k, that belong to the sky position and
the energy interval of bin i.
NGB·FGB,i and
NEGB·FEGB,i
denote the photon fluxes predicted for bin i, where
NGB and NEGB are the
corresponding normalization parameters that are free during the likelihood fit. While
FEGB,i is uniform for all the bins of a
given energy and is derived from a fixed spectrum3,
FGB,i is derived from a three-dimensional
distribution map of differential photon fluxes4. For
this reason, the SourceMap of the galactic diffuse emission, that is created with the
Science Tools, incorporates the factor FGB,i.
In the following,
(5)where
SGB,i,
SEGB,i and
Sk,i represent the SourceMap values for
the GB, EGB and the point sources k, that belong to the sky position and
the energy interval of bin i.
NGB·FGB,i and
NEGB·FEGB,i
denote the photon fluxes predicted for bin i, where
NGB and NEGB are the
corresponding normalization parameters that are free during the likelihood fit. While
FEGB,i is uniform for all the bins of a
given energy and is derived from a fixed spectrum3,
FGB,i is derived from a three-dimensional
distribution map of differential photon fluxes4. For
this reason, the SourceMap of the galactic diffuse emission, that is created with the
Science Tools, incorporates the factor FGB,i.
In the following, 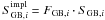 denotes the SourceMap of the GB model as it is implemented in the Science Tools. The
photon flux of source k is denoted by
N0,k·Fk,i(α,...),
based on a source spectrum that may depend on several parameters, e.g. a prefactor
N0 and a photon index α in the case of a
power-law spectrum5.
denotes the SourceMap of the GB model as it is implemented in the Science Tools. The
photon flux of source k is denoted by
N0,k·Fk,i(α,...),
based on a source spectrum that may depend on several parameters, e.g. a prefactor
N0 and a photon index α in the case of a
power-law spectrum5.
2.2. Co-adding of data
ROIs, selected and prepared as previously described, are combined by adding up their
corresponding CountCubes. For this purpose, we introduce a new coordinate system in which
the origin is defined to be at the center of the combined ROI. All sources of interest are
thus located at the origin. The goal is to analyze the co-added data with the maximum
likelihood method implemented in the Science Tools. We model the co-added diffuse
backgrounds, GB and EGB, by building a weighted sum of the SourceMaps. This takes into
account that the contributions of the diffuse backgrounds are different for each ROI and
that the co-adding adds up the exposures. 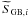 and
and  are the stacked SourceMaps for the GB and EGB model, respectively:
are the stacked SourceMaps for the GB and EGB model, respectively: ![\begin{eqnarray} \label{sourcemap_diffuseBG_coadded} \widetilde{S}_{{\rm{GB}},i} &&= \sum_{m} \left[N_{\rm{GB}}\cdot S^{\rm{impl}}_{{\rm{GB}},i}\right]_m {\rm{\,and}}\\ \label{sourcemap_diffuseBG_coadded2} \widetilde{S}_{{\rm{EGB}},i} &&= \sum_{m} \left[N_{\rm{EGB}}\cdot S_{{\rm{EGB}},i}\right]_m, \end{eqnarray}](/articles/aa/full_html/2012/11/aa19688-12/aa19688-12-eq36.png) where
m denotes the different ROIs. The factors
NGB and NEGB are used to
normalize the SourceMaps according to the diffuse background contributions in each region,
known from individual region analyses (see below).
where
m denotes the different ROIs. The factors
NGB and NEGB are used to
normalize the SourceMaps according to the diffuse background contributions in each region,
known from individual region analyses (see below).
Depending on the ROI size, the number of detected point sources increases rapidly and leads for the co-adding to a model with a large number of components. In order to keep the model simply structured, we follow a different strategy. Before co-adding the data, a binned likelihood analysis6 is performed on each individual ROI using models that contain the diffuse backgrounds and the Fermi-LAT detected point sources from the LAT 2-year point source catalog, within and close to the ROIs. These analyses yield the normalizations of the diffuse backgrounds and the parameters of the point sources for each individual ROI. More than 99% of the sources in the LAT 2-year point source catalog are characterized by a point-like gamma-ray emission, only very few sources may appear extended with extensions on the order of the PSF. In the following, we treat all point sources that are included in the models as point-like emissions. All Fermi-LAT detected point sources are then declared as background and simulated using the tool gtobssim, in order to subtract them from the measured data. This leads to a simpler form of Eq. (5), in which the last term is suppressed. The resulting CountCubes, that is the data minus the simulated point sources, are finally co-added.
In order to investigate sources at the center of the ROIs, the model that we apply for
the analysis of the co-added CountCubes contains, besides the diffuse backgrounds, a
common source of interest at the ROI center, that is denoted as test source. For the
analyses in the following sections, the test source is described as a point-like source
located at the ROI center using a power-law spectrum with a prefactor
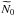 and a photon index
and a photon index 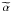 as model
parameters (see Sect. 2.1). Similar to the case of
the diffuse backgrounds, the SourceMaps for the test source are first produced
individually for each ROI m and then added up in order to take the total
exposure into account. The bin values of the co-added SourceMaps for the test source,
as model
parameters (see Sect. 2.1). Similar to the case of
the diffuse backgrounds, the SourceMaps for the test source are first produced
individually for each ROI m and then added up in order to take the total
exposure into account. The bin values of the co-added SourceMaps for the test source,
 ,
are then given by:
,
are then given by: ![\begin{eqnarray} \label{sourcemap_testsource_coadded} \widetilde{S}_{{\rm{test\,source}},i} = \sum_m \left[S_{{\rm{test\,source}},i}\right]_m. \end{eqnarray}](/articles/aa/full_html/2012/11/aa19688-12/aa19688-12-eq40.png) (8)From
the stacked SourceMaps defined in Eqs. (6)–(8), the number of co-added
model-predicted counts
(8)From
the stacked SourceMaps defined in Eqs. (6)–(8), the number of co-added
model-predicted counts 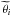 is derived by:
is derived by: 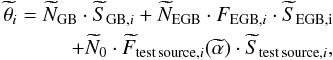 (9)where
the normalizations of the diffuse backgrounds
(9)where
the normalizations of the diffuse backgrounds 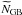 ,
,
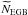 and the test source parameters, prefactor
and the test source parameters, prefactor 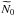 and photon index
and photon index 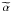 , may be
free during the likelihood fit. Due to the normalized sum of SourceMaps in Eqs. (6) and (7), the values of
, may be
free during the likelihood fit. Due to the normalized sum of SourceMaps in Eqs. (6) and (7), the values of 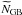 and
and 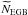 are expected to be close to 1 and FEGB,i is
derived from the same fixed spectrum as in Eq. (5). Since the SourceMaps of the test source are summed in Eq. (8), the test source parameters and the
resulting flux
are expected to be close to 1 and FEGB,i is
derived from the same fixed spectrum as in Eq. (5). Since the SourceMaps of the test source are summed in Eq. (8), the test source parameters and the
resulting flux 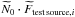 represent values that are averaged by the total stacked exposure.
represent values that are averaged by the total stacked exposure.
The log -likelihood function of the co-adding analysis
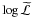 is given in Eq. (3), where
is given in Eq. (3), where
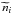 is the number of co-added measured counts in bin i after the subtraction
of the simulated point-like sources. Both Eqs. (4) and (3) represent a likelihood
that is derived from Poisson-distributed numbers of observed counts. The subtraction of
the simulated counts transforms, for a fraction of bins, the Poisson distribution into a
Skellam probability distribution (Skellam 1946).
For regions located at galactic
latitutes |b| > 25° (to avoid
the high number of contributing background sources close to the galactic plane and to be
consistent with the analyses performed in Sects. 3
and 4), about 3% of the bins in a CountCube are
affected by the subtraction. Therefore, the likelihood defined in Eq. (3) is used for the co-adding analysis in good
approximation.
is the number of co-added measured counts in bin i after the subtraction
of the simulated point-like sources. Both Eqs. (4) and (3) represent a likelihood
that is derived from Poisson-distributed numbers of observed counts. The subtraction of
the simulated counts transforms, for a fraction of bins, the Poisson distribution into a
Skellam probability distribution (Skellam 1946).
For regions located at galactic
latitutes |b| > 25° (to avoid
the high number of contributing background sources close to the galactic plane and to be
consistent with the analyses performed in Sects. 3
and 4), about 3% of the bins in a CountCube are
affected by the subtraction. Therefore, the likelihood defined in Eq. (3) is used for the co-adding analysis in good
approximation.
We perform the binned likelihood analysis of the co-added data through the likelihood python interface of the Science Tools7 using the minimizer Minuit8. During the likelihood analysis, Eq. (3) is maximized, which results in maximum likelihood estimators for the free parameters in the applied model. As a measure of the test source significance, we compute the test statistic TS = −2(log ℒ0−log ℒ1), in which ℒ0 and ℒ1 are the maximized likelihood-values given that only the diffuse backgrounds are present in the model (null hypothesis) and that a test source is present in addition to the diffuse backgrounds (alternative hypothesis), respectively.
For the analyses in the following sections, the prefactor
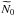 is the only free parameter in the spectral model of the test source. Hence, if the photons
were only due to the background fluctuations from the sources defined in the null
hypothesis, then the TS values would follow approximately a
is the only free parameter in the spectral model of the test source. Hence, if the photons
were only due to the background fluctuations from the sources defined in the null
hypothesis, then the TS values would follow approximately a
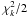 -distribution
with k = 1 free parameter. The significance level of the test source
can then be denoted as
-distribution
with k = 1 free parameter. The significance level of the test source
can then be denoted as 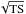 in units of sigma (σ) (Mattox et al.
1996; Particle Data Group 2010), based on a
one-sided Gaussian quantile. Simulations showed that a
in units of sigma (σ) (Mattox et al.
1996; Particle Data Group 2010), based on a
one-sided Gaussian quantile. Simulations showed that a
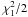 -distribution is still true when
simulated point sources are subtracted from the data and when stacking is performed. In
the following sections, we use a detection threshold of TS ≥ 25, corresponding to a
5σ detection level, based on one more free parameter in the alternative
hypothesis compared to the null hypothesis.
-distribution is still true when
simulated point sources are subtracted from the data and when stacking is performed. In
the following sections, we use a detection threshold of TS ≥ 25, corresponding to a
5σ detection level, based on one more free parameter in the alternative
hypothesis compared to the null hypothesis.
 |
Fig. 1 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The co-adding is performed for simulated regions that only contain EGB and GB and for regions that additionally contain a simulated point-like source (PS) at the center. Three samples with different integrated fluxes of the point-like source, 2.5 × 10-10, 5.0 × 10-10 and 7.5 × 10-10 ph/(cm2 s), are used. The detection threshold TS ≥ 25 is indicated by the dashed line. |
3. Tests with simulated data
In the following, the co-adding is tested using 40 simulated ROIs that are randomly distributed at high galactic latitudes |b| > 25°. Sources close to the galactic plane are excluded to avoid potential mis-modelings of the galactic diffuse emissions and to avoid a high number of background point sources in the analyzed ROIs. This is mainly relevant for the analysis of real data in Sect. 4 and applied here for consistency. The simulations are performed with gtobssim for 162 weeks of Fermi operation using the real spacecraft information (2008-08-04 to 2011-09-13) and for energies from 200 MeV to 100 GeV. The resulting photon data is filled into CountCubes with 100 × 100 pixels and 40 energy intervals in logarithmic scale, corresponding to square-shaped ROIs with an angular sidelength of 20°.
We made use of 40 ROIs because the available number of real sources used to test this method in Sect. 4.3 is on the order of 30. Furthermore, the co-adding method will be applied to search for gamma-ray emission from a sample of galaxy clusters in an upcoming paper (Huber et al., in prep.). The available number of clusters, after selection cuts similar to those used by (Reimer et al. 2003), is expected to be on the same order.
3.1. Robustness against false detections
First, we investigate the probability of a false detection of a point-like emission due
to statistical fluctuations of the co-added diffuse emissions. The model used to describe
the test source at the ROI center is defined by a power law with a fixed photon index of
−2.0. The normalizations of EGB and GB and the prefactor of the test source are free
parameters during the likelihood fit. As expected, co-adding of diffuse background yields
no significant signal at the position of the test source. As shown by the dark grey solid
line in Fig. 1, the TS values take values close to
zero for any number of co-added ROIs. Although this curve appears flat, the TS values
underlie the fluctuations expected for the analysis of pure diffuse background. Since the
TS values stay below TS = 25, we compute the 90% confidence level (CL) upper limits (UL).
To obtain the 90% CL UL on the gamma-ray flux, the prefactor of the test source spectrum
is stepwise-increased until 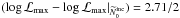 (Cowan 1997), where ℒmax is the maximized
likelihood-function and
(Cowan 1997), where ℒmax is the maximized
likelihood-function and 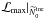 is the likelihood-function recomputed after
is the likelihood-function recomputed after 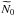 has been incremented. The resulting test source spectrum is then integrated over the full
simulated energy range from 200 MeV to 100 GeV.
has been incremented. The resulting test source spectrum is then integrated over the full
simulated energy range from 200 MeV to 100 GeV.
 |
Fig. 2 Integrated photon flux or 90% CL upper limit (UL) with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The co-adding is performed for simulated regions that only contain EGB and GB and for regions that additionally contain a point-like source (PS) at the center. Three samples with different integrated fluxes of the point-like source, 2.5 × 10-10, 5.0 × 10-10 and 7.5 × 10-10 ph/(cm2 s), are used. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. |
The UL development for the test source is shown by the dark grey solid line in Fig. 2. With an increasing number of co-added ROIs the probability of false signals due to Poissonian fluctuations is reduced. The computed UL decreases until it reaches an asymptote after approximately 25 co-adding steps. By co-adding 40 ROIs, an upper limit on the integrated flux of approximately 3 × 10-11 ph/(cm2 s) is obtained.
3.2. Detectability of weak signals
In a second step, we test the ability of the method to detect a signal from weak point-like emissions. Additional sets of simulations are performed that add a point-like source, denoted as central source, to the center of the previously simulated diffuse background regions. The central sources are simulated for different integrated fluxes [2.5, 5.0 and 7.5 × 10-10 ph/(cm2 s)] using a power-law spectrum with a photon index −2.0. Standard analyses of the individual ROIs (no co-addition applied) reveal no significant signal (TS ≥ 25) associated with the test source for any of these data sets. We perform the co-adding method independently for the different integrated fluxes using a power-law test source with a photon index −2.0, for which the resulting developments of the TS values are shown in Fig. 1. Central sources with a flux of 2.5 × 10-10 ph/(cm2 s) remain undetected during 40 co-adding steps. In contrast, sources with twice this integrated flux yield a clear detection after 15 co-added ROIs, and sources with a flux of 7.5 × 10-10 ph/(cm2 s) are detected after 10 co-additions. The high TS values, on the order of 100 and 200, after 40 stacking steps show clearly the power of this method to detect weak emissions from combined regions.
In each co-adding step, we also compute integrated flux values for the detected and 90% CL UL for the undetected samples, which are shown in Fig. 2. The UL values for the sources with 2.5 × 10-10 ph/(cm2 s) decrease strongly at the beginning and reach an asymptote after 10 co-adding steps, that is significantly higher than the one obtained from the diffuse background. This can be explained by the fact that the co-added central sources in this sample almost reach detection level. It can be seen from the same figure that the statistical uncertainties (grey and blue shaded areas) on the integrated fluxes of the detected samples are reduced with an increasing number of co-additions.
3.3. Dependence on the spectral hardness
In the following, the dependence of the source significance on different spectral shapes is tested. For this, four samples of simulated ROIs in which the central sources have a common integrated flux of 7.5 × 10-10 ph/(cm2 s) but different photon indices [−2.0, −2.4, −2.8 and −3.2] were produced. The samples are co-added and analyzed separately using a test source model that applies the same spectral shape as in the respective simulation. The resulting TS values are shown in Fig. 3. The two samples with photon indices −2.0 and −2.4 are clearly detected after 10 and 28 co-additions, respectively. Although the simulated integrated flux is the identical, we find no significant signal for the two softer spectra. Hard spectra provide, compared to soft spectra, an increased number of events in high energy bins, which make the likelihood, due to an improved PSF at high energies, more sensitive to a spatial correspondence between model and data.
 |
Fig. 3 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for simulated ROI samples that contain central sources with photon indices −2.0, −2.4, −2.8 and −3.2. For the analysis, power-law spectra are used that apply the same fixed photon indices as in the corresponding simulations. The stacking is also performed for ROIs that contain central sources with photon index −2.0 using a test source with photon index −2.4 in the analysis. |
In Fig. 4, the integrated flux of the test source is reported for the samples with photon indices −2.0 and −2.4, for which the values obtained after 40 co-additions are consistent with the simulated value of 7.5 × 10-10 ph/(cm2 s). Since a TS ≥ 25 is not reached for the samples with photon indices −2.8 and −3.2, 90% CL flux UL are computed instead.
 |
Fig. 4 Integrated photon flux or 90% CL upper limit (UL) with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for simulated ROI samples that contain central sources with photon indices −2.0, −2.4, −2.8 and −3.2. For the analysis, power-law spectra are used that apply the same fixed photon indices as in the corresponding simulations. The stacking is also performed for ROIs that contain central sources with photon index −2.0 using a test source with photon index −2.4 in the analysis. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. All central sources are simulated with an integrated flux of 7.5 × 10-10 ph/(cm2 s), indicated by the dashed line. |
 |
Fig. 5 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for a simulated source sample with mixed spectral shapes using analysis test sources with photon indices −2.0, −2.4 and −2.8. The detection threshold TS ≥ 25 is indicated by the dashed line. |
In cases in which the exact spectral features in the data are unknown, it may help to investigate the data using different spectral shapes. In Fig. 3, the TS values are computed for sources simulated with a photon index of −2.0 and analyzed with a photon index of −2.4. Applying an analysis spectrum that is softer than the spectrum in the data decreases the TS increment per stacking step, which is also the case if a harder analysis spectrum, e.g. with a photon index of −1.6, is used. The method is thus sensitive to the correspondence between the spectral shape in the model and the spectral shape in the data, which is a useful feature to investigate the combined spectrum of the sources in the sample.
The sensitivity of the likelihood analysis to events in high energy bins leads in this case to an increased integrated test source flux if a photon index −2.4 is used, as it is shown in Fig. 4, and to a decreased flux applying a photon index of −1.6.
3.4. Detectability of a source sample with mixed spectral shapes
In the following, we investigate the impact of having a source sample with mixed spectra, as it might be the case for different astrophysical sources. For this, simulated source spectra with different photon indices [−2.0, −2.4, −2.8 and −3.2] are mixed during the co-adding. We analyze the mixed sample for three different photon indices of the test source, [−2.0, −2.4, −2.8], and compute the TS values after each stacking step. The common integrated flux of the simulated central sources is again 7.5 × 10-10 ph/(cm2 s). The results are shown in Fig. 5. All three cases reach the detection threshold after 30 to 35 stacking steps. The co-adding hence allows sources to be detected even if different spectral shapes are involved. The analysis with photon index −2.4 yields the highest significance, indicating that this spectral shape yields, in this example, the best agreement with the mixed spectrum. The corresponding integrated test source fluxes for each stacking step are shown in Fig. 6. The flux that we find analyzing the mixed source spectrum with a photon index of −2.4 is slightly below the input flux of 7.5 × 10-10 ph/(cm2 s). Relative to this value, we obtain an increased and decreased integrated flux using photon indices −2.8 and −2.0, respectively, which can be explained again by the sensitivity of the likelihood fit to events in high energy bins as discussed previously.
It is possible to detect the spectral shape in the data using the photon index as an additional free parameter during the fitting procedure. This works well if sources with the same spectral shapes are stacked. In case of the present mixed spectra, however, it is not possible to achieve a sufficient likelihood fit quality if both the prefactor and the spectral index are free to vary.
 |
Fig. 6 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for a simulated source sample with mixed spectral shapes using analysis test sources with photon indices −2.0, −2.4 and −2.8. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. All central sources are simulated with an integrated flux of 7.5 × 10-10 ph/(cm2 s), indicated by the dashed line. |
4. Tests with real data
4.1. Robustness against false detections
Using real data, downloaded from the Fermi Science Support Center9, we again investigate the probability of false source detections due to diffuse background fluctuations, as in Sect. 3.1. The stacking is first performed with a sample of ROIs that contain as few Fermi-LAT detected sources as possible, and next with ROIs that contain Fermi-LAT sources with 5° to 10° angular separation from the ROI center. From all-sky data obtained during 162 weeks of LAT observations (2008-08-04 to 2011-09-13), 40 ROIs are selected for each of the two samples while galactic latitutes |b| < 25° are again excluded. In the following, we denote these ROIs as dark patches. The same energy and ROI size cuts are applied as in Sect. 3 and the identical spacecraft information is used. The selected events belong to the SOURCE class10. Before stacking, individual binned likelihood analyses are performed on each ROI, as it is described in Sect. 2, and the Fermi-LAT detected point sources are simulated and subtracted from the data. The resulting maps of counts (data minus simulated Fermi-LAT sources) are co-added. For the co-adding analysis, a model is applied that includes the EGB, GB emissions and a power-law test source with photon index −2.0. The normalizations of EGB and GB and the prefactor of the test source are, as in Sect. 3, free parameters during the fitting procedure. For both samples, the TS values computed for the test source remain <1 for all numbers of co-added ROIs.
 |
Fig. 7 The 90% CL upper limit (UL) on the integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The first sample consists of isolated dark patches that contain as few detected Fermi-LAT sources as possible. The second sample consists of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. |
The resulting 90% CL UL on the integrated test source flux are shown in Fig. 7. A flux upper limit of approximately 3 × 10-11 ph/(cm2 s) is obtained after 40 stackings for the first sample, which is consistent with the results for the simulated dark regions in Fig. 2. In the second sample, the flux upper limit rises during the stacking and results in approximately 5 × 10-11 ph/(cm2 s) after 40 co-additions. This behaviour can be explained by slight mis-modelings of the background point sources or the diffuse backgrounds in the vicinity of the source of interest.
4.2. Detectability of weak signals
We perform a consistency check by repeating the study discussed in Sect. 3.2, but this time the diffuse background is obtained from real data. As before, a simulated point-like source with an integrated flux of 7.5 × 10-10 ph/(cm2 s) is added at the center of each dark patch. The detected Fermi-LAT sources are fit and subtracted from each ROI prior the stacking. Using again a test source with photon index −2.0 in the model, we obtain a TS value for each co-adding step. The results are shown in Fig. 8 and compared with the results previously obtained for the simulated diffuse backgrounds. In all three cases, the detection threshold is reached within 5 to 10 stacking steps.
 |
Fig. 8 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed separately for three cases: simulated point-like sources (PS) with an integrated flux of 7.5 × 10-10 ph/(cm2 s) are added to simulated diffuse background regions, the first sample of dark patches that contain as few sources as possible and to the second sample of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. The detection threshold TS ≥ 25 is indicated by the dashed line. |
 |
Fig. 9 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed separately for three cases: simulated point-like sources (PS) with an integrated flux of 7.5 × 10-10 ph/(cm2 s) (dashed line) are added to simulated diffuse background regions, the first sample of dark patches that contain as few sources as possible and to the second sample of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. |
The corresponding developments of the integrated flux values are shown in Fig. 9. The final values obtained after 40 co-additions are consistent with the input flux of 7.5 × 10-10 ph/(cm2 s).
4.3. Application to real point-like emissions
In a further test, the method is applied to real point-like sources that are listed in the LAT 2-year point source catalog. 33 weak Fermi-LAT detected sources with average source significances close to 5σ are selected for this purpose from galactic latitudes |b| > 25°. As before, binned likelihood analyses are performed on the individual ROIs, in order to subtract the known Fermi-LAT sources from the data. The 33 selected Fermi-LAT sources are treated as undetected and therefore not included in the models. For the co-adding analysis, a model is applied that includes EGB and GB emissions and a point-like test source with photon index −2.0. We determine the TS values for each stacking step and find them approximately linearly increasing during the stacking, until a final value ~1000 is reached after 33 co-additions. Figure 10 illustrates the development of the integrated test source flux during the stacking, which yields a final integrated flux of 2 × 10-9 ph/(cm2 s). We find an excellent agreement with the averaged integrated fluxes that are obtained from individual ROI analyses (no subtraction of simulated sources, no co-adding).
 |
Fig. 10 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for Fermi-LAT detected point-like sources using the co-adding method (the grey shaded area corresponds to the statistical uncertainty). The results obtained with the Composite2 analysis are plotted for comparison. |
As a further consistency check, we apply the stacking tool Composite2, provided as part of the Science Tools, to the 33 Fermi-LAT sources. Since the ROIs are kept seperate in this case, we can not subtract the detected background point sources but need to provide individual models for each ROI that take into account these sources, the diffuse backgrounds as well as a test source at the center. The ROIs are then stepwise-added to the composite analysis and the integrated test source flux is determined after each stacking step. In Fig. 10, the resulting integrated fluxes are compared to the values obtained with the co-adding method. The flux developments for both methods, the co-adding and the Composite2 analysis, are in good agreement with each other, particularly for >4 stacking steps. Due to the subtraction of point sources from the data, there is a departure between the co-adding and the Composite2 method during the first stacking steps, clearing away after a few co-additions since potential mis-modelings of the subtracted sources and resulting negative counts vanish in the diffuse background fluctuations.
4.4. Visibility of stacked sources
The 33 Fermi-LAT sources from the previous section are used to illustrate the effect of the co-adding method on the maps of counts. Figure 11 shows the map of counts for one of the 33 regions containing a weak but known point-like source at the center, as it is obtained from Fermi-LAT all-sky data. This map corresponds to the CountCube of this region summed over all energies. The simulated background point sources have not yet been subtracted. After preparing the 33 regions according to Sect. 2.2, i.e. by subtracting the non-central point sources, stacking of these regions results in the map of counts shown in Fig. 12. The background appears smooth, while the cumulative emission of the 33 sources is clearly visible at the center.
 |
Fig. 11 Map of gamma-ray counts of a region that hosts a weak but known point-like emission at its center. This map corresponds to the CountCube of this region, summed over all energies. |
5. Summary and discussion
The stacking method presented in the previous sections is based on stacked maps of LAT counts and applies the public Fermi Science Tools for data preparation and maximum likelihood analysis. This method combines regions of potential gamma-ray sources in such a way that potential signals add constructively to increase the cumulative significance of these sources. We demonstrate with the aid of simulations that the method is capable to detect weak point-like emissions from sources that are individually not significant and to determine the corresponding average photon flux and flux upper limits. The method is sensitive to the correct choice of the spectral model for the sources to investigate, a feature that can be used for a systematic examination of the combined source spectrum. We find that the stacking of hard emission spectra leads to a higher source significance compared to the stacking of soft spectra, due to the improvement of the Fermi-LAT PSF at high energies. Furthermore, the source significance is generally higher if the individual spectral contributors are of similar spectral shape, and the significance is decreased if the spectra deviate strongly from each other. The method is successfully applied to real data, and an excellent agreement between the input and reconstructed source fluxes is found.
 |
Fig. 12 Map of gamma-ray counts of 33 stacked regions. Each of these regions hosts a weak but known point-like emission at the center. This map corresponds to the CountCube of these stacked regions, summed over all energies. |
Although the likelihood functions of the co-adding and the existing Composite2 method differ from each other, we show that both methods lead to similar results. The co-adding of maps of counts allows background point sources to be subtracted from the data and the model-predicted contribution of the diffuse backgrounds to be combined. This leads to a simple model for the likelihood analysis, that consists of only three components, i.e. the diffuse backgrounds and a common spectral model for the sources of interest, for any number of stacked sources. The co-adding method correlates the counts of the investigated sources in a defined way which can even help to make these sources visible in the count maps.
References
- Ackermann, M., Ajello, M., Albert, A., et al. 2011, Phys. Rev. Lett., 107, 241302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Cillis, A. N., Hartman, R. C., & Bertsch, D. L. 2004, ApJ, 601, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Cillis, A. N., Torres, D. F., & Reimer, O. 2005, ApJ, 621, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Cillis, A. N., Reimer, O., & Torres, D. F. 2007, Ap&SS, 309, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Cowan, G. 1997, Statistical data analysis (Oxford science publications) [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Particle Data Group. 2010, J. Phys. G: Nucl. Part. Phys., 37, equation (33.35) [Google Scholar]
- Petry, D. 2005, in High Energy Gamma-Ray Astronomy, eds. F. A. Aharonian, H. J. Völk, & D. Horns, AIP Conf. Ser., 745, 709 [Google Scholar]
- Reimer, O., Pohl, M., Sreekumar, P., & Mattox, J. R. 2003, ApJ, 588, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Skellam, J. G. 1946, J. Royal Stat. Soc., 109, 296 [CrossRef] [Google Scholar]
- The Fermi-LAT Collaboration 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The co-adding is performed for simulated regions that only contain EGB and GB and for regions that additionally contain a simulated point-like source (PS) at the center. Three samples with different integrated fluxes of the point-like source, 2.5 × 10-10, 5.0 × 10-10 and 7.5 × 10-10 ph/(cm2 s), are used. The detection threshold TS ≥ 25 is indicated by the dashed line. |
| In the text | |
 |
Fig. 2 Integrated photon flux or 90% CL upper limit (UL) with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The co-adding is performed for simulated regions that only contain EGB and GB and for regions that additionally contain a point-like source (PS) at the center. Three samples with different integrated fluxes of the point-like source, 2.5 × 10-10, 5.0 × 10-10 and 7.5 × 10-10 ph/(cm2 s), are used. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. |
| In the text | |
 |
Fig. 3 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for simulated ROI samples that contain central sources with photon indices −2.0, −2.4, −2.8 and −3.2. For the analysis, power-law spectra are used that apply the same fixed photon indices as in the corresponding simulations. The stacking is also performed for ROIs that contain central sources with photon index −2.0 using a test source with photon index −2.4 in the analysis. |
| In the text | |
 |
Fig. 4 Integrated photon flux or 90% CL upper limit (UL) with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for simulated ROI samples that contain central sources with photon indices −2.0, −2.4, −2.8 and −3.2. For the analysis, power-law spectra are used that apply the same fixed photon indices as in the corresponding simulations. The stacking is also performed for ROIs that contain central sources with photon index −2.0 using a test source with photon index −2.4 in the analysis. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. All central sources are simulated with an integrated flux of 7.5 × 10-10 ph/(cm2 s), indicated by the dashed line. |
| In the text | |
 |
Fig. 5 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for a simulated source sample with mixed spectral shapes using analysis test sources with photon indices −2.0, −2.4 and −2.8. The detection threshold TS ≥ 25 is indicated by the dashed line. |
| In the text | |
 |
Fig. 6 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for a simulated source sample with mixed spectral shapes using analysis test sources with photon indices −2.0, −2.4 and −2.8. The grey and blue shaded areas correspond to the statistical uncertainties on the integrated flux values. All central sources are simulated with an integrated flux of 7.5 × 10-10 ph/(cm2 s), indicated by the dashed line. |
| In the text | |
 |
Fig. 7 The 90% CL upper limit (UL) on the integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The first sample consists of isolated dark patches that contain as few detected Fermi-LAT sources as possible. The second sample consists of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. |
| In the text | |
 |
Fig. 8 Test statistic values with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed separately for three cases: simulated point-like sources (PS) with an integrated flux of 7.5 × 10-10 ph/(cm2 s) are added to simulated diffuse background regions, the first sample of dark patches that contain as few sources as possible and to the second sample of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. The detection threshold TS ≥ 25 is indicated by the dashed line. |
| In the text | |
 |
Fig. 9 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed separately for three cases: simulated point-like sources (PS) with an integrated flux of 7.5 × 10-10 ph/(cm2 s) (dashed line) are added to simulated diffuse background regions, the first sample of dark patches that contain as few sources as possible and to the second sample of dark patches that contain Fermi-LAT sources with an angular separation between 5° and 10° from the ROI center. |
| In the text | |
 |
Fig. 10 Integrated photon flux with respect to point-like emission at the center of the ROIs versus the number of co-added ROIs. The stacking is performed for Fermi-LAT detected point-like sources using the co-adding method (the grey shaded area corresponds to the statistical uncertainty). The results obtained with the Composite2 analysis are plotted for comparison. |
| In the text | |
 |
Fig. 11 Map of gamma-ray counts of a region that hosts a weak but known point-like emission at its center. This map corresponds to the CountCube of this region, summed over all energies. |
| In the text | |
 |
Fig. 12 Map of gamma-ray counts of 33 stacked regions. Each of these regions hosts a weak but known point-like emission at the center. This map corresponds to the CountCube of these stacked regions, summed over all energies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


