| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201118511 | |
| Published online | 29 October 2012 | |
Angular momentum transport and turbulence in laboratory models of Keplerian flows
1
Department of Physics and Center for Nonlinear DynamicsUniversity of
Texas,
Austin,
TX,
78712,
USA
e-mail: mpaolett@gmail.com
2
Physics of Fluids Group, Faculty of Science and Technology, Mesa+
Institute and Burgers Center for Fluid Dynamics, University of Twente,
7500AE
Enschede, The
Netherlands
3
CNRS URA 2464 SPHYNX/SPEC/IRAMIS/DSM, CEA Saclay,
91191
Gif-sur-Yvette,
France
4
Departments of Physics and Geology, Institute for Research in
Electronics and Applied Physics, Institute for Physical Science and Technology,
University of Maryland, College
Park, MD
20742,
USA
e-mail: lathrop@umd.edu
Received:
23
November
2011
Accepted:
5
September
2012
We present angular momentum transport (torque) measurements in two recent experimental studies of the turbulent flow between independently rotating cylinders. In addition to these studies, we reanalyze prior torque measurements to expand the range of control parameters for the experimental Taylor-Couette flows. We find that the torque may be described as a product of functions that depend only on the Reynolds number, which describes the turbulent driving intensity, and the rotation number, which characterizes the effects of global rotation. For a given Reynolds number, the global angular momentum transport for Keplerian-like flow profiles is approximately 14% of the maximum achievable transport rate. We estimate that this level of transport would produce an accretion rate of Ṁ/Ṁ0~10-3 in astrophysical disks. We argue that this level of transport from hydrodynamics alone could be significant. We also discuss the possible role of finite-size effects in triggering or sustaining turbulence in our laboratory experiments.
Key words: accretion, accretion disks / turbulence / methods: laboratory / hydrodynamics
© ESO, 2012
1. Introduction
Astrophysical disks are ubiquitous in the universe, orbiting around a wide panel of massive objects, from black holes to stars. An essential ingredient of their dynamics is the radial transport of angular momentum that governs the rate of material falling onto the central object. Realistic models of this process are impeded by the complexity of the disk dynamics, including a wide variety of processes such as general relativistic effects, self-gravitation, radiation, dynamics of plasma magnetic fields and turbulence. In particular, the contribution from hydrodynamics to the angular momentum transport in such astrophysical flows is not yet understood.
A natural first-step in the construction of a robust model is to consider the minimal list of ingredients that can capture and reproduce the observed disk properties. Such a model has been proposed several decades ago by Shakura & Sunyaev (1973) and Pringle (1981), and was given the name α disks. In that model, the radial transport of angular momentum is parameterized by a turbulent viscosity coefficient that needs to be prescribed or measured. In the past, there have been several attempts to estimate this coefficient from an analytical closure model (Dubrulle 1992), numerical simulations (see e.g. Rozyczka & Spruit 1993; Brandenburg et al. 1995; Abramowicz et al. 1996; Stone et al. 1996; Drecker et al. 1998; Beckwith et al. 2011; and a recent review by King et al. 2007, and references therein), or using theoretical arguments (Canuto et al. 1984; Mukhopadhyay 2008).
An alternative promising option, as recognized by Zeldovich (1981) and Richard & Zahn (1999), is offered by instead focusing on laboratory experiments. Indeed, it may be shown (Hersant et al. 2005) that under simple but well founded approximations the equations governing an α disk are similar to the equation of motion of an incompressible rotating shear flow, with penetrable boundary conditions and cylindrical geometry. This can be modeled in the Taylor-Couette flow (see Fig. 1), a fluid layer sheared between two independently rotating, coaxial cylinders.
These proposals motivated several studies of the transport properties in rotating shear flows, with contradicting conclusions. From the numerical point of view, the problem has been mainly tackled in the astrophysical community using the so-called shearing sheet approximation either without explicit viscosity (Balbus et al. 1996; Hawley et al. 1999), or with explicit viscosity (Lesur & Longaretti 2005) at resolutions ranging from 323 to 2563. This method is often seen as the simplest way to deal with the (unknown) disk boundary conditions, but it has some limitations as discussed in past work (Pumir 1996; Umurhan & Regev 2004; Fromang & Papaloizou 2007). While Balbus et al. (1996); Hawley et al. (1999) did not use explicit viscosity, thereby making it difficult to directly define a Reynolds number, they estimated that their simulations achieved Re ~ 103−104. In their case, they did not find any evidence for a subcritical transition to turbulence for Keplerian flows, which they determined to be completely stabilized by the Coriolis force. The simulations of Lesur & Longaretti (2005) at N3 = 1283 could achieve Re ≈ 4 × 104, according to their estimation. They concluded, on the other hand, that Keplerian like flows could exhibit turbulence, although the turbulence intensity may be too weak to account for the rate of energy dissipation observed. This has motivated us to experimentally explore Reynolds number up to Re = 4 × 106, a value that is beyond present computational efforts.
The overwhelming computational requirements needed to obtain larger Reynolds numbers
motivate an alternate approach to explore the transport properties of Taylor-Couette flow
through laboratory experiments, which can obtain much larger Reynolds numbers, as we present
here. Depending upon the community, the strength of the turbulent transport is quantified in
various ways. The most basic quantification (Wendt
1933) is the one through the torque T which is necessary to keep
the inner cylinder rotating at a given velocity. The dimensionless version thereof is
G = T/(Lmidρν2),
where ρ is the fluid density, ν its kinematic viscosity
and Lmid the effective length of the cylinders (Paoletti & Lathrop 2011). Eckhardt et al. (2007b) and van Gils
et al. (2011b) used
Nuω = G/Glam,
where Glam is the laminar torque, to quantify the angular
velocity flux from the inner to the outer cylinder, in order to highlight the analogy
between Taylor-Couette and Rayleigh-Bénard flow (Dubrulle
& Hersant 2002; Eckhardt et al.
2007b,a). The engineering community prefers
the drag-coefficient
cf = G/Re2,
where  and
η = a/b is the
radius ratio and Re1/2 the
Reynolds number of the inner/outer cylinder. In the astrophysics community, the same
information is often expressed in terms of the β coefficient, defined by
β = 2Gη2/(π(1 − η)4Re2) = 2η2cf/(π(1 − η)4),
which can be interpreted as a dimensionless turbulent viscosity.
and
η = a/b is the
radius ratio and Re1/2 the
Reynolds number of the inner/outer cylinder. In the astrophysics community, the same
information is often expressed in terms of the β coefficient, defined by
β = 2Gη2/(π(1 − η)4Re2) = 2η2cf/(π(1 − η)4),
which can be interpreted as a dimensionless turbulent viscosity.
By reexamining previous data obtained by Wendt (1933) and Taylor (1936), Richard & Zahn (1999) showed that the β-parameter is on the order of βRZ ~ 10-5 for Keplerian disks. A more complete analysis, including results of new experiments on a classical Taylor-Couette flow from Richard (2001), led to the same conclusion (Dubrulle et al. 2005). In contrast, an original experiment, built in Princeton (Ji et al. 2006) so as to minimize end effects, measured a β coefficient through radial Reynolds stresses and obtained a value smaller by more than an order of magnitude βP ~ 7 × 10-7. Furthermore, the Princeton experiments could not distinguish the angular momentum transport in Keplerian flows from their measurements in solid-body rotation, where the cylinders rotate together thereby resulting in zero angular momentum transport.
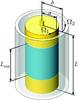 |
Fig. 1 Taylor-Couette flow may be used to study angular momentum transport in rotating shear flows. The fluid is sheared between two independently rotating cylinders of radii a < b that rotate at angular velocities Ω1 and Ω2 for the inner and outer cylinders, respectively. Although the total fluid height is given by L, some experiments only measure the contribution to the torque over a central section of length Lmid to minimize end effects, as in (Lathrop et al. 1992b,a; Lewis & Swinney 1999; van den Berg et al. 2003, 2005, 2007; Paoletti & Lathrop 2011; van Gils et al. 2011b). |
In the present contribution, we report precise global angular momentum transport (torque) measurements in two independent experiments performed at very large Reynolds number and compute the resulting β coefficient for different rotation profiles. To further study the scaling of angular momentum transport in rotating shear flows, we compare our measurements to those of Wendt (1933), Taylor (1936) and Richard (2001), Dubrulle et al. (2005). We find a universal scaling of the torque for various rotation profiles that captures the effects of the various geometries used in the experiments summarized here.
2. Apparatus and experimental details
2.1. Apparatus: generalities
The experiments presented here all examine the transport of angular momentum (torque) in classical Taylor-Couette flow. Figure 1 shows a schematic representation of our experiments. The fluid is contained between concentric cylinders of radii a < b. The inner (outer) cylinder rotates at an angular velocity of Ω1(Ω2). The overall height of the fluid contained between the axial boundaries is given by the length L. The geometry of a particular Taylor-Couette flow apparatus is often defined in dimensionless form by the radius ratio η ≡ a/b and the aspect ratio Γ ≡ L/(b − a).
The ideal Couette flow is infinite in axial extent. As such, several methods have been employed to handle the finite-size effects that are present in any laboratory experiment. The most common case has the axial boundaries rotate with one of the two cylinders. In other experiments, the axial boundaries are divided at the mid-gap and have the inner (outer) portion rotate with the inner (outer) cylinder. This split-ring approach has been further developed to allow for pairs of rings that can independently rotate with respect to the cylinders. Allowing the axial boundaries to independently rotate aids in the suppression of finite-size effects (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010).
Parameters used in the experiments discussed here.
The data that we analyze and present stems from several different experiments, which are summarized in Table 1. The early experiments by Wendt (1933) measured the torque required to drive the inner cylinder for three values of η. The system had a free surface at the top, although we quote an effective aspect ratio defined using the axial length of the apparatus. The data from Taylor (1936) determined the scaling of the torque for several values of η with the inner cylinder stationary (Ω1 = 0). Richard’s experiments (Richard 2001; Dubrulle et al. 2005) did not directly measure the torque. Instead, critical Reynolds numbers for various transitions were observed and the analysis presented by Dubrulle et al. (2005) was used to estimate the corresponding torque. We do not present data from the experiments of Ji et al. (2006), but rather use their reported measurements as a basis for comparison, as detailed in Sect. 4. The two most recent experiments by Paoletti & Lathrop (2011) and van Gils et al. (2011b) are further described in the forthcoming sections.
2.2. Apparatus: the Maryland experiment
The experiments presented by Paoletti & Lathrop (2011), henceforth referred to as the Maryland experiment, are conducted in the apparatus constructed by Lathrop et al. (1992b,a), which was modified to allow the outer cylinder to rotate independently. The outer cylinder is an anodized aluminum cylinder with the same physical dimensions as in Lathrop et al. (1992b,a); Lewis & Swinney (1999), specifically b = 22.085 cm and a working fluid height L = 69.50 cm. The inner cylinder is stainless steel with a radius a = 16.000 cm yielding a radius ratio η = 0.7245 and an aspect ratio Γ = 11.47. The inner cylinder is rotated up to Ω1/2π = 20 s-1 while the outer cylinder may be rotated in either direction up to |Ω2/2π| = 10 s-1. Both angular velocities are measured by shaft encoders and controlled to within 0.2% of the set value.
The axial boundaries in the Maryland experiment rotate with the outer cylinder. To reduce end effects in the torque measurements the inner cylinder is divided axially into three sections of length 15.69, 40.64 and 15.69 cm (see schematics in Lathrop et al. 1992b,a). Only the central section of length Lmid = 40.64 cm (see Fig. 1) senses the torque of the fluid as described in Lathrop et al. (1992b,a). The regions of the flow within 2.58 gap widths from each of the axial boundaries, where secondary circulation setup by finite boundaries is strongest, are avoided in the torque measurements.
Taylor-Couette control parameters related to some astrophysical disks, as computed by Hersant et al. (2005).
The desired accuracy of our measurements requires that the temperature of the water be precisely controlled. In contrast to prior experiments (Lathrop et al. 1992b,a; Lewis & Swinney 1999; van den Berg et al. 2003, 2005, 2007; van Gils et al. 2011b) where the system was cooled at the axial boundaries, we control the temperature of the water by heating and cooling the outer cylinder. This allows the working fluid to be temperature-controlled along the entire axial length of the experiment, yielding a 6.5 fold increase in the temperature-controlled surface area. This is particularly important for Rayleigh-stable flows, where mixing is greatly reduced. In our experiments the temperature is 50 ± 0.02 °C yielding a kinematic fluid viscosity of ν = 5.5 × 10-3 cm2/s, except for Re > 2 × 106 where T = 90 °C and ν = 3.2 × 10-3 cm2/s.
2.3. Apparatus: the Twente experiment
The Twente turbulent Taylor-Couette (called T3C) facility, here referred to as the Twente experiment, is described in great detail in van Gils et al. (2011a). In short, the working fluid height is L = 92.7 cm, has an inner radius of a = 20.0 cm and an outer radius of b = 27.94 cm. The maximum inner and outer angular velocities are Ω1/2π = 20 Hz and |Ω2/2π| = 10 Hz, respectively. The system is fully temperature controlled through cooling of the upper and lower end plates, which co-rotate with the outer cylinder. The system is operated with water at a temperature of 20 °C, resulting in a kinematic viscosity of ν = 1.04 × 10-2 cm2/s. The torque is measured over the middle part of the inner cylinder of height Lmid = 53.6 cm to minimize the influence of the end-plates (similar to Lathrop et al. 1992b,a). The torque is measured by a load cell imbedded inside the middle section of the inner cylinder in both the Twente and Maryland experiments, in contrast to measuring the torque on the drive shaft that would be affected by mechanical seals in the end plates or by velocimetry measurements, as in the Princeton experiments (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012).
2.4. Control parameters
The analysis of our results is simplified by a proper choice of the control parameters.
As in Dubrulle et al. (2005), we use the following
three dimensionless control parameters, which fully describe the geometry and specify the
state of the dynamical Taylor-Couette system: 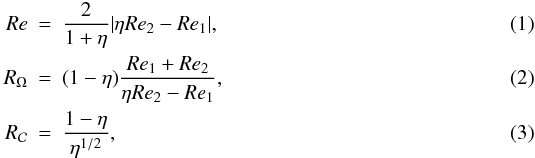 where
Re1 = aΩ1d/ν
and
Re2 = bΩ2d/ν
are the Reynolds number of the inner and outer cylinder and
d = (b − a) is the gap width.
where
Re1 = aΩ1d/ν
and
Re2 = bΩ2d/ν
are the Reynolds number of the inner and outer cylinder and
d = (b − a) is the gap width.
The above control parameters have been introduced so that their definitions apply to
rotating shear flows in general and not strictly only to the Taylor-Couette geometry. It
is very easy in this formulation to relate the Taylor-Couette flow to the shearing sheet
(plane Couette flow with rotation), by considering the limit
RC → 0. The linear stability properties of the fluid can
also be neatly recast using these control parameters. In the inviscid limit
(Re → ∞), and for axisymmetric disturbances, the linear stability
properties of the flow are governed by the Rayleigh criterion, namely that the fluid is
stable if the Rayleigh discriminant is everywhere positive: 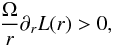 (4)where
L(r) = r2Ω(r)
is the specific angular momentum. Applying this criterion to the laminar profile leads to
(4)where
L(r) = r2Ω(r)
is the specific angular momentum. Applying this criterion to the laminar profile leads to
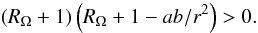 (5)Since
ab/r2 varies between
1/η and η, one obtains that in the
inviscid limit, the flow is unstable against infinitesimal axisymmetric disturbances when
(5)Since
ab/r2 varies between
1/η and η, one obtains that in the
inviscid limit, the flow is unstable against infinitesimal axisymmetric disturbances when
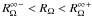 , where
, where
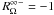 , respectively
, respectively
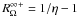 , are
the marginal stability thresholds in the inviscid limit (superscript ∞) in the cyclonic
case (RΩ > 0, subscript + ), and
anticyclonic case (RΩ < 0, subscript
−). This means that, in the anticyclonic case, any flow such that
RΩ < −1 is linearly stable against
axisymmetric disturbances. However, it may be non-linearly stable or unstable against
non-axisymmetric disturbances, as found in the experiments described here.
, are
the marginal stability thresholds in the inviscid limit (superscript ∞) in the cyclonic
case (RΩ > 0, subscript + ), and
anticyclonic case (RΩ < 0, subscript
−). This means that, in the anticyclonic case, any flow such that
RΩ < −1 is linearly stable against
axisymmetric disturbances. However, it may be non-linearly stable or unstable against
non-axisymmetric disturbances, as found in the experiments described here.
In the present paper, we determine the intensity of the momentum transport by measuring the torque required to drive the inner cylinder for a given set of parameters (Re,RΩ). Measurements described here suggest that at large enough Reynolds number, the nondimensional torque G = T/(ρν2Lmid), where T is the torque, ρ the fluid density, ν the kinematic viscosity and Lmid is defined in Fig. 1, varies approximately as G ~ Reα with 1.75 < α(Re) < 1.85, even for Rayleigh-stable flows. While this scaling exceeds the laminar case (G ~ Re), we note that these exponents are less than a simple dimensional argument would give: Such an argument would say that in a fully turbulent regime the transport properties could not depend on the molecular viscosity, which would imply that the quantity cf ~ G/Re2 is Reynolds number independent. The deviations from G ~ Re2 mean that the viscosity is always relevant for the transport, due to its dominance in the boundary layers. Only when the boundary layers are sufficiently disturbed by introducing wall roughness does one obtain G ~ Re2, as we have shown in our previous work (van den Berg et al. 2003).
2.5. Astrophysically relevant quantity
In the astrophysical context, one often considers asymptotic angular velocity profiles of the form Ω(r) ~ r−q where q characterizes the flow. In that case q = −∂lnΩ/∂lnr = −2/RΩ, which relates astrophysical profiles in the control parameters space of Taylor-Couette flows. For Keplerian flow, q = 3/2 resulting in RΩ = −4/3, which is an example of a linearly stable, anticyclonic flow. While Keplerian profiles cannot be precisely achieved by Taylor-Couette flows, states with RΩ < −1 are all linearly stable, anticyclonic flows that may be used to approximate astrophysical settings. We will refer to cases with RΩ < −1 as quasi-Keplerian, as in Ji et al. (2006).
Astrophysical disks are very wide with a ≪ b. Therefore, their geometrical global value of RC → ∞. In a local description of disks, one often considers the shearing sheet approximation, in which η → 1, so that RC → 0, as in plane-Couette flow. Here, we focus on global properties and consider only the limit η → 0 applicable to disks in the discussion. As a result of their astronomical size, the Reynolds numbers associated with accretion disks are very large. To give a few specific examples, parameters for typical T Tauri and Fu Ori stars have been computed by Hersant et al. (2005) and are given in Table 2.
In disks, angular momentum transport intensity is quantified through the accretion rate
Ṁ. In fact, as was shown in (Dubrulle
et al. 2005; Hersant et al. 2005), this
rate is directly related to the turbulent viscosity and the dimensionless torque. This
concept may be understood in the following way: pressure gradients substantially balance
centrifugal forces that develop in (incompressible) laboratory flows. Keplerian disks,
however, balance the centrifugal force with gravitational attraction. Thus when angular
momentum is transported radially outward, accretion disk matter responds by falling
radially inward at the rate Ṁ. The flux of angular momentum, which is
proportional to G, is thereby related to the accretion rate
Ṁ by (Dubrulle et al. 2005;
Hersant et al. 2005), 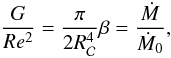 (6)where β
is a turbulent viscosity parameter such that
νt = βSr2, with
S a velocity shear, and Ṁ0 is an effective
accretion rate given by the mean surface density
(6)where β
is a turbulent viscosity parameter such that
νt = βSr2, with
S a velocity shear, and Ṁ0 is an effective
accretion rate given by the mean surface density 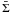 ,
the disk inner radius a, mean radius
,
the disk inner radius a, mean radius
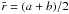 ,the
mean angular velocity
,the
mean angular velocity 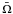 and the mean disk height
and the mean disk height 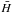 through
through 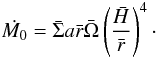 (7)As such, measurements
of G/Re2
in laboratory experiments may be used to estimate the hydrodynamical contribution to
angular momentum transport in accretion disks.
(7)As such, measurements
of G/Re2
in laboratory experiments may be used to estimate the hydrodynamical contribution to
angular momentum transport in accretion disks.
 |
Fig. 2 a) Our experiments span a large range of the Reynolds number Re, which controls the turbulence intensity, and the rotation number RΩ, introduced by Dubrulle et al. (2005), which compares shear to overall rotation. The rotation number can be used to distinguish between Rayleigh-stable flows (RΩ ≤ −1 or RΩ ≥ (1 − η)/η) and those that are linearly unstable (−1 < RΩ < (1 − η)/η). b) All of our measurements for −1 < RΩ < 0.38 are well above the linear stability curve (blue line) described by Esser & Grossmann (1996) and given by Eq. (8). The data are taken from separate experiments by van Gils et al. (2011b) (red squares) and (Paoletti & Lathrop 2011) (black circles). |
 |
Fig. 3 The scaling of the dimensionless torque G with the Reynolds number Re is independent of the rotation number RΩ, however the amplitude varies as in Paoletti & Lathrop (2011); van Gils et al. (2011b). The measurements by Paoletti & Lathrop (2011) are in black circles while the data from van Gils et al. (2011b) are shown by red squares. The thick blue line indicates the theoretical value for purely laminar flow, where angular momentum is transported only by molecular viscosity. |
3. Results
We study the scaling of the dimensionless torque G over a range of
Reynolds numbers for various constant rotation numbers (see Fig. 2), spanning a wide variety of flow states, including linearly stable
cyclonic and anticyclonic flows as well as linearly unstable states. Esser & Grossmann (1996) derived an analytical expression that
approximates the boundary for linear stability for all radius ratios and cylinder rotation
rate ratios. Their result for the critical Reynolds number
Rec may be expressed using the above control
parameters, as in Eqs. (16) and (17) in Dubrulle et al.
(2005): ![\begin{equation} Re_{\rm c}^2\(\Rom + 1\)\(\Rom +1 -\frac{1}{\eta x(\eta)^2}\) = -1708\(\frac{1-\eta}{2\eta[x(\eta)-1]}\)^4, \label{eq:Re_c} \end{equation}](/articles/aa/full_html/2012/11/aa18511-11/aa18511-11-eq144.png) (8)with
(8)with
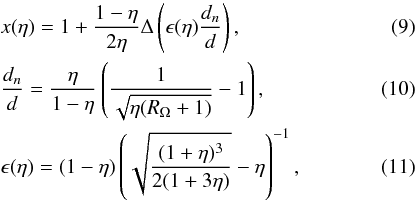 where
Δ(x) is a function equal to x if
x < 1 and equal to 1 if
x > 1. Equation (8) may be used to determine the stability boundary for the experiments
described in Table 1. As shown in Fig. 2b, all of our measurements for
−1 < RΩ < 0.38
are orders of magnitude above the laminar stability boundary. For
RΩ < −1 or
RΩ > 0.38 the system is linearly
stable for our radius ratios, although it may be possible for the system to undergo a
subcritical transition to turbulence. Corresponding torque measurements from the Twente
experiment are shown as red squares in Fig. 3 while the
data from Maryland are represented by black circles.
where
Δ(x) is a function equal to x if
x < 1 and equal to 1 if
x > 1. Equation (8) may be used to determine the stability boundary for the experiments
described in Table 1. As shown in Fig. 2b, all of our measurements for
−1 < RΩ < 0.38
are orders of magnitude above the laminar stability boundary. For
RΩ < −1 or
RΩ > 0.38 the system is linearly
stable for our radius ratios, although it may be possible for the system to undergo a
subcritical transition to turbulence. Corresponding torque measurements from the Twente
experiment are shown as red squares in Fig. 3 while the
data from Maryland are represented by black circles.
3.1. Existence of turbulence
In laminar flow, angular momentum is transported only by molecular viscosity, so that the dimensionless torque G is proportional to Re, with the prefactor depending upon RΩ. In Fig. 3, we show the expected laminar angular momentum transport (blue line) for the range of Re explored in this study for the case Ω2 = 0. As can be seen all the torque measurements considered differ from the theoretical expectation for laminar flow in two ways: (i) they increase faster than Re and (ii) they are much higher than the theoretical laminar value. This is an indication that the fluid is turbulent, with enhanced angular momentum transport in all the cases reported here. Note that these cases encompass several situations with RΩ < −1 (linearly stable anticyclonic flow) and RΩ > 0.4 (linearly stable cyclonic flow) in addition to many unstable states.
In particular, (approximate) Keplerian flows at RΩ = −4/3 are turbulent at Re ~ 105 in our experiments. This is in agreement with direct, visual observations of Richard (2001), performed at somewhat lower Reynolds number. We argue that this indicates that quasi-Keplerian flows can efficiently transport angular momentum in spite of their linear stability. However, the nature of this nonlinear instability remains unclear. We suggest that systematically perturbing quasi-Keplerian flow states at lower values of Re while measuring the torque, as in the experiments by Taylor (1936), could aid in the description of this likely nonlinear instability.
3.2. Enhancement of momentum transport
We now try to quantify the enhancement of angular momentum transport with respect to its laminar value, as a function of both Re and RΩ. As in Paoletti & Lathrop (2011); van Gils et al. (2011b), the torque at a given Re may be either increased or reduced depending upon RΩ; the Reynolds number alone is insufficient to describe the transport.
3.2.1. Variation with RΩ
Paoletti & Lathrop (2011) observed that variation of the torque at a given Re shows a pronounced maximum as a function of RΩ. An analogous dependence of the amplitude of an effective power-law scaling was also observed by van Gils et al. (2011b). To determine the effects of global rotation, we normalize G for each Re by G(Re,RΩ = 0) (Dubrulle et al. 2005), which we denote as G0. This normalization is different from Fig. 16 in Dubrulle et al. (2005) where G is normalized by G∞ ≡ G(Re,Ω2 = 0). The dependence of G/G0 on RΩ is shown in Fig. 5 with the data from Maryland shown as black circles and Twente in red squares.
 |
Fig. 4 a) The dimensionless torque G normalized by G0 ≡ G(Re,RΩ = 0) for different values of the radius ratio η nicely collapses when plotted as function of RΩ. The data from Wendt (1933) are shown as cyan (η = 0.68), blue (η = 0.85) and green (η = 0.935) triangles. Additional radius ratios are examined using the data from Taylor (1936), shown as orange diamonds, Richard (Richard 2001; Dubrulle et al. 2005), given by magenta squares, Paoletti & Lathrop (2011) indicated by black circles and van Gils et al. (2011b) by red circles. The solid lines are fits given by Eq. (12). Keplerian flow states are indicated by the dashed line at RΩ = −4/3. In b) we focus on the peak of the curve shown in a), but only present the data from Twente (van Gils et al. 2011b) (red) and Maryland (Paoletti & Lathrop 2011) (black). The solid line is the fit (12). |
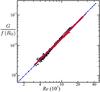 |
Fig. 5 The dimensionless torque G may be compensated by the fit f(RΩ) given by Eq. (12). The data from both Paoletti & Lathrop (2011) (black circles) and van Gils et al. (2011b) (red squares) agree with the best fit from Lewis & Swinney (1999) for the case where the outer cylinder was stationary (blue line). |
The agreement between the Twente and Maryland measurements is an important check, but not surprising given that the experiments have very similar geometries, measurement techniques and control parameters (see Table 1). Therefore, it remains unclear if the scaling of the normalized torque with RΩ is universal or if it depends upon other parameters, such as the radius ratio η. While the Twente experiment is capable of examining other values of η in future measurements, we may compare our results to previous experiments by Wendt (1933), Taylor (1936) and Richard (2001), which were analyzed by Dubrulle et al. (2005). The parameters of these past experiments are also summarized in Table 1. The measurements of Wendt (triangles), Taylor (orange diamonds) and Richard (magenta squares) are also shown in Fig. 4a.
As can be seen in Fig. 4, the dependence of the
normalized torque G/G0
on RΩ for various radius ratios in the range
0.68 ≤ η ≤ 0.973 collapse well. The data appear to follow distinct
approximate scalings given by 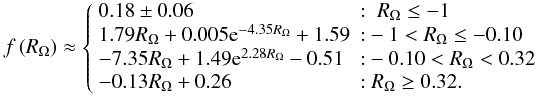 (12)Given
the rather different span of Re in each experiment and the varying
measurement techniques, it is not surprising that a few outliers remain. For example,
the values of G/G0 from
Richard’s experiments (Richard 2001) (magenta
squares) were computed using theoretical predictions regarding the correlation between
the torque and critical numbers for stability, as described in Dubrulle et al. (2005). The data from Wendt (1933), Taylor (1936), Paoletti & Lathrop (2011) and van Gils et al. (2011b) are direct measurements of
the torque, albeit with different apparati and measurement techniques.
(12)Given
the rather different span of Re in each experiment and the varying
measurement techniques, it is not surprising that a few outliers remain. For example,
the values of G/G0 from
Richard’s experiments (Richard 2001) (magenta
squares) were computed using theoretical predictions regarding the correlation between
the torque and critical numbers for stability, as described in Dubrulle et al. (2005). The data from Wendt (1933), Taylor (1936), Paoletti & Lathrop (2011) and van Gils et al. (2011b) are direct measurements of
the torque, albeit with different apparati and measurement techniques.
3.2.2. Variation with Reynolds number
The fits given in Eq. (12) may be used
to compensate the torque to account for the effects of global rotation. Figure 5 shows the dimensionless torque G
compensated by the fit f(RΩ) given in
Eq. (12) as a function of
Re. The data from Twente are shown as red squares while those of
Maryland are given by black circles. In both cases, the data agree well with the best
fit given by Lewis & Swinney (1999) for
the case Ω2 = 0 (blue line). This indicates that the amplitude of the torque
is affected by global rotation, as measured by
G/G0, while the
scaling with Re seems to be independent of
RΩ in the regime of our investigation. Therefore the
torque may be approximately factorized and written as 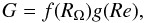 (13)where
f(RΩ) is measured in Fig. 4 and fit by Eq. (12) and our measurements of g(Re),
shown in Fig. 5, agree with previous measurements,
and may be fit by effective power-laws or logarithmically varying functions such as the
Prandtl-von Kármán form (Lathrop et al.
1992b,a; Lewis & Swinney 1999).
(13)where
f(RΩ) is measured in Fig. 4 and fit by Eq. (12) and our measurements of g(Re),
shown in Fig. 5, agree with previous measurements,
and may be fit by effective power-laws or logarithmically varying functions such as the
Prandtl-von Kármán form (Lathrop et al.
1992b,a; Lewis & Swinney 1999).
3.2.3. Comments
In addition to the observed data collapse, other interesting features arise in the normalized torque scaling with RΩ. The data from Taylor’s experiments (Taylor 1936) were obtained with a stationary inner cylinder (Ω1 = 0), and the flow is therefore Rayleigh-stable. However, the data from Wendt (1933), Maryland (Paoletti & Lathrop 2011) and Twente (van Gils et al. 2011b) over the same range of the rotation number, namely 0 < RΩ < 0.27, are obtained with counter-rotating cylinders. This configuration is linearly unstable, yet the measured values of G/G0 agree between all four experiments. We argue, as done by Taylor (1936), that the flow states in Taylor’s experiments could not have been laminar and must have undergone a subcritical transition to turbulence.
Paoletti & Lathrop (2011) observed that the torque scaling varied linearly with RΩ in four regions of the parameter space corresponding to: region I: RΩ ≤ −1, region II: −1 < RΩ ≤ −0.10, region III: −0.10 < RΩ < 0.38 and region IV: 0.38 < RΩ, where we have reordered the region numbers to correspond to increasing RΩ. Figure 4 shows that all of the data described here follow the region I–region II and region II–region III crossovers. The crossover between regions I and II corresponds to the Rayleigh stability criterion for all values of η. The crossover between regions II and III occurs at the observed maximum in the normalized torque G/G0 as a function of RΩ. While this maximum occurs for all of the Wendt (1933), Maryland (Paoletti & Lathrop 2011) and Twente (van Gils et al. 2011b) datasets, there is no general theoretical prediction for the exact location of this maximum yet.
The last crossover observed by Paoletti and Lathrop, between regions III and IV, corresponded to Ω1 = 0 with Ω1 > 0 and Ω2 < 0 in region III (counter-rotation) to Ω1 > 0 and Ω2 > 0 in region IV (co-rotation). It is unclear whether this crossover is set by RΩ = 0.38 or whether it always occurs at RΩ(Ω1 = 0). The data from Taylor (1936) has Ω1 = 0 but given the values of η used in those experiments RΩ < 0.38. The Richard data for RΩ > 0.38 fall below the observations by Maryland, although the scaling with RΩ is similar. It is unclear if this disparity is a result of the analysis used to deduce the torques from Richard’s measurements or the difference in the control parameters from the Maryland experiment (see Table 1). It would be fruitful to have independent, direct measurements of the torque in region IV to compare against those of Maryland at different radius ratios to better understand this final crossover.
 |
Fig. 6 The scaling of a) G/Re2, which is proportional to the accretion rate Ṁ and viscosity parameter β, decays slowly with Re while having an amplitude that varies with the rotation number RΩ (see Fig. 4). b) The effects of global rotation can be accounted for by compensating G/Re2 by the fits f(RΩ) given in Eq. (12). The measurements from Twente are shown as red squares. The Maryland data are given by black circles, except for quasi-Keplerian flows (RΩ ≤ −1), which are indicated by blue diamonds. The green continuous line is the theoretical fit given in Eq. (14) normalized by f(RΩ = −0.2755), which corresponds to Ω2 = 0. |
The Richard and Maryland data both indicate that the observed torque for quasi-Keplerian flows states (RΩ ≤ −1) is approximately 14% of the maximum observed torque for a given Reynolds number. This is in contrast to the results of Ji et al. (2006), who deduced that such flow states are “essentially steady” and unable to transport angular momentum hydrodynamically. In addition to the different geometries between the experiments in Ji et al. (2006) and those of Richard and Maryland (see Table 1), the measurement techniques and finite-size effects were different between the experiments. This contrast is further discussed in Sect. 4. Clearly, additional independent measurements of the angular momentum flux for quasi-Keplerian flows could aid this debate, as recently discussed by Balbus (2011).
3.2.4. Astrophysical implications
As described in Sect. 2.5, the scaling of the
torque with Reynolds number may be used to determine either the turbulent viscosity
parameter β or the accretion rate Ṁ through Eq. (6). Our measurements of
G/Re2,
which is proportional to both β and Ṁ, are shown in
Fig. 6a. The measurements from Twente are shown
as red squares while those of Maryland are given by black circles. The data indicated by
blue diamonds are quasi-Keplerian flow states (RΩ ≤ −1)
from the Maryland experiment. The quantity
G/Re2
decreases slowly with Re (only logarithmically, see Dubrulle et al. 2005; Hersant et al. 2005; Grossmann & Lohse
2011) as expected since
G ∝ Reα
with 1.8 < α(Re) ≤ 2.0 for
105 < Re < ∞
(Lathrop et al. 1992b,a; Lewis & Swinney
1999). The amplitude of
G/Re2
for a given Re is determined by RΩ. The
effects of global rotation may be accounted for by compensating the measurements of
G/Re2
by f(RΩ) (see. Eq. (12)), as shown in Fig. 6b. As discussed in Dubrulle &
Hersant (2002), the scaling may be fit by a logarithmically decaying function,
such as: ![\begin{equation} \frac{G}{Re^2}=K_7\frac{\eta^2}{(1-\eta)^{3/2}}\frac{1}{\ln[\eta^2(1-\eta)Re^2/K_8]^{3/2}}, \label{regime3taylor} \end{equation}](/articles/aa/full_html/2012/11/aa18511-11/aa18511-11-eq186.png) (14)with the values chosen
to be K7 = 0.4664 and
K8 = 104 to describe the best fit for the
torque scaling provided by Lewis & Swinney
(1999) for the case Ω2 = 0. An alternative logarithmic dependence
between
G/Re2
and Re has been suggested by Grossmann
& Lohse (2011) (for the analogous case of ultimate Rayleigh-Bénard
flow), and it equally well fits the data.
(14)with the values chosen
to be K7 = 0.4664 and
K8 = 104 to describe the best fit for the
torque scaling provided by Lewis & Swinney
(1999) for the case Ω2 = 0. An alternative logarithmic dependence
between
G/Re2
and Re has been suggested by Grossmann
& Lohse (2011) (for the analogous case of ultimate Rayleigh-Bénard
flow), and it equally well fits the data.
The expected accretion rate, measured by G/Re2 = 3.3 × 10-3, for quasi-Keplerian flows (blue diamonds in Fig. 6) is approximately 14% of the maximum accretion rate, which occurs for RΩ = −0.10. This corresponds to a value of βMd = 2 × 10-5 or Ṁ/Ṁ0 = 3.3 × 10-3 at Re = 7 × 105. Extrapolating towards astrophysical Reynolds numbers by using the formula of Hersant et al. (2005, see Eq. (6)), we get a value of Ṁ/Ṁ0 = 10-3 that is consistent with values observed in disks around T Tauri stars.
4. Discussion
The measured accretion rate for all of our quasi-Keplerian flows (RΩ ≤ −1) is approximately 14% of the maximum accretion rate, which occurs at RΩ = −0.10, resulting in βMd = 2 × 10-5. This is close to the value computed by Richard and Zahn βRZ = 10-5 and to the value of Dubrulle et al. (2005)βD = 8 × 10-6. This is somewhat surprising given that quasi-Keplerian flow profiles are linearly stable while the maximum accretion rate occurs when the cylinders counter-rotate, which produces destabilizing shear that dominates the dynamics. This result is in stark contrast to the results presented by Ji et al. (2006) and Schartman et al. (2012), where βP was measured to be an order of magnitude smaller, specifically βP = 7 × 10-7. Thus, they concluded that hydrodynamics alone cannot efficiently transport angular momentum in quasi-Keplerian flows.
Schartman et al. (2012) state that these incompatible results are caused by differing interpretations of finite-size effects, namely Ekman circulation produced by the axial boundaries. In the Princeton experiments (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012) the aspect ratio is small (Γ ≈ 2) and therefore finite-size effects would likely dominate. To minimize Ekman circulation, their axial boundaries are split into pairs of rings that can independently rotate with respect to the cylinders. This method has been shown to reduce the effects of Ekman circulation in the bulk of the fluid (Schartman et al. 2009). Furthermore, when Ekman circulation is not minimized their measured values of β for quasi-Keplerian flows are approximately half of the typical values presented here. Thus, Schartman et al. (2012) argue that our larger values of β are the result of Ekman circulation that is present in other experiments, but is minimized in their apparatus.
We argue, on the other hand, that while finite-size effects are certainly present in our experiments, we believe that they do not dominate our measured torques. Before presenting these arguments, we would like to preface the discussion with a summary of past studies that have examined the role of finite-size effects on angular momentum transport in rotating shear flows. The work of Lesur & Longaretti (2005) used numerical simulations of rotating plane-Couette flow up to Re ~ 104 in the shearing-sheet limit to conclude that Keplerian-like flows in Taylor-Couette systems are strongly affected by Ekman circulation. The aforementioned experiments by the Princeton group (Ji et al. 2006) experimentally observed that angular momentum transport in their apparatus was only significant when they did not actively minimize Ekman circulation by varying the rotation rate of their axial end rings.
To further address this issue from a numerical standpoint, Avila (2012) performed direct numerical simulations of our experimental geometry as well as the Princeton apparatus (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012). Avila found that the axial boundaries drive secondary flows that enhance the global angular momentum transport. The measured torques in those simulations were equal to the laminar value near Re = 0 and increased (approximately linearly) to be twice the laminar value in both the Maryland and Princeton geometry near his maximum Re ≈ 5000. While it was clear that finite-size effects played a dominant role for Re < 5000, Avila concluded by stating that the universal scaling of the torque with Reynolds number observed by Paoletti & Lathrop (2011) indicates that shear mechanisms might overwhelm finite-size effects at the values of Re explored here.
The role of finite-size effects at the values of Re that we have explored remains an open question. In order to quantitatively determine their effects at Re ~ 106 a series of future studies will be required, as discussed at the end of this section. We now turn to our arguments as to why finite-size effects may not dominate the flows that we have examined, with the caveat that we cannot rule out the possibility that secondary flows produced by end-wall effects are one of the different mechanisms that may perturb our quasi-Keplerian flows into a turbulent state (see e.g. Mukhopadhyay et al. 2005; Mukhopadhyay & Saha 2011, and references therein).
The normalized torque G/G0 is approximately constant for each value of RΩ characterized by the present experiments. This indicates that the amplitude of the torque varies with RΩ, however the scaling with Re is unchanged (see Fig. 5). Paoletti & Lathrop (2011) observed that their torque scaling for Rayleigh-stable and unstable flows agreed with the Prandtl-von Kármán description of Lathrop et al. (1992a); Lewis & Swinney (1999). The Twente data, initially presented by van Gils et al. (2011b), was well-described by the theoretical predictions of Eckhardt et al. (2007b) for all rotation numbers explored. If Ekman circulation significantly contributed to the torque for Rayleigh-stable flows, as argued by Schartman et al. (2012), then one would expect systematic disparities between these theoretical descriptions and the measured torques. As shown in Fig. 5, though, the torque scaling agrees well with the observations of Lewis & Swinney (1999) for the case Ω2 = 0 for all values of RΩ. Avila (2012) also argued that this universal scaling with Re indicates that shear turbulence dominates at the Reynolds numbers that we have explored, although this does not prove that secondary flows did not have a role in initiating the shear turbulence.
The torques in the Maryland and Twente experiments are measured over only 56% of the axial length of the flow centered at the mid-height of the apparatus. This design has been intentionally implemented such that the torque measurements are unaffected by flows within 2.58 radial gap widths of either axial boundary where Ekman circulation is strongest. Wendt’s experiments (Wendt 1933) had a free upper surface, which is therefore devoid of Ekman circulation. Even though Taylor’s measurements (Taylor 1936) were affected by Ekman circulation for Γ > 100, his measurements of the torque for Rayleigh-stable flows that are expected to be most affected by Ekman circulation agree with our measurements of counter-rotating flows for the same value of RΩ, where Ekman circulation is dwarfed by the dominant shear.
One of course wonders on whether this Ekman circulation caused by the co-rotating upper and lower plates affect the flow patterns. For laminar flow e.g. for purely outer cylinder rotation this clearly is the case (Coles & van Atta 1966; Hollerbach & Fournier 2004). However, we argue that the strong turbulence destroys such an axial dependence of the flow field. To check this assumption, we have measured the full turbulent velocity profile with laser doppler anemometry (LDA; van Gils et al. 2012). The result is shown in Fig. 7. Evidently, over the length of the central section of the inner cylinder where we measure the torque there is no visible z-dependence of the mean velocity; the plate boundary layers only produce an axial dependence far above the domain of the central section of the inner cylinder.
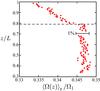 |
Fig. 7 Finite-size effects may be characterized by axial profiles of the angular velocity Ω measured at the mid-gap (r = (a + b)/2) in the Twente experiment. In this example, the cylinder Reynolds numbers are Re1 = 1.0 × 106 and Re2 = 0 (outer cylinder stationary). The global torque measurements are taken for 0.22 < z/L < 0.78 with the top boundary of these measurements indicated by the dashed line at z/L = 0.78. The resolution of the laser-doppler anemometry prohibits measurements of the angular velocity in the boundary layer near z/L = 1 where Ω = Ω2 = 0, in this case. |
The Princeton experiments (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012)
measure local velocity correlations to determine the global angular
momentum flux, whereas the Maryland and Twente
experiments directly measure the global angular momentum flux using precision calibrated
force-arm measurements. The distinction between the measured quantities has made direct
comparisons of the experiments difficult. To bridge this gap, Burin et al. (2010) recently used their local velocity measurements to determine
the corresponding torque G. To compare to previous studies with
Ω2 = 0 (Lathrop et al. 1992b,a; Lewis &
Swinney 1999) Burin et al. (2010) fit the
scaling of 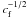 to
log 10(Re ∗ cf), where
cf ≡ G/Re2,
and determined a slope of 1.40 ± 0.16. The authors claim that this value agrees with the
measured value of 1.52 reported by Lathrop et al.
(1992b,a) and 1.56 measured in Lewis & Swinney (1999). However, the appropriate
Prandtl-von Kármán scaling predicts the following relationship (Lathrop et al. 1992b,a; Lewis & Swinney 1999)
to
log 10(Re ∗ cf), where
cf ≡ G/Re2,
and determined a slope of 1.40 ± 0.16. The authors claim that this value agrees with the
measured value of 1.52 reported by Lathrop et al.
(1992b,a) and 1.56 measured in Lewis & Swinney (1999). However, the appropriate
Prandtl-von Kármán scaling predicts the following relationship (Lathrop et al. 1992b,a; Lewis & Swinney 1999)
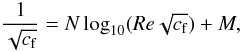 (15)in contrast to the scaling
shown in Fig. 5 of Burin et al. (2010). Furthermore,
the fit parameters N and M are predicted to depend upon
the radius ratio in the following way
(15)in contrast to the scaling
shown in Fig. 5 of Burin et al. (2010). Furthermore,
the fit parameters N and M are predicted to depend upon
the radius ratio in the following way ![\begin{eqnarray} &&N = [(1-\eta^2)\ln 10]/(\eta\kappa\sqrt{2\pi}), \\ &&M = \frac{N}{\ln 10}\[\ln \left\{\(\frac{1-\eta}{1+\eta}\)\frac{1}{y_0^+\sqrt{2\pi}}\right\} + \kappa y_0^+\], \end{eqnarray}](/articles/aa/full_html/2012/11/aa18511-11/aa18511-11-eq223.png) where
κ = 0.40 is the von Kármán constant and
where
κ = 0.40 is the von Kármán constant and
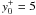 . The radius ratio
η = 0.35 in the Princeton experiments, therefore the Prandtl-von Kármán
skin friction law predicts N = 5.76 and M = −3.15. These
values do not agree with our analysis of the data in Burin
et al. (2010) where N ≈ 2 and M ≈ −0.4. In
fact, the measured values of G determined by the local velocity
fluctuations are on average five times larger than those predicted by the Prandtl-von Kármán
skin friction law that has been verified using direct torque measurements (Lathrop et al. 1992b,a; Lewis & Swinney 1999; Paoletti & Lathrop 2011). Therefore, we argue
that the local velocity fluctuation measurements used in the Princeton experiments (Ji et al. 2006; Schartman
et al. 2009; Burin et al. 2010; Schartman et al. 2012) face severe experimental
challenges. In fact, Huisman et al. (2012) showed
that the local angular momentum transport undergoes fluctuations that are two orders of
magnitude larger than the mean value. However, once the local angular momentum transport is
averaged long enough and over a large enough region, Huisman
et al. (2012) achieved perfect agreement between the local and the global
measurements.
. The radius ratio
η = 0.35 in the Princeton experiments, therefore the Prandtl-von Kármán
skin friction law predicts N = 5.76 and M = −3.15. These
values do not agree with our analysis of the data in Burin
et al. (2010) where N ≈ 2 and M ≈ −0.4. In
fact, the measured values of G determined by the local velocity
fluctuations are on average five times larger than those predicted by the Prandtl-von Kármán
skin friction law that has been verified using direct torque measurements (Lathrop et al. 1992b,a; Lewis & Swinney 1999; Paoletti & Lathrop 2011). Therefore, we argue
that the local velocity fluctuation measurements used in the Princeton experiments (Ji et al. 2006; Schartman
et al. 2009; Burin et al. 2010; Schartman et al. 2012) face severe experimental
challenges. In fact, Huisman et al. (2012) showed
that the local angular momentum transport undergoes fluctuations that are two orders of
magnitude larger than the mean value. However, once the local angular momentum transport is
averaged long enough and over a large enough region, Huisman
et al. (2012) achieved perfect agreement between the local and the global
measurements.
Clearly the contrasting conclusions of the Princeton experiments (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012) and those presented here warrant further experimental and theoretical investigation, as suggested by Balbus (2011). In particular the role of finite-size effects must be better understood at Re ~ 106. It may be that the Princeton measurements of the local velocity fluctuations may not accurately determine the global angular momentum transport (Burin et al. 2010), due to lack of convergence. On the other hand, the effects of the axial boundaries on the global torque measurements presented here have not yet been characterized in detail. The Twente experiments (Huisman et al. 2012) provide both local velocities as well as the global torque, which thereby presents future opportunities to clarify these distinctions. Vice versa, direct global torque measurements in a split axial-ring apparatus, such as the Princeton device, would also be scientifically useful. New experiments that also measure the angular momentum transport as a function of aspect ratio would also be very interesting.
An explanation for the contrasting results of our measurements with those of past studies can be sought in both future experiments and numerical simulations. From an experimental point of view, an apparatus that is capable of simultaneously measuring the global angular momentum transport and controlling secondary circulation by independently varying the rotation rate of split axial-rings would be particularly fruitful. In essence, such an apparatus would combine the techniques utilized in the Twente and Maryland experiments with the apparatus of the Princeton group (Ji et al. 2006; Schartman et al. 2009; Burin et al. 2010; Schartman et al. 2012). This would remove the ambiguities that are present in interpreting data from these experiments.
Avila (2012) observed that the torque increased (approximately) linearly with Re and was no more than twice the laminar value for Re < 5000. However, our measured torques are typically two orders of magnitude greater than the laminar value and increase faster than G ∝ Re, thus indicating a transition. Additional experiments could aid future numerical studies by performing measurements at lower Reynolds number to determine when the transition to turbulence occurs. In this way, computational studies could focus their efforts on examining values of the Reynolds number that straddle the transition point. Furthermore, experimentally characterizing the angular momentum transport below the transition will also be important in determining the torque produced by secondary flows.
In addition to overcoming these experimental challenges, efforts must be made to design laboratory systems that more closely resemble the astrophysical flows of interest. In accretion disks the radial and axial length scales are comparable (Regev & Umurhan 2008). However, many laboratory experiments (see Table 1) are designed with large aspect ratios to minimize finite-size effects. While the results in Fig. 4 seem to capture some of the dependence on the radius ratio, systematic studies with varying η are still required to determine the precise scaling. It also remains to be seen if our results are broadly applicable to smaller aspect ratios. The radial boundaries present in laboratory experiments produce boundary layers that affect the global angular momentum transport (Eckhardt et al. 2007b). Such boundaries may be less important in accretion flows and therefore one must account for these effects when extrapolating to astrophysically-relevant control parameters. Furthermore, recent numerical simulations by Meheut et al. (2010) have indicated that stratification may also play an important role in the dynamics of accretion disks, but such effects have not been experimentally examined in high Reynolds number Taylor Couette flow. Although these flows do not capture the full complexity of astrophysical systems, they do serve as an indication that hydrodynamic instabilities can occur in Rayleigh-stable flows. The detailed mechanism that produces the instability remains an open question for future endeavor.
5. Conclusions
The measurements that we present here indicate that the dimensionless torque G may be described as a product of functions that separately depend upon the Reynolds number Re and the rotation number RΩ. The rotation number RΩ introduced by Dubrulle et al. (2005) collapses all of the experimental data presented here for various radius ratios, aspect ratios and Reynolds numbers (see Table 1). The effects of global rotation, measured by G/G0, where G0 ≡ G(Re,RΩ = 0), are shown to be well-described by the function f(RΩ) given in Eq. (12) for the entire range of RΩ explored in the present studies.
The most astrophysically relevant result is the scaling of
G/Re2,
which is proportional to both the turbulent viscosity parameter β and the
accretion rate Ṁ. We observe that the expected accretion rate for
quasi-Keplerian flows (RΩ ≤ −1) is approximately 14% of the
maximum attainable rate for a given Reynolds number. We therefore get a dimensionless
angular transport parameter βMd = 2 × 10-5, in
agreement with Richard and Zahn but more than an order of magnitude larger than the
Princeton experiments. Such angular momentum transport is able to produce dimensionless
accretion rates on the order of 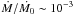 ,
which are compatible with observations in disks around T Tauri stars (Hersant et al. 2005). We have argued that our results are not easily
attributed to finite-size effects, such as Ekman circulation. As such, we conclude that
hydrodynamics may be able to transport angular momentum at astrophysical rates in spite of
the linear stability provided by the radially-increasing angular momentum profile. This
level of transport must result from turbulent means, thereby implying that quasi-Keplerian
flows can be nonlinearly unstable to finite amplitude disturbances.
,
which are compatible with observations in disks around T Tauri stars (Hersant et al. 2005). We have argued that our results are not easily
attributed to finite-size effects, such as Ekman circulation. As such, we conclude that
hydrodynamics may be able to transport angular momentum at astrophysical rates in spite of
the linear stability provided by the radially-increasing angular momentum profile. This
level of transport must result from turbulent means, thereby implying that quasi-Keplerian
flows can be nonlinearly unstable to finite amplitude disturbances.
Acknowledgments
The Maryland group would like to thank B. Eckhardt, Michael E. Fisher, C. Kalelkar, D. Martin, Harry L. Swinney and D. S. Zimmerman and acknowledge the support of Grant No. NSF-DMR 0906109. B.D. thanks the CNRS for its continuous unconditional financial support that made this fundamental research possible. The Twente collaboration thanks G. W. Bruggert for crucial work in building the T3C device, S. Grossmann and S. G. Huisman for discussions, and STW, which is financially supported by NWO, for financial support of this project.
References
- Abramowicz, M., Brandenburg, A., & Lasota, J.-P. 1996, MNRAS, 281, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Avila, M. 2012, Phys. Rev. Lett., 108, 124501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Balbus, S. A. 2011, Nature, 470, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., Hawley, J. F., & Stone, J. M. 1996, ApJ, 467, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, K., Armitage, P. J., & Simon, J. B. 2011, MNRAS, 416, 361 [NASA ADS] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Burin, M. J., Schartman, E., & Ji, H. 2010, Exp. Fluids, 48, 763 [CrossRef] [Google Scholar]
- Canuto, V. M., Goldman, I., & Hubickyj, O. 1984, ApJ, 280, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, D., & van Atta, C. 1966, J. Fluid Mech., 25, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Drecker, A., Hollerbach, R., & Rudiger, G. 1998, MNRAS, 298, 1030 [NASA ADS] [CrossRef] [Google Scholar]
- Dubrulle, B. 1992, A&A, 266, 592 [NASA ADS] [Google Scholar]
- Dubrulle, B., & Hersant, F. 2002, EPJ B, 26, 379 [NASA ADS] [Google Scholar]
- Dubrulle, B., Dauchot, O., Daviaud, F., et al. 2005, Phys. Fluids, 17, 095103 [Google Scholar]
- Eckhardt, B., Grossmann, S., & Lohse, D. 2007a, Europhys. Lett., 78, 24001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckhardt, B., Grossmann, S., & Lohse, D. 2007b, J. Fluid Mech., 581, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Esser, A., & Grossmann, S. 1996, Phys. Fluids, 8, 1814 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., & Papaloizou, J. 2007, A&A, 476, 1113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossmann, S., & Lohse, D. 2011, Phys. Fluids, 23, 045108 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Balbus, S. A., & Winters, W. F. 1999, ApJ, 518, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Hersant, F., Dubrulle, B., & Huré, J.-M. 2005, A&A, 429, 531 [Google Scholar]
- Hollerbach, R., & Fournier, A. 2004, in MHD Couette Flows: Experiments and Models, eds. R. Rosner, G. Rüdiger, & A. Bonanno, AIP Conf. Ser., 733, 114 [Google Scholar]
- Huisman, S. G., van Gils, D. P. M., Grossmann, S., Sun, C., & Lohse, D. 2012, Phys. Rev. Lett., 108, 024501 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, H., Burin, M., Schartman, E., & Goodman, J. 2006, Nature, 444, 343 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- King, A. R., Pringle, J. E., & Livio, M. 2007, MNRAS, 376, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Lathrop, D. P., Fineberg, J., & Swinney, H. L. 1992a, Phys. Rev. A, 46, 6390 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lathrop, D. P., Fineberg, J., & Swinney, H. L. 1992b, Phys. Rev. Lett., 68, 1515 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2005, A&A, 444, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, G. S., & Swinney, H. L. 1999, Phys. Rev. E, 59, 5457 [NASA ADS] [CrossRef] [Google Scholar]
- Meheut, H., Casse, F., Varniere, P., & Tagger, M. 2010, A&A, 516, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mukhopadhyay, B. 2008, Int. J. Mod. Phys. D, 17, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Mukhopadhyay, B., & Saha, K. 2011, Res. Astron. Astrophys., 11, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Mukhopadhyay, B., Afshordi, N., & Narayan, R. 2005, ApJ, 629, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Paoletti, M. S., & Lathrop, D. P. 2011, Phys. Rev. Lett., 106, 024501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Pumir, A. 1996, Phys. Fluids, 8, 3112 [NASA ADS] [CrossRef] [Google Scholar]
- Regev, O., & Umurhan, O. M. 2008, A&A, 481, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, D. 2001, Ph.D. Thesis, Univ. Paris VII [Google Scholar]
- Richard, D., & Zahn, J. 1999, A&A, 347, 734 [NASA ADS] [Google Scholar]
- Rozyczka, M., & Spruit, H. C. 1993, ApJ, 417, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Schartman, E., Ji, H., & Burin, M. J. 2009, Rev. Sci. Instrum., 80, 024501 [NASA ADS] [CrossRef] [Google Scholar]
- Schartman, E., Ji, H., Burin, M. J., & Goodman, J. 2012, A&A, 543, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, G. I. 1936, Roy. Soc. London Proc. A, 157, 546 [Google Scholar]
- Umurhan, O. M., & Regev, O. 2004, A&A, 427, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Berg, T. H., Doering, C. R., Lohse, D., & Lathrop, D. P. 2003, Phys. Rev. E, 68, 036307 [NASA ADS] [CrossRef] [Google Scholar]
- van den Berg, T. H., Luther, S., Lathrop, D. P., & Lohse, D. 2005, Phys. Rev. Lett., 94, 044501 [NASA ADS] [CrossRef] [Google Scholar]
- van den Berg, T. H., van Gils, D. P. M., Lathrop, D. P., & Lohse, D. 2007, Phys. Rev. Lett., 98, 084501 [NASA ADS] [CrossRef] [Google Scholar]
- van Gils, D. P. M., Bruggert, G.-W., Lathrop, D. P., Sun, C., & Lohse, D. 2011a, Rev. Scientific Instrum., 82, 025105 [NASA ADS] [CrossRef] [Google Scholar]
- van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C., & Lohse, D. 2011b, Phys. Rev. Lett., 106, 024502 [NASA ADS] [CrossRef] [Google Scholar]
- van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C., & Lohse, D. 2012, J. Fluid Mech., 706, 118149 [CrossRef] [Google Scholar]
- Wendt, F. 1933, Ing. Arch., 4, 577 [Google Scholar]
- Zeldovich, Y. B. 1981, Roy. Soc. London Proc. A, 374, 299 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Taylor-Couette control parameters related to some astrophysical disks, as computed by Hersant et al. (2005).
All Figures
 |
Fig. 1 Taylor-Couette flow may be used to study angular momentum transport in rotating shear flows. The fluid is sheared between two independently rotating cylinders of radii a < b that rotate at angular velocities Ω1 and Ω2 for the inner and outer cylinders, respectively. Although the total fluid height is given by L, some experiments only measure the contribution to the torque over a central section of length Lmid to minimize end effects, as in (Lathrop et al. 1992b,a; Lewis & Swinney 1999; van den Berg et al. 2003, 2005, 2007; Paoletti & Lathrop 2011; van Gils et al. 2011b). |
| In the text | |
 |
Fig. 2 a) Our experiments span a large range of the Reynolds number Re, which controls the turbulence intensity, and the rotation number RΩ, introduced by Dubrulle et al. (2005), which compares shear to overall rotation. The rotation number can be used to distinguish between Rayleigh-stable flows (RΩ ≤ −1 or RΩ ≥ (1 − η)/η) and those that are linearly unstable (−1 < RΩ < (1 − η)/η). b) All of our measurements for −1 < RΩ < 0.38 are well above the linear stability curve (blue line) described by Esser & Grossmann (1996) and given by Eq. (8). The data are taken from separate experiments by van Gils et al. (2011b) (red squares) and (Paoletti & Lathrop 2011) (black circles). |
| In the text | |
 |
Fig. 3 The scaling of the dimensionless torque G with the Reynolds number Re is independent of the rotation number RΩ, however the amplitude varies as in Paoletti & Lathrop (2011); van Gils et al. (2011b). The measurements by Paoletti & Lathrop (2011) are in black circles while the data from van Gils et al. (2011b) are shown by red squares. The thick blue line indicates the theoretical value for purely laminar flow, where angular momentum is transported only by molecular viscosity. |
| In the text | |
 |
Fig. 4 a) The dimensionless torque G normalized by G0 ≡ G(Re,RΩ = 0) for different values of the radius ratio η nicely collapses when plotted as function of RΩ. The data from Wendt (1933) are shown as cyan (η = 0.68), blue (η = 0.85) and green (η = 0.935) triangles. Additional radius ratios are examined using the data from Taylor (1936), shown as orange diamonds, Richard (Richard 2001; Dubrulle et al. 2005), given by magenta squares, Paoletti & Lathrop (2011) indicated by black circles and van Gils et al. (2011b) by red circles. The solid lines are fits given by Eq. (12). Keplerian flow states are indicated by the dashed line at RΩ = −4/3. In b) we focus on the peak of the curve shown in a), but only present the data from Twente (van Gils et al. 2011b) (red) and Maryland (Paoletti & Lathrop 2011) (black). The solid line is the fit (12). |
| In the text | |
 |
Fig. 5 The dimensionless torque G may be compensated by the fit f(RΩ) given by Eq. (12). The data from both Paoletti & Lathrop (2011) (black circles) and van Gils et al. (2011b) (red squares) agree with the best fit from Lewis & Swinney (1999) for the case where the outer cylinder was stationary (blue line). |
| In the text | |
 |
Fig. 6 The scaling of a) G/Re2, which is proportional to the accretion rate Ṁ and viscosity parameter β, decays slowly with Re while having an amplitude that varies with the rotation number RΩ (see Fig. 4). b) The effects of global rotation can be accounted for by compensating G/Re2 by the fits f(RΩ) given in Eq. (12). The measurements from Twente are shown as red squares. The Maryland data are given by black circles, except for quasi-Keplerian flows (RΩ ≤ −1), which are indicated by blue diamonds. The green continuous line is the theoretical fit given in Eq. (14) normalized by f(RΩ = −0.2755), which corresponds to Ω2 = 0. |
| In the text | |
 |
Fig. 7 Finite-size effects may be characterized by axial profiles of the angular velocity Ω measured at the mid-gap (r = (a + b)/2) in the Twente experiment. In this example, the cylinder Reynolds numbers are Re1 = 1.0 × 106 and Re2 = 0 (outer cylinder stationary). The global torque measurements are taken for 0.22 < z/L < 0.78 with the top boundary of these measurements indicated by the dashed line at z/L = 0.78. The resolution of the laser-doppler anemometry prohibits measurements of the angular velocity in the boundary layer near z/L = 1 where Ω = Ω2 = 0, in this case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


