| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219326 | |
| Published online | 08 October 2012 | |
Constraints on the relative sizes of intervening Mg II-absorbing clouds and quasar emitting regions⋆
1
Dark Cosmology Centre, Niels Bohr Institute, University of
Copenhagen,
Juliane Maries Vej 30,
2100
Copenhagen,
Denmark
e-mail: unclellama@gmail.com
2
Steward Observatory, University of Arizona,
933 N. Cherry Avenue, 85721
Tucson, AZ, USA
Received: 1 April 2012
Accepted: 31 July 2012
Context. A significantly higher incidence of strong (rest equivalent width Wr > 1 Å) intervening Mg ii absorption is observed along gamma-ray burst (GRB) sight-lines relative to those of quasar sight-lines. A geometrical explanation for this discrepancy has been suggested: the ratio of the beam size of the source to the characteristic size of an Mg ii absorption system can influence the observed Mg ii equivalent width, if these two sizes are comparable.
Aims. We investigate whether the differing beam sizes of the continuum source and broad-line region of Sloan Digital Sky Survey (SDSS) quasars produce a discrepancy between the incidence of strong Mg ii absorbers illuminated by the quasar continuum region and those of absorbers illuminated by both continuum and broad-line region light.
Methods. We performed a semi-automated search for strong Mg ii absorbers in the SDSS Data Release 7 quasar sample. The resulting strong Mg ii absorber catalog is available at the CDS. We measured the sight-line number density of strong Mg ii absorbers superimposed on and off the quasar C iv λ 1550 and C iii] λ 1909 emission lines.
Results. We see no difference in the sight-line number density of strong Mg ii absorbers superimposed on quasar broad emission lines compared to those superimposed on continuum-dominated spectral regions. This suggests that the Mg ii absorbing clouds typically observed as intervening absorbers in quasar spectra are larger than the beam sizes of both the continuum-emitting regions and broad line-emitting regions in the centers of quasars, corresponding to a lower limit of the order of 1017 cm for the characteristic size of an Mg ii absorbing cloud.
Key words: quasars: emission lines / Gamma-ray burst: general / ultraviolet: ISM
Catalog of Mg II absorbers is available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/546/A67
© ESO, 2012
1. Introduction
Both quasar and gamma-ray burst (GRB) spectra sometimes display intervening absorption lines. The Mg ii λλ 2796, 2803 doublet is identifiable even in low-resolution spectroscopy and is therefore well-suited for statistical studies. Intervening Mg ii absorption systems are associated with galaxy haloes, and may be due to galactic outflows produced by supernovae, as they do not appear to be virialized (Bouché et al. 2006). Intervening absorption systems may therefore trace the star formation rate of their host galaxies. For example, the equivalent width of strong (rest-frame equivalent width, Wr, greater than 1 Å for the 2796 Å component) Mg ii absorbers appears to be correlated with the [O iii] luminosity of their associated galaxies (Ménard et al. 2011), making them possible tracers of star formation rate at high redshift (Matejek & Simcoe 2012). Alternatively, intervening Mg ii lines could represent a reservoir of cool (T ≈ 104 K) gas in galaxy haloes, providing raw materials for galaxy growth (White & Frenk 1991) – in this case at least some of the absorption systems should trace inflowing material. Kacprzak & Churchill (2011) suggest a bimodal Mg ii absorber population where weak absorbers trace infalling gas and strong absorbers trace outflows.
Prochter et al. (2006b) report a surprising discrepancy in the statistics of Mg ii absorption along quasar and GRB sight lines, finding roughly four times as many strong intervening absorbers in GRB spectra. This is puzzling, as both quasar and GRB sight-lines are a priori assumed to be randomly distributed. Vergani et al. (2009) study a longer GRB-spectrum redshift path (Δz = 31.5) than previous work, yet they still find the sight-line number density of strong absorbers toward GRBs is a factor 2.1 ± 0.6 higher than toward quasars. They are also able to extend their study to lower equivalent widths. Interestingly, they find that the number of weak absorbers (0.3 Å < Wr < 1 Å) is similar along quasar and GRB sight lines. Sudilovsky et al. (2007) find no statistical difference between the sight-line number density of C iv absorbers along quasar and GRB sight lines.
Prochter et al. (2006b) discuss various explanations for their result: (a) dust obscuration by the galaxies associated with the absorption systems could alter the apparent magnitudes of those quasars richest in strong intervening absorbers, causing them to be excluded from magnitude-limited quasar samples; (b) a subset of absorption systems in the GRB sample could be intrinsic to the GRB event (implying very large outflow velocities if we are to observe them as intervening – see also Cucchiara et al. 2009, who find no significant difference between the properties of strong Mg ii absorbers in GRB and quasar spectra); or (c) there could be a selection bias toward detecting those GRBs that are gravitationally lensed by intervening galaxies, leading to a higher instance of absorption systems toward the GRBs that we detect compared to random sight-lines (as the Mg ii absorbers are associated with galaxies). Frank et al. (2007) suggest a model based on the relative sizes of Mg ii absorbing clouds to quasar and GRB emitting regions to explain the Prochter et al. (2006b) result – see Sect. 1.3.
1.1. Implications of dust extinction
The galaxies associated with Mg ii absorbers may both extinguish and redden background quasars. A few recent studies have addressed this issue. Ménard et al. (2008) investigate whether these effects could cause quasars with strong intervening absorbers to drop out of quasar catalogs due to selection effects – for example, the SDSS DR7 catalog is limited to objects with absolute i-band magnitudes brighter than −22 (Schneider et al. 2010), and quasar candidates are initially selected based on color cuts. They estimate that about 2% of quasars with strong Mg ii absorbers drop out of the SDSS quasar sample due to a combination of extinction and reddening associated with the Mg ii absorber alone. This selection effect is strongly dependent on the equivalent width of the absorber – they find that about 50% of quasars with an intervening Mg ii absorber with Wr > 6 Å drop out of the SDSS quasar sample. Very strong absorbers are, however, rare (only 1.2% of strong Mg ii absorbers in the Mg ii absorber sample described in Sect. 3 have Wr > 4 Å – only 0.06% have Wr > 6 Å), so the effect of this bias on strong absorber statistics is negligible. The selection mechanism for GRBs is different: they are detected via the transient gamma-ray flux and accurately localized in X-ray and optical emission, allowing a follow-up spectrum to be obtained. In the case of “dark GRBs”, a subgroup of GRBs with low optical flux relative to their X-ray flux (e.g., Jakobsson et al. 2004), it is not always possible to locate the burst accurately – a high signal-to-noise follow-up spectrum is in any case difficult to obtain for these bursts. The optical faintness of dark GRBs is likely a consequence of dust in their host galaxies (e.g., Krühler et al. 2011), and therefore unrelated to intervening Mg ii absorption systems.
Sudilovsky et al. (2009) perform Monte Carlo simulations investigating the effect of dust extinction by strong absorbers and find that only about 10% of the quasar-GRB absorber discrepancy can be accounted for by this effect. Stocke & Rector (1997) find five strong Mg ii absorbers in the spectra of ten BL Lac objects – this is larger by a factor of 4–5 than the number of strong absorbers expected based upon quasar sight-lines. Bergeron et al. (2011) investigate strong intervening Mg ii absorption for blazars in general (of which BL Lac objects are a subtype) – they find a factor 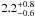 higher incidence of strong absorbers in blazar spectra compared to quasars. They argue that dust obscuration affects the quasar sample and not the blazar sample, as blazars are usually identified in bands that are not sensitive to dust obscuration. However, based on the dust obscuration quasar drop-out fraction of 2% reported by Ménard et al. (2008) they conclude that the resulting selection bias is too small to explain the discrepancy.
higher incidence of strong absorbers in blazar spectra compared to quasars. They argue that dust obscuration affects the quasar sample and not the blazar sample, as blazars are usually identified in bands that are not sensitive to dust obscuration. However, based on the dust obscuration quasar drop-out fraction of 2% reported by Ménard et al. (2008) they conclude that the resulting selection bias is too small to explain the discrepancy.
Budzynski & Hewett (2011) recently reexamined the dust obscuration bias in SDSS quasar samples, including an extra effect not discussed in the studies mentioned above: degradation of signal-to-noise ratio (S/N) of heavily dust-attenuated quasar spectra. If Mg ii absorbers are dusty, spectra with absorption lines will generally have a lower signal-to-noise ratio than those without, lowering the significance of detection of absorption lines. They find that a combination of signal-to-noise and dust obscuration could, in fact, account for a large part of the GRB-quasar absorber statistics discrepancy (up to a factor of 2).
1.2. Implications of gravitational lensing
Rapoport et al. (2011) examine the possibility that many of the GRBs we see are gravitationally lensed by foreground galaxies which also harbor Mg ii absorbing clouds, giving rise to a bias in the GRB sample toward sight-lines with absorbers. Using archival Hubble Space Telescope (HST) imaging, they report that galaxies are located systematically closer to the GRB sight lines than would be expected from a random distribution of sight lines. This is expected if the GRB sample has a large proportion of gravitationally lensed GRBs. Porciani et al. (2007) find that GRB afterglows with more than one Mg ii absorber are, on average, a factor of 1.7 brighter in the optical band than the other afterglows. However, this result has a low statistical significance due to the lack of GRBs with more than one absorption system. They also suggest a multi-band magnification bias for GRBs: sources such as GRBs that are particularly bright in more than one band are more likely to be lensed, irrespective of the nature of the lens. If Mg ii absorbers are more likely to lens GRBs than quasars due to this magnification bias, the result would be a subset of GRBs that would otherwise be too faint to be detected, all displaying Mg ii absorption. Chen et al. (2009) find suggestive evidence for lensing of the GRB in one of the five systems displaying strong Mg ii absorption in their sample.
1.3. Implications of beam-size dilution
Frank et al. (2007) propose a geometric model in which the different beam sizes of quasars and GRBs affect the fraction of Mg ii systems observed as strong absorbers. The argument is as follows: if a background source has a larger angular size than the Mg ii absorbing cloud, some of the light will avoid the cloud completely, giving a “dilution” of the equivalent width compared to a beam where all photons pass through the absorbing cloud. They model this effect using spherically symmetric clouds of a fixed core radius rc, with a power-law decline in column density outside this core radius, testing the total column density sampled by various beam sizes (relative to rc). They show that, in the case of beams hitting the core centrally, small beams will sample a higher average column density than beams larger than the core. At an impact parameter b = rc, this trend is weakened. At b = 5rc the effect is reversed: while all beams sample a reduced column density compared to b = 0, large beams sample a larger effective column density as they cover more of the core. For this beam dilution effect to explain the quasar-GRB discrepancy in absorber statistics, it requires that the beam size of quasars and the characteristic size of a Mg ii absorbing cloud (or substructure) are comparable, while the beam sizes of GRBs must be somewhat smaller: if both GRB and quasar beam sizes are much smaller than the absorbing clouds, only a small fraction of Mg ii-absorbed beams will sample the edge of the cloud, rendering the beam dilution effect insignificant. One prediction of this model is that absorbers in GRB spectra should vary in strength over time, as different parts of the GRB fireball are expected to dominate the emission at different stages of the burst. While such a variation has been reported for GRB 060206 (Hao et al. 2007), this claim was later refuted (Thöne et al. 2008; Aoki et al. 2009). Variable-strength intervening absorbers do not appear to be a common phenomenon in GRB spectra, although the need for high-resolution, high signal-to-noise time sequenced spectra limits the amount of observations for which it is possible to detect such variations. D’Elia et al. (2010) examine the very bright GRB 080319B (z = 0.937), which displayed four intervening Mg ii absorption systems in the redshift range 0.5 < z < 0.8, and find no evidence for variability in the intervening lines.
Quasars are almost certainly powered by an accretion disk around a central supermassive black hole (e.g., Peterson 1997). The UV-optical continuum spectrum is expected to be emitted by the central part of the accretion disk. The broad emission lines are emitted by photoionized gas. The detailed structures, geometries, and sizes of the continuum-emitting and broad line-emitting regions (BLR) are not accurately known, as they are too compact to be resolved even for the nearest active galactic nuclei. However, the measured time delays in the response of the broad lines to continuum luminosity variations (e.g., Peterson 2008; Peterson et al. 2004) indicate that the BLR extends to significantly larger radii (of order light-weeks to light-months) than the UV-optical continuum (of order light-days). Much of the broad-line radiation is therefore emitted at large radii from the continuum source, giving a larger effective beam size for the quasar light (BLR plus continuum) at these wavelengths.
Depending on the relative redshifts of a given absorption system and the quasar, the Mg ii line will either absorb the continuum emission alone or the continuum-plus-BLR emission. If the Frank et al. (2007) geometric model is the correct explanation for the different absorber statistics between GRBs and quasars, we also expect to see different absorber statistics for the different emission regions in the quasar system itself. The reasons are as follows. For the Frank et al. (2007) explanation to work, the “average” absorber in a quasar spectrum must suffer a dilution effect compared to a GRB-absorber. Therefore, the quasar continuum beam size must be large enough for the dilution effect to come into play. On the other hand, the continuum beam cannot be much larger than the absorbers, as we in that case would not expect to see any strong absorption in quasar spectra. This in turn implies that absorbers backlit by continuum plus BLR light would suffer an even larger dilution effect (Pontzen et al. 2007), as the BLR is larger than the continuum region. A comparison of absorber statistics for those absorbers only receiving continuum light and those also illuminated by BLR light is therefore a test of the geometric explanation. Note that since the two beam sizes reside in the same quasar systems, selection biases in the quasar sample play no role.
1.4. Outline of this study
The aim of this study is to test for a difference between the sight-line number density of strong Mg ii absorbers backlit by BLR light and that of absorbers illuminated by continuum-dominated emission. We identify a sample of strong Mg ii absorbers in SDSS DR7 quasar spectra (Schneider et al. 2010), measure the comoving sight-line number density of these absorbers (Sect. 2), and test it for a dependence on the quasar rest-frame wavelength of the absorbed light (Sect. 3). The outcome of this study has implications for the characteristic sizes of Mg ii-absorbing clouds relative to the sizes of quasar BLR and continuum-emitting regions. Detection of a significantly lower sight-line number density of strong Mg ii absorbers projected onto the quasar broad C iv and C iii] emission lines would directly support the Frank et al. (2007) geometrical explanation for the quasar-GRB strong absorber statistics discrepancy found in Prochter et al. (2006b).
2. Data: the Mg II absorber catalog
2.1. Method: identifying strong Mg II absorbers
We searched the SDSS Data Release 7 quasar sample (Schneider et al. 2010) for strong Mg ii absorption. For this study we used the 1D spectra processed by the SpecBS algorithm (the Princeton reductions). These spectra are binned as log (λ) with a pixel width corresponding to 69 km s-1. The spectrograph has a wavelength-dependent resolving power of between 1850 and 2200.
We developed a semi-automatic algorithm1 to find strong Mg ii absorbers in the spectra. This algorithm can be summarized as follows: an approximation Fs(λ) of the quasar’s intrinsic spectrum was first made via a combination of box-car median smoothing of the observed spectrum F(λ) and Gaussian fits to residuals corresponding to the peaks of broad emission lines. We experimented with the size of the boxcar and found that a width of 121 pixels is a good compromise: the box must be large enough that the smoothed spectrum does not trace absorption features with strengths corresponding to strong Mg ii absorbers, yet small enough that the median smoothing follows the broad wings of quasar emission lines adequately. This smooth spectrum serves as a reference spectrum against which candidate Mg ii absorbers are selected. The standard deviation, S(λ), of the residuals after subtraction of the smoothed spectrum (measured over a 121-pixel box centered on each pixel) was then calculated. Any pixel with F(λ) < (Fs(λ) − 3.5S(λ)) and a signal-to-noise ratio (averaged over a 121-pixel box centered on the pixel in question) of 8 or above was considered for inclusion in an Mg ii doublet. The latter constraint was imposed due to our line-finding algorithm becoming increasingly unreliable at lower signal-to-noise – we set the cutoff at the lowest signal-to-noise ratio where the algorithm retrieved more than 99% of strong absorbers in the Bouché et al. (2006) comparison sample described in Sect. 2.2, ignoring any absorption systems in the comparison sample located at spectral regions that fell below our signal-to-noise cutoff. Spurious identifications sometimes occurred with this signal-to-noise cutoff, however they were reliably flagged for visual inspection according to the criteria described below. Each of these candidate absorption features was fitted with a single Gaussian profile. Each absorption feature was then searched for additional structure within a 5-pixel (345 km s-1, corresponding to 2.5 times the spectral resolution at 4000 Å) interval, and refitted as a double-Gaussian composite if a non-negligible extra peak was found.
The resulting list of candidate absorption line positions was then searched for line pairs with a rest-frame wavelength separation of δλ = 7.178 Å (in vacuum), corresponding to the separation of the Mg ii λλ2796, 2803 doublet. These candidates were re-fitted simultaneously using a Gaussian for each line, with the wavelength separation between the two centroids fixed. The equivalent widths of the Gaussian line profiles were recorded. We limited our search to wavelengths longer than 1250 Å (1 + zem) due in part to the severe contamination by Lyman-α absorbers shortward thereof and, in part, to the fact that our smoothed spectrum does not follow the quasar’s Lyman-α emission profile adequately.
Spectra with intrinsic broad absorption lines were discarded from the sample using the catalog produced by Shen et al. (2011) for two reasons. Firstly, it proved difficult to measure the equivalent width of a bona fide Mg ii absorber superimposed on a BAL trough. Secondly, the automatic procedure occasionally misinterpreted broad C iv absorption as an Mg ii doublet.
The expected doublet ratio for Mg ii is W2796/W2803 ≈ 2 if the absorber is optically thin, and W2796/W2803 ≈ 1 in the optically thick limit. The initial constraint imposed on the ratio of equivalent widths for Mg ii doublet candidates was 0.33 < W2796/W2803 < 2.9. These limits were chosen to ensure that the automatic procedure includes all strong Mg ii absorbers in the sample of Bouché et al. (2006), even for cases where the initial measurement of Wr for one of the doublet components was impaired by line blending. Doublets with W2796/W2803 < 1 or W2796/W2803 > 2 were then flagged for visual inspection. Very strong absorbers (Wr > 4 Å), absorbers with narrow Gaussian widths (σ < 0.3 Å), and fits with large residuals within three pixels of the line center, were also flagged for visual inspection. Candidate systems at observed wavelengths between 7000 Å and 8000 Å were also inspected, as several SDSS spectra displayed artifacts of atmospheric-line removal in this interval which could be misinterpreted as Mg ii absorption.
In the relatively few cases where the Mg ii doublet profile is not fully convincing to the eye (e.g. because one of the components is blended with another absorption line, making the line center uncertain), we searched for the presence of other metal absorption lines, such as Fe ii λ 2600 and Mg i λ 2852, at the same redshift.
The resulting Mg ii absorber catalog comprises 10 367 strong Mg ii absorption systems, of which 2084 have been visually inspected.
2.2. Completeness of the Mg II absorber catalog
The completeness of the sample was tested against the SDSS-DR3 intervening Mg ii absorber sample of Bouché et al. (2006) which comprises 1806 Mg ii absorbers at redshifts 0.37 < zabs < 0.80, of which 1269 have Wr > 1 Å, in spectra of quasars with redshift zem < 3.193. The original purpose of the Bouché et al. (2006) sample was to investigate the cross-correlation of the Mg ii absorbers with the presence of galaxies. Their upper zabs limit is due to a completeness requirement for their galaxy sample. Thus, the Bouché et al. (2006) comparison sample does not cover all of the zabs range we search. However, the wide redshift range of their quasar sample ensures that their database contains representative examples of absorbers both blueward and redward of the C iv λ 1550 emission line as well as absorbers superimposed on it. These wavelength regions are the focus of our investigation in Sect. 3.2. Our algorithm retrieved 99.2% of the Bouché et al. (2006) absorbers with Wr > 1 Å (as measured by our fitting procedure). Quider et al. (2011) have released a catalog of Mg ii absorbers in SDSS DR4. They search all targets flagged as quasars by the SDSS spectroscopic pipeline with an apparent i-magnitude brighter than 20, and find 17042 Mg ii absorbers, of which 9942 have Wr > 1 Å. Our algorithm retrieves 96.2% of the strong absorbers in that sample. Including the strong absorbers from the Quider et al. (2011) sample that our algorithm missed does not significantly affect the analysis of Sect. 3.2.
For this study it is crucial that we have a uniform sensitivity to strong Mg ii absorbers superimposed on the quasar continuum and on the broad emission lines, respectively. Emission lines generally have a higher signal-to-noise than the rest of the spectrum. We tested the sensitivity by means of the detection limit σdet(λ), defined as the integrated noise spectrum over a resolution element around each pixel divided by the flux integrated over the same resolution element (e.g., Vestergaard 2003). This gives a minimum equivalent width (Wr,min > 3σdet) that can be detected at that pixel.
The detection limit σdet(λ) of absorbers was measured for all pixels searched (i.e. all pixels fulfilling our S/N criterion) within the quasar rest-frame wavelength intervals 1450–1500 Å, 1522–1570 Å and 1650–1700 Å (i.e., bluewards of, superimposed on, and redwards of the C iv line, respectively), for the entire quasar sample. The cumulative distributions of σdet for these intervals are shown in Fig. 1. Based thereon, we define the minimum rest-equivalent width Wr,min for each wavelength interval such that 95% of the pixels searched in that interval allow the detection of an absorption line of strength Wr,min at a 3σ significance. The best case was for pixels superimposed on the C iv emission line, for which Wr,min = 1.02 Å. The worst case was for the interval 1450–1500 Å, for which Wr,min = 1.16 Å. Discarding all absorbers with Wr < 1.16 Å reduces the total sample size by 20% without significantly affecting the analysis and conclusions discussed in Sect. 3.2.
 |
Fig. 1 The cumulative distribution of the 3-sigma detection limit, 3σdet, measured for all quasar spectra in our sample, for three quasar rest-frame wavelength intervals; the detection limit is defined in Sect. 2. Only the spectral regions in which we actually searched for absorbers (i.e. those that fulfill our signal-to-noise criterion, see Sect. 2) are included in the cumulative distributions. For comparison, the brown curve shows the cumulative distribution of equivalent widths of Mg ii absorbers detected by our algorithm within the quasar rest-frame wavelength interval 1450–1700 Å. The horizontal green line shows the 95% completeness limit. |
For Mg ii absorption systems with one of the doublet components superimposed on the central peak of a quasar broad emission line there is an additional uncertainty in the equivalent width measurement, as the emission line profile fits were less reliable for partially absorbed lines. We found that absorption lines that were superimposed within 3 Å (in the quasar rest-frame) of the emission line peak adversely affected the Gaussian fit of the emission line profile. This typically led to an underestimation of the absorption line’s equivalent width of order 0.1−0.2 Å, with stronger absorption generally leading to a more severe underestimation. This underestimation caused a few marginally strong Mg ii absorbers superimposed within 3 Å of the emission line peaks to drop out of our catalog.
To quantify this effect we interactively re-fit the emission line profile for all 0.8 Å < Wr < 1 Å absorption systems for which the Mg ii 2796 Å component was located within 3 Å of a quasar’s C iv emission peak. This led to the reexamination of 16 absorption systems. Ignoring the few strongly absorbed systems where the “correct” emission line profile was difficult to discern by eye, our updated, improved measurements show that the automated algorithm on average underestimates the equivalent width of these absorbers by 0.07 Å. Four of the tested systems were revealed as Wr > 1 Å absorbers after adjustment of the emission line fits. Based in Fig. 1, the completeness of our sample for absorbers near the quasar’s C iv emission line with Wr ≈ 0.8 Å is around 70% – this implies that around six strong absorbers on the C iv emission line peak are missed due to poor fitting of the emission line profile.
Another estimate of the amount of missed systems on the C iv emission line peak can be obtained by counting the systems within 3 Å of the C iv emission line peak that have 0.93 Å < Wr < 1 Å, i.e., all lines that, according to the equivalent width underestimation described above, would (on average) cross the Wr > 1 Å threshold. There are 7 of these systems. Correcting for completeness (around 90% at Wr > 0.93 Å) gives an estimated 8 missed Mg ii absorbers.
The effect of these missed systems on our result is discussed in Sect. 3.2. The redshift path covered by this survey within 3 Å of the C iv emission line peak is only 0.3% of the total redshift path covered by the survey. Therefore the effect of this bias on the total path length density found for Mg ii absorbers is negligible, even if a similar effect is present in previous surveys. In general we advise caution in the use of the equivalent widths quoted in our Mg ii absorber catalog for absorbers that are close to emission line peaks and that are not flagged as having been visually inspected.
3. Results
In the following, we first establish the redshift path distribution of our Mg ii absorber catalog (Sect. 3.1) and then examine the wavelength-dependent frequency of absorbers in the quasar frame of reference (Sect. 3.2) in order to address the issue of the sizes of Mg ii absorbers relative to the background quasar continuum and emission-line beam-sizes.
3.1. Redshift distribution of strong Mg II absorbers
 |
Fig. 2 Top panel: the redshift path density g(z) of this survey, i.e. the number of sight-lines that were searched for Mg ii absorption for a given absorber redshift zabs. Bottom panel: the distribution of equivalent widths of the Mg ii 2796 Å component of the absorption systems in our sample. |
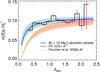 |
Fig. 3 The redshift distribution of the sight line number density n(X) of strong Mg ii absorption systems per comoving Mpc (bins of Δz = 0.15). The blue curve shows an exponential fit to this number density. The yellow curve shows the fit of Prochter et al. (2006a) to their strong Mg ii absorber sample. The shaded areas show the 1σ uncertainties on the exponential fits. |
The Mg ii absorber catalog on which Prochter et al. (2006b) base their comparison of GRB and quasar absorber statistics is that presented by Prochter et al. (2006a), where 45023 SDSS DR3 quasar spectra were searched, resulting in 4835 strong Mg ii absorbers. Before addressing the main question of the present study, it is therefore important to compare the properties of the Prochter et al. (2006a) absorber catalog to the properties of the absorber catalog presented here. While our sample of quasar spectra is larger, we expect the statistical properties of the absorber populations to be similar: there are no obvious reasons to think that the Mg ii absorber properties and typical quasar sight lines will be significantly different between the SDSS DR3 and DR7 releases.
The redshift path density g(z) of an absorber survey represents the number of spectra in which it is possible to detect strong Mg ii absorption at a given redshift. A value of 1 is added to a g(z) bin (corresponding to a redshift interval between z and z + Δz – we set Δz = 0.01 in Fig. 2 and Δz = 0.15 in Figs. 3 and 4) for each quasar spectrum that is searched for Mg ii absorption at the corresponding redshift. Here, individual pixels in the spectrum were searched if the signal-to-noise ratio, averaged over a 121-pixel box centered on the pixel in question (corresponding to δz = 0.04 when centered at λ = 4000 Å) was above 8. This often caused a fraction of the pixels in a redshift interval corresponding to a g(z) bin to be skipped, while other pixels were searched for absorption – in this case the fraction of the relevant redshift interval that was actually searched was added to the g(z) bin. We show g(z) as a function of redshift in Fig. 2. We attribute the dip in g(z) around z = 1 to a combination of a prominent sky emission line near 5570 Å, for which the SDSS pipeline removal often results in a noise spike, and to the decrease in signal-to-noise of SDSS spectra near the wavelength corresponding to the split between the two CCD detectors. Either of these issues can cause the signal-to-noise in this spectral region to fall below our cutoff, thereby decreasing the effective redshift path length of our study. The sight-line number density n(z) of strong Mg ii absorbers in a given redshift bin is then n(z) = N(z)/(g(z)Δz), where N(z) is the number of absorbers found between redshifts z and z + Δz, and Δz is the size of a redshift bin.
Following Prochter et al. (2006a), we convert n(z) to the sight-line number density of strong absorbers per comoving Mpc, n(X): ![\begin{equation} n(z)=n(X)(c/H_0)(1+z)^2[\Omega_{\rm M} (1+z)^3+\Omega_{\Lambda}]^{-1/2}\rm, \end{equation}](/articles/aa/full_html/2012/10/aa19326-12/aa19326-12-eq73.png) (1)assuming a cosmology with density parameters ΩΛ = 0.73, ΩM = 0.27 (Larson et al. 2011). The redshift distribution of
(1)assuming a cosmology with density parameters ΩΛ = 0.73, ΩM = 0.27 (Larson et al. 2011). The redshift distribution of 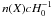 is shown in Fig. 3.
is shown in Fig. 3.
 |
Fig. 4 The redshift distribution of the sight line number density n(X) of strong Mg ii absorption systems per comoving Mpc (bins of Δz = 0.15), divided into three subsamples according to the u-band (top panel) and i-band (bottom panel) apparent magnitude of the background quasar. |
Prochter et al. (2006a) find that an exponential relationship between redshift and n(X) is a reasonable fit to their data, giving 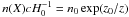 with n0 = 0.11(± 0.006), z0 = −0.28(± 0.05), for their Wr > 1 Å sample. Fitting an exponential function to our data gives n0 = 0.11(± 0.005), z0 = −0.11(± 0.03), i.e. we found a higher n(X) than Prochter et al. (2006a) at low absorber redshift; the exponential fits to n(X) agree for both studies at z ≳ 1.0 to within the quoted 1-σ errors. When we integrate the fit to n(X) of our absorber sample along the redshift path of GRB spectra searched for Mg ii absorption in Vergani et al. (2009), we obtain the number of Mg ii absorbers that would be expected along quasar sight lines covering the same redshift path,
with n0 = 0.11(± 0.006), z0 = −0.28(± 0.05), for their Wr > 1 Å sample. Fitting an exponential function to our data gives n0 = 0.11(± 0.005), z0 = −0.11(± 0.03), i.e. we found a higher n(X) than Prochter et al. (2006a) at low absorber redshift; the exponential fits to n(X) agree for both studies at z ≳ 1.0 to within the quoted 1-σ errors. When we integrate the fit to n(X) of our absorber sample along the redshift path of GRB spectra searched for Mg ii absorption in Vergani et al. (2009), we obtain the number of Mg ii absorbers that would be expected along quasar sight lines covering the same redshift path, 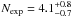 . This is consistent with the values of Nexp that Vergani et al. (2009) present in their Table 3, based on the absorber samples of Prochter et al. (2006b) and Nestor et al. (2005), and approximately a factor 2 smaller than the sight-line density they find for GRBs2.
. This is consistent with the values of Nexp that Vergani et al. (2009) present in their Table 3, based on the absorber samples of Prochter et al. (2006b) and Nestor et al. (2005), and approximately a factor 2 smaller than the sight-line density they find for GRBs2.
We find that the sight-line number density of strong absorbers in our sample depends on the apparent magnitude of the background quasar. In the u band (effective wavelength 3551 Å) a significantly higher sight-line number density of strong absorbers is found in spectra of faint (mu > 19.5 mag) quasars. For the i band (effective wavelength 7481 Å) the trend is reversed: we find a higher sight-line number density of absorbers in spectra of bright (mi < 18.2 mag) quasars, see Fig. 4. In the g and r bands the bright and faint quasar samples generally have the same sight-line number density of strong absorbers (within Poissonian errors). This appears to be analogous to the result presented by Ménard et al. (2008) based on an investigation of extinction, reddening, and gravitational lensing effects for an SDSS DR4 Mg ii absorber sample. They find apparent magnitude offsets for a sample of quasars with intervening Mg ii absorption compared to an unabsorbed reference sample, with the amplitude and sign of the offset depending on the SDSS filter band-pass – their results (described in Sect. 4.4) are consistent with our findings.
3.2. Incidence of strong Mg II absorbers on quasar emission regions
Here, we investigate the relative frequencies of Mg ii absorbers superposed on the quasar continuum and broad line emission, respectively. First, we define the superposition wavelength of each Mg ii absorber as λsup = λobs/(1 + zem), where λobs is the observed wavelength of the Mg ii λ 2796 component and zem is the emission redshift of the background quasar. That is, λsup is the wavelength of the Mg ii absorber in the quasar rest-frame. We split each quasar spectrum into bins of width 50 Å in the quasar rest-frame, and recorded the redshift path along which the Mg ii absorption is searched in each bin for this sight-line. Summing this quantity over all spectra searched gives the redshift path density (gλsup), analogously to g(z) defined in Sect. 3.1, but now as a binned function of λsup.
Next, we calculate the sight-line number density of strong Mg ii absorbers for a given superimposition wavelength: n(λsup) = N(λsup)/(g(λsup)Δz), where N(λsup) is the number of absorbers found in each quasar rest-frame wavelength bin, Δz. We converted this quantity to the number density of strong absorbers per comoving Mpc, as in Sect. 3.1 but now as a function of quasar rest-frame wavelength. We fitted a power-law 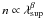 to quasar rest-frame wavelength bins mostly free of BLR emission – these bins are centered at 1320, 1355, 1452, 1690, 2030, 2160 and 2220 Å – and found β = 0.13 ± 0.11. We also fitted a power-law to the entire n(λsup) data set, yielding β = 0.17 ± 0.10. These fits are shown in Fig. 5.
to quasar rest-frame wavelength bins mostly free of BLR emission – these bins are centered at 1320, 1355, 1452, 1690, 2030, 2160 and 2220 Å – and found β = 0.13 ± 0.11. We also fitted a power-law to the entire n(λsup) data set, yielding β = 0.17 ± 0.10. These fits are shown in Fig. 5.
The C iv emission line in the composite SDSS quasar spectrum presented by Vanden Berk et al. (2001) is centered at 1546.15 Å and has a full-width half-maximum (FWHM) of 23.78 Å. Here we regard Mg ii absorbers with the quasar rest-frame wavelength of the 2796 Å doublet component located within this FWHM as being superimposed on the C iv line. The sight-line number density of strong Mg ii absorbers superimposed on C iv is 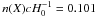 . The power-law fit to the entire data set gave
. The power-law fit to the entire data set gave 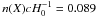 at λsup = 1546 Å, while the power-law fit to the continuum-only quasar rest-frame wavelengths gave
at λsup = 1546 Å, while the power-law fit to the continuum-only quasar rest-frame wavelengths gave 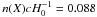 at λsup = 1546 Å. Adopting Poisson statistics, this corresponds to a significance of 1.08σ and 1.24σ, respectively, for the peak in number density of absorbers superimposed on C iv compared to the whole-spectrum fit and continuum-only fit, respectively. In other words, we found no significant increase or decrease in the number of absorbers superimposed on the C iv emission line relative to that of the continuum emission. The slight overabundance of absorbers superimposed on the C iv peak could possibly be due to the higher signal-to-noise level at the position of the emission line, if the completeness of our search is significantly decreased at relatively low signal-to-noise levels near our cutoff of S/N > 8. This does not introduce a significant systematic error; see Sect. 4.4.
at λsup = 1546 Å. Adopting Poisson statistics, this corresponds to a significance of 1.08σ and 1.24σ, respectively, for the peak in number density of absorbers superimposed on C iv compared to the whole-spectrum fit and continuum-only fit, respectively. In other words, we found no significant increase or decrease in the number of absorbers superimposed on the C iv emission line relative to that of the continuum emission. The slight overabundance of absorbers superimposed on the C iv peak could possibly be due to the higher signal-to-noise level at the position of the emission line, if the completeness of our search is significantly decreased at relatively low signal-to-noise levels near our cutoff of S/N > 8. This does not introduce a significant systematic error; see Sect. 4.4.
The sight-line number density of strong Mg ii absorbers superimposed on the C iii] emission line (centered at 1905.97 Å with a FWHM of 21.19 Å) is 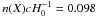 . The power-law fits gave
. The power-law fits gave 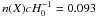 and
and 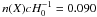 at λsup = 1906 Å for the whole-spectrum and continuum-only data, respectively. Adopting Poisson statistics, the significance of this peak is less than 1σ for both fits.
at λsup = 1906 Å for the whole-spectrum and continuum-only data, respectively. Adopting Poisson statistics, the significance of this peak is less than 1σ for both fits.
Due to the completeness considerations discussed in Sect. 2.2, we repeat this analysis for absorbers with Wr > 1.16 Å. In this case the significance of the overabundance of absorbers superimposed on C iv emission is reduced slightly, to 0.90σ and 1.06σ for the peak compared to the whole-spectrum and continuum-only fit, respectively. We also perform the same analysis including those absorbers from the sample of Quider et al. (2011) that our algorithm missed; doing so increased the significance of the C iv overabundance slightly, to 1.18σ and 1.27σ for the whole-spectrum and continuum-only fit, respectively. Thus, these considerations do not change our main results summarized above.
 |
Fig. 5 Distribution of the number density of strong Mg ii absorbers per comoving Mpc with respect to the absorbers’ wavelength in the quasar rest-frame, λsup = λobs/(1 + zem). We fit two power laws to the distribution: one is fitted to the number densities at continuum dominated wavelength bins only (violet curve), while the other is fitted to the entire dataset (blue curve). Error bars are Poissonian. Vertical lines indicate the wavelengths of the quasar broad emission lines C iv λ 1550, C iii] λ 1909, and Mg ii λ 2800. The peak at Mg ii (i.e., zabs ≈ zem) is expected, as some quasars display intrinsic Mg ii absorption. |
As discussed in Sect. 2.2, our algorithm misses some absorption lines superimposed on the central peak of the quasar broad emission lines, due to the absorption interfering with the emission line fitting. We estimate that around six strong Mg ii absorbers superimposed on the C iv emission line are missed due to this issue. The addition of six extra absorbers at λsup = 1550 Å increases the significance of the overabundance of absorbers superimposed on the C iv emission line to 1.48σ.
4. Discussion
As outlined in Sect. 1, different source beam-sizes can alter the observed equivalent width of an intervening absorber. A simple model to illustrate this is to imagine all Mg ii absorbing clouds as discrete, perfectly-absorbing spheres with solid boundaries. Consider a single Mg ii-absorbing cloud on or near the quasar sight-line. In the limit of a point-source, we either observe a strong (Wr > 1 Å) absorption or none at all. In the case of a background source (i.e., beam-size) much larger than the absorber radius, we will only observe weak absorption, as most photons from the source do not pass through the absorbing region at all. Between these two extremes we can observe strong absorption, depending on how close the absorbing cloud is to the quasar sight-line. For a random spatial distribution of sources and absorbers, a smaller source beam-size will therefore result in a larger number of strong absorbers than will a larger beam-size.
4.1. Size estimates of source beams and Mg II absorbers
In recent years, microlensing studies have been used to obtain approximate sizes of the continuum and line emitting regions in individual quasars. For example, Mediavilla et al. (2011) estimate the size of the continuum-emitting region of the quasar SBS 0909+532 (z = 1.38), and obtain a radius of around 1.81 × 1016 cm. For the quasar QSO 2237+0305 (z = 1.7) Wayth et al. (2005) find a size of the C iii] emitting regions of about 1.85 × 1017 cm and an upper limit on the continuum-emitting radius of 6.1 × 1016 cm. Mosquera & Kochanek (2011) obtain microlensing measurements of 87 quasar continuum-emitting regions, finding radii of around 1015 cm. They also estimate the size of the Hα BLR of the same quasars using the radius-luminosity relationship given by Bentz et al. (2009), and find BLR radii of ~1017 cm. Owing to the ionization stratification of the BLR (Clavel et al. 1991), higher ionization lines such as C iv are expected to be emitted closer to the ionizing continuum region than the C iii] and Balmer lines. The size of the BLR scales with quasar luminosity (see, e.g., Bentz et al. 2009); the quoted figures serve as order-of-magnitude estimates of the relative sizes of continuum and C iv BLR in an “average” quasar in our sample. As an example of a quasar at z ~ 2, Kaspi et al. (2004) report a tentative C iv broad-line rest-frame lag of 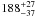 days with respect to variations in the continuum for the quasar S5 0836+71. This corresponds to a C iv BLR radius of 4.9 × 1017 cm for this luminous quasar. Sluse et al. (2011) perform a microlensing study of the z = 1.695 lensed quasar QSO 2237+0305 and find a radius of 1.71 × 1017 cm for the C iv BLR, while Balashev et al. (2011) study the partial coverage of the quasar Q1232+082 (z = 2.57) by an intervening damped Lyman-α absorber and find a C iv BLR radius of 2.78 × 1017 cm, using photoionization considerations to estimate the size of the absorbing cloud. These considerations show that it is reasonable to assume that quasar BLRs are, in general, located at radii from the central black hole that are one or two orders of magnitude larger than the extent of the continuum-emitting region.
days with respect to variations in the continuum for the quasar S5 0836+71. This corresponds to a C iv BLR radius of 4.9 × 1017 cm for this luminous quasar. Sluse et al. (2011) perform a microlensing study of the z = 1.695 lensed quasar QSO 2237+0305 and find a radius of 1.71 × 1017 cm for the C iv BLR, while Balashev et al. (2011) study the partial coverage of the quasar Q1232+082 (z = 2.57) by an intervening damped Lyman-α absorber and find a C iv BLR radius of 2.78 × 1017 cm, using photoionization considerations to estimate the size of the absorbing cloud. These considerations show that it is reasonable to assume that quasar BLRs are, in general, located at radii from the central black hole that are one or two orders of magnitude larger than the extent of the continuum-emitting region.
The radius of the GRB afterglow ring is expected to evolve with time (e.g., Waxman 1997). Based on this theoretical expectation Hao et al. (2007) estimate the radius of the GRB beam in GRB 060206 to be 5.1 × 1015 cm at the time that their spectra were obtained. Frank et al. (2007) suggest that the effective beam size could be an order of magnitude smaller than this due to an uneven luminosity distribution over the GRB emission ring. This is smaller than the quoted size of the typical quasar continuum region by a factor of ≈10 or more.
While entire Mg ii-absorbing complexes are thought to be similar in size to the gaseous haloes of their host galaxies (Smette et al. 1995), there are signs of a clumpy substructure with individual clouds smaller than a kiloparsec in diameter as evidenced by lensed quasars (Rauch et al. 2002). This upper limit is very large compared to the beam-size estimates quoted above; thus the size of an Mg ii-absorbing cloud itself is the main unknown in the present discussion.
4.2. Our results in context of the beam-size dilution scenario
In the context of the simple model described in Sect. 1.3, the beam-size interpretation (Frank et al. 2007) implies that one of two relationships exists between the characteristic sizes of Mg ii absorbing clouds and the background beams produced by (a) the quasar continuum emission, and by (b) the quasar BLR-plus-continuum emission, respectively. One possibility is that the Mg ii absorber size could be slightly smaller than the beam size emitted by a quasar continuum region. In this case, beam dilution always occurs for intrinsically strong absorbers in quasar spectra (regardless of the light source beam is the continuum or the BLR-plus-continuum), leading to the observed lack of strong absorbers along quasar sight-lines compared to GRB sight-lines. Alternatively, the Mg ii absorber could be comparable to or larger than the quasar continuum beam size but significantly smaller than the BLR beam size, in which case beam dilution only occurs for absorbers superimposed on BLR emission lines, and the discrepancy between quasar and GRB absorber statistics would be wholly due to a severe underabundance of strong absorbers superimposed on BLR emission.
In both of these scenarios we expect to find an underabundance of strong Mg ii absorbers superimposed on quasar C iv λ1550 (and C iii] λ1909) emission lines compared to the quasar continuum, as the C iv (and C iii] ) BLR extends to larger radii compared to the continuum region and contributes a significant amount of the total luminosity at 1550 Å. Figure 5 and Sect. 3.2 present a clear non-detection of such an underabundance. Therefore, the average size of Mg ii absorbing clouds must be larger than the typical quasar continuum beam size. In fact the lower limit on the size of an absorbing cloud must be comparable to the BLR beam size, i.e., on the order of 1017 cm, as we see no evidence of beam dilution for absorbers superimposed on BLR emission. This result is in broad agreement with the analysis of Pontzen et al. (2007) for the C iii] emission line. A detailed comparison with the Pontzen et al. (2007) study is, however, difficult as they do not estimate the completeness of their absorber sample (or, alternatively, test for a difference in their completeness on and off the C iii] emission line).
The simple picture described above is complicated somewhat by our ignorance of the true spatial distribution of the BLR gas, which is treated here as a spherical source of a given radius. Models in which the BLR emission is concentrated into smaller physical volumes (e.g. a rotating ring) for a given BLR radius may produce a less prominent dilution effect (averaged out over a large number of systems). Future quasar reverberation mapping studies aimed at retrieving the structure of the BLR (Horne et al. 2004) may give a better idea of the BLR beam morphology. However, we note that the BLR cannot be concentrated into an arbitrarily small spatial region with a negligible beam size, as the broad-line velocity distribution shows little structure at high resolution; this indicates that at least 5 × 104 broad-line emitting clouds orbit the central source (Peterson 1997).
4.3. Density considerations for gas in a galaxy halo
It is tempting to use the lower limit (of order ≈1017 cm) obtained in this study to place limits on the volume density of the clouds using column density estimates gleaned from the equivalent width of the Mg ii absorbers, thereby constraining the conditions of the absorbing galaxy halo. Here we consider the implications of our constraint on Mg ii absorption cloud size for the density in the clouds; to do so we must rely on knowledge of the cloud structure of Mg ii absorbers inferred from high-resolution spectroscopy.
Due to the geometrical nature of the beam dilution effect, the lower limit on Mg ii cloud sizes obtained in the present study (≈1017 cm) in principle only applies to a single absorbing cloud. Most Mg ii absorption systems in the SDSS display a saturated 2796,2803 Å doublet, and therefore the column density of strong Mg ii absorbers in the SDSS cannot be determined from the absorption line profile alone (Nestor et al. 2005). However, Mg ii absorbers with Wr > 1 Å as observed in moderate-resolution spectroscopy often turn out to be made up of a number of smaller, kinematically distinct components when seen in higher-resolution spectra. For example, Churchill & Vogt (2001) used Keck HIRES quasar spectra to study 23 Mg ii absorption systems, of which five displayed strong (Wr > 1 Å) absorption. Their strong systems split into an average of 2.2 resolved components, with the strongest component of each system having an average Wr of 1.09 Å for the 2796 Å transition. Voigt profile fits suggest a further division of these resolved components. An extreme example is the strong Mg ii absorption system at z = 0.911 in the spectrum of quasar PKS 0823-223; this profile splits up into 18 Voigt profile cloudlets, with Mg ii column densities 11.45 < log (Ncm-2) < 13.25 cm-2.
Ménard & Chelouche (2009) performed a study of the H i content of Mg ii absorbers. They generally found NH i > 1018 cm-2 for Mg ii absorbers with Wr > 0.45 Å, with a large scatter – see their Fig. 1. The median H i column densities in their sample for Mg ii absorbers with Wr ≈ 1 Å is 3 × 1019 cm-2. Assuming a single spherical absorption cloud and applying our lower limit for the cloud size, ≈1017 cm, this implies a H i volume number density of 300 cm-3. The expected upper limit for the number density of gas in galaxy halos is 10 cm-3 (e.g., Ding et al. 2005). Our lower limit on cloud size is therefore a very weak constraint when considering a one-cloud model.
Alternatively one could assume that most strong Mg ii absorption systems in the SDSS are comprised of several absorbing clouds, as the Churchill & Vogt (2001) results imply. The equivalent widths of individual cloud components could plausibly be of order 0.3−0.6 Å if the Voigt profile fits of Churchill & Vogt (2001) reliably reflect the substructure of strong Mg ii absorbers. This corresponds to the smallest column densities found by Ménard & Chelouche (2009), NHI ≈ 1018 cm-2. This column density gives a H i number density of 10 cm-3 for our lower limit on Mg ii cloud size, consistent with expectations for the densest halo gas (e.g., Ding et al. 2005).
Ding et al. (2005) performed photoionization modeling on weak and intermediate-strength Mg ii absorption systems. For example, they estimate the size of the highest column-density velocity component in the z = 0.6600, Wr = 0.34 Å Mg ii absorption system toward the quasar PG 1317+274 to be 6.17 × 1017 cm, with a H i density of ≈2 cm-3; they estimate the size of the highest column density component of the z = 0.7729, Wr = 0.694 Mg ii absorption system toward quasar PG 1248+401 to be 6.17 × 1018 cm, with a H i density of ≈0.9 cm-3. Our lower absorber size limit is thus fully consistent with existing photoionization models for intermediate-strength Mg ii absorption clouds, allowing for a scenario where strong absorbers in the SDSS are composed of multiple intermediate-strength components. It does not, however, strongly constrain such a scenario with respect to the sizes of the individual component clouds. According to the Ding et al. (2005) models, very weak Mg ii absorbers will have kpc-scale sizes, much larger than the lower limit presented here.
4.4. Bias due to low signal-to-noise?
In Sect. 3.1 we describe a dependence of the sight-line number density of strong absorbers on the apparent magnitude of the background quasar (Fig. 4). Ménard et al. (2008) find a similar dependence, and explain it as a combination of two effects: firstly a reddening of those quasar spectra with intervening absorbers due to dust associated with the absorption systems, and secondly a bias due to their line-finding algorithm. They measure this second effect using Monte Carlo simulations and find it to be independent of wavelength (i.e., producing a similar offset in all SDSS bands). This bias may be due to complications of continuum and emission line fitting in low-flux spectra – such complications could affect the identification of Mg ii doublets or the measurement of equivalent widths. But signal-to-noise may also be an issue as the ability to find an absorber decreases in spectral regions with low flux; this presents itself as a tendency to find more (and weaker) absorbers in high-flux spectra (as discussed in Sect. 3). Based on the discussion of completeness and sensitivity at the end of Sect. 3 this is not likely to affect our study given the high signal-to-noise cutoff (S/N > 8) and completeness level (>95%) of our catalog. Nonetheless, we note that any potential bias of this nature in our algorithm must also be present to some degree in the Mg ii absorber sample of Quider et al. (2011), as the inclusion of absorbers from their catalog, missed by our algorithm, does not affect our main results.
5. Summary
We have searched the SDSS DR7 quasar catalog for strong (Wr > 1 Å) Mg ii absorption systems, and tested for a difference in sight-line number density of absorbers illuminated by quasar broad emission line photons compared to that of absorbers illuminated by continuum photons only. There is no significant difference in these number densities. This constrains the size of the Mg ii absorbing clouds that give rise to strong absorption to be (as a lower limit) comparable to the size of quasar broad-line emitting regions, i.e., of the order of 1017 cm. The model proposed by Frank et al. (2007) to explain the difference in absorber sight-line number densities between quasar and GRB sight-lines appears to be excluded by our result as it implies an underabundance of absorbers on the C iv emission line relative to the continuum regions. This is in broad agreement with the test performed by Pontzen et al. (2007) for the C iii] broad emission line, and extends their result to the C iv broad emission line.
Note that the n(z) fit quoted in Prochter et al. (2006b), n(z) = −0.026 + 0.374z − 0.145z2 + 0.026z3, is based on their updated absorber catalog covering SDSS Data Release 4. This fit is in better agreement with our measurement of n(X) than that of Prochter et al. (2006a), but the updated absorber catalog is not described in detail.
Acknowledgments
The Dark Cosmology Centre is funded by the Danish National Research Foundation. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/.
References
- Aoki, K., Totani, T., Hattori, T., et al. 2009, PASJ, 61, 387 [NASA ADS] [Google Scholar]
- Balashev, S. A., Petitjean, P., Ivanchik, A. V., et al. 2011, MNRAS, 418, 357 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Bentz, M. C., Peterson, B. M., Netzer, H., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 697, 160 [Google Scholar]
- Bergeron, J., Boissé, P., & Ménard, B. 2011, A&A, 525, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouché, N., Murphy, M. T., Péroux, C., Csabai, I., & Wild, V. 2006, MNRAS, 371, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Budzynski, J. M., & Hewett, P. C. 2011, MNRAS, 416, 1871 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-W., Perley, D. A., Pollack, L. K., et al. 2009, ApJ, 691, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Churchill, C. W., & Vogt, S. S. 2001, AJ, 122, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Clavel, J., Reichert, G. A., Alloin, D., et al. 1991, ApJ, 366, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchiara, A., Jones, T., Charlton, J. C., et al. 2009, ApJ, 697, 345 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Fiore, F., Goldoni, P., et al. 2010, MNRAS, 401, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Ding, J., Charlton, J. C., & Churchill, C. W. 2005, ApJ, 621, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, S., Bentz, M. C., Stanek, K. Z., et al. 2007, Ap&SS, 312, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, H., Stanek, K. Z., Dobrzycki, A., et al. 2007, ApJ, 659, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K., Peterson, B. M., Collier, S. J., & Netzer, H. 2004, PASP, 116, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Jakobsson, P., Hjorth, J., Fynbo, J. P. U., et al. 2004, ApJ, 617, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Kacprzak, G. G., & Churchill, C. W. 2011, ApJ, 743, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Netzer, H., Maoz, D., et al. 2004, Coevolution of Black Holes and Galaxies (Cambridge: CUP) [Google Scholar]
- Krühler, T., Greiner, J., Schady, P., et al. 2011, A&A, 534, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larson, D., Dunkley, J., Hinshaw, G., et al. 2011, ApJS, 192, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Matejek, M. S., & Simcoe, R. A. 2012, ApJ, submitted [arXiv:1201.3919] [Google Scholar]
- Mediavilla, E., Muñoz, J. A., Kochanek, C. S., et al. 2011, ApJ, 730, 16 [Google Scholar]
- Ménard, B., & Chelouche, D. 2009, MNRAS, 393, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Ménard, B., Nestor, D., Turnshek, D., et al. 2008, MNRAS, 385, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Ménard, B., Wild, V., Nestor, D., et al. 2011, MNRAS, 417, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Mosquera, A. M., & Kochanek, C. S. 2011, ApJ, 738, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Nestor, D. B., Turnshek, D. A., & Rao, S. M. 2005, ApJ, 628, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. A. 1997, An Introduction To Active Galactic Nuclei (Cambridge: University Press) [Google Scholar]
- Peterson, B. M. 2008, New A R., 52, 240 [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pontzen, A., Hewett, P., Carswell, R., & Wild, V. 2007, MNRAS, 381, L99 [NASA ADS] [Google Scholar]
- Porciani, C., Viel, M., & Lilly, S. J. 2007, ApJ, 659, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Prochter, G. E., Prochaska, J. X., & Burles, S. M. 2006a, ApJ, 639, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Prochter, G. E., Prochaska, J. X., Chen, H.-W., et al. 2006b, ApJ, 648, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Quider, A. M., Nestor, D. B., Turnshek, D. A., et al. 2011, AJ, 141, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rapoport, S., Onken, C. A., Schmidt, B. P., et al. 2012, ApJ, 754, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, M., Sargent, W. L. W., Barlow, T. A., & Simcoe, R. A. 2002, ApJ, 576, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Sluse, D., Schmidt, R., Courbin, F., et al. 2011, A&A, 528, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smette, A., Robertson, J. G., Shaver, P. A., et al. 1995, A&AS, 113, 199 [Google Scholar]
- Stocke, J. T., & Rector, T. A. 1997, ApJ, 489, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Sudilovsky, V., Savaglio, S., Vreeswijk, P., et al. 2007, ApJ, 669, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Sudilovsky, V., Smith, D., & Savaglio, S. 2009, ApJ, 699, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., Wiersema, K., Ledoux, C., et al. 2008, A&A, 489, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, S. D., Petitjean, P., Ledoux, C., et al. 2009, A&A, 503, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestergaard, M. 2003, ApJ, 599, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Waxman, E. 1997, ApJ, 491, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Wayth, R. B., O’Dowd, M., & Webster, R. L. 2005, MNRAS, 359, 561 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Frenk, C. S. 1991, ApJ, 379, 52 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The cumulative distribution of the 3-sigma detection limit, 3σdet, measured for all quasar spectra in our sample, for three quasar rest-frame wavelength intervals; the detection limit is defined in Sect. 2. Only the spectral regions in which we actually searched for absorbers (i.e. those that fulfill our signal-to-noise criterion, see Sect. 2) are included in the cumulative distributions. For comparison, the brown curve shows the cumulative distribution of equivalent widths of Mg ii absorbers detected by our algorithm within the quasar rest-frame wavelength interval 1450–1700 Å. The horizontal green line shows the 95% completeness limit. |
| In the text | |
 |
Fig. 2 Top panel: the redshift path density g(z) of this survey, i.e. the number of sight-lines that were searched for Mg ii absorption for a given absorber redshift zabs. Bottom panel: the distribution of equivalent widths of the Mg ii 2796 Å component of the absorption systems in our sample. |
| In the text | |
 |
Fig. 3 The redshift distribution of the sight line number density n(X) of strong Mg ii absorption systems per comoving Mpc (bins of Δz = 0.15). The blue curve shows an exponential fit to this number density. The yellow curve shows the fit of Prochter et al. (2006a) to their strong Mg ii absorber sample. The shaded areas show the 1σ uncertainties on the exponential fits. |
| In the text | |
 |
Fig. 4 The redshift distribution of the sight line number density n(X) of strong Mg ii absorption systems per comoving Mpc (bins of Δz = 0.15), divided into three subsamples according to the u-band (top panel) and i-band (bottom panel) apparent magnitude of the background quasar. |
| In the text | |
 |
Fig. 5 Distribution of the number density of strong Mg ii absorbers per comoving Mpc with respect to the absorbers’ wavelength in the quasar rest-frame, λsup = λobs/(1 + zem). We fit two power laws to the distribution: one is fitted to the number densities at continuum dominated wavelength bins only (violet curve), while the other is fitted to the entire dataset (blue curve). Error bars are Poissonian. Vertical lines indicate the wavelengths of the quasar broad emission lines C iv λ 1550, C iii] λ 1909, and Mg ii λ 2800. The peak at Mg ii (i.e., zabs ≈ zem) is expected, as some quasars display intrinsic Mg ii absorption. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


