EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) L2 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number L2
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201219906
Published online 29 August 2012

© ESO, 2012

1. Introduction

In recent years, many Galactic pulsar wind nebulae (PWNe) have been discovered to be gamma-ray emitters (for a review, see e.g. de Oña Wilhelmi 2011).

thumbnail Fig. 1

Gamma-ray and X-ray view of N 157B. a) Image of the TeV gamma-ray excess obtained with H.E.S.S. The image was smoothed with the instrument’s point-spread function, which is shown in the inset. The green contour lines denote 6, 9, and 12σ statistical significances. The black box outlines the region shown in the X-ray image. b) Image of the X-ray flux in the energy band from 0.8 keV to 8 keV (Chandra ACIS-S, observation no. 2783, 48.2 ks dead-time corrected exposure). The data were smoothed with a Gaussian of σ = 1.5″ and the exposure map was computed with an assumed spectral index of 2.3, which is the average index of the nebula. The colour coding represents the X-ray flux in photons cm-2 s -1; for better visibility, it is clipped at 10-13 photons cm-2 s-1 at the lower end and saturates at 10-5 photons cm-2 s-1. The white contour lines denote regions of 68%, 95%, and 99% confidence for the position of the gamma-ray source HESS J0537 − 691. The position of the pulsar PSR J0537 − 6910 is indicated by a black cross. The green cross marks the best-fit position and the systematic uncertainty in the pointing of the H.E.S.S. telescopes.
Open with DEXTER

It was predicted by Aharonian et al. (1997) that the gamma-ray luminosity of these nebulae is connected to the spin-down power Ė, i.e. the loss rate of rotational energy of the pulsar, and that pulsars with Ė > 1034 − 35(d/1 kpc)2 erg s-1 (with d being the distance to the pulsar) power nebulae that are detectable in gamma rays. On the basis of the Galactic plane survey carried out by H.E.S.S. (Aharonian et al. 2005; Aharonian et al. 2006b; Gast et al. 2012), Carrigan et al. (2008) suggested that pulsars with a spin-down power of Ė ≳ 1034(d/1 kpc)2 erg s-1 may be correlated with nebulae detectable by H.E.S.S.

The most energetic pulsar known is PSR J0537 − 6910, with a spin-down power of Ė = 4.9 × 1038 erg s-1 (Marshall et al. 1998; Manchester et al. 2005). PSR J0537 − 6910 is also one the most distant pulsars known to date: located in the LMC, it has an estimated distance of (48.1 ± 2.3stat ± 2.9syst) kpc (Macri et al. 2006). This pulsar is the compact central object of the supernova remnant (SNR) N 157B (also called LHA 120-N 157B, SNR B0538 − 691, or NGC 2060). N 157B has been observed extensively in X-rays (Wang & Gotthelf 1998; Wang et al. 2001; Chen et al. 2006). N 157B is a Crab-like SNR (Gotthelf & Wang 1996): the emission from N 157B is dominated by synchrotron radiation from the PWN, which shows a bar-like feature surrounding the pulsar representing the reverse shock of a toroidal wind from the pulsar as well as a long tail of diffuse emission of about 20″ × 30″ in the north-west direction from the bar Wang et al.; Chen et al. (2001; 2006, see also Fig. 1b). Chen et al. (2006) show that faint thermal emission with a diameter of about 100″ is observed from the supernova ejecta and, unlike shell-type or composite SNRs, no emission from the supernova forward shock is detected. The supernova ejecta apparently expand into the low-density interior of the superbubble formed by the stellar association LH 99 (Chen et al. 2006). The characteristic age of the pulsar is about 5000 years (Marshall et al. 1998), which is consistent with estimates of the SNR’s age (Wang & Gotthelf 1998). Large-scale diffuse emission from the general direction of N 157B was discovered with the Fermi satellite (Abdo et al. 2010), which was interpreted as emission from massive star-forming regions. No significant emission, in addition to the diffuse emission, has been detected from N 157B.

Despite its extreme distance, PSR J0537 − 6910 has a large enough spin-down flux of Ė/d2 = 2 × 1035 erg s-1 kpc-2 to power a nebula detectable with H.E.S.S.

2. H.E.S.S. observations and results

The High Energy Stereoscopic System (H.E.S.S.; Aharonian et al. 2006a) is a system of four Imaging Cherenkov Telescopes, located in the Khomas Highland of Namibia at an altitude of 1800 m. The H.E.S.S. telescope array’s location in the southern hemisphere is ideal for observing the Magellanic Clouds. Furthermore, H.E.S.S. is sensitive to gamma rays at energies above 100  GeV up to several 10 TeV. The arrival direction of individual gamma rays can be reconstructed with an angular resolution of higher than 0.1°, and their energy is estimated with an relative uncertainty of 15%.

The region containing N 157B was observed with H.E.S.S., the data presented having been recorded from 2004 to 2009, with a dead-time corrected exposure of 46 h after data quality selection. The observations were carried out at large zenith angles (with a mean of 47°) leading to an elevated energy threshold of about 600 GeV. The data were analysed using Model analysis with standard cuts (de Naurois & Rolland 2009), where the camera images are compared with simulations using a log-likelihood minimisation. The remaining background was estimated from both rings around each sky position to generate the gamma-ray image and spatial analysis (ring background, Berge et al. 2007) and test regions with similar offsets from the camera centre for the spectral analysis (reflected background, Berge et al. 2007).

Figure 1a shows a gamma-ray excess image of N 157B. The image was smoothed with the H.E.S.S. point-spread function, where 68% of the events were contained in a circle with a radius of 0.06°. The significance was calculated from the counts in a circular integration region with a radius of 0.06° around each sky bin. Fitting a point-like source folded with the instrument’s point spread function results in a best-fit position of the source of RA = 5h37m44s, Dec =  −69°9′57″, equinox J2000, with a statistical uncertainty of  ± 11″ in each direction; the source is hence labelled HESS J0537 − 691. With the H.E.S.S. standard pointing correction, point-like sources can be localised with a systematic uncertainty of 20″ per axis (Acero et al. 2010). Figure 1b shows an X-ray image of the supernova remnant and its central PWN with overlaid confidence contours of the gamma-ray source position. The best-fit position is consistent with the pulsar position; the slight offset from the pulsar along the tail of the PWN is not significant (1.3σ of the combined statistical and systematic error).

In a circular region with a radius of 0.1° around the pulsar position, 395 gamma-ray candidate events were found. A total number of 3152 events were found in a background region with an area that is larger by a factor of 18.62. The corresponding gamma-ray excess is 226 events with a statistical significance of 14σ (calculated using formula (17) of Li & Ma 1983). The photon spectrum between 600 GeV and 12 TeV of the gamma-ray excess can be described by a pure power-law, dN/dE = Φ0(E/1 TeV) − Γ, with a normalisation at 1 TeV of Φ0 =  (8.2 ± 0.8stat) × 10-13 cm-2 s-1 TeV-1 and a photon index of Γ =  2.8 ± 0.2stat, which corresponds to an energy flux between 1 TeV and 10 TeV of (1.4 ± 0.1) × 10-12 erg cm-2 s-1 or 2% of the energy flux of the Crab Nebula (Aharonian et al. 2006a). The gamma-ray luminosity between 1 TeV and 10 TeV for a distance of 48 d48 kpc is 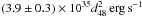. This result was derived from data accumulated over 4 years during the summer rainy seasons with varying atmospheric conditions. From the analysis of different subsets of the data, a systematic uncertainty of 30% in the flux and 0.3 in the photon index is estimated1.

3. Discussion

The observed gamma-ray luminosity between 1 TeV and 10 TeV of the PWN corresponds to (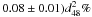 of the spin-down power of the pulsar, a value typical of young PWNe (for a review see e.g. de Oña Wilhelmi 2011). Pulsar wind nebulae are very efficient in producing TeV gamma rays via the inverse Compton (IC) up-scattering of lower-energy photons by relativistic electrons2. This makes them not only the most abundant source type among the TeV emitters in the Milky Way, but also with HESS J0537 − 691 the first extragalactic TeV source that is unrelated to a galaxy or an active galactic nucleus. N 157B can be detected at such a large distance not only because of the high spin-down power of the pulsar but also because of the strong infrared-photon fields from nearby sources serving as additional targets for the IC scattering.

Figure 2 shows the spectral energy distribution (SED) of N 157B. It exhibits synchrotron emission that has been detected at radio wavelengths (see Lazendic et al. 2000, and references therein) and in X-rays (Chen et al. 2006; Dennerl et al. 2001), as well as TeV gamma-ray emission from IC scattering. In addition to the cosmic microwave background (CMB), far-infrared photons from the OB association LH 99 and the nearby star-forming region 30 Doradus are important targets for IC scattering. Using observations from Spitzer (Indebetouw et al. 2009), the infrared photon fields are modelled as black-body radiation with a temperature of 80 K and an energy density of 8.9 eV cm-3 for LH 99, and a temperature of 88 K and an energy density of 2.7 eV cm-3 for 30 Doradus. These are only upper limits to the infrared fields, as the (unprojected) distances of N 157B to these objects are unknown.

thumbnail Fig. 2

Spectral energy distribution of N 157B. The data shown are radio emission (Lazendic et al. 2000, blue triangles), non-thermal X-rays (Chen et al. 2006, blue band), and TeV gamma rays (H.E.S.S., this work, black circles). The green, thick lines represent the model with a cooling break depending on the magnetic field and the age of the remnant. The red, thin lines denote the conservative model that minimises the energy content of electrons. The blue, long-dashed line represents a hadronic scenario.
Open with DEXTER

There is no evidence of extended emission beyond the angular resolution of H.E.S.S., thus the synchrotron and IC emission regions cannot be separated spatially. Hence, a simple one-zone model is assumed, where only a single electron population is responsible for both the synchrotron and IC emission. An electron spectrum following a broken power-law with two breaks and covering the energy band from 1 eV to 1015 eV is adopted. The low energy break is an intrinsic break of the injection spectrum proposed by Venter & de Jager (2007); the high energy break arises from the cooling of the particles. It is assumed that the cooling break appears at the energy where the synchrotron loss time (which depends on the magnetic field) is equal to the age of the remnant (which is assumed to be 5000 years). A low-energy spectral index of 1.33 is used to reproduce the radio spectrum, and a spectral index of 3.60 above the cooling break is consistent with both the X-ray and TeV data. Assuming that the cooling steepens the spectral index by one (Kardashev 1962), the uncooled high-energy spectral index is 2.60. This model, which is represented by the green lines in Fig. 2, requires an intrinsic break at 54 GeV and a magnetic field of 41 μG, the corresponding cooling break being at 1.1 TeV. Assuming a distance of 48 kpc, the total energy Wtot stored in electrons is 4 × 1049 erg. In a second, more conservative model, any assumptions about the age and cooling of the particles are abandoned to minimise the total energy stored in electrons. The intrinsic break is set to 7 GeV, the lowest energy still being compatible with the radio data, and the cooling break is set to 4.22 TeV, the highest energy being compatible with the TeV data points. These prerequisites require an uncooled high-energy spectral index of 2.57 and a low-energy spectral index of 0.93 to reproduce the radio data. This model is represented by the red lines in Fig. 2; it requires a magnetic field of 47 μG and the total energy is only 50% of the energy in the first model. The uncertainty in the distance measurement adds an error of 15% to the estimate of Wtot. Major uncertainties in the estimation of Wtot lie in the uncertainties in the gamma-ray spectrum. Varying the TeV flux by 30% while fixing the radio and X-ray points changes the total energy by 25%. The total energy content Wtot cannot be determined from the radio and X-ray data alone, since the strength of the synchrotron emission is governed by the a priori unknown magnetic field. Using the observed TeV spectrum presented here, it is possible to derive the magnetic field in the PWN and thus the energy content in electrons in the PWN. In a hadronic scenario, gamma-ray emission is produced in the decay of π0 mesons produced by inelastic interactions of accelerated protons with ambient material. The observed TeV emission can be described by the emission of a proton population following a power-law with an index 2 and an exponential cut-off at 23 TeV (blue, long-dashed line in Fig. 2). The total energy in this proton population is 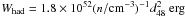. An ambient density of at least 100 cm-3 would be necessary to produce this emission by a single supernova. That the SNR is expected to expand into the low-density interior of a superbubble makes this scenario unlikely.

As proposed by de Jager (2008), Wtot can be used to estimate the birth period of the pulsar. PSR J0537−6910 is relatively young, its characteristic age being shorter than the cooling time of most of the electrons. Particles have survived since the earliest epoch when the pulsar’s spin was close to its birth period. Therefore, Wtot can be related to the pulsar’s birth and current period by the calorimetric expression 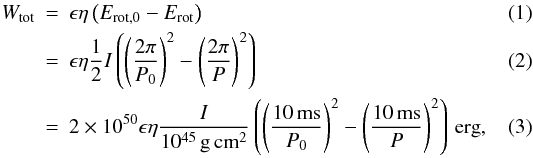where P0 is the birth period of the pulsar, P is the current period of 16.1 ms (Marshall et al. 1998), η denotes the conversion efficiency of spin-down power into accelerated electrons, and ϵ is the relative average energy-loss rate, which takes into account the energy already radiated by the particles during earlier epochs and adiabatic losses of the energy. For the pulsar’s moment of inertia, the canonical value of I = 1045 g cm2 is adopted (Lattimer & Prakash 2001); the moment of inertia could be higher owing to variations in the pulsar mass between 1.4 and 2.5 M⊙ as proposed by Belczynski & Taam (2008). Models indicate that η can be as low as 0.3 (Schöck et al. 2010, for MSH 15–52) or as high as 0.7 (de Jager et al. 2008, for G21.5−0.9). Magnetohydrodynamical simulations (de Jager et al. 2009) show that the adiabatic energy loss is around ϵ ~ 0.5. Further radiation losses during earlier epochs of the nebula reduce ϵ to less than 0.5. Choosing 0.7 and 0.5 for η and ϵ, respectively, shows that the birth period must have been shorter than 10 ms. Using the conservative model, the birth period increases by 23%. This result is consistent with earlier estimations of the pulsar’s birth period, Marshall et al. (1998) estimated the birth period by comparing the pulsar’s characteristic age with the age of the SNR for different braking indices, for SNR ages of more than 4000 years the birth period is shorter than 10 ms for a large range of braking indices. From the extrapolation of glitch data, Marshall et al. (2004) found that 5000 years ago the pulsar period was 11 ms. In the present paper, for the first time the birth period of a pulsar is obtained directly using a calorimetric technique, which depends on neither the glitch history nor the braking index and is – for the conservative model – completely independent of the age of the remnant.

This result confirms that PSR J0537-6910 has, with a birth period of less than about 10 ms, the shortest birth period ever derived for a pulsar. These short rotation periods are only known for millisecond pulsars that have been spun up after their birth by a companion star. Simulations show that pulsar birth periods can be related to some parameters of the progenitor stars. Heger et al. (2005) show that more massive progenitor stars produce heavier and more rapidly rotating pulsars: stars of 15, 20 and 35 M⊙ are required to produce pulsars with 11 ms, 7 ms and 3 ms, respectively. This is consistent with an earlier estimate of the PSR J0537 − 6910 progenitor mass of 20–35 M⊙ based on the comparison of the observed metal abundances in the supernova ejecta of SNR N 157B with supernova models (Chen et al. 2006). Such massive stars are close to the threshold for the formation of black holes in the supernova explosion. Fryer (1999) show, for instance, that 25 M⊙ is roughly the limit for black hole formation. On the other hand, Ott et al. (2006) show that the pulsar’s birth period is rather unrelated to the progenitor’s mass but roughly linearly dependent on the initial central iron-core spin. Birth periods of less than 10 ms require initial iron core periods of less than about 8 s. A very massive and/or rapidly spinning progenitor star therefore appears to be required to produce a neutron star with a birth period as short as 10 ms.

Alternatively, the pulsar could be part of a binary system that has been spun up by its companion star, a scenario typically assumed for millisecond pulsars. A very massive and rapidly rotating star at a distance of about 0.8′ from PSR J0537 − 6910 has been identified (Dufton et al. 2011). It was proposed that both objects were part of a binary system where mass was transferred from the pulsar’s progenitor to its companion and that both stars experienced radial velocity kicks in the supernova explosion. Nonetheless, in this scenario, the general picture of a very massive star producing a rapidly spinning neutron star remains unchanged.

4. Conclusions

Our principal conclusions are as follows:

  • 1.

    Gamma-ray emission from the PWN inN 157B was discovered withH.E.S.S. observations. The energy flux between1 TeV and 10 TeV is (1.4 ± 0.1) × 10-12 erg cm-2 s-1. Locatedin the LMC at a distance of 48 kpc, this is the mostdistant PWN ever detected in gamma rays and is the firstindividual stellar extragalactic TeV gamma-ray source. ThePWN is powered by the most energetic pulsar known:PSR J0537 − 6910.

  • 2.

    The TeV photon spectrum, in connection with radio and X-ray measurements, can be described with a one-zone leptonic model. From this model, the total energy stored in electrons in the nebula can be estimated to be 4 × 1049 erg.

  • 3.

    For the pulsar to provide this energy from its rotational energy loss, the pulsar’s birth period must have been shorter than about 10 ms. This is the shortest birth period ever inferred for a pulsar. In an alternative scenario, the pulsar might have been spun up by a companion star in a binary system.

  • 4.

    Assuming a direct connection between the pulsar’s birth period and the mass of the progenitor star, the progenitor must have had a mass of at least 15 M⊙. This is close to the limit for black hole formation. The pulsar PSR J0537 − 6910 is therefore at the upper mass limit for neutron star production.

1

These uncertainties are specific to this data set and should not be used for any other H.E.S.S. result.

2

The term electrons refers to electrons and positrons.

Acknowledgments

The support of the Namibian authorities and of the University of Namibia in facilitating the construction and operation of H.E.S.S. is gratefully acknowledged, as is the support by the German Ministry for Education and Research (BMBF), the Max Planck Society, the German Research Foundation (DFG), the French Ministry for Research, the CNRS-IN2P3 and the Astroparticle Interdisciplinary Programme of the CNRS, the UK Science and Technology Facilities Council (STFC), the IPNP of the Charles University, the Czech Science Foundation, the Polish Ministry of Science and Higher Education, the South African Department of Science and Technology and National Research Foundation, and by the University of Namibia. We appreciate the excellent work of the technical support staff in Berlin, Durham, Hamburg, Heidelberg, Palaiseau, Paris, Saclay, and in Namibia in the construction and operation of the equipment.

References

  1. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, A&A, 512, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Acero, F., Aharonian, F., Akhperjanian, A. G., et al. (HESS collaboration) 2010, MNRAS, 402, 1877 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aharonian, F. A., Atoyan, A. M., & Kifune, T. 1997, MNRAS, 291, 162 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. (HESS collaboration) 2005, Science, 307, 1938 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  5. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS collaboration) 2006a, A&A, 457, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. (HESS collaboration) 2006b, ApJ, 636, 777 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  7. Belczynski, K., & Taam, R. E. 2008, ApJ, 685, 400 [NASA ADS] [CrossRef] [Google Scholar]
  8. Berge, D., Funk, S., & Hinton, J. 2007, A&A, 466, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  9. Carrigan, S., Hinton, J. A., Hofmann, W., et al. 2008, in International Cosmic Ray Conference, 2, 659 [Google Scholar]
  10. Chen, Y., Wang, Q. D., Gotthelf, E. V., et al. 2006, ApJ, 651, 237 [NASA ADS] [CrossRef] [Google Scholar]
  11. de Jager, O. C. 2008, ApJ, 678, L113 [NASA ADS] [CrossRef] [Google Scholar]
  12. de Jager, O. C., Ferreira, S. E. S., & Djannati-Ataï, A. 2008, in AIP Conf. Ser. 1085, eds. F. A. Aharonian, W. Hofmann, & F. Rieger, 199 [Google Scholar]
  13. de Jager, O. C., Ferreira, S. E. S., Djannati-Ataï, A., et al. 2009 [arXiv:0906.2644] [Google Scholar]
  14. de Naurois, M., & Rolland, L. 2009, Astropart. Phys., 32, 231 [NASA ADS] [CrossRef] [Google Scholar]
  15. de Oña Wilhelmi, E. 2011, in High-Energy Emission from Pulsars and their Systems, eds. D. F. Torres, & N. Rea, 435 [Google Scholar]
  16. Dennerl, K., Haberl, F., Aschenbach, B., et al. 2001, A&A, 365, L202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Dufton, P. L., Dunstall, P. R., Evans, C. J., et al. 2011, ApJ, 743, L22 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fryer, C. L. 1999, ApJ, 522, 413 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gast, H., Brun, F., Carrigan, S., et al. 2012 [arXiv:1204.5860] [Google Scholar]
  20. Gotthelf, E. V., & Wang, Q. D. 1996, in Roentgenstrahlung from the Universe, eds. H. U. Zimmermann, J. Trümper, & H. Yorke, 255 [Google Scholar]
  21. Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
  22. Indebetouw, R., de Messières, G. E., Madden, S., et al. 2009, ApJ, 694, 84 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kardashev, N. S. 1962, AZh, 39, 393 [NASA ADS] [Google Scholar]
  24. Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  25. Lazendic, J. S., Dickel, J. R., Haynes, R. F., Jones, P. A., & White, G. L. 2000, ApJ, 540, 808 [NASA ADS] [CrossRef] [Google Scholar]
  26. Li, T., & Ma, Y. 1983, ApJ, 272, 317 [NASA ADS] [CrossRef] [Google Scholar]
  27. Macri, L. M., Stanek, K. Z., Bersier, D., Greenhill, L. J., & Reid, M. J. 2006, ApJ, 652, 1133 [NASA ADS] [CrossRef] [Google Scholar]
  28. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  29. Marshall, F. E., Gotthelf, E. V., Zhang, W., Middleditch, J., & Wang, Q. D. 1998, ApJ, 499, L179 [NASA ADS] [CrossRef] [Google Scholar]
  30. Marshall, F. E., Gotthelf, E. V., Middleditch, J., Wang, Q. D., & Zhang, W. 2004, ApJ, 603, 682 [NASA ADS] [CrossRef] [Google Scholar]
  31. Ott, C. D., Burrows, A., Thompson, T. A., Livne, E., & Walder, R. 2006, ApJS, 164, 130 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schöck, F. M., Büsching, I., de Jager, O. C., Eger, P., & Vorster, M. J. 2010, A&A, 515, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Venter, C., & de Jager, O. C. 2007, in WE-Heraeus Seminar on Neutron Stars and Pulsars 40 years after the Discovery, eds. W. Becker, & H. H. Huang, 40 [Google Scholar]
  34. Wang, Q. D., & Gotthelf, E. V. 1998, ApJ, 494, 623 [NASA ADS] [CrossRef] [Google Scholar]
  35. Wang, Q. D., Gotthelf, E. V., Chu, Y.-H., & Dickel, J. R. 2001, ApJ, 559, 275 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Gamma-ray and X-ray view of N 157B. a) Image of the TeV gamma-ray excess obtained with H.E.S.S. The image was smoothed with the instrument’s point-spread function, which is shown in the inset. The green contour lines denote 6, 9, and 12σ statistical significances. The black box outlines the region shown in the X-ray image. b) Image of the X-ray flux in the energy band from 0.8 keV to 8 keV (Chandra ACIS-S, observation no. 2783, 48.2 ks dead-time corrected exposure). The data were smoothed with a Gaussian of σ = 1.5″ and the exposure map was computed with an assumed spectral index of 2.3, which is the average index of the nebula. The colour coding represents the X-ray flux in photons cm-2 s -1; for better visibility, it is clipped at 10-13 photons cm-2 s-1 at the lower end and saturates at 10-5 photons cm-2 s-1. The white contour lines denote regions of 68%, 95%, and 99% confidence for the position of the gamma-ray source HESS J0537 − 691. The position of the pulsar PSR J0537 − 6910 is indicated by a black cross. The green cross marks the best-fit position and the systematic uncertainty in the pointing of the H.E.S.S. telescopes.
Open with DEXTER
In the text
thumbnail Fig. 2

Spectral energy distribution of N 157B. The data shown are radio emission (Lazendic et al. 2000, blue triangles), non-thermal X-rays (Chen et al. 2006, blue band), and TeV gamma rays (H.E.S.S., this work, black circles). The green, thick lines represent the model with a cooling break depending on the magnetic field and the age of the remnant. The red, thin lines denote the conservative model that minimises the energy content of electrons. The blue, long-dashed line represents a hadronic scenario.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.