| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 4 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219826 | |
| Published online | 12 September 2012 | |
ACME stellar spectra
I. Absolutely calibrated, mostly empirical flux densities of 55 Cancri and its transiting planet 55 Cancri e⋆
1
Max-Planck Institüt für Astronomie, Königstuhl 17,
69117
Heidelberg,
Germany
2
Department of Physics & Astronomy, University of
California Los Angeles, Los
Angeles, CA
90095,
USA
e-mail: ianc@astro.ucla.edu
Received: 15 June 2012
Accepted: 24 July 2012
The ACME Spectra project provides absolutely calibrated, mostly empirical spectra of exoplanet host stars for use in analysis of the stars and their planets. Spectra are obtained from ground-based telescopes and are tied directly to calibrated ground- and space-based photometry. The spectra remain only “mostly” empirical because of telluric absorption, but interpolation of stellar models over the gaps in wavelength coverage provides continuous stellar spectra. Among other uses, the spectra are suitable for precisely converting observed secondary eclipses (occultations) into absolute flux units with minimal recourse to models. In this paper, I introduce ACME’s methods and present a calibrated spectrum of the nearby, super-Earth hosting star 55 Cancri that spans the range from 0.81–5.05 μm. This spectrum is well-suited for interpreting near- and thermal-infrared eclipse observations. With this spectrum I show that the brightness temperature of the small, low-mass transiting planet 55 Cnc e is 1950-190+260 K at 4.5 μm (cooler than previously reported), which corresponds to a planetary flux of 0.44-0.08+0.12 mJy. This result suggests the planet has some combination of a nonzero albedo, a moderately efficient redistribution of absorbed stellar irradiation, and/or an optically thick atmosphere, but more precise eclipse measurements are required to distinguish between these scenarii.
Key words: methods: observational / techniques: spectroscopic / techniques: high angular resolution / infrared: stars / planets and satellites: atmospheres / stars: individual: 55 Cnc
The calibrated spectrum of the planet-hosting star 55 Cancri is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A97
© ESO, 2012
1. Introduction
Measurements of flux densities are the primary diagnostic of conditions in stellar and planetary atmospheres, and are used to constrain albedos, sizes, temperatures abundances, temperature profiles, and even interior conditions of stars and planets. In the last decade observations of transiting planets during eclipse have begun to reveal the intrinsic emission of these externally irradiated bodies (e.g., Deming et al. 2005; Charbonneau et al. 2005). Though initially confined to space-based observatories such as Spitzer (and, more recently, Hubble; Swain et al. 2012), more favorable targets and improved observing strategies have recently enabled a growing number of ground-based measurements (e.g., Sing & López-Morales 2009; de Mooij & Snellen 2009).
Because eclipse measurements are inherently relative, precise planetary fluxes require stellar fluxes yet more precise. The state of the art is now reaching the point at which this condition is no longer met; for example, recent measurements of eclipses with Spitzer/IRAC have attained relative precisions of 1−4% (e.g., Agol et al. 2010; Campo et al. 2011), comparable to the instrument’s 3% absolute calibration accuracy (Spitzer Science Center 2012).
The goal of the ACME project is to provide a catalog of Absolutely Calibrated, Mostly Empirical (ACME) spectra of exoplanet host stars with high accuracy and precision. In the rapidly approaching era of exoplanet spectroscopy (e.g., Swain et al. 2012) it is imperative that such an effort advance beyond standard photometric calibrations and focus on calibrated spectroscopy. In addition to the aforementioned conversion of planetary eclipse depths into absolute flux units, other potential uses for such a catalog include the study of the planets’ host stars: abundance analyses, spectral typing, and refined bolometric luminosities and effective temperatures are all enabled by such data.
I describe the observation, reduction, and calibration of ACME spectra in Sect. 2. As a particular case study I present a calibrated spectrum of the nearby star 55 Cancri (55 Cnc) in Sect. 3. With this calibrated spectrum I provide an improved measurement of 55 Cnc e’s flux at 4.5 μm in light of recent observations (Demory et al. 2012), and I conclude with future prospects.
SpeX Observations of 55 Cnc.
2. Observations and methods
2.1. Summary of observations
Observations thus far have been made solely with SpeX (Rayner et al. 2003), a cryogenic, cross-dispersed, near-infrared echelle spectrograph at the NASA InfraRed Telescope Facility (IRTF). Observations and reduction of SpeX data generally follow the steps used in compilation of the IRTF Spectral Library (Cushing et al. 2005; Rayner et al. 2009); below I review briefly these steps and highlight the differences between my analysis and that of the IRTF Library’s.
All objects are observed using SpeX’s short-wavelength (SXD) mode. This mode offers continuous wavelength coverage from 0.8–2.4 μm (except for the gap at 1.81–1.87 μm) at a spectral resolution of 2000 for the standard 0.3′′ slit. For bright targets such as 55 Cnc (Ks = 4), wavelength coverage can be extended into the thermal infrared using one of the several long-wavelength (LXD) modes, which offer a resolution of 2500.
For each target, observations of a nearby A0 V star allows telluric calibration (Vacca et al. 2003); these stars are typically chosen to be located within 15° and 0.1 airmass unit of the primary observation. Observations are taken at the parallactic angle to avoid spurious spectral slopes induced by differential atmospheric refraction. I use the standard SpeX calibration macros to generate the dark, flat, and arc frames used to calibrate the data. Table 1 shows a log of the observations of 55 Cnc discussed in Sect. 3.
2.2. Initial spectral reduction
I use the excellent SpeXTool software package (Cushing et al. 2004) to reduce, combine, and clean the data, a process that consists of the following steps1. First, optimal extraction converts the differences of pairs of nodded frames into uncalibrated spectra in flux density units. I use a constant background level and large apertures (2−3′′ radii) in the extraction; note that the particular choice of reduction parameters is retained in the headers of the FITS files generated by SpeXTool. Individual spectra for an object are then combined using a robust weighted mean, and the mean target spectrum is corrected for telluric absorption using the mean A0 V spectrum (Vacca et al. 2003). If an object was not observed at the parallactic angle, I correct the spectrum for losses resulting from chromatic seeing and atmospheric dispersion. Finally, the individual echelle orders are combined by applying small (≲2%) offsets to the individual orders. The final result is a spectrum with well-determined uncertainties at all wavelengths. In most cases an additional step is the trimming of pixels located in regions of extremely low telluric transmission or with S/N < 5.
Note that unlike objects catalogued in the IRTF Spectral Library (Cushing et al. 2005; Rayner et al. 2009) the spectra of ACME targets are not shifted to zero radial velocity; but such corrections can easily be made by using the copious body of high-precision radial velocity characterization of these systems (e.g., Fischer et al. 2008). Future ACME spectra will be corrected for interstellar reddening, but owing to its proximity 55 Cnc requires no such correction (von Braun et al. 2011).
2.3. Spectral calibration
To place an extracted spectrum on an absolute flux scale I follow Rayner et al. (2009), whose Eq. (1) computes the correction factor CX for each bandpass X by comparing to catalog photometry. These factors provide the ratios by which the uncalibrated spectrum should be scaled in each bandpass: multiplying the spectrum by the weighted average of the CX calibrates the flux scale of the spectrum. Fainter objects observed at <2.5 μm use only 2MASS photometry (Skrutskie et al. 2006) and the spectral response curves from Cohen et al. (2003); targets observed at longer wavelengths (such as 55 Cnc) also use WISE W1 and/or W2 photometry (Wright et al. 2010) and the spectral response curves from Jarrett et al. (2011).
Telluric absorption causes several gaps in the observed spectrum: in addition to several smaller regions, the largest gaps span 1.81−1.87 μm, and (for longer-wavelength data) from 2.50−2.95 μm and 4.18−4.59 μm. These last two gaps intersect the WISE W1 and W2 response curves and so must be accounted for before flux calibration can take place; this step is also required to best constrain bolometric luminosities and for future application to space-based observations not necessarily restricted to telluric windows. As described below, to fill these gaps I use the BT-Settl library2 (Allard et al. 2012), which provides high-resolution model spectra across a wide range of Teff, log g and [Fe/H].
I interpolate the model spectra to obtain a spectrum with the stellar parameters appropriate for the target star; for 55 Cnc, these are 5196 ± 24 K, log g(cgs) = 4.45 ± 0.01, and [Fe/H] = 0.315 ± 0.03 (Valenti & Fischer 2005; von Braun et al. 2011). Convolution of the resultant model with a Gaussian profile brings the model to an approximate resolution of 2000, and computation of CX factors for the model place it on the same flux scale as the observed spectrum. At this point the observed and model spectra sometimes exhibit mismatched spectral slopes at gap edges. To mitigate these discrepancies I measure the weighted mean flux density in the 10 nm adjacent to the gap boundary for both model and observed spectra; from these measurements I compute a weighted linear fit that I apply to the model spectrum. Thus the details of spectral features in the model are retained, while the spectral slope is adjusted to match the observations. I re-compute the weighted mean of the CX factors using the continuous, hybrid spectrum; the uncertainty on this quantity provides an estimate of the uncertainty in the absolute flux calibration. Applying this mean factor to the data produces an absolutely calibrated, mostly empirical spectrum of the target star.
 |
Fig. 1 Absolutely calibrated, mostly empirical spectrum of 55 Cnc. The data in black are measured, while those in gray are modeled. At bottom are the response curves from 2MASS (dotted; Cohen et al. 2003), WISE (dashed; Jarrett et al. 2011), and Spitzer/IRAC (solid; Spitzer Science Center 2012). |
The situation is slightly more complicated for 55 Cnc, which exceeds the nominal WISE saturation limits in the W1 and W2 bands. For a star of this magnitude, WISE overestimates the flux in the W1 and W2 bands by, respectively, 0.1 mag and 0.8 mag when compared to fainter stars (Sect. VI.4 of Cutri et al. 2012, updated 2011 April 26). I therefore apply these offsets to the reported magnitudes before flux-calibrating the spectrum.
As an additional check, I measure 55 Cnc’s flux at 3.6 μm and 4.5 μm in archival IRAC photometry (Spitzer Programs 48, 33970, 40976, 70076, and 80231; P.I.s G. Fazio, K. Luhman, M. Marengo, K. Su, and M. Gillon, respectively). I determine the stellar flux densities in these bands to be 7.2 ± 0.3 Jy and 4.3 ± 0.1 Jy, where the uncertainties represent the spread in values across several observing programs. These flux values exceed the WISE catalogue fluxes (after applying corrections for the slightly different isophotal wavelengths and for partial saturation, as described above) by 22%.
Both the IRAC and WISE measurement pairs are internally self-consistent, as demonstrated by the fact that both sets yield 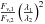 equal to 1.05, near the value of unity expected near the Rayleigh-Jeans limit. The deciding factor is the comparison with the calibrated model spectrum of von Braun et al. (2011) described in the following section. Spectral calibration using the WISE photometry provides an excellent agreement with von Braun et al.’s model spectrum, but the agreement becomes worse by a factor of ~8 when calibrating with the IRAC photometry.
equal to 1.05, near the value of unity expected near the Rayleigh-Jeans limit. The deciding factor is the comparison with the calibrated model spectrum of von Braun et al. (2011) described in the following section. Spectral calibration using the WISE photometry provides an excellent agreement with von Braun et al.’s model spectrum, but the agreement becomes worse by a factor of ~8 when calibrating with the IRAC photometry.
The 2MASS Ks band measurement of 55 Cnc has a quality flag of E, indicating a poorly determined flux; therefore I do not use this bandpass for flux calibration. In addition, the final calibration suggests that the 2MASS J and H measurements underestimate the stellar flux by roughly 25%. The calibration is dominated by the smaller uncertainties of the WISE photometry, and I use J, H, W1, and W2 in the final calibration. 55 Cnc’s calibrated spectrum is shown in Fig. 1 and is available at the CDS. Comparison of this spectrum with the photometrically-calibrated Pickles (1998) spectrum of von Braun et al. (2011) indicates a good match between the two, as described below.
3. Results: Stellar and planetary fluxes
3.1. Spectrum and bolometric flux of 55 Cnc
The star 55 Cnc hosts five planets (Fischer et al. 2008; Dawson & Fabrycky 2010), including the small transiting planet 55 Cnc e (Winn et al. 2011; Demory et al. 2011; Gillon et al. 2012). Because of these planets, and by virtue of its proximity, the star has been the subject of detailed characterization. Recently von Braun et al. (2011) used new interferometric and archival photometric measurements to determine the star’s bolometric flux (using models from Pickles 1998) to be (1.227 ± 0.0177) × 10-10 W m-2. The calibrated spectrum of 55 Cnc shown in Fig. 1 emits a flux consistent with that of von Braun et al.’s spectrum from 0.81–2.49 μm: the difference between the two is only (1.8 ± 7.2) × 10-12 W m-2, which independently confirms the calibration of both spectra.
In the IRAC1 and 2 bands the flux densitites of 55 Cnc are 6.153 ± 0.006 Jy and 3.444 ± 0.006 Jy, respectively, where these uncertainties represent only the precision (not the accuracy) of the measurements. The formal uncertainty on these values is in fact dominated by the absolute calibration of the ACME spectrum: the weighted mean of the CX factors for 55 Cnc has an uncertainty of 12%. Considering this level of accuracy, the stellar fluxes are in good agreement with the stellar flux densities inferred solely from the calibrated BT-Settl model: 6.03 Jy and 3.78 Jy, respectively. This situation will improve for fainter stars (which avoid saturation and are measured more precisely by 2MASS and WISE), but even here the close correspondence (1.4%) between my and von Braun et al.’s in-band fluxes suggests that the true accuracy of 55 Cnc’s spectrum may be better than 12%.
3.2. Brightness temperature and flux of 55 Cnc e
By dint of its high temperature and its host star’s apparent brightness, and despite its small transit depth, 55 Cnc e is the planet whose intrinsic emission spectrum is most amenable to characterization (Winn et al. 2011; Gillon et al. 2012). At least in the near term, this planet will be our sole source of detailed information as to the nature of small, highly irradiated planets and their atmospheres.
The mass, size, and density of 55 Cnc e are all intermediate between the Solar System’s terrestrial and gas giant planets (Dawson & Fabrycky 2010; Gillon et al. 2012), so its composition cannot be determined solely on the basis of these bulk properties (cf. Valencia et al. 2010). However, models of planetary interiors suggest that 55 Cnc e hosts a substantial envelope of volatile materials (Gillon et al. 2012). The planet’s mass and radius can be fit with an Earthlike core and an envelope of either a H2/He (~0.03% by mass) or H2O (~20%) (Valencia et al. 2010). Models of atmospheric mass loss for CoRoT-7b (a smaller, denser, and hotter planet; Léger et al. 2009) reveal that it is difficult for such a small, highly irradiated planet to retain substantial amounts of H2/He (Valencia et al. 2010; Heng & Kopparla 2012), and models of sublimated rock atmospheres suggest that even heavier species will not remain aloft beyond the highly irradiated dayside (Castan & Menou 2011). Thus it is unlikely that 55 Cnc e’s volatile component is a H2/He envelope, and it seems more likely to be made up of heavier species.
At present, only observations during transit and/or eclipse can constrain the atmospheric properties of such a planet (e.g., Miller-Ricci et al. 2009). The first thermal emission from 55 Cnc e has recently been reported (Demory et al. 2012) via detection with Spitzer/IRAC at 4.5 μm of an eclipse whose depth is only 131 ± 28 ppm (Demory et al. 2012). This result provides a timely opportunity to demonstrate the utility of ACME spectra: I now demonstrate that the planet’s brightness temperature, TB, is cooler than the initially reported value of 2360 ± 300 K (Demory et al. 2012).
The brightness temperature TB of an eclipsing planet can be determined by solving the following relation: 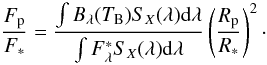 (1)Here
(1)Here 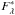 is the stellar flux density, SX(λ) is the system response in bandpass X, Bλ is the Planck function, and the other symbols have their usual meanings. In a typical eclipse observation the planet/star radius ratio is known to high precision from transits and the planet/star flux ratio is measured from eclipses. The ACME Spectra project provides
is the stellar flux density, SX(λ) is the system response in bandpass X, Bλ is the Planck function, and the other symbols have their usual meanings. In a typical eclipse observation the planet/star radius ratio is known to high precision from transits and the planet/star flux ratio is measured from eclipses. The ACME Spectra project provides 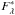 , so TB is the only unknown quantity.
, so TB is the only unknown quantity.
Combining the eclipse depth (Demory et al. 2012), planetary properties from Gillon et al. (2012), stellar properties from Valenti & Fischer (2005) and von Braun et al. (2011), the stellar spectrum shown in Fig. 1, and propagating the uncertainties in all these quantities using a Monte Carlo approach yields  (corresponding to
(corresponding to 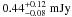 ), lower than previously reported by 400 K. If 55 Cnc has an exposed, rocky component then this new, lower temperature suggests that atomic Fe would be more prevalant in the planet’s Na-dominated atmosphere than SiO, and in general outgassed materials would be rather less common than in the hotter case (Castan & Menou 2011; Miguel et al. 2011).
), lower than previously reported by 400 K. If 55 Cnc has an exposed, rocky component then this new, lower temperature suggests that atomic Fe would be more prevalant in the planet’s Na-dominated atmosphere than SiO, and in general outgassed materials would be rather less common than in the hotter case (Castan & Menou 2011; Miguel et al. 2011).
Using a blackbody for 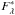 instead of the stellar spectrum I obtain the published value of
instead of the stellar spectrum I obtain the published value of 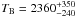 , a result which emphasizes the point that a star does not emit the same flux density as a blackbody at the stellar effective temperature. However, note that in converting TB into a flux density I have assumed the planet emits like a blackbody in the IRAC2 band; this is probably not the case, but it is forgivable considering our current ignorance of the planet’s true emission spectrum. Table 2 shows the stellar fluxes and planetary 4.5 μm brightness temperatures inferred from flux calibration of several different model stellar specta using the same techniques described above for the mostly-empirical spectrum. The precision to which 55 Cnc e’s eclipse depth is known currently precludes any discussion of the relative merits of these models, but more precise observations should permit the exclusion of some stellar models.
, a result which emphasizes the point that a star does not emit the same flux density as a blackbody at the stellar effective temperature. However, note that in converting TB into a flux density I have assumed the planet emits like a blackbody in the IRAC2 band; this is probably not the case, but it is forgivable considering our current ignorance of the planet’s true emission spectrum. Table 2 shows the stellar fluxes and planetary 4.5 μm brightness temperatures inferred from flux calibration of several different model stellar specta using the same techniques described above for the mostly-empirical spectrum. The precision to which 55 Cnc e’s eclipse depth is known currently precludes any discussion of the relative merits of these models, but more precise observations should permit the exclusion of some stellar models.
Model-dependent stellar and planetary fluxes.
This new and improved temperature estimate is mildly lower (by 1.4σ) than the 2300 K expected in the zero albedo, zero redistribution case discussed by Demory et al. (2012). Kepler-10b is another small, low-mass, highly irradiated planet whose albedo has been inferred from its optical phase curve to be 0.48 ± 0.35 (Batalha et al. 2011; Rouan et al. 2011). It is intriguing to note that such an albedo for 55 Cnc e would make the 4.5 μm brightness temperature quite consistent with the no-redistribution case (1930 K). However, this agreement is probably coincidental: in contrast to 55 Cnc e, Kepler-10b contains few or no volatiles (Batalha et al. 2011) and is presumably of an altogether different nature.
The large uncertainty on the 4.5 μm eclipse depth precludes any unambiguous inferences as to the nature of 55 Cnc e’s emission spectrum. However, if the brightness temperature reported here is characteristic of the temperature in the planet’s atmosphere, some combination of the following three scenarios may therefore be required. The planet has a nonzero albedo, caused either by clouds (Schaefer & Fegley 2009; Castan & Menou 2011; but see also Léger et al. 2011) or perhaps by the planet’s surface; the planet exhibits some redistribution of absorbed stellar irradiation, suggesting a dense atmosphere (a more tenuous atmosphere or a lava ocean cannot transport the requisite heat flux; Castan & Menou 2011; Léger et al. 2011); or the planet has an optically thick atmosphere, of which the IRAC2 observations probe a particular layer (one not necessarily indicative of the planet’s surface or equilibrium temperature). Further observations at higher precision are of the utmost important if we are to distinguish between these scenarii.
These results demonstrate the utility of calibrated stellar spectra for determining the properties of transiting planets and their host stars. In particular, the spectrum presented here should be of great utility in planning and interpreting future observations of 55 Cnc e with Spitzer/IRAC and the Hubble Space Telescope. A forthcoming paper will present the first large batch of approximately one dozen ACME spectra, several of which extend into the thermal infrared. Secondary eclipses have been observed for all these targets, and such calibrated spectra should provide a useful tools with which to study these systems.
Available online at http://phoenix.ens-lyon.fr/
Acknowledgments
I thank T. Guillot and the anonymous referee for insightful comments and suggestions which improved the quality of this paper. I was supported by the UCLA Dissertation Year Fellowship and by EACM. This research has made use of the Exoplanet Orbit Database at http://www.exoplanets.org, the Extrasolar Planet Encyclopedia Explorer at http://www.exoplanet.eu, and free and open-source software provided by the Python, SciPy, and Matplotlib communities. I will gladly distribute my raw data products, and many of my algorithms, to interested parties upon request.
References
- Agol, E., Cowan, N. B., Knutson, H. A., et al. 2010, ApJ, 721, 1861 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun., eds. C. M. Johns-Krull, et al. (San Francisco: ASP), ASP Conf. Ser., 448, 91 [Google Scholar]
- Batalha, N. M., Borucki, W. J., Bryson, S. T., et al. 2011, ApJ, 729, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Campo, C. J., Harrington, J., Hardy, R. A., et al. 2011, ApJ, 727, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Castan, T., & Menou, K. 2011, ApJ, 743, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Wheaton, W. A., & Megeath, S. T. 2003, AJ, 126, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Vacca, W. D., & Rayner, J. T. 2004, PASP, 116, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2012, Explanatory Supplement to the WISE All-Sky Data Release Products, Tech. Rep. [Google Scholar]
- Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., & Snellen, I. A. G. 2009, A&A, 493, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Brown, T. M., Charbonneau, D., Harrington, J., & Richardson, L. J. 2005, ApJ, 622, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Seager, S., Madhusudhan, N., et al. 2011, ApJ, 735, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Gillon, M., Seager, S., et al. 2012, ApJ, 751, L28 [Google Scholar]
- Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 675, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Demory, B.-O., Benneke, B., et al. 2012, A&A, 539, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heng, K., & Kopparla, P. 2012, ApJ, 745, 60 [Google Scholar]
- Jarrett, T. H., Cohen, M., Masci, F., et al. 2011, ApJ, 735, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Grasset, O., Fegley, B., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Léger, A., Grasset, O., Fegley, B., et al. 2011, Icarus, 213, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miguel, Y., Kaltenegger, L., Fegley, B., & Schaefer, L. 2011, ApJ, 742, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Miller-Ricci, E., Seager, S., & Sasselov, D. 2009, ApJ, 690, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Rouan, D., Deeg, H. J., Demangeon, O., et al. 2011, ApJ, 741, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, L., & Fegley, B. 2009, ApJ, 703, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Sing, D. K., & López-Morales, M. 2009, A&A, 493, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer Science Center 2012, IRAC Instrument Handbook, v2.0.2, ed. IRAC Instrument and Instrument Support Teams [Google Scholar]
- Swain, M., Deroo, P., Tinetti, G., et al. 2012, Icarus, submitted [arXiv:1205.4736] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Ikoma, M., Guillot, T., & Nettelmann, N. 2010, A&A, 516, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- von Braun, K., Boyajian, T. S., Ten Brummelaar, T. A., et al. 2011, ApJ, 740, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Holtzman, W., Dooley, K. L., et al. 2011, ApJ, 737, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Absolutely calibrated, mostly empirical spectrum of 55 Cnc. The data in black are measured, while those in gray are modeled. At bottom are the response curves from 2MASS (dotted; Cohen et al. 2003), WISE (dashed; Jarrett et al. 2011), and Spitzer/IRAC (solid; Spitzer Science Center 2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


