| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219555 | |
| Published online | 05 September 2012 | |
Self-similarity of temperature profiles in distant galaxy clusters: the quest for a universal law⋆
1
Dipartimento di AstronomiaUniversità di Bologna,
via Ranzani 1, 40127
Bologna, Italy
e-mail: alessandro.baldi@oabo.inaf.it
2
INAF, Osservatorio Astronomico di Bologna,
via Ranzani 1, 40127
Bologna,
Italy
3
INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127
Bologna,
Italy
4
INAF-IASF, via
Bassini 15, 20133
Milan,
Italy
5
Department of Physics and Astronomy, University of California at
Irvine, 4129 Frederick Reines
Hall, Irvine,
CA
92697–4575,
USA
Received:
7
May
2012
Accepted:
27
June
2012
Context. We present the XMM-Newton temperature profiles of 12 bright (LX > 4 × 1044 erg s-1) clusters of galaxies at 0.4 < z < 0.9, having an average temperature in the range 5 ≲ kT ≲ 11 keV.
Aims. The main goal of this paper is to study for the first time the temperature profiles of a sample of high-redshift clusters, to investigate their properties, and to define a universal law to describe the temperature radial profiles in galaxy clusters as a function of both cosmic time and their state of relaxation.
Methods. We performed a spatially resolved spectral analysis, using Cash statistics, to measure the temperature in the intracluster medium at different radii.
Results. We extracted temperature profiles for the clusters in our sample, finding that all profiles are declining toward larger radii. The normalized temperature profiles (normalized by the mean temperature T500) are found to be generally self-similar. The sample was subdivided into five cool-core (CC) and seven non cool-core (NCC) clusters by introducing a pseudo-entropy ratio σ = (TIN/TOUT) × (EMIN/EMOUT)−1/3 and defining the objects with σ < 0.6 as CC clusters and those with σ ≥ 0.6 as NCC clusters. The profiles of CC and NCC clusters differ mainly in the central regions, with the latter exhibiting a slightly flatter central profile. A significant dependence of the temperature profiles on the pseudo-entropy ratio σ is detected by fitting a function of r and σ, showing an indication that the outer part of the profiles becomes steeper for higher values of σ (i.e. transitioning toward the NCC clusters). No significant evidence of redshift evolution could be found within the redshift range sampled by our clusters (0.4 < z < 0.9). A comparison of our high-z sample with intermediate clusters at 0.1 < z < 0.3 showed how the CC and NCC cluster temperature profiles have experienced some sort of evolution. This can happen because higher z clusters are at a less advanced stage of their formation and did not have enough time to create a relaxed structure, which is characterized by a central temperature dip in CC clusters and by flatter profiles in NCC clusters.
Conclusions. This is the first time that a systematic study of the temperature profiles of galaxy clusters at z > 0.4 has been attempted. We were able to define the closest possible relation to a universal law for the temperature profiles of galaxy clusters at 0.1 < z < 0.9, showing a dependence on both the relaxation state of the clusters and the redshift.
Key words: galaxies: clusters: intracluster medium / X-rays: galaxies: clusters
Appendix A is only available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Clusters of galaxies are the largest virialized structures in the Universe, arising from the gravitational collapse of high peaks of primordial density perturbations. They represent unique signposts where the physical properties of the cosmic diffuse baryons can be studied in great detail and can be used to trace the past history of cosmic structure formation (e.g. Peebles 1993; Coles & Lucchin 1995; Peacock 1999; Rosati et al. 2002; Voit 2005). As a result of adiabatic compression and shocks generated by supersonic motion during shell crossing and virialization, a hot thin gas permeating the cluster’s gravitational potential well is formed. This gas reaches temperatures of several 107 K and therefore emits mainly via thermal bremsstrahlung and is easily detectable in the X-rays. The gas key observable quantities are its density, temperature, and metallicity. Assuming hydrostatic equilibrium, the gas temperature and density profiles allow one to derive the total cluster mass and thus to use galaxy clusters as cosmological probes (e.g. Voit 2005). Temperature and density profiles can also be combined to determine the intracluster medium (ICM) entropy distribution, which provides valuable information on the cluster thermodynamic history and has proven to be a powerful tool in investigating non-gravitational processes (e.g. Pratt et al. 2006). Radial temperature profiles of the hot ICM in galaxy clusters are therefore very important for studying the gravitational processes responsible for large-scale structure formation and non-gravitational energy input into the ICM.
Early measurements of cluster temperature profiles were obtained by ASCA and Beppo-SAX (e.g. Ikebe et al. 1997; Markevitch et al. 1998; Ettori et al. 2000; Finoguenov et al. 2001; Nevalainen et al. 2001; De Grandi & Molendi 2002). In particular, using ASCA data, Markevitch et al. (1998) obtained temperature profiles for a sample of 32 nearby clusters, which showed significant declines with radius between r = 0.1rvir and r = 0.6rvir. These authors also found that in clusters without obvious mergers, the radial temperature profiles outside the cool cores were similar when normalized to the virial radius. Consistent results were obtained using the spatially resolved spectroscopic capabilities of BeppoSAX. In their analysis of 21 clusters, De Grandi & Molendi (2002) found declining temperature profiles, in good agreement with Markevitch et al. (1998) outside the cores [r > 0.15−0.2rvir], although they were less peaked at the center. De Grandi and Molendi also found that for r > 0.2r180, where the gas can be treated as a polytrope, the polytropic index derived for cool-core (CC) clusters is significantly flatter than the index derived for non cool-core (NCC) clusters, corresponding to 1.20 ± 0.06 for CC clusters and to 1.46 ± 0.06 for NCC clusters.
More recently, Chandra and XMM-Newton allowed measuring the temperature profiles of galaxy clusters with better accuracy and improved spatial resolution, especially in their central regions (e.g. Vikhlinin et al. 2005, 2006; Baldi et al. 2007; Pratt et al. 2007; Leccardi & Molendi 2008), without the complications introduced by the point spread function (PSF) of ASCA and BeppoSAX. In particular, using Chandra data, Baldi et al. (2007) were able to study the temperature profiles of 12 clusters in the redshift range 0.1 < z < 0.3, dividing the clusters into CC and NCC clusters in a systematic fashion. These authors found that the profiles in the inner 0.1r180 were showing a positive gradient kT(r) ∝ rμ, with μ ~ 0.25 in CC clusters and μ ~ 0 in NCC clusters. Moreover Baldi et al. found that the outer region profiles were significantly steeper in the NCC systems than in the CC systems. This behavior agrees with the recent findings of Arnaud et al. (2010), who derived a universal pressure profile of galaxy clusters (including CC and NCC clusters) in the REXCESS local sample (z < 0.2) with low dispersion, especially in the external regions. Steeper temperature gradients in the profiles of NCC systems than in those of CC systems are indeed expected if this pressure profile, analogous for both cluster categories, is combined with the density profiles (steeper in CC and flatter in NCC clusters, see e.g. Cavaliere et al. 2009). Probing a similar redshift range, Leccardi & Molendi (2008) analyzed a sample of ≈ 50 galaxy clusters observed by XMM-Newton to measure their radial temperature profiles. In agreement with previous results, these authors found a decline of the temperature in the 0.2−0.6r180 range. In contrast with De Grandi & Molendi (2002) and Baldi et al. (2007), Leccardi and Molendi did not find any evidence of a dependence in the slope of the outer regions from the presence or absence of a cool core, nor did they find evidence of profile evolution with redshift out to z ≈ 0.3.
Cosmological simulations have also tackled the measure of temperature profiles in galaxy clusters. However, the existing simulations (e.g. Loken et al. 2002; Roncarelli et al. 2006) are not able to account for the physics at small radii (i.e. in the cluster core regions) and are not considering the evolution of the profiles through cosmic time.
In this work we aim at studying for the first time the temperature profiles in a sample of galaxy clusters at z > 0.4, i.e. in a redshift range where no comprehensive study is present in the literature. The plan of the paper is as follows. In Sect. 2 we describe how we selected our XMM-Newton sample and the data reduction procedure we followed. We describe our spectral analysis strategy in Sect. 3, with particular focus on the background treatment procedure (Sect. 3.1) and the correction we applied to take into account the PSF of XMM-Newton (Sect. 3.2). In Sect. 4 we present the results obtained in our analysis, presenting the temperature profiles of individual clusters in the sample and the classification method we used to divide them into CC and NCC (Sect. 4.1), their profiles by the overdensity radius r500 and by the average temperature T500, and the properties of self-similarity they exhibit (Sect. 4.2). We also present several fits of the normalized profiles of the total sample (Sect. 4.2.1), of the CC and NCC clusters samples individually (Sect. 4.2.2), and of the external regions of the profiles (Sect. 4.2.3). In Sect. 5, we discuss our results and compare our sample with the Leccardi & Molendi (2008) intermediate redshift cluster sample (Sect. 5.1) to attempt to define a universal law for temperature profiles for galaxy clusters at 0.1 < z < 0.9 (Sect. 5.2). Our conclusions are summarized in Sect. 6.
We adopt a cosmological model with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7 throughout the paper. Confidence intervals are quoted at 1σ unless otherwise stated.
 |
Fig. 1 Redshift distribution of the XMM-Newton galaxy cluster bright sample presented in this paper. |
XMM-Newton archival observations of the 12 bright galaxy clusters analyzed in this paper.
2. Sample selection and data reduction
In Table 1, we present the list of galaxy clusters analyzed in this paper. The clusters considered are picked from the XMM-Newton archive sample presented in Baldi et al. (2012, hereafter BAL12). Here we selected all clusters with at least 3000 MOS net counts to obtain temperature radial profiles with a sizeable number of bins (from 3 to 9, depending on the cluster luminosity) and reasonable errors on kT (σkT/kT < 15%). Thus, a sample of twelve galaxy clusters was selected, with a redshift range of 0.4 ≲ z ≲ 0.9 although half of the clusters are located at z < 0.5 (Fig. 1). Since this sample was simply taken from the archive without any selection criteria apart from the number of counts available and the redshift, we caution that our cluster sample is far from being a complete sample and the relative proportion of CC and NCC clusters may not be representative of the relative fraction of CC and NCC clusters present in the Universe, within the redshift range explored. The full details of data reduction are described in BAL12; here we summarize only the main steps used in processing the data.
The observation data files (ODF) were processed to produce calibrated event files using the XMM-Newton science analysis system (SAS v11.0.1). As described in BAL12, the pn data were not used in the spectral analysis because of problems in the characterization of the background in pn spectra of extended sources (see e.g. Leccardi & Molendi 2008, and the XMM-ESAS cookbook1) and inconsistencies with the measures of temperature and abundance with the MOS detectors.
The soft proton cleaning was performed using a double filtering process. First, we extracted a light curve in 100 s bins in the 10−12 keV energy band by excluding the central CCD, applied a threshold of 0.20 cts s-1, produced a GTI file and generated the filtered event file accordingly, to remove the majority of the flares. The remaining softer flares (that do not contribute significantly to the emission at E > 10 keV) were removed by extracting a light curve in the 2−5 keV. The resulting histogram was fit with a Gaussian distribution with a mean count rate μ, and the standard deviation σ. A 3σ clipping algorithm (excluding all time intervals with a count rate higher than μ + 3σ) and visual inspection of the light curves were then used to remove the remaining background flaring periods. In Table 1 we list the resulting clean exposure times for the MOS and pn detectors.
After additional filtering was applied to remove events with low spectral quality, we merged the event files from each detector to create a single event file and created a 0.5−8 keV band image of each cluster. The resulting image was used to define the extraction regions for the temperature profiles and to create a list of point sources (using both the EBOXDETECT task and a visual inspection of the field to check for false detections). If a point source is located inside an extraction region, a circular region of radius ≳ 15′′ (depending on the source brightness), centered at the position of the point source is excised from the spectral extraction region. As in BAL12, the pn data were used to create the merged image to detect the point sources that needed to be removed from the cluster spectra at a lower flux limit.
Values of T500 and r500 (expressed in Mpc and in arcsec, as computed in BAL12) for the XMM-Newton galaxy cluster bright sample presented in this paper.
3. Spectral analysis strategy
The emission from each cluster was subdivided into several concentric annular regions, allowing each annulus to have a total of at least 1000 net MOS counts and a minimum thickness of 15′′. The number of annuli considered for each cluster is reported in Table 1.
3.1. Background spectral modeling
The background in our MOS spectra was modeled (instead of subtracted) following the procedure developed by Leccardi & Molendi (2008), which is also described extensively in BAL12. This procedure is preferrable to a direct background subtraction because it allows the use of Cash statistics (Cash 1979) and avoids problems caused by the vignetting of the background spectra, which would need to be extracted at larger off-axis angle than the cluster spectra. Here we summarize just the main aspects of this procedure, more details can be found in Leccardi & Molendi (2008) and in BAL12.
The background model consists mainly of five components: a thermal emission from the Galaxy halo (HALO), the cosmic X-ray background (CXB), a residual from the filtering of quiescent soft protons (QSP), the cosmic ray induced continuum (NXB) and the fluorescence emission lines. The parameters for this model were first estimated (using Cash statistics and considering the 0.7−8 keV band) from a spectrum extracted in an annulus located between 10′ and 12′ from the center of the field of view for MOS1 and MOS2. To fit the cluster spectra, the background parameters (and their 1σ errors) were then rescaled by the area in which the cluster spectra were extracted. Appropriate correction factors (Leccardi & Molendi 2008, dependent on the off-axis angle) were considered for the HALO and CXB components and a vignetting factor (corresponding to 1.858−0.078r, with r the distance from the center of the annulus) was applied to the QSP component. All these rescaled values (and their 1σ errors) were transferred to an XSPEC model with the same background components used in the fit of the 10′−12′ annulus plus a thermal mekal model (Liedahl et al. 1995) for the emission of the cluster, leaving its temperature, abundance and normalization free to vary. The 1σ errors on the parameters were used to fix a range where the normalizations of the background components are allowed to vary. This model was tailored to each cluster and used to fit all spectra in our sample. A joint MOS1 plus MOS2 fit (using Cash statistics and therefore requiring simply minimal grouping to avoid spectral bins with no counts) was performed to increase statistics. We were able to do that because there are no calibration problems between the two detectors and an independent analysis of the spectra from MOS1 and MOS2 led to consistent results in the measurements of kT and Z.
3.2. XMM-Newton PSF correction and spectral fitting
In the present analysis we also considered the effect that PSF of EPIC XMM-Newton (HEW ~ 15′′) has on the determination of the temperature profiles in our cluster sample. This is a different approach than in BAL12, where we were interested only in the measure of the abundances in three different radial bins (r < 0.15r500, 0.15r500 < r < 0.4r500, r > 0.4r500), a measurement that we found not to be affected by the PSF. In the present sample we used the procedure developed in XMM-ESAS (Snowden et al. 2004) that considers the crosstalk ancillary response files (ARFs) between two regions to remove the contribution of each region from the other region and vice versa. Therefore, for each spectral annulus, we computed the crosstalk ARF relative to the contribution of this annulus to the emission in all remaining annuli and vice versa. All annuli were therefore fitted simultaneously to remove the effect of the non-negligible PSF of EPIC, an effect that is more significant in the core regions, especially if there are strong gradients in the emission and spectral parameters over the field (as is the case of cool core clusters).
The spectra were analyzed with XSPEC v12.7.0 (Arnaud 1996) and fitted with a single-temperature mekal model (Liedahl et al. 1995) with Galactic absorption (wabs model). The fits were performed over the energy range 0.7−8.0 keV for both of the two MOS detectors, which were fitted simultaneously to increase the statistics. In our spectral fits, we left the temperature, the abundance, and normalization free to vary. Local absorption was fixed to the Galactic neutral hydrogen column density, as obtained from radio data (Kalberla et al. 2005), and the redshift to the value measured from optical spectroscopy (z in Table 1). We used Cash statistics applied to the source plus background2, which requires a minimum grouping of the spectra (at least one count per spectral bin). A goodness-of-fit for the best-fit models was computed with the XSPEC command goodness, as described in BAL12. In this way, we simulated for each spectrum in the sample 10 000 spectra from the best fit model, whose C-statistic values were compared with the value obtained from the original spectrum. For each cluster, we found that the percentage of simulations with a value of the C-statistic lower than that for the data is always below 20%, an indication that the one-temperature model used to determine the temperature profiles is always a good fit.
3.3. Determination of r500
Our analysis strategy, which involves testing for self-similarity in the temperature
profiles at z > 0.4, requires determining the overdensity radius
r500 and the average temperature
T500 relative to that radius, computed as described in
BAL12, adopting the formula derived by Vikhlinin et al.
(2006): 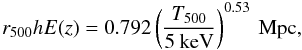 (1)where
E(z) = (Ωm(1 + z)3 + ΩΛ)0.5.
(1)where
E(z) = (Ωm(1 + z)3 + ΩΛ)0.5.
For each cluster, T500 was estimated by extracting a spectrum in the 0.15r500 < r < 0.6r500 radial range, assuming a first-guess value of T500 = 5 keV to compute an initial value of r500. The values of T500 and r500 were then evaluated iteratively until a convergence to a stable value of the temperature was obtained (ΔT500 ≤ 0.01 keV between two successive iterations). The values of T500 and r500 for each of the clusters are reported in Table 2, which shows that we sampled mostly high-temperature clusters; 75% of the clusters in the sample have a temperature kT > 6 keV.
4. Results
4.1. CC/NCC classification of the clusters
Although the spatial resolution of XMM and the redshift of the clusters in our sample
could in principle represent a complication and may not allow a trivial method to classify
galaxy clusters, we divided our sample into CC and NCC clusters based on a comparison of
the entropy measured in their core with the entropy measured outside the central regions.
In particular, we considered the regions corresponding to
r < 0.15r500 and to
0.15r500 ≤ r ≤ 0.4r500,
defining a pseudo-entropy ratio 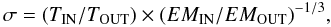 (2)where TIN and
TOUT are the temperature measured in the
r < 0.15r500 region and in the
0.15r500 ≤ r ≤ 0.4r500
annulus, respectively, and EMIN and
EMOUT are the corresponding emission
measures. This ratio is very similar to the parameter defined in Leccardi et al. (2010) to classify their low-z cluster
sample (z < 0.24), with the exception of the radial range, which in
their case was r < 0.05r200 for the IN
region (corresponding to ~0.08r500) and
0.05r200 ≤ r ≤ 0.2r200
for the OUT region (corresponding approximately to
0.08r500 ≤ r ≤ 0.3r500).
The choice of a different radial range was motivated by the higher redhift of the clusters
in our sample, which would make the IN region smaller (~10′′) than the PSF of
XMM-Newton, in most cases. To test whether this choice may introduce a
bias in the classification, we computed the pseudo-entropy ratio for the cluster sample
presented in Leccardi & Molendi (2008) using
both methods, and compared the results in Fig. 2.
Clearly, the pseudo-entropy ratios calculated with the two different choices of radial
range show a good correlation with low dispersion especially at low values of
σ. In both methods, σ is expected to be higher for
NCC clusters and lower for CC clusters. Leccardi et al.
(2010) divided their sample into three different classes: low-entropy core (LEC,
corresponding to σ < 0.45), medium-entropy core (MEC,
0.45 < σ < 0.64), and high-entropy core (HEC,
σ > 0.64) clusters. For our purposes, we do not need such a detailed
classification, hence we decided to classify our clusters into only two categories: the
LEC/CC, with σ < 0.6, and the HEC/NCC, with σ ≥ 0.6.
Figure 2 shows that the choice of
σ = 0.6 as a boundary between CC and NCC clusters is reasonable and
agrees well with the independent methods of cluster classification in CC and NCC presented
in Ettori et al. (2010). Our sample would then be
divided into five CC clusters and seven NCC clusters, indicating a prevalence of
non-relaxed NCC systems that is fully expected in our redshift range (see e.g. Vikhlinin et al. 2007; Santos et al. 2010). The values of σ for each cluster are also
reported in Table 2. In Fig. 3 we show the temperature profiles derived for each cluster in the
sample with the analysis procedure described above.
(2)where TIN and
TOUT are the temperature measured in the
r < 0.15r500 region and in the
0.15r500 ≤ r ≤ 0.4r500
annulus, respectively, and EMIN and
EMOUT are the corresponding emission
measures. This ratio is very similar to the parameter defined in Leccardi et al. (2010) to classify their low-z cluster
sample (z < 0.24), with the exception of the radial range, which in
their case was r < 0.05r200 for the IN
region (corresponding to ~0.08r500) and
0.05r200 ≤ r ≤ 0.2r200
for the OUT region (corresponding approximately to
0.08r500 ≤ r ≤ 0.3r500).
The choice of a different radial range was motivated by the higher redhift of the clusters
in our sample, which would make the IN region smaller (~10′′) than the PSF of
XMM-Newton, in most cases. To test whether this choice may introduce a
bias in the classification, we computed the pseudo-entropy ratio for the cluster sample
presented in Leccardi & Molendi (2008) using
both methods, and compared the results in Fig. 2.
Clearly, the pseudo-entropy ratios calculated with the two different choices of radial
range show a good correlation with low dispersion especially at low values of
σ. In both methods, σ is expected to be higher for
NCC clusters and lower for CC clusters. Leccardi et al.
(2010) divided their sample into three different classes: low-entropy core (LEC,
corresponding to σ < 0.45), medium-entropy core (MEC,
0.45 < σ < 0.64), and high-entropy core (HEC,
σ > 0.64) clusters. For our purposes, we do not need such a detailed
classification, hence we decided to classify our clusters into only two categories: the
LEC/CC, with σ < 0.6, and the HEC/NCC, with σ ≥ 0.6.
Figure 2 shows that the choice of
σ = 0.6 as a boundary between CC and NCC clusters is reasonable and
agrees well with the independent methods of cluster classification in CC and NCC presented
in Ettori et al. (2010). Our sample would then be
divided into five CC clusters and seven NCC clusters, indicating a prevalence of
non-relaxed NCC systems that is fully expected in our redshift range (see e.g. Vikhlinin et al. 2007; Santos et al. 2010). The values of σ for each cluster are also
reported in Table 2. In Fig. 3 we show the temperature profiles derived for each cluster in the
sample with the analysis procedure described above.
4.2. Self-similarity of temperature profiles
The values of r500 and of T500,
computed in Sect. 3.3 and reported in Table 2, were used to normalize the average distance from the
center of each annulus and the corresponding observed temperature. The normalized
temperature profiles are plotted in Fig. 4. At first
glance, a self-similarity of the temperature profiles of the clusters in our sample can be
observed, although with non-negligible scatter. With the aim of quantifying the
self-similarity, we considered a function derived from the relation introduced by Vikhlinin et al. (2006) to fit the deprojected
temperature profiles of their low-redshift CC cluster sample: 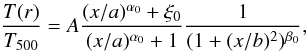 (3)where
x = r/r500 and
A is a normalization parameter. The parameters a and
b describe the core radius of the inner and outer regions of the
profiles, respectively, while α0 and
β0 represent the inner and the outer slope of the
temperature profiles, respectively. The additional parameter
ξ0 is introduced to adjust the relative normalization of the
inner profile with respect to the outer profile. Figure 5 shows how each of the fitting parameters affects the shape of the temperature
profiles described in Eq. (3). The best-fit
values of these parameters found by Vikhlinin et al.
(2006) were A = 1.35, a = 0.045,
b = 0.6, α0 = 1.9,
β0 = 0.45, and ξ0 = 0.45.
Because of the spatial resolution of XMM-Newton, the parameter
a is clearly insensitive to our data and it was therefore fixed to the
value of 0.045, defined by Vikhlinin et al. (2006).
The other parameters are expected to be different by fitting our data since we are
considering projected temperature profiles (and not 3-D profiles) of a sample not
exclusively built of CC clusters. However, the best-fit values of these parameters
obtained by Vikhlinin et al. (2006) were used when
we needed to freeze one parameter to obtain meaningful constraints on the others.
(3)where
x = r/r500 and
A is a normalization parameter. The parameters a and
b describe the core radius of the inner and outer regions of the
profiles, respectively, while α0 and
β0 represent the inner and the outer slope of the
temperature profiles, respectively. The additional parameter
ξ0 is introduced to adjust the relative normalization of the
inner profile with respect to the outer profile. Figure 5 shows how each of the fitting parameters affects the shape of the temperature
profiles described in Eq. (3). The best-fit
values of these parameters found by Vikhlinin et al.
(2006) were A = 1.35, a = 0.045,
b = 0.6, α0 = 1.9,
β0 = 0.45, and ξ0 = 0.45.
Because of the spatial resolution of XMM-Newton, the parameter
a is clearly insensitive to our data and it was therefore fixed to the
value of 0.045, defined by Vikhlinin et al. (2006).
The other parameters are expected to be different by fitting our data since we are
considering projected temperature profiles (and not 3-D profiles) of a sample not
exclusively built of CC clusters. However, the best-fit values of these parameters
obtained by Vikhlinin et al. (2006) were used when
we needed to freeze one parameter to obtain meaningful constraints on the others.
 |
Fig. 2 Distribution of the values of the pseudo-entropy ratio σ computed using the radial regions adopted in this paper vs. the values of σ computed using the radial range used in Leccardi et al. (2010) for the intermediate redshift cluster sample of Leccardi & Molendi (2008). The red, green, and blue squares represent the systems classified in the literature as CC, uncertain, and NCC , respectively. The purple squares are the clusters classified in the literature as “dubious” CC. The dotted horizontal lines represents the boundary chosen by Leccardi et al. (2010) to separate among LEC, MEC and HEC clusters. The dashed thick vertical line represent the boundary we have chosen to distinguish between LEC/CC and HEC/NCC clusters. Evidently, our classification method for CC and NCC agrees very well with the literature and with the method of Leccardi et al. (2010). |
 |
Fig. 3 Temperature profiles for the twelve galaxy clusters in our sample ordered according to redshift from left to right and from top to bottom. The notes on individual clusters are reported in Appendix A. |
 |
Fig. 4 Normalized temperature profiles for all clusters in the sample. CC clusters are plotted with filled squares, while NCC clusters are shown as open squares (see Sect. 4.2.1). The best fit to the Vikhlinin et al. (2006) relation, freeing the normalization, is drawn as a blue solid line. The blue dotted line represents the best fit to the relation in Eq. (3) (with ξ0 = 0.45), while the blue dashed line is the best fit of Eq. (5) for r > 0.15r500. |
For completeness, we also computed the projected equivalent of the Vikhlinin et al. (2006) relation. The best-fit parameters of the projected relation are slightly different from those derived for the 3-D profiles, with the most significant variation observed in the inner core radius a (from 0.045 to 0.03), to which our data are not sensitive. We ran the fits of the temperature profiles using also the projected parameters when freezing one of the fit parameters became necessary, finding consistent results with respect to the fits performed using the corresponding 3-D parameters. These findings show that a slight change in the value of a frozen parameter does not significantly affect the best fits of the others, therefore we can conclude that the results of the fits presented in the forthcoming sections are quite robust.
4.2.1. Fits of CC and NCC temperature profiles
The temperature profiles of galaxy clusters are known to be generally self-similar, showing a decline beyond ~15% of their virial radius (e.g. Vikhlinin et al. 2005; Baldi et al. 2007; Pratt et al. 2007; Leccardi & Molendi 2008). However, an apparent difference is present in their center, with the relaxed CC clusters showing a temperature drop, while such drop is not observed in the NCC clusters, which are generally not relaxed. Moreover, in a few studies based on low- and intermediate-redshift clusters, the NCC clusters were found to present a steeper temperature decline in the outer regions with respect to the CC clusters (e.g. Baldi et al. 2007), although this still remains a debated question (e.g. Leccardi & Molendi 2008).
As shown in Sect. 4.1, we divided our sample into CC and NCC based on their pseudo-entropy ratio σ. In particular, we defined as CC clusters the objects having σ < 0.6, while the objects with σ ≥ 0.6 were classified as NCC clusters. The two different categories were analyzed individually in this section. Figure 6 shows the normalized temperature profiles for CC and NCC clusters separately. We also computed an emission-weighted average for both subsamples, which, as expected, shows the temperature drop typical of CC clusters in the central regions, while a flat (or increasing) temperature profile is observed at the center of NCC clusters.
 |
Fig. 5 Temperature profiles as described by the relation of Vikhlinin et al. (2006) (solid black line) and by varying some of its parameters. Decreasing the inner slope parameter α0 (green dashed line) creates a shallower temperature dip in the center. If the relative normalization ξ0 between the inner and the outer profile is increased (blue dashed line), the profile transitions toward the typical shape of NCC clusters. A decrease in the outer slope β0 (red dashed line) flattens the external part of the temperature profile. |
 |
Fig. 6 Left: normalized temperature profiles for the CC clusters in the sample. Shaded areas show the error-weighted mean of the normalized temperature with its error (red) and rms dispersion (magenta) in 4 radial bins. The best fit to Vikhlinin et al. (2006) relation freeing the normalization is plotted as a blue solid line, while the blue dotted line and the blue dashed line represent the best fits to the relation in Eq. (3) (with ξ0 = 0.45) and to Eq. (5) (for r > 0.15r500), respectively. Right: normalized temperature profiles for the NCC clusters in the sample. Shaded areas show the error-weighted mean of the normalized temperature with its error (blue) and rms dispersion (cyan) in 6 radial bins. The best fit to Vikhlinin et al. (2006) relation (leaving the normalization free to vary), to the adaptation of the relation in Eq. (3) (with ξ0 = 0.45), and to Eq. (5) are plotted as a red solid, dotted and dashed line, respectively. |
 |
Fig. 7 Expected values for the function φ + introduced in Eq. (4) in the z − σ parameter space. The black lines represent the loci where a combination of the values of z and σ are expected to yield identical values of φ + . The dashed red line represent the boundary between CC and NCC clusters. |
To quantify the differences between the two subsamples, we fitted the relation in Eq. (3) separately to CC and NCC cluster normalized temperature profiles (Table 3). Running a fit leaving all the parameters in Eq. (3) free to vary (except for a, which is insensitive to our data, and was therefore fixed to 0.045), no meaningful constraint could be obtained either on the CC or on the NCC cluster temperature profiles. Hence, it was necessary to alternately freeze one of the parameters (except for the normalization A) to the value found in Vikhlinin et al. (2006) (reported in Sect. 4.2), and allow the other parameters to fit the data. For CC clusters, the better fits are obtained by freezing the parameter ξ0 or the parameter β0, but in the latter case the value of the free parameter ξ0 was frozen to zero by the fit. For the NCC clusters the better fits to Eq. (3) are obtained when we freeze α0 or ξ0. If we compare the fits with the parameter ξ0 frozen, which are showing one of the lowest χ2 and reasonable constraints on the free parameters in both samples, CC and NCC clusters differ mainly for the best fit of the inner slope parameter α0, which assumes a positive value for the CC sample (α0 = 1.14 ± 0.59), to fit the temperature drop in the center, and a value consistent with zero for the NCC sample (α0 = 0.18 ± 0.66), to fit their flat temperature profile in the central regions. No significant difference in the external slope β0 could be detected, being β0 = 0.35 ± 0.32 in CC clusters and β0 = 0.30 ± 0.10 in NCC clusters. Interestingly, the parameter ξ0 in NCC clusters is always found to be ~1 (when not frozen to 0.45). A value of ξ0 ~ 1 makes the first term in Eq. (3) approximately equal to unity, with the effect of removing the temperature dip in the center, as expected in the profiles of NCC clusters. In the successive fits of NCC clusters presented in this paper we adopted a value of ξ0 = 1.
Fit results using the functions similar to Vikhlinin et al. (2006), defined in Sect. 4.2, obtained by fixing a = 0.045 and by alternately freezing each one of the other free parameters, except the normalization A, which was always left free to vary.
4.2.2. General fits of the whole cluster sample
We fit the relation in Eq. (3) to the normalized temperature profiles of the whole sample, including both CC and NCC clusters. Leaving all fit parameters free to vary (except for a, which is insensitive to our data, and was therefore fixed to 0.045), we obtain that three of them (A, α0 and b) are unconstrained and able to vary throughout the whole parameter space without introducing any difference in the value of the statistics, with the other two being loosely constrained (ξ0 = 0.19 ± 0.21, β0 = 0.35 ± 1.08). Therefore, as we did for the separate fits of CC and NCC clusters (Sect. 4.2.1), we alternately froze one of the parameters (except the normalization A) to the value found by Vikhlinin et al. (2006) (reported in Sect. 4.2), and allowed the other four parameters to fit the data. The results of the fits are presented in Table 4. The better fits were obtained when we froze α0 or ξ0 (with a minimum difference in their respective χ2), yielding a best-fit value of ξ0 = 0.56 ± 0.11 and α0 = 1.39 ± 0.46, respectively. These fits also give fully consistent values of the normalization A and of the parameters b and β0, which describe the external region of the profiles.
We also adopted a more general approach to test the dependence of the profiles on the pseudo-entropy ratio σ (that we used to classify the clusters in our sample as CC or NCC), and/or on the cluster redshift, by fitting the data with a function of the
distance from the center r, the pseudo-entropy ratio
σ, and the redshift z. Equation (3) was modified accordingly in the form
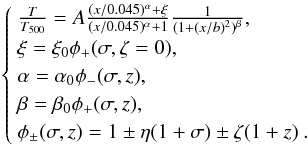 (4)In the function
φ ± (σ,z), the parameters
η and ζ take into account the dependence of the
temperature profiles on the pseudo-entropy ratio σ and on the redshift
z, respectively (Fig. 7). Owing
to the expected evolution of the temperature profiles in CC clusters (e.g. Ettori & Brighenti 2008), β is
expected to increase at high redshift in CC systems and therefore we considered the
function φ + to model their evolution. On the other hand,
α is expected to decrease with redshift and the function
φ− was considered for the evolution of this parameter.
Although in principle ξ is expected to have a dependence on
z, no meaningful constraint could be obtained for its evolution and
therefore we imposed this parameter to have a dependence only on σ (by
setting ζ = 0 in the function φ + ).
(4)In the function
φ ± (σ,z), the parameters
η and ζ take into account the dependence of the
temperature profiles on the pseudo-entropy ratio σ and on the redshift
z, respectively (Fig. 7). Owing
to the expected evolution of the temperature profiles in CC clusters (e.g. Ettori & Brighenti 2008), β is
expected to increase at high redshift in CC systems and therefore we considered the
function φ + to model their evolution. On the other hand,
α is expected to decrease with redshift and the function
φ− was considered for the evolution of this parameter.
Although in principle ξ is expected to have a dependence on
z, no meaningful constraint could be obtained for its evolution and
therefore we imposed this parameter to have a dependence only on σ (by
setting ζ = 0 in the function φ + ).
Initially, we tested the dependence of the temperature profiles only on the parameter σ (an indicator of their state of relaxation) by fitting Eq. (4) to the profiles and considering no redshift dependence at this stage (i.e. fixing the parameter ζ = 0). Similarly to the fits of Eq. (3), we froze one of the free parameters to obtain reasonable constraints on the others. In particular, we chose to freeze the value of ξ0 = 0.45, corresponding to the case with the lowest value of χ2. This fit, however, is not able to meaningfully constrain any of the free parameters. Therefore we decided to also fix the value of the external core radius to b = 0.4, a value consistent with the results of the fits in Table 4. The fit yields a χ2 ~ 109.7 with 68 d.o.f. and points out a mild dependence on σ of the temperature profiles, as indicated by the best-fit value of η = 0.33 ± 0.18 (Table 4). Even taking into account the uncertainties in the measurement of η and of the other parameters, the outer part of the profiles clearly becomes steeper for higher values of σ (i.e. transitioning toward the NCC clusters). This behavior agrees with the results obtained in lower redshift galaxy cluster samples (e.g. Baldi et al. 2007) and with the universal pressure profile derived by Arnaud et al. (2010) in galaxy clusters in the REXCESS local sample (z < 0.2), showing a low dispersion, especially in the external regions. An analogous behavior of the pressure profiles for both CC and NCC clusters, combined with that of the density profiles, which are known to be flatter at large radii in NCC clusters than in CC clusters (see e.g. Cavaliere et al. 2009; Eckert et al. 2012), would indeed yield steeper temperature profiles in NCC than in CC systems.
We also added a redshift dependence of the temperature profiles by fitting Eq. (4) to the data, this time also leaving the parameter ζ free to vary. Fixing again ξ0 = 0.45 and b = 0.4, we obtain a χ2 = 110.3 with 67 degrees of freedom, i.e. no improvement in the fit quality. The best-fit value of ζ is found to be consistent with zero (ζ = 0.12 ± 0.39), pointing to no significant evolution with the redshift within the redshift range considered (0.4 < z < 0.9). In this fit, the parameter η is also consistent with zero, an indication that also introducing a redshift dependence removed the mild dependence of the profiles on σ detected in the previous fit.
We caution, however, that our sample is not a complete sample at z > 0.4 with representative fractions of CC and NCC clusters (Sect. 2) and the value of the parameter η may change if we use a different cluster sample than this present one.
4.2.3. Fits of the cluster external regions
As shown before, the shape of temperature profiles in galaxy clusters is not easy to
describe by using a simple function with few free parameters, to fit the observed data.
Indeed, in the previous subsections the relations we considered have at least five free
parameters, which makes it harder to obtain meaningful constraints on the best-fit
values and complicates the interpretation of the resulting best-fit functions. The
modeling of the temperature profiles can be simplified if we consider only the external
regions of the clusters (r > 0.15r500)
in a radial range in which the influence of a possible cool core is marginal. To fit the
profiles in these regions we considered Eq. (4) and imposed that the parameters α and ξ
are frozen to zero. Thuse we obtain 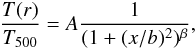 (5)where the parameters b and
β have the same meaning as in Eq. (4). To simplify the fit and have just two free parameters, we also
fixed the value of the core radius b to 0.4, a value that is more
appropriate to the best fits found previously in Sect. 4.2.2 for our sample than the value of 0.6 measured by Vikhlinin et al. (2006) in their low-redshift CC clusters. Without
considering any dependence on σ and/or z, the best
fits to the data of Eq. (5) yield a
χ2 = 73.2 (both with 51 d.o.f.) with best-fit values of
the normalization A = 1.13 ± 0.05 and of
β0 = 0.37 ± 0.06 (Table 5).
(5)where the parameters b and
β have the same meaning as in Eq. (4). To simplify the fit and have just two free parameters, we also
fixed the value of the core radius b to 0.4, a value that is more
appropriate to the best fits found previously in Sect. 4.2.2 for our sample than the value of 0.6 measured by Vikhlinin et al. (2006) in their low-redshift CC clusters. Without
considering any dependence on σ and/or z, the best
fits to the data of Eq. (5) yield a
χ2 = 73.2 (both with 51 d.o.f.) with best-fit values of
the normalization A = 1.13 ± 0.05 and of
β0 = 0.37 ± 0.06 (Table 5).
Introducing a dependence on σ (i.e. leaving ζ = 0 in Eq. (5) and freeing the parameter η), a mild dependence on this parameter could be found, with the value of η = −0.37 ± 0.08). Freeing also the parameter ζ, no redshift dependence could be found (ζ = 0.30 ± 0.64) within our redshift range.
By separately fitting the CC and NCC samples to Eq. (5) we obtained a χ2/d.o.f. = 42.2/21 and a χ2/d.o.f. = 28.2/28, respectively, indicating that the function is a good fit for NCC cluster profiles and pointing to more scattered profiles in CC clusters. Both profiles show consistent values of the external slope β0 (β0 = 0.37 ± 0.06 for NCC, β0 = 0.39 ± 0.12 for CC clusters).
We also tested the dependence of the profiles of CC and NCC clusters on the redshift, considering the relation in Eq. (5) and fixing η = 0 (Table 6). The fit yielded an improvement in the fit quality of CC clusters (F-test probability ~82%), while no F-test could be computed for the NCC clusters because the parameter ζ was frozen to the upper limit allowed by the fit. In CC clusters, we detect a significant dependence of the slope from the redshift, as shown by the value of ζ = −0.48 ± 0.09 significantly different from zero. However, the error on the slope is quite large (β0 = 1.66 ± 0.92), preventing any quantitative conclusion on the evolution of the external temperature profiles in CC clusters within the redshift range probed by our sample.
5. Discussion
In Sect. 4, we presented the normalized temperature profiles of our galaxy cluster sample, showing that they are generally self-similar at large radii (r > 0.15r500). The profiles exhibit a clear decline of the temperature with the radius, although a non-negligible scatter is present, especially among the CC clusters. The function we used to fit the profiles (derived from Vikhlinin et al. 2006) represents a good fit to the data in most cases, with the largest χ2 observed for the CC sample (where the scatter is larger). Although the profiles showed some dependence from the pseudo-entropy ratio σ (that we used to classify the clusters based on their state of relaxation), dividing the sample into CC and NCC cluster, no difference in the external slope between CC and NCC clusters was found, in contrast with some of the previous works performed at lower redshift (e.g. De Grandi & Molendi 2002; Baldi et al. 2007). Moreover, an attempt to introduce a dependence also on the redshift gave inconclusive results. These facts may be mostly due to the sample size, which consists of 12 galaxy clusters (five CC and seven NCC clusters), for a total of ~70 data points (~30 and ~45 data points for the CC and NCC sample, respectively). Moreover, a reduced redshift range (0.4 < z < 0.9) may factor in a lack of evidence of temperature profile evolution within our sample.
Both of these problems could be tackled considering a larger sample of clusters, spanning a different redshift range. To this aim, the most suitable sample clearly is the sample of 44 XMM-Newton clusters presented in Leccardi & Molendi (2008), which spans a lower redshift range than our sample (0.1 < z < 0.3) and whose data were reduced and analyzed using a procedure similar to that adopted in this paper, especially concerning the XMM background treatment.
 |
Fig. 8 Top: average temperature profiles measured for the CC clusters presented in this paper and for the CC clusters of Leccardi & Molendi (2008), examined in three redshift bins: 0.1 < z < 0.2 (red triangles), 0.2 < z < 0.3 (green squares), and 0.4 < z < 0.9 (blue dots). The profiles are consistent to be similar except for the central radial bin where the temperature dip in the high-redshift clusters is less pronounced. High-redshift clusters are indeed expected to be at a less advanced stage of their formation and are expected to have not grown enough mass to create a deep potential well and establish an efficient cooling in the central regions. We caution, however, that another concurring factor may be the difficulty to fully resolve the core at high redshift. Bottom: average temperature profiles measured for the NCC clusters presented in this paper and for the NCC clusters of Leccardi & Molendi (2008), examined in three redshift bins: 0.1 < z < 0.2 (red triangles), 0.2 < z < 0.3 (green squares), and 0.4 < z < 0.9 (blue dots). Although the average profiles are consistent at every radius, the slope of the high-redshift sample seems slightly steeper than that of the lower redshift samples, which is fully expected because of the less advanced stage of formation (and consequently less massive hot gas halos) of higher redshift clusters. |
5.1. Comparison with intermediate redshift clusters
The normalized temperature profiles for the sample of Leccardi & Molendi (2008) were obtained using the values of r500 reported in Ettori et al. (2010) and the values of T500 were computed using emission-weighted averages of the temperatures measured in the radial bins comprised in the 0.15−0.6 r500 radial range. We computed the emission-weighted average temperature profiles of CC and NCC clusters in different radial bins to achieve a direct comparison between the two samples (probing different redshift ranges). Since the size of the Leccardi & Molendi (2008) sample is quite large (44 clusters), we divided it into two subsamples, considering two redshift bins: 0.1 < z < 0.2 and 0.2 < z < 0.3. The 0.4 < z < 0.9 redshift range is covered by the sample presented in this work. The emission-weighted average temperature profiles in the three redshift bins are shown in Fig. 8.
The profiles of CC clusters are consistent within the errors at every radius except for the central radial bin where the high-redshift cluster sample shows a shallower temperature dip with respect to the lower redshift clusters. This may indicate a difference between CC clusters at z > 0.4 with respect to CC clusters located at z < 0.3. A possible reason for this is that the former are at less advanced stage of their formation and would not have had enough time to accrete enough mass to create a deeper potential well and therefore establish a more efficient cooling in the central regions. However, in this case we have to be cautious about any claim about evolution for two reasons. First of all, it may be very difficult to fully resolve the cluster core regions at z > 0.4 because of the XMM-Newton PSF. Although a PSF correction was applied (Sect. 3.2), the size of the region corresponding to the central bin (r < 0.1r500) in some cases could be about that of the XMM-Newton PSF itself. Moreover, selection effects could affect this result. Indeed, our high-redshift sample consists of only five clusters and cannot be considered complete in any sense (Sect. 2).
Fit results for the CC clusters in our sample and in the Leccardi & Molendi (2008) sample considering three different redshift bins and using the relation in Eq. (3) obtained by fixing the value of the relative normalization between the internal and external region of the profiles to ξ0 = 0.45 and the values of the external core radius to b = 0.4.
For the NCC clusters, the average profiles in the three redshift bins are consistent within the errors at every radius. It is worth noticing, however, that the slope of our high-redshift sample seems to be slightly steeper than that of the lower redshift samples, although no quantitative claim can be obtained from this plot. In this case the PSF of XMM is not a biasing factor, but selection effects may also play a role in NCC clusters (Sect. 2).
A more quantitative comparison could be performed by considering the relations introduced in Sect. 4.2 to fit the data points from the samples in the three different redshift bins. For the CC clusters, where the main differences are observed in the central regions, the most suitable comparison can be made using Eq. (3) and fixing the value of the relative normalization between the internal and external region of the profiles to ξ0 = 0.45. Since we are not interested in the external regions of the profiles, at this stage we can also fix the external core radius to b = 0.4. The results of the fits for the three different redshift bins are shown in Table 7. The inner slope α0 is flatter in the high-z sample presented in this paper with respect to the two lower redshift samples extracted from Leccardi & Molendi (2008), although the difference is statistically significant only in the comparison with the 0.1 < z < 0.2 redshift bin (> 2σ). It is worth noticing, however, that also this comparison could be biased by the XMM PSF and by possible selection effects. Moreover, there is a significant difference in the external slope β0, but no quantitative claim could be made about this point because fixing the external core radius to b = 0.4 may have biased the determination of the slope, especially at lower redshift.
In the NCC clusters the average profiles are showing a slightly steeper slope in our high-z sample with respect to the intermediate cluster sample of Leccardi & Molendi (2008). The difference could be quantified by fitting the data points for both samples using a simplified function as described in Sect. 4.2.3 (Eq. (5)) and considering only the external regions of the clusters (r > 0.15r500). We used this function also to compare the external slopes at different redshifts in CC clusters, a task not attainable with the more complex function in Eq. (3). The results of the power-law fits are shown in Table 8.
Fit results using the functions similar to Vikhlinin et al. (2006) (defined in Sect. 4.2) for our sample and the Leccardi & Molendi (2008) sample together, obtained by fixing a = 0.045 and the relative normalization xi0 = 0.45.
For the CC clusters there is no significant difference in the power-law slope between the two intermediate redshift bins, where the value of β is consistent within the 1σ errors. A difference just above 1σ is observed instead between the slope of the high-z CC clusters and the slope of the intermediate redshift CC clusters. For the NCC no difference in the slope β is observed either between the two intermediate redshift bins. The value of β in our high-z NCC sample is in this case significantly higher than in the NCC clusters at z < 0.3 in the Leccardi & Molendi (2008) sample (~2σ). As stated before, this difference could be caused by selection effects introduced by our sample selection. However, it is very likely that it is instead related to the different stages of the evolution of the clusters at z > 0.4 with respect to clusters at z < 0.3. It is indeed expected that the former would be younger clusters with a smaller sized hot gas halo with respect to the latter, and therefore would show lower temperatures at large radii.
5.2. A universal law for temperature profiles
The data points of the clusters in the Leccardi &
Molendi (2008) sample can be used together with our sample to help us define a
universal behavior of temperature profiles in galaxy clusters at
0.1 < z < 0.9 as a function of both cosmic time and state of
relaxation (as defined by the pseudo-entropy ratio σ). The relations
introduced in Sect. 4.2 could indeed be used to
jointly fit the data points from our high-z cluster sample and the
intermediate-redshift sample of Leccardi & Molendi
(2008). The results are presented in Table 9. For simplicity, we considered only the case of Eq. (3) where the value of the external core radius
has been set at b = 0.4. In all cases, the fit quality is poor
(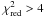 ), indicating a consistent scatter in the
normalized temperature profiles. Introducing a dependence on σ
(Eq. (4), with ζ = 0)
clearly improves the fit (F-test probability ~99.96%). The best-fit values indicate
that the external part of the profiles is steeper for increasing values of
σ, i.e. transitioning from CC to NCC clusters. If we also take into
account a dependence on the redshift of the temperature profiles (by fitting Eq. (4) and leaving both η and
ζ free to vary), we obtain the following relation that
can be considered to be the closest possible to a universal law for temperature profiles
of clusters at 0.1 < z < 0.9 that can be attained with the present
data
), indicating a consistent scatter in the
normalized temperature profiles. Introducing a dependence on σ
(Eq. (4), with ζ = 0)
clearly improves the fit (F-test probability ~99.96%). The best-fit values indicate
that the external part of the profiles is steeper for increasing values of
σ, i.e. transitioning from CC to NCC clusters. If we also take into
account a dependence on the redshift of the temperature profiles (by fitting Eq. (4) and leaving both η and
ζ free to vary), we obtain the following relation that
can be considered to be the closest possible to a universal law for temperature profiles
of clusters at 0.1 < z < 0.9 that can be attained with the present
data 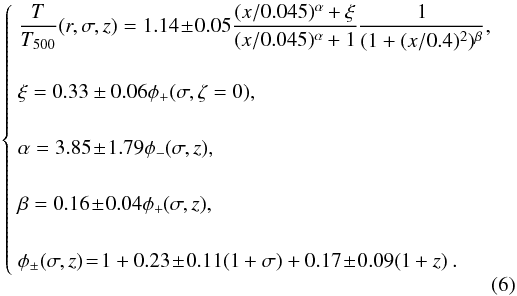 (6)This relation shows that the steepening of
the profiles with increasing σ is still robust, and the behavior with the
redshift agrees with the results of Sect. 5.1, i.e.,
higher z corresponds to steeper profiles.
(6)This relation shows that the steepening of
the profiles with increasing σ is still robust, and the behavior with the
redshift agrees with the results of Sect. 5.1, i.e.,
higher z corresponds to steeper profiles.
6. Conclusions
We analyzed an XMM-Newton sample of 12 bright (LX > 4 × 1044 erg s-1) galaxy clusters in the redshift range 0.4 < z < 0.9 with an average temperature kT > 4.5 keV. This sample was extracted from the XMM-Newton sample analyzed in BAL12 by selecting all clusters with at least 3000 MOS net counts to obtain radial temperature profiles with a sizeable number of radial bins and reasonable errors on the temperature (σkT/kT < 15%).
Taking advantage of EPIC XMM-Newton’s high throughput and effective area, which makes it an ideal instrument for performing a spatially resolved spectral analysis, this paper aimed at a systematic study of the temperature profiles in galaxy clusters at z > 0.4, which is not currently provided in the literature. The results we obtained can be summarized as follows:
-
We extracted temperature profiles for the 12 clusters in our sample. The cluster extension ranged from ~500 kpc to ~1.3 Mpc from the center. All profiles were found to be declining toward larger radii.
-
The temperature profiles of the galaxy clusters in our sample, normalized by the mean temperature T500, were found to be generally self-similar and could be well described by a function obtained by adapting the relation of Vikhlinin et al. (2006) derived for lower redshift clusters.
-
We divided the sample into five CC and seven NCC clusters by introducing a pseudo-entropy ratio σ and defining a threshold σ = 0.6 between CC and NCC clusters with the latter having σ ≥ 0.6. The profiles of the two subsamples were found to be different mainly in the inner regions, with the inner slope parameter assuming a positive value in the CC clusters (α = 1.14 ± 0.59), to fit the temperature drop in the center, and a value consistent with zero in the NCC clusters (α = 0.18 ± 0.66), to fit their flat central profile. The large errors on the measurement of the external slope β0 gave inconclusive results on the differences between the samples. Fitting the external regions (r > 0.15r500) with a simpler function yielded no significant difference between the slopes of CC and NCC clusters (β0 = 0.39 ± 0.12 and β0 = 0.37 ± 0.06, respectively). The lack of any significant difference between the two samples could be attributed to the small sample size, and therefore to the few data points available for the fit, especially for the CC clusters.
-
We introduced a function of both r and σ to fit the data points of CC and NCC clusters together. In this case, the improved statistics allowed us to detect a significant dependence of the temperature profiles on the pseudo-entropy ratio σ, showing an indication that the outer part of the profiles becomes steeper for higher values of σ (i.e. transitioning toward the NCC clusters). This behavior would agree with the results obtained in lower redshift galaxy cluster samples (e.g. Baldi et al. 2007) and with the universal pressure profile derived by Arnaud et al. (2010) in galaxy clusters in the REXCESS local sample (z < 0.2), which show a low dispersion, especially in the external regions.
-
In all attempted fits, no evidence of redshift evolution could be found within the redshift range sampled by our clusters (0.4 < z < 0.9).
-
We compared our sample with the intermediate cluster sample of Leccardi & Molendi (2008) at 0.1 < z < 0.3, finding significant differences in both the CC and the NCC cluster samples. In particular, we found that CC clusters at z > 0.4 shows a temperature dip in the center less deep with respect to CC clusters at z < 0.3, while NCC clusters at z > 0.4 showed steeper temperature profiles with respect to NCC clusters at z < 0.3. This can be caused by the circumstance that higher z clusters are at a less advanced stage of their formation and did not have enough time to create a large massive hot gas halo comparable in size and mass with that of lower redshift clusters.
-
We defined for the first time the closest possible relation to a universal law for the temperature profiles of galaxy clusters at 0.1 < z < 0.9. This relation shows a dependence on the state of relaxation of the clusters and the redshift.
Although some of the results obtained in this paper can in principle be biased by possible selection effects introduced in extracting the sample from the XMM archive (Sect. 2), we stress that this is the first time that a systematic study of the temperature profiles in galaxy clusters at z > 0.4 has been attempted. Additional deep XMM-Newton and Chandra observations, and most likely a new generation of X-ray observatories, would be
needed to improve the current knowledge of the temperature distribution in the hot gas of galaxy clusters at high redshift.
Online material
Appendix A: Notes on individual clusters
A851 – A851, the lowest redshift cluster in the sample
(z = 0.407), has been observed by EPIC XMM-Newton
for ~56 ks (ObsID: 0106460101), of which ~41 ks were useful for
scientific analysis after removing the periods of high flares. Its temperature profile
is quite flat in the central regions with a temperature of ~6 keV, showing a
significant decline only in the outer radial bin (r > 700 kpc). As
indicated by a value of 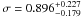 , this cluster is classified as NCC.
, this cluster is classified as NCC.
RXCJ0856.1+3756 – RXCJ0856.1+3756 (z = 0.411) has
been observed by XMM for ~29 ks (ObsID: 0302581801), with ~24 ks available
for our analysis after cleaning the event files from soft proton flares. Although the
temperature profile consists of only four radial bins, a hint of a temperature drop in
the central bin (r < 170 kpc) is observed, although its value of
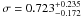 puts this cluster in the NCC category.
The temperature profile then declines from kT ≈ 9 keV down to
kT ≈ 5.5 keV) in the outer two bins
(r > 250 kpc).
puts this cluster in the NCC category.
The temperature profile then declines from kT ≈ 9 keV down to
kT ≈ 5.5 keV) in the outer two bins
(r > 250 kpc).
RXJ2228.6+2037 – EPIC XMM-Newton observed the cluster
RXJ2228.6+2037 (z = 0.412) for a total of ~26 ks (ObsID:
0147890101), almost entirely useful for our analysis. Although a hint of a drop in the
temperature is observed in the central two radial bins
(r < 150 kpc), with kT ≈ 8 keV in the central
region, this cluster is classified as NCC (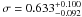 ). The temperatures reaches its maximum
(kT ≈ 9 keV) at r ~ 200 kpc and then declines
smoothly down to ~4 keV at radii larger than ~850 kpc.
). The temperatures reaches its maximum
(kT ≈ 9 keV) at r ~ 200 kpc and then declines
smoothly down to ~4 keV at radii larger than ~850 kpc.
RXCJ1206.2-0848 – The cluster RXCJ1206.2-0848
(z = 0.440) has been observed twice by EPIC XMM-Newton
(ObsIds: 0302581901, 0502430401), but one of the two observation (ObsID:
0302581901) was heavily affected by soft proton flares and was therefore discarded. The
~30 ks of the other observation were almost entirely available for scientific
analysis. The temperature profile can be considered approximately constant around
kT ≈ 10 keV, although several fluctuations are observed in the
profile and the temperature shows a drop of ~3.5 keV between the center and the
adjacent radial bin. This cluster is classified as CC, presenting a value of
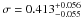 .
.
IRAS09104+4109 – IRAS09104+4109 (z = 0.442) has been
observed by EPIC XMM-Newton for a total of ~14 ks (~12 ks of
clean exposure time, ObsID: 0147671001). The temperature shows a hint of a temperature
drop in the center (ΔkT ~ 0.5 keV), and decreases from
~6.5 keV to ~4.5 keV between the region located at ~100 kpc from the
center and the one located at ~200 kpc, remaining constant around the latter value
going toward larger radii. This cluster shows a value of
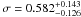 and is therefore classified as NCC.
and is therefore classified as NCC.
RXJ1347.5-1145 – RXJ1347.5-1145 (z = 0.451),
representing the brightest cluster in our sample with its X-ray luminosity of
4.2 × 1045 erg s-1 (0.1–2.4 keV band, Ebeling et al. 2010), has been observed for ~38 ks
(~32 ksec after cleaning for flares) by XMM-Newton (ObsID:
0112960101). This cluster shows evidence of a very strong cool core with the temperature
dropping from kT ≈ 13.5 keV to kT ≈ 10 keV in the
central bin (r < 90 kpc) and is classified as a CC cluster
(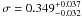 , the lowest value among the clusters in
our sample). Although some irregularities in the profile are present, the temperature
, the lowest value among the clusters in
our sample). Although some irregularities in the profile are present, the temperature
then declines smoothly toward the outer regions, reaching a value around ~6 keV at r > 750 kpc.
CLJ0030+2618 – The cluster CLJ0030+2618 (z = 0.500)
has been observed three times by XMM-Newton (ObsIds: 0302581101,
0402750201, 0402750601) for a total of ~94 ks, of which ~70 ks were
available after removing the high-flaring intervals. The number of counts available did
not allow us to divide the emission into more than three radial bins, with the
temperature profiles being approximately constant around ~5 keV. CLJ0030+2618 is
classified as a NCC cluster, as indicated by a 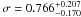 .
.
MS0015.9+1609 – MS0015.9+1609 (z = 0.541) has been
observed twice by XMM (ObsIds: 0111000101, 0111000201) for a total of ~45 ks
(~36 ks of clean exposure time). The temperature profile declines smoothly from
kT ≈ 12 keV measured at the center down to a minimum of ~7 keV
observed as far as ~900 kpc from the center, making of it a clear example of a
NCC cluster (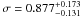 ).
).
MS0451.6-0305 – The galaxy cluster MS0451.6-0305
(z = 0.550) has been observed by XMM-Newton (ObsId:
0205670101) for a total of ~45 ks. The observation was heavily affected by soft
proton flares and we were able to use only ~26 ks of the original exposure. The
observed temperature shows a drop in the central 200 kpc
(kT ~ 9 keV) and is then quite constant around ~11 keV
between 200 and 450 kpc. It then declines to ~6 keV at
r > 450 kpc. The value of 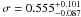 measured for this cluster puts it in the
CC category.
measured for this cluster puts it in the
CC category.
MACSJ0647.7+7015 – EPIC XMM-Newton observed twice
(ObsIDs: 0551850401, 0551851301) the galaxy cluster MACSJ0647.7+7015
(z = 0.591) for a total of ~145 ks (~88 keV of clean
exposure time). The temperature observed in this cluster shows a smooth decline from the
center (kT ≈ 12 keV) toward the outskirts
(kT ≈ 6−7 keV at r > 450 kpc), making of it
another obvious example of NCC cluster (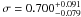 ).
).
MACSJ0744.9+3927 – Two EPIC observations of the cluster of galaxy
MACSJ0744.9+3927 (z = 0.698) are present in the XMM-Newton
archive (ObsIDs: 0551850101, 0551851201) accounting for a total exposure time
of ~154 ks (~106 ks after cleaning for high-flaring periods).
MACSJ0744.9+3927 is another examples of strong CC present in our sample (as indicated
also by 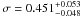 ), showing a temperature drop from
~10 keV (at ~150 kpc from the center) to ~7.5 keV in the central
radial bin (r < 100 kpc). The temperature smoothly declines toward
the outskirts and stabilizes around a value of ~6 keV at
r > 500 kpc.
), showing a temperature drop from
~10 keV (at ~150 kpc from the center) to ~7.5 keV in the central
radial bin (r < 100 kpc). The temperature smoothly declines toward
the outskirts and stabilizes around a value of ~6 keV at
r > 500 kpc.
CLJ1226.9+3332 – CLJ1226.9+3332, the farthest cluster in our sample
(z = 0.890), has been observed twice by EPIC XMM-Newton
(ObsIds: 0070340501, 0200340101) for a total of ~139 ks. Both observation
were heavily affected by soft proton flares (in particular ~75% of ObsID
0070340501 was affected by soft protons), leaving just ~77 ks of clean exposure
time available for scientific analysis. The temperature shows a sharp decline from the
center (kT ≈ 13 keV) toward the outer radial bin as far as
~500 kpc from the core (kT ≈ 6 keV). This cluster is classified
as a NCC (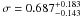 ).
).
Acknowledgments
We acknowledge financial contribution from contracts ASI-INAF I/023/05/0 and I/088/06/0. F.G. acknowledges financial support from contract ASI-INAF I/009/10/0.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, A., Ettori, S., Mazzotta, P., Tozzi, P., & Borgani, S. 2007, ApJ, 666, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, A., Ettori, S., Molendi, S., et al. 2012, A&A, 537, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Lapi, A., & Fusco-Femiano, R. 2009, ApJ, 698, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, P., & Lucchin, F. 1995, Cosmology. The origin and evolution of cosmic structure [Google Scholar]
- De Grandi, S., & Molendi, S. 2002, ApJ, 567, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Mantz, A., et al. 2010, MNRAS, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Eckert, D., Vazza, F., Ettori, S., et al. 2012, A&A, 541, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S., & Brighenti, F. 2008, MNRAS, 387, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Bardelli, S., De Grandi, S., et al. 2000, MNRAS, 318, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Gastaldello, F., Leccardi, A., et al. 2010, A&A, 524, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finoguenov, A., Arnaud, M., & David, L. P. 2001, ApJ, 555, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Ikebe, Y., Makishima, K., Ezawa, H., et al. 1997, ApJ, 481, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., Rossetti, M., & Molendi, S. 2010, A&A, 510, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Loken, C., Norman, M. L., Nelson, E., et al. 2002, ApJ, 579, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Forman, W. R., Sarazin, C. L., & Vikhlinin, A. 1998, ApJ, 503, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Nevalainen, J., Kaastra, J., Parmar, A. N., et al. 2001, A&A, 369, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peacock, J. A. 1999, Cosmological Physics (Cambridge University Press) [Google Scholar]
- Peebles, P. J. E. 1993, Principles of Physical Cosmology (Princeton: Princeton University Press) [Google Scholar]
- Pratt, G. W., Arnaud, M., & Pointecouteau, E. 2006, A&A, 446, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Böhringer, H., Croston, J. H., et al. 2007, A&A, 461, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roncarelli, M., Ettori, S., Dolag, K., et al. 2006, MNRAS, 373, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Rosati, P., Borgani, S., & Norman, C. 2002, ARA&A, 40, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., & Böhringer, H. 2010, A&A, 521, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snowden, S. L., Collier, M. R., & Kuntz, K. D. 2004, ApJ, 610, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Markevitch, M., Murray, S. S., et al. 2005, ApJ, 628, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R., Forman, W. R., et al. 2007, in Heating versus Cooling in Galaxies and Clusters of Galaxies, eds. H. Böhringer, G. W. Pratt, A. Finoguenov, & P. Schuecker, 48 [Google Scholar]
- Voit, G. M. 2005, Rev. Mod. Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
XMM-Newton archival observations of the 12 bright galaxy clusters analyzed in this paper.
Values of T500 and r500 (expressed in Mpc and in arcsec, as computed in BAL12) for the XMM-Newton galaxy cluster bright sample presented in this paper.
Fit results using the functions similar to Vikhlinin et al. (2006), defined in Sect. 4.2, obtained by fixing a = 0.045 and by alternately freezing each one of the other free parameters, except the normalization A, which was always left free to vary.
Fit results for the CC clusters in our sample and in the Leccardi & Molendi (2008) sample considering three different redshift bins and using the relation in Eq. (3) obtained by fixing the value of the relative normalization between the internal and external region of the profiles to ξ0 = 0.45 and the values of the external core radius to b = 0.4.
Fit results using the functions similar to Vikhlinin et al. (2006) (defined in Sect. 4.2) for our sample and the Leccardi & Molendi (2008) sample together, obtained by fixing a = 0.045 and the relative normalization xi0 = 0.45.
All Figures
 |
Fig. 1 Redshift distribution of the XMM-Newton galaxy cluster bright sample presented in this paper. |
| In the text | |
 |
Fig. 2 Distribution of the values of the pseudo-entropy ratio σ computed using the radial regions adopted in this paper vs. the values of σ computed using the radial range used in Leccardi et al. (2010) for the intermediate redshift cluster sample of Leccardi & Molendi (2008). The red, green, and blue squares represent the systems classified in the literature as CC, uncertain, and NCC , respectively. The purple squares are the clusters classified in the literature as “dubious” CC. The dotted horizontal lines represents the boundary chosen by Leccardi et al. (2010) to separate among LEC, MEC and HEC clusters. The dashed thick vertical line represent the boundary we have chosen to distinguish between LEC/CC and HEC/NCC clusters. Evidently, our classification method for CC and NCC agrees very well with the literature and with the method of Leccardi et al. (2010). |
| In the text | |
 |
Fig. 3 Temperature profiles for the twelve galaxy clusters in our sample ordered according to redshift from left to right and from top to bottom. The notes on individual clusters are reported in Appendix A. |
| In the text | |
 |
Fig. 4 Normalized temperature profiles for all clusters in the sample. CC clusters are plotted with filled squares, while NCC clusters are shown as open squares (see Sect. 4.2.1). The best fit to the Vikhlinin et al. (2006) relation, freeing the normalization, is drawn as a blue solid line. The blue dotted line represents the best fit to the relation in Eq. (3) (with ξ0 = 0.45), while the blue dashed line is the best fit of Eq. (5) for r > 0.15r500. |
| In the text | |
 |
Fig. 5 Temperature profiles as described by the relation of Vikhlinin et al. (2006) (solid black line) and by varying some of its parameters. Decreasing the inner slope parameter α0 (green dashed line) creates a shallower temperature dip in the center. If the relative normalization ξ0 between the inner and the outer profile is increased (blue dashed line), the profile transitions toward the typical shape of NCC clusters. A decrease in the outer slope β0 (red dashed line) flattens the external part of the temperature profile. |
| In the text | |
 |
Fig. 6 Left: normalized temperature profiles for the CC clusters in the sample. Shaded areas show the error-weighted mean of the normalized temperature with its error (red) and rms dispersion (magenta) in 4 radial bins. The best fit to Vikhlinin et al. (2006) relation freeing the normalization is plotted as a blue solid line, while the blue dotted line and the blue dashed line represent the best fits to the relation in Eq. (3) (with ξ0 = 0.45) and to Eq. (5) (for r > 0.15r500), respectively. Right: normalized temperature profiles for the NCC clusters in the sample. Shaded areas show the error-weighted mean of the normalized temperature with its error (blue) and rms dispersion (cyan) in 6 radial bins. The best fit to Vikhlinin et al. (2006) relation (leaving the normalization free to vary), to the adaptation of the relation in Eq. (3) (with ξ0 = 0.45), and to Eq. (5) are plotted as a red solid, dotted and dashed line, respectively. |
| In the text | |
 |
Fig. 7 Expected values for the function φ + introduced in Eq. (4) in the z − σ parameter space. The black lines represent the loci where a combination of the values of z and σ are expected to yield identical values of φ + . The dashed red line represent the boundary between CC and NCC clusters. |
| In the text | |
 |
Fig. 8 Top: average temperature profiles measured for the CC clusters presented in this paper and for the CC clusters of Leccardi & Molendi (2008), examined in three redshift bins: 0.1 < z < 0.2 (red triangles), 0.2 < z < 0.3 (green squares), and 0.4 < z < 0.9 (blue dots). The profiles are consistent to be similar except for the central radial bin where the temperature dip in the high-redshift clusters is less pronounced. High-redshift clusters are indeed expected to be at a less advanced stage of their formation and are expected to have not grown enough mass to create a deep potential well and establish an efficient cooling in the central regions. We caution, however, that another concurring factor may be the difficulty to fully resolve the core at high redshift. Bottom: average temperature profiles measured for the NCC clusters presented in this paper and for the NCC clusters of Leccardi & Molendi (2008), examined in three redshift bins: 0.1 < z < 0.2 (red triangles), 0.2 < z < 0.3 (green squares), and 0.4 < z < 0.9 (blue dots). Although the average profiles are consistent at every radius, the slope of the high-redshift sample seems slightly steeper than that of the lower redshift samples, which is fully expected because of the less advanced stage of formation (and consequently less massive hot gas halos) of higher redshift clusters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


