| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219364 | |
| Published online | 12 September 2012 | |
The rate of supernovae at redshift 0.1–1.0⋆,⋆⋆
The Stockholm VIMOS Supernova Survey III
1
Department of Astronomy, Oskar Klein CentreStockholm University, AlbaNova
University Centre,
10691
Stockholm,
Sweden
e-mail: jens@astro.su.se
2
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD
21218,
USA
3
Tuorla Observatory, Department of Physics and Astronomy,
University of Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
4
CNRS, Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse,
France
5
Argelander-Institut für Astronomie, Universität Bonn,
Auf dem Hügel 71,
53121
Bonn,
Germany
Received:
7
April
2012
Accepted:
20
July
2012
We present supernova rate measurements at redshift 0.1–1.0 from the Stockholm VIMOS Supernova Survey (SVISS). The sample contains 16 supernovae in total. The discovered supernovae have been classified as core collapse or type Ia supernovae (9 and 7, respectively) based on their light curves, colour evolution and host galaxy photometric redshift. The rates we find for the core collapse supernovae are 3.29-1.78 -1.45+3.08 +1.98 × 10-4 yr-1 Mpc-3 h703 (with statistical and systematic errors respectively) at average redshift 0.39 and 6.40-3.12 -2.11+5.30 +3.65 × 10-4 yr-1 Mpc-3 h703 at average redshift 0.73. For the type Ia supernovae we find a rate of 1.29-0.57 -0.28+0.88 +0.27 × 10-4 yr-1 Mpc-3 h703 at ⟨z⟩ = 0.62. All of these rate estimates have been corrected for host galaxy extinction, using a method that includes supernovae missed in infrared bright galaxies at high redshift. We use Monte Carlo simulations to make a thorough study of the systematic effects from assumptions made when calculating the rates and find that the most important errors come from misclassification, the assumed mix of faint and bright supernova types and uncertainties in the extinction correction. We compare our rates to other observations and to the predicted rates for core collapse and type Ia supernovae based on the star formation history and different models of the delay time distribution. Overall, our measurements, when taking the effects of extinction into account, agree quite well with the predictions and earlier results. Our results highlight the importance of understanding the role of systematic effects, and dust extinction in particular, when trying to estimate the rates of supernovae at moderate to high redshift.
Key words: supernovae: general / surveys / galaxies: stellar content
Table 4 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The cosmic rate of supernovae is an important observable that can be used to constrain the properties of galaxies at high redshifts and to study the supernovae (SNe) themselves. Depending on the origin of the SN explosion, thermonuclear or core collapse, different aspects can be studied. The first measurement of the cosmic SN rate (SNR) was done by Zwicky (1938) who found that “the average frequency of occurrence of supernovae is about one supernova per extra-galactic nebula per six hundred years” for the local volume. It is not until the latest decades that the higher redshift regimes have been possible to reach.
More recently, large programmes targeting type Ia supernovae at intermediate and high (≳ 0.1) redshifts have been conducted to measure the expansion of the universe and do precision cosmology (e.g. Perlmutter et al. 1997; Schmidt et al. 1998; Astier et al. 2006; Riess et al. 2007; Miknaitis et al. 2007). Some of these surveys also report supernova rates for Ia SNe (e.g. Neill et al. 2006; Dahlen et al. 2008) out to z ~ 1.5 and core collapse supernovae (CC SNe) (Dahlen et al. 2004; Bazin et al. 2009) out to z ~ 0.7. Large surveys targeting SNe of any type have also been successful in finding and characterising supernovae as well as determining both local and intermediate redshift cosmic supernova rates (Botticella et al. 2008; Dilday et al. 2010b; Li et al. 2011b). Sharon et al. (2010), Dilday et al. (2010a), and Barbary et al. (2012a) survey galaxy clusters, where the SN Ia rates are likely to be enhanced, to find supernovae and have reported cluster SN rates out to redshift 0.9. Barbary et al. (2012b) also report SN Ia rates from detections in the foreground and background of the targeted galaxy clusters out to z ~ 1.5.
The standard observational strategy for finding SNe at high redshift is to perform survey observations on a given field and then monitor the same field over a long period of time. Supernovae are discovered by searching the images for variable sources using image subtraction tools (such as Alard 2000) to minimise subtraction residuals. The cadence of observations during the survey period is normally chosen to sample signature features of the SN light curves and colour evolution at the target redshifts. In this way photometric typing of the SNe is possible and the light curves can be used to study the SN characteristics. For the Ia surveys with cosmology as the main goal, follow-up spectroscopy of SN Ia candidates is needed to get a secure determination of the redshift, to improve the accuracy in the distance measurement, and confirmation of the type. When calculating supernova rates from this kind of survey, care has to be taken to avoid selection effects from the spectroscopic observations.
Supernova typing normally includes studying the spectra of the SNe close to their peak luminosity and identifying spectral lines, notably H, He and SiII lines, something which is observationally very expensive and in practice unfeasible at high redshift for fainter SN types. Another method to type SNe is to compare the observed light curves and colour evolution to pre-existing templates of different SN types, i.e. photometric SN typing. These methods have been demonstrated to work (e.g. Kuznetsova & Connolly 2007; Poznanski et al. 2007; Rodney & Tonry 2009; Kessler et al. 2010) using somewhat different techniques. Better typing accuracy is achieved with prior information on the redshift through photometric or spectroscopic redshift of the host galaxy (Kessler et al. 2010; Melinder et al. 2011).
Thermonuclear supernovae (or SN Ia’s) are thought to be white dwarfs that explode when they accrete matter and approach the Chandrasekhar limit (for a review, see Leibundgut 2000). When taking the luminosity-stretch relation (Phillips 1993) into account the peak luminosity of these SNe exhibit a very narrow spread and can thus be used to accurately measure cosmological distances. The exact details of the explosions and of the progenitor system are not fully understood. For example, the time between formation of the progenitor system and the supernova explosion – the so called delay time – is unknown. This delay time depends on the nature of the companion star to the white dwarf (Greggio 2005). By studying the rates of Ia supernovae and comparing to either the cosmic star formation history (e.g. Dahlén & Fransson 1999; Neill et al. 2006; Strolger et al. 2010), or the star formation rates and stellar masses of the host galaxies (Sullivan et al. 2006; Totani et al. 2008; Maoz et al. 2011) it is possible to set constraints on the delay time and thereby also on the progenitor system.
Core collapse supernova explosions (CC SNe) are the end-points of the lives of massive stars, with masses between ~8 M⊙ and ~50 M⊙ (Nomoto 1984; Tsujimoto et al. 1997; Smartt 2009). Since massive stars are short-lived compared to the cosmic time-scales the CC SNe trace active star formation. By averaging the CC SN rate over cosmic volume the rest frame rate of star formation in that volume can be studied. In this way an independent measure of the star formation history at high redshift can be obtained (Dahlen et al. 2004; Cappellaro et al. 2005; Botticella et al. 2008; Bazin et al. 2009). More conventional methods of finding the cosmic star formation rates include measuring the rest-frame UV light from galaxies at a given redshift (e.g. Giavalisco et al. 2004; Bouwens et al. 2009), measuring the far-infrared (FIR) light to take star formation hidden by dust into account (e.g. Le Floc’h et al. 2005) and deriving the rates from Hα measurements (Shim et al. 2009; Hayes et al. 2010). The UV and Hα-based methods have a drawback, that is also present for the SNR method, in that a correction for dust extinction needs to be applied. Methods based on using the FIR light to estimate the added star formation from re-radiated UV light make it possible to correct the star formation history for dust extinction effects. Hopkins & Beacom (2006) presented a compilation of the star formation history from multiple sources for z ~ 0−6, taking the obscured star formation into account, and fitted an analytical function to the data.
The light from a supernova has to pass through its host galaxy before starting on the long trip to reach our telescopes. When travelling through the gas and dust inside its host the supernova light will be subject to varying degrees of extinction, depending on the dust content of the galaxy and the position of the SN with respect to the observer (e.g. a SN situated in an edge-on galaxy will suffer from higher extinction, on average, than one in a face-on galaxy). Hatano et al. (1998) and Riello & Patat (2005) present models of extinction for core collapse and thermonuclear SNe in normal spiral galaxies. These models are built by using Monte Carlo simulations of supernova positions within a galaxy with given morphology and dust content. By using the extinction models it is possible to estimate the effect on the observed supernova rates (Dahlen et al. 2004). It should be noted that this method is mainly applicable to normal galaxies with low to medium amounts of gas/dust, typical of galaxies in the local volume of the universe.
As the redshift increases, more and more of the star formation takes place inside dusty galaxies. Le Floc’h et al. (2005); Magnelli et al. (2009, 2011) find that the star formation from these infrared bright galaxies dominate the global star formation at redshift 0.7 and higher. In these galaxies the SN explosions can be completely obscured by the large amounts of dust within the nuclear regions. For low to moderate amounts of extinction this can be estimated and taken into account in the light curve analysis. But for host galaxies with high dust content (such as luminous and ultra-luminous infrared galaxies, LIRGs and ULIRGs) most of the SNe may not be detectable, even in the near-infrared (NIR) where the extinction is strongly reduced (e.g. Mattila & Meikle 2001). When calculating the rates, the number of missing SNe due to the change in average extinction in star forming galaxies with redshift needs to be compensated for (Mannucci et al. 2007). The derivation of the de-bias factors that are needed to correct the rates for this effect is further complicated by the recent discovery that the population of U/LIRGs at low redshift is quite different from the ones at high redshift (e.g. Daddi et al. 2010; Elbaz et al. 2011; Kartaltepe et al. 2012). Mattila et al. (2012) have recently estimated the fraction of SNe missed in such galaxies both locally and as a function of redshift making use of the most recent results on the nature of U/LIRGs at different redshifts.
The Stockholm VIMOS Supernova Survey (SVISS) is a multi-band (R + I) imaging survey aimed at detecting supernovae at redshift ~0.5 and derive thermonuclear and core collapse supernova rates. The supernova survey data were obtained over a six month period with VIMOS/VLT. Melinder et al. (2008) describe the supernova search method along with extensive testing of the image subtraction, supernova detection and photometry. The discovery and typing of 16 supernovae in one of the search fields is reported in Melinder et al. (2011). Here we present the supernova rates estimated from the survey data along with delay time distributions for the Ia SNe and star formation rates (SFR) calculated from the CC SNe rates.
The first part of the paper contains a description of the observations and supernova sample. In Sect. 3 we describe the method used to determine the supernova rates and in Sect. 4 the resulting supernova rates, delay time distribution and star formation rates are presented. In the final section of the paper, Sect. 5, we discuss the results and compare them to the work of other authors. The Vega magnitude system and a standard ΛCDM cosmology with { H0,ΩM,ΩΛ } = { 70,0.3,0.7 } have been used throughout the paper.
2. The data
2.1. Observations
The data used in this paper were obtained with the VIMOS instrument (Le Fèvre et al. 2003) mounted on the ESO Very Large Telescope (UT3) at several epochs during 2003–2006. The VIMOS instrument has four CCDs, each 2k × 2.4k pixels with a pixel scale of 0.205′′/pxl, covering a total area of roughly 4 × 56 sq. arcmin. The observations were obtained in the ELAIS-S1 field (La Franca et al. 2004), in five broad band filters (U, B, V, R and I) centred at α = 00h32m13s, δ = −44°36′27″ (J2000). The supernova search filters were R and I. Observations in these filters were divided into seven search epochs and 2 additional reference epochs (one before and one after). The search epochs were separated by roughly one month. The observational programme did not include any spectroscopy of the detected SNe and the analysis presented here is based on the R + I photometric data exclusively.
The individual frames in each epoch were reduced, including removal of fringes, registered to a common frame of reference and stacked. Each epoch image was photometrically calibrated using photometric standard stars observed during one of the nights and local standard stars selected in the field. Detailed measurements of the seeing in each of the frames were done by modelling the point spread function. For more details on the observations and data reduction, see Mencía Trinchant et al. (2012) and Melinder et al. (2011).
2.2. The supernova sample
The supernovae were detected by using a dedicated pipeline that was developed and thoroughly tested by our team. For a detailed description along with the results of the testing see Melinder et al. (2008). The pipeline includes the following steps, first the reference image and the search image are scaled to a common seeing using the ISIS 2.2 code (Alard 2000) and the reference image subtracted from the search image. Automatic source detection using SExtractor (Bertin & Arnouts 1996) together with a by-eye inspection is then done on the subtracted image to find variable objects. The final step is the aperture photometry, and point spread function (PSF) modelling based photometry, of the sources. Detailed simulations of the photometric accuracy are done to make sure that the error estimates are valid.
To avoid including spurious detections in the output catalogues we required that the supernova candidates were detected in both bands in two consecutive epochs. A detection is here defined as being brighter than the 3σ limiting magnitude in that epoch. Furthermore, we used the late control epoch to remove non-SNe (most likely active galactic nuclei, AGN) from the sample, since no SNe are expected to be visible ~1 year after explosion at the wavelengths and redshifts considered here. It should be noted that the decision to require detection in both the R and I filters has a significant impact on the number of detected SN Ia’s. These SNe are inherently redder than the CC SNe. At z ≳ 0.8 their light starts to become redshifted beyond the R filter and they are less likely to be detected in both of the filters used in this survey. This effect is taken into account in the rate calculations (see Sect. 3).
Supernovae in the SVISS.
Properties of the supernova photometric templates.
For the sample of supernovae considered in this paper we used the pipeline described above on the ELAIS-S1 R + I data and found a total of 16 supernovae, seven Ia SNe and nine CC SNe, ranging from z ~ 0.1 to z ~ 1.4 (see Table 1). The light curves and colour evolution of the SNe were used to classify them into either Ia-like or CC types (9 different subtypes, see Table 2). We then co-added the likelihoods for all subtypes belonging to the type Ia or CC SNe, respectively, to find the most likely type. This was done using a Bayesian model selection code, where priors were used for the redshift (host galaxy photometric redshift), absolute magnitude distribution, extinction and time after explosion. In Melinder et al. (2011) we describe in detail how the sample was obtained together with the typing code. In that paper we also investigated the misclassification errors when applying our code to the SN sample by using a Monte Carlo simulated sample of ~18 000 SNe and a local SN sample from SDSS-II containing 87 SNe. The resulting errors are used to estimate systematic errors for the SN rates (see Sect. 4.3).
Over the full redshift range where we have found SNe (z ≲ 1.4) we expect approximately 8% of the found Ia SNe, and 2% of the CC SNe, to be false positives. On the other hand, it then follows that only about 2% of the Ia SNe are mistyped compared to about 8% of the CC SNe. This systematic effect is thus not symmetric, overall we expect the Ia count to be slightly inflated and the CC count slightly deflated.
2.3. Supernova redshifts
The reference epoch R and I images were used together with the UBV deep images to obtain photometric redshifts for the supernova host galaxies. The redshifts are calculated using the GOODSZ code (Dahlen et al. 2010). This is a χ2 template fitting code that uses empirical spectral energy distributions from Coleman et al. (1980) and Kinney et al. (1996). The photometric redshifts were found to have an accuracy of σz = 0.07 where the redshift scatter Δz is given by Δz = σz(1 + z). Details on the photometric redshift technique will be presented in Mencía Trinchant et al. (2012). We require the galaxies to be detected in at least 3 filters to trust the resulting redshifts, something which is fulfilled for all of the 16 supernovae. The hosts were selected by choosing the closest galaxy in physical distance, calculating the distance from the photometric redshift and the angular distance. For two of the supernovae (SN309 and SN357) this means that the closest galaxy in terms of angular distance is not the host galaxy. These galaxies are at much higher redshifts (z ≳ 3), thus it is extremely unlikely we would be able to detect a supernova in them. More details on the host galaxy identification is presented in Melinder et al. (2011).
The photometric redshifts, together with the 68% confidence limits (as estimated by the χ2 fitting), were used to construct a Bayesian prior for the supernova typing. The typing code then outputs a most likely redshift for the best fitting supernova type for each supernova (details are given in Melinder et al. 2011). This is the redshift estimate used for the supernovae in the rate calculations. Figure 1 shows the redshift accuracy for the Monte Carlo simulated supernova sample described in Sect. 2.2. When typing the simulated supernovae we assume that the redshift errors for the host galaxies are equal to the redshift scatter, Δz. The resulting redshift accuracy for the SNe with host galaxy redshifts is given by σz = 0.07 with an outlier fraction (defined as having |zsim − zfit| > 0.15) of 3% over the full range of redshifts. The resulting redshift accuracy from the “photometric redshift + SN typing” scheme is thus unchanged from the pure photometric redshift scheme.
For reference, we also show the accuracy for SNe typed with a flat redshift prior (i.e. sources without any photometric redshift information). This is worse, with σz = 0.11 and an outlier fraction of 4%. For both populations it should be noted that the majority of the outliers comes from the zsim = 0.2−0.4 region and is due to mistyping of the supernovae.
The typing was also rerun using a flat redshift prior for all of the discovered SNe. The fitted redshifts from this run were all within the 68% confidence limit of the host photometric redshifts and none of the SNe changed main type. Based on this the chosen hosts are thus likely to be the correct ones, although it is certainly possible that some hosts have been misidentified. In any case, neither the typing nor redshifts are appreciably affected by the possible host misidentification.
3. Supernova rate determination
 |
Fig. 1 The redshift accuracy for simulated supernovae with (upper panel) and without (lower panel) a host galaxy photometric redshift. The ~2000 SNe of all different subtypes used to make this figure are a sub-sample of the full sample of simulated light curves. The redshift on the x axis (zsim) is the initial adopted redshift of the supernovae. The dotted lines indicate the |zfit − zsim|/(1 + zsim) > 0.15 limits. |
The supernova rates were determined using a Monte Carlo method (Dahlen et al. 2004). Using a set of supernova templates (see Table 2) we simulate a number of supernova light curves of different types and at different redshifts with time of explosion set within our detection window. The requirement that each SN has to be detected in two consecutive epochs means that this window stretches from approximately 5 months before until five months after the start of monitoring. The main input parameters are the intrinsic supernova rates (Ia and CC) for a given redshift bin and volume-limited fractions of the different types. The template light curves are calculated from absolute magnitude light curves (mainly from Richardson et al. 2002, 2006; Dahlen et al. 2004) and a set of spectra from Nugent (2007). For more information on how the template light curves are built see Melinder et al. (2011) and references therein.
The volumetric fractions for the Ia subtypes are adapted from Li et al. (2011b), treating their Ia-HV sub-category as Ia-normal SNe. The Ia-faint category is used in the typing of supernovae to be able to better characterise normal Ia supernovae with a somewhat lower value of stretch. The fraction of low-stretch Ia SNe is estimated from the distribution of stretch value in the Supernova Legacy Survey (Sullivan et al. 2006) Ia sample. The core collapse fractions are based on a compilation of supernovae from Smartt et al. (2009) and Li et al. (2011b), treating IIb SNe as Ibc-normal supernovae, since, with our time sampling of the light curves, these subtypes will look very similar.
Each supernova is also given a host galaxy extinction. For type Ia SNe we use the parametrisation of the Riello & Patat (2005) simulations presented in Neill et al. (2006), while for core collapse SNe we use Monte Carlo simulations based on the models of Riello & Patat (2005). The effects of spiral arms and the bulge component are considered negligible in the core collapse SN simulations and are not included. The extinction is scaled with the V-band optical depth through a simulated face-on galaxy at zero radius with τV(0) = 2.5, which provides a reasonable match to the observed host galaxy extinction distribution for CC SNe within 12 Mpc (Mattila et al. 2012). To calculate the wavelength dependence of the extinction, we use a Cardelli extinction law (Cardelli et al. 1989) with RV = 3.1 for Type Ia SNe and a Calzetti attenuation law (Calzetti et al. 2000) with RV = 4.05 for core collapse SNe. In Sect. 4.3, we investigate how the choice of extinction models and extinction laws affects the results. It is important to note that this extinction is the result of simulations of normal spiral/elliptical galaxies. In this case the modelled mean extinction only goes above AV ~ 1 mag. for galaxies with inclination higher than 60 degrees. According to the simulations, no supernovae in these normal galaxies exhibit very high extinctions. But observations of local supernovae show that this is untrue, e.g. SN 2002hh (Pozzo et al. 2006) and SN 2009hd (Elias-Rosa et al. 2011) both have host galaxy extinctions of AV ~ 4 mag. The extinction adopted for our simulated supernova light curves thus only include the effect of small to moderate levels of extinction. In Sect. 3.2 we describe how the output rates are de-biased to account for the missing population of highly extinguished supernovae in normal galaxies as well as in U/LIRGs.
The light curves are then fed through the same detection procedure as the real supernova light curves (see Sect. 2.2). It should be noted that even with a quite conservative photometric limit (3σ in four data points) there are issues with completeness. The detection efficiency of the survey does affect the observed rates since it starts to drop below one before the 3σ-limit is reached. The detection efficiencies described below are thus used to give a probability that a supernova is detected in a certain epoch and filter, and are included in the Monte Carlo simulations. We have used the detection efficiencies derived for hosts of intermediate brightness for all supernovae. The effect of this choice on the rates is small (see Sect. 4.3).
The output number of detectable SNe from the simulations is then compared to the observed number in the chosen redshift bin. Since the redshifts for the SNe have quite high uncertainties (being based on photometric redshifts) we distribute the SNe in the bins according to a Gaussian distribution with the redshift uncertainty Δz = 0.07(1 + z). We denote the number of redistributed SNe in each bin Nredist. The simulations are then iterated until the output number matches Nredist. At that point the input intrinsic SN rate that produces the correct number of observed SNe is chosen as the true supernova rate.
3.1. Detection efficiencies
 |
Fig. 2 An example of the detection efficiency for a given epoch for different host galaxy brightness. The efficiencies from simulations of supernovae in the field are given by the points while the lines are the S-curve fits to the efficiencies as described in the text. Errors for the measured efficiencies are binomial. Note that a total of 30 (one for each of five epochs × , two filters × , and three host galaxy types) S-curve fits have been used to estimate the detection efficiencies of the full survey. This figure is available in colour in the electronic version of the article. |
The detection efficiency for each epoch and filter was determined by simulating supernovae at variable brightness in the actual search images and then running the standard detection pipeline on the simulated frames. The procedures used are described in Melinder et al. (2008). We placed supernovae in different environments, i.e. with different host galaxy brightness, to study the effect of background light on the efficiencies. The detection efficiencies are notably worse when the SNe are situated in bright galaxies (defined as having mI < 22). In Fig. 2 a sample of the detection efficiency testing is presented, showing the efficiencies for the three different host galaxy brightness modes. It should be noted that the 50% efficiency limits roughly corresponds to the 3σ rejection limits.
To use the efficiency curves in the Monte Carlo simulations, and to smooth out possible
outliers in the measured efficiency, we parametrise the efficiencies using a S-curve
parametrisation (as previously used by, e.g. Strolger
et al. 2004) given by: 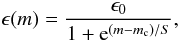 (1)where
ϵ(m) is the fitted detection efficiency and
m the magnitude. ϵ0 is the maximum
efficiency (which is very close to one for most of our fits),
mc the magnitude when the efficiency has dropped to 50%, and
S a parameter that determines how fast the drop occurs. The
best-fitting parameters for each epoch, filter and host galaxy brightness are found with a
simple χ2 optimisation algorithm and are shown as lines in
Fig. 2.
(1)where
ϵ(m) is the fitted detection efficiency and
m the magnitude. ϵ0 is the maximum
efficiency (which is very close to one for most of our fits),
mc the magnitude when the efficiency has dropped to 50%, and
S a parameter that determines how fast the drop occurs. The
best-fitting parameters for each epoch, filter and host galaxy brightness are found with a
simple χ2 optimisation algorithm and are shown as lines in
Fig. 2.
3.2. De-biasing the rates for extreme host galaxy extinction
The star formation in the local universe takes place mostly in galaxies with low amounts of dust and thus the supernovae discovered in the local universe often have low extinctions. The use of core collapse supernovae as tracers of recent star formation is thus feasible at low redshifts (e.g. Botticella et al. 2012). However, as we go to higher redshifts the bulk of the star formation takes place in dusty galaxies with high infrared luminosities (LIRGs and ULIRGs). A number of studies (e.g. Le Floc’h et al. 2005; Magnelli et al. 2009, 2011) have found the fraction of star formation taking place in LIRGs and ULIRGs to increase rapidly towards z ~ 1, such that approximately half of the star formation at z ~ 1 is taking place in these galaxies. Furthermore, highly extinguished supernovae are present also in normal spiral galaxies (e.g. Mattila et al. 2012). From now on we denote the effect these two factors have on the supernova rates obscuration, to distinguish it from the standard host galaxy extinction of light from SNe in normal spiral and elliptical galaxies.
Mannucci et al. (2007) compiled the star formation densities for different redshifts derived from UV and infrared observations in a number of studies. They used these results together with their own estimates on how many SNe are lost due to obscuration by dust in local starburst galaxies, LIRGs and ULIRGs to derive a correction for supernova rates at high redshifts. The estimates were based on SN searches conducted in such galaxies by that time (Maiolino et al. 2002; Mannucci et al. 2003), which had found few SNe. Another caveat with the previous studies of this effect is that it was, at that time, almost completely unknown what kind of galaxies the high redshift LIRGs and ULIRGs were. They were selected based on high luminosities in the mid- and far-infrared wavelengths, and the assumption made in Mannucci et al. (2007) was that they were the same kind of starbursting, irregular and compactly star forming galaxies as in the local universe. At the time this was not an unreasonable assumption, but later developments (Spitzer and Herschel observations in particular) have shown that the high redshift U/LIRG population is dominated by disk galaxies with more constant, although high, star formation rates (Daddi et al. 2010; Elbaz et al. 2011; Kartaltepe et al. 2012), the so called main sequence (MS) galaxies. These galaxies have a higher content of gas and dust than local disk galaxies, but they do not exhibit the kind of compact star formation found in local U/LIRGs. A smaller fraction of the high redshift U/LIRGs are more similar to the local counterparts (Elbaz et al. 2011; Kartaltepe et al. 2012).
3.2.1. De-bias factors for the core collapse supernovae
For SNe in normal galaxies we have already taken into account the effect of low to
moderate amounts of extinction, but, as previously mentioned, there are supernovae with
extreme extinction also in normal disk galaxies. Mattila
et al. (2012) find that 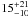 %
of the supernovae in these galaxies have extinctions significantly higher than predicted
by simulations following the recipe in Riello &
Patat (2005). These are SNe that would likely be missed in dusty regions of the
normal galaxies by magnitude limited surveys. In the local universe almost all U/LIRGs
are also characterized as starburst galaxies (e.g. Pereira-Santaella et al. 2010). In these galaxies less than ~20% of the
CC SNe can be detected in optical searches and in some extreme cases, such as Arp 220,
the entire SN population is obscured by the large amounts of dust and can only be
detected in radio (e.g. Parra et al. 2007). Mattila et al. (2012) investigated the SN population
of the nearby LIRG Arp 299 and found that
%
of the supernovae in these galaxies have extinctions significantly higher than predicted
by simulations following the recipe in Riello &
Patat (2005). These are SNe that would likely be missed in dusty regions of the
normal galaxies by magnitude limited surveys. In the local universe almost all U/LIRGs
are also characterized as starburst galaxies (e.g. Pereira-Santaella et al. 2010). In these galaxies less than ~20% of the
CC SNe can be detected in optical searches and in some extreme cases, such as Arp 220,
the entire SN population is obscured by the large amounts of dust and can only be
detected in radio (e.g. Parra et al. 2007). Mattila et al. (2012) investigated the SN population
of the nearby LIRG Arp 299 and found that 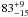 %
of SNe exploding in this galaxy will remain undetected by optical SN searches. They then
assume that Arp 299 is representative of compact starbursting U/LIRGs and adopt this
figure as the missing fraction of supernovae in these galaxies. The missing fraction of
SNe in high redshift U/LIRGs is highly uncertain. For the main sequence (i.e.
non-starburst) galaxies little is known about the extinction, although they have been
found to be disk-like and not as compact as their local counterparts (Kartaltepe et al. 2012). Mattila et al. (2012) assume a missing fraction of
%
of SNe exploding in this galaxy will remain undetected by optical SN searches. They then
assume that Arp 299 is representative of compact starbursting U/LIRGs and adopt this
figure as the missing fraction of supernovae in these galaxies. The missing fraction of
SNe in high redshift U/LIRGs is highly uncertain. For the main sequence (i.e.
non-starburst) galaxies little is known about the extinction, although they have been
found to be disk-like and not as compact as their local counterparts (Kartaltepe et al. 2012). Mattila et al. (2012) assume a missing fraction of
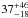 %
for these galaxies (see Sect. 4.3 for a discussion
on the systematic errors resulting from this decision).
%
for these galaxies (see Sect. 4.3 for a discussion
on the systematic errors resulting from this decision).
Mattila et al. (2012) calculate the de-bias factor as a function of redshift by using the relative contributions to the cosmic star formation density of normal galaxies (defined as galaxies with LIR < 1011 L⊙), LIRGs, and ULIRGs from Magnelli et al. (2011) and the relative contributions of the compact and main sequence channels from Kartaltepe et al. (2012). Furthermore, they assume that Arp 299 only represents the U/LIRGs that are starbursting, i.e. lie more than three times above the specific star formation rate (sSFR) MS locus at high redshift.
We adopt the de-biasing factors for the CC SN rates in the two redshift bins under consideration from Mattila et al. (2012). The final de-bias factors to correct the CC SN rates for obscuration in our two redshift bins is 1.34 at 0.1 < z < 0.5 and 1.52 at 0.5 ≤ z < 0.9. In Sect. 4.3 we give the errors on these factors and discuss the systematic errors on the rates resulting from the calculation.
3.2.2. De-bias factors for the type Ia supernovae
The previous section dealt with de-biasing the CC SN rate, but it should be noted that also Ia supernovae may be missed in SN surveys due to high extinction in star forming galaxies. Multiple studies have shown that the rate of Ia SNe is correlated with the current star formation rate in the host galaxies (Mannucci et al. 2006; Sullivan et al. 2006). This indicates that there is a so called prompt channel of thermonuclear explosion (Scannapieco & Bildsten 2005), or that the delay time distribution extends to time intervals as short as ~420 Myr (Maoz et al. 2011).
No Ia SN has ever been detected in the compact star forming cores of starburst galaxies. But, given that the extinction is extreme in such environments and that Ia SNe are faint in radio, this may be the result of selection effects. However, the delay time distribution of Ia SNe has so far only been determined down to a time difference of 420 Myr (Maoz et al. 2011), while the starburst phase in U/LIRG starbursts normally has a duration of ~100 Myr (e.g. Marcillac et al. 2006). After this time the starburst normally enters the post-starburst phase where the lack of gas makes the star formation stop (e.g. Goto 2007). Most of the dense dust and gas shroud in a starburst core will likely have been disrupted and blown off in the post-starburst phase (e.g. Tremonti et al. 2007), and any Ia SNe exploding after a delay time of ≳ 100 Myr will thus not experience higher extinction than a supernova in a normal star forming galaxy.
Similar to what has been found for CC SNe, also a small fraction of the Ia SNe will be subject of extreme extinction in normal star forming disk galaxies. This fraction will depend on the delay time distribution and is likely significantly lower than the fractions found for CC SNe. At higher redshifts a fraction of type Ia SNe will explode in the main sequence channel of the U/LIRG population. These SNe will, as the CC SNe, suffer from higher extinction than the normal extinction models predict, but no estimates on this effect can be found in the literature and a detailed study is outside the scope of this paper.
The fraction of Ia SNe missed at high redshift has been estimated by Mannucci et al. (2007), but suffers from the same problems as the core collapse estimate in addition to systematic errors from the assumptions on delay time distribution and starburst lifetime (few details on the calculations are given in that paper) as described above. Because of the added uncertainties inherent in estimating a missing fraction for type Ia SNe we do not try to compute any missing fraction for the Ia SNe. Furthermore, it should be noted that any assumptions on the delay time distribution may introduce a circular argument. To limit the circularity, and to avoid using a de-bias factor for which the systematic error is unknown, we assume that no Ia SNe will be missed because of obscuration (but note that we do apply a correction for the normal host galaxy extinction). In Sect. 4.3 we estimate the systematic error resulting from this assumption.
4. Results
 |
Fig. 3 Core collapse supernova rates determined from the SVISS SNe (black stars). Grey stars are displaced by + 0.01 in z and show the SVISS rates without extinction correction. Also shown is a collection of measured rates from other authors. We plot star formation histories from two different sources, scaled to supernova rates through the use of Eq. (2). Error bars are statistical with total errors (statistical and systematic added in quadrature) as a transparent/faded extra error bar for all surveys. Redshift bin sizes are not shown, but are given in Table 3. The rate from Cappellaro et al. (1999) has been rescaled from SNu to a volumetric rate by assuming a local B-band luminosity density 2.0 × 108 h70 L⊙ Mpc-3 at redshift ~0. The local CCSN rates from Botticella et al. (2012) and Mattila et al. (2012) have been measured in small volumes and are likely dominated by inhomogeneity. The star formation rate in the local volume is higher than the average over an extended volume and can therefore cause the SNR to be higher than expected. |
 |
Fig. 4 Type Ia supernova rates determined from the SVISS SNe (black star). The grey star is displaced by + 0.01 in z and show the rate without extinction correction. Also shown is a collection of published rates from the literature. We plot SN Ia rates resulting from assumptions on the delay time distribution combined with the star formation history. Error bars are statistical with total errors (statistical and systematic added in quadrature) as a transparent/faded extra error bar for all surveys. Redshift bin sizes are not shown, but are given in Table 3. The rate from Cappellaro et al. (1999) has been rescaled from SNu to a volumetric rate by assuming a local B-band luminosity density 2.0 × 108 h70 L⊙ Mpc-3 at redshift ~0. |
4.1. Core collapse supernova rates
SVISS supernova rates.
The core collapse supernova rate in two redshift bins (0.1–0.5, 0.5–0.9) is shown in Fig. 3 and in Table 3. The two bins do not include all of the SNe in the sample. By binning differently the total number can be increased, but this comes at the price of higher statistical uncertainty (with more bins) and higher systematic uncertainties (with wider bins). Both the rates corrected for extinction/obscuration and the raw rates are shown in the table but the figure show the corrected values. The two sets of error bars in Fig. 3 show the statistical errors, and statistical and systematic errors added in quadrature, unless otherwise noted.
In Table 4 and Fig. 3 we show a comparison of our rates with rates reported by other authors. At low redshift we plot the rate estimates of LOSS (Li et al. 2011a), which is the largest SN survey to date in the local volume with a total number of core collapse SNe of 440. We also plot the low redshift rates determined by Cappellaro et al. (1999), Botticella et al. (2012), and Mattila et al. (2012). At slightly higher redshifts we plot the results from Botticella et al. (2008), which also includes the data presented in Cappellaro et al. (2005). The second survey with rates based on a large number of CC SNe (117 SNe) is the Supernova Legacy Survey (SNLS, Bazin et al. 2009) which provides a data point with small error at z = 0.3. None of these surveys include de-biasing for obscuration.
At higher redshifts we plot the rates from the GOODs determined by Dahlen et al. (2004), which includes the effect of extinction in normal spiral galaxies, but not de-biasing for obscuration and the recent measurements from the Subaru Deep Field (Graur et al. 2011), which includes de-biasing for obscuration and extinction in normal galaxies. For comparison, the figure also shows estimates of the star formation history from two different sources, Strolger et al. (2004) and Hopkins & Beacom (2006), scaled to supernova rates (see Sect. 4.4). Both are corrected for extinction.
The rate at z = 0.39 is consistent with the rates reported by other authors, even though different approaches to extinction correction is used. Our CC rate at high redshift agrees well with the observations of Dahlen et al. (2004) and Graur et al. (2011). For a discussion on how our supernova rate measurements compares to the star formation history, see Sect. 5.
4.2. Ia supernova rates
The Ia supernova rate in one redshift bin (0.3–0.8) is shown in Fig. 4 and in Table 3. The rates in the table are given with and without extinction correction (no de-biasing to account for obscuration have been done on the Ia rate). The choice of using one bin for the Ia SNe is motivated by the low number of supernovae found at both low (z < 0.3) and high (z > 0.8) redshifts. By using the redshift bin given above we minimise the statistical errors. It should also be noted that the SNe outside the bin have not been excluded from the rate calculation. They contribute to the Nredist of the bin, because they have redshift probability distributions that stretches into the redshift interval.
In Table 4 and Fig. 4 we show a comparison of our rate with rates reported by other authors. At low z we show the Ia rates from the LOSS (Li et al. 2011a) and Cappellaro et al. (1999). At slightly higher z we compare with the rates calculated from the SDSS supernova search (Dilday et al. 2010b) and with the results from the STRESS (Botticella et al. 2008). Rodney & Tonry (2010) presented revised Ia rates from the IfA Deep Survey out to z = 1.05 using new techniques, lower than those previously reported. The SNLS measured the Ia rate at z = 0.47 using a large sample of supernovae, at similar redshift Pain et al. (2002) presented some of the first rates determined from cosmological survey data. At higher redshifts Dahlen et al. (2008) determined Ia rates from the GOODS (extending their sample from 2004). Barbary et al. (2012b) has measured the volumetric SN Ia rate in the background galaxies of the Hubble Space Telescope Cluster Supernova Survey. Graur et al. (2011) reported the findings of the supernova search in the Subaru Deep Field, their rate measurements are the highest redshift measurements available and reach z ~ 1.7.
Systematic errors.
Our rate measurement is higher than the results from many other surveys at this redshift, but marginally consistent with all other measurements when taking statistical and systematic errors into account. While the uncertainty of our rate measurement is too high and the redshift coverage too small to allow for detailed fitting of different DTD models, we can compare our rates to models introduced by other authors (Sullivan et al. 2006; Neill et al. 2006; Strolger et al. 2010; Graur et al. 2011) together with their chosen star formation history (see Sect. 4.5, for details).
4.3. Analysis of errors for the supernova rates
The statistical errors are calculated using the prescription of Gehrels (1986). The redshift bins have been chosen to provide a reasonable number of sources in each bin to get similar statistical errors in each bin.
We now proceed to study the systematic errors of our rate estimates. Given that the total number of SNe is quite low, the statistical errors are high. One of the goals of this study is thus to find out whether any of the systematic effects can introduce errors larger than these. Calculating the mean statistical relative error (mean of the upper and lower limit differences) for the two types and all redshift bins we arrive at the following: 74% for CC at low z; 67% for CC at high z; and 56% for the Ia bin. These can be compared to the relative systematic errors calculated below. The second goal of the study is to make an extensive list of systematic effects that can affect supernova rate measurements and to try and estimate them. These effects will be very similar for all supernova rate measurements of similar type and our compilation can thus be of use in future surveys which may be limited by systematic rather than statistical errors. A thorough study of the systematic effects is also of great help when trying to find better observational strategies in future surveys.
A compilation of the systematic errors can be found in Table 5.
Misclassification errors.
The systematic errors due to misclassification in our sample are given in Melinder et al. (2011) and are on the order of 5–10 %. However, these estimates are really only valid when the number of detected SNe is large enough. For the small number statistic estimates presented here the systematic errors have to be estimated in a different way. The expected numbers of misclassified SNe in each type and redshift bin is below one in all cases. To get a conservative estimate of the misclassification systematic error we thus vary the observed number of SNe by one (positive and negative) and recalculate the rates. This test gives an error of approximately 20%, but is dependent on the actual number of sources in the given bin (a low source count gives a higher error). For bins with more than two SNe the error is smaller than the statistical errors.
The systematic misclassification errors are overestimated when computed with this method, on average one SNe in our sample will have been misclassified, not one per bin and type as the estimate indicates. But it is impossible to say which bin and type that is affected by misclassification, hence we give this error estimate.
Redshift.
The redshifts of the supernovae have uncertainties on the order of 0.1 when using the host photometric redshifts as a prior for the typing. This leads to a redistribution in redshift which affects the rates. To study this effect we redistribute the simulated SNe according to a Gaussian distribution assuming σ = 0.07(1 + z) and recalculate the rates. This test is repeated 10 000 times to find the spread in the rates. The systematic error varies between ~15 to ~30% for the different types and redshift bins, lower than the statistical errors in all cases.
Detection efficiencies.
We determine the systematic errors from the detection efficiency assumptions using the faint and bright host galaxy detection efficiency estimates. The binomial errors of the efficiencies are smaller than the difference between the results for the different host types in almost all cases. The effect on the rates is on the order of ± 2%, significantly lower than the statistical errors.
Photometric errors.
The SVISS photometric zero point calibration is accurate to within ~5%. Since we apply an absolute 3σ detection limit on our sample (see Sect. 2.2) the estimated rates will be affected by a slight shift in the photometric zero points. This effect will in reality be random over the two filters and seven epochs, to get a conservative estimate we vary the detection limits by 0.1 mag. The resulting rates vary by ~5%.
Template choices.
Our selection of subtype light curve templates and their assumed fractions influence the rates as well. The choices and assumptions we have made are based on observational results (Richardson et al. 2002, 2006; Li et al. 2011b). The fractions are subject to statistical uncertainties as well as systematic uncertainties (e.g., evolution with redshift, selective obscuration). There is also the possibility that very faint supernovae are under-represented in magnitude-limited SN surveys (Horiuchi et al. 2011).
For the CC SNe we study the effect of introducing an additional light curve template, a IIP template with a peak MB of −14.39 (as for the faint core collapse SN 1987A) with fraction that changes the percentage of CC SNe with MB > −15 from 7% to 30%. The effect of this change on the rates is quite large, it makes the rates go up by approximately 30%. This is smaller than the statistical errors but could help to explain any possible mismatch with the star formation history (as identified by Horiuchi et al. 2011). Varying the fractions randomly have a very small effect on the rates since the changes tend to cancel out.
For the Ia SNe we have made tests with different combinations of using or not using the peculiar (91T and 91bg-like) and non-standard (Ia-faint) templates. We get the largest positive change in the rates when putting the fraction of 91T SNe to zero (treating them as normal SN Ia’s), on the order of 1–2%. The largest negative change is found when setting the fraction of faint Ia supernovae (91bg and the Ia–faint subtypes) to zero, treating them as Ia-normal SNe, which results in a change of 10–15% in the rates. These errors should be considered to be the extreme limits, since there is plenty of evidence that these faint Ia SNe do exist.
Peak magnitudes.
As described above the choice of template distribution also affects the distribution of peak magnitudes for the simulated SNe. However, the average peak magnitudes used in this work have associated uncertainties (note that this is not the same as the scatter).
For the CC SNe the template peak magnitudes have uncertainties given by Richardson et al. (2002) and Richardson et al. (2006). As conservative estimate we allow the peak magnitudes of CC SNe to vary by the 1σ errors given in these papers and recompute the rates. The resulting rates change by approximately 10%, which is smaller than the statistical errors.
For the Ia SNe the peak magnitudes are much better constrained (due to their use in precision cosmology). Assuming an uncertainty of 0.05 mag for the Ia subtype and 0.1 for the 91bg/91T subtypes we calculate the impact on the Ia rates. The effect is small, on the order of 3%, much smaller than the statistical errors.
Host galaxy extinction.
The effect of host galaxy extinctions are based on models by Riello & Patat (2005) for type Ia and core collapse SNe. For the type Ia SNe these models were used as given, while a different scaling was used for the CC SNe (see Sect. 3). Using instead a positive Gaussian distribution of E(B − V) with σE(B − V) = 0.2 mag as in Neill et al. (2006) for Type Ia only changes the rate by ~2%. For core collapse SNe, we have examined the effect of applying an extinction model following Riello & Patat (2005) as given. This has marginal effect on the rate in the low redshift bin (1%) and may affect the high redshift bin by 10%.
Using the estimates from Hatano et al. (1998) change the resulting rates by a very small amount (<1%). We also study the effect of using different extinction laws for the extinction. For the CC SNe we use a Cardelli/RV = 3.1 law instead of the Calzetti law and for the Ia we use a steeper Cardelli law with RV = 2.1 (as advocated by Goobar 2008). The impact on the rates is small, on the order of 1%.
Dust obscuration in the host galaxy.
Mattila et al. (2012) estimate lower and upper limits on the de-bias factors for CC SNe from different assumptions on the amount of obscuration in the SN host galaxies. The systematic errors on the CC SN rate resulting from these limits are: −10%/ + 28% at z = 0.39, and −10%/ + 33% at z = 0.73. The upper and lower limits on the de-bias factors corresponds to the upper and lower limits on the rates.
For the Ia SNe we assumed a nominal de-bias factor of 1.0 (i.e. a missing fraction of zero). As an upper limit to this value we have chosen to use a de-bias factor calculated from the formula given in Mannucci et al. (2007) for the redshift in question. The resulting systematic error on the Ia rates is then +8% at z = 0.62.
AGN contamination.
We used a control epoch with observations obtained one year after our search period had ended to check whether any of our supernova candidates showed variability over this longer period. Except for the possibility of very rare peculiar SNe none of the SN subtypes should be detected one year later. The list of variable sources originally contained 31 entries, about ten of which showed variability over a long time-scale and were excluded from the final list of SNe. This routine is enough to limit the amount of AGN contamination to very low levels. We do not give this error in Table 5 since we estimate it to be smaller than all other systematic effects.
Cosmic variance.
The size of the SVISS field is fairly small (4 × 56 sq. arcmin). Cosmic variance is therefore a possible uncertainty in the rate estimates. We have estimated the cosmic variance by using the work of Trenti & Stiavelli (2008)1, and assuming that the variance of SNe follow that of the overall galaxy population. The relative cosmic variance for the type Ia SNe redshift bin is then 9%. For the CC SNe low redshift bin we estimate a relative variance of 12%, and 10% for the high redshift bin.
In Table 5 we also give the sum of all the systematic errors (added in quadrature). These are also the systematic error estimates given in Table 3. The co-added systematic errors are all smaller than the statistical errors. The major contributions to the systematic errors comes from misclassification, template choices redshift uncertainties, and the obscuration correction.
4.4. Comparing the CC supernova rate to the cosmic star formation history
The core collapse supernova rate can be compared to the cosmic star formation history
(SFH), since the time-scale for CC progenitors to explode is much shorter than the cosmic
time-scale. The supernova rate is derived from the star formation history by assuming an
initial mass function (IMF, denoted by ξ below) and the mass range of the
SN progenitors (Ml and Mu for the
lower and upper mass limits, respectively). The volumetric rate of CC SNe,
RCC in units of yr-1 Mpc-3 is then:
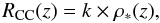 (2)where
ρ∗(z) is the star formation history in
units of M⊙ yr-1 Mpc-3.
RCC is a volumetric rate, and thus scales as
h3, this needs to be addressed when comparing to star
formation histories which may have a different scaling. The constant k is
the percentage of stars that explode as SNe per unit mass and is given by:
(2)where
ρ∗(z) is the star formation history in
units of M⊙ yr-1 Mpc-3.
RCC is a volumetric rate, and thus scales as
h3, this needs to be addressed when comparing to star
formation histories which may have a different scaling. The constant k is
the percentage of stars that explode as SNe per unit mass and is given by:
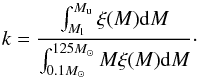 (3)For this work we
choose to use a Salpeter IMF (Salpeter 1955) with
progenitor masses between 8 M⊙ and
50 M⊙. The constant k is then equal
to 0.0070.
(3)For this work we
choose to use a Salpeter IMF (Salpeter 1955) with
progenitor masses between 8 M⊙ and
50 M⊙. The constant k is then equal
to 0.0070.
The choice to use a Salpeter IMF is based on that most SFH measurements and other supernova rate measurements are using this IMF. Recently a number of authors have argued that the Salpeter IMF is not consistent with recent observations (see, e.g. Hopkins & Beacom 2006), and claim that an IMF with a flatter shape is better. The choice to use different IMFs introduce a systematic uncertainty to the comparison. However, the IMF dependence is partly cancelled out by the dependence on IMF of the star formation history (where the IMF is used to normalise the star formation measurements). To investigate this we compute k for the flattest IMF given in Hopkins & Beacom (2006) which is a modified Salpeter form from Baldry & Glazebrook (2003) with a high mass slope of −1.15 (compared to −1.35 for the normal Salpeter IMF). While the k factor changes to 0.0141 (a factor of ~2) this is countered by the change of the SFH normalisation by a factor of 0.5, given by Hopkins & Beacom (2006). The total change of the SNR-SFR comparison is on the order of 2%, significantly less than the statistical errors. Incidentally, this also tells us that there is little hope in trying to use the comparisons between SNR and star formation rates to constrain a possible universal IMF unless much larger supernova samples can be obtained.
The upper limit for the progenitor mass comes from Tsujimoto et al. (1997) and is essentially the limit at which massive stars will produce black holes instead of neutron stars with an associated supernova explosion. Varying the upper limit between Mu = [30,125] M⊙ has a small effect on the SNR-SFR comparison, less than 10%, although this could be slightly higher with a flatter IMF. The lower limit of 8 M⊙ is grounded on observations of supernova progenitors (Smartt et al. 2009). The choice of lower limit strongly affects the rate scaling but is luckily well constrained by these observations, varying the lower limit between their 68% confidence limits (7–9.5 M⊙) changes k by ± 20%, also this lower than the statistical errors for our supernova rates.
4.4.1. Star formation history parametrisations
We use star formation histories, ρ∗(z),
from two different sources as input for Eq. (2). Hopkins & Beacom (2006)
compile star formation measurements from many sources and correct them for dust
extinction based on the work done by Le Floc’h et al.
(2005). The observations are then fit by the simple analytical parametrisation
introduced by Cole et al. (2001): 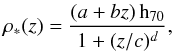 (4)where
a, b, c and d are
fitting parameters and h70 is the Hubble constant to account for changes to
the assumed cosmology. The best fit from Hopkins
& Beacom (2006) gives parameter values: a = 0.0170,
b = 0.13, c = 3.3 and d = 5.3. They
give a conservative error estimate by plotting the confidence regions of the fit, at
z ~ 1 the uncertainty is on the order of 30%.
(4)where
a, b, c and d are
fitting parameters and h70 is the Hubble constant to account for changes to
the assumed cosmology. The best fit from Hopkins
& Beacom (2006) gives parameter values: a = 0.0170,
b = 0.13, c = 3.3 and d = 5.3. They
give a conservative error estimate by plotting the confidence regions of the fit, at
z ~ 1 the uncertainty is on the order of 30%.
Strolger et al. (2004) fit the data compilation
of Giavalisco et al. (2004) by using a
parametrisation of the form: 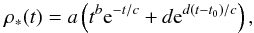 (5)where
a, b, c and d are
parameters, t is the age of the universe and
t0 the age of the universe at z = 0
(13.47 Gyr with our chosen cosmology). The best fit parameter values are:
a = 0.182, b = 1.26, c = 1.865 and
d = 0.071. To compare this with our results we convert it
to ρ∗(z).
(5)where
a, b, c and d are
parameters, t is the age of the universe and
t0 the age of the universe at z = 0
(13.47 Gyr with our chosen cosmology). The best fit parameter values are:
a = 0.182, b = 1.26, c = 1.865 and
d = 0.071. To compare this with our results we convert it
to ρ∗(z).
4.5. Delay time distributions for Ia supernovae
The delay time distribution (DTD) for Ia supernovae is the subject of controversy in
current research. By convolving an assumed DTD with the underlying star formation history
the Ia rate can be calculated. This can then be compared with the observed rates to put
constraints on the DTDs. The Ia rate can thus be written (Strolger et al. 2004): 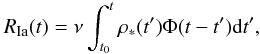 (6)where
ν is the number of SNe formed per unit stellar mass,
ρ∗(t) the star formation history and
Φ(τ) the delay time distribution which represents the percentage of
supernovae that go off at time τ after a single burst of star formation.
Also, t0 is the time at which stars start to form in the
universe, we assume this happens at z = 10; corresponding to a time of
0.45 Gyr after the big bang (with our chosen cosmology). The integral can easily be
converted to redshift space to yield RIa(z)
by performing a variable substitution.
(6)where
ν is the number of SNe formed per unit stellar mass,
ρ∗(t) the star formation history and
Φ(τ) the delay time distribution which represents the percentage of
supernovae that go off at time τ after a single burst of star formation.
Also, t0 is the time at which stars start to form in the
universe, we assume this happens at z = 10; corresponding to a time of
0.45 Gyr after the big bang (with our chosen cosmology). The integral can easily be
converted to redshift space to yield RIa(z)
by performing a variable substitution.
As noted above, the uncertainties in our rate estimates make it quite fruitless to try and fit different DTDs to our data. Instead we choose to compare our rates to the best-fitting DTDs from the literature. In Fig. 4 we show four different choices of DTD. The simplest one is just a rescaling of the star formation history assuming that one Ia SN explode per 1000 M⊙ of stellar mass formed (Neill et al. 2006). This corresponds to using a Dirac delta function DTD with the peak at τ = 0, i.e. no delay time between the SN explosion and star formation or, in other words, a prompt channel for the Ia progenitor-to-supernova process.
In Strolger et al. (2010) and Strolger et al. (2004) a Gaussian shaped (or close to
Gaussian) DTD with a mean delay time of ~3 Gyr is found to give the best fit to the
GOODs Ia supernova rates. We use the unimodal skew-normal DTD parametrisation and best
fitting parameters from Strolger et al. (2010) and
convolve this with the star formation history given in Eq. (5) (the same SFH as the one used by these authors). The DTD
parametrisation is: 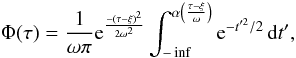 (7)with the best fitting
parameters ω = 0.2, ξ = 3.2 and
α = 2.2.
(7)with the best fitting
parameters ω = 0.2, ξ = 3.2 and
α = 2.2.
Graur et al. (2011) fit the results from the
Subaru Deep Field supernova search together with the rates of many other surveys using
different power law DTDs. The DTD models and SFHs they try show quite similar fitting
quality, the rate we show in Fig. 4 uses a power law
DTD with an exponent β equal to 0.97, their best fitting value:
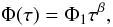 (8)where Φ1
is a normalisation parameter. Φ is also set to 0 for
τ < 40 million years. This is then convolved
with the SFH given in Eq. (4) to get the
rates plotted in the Fig. 4.
(8)where Φ1
is a normalisation parameter. Φ is also set to 0 for
τ < 40 million years. This is then convolved
with the SFH given in Eq. (4) to get the
rates plotted in the Fig. 4.
Scannapieco & Bildsten (2005), Mannucci et al. (2006) and Sullivan et al. (2006) find strong evidence for the existence of a
prompt channel for Ia SNe by looking at the properties of the host galaxies of Ia SNe (and
other data). Maoz et al. (2011) study the hosts of
the local SNe found in the LOSS and find a prompt channel (with
τ < 420 Myr) with 99% significance. Models of
Ia explosions also show the possibility of such a channel (Nomoto et al. 2009; Ruiter et al. 2011).
The Ia rates are then modelled with one prompt component, directly proportional to the
SFH, and one delayed component. We plot the resulting Ia rate from the work by Sullivan et al. (2006), who use a parametrisation of
the form 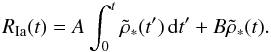 (9)Note that the SFH used
by us is not strictly the same as the one used by these authors and can thus not be used
directly in this equation. We plot the SNR as given in Sullivan et al. (2006) in Fig. 4.
(9)Note that the SFH used
by us is not strictly the same as the one used by these authors and can thus not be used
directly in this equation. We plot the SNR as given in Sullivan et al. (2006) in Fig. 4.
5. Discussion and summary
We have presented supernova rates from the SVISS along with a description of the methods
used to compute them and an extensive analysis of systematic errors for the rates. The
resulting rates for the core collapse SNe are: 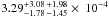 yr-1
yr-1 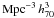 (with statistical and
systematic errors respectively) at ⟨z⟩ = 0.39 and
(with statistical and
systematic errors respectively) at ⟨z⟩ = 0.39 and
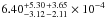 yr-1
yr-1 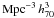 at
⟨z⟩ = 0.73. The CC rates have been corrected for obscuration in dusty
environments using the results of Mattila et al.
(2012), as described in Sect. 3.2 and host
galaxy extinction based on the models in Riello &
Patat (2005). Uncorrected values can be found in Table 3.
at
⟨z⟩ = 0.73. The CC rates have been corrected for obscuration in dusty
environments using the results of Mattila et al.
(2012), as described in Sect. 3.2 and host
galaxy extinction based on the models in Riello &
Patat (2005). Uncorrected values can be found in Table 3.
The rate estimates follow the star formation history well. Horiuchi et al. (2011) point out that the core collapse supernova rates found in both local and high redshift searches seem to be too low by a factor of two when compared to the star formation history compiled in Hopkins & Beacom (2006). Our results do not show this difference, both of our rate estimates are consistent with the star formation history within the statistical errors. But our errors are quite large, the rates estimated by other authors, in particular at low z, do in fact differ significantly from the SFH. The strongest evidence for this comes from the rate estimate by Li et al. (2011a) at low z which has small errors and is clearly below the SFH. At higher redshift the problem is less severe, which could be due to the increased statistical errors. At high redshift the problem may also be somewhat alleviated by the obscuration corrections, which we have included in our plotted rates in Fig. 3, the rates from other surveys plotted in this figure do not include this correction (with the exception of the data point from Graur et al. 2011). Recently Dahlen et al. (2012) presented their measurements of the CC SN rate. They use a similar method as the one described in this paper but a different data set, and arrive at SN rates that are consistent with the ones presented in this paper.
Horiuchi et al. (2011) suggest that taking missed SNe due to extinction and dust obscuration in LIRGs and ULIRGs into account is not enough to explain the difference. Instead they suggest that the reason is that the assumed fractions of faint and very faint CC SNe are too low. In our tests of the systematic uncertainties we find that assuming 30% of the CC SNe to be faint (MB > −15) boosts the rates by ~30%, not enough to bridge the factor of two gap found for the local SN searches. Of course, the assumption on fractions of faint CC SNe may be very different for the different surveys, making it possible that other data points may go up more than this. While the SFHs we compare with have also been corrected for dust and hidden star formation, the supernovae are probably affected differently by the presence of obscuring dust. The number of supernovae that are missed in dusty starburst galaxies and LIRGs is currently not well constrained even in the local universe (e.g. Mannucci et al. 2003; Mattila et al. 2004). The de-bias factors for extinction and dust obscuration in normal galaxies and U/LIRGs derived by Mattila et al. (2012) can make the difference between the predicted and observed CC SN rates disappear. In this paper we have used these factors to de-bias the core collapse supernova rates. The de-bias factors from this study are slightly larger at low redshifts, but lower at high redshift, than the factors from Mannucci et al. (2007). The uncertainties – both statistical and systematic – of the de-bias factors derived in Mattila et al. (2012) have been thoroughly studied, and will hopefully decrease as more observations of SNe in dusty galaxies are obtained. High angular resolution observations at near-IR (e.g. Mattila et al. 2007; Kankare et al. 2008, 2012) and radio (e.g., Pérez-Torres et al. 2010; Romero-Cañizales et al. 2011) wavelengths have recently been used to detect and characterise the hidden SN populations in the nearest LIRGs. Such studies are needed to constrain the complete rates, properties and extinction distributions towards the CC SNe buried in such dusty galaxies. Eventually, these studies will hopefully provide a robust estimate for the numbers of SNe missed by optical searches both locally and at high-z.
The resulting rate for the Ia supernovae is: 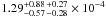 yr-1
yr-1 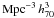 at
⟨z⟩ = 0.62. This rate has been corrected for host galaxy extinction,
but not for high redshift obscuration (a positive correction for this is included in the
systematic error).
at
⟨z⟩ = 0.62. This rate has been corrected for host galaxy extinction,
but not for high redshift obscuration (a positive correction for this is included in the
systematic error).
Because of the quite high statistical errors and the lack of Ia SNe beyond z = 1 we do not try to fit any DTDs to our Ia rate measurements. The comparison to the plotted models show that all these models are consistent with our rates. The high rate of Ia SNe at z ~ 0.5 measured by SVISS is in strong agreement with the results of Dahlen et al. (2008), and thus in support of a Gaussian-like, fairly wide, DTD for Ia SNe. However, it should be noted that our measurement is also consistent with the distributions proposed by other authors. The type Ia SN rate measurements at z ≳ 0.4 differ by up to a factor of ~2. We believe that the cause of this large scatter is the large statistical and systematic errors that the SN surveys suffer from in this redshift range. It should also be noted that there are differences in the methods used to calculate the rates in the different surveys. It is therefore of utmost importance that the systematic errors are correctly estimated. Strolger et al. (2010) find that models with a prompt Ia component are hard to reconcile with the rates measured at redshifts higher than one. Increased sample sizes at these high redshifts, or more studies of Ia host galaxies (Gallagher et al. 2005; Sullivan et al. 2006) are needed to constrain the contribution from this channel.
In Sect. 3.2.2 we outline our motivation for not de-biasing the type Ia SN rates to account for extremely high extinction in U/LIRGs. It is very important to understand that the missing fractions of type Ia SNe situated in U/LIRGs similar to Arp 299 very likely depend on the DTDs. It is likely that also the missing fractions in other types of galaxies will depend on the DTD, although to a lesser extent. Using the type Ia SN rates to estimate the DTD thus inherently suffers from circularity to some extent. Assuming a zero missing fraction is a choice in itself – the DTD implicit to such an assumption has a cut-off at some delay time τ ≲ 200 Myr. If the DTD has no such cut-off, and a significant number of type Ia SNe have very short delay times, our assumption is faulty. In that case the resulting rates may be off by more than the adopted systematic error.
The determination of supernova rates at high redshift is difficult. The SNe detected at high redshift will only be sampling the bright end of the SN luminosity function. This means that any global statistics estimated from such measurements will be sensitive to assumptions on the luminosity function made during the calculations. There are a number of additional assumptions going into the rate calculations that affect the rates differently. It is important to estimate the systematic errors these assumptions give rise to. With the exception of the misclassification error, that essentially scales with the sample size for samples smaller than ten given a misclassification ratio of 10%, we have shown that the systematic errors are on the order of 50% when using photometric redshifts and with the present uncertainties in template fractions and peak magnitudes. Furthermore, the assumptions made when correcting the rates for extinction/obscuration are shown to have a large effect on the systematics. Presently little is known about the number of SNe missed in LIRGs and ULIRGs, especially important at high redshift, which is evident in the large uncertainties on the de-bias factors.
Given the low numbers of SNe for most high redshift surveys it is perhaps tempting to try and use the rates found in different surveys together when comparing to models (for the Ia SNe) and other sources (SFH for CC SNe). However, it’s not straight-forward to do this. Different surveys estimate systematic errors in different ways, some include more sources and some less. If combined as given using co-added statistical and systematic errors, the risk is that greater weight is given to surveys where fewer systematic error estimates are included (given that the sample sizes are similar). We believe that the work presented in this paper shows the importance of including a variety of systematic effects to correctly estimate the uncertainties of supernova rates at high redshift. This will be even more important for future surveys with larger sample sizes and therefore lower statistical errors.
Online material
Supernova rates in the literature.
Web based calculator available at http://casa.colorado.edu/~trenti/CosmicVariance.html
Acknowledgments
We are grateful for financial support from the Swedish Research Council. S.M., J.M., and E.K. acknowledge financial support from the Academy of Finland (project:8120503). We also thank D. F. de Mello for interesting input on the manuscript. We thank the anonymous referee for useful comments.
References
- Alard, C. 2000, A&AS, 144, 363 (A00) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., & Glazebrook, K. 2003, ApJ, 593, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Barbary, K., Aldering, G., Amanullah, R., et al. 2012a, ApJ, 745, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Barbary, K., Aldering, G., Amanullah, R., et al. 2012b, ApJ, 745, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Bazin, G., Palanque-Delabrouille, N., Rich, J., et al. 2009, A&A, 499, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botticella, M. T., Riello, M., Cappellaro, E., et al. 2008, A&A, 479, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Botticella, M. T., Smartt, S. J., Kennicutt, R. C., et al. 2012, A&A, 537, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Illingworth, G. D., Franx, M., et al. 2009, ApJ, 705, 936 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., Evans, R., & Turatto, M. 1999, A&A, 351, 459 [NASA ADS] [Google Scholar]
- Cappellaro, E., Riello, M., Altavilla, G., et al. 2005, A&A, 430, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Norberg, P., Baugh, C. M., et al. 2001, MNRAS, 326, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. D., Wu, C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Bournaud, F., Walter, F., et al. 2010, ApJ, 713, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlén, T., & Fransson, C. 1999, A&A, 350, 349 [NASA ADS] [Google Scholar]
- Dahlen, T., Strolger, L.-G., Riess, A. G., et al. 2004, ApJ, 613, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Strolger, L.-G., & Riess, A. G. 2008, ApJ, 681, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Mobasher, B., Dickinson, M., et al. 2010, ApJ, 724, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Strolger, L., Riess, A. G., et al. 2012, ApJ, in press [arXiv:1208.0342] [Google Scholar]
- Dilday, B., Bassett, B., Becker, A., et al. 2010a, ApJ, 715, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Dilday, B., Smith, M., Bassett, B., et al. 2010b, ApJ, 713, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elias-Rosa, N., Van Dyk, S. D., Li, W., et al. 2011, ApJ, 742, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., Garnavich, P. M., Berlind, P., et al. 2005, ApJ, 634, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Giavalisco, M., Dickinson, M., Ferguson, H. C., et al. 2004, ApJ, 600, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Goobar, A. 2008, ApJ, 686, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T. 2007, MNRAS, 377, 1222 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., Poznanski, D., Maoz, D., et al. 2011, MNRAS, 1508 [Google Scholar]
- Greggio, L. 2005, A&A, 441, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatano, K., Branch, D., & Deaton, J. 1998, ApJ, 502, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, M., Schaerer, D., & Östlin, G. 2010, A&A, 509, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Horiuchi, S., Beacom, J. F., Kochanek, C. S., et al. 2011, ApJ, 738, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Kankare, E., Mattila, S., Ryder, S., et al. 2008, ApJ, 689, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Kankare, E., Mattila, S., Ryder, S., et al. 2012, ApJ, 744, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Kartaltepe, J. S., Dickinson, M., Alexander, D. M., et al. 2012, ApJ, 757, 23 [CrossRef] [Google Scholar]
- Kessler, R., Bassett, B., Belov, P., et al. 2010, PASP, 122, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kuznetsova, N. V., & Connolly, B. M. 2007, ApJ, 659, 530 [NASA ADS] [CrossRef] [Google Scholar]
- LaFranca, F., Gruppioni, C., Matute, I., et al. 2004, AJ, 127, 3075 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Proc. SPIE, 4841, 1670 [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Leibundgut, B. 2000, A&ARv, 10, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Chornock, R., Leaman, J., et al. 2011a, MNRAS, 317 [Google Scholar]
- Li, W., Leaman, J., Chornock, R., et al. 2011b, MNRAS, 413 [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2009, A&A, 496, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Elbaz, D., Chary, R. R., et al. 2011, A&A, 528, A35 [Google Scholar]
- Maiolino, R., Vanzi, L., Mannucci, F., et al. 2002, A&A, 389, 84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Maiolino, R., Cresci, G., et al. 2003, A&A, 401, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2007, MNRAS, 377, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 307 [Google Scholar]
- Marcillac, D., Elbaz, D., Charlot, S., et al. 2006, A&A, 458, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattila, S., & Meikle, W. P. S. 2001, MNRAS, 324, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Meikle, W. P. S., & Greimel, R. 2004, New Astron. Rev., 48, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Väisänen, P., Farrah, D., et al. 2007, ApJ, 659, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, S., Dahlen, T., Efstathiou, A., et al. 2012, ApJ, 756, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Melinder, J., Mattila, S., Östlin, G., Mencía Trinchant, L., & Fransson, C. 2008, A&A, 490, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melinder, J., Dahlen, T., Mencía Trinchant, L., et al. 2011, A&A, 532, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mencía Trinchant, L., Melinder, J., Dahlen, T., et al. 2012, A&A, submitted [Google Scholar]
- Miknaitis, G., Pignata, G., Rest, A., et al. 2007, ApJ, 666, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Balam, D., et al. 2006, AJ, 132, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Kamiya, Y., Nakasato, N., Hachisu, I., & Kato, M. 2009, in AIP Conf. Proc., 1111, 267 [Google Scholar]
- Nugent, P. 2007, Peter Nugent’s Spectral Templates, http://supernova.lbl.gov/~nugent/nugent_templates.html [Google Scholar]
- Pain, R., Fabbro, S., Sullivan, M., et al. 2002, ApJ, 577, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Parra, R., Conway, J. E., Diamond, P. J., et al. 2007, ApJ, 659, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Rieke, G. H., et al. 2010, ApJS, 188, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez-Torres, M. A., Alberdi, A., Romero-Cañizales, C., & Bondi, M. 2010, A&A, 519, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perlmutter, S., Gabi, S., Goldhaber, G., et al. 1997, ApJ, 483, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Maoz, D., & Gal-Yam, A. 2007, AJ, 134, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzo, M., Meikle, W. P. S., Rayner, J. T., et al. 2006, MNRAS, 368, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, D., Branch, D., Casebeer, D., et al. 2002, AJ, 123, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, D., Branch, D., & Baron, E. 2006, AJ, 131, 2233 [NASA ADS] [CrossRef] [Google Scholar]
- Riello, M., & Patat, F. 2005, MNRAS, 362, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., & Tonry, J. L. 2009, ApJ, 707, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Rodney, S. A., & Tonry, J. L. 2010, ApJ, 723, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Romero-Cañizales, C., Mattila, S., Alberdi, A., et al. 2011, MNRAS, 415, 2688 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., Sim, S. A., et al. 2011, MNRAS, 417, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Scannapieco, E., & Bildsten, L. 2005, ApJ, 629, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Sharon, K., Gal-Yam, A., Maoz, D., et al. 2010, ApJ, 718, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Shim, H., Colbert, J., Teplitz, H., et al. 2009, ApJ, 696, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Smartt, S. J., Eldridge, J. J., Crockett, R. M., & Maund, J. R. 2009, MNRAS, 395, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Strolger, L., Riess, A. G., Dahlen, T., et al. 2004, ApJ, 613, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Strolger, L., Dahlen, T., & Riess, A. G. 2010, ApJ, 713, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Le Borgne, D., Pritchet, C. J., et al. 2006, ApJ, 648, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Moustakas, J., & Diamond-Stanic, A. M. 2007, ApJ, 663, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., & Stiavelli, M. 2008, ApJ, 676, 767 [Google Scholar]
- Tsujimoto, T., Yoshii, Y., Nomoto, K., et al. 1997, ApJ, 483, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1938, ApJ, 88, 529 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The redshift accuracy for simulated supernovae with (upper panel) and without (lower panel) a host galaxy photometric redshift. The ~2000 SNe of all different subtypes used to make this figure are a sub-sample of the full sample of simulated light curves. The redshift on the x axis (zsim) is the initial adopted redshift of the supernovae. The dotted lines indicate the |zfit − zsim|/(1 + zsim) > 0.15 limits. |
| In the text | |
 |
Fig. 2 An example of the detection efficiency for a given epoch for different host galaxy brightness. The efficiencies from simulations of supernovae in the field are given by the points while the lines are the S-curve fits to the efficiencies as described in the text. Errors for the measured efficiencies are binomial. Note that a total of 30 (one for each of five epochs × , two filters × , and three host galaxy types) S-curve fits have been used to estimate the detection efficiencies of the full survey. This figure is available in colour in the electronic version of the article. |
| In the text | |
 |
Fig. 3 Core collapse supernova rates determined from the SVISS SNe (black stars). Grey stars are displaced by + 0.01 in z and show the SVISS rates without extinction correction. Also shown is a collection of measured rates from other authors. We plot star formation histories from two different sources, scaled to supernova rates through the use of Eq. (2). Error bars are statistical with total errors (statistical and systematic added in quadrature) as a transparent/faded extra error bar for all surveys. Redshift bin sizes are not shown, but are given in Table 3. The rate from Cappellaro et al. (1999) has been rescaled from SNu to a volumetric rate by assuming a local B-band luminosity density 2.0 × 108 h70 L⊙ Mpc-3 at redshift ~0. The local CCSN rates from Botticella et al. (2012) and Mattila et al. (2012) have been measured in small volumes and are likely dominated by inhomogeneity. The star formation rate in the local volume is higher than the average over an extended volume and can therefore cause the SNR to be higher than expected. |
| In the text | |
 |
Fig. 4 Type Ia supernova rates determined from the SVISS SNe (black star). The grey star is displaced by + 0.01 in z and show the rate without extinction correction. Also shown is a collection of published rates from the literature. We plot SN Ia rates resulting from assumptions on the delay time distribution combined with the star formation history. Error bars are statistical with total errors (statistical and systematic added in quadrature) as a transparent/faded extra error bar for all surveys. Redshift bin sizes are not shown, but are given in Table 3. The rate from Cappellaro et al. (1999) has been rescaled from SNu to a volumetric rate by assuming a local B-band luminosity density 2.0 × 108 h70 L⊙ Mpc-3 at redshift ~0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


