| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 33 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219188 | |
| Published online | 10 September 2012 | |
Type Ia supernova host galaxies as seen with IFU spectroscopy⋆,⋆⋆
1
CENTRA – Centro Multidisciplinar de Astrofísica, Instituto
Superior Técnico, Av. Rovisco Pais
1, 1049-001
Lisbon,
Portugal
e-mail: vallery.stanishev@ist.utl.pt
2
GEPI, Observatoire de Paris, CNRS, University Paris
Diderot, 5 place Jules
Janssen, 92195
Meudon,
France
3
European Southern Observatory, Alonso de Cordova 3107, Casilla 19001, Vitacura,
Santiago,
Chile
Received: 8 March 2012
Accepted: 17 May 2012
Context. Type Ia supernovae (SNe Ia) have been widely used in cosmology as distance indicators. However, to fully exploit their potential in cosmology, a better control over systematic uncertainties is required. Some of the uncertainties are related to the unknown nature of the SN Ia progenitors.
Aims. We aim to test the use of integral field unit (IFU) spectroscopy for correlating the properties of nearby SNe Ia with the properties of their host galaxies at the location of the SNe. The results are to be compared with those obtained from an analysis of the total host spectrum. The goal is to explore this path of constraining the nature of the SN Ia progenitors and further improve the use of SNe Ia in cosmology.
Methods. We used the wide-field IFU spectrograph PMAS/PPAK at the 3.5 m telescope of Calar Alto Observatory to observe six nearby spiral galaxies that hosted SNe Ia. Spatially resolved 2D maps of the properties of the ionized gas and the stellar populations were derived.
Results. Five of the observed galaxies have an ongoing star formation rate of 1–5 M⊙ yr-1 and mean stellar population ages ~5 Gyr. The sixth galaxy shows no star formation and has an about 12 Gyr old stellar population. All galaxies have stellar masses larger than 2 × 1010 M⊙ and metallicities above solar. Four galaxies show negative radial metallicity gradients of the ionized gas up to −0.058 dex kpc-1 and one has nearly uniform metallicity with a possible shallow positive slope. The stellar components show shallower negative metallicity gradients up to −0.03 dex kpc-1. We find no clear correlation between the properties of the galaxy and those of the supernovae, which may be because of the small ranges spanned by the galaxy parameters. However, we note that the Hubble residuals are on average positive while negative Hubble residuals are expected for SNe Ia in massive hosts such as the galaxies in our sample.
Conclusions. The IFU spectroscopy on 4-m telescopes is a viable technique for studying host galaxies of nearby SNe Ia. It allows one to correlate the supernova properties with the properties of their host galaxies at the projected positions of the supernovae. Our current sample of six galaxies is too small to draw conclusions about the SN Ia progenitors or correlations with the galaxy properties, but the ongoing CALIFA IFU survey will provide a solid basis to exploit this technique more and improve our understanding of SNe Ia as cosmological standard candles.
Key words: galaxies: abundances / supernovae: general / galaxies: general / galaxies: ISM / galaxies: stellar content
Based on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC).
Figures 7–15 and Appendices are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
More than a decade ago the observations of Type Ia supernovae (SNe Ia) led to the discovery of the accelerating expansion of the Universe and the need for an unknown repulsive force to drive it (Riess et al. 1998; Perlmutter et al. 1999). Understanding the nature of this force – now dubbed “dark energy” – is an outstanding goal of astrophysics and cosmology. It is now well-understood that no single observational technique will be able to achieve this alone (e.g. Albrecht et al. 2006). The combined constraints of many techniques will be needed to measure the equation-of-state parameter of the dark energy (the ratio between the pressure and the density) and eventually its evolution over the cosmic time. At present, SNe Ia is the most matured and well-understood technique to accurately trace the cosmic expansion history and will continue to play an essential role in future cosmological experiments (Albrecht et al. 2006). However, the SNe Ia technique is affected by several systematic uncertainties, which need to be reduced to a level below ~2% to differentiate between different dark energy models.
The use of SNe Ia in cosmology relies on the empirically established tight relation between their light curve width and peak luminosity, which allows one to measure the luminosity distance with an accuracy of ~7% (Phillips et al. 1999), and on the assumption that the (standardized) peak luminosity of SNe Ia does not change over the cosmic time. There is now observational evidence that the slope of the “light curve shape – peak luminosity” relation does not depend on the redshift or the host galaxy mass (Conley et al. 2011; Sullivan et al. 2011). However, Sullivan et al. (2010) and Kelly et al. (2010) have found that the offsets of the SN Ia peak magnitudes from the best-fitting Hubble line (from now on Hubble residuals or HR) correlate with the host stellar mass. Together with the mass-metallicity relation for galaxies (e.g., Tremonti et al. 2004) and the overall increase of the metal content of the universe with the cosmic time, this may be an indication for possible luminosity evolution of SNe Ia at a level of 0.05–0.10 mag.
It is now generally agreed that SNe Ia are the result of thermonuclear disruption of carbon/oxygen (C/O) white dwarfs (WD), which ignite explosively when they approach the Chandrasekhar limit MCh ~ 1.38 M⊙ (Hoyle & Fowler 1960). However, there has been little observational evidence of the exact evolutionary scenario that leads to the explosion. C/O WDs are the end product of the evolution of stars with masses ~1.5–7 M⊙ (e.g., see Becker & Iben 1980; Domínguez et al. 1999). The upper mass limit for C/O WDs is ~1.1 M⊙ (e.g., see Weidemann 1987; Domínguez et al. 1999; Salaris et al. 2009) and therefore a mechanism that allows the WD to gain additional mass of at least ~0.3–0.4 M⊙ is needed. In the single-degenerate (SD) scenario the WD accretes mass from a non-degenerate companion star in a binary system (Whelan & Iben 1973). However, the exact physical mechanism of the WD mass growth has not yet been identified. In the double-degenerate (DD) scenario two C/O WDs in a binary merge after loosing orbital angular momentum by gravitational wave radiation (Iben & Tutukov 1984; Webbink 1984; Paczynski 1985). While considered the most viable, both scenarios have considerable uncertainties (see, e.g. Hillebrandt & Niemeyer 2000; Maoz & Mannucci 2011).
The numerical simulations of thermonuclear SN Ia explosions suggest that the properties of the exploding WD may significantly influence the peak luminosity, the “light curve width – luminosity” relation and colors of the resulting supernovae (e.g., Höflich et al. 1998; Umeda et al. 1999; Domínguez et al. 2001; Röpke et al. 2006; Kasen et al. 2009; Bravo et al. 2010). On the other hand, the properties of the WD just before the ignition (the central density, metallicity and C/O ratio) are sensitive to the properties and the evolution of its progenitor binary star, and to the subsequent WD mass growth mechanism. For example, the SD channel can produce MCh WDs with slightly different structure and chemical composition depending on the mass of the WD at the moment when the accretion started (e.g., Domínguez et al. 2001). In the DD scenario, the outcome of the merger may depend on the mass ratio of the two WDs. In addition, one may expect that some properties of SN Ia progenitor stars will evolve with cosmic time, e.g. metallicity. Therefore, possible evolution of the properties of SN Ia progenitors or, if more than one evolutionary channel exist, evolution of their relative contribution to the SNe Ia population, may introduce systematic uncertainties in SN Ia cosmology and potentially bias the cosmological results from the future large SN surveys (e.g., see Sarkar et al. 2008; Nordin et al. 2008).
To date no progenitor of a SN Ia has been unambiguously identified and/or observed and information about the SNe Ia progenitors has been inferred indirectly. Mannucci et al. (2005) and Scannapieco & Bildsten (2005) studied the SN Ia rate as a function of redshift and host galaxies properties. Both studies found that the SN Ia rate depends on both the on-going star formation rate (SFR) and total galaxy stellar mass. This result was also confirmed by others (Sullivan et al. 2006; Neill et al. 2006; Mannucci et al. 2006; Pritchet et al. 2008; Dahlen et al. 2008; Maoz et al. 2011) and appears to suggest that at least part of SNe Ia are associated with the young stellar population capable of producing SN Ia with short delay time ≤ 400 Myr. Totani et al. (2008) and Maoz et al. (2010) have shown that the delay times from star formation to SN Ia explosions between the shortest time probed <400 Myr and 10 Gyr are distributed as a power law with slope ~− 1. This delay time distribution (DTD) strongly favors the DD scenario. The SD scenario may also explain this DTD (Hachisu et al. 2008) but the efficiency of the symbiotic channel (WD+red giant) needs to be significantly increased (see, e.g., Maoz & Mannucci 2011). The early discovery of SN 2011fe in M101, the nearest SN Ia in 25 years, provided the first real possibility to constrain the properties of a progenitor star of an SN Ia (Bloom et al. 2012; Chomiuk et al. 2012; Nugent et al. 2011). The results reinforce the conclusion that the exploding star is a C/O WD and seem to rule out all but a degenerate star as its companion, thus favoring the DD scenario. On the other hand, based on high-resolution spectroscopy of a sample of nearby SNe Ia Sternberg et al. (2011) favor the SD scenario.
Many studies have shown that the intrinsically luminous SNe tend to occur in star-forming hosts, while the faint SNe prefer passive ones (e.g., Hamuy et al. 1996, 2000; Gallagher et al. 2005, 2008; Howell et al. 2009; Neill et al. 2009; Sullivan et al. 2006, 2010; Kelly et al. 2010; Brandt et al. 2010; Raskin et al. 2009). Gallagher et al. (2008) found that the Hubble residuals correlate with the global host metallicity. Sullivan et al. (2010) and Kelly et al. (2010) found such a correlation with the host stellar mass. However, Howell et al. (2009), who used the galaxy stellar mass as a proxy for the metallicity, found no such correlation and suggested that instead the progenitor age may be a more important parameter.
All studies of SN Ia hosts galaxies conducted so far, except that by Raskin et al. (2009), were based on an analysis of the global photometric or spectroscopic properties of the host galaxies. In this paper we take a different approach. We use for the first time integral field unit (IFU) spectroscopy at intermediate spectral resolution to study a sample of host galaxies of local SNe Ia (z ~ 0.02). This approach has an advantage over the previous studies because it allows us to derive spatially-resolved two-dimensional (2D) maps of host galaxy properties, e.g. the heavy element abundance in the interstellar medium (ISM). The intermediate spectral resolution makes it also possible to use full-spectrum fitting techniques to derive 2D maps of the properties of the stellar populations. The main objective of this pilot work is to test the methodology to correlate the properties of the SNe with the properties of the gas and the stellar populations at the location of the SN explosion, in addition to the global host properties. By analyzing the properties of the stellar populations we also aim to constrain the nature of the SNe Ia progenitors.
Throughout the paper we assume the concordance cosmological model with ΩM = 0.27, ΩΛ = 0.73, w = −1 and h = 0.71.
Supernovae and details of their host galaxies: morphological type, Milky Way dust reddening, offsets from the host nucleus, de-projected galactocentric distance, inclination, and position angle.
SALT2 (Guy et al. 2007) x1 and C parameters of the SNe from Amanullah et al. (2010), the offset from the best-fit Hubble line Δμ, and the ΔM15 parameter.
2. Observations and data reduction
2.1. Target selection
The list of targets for this program was selected from a sample of spiral galaxies that hosted SNe Ia for which the important parameters such as luminosity, extinction, intrinsic color indices, luminosity decline rate, and deviation from the Hubble diagram have been accurately measured. The galaxies were carefully examined and selected to fulfill four additional criteria:
-
1.
to have angular size ≃ 40–60 arcsec;
-
2.
to be nearly face-on;
-
3.
the SN lies on a high surface brightness location in the galaxy;
-
4.
be observable at airmass less that 1.3 to minimize the effect of the differential atmospheric refraction.
The first two requirements maximize the use of the large field-of-view (FOV) of the IFU instrument and minimize the projection effects when correlating the SN and its local host galaxy properties. The third requirement ensures that we will obtain a good signal-to-noise ratio (S/N) of the spectra at the location of the SN, and in particular will allow us to access the absorption and emission line spectra. From the large sample of galaxies six objects were observed. The galaxy details and the SNe offset from the nucleus are given in Table 1. All SNe are normal SNe Ia, except for SN 1999dq, which was classified as a peculiar 1991T-like event (Jha et al. 1999). Table 2 gives the SALT2 x1 and C parameters of the supernova light curves (Guy et al. 2007) taken from Amanullah et al. (2010), the offset from the best-fit Hubble line Δμ, and the ΔM15 parameter, which shows how much the SN B-band magnitude has declined during the first 15 days after the time of the B band maximum. x1 and C are parameters related to the SN light curve shape and B − V color index at maximum, respectively. They are used to standardize the observed B-band peak magnitude Bobs via the relation Bstd = Bobs + αx1 − βC, with α = 0.121 and β = 2.51 as per Amanullah et al. (2010). Δμ was computed after first correcting the redshifts of the SNe for large-scale coherent galaxy motions in the local universe based on the models of Hudson et al. (2004). The accuracy of this correction is estimated to be ~150 km s-1 and a random peculiar velocity of 150 km s-1 is added to the uncertainty of Δμ.
It should be noted that for this pilot project the selection criteria are solely optimized to maximize the quality of the observations and facilitate the analysis. We focus on late-type galaxies because one of our goals is to correlate the SN properties with the properties of the ISM determined from the ionized gas. This leads to strong biases, however, e.g. the galaxies in our sample are bright, massive, and likely metal-rich.
2.2. Observations
The six galaxies were observed on November 14 and 15, 2009 at the 3.5 m telescope of the Calar Alto observatory using the Potsdam Multi-Aperture Spectrograph (PMAS, Roth et al. 2005) in the PPAK mode (Verheijen et al. 2004; Kelz et al. 2006). The atmospheric conditions were variable with occasional thin clouds interrupting the observations. The seeing varied between 1.5′′ and 2.2′′.
The PMAS instrument is equipped with a 4k × 4k E2V#231 CCD. We used a set-up with the 600 lines mm-1 grating V600 and 2 × 2 binned CCD, which provided a wavelength range of ~3700–7000 Å with a spectral resolution of ~5.5 Å. The PPAK fiber bundle of PMAS consists of 382 fibers with 2.7′′ diameter each, 331 of which (science fibers) are ordered in a single hexagonal bundle that covers a FOV of 72′′ × 64′′. Thirty-six additional fibers form six mini-bundles (sky-bundles), which are evenly distributed along a circle of ~90′′ radius and face the edges of the central hexagon (see Fig. 5 in Kelz et al. 2006). The remaining 15 fibers are used for calibration and can only be illuminated with the PMAS internal calibration unit. For a detailed description of the PPAK fiber bundle we refer the reader to Kelz et al. (2006). Some details that are relevant for the data reduction are also given in Appendix A.
For each object three 1800-s long exposures were obtained. Because the filling factor of a single PPAK exposure is ~65%, we adopted a dithering pattern with the second and the third exposures offset by Δ(RA, Dec) = (1.56, 0.78) and (1.56, −0.78) arcsec with respect to the first exposure to ensure that every point within the FOV was spectroscopically sampled. Before and after the science exposures, spectra of HgNe and continuum halogen lamp were obtained to wavelength-calibrate and trace the spectra. The spectrophotometric standard stars Feige 34 and BD+25 3941 were observed to measure the sensitivity function of the instrument. In addition, series of exposures of blank sky regions were obtained during twilight and were used to equalize the fiber-to-fiber throughput variations.
2.3. Data reduction
The pre-reduction of the CCD images was performed with IRAF1 and the rest of the reduction with our own programs written in IDL. Each individual science pointing was reduced independently. After the standard CCD reduction steps of bias subtraction, flat-field correction and removal of cosmic ray hits, the spectra were traced, extracted, wavelength- and flux-calibrated, and finally sky-subtracted. At the final step the three pointings were combined into a final 3D data-cube, taking into account the differential atmospheric diffraction. The full details of the data reduction are given in Appendix B.
Three of the galaxies in our sample also have SDSS spectra. This allowed us to check the relative flux calibration of our spectroscopy. Spectra within an aperture of 3′′ diameter centered on the galaxy nucleus were extracted from the data-cubes to emulate the SDSS spectra. The comparison, after our spectra were scaled to match the flux level of the SDSS spectra, is shown in Fig. 1. It demonstrates that the relative flux calibration of our spectra is excellent and matches SDSS to within a few percent.
The absolute flux scale of the data-cubes was set using the SDSS imaging. SDSS g and r magnitudes of the galaxies were computed within an aperture of 20′′ diameter. Spectra within the same aperture size were extracted from the data-cubes and synthetic g and r magnitudes were computed. The g and r scale factors that provided the match of the synthetic magnitudes to the observed ones were computed and the average of the two was applied to the data-cubes. We note that the g and r scale factors coincided to within 3%, which additionally supports our conclusion that the relative flux calibration is accurate.
 |
Fig. 1 Comparison between SDSS spectra (red) and spectra extracted from our data-cubes within an aperture of 3′′ diameter centered on the galaxy nuclei (black). |
3. Data analysis
The individual spectra in the data-cubes were analyzed to derive 2D maps of the properties of the galaxies. This included the properties of the ionized gas and the stellar populations. The properties of the galaxies at the SN position and the galaxy center were derived by interpolating the 2D maps. The galaxy centers were computed from the data-cubes and the SN positions were computed with respect to it, using the offsets quoted in the discovery IAU circulars and Jha et al. (2006).
As previously mentioned, one of the main goals of this study is to test the feasibility of using IFU spectroscopy to compare the properties of the host as derived from integrated spectroscopy to those derived from spatially resolved spectroscopy. For this purpose, we also analyzed for each galaxy the total spectrum formed by simply summing all spaxel spectra in the data-cube. This simulates an observation of the same galaxy with long-slit spectroscopy as is performed for high-redshift galaxies.
For each galaxy the analysis was also performed on azimutally averaged spectra at several de-projected galactocentric radii. This was performed as an alternative way to derive the radial dependence of the galaxy properties such as the metallicity. To compute the azimutally averaged spectra we first computed the de-projected galactocentric distance of each spaxel with the position angle and inclination (Table 1) computed from the analysis of the Hα velocity maps2 (see Sect. 3.1.2). The spectra were corrected to rest-frame wavelength with the stellar velocities estimated from the fits to the absorption line spectrum (Sect. 3.2.4). Finally, for each galaxy the spectra within several (4 to 6) radial bins were averaged. Because the stellar velocities were used to correct the spectra to rest frame, we used only the spectra that had a sufficiently high S/N to allow fitting with STARLIGHT.
All quoted uncertainties of the derived quantities are statistical and do not include systematic and intrinsic uncertainties of the methods, which will be additionally discussed when appropriate. In the next sections we present the main steps in the data analysis.
3.1. Properties of the ionized gas
The presence of nebular emission lines in the galaxy spectra allows us to study the properties of the ionized gas such as its oxygen abundance and ionization state, and to derive other important properties such as the star formation rate, dust extinction, etc. Some of the methods used to derive these quantities, for example the strong line methods to estimate the gas metallicity, can only be applied if the ionization source is exclusively arising from the stellar radiation. For this reason and to search for possible AGN contamination, we used the diagnostic diagram [O iii] λ5007/Hβvs. [N ii] λ6584/Hα (BPT diagram; Baldwin et al. 1981) (Fig. 2). The central spaxels that fall in the AGN area of the diagnostic diagram according to the Kauffmann et al. (2003) criterion were excluded from the relevant parts of the analysis.
 |
Fig. 2 BPT diagram (Baldwin et al. 1981). The contours show the density of SDSS emission line galaxies. The dotted and the dashed lines of Kewley et al. (2001) and Kauffmann et al. (2003), respectively, separate star-forming galaxies, AGNs, and composite galaxies. The filled circles, filled triangles, and crosses show the measurements at the position of the SN, the galaxy nucleus, and the total galaxy spectrum, respectively. |
3.1.1. Emission line fluxes
Five of the six galaxies in our sample show strong nebular emission lines. The fluxes of the prominent emission lines [O ii] λ3727, Hβ, [O iii] λλ4959/5007, Hα, and [N ii] λλ6549/6584 were used in the analysis. Whenever possible, the [S ii] λλ6716/6731 lines were also measured. In the spectra of galaxies the emission lines are superimposed on the underlying stellar absorption spectrum. The stellar absorption lines can bias the measurement of the emission line fluxes, an effect that is especially prominent in the Hβ line (Fig. C.1). Therefore, to measure the emission line fluxes accurately, the stellar absorption spectrum needs to be subtracted first. For this we used the STARLIGHT software (Cid Fernandes et al. 2005). All spectra that had S/N greater than 5 at ~4600 Å were fitted with STARLIGHT and the emission line fluxes were measured on the continuum-subtracted spectrum. For the remaining the spectra the measurements were made without continuum subtraction. Each emission line was fitted with a single Gaussian plus a linear term, and the area under the Gaussian was taken as flux estimate. Details of the adopted procedure and the Monte Carlo simulations that were performed to estimate the uncertainties of the line fluxes are given in Appendix C.
3.1.2. Hα velocity field
The fitted positions of the strongest of all emission lines, Hα, provide the best estimate of the gas velocity field. These fields, shown in Figs. 3–5, were analyzed with the methods and IDL programs developed by Krajnović et al. (2006). The program analyzes the velocity field at several radii and for each of them returns the inclination and position angle and quantifies the degree of deviation from pure disk rotation. From this analysis we also derived the redshift, the average position angle (PA) and inclination i for each galaxy, which are listed in Table 1.
 |
Fig. 3 Upper row: from left to right, the color SDSS image of NGC 976, the observed Hα flux and velocity maps. Lower row: the ionization parameter log (U), the visual extinction AV estimated from the Balmer decrement and the metallicity map derived with the Pettini & Pagel (2004) O3N2 method. In all maps presented in this paper, × marks the galaxy center and + the SN position. The four contour levels overplotted on the extinction and metallicity maps are derived from the Hα map. The four levels are 0.8, 0.6, 0.4 and 0.2 of the maximum Hα flux. The x,y coordinates are in arcsec with respect to the map centers. The orientation of the images is north – up, east – left. |
 |
Fig. 4 Same as Fig. 3 but for UGC 5129 and CGCG 207-042. |
 |
Fig. 5 Same as Fig. 3 but for NGC 105 NED02 and UGC 4008 NED01. |
3.1.3. Extinction, Hα flux, and star formation rate maps
For the purpose of the following analysis the measured line fluxes were corrected for dust extinction using the observed Balmer decrement I(Hα)/I(Hβ) and assuming a foreground dust screen. For the intrinsic Balmer decrement I(Hα)/I(Hβ)intr a value of 2.86 was assumed, which is appropriate for case-B recombination with electron temperature Te = 10 000 K and electron density 102 cm3 (e.g., Osterbrock & Ferland 2006). The dust is described by the Fitzpatrick (1999) law with RV = 3.1.
The extinction-corrected Hα flux was converted into instantaneous SFR
using the Kennicutt (1998) relation:
![\begin{equation} {\it SFR}\,[M_{\sun}\,\mathrm{yr}^{-1}]=7.9\times 10^{-42}\,L(\mathrm{H}\alpha), \end{equation}](/articles/aa/full_html/2012/09/aa19188-12/aa19188-12-eq58.png) (1)where L(Hα) is the Hα
luminosity in units of erg s-1.
(1)where L(Hα) is the Hα
luminosity in units of erg s-1.
3.1.4. ISM oxygen abundance
The most accurate method to measure the ISM abundances – the so-called direct method – involves determining of the ionized gas electron temperature, Te, which is usually estimated from the flux ratios of auroral to nebular emission lines, e.g. [O iii] λλ4959/5007/[O iii] λ4363 (e.g. Stasińska 2006; Izotov et al. 2006). However, the temperature-sensitive lines such as [O iii] λ4363 are very weak and difficult to measure, especially in metal-rich environments. A careful examination of our data-cubes revealed that the [O iii] λ4363 line was not present. For this reason we used other strong emission line methods to determine the gas oxygen abundance. Many such methods have been developed throughout the years, the most commonly used being R23 = ([O ii] λ3727+[O iii] λλ4959/5007)/ Hβ ratio-based methods (Pagel et al. 1979; McGaugh 1991; Zaritsky et al. 1994; Tremonti et al. 2004; Kewley & Dopita 2002; Kobulnicky & Kewley 2004; Pilyugin 2001; Pilyugin & Thuan 2005), N2 = log[[N ii] λ6584/Hα] (Storchi-Bergmann et al. 1994; Pettini & Pagel 2004) and O3N2 = log[([O iii] λ5007)/Hβ)/([N ii] λ6584/Hα)] (Alloin et al. 1979; Pettini & Pagel 2004). More recently, Liang et al. (2006, 2007) and Yin et al. (2007) have verified and re-calibrated these and other strong-line methods using Sloan Digital Sky survey (SDSS) spectroscopy.
Unfortunately, there are large systematic differences between the methods, which translate into a considerable uncertainty in the absolute metallicity scale (for a recent review see, e.g., Kewley & Ellison 2008). In particular, there is ~0.4 dex difference between the so-called empirical and theoretical strong-line methods. The empirical methods are calibrated against H II regions and galaxies whose metallicities have been previously determined by the direct method, e.g. O3N2 and N2 (Pettini & Pagel 2004), R23 − P (Pilyugin & Thuan 2005). The theoretical methods, on the other hand, are calibrated by matching the observed line fluxes with those predicted by theoretical photoionization models (most of the R23-based methods, e.g., McGaugh 1991; Kobulnicky & Kewley 2004; Tremonti et al. 2004; Kewley & Dopita 2002). The cause of these discrepancies is still not well-understood. Recently Moustakas et al. (2010) discussed this problem and concluded that the empirical methods may underestimate the metallicity by a few tenths of dex (see also Peimbert et al. 2007), while the theoretical methods overestimate it. In this situation, we followed the recommendation of Kewley & Ellison (2008) to use one method to compute the metallicities in all galaxies and discuss the results in relative sense, and use another method to confirm the observed trends. As our primary method we used the empirical O3N2 method of Pettini & Pagel (2004, PP04 from now on) and checked the results with the theoretical R23 method of Kobulnicky & Kewley (2004, KK04 from now on). Both methods have advantages and disadvantages, which have been discussed in several papers (e.g., Kewley & Ellison 2008; Yin et al. 2007).
3.2. Stellar populations
The star formation history and chemical evolution of a galaxy is imprinted in the properties of its present-day stellar populations. Determining the properties of the stellar populations in the galaxies has been a major research topic in astrophysics and through the years many different methods have been used, ranging from analysis of the color-magnitude diagrams (CMD, Faber 1972) to equivalent widths of absorption lines (e.g., the Lick indices, Worthey et al. 1994). However, in most galaxies several stellar population are simultaneously present. Disentangling their contribution to the galaxy spectrum is a very difficult task because of various astrophysical and numerical degeneracies.
3.2.1. Full-spectrum fitting technique
Recently, the so-called evolutionary population synthesis methods (Tinsley 1968; Vazdekis et al. 1996; Bruzual & Charlot 2003) coupled with full-spectrum fitting techniques (e.g., Vazdekis & Arimoto 1999; Reichardt et al. 2001; Cid Fernandes et al. 2005; Koleva et al. 2008; MacArthur et al. 2009) have emerged as powerful means to analyze galaxy spectra. The evolutionary population synthesis methods produce synthetic galaxy spectra using as input theoretical evolutionary tracks, libraries of stellar spectra, initial mass function (IMF), and prescriptions for star formation and chemical evolution. The models are then compared to the observed spectra to infer the properties of the stellar populations that contribute to the formation of the observed spectrum. One possible approach is to fit the observed spectrum with a linear combination of model spectra of single stellar populations (SSP) of different ages and metallicities (e.g., Cid Fernandes et al. 2005; Koleva et al. 2008; MacArthur et al. 2009). The fitting returns the contribution of the different SSPs (called population vector) that best describe the observed spectrum, which then can be used to study the stellar populations of the galaxy. However, because of astrophysical and numerical degeneracies, and the presence of noise in the observed spectra, it is well-known that the solution may not be unique and the results should be interpreted with caution (e.g., see the discussion in Cid Fernandes et al. 2005). The best known is the age-metallicity degeneracy3 where young metal-rich stellar populations are confused with older metal-poor ones (see for example Fig. 10 in Bruzual & Charlot 2003). As noted by Bruzual & Charlot (2003), while the shape of the stellar continuum is roughly the same, the strength of the metal lines increases. Therefore, analyzing well-calibrated spectra with high S/N and spectral resolution to resolve the absorption lines has the potential to brake the age-metallicity degeneracy. In addition, uncertainties in the input ingredients needed for computing the SSPs, such as non-uniform coverage of the age/metallicity parameter space of the stellar libraries, IMF and the difficulties in describing some phases of the stellar evolution (e.g., the thermal-pulsating asymptotic giant branch phases), add even more uncertainties when interpreting the results (see, e.g., Conroy et al. 2009).
3.2.2. Choice of the base
In this study we used the STARLIGHT code described in Cid Fernandes et al. (2005) and Asari et al. (2007) coupled with a version of the Bruzual & Charlot4 SSP models based on the new MILES spectral library (Sánchez-Blázquez et al. 2006). The selection of the SSP basis is important for any full-spectrum fitting algorithm and the interpretation of the results. To minimize the computing time one should select few SSPs that are maximally independent and at the same time are capable of reproducing the variability of the full SSP set for a given metallicity. If a large basis is selected, many of its components will be close neighbors. This will lead to increased non-uniqueness of the solution and increase the time for the fitting algorithm to converge. On the other hand, if too small a basis is selected, it will not be able to capture the full variability of the SSP models, the fits may be poor, and the results will be unreliable.
In our work we used the following approach to select the basis. For a given metallicity all SSPs were normalized to the flux in the 4600–4800 Å interval. Then the evolution of the flux in seven spectral windows in the range 3700–7000 Å was tracked as a function of the SSP age. The goal was to identify age intervals where the flux in all seven spectral windows evolves linearly (or close to) with time. If such intervals exist, then the SSPs within them are not independent; all SSPs in a given interval can be closely reproduced as a linear combination of the two SSPs at the extremes. By selecting the basis at the ages connecting the linear intervals we form a small independent set of basis vectors, which at the same time can reproduce the SSPs at all other ages. Following this approach we were able to select N∗ = 16 or 17 SSPs per metallicity that formed our fitting basis of 66 SSP models with ages between 1 Myr and 18 Gyr, and four metallicities Z = 0.004, 0.008, 0.02 (the solar metallicity) and 0.05.
3.2.3. Voronoi binning
To increase the S/N in the outer parts of the galaxies the data cubes were spatially binned using adaptive Voronoi tessellations (Cappellari & Copin 2003; Diehl & Statler 2006). The binning of the spaxels was determined from the S/N measured in the interval 4580–4640 Å, after discarding the spectra with S/N < 1. The targeted S/N of the binned spaxels was S/N ~ 20, with the exception of the host of SN 2006te, for which a lower S/N of 15 was used. To keep the spatial resolution reasonably small, an upper limit of the size of the bins was also imposed: 5 for NGC976, 17 for NGC495, and 12 for the remaining four.
3.2.4. STARLIGHT fits
The Voronoi-binned spectra along with the un-binned ones were fitted with the STARLIGHT
code allowing for all SSPs to be reddened by the same amount of dust
described by the Cardelli et al. (1989) law. In
our analysis, the spectra and the basis were normalized to the mean flux in the region
4580–4620 Å. Thus the population vector is the fractional contribution
xj of the different SSP models at
~4600 Å. In addition to the population vector the code also returns the fractional
contributions μj of each SSP to the total
stellar mass of the galaxy, which is the more relevant physical quantity. The code also
returns the velocity shift and the Gaussian broadening that need to be applied to the
model in order to fit the observed spectrum. The shifts provide the velocity maps for
the stars and the broadening is related to the velocity dispersion of the stars. From
the population vectors we can compute the mass- and light-weighted mean age and
metallicity following Cid Fernandes et al.
(2005):  where
tj and
Zj are the age and the metallicity of
the jth SSP model, and
wj = xj
or
wj = μj
for light- and mass-weighted quantities, respectively.
where
tj and
Zj are the age and the metallicity of
the jth SSP model, and
wj = xj
or
wj = μj
for light- and mass-weighted quantities, respectively.
3.2.5. Compressed population vectors
The simulations performed by Cid Fernandes et al. (2005) demonstrated that the individual components of the population vectors computed by STARLIGHT are very uncertain. Instead of analyzing the individual components, Cid Fernandes et al. (2005) showed that a coarsely binned version of the population vectors provides a more robust description of the current stellar content of the galaxies. Thus, following Cid Fernandes et al. (2004) and Cid Fernandes et al. (2005), we formed compressed the population vectors in three age bins: young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar populations.
4. Results
4.1. Ionized gas
Figures 2–6 show the main results obtained from the analysis of the emission line fluxes. The 2D maps of the galaxy properties that are discussed in this section are shown by galaxy in Figs. 3–5.
4.1.1. BPT diagnostic diagram
Baldwin et al. (1981) introduced several diagnostic diagrams to segregate spectra of emission-line galaxies and AGNs according to their main excitation mechanism. These diagrams are based on easily measured optical emission line flux ratios. Figure 2 shows the positions of the galaxies in our sample on the log([N ii] λ6584/Hα) – log([O iii] λ5007/Hβ) diagnostic diagram. The filled circles, filled triangles, and crosses show the measurements at the position of the SN, the galaxy nucleus, and the total galaxy spectrum, respectively. The dotted and dashed lines show two widely used criteria to separate emission-line galaxies and AGNs introduced by Kewley et al. (2001) and Kauffmann et al. (2003), respectively. From Fig. 2 it is evident that the hosts of SNe 2001fe and 2007A/1997cw harbor AGNs and the host of SN 199dq is on the border of composite galaxies and AGNs. However, the line ratios measured in the total spectra of these three galaxies still fall into the star-forming region of the BPT diagram, which suggests that the AGNs are not strong enough to significantly affect the total galaxy spectra. At high redshift good S/N, spatially resolved spectroscopy is difficult to obtain and weak AGNs may remain unrecognized in slit spectroscopy because typically the whole galaxy falls into the slit. The presence of AGNs, even though weak, may still bias the metallicity estimation from integrated galaxy spectra.
 |
Fig. 6 Radial dependence of 12 + log(O/H)PP04. The red dots show the measurement at the SN position. The horizontal dashed lines indicate the metallicity measured from the total galaxy spectra (Table 4). As a guide to the eye, we plot metallicity gradients of −0.022, −0.035, −0.030, −0.058 and + 0.007 dex kpc-1 (from top to bottom) with the solid lines. We estimate that the accuracy of these gradients is ~0.005. The blue squares show the metallicities measured from the azimuthally averaged spectra. The points shown with the cross and plus signs are the metallicities of the H ii regions discussed in Sect. 4.1.6. |
The locations of the SNe fall into the (small) region of the BPT diagram with the highest density of SDSS galaxies. This is the region where the metal-rich galaxies are typically found (see, e.g., Cid Fernandes et al. 2007). High metallicity in this region of the BPT diagram is also expected from the O3N2 method for metallicity estimation (Alloin et al. 1979; Pettini & Pagel 2004). These are indications that for the emission line galaxies in our sample, the SNe likely exploded in metal-rich environments.
4.1.2. Hα velocity field
The gas velocity maps derived from the Hα emission line show smooth gradients and no apparent irregularities. The analysis with the method of Krajnović et al. (2006) shows that the velocity fields of all five galaxies are consistent with pure disk rotation without signs of significant disturbances. The σ-maps (not shown here) derived form the width of Hα emission line also show a simple structure with a single peak at the center. These results suggest that the galaxies in our sample are likely relaxed systems.
4.1.3. Hα flux, extinction, and star formation rate
On small scales the Hα flux distribution follows the spiral arms visible in the broad-band images. Overall, the Hα flux increases toward the centers of the galaxies. It can be seen that all six SNe in these galaxies are projected onto regions with strong Hα emission with fluxes above the galaxy-average. In the late-type spirals NGC 976, UGC 5129, and NGC 105 NED02 there is a clear Hα flux deficit in the bulge. Interestingly, these are also the galaxies that have AGNs. However, these two phenomena are probably unrelated. James et al. (2009) studied the radial distribution of Hα emission in a large sample of spiral galaxies and found that the late-type spirals (Sc+) show a Hα flux deficit in the bulge regardless of the presence of bars. This effect is much less pronounced in the Sa-type spirals or even absent in their barred counterparts, which tend to have a high concentration of the Hα emission toward the center. This is clearly the case for UGC 4008 NED01, which is the only Sa emission line galaxy in our sample.
Total galaxy SFR, SFR surface density ΣSFR and gas extinction AV at the SN location derived from our observations.
According to James et al. (2009), there is a significant difference in the Hα radial profile of barred and unbarred Sb galaxies. The unbarred Sb galaxies show a smooth profile similar to Sa galaxies. The barred counterparts have a strong peak of Hα emission at the centers, followed by a decrease of the Hα flux, before it increases again because of the Hα emission ring at the outer radius of the bar. The barred Sb galaxy CGCG 207-042 shows exactly the same characteristics with a clear Hα emission ring at the outer radius of the bar. Thus, the radial Hα emission profiles in our galaxies are consistent with the findings of James et al. (2009).
The gas extinction maps presented in Figs. 3–5 also show increase of the extinction toward the galaxy center. Although the extinction maps do not show small-scale structures as clearly as in the Hα flux maps, there is a general trend that the extinction increases with the Hα flux. This is expected because an increased amount of dust is typically observed in the regions of active star formation. The total extinction along the lines of sights of the SN position is low, except for SN 1997cw (marked with the leftmost of the three signs). The extinction along the SN lines-of-sight is given in Table 3.
Table 3 lists the total on-going SFR and the SFR surface density, ΣSFR, at the SN positions derived from the extinction-corrected Hα flux map. The ΣSFR values at the SN position are consistent with the disk-averaged values for normal spiral galaxies (see Fig. 5 in Kennicutt 1998). Our values fall in the upper half of the Kennicutt (1998) distribution, which can be attributed to the SN being projected on regions with higher-than-average Hα flux.
For comparison the total SFR and its confidence intervals derived by Neill et al. (2009) are also given in Table 3. In general, our values are consistent with Neill et al. (2009), although in all cases but one we derive lower values. However, it should be noted that the values of Neill et al. (2009) were derived with a completely different technique – fitting model galaxy SEDs to broad-band photometry – and represent the average SFR during the last 0.5 Gyr, while our estimates from the Hα flux represent the very recent, <20 Myr, SFR.
4.1.4. Ionization parameter and electron density
The ionization parameter log (U) – the ratio of the ionizing photon density to the gas density – is a measure of the degree of ionization of the nebula and can be determined from the ratio of two lines of the same element corresponding to two different ionization states. The ionization maps of the galaxies were computed from the ratio of the [O ii] λ3727 and [O iii] λ5007 lines using the relation of Díaz et al. (2000).
The three AGN galaxies clearly show an increased degree of ionization toward the center, while the remaining two galaxies do not. In three of the galaxies, NGC 976, CGCG 207-042, and NGC 105 NED02, there is also a hint of increasing of the ionization parameter toward the outer spirals. The mean ionization parameters for all five galaxies fall into a rather narrow interval of log (U) = −3.6 ÷ −3.4. The [O ii] λ3727/ [O iii] λ5007 line ratio is known to provide lower values for the ionization parameters compared to other available methods (e.g., Díaz et al. 2000). In comparison with the ionization parameter maps that were computed as part of the Kobulnicky & Kewley (2004) method for oxygen abundance determinations, the [O ii] λ3727/ [O iii] λ5007-based maps show very similar features, but are shifted toward lower values by ~0.3–0.4 dex. Even taking this offset into account, the average values for our galaxies fall into the lower end of the distribution of the H ii galaxies studied by Díaz (1998). This part of the distribution is mostly populated with H ii galaxies without measurable [O iii] λ4363 line, which tend to be metal-rich.
Given the spectral resolution and wavelength range of our spectroscopy, the electron density, ne, can be estimated only from the flux ratio of the [S ii] λλ6716/6731 lines (Osterbrock & Ferland 2006). The ratio of these two lines is sensitive to ne in the range ~102−104 cm-3. Unfortunately, for the two highest redshift galaxies in our sample, CGCG 207-042 and UGC 4008 NED01, the [S ii] lines are outside the covered wavelength range. For the remaining three galaxies the ratio is constant ~1.4 across the galaxy and no apparent structure is visible. Ratios of ~1.4 indicate low electron density ne ≤ 102 cm-3 and are similar to the measurements of ne in other galaxies, e.g. the sample of SDSS galaxies studied by Kniazev et al. (2004). The low electron density suggests that there are no shocks in the galaxy.
4.1.5. ISM oxygen abundance
Figures 3–5 also show the distributions of the metallicity (indicated as 12+log(O/H)PP04) estimated with the O3N2 method of Pettini & Pagel (2004). For the three galaxies that likely harbor AGNs, namely, NGC 976, UGC 5129, and NGC 105 NED02, the central regions affected by the AGN are masked. The decrease of the S/N in the outer parts of the galaxies affects the measurements of the line ratios and some spaxels are also marked as affected by AGN according to the Kewley et al. (2001) criterion. Because no AGN activity is expected in the outer parts of the galaxies the line ratios measured in those spaxels are likely dominated by the noise and have also been masked in the plots. In these three galaxies there are indications for ring-like structures with enhanced metallicity and Hα flux. However, it is difficult to assess whether these are real structures or artifacts caused by the central AGN altering the line ratios. Thus, these ring-like structures should be regarded with caution.
Figure 6 shows the dependence of the metallicity on the de-projected galactocentric distance, which was computed from the position angle and inclination derived from the analysis of the Hα velocity fields. Excluding the host of SN 2007R, which has a quite uniform metallicity distribution, the other four galaxies show decreasing of the metallicity with the radius. The plots also suggest that the high metallicities measured in some of the outermost spaxels in UGC 5129, CGCG 207-042, and NGC 105 NED02 are most likely due to noise in the line flux measurements. The solid lines are guides to the eye, showing metallicity gradients of −0.022, −0.035, −0.030 and −0.058 dex kpc-1 for NGC 976, CGCG 207-042, UGC 5129, and NGC 105 NED02, respecively. These metallicity gradients fall well into the range observed in other nearby galaxies, e.g. M51 (Bresolin et al. 2004), NGC 300 (Bresolin et al. 2009), and NGC 628 (Rosales-Ortega et al. 2011). In contrast, in UGC 4008 NED01 the metatllicity is nearly uniformly distributed with a hint of a very small positive gradient of + 0.007 dex kpc-1. The blue squares in Fig. 6 show the metalliciy estimates from the azimutally averaged spectra described in Sect. 3. These estimates trace the measurements on the individual spaxel spectra very well.
Figure 6 and the inspection of the 2D maps reveals that the SN explosion sites are projected onto regions that have the highest, or close to the highest, metallicity within the corresponding galaxy. Table 4 shows the metallicity measurements in the total galaxy spectra, at the nucleus, and at the SN position. The metallicities at the SN positions in all five galaxies are very similar to each other, 12 + log(O/H)PP04 ~ 8.8 and 12 + log(O/H)KK04 ~ 9.1, and are on average by 0.1 dex higher than the metallicities measured from the total galaxy spectra. For the three galaxies that host AGNs we also computed the metallicity in the total spectra, excluding the central spaxels, which are affected by the AGNs. The metallicity was in all cases identical to the one measured from the total spectra that included the central spaxels (the latter are given in Table 4). This result shows that in these cases the AGNs are too weak to significantly affect the total galaxy spectrum and the metallicity estimation.
ISM metallicity estimates from the total galaxy spectra, at the nucleus, and at the position of the SN using the PP04 and KK04 methods.
4.1.6. Notes on the individual galaxies
NGC 976: the metallicity distribution is nearly symmetric around the galaxy center except for a somewhat extended region located at coordinates (+8, +22). The metallicity of this region is higher compared to the other parts of the galaxy at the same radial distance. Examining the [ O iii] 5007/Hβ and [ N ii] 6584/Hα maps (not shown in the paper), we noted that this is caused by an asymmetry in [ O iii] 5007/Hβ. Both ratios are nearly symmetrically distributed around the galaxy center except for the region at (+8, +22), which has a lower [ O iii] 5007/Hβ ratio resulting in a higher metallicity estimate. There is also a slight decrease of the degree of ionization at the same location. The galaxy was included by Maiolino et al. (1997) in the control sample for their study of the cause of the elevated star formation in Seyfert 2 compared with Seyfert 1 galaxies. The authors found no obvious trigger of star formation in NGC 976.
NGC 495: this red barred Sa galaxy shows no emission lines. Miller et al. (2002) found it to be a member of a poor galaxy cluster, which was the richest cluster among those studied in their work, however. It is therefore possible that the gas component of NGC 495 was separated from the galaxy by the tidal interaction with the other cluster members.
UGC 5129: this galaxy was included in the study of isolated disk galaxies by Varela et al. (2004). It was included in the final list of 203 galaxies (out of an initial 1706) that were likely not affected by other galaxies during the last few Gyr of their evolution.
CGCG 207-042: the spirals arms of the galaxy are barely visible in the SDSS image. However, there are three H ii regions along one of them that are clearly visible in the Hα map. They are roughly located at (x,y) coordinates (+8, −27), (+27, −10) and (+20, +27). The metallicity decreases considerably along the spiral arm, which is also accompanied by a strong increase of the ionization parameter. The two outermost H ii regions are shown with blue and magenta points in Fig. 6.
NGC 105 NED02: in the Hα velocity map there is a spot located at (+28, +4) that clearly does not follow the velocity of the underlying part of the galaxy but moves away ~120 km s-1 faster. At the same position there is a very faint spot in the broad-band images. This sport also clearly shows increased Hα emission and a marginal increase of the ionization parameter. The metallicity of the spot is lower than the rest of the galaxy by at least 0.2 dex. The points corresponding to this spot are shown with blue points in Fig. 6. Given the properties of this feature, it is possible that this is a dwarf satellite galaxy of NGC 105 NED02. Another interesting feature is that the central ring-like pattern of increased metallicity is interrupted by a region of slightly lower metallicity located at coordinates (− 3, −2). Examining the [ O iii] 5007/Hβ and [ N ii] 6584/Hα maps, we again noted that this is caused by an asymmetry in [ O iii] 5007/Hβ. The [ O iii] 5007/Hβ ratio at (− 3, −2) is slightly higher and causes the lower metallicity estimate.
UGC 4008 NED01: this is the only galaxy in our sample that shows a positive metallicity gradient.
4.2. Stellar populations
4.2.1. Stellar vs. gas dust extinction
STARLIGHT fits provide an estimate of the extinction by dust suffered by the stellar light. The assumption that the stellar populations of different age are subject to the same extinction is probably not entirely correct. It is reasonable to assume that the young populations can be still embedded in the dusty nebula where the stars formed and can be subject to higher extinction. STARLIGHT has the capability to take this into account and can determine different extinctions for the different SSP models. However, this approach adds additional uncertainty to the already complex problem of recovering the properties of the stellar populations. We have chosen to assume a single extinction for all SSPs.
The extinction maps of the star light are shown in Fig. 7 and there were no easily identifiable features in them. In comparison with the extinction derived from the emission lines (Figs. 3–5), the extinction derived by STARLIGHT fits is lower. The relation between the star and gas extinction shows considerable scatter and the two quantities appear to be uncorrelated, except for NGC 105 NED02. In this galaxy there is a clear linear relation between the star and gas extinction, with the gas extinction being about twice the star’s extinction. A similar relation was also derived by Cid Fernandes et al. (2005) in their analysis of a sample of SDSS galaxies.
4.2.2. Mean stellar age and metallicity
Stellar population metallicity and age estimates from the STARLIGHT fits.
Table 5 lists the mass- and light-weighted mean stellar population age and metallicity determined from fitting the total galaxy spectrum formed as the sum of all spaxels with (these fits are shown in Fig. 8) and without the AGN-affected central spaxels. The results show that all galaxies in our sample have a higher mean stellar metallicity than solar. This is in accord with the findings from the emission lines analysis. The mean mass-weighted stellar age of the five emission line galaxies is ~5 Gyr. NGC 495, which shows no emission lines, has an older stellar population of about 12 Gyr. These values can be compared with studies based on total galaxy spectra, e.g. obtained with drift-scanning with a long-slit of local galaxies (e.g., Gallagher et al. 2005) or spectroscopy of high-redshift galaxies when practically the whole galaxy light falls into the slit. Note that the residuals show a large-scale pattern with a full amplitude of up to ~4% (Fig. 8). This signals either a problem with the relative flux calibration of the observed spectra or a problem in the SSP models. At present it is difficult to quantify what effect this would have on the results that are based on the spectral fitting.
Figure 7 shows the mass- and light-weighted mean stellar population age and metallicity maps of the six galaxies. In Table 5 are given the measurements for the total galaxy and at the SN position. The maps show considerable scatter and it is difficult to identify clear structures in them. Many spaxels that indicate high metallicity appear in the outer parts. This is most likely not real but rather a result of the insufficient S/N of the spectra even after applying the Voronoi binning. Nevertheless, there may be a slight increase of the metallicity toward the center, especially in NGC 495 and UGC 4008 NED01. The same is also true for the stellar age maps, and again there is an indication of an older stellar population toward the nucleus, which can be expected.
To investigate the matter in more detail, we plot in Fig. 9 the mass- and light-weighted mean stellar population age and metallicity measurements as a function of the de-projected galactocentric distance. Unfortunately, the plot confirms that the measurements from the individual spaxels spectra show too large scatter. Unlike the ionized gas metallicity measurements, which show a small scatter of ≤ 0.05 dex at a given radius (Fig. 6), the stellar metallicities estimated from the STARLIGHT fits show scatter as large as 0.3 dex, for example at a radial distance of 6 kpc in NGC 976, UGC 5129, and NGC 105 NED02. The age estimates also show considerable scatter.
Compressed population vectors showing the contribution of the young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar populations to the formation of the observed total galaxy spectrum.
The analysis of the emission lines shows that most of the ISM properties have a well-defined axial symmetry. One can expect this to be also the case for the stellar populations and hence asymmetries are unlikely to be responsible for the observed scatter in the outer parts of the galaxies. The scatter clearly increases with the radial distance (Fig. 9), suggesting that the lower S/N of the spectra in the outer parts of the galaxies is causing it. After the Voronoi binning the analyzed spectra a have minimum S/N ~ 15–20 at 4600 Å. The large scatter that we observe in the derived quantities demonstrates the limitations of the full-spectrum fitting technique in the low-S/N regime and suggests that an S/N significantly higher than 20 is needed to achieve reliable results.
Given the large scatter of the measurements from the individual spaxel spectra, interpolating at the location of the SNe from the 2D maps is not recommended. An alternative approach is to use the measurements obtained from the azimuthally averaged spectra and interpolate them at the radial location of the SNe. This approach is better when there is evidence that the galaxy properties are symmetric around the nucleus. In Fig. 9 the blue symbols show the values estimated from the fits of the azimuthally averaged spectra and the vertical dashed lines show the radial distance of the SNe. The corresponding fits are shown in Figs. 10–12. The mean age and metallicity show a smooth radial dependence. In some cases the metallicity derived from the azimutally averaged spectra suggests negative gradients of up to −0.03 dex kpc-1. However, given the large uncertainty with which the stellar metallicity is estimated (≥ 0.2 dex), the significance of these gradients is difficult to assess. The mean ages qualitatively show the same behavior with decreasing age outward. We note that the different types of weighting, mass or light, lead to different radial dependencies, with the light-weighted quantities showing stronger variation. The metallicity and the age at the locations of the SNe linearly interpolated from these radial dependencies are given in Table 5. It is also worth mentioning that the light-weight quantities appear to have a slightly lower scatter, most pronounced in the inner regions where the spectra have a higher S/N. In most cases the light-weighted metallicies are lower than the mass-weight ones. The light-weighting gives much more weight to the younger stellar population and this result may imply that the younger populations have lower metallicity.
4.2.3. Binned population vectors
The 2D maps representing the fractional contribution of the young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar populations are shown in Fig. 13. In Fig. 14 the measurement from the individual spaxel spectra and the azimutally averaged spectra are plotted vs. the de-projected galactocentric distance. The measurements from the individual spectra again show considerable scatter in the outer parts of the galaxies. For this reason we again estimated the values at the radial distance SN from the azimutally averaged spectra and not from interpolation of the 2D maps. The estimated stellar population fractions at the SN radial distances are given in Table 6 along with the values derived from the total galaxy spectra. The S/N of the spectra used to derive these values are also shown. The analysis shows that the five emission line galaxies contain stellar populations of different ages, including a considerable fraction of young stars. In general, there is a clear trend of increasing the fraction of young stars with the radial distance. Depending on the galaxy, at a distance of 4–8 kpc the trend is reversed and the fraction of young stars starts to decrease. In four of the galaxies the fraction of old stellar populations monotonically increases toward the galaxy nucleus, which is expected for most star-forming spiral galaxies. The exception is CGCG 207-042, the host of SN 2006te, which shows a decrease of the fraction of old stellar populations toward the center. NGC 495 is dominated by old stellar populations with possibly a small fraction of younger stars in the central few kpc. The contribution of the younger population is small, however, and its presence cannot be confidently confirmed. The behavior of the intermediate age stellar populations is the opposite to that of the old ones.
Cid Fernandes et al. (2005) showed that the compressed population vectors can be recovered with an accuracy better than ~10% for S/N > 10. However, considering the uncertainties involved in the computation of the SSP models as well as other uncertainties such as the correlations between the fitted parameters, the relative flux calibration and the dust extinction laws in the galaxies, the accuracy is probably no better than ~10%. This is also supported by the level of the scatter in Fig. 14. In this context, the population vectors at the locations of SNe 1999dq, 2007A, 1997cw, and 2007R are un-distinguishable from those of the whole galaxies (Table 6). At the location of SN 2006te there is a larger contribution from old populations at the expense of the intermediate age, while the fraction of young stars is the same as for the whole galaxy. For SN 2001fe there is marginal evidence for an increased contribution of a young population at the position of the SN. The host of SN 1999ej formed the bulk of its stars about 13 Gyr ago followed by a less intense star-forming period about 2 Gyr ago. At the distance of SN 1999ej we only find evidence for the older population.
4.2.4. Stellar kinematics
The velocity dispersion maps derived from the STARLIGHT fits show a simple morphology with a single peak centered at the galaxy nucleus. In Fig. 15 the velocity fields of the stars in the five emission line galaxies are compared to the velocity fields derived from the Hα emission line. The two maps are very similar and small systematic differences are only revealed after subtracting the two maps (the last column in Fig. 15). Evidently, the gas rotates faster in the central regions than the stars, with the difference being largest in UGC 4008 NED01. These differences between the rotation of stars and ionizied gas in the central regions of galaxies are well-known and have been extensively studied (see, e.g., Pizzella et al. 2004, and references therein). We note that none of the galaxies shows a sign of counter-rotating gaseous disk (e.g., Bertola et al. 1996; Rubin et al. 1992).
The stellar velocity fields were also analyzed with the methods of Krajnović et al. (2006). As with the Hα velocity map, within the uncertainty we also found no evidence for deviations from pure disk rotation.
4.2.5. Current stellar mass
An estimate of the present-day stellar mass of the galaxies was obtained from the STARLIGHT fits of the total galaxy spectra. The fits are shown in Fig. 8 and the masses are given in Table 6. All the galaxies have masses exceeding 2 × 1010 M⊙ and can be classified as quite massive. The fairly high metallicity that we derived for both the ionized gas and the stellar component are therefore in line with the expectation from the mass-metallicity relation, e.g. Tremonti et al. (2004). We note that the values that we obtain are very close to those of Neill et al. (2009), which were obtained by a different methodology (see Sec. 4.1.3).
5. Discussion
5.1. Galaxy mass and metallicity
We used IFU spectroscopy to derive the spatially resolved properties of six face-on spiral galaxies that hosted seven nearby SNe Ia. The masses of the galaxies derived from the analysis of the total spectra with the STARLIGHT code are all higher than 2 × 1010 M⊙. Recently, Kelly et al. (2010), Sullivan et al. (2010), and Lampeitl et al. (2010) have claimed that the residuals from the best-fit Hubble line correlate with the SN host stellar mass. Furthermore, Sullivan et al. (2010) proposed to incorporate into the cosmological SN Ia analyses two different absolute peak magnitudes for SNe in hosts with masses lower or higher than 1010 M⊙; after the “lightcurve width – luminosity” and color corrections the SNe in the more massive hosts are found to be ~0.06–0.09 mag brighter than their counterparts in lower mass hosts. The galaxies in our sample fall into the high-mass/low-specific SFR bins defined by Sullivan et al. (2010). Accordingly, one can expect the SN in these galaxies to have on average negative Hubble residuals. From Table 2 one can see that four of the SNe have significant positive residuals (>2σ). The other three have negative residuals, but only one of them is bigger than the uncertainly. The mean weighted residual is positive, + 0.07 ± 0.22; however, one should keep in mind that we used only very few SNe in our analysis.
The cause of the apparent dependence of the SN Ia luminosity on the host galaxy stellar mass is still unclear. Theoretical investigations have shown that various parameters of the exploding WD, such as its metallicity, C/O ratio, central density, and progenitor age can affect the amount of 56Ni synthesized in the explosion to a different degree and hence the SN luminosity (see, e.g., Timmes et al. 2003; Röpke et al. 2006; Howell et al. 2009; Bravo et al. 2010,and references therein). Among these parameters, the metallicity is known to correlate with the galaxy mass (see, e.g., Tremonti et al. 2004) and is likely to have the strongest impact. Our analysis of the emission line fluxes and the stellar populations revealed that the galaxies in our sample have on average solar and higher metallicity (Tables 4 and 5). This is not surprising because the galaxies are quite massive and by the virtue of the mass-metallicity relation (see, e.g., Tremonti et al. 2004) may be expected to have high metallicities. For five of the SNe, the ISM metallicity measured at the location of the SN is higher than the galaxy average by about 0.1 dex (Table 4). This can be explained by the presence of radial metallicity gradients and our target selection criteria. Figures 6 and 9 show that the galaxies in our sample have radial metallicity gradients. At the same time, the selection criterion that the SNe are located on a high surface brightness location in the galaxies led to a SN sample that is biased toward SNe close to the galaxy nuclei. Together with the presence of the metallicity gradients, this resulted in most of the SNe being at locations with higher-than-average metallicity within the galaxies (see also Kewley et al. 2005).
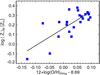 |
Fig. 16 Mass-weighted stellar metallicity vs. gas-phase oxygen abundance estimated from the azimutally averaged spectra. |
While the gas-phase metallicity is easier to estimate, a more relevant quantity is the stellar metallicity. Figure 16 shows the mass-weighted stellar metallicity vs. the gas-phase oxygen abundance estimated from the azimutally averaged spectra. The two quantities appear to be correlated. The slope of the linear fit is ~1.8 with a dispersion of ~0.1 dex. Note that Cid Fernandes et al. (2005) also found that the gas-phase and the stellar metallicities are correlated from an analysis of a large sample of SDSS galaxies. However, the two relations are difficult to compare because the Cid Fernandes et al. (2005) analysis also included low-metallicity galaxies and galaxies in a somewhat higher redshift interval.
5.2. The impact of the metallicity gradient
The presence of abundance gradients in both spiral and elliptical galaxies is now a well-established fact (e.g., Zaritsky et al. 1994; Henry & Worthey 1999). If not taken into account, the gradients will affect any attempt to study the properties of SNe Ia and/or their progenitors as a function of their host galaxy metallicity. The values of the gradients seen in the galaxies in our sample suggest that SN Ia progenitors that form at radial distances greater than ~15 kpc may have metallicities that are lower by a factor at least 2–3 than progenitors in the central parts. Studies of the radial distribution of SNe Ia within their hosts galaxies have shown that more SNe explode in the central regions (e.g., Ivanov et al. 2000; Wang et al. 1997; van den Bergh 1997; Bartunov et al. 2007). However, SNe Ia are also found at large galactocentric distances in both spiral and elliptical galaxies. In Fig. 17 we show the distribution of the projected galactocentric distances (PGD) for a sample of 305 SNe with modern CCD observations (observed after 1990) and with known host galaxy type, redshift, and offset from the center. About 7% of the SNe in spiral galaxies and 20% in the ellipticals are found at PGD > 20 kpc. Since the real galactocentric distances are always greater than, or equal to, the PGD, the above-mentioned fractions are lower limits. Therefore, a significant fraction of SNe may have progenitors with a metallicity that is much lower than that of the host average.
 |
Fig. 17 Distribution of the observed galactocentric distance for a sample of 305 nearby SNe Ia in late- and early-type hosts. Because the distances have not been de-projected these are the minimum galactocentric distances. |
An important question is whether the present-day galaxy metallicity is a good proxy of the metallicity of SN Ia progenitors. This was recently studied by Bravo & Badenes (2011), who used simplified one-zone galaxy evolution models coupled with the SN delay-time distribution (DTD) functions of Pritchet et al. (2008) and Maoz et al. (2010). The authors concluded that the galaxy ISM metallicity is a good proxy for the SN progenitor metallicity and derived simple linear relations to estimate the progenitor metallicity from the present-day host metallicity. However, Bravo & Badenes (2011) did not include metallicity gradient, and more importantly, its possible evolution with time. There is growing evidence that the disks in late-type galaxies formed and evolved slowly under the constant inflow of metal-pool gas from the galactic halo. The galaxy chemical evolution models and hydrodynamical simulations have shown that the metallicity gradient evolves considerably during the last 10 Gyr of the galaxy evolution (Pilkington et al. 2012; Fu et al. 2009; Naab & Ostriker 2006; Sánchez-Blázquez et al. 2009; Mollá & Díaz 2005; Chiappini et al. 2001; Molla et al. 1997). Although the exact results depend of the particular code and model used (Pilkington et al. 2012), all studies but one (Chiappini et al. 2001) show that the metallicity gradient was steeper in the past and gradually flattens out to reach present-day values similar to those observed in local spiral galaxies. Recently, there has also been observational support for this conclusion. Yuan et al. (2011) and Jones et al. (2010) reported metallicy gradients of −0.16 dex kpc-1 and −0.27 dex kpc-1 for galaxies at redshifts z = 1.5 and z = 2.0, respectively. We note that the galaxy chemical evolution studies show that the mean disk metallicity has increased slowly by ~0.3–0.5 dex during the last several Gyr. The gradients seen in the galaxies in our sample and in other galaxies at low and high redshift imply that the metallicity differences within the same galaxy may exceed the cosmological increase of the mean metallicity. In addition, some studies have pointed out that the metallicity gradient in the outermost parts of the galaxies may be steeper than in the inner disk (see, e.g., Fu et al. 2009).
The above studies highlight the complexity of estimating the metallicity of the SN Ia progenitors from their host galaxy present-day metallicity. The difference between the present host metallicity and the SN progenitor metallicity is a complex function of several factors, some of which are poorly understood and not very well constrained with observations: the radial distance at which the progenitor formed, the age of the progenitor, and the evolution of the metallicity gradient. For example, a progenitor that formed at large radial distance will have increasingly larger difference from the preset-day metallicity at the same radius as the progenitor ages. Another uncertainty can be added if the galaxies have experienced major mergers and radial star migrations, which tend to flatted the metallicity gradient (see, e.g., Kewley et al. 2010; Sánchez-Blázquez et al. 2009). This complexity may be the reason why the attempts to correlate the Hubble residual with the host global metallicity have not led to conclusive results (Gallagher et al. 2008; Howell et al. 2009; Gallagher et al. 2005; D’Andrea et al. 2011). Note however that Howell et al. (2009) did not directly measure the metallicity but rather estimated it from a mass-metallicity relation.
All SNe in our sample but one are within 5 kpc from the galaxy centers. Generally, the chemical evolution models show that the metallicity close to the galaxy nuclei changes least. Therefore, the metallicity of the SN progenitors that formed near the center should be closer to the present-day galaxy metallicity compared to the progenitors that formed in the outer parts. Together with the fact that we measured fairly high present-day metallicity at the locations of all SNe, this suggests that their progenitors did not form in metal-poor environments, unless they came from very old stellar population with a long delay time.
5.3. Star formation history
Much of the recent progress on the question of SN Ia progenitors has been achieved through studies of the SN rates. It is now well-established that the SN Ia rate depends on both the total stellar mass and the recent SFR in the host galaxy (e.g., Mannucci et al. 2005; Scannapieco & Bildsten 2005; Sullivan et al. 2006; Maoz et al. 2010; Brandt et al. 2010), which led to a two component model for the SN Ia rate, the co-called A+B model. Along with the fact that SNe Ia are also observed in old, passive galaxies, this points to the existence of at least two evolution channels for SNe Ia associated with young and old stellar populations.
Except for NGC 495, all other galaxies in our sample contain a considerable fraction of young stars and strong Hα emission, indicating ongoing star formation activity. The STARLIGHT fits of the total galaxy spectra are shown in Fig. 8. Except for NGC 495, all other galaxies show a similar pattern, namely, the population vectors xj show the largest contribution from SSPs with ages 0.5–5 Gyr. Young populations, ~50 Myr, are also confidently detected in all cases. From Figs. 13 and 9 it can be seen that the fraction of young stars increases with increasing the radial distance. It is known that the full-spectrum fitting techniques tend to estimate suspiciously large components with ages ~1 Gyr (see, e.g., Asari et al. 2007; Mathis et al. 2006; Panter et al. 2007) and one may ask whether the large contribution of SSPs of similar ages that we see in our analysis is real. Asari et al. (2007) and Cid Fernandes et al. (2009) report that the problem disappeared once they switched from the original Bruzual & Charlot (2003) fitting basis based on STELIB to a new basis that uses the MILES spectral library. Because we also used the newer Bruzual & Charlot basis based on MILES, our results are also likely unaffected by the above-mentioned problem.
We estimated the current SFR rate from the Hα emission line flux (Table 3). Because most of the ionizing photons are produced by massive, short-lived stars, the Hα flux is a tracer of the very recent star formation, ≤ 20 Myr. Another estimate of the SFR can be obtained from the STARLIGHT fits following the methodology described in Asari et al. (2007). We estimated the mean SFRs during the last 0.5 Gyr and last 50 Myr. The values are given in Table 3. The mean SFRs over the last 50 Myr are very similar to the estimates obtained from the Hα flux; Asari et al. (2007) have already demonstrated that there is a tight correlation between these two estimations using a large sample of SDSS galaxies. On the other hand, the mean SFRs during the last 0.5 Gyr are by a factor 3–5 higher than the SFR estimates from Hα flux, but are similar to those of Neill et al. (2009). The only exception is UGC 4008 NED01, for which we obtain a much higher value; note, however, that the confidence interval quoted by Neill et al. (2009) has an upper limit higher by an order of magnitude than our estimate. Note also that the model SEDs that Neill et al. (2009) fitted to the broad-band photometry are based on eight galaxy models with pre-defined SFHs, which were meant to represent the Hubble galaxy types plus one star-burst galaxy model. STARLIGHT does not assume any pre-defined SFH and the contributions of all SSPs are free parameters. Therefore, STARLIGHT is much more flexible to describe galaxies with arbitrary SFHs.
If the two components of the A+B model represent the contribution of two different channels to produce SNe Ia, we can estimate the probability from which channel the SNe in our galaxies were produced. With the A and B constants estimated by Sullivan et al. (2006) and our measurement of the galaxies’ total mass and SFR, the SNe in the five star-forming galaxies have an about equal chance to have come from the young or the old channel.
5.4. Correlation between the SN and host galaxy properties
Despite the low statistics of our sample, we can still test correlations between the SALT2 x1 parameter and the Hubble residuals of the SNe with the various parameters that we derived for the total galaxy and at the SN locations (Tables 3–6). We found no statistically significant correlations. The small number of objects is certainly not ideal for this analysis, but the metallicity and the masses of the galaxies in our sample also span quite a small range. To search for correlations it is necessary to expand the sample toward lower masses and metallicities. This may not be an easy task because SNe Ia in metal-poor galaxies in the local Universe are rare. Besides, the low-mass, low-metallicity galaxies tend to be faint and are more difficult to observe with a sufficient S/N.
In addition to the above concerns, when correlating the SN properties with the properties of their host galaxies at the location of the SN one should always bear in mind that the SN progenitors may be very old stars (e.g., Maoz et al. 2011). The progenitor system may have migrated from its birth place and the galaxy properties at its present location may be different from those where the progenitor has formed. Maoz et al. (2011) discussed that random stellar motions will affect the SN progenitor and its surroundings in the same way. As a result, the population that gave birth to the SN progenitor will also be present in the new SN location. Following the same argument, the radial star migrations should not have a significant effect either. Additionally, Sánchez-Blázquez et al. (2009) found that within the central 5–10 kpc the radial star migration during the whole galaxy evolution is fairly small ~1.5 kpc and increases to only ~3.5 kpc in the outer parts.
Another problem is related to the projection effects. Because the SN Ia progenitors have a broad range of ages between ~100 Myr and 10 Gyr, SNe can explode anywhere along the line of sight. An SN produced by an young progenitor would have most likely exploded in the galactic disk, where the newly formed stars and the ionized gas typically reside. In this case the progenitor star’s metallicity should be close to that of the ionized gas at the (projected) location of the SN. In the case of old progenitors, however, the SN may have exploded in the galactic halo and the metallicity of its progenitor may be very different from the gas. Similarly, the stellar continuum at a given spaxel is the sum of all star light along the light of sight. All these effects indicate that the correlation of the SN properties with the properties of its local environment is not unambiguous.
Clearly, to study the correlation between the SN properties and its local environment, a large, unbiased sample of galaxies observed with a large-field IFU spectrograph is needed. Our sample of seven SNe Ia in six galaxies is not large enough to draw any conclusion. The ongoing CALIFA5 survey (Sanchez et al. 2012) will provide IFU observations of about 600 galaxies at redshift z ~ 0.02. CALIFA uses the same instrument as the observations presented in this paper with similar setup and exposure times, and will provide data of similar quality as ours. The CALIFA targets are selected from a larger pool of about 1000 galaxies based only on the visibility of the targets at the time of the observations. Many of these galaxies are known to have hosted SNe. In addition, there are several ongoing large-field SN searches with that will potentially discover many new SNe in CALIFA-targeted galaxies. Thus, the CALIFA survey will provide a solid base to further expand the studies SNe Ia properties as a function of their local environment to all SN types. In addition, CALIFA will provide the full galaxy spectra that will allow one to avoid the aperture effects to which the SDSS spectroscopy is subject. At low redshift the 3′′-diameter fibers of the SSDS spectrograph cover only the galaxy nucleus, whose properties may be very different from those of the disk and may not be representative for the environment of the SNe that exploded elsewhere in the galaxy, for example because of the radial gradients of these properties.
6. Conclusions
In this pilot study we have obtained and analyzed IFU spectroscopy of six nearby spiral galaxies that hosted seven SNe Ia. For the data reduction we developed and tested a robust reduction pipeline. A set of tools that implement various methods to derive the properties of the ionized gas and the stellar populations from the data-cube were also developed. This allowed us to generate 2D maps of the galaxies properties. The analysis of the maps showed that the quality of the data is sufficient to accurately derive the properties of the ionized gas even in the outer low surface brightness parts of the galaxies. However, the parameters of the stellar populations are determined with much larger uncertainties. We showed that analysis of azimutally averaged spectra at several de-projected galactocentric radii instead of the 2D maps provides a more robust way to derive the radial dependencies of the stellar population properties in galaxies with well-defined axial symmetry. The main results of our study can be summarized as follows:
-
The six galaxies are quite massive with masses exceeding 2 × 1010 M⊙.
-
The ionized gas and the stellar populations both indicate metallicities above the solar value.
-
Five of the galaxies are currently forming stars at a rate of 1–5 M⊙ yr-1, which is typical for spiral galaxies at z ≃ 0. The sixth galaxy shows no signs of star formation.
-
The five star-forming galaxies have mean mass-weighted stellar age ~5 Gyr and the passive one ~12 Gyr.
-
Four of the five star-forming galaxies show radial gradients of their ionized gas metallicity in the range from −0.022 to −0.058 dex kpc-1. These values are typical for other spiral galaxies in the local universe. The fifth galaxy has a nearly uniformly distributed metallicity with a hint of a very low positive gradient of + 0.007 dex kpc-1.
-
The radial dependence of the stellar population properties can be more robustly derived if azimutally averaged spectra at several de-projected galactocentric radii are analyzed. By this analysis we found indication of low negative radial metallicity gradients of the stellar populations in some galaxies of up to −0.03 dex kpc-1. Given the large uncertainties with which the stellar metallicity is estimated, the significance of these gradient is difficult to assess.
-
In the five star-forming galaxies the fraction of young stellar populations increases until 4–8 kpc and shows signs of a subsequent decrease. In four of them the fraction of old stars monotonically decreases in the disk and one galaxy shows a more complex behavior.
-
The passive galaxy has mostly old stars, with a possible small fraction of younger stars in the central few kpc.
-
The kinematic analysis indicates that the galaxies are relaxed systems that most likely have not experienced recent a major merger.
-
Most of the SNe in our sample are projected on regions with metallicity and star formation rates above the galaxy average, likely as a result of our target selection criteria and the radial metallicity gradients.
-
The BPT diagnostic diagram revealed that two of the galaxies host AGNs. Another galaxy is on the border between the AGNs and the star-forming galaxies. Our analysis shows that the AGNs are not strong enough to affect the quantities derived from the total galaxy spectra. This AGNs may not be recognized in studies of host galaxies of SNe Ia at high redshift.
-
The correlation of the SALT2 x1 parameter of the SNe and the Hubble residuals with the various parameters of the host galaxies did not lead to conclusive results. The low statistics and the small ranges spanned by the galaxy parameters render such an attempt still premature. We also note that the HRs of our SNe are on average positive, although their host galaxies have masses in the range where the other studies have shown negative HRs.
In conclusion, we have demonstrated the viability to study the host galaxies of SNe Ia at low redshift using wide-field IFU spectroscopy at 4 m-class telescopes. Intermediate-resolution spectra with sufficient S/N can be obtained out to the outer low-surface brightness parts of the galaxies with a reasonably long exposure time of ~1.5 h. Compared to a integrated spectroscopy and analysis of multi-color broad-band imaging, the IFU spectroscopy provides much more detailed information about the properties of the galaxies, e.g. metallicity and age gradients, detailed star formation histories, etc. In principle, the S/N of our data is sufficient to perform correlation analyses between the SN properties and the properties of the host galaxies at the location of the SN. However, our current sample it too small and suffers from strong selection biases to provide robust correlation results. The ongoing CALIFA survey may soon provide IFU spectroscopy of a larger sample of SNe Ia host galaxies, which will be a solid basis to further explore this path to study the SNe Ia progenitors and improve SNe Ia as distance indicators. We have tested the methodology and developed semi-automated tools that will allow expanding our analysis once the CALIFA data become available.
Online material
Appendix A: PMAS/PPAK instument details
In this section we provide some details on the PPAK instrument that are relevant for the data reduction. For a full description of the instrument see Verheijen et al. (2004), Roth et al. (2005), and Kelz et al. (2006).
The PPAK fiber bundle consists of 382 fibers with 2.7′′ diameter each, 331 of which (science fibers) are ordered into a single hexagonal bundle that covers a field-of-view (FOV) of 72′′ × 64′′. Thirty-six additional fibers form six mini-bundles of six fibers each (sky-bundles). The sky-bundles are evenly distributed along a circle of radius ~90′′ and face the edges of the central hexagon (see Fig. 5 in Kelz et al. 2006). The remaining 15 fibers are used for calibration and can only be illuminated with the PMAS internal calibration unit.
The fibers are ordered into 12 slitlets. Each slitlet typically holds 28 science fibers, three sky-fibers from three different sky-bundles and one calibration fiber. The three sky-fibers are evenly distributed between the science fibers in the slitlet. The 12 slitlets are ordered to form a pseudo-slit. When projected onto the CCD in 2 × 2 binned mode, the separation between the spectra along the cross-dispersion direction is ~4.8 pixels and the full-width at half-maximum (FWHM) of the spectral traces is ~2.5 pixels. Between the slitlets there are gaps about two fibers wide, with the exception of the two central slitlets, which are separated by wider gap of ~10 fibers (see Fig. A.1; and also Figs. 13 and 14 in Kelz et al. 2006).
 |
Fig. A.1 Part of one of the science images that demonstrates the configuration of the fibers on the CCD. The calibration fibers are not visible because they are not illuminated during the science exposures. The calibration fibers are normally last within the slitlets. Slitlet #6 holds two calibration fibers, and two more are placed at the beginning of the fiber sequence and one is at the end. |
Because the fibers are circular, only ~65% of the FOV is spectroscopically sampled in a single exposure. Therefore, at least three suitably offset pointings are needed to spectroscopically sample every point in the PPAK FOV.
Appendix B: Data reduction
The pre-reduction of the CCD images was performed with IRAF and the remaining reduction with our own programs written in IDL.
B.1. Pre-reduction
The PMAS 4k × 4k CCD is read by four amplifiers and for each exposure four separate FITS files are created. These were individually pre-reduced. The bias frames showed no significant large-scale structures and the bias was corrected by subtracting the average value computed from the CCD overscans. The images were then trimmed, converted from ADUs into electrons using the gain values measured during the commissioning of the CCD and finally combined into a single 2D image, on which the spectra were oriented roughly along the rows.
To create a master flat-field image, all halogen lamp exposures obtained during the run where summed. The separation between the spectra along the cross-dispersion direction is ~4.8 pixels and the full-width at half-maximum (FWHM) of the spectral traces is ~2.5 pixels. As a result, the intensity of the pixels between the spectra is ~20% of the peak value (e.g., see Fig. 18 in Kelz et al. 2006). Therefore, when all the images of the halogen lamp spectra are combined, there will be enough counts even in between the spectra. Moreover, because of the instrument flexure the positions of the spectra change by up to ~1–2 pixels, depending on the pointing of the telescope. As a result, in the combined image the intensities between the spectra were ~80% of the peak values. Because the intensity changes smoothly along the dispersion axis, each image row was smoothed with running median in a window of 20 pixels to normalize the master flat-field image. The flat-field image was divided into its smoothed version to derive the final normalized flat-field that contained only the pixel-to-pixel variations.
Because of the relatively long exposures used, the images contain many pixels that are affected by cosmic ray (CR) hits. The complexity of PPAK images makes it very difficult to use conventional methods for CRs rejection. We experimented with different approaches and found that the CRREJ algorithm (developed for WFPC on HST6) gave the best results. We tried different parameter settings, each time carefully examining the CR masks to verify that no sky lines or galaxy emission lines were identified as CRs and at the same time as many as possible CRs were identified. It was occasionally necessary to manually mark some CRs. Finally, the values of the CR hit pixels were replaced with the values derived by interpolating the adjacent good pixels. We used cubic-spline interpolation and the direction of the interpolation depended on the extent of the CR-affected region along the image rows and columns
B.2. Spectra tracing
The continuum lamp exposures that were obtained before and/or after the science exposures were used to trace the positions of the spectra on the CCD. The spectra tracing was performed in two steps. First, 20 columns at the middle of the image were averaged and used to determine the location of all 382 spectra. Then moving left and right and averaging 20 columns, the position of each spectrum at each CCD column was determined using the peak positions of the previous column as starting points. The positions of the maxima were determined by fitting a parabola to either the three or the four highest intensity points. When the ratio between the two highest points was lower than 0.9, three points were used, in which case the parabola passes exactly through all three points and the maximum can be computed. Otherwise, a least-squares fit was used to determine the maximum.
The space between the adjacent spectra is ~4.8 pixels, which prevented us from using a more accurate scheme to compute the positions of the spectra. The traces determined at the first step were clearly oscillating with an amplitude ~1/3 pixels and it was necessary to additionally smooth them. The traces were fit with a sixth-order polynomial function and the results were stored in a FITS file.
Because of the mechanical flexures of PMAS the positions of the spectra moved slightly (at sub-pixel level) between the exposures, even within the sequence of exposures of a given galaxy. This effect can be accurately accounted for by a constant shift of the derived spectral traces. To derive these shifts, the average of 20 columns taken at the middle of the 2D image was cross-correlated with the same average in the halogen 2D image that was used to trace the spectra. In the subsequent reduction steps these shifts were always accounted for.
B.3. Scattered light
A small amount of scattered light is present in the images and it needs to be subtracted to achieve an accurate flux calibration. To derive a 2D model of the scattered light, we used the gaps between the slitlets (Fig. A.1), which contain no light from the object. Bands of five pixels width were extracted from the gaps (wider band was extracted between the sixth and the seventh slitlets) using the information from the spectra tracing. The bands were converted into 1D vectors by running median in 5 × 5 pixel window and the positions along the y-axis were also computed. The scattered light pattern along the dispersion axis is fairly complex and the attempts to directly fit a 2D polynomial surface yielded no satisfactory results. Instead, the scattered light vectors were cubic-spline-interpolated along all image columns (in the spatial direction) to derive the amount of scattered light at each image pixel. The resulting 2D model image of the scattered light was smoothed by 50 × 50 pixel running median and subtracted from the original image.
B.4. Spectra extraction and cross-talk correction
The spectra were extracted from the 2D images using a simplified version of the optimal extraction algorithm of Horne (1986). In this method the spatial profile of the spectral trace is determined from the data themselves and is used to form a weighted sum of the pixels in a given aperture, giving larger weights to the pixels that received more light. In the conventional longslit spectroscopy the profile is determined by the seeing and the telescope guiding, and may change considerably from exposure to exposure. In the case of PPAK the spatial profiles are almost entirely determined by the size of the fibers and have a stable shape that can be accurately described by a Gaussian. Thus, we determined the FWHMs of the Gaussians that describe the profiles of all 382 spectra and used this information to compute the weights for the optimal extraction. Series of halogen lamp spectra were obtained and added to increase the signal-to-noise ratio (S/N). For each image column 382 Gaussians were simultaneously fitted to derive the FWHMs. The fitting was performed with the MPFIT IDL package7 and special care was taken to provide accurate starting values; otherwise the fit with so many Gaussians would fail. The resulting 2D FWHM image (382 spectra by 2048 spectral elements) was somewhat noisy and was smoothed by running median within 11 × 11 elements window. The mean FWHM is 2.46 pixels and the covered range is 2.12–2.85.
With the positions of the spectra and the spatial profiles determined, the spectra were extracted with the optimal extraction algorithm. The separation between the spectra within the slitlets is fairly constant ~4.8–4.9 pixels, both from spectrum to spectrum and along the trace. The extraction apertures were automatically computed as half the average distance from closest spectrum. This means that for a given spectrum the extraction aperture may be slightly asymmetric with respect to the trace center and that different spectra may have slightly different aperture sizes.
Within a given slitlet the spectra are separated by only ~2 × FWHM, which leads to an effect known as cross-talk, i.e. contamination by adjacent spectra8. Sánchez (2006) proposed the iterative Gaussian-suppression technique and we followed this approach with small modifications. After the first optimal extraction, the contamination from the adjacent spectra for a given spectrum was estimated as follows. Using the estimated flux, trace positions and FWHMs of the Gaussians that describe the spatial profiles of the adjacent spectra, and taking into account the finite size of the extraction apertures, we computed the height of the Gaussian functions that would have produced the fluxes of the adjacent spectra were. This was performed for all columns and the contamination of the adjacent spectra was subtracted. Then a new optimal extraction was performed on the corrected image using the same extraction aperture as before. This was performed for all spectra and the process was iterated once more.
B.5. Wavelength calibration
The HgNe and ThAr arc-lamp spectra were used to derive separate wavelength calibrations for each individual spectrum. The arc-lamp spectra were extracted in exactly the same way as the science ones and the positions of all Hg, Ne and Cd9 lines with known laboratory wavelengths were determined by a least-squares fit with Gaussian function. A sixth-order polynomial fit was then used to derive accurate pixel-to-wavelength transformations. The spectra extend from about 3700 Å to 7000 Å. The bluest line in the HgNe spectrum is at ~4047 Å. Thus, the wavelength solution below ~4000 Å may not be accurate. On the other hard, the two reddest arc lines are at 6717 Å and 6929 Å. Because of the field vignetting (see below) the 6929 Å line was not detected in all fibers and as a result for those fibers the red part of the wavelength solution may also be inaccurate. To work around this problem, the 15 calibration fibers that were illuminated with a ThAr lamp were used to improve the wavelength solutions in the two extremes of the covered wavelength range. The dispersion over the wavelength range is between 1.5 Å pixel-1 and 1.7 Å pixel-1
B.6. Background subtraction
The spectra extracted from fiber-fed or IFU spectrographs contain not only the object light, but also the sky background, which needs to be subtracted. For faint objects the background may exceed the object flux by far and accurate background subtraction is essential to obtain reliable results. The PPAK design with the separate sky-fibers, which are distributed evenly between the science fibers, gives the flexibility to apply different approaches to the background subtraction. The following method was found to work best. The sky-fibers were first examined to check if some of them were accidentally contaminated by background objects. No such cases were found. Each element of the 331 science spectra was labeled with a pair of numbers (λi, N), its wavelength and fiber number as is recorded on the CCD, respectively. For a given element (λi, N) all sky-spectra were interpolated at a common wavelength λi using forth-order B-spline interpolation10, which has one of the best interpolation properties of all known interpolation schemes (e.g., Thèvenaz et al. 2000). The interpolated sky-spectra were fitted as a function of their fiber position with least-squares fifth order polynomial fit and the value of the sky at the element position N was recorded. Repeating this for all elements gives a 2D model of the sky-background, which was subtracted from the science fibers. The sky-subtracted 2D images were carefully examined and no visible systematic residuals were noticed, except at the position of the few strongest sky-lines.
B.7. Flux calibration
The flux calibration of the spectra was a two-step process: (i) normalization for the fiber-to-fiber throughput variations and (ii) correcting for the wavelength-dependent system response. To account for the fiber-to-fiber throughput variations the series of twilight sky exposures were used. The individual images were added to increase the S/N and all spectra were extracted and wavelength-calibrated in the same way as the science ones. Unfortunately, with the new larger CCD11 the images suffer from vignetting at the corners. The sensitivity of the parts of the spectra that are projected at the CCD corners falls sharply as function of the distance from the CCD center (Fig. B.1). The relation between the on-sky fiber positions and the fiber position on the CCD is such that the most affected fibers are those adjacent to the central hexagon of 37 fibers (see Fig. 7 in Kelz et al. 2006) and not the outermost fibers. The fibers of the central hexagon are projected at the middle of the CCD and are practically un-affected by the vignetting.
To derive the relative throughput of the fibers, all spectra were interpolated on a common wavelength frame. The 37 spectra of the central hexagon were averaged and all spectra were divided by this average spectrum. The resulting ratios were least-squares fitted with polynomials of different degrees (high orders were needed for the fibers most affected by the vignetting) to derive the throughput map of the fibers. The map is shown in Fig. B.1 and the vignetting at the corners is clearly visible. This map was used to equalize the throughput of the fibers by dividing all science exposures by it.
 |
Fig. B.1 Throughput map of the PPAK fibers. Note the vignetting in the corners. |
During the analysis it was found that for several of the fibers that were most severely affected by the vignetting the drop of the throughput in the extreme blue and red parts could not be corrected well. This resulted in several spaxel spectra having incorrect relative flux calibration at the two extreme ends. This affected the spectrum fitting of these spaxels with STARLIGHT. Because the Hα flux was also affected, the estimation of the extinction was unreliable and hence part of the emission line analysis. The “bad” spaxels were masked in the 2D maps of the affected properties. It should be noted, however, that our primary gas metallicity indicator, the O3N2 method, was not affected because it only involves flux ratios of emission lines at close wavelengths.
The two spectrophotometric standard stars that were observed on 15 November were used to derive the system response. The spectra of the standards were extracted, wavelength-calibrated, background-subtracted and fiber-throughput-corrected in the same way as the rest of the science exposures. The presence of gaps between the fibers in combination with the point source nature of the standards makes it difficult to recover the whole flux of the star from a single exposure. In addition, because of the differential atmospheric refraction (DAR) there may be significant differential flux losses. By taking the observations of the standards at five different points on the PPAK FOV, we aimed to minimize these effects. First, the differential flux losses may cancel out when the five spectra are summed. Second, it gives more control, for example, too discard a clearly deviating observation.
To minimize the flux losses instead of summing all spectra that contain object flux, we adopted a different approach. The spectra were interpolated at a common wavelength scale and each fiber was associated with its on-sky position. For each wavelength plane a symmetric 2D Gaussian function (without constant term) was fitted and the flux was taken to be the integral over the Gaussian. So extracted spectra were compared with the result of simply suming the fibers. The spectra extracted with the Gaussian fitting were clearly more consistent between the five pointings. With the exception of one pointing for each standard, the systematic difference between the spectra were less than ~3–4%. The deviating spectra for each star were discarded and the remaining four were averaged. After correcting for the atmospheric extinction using a mean extinction curve for Calar Alto Observatory, the ratio between the observed counts and the tabulated fluxes of the standard were fitted with a polynomial function to derive the sensitivity function of the system. The sensitivities derived from the two standards agreed well and the average of the two sensitivities was used to calibrate all science observations.
 |
Fig. C.1 Example of the effect of the stellar spectrum subtraction in the regions of Hβ and Hα emission lines. In the top panels we show the observed spectrum with the best fit overplotted. The bottom panels show the observed spectrum minus the best fit. Clearly, the fluxes of the emission line cannot be accurately measured without a proper subtraction of the stellar spectrum. |
B.8. Final data-cubes
The final step in the reduction was to combine the three pointings into a data cube. The spectra were re-sampled into a common linear wavelength scale with a sampling of 1.5 Å per element. Taking into account the offset between the exposures, the circular fibers were mapped onto an output grid of square 2′′ × 2′′ pixels. The flux of a given fiber was distributed between the output pixels according to the overlap area between the fiber and the output pixels. No attempt was made to first shrink the fibers and emulate the Drizzle algorithm used for HST images (Fruchter & Hook 2002); with only three barely overlapping pointing this would not gain any improvement. However, with five or more carefully selected pointings it may be possible to use Drizzle to improve the spatial sampling of the final cubes.
Two important effects were taken into account two when creating the data-cubes – the non-photometric condition and the differential atmospheric refraction (DAR). To account for the first, for each galaxy and pointing the total flux within an aperture of 12′′ centered on the galaxy core was computed and the observations of given galaxy were scaled to the exposure with the highest flux. With one exception all corrections were smaller than 15%; the remaining pointing required a correction factor of ~2.
The observations were obtained at an airmass of less that 1.3 and the effect of DAR was small, but we nevertheless corrected for it. To compute the DAR we used the formulas from Szokoly (2005) and the ambient conditions as recorded in the FITS image headers. To combine the three pointings, we shifted the positions of the fibers for each wavelength slice along the x and y axes by the values computed from the value of the DAR at that wavelength (with respect to the refraction at 6300 Å) and the effective parallactic angle of the observations (see also Walsh & Roy 1990). For both the DAR-corrected and un-corrected data-cubes, the positions of the galaxy nuclei were computed in the blue (average in 3800–4000 ÅÅ) and red (6600–6800 ÅÅ) wavelength ranges. The two positions measured in the DAR-corrected cubes matched very well, but not in the un-corrected cubes, which shows that the DAR was correctly accounted for.
Three of the galaxies in our sample also have SDSS spectroscopy. This allowed us to check the relative flux calibration of our spectra. To emulate the SDSS spectroscopy, we extracted from our data-cubes the flux within an aperture of 3′′ diameter centered on the galaxy nucleus and scaled it to match the mean flux level of the SDSS spectra. The comparison between the SDSS spectra and those extracted from our date-cubes is shown in Fig. 1. It shows that the relative flux calibration of our spectra is excellent and matches SDSS to within a few percent.
To set the absolute flux scale of the data-cubes we used the SDSS imaging. SDSS g and r magnitudes of the galaxies were computed within an aperture of 20′′ diameter. Spectra within the same aperture size were extracted from the data-cubes and synthetic g and r magnitudes were computed. The g and r scale factors that made the synthetic magnitudes match the observed ones were computed and the average of the two was applied to the data-cubes. It should be noted that the g and r scale factors coincided to within a few percent, which supports our conclusion that the relative flux calibration is accurate.
Appendix C: Measurement of emission line fluxes
Five of the six galaxies show strong nebular emission lines. This enabled us to study the properties of the gas phase in the galaxies through measuring the fluxes of the most prominent emission lines [O ii] λ3727, Hβ, [O iii] λλ4959/5007, Hα, and [N ii] λλ6549/6584, and when possible also [S ii] λλ6716/6731. In spectra of galaxies the nebular emission lines are superimposed on the underlying stellar continuum. The stellar absorption lines can bias the measurement of the emission line fluxes, an effect that is especially prominent in Hβ (Fig. C.1). Therefore, the stellar continuum needs to be subtracted first to measure the emission line fluxes accurately. For this we used the STARLIGHT software (Cid Fernandes et al. 2005). Briefly, after masking the regions of known nebular emission lines, telluric absorptions, and strong night-sky emission lines, the spectrum was fitted with a linear combination of model spectra of single stellar populations (SSP) of different ages and metallicities. The best fit was subtracted to derive the pure emission line spectrum, where the emission line fluxes can be measured without bias, see Fig. C.1. The parameters of the fitted SSPs can be used to derive the properties of the galaxy stellar population, but here we regarded the fits as a means to subtract the underlying stellar absorption. All spectra that had S/N higher than 5 at ~4600 Å were fitted and the emission line fluxes were measured on the continuum-subtracted spectrum. For the remaining spectra the measurements were made without continuum subtraction. A weighted non-linear least-squares fit with a single Gaussian plus a linear term was performed for each emission line, and the area below the Gaussian was taken as an estimate of the flux. The weights were the error spectrum produced during the spectral extraction. Including the linear term is necessary to account for possible systematic residuals due to imperfect subtraction of the the stellar absorption spectrum. The close lines Hα, [N ii] λ6549 and [N ii] λ6584 were simultaneously fitted. [O ii] λ3727 is a blend of two lines – [O ii] λλ3726.04/3728.80. This blend was fitted with two Gaussians with equal width and a fixed separation of 2.76 Å. In addition, a robust standard deviation of the adjacent continuum was also measured from the regions more then 3σ away from the line centers.
The uncertainty of the line fluxes was estimated by propagating the uncertainties of the fitted amplitude and σ of the Gaussians. To check the reliability of this estimate, we performed Monte Carlo simulations. We assumed that the lines have a Gaussian shape with σ = 2, representative for our spectra, and that they were superimposed on constant background with standard deviation one and mean zero. The noise across the line was assumed to follow a Poisson distribution – if a given datum has N counts, the 1σ uncertainty of this datum is (1 + N)1/2. This noise model was used to generate pseudo-random numbers, which were added to the line and the line was fitted (weighted by the noise model). This was repeated 1000 times and the mean values and the standard deviation of σ, the amplitude, and the area below the Gaussian were computed. This procedure was repeated for Gaussians with amplitudes 2 to 1000, i.e. exceeding the continuum noise by the same numbers.
The results of these simulations show that propagating the errors of the fitted parameters to the total flux overestimates the
uncertainty by about a factor of 2. The simulations also showed that the area below the Gaussian can be recovered with ~30% accuracy and without significant bias for lines that exceed the continuum noise by only three times. The S/N of the measured line flux was tabulated as a function of the ratio of the fitted amplitude of the Gaussian to the standard deviation of the adjacent continuum and was used to assign realistic errors to the line fluxes measured by fitting a Gaussian function. For example, a 10% accuracy is achieved when the amplitude of the Gaussian is 20 times the continuum noise. A possible concern is that the shape of the lines in the real spectra may deviate from Gaussian, in which case additional uncertainty will be introduced. Close inspection of the line fits revealed that the line shape in our spectra is well represented by a Gaussian function and we do not expect problems related to a non-Gaussian line shape.
 |
Fig. 7 From left to right: SDSS color images of the galaxies, the light-weighted average stellar population age ⟨ log t∗ ⟩ L and metallicity ⟨ Z∗ ⟩ L, and the visual extinction AV determined by STARLIGHT fits to the stellar spectra. |
 |
Fig. 8 STARLIGHT fits to the total galaxy spectra. For each galaxy we also show the ratio between the observed and the best-fit spectrum. The vertical brown lines in the spectrum panels show the location of the strongest night-sky lines, which could not be cleanly subtracted and the corresponding wavelength regions were excluded from the fits. To the right of the plots are shown the population vectors and the mass-fraction vectors along with the extinction, the mass- and light-averaged age and metallicity, and the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age > 2.4 Gyr) stellar populations. The short brown bars show the ages of the SSPs used in the fits and the two vertical dotted lines separate the young, intermediate and old populations. |
 |
Fig. 9 Mass- and light-weighted average stellar populations metallicity (left panel) and age (right panel) from the STARLIGHT fits as function of the de-projected galactocentric distance. The small black dots are the measurements on the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
 |
Fig. 13 From left to right: SDSS color images of the galaxies and the maps of the fraction of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age < 2.4 Gyr) stellar populations. |
 |
Fig. 14 Compressed population vectors corresponding to the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar population to the formation of the observed spectra as function of the de-projected galactocentric distance. The small black dots are the measurements obtained from the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
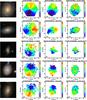 |
Fig. 15 From left to right for each galaxy we show the color SDSS image, Hα velocity map, the star velocity map, and the difference between them. The x,y coordinates are in arcsec with respect to the map centers. The orientation of the images is north – up, east – left. |
For NGC 495 the stellar velocity map was used because this galaxy shows no emission lines.
We use the IDL implementation available in the IDL Astronomy User’s Library maintained by Wayne Landsman and available at http://idlastro.gsfc.nasa.gov/
Available at http://cow.physics.wisc.edu/~craigm/idl/idl.html
Acknowledgments
V.S. acknowledges financial support from Fundação para a Ciência e a Tecnologia (FCT) under program Ciência 2008. This work was partly funded by FCT with the research grant PTDC/CTE-AST/112582/2009 and a Ph.D. scholarship SFRH/BD/28082/2006, and under the Marie Curie Actions of the European Commission (FP7-COFUND). This work has made use of the NASA/IPAC Extragalactic Database (NED), NASA’s Astrophysics Data System, and data products from SDSS and SDSS-II surveys. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/.
References
- Albrecht, A., Bernstein, G., Cahn, R., et al. 2006 [arXiv:astro-ph/0609591] [Google Scholar]
- Alloin, D., Collin-Souffrin, S., Joly, M., & Vigroux, L. 1979, A&A, 78, 200 [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Asari, N. V., Cid Fernandes, R., Stasińska, G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartunov, O. S., Tsvetkov, D. Y., & Pavlyuk, N. N. 2007, Highlights of Astronomy, 14, 316 [NASA ADS] [Google Scholar]
- Becker, S. A., & Iben, Jr., I. 1980, ApJ, 237, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bertola, F., Cinzano, P., Corsini, E. M., et al. 1996, ApJ, 458, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kasen, D., Shen, K. J., et al. 2012, ApJ, 744, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Brandt, T. D., Tojeiro, R., Aubourg, É., et al. 2010, AJ, 140, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E., & Badenes, C. 2011, MNRAS, 414, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E., Domínguez, I., Badenes, C., Piersanti, L., & Straniero, O. 2010, ApJ, 711, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Garnett, D. R., & Kennicutt, Jr., R. C. 2004, ApJ, 615, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., Soderberg, A. M., Moe, M., et al. 2012, ApJ, 750, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Gu, Q., Melnick, J., et al. 2004, MNRAS, 355, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Asari, N. V., Sodré, L., et al. 2007, MNRAS, 375, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Schoenell, W., Gomes, J. M., et al. 2009, in Rev. Mex. Astron. Astrofis. Conf. Ser., 35, 127 [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conroy, C., Gunn, J. E., & White, M. 2009, ApJ, 699, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlen, T., Strolger, L.-G., & Riess, A. G. 2008, ApJ, 681, 462 [NASA ADS] [CrossRef] [Google Scholar]
- D’Andrea, C. B., Gupta, R. R., Sako, M., et al. 2011, ApJ, 743, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, Á. I. 1998, Ap&SS, 263, 143 [Google Scholar]
- Díaz, A. I., Castellanos, M., Terlevich, E., & Luisa García-Vargas, M. 2000, MNRAS, 318, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, S., & Statler, T. S. 2006, MNRAS, 368, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Chieffi, A., Limongi, M., & Straniero, O. 1999, ApJ, 524, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Höflich, P., & Straniero, O. 2001, ApJ, 557, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M. 1972, A&A, 20, 361 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J., Hou, J. L., Yin, J., & Chang, R. X. 2009, ApJ, 696, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., Garnavich, P. M., Berlind, P., et al. 2005, ApJ, 634, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., Garnavich, P. M., Caldwell, N., et al. 2008, ApJ, 685, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 2008, ApJ, 683, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996, AJ, 112, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Trager, S. C., Pinto, P. A., et al. 2000, AJ, 120, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, R. B. C., & Worthey, G. 1999, PASP, 111, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., & Niemeyer, J. C. 2000, ARA&A, 38, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howell, D. A., Sullivan, M., Brown, E. F., et al. 2009, ApJ, 691, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, M. J., Smith, R. J., Lucey, J. R., & Branchini, E. 2004, MNRAS, 352, 61 [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJ, 284, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, V. D., Hamuy, M., & Pinto, P. A. 2000, ApJ, 542, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Stasińska, G., Meynet, G., Guseva, N. G., & Thuan, T. X. 2006, A&A, 448, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- James, P. A., Bretherton, C. F., & Knapen, J. H. 2009, A&A, 501, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jha, S., Garnavich, P., Challis, P., Kirshner, R., & Berlind, P. 1999, IAU Circ., 7250, 1 [NASA ADS] [Google Scholar]
- Jha, S., Kirshner, R. P., Challis, P., et al. 2006, AJ, 131, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T., Ellis, R., Jullo, E., & Richard, J. 2010, ApJ, 725, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kelly, P. L., Hicken, M., Burke, D. L., Mandel, K. S., & Kirshner, R. P. 2010, ApJ, 715, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Rupke, D., Zahid, H. J., Geller, M. J., & Barton, E. J. 2010, ApJ, 721, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kniazev, A. Y., Pustilnik, S. A., Grebel, E. K., Lee, H., & Pramskij, A. G. 2004, ApJS, 153, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Koleva, M., Prugniel, P., Ocvirk, P., Le Borgne, D., & Soubiran, C. 2008, MNRAS, 385, 1998 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Lampeitl, H., Smith, M., Nichol, R. C., et al. 2010, ApJ, 722, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, Y. C., Yin, S. Y., Hammer, F., et al. 2006, ApJ, 652, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, Y. C., Hammer, F., Yin, S. Y., et al. 2007, A&A, 473, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacArthur, L. A., González, J. J., & Courteau, S. 2009, MNRAS, 395, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Ruiz, M., Rieke, G. H., & Papadopoulos, P. 1997, ApJ, 485, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Della Valle, M., & Panagia, N. 2006, MNRAS, 370, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Mannucci, F. 2011, PASA [arXiv:astro-ph/1111.4492] [Google Scholar]
- Maoz, D., Sharon, K., & Gal-Yam, A. 2010, ApJ, 722, 1879 [Google Scholar]
- Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 412, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, H., Charlot, S., & Brinchmann, J. 2006, MNRAS, 365, 385 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 1991, ApJ, 380, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N. A., Ledlow, M. J., Owen, F. N., & Hill, J. M. 2002, AJ, 123, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Molla, M., Ferrini, F., & Diaz, A. I. 1997, ApJ, 475, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., & Ostriker, J. P. 2006, MNRAS, 366, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Balam, D., et al. 2006, AJ, 132, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Howell, D. A., et al. 2009, ApJ, 707, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Nordin, J., Goobar, A., & Jönsson, J. 2008, J. Cosmol. Astro-Part. Phys., 2, 8 [CrossRef] [Google Scholar]
- Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Sausalito, CA: University Science Books) [Google Scholar]
- Paczynski, B. 1985, in Cataclysmic Variables and Low-Mass X-ray Binaries, eds. D. Q. Lamb, & J. Patterson, Astrophys. Space Sci. Lib., 113, 1 [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Panter, B., Jimenez, R., Heavens, A. F., & Charlot, S. 2007, MNRAS, 378, 1550 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M., Peimbert, A., Esteban, C., et al. 2007, in Rev. Mex. Astron. Astrofis. Conf. Ser., eds. R. Guzmán, et al., 29, 72 [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Lira, P., Suntzeff, N. B., et al. 1999, AJ, 118, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Pilkington, K., Few, C. G., Gibson, B. K., et al. 2012, A&A, 540, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S. 2001, A&A, 374, 412 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Pizzella, A., Corsini, E. M., Vega Beltrán, J. C., & Bertola, F. 2004, A&A, 424, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pritchet, C. J., Howell, D. A., & Sullivan, M. 2008, ApJ, 683, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, C., Scannapieco, E., Rhoads, J., & Della Valle, M. 2009, ApJ, 707, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Reichardt, C., Jimenez, R., & Heavens, A. F. 2001, MNRAS, 327, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., Gieseler, M., Reinecke, M., Travaglio, C., & Hillebrandt, W. 2006, A&A, 453, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, V. C., Graham, J. A., & Kenney, J. D. P. 1992, ApJ, 394, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F. 2006, Astron. Nach., 327, 850 [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarkar, D., Amblard, A., Cooray, A., & Holz, D. E. 2008, ApJ, 684, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E., & Bildsten, L. 2005, ApJ, 629, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Stasińska, G. 2006, A&A, 454, L127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., Gal-Yam, A., Simon, J. D., et al. 2011, Science, 333, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Calzetti, D., & Kinney, A. L. 1994, ApJ, 429, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Le Borgne, D., Pritchet, C. J., et al. 2006, ApJ, 648, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Conley, A., Howell, D. A., et al. 2010, MNRAS, 406, 782 [NASA ADS] [Google Scholar]
- Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Szokoly, G. P. 2005, A&A, 443, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thèvenaz, P., Blu, T., & Unser, M. 2000, IEEE Trans. Med. Imag., 19, 739 [Google Scholar]
- Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Tinsley, B. M. 1968, ApJ, 151, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Umeda, H., Nomoto, K., Kobayashi, C., Hachisu, I., & Kato, M. 1999, ApJ, 522, L43 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1997, AJ, 113, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Varela, J., Moles, M., Márquez, I., et al. 2004, A&A, 420, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazdekis, A., & Arimoto, N. 1999, ApJ, 525, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Casuso, E., Peletier, R. F., & Beckman, J. E. 1996, ApJS, 106, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Verheijen, M. A. W., Bershady, M. A., Andersen, D. R., et al. 2004, Astron. Nach., 325, 151 [Google Scholar]
- Walsh, J. R., & Roy, J. R. 1990, in ESO Conf. and Workshop Proc., 34, eds. D. Baade, & P. J. Grosbol, 95 [Google Scholar]
- Wang, L., Höflich, P., & Wheeler, J. C. 1997, ApJ, 483, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Weidemann, V. 1987, A&A, 188, 74 [NASA ADS] [Google Scholar]
- Whelan, J., & Iben, I. J. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., Faber, S. M., Gonzalez, J. J., & Burstein, D. 1994, ApJS, 94, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, S. Y., Liang, Y. C., Hammer, F., et al. 2007, A&A, 462, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yuan, T.-T., Kewley, L. J., Swinbank, A. M., Richard, J., & Livermore, R. C. 2011, ApJ, 732, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Supernovae and details of their host galaxies: morphological type, Milky Way dust reddening, offsets from the host nucleus, de-projected galactocentric distance, inclination, and position angle.
SALT2 (Guy et al. 2007) x1 and C parameters of the SNe from Amanullah et al. (2010), the offset from the best-fit Hubble line Δμ, and the ΔM15 parameter.
Total galaxy SFR, SFR surface density ΣSFR and gas extinction AV at the SN location derived from our observations.
ISM metallicity estimates from the total galaxy spectra, at the nucleus, and at the position of the SN using the PP04 and KK04 methods.
Compressed population vectors showing the contribution of the young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar populations to the formation of the observed total galaxy spectrum.
All Figures
 |
Fig. 1 Comparison between SDSS spectra (red) and spectra extracted from our data-cubes within an aperture of 3′′ diameter centered on the galaxy nuclei (black). |
| In the text | |
 |
Fig. 2 BPT diagram (Baldwin et al. 1981). The contours show the density of SDSS emission line galaxies. The dotted and the dashed lines of Kewley et al. (2001) and Kauffmann et al. (2003), respectively, separate star-forming galaxies, AGNs, and composite galaxies. The filled circles, filled triangles, and crosses show the measurements at the position of the SN, the galaxy nucleus, and the total galaxy spectrum, respectively. |
| In the text | |
 |
Fig. 3 Upper row: from left to right, the color SDSS image of NGC 976, the observed Hα flux and velocity maps. Lower row: the ionization parameter log (U), the visual extinction AV estimated from the Balmer decrement and the metallicity map derived with the Pettini & Pagel (2004) O3N2 method. In all maps presented in this paper, × marks the galaxy center and + the SN position. The four contour levels overplotted on the extinction and metallicity maps are derived from the Hα map. The four levels are 0.8, 0.6, 0.4 and 0.2 of the maximum Hα flux. The x,y coordinates are in arcsec with respect to the map centers. The orientation of the images is north – up, east – left. |
| In the text | |
 |
Fig. 4 Same as Fig. 3 but for UGC 5129 and CGCG 207-042. |
| In the text | |
 |
Fig. 5 Same as Fig. 3 but for NGC 105 NED02 and UGC 4008 NED01. |
| In the text | |
 |
Fig. 6 Radial dependence of 12 + log(O/H)PP04. The red dots show the measurement at the SN position. The horizontal dashed lines indicate the metallicity measured from the total galaxy spectra (Table 4). As a guide to the eye, we plot metallicity gradients of −0.022, −0.035, −0.030, −0.058 and + 0.007 dex kpc-1 (from top to bottom) with the solid lines. We estimate that the accuracy of these gradients is ~0.005. The blue squares show the metallicities measured from the azimuthally averaged spectra. The points shown with the cross and plus signs are the metallicities of the H ii regions discussed in Sect. 4.1.6. |
| In the text | |
 |
Fig. 16 Mass-weighted stellar metallicity vs. gas-phase oxygen abundance estimated from the azimutally averaged spectra. |
| In the text | |
 |
Fig. 17 Distribution of the observed galactocentric distance for a sample of 305 nearby SNe Ia in late- and early-type hosts. Because the distances have not been de-projected these are the minimum galactocentric distances. |
| In the text | |
 |
Fig. A.1 Part of one of the science images that demonstrates the configuration of the fibers on the CCD. The calibration fibers are not visible because they are not illuminated during the science exposures. The calibration fibers are normally last within the slitlets. Slitlet #6 holds two calibration fibers, and two more are placed at the beginning of the fiber sequence and one is at the end. |
| In the text | |
 |
Fig. B.1 Throughput map of the PPAK fibers. Note the vignetting in the corners. |
| In the text | |
 |
Fig. C.1 Example of the effect of the stellar spectrum subtraction in the regions of Hβ and Hα emission lines. In the top panels we show the observed spectrum with the best fit overplotted. The bottom panels show the observed spectrum minus the best fit. Clearly, the fluxes of the emission line cannot be accurately measured without a proper subtraction of the stellar spectrum. |
| In the text | |
 |
Fig. 7 From left to right: SDSS color images of the galaxies, the light-weighted average stellar population age ⟨ log t∗ ⟩ L and metallicity ⟨ Z∗ ⟩ L, and the visual extinction AV determined by STARLIGHT fits to the stellar spectra. |
| In the text | |
 |
Fig. 8 STARLIGHT fits to the total galaxy spectra. For each galaxy we also show the ratio between the observed and the best-fit spectrum. The vertical brown lines in the spectrum panels show the location of the strongest night-sky lines, which could not be cleanly subtracted and the corresponding wavelength regions were excluded from the fits. To the right of the plots are shown the population vectors and the mass-fraction vectors along with the extinction, the mass- and light-averaged age and metallicity, and the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age > 2.4 Gyr) stellar populations. The short brown bars show the ages of the SSPs used in the fits and the two vertical dotted lines separate the young, intermediate and old populations. |
| In the text | |
 |
Fig. 9 Mass- and light-weighted average stellar populations metallicity (left panel) and age (right panel) from the STARLIGHT fits as function of the de-projected galactocentric distance. The small black dots are the measurements on the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
| In the text | |
 |
Fig. 10 Same as in Fig. 8, but for the azimutally averaged spectra. |
| In the text | |
 |
Fig. 11 Same as in Fig. 8, but for the azimutally averaged spectra. |
| In the text | |
 |
Fig. 12 Same as in Fig. 8, but for the azimutally averaged spectra. |
| In the text | |
 |
Fig. 13 From left to right: SDSS color images of the galaxies and the maps of the fraction of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age < 2.4 Gyr) stellar populations. |
| In the text | |
 |
Fig. 14 Compressed population vectors corresponding to the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar population to the formation of the observed spectra as function of the de-projected galactocentric distance. The small black dots are the measurements obtained from the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
| In the text | |
 |
Fig. 15 From left to right for each galaxy we show the color SDSS image, Hα velocity map, the star velocity map, and the difference between them. The x,y coordinates are in arcsec with respect to the map centers. The orientation of the images is north – up, east – left. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


