| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 33 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201219188 | |
| Published online | 10 September 2012 | |
Online material
Appendix A: PMAS/PPAK instument details
In this section we provide some details on the PPAK instrument that are relevant for the data reduction. For a full description of the instrument see Verheijen et al. (2004), Roth et al. (2005), and Kelz et al. (2006).
The PPAK fiber bundle consists of 382 fibers with 2.7′′ diameter each, 331 of which (science fibers) are ordered into a single hexagonal bundle that covers a field-of-view (FOV) of 72′′ × 64′′. Thirty-six additional fibers form six mini-bundles of six fibers each (sky-bundles). The sky-bundles are evenly distributed along a circle of radius ~90′′ and face the edges of the central hexagon (see Fig. 5 in Kelz et al. 2006). The remaining 15 fibers are used for calibration and can only be illuminated with the PMAS internal calibration unit.
The fibers are ordered into 12 slitlets. Each slitlet typically holds 28 science fibers, three sky-fibers from three different sky-bundles and one calibration fiber. The three sky-fibers are evenly distributed between the science fibers in the slitlet. The 12 slitlets are ordered to form a pseudo-slit. When projected onto the CCD in 2 × 2 binned mode, the separation between the spectra along the cross-dispersion direction is ~4.8 pixels and the full-width at half-maximum (FWHM) of the spectral traces is ~2.5 pixels. Between the slitlets there are gaps about two fibers wide, with the exception of the two central slitlets, which are separated by wider gap of ~10 fibers (see Fig. A.1; and also Figs. 13 and 14 in Kelz et al. 2006).
 |
Fig. A.1
Part of one of the science images that demonstrates the configuration of the fibers on the CCD. The calibration fibers are not visible because they are not illuminated during the science exposures. The calibration fibers are normally last within the slitlets. Slitlet #6 holds two calibration fibers, and two more are placed at the beginning of the fiber sequence and one is at the end. |
| Open with DEXTER | |
Because the fibers are circular, only ~65% of the FOV is spectroscopically sampled in a single exposure. Therefore, at least three suitably offset pointings are needed to spectroscopically sample every point in the PPAK FOV.
Appendix B: Data reduction
The pre-reduction of the CCD images was performed with IRAF and the remaining reduction with our own programs written in IDL.
B.1. Pre-reduction
The PMAS 4k × 4k CCD is read by four amplifiers and for each exposure four separate FITS files are created. These were individually pre-reduced. The bias frames showed no significant large-scale structures and the bias was corrected by subtracting the average value computed from the CCD overscans. The images were then trimmed, converted from ADUs into electrons using the gain values measured during the commissioning of the CCD and finally combined into a single 2D image, on which the spectra were oriented roughly along the rows.
To create a master flat-field image, all halogen lamp exposures obtained during the run where summed. The separation between the spectra along the cross-dispersion direction is ~4.8 pixels and the full-width at half-maximum (FWHM) of the spectral traces is ~2.5 pixels. As a result, the intensity of the pixels between the spectra is ~20% of the peak value (e.g., see Fig. 18 in Kelz et al. 2006). Therefore, when all the images of the halogen lamp spectra are combined, there will be enough counts even in between the spectra. Moreover, because of the instrument flexure the positions of the spectra change by up to ~1–2 pixels, depending on the pointing of the telescope. As a result, in the combined image the intensities between the spectra were ~80% of the peak values. Because the intensity changes smoothly along the dispersion axis, each image row was smoothed with running median in a window of 20 pixels to normalize the master flat-field image. The flat-field image was divided into its smoothed version to derive the final normalized flat-field that contained only the pixel-to-pixel variations.
Because of the relatively long exposures used, the images contain many pixels that are affected by cosmic ray (CR) hits. The complexity of PPAK images makes it very difficult to use conventional methods for CRs rejection. We experimented with different approaches and found that the CRREJ algorithm (developed for WFPC on HST6) gave the best results. We tried different parameter settings, each time carefully examining the CR masks to verify that no sky lines or galaxy emission lines were identified as CRs and at the same time as many as possible CRs were identified. It was occasionally necessary to manually mark some CRs. Finally, the values of the CR hit pixels were replaced with the values derived by interpolating the adjacent good pixels. We used cubic-spline interpolation and the direction of the interpolation depended on the extent of the CR-affected region along the image rows and columns
B.2. Spectra tracing
The continuum lamp exposures that were obtained before and/or after the science exposures were used to trace the positions of the spectra on the CCD. The spectra tracing was performed in two steps. First, 20 columns at the middle of the image were averaged and used to determine the location of all 382 spectra. Then moving left and right and averaging 20 columns, the position of each spectrum at each CCD column was determined using the peak positions of the previous column as starting points. The positions of the maxima were determined by fitting a parabola to either the three or the four highest intensity points. When the ratio between the two highest points was lower than 0.9, three points were used, in which case the parabola passes exactly through all three points and the maximum can be computed. Otherwise, a least-squares fit was used to determine the maximum.
The space between the adjacent spectra is ~4.8 pixels, which prevented us from using a more accurate scheme to compute the positions of the spectra. The traces determined at the first step were clearly oscillating with an amplitude ~1/3 pixels and it was necessary to additionally smooth them. The traces were fit with a sixth-order polynomial function and the results were stored in a FITS file.
Because of the mechanical flexures of PMAS the positions of the spectra moved slightly (at sub-pixel level) between the exposures, even within the sequence of exposures of a given galaxy. This effect can be accurately accounted for by a constant shift of the derived spectral traces. To derive these shifts, the average of 20 columns taken at the middle of the 2D image was cross-correlated with the same average in the halogen 2D image that was used to trace the spectra. In the subsequent reduction steps these shifts were always accounted for.
B.3. Scattered light
A small amount of scattered light is present in the images and it needs to be subtracted to achieve an accurate flux calibration. To derive a 2D model of the scattered light, we used the gaps between the slitlets (Fig. A.1), which contain no light from the object. Bands of five pixels width were extracted from the gaps (wider band was extracted between the sixth and the seventh slitlets) using the information from the spectra tracing. The bands were converted into 1D vectors by running median in 5 × 5 pixel window and the positions along the y-axis were also computed. The scattered light pattern along the dispersion axis is fairly complex and the attempts to directly fit a 2D polynomial surface yielded no satisfactory results. Instead, the scattered light vectors were cubic-spline-interpolated along all image columns (in the spatial direction) to derive the amount of scattered light at each image pixel. The resulting 2D model image of the scattered light was smoothed by 50 × 50 pixel running median and subtracted from the original image.
B.4. Spectra extraction and cross-talk correction
The spectra were extracted from the 2D images using a simplified version of the optimal extraction algorithm of Horne (1986). In this method the spatial profile of the spectral trace is determined from the data themselves and is used to form a weighted sum of the pixels in a given aperture, giving larger weights to the pixels that received more light. In the conventional longslit spectroscopy the profile is determined by the seeing and the telescope guiding, and may change considerably from exposure to exposure. In the case of PPAK the spatial profiles are almost entirely determined by the size of the fibers and have a stable shape that can be accurately described by a Gaussian. Thus, we determined the FWHMs of the Gaussians that describe the profiles of all 382 spectra and used this information to compute the weights for the optimal extraction. Series of halogen lamp spectra were obtained and added to increase the signal-to-noise ratio (S/N). For each image column 382 Gaussians were simultaneously fitted to derive the FWHMs. The fitting was performed with the MPFIT IDL package7 and special care was taken to provide accurate starting values; otherwise the fit with so many Gaussians would fail. The resulting 2D FWHM image (382 spectra by 2048 spectral elements) was somewhat noisy and was smoothed by running median within 11 × 11 elements window. The mean FWHM is 2.46 pixels and the covered range is 2.12–2.85.
With the positions of the spectra and the spatial profiles determined, the spectra were extracted with the optimal extraction algorithm. The separation between the spectra within the slitlets is fairly constant ~4.8–4.9 pixels, both from spectrum to spectrum and along the trace. The extraction apertures were automatically computed as half the average distance from closest spectrum. This means that for a given spectrum the extraction aperture may be slightly asymmetric with respect to the trace center and that different spectra may have slightly different aperture sizes.
Within a given slitlet the spectra are separated by only ~2 × FWHM, which leads to an effect known as cross-talk, i.e. contamination by adjacent spectra8. Sánchez (2006) proposed the iterative Gaussian-suppression technique and we followed this approach with small modifications. After the first optimal extraction, the contamination from the adjacent spectra for a given spectrum was estimated as follows. Using the estimated flux, trace positions and FWHMs of the Gaussians that describe the spatial profiles of the adjacent spectra, and taking into account the finite size of the extraction apertures, we computed the height of the Gaussian functions that would have produced the fluxes of the adjacent spectra were. This was performed for all columns and the contamination of the adjacent spectra was subtracted. Then a new optimal extraction was performed on the corrected image using the same extraction aperture as before. This was performed for all spectra and the process was iterated once more.
B.5. Wavelength calibration
The HgNe and ThAr arc-lamp spectra were used to derive separate wavelength calibrations for each individual spectrum. The arc-lamp spectra were extracted in exactly the same way as the science ones and the positions of all Hg, Ne and Cd9 lines with known laboratory wavelengths were determined by a least-squares fit with Gaussian function. A sixth-order polynomial fit was then used to derive accurate pixel-to-wavelength transformations. The spectra extend from about 3700 Å to 7000 Å. The bluest line in the HgNe spectrum is at ~4047 Å. Thus, the wavelength solution below ~4000 Å may not be accurate. On the other hard, the two reddest arc lines are at 6717 Å and 6929 Å. Because of the field vignetting (see below) the 6929 Å line was not detected in all fibers and as a result for those fibers the red part of the wavelength solution may also be inaccurate. To work around this problem, the 15 calibration fibers that were illuminated with a ThAr lamp were used to improve the wavelength solutions in the two extremes of the covered wavelength range. The dispersion over the wavelength range is between 1.5 Å pixel-1 and 1.7 Å pixel-1
B.6. Background subtraction
The spectra extracted from fiber-fed or IFU spectrographs contain not only the object light, but also the sky background, which needs to be subtracted. For faint objects the background may exceed the object flux by far and accurate background subtraction is essential to obtain reliable results. The PPAK design with the separate sky-fibers, which are distributed evenly between the science fibers, gives the flexibility to apply different approaches to the background subtraction. The following method was found to work best. The sky-fibers were first examined to check if some of them were accidentally contaminated by background objects. No such cases were found. Each element of the 331 science spectra was labeled with a pair of numbers (λi, N), its wavelength and fiber number as is recorded on the CCD, respectively. For a given element (λi, N) all sky-spectra were interpolated at a common wavelength λi using forth-order B-spline interpolation10, which has one of the best interpolation properties of all known interpolation schemes (e.g., Thèvenaz et al. 2000). The interpolated sky-spectra were fitted as a function of their fiber position with least-squares fifth order polynomial fit and the value of the sky at the element position N was recorded. Repeating this for all elements gives a 2D model of the sky-background, which was subtracted from the science fibers. The sky-subtracted 2D images were carefully examined and no visible systematic residuals were noticed, except at the position of the few strongest sky-lines.
B.7. Flux calibration
The flux calibration of the spectra was a two-step process: (i) normalization for the fiber-to-fiber throughput variations and (ii) correcting for the wavelength-dependent system response. To account for the fiber-to-fiber throughput variations the series of twilight sky exposures were used. The individual images were added to increase the S/N and all spectra were extracted and wavelength-calibrated in the same way as the science ones. Unfortunately, with the new larger CCD11 the images suffer from vignetting at the corners. The sensitivity of the parts of the spectra that are projected at the CCD corners falls sharply as function of the distance from the CCD center (Fig. B.1). The relation between the on-sky fiber positions and the fiber position on the CCD is such that the most affected fibers are those adjacent to the central hexagon of 37 fibers (see Fig. 7 in Kelz et al. 2006) and not the outermost fibers. The fibers of the central hexagon are projected at the middle of the CCD and are practically un-affected by the vignetting.
To derive the relative throughput of the fibers, all spectra were interpolated on a common wavelength frame. The 37 spectra of the central hexagon were averaged and all spectra were divided by this average spectrum. The resulting ratios were least-squares fitted with polynomials of different degrees (high orders were needed for the fibers most affected by the vignetting) to derive the throughput map of the fibers. The map is shown in Fig. B.1 and the vignetting at the corners is clearly visible. This map was used to equalize the throughput of the fibers by dividing all science exposures by it.
 |
Fig. B.1
Throughput map of the PPAK fibers. Note the vignetting in the corners. |
| Open with DEXTER | |
During the analysis it was found that for several of the fibers that were most severely affected by the vignetting the drop of the throughput in the extreme blue and red parts could not be corrected well. This resulted in several spaxel spectra having incorrect relative flux calibration at the two extreme ends. This affected the spectrum fitting of these spaxels with STARLIGHT. Because the Hα flux was also affected, the estimation of the extinction was unreliable and hence part of the emission line analysis. The “bad” spaxels were masked in the 2D maps of the affected properties. It should be noted, however, that our primary gas metallicity indicator, the O3N2 method, was not affected because it only involves flux ratios of emission lines at close wavelengths.
The two spectrophotometric standard stars that were observed on 15 November were used to derive the system response. The spectra of the standards were extracted, wavelength-calibrated, background-subtracted and fiber-throughput-corrected in the same way as the rest of the science exposures. The presence of gaps between the fibers in combination with the point source nature of the standards makes it difficult to recover the whole flux of the star from a single exposure. In addition, because of the differential atmospheric refraction (DAR) there may be significant differential flux losses. By taking the observations of the standards at five different points on the PPAK FOV, we aimed to minimize these effects. First, the differential flux losses may cancel out when the five spectra are summed. Second, it gives more control, for example, too discard a clearly deviating observation.
To minimize the flux losses instead of summing all spectra that contain object flux, we adopted a different approach. The spectra were interpolated at a common wavelength scale and each fiber was associated with its on-sky position. For each wavelength plane a symmetric 2D Gaussian function (without constant term) was fitted and the flux was taken to be the integral over the Gaussian. So extracted spectra were compared with the result of simply suming the fibers. The spectra extracted with the Gaussian fitting were clearly more consistent between the five pointings. With the exception of one pointing for each standard, the systematic difference between the spectra were less than ~3–4%. The deviating spectra for each star were discarded and the remaining four were averaged. After correcting for the atmospheric extinction using a mean extinction curve for Calar Alto Observatory, the ratio between the observed counts and the tabulated fluxes of the standard were fitted with a polynomial function to derive the sensitivity function of the system. The sensitivities derived from the two standards agreed well and the average of the two sensitivities was used to calibrate all science observations.
 |
Fig. C.1
Example of the effect of the stellar spectrum subtraction in the regions of Hβ and Hα emission lines. In the top panels we show the observed spectrum with the best fit overplotted. The bottom panels show the observed spectrum minus the best fit. Clearly, the fluxes of the emission line cannot be accurately measured without a proper subtraction of the stellar spectrum. |
| Open with DEXTER | |
B.8. Final data-cubes
The final step in the reduction was to combine the three pointings into a data cube. The spectra were re-sampled into a common linear wavelength scale with a sampling of 1.5 Å per element. Taking into account the offset between the exposures, the circular fibers were mapped onto an output grid of square 2′′ × 2′′ pixels. The flux of a given fiber was distributed between the output pixels according to the overlap area between the fiber and the output pixels. No attempt was made to first shrink the fibers and emulate the Drizzle algorithm used for HST images (Fruchter & Hook 2002); with only three barely overlapping pointing this would not gain any improvement. However, with five or more carefully selected pointings it may be possible to use Drizzle to improve the spatial sampling of the final cubes.
Two important effects were taken into account two when creating the data-cubes – the non-photometric condition and the differential atmospheric refraction (DAR). To account for the first, for each galaxy and pointing the total flux within an aperture of 12′′ centered on the galaxy core was computed and the observations of given galaxy were scaled to the exposure with the highest flux. With one exception all corrections were smaller than 15%; the remaining pointing required a correction factor of ~2.
The observations were obtained at an airmass of less that 1.3 and the effect of DAR was small, but we nevertheless corrected for it. To compute the DAR we used the formulas from Szokoly (2005) and the ambient conditions as recorded in the FITS image headers. To combine the three pointings, we shifted the positions of the fibers for each wavelength slice along the x and y axes by the values computed from the value of the DAR at that wavelength (with respect to the refraction at 6300 Å) and the effective parallactic angle of the observations (see also Walsh & Roy 1990). For both the DAR-corrected and un-corrected data-cubes, the positions of the galaxy nuclei were computed in the blue (average in 3800–4000 ÅÅ) and red (6600–6800 ÅÅ) wavelength ranges. The two positions measured in the DAR-corrected cubes matched very well, but not in the un-corrected cubes, which shows that the DAR was correctly accounted for.
Three of the galaxies in our sample also have SDSS spectroscopy. This allowed us to check the relative flux calibration of our spectra. To emulate the SDSS spectroscopy, we extracted from our data-cubes the flux within an aperture of 3′′ diameter centered on the galaxy nucleus and scaled it to match the mean flux level of the SDSS spectra. The comparison between the SDSS spectra and those extracted from our date-cubes is shown in Fig. 1. It shows that the relative flux calibration of our spectra is excellent and matches SDSS to within a few percent.
To set the absolute flux scale of the data-cubes we used the SDSS imaging. SDSS g and r magnitudes of the galaxies were computed within an aperture of 20′′ diameter. Spectra within the same aperture size were extracted from the data-cubes and synthetic g and r magnitudes were computed. The g and r scale factors that made the synthetic magnitudes match the observed ones were computed and the average of the two was applied to the data-cubes. It should be noted that the g and r scale factors coincided to within a few percent, which supports our conclusion that the relative flux calibration is accurate.
Appendix C: Measurement of emission line fluxes
Five of the six galaxies show strong nebular emission lines. This enabled us to study the properties of the gas phase in the galaxies through measuring the fluxes of the most prominent emission lines [O ii] λ3727, Hβ, [O iii] λλ4959/5007, Hα, and [N ii] λλ6549/6584, and when possible also [S ii] λλ6716/6731. In spectra of galaxies the nebular emission lines are superimposed on the underlying stellar continuum. The stellar absorption lines can bias the measurement of the emission line fluxes, an effect that is especially prominent in Hβ (Fig. C.1). Therefore, the stellar continuum needs to be subtracted first to measure the emission line fluxes accurately. For this we used the STARLIGHT software (Cid Fernandes et al. 2005). Briefly, after masking the regions of known nebular emission lines, telluric absorptions, and strong night-sky emission lines, the spectrum was fitted with a linear combination of model spectra of single stellar populations (SSP) of different ages and metallicities. The best fit was subtracted to derive the pure emission line spectrum, where the emission line fluxes can be measured without bias, see Fig. C.1. The parameters of the fitted SSPs can be used to derive the properties of the galaxy stellar population, but here we regarded the fits as a means to subtract the underlying stellar absorption. All spectra that had S/N higher than 5 at ~4600 Å were fitted and the emission line fluxes were measured on the continuum-subtracted spectrum. For the remaining spectra the measurements were made without continuum subtraction. A weighted non-linear least-squares fit with a single Gaussian plus a linear term was performed for each emission line, and the area below the Gaussian was taken as an estimate of the flux. The weights were the error spectrum produced during the spectral extraction. Including the linear term is necessary to account for possible systematic residuals due to imperfect subtraction of the the stellar absorption spectrum. The close lines Hα, [N ii] λ6549 and [N ii] λ6584 were simultaneously fitted. [O ii] λ3727 is a blend of two lines – [O ii] λλ3726.04/3728.80. This blend was fitted with two Gaussians with equal width and a fixed separation of 2.76 Å. In addition, a robust standard deviation of the adjacent continuum was also measured from the regions more then 3σ away from the line centers.
The uncertainty of the line fluxes was estimated by propagating the uncertainties of the fitted amplitude and σ of the Gaussians. To check the reliability of this estimate, we performed Monte Carlo simulations. We assumed that the lines have a Gaussian shape with σ = 2, representative for our spectra, and that they were superimposed on constant background with standard deviation one and mean zero. The noise across the line was assumed to follow a Poisson distribution – if a given datum has N counts, the 1σ uncertainty of this datum is (1 + N)1/2. This noise model was used to generate pseudo-random numbers, which were added to the line and the line was fitted (weighted by the noise model). This was repeated 1000 times and the mean values and the standard deviation of σ, the amplitude, and the area below the Gaussian were computed. This procedure was repeated for Gaussians with amplitudes 2 to 1000, i.e. exceeding the continuum noise by the same numbers.
The results of these simulations show that propagating the errors of the fitted parameters to the total flux overestimates the
uncertainty by about a factor of 2. The simulations also showed that the area below the Gaussian can be recovered with ~30% accuracy and without significant bias for lines that exceed the continuum noise by only three times. The S/N of the measured line flux was tabulated as a function of the ratio of the fitted amplitude of the Gaussian to the standard deviation of the adjacent continuum and was used to assign realistic errors to the line fluxes measured by fitting a Gaussian function. For example, a 10% accuracy is achieved when the amplitude of the Gaussian is 20 times the continuum noise. A possible concern is that the shape of the lines in the real spectra may deviate from Gaussian, in which case additional uncertainty will be introduced. Close inspection of the line fits revealed that the line shape in our spectra is well represented by a Gaussian function and we do not expect problems related to a non-Gaussian line shape.
 |
Fig. 7
From left to right: SDSS color images of the galaxies, the light-weighted average stellar population age ⟨ log t∗ ⟩ L and metallicity ⟨ Z∗ ⟩ L, and the visual extinction AV determined by STARLIGHT fits to the stellar spectra. |
| Open with DEXTER | |
 |
Fig. 8
STARLIGHT fits to the total galaxy spectra. For each galaxy we also show the ratio between the observed and the best-fit spectrum. The vertical brown lines in the spectrum panels show the location of the strongest night-sky lines, which could not be cleanly subtracted and the corresponding wavelength regions were excluded from the fits. To the right of the plots are shown the population vectors and the mass-fraction vectors along with the extinction, the mass- and light-averaged age and metallicity, and the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age > 2.4 Gyr) stellar populations. The short brown bars show the ages of the SSPs used in the fits and the two vertical dotted lines separate the young, intermediate and old populations. |
| Open with DEXTER | |
 |
Fig. 9
Mass- and light-weighted average stellar populations metallicity (left panel) and age (right panel) from the STARLIGHT fits as function of the de-projected galactocentric distance. The small black dots are the measurements on the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
| Open with DEXTER | |
 |
Fig. 10
Same as in Fig. 8, but for the azimutally averaged spectra. |
| Open with DEXTER | |
 |
Fig. 11
Same as in Fig. 8, but for the azimutally averaged spectra. |
| Open with DEXTER | |
 |
Fig. 12
Same as in Fig. 8, but for the azimutally averaged spectra. |
| Open with DEXTER | |
 |
Fig. 13
From left to right: SDSS color images of the galaxies and the maps of the fraction of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr) and old (age < 2.4 Gyr) stellar populations. |
| Open with DEXTER | |
 |
Fig. 14
Compressed population vectors corresponding to the contribution of young (age < 300 Myr), intermediate (300 Myr < age < 2.4 Gyr), and old (age > 2.4 Gyr) stellar population to the formation of the observed spectra as function of the de-projected galactocentric distance. The small black dots are the measurements obtained from the individual spaxels and the large blue dots are from the azimuthally averaged spectra. |
| Open with DEXTER | |
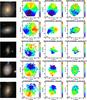 |
Fig. 15
From left to right for each galaxy we show the color SDSS image, Hα velocity map, the star velocity map, and the difference between them. The x,y coordinates are in arcsec with respect to the map centers. The orientation of the images is north – up, east – left. |
| Open with DEXTER | |
© ESO, 2012
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


