| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A42 | |
| Number of page(s) | 23 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219135 | |
| Published online | 05 September 2012 | |
Constraining γ-ray pulsar gap models with a simulated pulsar population⋆
1
Laboratoire AIM, Université Paris Diderot/CEA-IRFU/CNRS, Service
d’Astrophysique, CEA Saclay,
91191
Gif-sur-Yvette,
France
e-mail: marco.pierbattista@cea.fr
2
François Arago Centre, APC, Université Paris Diderot, CNRS/IN2P3,
CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue A. Domon et L. Duquet, 75205
Paris Cedex 13,
France
3 Institut Universitaire de France France
4
Astrophysics Science Division, NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
5
Hope College, Department of Physics, Holland
MI,
USA
Received:
29
February
2012
Accepted:
23
June
2012
With the large sample of young γ-ray pulsars discovered by the Fermi Large Area Telescope (LAT), population synthesis has become a powerful tool for comparing their collective properties with model predictions. We synthesised a pulsar population based on a radio emission model and four γ-ray gap models (Polar Cap, Slot Gap, Outer Gap, and One Pole Caustic). Applying γ-ray and radio visibility criteria, we normalise the simulation to the number of detected radio pulsars by a select group of ten radio surveys. The luminosity and the wide beams from the outer gaps can easily account for the number of Fermi detections in 2 years of observations. The wide slot-gap beam requires an increase by a factor of ~10 of the predicted luminosity to produce a reasonable number of γ-ray pulsars. Such large increases in the luminosity may be accommodated by implementing offset polar caps. The narrow polar-cap beams contribute at most only a handful of LAT pulsars. Using standard distributions in birth location and pulsar spin-down power (Ė), we skew the initial magnetic field and period distributions in a an attempt to account for the high ĖFermi pulsars. While we compromise the agreement between simulated and detected distributions of radio pulsars, the simulations fail to reproduce the LAT findings: all models under-predict the number of LAT pulsars with high Ė, and they cannot explain the high probability of detecting both the radio and γ-ray beams at high Ė. The beaming factor remains close to 1.0 over 4 decades in Ė evolution for the slot gap whereas it significantly decreases with increasing age for the outer gaps. The evolution of the enhanced slot-gap luminosity with Ė is compatible with the large dispersion of γ-ray luminosity seen in the LAT data. The stronger evolution predicted for the outer gap, which is linked to the polar cap heating by the return current, is apparently not supported by the LAT data. The LAT sample of γ-ray pulsars therefore provides a fresh perspective on the early evolution of the luminosity and beam width of the γ-ray emission from young pulsars, calling for thin and more luminous gaps.
Key words: stars: neutron / pulsars: general / gamma rays: stars / radiation mechanisms: non-thermal / methods: numerical / surveys
Appendix A and a colour version of Figs. 1–18 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
After the radio detection of the first pulsar signal in 1967 (Hewish et al. 1968), a pulsar magnetosphere model was formulated by Goldreich & Julian (1969). A direct consequence of the Goldreich & Julian model is the establishment of a magnetospheric charge density that creates a force-free pulsar magnetosphere. However, such a magnetosphere has no electric field along the magnetic field to accelerate charges and produce γ-rays.
The detection, a few years later, of pulsed emission at γ-ray energies from the Crab (McBreen et al. 1973) and Vela (Thompson et al. 1975) pulsars, and the detection of four more γ-ray pulsars by Thompson et al. (1994) established that pulsars accelerate particles to energies of at least a few TeV suggesting that there are magnetospheric regions where the charge density departs from that of Goldreich & Julian, locally violating the force-free condition and allowing particle acceleration. These regions were identified in two magnetospheric zones. In the inner magnetosphere, acceleration can take place both above the polar cap and in the slot gap, which extends to high-altitude along the last open magnetic field lines. In the outer magnetosphere, the outer gap extends from the null charge surface to the light cylinder. These gap regions correspond to three models: the low-altitude slot-gap model, hereafter Polar Cap (PC, Muslimov & Harding 2003), the Slot Gap model (SG, Muslimov & Harding 2004), and the Outer Gap model (OG, Cheng et al. 2000).
In the polar-cap model the emission comes from a region close to the neutron star (NS) surface and well confined above the magnetic polar cap. Charged particles from the neutron star are initially accelerated in the strong electrostatic field generated by a departure from the Goldreich-Julian charge density (Arons & Scharlemann 1979). Aided by inertial frame dragging (Muslimov & Tsygan 1992), pulsars emit high energy photons by curvature radiation (CR) and inverse Compton scattering (ICS). The most energetic of these photons reach threshold for electron-positron pair production in the strong magnetic field at a pair formation front (PFF), above which the secondary pairs can screen the electric field in a short distance. The pairs, produced in excited Landau states, emit synchrotron photons which trigger a pair cascade with high multiplicity. A small fraction of the pairs is actually accelerated. The pair plasma likely establishs force-free conditions along the magnetic field lines above the PFF, as well as radiate γ-rays. Over most of the polar cap, the PFF and γ-ray emission occurs well within a few stellar radii of the NS surface. The main contribution to the γ-ray emission comes from CR from the pairs moving upward. Since the CR intensity scales with the magnetic field lines curvature, it decreases from the polar cap edge toward the magnetic axis, conferring to the emission beam the structure of an hollow cone.
The slot-gap emission is generated from the same polar cap electromagnetic pair cascade near the boundary of the closed magnetic field lines region where the parallel electric field E ∥ → 0 and the PFF rises to higher altitude. Here electrons are accelerated over longer distances to produce the pair cascade. A narrow gap, the slot gap, is formed along the closed magnetic field surface where the PFF is never established, and electrons continue to be accelerated and radiating γ-rays by self-limited curvature radiation into the outer magnetosphere. The resulting hollow beam is much broader and less collimated near the magnetic axis than the lower-altitude PC emission (see Sect. 7).
The outer gaps are vacuum regions characterised by a strong electric field along the magnetic field lines (Holloway 1973; Cheng et al. 1976) above the null charge surface. Two outer gap regions (Cheng et al. 1976; Romani & Yadigaroglu 1995; Cheng et al. 2000; Hirotani 2006) can exist in the angular velocity-magnetic momentum plane, one for each pole. In the physical OG model, in the case of a non-aligned rotator, the gap region closer to the pulsar surface is more active than the other gap further away from the surface due to the pair production screening operating more efficiently at lower altitude. In the OG model a charge-deficient region forms in the outer magnetosphere above the null charge surface where a charge-separated flow is formed. The induced electric field accelerates pairs radiating γ-rays in a direction tangent to the B lines. The γ-ray photons interact with thermal X-rays from the NS surface to produce pairs on field lines interior to the last open field line. The pair formation surface screening the electric field defines the interior surface of the gap.
More than 2000 pulsars are listed in the ATNF database (Manchester et al. 2005), most of which were first observed at radio wavelength. We employ the following ten selected pulsar radio surveys in this study: Molonglo2 (Manchester et al. 1978), Green Bank 2 & 3 (Dewey et al. 1985; Stokes et al. 1985), Parkes 2 (70 cm) (Lyne et al. 1998), Arecibo 2 and 3 (Stokes et al. 1986; Nice et al. 1995), Parkes 1 (Johnston et al. 1992), Jodrell Bank 2 (Clifton & Lyne 1986), Parkes Multi-beam (Manchester et al. 2001) and the extended Swinburne surveys (Edwards et al. 2001; Jacoby et al. 2009). For these, the survey parameters are known with a high accuracy and they cover the largest possible sky surface while minimising the overlapping regions.
The advent of the LAT telescope on the Fermi satellite (Atwood et al. 2009) led to a drastic increase in the number of γ-ray pulsars. After three years of observations the LAT detected about 106 pulsars, more than doubling the number of detections listed in the first pulsar catalog (Abdo et al. 2010) leading to the discovery of two well defined γ-ray pulsar populations consisting of 31 millisecond pulsars, and 75 young or middle aged isolated, normal pulsars. To study and compare the collective properties of the LAT normal isolated pulsars and investigate the emission mechanisms that best explain the observed emission, we synthesised a pulsar population incorporating four important high-energy radiation gap models. The simulation takes into account the axisymmetric structure of our Galaxy and is designed to match the known characteristics of the group of older radio pulsar population than the younger group of pulsars sampled in γ-rays. Four γ-ray emission gap models have been assumed: the previously described Polar Cap (PC), Slot Gap (SG), and Outer Gap (OG), and a variation of the OG, hereafter the One Pole Caustic (OPC; Romani & Watters 2010; Watters et al. 2009) that differs from the OG in the energetics. We model the radio emission at two different frequencies, 1400 MHz and 400 MHz (Gonthier et al. 2004; Harding et al. 2007), comparing simulated radio fluxes with the flux thresholds of existing surveys.
The outline of this paper is as follows. In Sects. 2 and 3, we describe the neutron star characteristics and evolution. In Sects. 4–6, we give a brief overview of the radio luminosity computation, γ-ray gap widths, and γ-ray luminosities computations. Sections 7 and 8 describe the pulsar light-curve and flux computation. Section 9 reviews the radio and γ-ray pulsar visibility calculations. We present the results in the final Sect. 10.
2. Neutron star characteristics
The neutron star mass, radius, and moment of inertia used in this paper have been chosen according to the experimental mass measurements in binary NS-NS systems, X-ray binaries, and NS-white dwarf binaries shown in Fig. 3 of Lattimer & Prakash (2007).
The assumed NS mass and radius are MNS = 1.5 M⊙ and RNS = 13 km. The mass value lies between the weighted average and average values of X-ray and white dwarf-NS binaries estimates and, with the RNS = 13 km, represent, a possible solution for the EOS that describe the NS interior (Fig. 2 of Lattimer & Prakash 2007).
The moment of inertia of a NS is evaluated by Eq. (35) of Lattimer & Prakash (2007). For the 13 km radius and the 1.5 M⊙ mass of our standard NS, we obtain I ~ 1.8 × 1038 kg m2. Because of the uncertainty on the mass and radius estimates, this value has an uncertainty of about 70%.
For each simulated NS we have generated a value of the magnetic obliquity α (angle between the pulsar rotation and magnetic axes) and of the observer line of sight ζ (angle between the pulsar rotation axis and the observer line of sight). After the supernova explosion that generates the neutron star, the magnetic axis α has equal probability to point in any direction of a 3 dimensional space. This is also true for the observer line of sight direction ζ with respect to the pulsar rotational axis. The α and ζ distributions are isotropic.
The spin-down power Ė is defined as the rate with which the pulsar loses
rotational kinetic energy, as 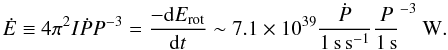 (1)The latter equation is
based on the NS structure assumptions through the moment of inertia I.
Since mass and radius are chosen inside intervals of allowed values, the Ė
estimate is affected by an uncertainty of at least a factor 3.
(1)The latter equation is
based on the NS structure assumptions through the moment of inertia I.
Since mass and radius are chosen inside intervals of allowed values, the Ė
estimate is affected by an uncertainty of at least a factor 3.
The choice of mass, radius, and moment of inertia formulation yields a moment of inertia value that is 1.5 times higher than in the ATNF catalog. This helps to reduce the discrepancy found between the simulated and observed Ė distributions (Sect. 10.3), while remaining well within the range of parameters allowed by the binary data and equations of state in Lattimer & Prakash (2007). The choice of different values for mass and radius would also impact the range of the P and Ṗ distributions of the evolved pulsar population (Sect. 10.2).
3. Neutron stars at birth and their evolution
We synthesised ~2.7 × 108 NSs with mass, radius, and moment of inertia as described in Sect. 2, and assuming a constant birth rate over the last 1 Gyr. It yields 2.5 × 106 isolated ordinary pulsars to the left of the radio death line (see below). To match the observed radio pulsars P and Ṗ distributions, an exponential magnetic field decay with a time scale of 2.8 × 106 yr has been assumed (Gonthier et al. 2004). The choice of such a short timescale decay is justified by the need to slow down the birth population enough to reproduce the characteristics of the observed radio sample. It provides a simple mathematical solution to a more physical model of the rotational evolution of the NS, yet to be developed. For our study, since we are dealing with young ordinary pulsars, this choice has been checked not to affect the obtained results.
The radio death line we used is defined as 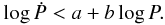 (2)It is composed by three
different segments (Story et al. 2007; Zhang et al. 2000), each one refers to a specific period
interval characterised by the following a and b values
(2)It is composed by three
different segments (Story et al. 2007; Zhang et al. 2000), each one refers to a specific period
interval characterised by the following a and b values
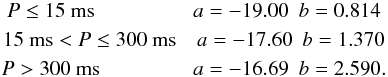 (3)
(3)
3.1. Birth spinning and magnetic characteristics
The distribution of period at birth, P0, plotted in the right panel of Fig. 1, follows a single Gaussian of width 50 ms, centred at 50 ms, and truncated at 0 to avoid negative periods. The same distribution was adopted by Watters & Romani (2011) on the basis of radio luminosity arguments but it differs from the choice of Takata et al. (2011) who selected the birth period randomly in the range 20 ≤ P0 ≤ 30 ms.
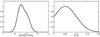 |
Fig. 1 Left: the assumed surface magnetic field distribution at birth. Right: the assumed spin period distribution at birth. |
The magnetic field birth distribution B0 shown in the left panel of Fig. 1 has been built as the sum of two Gaussians in log 10B0 [Tesla], both 0.4 in width, respectively centred at 8.5 and 9.1, and with an amplitude ratio of 1:7/12. Our choice represents a compromise between that of Watters & Romani (2011), a single Gaussian centred at 8.65 and width 0.3, and the Takata et al. (2011) one, a single Gaussian centred at 8.6 and width 0.1. The high-B0 Gaussians provide energetic pulsars when evolved.
Both the P0 and
B0 distributions have been optimized
a posteriori to obtain, after evolution, a simulated pulsar sample as close as possible to
the observed one by minimizing the observed lack of high Ė objects
(Sect. 10.3). The
Ṗ0 birth distribution has been derived from
P0 and
B0 by using the equation 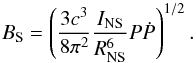 (4)This formulation includes
no dependence on the magnetic obliquity alpha, as proposed by Ruderman & Sutherland (1975) for the spinning down of
magnetospheres carrying current flows. More recently, Spitkovsky (2006) numerically showed for force-free magnetospheres that the spin
down of orthogonal rotators is twice that of aligned rotators. In the non-ideal case of a
magnetosphere accelerating charges to produce pulsed emission the impact of alpha on
Ė is still under discussion, so we chose for this paper the alpha
independent prescription of Ruderman & Sutherland
(1975). Hereinafter, all luminosities are given as a function of
Ė to judge how the uncertainty on the spin-down rate propagates.
(4)This formulation includes
no dependence on the magnetic obliquity alpha, as proposed by Ruderman & Sutherland (1975) for the spinning down of
magnetospheres carrying current flows. More recently, Spitkovsky (2006) numerically showed for force-free magnetospheres that the spin
down of orthogonal rotators is twice that of aligned rotators. In the non-ideal case of a
magnetosphere accelerating charges to produce pulsed emission the impact of alpha on
Ė is still under discussion, so we chose for this paper the alpha
independent prescription of Ruderman & Sutherland
(1975). Hereinafter, all luminosities are given as a function of
Ė to judge how the uncertainty on the spin-down rate propagates.
3.2. Birth location and velocity in the Galactic plane
To follow the dynamical evolution of the pulsars in the Galactic reference frame, we synthesised their birth position x, y, z in the Galaxy as well as their kick velocity and direction.
We emulated the distribution of the NS progenitors by using the location of the HII regions in the Galaxy. The latter are good tracers of massive stars because O-B stars are required to ionise the hydrogen bubbles. For the number density of pulsars at birth as a function of Galactocentric distance, we used the HII region profile recently obtained by Bania et al. (2010) from radio observations that can probe HII regions to large distance with little absorption. Figure 2 shows the comparison between the Paczyński (1990) birth distribution used in earlier publications (Gonthier et al. 2004; Takata et al. 2011) and the HII region profile used here. Both distributions extend from the Galactic centre up to 40 kpc and have been normalised to 1 over the Galaxy.
 |
Fig. 2 Surface density of the new born neutron stars. The dashed curve represents the Paczyński distribution (Paczyński 1990), while the adopted one following the distribution of radio HII regions, is shown as a solid curve. Both curves are normalised. |
We assume that all the NSs are born in the Galactic disk, with an exponential thin disk distribution with a scale height of 50 pc (consistent with Watters & Romani 2011 that adopted an exponential thin disk with a 75 pc scale height) and with a surface density distribution defined in Fig. 2. Due to the large supernova kick velocity, the neutron stars evolve quickly out of the plane of the Galaxy. The assumed kick velocity distribution is the same as in Watters & Romani (2011) and Takata et al. (2011). It is described by a Maxwellian distribution, characterised by a mean of 400 km s-1 and a width of 256 km s-1 (Hobbs et al. 2005).
3.3. Evolution
We have evolved both the pulsar position and velocity in the Galactic gravitational potential (described in Paczyński 1990 and Gonthier et al. 2002, Eqs. (17)–(19); and Takata et al. 2011). The spin characteristics have been evolved to the present time assuming a magnetic dipole.
The simulated pulsar population at birth is shown, in red, in the
P − Ṗ diagram of Fig. 3. Following Gonthier et al. (2002), by
knowing the analytical expression for
B(t) = f(B0,t),
it is possible to follow the evolution of the spin parameters from the birth time
t0 to the present time
tp. The magnetic decay is described by
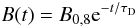 (5)where
τD = 2.8 Myr is the decay timescale, and
B0,8 is the birth magnetic field in units
of 108 Tesla.
(5)where
τD = 2.8 Myr is the decay timescale, and
B0,8 is the birth magnetic field in units
of 108 Tesla.
Assuming magnetic dipole spin-down and initial period P0, the period and the period first time derivative at the present time can be obtained from Eqs. (7) and (8) of Gonthier et al. (2002). The simulated pulsar population after evolution is shown, in blue, in Fig. 3.
 |
Fig. 3 P − Ṗ diagram of the pulsar population at birth (in red), and the population evolved to the present (blue). |
4. Radio emission model
After evolving the neutron stars in the Galactic frame, values of the radio dispersion measure (DM), and the radio scattering measure (SM), are assigned to each star using the NE2001 model (Cordes & Lazio 2001). The sky temperature at 408 MHz (Tsky, 408) for each star is obtained using the all-sky map from the study of Haslam et al. (1982).
The empirical radio emission model we have implemented in our simulations follows the work
of Gonthier et al. (2004) and Harding et al. (2007). We assume that the radio beam is composed of a
core component originating relatively near the neutron star surface and a conical component
radiated at higher altitude, both centered on the magnetic axis in the co-rotating frame.
The adopted form of this model is similar to that proposed by Arzoumanian et al. (2002), based on the work of Rankin (1983) and Kijak & Gil
(2003) and modified to include frequency dependence by Gonthier et al. (2004). The total flux at a given frequency from the two
components seen at angle θ to the magnetic field axis is 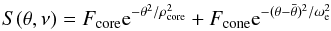 (6)where
(6)where
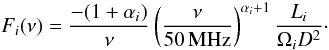 (7)The index
i refers to the core or cone,
αi is the spectral index of the total angle
and frequency integrated flux for each component,
Li is the component luminosity, and
D is the distance to the pulsar. The total solid angles of the Gaussian
beams describing the core and cone components are
(7)The index
i refers to the core or cone,
αi is the spectral index of the total angle
and frequency integrated flux for each component,
Li is the component luminosity, and
D is the distance to the pulsar. The total solid angles of the Gaussian
beams describing the core and cone components are 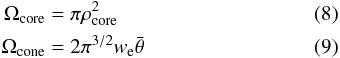 where
the latter can be written as
where
the latter can be written as 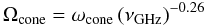 (10)where
νGHz is the frequency expressed in Giga-Hertz. The factor
ωcone represents the portion of Ωcone that is
independent of the frequency and used later in Eq. (14). The width of the Gaussian describing the core beam is
(10)where
νGHz is the frequency expressed in Giga-Hertz. The factor
ωcone represents the portion of Ωcone that is
independent of the frequency and used later in Eq. (14). The width of the Gaussian describing the core beam is 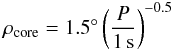 (11)where
P is the pulsar period in seconds. The annulus and width of the cone beam
are
(11)where
P is the pulsar period in seconds. The annulus and width of the cone beam
are  where
δw = 0.18 (Gonthier et al. 2006), and
where
δw = 0.18 (Gonthier et al. 2006), and 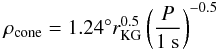 (14)is
the radius of the open field volume at the emission altitude derived by Kijak & Gil (2003), and
(14)is
the radius of the open field volume at the emission altitude derived by Kijak & Gil (2003), and 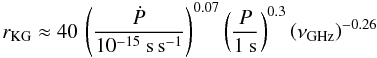 (15)rKG
is in units of stellar radius. The ratio of the core-to-cone peak flux r is
expressed as
(15)rKG
is in units of stellar radius. The ratio of the core-to-cone peak flux r is
expressed as 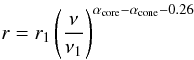 (16)and
requires αcore − αcone − 0.26 = 0.9,
αcore − αcone = >0.64 where
ν1 = 1 MHz. Gonthier et al.
(2006), who carried out a study of 20 pulsars having three peaks in their
average-pulse profiles at frequencies 400, 600 and 1400 MHz, found a core-to-cone peak-flux
ratio
(16)and
requires αcore − αcone − 0.26 = 0.9,
αcore − αcone = >0.64 where
ν1 = 1 MHz. Gonthier et al.
(2006), who carried out a study of 20 pulsars having three peaks in their
average-pulse profiles at frequencies 400, 600 and 1400 MHz, found a core-to-cone peak-flux
ratio 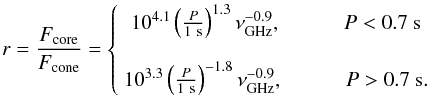 (17)It
is consistent with the ratio of Arzoumanian et al.
(2002) at periods above about 1 s, and predicts that pulsars with
P ≲ 0.05 s are cone dominated. Such a picture is supported by the
study of Crawford et al. (2001) who measured the
polarisation of a number of pulsars younger than 100 kyr, finding that they possess a high
degree of linear polarisation and very small circular polarisation, typical of cone beams.
The luminosities of the core and cone components are
(17)It
is consistent with the ratio of Arzoumanian et al.
(2002) at periods above about 1 s, and predicts that pulsars with
P ≲ 0.05 s are cone dominated. Such a picture is supported by the
study of Crawford et al. (2001) who measured the
polarisation of a number of pulsars younger than 100 kyr, finding that they possess a high
degree of linear polarisation and very small circular polarisation, typical of cone beams.
The luminosities of the core and cone components are 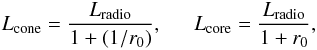 (18)where
(18)where 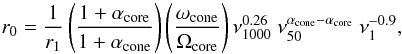 (19)r1
is evaluated from Eqs. (16) and (17),
αcore = >1.96, αcone = >1.32,
ν1000 = 1000 MHz and ν50 = 50 MHz,
and
(19)r1
is evaluated from Eqs. (16) and (17),
αcore = >1.96, αcone = >1.32,
ν1000 = 1000 MHz and ν50 = 50 MHz,
and 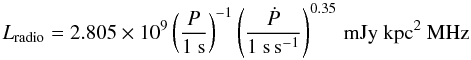 (20)as modified
from Arzoumanian et al. (2002).
(20)as modified
from Arzoumanian et al. (2002).
5. PC and SG: particle luminosity and gap width
5.1. Particle luminosity
The slot gap region is defined between the last open magnetic field line, defined by the colatitude θ0 ≃ (ΩR/cf(1))1/2, and the magnetic field line with a colatitude value (1 − wSG) where wSG is the SG width expressed in units of the dimensionless colatitude of a PC magnetic field line, ξ ≡ θ/θ0.
It is possible to define the emission component from the PC pair cascades along the PFF
that forms on the inside surface of the SG by assuming that mono-energetic radiation is
emitted tangent to field lines (Muslimov & Harding
2003). wSG is a function of pulsar period,
P, and surface magnetic field, BNS (Muslimov & Harding 2003). The photons from the
polar cap pair cascade are emitted in the region defined by
1 − wSG. The luminosity of the SG from each pole is
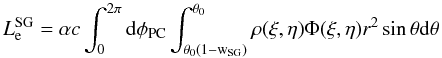 (21)where
ρ(ξ,η) and Φ(ξ,η) are the primary
charge density and potential as a function of the emission altitude
η ≡ r/RNS
and of ξ, in units of NS radius, and φPC is
the magnetic azimuthal angle. Using the expressions for Φ and for ρ from
Muslimov & Harding (2003), the PC
particle luminosity (from the low-altitude SG) is
(21)where
ρ(ξ,η) and Φ(ξ,η) are the primary
charge density and potential as a function of the emission altitude
η ≡ r/RNS
and of ξ, in units of NS radius, and φPC is
the magnetic azimuthal angle. Using the expressions for Φ and for ρ from
Muslimov & Harding (2003), the PC
particle luminosity (from the low-altitude SG) is ![\begin{eqnarray} &&\label{eqn:Lglow}L_\mathrm{e}^{\rm PC} = \dot{E} w_\mathrm{SG}^3 \left(1 - {w_\mathrm{SG}\over 2}\right)\left[\kappa \left(1-\kappa\right)\left(1-{1\over \eta^3}\right)\cos^2\alpha + {9\over 8} \theta_0^2\phantom{\left[{H(\eta)\over H(1)}\sqrt{\eta{f(1)\over f(\eta)}}-1\right]}\right. \nonumber\\&& \times \left.\left(1 - {w_\mathrm{SG} + {3 \over 10} w_\mathrm{SG}^2 }\right) H^2(1) \left[{H(\eta)\over H(1)}\sqrt{\eta{f(1)\over f(\eta)}}-1\right]\sin^2\alpha\right] \end{eqnarray}](/articles/aa/full_html/2012/09/aa19135-12/aa19135-12-eq95.png) (22)where
(22)where
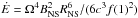 is the spin-down power,
is the spin-down power,
 ,
I38 is the NS moment of inertia in unit of
1038 kg m2, R6 is the NS radius
RNS in unit of 106 m,
H(η) is a relativistic correction factor of order 1,
f(η) is the correction factor for the dipole component
of the magnetic field in a Schwarzschild metric, and α is the pulsar
obliquity (Muslimov & Tsygan 1992; Harding & Muslimov 1998).
,
I38 is the NS moment of inertia in unit of
1038 kg m2, R6 is the NS radius
RNS in unit of 106 m,
H(η) is a relativistic correction factor of order 1,
f(η) is the correction factor for the dipole component
of the magnetic field in a Schwarzschild metric, and α is the pulsar
obliquity (Muslimov & Tsygan 1992; Harding & Muslimov 1998).
Using the equations for Φ and for ρ from Muslimov & Harding (2004), the high-altitude SG particle luminosity from
each pole can also be determined from Eq. (21) as 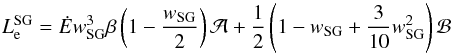 (23)where
β = (1>3η/4ηlc)1/2
and
ηlc = rlc/RNS = c/ΩRNS.
The parameters
(23)where
β = (1>3η/4ηlc)1/2
and
ηlc = rlc/RNS = c/ΩRNS.
The parameters 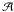 and ℬ, are defined as: where
ηLC = RLC/RNS,
β = (1>0.75η/ηLC),
and ηc = 1.3. According to Muslimov & Harding (2004), the energies of the primary electrons in the
SG quickly become radiation-reaction limited, with the rate of acceleration balancing the
curvature radiation loss rate, resulting in 100% efficiency with
and ℬ, are defined as: where
ηLC = RLC/RNS,
β = (1>0.75η/ηLC),
and ηc = 1.3. According to Muslimov & Harding (2004), the energies of the primary electrons in the
SG quickly become radiation-reaction limited, with the rate of acceleration balancing the
curvature radiation loss rate, resulting in 100% efficiency with
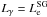 in this
case.
in this
case.
5.2. Gap width
In the SG model, the width of the slot gap wSG can be
estimated as the magnetic colatitude where the variation in height of the curvature
radiation PFF z0 (in units of stellar radius) becomes
comparable to a fraction λ of the stellar radius
RNS (Muslimov &
Harding 2003): 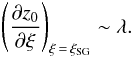 (24)In Eq. (24), z0 represents
the dimensionless altitude, above the polar cap, of pair formation due to curvature
radiation
(24)In Eq. (24), z0 represents
the dimensionless altitude, above the polar cap, of pair formation due to curvature
radiation 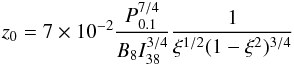 (25)where
P0.1 = P/0.1 s, and
B8 is the magnetic field in units of 108 Tesla.
By solving numerically Eq. (24) with
z0 defined in Eq. (25), one obtains ξSG for a specific pulsar. The
wSG gap width value is then obtained as
(25)where
P0.1 = P/0.1 s, and
B8 is the magnetic field in units of 108 Tesla.
By solving numerically Eq. (24) with
z0 defined in Eq. (25), one obtains ξSG for a specific pulsar. The
wSG gap width value is then obtained as 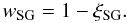 (26)The
λ parameter constrains both the energetics and emission pattern of the
SG emission and impacts both the SG and PC luminosity (Sect. 10.6) and light-curve sharpness and shape. For large λ
values the light-curve peaks appear too sharp compared with the observed LAT profiles,
therefore the slot gap is too narrow and not energetic enough to explain the observed LAT
fluxes. On the other hand, smaller λ values imply wider slot gaps,
sufficiently luminous when compared with the observations, but light-curve peaks too broad
when compared with the observed ones.
(26)The
λ parameter constrains both the energetics and emission pattern of the
SG emission and impacts both the SG and PC luminosity (Sect. 10.6) and light-curve sharpness and shape. For large λ
values the light-curve peaks appear too sharp compared with the observed LAT profiles,
therefore the slot gap is too narrow and not energetic enough to explain the observed LAT
fluxes. On the other hand, smaller λ values imply wider slot gaps,
sufficiently luminous when compared with the observations, but light-curve peaks too broad
when compared with the observed ones.
As a result we compromise between the narrow light-curve structures and the γ-ray luminosity through a reasonable radiation efficiency ϵγ. We tried two different approaches to constrain λ: one based on energetic arguments, and one based on the optimisation of the expected light-curves for some of the LAT pulsars.
Since Lγ scales as
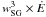 and
since we want the luminosity to be close to
Lγ ∝ Ė1/2
(Abdo et al. 2010, First pulsar catalog) we need
to have
wSG ∝ Ė − 1/6
to obtain a reasonable agreement with the LAT data. The luminosity remains close to
Ė0.5 for all the tested λ values, but
favours λ < 0.4 to explain the bright LAT
pulsars. A good compromise is found for λ = 0.35.
and
since we want the luminosity to be close to
Lγ ∝ Ė1/2
(Abdo et al. 2010, First pulsar catalog) we need
to have
wSG ∝ Ė − 1/6
to obtain a reasonable agreement with the LAT data. The luminosity remains close to
Ė0.5 for all the tested λ values, but
favours λ < 0.4 to explain the bright LAT
pulsars. A good compromise is found for λ = 0.35.
One can calculate numerically the PFF shape for the P and B values of some of the best known pulsars, Crab, Vela, CTA1, and Geminga, to obtain an approximate wSG value (Muslimov & Harding 2003). The results yield wSG,Crab = 0.03, wSG,Vela = 0.1, wSG,CTA1 = 0.16, wSG,Geminga = 0.3 for λ values between 0.02>0.6.
To investigate how the pulsar light-curve changes as a function of λ, we performed a fit to some LAT light-curves with the SG phase-plots (see Sect. 7), evaluated for a set of wSG values obtained for different λ values. We studied the behaviour of the best-fit likelihood value as a function of λ for Vela, Crab, J1028-5820, J1048-5832, J2021+3651, and J2229+6114. For all the studied pulsars, in the λ < 0.4 range that allows bright enough pulsars, the maximum-likelihood value presents a local maximum between 0.2 and 0.4. This result is consistent with the λ estimate obtained from the luminosity study and the PFF evaluation from Crab, Vela, CTA1, and Geminga.
In this paper, we set λ = 0.35. This value reproduces the bulk of the light-curve structure of the observed objects and yields a reasonable estimate of the SG luminosity. In choosing λ, we put more emphasis on matching the sharply peaked light-curves often recorded by the LAT than on achieving bright luminosities. This selection of λ was driven by the need to preserve realistic beam patterns (thus their brightness and visibility across the beam) and is a key assumption that contains the results of our population studies. We mitigated the low SG gamma-ray luminosities by using a radiative efficiency greater than 1 as discussed in Sect. 8.2.
6. OG and OPC: particle luminosity and gap width
6.1. Gap width
To determine the gap width, we consider two different prescriptions. The first one (Watters et al. 2009) simply assumes that the gap width
is equal to the γ-ray radiation efficiency. Because of the
Lγ ∝ Ė0.5
relation observed in the first LAT pulsar catalog (Abdo
et al. 2010), the gap width should follow as 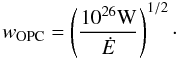 (27)Our second
prescription follows the calculations of the self sustaining OG model presented in Zhang et al. (2004). In this formulation, the X-rays
that trigger the pair production come from the bombardment of the NS surface by the full
return current from the OG. The bright X-ray luminosity allows active OGs and
γ-ray emission for many old pulsars. The outer gap width across
magnetic field lines is determined by computing the location of the pair formation
surface. From Kapoor & Shukre (1998), the
polar angle θc corresponding to the magnetic field line
tangent to the light cylinder is:
(27)Our second
prescription follows the calculations of the self sustaining OG model presented in Zhang et al. (2004). In this formulation, the X-rays
that trigger the pair production come from the bombardment of the NS surface by the full
return current from the OG. The bright X-ray luminosity allows active OGs and
γ-ray emission for many old pulsars. The outer gap width across
magnetic field lines is determined by computing the location of the pair formation
surface. From Kapoor & Shukre (1998), the
polar angle θc corresponding to the magnetic field line
tangent to the light cylinder is: ![\begin{equation} \tan\theta_\mathrm{c} = -\frac{3}{4\tan\alpha}\left[1+\left(1+\frac{8}{9}\tan^2 \alpha\right)^{0.5}\right] \end{equation}](/articles/aa/full_html/2012/09/aa19135-12/aa19135-12-eq141.png) (28)with
the light cylinder radius given by
(28)with
the light cylinder radius given by
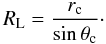 (29)Here
rc is the distance between the pulsar and the point where
the light cylinder is tangent to the magnetic field line corresponding to
θc. The lower boundary of the outer gap is estimated from
the null-charge surface, Ω·B = 0,
that in two dimensions is described by
(rin,θin). By
definition, the polar angle at the inner edge of the outer gap is
(29)Here
rc is the distance between the pulsar and the point where
the light cylinder is tangent to the magnetic field line corresponding to
θc. The lower boundary of the outer gap is estimated from
the null-charge surface, Ω·B = 0,
that in two dimensions is described by
(rin,θin). By
definition, the polar angle at the inner edge of the outer gap is
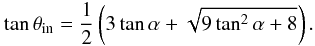 (30)The computation of
rin is obtained from the relation
(30)The computation of
rin is obtained from the relation
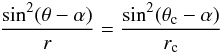 (31)which
results in
(31)which
results in 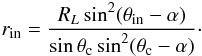 (32)The relation that defines
the fractional OG size in this case is:
(32)The relation that defines
the fractional OG size in this case is: 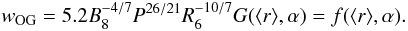 (33)where
G(r,α) is a factor that is numerically solved for each
pulsar by taking into account the average distance ⟨ r ⟩ at which
primary γ-rays are produced and along which magnetic field line they pair
produce when they interact with an X-ray coming radially from the NS surface. The average
distance ⟨ r ⟩ is defined in Zhang
et al. (2004) as
(33)where
G(r,α) is a factor that is numerically solved for each
pulsar by taking into account the average distance ⟨ r ⟩ at which
primary γ-rays are produced and along which magnetic field line they pair
produce when they interact with an X-ray coming radially from the NS surface. The average
distance ⟨ r ⟩ is defined in Zhang
et al. (2004) as 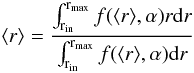 (34)where
rmax = min(rc,rb)
and rb is the radius at which the fractional size of the outer
gap stops to grow:
f(rb,α) = 1.
(34)where
rmax = min(rc,rb)
and rb is the radius at which the fractional size of the outer
gap stops to grow:
f(rb,α) = 1.
A full calculation of the width of the OG radiating layer is complicated (Hirotani 2006, 2008) since both the screening and the radiation occur in the same location. For this paper, we assume that this is an infinitely thin layer on the gap inner edge and that it is uniform in azimuth around the magnetic axis whereas Hirotani (2006) finds a significant azimuthal dependence.
6.2. Particle luminosities
The assumed gap width wOPC defined in Sect. 6.1 is not based on any physical prescription and is very different from the usual dependence luminosity ∝ (gap width)3 (both SG and OG) based on the electrodynamics.
The gap width luminosity is evaluated as 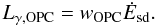 (35)In the OG case, from
Zhang et al. (2004) and previous papers dealing
with OG gap geometry, the total γ-ray luminosity is
(35)In the OG case, from
Zhang et al. (2004) and previous papers dealing
with OG gap geometry, the total γ-ray luminosity is 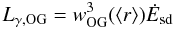 (36)where
wOG is the fractional width of the gap at the average gap
radius ⟨ r ⟩ .
(36)where
wOG is the fractional width of the gap at the average gap
radius ⟨ r ⟩ .
7. Phase-plot and light-curve generation
7.1. Assumptions and photon distributions
To provide the γ-ray emission pattern for each emission mechanism, we used the geometric emission model from Dyks et al. (2004) based on the following assumptions: (i) the pulsar magnetic field is dipolar and swept-back by the pulsar rotation (retarded potentials) (Deutsch 1955); (ii) the γ-ray emission is tangent to the magnetic field line and oriented in the direction of the accelerated electron velocity in the star frame. Relativistic aberration and time of flight delays are taken into account.
In the computation of the emission pattern, the first step consists in localising the position of the magnetic field line from which the radiation is produced. Each field line is then divided into segments and for each segment the tangent direction and height with respect to the NS surface is evaluated. Since the emission gap is located, for each model, in a different magnetospheric region, the emission patterns are obtained by selecting the segments corresponding to the gap position in each model. The γ-ray emission is assumed to be uniform along the field lines in the co-rotating frame. The phase φ of the pulsar emission is defined by the direction of the emitted photons with respect to the corotating frame. The result of this computation is the two-dimensional emission pattern in the plane (φ,ζ), shown for each implemented emission model in Fig. 4, which we refer to as a phase-plot. Figure 4 also shows the evolution of the emission pattern as a pulsar ages.
To incorporate the radio emission geometry we modulate the field lines with the flux
S(θ,ν) given by Eq. (6). The differential flux radiated from a bundle of field lines centred
at open-volume coordinates (r, l) (see Dyks et al. 2004) is 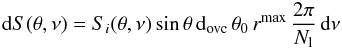 (37)where
Nl is the number of azimuthal divisions of
each polar cap ring, rmin = 0.1 and
rmax = 1.0 are the lower and upper boundary of the emission
region, and dovc (=0.1 for the radio phase-plot) is the
spacing of the rings on the PC in open volume coordinates. For the SG model
dovc is adjusted to have 20 rings within the gap. The flux
is assumed to be emitted at an altitude of 1.8RNS for the core
component and at an altitude given by Eq. (15) for the cone component.
(37)where
Nl is the number of azimuthal divisions of
each polar cap ring, rmin = 0.1 and
rmax = 1.0 are the lower and upper boundary of the emission
region, and dovc (=0.1 for the radio phase-plot) is the
spacing of the rings on the PC in open volume coordinates. For the SG model
dovc is adjusted to have 20 rings within the gap. The flux
is assumed to be emitted at an altitude of 1.8RNS for the core
component and at an altitude given by Eq. (15) for the cone component.
 |
Fig. 4 The top to bottom panels illustrate the γ-ray emission pattern obtained for a young (left) and old (right) pulsar, respectively for the PC, SG, OG/OPC, and radio (core plus cone) models. For the PC and Radio models, the time evolution is obtained for B = 108 T and period increasing from 30 to 1000 ms. In the SG and OG/OPC models, the time evolution is obtained for a gap width wSG increasing from 0.04 to 0.5 and wOG/OPC increasing from 0.01 to 0.4 respectively. All the plots are given for an obliquity α = 45°. |
In the PC model, the emission profile in colatitude is infinitely thin along the inner
edge of the slot gap (with wSG defined in Sect. 5.2) and the intensity of the emission along the field
line, IPC, exponentially decreases from the polar cap edges to
the magnetic pole 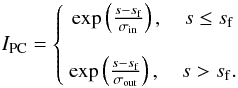 (38)Here
sf = 2.5,σin = 1.0,σout = 2.0,
and s is the curvilinear distance along the field line starting from the
NS surface. Both s and sf are in unit of
RNS.
(38)Here
sf = 2.5,σin = 1.0,σout = 2.0,
and s is the curvilinear distance along the field line starting from the
NS surface. Both s and sf are in unit of
RNS.
To model the emission component from primary electrons in the SG model, we assume that
radiation is emitted along the field lines in the slot gap, up to altitude
η = ηmax (where
η = r/RNS).
We assume an emissivity distribution across the SG as:
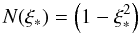 (39)where
ξ ∗ = 0 at the center of the SG and
(39)where
ξ ∗ = 0 at the center of the SG and
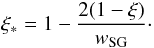 (40)Such a
distribution, that peaks in the centre of the gap and decreases to zero at the gap edges,
follows from the ξ ∗ distribution of the SG potential (Muslimov & Harding 2004).
(40)Such a
distribution, that peaks in the centre of the gap and decreases to zero at the gap edges,
follows from the ξ ∗ distribution of the SG potential (Muslimov & Harding 2004).
Magnetic field, period, and gap width values for which the phase-plots have been evaluated for each emission model.
For the OG/OPC model, we describe the emitting region as an infinitely thin layer along the inner surface of the gap. The radio and PC phase-plots show the hollow cone patterns centered on the magnetic pole, while the SG and OG phase-plots show the caustic emission patterns characteristic of outer magnetosphere emission (Dyks et al. 2004).
7.2. Light-curve generation
The (φ,ζ) phase-plot space has been sampled in
180 × 90 bins. Each bin n(φ,ζ) of the phase-plot gives
the number of photons per solid angle per primary particle that can be observed in the
ζ direction at the rotational phase φ: 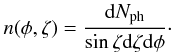 (41)Each phase-plot
is obtained for a specific set of pulsar parameters that define its magnetospheric
structure: the spin period P, the surface magnetic field
BNS, and the magnetic
obliquity α. For the studied models, the phase-plot has the following
dependencies: For each emission model, we have evaluated phase-plots for
α values, from 5° to 90°, with a step of
5°. For each α value, the phase-plots have been evaluated
for 2 magnetic field values and 9 spin period values for the PC and radio models, and for
16 gap width values in the SG and OG/OPC cases. The complete set of sampled parameters is
listed in Table 1.
(41)Each phase-plot
is obtained for a specific set of pulsar parameters that define its magnetospheric
structure: the spin period P, the surface magnetic field
BNS, and the magnetic
obliquity α. For the studied models, the phase-plot has the following
dependencies: For each emission model, we have evaluated phase-plots for
α values, from 5° to 90°, with a step of
5°. For each α value, the phase-plots have been evaluated
for 2 magnetic field values and 9 spin period values for the PC and radio models, and for
16 gap width values in the SG and OG/OPC cases. The complete set of sampled parameters is
listed in Table 1.
To obtain the light-curve of a given NS, with a particular set of P, BNS, α, and gap width parameters, we interpolated the phase-plots noted in Table 1. When comparing phase profiles for a different set of parameters, typically one profile will be narrower than another one making it nontrivial to interpolate between them. We adopted a non-linear interpolation which expands the narrower light-curve covering the smallest phase range up to the phase extent of the wider profile, then applies a linear interpolation, and contracting the expanded profile back down to the extent of the original parent profiles. This strategy preserves the thin peaks and high degree of modulation that characterises the pulsar emission profiles at radio and γ-ray wavebands.
8. Flux calculations
8.1. Phase-plot normalisation and energy flux
Let us define Lpole as the radiative luminosity from each
pole, either in the γ-rays or in the radio. Assuming a value for the
primary particle production rate Ṅe and the energy
E of each photon, one obtains a radiation luminosity per phase-plot
bin: 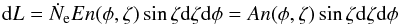 (42)where A
is a proportionality constant. One can normalise the phase-plot to the total radiation
luminosity over the two poles according to:
(42)where A
is a proportionality constant. One can normalise the phase-plot to the total radiation
luminosity over the two poles according to:
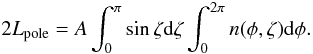 (43)We define the specific
intensity I as
(43)We define the specific
intensity I as 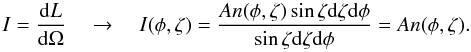 (44)It is now possible to
obtain the average energy flux observed by an Earth observer for a line of sight
ζobs:
(44)It is now possible to
obtain the average energy flux observed by an Earth observer for a line of sight
ζobs: 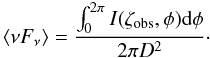 (45)Here, D
is the pulsar distance.
(45)Here, D
is the pulsar distance.
From the Eqs. (44) and (45), we can write the average energy flux
observed at the Earth as: 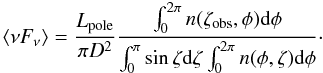 (46)The latter equation
establishes the relation between the luminosity derived in the framework of a given model,
Lpole, and the integral of the pulsar light-curve
(46)The latter equation
establishes the relation between the luminosity derived in the framework of a given model,
Lpole, and the integral of the pulsar light-curve
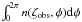 ,
obtained, from the phase-plot, for ζ = ζobs.
This is related to the beaming factor fΩ discussed in
Sect. 10.5
,
obtained, from the phase-plot, for ζ = ζobs.
This is related to the beaming factor fΩ discussed in
Sect. 10.5
8.2. Computations: gap width and energy flux
We calculated the γ-ray and radio light-curve for each pulsar of the
sample, storing the value of the integral 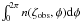 for the
flux computation. The width of the emission gaps is computed using Eq. (26) for the SG, and Eqs. (33) and (27) for the OG and OPC. Because the PC and SG models do not apply when
the gap becomes too large (pair-starved gaps should then be used), the flux for gap widths
larger than 0.5 has been set to 0. Because no emission remains visible from the thin inner
edge of OG/OPC gaps when the gap width exceeds 0.7 the flux for gap widths larger than 0.7
has been set to 0. So all the pulsars with a gap width above these threshold levels are
assumed to not produce any γ-ray emission.
for the
flux computation. The width of the emission gaps is computed using Eq. (26) for the SG, and Eqs. (33) and (27) for the OG and OPC. Because the PC and SG models do not apply when
the gap becomes too large (pair-starved gaps should then be used), the flux for gap widths
larger than 0.5 has been set to 0. Because no emission remains visible from the thin inner
edge of OG/OPC gaps when the gap width exceeds 0.7 the flux for gap widths larger than 0.7
has been set to 0. So all the pulsars with a gap width above these threshold levels are
assumed to not produce any γ-ray emission.
 |
Fig. 5 Number density of the visible γ-ray pulsars obtained for each model as a function of characteristic age and energy flux times the square of the pulsar distance. These parameters can all be measured from the observations. The linear grey scale saturates at 1 star/bin for the polar cap and 2.5 star/bin for the other models. The pink contours outline the region where simulated radio-loud γ-ray pulsars are found (at 20% of the maximum density). The pink and green lines show the data for the radio-loud and radio-quiet LAT pulsars, respectively. |
For the radio luminosity computation, Lpole, we have used Eq. (20) to evaluate the total radio luminosity and Eq. (18) to evaluate the luminosities of each core and cone component. The γ-ray luminosity has been obtained by scaling the particle luminosities derived in Eqs. (22), (23), (36), and (35), for the PC, SG, OG and OPC models respectively by using a radiative eficiency εγ. The latter has been chosen to provide a good agreement between the observed and simulated SγD2 distributions as a function of characteristic age (Sγ is the photon flux and D the pulsar distance). This distribution involves only readily observable quantities. The solution adopted for each model is shown in Fig. 5. The choice of radiative efficiencies are: ϵPC = 1.0, ϵSG = 12.0, ϵOG = 1.0, and ϵOPC = 0.5. The high value of ϵSG needed for the SG requires either a super Goldreich-Julian current or a stronger value of the accelerating electric field in the gap compared to the original calculation by Muslimov & Harding (2004). This is quite possible if the polar cap is slightly offset, i.e., non-symmetrical around the magnetic axis, as one expects from the shape of the magnetic field lines distorted by the stellar rotation. Harding & Muslimov (2011) show that this distortion leads to a larger pair multiplicity as well as an increased electrical field along the field lines, thus an enhanced luminosity. Offset polar caps can sustain the modest increase in particle energy that is required in the present population study to account for the flux and pulsar counts observed by the LAT without invoking a radiation efficiency larger than one. The offset polar cap prediction was not available at the time of the population synthesis work, so we keep here the original polar cap luminosity and ϵSG = 1200%.
8.3. Gamma-ray energy and photon flux
To evaluate the photon flux from the energy flux and to compare it with the LAT
sensitivity in photon flux, we need to assume an emission spectrum for the pulsars. The
typical photon spectrum of a LAT pulsar is well fitted by a power-law with an exponential
cutoff, like 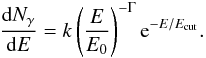 (47)In the first LAT pulsar
catalog (Abdo et al. 2010), the distribution of the
parameters Γ and Ecut can be described by two Gaussians:
(47)In the first LAT pulsar
catalog (Abdo et al. 2010), the distribution of the
parameters Γ and Ecut can be described by two Gaussians:
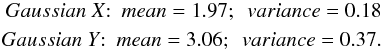 (48)The
spectral index Γ and the log 10(Ecut) are defined
as:
(48)The
spectral index Γ and the log 10(Ecut) are defined
as: ![\begin{eqnarray} &&\theta = 0.5982~~~[{\rm rad}] \notag \nonumber\\ &&\Gamma = X\cos\theta - Y\sin\theta\notag \nonumber\\ &&\log_\mathrm{10}(E_\mathrm{cut})=X\sin\theta + Y\cos\theta. \label{twogaussSpec} \end{eqnarray}](/articles/aa/full_html/2012/09/aa19135-12/aa19135-12-eq224.png) (49)The
Gaussian widths, centroids, and correlation angle had been derived from the analysis of
the spectral parameters measured for the 1st LAT pulsar catalogue. We took here the same
values.
(49)The
Gaussian widths, centroids, and correlation angle had been derived from the analysis of
the spectral parameters measured for the 1st LAT pulsar catalogue. We took here the same
values.
The photon flux computation has been done using Eqs. (46)–(49) by assuming that the luminosity is mainly produced at photon energies ≥ 100 MeV. The choice of this threshold and the choice of radiative efficiencies to match the data in Fig. 5 are linked.
9. Gamma-ray and radio visibilities
9.1. γ-ray pulsar visibility
To select the simulated pulsars that could be detected by the LAT during two years of observation, we made use of the 6 month pulsar visibility map published for the 1st LAT pulsar catalogue (Abdo et al. 2010) and of the 1 year pulsar visibility of blind pulsar searches (Dormody et al. 2011). The two maps have been used to estimate the γ-ray detectability of the radio-loud pulsars (corresponding to the LAT radio selected objects) and the radio-quiet ones (corresponding to the LAT blind search objects) respectively. The maps give the minimum visible photon flux Smin.ph and have been obtained taking into account the real LAT observation time in the sky, the photon energy, and the effective collection area corrected for the different incidence directions. Since the sky survey mode for LAT observations has been continued after 6 months, the maps have been scaled to 2 years as the square root of time for the radio-selected sensitivity map and linearly with time for the blind search sensitivity map. Very few pointed observations were programmed that would significantly alter the shape of the visibility map. Photons collected in survey mode largely dominate and the flux threshold for detectability is primarily limited by the intensity of the interstellar background.
9.2. Radio visibility
The synthesis of the population is not based on any assumed NS birth rate; we assume a flat star formation rate over the last 1 Gyr. Instead, the simulated sample was scaled to the real number of pulsars detected in the Galaxy. The scaling factor has been evaluated by selecting all the ATNF radio pulsars present in a select group of ten surveys and comparing this number with simulated radio pulsars visible in the same region. We have generated a large enough population to reduce the Poisson fluctuations and to improve the statistics in the analysis results.
Instrumental parameters of the radio surveys.
We selected the simulated pulsars within the visibility criteria of 10 radio surveys from
the ATNF database1 for which the survey parameters
are well known and that cover the largest possible sky surface while minimising the
overlapping regions. These surveys are: Molonglo2 (Manchester et al. 1978), Green Bank 2 and 3 (Dewey et al. 1985; Stokes et al. 1985),
Parkes 2 (70 cm) (Lyne et al. 1998), Arecibo 2
and 3 (Stokes et al. 1986; Nice et al. 1995), Parkes 1 (Johnston
et al. 1992), Jodrell Bank 2 (Clifton &
Lyne 1986), Parkes Multi-beam (Manchester et al.
2001) and the extended Swinburne surveys (Edwards
et al. 2001; Jacoby et al. 2009). The
ratio between the number of simulated pulsars meeting the surveys’ visibility criteria and
the number of objects actually detected is 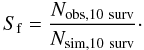 (50)This is the factor we
used to scale the simulated pulsar sample.
(50)This is the factor we
used to scale the simulated pulsar sample.
9.2.1. Radio pulsar selection
During a radio survey, the edges of the survey region are defined by the position of the radio-telescope beam centre. Nevertheless, because of the solid angle extension and complexity of the beam, it is possible to observe a pulsar slightly out of the declared survey region. Thus, to say that all the pulsars observed during a survey fall inside the declared survey coordinates edges is not totally correct. The first parameter we re-evaluated for each survey is the number of pulsars seen inside a given region.
The second important parameter is the survey efficiency ϵsurv. It is defined as a filling factor, e.g. the ratio between the actual solid angle covered by the radio telescope beam during the observations, and the area within the declared survey boundaries. The survey efficiency can be considered as the probability of observing a pulsar present in the survey region only if the parent spatial distribution is uniform. To evaluate the boundaries of the survey region and to define the survey efficiency we decided:
-
1.
to slightly extend the sky survey boundaries in order to includethe largest number of pulsars actually detected by a survey,without changing too much the original boundaries;
-
2.
to evaluate the detection flux threshold for each pulsar within a survey by scaling the Dewey formula (Dewey et al. 1985) with a free parameter, ϵDewey, to match the observations.
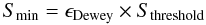 (51)where
the threshold flux Sthreshold is expressed by the
Dewey formula
(51)where
the threshold flux Sthreshold is expressed by the
Dewey formula ![\begin{equation} \label{DeweyEq} S_\mathrm{threshold}=\frac{\sigma_\mathrm{S/N}[T_\mathrm{rec}+T_\mathrm{sky}(l,b)]}{G\sqrt{N_\mathrm{p}Bt}}\sqrt{\frac{W}{P-W}}\cdot \end{equation}](/articles/aa/full_html/2012/09/aa19135-12/aa19135-12-eq245.png) (52)
(52)
 (53)Here,
W0 is the intrinsic pulse width (Duty Cycle),
τsamp is a low-pass filter time constant applied before
sampling (when this parameter is unknown, a value equal to twice the sampling time has
been used), τDM is the pulse smearing due to the DM over one
frequency interval Δν, and τscat is the
pulse broadening due to interstellar scattering (Dewey
et al. 1985). The dispersion broadening time, τDM
(ms), across one frequency channel, Δν, is related to the dispersion
measure (DM) as
(53)Here,
W0 is the intrinsic pulse width (Duty Cycle),
τsamp is a low-pass filter time constant applied before
sampling (when this parameter is unknown, a value equal to twice the sampling time has
been used), τDM is the pulse smearing due to the DM over one
frequency interval Δν, and τscat is the
pulse broadening due to interstellar scattering (Dewey
et al. 1985). The dispersion broadening time, τDM
(ms), across one frequency channel, Δν, is related to the dispersion
measure (DM) as  (54)where
me is the mass of the electron, c is the
speed of the light, and ν1, ν2
are the edges of the frequency channel. The dispersion measure, DM (pc cm-3),
is obtained using the Cordes & Lazio
(2001) NE2001 model. The same model provides the scattering measure, SM (kpc
m−20/3), which allows to estimate the broadening time
due to interstellar scattering as
(54)where
me is the mass of the electron, c is the
speed of the light, and ν1, ν2
are the edges of the frequency channel. The dispersion measure, DM (pc cm-3),
is obtained using the Cordes & Lazio
(2001) NE2001 model. The same model provides the scattering measure, SM (kpc
m−20/3), which allows to estimate the broadening time
due to interstellar scattering as
 (55)where
d is the pulsar distance in kpc (Johnston et al. 1992; Sturner & Dermer
1996). The last term of Eq. (53),
(55)where
d is the pulsar distance in kpc (Johnston et al. 1992; Sturner & Dermer
1996). The last term of Eq. (53),  , is an
additional time broadening added when the sampling is performed for a DM value different
from the real one. It corresponds to the fourth term of Eq. (2) in Dewey et al. (1985) and becomes important just for low period
pulsars.
, is an
additional time broadening added when the sampling is performed for a DM value different
from the real one. It corresponds to the fourth term of Eq. (2) in Dewey et al. (1985) and becomes important just for low period
pulsars.
Estimated survey parameters.
For each model and for the observed dataset, we give from left to right the scaled numbers of pulsars visible in the radio or γ-ray band, in the radio and γ-ray bands, in γ-rays only, and the fraction of radio loud objects in the γ visible sample.
The sky temperature at frequencies other than 408 MHz is obtained as:
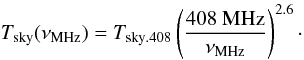 (56)Tables 2 and 3 list
all the radio telescope and detector characteristics of the surveys we took into
account. Some of the survey parameters in the literature listed as average values have
been re-evaluated using the above mentioned prescription.
(56)Tables 2 and 3 list
all the radio telescope and detector characteristics of the surveys we took into
account. Some of the survey parameters in the literature listed as average values have
been re-evaluated using the above mentioned prescription.
The scaling of the radiometer equation was motivated by the uncertainties related to the Dewey formula, because of flux oscillations due to scintillation. The scintillation is caused by the turbulent variation of the interstellar medium that the pulsar light has to cross before reaching the observer. The consequence is an oscillation (scintillation) of the pulsar flux that can introduce spurious detections of pulsars with a flux lower than the survey threshold or that can cause the non-detection of pulsars with a flux higher than the survey threshold. So we scaled the Sthreshold level to take into account possible spurious detections or missed detections due to scintillation. Sthreshold should not be lower than the flux of the weakest pulsar of the survey. A reasonable estimate is to employ the average of the low-flux tail of the pulsars of the survey.
In the ATNF database we can count how many pulsars fall within a survey boundary, how many would match the survey visibility criterion (flux > Sthreshold), and how many of these pulsars have really been observed by the survey. The comparison of the ratios of the radio flux recorded for each pulsar to the minimum visible flux Smin in its direction provides an estimate of the Dewey scaling factor. The scaling values ϵDewey are given in Table 3 and the distribution of the flux ratios is shown in Figs. A1–A3 (right plots) for each survey (only the ratios below 10 are displayed to focus near the visibility threshold).
Then, for each survey, we derived the ratio between the number of pulsars really detected by the survey and the total number of observable ATNF pulsars (the sum of the detected ones plus those that match the position and flux survey criteria but were not detected). We consider this last ratio as the new survey efficiency, ϵsurv, i.e., the percentage of pulsars detected by the survey with respect to all the detectable ATNF pulsars in the survey region. The new efficiency ϵsurv is listed, for each survey, in Table 3.
By using the newly estimated survey parameters listed in Tables 2 and 3, and by using the radiometer Eq. (52), the number of real pulsars that meet the visibility criteria of our surveys is 1430 (ATNF database, January 2012). We use this number and the number of simulated pulsars that match the same criteria to scale the visible component of the simulated γ-ray pulsar population in Eq. (50).
10. Results
10.1. Detection statistics
Table 4 indicates, for each model, the numbers of NSs that passed the radio and/or γ visibility criteria and their comparison with the LAT detections after 2 years of observations. The number of radio visible pulsars in the simulation has been scaled to the 1430 ATNF radio pulsars that passed the same selection criteria. The scale factor of 0.136 is required to match the simulated and observed radio samples and has been applied to all star counts quoted hereafter, in particular to the γ-ray simulated samples. This scale factor implies a NS birth rate of ~3.7 NS/century over the last 1 Gyr. The choice of radiative efficiencies driven by a reasonable agreement in the SγD2 evolutions with characteristic age shows that the wide beams produced in the intermediate-high (SG) and outer models provide enough detections to account the LAT findings. The low-luminosity narrow PC beam fails in predicting the LAT detection number and the fraction of radio-quiet objects because of the large overlap between the γ-ray and radio beams.
 |
Fig. 6 Number density of the visible radio pulsars as a function of period and period derivative. The left and right plots respectively show the simulation and observed data with the same grey scale saturating at 25 star/bin and the same visibility criteria. The rising grey line marks the slot-gap death line. The declining grey lines mark the iso-magnetic lines at 107, 108, and 109 Tesla. |
 |
Fig. 7 Number density of the visible γ-ray pulsars obtained for each model as a function of period and period derivative. The linear grey scale saturates at 1.5 star/bin. The pink triangles and green dots show the radio-loud and radio-quiet LAT pulsars, respectively. The rising grey line in the slot-gap subplot marks the slot-gap death line. The declining grey lines mark the iso-magnetic lines at 107, 108, and 109 T. |
10.2. Comparison of the total simulated and observed samples
Figures 6 and 7 show the comparison between the simulated distributions in the P − Ṗ diagram for the radio visible component and for the γ-ray visible population for each model. The simulated distributions reasonably describe the observed samples and are in nice agreement with the same distributions obtained by Takata et al. (2011). The simulated radio population is able to describe the observed P − Ṗ distribution for the fastest rotators that are likely to sustain substantial γ-ray emission and represent the LAT pulsar population. The PC model reproduces poorly the observed population. Both the SG and OG models over predict the number of middle aged γ-ray pulsars and under predict the number of young γ-ray objects. Of those, the OG shows the poorer description of the data; the core of the distribution is too close to the pulsar death line and it lacks energetic pulsars. The OPC γ-visible population best describes the observed P and Ṗ of the LAT population with a core centred on the observed objects and tails that cover the overall dispersion.
 |
Fig. 8 Number distributions in period, period first time derivative, surface magnetic field strength, and distance obtained for the whole populations of radio or γ-ray visible pulsars in the simulations (light grey histogram) and in the LAT and radio survey data (thick line). The ATNF radio sample has been restricted to the objects that pass the same position and flux selection criteria as in the simulation. The slot-gap model has been used as an example for the γ-ray simulation. The dark shaded histograms show the distributions of the gamma active subsample of the whole simulated population. The abundances of simulated objects at low P, high Ṗ, and high B are dominated by γ-ray active pulsars. The excess of energetic and nearby simulated objects reflects the set of assumptions adopted for the birth distributions to provide a better match to the LAT data. |
Figure 8 compares the total simulated populations and its γ-ray sub-sample to the observed total sample of radio and/or γ-ray visible objects for key characteristics: period, period first time derivative, surface magnetic field, and distance. The simulated spin period distribution is too broad to describe the observed proportion between the number of intermediate period objects (~50 ms) and the wings of the distribution. The range of spin periods is well covered and well centred, but we lack simulated objects in the 0.3>1.0 s range. The simulated distributions in Ṗ, B, and D are all shifted to an excess of young, energetic, and nearby pulsars compared to the observed ones. This results from the choice of birth characteristics and NS intrinsic characteristics (MNS, RNS, and I formulation) that emphasised nearby and high-Ė objects while preserving the bulk of the radio distributions. This choice has been made a posteriori to minimise the lack of high-Ė objects discussed in Sect. 10.3. Nevertheless, the discrepancies observed in Figs. 6 and 8 are not only due to the choice of birth distributions, but also to a radio model ill adapted to explain the observed radio population at the highest Ės. Whereas this would be problematic to study radio beam models, the reasonable representation at P < 500 ms and the excess of objects with Ṗ > 3 × 10-15 s s-1, B > 108 T, and D ≤ 4 kpc, where most of the LAT pulsars are found, supports the study of γ-ray models. The necessity of an improved radio model is a result of this paper and its formulation, beyond the purpose of this study, will be the subject of future work. In the histograms shown in Fig. 8, the total distributions are dominated by the radio sample since the γ-ray pulsars’ contribution is much smaller.
 |
Fig. 9 Spin-down power distributions obtained for each model for the visible γ-ray pulsars. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible pulsars for each model to ease the comparison and show the relative lack of young energetic pulsars with Ė > 3 × 1028 W. |
10.3. The spin-down power
Figures 9 and 10 compare the distributions in spin-down power and characteristic age for the LAT and the γ-visible simulated pulsars. All models are significantly lacking simulated pulsars with spin-down power Ė > 3 × 1028 W and characteristic age tchar < 100 kyr. Additionally, all the models over-predict the number of low Ė pulsars and favour a pulsar population older than that observed by the LAT. The difference in shape of the observed and simulated histograms suggests that the Ė inconsistency is not due to a simple scale mismatch, but to a deficiency in modelling the pulsar evolution: even by scaling the spin down power upward none of the models would be able to describe the observed distribution.
Even though the PC model fails to produce enough visible gamma-ray pulsars because its narrow beam is under luminous and rarely visible, its evolution with Ė or age is less skewed to old age than the high-altitude SG or the outer-gap models.
The OG model provides the poorest description of the γ-ray evolution. A strong evolution with age is predicted by the classical formulation of the OG because the gap size is controlled by the amount of X-rays emitted by the stellar surface heated by the back-flow of primary charges returning from the gap (self-sustaining OG model). The strong evolution driven by this feedback is apparently not supported by the LAT data. The OPC model gives slightly better results but still fails to predict enough high Ė pulsars. The similarity of the Ė profiles obtained for the SG and OPC models shows that the relative lack of energetic γ-ray pulsars is not related to the number of visible hemispheres (two pole caustic SG, one pole caustic OPC), or to the evolution of the emission region with age within the open magnetosphere (the emitting layer moves closer to the magnetic axis with increasing age in the OPC case while it remains near the last closed B line, but widens with age in the SG model).
 |
Fig. 10 Age distributions obtained for each model for the visible γ-ray objects. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible objects for each model to ease the comparison and show the relative lack of visible objects with age <100 kyr. |
The under-prediction of high-Ė visible γ-ray pulsars is rather puzzling since they are the intrinsically brightest objects (high particle power and large fΩ) with the widest beams (large open magnetosphere and thin gaps emitting near the closed field lines) sweeping widely across the sky. The problem affects all the models, so its origin does not depend much on the emission pattern or the luminosity trend with Ė. For instance, the luminosity evolution of the OPC model was constructed to agree with the LAT data, yet the deficit of energetic γ-ray visible pulsars is still present. For a given luminosity the effective flux intercepted by the observer strongly depends on the gap thickness. For Ė > 1028 W, the OPC gap width is 10 to 100 times smaller than the SG one, concentrating the photons in sharp caustics that remain visible to large distances and over many aspect angles, yet both the OPC and SG models produce a deficit of high Ė pulsars in a rather similar way. The discrepancy is also insensitive to the relative orientation of the radio and γ-ray beams since both radio-loud and radio-quiet simulated pulsars are missing at high Ė. Nor is the problem related to the sensitivity horizon since all the models over-predict the fainter objects at low Ė. By testing different population configurations we have tried to understand which pulsar parameter has the largest impact on the high Ė tail of the γ-ray sample. Different birth distributions in period and magnetic field have been tested. Decreasing the birth spin period in order to increase the fraction of very young and energetic pulsars (Sect. 3.1) yields a very small gain in the number of γ-visible energetic pulsars. Scanning the allowed domain of intrinsic luminosities (e.g., SG λ parameter) also failed to produce an increase in the young, energetic population.
A different choice of MNS, RNS, or I would shift the simulated distributions horizontally in Ė, but would not alter their shape. The range of acceptable masses and radii given in Lattimer & Prakash (2007) limits an increase in the moment of inertia of the stars (thus Ė) to within a factor of 2 or 3 beyond our present choice. This is too small a factor to address the lack of high-Ė pulsars in the simulations. One of the tested configurations, illustrated in Fig. 11, shows how the lack of high-Ė pulsars remains, even after choosing a more energetic pulsar population at birth and a much broader distribution for their birth places across the Galaxy, Paczyński (1990), as used in previous work e.g., Gonthier et al. (2004) and Takata et al. (2011).
Despite the stronger bias to energetic objects at birth adopted in Fig. 11 as compared to Fig. 9, the lack of high-Ėγ-ray pulsars is less severe in the latter. This is due to the much larger fraction of births occurring in the inner Galaxy for the population shown in Fig. 9. Because of the constraints on the supernova rate in the Galaxy, we cannot significantly increase the number of recent births, but the distribution provided by the HII region profile concentrates a larger fraction of the recent births in the inner Galaxy, within the LAT visibility horizon. So, the Ė problem seems related both to the birth location and spin-down evolution of the pulsars.
It is possible that the magnetic obliquity α decreases with age, as suggested by Young et al. (2010). First, the solid angle swept by the pulsar beam would decrease as α gradually decreases with age, so pulsars detected originally will later become invisible. Second, α has an impact on visibility through the gap width. This is illustrated by the difference in the Ė histograms obtained for the OG and OPC cases. They share the same emission pattern, but the OG gap width depends on α while the OPC gap width is just proportional to Ė. Another speculative explanation would be a slower evolution of the dipole spin-down for very young and energetic objects, within the first 100 kyr. This hypothesis would need to be justified on the basis of theory.
 |
Fig. 11 Spin-down power distributions obtained for each model for the visible γ-ray objects for a different set of birth distributions: a Gaussian of width 200 ms centred at 0 for the periods; the sum of two Gaussians in log 10BNS [Tesla], both 0.6 in width, respectively centred at 8.4 and 9.1, and with an amplitude ratio 1:7/12 for the surface magnetic fields; and the Paczyński (1990) surface density in the Galaxy. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution, scaled to the total number of visible objects, is plotted as a black contour. |
 |
Fig. 12 Number density of the visible radio and/or γ-ray pulsars in the Milky Way (polar view). The left and right plots respectively show the simulation and observed data with the same logarithmic gray scale saturating at 100 star/bin and the same visibility criteria. The cyan contour outlines the region where simulated SG γ-ray pulsars are detectable. The cyan triangles show the location of the LAT pulsars. The yellow dot marks the Sun. |
 |
Fig. 13 Distance distributions obtained for each model for the visible γ-ray objects. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible objects for each model to ease the comparison and show the relative overabundance of nearby objects for the PC and SG models and under abundance of nearby objects for the OG and OPC models. |
 |
Fig. 14 Distribution of the γ-ray beaming factors obtained for each model as a function of the spin-down power. Pink and green dots refer to radio-loud and radio-quiet γ-ray visible objects, respectively. The solid and dotted lines give the best exponential fit to the radio-loud and radio-quiet data points, respectively. For the PC case, a unique fit was applied to the whole sample of radio-loud and radio-quiet objects. |
10.4. Spatial distribution in the Milky Way
Figure 12 shows a polar view of the spatial density of visible radio or γ-ray pulsars in the Galaxy, resulting from the birth location profile described in Sect. 3.2.
The majority of these pulsars are born within the solar circle and the γ-ray visibility contour agrees well with the Galactic region where the bulk of the LAT pulsars have been detected. The radio visibility horizon is closer in the simulation than in reality, but the γ-ray visibility horizon spans the right distance range. The visibility is therefore not the primary cause for the lack of high-Ėγ-ray predictions discussed in the previous section.
Figure 13 gives the distance distributions of the visible γ-ray pulsars. An interesting trend, observed in all the models except for the PC, is that the radio loud to radio quiet ratio increases up to 4 or 5 kpc, and decreases down to zero at larger distance, implying that we lose the radio emission with distance more rapidly than we lose the γ-ray signal.
Since the measurement of the LAT pulsar distances is often affected by large uncertainties, the comparison between models and data in Figs. 12 and 13 should be taken with care.
10.5. The beaming factor fΩ
The beaming factor (Watters et al. 2009) is
defined as 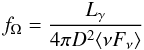 (57)where
Lγ, D, and
⟨ νFν ⟩ are respectively
the pulsar γ-ray luminosity, distance, and average energy flux. The
beaming factor is the ratio of the total energy flux radiated over the 4π
sr solid angle swept by the pulsar beam, after one complete rotation, to the
phase-averaged energy flux observed at a given ζobs angle. Its
value depends both on the intrinsic solid angle of the emission beam, on the beam
inclination, and on the amount of energy that it contains. From Eqs. (57) and (46), the beaming fraction is calculated for each simulated light-curve
as:
(57)where
Lγ, D, and
⟨ νFν ⟩ are respectively
the pulsar γ-ray luminosity, distance, and average energy flux. The
beaming factor is the ratio of the total energy flux radiated over the 4π
sr solid angle swept by the pulsar beam, after one complete rotation, to the
phase-averaged energy flux observed at a given ζobs angle. Its
value depends both on the intrinsic solid angle of the emission beam, on the beam
inclination, and on the amount of energy that it contains. From Eqs. (57) and (46), the beaming fraction is calculated for each simulated light-curve
as: 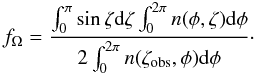 (58)Figure 14 shows the behaviour of the beaming factor as a
function of Ė. For each model we have fitted the trend for the radio-loud
and radio-quiet components of the population by using an exponential function. In the PC
case there are too few visible γ-ray pulsars, both radio-loud or
radio-quiet, to fit the evolution of the beaming factor with Ė for each
type separately. The PC fΩ(Ė) has been
evaluated by merging the samples and fitting the global trend. The best-fit functions
(fΩ,RL(Ė) and
fΩ,RQ(Ė)) are indicated in
Fig. 14.
(58)Figure 14 shows the behaviour of the beaming factor as a
function of Ė. For each model we have fitted the trend for the radio-loud
and radio-quiet components of the population by using an exponential function. In the PC
case there are too few visible γ-ray pulsars, both radio-loud or
radio-quiet, to fit the evolution of the beaming factor with Ė for each
type separately. The PC fΩ(Ė) has been
evaluated by merging the samples and fitting the global trend. The best-fit functions
(fΩ,RL(Ė) and
fΩ,RQ(Ė)) are indicated in
Fig. 14.
 |
Fig. 15 Distribution of the γ-ray luminosities obtained for each model as a function of the spin-down power. Pink and green dots refer to radio-loud and radio-quiet γ-ray visible objects, respectively. The LAT luminosities (black circles and crosses for radio-loud and radio-quiet objects respectively) have been derived using the energy-flux measurement and the fΩ value estimated from the fit to the simulated data for the particular spin-down power and radio-loud or quiet state of the LAT pulsars. The dotted line shows the 100% efficiency boundary. |
For all models, the small decrease of fΩ with age (decreasing Ė) is due to the shrinking of the polar cap as the pulsar slows down. In the PC case, both the radio-quiet and radio-loud fΩ values are very dispersed and very small because of the collimated PC beam. For the SG, OG, and OPC, the fΩ distribution of the radio-quiet population component appears always more dispersed than the radio-loud one and it spans lower fΩ values, while the radio-loud objects exhibit higher and more highly constrained beaming factors. Radio-quiet pulsars are generally seen at large |α − ζ| impact angle where the γ-ray caustics are fainter, so fΩ can reach low values.
The SG case shows a minimal change in beaming factor with age for both the radio-loud and radio quiet pulsars because emission from the bright caustic can be seen over most ζ directions in the sky and because this model predicts a strong off-peak emission. The SG radio-quiet and radio-loud beaming factors are centred around fΩ = 1.
In the OG and OPC cases, we note a pronounced dispersion in fΩ, over 1 or 2 orders of magnitude, for the radio-quiet pulsars. The OG and OPC models share the same emission pattern (phase-plot), thus the dispersion covers the same range of values. In the OPC case, the beaming factor increases up to Ė ~ 1028 W and then stays constant around 0.8. Since all the OPC simulated pulsars at a given Ė have the same γ-ray luminosity (by construction), the observed spread in the fΩ values reflects the spread in beam flux as seen from different perspectives. It amounts typically to less than a factor of 2 for radio-loud objects and more than one order of magnitude for radio-quiet ones. As the pulsars age in the OG and OPC models, there is an increasing separation of the gamma-ray and radio beams on the sky as the gamma-ray beam shrinks towards the the spin equator, producing a greater number of radio-quiet pulsars with small fΩ.
In the outer gap models, the core of the fΩ distributions is consistent with the beaming factor obtained by Takata et al. (2011)fΩ ~ 0.4.
10.6. γ-ray luminosity trend with Ė
Figure 15 shows, for each emission model, the evolution of the γ-ray luminosity with the spin-down power and its comparison with the LAT results. The luminosity of the LAT pulsars has been computed from the measured pulsed flux using Eq. (57) with a beaming factor fΩ(Ė) obtained from the best fit plotted in Fig. 14, according to their radio-loud or radio-quiet state.
The observed evolution is roughly predicted by all the models. Given the large dispersion in both the data and model predictions, the luminosity trend with Ė cannot be used to discriminate between the gap models. In the OPC case, the Lγ(Ė) evolution is a built-in assumption of the model chosen to follow the observations.
The comparison with the LAT population indicates that the PC model is not luminous enough to account for the observed pulsars. Because of the large radiative efficiency (increased power in the gap), the SG luminosity reasonably follows the LAT data and the SG population best describes the observed trend. Since the γ-ray emission is sustained by the particles generating the same polar cap electromagnetic cascade, Lγ in both the PC and SG models follows the same trend, steepening from Lγ ∝ E1/2 to Lγ ∝ E with decreasing Ė when the pulsar puts out most of its spin-down power into γ-rays. This trend is predicted but not yet observed because of the large dispersion in the LAT data points and large uncertainties in LAT pulsar distances. It is possible, however, that a more pronounced break to lower γ-ray luminosities is required at low Ė.
The OG luminosity evolution shows a different behaviour for high and low spin-down values. At Ė < 1028 W, the gap width quickly saturates to a constant value which covers about three quarters of the open field volume. Only objects with large obliquities α remain visible and their luminosity scales linearly with Ė. They exhibit a small dispersion that is not consistent with the LAT data. At higher Ė values, the LAT pulsars fall within the range of predicted luminosities but they exhibit less dispersion than predicted by the model.
 |
Fig. 16 For each model, the linear gray scale shows the number density of the radio- or γ-visible population, with a saturation at 10 star/bin. Contours are given for the radio-only visible (cyan), γ-only visible (green), and radio plus γ visible (red) objects at 1% of the maximum number density for each type. The red triangles and green dots mark the location of the radio-quiet and radio-loud LAT pulsars, respectively. |
The Lγ ∝ Ė0.5 evolution predicted by the OG and SG models at high Ė is driven primarily by the evolution of the Goldreich-Julian current across the open magnetosphere. This is true if the feedback between particle acceleration and electrical screening from the cascading yields a rather stable maximum energy for the primaries and a stable fraction of this energy is radiated away in the cascade. A steeper evolution (Lγ ∝ Ė) is expected for both polar-cap and outer-gap accelerators when the electrical screening becomes inefficient and the gap fills a large part of the open magnetosphere. The LAT data in Fig. 15 suggest a stronger luminosity evolution at Ė > 1029 W than proposed by the current models. This conclusion appears to be robust because it applies to the very different radiation patterns tested in the OG and SG cases and because the beaming factors that have been used to derive the LAT luminosities show little evolution and little scatter from one pulsar to the next for Ė > 1029 W for both models.
One can note a larger scatter in the SG and OG luminosities plotted in Fig. 15 than in the beaming factors for the same Ė range. This is due to the intrinsic variation in gap width resulting from the variety of NS properties, amplified by the fact that the luminosity is proportional to the gap width cubed. The scatter in the SG luminosity distribution is driven by the spread in period and stellar magnetic field at each value of Ė. The scatter in the OG luminosity further builds on a strong dependence of the gap width with obliquity. In that sense, looking forward to a time when more precise distance estimates are obtained and when tighter constraints on the gap location in the outer magnetosphere (from phase-resolved spectroscopy and light-curve studies) provide more reliable beaming factors for each pulsar, the dispersion in the luminosity plot can teach us about the diversity of young neutron stars that compose the LAT pulsar sample.
10.7. Fractions of γ-ray loud and radio-loud pulsars
Figure 16 illustrates the change in visibility distance for pulsars of different ages (Ė) and emission types (loud or quiet in the radio and γ-ray bands). A similar figure has been shown in Watters & Romani (2011) to study the evolution of the pulsar visibility horizon. Data points for the LAT pulsars have been overlaid, but one should note that very few distance estimates exist for the new LAT pulsars that have been found through blind periodicity searches, because of the lack of radio dispersion measures. Given the large uncertainties in distance, the agreement between the SG and OPC predictions and the LAT data is reasonable.
Figure 17 shows the fraction of radio loud pulsars in the cumulative distribution of γ-ray visible pulsars with Ė larger than the plotted value, and Fig. 18 shows the fraction of γ-loud pulsars in the cumulative distribution of radio-visible pulsars above the given Ė (see Ravi et al. 2010).
They jointly illustrate the high probability of detecting both the radio and γ-ray beams in LAT objects with Ė > 1030 W, in contrast to the predictions of all the models. This fraction remains high at all Ė values for the PC prediction, at variance with the data, because the radio and γ-ray beams are produced in nearby regions of the magnetosphere.
Figure 16 shows that the LAT visibility horizon for radio-loud and radio-quiet objects shrinks similarly with pulsar age (decreasing Ė), so we lose both types at the same rate. The radio-loud to radio-quiet ratio evolves little for Ė < 1030 W, so the radio-loud fraction in the whole γ-ray sample (Fig. 17) flattens with age to about 0.5 in good agreement with the LAT data.
The value of this fraction is controlled by the effective difference in flux sensitivity for the detection of a radio-loud or radio-quiet pulsar in the LAT data. Detecting a γ-ray pulsation after phase-folding with the radio ephemerides requires fewer photon counts and trials than for blind periodicity searches.
 |
Fig. 17 Spin-down power evolution of the fraction of radio loud pulsars in the cumulative distribution of γ-ray visible pulsars with Ė larger than the plotted value. The thin lines give the simulation results for each model. The thick line gives the fraction evolution in the LAT sample. |
 |
Fig. 18 Spin-down power evolution of the fraction of γ-loud pulsars in the cumulative distribution of radio-visible pulsars with Ė larger than the plotted value. The thin lines give the simulation results for each model. The thick line gives the fraction evolution in the LAT sample. |
The use of the first pulsar catalogue sensitivity map for the radio-loud objects (Abdo et al. 2010) and of the blind-search sensitivity map for the radio-quiet objects (Dormody et al. 2011), both scaled to 2 years, brings an excellent agreement between the model predictions and data at Ė < 1030 W. The use of the catalogue map (presenting the lowest flux thresholds) for both types of pulsars lowers the predicted fraction by a factor of 2. Figure 16 shows that the γ-ray visibility horizon shrinks much more rapidly than the radio one with pulsar power. So γ-ray pulsars become undetectable faster than radio pulsars and the γ-loud fraction in the radio-visible sample falls continuously down to a few percent at low Ė in Fig. 18.
Figure 17 shows that the radio-loud fraction in the LAT sample becomes 1 at high Ė while the SG and OPC predictions remain flat or decrease. The outer-gap predictions decline at high Ė because of a relative increase in the number of radio-quiet γ-ray pulsars seen at large distances (see Fig. 16 for the OPC). We checked that the SG prediction behaves similarly if we increase its radiative efficiency to match that of the OPC model at high Ė, so the radio-loud deficit is rather independent of the 1-pole versus 2-pole radiation pattern from the outer regions. The open magnetosphere widens with Ė and wide beams are produced near the edge of the open volume by the efficiently screened, thin gaps. One would thus expect a larger overlap between the radio and γ-ray beams (i.e. an increase in the radio-loud to radio-quiet ratio) as Ė increases. Another effect must overcome this trend. It is related to the detectability of the large reservoir of faint radio-quiet pulsars in the outer magnetosphere gap models. The latter exist at large |α − ζ| impact angles and they dominate in potential number. The γ-ray caustic emission extends to larger |α − ζ| angles as Ė increases, so the number of potentially visible γ-ray pulsars (radio-quiet) increases. Then, as the dimmer parts of the caustic emission intercepted at high impact angle gradually passes the sensitivity threshold as the luminosity increases, a larger fraction of the potential reservoir becomes γ-ray visible. In other words, the radio-loud probability increases because of the widening of the radio and γ-ray beams, but the flux detectability of the large reservoir of faint radio-quiet objects increases even more and the net result is that the radio-loud to radio-quiet ratio can remain constant or decrease at high Ė. We checked, by lowering the luminosity of the SG and OPC models or by increasing the flux sensitivity threshold, that the radio beam widening effect becomes dominant when it is harder to detect faint radio-quiet objects.
The LAT visibility is good enough for the simulations to predict a small fraction of radio-loud objects at high Ė, at variance with the LAT data. The use of higher flux thresholds for γ-ray detection would alleviate this deficit, but it would significantly deteriorate all the other observable distributions. The predicted deficit is robust against different gap locations and extents in the outer magnetosphere (2 pole or 1 pole emission, infinitely thin emitting layer for OPC and emission across a gap thinning with increasing Ė for the slot gap, emission above the null surface or reaching to lower altitudes). It is also robust against the gap width estimation (which impacts the caustic extent) since the SG and OPC gap width values we obtained differ by 10 to 30 at high Ė. The pronounced discrepancy suggests that the assumed radio beam is too narrow at young ages. A broader beam of radio emission at higher altitude has also been suggested by Manchester (2005) and Ravi et al. (2010).
We have tested flat distributions in α and ζ instead of isotropic ones. The flat distributions give more weight to small angles, therefore bias the samples toward more numerous radio-quiet pulsars. Adopting isotropic distributions in α and ζ results in lower fractions of both radio and γ-ray, with even lower predictions at medium and high Ė for all models compared to the predictions shown in Figs. 17 and 18. A rapid decrease of the magnetic obliquity, over a timescale of 1 Myr, has been suggested by Young et al. (2010) from their study of radio pulse widths. The discrepancy we find here applies to ages less than 30 kyr, so magnetic alignment is unlikely to play a key role in reconciling the observed overabundance of young radio and γ-ray pulsars and the model predictions.
11. Summary
The exceptional results obtained with the Fermi LAT telescope in the last few years offer the unique and exciting opportunity to constrain the physics of the pulsed γ-ray emission by studying the early evolution of the pulsar population and its collective properties. We compared simulation predictions with Fermi LAT observations for this young ordinary pulsar population.
We synthesised a radio and γ-ray pulsar sample, assuming a core and cone model for the radio emission and γ-ray emission according to four gap models, the Polar cap (PC), Slot Gap (SG), Outer Gap (OG), and an alternative outer gap, the One Pole Caustic model (OPC), that uses the OG beam geometry and a simple luminosity evolution with Ė consistent with the LAT data (Watters et al. 2009). We compared model expectations and LAT data by applying γ-ray and radio visibility criteria to our sample and by scaling it to the number of radio pulsars observed in the Milky Way.
We found that the narrow beam of the low-altitude polar cap emission contributes at most a handful of pulsars in the LAT sample. The modelled luminosity is also too faint by an order of magnitude to account for the LAT data if one applies the average PC beaming factors we found for the given spin-down powers of the LAT pulsars. The large dispersion found in PC beaming factors, however, can substantially solve the luminosity discrepancy. We find that all the LAT pulsars are much more luminous (by 1 order of magnitude) than the PC expectations. Yet, there is a huge dispersion (1 or 2 orders of magnitude) in fΩ for the PC beams, so applying the average fΩ(Ė) trend to he LAT pulsars could be off by more than one order of magnitude in reality, so all the LAT points could go up and down by more than 1 decade in Fig. 15 without problems. The wide beams from the outer gaps and slot gap models can easily account for the Fermi LAT detection number in 2 years, provided an increase of a factor of ~10 of the standard slot-gap luminosity. The required increase may result from an enhanced accelerating electric field in the context of offset polar caps (Harding & Muslimov 2011). The evolution of the enhanced SG luminosity with spin-down power is compatible with the large dispersion seen in the LAT data.
We took into account the difference in the LAT flux sensitivity for detecting pulsed emission from radio-selected pulsars and for blind periodicity searches. The use of the two different sensitivity maps explained the almost equal amounts of radio-loud and radio-quiet pulsars found by the LAT. For all models, we found that the γ-ray visibility horizon extends to comparable distances for radio-loud and radio-quiet pulsars as a function of Ė, from 6 to 8 kpc at the highest powers down to 2 kpc for the least energetic LAT pulsars. The radio visibility horizon compares well with the γ-ray horizon at high Ė, but it extends to much larger distances for less energetic pulsars, except for the rapidly evolving OG case for which the pulsars with Ė ≲ 3 × 1027 W put 58% of their spin-down power into γ-rays and remain visible to 5 kpc.
All the γ-ray models fail to reproduce the high probability of detecting both the radio and γ-ray beams at high Ė. The OPC prediction for the fraction of γ-loud pulsars among the radio pulsars is consistent with the radio and LAT data, but the model significantly under-predicts the fraction of γ-ray pulsars that are radio-loud. The SG model also over-predicts the number of radio-quiet γ-ray pulsars. These discrepancies may indicate that pulsar radio beams are larger than those we have modeled, either because they are intrinsically wider or because the emission occurs at higher altitude (Manchester 2005), or both. The same conclusion has been argued by Karastergiou & Johnston (2007), that postulates emission over a wide range of emission heights rather than over a wide range of beam longitudes, and more recently by Ravi et al. (2010) and Watters & Romani (2011) in the light of the Fermi observations.
The beaming factor fΩ hardly evolves with Ė in the SG case. It is well constrained around 1 for both radio-loud and radio-quiet pulsars. In the OPC case, fΩ ~ 0.8 for radio-loud objects with Ė > 1028 W, and it decreases by a factor of 2 for the less energetic objects detected by the LAT. In the OG case, fΩ decreases from 1 to 0.3 with Ė decreasing down to 1028 W and the evolution flattens around ~0.2 for lower powers. In all the models, the beaming factor of radio-quiet pulsars follow the average trend found for radio-loud pulsars, but with a large dispersion than spans 1 or 2 orders of magnitude.
The classical outer-gap model (OG) fails to explain many of the most important pulsar population characteristics, such as spin-down power distribution and luminosity evolution, whereas the outer-gap alternative (OPC), which is based on a simple scaling of the gap width with Ė − 1/2, provides the best agreement between model predictions and data, as concluded by Watters & Romani (2011). This agreement relies on the very narrow gaps assumed in the OPC case. They are 10 to 100 times thinner than the values obtained for the SG for the same spin-down power, so the γ-ray luminosity is concentrated in thin and wide beams along the edge of the open magnetosphere. The OG model predicts a stronger luminosity evolution because it uses the polar cap heating by the returning particles to close the gap. The stronger evolution driven by this feedback is apparently not supported by the LAT data. Takata et al. (2011) studied the evolution of the two layer OG luminosity as a function of Ė. Its result is consistent with the one we plot in Fig. 15 for the OG model. The less pronounced dispersion observed in Takata et al. (2011) is due to the choice of a fΩ = 1 for all the pulsars.
All models studied here significantly under-predict the number of visible γ-ray pulsars seen at high Ė. This inconsistency does not depend on the modelling of the γ-ray and radio visibility thresholds. The discrepancy with the observations is significant despite our choice of birth distributions skewed to young energetic pulsars, at slight variance with the constraints imposed by the total radio and γ-ray pulsar sample observed. The fact that the four models have different γ-ray luminosity evolutions and different beam patterns suggests a different cause for the discrepancy. Concentrating the birth location in the inner Galaxy lessened but did not resolve the discrepancy. Further increasing the number of energetic pulsars near the Sun would conflict with the observed pulsar distances. The estimate of the visibility threshold in radio or γ-ray flux is not at stake since all models over-predict the number of older, fainter, visible objects.
The set of present results suggests that the observations require rather luminous albeit thin gaps in the magnetospheres of young pulsars. It will be a challenge for models to match this behaviour. The impact of a magnetic alignment with age (Young et al. 2010), of an azimuthal variation of the accelerating field, or the choice of different braking indices for the pulsar spin-down may be important and will be included in future population studies to explore the origin of the scarcity of young energetic γ-ray pulsars in the model predictions.
Online material
Appendix A: Radio survey sensitivity plots
 |
Fig. A.1 Definition of the radio visibility criteria for the surveys Molonglo 2, Green Bank 2, Green Bank 3, and Parkes 2. For each survey we show the pulsar selection, classification, and counting in the redefined survey coordinates region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; ATNF NaN (green dot): pulsars listed in the ATNF catalogue for which it is not possible to evaluate the threshold flux; Detected (red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
 |
Fig. A.2 Definition of the radio visibility criteria for the surveys Arecibo 2, Arecibo 3, Parkes 1, and Jodrell Bank 2. For each survey we show the pulsar selection, classification, and counting in the redefined survey sky region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; Detected(red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
 |
Fig. A.3 Definition of the radio visibility criteria for the surveys Parkes Multibeam and Swinburne. It is shown the pulsar selection, classification, and counting in the redefined survey sky region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; ATNF NaN (green dot): pulsars listed in the ATNF catalogue for which it is not possible to evaluate the threshold flux; Detected (red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
Acknowledgments
M.P. acknowledges Patrizia Caraveo and the IASF-INAF of Milan for the hospitality and help, thanks Damien Parent for the helpful suggestions, and acknowledges Volker Beckmann and the François Arago Centre for hospitality. M.P. acknowledges P and Isabel Caballero for the help. A.K.H. and P.L.G. acknowledges support from the NASA Astrophysics Theory and Fermi GI programs. P.L.G. also appreciates the support from NSF under the RUI program. We acknowledge the referee for the useful suggestions.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 187, 460 [Google Scholar]
- Arons, J., & Scharlemann, E. T. 1979, ApJ, 231, 854 [NASA ADS] [CrossRef] [Google Scholar]
- Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ, 568, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bania, T. M., Anderson, L. D., Balser, D. S., & Rood, R. T. 2010, ApJ, 718, L106 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, A., Ruderman, M., & Sutherland, P. 1976, ApJ, 203, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, K. S., Ruderman, M., & Zhang, L. 2000, ApJ, 537, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Clifton, T. R., & Lyne, A. G. 1986, Nature, 320, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2001, ApJ, 549, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, F., Manchester, R. N., & Kaspi, V. M. 2001, AJ, 122, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Deutsch, A. J. 1955, Ann. Astrophys., 18, 1 [NASA ADS] [Google Scholar]
- Dewey, R. J., Taylor, J. H., Weisberg, J. M., & Stokes, G. H. 1985, ApJ, 294, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Dormody, M., Johnson, R. P., Atwood, W. B., et al. 2011, ApJ, 742, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Dyks, J., Harding, A. K., & Rudak, B. 2004, ApJ, 606, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Edwards, R. T., Bailes, M., van Straten, W., & Britton, M. C. 2001, MNRAS, 326, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gonthier, P. L., Ouellette, M. S., Berrier, J., O’Brien, S., & Harding, A. K. 2002, ApJ, 565, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Gonthier, P. L., Van Guilder, R., Harding, A. K., Greneir, I., & Perrot, C. 2004, BAAS, 36, 918 [NASA ADS] [Google Scholar]
- Gonthier, P. L., Story, S. A., Giacherio, B. M., Arevalo, R. A., & Harding, A. K. 2006, Chinese J. Astron. Astrophys. Suppl., 6, 020000 [CrossRef] [Google Scholar]
- Harding, A. K., & Muslimov, A. G. 1998, ApJ, 500, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., & Muslimov, A. G. 2011, ApJ, 726, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K., Grenier, I. A., & Gonthier, P. L. 2007, Astrophys. Space Sci., 309, 221 [Google Scholar]
- Haslam, C. G. T., Stoffel, H., Salter, C. J., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [Google Scholar]
- Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F., & Collins, R. A. 1968, Nature, 217, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K. 2006, Mod. Phys. Lett. A, 21, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Hirotani, K. 2008, in AAS/High Energy Astrophysics Division, AAS/High Energy Astrophysics Division, 10, 12 [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Holloway, N. J. 1973, Nature, 246, 6 [NASA ADS] [Google Scholar]
- Jacoby, B. A., Bailes, M., Ord, S. M., Edwards, R. T., & Kulkarni, S. R. 2009, ApJ, 699, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Johnston, S., Lyne, A. G., Manchester, R. N., et al. 1992, MNRAS, 255, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Kapoor, R. C., & Shukre, C. S. 1998, ApJ, 501, 228 [NASA ADS] [CrossRef] [Google Scholar]
- Karastergiou, A., & Johnston, S. 2007, MNRAS, 380, 1678 [NASA ADS] [CrossRef] [Google Scholar]
- Kijak, J., & Gil, J. 2003, A&A, 397, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lyne, A. G., Manchester, R. N., Lorimer, D. R., et al. 1998, MNRAS, 295, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N. 2005, Astrophys. Space Sci., 297, 101 [Google Scholar]
- Manchester, R. N., Lyne, A. G., Taylor, J. H., et al. 1978, MNRAS, 185, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Lyne, A. G., Camilo, F., et al. 2001, MNRAS, 328, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- McBreen, B., Ball, Jr., S. E., Campbell, M., Greisen, K., & Koch, D. 1973, ApJ, 184, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Harding, A. K. 2003, ApJ, 588, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Harding, A. K. 2004, ApJ, 606, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Muslimov, A. G., & Tsygan, A. I. 1992, MNRAS, 255, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Nice, D. J., Fruchter, A. S., & Taylor, J. H. 1995, ApJ, 449, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1990, ApJ, 348, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Rankin, J. M. 1983, ApJ, 274, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ravi, V., Manchester, R. N., & Hobbs, G. 2010, ApJ, 716, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Watters, K. P. 2010, ApJ, 714, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Romani, R. W., & Yadigaroglu, I.-A. 1995, ApJ, 438, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitkovsky, A. 2006, ApJ, 648, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Stokes, G. H., Taylor, J. H., Weisberg, J. M., & Dewey, R. J. 1985, Nature, 317, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Stokes, G. H., Segelstein, D. J., Taylor, J. H., & Dewey, R. J. 1986, ApJ, 311, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Story, S. A., Gonthier, P. L., & Harding, A. K. 2007, ApJ, 671, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Sturner, S. J., & Dermer, C. D. 1996, ApJ, 461, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, J., Wang, Y., & Cheng, K. S. 2011, ApJ, 726, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, D. J., Fichtel, C. E., Kniffen, D. A., & Ogelman, H. B. 1975, ApJ, 200, 79 [Google Scholar]
- Thompson, D. J., Arzoumanian, Z., Bertsch, D. L., et al. 1994, ApJ, 436, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Watters, K. P., & Romani, R. W. 2011, ApJ, 727, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Watters, K. P., Romani, R. W., Weltevrede, P., & Johnston, S. 2009, ApJ, 695, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M. D. T., Chan, L. S., Burman, R. R., & Blair, D. G. 2010, MNRAS, 402, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B., Harding, A. K., & Muslimov, A. G. 2000, ApJ, 531, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Cheng, K. S., Jiang, Z. J., & Leung, P. 2004, ApJ, 604, 317 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Magnetic field, period, and gap width values for which the phase-plots have been evaluated for each emission model.
For each model and for the observed dataset, we give from left to right the scaled numbers of pulsars visible in the radio or γ-ray band, in the radio and γ-ray bands, in γ-rays only, and the fraction of radio loud objects in the γ visible sample.
All Figures
 |
Fig. 1 Left: the assumed surface magnetic field distribution at birth. Right: the assumed spin period distribution at birth. |
| In the text | |
 |
Fig. 2 Surface density of the new born neutron stars. The dashed curve represents the Paczyński distribution (Paczyński 1990), while the adopted one following the distribution of radio HII regions, is shown as a solid curve. Both curves are normalised. |
| In the text | |
 |
Fig. 3 P − Ṗ diagram of the pulsar population at birth (in red), and the population evolved to the present (blue). |
| In the text | |
 |
Fig. 4 The top to bottom panels illustrate the γ-ray emission pattern obtained for a young (left) and old (right) pulsar, respectively for the PC, SG, OG/OPC, and radio (core plus cone) models. For the PC and Radio models, the time evolution is obtained for B = 108 T and period increasing from 30 to 1000 ms. In the SG and OG/OPC models, the time evolution is obtained for a gap width wSG increasing from 0.04 to 0.5 and wOG/OPC increasing from 0.01 to 0.4 respectively. All the plots are given for an obliquity α = 45°. |
| In the text | |
 |
Fig. 5 Number density of the visible γ-ray pulsars obtained for each model as a function of characteristic age and energy flux times the square of the pulsar distance. These parameters can all be measured from the observations. The linear grey scale saturates at 1 star/bin for the polar cap and 2.5 star/bin for the other models. The pink contours outline the region where simulated radio-loud γ-ray pulsars are found (at 20% of the maximum density). The pink and green lines show the data for the radio-loud and radio-quiet LAT pulsars, respectively. |
| In the text | |
 |
Fig. 6 Number density of the visible radio pulsars as a function of period and period derivative. The left and right plots respectively show the simulation and observed data with the same grey scale saturating at 25 star/bin and the same visibility criteria. The rising grey line marks the slot-gap death line. The declining grey lines mark the iso-magnetic lines at 107, 108, and 109 Tesla. |
| In the text | |
 |
Fig. 7 Number density of the visible γ-ray pulsars obtained for each model as a function of period and period derivative. The linear grey scale saturates at 1.5 star/bin. The pink triangles and green dots show the radio-loud and radio-quiet LAT pulsars, respectively. The rising grey line in the slot-gap subplot marks the slot-gap death line. The declining grey lines mark the iso-magnetic lines at 107, 108, and 109 T. |
| In the text | |
 |
Fig. 8 Number distributions in period, period first time derivative, surface magnetic field strength, and distance obtained for the whole populations of radio or γ-ray visible pulsars in the simulations (light grey histogram) and in the LAT and radio survey data (thick line). The ATNF radio sample has been restricted to the objects that pass the same position and flux selection criteria as in the simulation. The slot-gap model has been used as an example for the γ-ray simulation. The dark shaded histograms show the distributions of the gamma active subsample of the whole simulated population. The abundances of simulated objects at low P, high Ṗ, and high B are dominated by γ-ray active pulsars. The excess of energetic and nearby simulated objects reflects the set of assumptions adopted for the birth distributions to provide a better match to the LAT data. |
| In the text | |
 |
Fig. 9 Spin-down power distributions obtained for each model for the visible γ-ray pulsars. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible pulsars for each model to ease the comparison and show the relative lack of young energetic pulsars with Ė > 3 × 1028 W. |
| In the text | |
 |
Fig. 10 Age distributions obtained for each model for the visible γ-ray objects. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible objects for each model to ease the comparison and show the relative lack of visible objects with age <100 kyr. |
| In the text | |
 |
Fig. 11 Spin-down power distributions obtained for each model for the visible γ-ray objects for a different set of birth distributions: a Gaussian of width 200 ms centred at 0 for the periods; the sum of two Gaussians in log 10BNS [Tesla], both 0.6 in width, respectively centred at 8.4 and 9.1, and with an amplitude ratio 1:7/12 for the surface magnetic fields; and the Paczyński (1990) surface density in the Galaxy. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution, scaled to the total number of visible objects, is plotted as a black contour. |
| In the text | |
 |
Fig. 12 Number density of the visible radio and/or γ-ray pulsars in the Milky Way (polar view). The left and right plots respectively show the simulation and observed data with the same logarithmic gray scale saturating at 100 star/bin and the same visibility criteria. The cyan contour outlines the region where simulated SG γ-ray pulsars are detectable. The cyan triangles show the location of the LAT pulsars. The yellow dot marks the Sun. |
| In the text | |
 |
Fig. 13 Distance distributions obtained for each model for the visible γ-ray objects. Pink and green refer to radio-loud and radio-quiet fractions of the total population, respectively. The LAT distribution (in black) has been scaled to the total number of visible objects for each model to ease the comparison and show the relative overabundance of nearby objects for the PC and SG models and under abundance of nearby objects for the OG and OPC models. |
| In the text | |
 |
Fig. 14 Distribution of the γ-ray beaming factors obtained for each model as a function of the spin-down power. Pink and green dots refer to radio-loud and radio-quiet γ-ray visible objects, respectively. The solid and dotted lines give the best exponential fit to the radio-loud and radio-quiet data points, respectively. For the PC case, a unique fit was applied to the whole sample of radio-loud and radio-quiet objects. |
| In the text | |
 |
Fig. 15 Distribution of the γ-ray luminosities obtained for each model as a function of the spin-down power. Pink and green dots refer to radio-loud and radio-quiet γ-ray visible objects, respectively. The LAT luminosities (black circles and crosses for radio-loud and radio-quiet objects respectively) have been derived using the energy-flux measurement and the fΩ value estimated from the fit to the simulated data for the particular spin-down power and radio-loud or quiet state of the LAT pulsars. The dotted line shows the 100% efficiency boundary. |
| In the text | |
 |
Fig. 16 For each model, the linear gray scale shows the number density of the radio- or γ-visible population, with a saturation at 10 star/bin. Contours are given for the radio-only visible (cyan), γ-only visible (green), and radio plus γ visible (red) objects at 1% of the maximum number density for each type. The red triangles and green dots mark the location of the radio-quiet and radio-loud LAT pulsars, respectively. |
| In the text | |
 |
Fig. 17 Spin-down power evolution of the fraction of radio loud pulsars in the cumulative distribution of γ-ray visible pulsars with Ė larger than the plotted value. The thin lines give the simulation results for each model. The thick line gives the fraction evolution in the LAT sample. |
| In the text | |
 |
Fig. 18 Spin-down power evolution of the fraction of γ-loud pulsars in the cumulative distribution of radio-visible pulsars with Ė larger than the plotted value. The thin lines give the simulation results for each model. The thick line gives the fraction evolution in the LAT sample. |
| In the text | |
 |
Fig. A.1 Definition of the radio visibility criteria for the surveys Molonglo 2, Green Bank 2, Green Bank 3, and Parkes 2. For each survey we show the pulsar selection, classification, and counting in the redefined survey coordinates region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; ATNF NaN (green dot): pulsars listed in the ATNF catalogue for which it is not possible to evaluate the threshold flux; Detected (red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
| In the text | |
 |
Fig. A.2 Definition of the radio visibility criteria for the surveys Arecibo 2, Arecibo 3, Parkes 1, and Jodrell Bank 2. For each survey we show the pulsar selection, classification, and counting in the redefined survey sky region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; Detected(red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
| In the text | |
 |
Fig. A.3 Definition of the radio visibility criteria for the surveys Parkes Multibeam and Swinburne. It is shown the pulsar selection, classification, and counting in the redefined survey sky region (Table 3), and the ratio between the pulsar fluxes and the threshold ones re-evaluated by taking into account the fudge factor defined in Table 3. The object categories listed in the legend are: ATNF (black cross): pulsars inside the new survey coordinates region defined in Table 3 that are listed in the ATNF catalogue; ATNF vis (blue dot): pulsars that are visible according to the new survey parameters listed in Tables 2 and 3 and/or listed in the ATNF catalogue; ATNF NaN (green dot): pulsars listed in the ATNF catalogue for which it is not possible to evaluate the threshold flux; Detected (red circle): pulsars that have been detected according to the new survey parameters listed in Tables 2 and 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


