EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) A6 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number A6
Number of page(s) 9
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201118425
Published online 28 August 2012

© ESO, 2012

1. Introduction

“To boldly go where no man has gone before!” This famous quote from the Star Trek saga is still wishful thinking, but the CoRoT space telescope brings us one step closer to foreign strange worlds. The combination of the transit method employed by CoRoT (Baglin et al. 2008) with spectroscopic and radial velocity measurements as follow-up observations from the ground allows us to fully characterize the planetary system and its host star: stellar mass and radius, spectral type, the planet’s orbital period, semi-major axis, eccentricity, orbit plane inclination, argument of periastron, and the planetary mass and radius. Finally, the most important parameter, the planetary bulk density derived from planetary mass and radius, characterizes the nature of the planet.

Since its launch in December 2006, CoRoT discovered 26 confirmed planets, many first discoveries among them:

  • the first terrestrial planet CoRoT-7b (Légeret al. 2009; Quelozet al. 2009), a member of amulti-planet system with possibly three planets (Hatzeset al. 2010) in which CoRoT-7c andCoRoT-7d have been discovered by radial velocity (RV)observations only because they do not transit the star due to theinclined orbit plane with respect to the plane-of-sky;

  • the first transiting brown dwarf CoRoT-3b (Deleuil et al. 2008) that covers the gap between planets and low-mass stellar companions. Another discovered brown dwarf is CoRoT-15b (Bouchy et al. 2011);

  • the first temperate Jupiter-like planet CoRoT-9b (Deeg et al. 2010).

CoRoT also discovered several hot-Jupiter planets. Five more confirmed planets are under publication and there are many more candidates from a long list pending confirmation. CoRoT is observing different star fields for a duration of approximately 150 days for each long run and 30 or 80 days for a short run since the start of the observations in early 2007.

The Kepler mission has announced the discovery of more than 1200 candidates (Borucki et al. 2011) from a single star field with many multi-planet system candidates and with Kepler-16b as the first transiting circumbinary planet (Doyle et al. 2011). Nineteen planets are confirmed at the time of writing.

There are about 140 transiting planets discovered from ground-based projects, mainly populating a parameter space with semi-major axis inside 0.08 AU and planetary masses above 0.1   MJ.

CoRoT-21 was observed from October 2007 to March 2008 during the Long Run LRa01 in the first winter field (constellation Monoceros, coordinates and target IDs in Table 1). It was not discovered, in contrast to all other CoRoT planets, by the alarm mode, but by the efforts of (at that time) six detection teams (Carone et al. 2012) that processed the raw light curves1. This candidate received a low priority for the follow-up observations because the transit duration is 4.8 h long, too long for a suspected G2 star, as which CoRoT-21 was classified within the EXODAT data base at that time. Because most of the available follow-up observation time for the LRa01 candidates had been exclusively used for CoRoT-7, there was little expectation of appreciable observation time for the faint CoRoT-21 star of visual magnitude V = 16 mag. After some consideration among the CoRoT detection groups, however, CoRoT-21 was given a higher priority and first follow-up observations started with HARPS in November 2009 and at Keck in December 2009.

2. Discovery and the analysis of the stellar light curve

2.1. Detection

Figure 1a is the normalized light curve of CoRoT-21 as a function of time observed continuously for about 130 days. The stellar flux varies by  ± 2% about the normalized value with a significant drop by 1.5% around day MJD 54 510 caused most probably by instrumental effects. Short term variations are obvious. The transit, however, is not readily identifiable in Fig. 1a. The transit detection is described here exemplarily with the software package EXOTRANS developed in Cologne (Grziwa et al. 2012). In preparation for the transit search among the 10 000 light curves of LRa01, a subset of 200 light curves was randomly selected from all light curves in LRa01. A general trend was derived, which may have been caused by instrumental and other systematic effects. This general trend was subtracted from all light curves including that of CoRoT-21. Other periodic flux variations caused by spacecraft orbital effects etc. are derived by a harmonic filter and were subtracted. The CoRoT-21 light curve is now clean of the general trend and any harmonic periodic fluctuations (Fig. 1b). The box-like transit is not deleted by the filtering because of its unharmonic nature (Grziwa et al. 2012).

Feeding the cleaned light curve into the EXOTRANS software routine, which uses a modified box-least-squares (BLS) algorithm (Kovács et al. 2002) for the search, a faint transit feature appears in the phase diagram at a period of 2.72482 days (Fig. 1c). The data in the phase diagram are binned by 50 points.

thumbnail Fig. 1

a) Normalized raw light curve of CoRoT-21 during the observation time from MJD 54 396 to MJD 54 529. Strong variations in stellar flux are obvious. b) Light curve after removing a common trend as computed from a subset of 200 light curves and after harmonic filtering. c) Phase diagram of the trend-filtered light curve at period 2.7472 days. The phase is divided into 300 bins with mean flux and standard deviation displayed for each bin.

2.2. Excluding a stellar binary system

A transit has been identified but the transiting object is still of unknown nature. A stellar binary system may produce a similar signature at twice the detected period. To rule out a binary system, an eclipsing stellar binary was simulated using the software package DEBIL (Devor 2005). It is part of the automated detection pipeline in Cologne and routinely applied to the candidate list. It identifies and extracts the obvious eclipsing binaries from the candidate list of the observation run. For CoRoT-21, DEBIL returned a ratio of R1/R2 ≈ 20 for the radius of the central star R1 and the radius of an eclipsing potential stellar companion R2, which supported the suspicion that CoRoT-21b may be of planetary nature. Finally, high-resolution spectroscopy performed with HARPS and HIRES as follow-up observations from the ground (see Sect. 3) after the light curve processing excluded any undiluted stellar companion in a 2.72 day orbit and confirmed the DEBIL result.

2.3. Multitransits

From a hypothetical stellar light curve containing transits from a multi-planetary system, the Cologne detection software package EXOTRANS would return first the transit events of the innermost planet, which produces the most numerous transits above the noise level. The power spectrum from the original raw light curve returns a strong signal at the 2.72 day period of CoRoT-21b and its harmonics (Fig. 2a). This detected transit is subtracted from the original CoRoT-21 light curve, which is then processed again with EXOTRANS and searched for more transits at longer periods. The comparison between the power spectrum before and after the transit subtraction (Fig. 2b) quite clearly shows a 10 day and a 11.5 day period peaking out of the spectrum. Note that the scale of the amplitudes in Fig. 2b is two orders of magnitude smaller than in Fig. 2a. A search for further transits with EXOTRANS was unsuccessful, however, and did not reveal transit features that stood out of the noise level in particular at these outstanding periods, concluding that there are unfortunately no further transits from an additional second planet detected.

thumbnail Fig. 2

a) Power spectrum of the trend-harmonic filtered light curve. The period of 2.72474 days and its harmonics are clearly identified. b) Power spectrum of the trend-filtered light curve after removing the transits at period 2.72474 days. Note the change in scale by two orders of magnitude compared to panel a). The periods at 10 days and 11.5 days did not return convincing detections of more transits and are probably caused by stellar activity at the rotation period.

2.4. Analysis of the transit

Figure 3 shows CoRoT-21 and its vicinity in a star field of 120 arcsec  ×  120 arcsec extension. The outline in Fig. 3 is the aperture mask for CoRoT-21. There is only one star at the immediate edge of the mask (labeled “1”). This star has the EXODAT ID 102725438 and visual magnitude V = 17.4 mag. The contamination into the CoRoT-21 mask is estimated to be 8.5% ± 1.1% (see Cabrera et al. 2010). The star is not a CoRoT target and a light curve is not available.

thumbnail Fig. 3

Immediate vincinity of CoRoT-21 in the star field covered by LRa01. The outline is the aperture mask of the target star CoRoT-21. A potential perturber of the photometry is the star labeled “1” at the immediate edge of the outline. This star is not a CoRoT target. The contamination of the target mask is estimated to be 8.5%.

The duration of the transit and the relative flux drop are directly related to the size of the planet relative to the stellar radius and the orbital distance. After removing stellar activity variations by fitting and subtracting a trend in between the transits and clipping 5σ outliers, the original light curve was phase-folded using the ephemeris 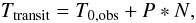(1)where T0,obs = JD   2   454   399.0299 is the determined transit epoch from the light curve, P = 2.724740 days is the orbit period, N is the cycle number of the transit since the start of the observation. The full phase is divided into 300 bins with approximately 50 data points each (Fig. 4). The model by Mandel & Agol (2002) was fit to the phase-folded light curve using the Genetic Algorithm (Kim et al. 2001) and to solve for the following parameters: (a) the epoch T0, (b) the ratio between the semi-major axis of the orbit and the stellar radius a/R∗, (c) the ratio between the planetary radius Rp and the stellar radius Rp/R∗, (d) the impact parameter B = acosi/R∗ where i is the inclination of the orbit plane for circular orbits (e = 0) and (e) the combinations u +  = ua + ub and u −  = ua − ub where ua and ub are the quadratic limb-darkening coefficients (Brown et al. 2001). See for example Guenther et al. (2012) and Fridlund et al. (2010) for a comparison with other approaches.

The coefficients were fixed at their theoretical values taken from the tables by Sing (2010). The stellar magnitude of CoRoT-21, however, is so faint that it seems hopeless to determine ua and ub from photometry. A much better agreement was found by leaving ua and ub as free parameters but constraining their variation within a 3σ range about their theoretical tabulated values. The tables by Sing (2010) predict ua = 0.65 ± 0.02 and ub = 0.10    ±    0.02 for the stellar parameters reported in Table 1 and Sect. 3. These predicted values agree very well with the measured values of ua = 0.66 ± 0.09 and ub = 0.13 ± 0.11. The uncertainty of these values was constrained by the uncertainty of the stellar parameters. For the best fit (Fig. 4 and Table 1), the fit epoch T0 = JD   2   454   399.0282 ± 0.0009 was found 150 ± 80 s earlier, however, still within the error range of T0,obs. The ratio a/R∗ = 4.60 ± 0.26 yields a stellar density parameter of 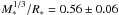, the lowest among all known transit host stars. A comparable case is the system TrES-4 (Southworth 2010) with a less massive Jupiter planet at a distance comparable to CoRoT-21b. The ratio Rp/R∗ = 0.067 ± 0.0018 is relatively low for a suspected close-in Jupiter-like planet. All parameters from the transit fit, however, would be consistent with considering CoRoT-21 as a sub-giant star of about 2 solar radii.

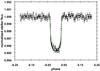thumbnail Fig. 4

Phase diagram of the raw light curve from  −0.25 to  +0.25 in phase. The phase has been divided into 300 bins with average flux and standard deviation shown for each bin. The solid line is the fit as described in the text. Fit results are given in Table 1.

2.5. Follow-up observations

Photometric follow-up of CoRoT-candidates is being performed to verify that a signal arises from a target star instead of any nearby stars that may contaminate the signal within CoRoT’s photometric aperture (Deeg et al. 2009). For CoRoT-21b, it was performed with the IAC 80 telescope during a transit on 29 Nov. 2008 and again off-transit on 03 Jan. 2009. The follow-up did not reveal any possible blends.

Radial velocity (RV) follow-up observations of CoRoT-21 were performed with the HARPS spectrograph in November 2009 only and the HIRES spectrograph (Vogt et al. 1994) at the 10-m Keck 1 telescope on top of Mauna Kea, Hawaii, as part of NASA’s key science program to support the CoRoT mission.

HIRES is used in combination with its iodine (I2) cell to measure precise differential RVs. All observations were taken with a 7 arcsec long slit to allow proper background subtraction, and 0.861 arcsec width, which yields a spectral resolving power of R ≈ 50   000. A total of 13 spectra of CoRoT-21 over four nights in January 2010 and one night in January 2011 were obtained. The signal-to-noise (S/N) ratios of these data range from 14:1 to 20:1 (with the I2 cell) per pixel in the spectral region used to determine the RVs ( ≈ 500   nm to 600   nm). Exposure times for the CoRoT-21 spectra were between 900 and 1800 s. Two spectra were also taken in December 2009, but under poor conditions (bad seeing), which resulted in S/N ratios of less than 10:1. These two specific spectra were finally not used for the RV determination. This also shows how challenging the RV follow-up for such a faint target is, even with a 10-m telescope at our disposal. The first template spectrum of CoRoT-21 (without the I2 cell) was also observed in December 2009 and has an S/N ratio of only 10:1 per pixel. A second template spectrum with a total exposure time of 2400 s was taken in the following next run. This new template has S/N    =    30:1 and was used to determine the stellar parameters for the host star. The I2 cell data Doppler code (Endl et al. 2000) was taken for the computation of precise differential RVs. A CoRoT-21 template spectrum was taken in a first step, but experience with such low S/N data has shown that the precision of the RV computation can be improved by using a HIRES template of a similar, but much brighter, star. Several different templates were tested; the template of HD 12800 (54 Cas, V = 6.55, F8) yielded the best results. The RV results given in Table 2 have a total rms-scatter of 178   ms-1 and an average uncertainty of 65   ms-1. Clearly, the large RV error is dominated by the low S/N, but the early spectral type (F8), combined with a significant stellar rotation of 11   km   s-1, contributes to the scatter as well.

thumbnail Fig. 5

Radial velocity curve fit on 19 observations. Blue data points are from HIRES, red data points are from HARPS. The eccentricity was forced to e = 0 for the fit.

HARPS is a cross-dispersed echelle spectrograph fiber-fed from the Cassegrain focus of the 3.6 m telescope at La Silla Observatory, Chile (Mayor et al. 2003). Four spectra with a spectral resolution R ≈ 115   000 were obtained, setting one of the two available fibers on the sky to monitor the presence of moonlight and to obtain an optimum sky background subtraction, which is important for faint targets such as Corot-21. The spectra were reduced and extracted using the HARPS processing pipeline. The radial velocity was measured on each extracted spectrum by means of a weighted cross-correlation (see Baranne et al. 1996; Bonomo et al. 2010, for details) with a numerical mask corresponding to a G2 star. The resulting cross-correlation functions (CCFs) were fit by Gaussians to derive the radial velocities. The HARPS automated data-reduction pipeline derives radial velocities by cross-correlating the observed spectra with a numerical mask computed for a star of similar spectral type. There are only four masks available within the HARPS data-reduction, namely, the F0, G2, K5, and M0 masks. The G2 mask was used for CoRoT-21, because this is the closest mask to the spectral type of CoRoT-21 (F8 IV). Cross-correlations with the F0 and K5 masks provided similar results. If the radial velocity measurements had shown a dependence on the selected mask, a non-planetary scenario would have been suspected.

All RV data are shown in Fig. 5 and are listed in Table 2. The solid curve in Fig. 5 is a (non-linear least-squares) sine-fit 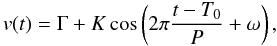(2)which allows solvong for the system velocity Γ = 101   m   s-1, the half-amplitude K = 274 ± 35   m   s-1 by enforcing the orbital eccentricity to zero (e = 0) and the argument of periastron to ω = 90°. The half amplitude K allows deriving the minimal planetary mass Mp   sin   i assuming again Mp ≪ M∗ and e = 0: 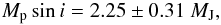(3)with MJ = 1.8986 × 1027   kg as the Jupiter mass.

Although the four HARPS RV data do not stand out among all residuals in Fig. 5, the inclusion of the HARPS data to the Keck data set decreased the value of K by 10% (by increasing the relative error) and therefore also decreased the derived planetary mass.

3. Spectroscopy

The photospheric fundamental parameters of CoRoT-21, i.e., the effective temperature Teff, the surface gravity log    g, the metallicity  [M/H] , and the projected rotational velocity v   sin   i, were derived using the co-added HARPS spectrum and the HIRES template. As described in detail by other CoRoT publications (e.g., Fridlund et al. 2010; Gandolfi et al. 2010), the HARPS and HIRES spectra were compared with a grid of synthetic spectra from Castelli & Kurucz (2004); Coelho et al. (2005) and Gustafsson et al. (2008) using spectral lines sensitive to different photospheric parameters. The spectral analysis package SME 2.1 (Valenti & Piskunov 1996; Valenti & Fischer 2005) was also used to determine the above mentioned parameters. Consistent results were obtained regardless of the used spectrum or method. The final adopted values are Teff = 6200 ± 100   K, log g = 3.7 ± 0.1   dex,  [M/H]  = 0.0 ± 0.1 and v   sin   i = 11 ± 1.0   km   s-1, which translate into a star of spectral type F8IV, in agreement with the low mean stellar density derived from the light curve analysis (Sect. 2.4).

To estimate stellar mass, radius and age, we used the mean stellar density along with the effective temperature and metallicity, as obtained from the spectral analysis. By comparing the location of the star on a log (M∗/R∗) vs. log (Teff) H-R diagram with evolutionary tracks computed with the CESAM code (Morel & Lebreton 2008), the star appears as a well evolved sub-giant star at a mass of M∗ = 1.29 ± 0.09 solar masses, a larger radius of R∗ = 1.95 ± 0.21 solar radii and at an age of 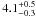 Gyr.

4. System parameters

The semi-major axis ap of the planetary orbit follows now directly from stellar mass using Keplers third law assuming for the moment Mp ≪ M∗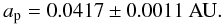(4)The inclination i of the planetary orbit versus the line-of-sight is derived from the impact parameter b = (a   sini)/R∗, which is known from the transit fit: With the stellar mass M∗ and the sin   i derived from evolution models and the transit fit, respectively, the planetary mass Mp is finally derived to be 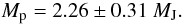(7)The transit fit also returns the ratio Rp/R∗ which yields for the mean planetary radius 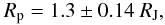(8)with RJ = 69   911 km as the equivalent radius of Jupiter assuming the volume is contained in a sphere of radius RJ. Finally, the most important planetary parameter of CoRoT-21b, the bulk density, is derived to be 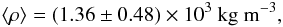(9)which is similar to the Jupiter bulk density. Figure 6a presents the CoRoT, the confirmed Kepler planets and transiting planets from ground-based observations within 0.25 AU. CoRoT-21b is one of the most massive planets. It is interesting to plot the planets in a mass-radius-relationship (Fig. 6b). The more massive planets stand out from the usual relationships with constant bulk density while CoRoT-21b lies, of course, near the 1.5 × 103   kg   m-3 curve, similar to Jupiter. CoRoT-21b and Jupiter are obviously following the same M1/3 − R relation.

thumbnail Fig. 6

a) Planetary mass vs. semi-major axis for all CoRoT planets, the confirmed Kepler planets (filled circles) and other transiting planets from ground-based observations (small open circles) within 0.25 AU. The large open circle is CoRoT-21b. b) Planetary mass-radius relationship for the CoRoT planets, confirmed Kepler planets (filled circles) and the transiting planets from ground-based observations (small open circles). Also drawn are lines of constant density. Jupiter and CoRoT-21b (circles) follow almost the same line of constant density and are directly comparable.

Table 1

Stellar and planetary parameters.

Table 2

RV observations.

5. Tides and orbit evolution

The large mass and size and the close proximity of CoRoT-21b to its star makes it worthwhile to look into the orbit evolution which is dominated by the exchange of tidal forces. One way to compare tidal forces among bodies is the Doodson constant Dp, which is the amplitude of the tidal potential (Pätzold et al. 2004) generated by a body of mass Mp acting on a body of radius R∗ at a distance a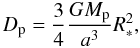(10)where G is the gravitational constant. The rate of orbital decay is defined by the property factor 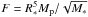(Pätzold & Rauer 2002), which is most efficient for evolved F-stars. The CoRoT-21 system has the sixth largest Dp and the third largest property factor F of all published CoRoT and Kepler objects (Figs. 7a and b), only beaten, not surprisingly, by the two brown dwarfs CoRoT-3b and CoRoT-15b (Deleuil et al. 2008; Bouchy et al. 2011) and the massive close-in planet CoRoT-14b (Tingley et al. 2011). All these host stars, including CoRoT-21, are F-stars.

The shape of the RV curve (Fig. 4) does not show any appreciable influence from the orbit eccentricity e. The RV data were fit by forcing e = 0. To demonstrate the validity of that assumption, the orbit circularization under tidal forces was simulated by the set of tidal equations from Matsumura et al. (2010). Starting at a stellar age of t0 = 60 Myr using an average planetary dissipation Qp/k2p = 105 (Lainey et al. 2009) and an already strong stellar dissipation Q∗/k2 ∗  = 107 (see the discussion in Pätzold & Rauer 2002; and Pätzold et al. 2004), the evolution of the orbit eccentricity e(t) and of the semi-major axis a(t) were simulated for different starting values of e(t0) such that the present value of the semi-major axis apresent = 0.0417 AU at t = 4.1 Gyr is always met. For starting values e(t0) = 0.1; 0.3; 0.5 and 0.7, the orbit circularizes fast, the maximal time is found for e(t0) = 0.7 within 600 Myr (Fig. 8a). The changes in a(t) following the circularization are slow, the present orbit radius is achieved after more than 3.5 Gyr. The overall behavior and conclusion does depend on the specific choice of Qp/k2p. The used Qp/k2p value is taken from the Jupiter example (Lainey et al. 2009) and may scale for Corot-21b by a factor of two (Ferraz-Mello 2012), which would also increase the time scales for circularization by a factor of two, but would not change the conclusion. Once the orbit is circularized (e = 0) and the planetary rotation has been synchronized with the orbit revolution, a set of simplified equations for the change in semi-major axis da/dt and the change in stellar rotation rate dΩ∗/dt may be used

thumbnail Fig. 7

a) Doodson constants for all CoRoT and confirmed Kepler planets within 0.15 AU. CoRoT-21b has the fourth largest Doodson constant and is subject to extreme exchange of tidal forces with his star. b) Property factors for all CoRoT and confirmed Kepler planets within 0.15 AU. The largest property factors are found with F-stars. Massive planets around F-stars are subject to extreme exchange of tidal forces, which may result in the decay of the planetary orbit.

where I∗ = 0.07 is the normalized moment of inertia of sun-like stars, M⊙ and R⊙ are the solar mass and radius, respectively. If the planetary orbit is within the synchronous orbit of the star defined by a < async and , then Ω∗ < n which is usually the case for orbits within 0.1 AU. sgn(Ω∗ − n) =  −1, which defines da/dt < 0. The first term in (12) is then greater than zero, which means that the star is spun-up by the tidal force. The second term in (12) describes the loss of stellar angular momentum by magnetic braking (Bouvier et al. 1997), which slows the stellar rotation down during the aging of the star. Magnetic braking with F-stars may be weaker than with G-stars (Barker & Ogilvie 2009). This is considered by an additional parameter f in (12), which is chosen f = 0.1 for F-stars in this example and unity for G-stars. The time required to spiral into the Roche zone of the host star at aRoche = 0.012 AU from the present circular orbit is (Pätzold & Rauer 2002)

thumbnail Fig. 8

a) Change in eccentricity and b) semi-major axis in the past starting at a), e) values which yield the observed values at the stellar age of 4.1 Gyr (dashed-dotted line) for Q∗/k2 ∗  = 107 and Qp/k2p = 105. The orbit is rapidly circularized within 600 Myr for any start value e0. b) The semi-major axis is decreasing until circularization and synchronization with the planetary rotation has been achieved. The current observed value of the orbital radius decays for Q∗/k2 ∗  = 107 within the next 800 Myr (dashed “doomsday line”) line when the planet enters the stellar Roche zone. The grey region marks the radius extension of the star, the horizontal dashed line marks the extent of the stellar Roche zone. c) The stellar rotation is spun-up until the planet gets lost in the stellar Roche zone. The tidal spin-up compensates and dominates the loss of angular momentum and slow-down of stellar rotation. After the loss of the planet, tidal friction has ceased and the stellar rotation is again slowed-down by the loss of angular momentum caused by magnetic braking. The extent of the slow-down of F-stars is modeled by different parameters f (see text) where f = 1 is for G-stars (not appropriate here, but shown for comparison), f = 0.1 is assumed for F-stars and f = 0 is neglecting the stellar angular momentum loss by magnetic braking.

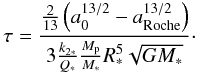(13)For a considered large Q∗/k2 ∗  = 107 the orbit decays rapidly (Fig. 8b) and the planet enters the stellar Roche limit at the dashed “Doomsday line” within 800 Myr (Fig. 8b). Figure 8c shows the evolution of the planetary revolution period, practically translated from the change in da/dt in Fig. 8b, into the future starting from the current stellar age of 4.1 Gyr. From the conservation of angular momentum, the star is equally rapidly spun-up until the planet enters the Roche zone. Depending on the magnetic braking model represented by the parameter f, magnetic braking is only partially compensating (for f = 1.0) the stellar spin-up before the planet reaches the Roche zone (the Doomsday line in Figs. 8b and c). Magnetic braking has no significant effect for f = 0.1. In any case, the star is significantly spun-up by the tides. Tidal spin-up of F-stars is very efficient (Dobbs-Dixon et al. 2004) and will even overcome the angular momentum loss and slow-down from magnetic braking (Barnes 2003; Bouvier et al. 1997), in particular during the end-run toward the Roche zone. When the planet eventually reaches the Roche zone in 800 Myr, CoRoT-21 will rotate extremely fast at a period of a few days regardless of the applied f parameter. Once the planet gets lost, tidal forces are no longer acting and the star now loses angular momentum by magnetic braking only and is slowed down afterward (Fig. 8c).

This scenario depends on the choice of Q∗/k2∗. Pätzold & Rauer (2002) concluded that Q∗/k2∗ must be greater than 106 because massive planets larger than 0.3 MJ are not expected within 0.05 AU about F-stars for Q∗/k2∗ ≤ 106. If so, however, the orbit would decay dramatically fast, too fast. CoRoT and Kepler, however, found quite a number of extremely massive planets within 0.05 AU, three of those around F-stars (Fig. 6a). In contrast to Jackson et al. (2008) and Jackson et al. (2009), Carone & Pätzold (2007) constrained the range of Q∗/k2 ∗  to 107 < Q∗/k2∗ < 109.

6. Summary

The light curve of CoRoT-21 was observed during the first Long Run in galactic anti-center direction, LRa01, in 2007/2008. The planetary transit was detected during the processing of the raw light curve. Follow-up observation opportunities were eventually given mostly in January 2010 with the Keck telescope. The planet CoRoT-21b is a hot Jupiter of 2.26 ± 0.31 Jupiter masses in a 2.72 day orbit about a sub-giant F-star. The bulk density of (1.36 ± 0.48) × 103   kg   m-3 is comparable to Jupiter and follows the same M1/3 − R relation. The CoRoT-21 system is a textbook example for studying tidal interaction between a star and a close-in massive planet on a circular orbit. The high mass and close proximity to its star will let the orbit decay strongly within the next 800 Gyr if Q∗/k2∗ ≤ 107. A potentially eccentric orbit has been circularized very fast in the first billion years of the stars life and resulted in the now observed circular and decaying orbit. The rotation of the star CoRoT-21 will be spun-up by tidal forces that strongly compensate for the loss of angular momentum and slow-down by magnetic braking till the planet will get lost in the stellar Roche zone. “May the Force be with them”.

1

The CoRoT detection teams of LRa01 are located at University Cologne, University Exeter, ESA-ESTEC Noordwijk, IAC Teneriffa, IAS Paris and LUTH Paris.

Acknowledgments

The authors wish to thank the staff at ESO La Silla Observatory for their support and for their contribution to the success of the HARPS project and operation. Some of the data presented are from on observations made with the IAC80 operated at Teide Observatory on the island of Tenerife by the Instituto de Astrofísica de Canarias. The team at the IAC acknowledges support by grants ESP2007-65480-C02-02 and AYA2010-20982-C02-02 of the Spanish Ministry of Science and Innovation (MICINN). The CoRoT/Exoplanet catalogue (Exodat) was made possible by observations collected for years at the Isaac Newton Telescope (INT), operated on the island of La Palma by the Isaac Newton group in the Spanish Observatorio del Roque de Los Muchachos of the Instituto de Astrophysica de Canarias. The German CoRoT team (TLS and University of Cologne) acknowledges DLR grants 50OW0204, 50OW0603, and 50QM1004. The French team wishes to thank the CNES and the French National Research Agency (ANR-08- JCJC- 0102-01) for their continuous support to our planet search. The Swiss team acknowledges the ESA PRODEX program and the Swiss National Science Foundation for their continuous support on CoRoT ground follow-up. A. S. Bonomo acknowledges a CNES grant. S. Aigrain acknowledges STFC grant ST/G002266. M. Gillon acknowledges support from the Belgian Science Policy Office in the form of a Return Grant. M. Endl, W. D. Cochran and P. J. MacQueen were supported by NASA Origins of Solar Systems grant NNX09AB30G. Part of the data presented herein were obtained at the W. M. Keck Observatory from telescope time allocated to the National Aeronautics and Space Administration through the agency scientific partnership with the California Institute of Technology and the University of California. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation.

References

  1. Baglin, A., Auvergne, M., Barge, P., Deleuil, M., & Michel, E. 2008, Proc. Int. Astron. Union, 4, 71 [Google Scholar]
  2. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Barker, A. J., & Ogilvie, G. I. 2009, MNRAS, 395, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barnes, S. A. 2003, ApJ, 586, 464 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonomo, A. S., Santerne, A., Alonso, R., et al. 2010, A&A, 520, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 728, 117 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bouchy, F., Deleuil, M., Guillot, T., et al. 2011, A&A, 525, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bouvier, J., Forestini, M., & Allain, S. 1997, A&A, 326, 1023 [NASA ADS] [Google Scholar]
  9. Brown, T. M., Charbonneau, D., Gilliland, R. L., Noyes, R. W., & Burrows, A. 2001, ApJ, 552, 699 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cabrera, J., Bruntt, H., Ollivier, M., et al. 2010, A&A, 522, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Carone, L., & Pätzold, M. 2007, Planet. Space Sci., 55, 643 [NASA ADS] [CrossRef] [Google Scholar]
  12. Carone, L., Gandolfi, D., Cabrera, J., et al. 2012, A&A, 538, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Castelli, F., & Kurucz, R. L. 2004, New Grids of ATLAS9 Model Atmospheres, eds. N. Piskunov et al. 2003, Proc. IAU Symp. 210, poster A20 [Google Scholar]
  14. Coelho, P., Barbuy, B., Meléndez, J., Schiavon, R. P., & Castilho, B. V. 2005, A&A, 443, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Deeg, H. J., Gillon, M., Shporer, A., et al. 2009, A&A, 506, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Deeg, H. J., Moutou, C., Erikson, A., et al. 2010, Nature, 464, 384 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  17. Deleuil, M., Deeg, H. J., Alonso, R., et al. 2008, A&A, 491, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Devor, J. 2005, ApJ, 628, 411 [NASA ADS] [CrossRef] [Google Scholar]
  19. Dobbs-Dixon, I., Lin, D. N. C., & Mardling, R. A. 2004, ApJ, 610, 464 [NASA ADS] [CrossRef] [Google Scholar]
  20. Doyle, L. R., Carter, J. A., Fabrycky, D. C., et al. 2011, Science, 333, 1602 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  21. Endl, M., Kürster, M., & Els, S. 2000, A&A, 362, 585 [Google Scholar]
  22. Ferraz-Mello, S. 2012 [arXiv:1204.3957] [Google Scholar]
  23. Fridlund, M., Hébrard, G., Alonso, R., et al. 2010, A&A, 512, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Gandolfi, D., Hébrard, G., Alonso, R., et al. 2010, A&A, 524, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Grziwa, S., Pätzold, M., & Carone, L. 2012, MNRAS, 420, 1045 [NASA ADS] [CrossRef] [Google Scholar]
  26. Guenther, E. W., Díaz, R. F., Gazzano, J.-C., et al. 2012, A&A, 537, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Hatzes, A. P., Dvorak, R., Wuchterl, G., et al. 2010, A&A, 520, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Jackson, B., Greenberg, R., & Barnes, R. 2008, ApJ, 678, 1396 [NASA ADS] [CrossRef] [Google Scholar]
  30. Jackson, B., Barnes, R., & Greenberg, R. 2009, ApJ, 698, 1357 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kim, J. H., Geem, Z. W., & Kim, E. S. 2001, J. Am. Water Res. Assoc., 37, 1131 [CrossRef] [Google Scholar]
  32. Kovács, G., Zucker, S., & Mazeh, T. 2002, A&A, 391, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Lainey, V., Arlot, J.-E., Karatekin, Ö., & van Hoolst, T. 2009, Nature, 459, 957 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  34. Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  35. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  36. Matsumura, S., Peale, S. J., & Rasio, F. A. 2010, ApJ, 725, 1995 [NASA ADS] [CrossRef] [Google Scholar]
  37. Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  38. Pätzold, M., & Rauer, H. 2002, ApJ, 568, L117 [NASA ADS] [CrossRef] [Google Scholar]
  39. Pätzold, M., Carone, L., & Rauer, H. 2004, A&A, 427, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Queloz, D., Bouchy, F., Moutou, C., et al. 2009, A&A, 506, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Sing, D. K. 2010, A&A, 510, A21 [Google Scholar]
  42. Southworth, J. 2010, MNRAS, 408, 1689 [NASA ADS] [CrossRef] [Google Scholar]
  43. Tingley, B., Endl, M., Gazzano, J.-C., et al. 2011, A&A, 528, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  45. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Vogt, S. S., Allen, S. L., Bigelow, B. C., et al. 1994, in SPIE Conf. Ser., 2198, eds. D. L. Crawford, & E. R. Craine, 362 [Google Scholar]

All Tables

Table 1

Stellar and planetary parameters.

In the text
Table 2

RV observations.

In the text

All Figures

thumbnail Fig. 1

a) Normalized raw light curve of CoRoT-21 during the observation time from MJD 54 396 to MJD 54 529. Strong variations in stellar flux are obvious. b) Light curve after removing a common trend as computed from a subset of 200 light curves and after harmonic filtering. c) Phase diagram of the trend-filtered light curve at period 2.7472 days. The phase is divided into 300 bins with mean flux and standard deviation displayed for each bin.
In the text
thumbnail Fig. 2

a) Power spectrum of the trend-harmonic filtered light curve. The period of 2.72474 days and its harmonics are clearly identified. b) Power spectrum of the trend-filtered light curve after removing the transits at period 2.72474 days. Note the change in scale by two orders of magnitude compared to panel a). The periods at 10 days and 11.5 days did not return convincing detections of more transits and are probably caused by stellar activity at the rotation period.
In the text
thumbnail Fig. 3

Immediate vincinity of CoRoT-21 in the star field covered by LRa01. The outline is the aperture mask of the target star CoRoT-21. A potential perturber of the photometry is the star labeled “1” at the immediate edge of the outline. This star is not a CoRoT target. The contamination of the target mask is estimated to be 8.5%.
In the text
thumbnail Fig. 4

Phase diagram of the raw light curve from  −0.25 to  +0.25 in phase. The phase has been divided into 300 bins with average flux and standard deviation shown for each bin. The solid line is the fit as described in the text. Fit results are given in Table 1.
In the text
thumbnail Fig. 5

Radial velocity curve fit on 19 observations. Blue data points are from HIRES, red data points are from HARPS. The eccentricity was forced to e = 0 for the fit.
In the text
thumbnail Fig. 6

a) Planetary mass vs. semi-major axis for all CoRoT planets, the confirmed Kepler planets (filled circles) and other transiting planets from ground-based observations (small open circles) within 0.25 AU. The large open circle is CoRoT-21b. b) Planetary mass-radius relationship for the CoRoT planets, confirmed Kepler planets (filled circles) and the transiting planets from ground-based observations (small open circles). Also drawn are lines of constant density. Jupiter and CoRoT-21b (circles) follow almost the same line of constant density and are directly comparable.
In the text
thumbnail Fig. 7

a) Doodson constants for all CoRoT and confirmed Kepler planets within 0.15 AU. CoRoT-21b has the fourth largest Doodson constant and is subject to extreme exchange of tidal forces with his star. b) Property factors for all CoRoT and confirmed Kepler planets within 0.15 AU. The largest property factors are found with F-stars. Massive planets around F-stars are subject to extreme exchange of tidal forces, which may result in the decay of the planetary orbit.
In the text
thumbnail Fig. 8

a) Change in eccentricity and b) semi-major axis in the past starting at a), e) values which yield the observed values at the stellar age of 4.1 Gyr (dashed-dotted line) for Q∗/k2 ∗  = 107 and Qp/k2p = 105. The orbit is rapidly circularized within 600 Myr for any start value e0. b) The semi-major axis is decreasing until circularization and synchronization with the planetary rotation has been achieved. The current observed value of the orbital radius decays for Q∗/k2 ∗  = 107 within the next 800 Myr (dashed “doomsday line”) line when the planet enters the stellar Roche zone. The grey region marks the radius extension of the star, the horizontal dashed line marks the extent of the stellar Roche zone. c) The stellar rotation is spun-up until the planet gets lost in the stellar Roche zone. The tidal spin-up compensates and dominates the loss of angular momentum and slow-down of stellar rotation. After the loss of the planet, tidal friction has ceased and the stellar rotation is again slowed-down by the loss of angular momentum caused by magnetic braking. The extent of the slow-down of F-stars is modeled by different parameters f (see text) where f = 1 is for G-stars (not appropriate here, but shown for comparison), f = 0.1 is assumed for F-stars and f = 0 is neglecting the stellar angular momentum loss by magnetic braking.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.